Изобретение относится к машиностроению, а именно к конструкциям бойков, и может быть использовано в механизмах ударного, ударно-вращательного и ударно-поворотного действия.
Известен боек, содержащий генерирующую часть с образующей боковой поверхностью криволинейной формы, ограниченную плоскими воспринимающим и ударным торцами [1]
При плоском ударном торце бойка практически невозможно обеспечить его касание с воспринимающей частью волновода (буровой штанги) одновременно по всей поверхности. Из-за зазоров в ударных механизмах плоский ударный торец бойка соприкасается с воспринимающим торцом волновода сначала в точке боковой кромки, затем в результате деформации этой кромки и воспринимающего торца волновода площадь контакта постепенно возрастает. Темп возрастания контакта зависит от начального угла между осями блока и волновода. Поскольку обеспечить стабильность этого угла практически невозможно, невозможно обеспечить и стабильность точки встречи ударного торца бойка с воспринимающим торцом волновода (центричность удара), а следовательно, и стабильность результатов удара. Более того, при нецентричном ударе в волноводе возникают изгибные волны деформации, снижающие коэффициент передачи энергии бойка обрабатываемой среде.
Известен боек, содержащий генерирующую поверхность произвольной формы, ограниченную воспринимающим торцом и ударным торцом, выполненным в форме шарового сегмента [2]
В известном бойке с закругленным по дугам окружности торцом недостаточно интенсивно возрастает площадь контакта ударного торца бойка при его взаимодействии с воспринимающим торцом волновода, что приводит к снижению передачи кинетической энергии бойка волноводу.
Цель изобретения повышение эффективности передачи кинетической энергии бойка волноводу.
Это достигается тем, что ударный торец бойка выполнен по укороченной циклоиде, кривизна которой переменна.
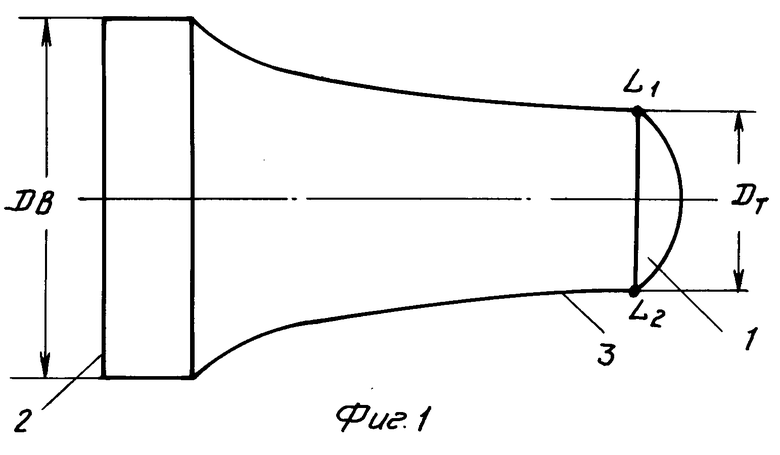
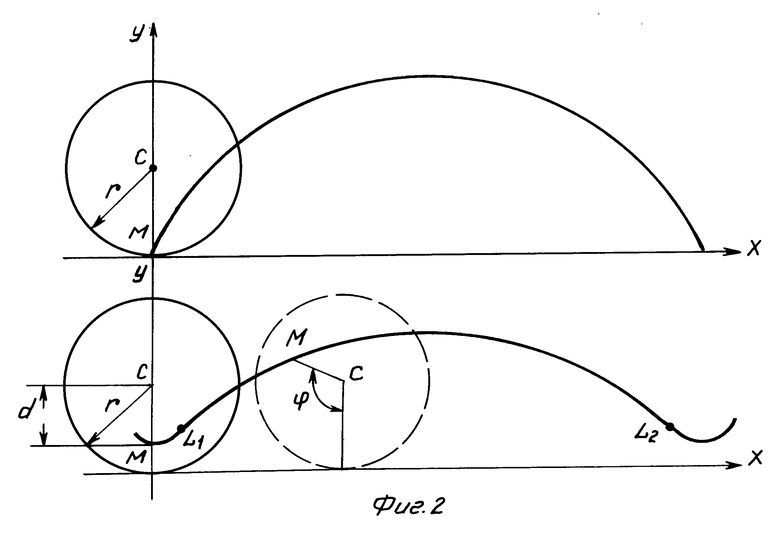
На фиг. 1 изображен предлагаемый боек; на фиг. 2 геометрическое объяснение изобретения, где Dт диаметр ударного торца; Dв диаметр воспринимающего торца.
Боек состоит из генерирующей части 1, ограниченной воспринимающим 2 и ударным торцами 3. Ударный торец 3 представляет собой поверхность, образованную вращением вокруг продольной оси бойка укороченной циклоиды.
Известна плоская кривая, называемая циклоидой. Если на катящемся без скольжения по прямой Х-Х круге 1 (см. фиг. 2) зафиксировать точку М, то она опишет циклоиду (построит арку циклоиды). При заданном радиусе круга r точка М может находиться от центра круга С на расстоянии d > r, d r и d < r, тогда соответственно будут описываться удлиненная, обыкновенная и укороченная циклоиды. Последняя имеет точки перегиба L1 и L2, а также при условии, что d стремится к нулю, она превращается в прямую линию, т.е. радиус ее кривизны в точке контакта (в наивысшей точке по оси Y) может возрасти до бесконечно большой величины.
В параметрической форме укороченная циклоида описывается уравнениями
x r (ϕ-λsinϕ);
y r (1 -λcosϕ), (4) где r радиус катящейся окружности (круга);
ϕ угол МСР (см. фиг. 2);
λ отношение d/r, названное параметром укороченной циклоиды.
Точки перегиба на ней L1 и L2 определяются из уравнения
cosϕ=λ  (5)
(5)
Если принять диаметр ударного торца бойка равным Dт (фиг. 1), то будем вписывать укороченную циклоиду так, что на краях торца бойка как раз разместятся точки перегиба L1 и L2.
Формула для определения радиуса кривизны любой точки циклоиды
R 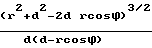 (6)
(6)
Применительно к бойку нас будет интересовать лишь верхняя точка арки укороченной циклоиды. Для этого случая ϕ=π, значит cos ϕ=cosπ 1 и если обозначить d/r λ, то формула (6) преобразуется к виду
R=r (7)
(7)
Используя уравнение (7) можно задать необходимый радиус кривизны R ударного торца бойка и выбрать нужное значение λ.
Теперь из уравнения (5) можно найти два значения ϕ, соответствующие условию cos ϕ= λ По этим ϕ можно определить координаты точек L1 и L2. Разница между координатами L2 и L1 по оси Х будет соответствовать диаметру ударного торца бойка, т.е.
X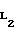 X
X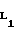 = Dт. (8)
= Dт. (8)
Имея теперь ϕ1 arccos λ и ϕ2=π-ϕ1 и используя первое уравнение системы (4) для заданных ϕ1 и ϕ2, находим XL1 и XL2. Решая уравнение (8), находим λ, которое удовлетворяет условию вписывания укороченной циклоиды в размер диаметра ударного торца бойка.
Решая далее совместно полученное уравнение с уравнением (7), находим необходимые значения r и d.
П р и м е р. Принимаем Dт 30 мм, выбираем радиус кривизны R ударного торца ударника 150 мм.
Из уравнения (7) получим
150 λ=r(1+2λ+λ2) (9) Так как ϕ1 arccos λ и ϕ2=π-ϕ1, находим
X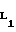 r[arccos λ λ sin (arccos λ)]
r[arccos λ λ sin (arccos λ)]
X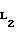 r[π arccos λ λ sin (π arccos λ)] Далее
r[π arccos λ λ sin (π arccos λ)] Далее
X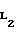 -X
-X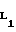 r[π arccos λ λ sin (π
r[π arccos λ λ sin (π
arccos λ) arccos λ + λ sin (arccos λ)]
30 мм (10)
Упростим последнее выражение
r(π 2 arccos λ) 30 мм.
Теперь имеем систему
r(1/λ + 2 + λ) 150 мм,
r(π 2 arccos λ) 30 мм.
Разделим левую и правую части
1/ λ + 2 + λ 5 (π arccos λ), откуда
10 arccos λ + λ + 1/ λ 13,7. (11) Численно решая уравнение (11), находим λ 0,45.
Подставляя это значение в уравнение (9), находим r 32,1 мм, тогда d λ˙ r 14,45 мм.
Аналогичные расчеты для Dт 30 мм и R 300 мм приводят к результатам: λ 0,29; r 52,2 мм; d 15,16 мм.
Наиболее целесообразным являются радиусы кривизны в точке контакта соударяющихся тел от 150 до 300 мм. Этим радиусом кривизны удовлетворяют условия λ0,3.0,5, именно эти значения и следует принимать за оптимальные.
Боек, изображенный на фиг. 1 с ударным торцом, образованным вращением вокруг продольной оси бойка укороченной циклоиды с параметром λ 0,3.0,5, работает следующим образом.
Усилие, приложенное к воспринимающему торцу 2, разгоняет боек для удара. Кинетическая энергия бойка преобразуется в генерирующей части 1 в продольные колебания, которые через ударный торец 3 передаются в волновод. Предлагаемая форма ударного торца бойка обеспечивает более интенсивный рост контакта ударяемого торца при его взаимодействии с волноводом. В связи с этим увеличивается коэффициент передачи кинетической энергии бойка в волновод при сохранении стабильности результатов удара.
| название | год | авторы | номер документа |
|---|---|---|---|
| УДАРНИК БУРИЛЬНОЙ МАШИНЫ | 1998 |
|
RU2137595C1 |
| СПОСОБ ОБРАЗОВАНИЯ ВИДОВ КАТЕНОИДНЫХ БОЙКОВ УДАРНЫХ МЕХАНИЗМОВ | 2000 |
|
RU2182953C1 |
| УДАРНИК БУРИЛЬНОЙ МАШИНЫ | 2011 |
|
RU2484944C1 |
| БОЕК УДАРНОГО МЕХАНИЗМА | 2003 |
|
RU2234583C1 |
| БОЁК ЦИЛИНДРО-ПСЕВДОСФЕРИЧЕСКИЙ | 2012 |
|
RU2486049C1 |
| БОЕК ЦИЛИНДРОКОНИЧЕСКИЙ | 2011 |
|
RU2484943C1 |
| Боек | 1987 |
|
SU1489980A1 |
| ШАРНИРНОЕ УСТРОЙСТВО | 2002 |
|
RU2235228C2 |
| СПОСОБ СТАТИКОИМПУЛЬСНОЙ ОБРАБОТКИ ПОВЕРХНОСТНЫМ ПЛАСТИЧЕСКИМ ДЕФОРМИРОВАНИЕМ | 1996 |
|
RU2098259C1 |
| СПОСОБ ПОЛУЧЕНИЯ ЗАКРУГЛЕННОЙ КРОМКИ ДЕТАЛИ, УСТРОЙСТВО ДЛЯ ЕГО ОСУЩЕСТВЛЕНИЯ И БОЕК, ИСПОЛЬЗУЕМЫЙ В ЭТОМ УСТРОЙСТВЕ | 2008 |
|
RU2373018C1 |
Использование: изобретение относится к машиностроению, а именно к конструкциям бойков, и может быть использовано в машинах ударного, ударно-вращательного и ударно-поворотного действия. Цель изобретения - повышение эффективности передачи кинетической энергии волноводу. Ударный торец бойка представляет собой поверхность, образованную вращением вокруг продольной оси бойка укороченной циклоиды с параметром λ 0,3.0,5. Предлагаемая форма ударного торца бойка с переменной кривизной обеспечивает более интенсивный рост контакта ударяемого торца при его взаимодействии с волноводом. В связи с этим увеличивается коэффициент передачи кинетической энергии бойка в волновод при сохранении стабильности результатов удара. 2 ил.
БОЕК, содержащий генерирующую часть с образующей боковой поверхностью, ограниченную воспринимающим и выпуклым ударным торцами, отличающийся тем, что выпуклый ударный торец выполнен в виде поверхности, образованной вращением вокруг продольной оси бойка укороченной циклоиды с отношением d/r, лежащим в пределах 0,3 0,5, где r радиус круга, а d расстояние точки, описывающей циклоиду от центра круга.
| Аппарат для очищения воды при помощи химических реактивов | 1917 |
|
SU2A1 |
| Иванов К.И | |||
| Варич М.С., Дусев В.И., Андреев В.Д | |||
| Техника бурения при разработке месторождений полезных ископаемых | |||
| М | |||
| : Недра, 1974, с.343. | |||
Авторы
Даты
1995-08-20—Публикация
1992-02-17—Подача