Изобретение относится к специализированной вычислительной технике и может быть использовано в оптических вычислительных машинах при решении функциональных уравнений.
Известны оптические вычислительные устройства, позволяющие решать дифференциальные уравнения в частных производных, являющиеся частным случаем функционального уравнения, на основе использования пары-преобразования Фурье [1] или метода Либмана [2] Наиболее близкой по техническому выполнению к предлагаемому устройству является оптоэлектронное устройство для решения дифференциальных уравнений [2] содержащее источник когерентного излучения, световодные каналы и вычислительные транспаранты, также позволяющее осуществлять решение дифференциальных уравнений в частных производных.
Недостатком данных устройств является отсутствие возможности решения функциональных уравнений.
Цель изобретения расширение функциональных возможностей устройства за счет решения функциональных уравнений.
Это достигается тем, что в устройство дополнительно введены входной оптический разветвитель, две группы вычислительных транспарантов, четыре световода, группа блоков модуляторов света, группа матричных селекторов минимального сигнала, а выход источника излучения подключен к входу входного оптического разветвителя, первое ответвление которого разветвляется на N разветвлений, каждое из которых, в свою очередь разветвляется на ответвления, выходы которых подключены к входу вычислительного транспаранта первой группы N транспарантов, выход которого через световодный жгут первого световода, содержащего N жгутов, подключен к входу матричного селектора минимального сигнала (МСМС), входящего в группу из N МСМС, выходы которого подключены к управляющим входам блока электрооптических модуляторов Керра, входящего в группу из N модуляторов, информационные входы каждого из которых оптически связаны с выходами N ответвлений соответствующего разветвления, одного из N второго ответвления входного оптического разветвителя, а выходы подключены к входам соответствующих оптических интеграторов, выходы которых подключены к входам соответствующих световодных жгутов второго световода, объединенных со световодными жгутами, образованными N ответвлениями соответствующего разветвления, одного из N третьего ответвления входного оптического разветвителя, оптически связанного с выходом источника излучения через транспарант начальных условий уравнения, причем каждый из световодных жгутов второго световода, содержащих N оптических волокон, имеет два разветвления: выходы первых разветвлений являются выходами устройства, а выходы i-х волокон всех жгутов подключены к входу i-го оптического дифференциатора, i=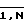 , выход которого подключен к входам i-x волокон всех N световодных жгутов третьего световода, разветвляющихся далее на N ответвлений, причем выходы N ответвлений j-го волокна k-го жгута третьего световода подключены к j-му столбцу k-й матрицы-транспаранта, j, k=
, выход которого подключен к входам i-x волокон всех N световодных жгутов третьего световода, разветвляющихся далее на N ответвлений, причем выходы N ответвлений j-го волокна k-го жгута третьего световода подключены к j-му столбцу k-й матрицы-транспаранта, j, k= 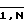 , входящего во вторую группу вычислительных транспарантов, выходы которых подключены ко входам N соответствующих световодных жгутов четвертого световода, объединенных с соответствующими жгутами первого световода и оптически связанных по выходу с входами соответствующих МСМС.
, входящего во вторую группу вычислительных транспарантов, выходы которых подключены ко входам N соответствующих световодных жгутов четвертого световода, объединенных с соответствующими жгутами первого световода и оптически связанных по выходу с входами соответствующих МСМС.
Функциональное уравнение Гамильтона-Якоби-Беллмана (далее уравнение Беллмана) имеет вид 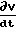 minL(x,u,t)+
minL(x,u,t)+ 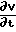 · f (x,u,t), (1) где V=V(x, t) определяемая в процессе решения (1) функция Беллмана;
· f (x,u,t), (1) где V=V(x, t) определяемая в процессе решения (1) функция Беллмана;
L(x, u, t), f(x, u, t) известные нелинейные функции, удовлетворяющие условию Липшица во всей области определения аргументов,
min{ операция вычисления значения функции, минимального по аргументу V.
Учитывая, что ∀x правая часть уравнения (1) удовлетворяет условию Липшица, а также то что 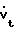 ≅0 ∀ x,t, решение (1) по координате t можно представить с помощью метода последовательных приближений следующим образом:
≅0 ∀ x,t, решение (1) по координате t можно представить с помощью метода последовательных приближений следующим образом:
Vi(x,t)= Vo+ 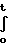 m
m n{L(x,u,S)+
n{L(x,u,S)+ 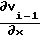 · f(x,u,s)}dS
· f(x,u,s)}dS
i=1,2, Vi(x,0)=Vo=const, (2) где Vo начальное значение функции Беллмана.
Следует отметить, что наряду с необходимостью решения уравнения Беллмана для случаев, когда Vо известна, существует ряд задач теории оптимального управления, когда задается лишь финальное значение функции Беллмана на заданном интервале времени решения: V(x,T)=VT=const. Это, в свою очередь, требует решения (1) "с конца" и не позволяет непосредственно использовать подход к решению (2).
Осуществив в (1) замену переменных τ=Т-t и используя аналогично изложенному метод последовательных приближений, в этом случае имеем
Vi(x,τ) Vт+ 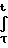 min{L(X,U,T-S)+
min{L(X,U,T-S)+ 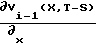 · f(x, U, T-S)}ds;
· f(x, U, T-S)}ds;
i=1,2, Vi(x,T)=VT=const (3)
Из сравнения (2) и (3) очевидно, что схемная реализация обоих вариантов решения уравнения Беллмана, определяемых соответствующим заданием краевых условий, одна и та же с той лишь разницей, что в случае (3) запись функций L, f на транспаранты осуществляется с учетом замены t на (T-τ ), а функция V(x, t) формируется не с Vо до VT, а наоборот. Для наглядности рассматриваем далее реализацию (2).
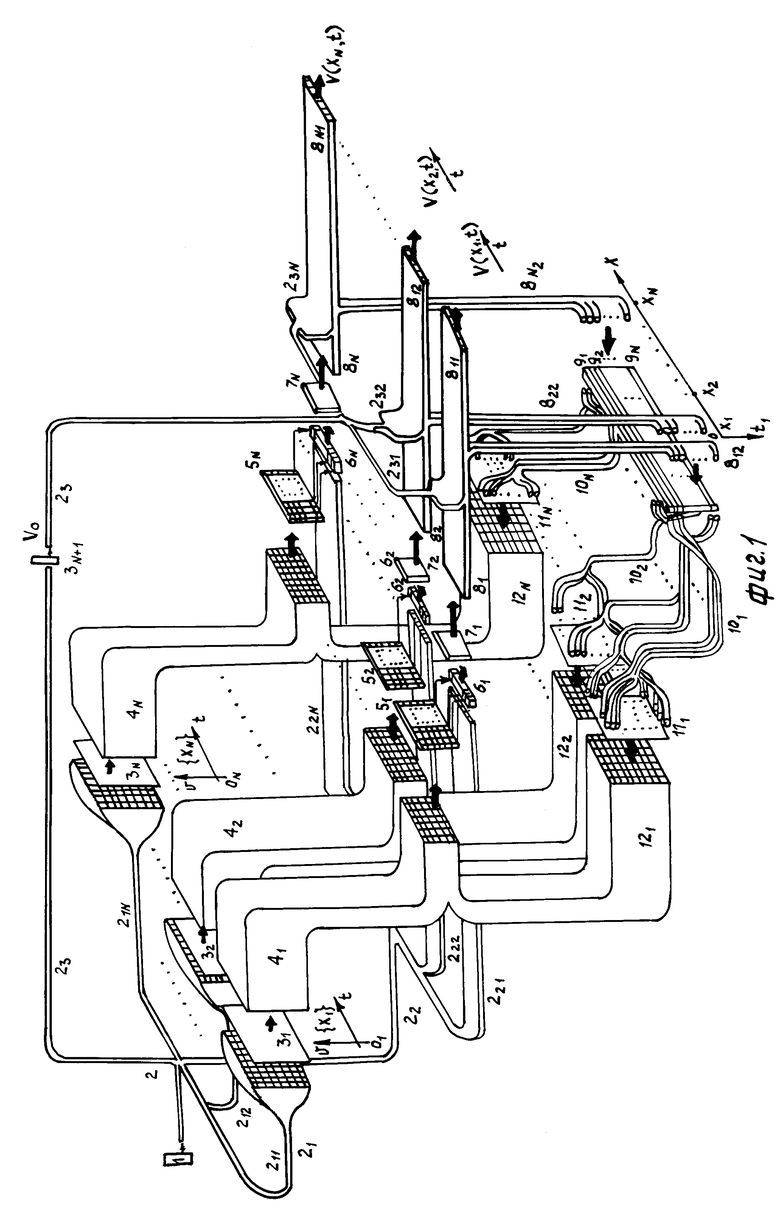
Решение уравнения (1) с учетом его возможных представлений (2, 3) осуществляется устройством, функциональная схема которого представлена на фиг. 1.
Устройство для решения функционального уравнения содержит источник когеpентного излучения 1, входной оптический разветвитель 2, содержащий три группы ответвлений 21, 22, 23, каждая из которых имеет N разветвлений 2i1. 2iN; первую группу из (N+1) вычислительных транспарантов 31, 3N+1; первый световод 4, состоящий из N световодных жгутов 41, 4N; группу матричных селекторов минимального сигнала (СМС) 51, 52, 5N; N групп электрооптических модуляторов Керра 61, 6N; оптических интеграторов 71, 7N; второй световод 8, содержащий N световодных жгутов 81, 8N, каждый из которых разветвляется на два 8i1, 8i2; N оптических дифференциаторов 91, 9N; третий световод 10, содержащий N световодных жгутов 101, 10N, каждый из которых имеет N ответвлений; вторую группу из N вычислительных транспарантов 111,11N; четвертый световод 12, содержащий световодных жгутов 121, 12N.
Световоды (световодные жгуты) могут быть выполнены в виде набора плотноупакованных оптических волокон (неуправляемых направленных ответвителей. Вычислительные транспаранты выполняются неуправляемыми в виде фотопластины, фотопленки или оптического стекла с заданной функцией пропускания. На фиг. 1 для удобства описания происходящих в устройстве информационных преобразований введены условные системы координат ОiVt, QiVt, i=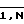 , 0xt1, показано направление изменения аргумента t на выходе устройства.
, 0xt1, показано направление изменения аргумента t на выходе устройства.
Функция пропускания i-го транспаранта 3i, i=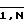 в плоскости QiVt пропорциональна двумерной функции L(X,V,t)|x=xi=L(Xi,U,t), где Хi значение аргумента Х на i-м интервале дискретизации всей области определения Х. Число интервалов дискретизации, а следовательно, и число N транспарантов 3i выбирается, исходя из точности описания функции L по Х. Функция пропускания транспаранта 3N+1 пропорциональна Nо=сonst. Аналогично функция пропускания j-го транспаранта 11j в плоскости QjVt пропорциональна функции f(xj, V, t) (число транспарантов 3i равно числу транспарантов 11i).
в плоскости QiVt пропорциональна двумерной функции L(X,V,t)|x=xi=L(Xi,U,t), где Хi значение аргумента Х на i-м интервале дискретизации всей области определения Х. Число интервалов дискретизации, а следовательно, и число N транспарантов 3i выбирается, исходя из точности описания функции L по Х. Функция пропускания транспаранта 3N+1 пропорциональна Nо=сonst. Аналогично функция пропускания j-го транспаранта 11j в плоскости QjVt пропорциональна функции f(xj, V, t) (число транспарантов 3i равно числу транспарантов 11i).
Число волокон в световодных жгутах выбирается большим или равным числу интервалов дискретизации, записанных на вычислительных транспарантах функций пропускания в соответствующем направлении. Матричный СМС 5i выполняется в виде набора из "М" СМС, каждый из которых представляет собой цепь К фотодиодов. Числа М и К соответствуют числу волокон световодного жгута в соответствующем направлении (для наглядности М= К=N). Набор выходных сигналов СМС образует выход матричного СМС.
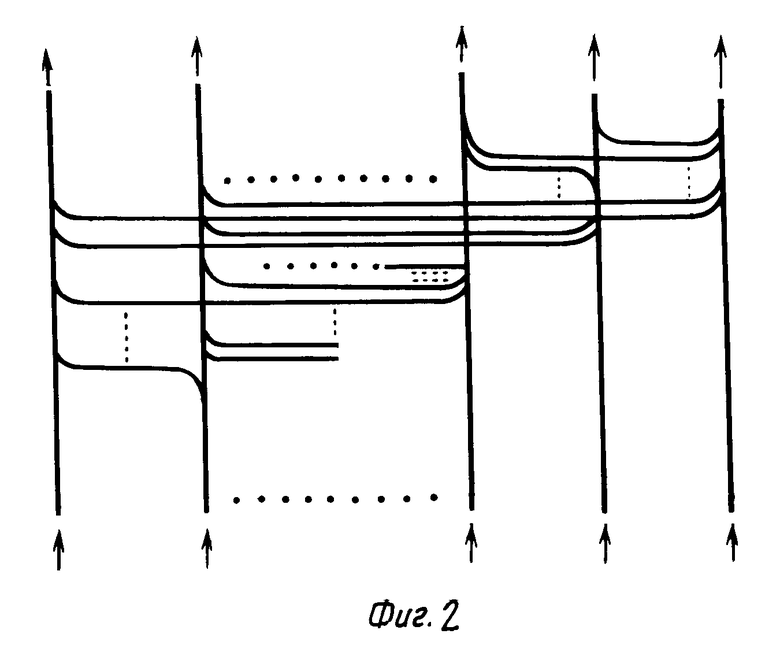
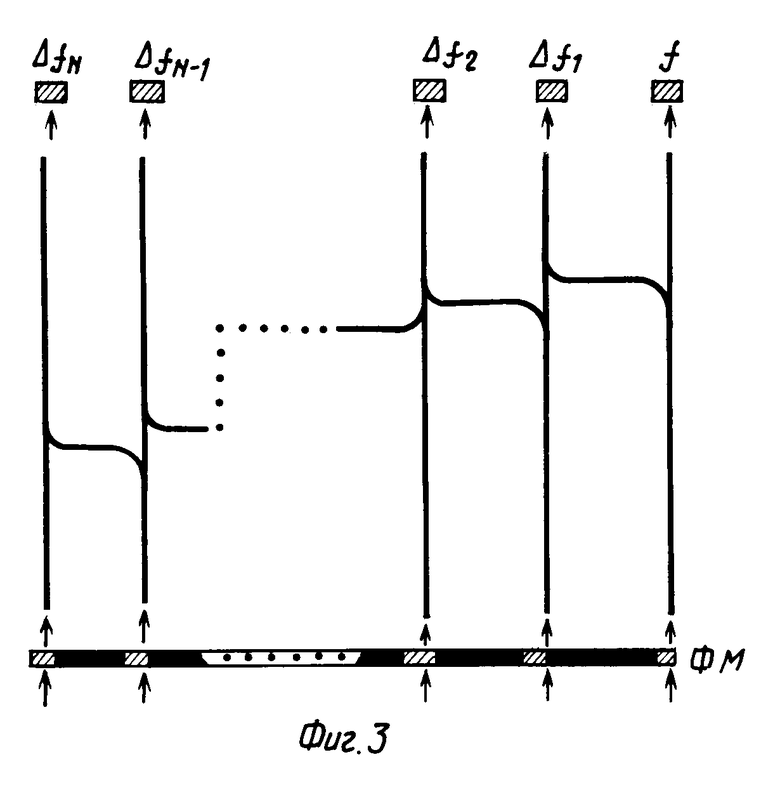
Блок (линейка) модуляторов света 6 состоит из N электрооптических модуляторов Керра, осуществляющих модуляцию светового потока по интенсивности. Оптические интеграторы и дифференциаторы могут быть выполнены как на основе когерентного аналогового оптического процессора, использующего методы пространственной фильтрации, так и в виде соответствующим образом соединенных N оптических волокон (фиг. 2, 3). На фиг. 3 использовано обозначение ФМ для оптического модулятора фазы входного когерентного потока, обеспечивающего сдвиг фаз соседних потоков на входах волокон (справа налево) на πи выполненного, например, в виде оптически прозрачной пластины с переменной толщиной.
Выход источника излучения 1 подключен к входу световода 2, разветвляющегося на 21, 22, 23. Световод 21 имеет N ответвлений 211, 21N, каждое из которых разветвляется на NxN ответвлений, выходы которых подключены к входам соответствующих транспарантов 31, 3N. Выходы транспарантов 31,3N подключены через световодные жгуты 41, 4N к входам матричных СМС 51,5N, выходы которых подключены к входам управления модуляторов 61, 6N. Информационные входы модуляторов 61,6N через ответвления 221,22N разветвления 22 световода 2 оптически связаны с выходом источника излучения 1, а выходы модуляторов 61,6N подключены к входам оптических интеграторов 71,7N, выходы которых подключены к входам световодных жгутов 81,8N. Со световодными жгутами 81,8N объединены соответствующие ответвления 231,23N третьего разветвления 23 световода 2, соединяющего выход источника излучения 1 через транспарант 3N+1 с выходом устройства. Выходы первых ответвлений 811,8N1 световодных жгутов 81, 8Nобъединены с выходами устройства для соответствующих значений решения уравнения V(X1, t),V(XN, t), а выходы вторых ответвлений 812,8N2, состоящих из N волокон, подключены к входам оптических дифференциаторов 9j следующим образом: выходы i-х волокон ответвлений 812,8N2подключены к входу i-го дифференциатора 9i так, что отсчет (изменение) аргумента дифференцируемой функции на входе дифференциатора происходит от ответвления 812 к 8N2 (в направлении ОХ). Выходы оптических дифференциаторов 9j подключены к входам разветвлений световода 10 таким образом, что входы i-х волокон ответвлений 101-10N оптически связаны с выходом i-го дифференциатора 9i, причем отсчет аргумента дифференцируемой функции осуществляется от ответвления 101 и 10N. В каждом жгуте-ответвлении 10j i-е волокно разветвляется на N волокон, выходы которых оптически связаны с i-м столбцом j-й матрицы-транспаранта 11j, j=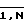 (т.е. по оси QjV). Выход j-го транспаранта 11j через j-е ответвление 12j четвертого световода 12, объединенное с j-м ответвлением 4j первого световода 4, оптически связан с входом j-го матричного СМС 5j, j=
(т.е. по оси QjV). Выход j-го транспаранта 11j через j-е ответвление 12j четвертого световода 12, объединенное с j-м ответвлением 4j первого световода 4, оптически связан с входом j-го матричного СМС 5j, j=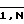 .
.
Устройство работает следующим образом.
Источник излучения 1 формирует когерентный монохроматический поток интенсивностью 3N3 усл. единиц, который, разветвляясь во входном оптическом разветвителе 2 на три потока, поступает по разветвлениям 21-23, соответственно на
входы ответвлений 211-21N,
входы ответвлений 221-22N,
транспарант 3N+1
Cветовой поток на выходах ответвлений 211-21N разветвляется на N2потоков, образуя тем самым, на входах транспарантов 31-3N двумерный световой поток единичной интенсивности. Световой поток на выходах ответвлений 221-22N разветвляется на N потоков, формируя на входах модуляторов 61-6N в направлении t световой поток интенсивности N усл. ед.
Световой поток ответвления 23, проходя через транспарант 3N+1 с функцией пропускания Vо (здесь и далее учитываем, что на функцию пропускания транспаранта умножается амплитуда потока, а не интенсивность), разветвляется в ответвлениях 231-23N на N потоков, формируя, таким образом, постоянный в направлении t световой поток с амплитудой Vo·  , поступающий в световодные жгуты 81-8N. Постоянные в течение времени работы устройства световые потоки с выхода транспарантов 31-3N, имеющие распределения амплитуд в пл. О, V, t-ONVt соответственно L(X1, V, t)-L(XN, V, t), через световодные жгуты 41-4N поступают на входы матричных СМС 51-5N, где суммируются по амплитуде со световыми потоками, поступающими по световодным жгутам 121-12N. В начальный момент времени амплитуды выходных потоков световодов 121-12N равны 0, в дальнейшем при осуществлении процесса последовательных приближений (2) соответственно
, поступающий в световодные жгуты 81-8N. Постоянные в течение времени работы устройства световые потоки с выхода транспарантов 31-3N, имеющие распределения амплитуд в пл. О, V, t-ONVt соответственно L(X1, V, t)-L(XN, V, t), через световодные жгуты 41-4N поступают на входы матричных СМС 51-5N, где суммируются по амплитуде со световыми потоками, поступающими по световодным жгутам 121-12N. В начальный момент времени амплитуды выходных потоков световодов 121-12N равны 0, в дальнейшем при осуществлении процесса последовательных приближений (2) соответственно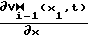 · f(x1, u, t) ÷
· f(x1, u, t) ÷ 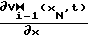 · f (xN, U, t)
· f (xN, U, t)
С выходов матричных СМС 51-5N снимаются сигналы, пропорциональные значениям функций (в направлении t): i
i L
L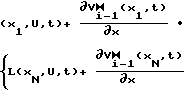 f
f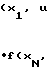 ,
,  )
)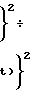 так как в каждом столбце i-го матричного СМС осуществляется формирование сигнала, пропорционального минимальной интенсивности входного светового сигнала из всех распределенных в направлении ОiV. Выходные сигналы матричных СМС 51-5N поступают на управляющие входы модуляторов 61-6N. Соотношение коэффициентов передачи СМС 5i"k" и модуляторов 6i "k"2выбирается, исходя из степени затухания интенсивности светового потока в кольце обратной связи "выход 6i_→7i_→8i_→9i_→10i_→11i_→12i_→ вход 5i" в ε раз: k1˙k2= ε. С выходов модуляторов 61-6N на i-м шаге процедуры (2) снимаются световые потоки с распределением амплитуд в направлении t:
так как в каждом столбце i-го матричного СМС осуществляется формирование сигнала, пропорционального минимальной интенсивности входного светового сигнала из всех распределенных в направлении ОiV. Выходные сигналы матричных СМС 51-5N поступают на управляющие входы модуляторов 61-6N. Соотношение коэффициентов передачи СМС 5i"k" и модуляторов 6i "k"2выбирается, исходя из степени затухания интенсивности светового потока в кольце обратной связи "выход 6i_→7i_→8i_→9i_→10i_→11i_→12i_→ вход 5i" в ε раз: k1˙k2= ε. С выходов модуляторов 61-6N на i-м шаге процедуры (2) снимаются световые потоки с распределением амплитуд в направлении t: 
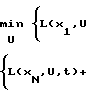 ,
,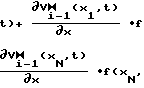 (
( ,
, 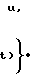 t
t ÷ которые, проходя через оптические интеграторы 71-7N, где осуществляется операция неопределенного интегрирования по t функции их амплитудного распределения, поступают в световодные жгуты 81-8N, где суммируются со световыми потоками, имеющими постоянную амплитуду Vo·
÷ которые, проходя через оптические интеграторы 71-7N, где осуществляется операция неопределенного интегрирования по t функции их амплитудного распределения, поступают в световодные жгуты 81-8N, где суммируются со световыми потоками, имеющими постоянную амплитуду Vo·  . Тем самым в световодном жгуте 8j на i-м шаге решения формируется световой поток, распределение амплитуды которого в направлении t пропорционально функции Vi(xi,t) т.е. i-му приближению к значению решения V(xj,t).
. Тем самым в световодном жгуте 8j на i-м шаге решения формируется световой поток, распределение амплитуды которого в направлении t пропорционально функции Vi(xi,t) т.е. i-му приближению к значению решения V(xj,t).
Данные потоки поступают далее на входы дифференциаторов 91-9N, "разворачиваясь" за счет конструктивного разведения волокон ответвлений 812-8N2 на 90о в пл. Охt1. На выходах дифференциаторов 91-9Nформируется двумерный световой поток с распределением амплитуды в пл. Охt1: ·
· 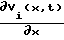 (с выхода 9j снимается световой поток с распределением амплитуды по Ох, пропорциональным
(с выхода 9j снимается световой поток с распределением амплитуды по Ох, пропорциональным 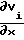 (xitj). За счет конструктивной разводки волокон ответвлений 101-10N световой поток с распределением амплитуды
(xitj). За счет конструктивной разводки волокон ответвлений 101-10N световой поток с распределением амплитуды  ·
· 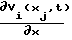 в направлении Оt1 "разворачивается" на 90о в направлении Qjt и разветвляется в направлении QjV на N потоков, обеспечивая тем самым формирование в пл. QjVt двумерного потока с амплитудой
в направлении Оt1 "разворачивается" на 90о в направлении Qjt и разветвляется в направлении QjV на N потоков, обеспечивая тем самым формирование в пл. QjVt двумерного потока с амплитудой 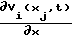 , постоянной при фиксированном t.
, постоянной при фиксированном t.
Далее происходит умножение амплитуд данных потоков на функции пропускания f(x1,V,t)-f(xN1,V,t) транспарантов 111-11N с последующей их передачей по ответвлениям 121-12N на входы матричных СМС 51-5N и суммированием с потоками, поступающими по световодам 41-4N. Процесс формирования очередного приближения функции V(x,t), т.е. решения (1), повторяется. По окончании переходного процесса, т. е. итеративной процедуры, на выходах ответвлений 811-8N1 формируются световые потоки с распределением амплитуды в направлении t, пропорциональной значениям решения уравнения (1), соответственно, V(x1, t)-V(xN,t).
| название | год | авторы | номер документа |
|---|---|---|---|
| ОПТОЭЛЕКТРОННОЕ УСТРОЙСТВО ДЛЯ РЕШЕНИЯ ДИФФЕРЕНЦИАЛЬНОГО ПАРАБОЛИЧЕСКОГО УРАВНЕНИЯ | 1989 |
|
RU2042179C1 |
| ОПТОЭЛЕКТРОННОЕ УСТРОЙСТВО ДЛЯ РЕШЕНИЯ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ В ЧАСТНЫХ ПРОИЗВОДНЫХ | 1991 |
|
RU2042181C1 |
| СТОХАСТИЧЕСКИЙ ФИЛЬТР | 1995 |
|
RU2100905C1 |
| ОПТИЧЕСКОЕ ВЫЧИСЛИТЕЛЬНОЕ УСТРОЙСТВО | 1991 |
|
RU2018920C1 |
| УСТРОЙСТВО ДЛЯ СИНТЕЗА ОПТИМАЛЬНОГО УПРАВЛЕНИЯ | 1994 |
|
RU2110086C1 |
| ОПТИЧЕСКИЙ УМНОЖИТЕЛЬ | 1994 |
|
RU2087028C1 |
| УСТРОЙСТВО ДЛЯ РЕШЕНИЯ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ | 1992 |
|
RU2021628C1 |
| ОПТИЧЕСКОЕ УСТРОЙСТВО ДЛЯ РЕШЕНИЯ ИНТЕГРОДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ В ЧАСТНЫХ ПРОИЗВОДНЫХ | 1992 |
|
RU2022329C1 |
| СТОХАСТИЧЕСКИЙ ФИЛЬТР | 1992 |
|
RU2050581C1 |
| ОПТИЧЕСКИЙ СТАТАНАЛИЗАТОР | 1990 |
|
RU2018917C1 |
Изобретение относится к вычислительной технике и может быть использовано в оптических вычислительных машинах при решении функциональных уравнений. Расширение функциональных возможностей устройства за счет решения функциональных уравнений достигается введением в устройство матричного электрооптического модулятора Керра и матричных оптических интегратора и дифференциатора, что позволяет, используя функцию определения минимума, осуществить решение уравнения Беллмана, представляющего собой более общий случай по сравнению с дифференциальным уравнением в частных производных, решение которого реализуется в прототипе. 3 ил.
ОПТОЭЛЕКТРОННОЕ УСТРОЙСТВО ДЛЯ РЕШЕНИЯ ФУНКЦИОНАЛЬНОГО УРАВНЕНИЯ, содержащее источник излучения, матричный вычислительный транспорант и разветвленные световодные жгуты, отличающееся тем, что в него введены матричный селектор минимального сигнала, матричный оптический интегратор, матричный оптический дефференциатор и матричный электрооптический модулятор Керра, выход источника излучения через первое ответвление первого разветвленного световодного жгута, N элементов матрицы вычислительных транспарантов, первое ответвление второго разветвленного световодного жгута, элементы матричного селектора минимального сигнала подключен к первым входам элементов матричного электрооптического модулятора Керра, выход источника излучения через второе ответвление первого разветвленного световодного жгута соединен с вторыми входами элементов матричного электрооптического модулятора Керра, выходы которых через элементы матричного оптического интегратора, первое ответвление третьего разветвленного световодного жгута, элементы матричного оптического дифференциатора, четвертый разветвленный световодный жгут, элементы с (N + 1)-го по 2N-й матричного вычислительного транспаранта, второе ответвление второго разветвленного световодного жгута подключены к входам элементов матричного селектора минимального сигнала, выход источника излучения через третье ответвление первого разветвленного световодного жгута, (2N+1)-й элемент матричного вычислительного транспаранта и второе ответвление третьего разветвленного световодного жгута соединен с входами элементов матричного оптического дифференциатора.
| Аппарат для очищения воды при помощи химических реактивов | 1917 |
|
SU2A1 |
| Оптоэлектронное устройство для ре-шения дифференциальных уравнений вчастных производных | 1974 |
|
SU508784A1 |
| Приспособление для точного наложения листов бумаги при снятии оттисков | 1922 |
|
SU6A1 |
Авторы
Даты
1995-11-10—Публикация
1989-12-26—Подача