Изобретение относится к нефтедобычи, к методам увеличения нефтеотдачи пластов, в частности к способу определения эффективности применяемых методов увеличения нефтеотдачи пластов.
Известен способ определения технологической эффективности методов увеличения нефтеотдачи пластов, включающий определение через определенные временные интервалы фактических текущих и накопленных отборов нефти до применения метода увеличения нефтеотдачи пластов (МУН), определение фактических отборов нефти в период после применения МУН, определение прогнозных накопленных отборов нефти путем экстраполирования на период после применения МУН фактических данных накопленных отборов нефти за базовый период, сравнение фактических накопленных отборов в период после применения МУН с прогнозными накопленными отборами и определение эффективности МУН по разнице между фактически прогнозным отбором нефти [1]
Известный способ не дает возможности точно определить эффективность методов увеличения нефтеотдачи и унифицировать способ определения эффективности МУН.
С целью оценки извлекаемых запасов нефти, темпа разработки, продолжительности времени доразработки и принятия решения об извлеченной части запасов за счет тех или иных интенсификационных технологий добычи нефти и методов увеличения нефтеотдачи, а также для прогноза широко используют, также как и в прототипе, двух-, трех-, четырехпараметрические характеристики вытеснения как в интегральной, так и в дифференциальной форме.
Однако применение того или иного метода характеристик вытеснения ограничивается определенными условиями при решении конкретных задач, что позволяет утверждать об отсутствии единых принципов определения технологической эффективности МУН. Так, в известном способе, также как и в других известных способах определения эффективности МУН, отсутствуют обоснования относительно количества точек, допускающих линеаризацию характеристики вытеснения, то есть обоснование базового периода. Существует ряд основополагающих причин, в силу которых недопустимо в качестве базы выбирать произвольное количество точек для выпрямления (линеаризации) конечного участка характеристики вытеснения и тем более, основываясь на этом, прогнозировать дальнейшее развитие процесса и принимать серьезные технологические решения. Произвол заключается в том, что, варьируя количеством точек в выборке для базового периода и подбирая наиболее "подходящую" модель из большого количества характеристик вытеснения, можно достигнуть приемлемого выпрямления конечного отрезка любой кривой характеристики вытеснения, тем самым при желании можно обеспечить формально эффективность для любой технологии или наоборот.
Целью изобретения является повышение точности определения эффективности МУН и установление единого принципа определения технологической эффективности методов увеличения нефтеотдачи пластов.
Цель достигается тем, что в способе, включающем определение через временные интервалы фактических текущих и накопленных отборов нефти до применения МУН, определение прогнозных накопленных отборов нефти в период после применения МУН, определение прогнозных накопленных отборов нефти путем экстраполирования на период после применения МУН фактических данных накопленных отборов нефти за базовый период, определение эффективности (или неэффективности) МУН по изменению фактических накопленных отборов за период после применения МУН в сравнении с прогнозными накопленными отборами нефти, фактические текущие и накопленные отборы нефти определяют с месячным временным интервалом с начала разработки залежи, строят кривую накопленного отбора нефти от времени, определяют время начала уменьшения фактических отборов нефти и его принимают за начало базового периода, при этом время начала уменьшения фактических отборов нефти находят путем определения времени, соответствующего точке перегиба кривой накопленного отбора нефти от времени.
Периодичность и продолжительность измерений технологических показателей процесса позволяет определить объективность и обоснованность замеров и параметров контроля, что необходимо при определении эффективности МУН.
В настоящее время временные ряды показателей разработки часто представляются с годовым или квартальным временными шагами, хотя продолжительность эффективности по методам увеличения нефтеотдачи исчисляется десятками месяцев. Поэтому динамику развития процесса в период реализации предложенной технологии целесообразно и оптимально выразить с месячным временным шагом, причем с начала разработки.
При обоснованной постановке задачи кривые падения (характеризуют динамику добычи нефти во времени и выражаются зависимостью между текущей или накопленной добычей нефти и временем) имеют вид S-образной или логистической кривой. Аппроксимация этих кривых с помощью известных характеристик вытеснения невозможна, так как исследования этих функций показали, что для этих зависимостей область вогнутости и выпуклости несовместима.
Кроме того, широко используемые кривые обводнения с временным шагом в один месяц свидетельствует о возможном хаотическом характере зависимостей текущего отбора нефти от жидкости, нефти и воды, отбираемой и закачиваемой в пласт соответственно. Линеаризация конечных участков этих кривых, выраженных через кривые обводнения, не дает права судить о характере процесса. При математической формализации по кривой накопленных отборов процесс разработки естественным образом в точке перегиба распадается на два этапа. Следовательно, процессы, происходящие в пластовой системе до точки перегиба и после нее, имеют принципиальное различие, то есть вторые производные функционала в точке перегиба меняют знак. Это играет ключевую роль в подборе базы для сравнения и оценки эффективности до и после проведения МУН. Таким образом, выбор более точного временного шага позволяет проследить логику развития процесса. Кривые падения с месячным временным шагом дают возможность получить более точную малопараметрическую модель эволюции пластовой системы.
Известно, что любую развивающуюся динамическую систему можно представить общим нелинейным уравнение эволюции: поскольку пластовая система является такой же системой, то временные ряды показателей разработки могут быть ярким примером, характеризующим эволюцию пластовой системы. Это позволяет представить изменение текущего отбора нефти во времени с помощью нелинейного уравнения эволюции.
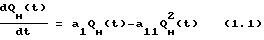
где
QH(t) накопленный отбор нефти,
a1 коэффициент роста отбора нефти,
a11 коэффициент потерь нефти;
a1 > 0, a11 > 0.
В уравнении (1.1) первое слагаемое показывает неограниченный экспоненциальный рост отбора нефти, а второе слагаемоe представляет ограничения, налагаемые на экспоненциальный рост отбора нефти за счет взаимодействия добывающих скважин, физико-химических свойств флюидов или топологией самой фильтрационной среды.
В данном случае вклад второго слагаемого можно объяснить следующим образом.
Если изначально применяется слишком плотная сетка скважин, или в процессе разработки произошло уплотнение сетки скважин, то в силу взаимодействия (интерференции) скважин одни скважины отбирают нефть у других соседних, что характеризуется слагаемым в (1.1) a11QH•QH. Это приводит к перераспределению ресурсов пласта на более плотную сетку скважин, что устанавливается с помощью корреляционной матрицы. Если корреляционная матрица, характеризующая взаимодействие между скважинами, имеет коэффициенты корреляции с отрицательным знаком, то это свидетельствует об интерференции скважин. Это налагает ограничения на экспоненциальный рост отбора нефти, приводящие к нелинейной эволюционной модели. Подобных причин можно выявить множество, особенно в пластовых условиях. Таким же примером, ограничивающим экспоненциальный рост отбора нефти, является обводненность QB продукции скважин и пласта. В этом случае в правой части уравнения (1.1) появляется дополнительное слагаемое, учитывающее взаимодействие двух фаз a12QH•QB, тогда уравнение (1.1) примет следующий вид,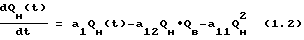
В итоге борьба двух фаз "нефть-вода" будет определять возможности пластовой системы. Поэтому часть методов увеличения нефтеотдачи пластов направлена на то, чтобы заставить воду выполнять полезную работу. Именно с помощью этих параметров делаются попытки смоделировать ситуацию.
Любой вид ограничения, налагаемого на экспоненциальный рост отбора нефти (1.2), можно преобразовать модификацией нелинейного эволюционного уравнения (1.1).
Таким образом, аналитическое решение уравнения (1.1) с начальными условиями при t=0 QH(t)=Qo имеет вид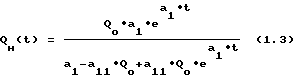
И, наконец, взяв предел QH(t) при t → ∞, получим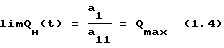
Это значит, что накопленный отбор будет стремиться к QМАХ и имеет определенный физический смысл.
Знаменатель и числитель функции (1.3) разделим на a11 и преобразуем к виду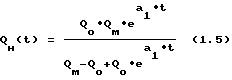
Для последующего исследования уравнения (1.1) преобразуем его к виду: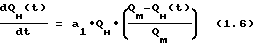
Заметим, что если начальное значение QО < QМ, то для t > 0, QH(t) < QM. Тогда из уравнения (1.6) следует, что при QH(t)<QM, производная 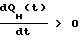 и, следовательно, QH(t) растет.
и, следовательно, QH(t) растет.
Кроме того, если взять вторую производную от уравнения (1.6), получим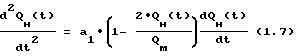
Подставив сюда выражения из (1.5), получим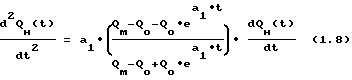
Из уравнения (1.8) следует, что при QM QО - QО•eat > 0 производная 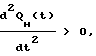 , значит, функция QH(t) выпукла, при QH QО QО•eat < 0 производная
, значит, функция QH(t) выпукла, при QH QО QО•eat < 0 производная 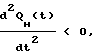 , следовательно, функция QH(t) вогнута. Из первого неравенства находим область выпуклости:
, следовательно, функция QH(t) вогнута. Из первого неравенства находим область выпуклости: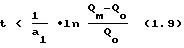
Аналогично находим область вогнутости: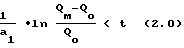
Таким образом, находим точку перегиба: 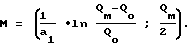 .
.
Так как производная 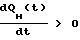 , то для любого t исследуемая зависимость QH(t) нигде не имеет экстремума.
, то для любого t исследуемая зависимость QH(t) нигде не имеет экстремума.
Таким образом, график функции QH(t) имеет вид логистической кривой и ассимптотически стремится к максимально возможному значению, что и требовалось доказать (фиг. 1). Практически все эволюционно развивающиеся системы и процессы при естественном стечении обстоятельств ведут себя идентично и проходят через три стадии развития, в том числе человеческая жизнь. В процессе разработки нефтяной залежи так же наблюдается "начальная стадия" развития пластовой системы (I стадия, отрезок O-N), "нормальная стадия" развития пластовой системы (II стадия, отрезок N-P) и естественное старение и "смерть" пластовой системы (III стадия, отрезок P-L), что подтверждает логистический характер развития пластовой системы. Поэтому кинетическую модель процесса разработки месторождения можно представить удобной с практической точки зрения модификацией эволюционного уравнения, имеющей логистический характер и охватывающей весь жизненный цикл процесса разработки.
Становится очевидным, что точка перегиба обязательно присутствует, и только модификация кинетического уравнения, обладающая вышеуказанными свойствами, может аппроксимировать процесс.
Исследованиями установлено, что такими свойствами обладает кинетическое уравнение Колмогорова А.Н. что является аналогом плотности распределения Вейбулла.
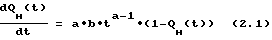
где
a и b коэффициенты аппроксимации; a > 1, b > 0.
Решение уравнения (2.1) имеет вид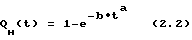
Решение уравнения Колмогорова А. Н. (2.2) совпадает со статистическим распределением Вейбулла, разработанного для задач теории надежности. Таким образом, статистическому распределению (2.2) соответствует кинетическое уравнение (2.1), что позволяет раскрыть физическую сущность статистического распределения.
Преобразовав уравнение (2.1) к виду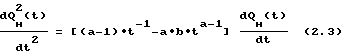
находим условия выпуклости и вогнутости.
Из уравнения (2.3) следует, что при [(a-l)•t-1 - a•b•ta-1] > 0 производная 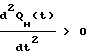 , значит QH(t) выпукла, при [(a-l)•t-1 a•b•ta-1] < 0 производная
, значит QH(t) выпукла, при [(a-l)•t-1 a•b•ta-1] < 0 производная 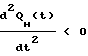 , значит QH(t) вогнута.
, значит QH(t) вогнута.
Зная область выпуклости и вогнутости, находим координаты точки перегиба на логистической кривой 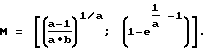 .
.
При заданном уровне извлекаемых запасов по зависимости (2.2) можно определить остаточное время (продолжительность) доразработки объекта.
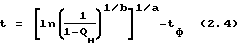
где
Q0 извлекаемые запасы нефти,
t продолжительность времени до разработки объекта,
tф фактическое время разработки объекта,
a, b коэффициенты аппроксимации.
После обоснованного выбора эволюционной модели необходимо оценить точность аппроксимации и чувствительность решения относительно коэффициентов аппроксимации.
Необходимость такой оценки вызвана тем, что часто предполагаемая "эффективность" становится сопоставима с величиной погрешности, допускаемой при расчете коэффициентов аппроксимации, а иногда и меньше ее. В такой ситуации исключается возможность принятия объективного решения.
Крайне важно определить степень точности коэффициентов аппроксимации a и b, поскольку это показывает адекватность модели самому процессу и дает возможность рассчитывать погрешность.
Эту задачу удалось решить с помощью метода теории чувствительности.
Суть метода заключается в том, что, определив погрешности оценки коэффициентов аппроксимации и функции чувствительности модели (2.2), можно определить погрешности в прогнозной области.
С этой целью зависимость (2.2) следует разложить в виде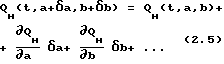
Из (2.5) находится погрешность ΔQн как разница между Qн(t,a+δa,b+δb). и QН(t, a, b)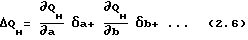
где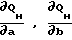 функции чувствительности,
функции чувствительности,
δa, δb погрешности при определении коэффициентов аппроксимации a и b,
Δ QH разница между нулевым и первым порядком разложения.
Для определения функций чувствительности из модели (2.2) находим производные по a и b: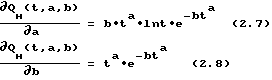
Погрешности δa, δb находим из условия минимума невязки (квадратическое отклонение) для базового периода: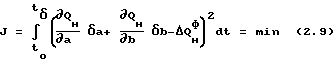
где
tб tо базовый период, j min невязки.
Раскроем под интегралом квадрат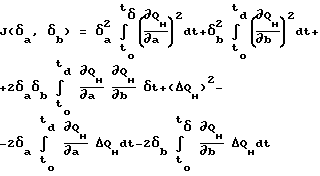
и введем вспомогательные обозначения: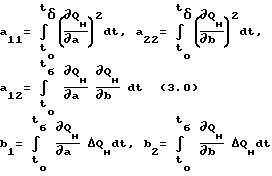
Таким образом, поставленная задача принимает вид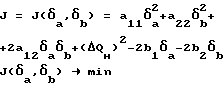
Посчитаем частные производные по δa и δb, и приравняем их к 0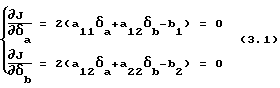
Решим систему и найдем погрешности δa и δb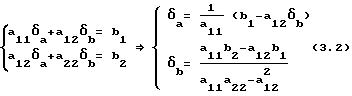
Примечательно то, что предлагаемая расчетная схема позволяет осуществить как линейную аппроксимацию и последующий прогноз, так и нелинейную аппроксимацию и соответствующий прогноз. Это дает возможность оценить адекватность выбранной эволюционной модели и объекта.
С этой целью уравнение (2.2) с помощью двойного логарифмирования линеаризуется: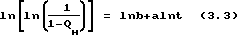
Коэффициенты аппроксимации a и b определяются методом наименьших квадратов из выражения (3.3).
Таким образом, осуществив линеаризацию, найденные значения a и b используем для нелинейной аппроксимации, подставляя числовые значения a и b в уравнение (2.2). Кроме того, с помощью прогноза по зависимости и графику (3.3) определяется величина извлекаемого запаса по годам.
Способ осуществляется следующим образом:
1. Определяют фактические текущие qH, фактические накопленные QH отборы нефти с месячным временным интервалом с начала разработки.
2. Строятся графики кривых текущего и накопленного отборов нефти от времени.
3. Полученная логистическая кривая накопленного отбора нефти аппроксимируется с помощью зависимости (2.2), и находятся коэффициенты аппроксимации a и b и точка перегиба M на логистической кривой, являющаяся точкой начала уменьшения текущих отборов нефти.
4. Выбирается базовый период, начало которого время, соответствующее точке перегиба M на логистической кривой, конец базового периода время, соответствующее концу разработки объекта базовым методом.
5. На базовом участке с помощью зависимости (3.3) проводится линеаризация кривой накопленного отбора нефти. Определяют прогнозные накопленные отборы нефти путем экстраполирования на период после применения МУН линеаризированного участка кривой фактического накопленного отбора нефти за базовый период.
6. Методом наименьших квадратов определяют коэффициенты a и b линейной аппроксимации на базовом участке по зависимости (3.3). Определяют прогнозируемые отборы нефти за период после применения МУН.
7. Сравнивают значения фактических и прогнозных накопленных отборов нефти за период после применения МУН и определяют эффективность по наличию дополнительно добытой нефти за этот период как разницу между фактическим и прогнозным (Qp) отбором нефти.
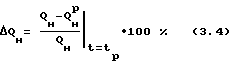
8. Оценивают точность расчета методом теории чувствительности по формулам (2.5-3.2).
Пример 1.
Начало разработки базовым методом 1970 г. конец разработки базовым методом 1990 г.
В 1990 г. на участке месторождения применили метод гидродинамического воздействия на пласт. 1990 г. начало оцениваемого периода, конец оцениваемого периода 1994 г.
1. С начала разработки пласта определяют фактические текущие и фактические накопленные отборы с месячным временным интервалом.
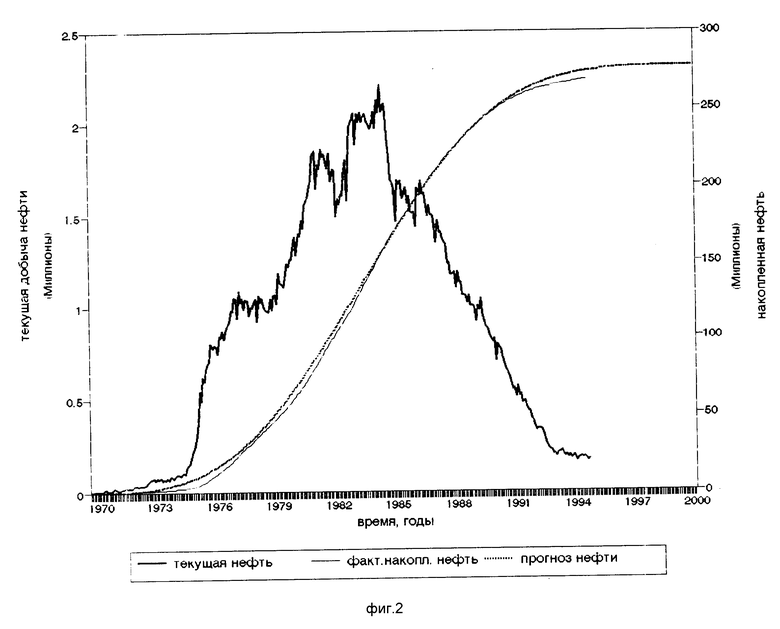
Строят графики зависимости текущего и накопленного отборов нефти от времени (фиг. 2).
3. Полученная логистическая кривая накопленного отбора нефти аппроксимируют с помощью зависимости (2.2) и находят коэффициенты аппроксимации a и b и точка перегиба M. Определяют время начала уменьшения текущих отборов нефти, соответствующее точке перегиба. В данном случае a 3,256785, b 3,92e-8, время 1983 г.
Таким образом, начало базового периода 1983 г. конец 1990 г.
4. На базовом участке (конечный участок логистической кривой накопленного отбора) с помощью зависимости (3.3) проводят линеаризацию кривой накопленного отбора нефти (фиг. 3).
5. Методом наименьших квадратов определяют коэффициенты a и b линейной аппроксимации на базовом участке a 3,188475, b 5,69e-8.
6. Определяют прогнозные отборы нефти за период после применения МУН.
7. Сравнивают значения фактических и прогнозных накопленных отборов нефти по формуле (3.4). В данном случае Δ QH -2715369 тонн или -1,01301%
Таким образом, примененный метод увеличения нефтеотдачи неэффективен, так как от неэффективного применения МУН нефтеотдача снизилась более чем на один процент.
8. Определяют точность расчета коэффициентов линейной аппроксимации da -0,0004, δb1,67e-10. Погрешность определения коэффициентов δ0,003161.
Пример 2.
Начало разработки базовым методом 1971 г. конец разработки базовым методом 1990 г.
В 1990 г. на участке месторождения применили метод полимерного заводнения пласта с системной обработкой призабойной зоны пласта.
Начало оцениваемого периода 1990 г. конец оцениваемого периода 1994 г.
1. Определяют фактические текущие и фактические накопленные отборы с месячным временным интервалом с начала разработки.
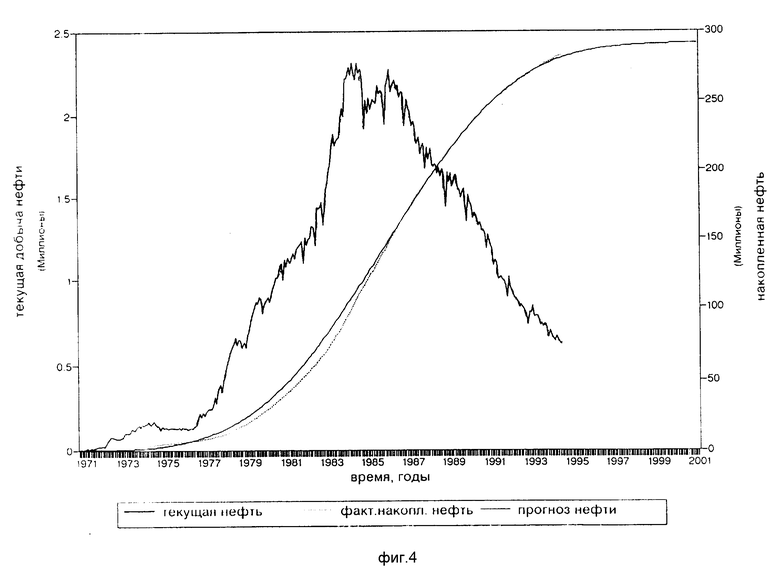
2. Строят графики зависимости текущего и накопленного отборов нефти от времени (фиг. 4).
3. Полученная логистическую кривую накопленного отбора нефти аппроксимируют с помощью зависимости (2.2) и находят коэффициенты аппроксимации a 3,620143, b 4,49e-9 и точку перегиба M.
4. Время, соответствующее точке перегиба M, (время начала уменьшения текущих отборов 1986 г.) является началом базового периода, конец базового периода 1990 г.
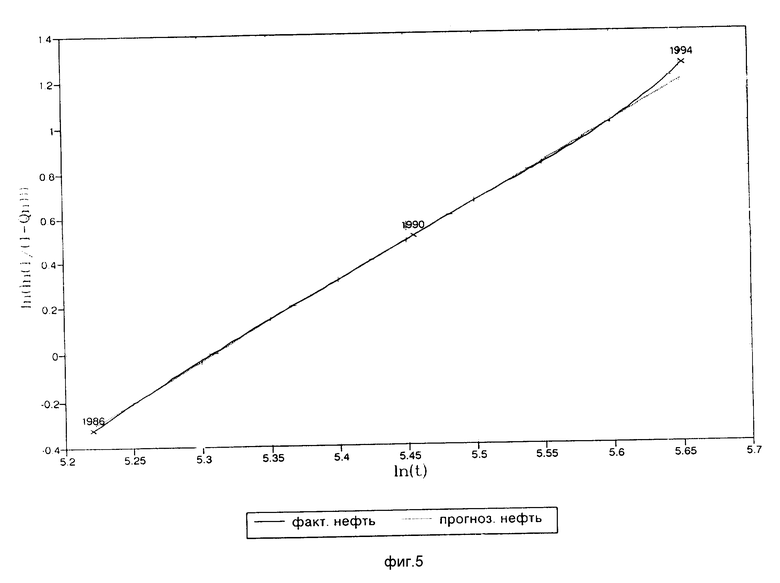
5. На базовом участке с помощью зависимости (3.3) проводится линеаризация кривой накопленного отбора нефти (фиг. 5).
6. Методом наименьших квадратов определяют коэффициенты линейной аппроксимации на базовом участке a 3,468854, b 1•e-8. Определяют прогнозные отборы нефти за период после применения МУН.
7. Определяют дополнительно добытую нефть (D QH) по формуле (3.4) D QH 0,74478% или 2104190 тонн.
Таким образом, применный МУН эффективен, так как дополнительная добыча нефти после МУН составила более 2 млн. тонн.
8. Определяют точность расчета коэффициентов линейной аппроксимации da 0,00352, δb 1,92•e-10, погрешность определения коэффициентов линейной аппроксимации δ -0,00951.
Таким образом, описываемый способ позволяет повысить точность определения технологической эффективности МУН, оценить допускаемые погрешности.
Литература
1. Методическое руководство по оценке технологической эффективности применения методов увеличения нефтеотдачи пластов, М. 1993, с. 10-13, 41-44.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ ОПРЕДЕЛЕНИЯ ТЕХНОЛОГИЧЕСКОЙ ЭФФЕКТИВНОСТИ МЕТОДОВ УВЕЛИЧЕНИЯ НЕФТЕОТДАЧИ ПЛАСТОВ | 1999 |
|
RU2149256C1 |
| Способ определения эффективности проведенного геолого-технического мероприятия | 2023 |
|
RU2820909C1 |
| Способ разработки нефтяных месторождений на поздней стадии эксплуатации | 2015 |
|
RU2611097C1 |
| Способ эксплуатации системы газлифтных скважин | 1991 |
|
SU1773273A3 |
| Способ повышения эффективности гидродинамических методов увеличения нефтеотдачи пласта | 2020 |
|
RU2759143C1 |
| АКУСТИЧЕСКИЙ СПОСОБ ВОЗДЕЙСТВИЯ НА СКВАЖИНУ И ПЛАСТ МЕСТОРОЖДЕНИЙ ПОЛЕЗНЫХ ИСКОПАЕМЫХ "АРСИП" | 1998 |
|
RU2143554C1 |
| СПОСОБ РАЗРАБОТКИ НЕФТЯНОЙ ЗАЛЕЖИ С УТОЧНЯЕМЫМИ ГРАНИЦАМИ | 1997 |
|
RU2095554C1 |
| СПОСОБ РАЗРАБОТКИ НЕФТЯНОГО ПЛАСТА | 2014 |
|
RU2539485C1 |
| СПОСОБ КОНТРОЛЯ ЗА РАЗРАБОТКОЙ НЕФТЯНОГО МЕСТОРОЖДЕНИЯ | 1999 |
|
RU2166630C1 |
| СПОСОБ РАЗРАБОТКИ ТРЕЩИННО-КАВЕРНОЗНОЙ ЗАЛЕЖИ С ГАЗОВОЙ ШАПКОЙ И ПОДСТИЛАЮЩЕЙ ВОДОЙ | 2022 |
|
RU2808627C1 |

Назначение: Изобретение относится к нефтедобыче, в частности, к способам определения технологической эффективности методов увеличения нефтеотдачи пластов (МУН). Сущность изобретения: В способе определяют через временные интервалы фактические текущие и накопленные отборы нефти до применения методов увеличения нефтеотдачи и фактические накопленные отборы нефти в период применения МУН. Затем определяют прогнозные накопленные отборы нефти путем экстраполирования на период применения МУН фактических данных накопленных отборов нефти до применения МУН за базовый период. А эффективность МУН определяют по увеличению фактических накопленных отборов нефти за период применения МУН в сравнении с прогнозными накопленными отборами. При этом фактические текущие и накопленные отборы нефти определяют с месячным временным интервалом с начала разработки залежи. Затем строят кривую накопленного отбора нефти от времени, определяют время начала уменьшения фактических отборов нефти и его принимают за начало базового периода. При этом время начала уменьшения фактических отборов нефти находят путем определения времени соответствующего точке перегиба кривой накопленного отбора нефти от времени унифицируя определение базового периода. 5 ил.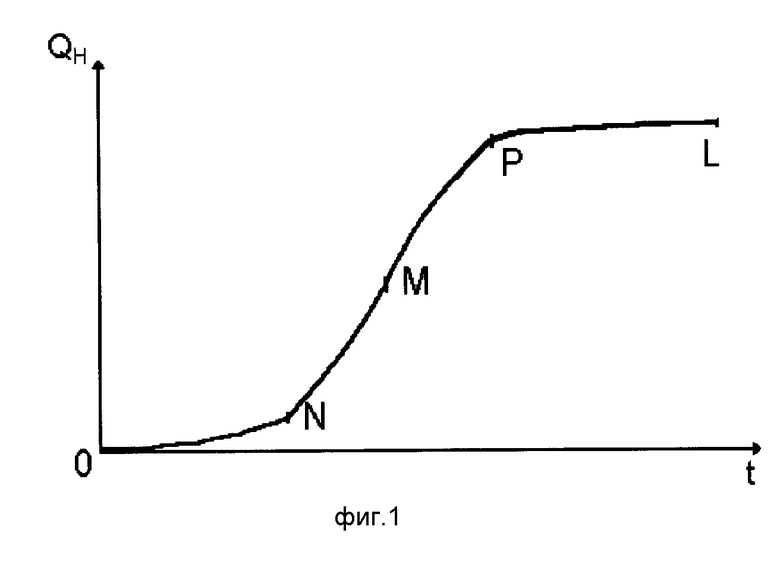
Способ определения технологической эффективности методов увеличения нефтеотдачи пластов, включающий определение через временные интервалы фактических текущих и накопленных отборов нефти до применения метода увеличения нефтеотдачи пласта, определение фактических накопленных отборов нефти в период после применения метода увеличения нефтеотдачи пластов, определение прогнозных накопленных отборов нефти путем экстраполирования на период после применения методов увеличения нефтеотдачи пласта фактических накопленных отборов нефти за базовый период, определение эффективности метода увеличения нефтеотдачи пласта по разнице между фактическим и прогнозным отбором нефти, отличающийся тем, что фактические текущие и накопленные отборы нефти определяют с месячным временным интервалом с начала разработки залежи, строят кривую накопленного отбора от времени, определяют время начала уменьшения фактических отборов нефти и его принимают за начало базового периода, при этом время начала уменьшения фактических отборов нефти находят путем определения времени, соответствующего точке перегиба кривой накопленного отбора нефти от времени.
| Методическое руководство по оценке технологической эффективности применения методов увеличения нефтеотдачи пластов | |||
| - М., 1993, с.10-13, 41-44. |
Авторы
Даты
1997-11-10—Публикация
1997-03-28—Подача