Изобретение относится к области физической акустики и может использоваться для определения интегральной (в полосе частот) эффективности звукоизоляции конструкций, предназначенных для локализации диффузных шумовых широкополосных и узкополосных стационарных акустических полей.
Известен способ определения эффективности звукоизоляции для звукоизолирующих конструкций, основанный на законе "массы" (Исакович М.А. Общая акустика.-М.: Наука, 1973, с. 149). Согласно этому закону коэффициент звукопрохождения пластины с поверхностной плотностью m = ρh определяется формулой
Kзвпр(ω) = 1/[1+(ωρh/2ρ0C0)2], (1/1)
где
ω - круговая частота падающей на пластину звуковой волны;
ρ0 - плотность воздуха;
C0 - скорость звука в воздухе;
ρ - плотность материала пластины;
C - скорость звука в материале пластины;
h - толщина пластины;
m = ρh - масса единицы площади пластины.
Фактически формула (1.1) моделирует звукоизолирующую конструкцию фильтром нижних частот.
Из курса статистической радиотехники известно, что при воздействии стационарного шума (в полосе B) на фильтр нижних частот, интегральный коэффициент звукопрохождения для фильтра нижних частот при стационарном входном воздействии определяется как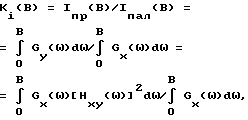
где
Iпад - интенсивность падающей на пластину звуковой волны;
Iпр - интенсивность прошедшей через пластину звуковой волны.
Если полоса частот входного воздействия B больше чем 2ρ0C0/ρh и имеет равномерную спектральную плотность в этой полосе частот, то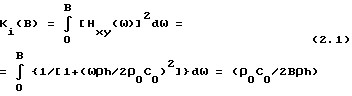
Соответственно эффективность звукоизоляции для данного коэффициента звукопрохождения определяется следующим образом (Скучик Е.. Основы акустики, т. 2. -М.: Изд-во Иностр. лит-ра, 1959, с. 186, формула (28.11)):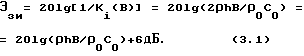
Это выражение имеет основное значение в прикладной акустике и является интегральным аналогом закона "массы" при широкополосном входном воздействии, когда измерения проводятся в некоторой полосе частот входного воздействия. Эффективность звукоизоляции в некоторой полосе частот определяется как величина, обратная интегральному коэффициенту звукопрохождения, т. е. как 1/Ki(B). Оценки эффективности звукоизоляции по формуле (2.1) или по формуле (3.1) всегда очень сильно расходятся с результатами эксперимента при исследованиях звукоизолирующих конструкций как в "свободном поле", так и в условиях помещений с реверберацией. Это связано с тем, что при выводе указанных формул в качестве модели процесса распространения звука в упругих конструкциях использованы продольные волны. В ряде публикаций указывается, что подобная модель на частотах ниже 100 кГц неприменима. Поэтому представляется целесообразным для расчета механизма звукоизоляции в звуковом диапазоне частот использовать модель в виде шарнирно закрепленной по периметру упругой панели с плотностью ρ, толщиной h, линейными размерами Lx и Ly.
Цель изобретения - исключение недопустимо больших расхождений практических изменений и теории при расчете эффективности звукоизоляции шумозащитных конструкций.
Заявляемый способ оценки эффективности звукоизоляции закрепленной по периметру упругой прямоугольной пластины в условиях стационарных широкополосных или узкополосных шумовых воздействий, основанный на законе "массы", по которому эффективность звукоизоляции Эзи определяют как
Эзи = 20 lg[1/Ki(B)],
где
Ki (B) - интегральный коэффициент звукопрохождения пластины, рассчитываемый с учетом полосы частот B = ω2-ω1 шумового воздействия, плотности ρ материала пластины и толщины h пластины, отличающийся тем, что определяют линейные размеры Lx и Ly пластины жесткостью D, а также собственные частоты ωmn колебаний пластины и граничную частоту ωгр пластины, а интегральный коэффициент звукопрохождения Ki(B) пластины на расстоянии z от пластины определяют при полосе частот B, лежащий ниже граничной частоты пластины, по формуле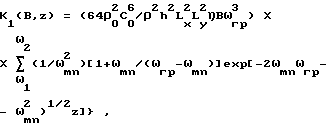
при полосе B частот, лежащей выше граничной частоты пластины, по формуле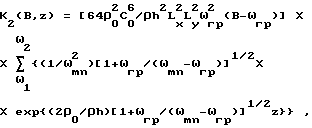
и при полосе B частот, включающей граничную частоту пластины, по формуле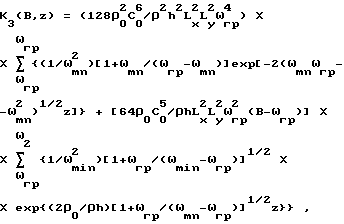
где
ρ0 - плотность воздуха;
C0 - скорость звука в воздухе;
η - коэффициент механических потерь материала пластины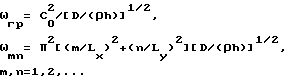 .
.
Расположим пластину по отношению к системе координат в соответствии с чертежом. Плоскость пластины совпадает с плоскостью z = 0. Если обозначить поперечное смещение точек пластины как u(x, y, t), то для поперечных отклонений от невозмущенного положения точек пластины получаем гиперболическое дифференциальное уравнение в частных производных четвертого порядка (первая краевая задача)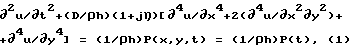
где граничные условия при z = 0 задаются выражениями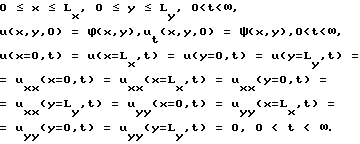
Указанные граничные условия определяют шарнирное закрепление пластины по периметру, здесь D - цилиндрическая жесткость пластины, h - толщина пластины, ρ - плотность пластины, η - коэффициент механических потерь в материале пластины, ρh = m, где m - поверхностная плотность пластины.
В уравнении (1) сделано предложение, что силы неупругого сопротивления пропорциональны деформации.
Решение уравнения (1) с граничными условиями (2) для гармоничного звукового воздействия частоты ω, амплитуда которого P0 не зависит от координат x, y, z, т.е. для падающей плоской волны вида
P(t,x,y,z) = P(t,z) = P0exp[j(-ωt+kz)],
для распределения нормальных смещений поверхности пластины u(x, y, t) имеет вид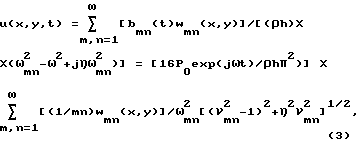
где νmn= ω/ωmn, wmn(x,y) = wm(x)wn(y) = sin(km(x)wn(y) = sin(kmx)sin(kny).
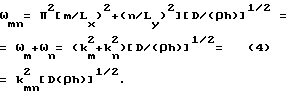
Значение kn= nπ/Ly, km= mπ/Lx, k
где ωгр - граничная частота пластины.
k
Учитывая, что kmn= ωmn/Cи, где Cи - скорость изгибной волны в материале пластины на частоте ωkn, для пластины получаем дисперсионное уравнение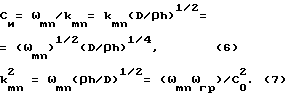
С физической точки зрения разложение в ряд (3) означает, что реальная механоакустическая система (упругая пластина) дает отклик на внешнее воздействие частоты ω на каждый из бесконечного числа собственных форм колебаний пластины и это бесконечное число откликов с тем или иным весом дает суммарное вынужденное колебание системы. Частоты вынужденных колебаний системы несколько отличаются от собственных частот системы и равны
ωdmn= ωmn(1-2η
Однако учитывая, что величина механических потерь η < 1 для реальных механоакустических систем типа упругих пластин, этим отличием частот вынужденных колебаний от собственных частот можно пренебречь и считать, что ωdmn = ωmn на частотах ниже граничной частоты пластины, равной
ωгр= C
а на частотах выше граничной частоты пластины появляются потери, связанные с излучением звука, и величина η = ηmn становится равной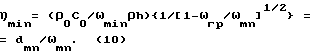
В упругой пластине величина механических потерь реально используемых материалов пластин η на частотах ниже граничной частоты составляет 10-3 - 10-4, т.е. много меньше единицы. На частотах выше граничной частоты пластины она также весьма мала. Исключение составляет небольшая область вблизи граничной частоты пластины. Следовательно, за исключением небольшой области собственных частот пластины вблизи граничной частоты речь идет о высокодобротной многорезонансной системе.
Предположим, что падающая на пластину звуковая волна P(t) - гармоническая и имеет вид P(t) = P0exp(jωt). Тогда, учитывая, что для данной ситуации z > 0 роль источника играют граничные условия, для определения прошедшей через пластину звуковой волны воспользуемся известным уравнением Эйлера
ρ0(∂2u/∂t2) = -∂p/∂z при z = 0. (11)
Теперь, воспользовавшись полученным для пластины уравнением для распределения смещений (3) и уравнением (11), можно получить распределение амплитуд создаваемого звукового давления, вызванного данным распределением нормальных скоростей на плоскости.
Из выражения (3) следует, что при воздействии волны P(t) на пластине образуется поле нормальных смещений, а следовательно, и поле нормальных скоростей. Это ведет к тому, что при колебаниях некоторых собственных форм пластины с частотой возбуждения ω по обе стороны пластины возникнут плоские звуковые волны частоты ω , а при колебании других собственных форм пластины образуются стоячие волны.
Рассмотрим колебание пластины на одной из собственных форм, т.е. один из членов бесконечной суммы (3)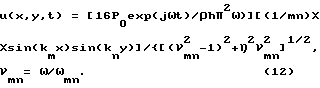
Выражение (10) описывает высокодобротное колебание пластины с ярко выраженными резонансными свойствами, определяемыми членом в фигурных скобках. Фактически выражение (12) означает, что при гармоническом воздействии частоты ω отклик системы (пластины) возможен только на собственной частоте пластины ωmn, расположенной вблизи частоты воздействия. Подобное распределение смещений на пластине приведет к излучению плоских звуковых волн или к созданию неоднородных стоячих волн, быстро убывающих по амплитуде при удалении от плоскости пластины по оси Z на длине изгибной волны в материале пластины. Тот или иной результат (плоские волны или стоячие) будет зависеть от соотношения длины изгибной волны для данной собственной формы колебания пластины на данной частоте с длиной волны излучаемого звука в воздухе. Если волновое число данной моды колебания пластины (kmn < k) меньше волнового числа звука в воздухе, то пластиной излучается плоская бегущая звуковая волна. Если kmn > k, то создается неоднородная стоячая волна. В частотной области это означает, что при частоте воздействия ω, меньшей чем ωгр пластины, излучение будет иметь вид стоячих волн, а при частоте воздействия ω, большей чем ωгр пластины, излучение будет иметь вид плоских бегущих волн.
При ω/C0= k<kmn, т.е. для ω < ωгр , из выражений (12) и (11) можно получить амплитуды стоячих волн. Для амплитуды стоячих волн получаем (с одной стороны пластины)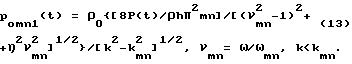
В выражении (11) последний член в квадратных скобках - мнимый, что приводит к экпоненциальному затуханию амплитуд стоячих волн вдоль оси Z на длине изгибной волны в материале пластины. Звуковое излучение в виде стоячих волн при этом описывается выражением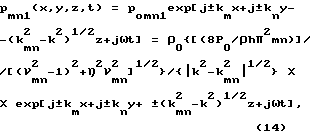
где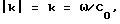 kmn > k, νmn= ω/ωmn.
kmn > k, νmn= ω/ωmn.
Для колебания пластины (11) на основании (12) при гармоническом входном воздействии P(t) = P0exp(jωt) получаем (для ω > ωгр) выражение для амплитуды давления в каждой из восьми плоских звуковых волн (при k = ω/C0> kmn или при ωmn > ωгр), по четыре с каждой стороны пластины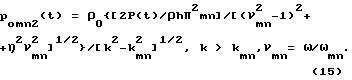
Общее выражение для излучаемых одной из собственных форм пластины при гармоническом входном воздействии принимает вид (при k > kmn или при ωmn > ωгр )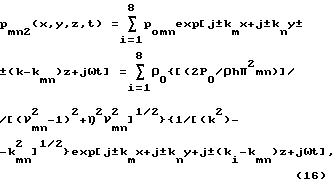
где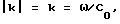 kmn < k, νmn= ω/ωmn.
kmn < k, νmn= ω/ωmn.
Направляющие косинусы этих i-х восьми волн равны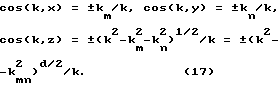
Каждому из восьми векторов ki соответствует одна из восьми комбинаций направляющих косинусов, взятых с положительным или отрицательным знаком.
Из указанных выражений можно получить амплитудно-частотную характеристику, связывающую входное воздействие P(t) и отклик собственной mn-й формы пластины на это воздействие - излучаемую пластиной часть, соответствующую данной форме колебаний, звукового излучения в виде плоских бегущих или стоячих волн. Для этого учтем, что при гармоническом воздействии вида P(t)= Poexp (ωt) отклик системы пластина - звук для каждой формы излучения дается выражением (14) или (15). Поэтому из выражений (14) и (15) следует, что амплитудно-частотная характеристика системы (АЧХ) системы пластина - звук при гармоническом воздействии имеет вид для ω > ωгр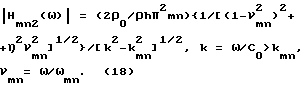
Аналогично для k < Kmn или ω > ωгр получаем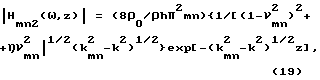
где
k = ω/C0 < kmn, νmn= ω/ωmn.
Звукопрохождение пластины определим как отношение интенсивностей процесса выходного (амплитуды интенсивности излучаемой звуковой волны) и входного (амплитуды интенсивности волны, падающей на пластину) в полосе частот B больше чем ΔB = 10ηωmn.
Необходимо иметь в виду, что на частотах ниже граничной частоты пластины это величина скалярная и от направления не зависит. Напротив, на частотах, выше граничной, предстоит "совмещать пространство и время", так как усреднение по частоте и сложение разнонаправленных звуковых волн вещь необычная, но в акустике встречается практически в любом учебнике. Причем считаем, что это настолько очевидно, что об этом нечего и говорить. Правда, и структура акустических полей в этих учебниках оказывается гораздо проще наблюдаемой на практике.
Предлагается раздельно оценивать коэффициенты звукопрохождения для пластины на частотах, выше граничной частоты пластины, и на частотах, ниже этой частоты. При этом с достаточной строгостью имеем право раздельно складывать скалярные величины на частотах, ниже граничной частоты, и складывать величины z-составляющих для векторных величин (или усреднять их в некоторой полосе частот) для частот, выше граничной частоты пластины.
Трудность заключается в том, что при широкополосном воздействии с полосой частот воздействия, включающей граничную частоту звукоизолирующей панели, добротность некоторых собственных форм колебаний пластины, собственные частоты которых расположены вблизи граничной частоты пластины, становится очень мала. Это приводит к тому, что полоса частот отклика этих форм становится очень широкой, сравнимой с полосой частот воздействия. Кроме того, они влияют на колебания других мод пластины и оказывают на них демпфирующее влияние.
Вторая особенность широкополосного возбуждения пластины с граничной частотой в полосе воздействия - отсутствие полосы "непрозрачности" пластины (в отличие от гармонического воздействия). Это связано со сдвигом частот, лежащих выше граничной частоты пластины (формула (8)), в сторону низких частот. При этом в полосе "непрозрачности" пластины оказываются колебания собственных форм пластины с более высоко расположенными собственными частотами. Фактически полоса "непрозрачности" пластины при подобном широкополосном воздействии превращается в "окно", через которое широкополосный сигнал достаточно хорошо проходит, т.е. открывается некий широкополосный фильтр пропускания входного сигнала.
Указанные особенности излучения звука пластиной при широкополосном ее возбуждении акустическим шумом приводят к необходимости раздельной оценки коэффициентов звукопрохождения для частот воздействия, выше граничной частоты пластины и ниже этой частоты.
Тогда для интегрального коэффициента звукопрохождения (в отличие от классического выражения (2.1) получаем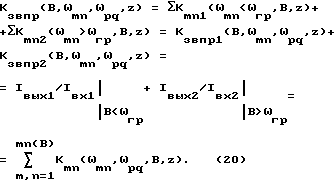
Оценка (20) интегрального коэффициента звукопрохождения пластины зависит от параметров пластины (распределения собственных частот пластины ωmn в полосе B), полосы частот B входного воздействия, величины граничной частоты пластины и соотношения этой частоты и полосы частот входного воздействия. Полоса частот входного воздействия должна разбиваться на часть полосы, лежащую ниже граничной частоты пластины, и часть, расположенную выше граничной частоты пластины. При этом имеем право на усреднение эффекта воздействия в некоторой полосе частот, так как оперируем с однородными величинами. Кроме того, необходимо рассматривать отдельно три ситуации излучения, о которых говорилось выше.
Для оценки коэффициента звукопрохождения упругой пластины, возбуждаемой воздействием в полосе частот B, рассмотрим еще раз выражения (19) и (18). На их основе можно рассчитать средний квадрат звукового процесса, излучаемого пластиной при воздействии на нее широкополосного звукового процесса, с шириной частотной полосы, равной B рад. Для этого учтем, что при стационарном воздействии широкополосного шума на резонансную систему типа (19) или (18), на которую воздействует стационарный звуковой шум со спектральной плотностью Go в полосе частот B > ΔB, для которой
(1-6ηmn)ωmn<ΔB<(1+6ηmn)ωmn, (21)
на ее выходе образуется стационарный случайный процесс, средний квадрат которого равен для излучающих форм пластины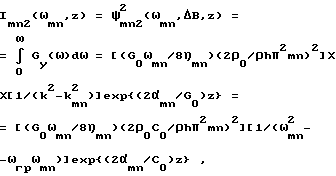 (22)
(22)
и для неизлучающих форм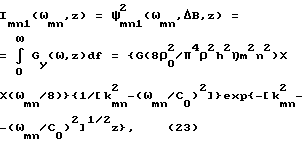
Для оценки полной интенсивности выходного процесса, излучаемого пластиной на частотах, ниже граничной частоты ωгр , необходимо взять конечную сумму выражений (23) по всем собственным частотам пластины от ωmn= ω11 (m,n= 1) до ωpq= ωгр. Для оценки полной интенсивности выходного процесса, излучаемого пластиной на частотах, выше граничной частоты ωгр, необходимо оценить величину бесконечной суммы выражений (22) по всем собственным частотам пластины от ωmn= ωгр до ωmn, стремящейся к бесконечности
Если входной процесс (стационарный шум) имеет интенсивность, постоянную в полосе частот B и равную G(ω) = G0, т.е. при B = ω2-ω1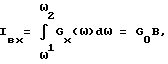
где ω1 и ω2>ωгр
то выходной процесс будет иметь интенсивность звукового процесса в полосе частот B > ωгр для излучения в виде бегущих волн (ωmn>ωгр,ω1,ω2>ωгр)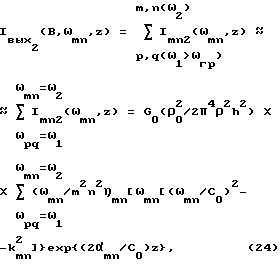
а для излучения в виде стоячих волн выходной процесс будет иметь интенсивность звукового процесса в полосе частот ω1 - ω2 рад при ω1,ω2<ωгр :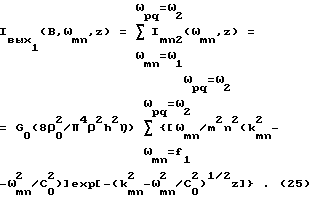
Третий случай излучения, когда полоса частот воздействия включает граничную частоту пластины, на основе вышеуказанных факторов приводит к следующему распределению выходного излучения пластины для B = ω2-ω1 при 0<ω1<ωгр и ω2>ωгр::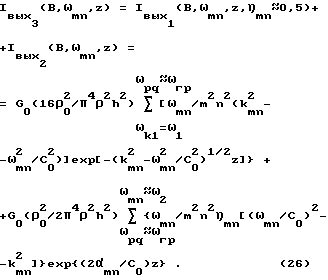
Теперь попробуем оценить реальную величину звукопрохождения (обратная величина звукопрохождения есть звукоизоляция) при стационарном воздействии на пластину случайного звукового процесса со спектральной плотностью G ω = G - постоянной в полосе частот B для указанных трех случаев. Звукопрохождение пластины определим как отношение интенсивностей процесса выходного (амплитуды интенсивности излучаемой звуковой волны) и входного (амплитуды интенсивности волны, падающей на пластину) в полосе частот B больше чем ΔB = 10ηωmn описываемого выражением (19). Тогда для интегрального коэффициента звукопрохождения для третьего случая получаем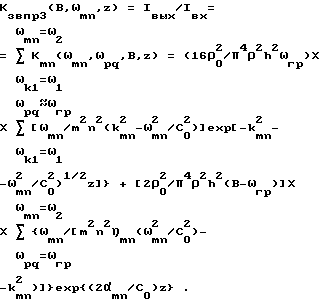
Из выражения (27) следует, что при совпадении полосы частот воздействия с граничной частотой пластины, коэффициент звукопрохождения пластины всегда будет весьма велик, хотя и конечен, т.е. пластина для звукоизоляции стационарных шумов будет малоэффективна. Из выражения (25) следует, что для того чтобы панель эффективно изолировала входное воздействие, полоса частот входного воздействия ω∈B = ω2-ω1 была или ниже граничной частоты пластины ωгр (27)
или выше ее.
Как видно из выражения (27), оно существенно отличается от классического закона "массы", описываемого выражением (2.1). Сумма (25) состоит из двух основных частей. Для частот, ниже граничной для пластины, т.е. для собственных частот ωmn , меньших по величине ωгр , под знаком суммы получаем суммирование выходов неизлучающих форм, т.е. суммируются амплитуды стоячих волн с частотами, близкими к резонансным частотам пластины. Вторая часть ряда (27) включает в себя члены с выходами излучающих форм, для которых ωmn > ωгр , и для каждой собственной излучающей формы и частоты получаем восемь звуковых волн одинаковой частоты и амплитуды и различно ориентированных в пространстве по отношению к плоскости пластины ωmn ≤ B . В выражении (27) над знаком второй суммы стоит индекс последней излучающей формы, для которой для данных параметров пластины выполняется условие kmn < k, где k - волновое число излучаемой звуковой волны.
Выражение (27) необходимо уточнить, так как рассматривали амплитуду только одной из возникающих четырех звуковых волн со стороны пластины, противоположной стороне, на которую звуковая волна падает. Таким образом, из детального рассмотрения механизма звукопрохождения реальной упругой пластины следует, что коэффициент звукопрохождения пластины является величиной, зависящей от ориентации пластины и измерительного микрофона в пространстве. В результате получаем полное выражение для оценки интегрального коэффициента звукопрохождения упругой пластины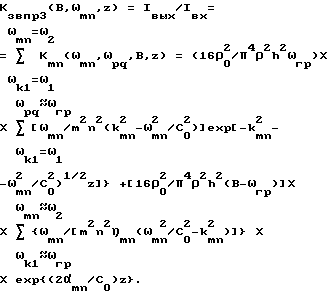 (28)
(28)
Для оценки эффективности звукоизоляции пластины в полосе частот B необходимо взять величину, обратную интегральному коэффициенту звукопрохождения.
Для большей наглядности полученных результатов преобразуем выражение (26) к некоторому другому виду. Для этого учтем, что k
С учетом этих соотношений из (26) получаем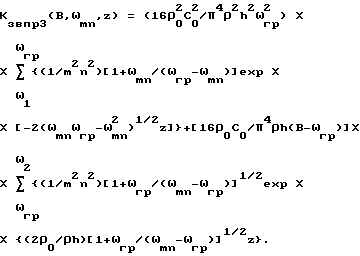 (29)
(29)
Из аналогичного рассмотрения первого и второго случая следует, что если полоса частот входного воздействия B выше граничной частоты пластины, то оценки коэффициента звукопрохождения необходимо пользоваться выражением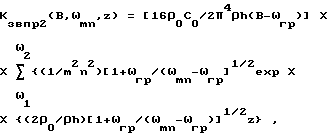 (30)
(30)
а если полоса частот входного воздействия ниже граничной частоты пластины, то необходимо использовать выражение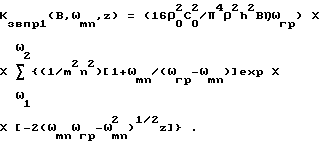 (31)
(31)
Проведем анализ полученных выражений (30) и (31). Рассмотрим выражение (30), которое при B ≫ ωгр, ωm ≫ ωгр и при z≈ 0 преобразуется к виду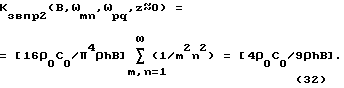
Напомним, что классический аналог-выражение (2.1) имеет вид
Ki(B) = ρ0C0/2ρhB.
Выражение (30) почти точно (отличие составляет 1/9 или менее 10%) совпадает с классическим выражением для интегрального коэффициента звукопрохождения, полученного на основе закона массы". Следовательно, закон "массы" - выражение (2.1) является частным случаем полученного более общего выражения (26). Рассмотрим выражение (31), которое при B < ωгр,, ωmn < ωгр и при z≈0 преобразуется к виду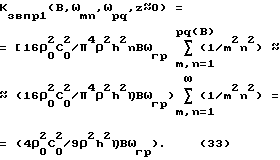
Последнее выражение можно сравнить с выражением (32). Это можно сделать при рассмотрении следующей задачи. Предположим, что заданы частотная полоса B входного воздействия на звукоизолирующую панель и ее нижняя и верхняя границы частотного диапазона ω1 и ω2. Как показано выше, эффект звукоизоляции будет достигнут в двух случаях: в первом - полоса входного воздействия должна быть ниже граничной частоты звукоизолирующей панели, а во втором - полоса входного воздействия должна быть выше граничной частоты панели. Во всех остальных случаях звукоизоляция будет для данной панели и для данного входного воздействия неэффективной. Следовательно, для решения поставленной задачи - локализации входного воздействия с помощью звукоизолирующей панели - есть два пути. В первом случае можно использовать тонкую пластину, граничная частота которой выше верхней границы частотной полосы входного воздействия (в два раза - оптимально). Во втором случае необходимо использовать толстую массивную панель, граничная частота которой ниже нижней границы частотной полосы входного воздействия.
На основании выражений (32) и (33) можно сравнить два этих подхода. Для этого будем полагать, что в результате расчетов получили равные коэффициенты звукопрохождения (или эффективности звукоизоляции) для обоих подходов, т.е. получили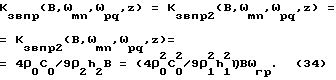
Из последнего выражения легко получить сравнение одинаково эффективных (по звукоизоляции) панелей с разной толщиной и плотностью. Фактически на основании этого выражения можно проводить оценки параметров звукоизолирующих конструкций при использовании двух наиболее оптимальных методов. Естественно, что первый подход позволяет не только снизить интенсивность входного процесса, но и локализовать его в определенной части пространства (за счет влияния экспоненциального множителя в выражении (27)), второй способ не позволяет этого сделать, так как амплитуда бегущих волн (т.е. излучение пластины) будет нарастать при удалении от пластины (за счет экспоненциального множителя в выражении (27)), но позволяет эффективно снизить мощность излучения пластины за счет ее толщины.
Приведем еще одно приближенное, но достаточно точное по акустическим меркам выражение для интегрального коэффициента звукопрохождения упругой звукоизолирующей пластины, шарнирно закрепленной по периметру и имеющей толщину h и линейные размеры Lx и Ly, при невырожденных линейных размерах пластины, когда величины Lx и Ly не слишком различны. При этом для пластины верны некоторые приближенные выражения: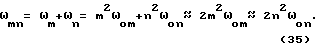
Заметим, что для пластины квадратной формы выражение (35) является точным. Тогда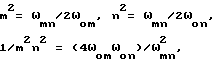
где
ωom= π2C
следовательно,
1/m2n2 = 4π4C
С учетом этих соотношений из (29) - (31) получаем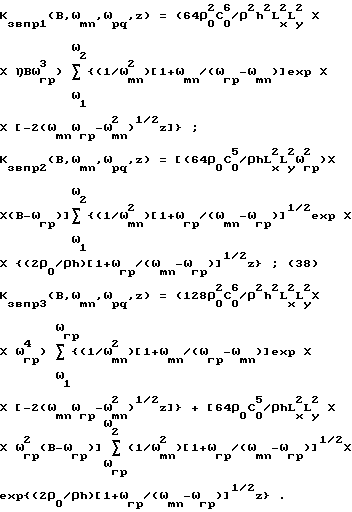
Уравнения (37) - (39) являются аналогами закона "массы" (2.1), но гораздо точнее отражают реальные процессы звукопреобразования реальных звукоизолирующих конструкций. Эффективность звукоизоляции пластины определяется как
Эзи = 20lg[1/Ki(B)],
где
Ki(B) определяется для каждого их трех случаев по формулам (37) - (39) и B определяется также как полоса частот (f2-f1) воздействующего на пластину плотности ρ и толщины h звукового шума;
ρ0 - плотность воздуха;
Co - скорость звука в воздухе.
Методика реализации заявляемого способа оценки эффективности звукоизоляции закрепленной по периметру упругой прямоугольной пластины в условиях стационарных широкополосных или узкополосных шумовых воздействий основана на измерениях линейных размеров и толщины пластины, экспериментальном определении собственных частот изгибных колебаний пластины и ее жесткости D. Далее для заданного (или определяемого) расстояния z от пластины определяются конкретные значения коэффициентов звукопрохождения для данного звукового воздействия по описанным в способе формулам, а затем и искомой величины эффективности звукоизоляции пластины.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ ОПРЕДЕЛЕНИЯ КОЭФФИЦИЕНТА ЗВУКОПРОХОЖДЕНИЯ ДЛЯ ЗАКРЕПЛЕННОЙ ПО ПЕРИМЕТРУ УПРУГОЙ ПРЯМОУГОЛЬНОЙ ПЛАСТИНЫ В УСЛОВИЯХ СТАЦИОНАРНОГО ГАРМОНИЧЕСКОГО ЗВУКОВОГО ВОЗДЕЙСТВИЯ | 1996 |
|
RU2111553C1 |
| Звукоизоляционное воздухопроницаемое ограждение | 1989 |
|
SU1768726A1 |
| СПОСОБ УПРАВЛЕНИЯ ПОВЕДЕНИЕМ МОРСКИХ МЛЕКОПИТАЮЩИХ ПРИ ПРОМЫСЛЕ РЫБЫ | 2004 |
|
RU2276386C1 |
| УСТРОЙСТВО ДЛЯ ОПТИЧЕСКОГО СМЕШЕНИЯ СИГНАЛОВ | 1995 |
|
RU2107997C1 |
| Низкошумное техническое помещение | 2017 |
|
RU2670309C2 |
| ВИБРОДЕМПФИРУЮЩИЙ ЗВУКОИЗОЛИРУЮЩИЙ ЭЛАСТОМЕРНЫЙ МАТЕРИАЛ | 2015 |
|
RU2595274C1 |
| СПОСОБ ВОЗДЕЙСТВИЯ НА ПРИЕМО-ПЕРЕДАЮЩЕЕ ЭЛЕКТРОННОЕ УСТРОЙСТВО | 2013 |
|
RU2533682C2 |
| Шумозащитный экран | 2016 |
|
RU2647542C2 |
| СПОСОБ ИЗМЕРЕНИЯ ХАРАКТЕРИСТИКИ НАПРАВЛЕННОСТИ ГИДРОАКУСТИЧЕСКОЙ АНТЕННЫ В УСЛОВИЯХ РАСПРОСТРАНЕНИЯ МНОГОЛУЧЕВОГО СИГНАЛА | 2007 |
|
RU2356060C1 |
| ПЛАВАЮЩАЯ КРЫШКА УСТАНОВКИ ДЛЯ УЛЬТРАЗВУКОВОЙ ОЧИСТКИ (ВАРИАНТЫ) | 1992 |
|
RU2005568C1 |
Использование: для определения интегральной (в полосе частот) эффективности звукоизоляции конструкций, предназначенных для локализации акустических полей. Сущность изобретения: эффективность звукоизоляции пластины оценивают по интегральному коэффициенту звукопрохождения. Для определения последнего определяют линейные размеры, собственные частоты колебаний и граничную частоту пластины. Эти параметры, а также толщину и жесткость пластины, плотность и коэффициент механических потерь материала пластины, плотность воздуха и скорость звука в воздухе используют для вычисления интегрального коэффициента звукопрохождения на заданном расстоянии от плоскости пластины при определенной полосе частот шумового воздействия. Предложены три разные формулы для вычисления упомянутого коэффициента для различных полос частот, лежащих ниже и выше граничной частоты пластины и включающей граничную частоту. Изобретение позволяет исключить недопустимо большие расхождения между экспериментально и аналитически определяемыми значениями коэффициента звукопрохождения. 1 ил.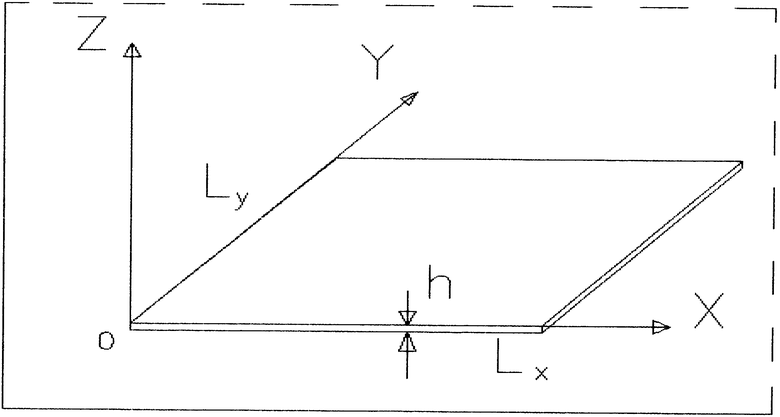
Способ оценки эффективности звукоизоляции закрепленной по периметру упругой прямоугольной пластины в условиях стационарных широко- или узкополосных шумовых воздействий, основанный на законе массы, по которому эффективность звукоизоляции Эз и определяют по формуле
Эз и = 20lg[1Ki(B)],
где Ki(B) - интегральный коэффициент звукопрохождения пластины, рассчитываемый с учетом полосы частот B = ω2-ω1 шумового воздействия, плотности ρ материала пластины и толщины h пластины, отличающийся тем, что определяют линейные размеры Lx и Ly пластины жесткостью D, а также собственные частоты ωmn колебаний пластины и граничную частоту ωгр пластины, а интегральный коэффициент звукопрохождения Ki(B) пластины на расстоянии z от пластины определяют при полосе частот B, лежащей ниже граничной частоты пластины, по формуле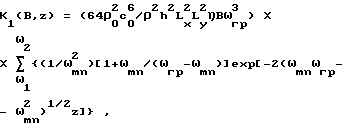
при полосе B частот, лежащей выше граничной частоты пластины, по формуле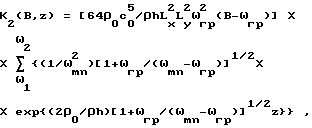
и при полосе B частот, включающей граничную частоту пластины, по формуле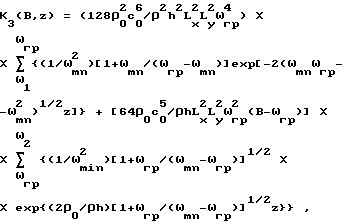
где ρ0 - плотность воздуха;
c0 - скорость звука в воздухе;
η - коэффициент механических потерь материала пластины;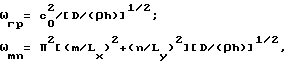 m, n = 1, 2, ... .
m, n = 1, 2, ... .
| Печь для непрерывного получения сернистого натрия | 1921 |
|
SU1A1 |
| Исакович М.А | |||
| Общая акустика | |||
| - М.: Наука, 1973, с | |||
| Подъемник для выгрузки и нагрузки барж сплавными бревнами, дровами и т.п. | 1919 |
|
SU149A1 |
| Аппарат для очищения воды при помощи химических реактивов | 1917 |
|
SU2A1 |
| Скучик Е | |||
| Основы акустики | |||
| Т | |||
| Аппарат для очищения воды при помощи химических реактивов | 1917 |
|
SU2A1 |
| иностр | |||
| лит., 1959, с | |||
| Пружинная погонялка к ткацким станкам | 1923 |
|
SU186A1 |
Авторы
Даты
1998-05-20—Публикация
1996-10-10—Подача