Изобретение относится к физической акустике и может использоваться для определения частотной зависимости коэффициента звукопрохождения упругих пластин - звукоизолирующих перегородок и кожухов прямоугольной формы при воздействии на них стационарных полигармонических или гармонических звуковых полей.
Известен способ определения коэффициента звукопрохождения для звукоизолирующих конструкций, основанный на законе массы (Исакович М.А. Общая акустика. - М.: Наука, 1973, с. 149). Согласно этому закону коэффициент звукопрохождения пластины с поверхностной плотностью m = ρh определяется формулой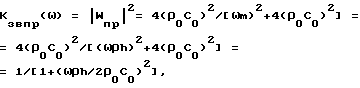
где
ω - круговая частота падающей на пластину звуковой волны; ρ0 - плотность воздуха; C0 - скорость звука в воздухе; ρ - плотность материала пластины; C - скорость звука в материале пластины; h - толщина пластины; m = ρh - масса единицы площади пластины.
Однако, измеряемые на практике частотные зависимости коэффициента звукопрохождения реальных перегородок существенно отличаются от данного в формуле. Они отличаются наличием множества минимумов и максимумов, а также частотных областей полного звукопрохождения. На фиг. 1 представлена частотная зависимость коэффициента звукопрохождения реальной пластины, измеренная при воздействии гармонических звуковых волн на расстоянии 1 м от пластины, и частотная зависимость коэффициента звукопрохождения этой же пластины, рассчитанная на основе указанной выше формулы, которая в свою очередь получена из так называемого закона массы. Как видно из фиг. 1, реально измеренная характеристика существенно отличается от расчетной. В большинстве публикаций по данному вопросу несовпадение теории с практикой списывается на ошибки экспериментов. Таков обычно итог классического подхода к проблеме звукоизоляции звукоизолирующей панели массы m=ρh при нормальном падении на нее звуковой волны амплитуды P0 с частотой ω. Расхождения в величине звукоизоляции реальной панели и теоретического расчета на 200-300% и более - обычное явление.
Еще один аспект противоречия классической теории звукоизоляции и практики - закон массы исключает возможность волнового совпадения при нормальном падении звуковой волны на преграду.
Целью изобретения является исключение подобных недопустимо больших расхождений практических измерений и теории.
Заявляемый способ определения коэффициента звукопрохождения для закрепленной по периметру упругой прямоугольной пластины в условиях стационарного гармонического звукового воздействия, основанный на законе массы, по которому коэффициент звукопрохождения рассчитывают с учетом круговой частоты ω падающей на пластину звуковой волны, плотности ρ материала пластины и толщины h пластины, отличающийся тем, что определяют линейные размеры Lx и Ly пластины и собственные частоты ωmn нормальных колебаний пластины, коэффициент звукопрохождения Kзвпр (ω,z) на расстоянии z от плоскости пластины определяют для частот ω, лежащих ниже граничной частоты ωгp пластины, по формуле: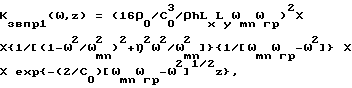
где
ρ0 - плотность воздуха; C0 - скорость звука в воздухе;
ωmn= π2[(m/Lx)2+(n/Ly)2][D(ρh)1/2; m, n = 1,2,3,...;
D - цилиндрическая жесткость пластины; ωгр= C
а для частот ω, лежащих выше частоты ωL > ωгр, равной
ωL= ωгр{1/2+[1/4+(ρ0C0/ρhωгр)2]1/2},
по формуле:
при этом для частот ω, для которых ωгр < ω < ωL, коэффициент звукопрохождения полагают равным нулю.
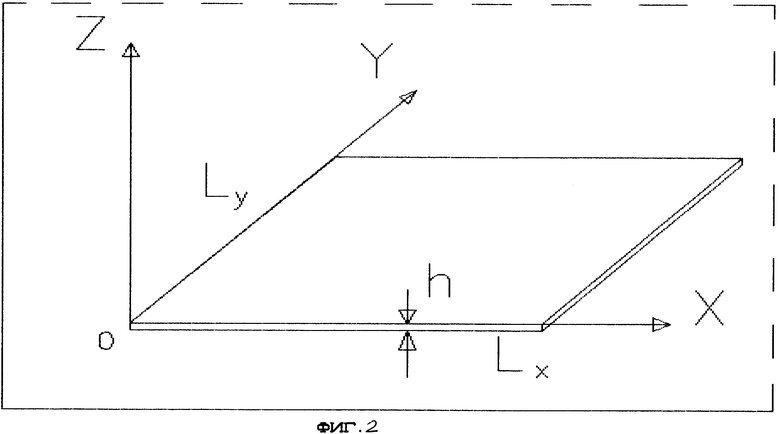
Расположим пластину по отношению к системе координат в соответствии с фиг. 2. Плотность пластины совпадает с плоскостью z = 0.
Если обозначить поперечное смещение точек пластины как u(x,y,t), то для поперечных отклонений от невозмущенного положения точек пластины получают гиперболическое дифференциальное уравнение в частных производных четвертого порядка (первая краевая задача):
где граничные условия при z = 0 задаются выражениями
0 ≤ x ≤ Lx, 0 ≤ y ≤ Ly, 0 < t < ∞ ,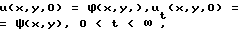
u(x= 0, t) = u(x=Lx, t) = u(y=0, t) = u(y=Ly, t) = uxx(x=0, t) = uxx(x= LX, t) = uxx(y=0, t) = uxx(y=Ly, t) = uyy (x=0, t) = uyy(x=Lx, t) = uyy(y=0, t) = uyy(y=Ly, t) = 0, 0< t < ∞ . II
Указанные граничные условия определяют шарнирное закрепление пластины по периметру, D - цилиндрическая жесткость пластины; h - толщина пластины; ρ - плотность пластины; η - коэффициент механических потерь в материале пластины, ρh = m, где m - поверхностная плотность пластины.
В уравнении (I) предположено, что силы неупругого сопротивления пропорциональны деформации.
Решим уравнение (I) с граничными условиями (II), полагая падающую звуковую волну гармонической частоты ω, амплитуда которой P0 не зависит от координат x, y, z, т.е. падающая волна плоская вида
P(t,x,y,z) = P(t,z) = P0exp[j(ωt+kz)],
используя метод разложения функций в ряд по собственным формам колебаний пластины. В соответствии с этим методом форму колебаний пластины можно представить в виде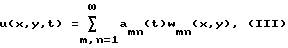
где коэффициенты amn(t) = Amnexp(jωt), а Wmn(x, y) - собственные формы колебаний, удовлетворяющие однородному уравнению
Функцию P (x, y,t) (звуковое давление падающей волны) также разложим в ряд по собственным формам колебаний пластины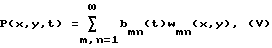
где коэффициенты bmn(t) = Bmnexp(jωt), а wmn(x, y) - те же, что и в уравнении (III).
Величину Bmn найдем из следующих соображений. Умножим обе части выражения P(x,y)
на собственную форму колебаний wmn(x, y) и проинтегрируем их по площади пластины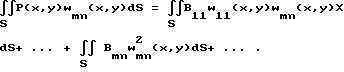
Из условия ортогональности собственных форм колебаний следует, что при mn ≠ if имеем
Следовательно,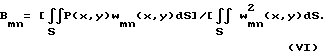
Амплитудная функция wmn(x, y), называемая собственной формой колебаний пластины, определяется выражением (VI). Учитывая ортогональность собственных функций и независимость колебаний пластины на собственных частотах друг от друга (принцип суперпозиции) для колебаний пластины, описываемых собственной функцией (формой) wmn(x, y) на собственных частотах ωkn, из выражений (III) и (IV) можно получить выражение для определения собственных частот колебаний пластины. Для этого учтем, что при колебаниях пластины на частоте ωmn в выражении (III) все члены бесконечного ряда, за исключением члена
u0(x,y,t) = Amnwmn(x,y)exp(jωmnt). (VII)
обращаются в нуль.
Подставляя выражение (VII) в уравнение движения (IV), получаем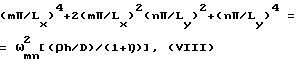
откуда получаем выражение для определения собственных частот нормальных колебаний пластины
учитывая, что η ≪ 1, полагаем, что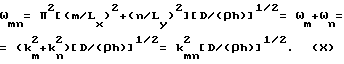
Кроме того, λn= 2π/kn(n=1,2,...),λm= 2π/km(m=1,2,...,), граничная частота пластины, равная ωгр= C
граничная частота пластины, равная ωгр= C
Следовательно,
k
Учитывая, что kmn= ωmn/Cи, где Cи - скорость изгибной волны в материале пластины на частоте ωkn, для пластины получаем дисперсионное уравнение (оно следует из уравнения (VIII),
k
Так как из условий краевой задачи (II) (шарнирное закрепление) для wmn(x, y) имеем
wmn(x, y) = wm(x)wn(y) = sin(kmx)sin(kny). (XIV)
Для P(x, y) = P0 из (V) и (VI) получаем
Из выражений (V) и (XV) для разложения падающей звуковой волны по собственным функциям пластины получаем
Подставив (III) и (V) в уравнение (I) вынужденных колебаний, после преобразований получим
Приравнивая коэффициенты при одинаковых wmn(x, y) справа и слева, получим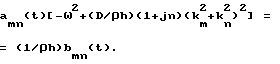
Учитывая, что k
amn(t) = bmn(t)/[(ρh)(ω
Подставив выражение (X) в разложение (XVI), получим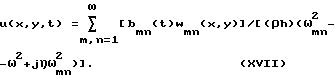
Учитывая, что bmn(t) = Bmnexp(jωt), а величина Bmn определена в выражении (XV), для bmn(t) получаем
bmn(t) = Bmnexp(jωt) = (16P0/mnπ2)exp(jωt).
Тогда из (VII) и (X) получаем
где νmn= ω/ωmn, wmn(x, y) = wm(x)wn(y) = sin(kmx)sin(kny).
С физической точки зрения разложение в ряд (XVIII) означает, что реальная механоакустическая система (упругая пластина) дает отклик на внешнее воздействие частоты ω на каждой из бесконечного числа собственных форм колебаний пластины и это бесконечное число откликов, с тем или иным весом дает суммарное вынужденное колебание системы. Частоты (IX) колебаний системы несколько отличаются от собственных частот недемпфированной системы (X) и равны
ωdmn= ωmn(1-2η2)1/2, (XIX)
однако, учитывая, что величина механических потерь η ≪ 1 для реальных механоакустических систем типа упругих пластин, этим отличием частот вынужденных колебаний от собственных частот можно пренебречь и считать, что ωdmn= ωmn.
В упругой пластине величина механических потерь реально используемых материалов пластин составляет 10-3 - 10-4, т.е. много меньше единицы. Следовательно, речь идет о высокодобротных многорезонансных системах
Вынужденные колебания пластины при стационарном гармоническом воздействии.
Предположим, что падающая на пластину звуковая волна P(t) - гармоническая и имеет вид P(t) = P0exp(jωt). Тогда, пользуясь уравнением Эйлера /1/, для данного случая получаем соотношение
ρ0(∂2u/∂t2) = -∂p/∂z при z = 0. (XX)
Теперь, воспользовавшись полученным для пластины уравнением для распределения смещений (XVIII) и уравнением (XX), можно получить распределение амплитуд создаваемого звукового давления, вызванного данным распределением нормальных скоростей на плоскости.
Из выражения (XVIII) следует, что при воздействии волны P(t) на пластине образуется поле нормальных смещений, а, следовательно, и поле нормальных скоростей. Это приведет к тому, что при колебаниях некоторых собственных форм пластины с частотой возбуждения ω по обе стороны пластины возникнут плоские звуковые волны частоты ω, а при колебаниях других собственных форм пластины образуются стоячие волны.
Рассмотрим колебание пластины на одной из собственных форм, т.е. один из членов бесконечной суммы (XVIII)
Выражение (XXI) описывает высокодобротное колебание пластины, с ярко выраженными резонансными свойствами, определяемыми членом в фигурных скобках. Фактически выражение (XXI) означает, что при гармоническом воздействии частоты ω отклик системы (пластины) возможен только на собственной частоте пластины ωmn, расположенной вблизи частоты воздействия. Подобное распределение смещений на пластине приведет к излучению плоских звуковых волн или к созданию неоднородных стоячих волн, быстро убывающих по амплитуде при удалении от плоскости пластины по оси Z на длине изгибной волны в материале пластины. Тот или иной результат (плоские волны или стоячие волны) будет зависеть от соотношения длины изгибной волны для данной собственной формы колебания пластины на данной частоте с длиной волны излучаемого звука в воздухе. Если волновое число данной моды колебания пластины (kmn < k) меньше волнового числа звука в воздухе, то пластиной излучается плоская бегущая звуковая волна. Если kmn > k, то создается неоднородная стоячая волна. В частотной области это означает, что при частоте воздействия ω,, меньшей чем ωгр пластины, излучение будет иметь вид стоячих волн, а при частоте воздействия ω, большей, чем ωгр пластины, излучение будет иметь вид плоских бегущих волн. Величина граничной частоты пластины определяется на основании дисперсионного уравнения пластины (XII) из условия равенства на этой частоте скорости изгибной волны в материале пластины скорости звука в окружающей среде, т.е. скорости звука в воздухе.
При ω/C0= k < kmn, т.е. для ω < ωгр из выражений (XX) и (XXI) можно получить амплитуды стоячих волн. Для амплитуды стоячих волн получаем (с одной стороны пластины)
В выражении (XXII) последний член в квадратных скобках - мнимый, что приводит к экспоненциальному затуханию амплитуд стоячих волн вдоль оси Z на длине изгибной волны в материале пластины.
Звуковое излучение в виде стоячих волн при этом описывается выражением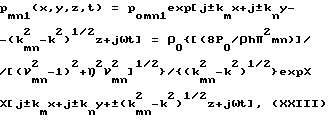
где  .
.
Следовательно, для АЧХ (амплитудно-частотной характеристики) звукопреобразования пластины на частотах ниже граничной получаем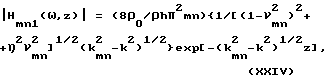
где k = ω/C0< kmn,νmn= /ωmn .
Из выражения (XXIV) следует, что пространственное распределение амплитуды стоячих волн (на частотах ниже граничной частоты пластины) зависит от точки наблюдения относительно пластины и амплитуды стоячих волн быстро убывают при удалении от пластины вдоль оси Z.
Для колебания пластины (XXI) на основании (XX) при гармоническом входном воздействии P(t) = P0exp(jωt) получаем для частот воздействия выше граничной частоты пластины (для ω > ωгр) выражение для амплитуды давления в каждой из 8 плоских звуковых волн (при k = ω/C0>kmn или при ωmn > ωгр ), по четыре с каждой стороны пластины
Общее выражение для излучаемых одной из собственных форм пластины при гармоническом входном воздействии принимает вид (при k > kmn или при ωmn > ωгр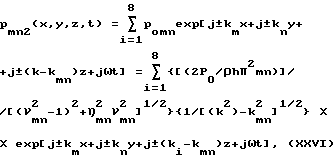
где .
.
Направляющие косинусы этих i-x восьми волн равны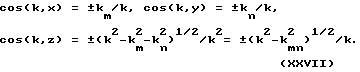
Каждому из 8 векторов ki соответствует одна из восьми комбинаций направляющих косинусов, взятых с положительным или отрицательным знаком.
Однако, для бегущих волн, описываемых выражением (XXVI), необходимо сделать существенное уточнение. Дело в том, что излучение энергии пластиной приводит к диссипации энергии пластины за счет излучения, что приводит к появлению мнимой части у волнового числа данной излучающей формы пластины. Это приводит к образованию волн с комплексной частотой (Исакович М.А. Общая акустика. -М.: Наука, 1973, с.102) и комплексным волновым числом той же комплексности, а именно с волновым числом kmnk и частоты ωmnk :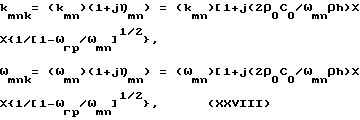
при
ωmn > ωгр .
В вещественном представлении эта волна будет иметь вид
где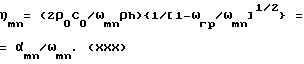
Фактически, речь идет о том, что при частотах воздействия выше граничной частоты пластины диссипативный член η в уравнении (IX) становится благодаря изучению звука пластиной настолько велик, что приближенное выражение (X) становится неверным без учета влияния этого члена, т.е. выражения (XXX).
При стационарном воздействии временной множитель в экспоненте выражения (XXIX) быстро затухает и обращается в единицу, а вот пространственный множитель определяет распределение амплитуд звукового давления и при стационарном воздействии. Из выражения (XXIX) следует, что благодаря комплексности волнового числа пластины kmn на частотах выше граничной частоты пластины ωгр величина амплитуды волны (XXIX) нарастает при удалении точки наблюдения от излучающей пластины вдоль оси Z.
Общее выражение (XXVI) для излучаемых одной из собственных форм пластины при гармоническом входном воздействии с учетом комплексности волнового числа пластины (XXVIII) принимает вид
(при k > kmn или при ωmn > ωгр)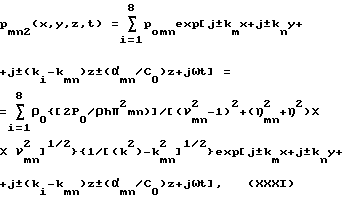
где .
.
При стационарном гармоническом воздействии рассмотренное явление проявляет себя в том, что в уравнении (I) величина η меняется на величину (η2+η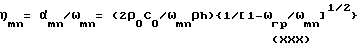
при ωmn > ωгр .
В звуковом диапазоне частот при ωmn > ωгр
ηmn ≫ η
и влияние выражения (XXX) на излучение звука пластиной весьма значительно. И только при очень высоких частотах выражение (XXX) стремится к нулю.
Из указанных выражений можно получить амплитудно-частотную характеристику, связывающую входное воздействие P(t) и отклик собственной mn-ой формы пластины на это воздействие - изучаемую пластиной часть, соответствующую данной форме колебаний, звукового излучения в виде плоских бегущих или стоячих волн. Для этого учтем, что при гармоническом воздействии вида P(t) = P0exp(ωt) отклик системы пластина-звук для каждой формы излучения дается выражением (XXIII) или (XXXI). Поэтому из выражений (XXIII) и (XXXI) следует, что АЧХ (амплитудно-частотная характеристика) системы пластина-звук при гармоническом воздействии имеет вид для ω > ωгр (для одной из восьми звуковых волн, направления которых определяются выражением (XXXI), а амплитуды равны и определяются выражением (XXV) при z≈0):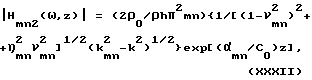
где
k = ω/C0>kmn, νmn= ω/ωmn.
Физическое обоснование процесса звукопреобразования пластины на частотах выше граничной частоты пластины.
Представляется интересным рассмотреть поставленный выше вопрос, связанный с изучением звука изгибно колеблющейся пластиной при возбуждении ее звуковой волной, частота которой выше граничной частоты fгр пластины. Речь идет о потерях при свободных колебаниях пластины, связанных с излучением звука.
Из выражений (XXII) и (XXIII) следует, что на частотах воздействующей волны ниже частоты волнового совпадения fгр (ωгр) пластина не излучает звука, в окружающем пространстве создается стоячая волна. При этих условиях пластина может весьма долго колебаться, время ее колебаний определяется коэффициентом механических потерь η (см. уравнение (I)). Например, хорошо известный прибор для настройки музыкальных инструментов - камертон - может совершать свои колебания в течение нескольких минут. Однако это всегда колебания низких частот (f < fгр) и излучение в ближней зоне (стоячие волны в непосредственной близости от прибора).
Совсем иначе ведут себя пластины при своих собственных колебаниях на частотах выше fгр. Это связано с тем, что при излучении звука характер диссипации энергии в пластине описывается не высокодобротным колебанием (с малой величиной η, а акустическим импедансом пластины (α2).

На частотах f < fгр пластина колеблется в режиме акустического короткого замыкания и не излучает звука. При граничной частоте акустический импеданс становится бесконечно большим. При повышении частоты выражение под знаком корня меняет знак - выражение под корнем становится положительной величиной, и соколеблющаяся масса переходит в сопротивление излучения.
Это сопротивление сначала бесконечно велико, но с повышением частоты асимптотически переходит в волновое сопротивление среды ρ0/C0. Бесконечно большое сопротивление излучения приводит к тому, что колебания на частотах волнового совпадения ( при ω ≈ ωгр ) практически мгновенно затухают. И лишь при конечном сопротивлении излучения колебания пластины существуют конечное время и мы их может фиксировать.
При создании звуковой волны заданным распределением нормальных скоростей на плоскости (пластине) весь набор спектров распадается на ближнее поле, состоящее из неоднородных волн, и на поле, излучаемое плоскостью (пластиной) в виде однородных распространяющихся волн. Нормальные смещения создаются изгибными волнами, бегущими по поверхности пластины. Но изгибные волны обладают большой дисперсией, а низкочастотные изгибные волны имеют малую фазовую скорость. Если скорость этих волн меньше скорости звука той же частоты в окружающей среде, то они создадут только ближнее поле, и вдали оно не будет заметно. Только волны, бегущие быстрее, чем волны в среде, дадут заметное излучение, которое будет принято на достаточно большом расстоянии от колеблющейся поверхности.
Из выражения (XXI) следует, что излучение звуковых волн происходит только на собственных частотах пластины, для остальных частот возбуждения оно пренебрежимо мало. Кроме того, пластина осуществляет пространственное разделение звуковых волн с разной частотой (селекцию по частоте). Для каждой частоты возбуждения имеется по четыре направления распространения звуковых волн одной частоты и равной амплитуды с каждой стороны пластины и симметричных относительно плоскости пластины. Эти направления однозначно связаны с ориентацией пластины в пространстве и определяются соотношением (XXVII).
Для частот ниже некоторой граничной частоты fгр направляющий косинус волнового вектора k вдоль оси Z, равный cos(k, z) в (XXVII), - мнимая величина и в направлении оси z излучения не происходит. При этом мы получаем экспоненциально убывающее с расстоянием стоячее звуковое поле. Для частот выше fгр cos(k, z) - действительная величина, и мы получаем решение в виде (XXXI). Проекция направления звуковой волны проходит через диагональ прямоугольника, образованного векторами km=kx, kn=ky и kz, согласно (XXVII). При частоте звуковой волны f = fгр она скользит по поверхности пластины, при повышении частоты ее направление поворачивает наружу (к оси Z) и в конце концов при бесконечно высокой частоте излучения становится перпендикулярной плоскости пластины.
Акустический импеданс пластины представляет собой отношение звукового давления (создаваемого пластиной) к нормальной скорости движения пластины, т.е.
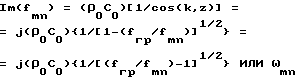
Im(ωmn) = α2= (ρ0/C0){1/[1-ωгр/ωmn)]1/2}. .
Для низких частот, когда f < fгр , т.е. до тех пор, пока длина волны в граничащей среде больше, чем длина волны изгибных колебаний пластины, акустический импеданс Im является мнимым .
.
Пластина колеблется в режиме акустического короткого замыкания и не излучает звука. При граничной частоте акустический импеданс становится бесконечно большим. При повышении частоты выражение под знаком корня меняет знак - направляющий косинус становится действительной величиной, и соколеблющаяся масса переходит в сопротивление излучения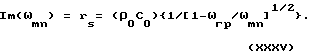 .
.
Это сопротивление сначала бесконечно велико, но с повышением частоты асимптотически переходит в волновое сопротивление среды.
При стационарном гармоническом воздействии рассмотренное явление проявляет себя в том, что в уравнении (1) величина η меняется на величину (η
ηmn= αmnωmn= (2ρ0C0/ωmnρh){1/[1-ωгр/ωmn]1/2}
при ωmn > ωL > ωгр .
В результате на частотах ωpq(ωгр < ωpq < ωL) , для которых декремент затухания больше единицы (αpqωpq > 1) , колебания собственных форм быстро затухают и их частоты в излучении отсутствуют.
Определим эти области частот следующим образом.
Нижняя граница первой области - области отсутствия колебаний для собственных частот пластины очевидна - это ближайшая собственная частота пластины, хотя бы немного превышающая величину граничной частоты, примерно ее величину можно положить равной граничной частоте пластины. Для определения верхнего предела указанной первой полосы неизлучаемых собственных частот (и форм) воспользуемся уравнением, вытекающим из неравенства ω
ωmn > ωгр , откуда получаем уравнение для собственной частоты пластины ωL
αL/ωL= (ρ0C0/ωLρh){1/[1-ωгр/ωL]1/2} = 1.
Отсюда получаем выражение для ωL
ωL= ωгр{1/2+[1/4+(ρ0C0/ρhωгр)2]1/2} (XXXVII)
При ωmn > ωL получаем для частоты свободных колебаний пластины
ωmn > ωL > ωгр.
Соответственно, полученное выражение для частоты ωL является выражением, определяющим верхнюю границу полосы частот пластины, для которой начинается излучение в виде плоских бегущих волн.
Для величины квадрата АЧХ получаем ωmn > ωL > ωгр. .

где
k = ω/C0>kmn, νmn= ω/ωmn .

ωmn > ωL > ωгр.
Излучение звуковой энергии пластиной означает, что амплитуда свободных колебаний пластины будет достаточно быстро уменьшаться. Слово быстро имеет смысл по отношению к величине затухания собственных колебаний, связанной с механическими потерями и описываемой коэффициентом ηmn . Из (XXX) следует, что наименьшие потери при излучении звука будут на высоких частотах, т.е. тогда, когда f>>fгр. Попробуем рассчитывать это затухание колебаний пластины, а следовательно, и затухание звуковых волн, излучаемых пластиной.
Выражение (XXXIX) определяет связь между колебаниями пластины и амплитудой каждой из восьми звуковых волн данной частоты ω и соответственно (по-разному) ориентированных в пространстве относительно пластины. При этом интенсивность выходного процесса равна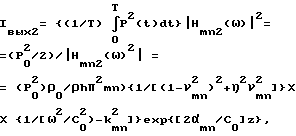
k = ω/C0>kmn, νmn= ω/ωmn.
Интенсивность входного процесса определяется как
Следовательно для этого случая (ω > ωL > ωгр) коэффициент звукопрохождения равен
где
k = ω/C0 > kmn, νmn= ω/ωmn.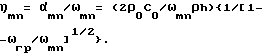
ωmn > ωL > ωгр, где
ωL= ωгр{1/2+[1/4+(ρ0C0/ρhωгр)2]1/2},
ωгр= C
Заметим, что величина Kзвпр2 существенно увеличивается при увеличении расстояния Z, т.е. при удалении точки наблюдения от пластины.
Аналогично для kmn или ω < ωгр получаем
где
k = ω/C0< kmn, νmn= ω/ωmn.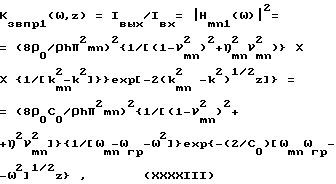
где
k = ω/C0< kmn, νmn= ω/ωmn.
Заметим, что величина Kзвпр1 существенно уменьшается при увеличении расстояния Z, т. е. при удалении точки наблюдения от пластины. Для анализа выражений (XXXXI) и (XXXXIII) преобразуем их к некоторому другому виду. Для этого учтем, что при невыраженных линейных размерах пластины, когда величина Lx и Ly не слишком различны, для пластины верны некоторые приближенные выражения: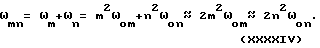
Заметим, что для пластины квадратной формы выражение (XXXIV) является точным.
Тогда 
где
ωom= π2C
1/m2n2= 4π4C
Далее учтем, что на основании дисперсионного уравнения пластины (XIII) для волнового числа mn-ой собственной формы пластины имеем выражение
k
Тогда учитывая, что при
ω > ωL > ωгр.
выражения (XXXXI) и (XXXXIII) можно привести к виду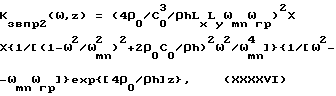
где
ω > ωL > ωгр,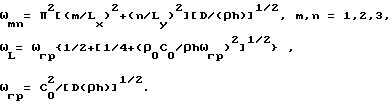
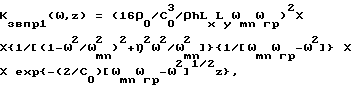
где
ωmn= π2[(m/Lx)2+(n/Ly)2][D/(ρh)]1/2,
ωгр= C
Полагая, что для частот воздействия ω, для которых ωгр < ω < ωL, коэффициент звукопрохождения равен нулю.
Уравнения (XXXXVI) и (XXXXVII) являются аналогами закона массы, но гораздо точнее отражают реальные процессы звукопреобразования реальных звукоизолирующих конструкций.
Реализация заявляемого способа определения коэффициента звукопрохождения для закрепленной по периметру упругой прямоугольной пластины в условиях стационарного гармонического звукового воздействия основана на измерениях круговой частоты ω падающей на пластину звуковой волны, плотности ρ материала пластины и толщины h пластины, затем измеряют линейные размеры Lx и Ly пластины и собственные частоты ωmn нормальных колебаний пластины, после чего определяется коэффициент звукопрохождения Kзвпр(ω,z) на расстоянии z от плоскости пластины по полученным формулам, а также определяется частотный диапазон акустической непрозрачности пластины. Аналогично полученные в данной работе выражения дают метод решения и обратной задачи.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ ОЦЕНКИ ВЛИЯНИЯ ПАРАМЕТРОВ ЗАКРЕПЛЕННОЙ ПО ПЕРИМЕТРУ УПРУГОЙ ПРЯМОУГОЛЬНОЙ ПЛАСТИНЫ НА ЭФФЕКТИВНОСТЬ ЕЕ ЗВУКОИЗОЛЯЦИИ ПРИ ВОЗБУЖДЕНИИ ПЛАСТИНЫ СТАЦИОНАРНЫМ СТОХАСТИЧЕСКИМ ЗВУКОВЫМ ВОЗДЕЙСТВИЕМ | 1996 |
|
RU2111552C1 |
| УСТРОЙСТВО ДЛЯ ПРЕДОТВРАЩЕНИЯ ПОПАДАНИЯ ЧАСТИЦ МЕХАНИЧЕСКОЙ ПРИМЕСИ В ЭЛЕКТРОЦЕНТРОБЕЖНЫЙ НАСОС | 2011 |
|
RU2499128C2 |
| СПОСОБ ОСАЖДЕНИЯ КАПЕЛЕК ПАРА В ГРАДИРНЕ | 2008 |
|
RU2360198C1 |
| УСТРОЙСТВО КОМПЕНСАЦИИ ШУМА ЭЛЕКТРОДВИГАТЕЛЕЙ | 2013 |
|
RU2528552C1 |
| СПОСОБ ВОССТАНОВЛЕНИЯ РЕЛЬЕФА МОРСКОГО ДНА ПРИ ИЗМЕРЕНИИ ГЛУБИН ПОСРЕДСТВОМ ГИДРОАКУСТИЧЕСКИХ СРЕДСТВ | 2011 |
|
RU2466426C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ОБЪЕМА ОСТАТКА ТВЕРДОГО НЕФТЕПРОДУКТА В ЖЕЛЕЗНОДОРОЖНОМ ВАГОНЕ-ЦИСТЕРНЕ | 2007 |
|
RU2348015C1 |
| СПОСОБ АКТИВНОГО ЗВУКОГАШЕНИЯ | 1999 |
|
RU2185666C2 |
| СПОСОБ ОСАЖДЕНИЯ ПАРА В ГРАДИРНЕ | 2005 |
|
RU2295684C1 |
| СПОСОБ ОСАЖДЕНИЯ ПАРА В ГРАДИРНЕ | 2007 |
|
RU2339888C1 |
| СПОСОБ ОЗВУЧИВАНИЯ ПОМЕЩЕНИЙ | 1996 |
|
RU2127495C1 |
Способ может быть использован для определения частотной зависимости коэффициента звукопрохождения звукоизолирующих перегородок и кожухов. Способ основан на законе массы. Коэффициент звукопрохождения на заданном расстоянии от плоскости пластины определяют с учетом круговой частоты падающей на пластину звуковой волны, плотности и коэффициента механических потерь материала пластины, ее толщины, линейных размеров и собственных частот нормальных колебаний. Предложены две различные формулы для вычисления упомянутого коэффициента для различных частот падающей волны, лежащих ниже граничной частоты ωгр и выше частоты ωL, превышающей ωгр. Для частот, лежащих в интервале между ωгр и ωL, коэффициент звукопрохождения полагают равным нулю. Изобретение позволяет исключить недопустимо большие расхождения между экспериментально и аналитически определяемыми значениями коэффициента звукопрохождения. 2 ил.
Способ определения коэффициента звукопрохождения для закрепленной по периметру упругой прямоугольной пластины в условиях стационарного гармонического звукового воздействия, основанный на законе массы, по которому коэффициент звукопрохождения рассчитывают с учетом круговой частоты ω падающей на пластину звуковой волны, плотности ρ материала пластины и толщины h пластины, отличающийся тем, что определяют линейные размеры Lx и Ly пластины и собственные частоты ωmn нормальных колебаний пластины, коэффициент звукопрохождения Кз в п р (ω, Z) на расстоянии z от плоскости пластины определяют для частот ω, лежащих ниже граничной частоты ωгр пластины, по формуле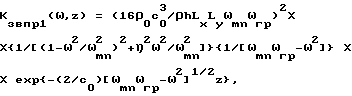
где ρ0 - плотность воздуха;
c0 - скорость звука в воздухе;
ωmn= π2[(m/Lx)2+(n/Ly)2][(D/ρh)]1/2, m, n = 1, 2, 3, ...;
D - цилиндрическая жесткость пластины;
ωгр= c
η - коэффициент механических потерь материала пластины,
а для частот ω, лежащих выше частоты ωL > ωгр, равной
ωL= ωгр{1/2+[1/4+(ρ0c0/ρhωгр)2]1/2},
по формуле
при этом для частот ω, для которых ωгр < ω < ωL, коэффициент звукопрохождения полагают равным нулю.
| SU, авторское свидетельство, 1756934, кл | |||
| Печь-кухня, могущая работать, как самостоятельно, так и в комбинации с разного рода нагревательными приборами | 1921 |
|
SU10A1 |
| Исакович М.А | |||
| Общая акустика | |||
| - М.: Наука, 1973, с.149. | |||
Авторы
Даты
1998-05-20—Публикация
1996-09-27—Подача