Изобретение относится к области вычислительной техники и предназначено для построения устройств цифровой обработки сигналов, в частности процессоров для быстрого преобразования Фурье и быстрого преобразования Хартли.
Известно арифметические устройство для процессора быстрого преобразования Фурье (авт. св. N 1631556, G 06 F 15/332, 20.03.1989).
Это устройство не обеспечивает:
а) необходимой простоты аппаратурной реализации;
б) необходимого быстродействия из-за сложности управления вычислительным процессом.
Наиболее близким к заявляемому техническому решению является принятое за прототип "Устройство для умножения комплексных чисел" (авт. св. N 1297034, G 06 F 7/49, 03.10.85), содержащее регистры, сумматоры, дешифраторы, коммутаторы, элементы ИЛИ, многовходовые сумматоры.
Данное устройство предназначено для построения процессоров быстрого преобразования Фурье, цифровых фильтров, вычислительных машин с комплексной арифметикой, решения систем линейных алгебраических уравнений.
Это устройство не обеспечивает:
а) необходимый простоты аппаратурной реализации;
б) необходимого быстродействия из-за сложности управления вычислительным процессом.
Сущность изобретения заключается:
- в упрощении схемы устройства за счет использования алгоритма скалярного произведения, обладающего регулярной структурой;
- в увеличении быстродействия за счет использования специализированной микросхемы - параллельного умножителя с накопителем;
- в увеличении быстродействия работы устройства, достигаемом за счет регулярности и простоты управления вычислительным процессом арифметического устройства для выполнения БПФ или БПХ.
Для этого, в устройство, содержащее пять регистров, два коммутатора, введены два умножителя с накопителями.
Изобретение будет понятно из следующего описания и приложенных к нему чертежей.
На фиг. 1 приведена схема арифметического устройства для выполнения БПФ;
на фиг. 2 приведена временная диаграмма работы арифметического устройства.
В чертежах и тексте приняты следующие обозначения:
1. Первый вход данных.
2. Второй вход данных.
3. Третий вход данных.
4. Первый вход управления записью.
5. Вход управления коммутаторами.
6. Вход признака кода операции.
7. Вход управления.
8. Вход тактовой частоты.
9. Второй вход управления записью.
10. Первый регистр.
11. Второй регистр.
12. Третий регистр.
13. Первый коммутатор.
14. Второй коммутатор.
15. Первый умножитель с накопителем.
16. Второй умножитель с накопителем.
17. Четвертый регистр.
18. Пятый регистр.
19. Первый выход результата.
20. Второй выход результата.
В состав арифметического устройства для выполнения быстрого преобразования Хартли-Фурье на основе алгоритма скалярного произведения (фиг. 1) входят пять регистров, два коммутатора, два умножителя с накопителями.
К информационным входам первого регистра 10, второго регистра 11 и третьего регистра 12 подключены соответственно первый вход данных 1, второй вход данных 2 и третий вход данных 3. Входы управления записью регистров 10, 11, 12 соединены с первым входом управления записью 4. Выход первого регистра 10 соединен с первыми информационными входами первого и второго коммутаторов 13, 14. Выход второго регистра 11 соединен со вторыми информационными входами первого и второго коммутаторов 13, 14. Управляющие входы коммутаторов 13 и 14 соединены со входом управления коммутаторами 5. Выход первого коммутатора 13 соединен с первым информационным входом первого умножителя с накопителем 15. Выход второго коммутатора 14 соединен с первым информационным входом второго умножителя с накопителем 16. Вторые информационные входы первого и второго умножителей с накопителями 15, 16 соединены с выходом третьего регистра 12. Входы задания кода операции (КОП) умножителей с накопителями 15, 16 соединены со входом признака кода операции 6. Входы импульсов управления умножителей с накопителями 15, 16 соединены со входом управления 7. Входы тактового сигнала (CLX) умножителей с накопителями 15 и 16 соединены со входом тактовой частоты 8.
Выходы первого и второго умножителей с накопителями 15 и 16 соединены с информационными входами четвертого и пятого регистров 17, 18 соответственно. Входы управления записью регистров 17, 18 соединены со вторым входом управления записью 9. Выходы четвертого и пятого регистров 17, 18 соединены соответственно с первым и вторым выходами результата 19, 20 и являются информационными выходами устройства.
Устройство работает следующим образом.
Матричный рекуррентный алгоритм БПФ, описанный в авт. св. N 1633426, G 06 А 15/332 13.03.89 г. представляется следующими формулами: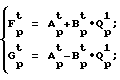 (1)
(1)
где
p, t - размерности матриц A, B, Q, F, G на разных итерациях;
P = 2m-1; t = 2r-m; p•t = 2r-1; r = log2N;
где
m - номер итерации, m = 1, 2, 3, ... r;
N = 2r - размерность обрабатываемого массива данных;
матрицы A
матрицы F
Q
Операция B
Весовые коэффициенты представляются следующим выражением:
Q(k) = exp(-j2π(k-1)/N;
где
k = 1, 2, 3,... N/2; 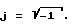
Если взять N = 2, то формулы (1) принимают вид: (2)
(2)
Формулы (2) представляют собой известное выражение базовой операции БПФ - "бабочки".
Арифметическое устройство выполняет "бабочку" БПФ в соответствии с формулами (2). Учтем, что числа A, B, Q, F и G являются комплексными. Обозначим: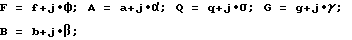
где
a, b, f, g, q - действительные части комплексных чисел A, B, F, G, Q, а α, β, γ, φ, σ - мнимые части этих чисел. Раскрывая формулы (2), получим: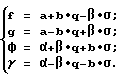 (3)
(3)
Формулы (3) можно представить в виде двух скалярных произведений матриц на вектор-столбцы: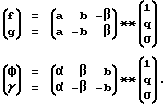 (4)
(4)
Предлагаемое арифметическое устройство вычисляет операцию "бабочка" как матричную: вычислением скалярного произведения (4).
Запишем выражение (4) в виде: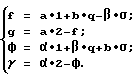 (5)
(5)
Можно представить вычислительный процесс по формулам (5) с использованием математического знака суммирования: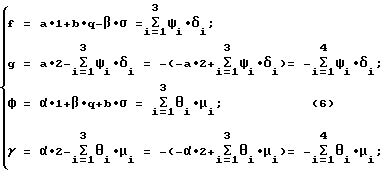
где
ψi и δi - числа а,b,-β,-а,1,q,σ,2, a θi и μi - числа α,β,b,-α,1,q,σ и 2.
Суммы 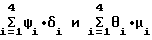 представляют собой операции скалярного умножения.
представляют собой операции скалярного умножения.
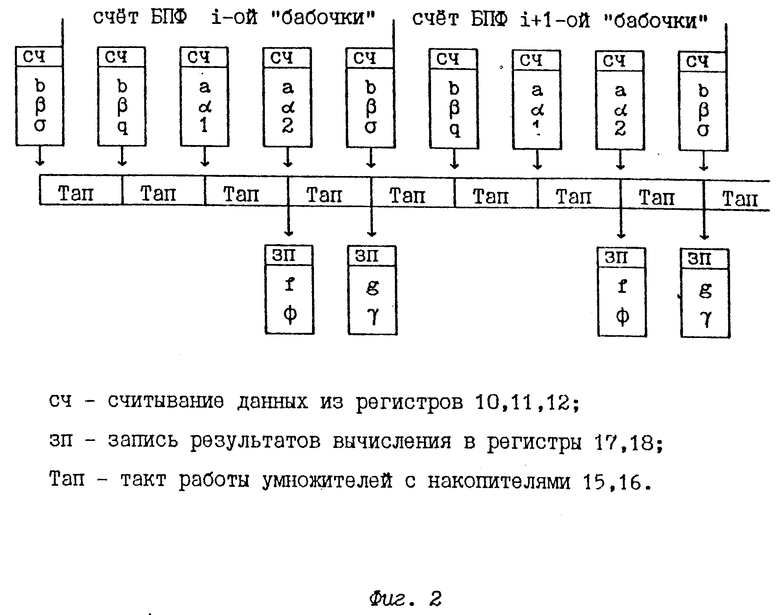
Таким образом, вычисления проходят за 4 такта работы умножителей с накопителями. На третьем такте появляются результаты f и φ. На четвертом такте появляются результаты -g и -γ. Для получения g и γ надо проинвертировать знак результата. Как будет показано далее, практически вычисления проходят еще проще и операция инверсии знака не нужна.
Матричный рекуррентный алгоритм быстрого преобразования Хартли (БПХ) с прореживанием по времени, описанный в заявке N 94-024301 (023698) (принято решение с выдаче патента на изобретение, название изобретения: "Процессор для быстрого преобразования Хартли", МПК G 06 F 15/332 (по новой классификации: МПК 6 G 06 F 17/14), дата поступления заявки 29.06.94 г.), представляется следующими формулами: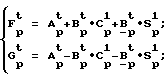 (7)
(7)
где
p=2m-1, t=2r-m, m = 1, 2, 3,...,r;
p, t - размерности матриц A, B, 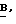 C, S, F, G на разных итерациях;
C, S, F, G на разных итерациях;
C
r - число итераций;
m - номер итерации;
N - длина исходного массива, N=2r.
Операция B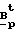 получена из матрицы B
получена из матрицы B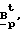 кроме первой, представлены строками матрицы B
кроме первой, представлены строками матрицы B
Весовые коэффициенты представляются следующими выражениями:
C(k) = cos(2π(k-1)/N); S(k) = sin(2π(k-1)/N;
где
k=1, 2, 3,... N/2.
Если взять N= 2, то базовая операция БПХ ("бабочка") будет описываться выражением: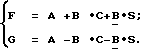 (8)
(8)
Формулы (8) можно представить в виде скалярного произведения матрицы на вектор-столбец: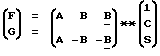 (9)
(9)
где
A, B и 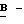 входные действительные числа; F, G - выходные действительные числа (результат счета); C и S - весовые коэффициенты.
входные действительные числа; F, G - выходные действительные числа (результат счета); C и S - весовые коэффициенты.
Запишем выражение (9) в виде: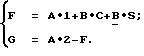 (10)
(10)
Выражения (10) также можно представить с использованием математического знака суммирования: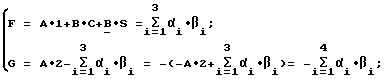 (11)
(11)
где
αi, βi - числа A, B 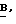 - A, 1, C, S, 2.
- A, 1, C, S, 2.
Сумма 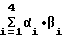 представляет собой операцию скалярного умножения.
представляет собой операцию скалярного умножения.
Вычисление "бабочки" БПХ проходит за 4 такта работы умножителей с накопителями. На третьем такте появляется результат F, а на четвертом - результат G. На практике операция инверсии знака результата здесь также не нужна.
Ясно, что выражения (10) можно записать и в таком виде: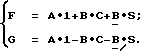 (12)
(12)
Для вычисления операции "бабочка" по формулам (10) достаточно одного умножителя с накопителем и вычисления производятся за 4 такта работы этой микросхемы. Если же использовать формулы (12), то необходимо два умножителя с накопителями, и вычисления займут 3 такта работы. Таким образом, формулы для вычисления операции "бабочка" аналогичны 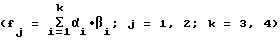 для БПФ и БПХ и поэтому в дальнейшем будет рассмотрен процесс вычисления "бабочки" БПФ.
для БПФ и БПХ и поэтому в дальнейшем будет рассмотрен процесс вычисления "бабочки" БПФ.
На фиг. 1 приведена схема арифметического устройства для выполнения базовой операции БПФ.
По входам 1, 2, 3 в арифметическое устройство поступают числа A, B, Q, 1 и 2. Регистры 10, 11 и 12 осуществляют прием и хранение действительных и мнимых компонент этих чисел. Указанные числа записываются в регистры параллельным кодом. Регистр 10 принимает и хранит числа b, a, регистр 11 - числа β, α, а регистр 12 - числа σ, q, 1 и 2. По входу 4 устройства на входы управления записью регистров поступает код записи.
Арифметическое устройство параллельно обрабатывает каналы действительных и мнимых компонент согласно формулам (4). Коммутаторы 13 и 14 мультиплексируют каналы между собой, подмешивая в скалярные произведения компоненты смежных каналов в соответствии с (4). По входу 5 устройства поступает код управления коммутаторами 13 и 14. Умножители с накопителями (специализированные интегральные микросхемы 15 и 16) выполняют операцию скалярного умножения по каналам. Три такта работы умножителей с накопителями затрачиваются на вычисление компонент f и φ и один такт на вычисление g и γ. Вычисления производятся следующим образом.
1. Из регистра 10 операнд b поступает на вход X микросхемы 16. Из регистра 12 операнд σ поступает на вход Y этой микросхемы. Операнды b и σ перемножаются и результат записывается в накапливающий регистр микросхемы 16.
Одновременно из регистра 11 операнд β поступает на вход X микросхемы 15. Из регистра 12 операнд σ поступает на вход Y этой микросхемы. Операнды β и σ перемножаются и результат записывается в накапливающий регистр микросхемы 15.
2. Из регистра 10 операнд b поступает на вход X микросхемы 15. Из регистра 12 операнд q поступает на вход Y этой микросхемы. Операнды перемножаются и из произведения вычитается содержимое накапливающего регистра микросхемы.
Одновременно из регистра 11 операнд β поступает на вход X микросхемы 16. Из регистра 12 операнд q поступает на вход Y этой микросхемы. Операнды перемножаются и результат суммируется с содержимым накапливающего регистра микросхемы.
3. Из регистра 10 операнд a поступает на вход X микросхемы 15. Из регистра 12 число 1 поступает на вход Y этой микросхемы. Операнды перемножаются и результат суммируется с содержимым накапливающего регистра микросхемы. Получен первый результат - число f.
Одновременно из регистра 11 операнд α поступает на вход X микросхемы 16. Из регистра 12 число 1 поступает на вход Y этой микросхемы. Операнды перемножаются и результат суммируется с содержимым накапливающего регистра. Получен второй результата - число φ. Числа f и φ записываются в регистры 17 и 18 соответственно.
4. Из регистра 10 операнд a поступает на вход X микросхемы 15. Из регистра 12 число 2 поступает на вход Y этой микросхемы. Операнды перемножаются и из произведения вычитается содержимое накапливающего регистра. Получен третий результат - число g.
Совершенно аналогично одновременно с этим на выходе микросхемы 16 будет получен четвертый результат - число γ. Числа g и γ записываются в регистры 17 и 18 соответственно. По входу 9 устройства на входы управления записью регистров 17 и 18 поступает код записи.
Импульсы управления, необходимые для работы умножителей с накопителями 15 и 16, поступают на вход 7 устройства. Тактовый сигнал (CLX) поступает на вход 8 устройства. Код операции (КОП) поступает на вход 6 устройства.
Таким образом, полный цикл вычисления базовой операции ("бабочки") БПФ занимает четыре такта работы умножителей с накопителями 15 и 16. Результаты вычисления базовой операции из регистров 17 и 18 поступают на выходы 19 и 20 устройства.
Временная диаграмма работы арифметического устройства приведена на фиг. 2.
| название | год | авторы | номер документа |
|---|---|---|---|
| АРИФМЕТИЧЕСКОЕ УСТРОЙСТВО ДЛЯ ВЫЧИСЛЕНИЯ БЫСТРОГО ПРЕОБРАЗОВАНИЯ ХАРТЛИ-ФУРЬЕ | 1999 |
|
RU2190874C2 |
| Арифметическое устройство для выполнения быстрого преобразования Хартли-фурье | 1990 |
|
SU1795473A1 |
| ПРОЦЕССОР С МАКСИМАЛЬНО ВОЗМОЖНОЙ ПРОИЗВОДИТЕЛЬНОСТЬЮ ДЛЯ БЫСТРОГО ПРЕОБРАЗОВАНИЯ ФУРЬЕ | 2005 |
|
RU2290687C1 |
| СПОСОБ ЦИФРОВОЙ ОБРАБОТКИ СИГНАЛОВ И УСТРОЙСТВО ДЛЯ ЕГО ОСУЩЕСТВЛЕНИЯ | 2000 |
|
RU2163391C1 |
| Арифметическое устройство для выполнения быстрого преобразования Хартли-Фурье | 1990 |
|
SU1756902A1 |
| Процессор быстрого преобразования Фурье | 1988 |
|
SU1667101A1 |
| УСТРОЙСТВО ДЕЛЕНИЯ И ИЗВЛЕЧЕНИЯ КВАДРАТНОГО КОРНЯ | 2012 |
|
RU2510072C1 |
| Устройство для реализации двумерного быстрого преобразования фурье | 1983 |
|
SU1142845A1 |
| Устройство для реализации быстрого преобразования Фурье последовательности с нулевыми элементами | 1983 |
|
SU1119025A1 |
| Устройство для выполнения быстрого преобразования Фурье | 1985 |
|
SU1337904A1 |
Изобретение относится к области вычислительной технике и предназначено для построения устройств цифровой обработки сигналов, в частности процессоров для быстрого преобразования Фурье (БПФ) и быстрого преобразования Хартли (БПХ). Сущность изобретения заключается в упрощении схемы за счет использования алгоритма скалярного произведения, обладающего регулярной структурой в увеличении быстродействия работы устройства, достигаемом за счет регулярности и простоты управления вычислительным процессом для выполнения БПФ или БПХ. Для этого в устройство, содержащее пять регистров 10 - 12, 17, 18, два коммутатора 13, 14, введены два умножителя с накопителем 15, 16. 2 ил.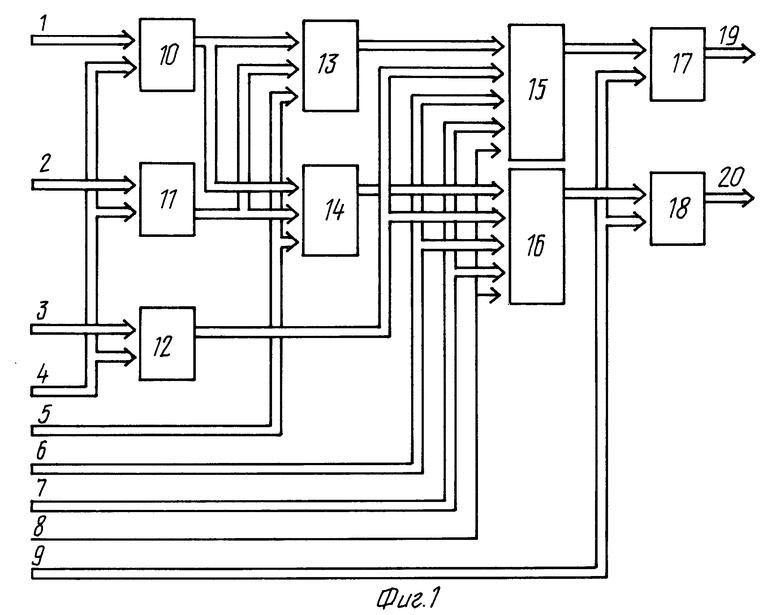
Арифметическое устройство для выполнения быстрого преобразования Хартли-Фурье, содержащее пять регистров, два коммутатора, причем первый, второй и третий входы данных устройства соединены с информационными входами с первого по третий регистров соответственно, входы управления записью которых соединены с первым входом управления записью устройства, выход первого регистра соединен с первыми информационными входами первого и второго коммутатора, выход второго регистра соединен с вторыми информационными входами первого и второго коммутаторов, входы управления записью четвертого и пятого регистров объединены, выходы четвертого и пятого регистров соединены соответственно с первым и вторым выходами результата устройства, отличающееся тем, что устройство содержит два умножителя с накопителем, причем управляющие входы первого и второго коммутаторов соединены с входом управления коммутаторами устройства, выход первого коммутатора соединен с первым информационным входом первого умножителя с накопителем, выход второго коммутатора соединен с первым информационным входом второго умножителя с накопителем, вторые информационные входы первого и второго умножителей с накопителями соединены с выходом третьего регистра, входы задания кода операции обоих умножителей с накопителями соединены со входом признака кода операции устройства, входы управления обоих умножителей с накопителями соединены со входом управления устройства, тактовые входы обоих умножителей с накопителями соединены со входом тактовой частоты устройства, выходы первого и второго умножителей с накопителями соединены с информационными входами четвертого и пятого регистров соответственно, входы управления записью которых соединены со вторым входом управления записью устройства.
Авторы
Даты
1999-01-20—Публикация
1996-03-20—Подача