Изобретение относится к вычислительной технике и может быть использовано в различных областях для повышения информационной емкости экрана монитора.
Известен способ перемещения объекта на экране монитора компьютера с помощью 2-D манипулятора типа компьютерной мыши, так называемый "drag & drop" - "схватил и перетащил" [1].
Этот способ предусматривает перемещение объектов по плоскости экрана, тождественным двумерному пространству. Для его реализации на экране монитора формируют изображения объекта. Путем перемещения мыши подводят ее курсор к нужному объекту и осуществляют "захват" путем нажатия левой клавиши мыши.
Перемещают объект по экрану монитора путем перемещения курсора мыши. Перемещение объекта происходит одновременно с перемещением курсора до тех пор, пока левая клавиша мывши остается нажатой. Сохраняют объект в измененном положении путем опускания нажатой клавиши мыши.
Способ характеризуется удобством и наглядностью для пользователя при перемещении объектов по экрану монитора, а также естественностью осуществления перемещений.
Его ограничением является то, что объект может перемещаться только в двумерном пространстве, отождествляемом с плоскостью экрана монитора.
Известен способ перемещения объекта на экране монитора компьютера с помощью 2-D манипулятора типа компьютерной мыши, включающий формирование на экране изображения трехмерного пространства при помощи аксонометрической проекции осей его системы координат, формирование изображения объекта в этом пространстве, перемещение в нем изображения объекта [2].
Способ предусматривает перемещение объекта в трехмерном пространстве. Для выбора направления перемещения относительно оси одной из координатных осей, которую предварительно активизируют, используют меню, а собственно для управления перемещением используют слайдеры.
Ограничениями этого способа являются: возможность перемещения объекта при помощи одного слайдера только относительно одной из координатных осей, необходимость предварительного активизирования осей, при этом производится манипуляция мышью не непосредственно перемещаемого объекта, а перемещение указателя слайдера, что затрудняет точность перемещения, увеличивает путь доступа к информации, ухудшает наглядность и удобство манипулирования.
Решаемая изобретением задача - повышение наглядности изображения перемещения объекта в пространстве и упрощение доступа к получению информации.
Технический результат, который может быть получен при осуществлении заявленного способа, - обеспечение естественного управления перемещением объекта в пространстве с размерностью больше двух, создание прямого доступа к любому объекту в пространстве, отображаемому на экране монитора, и обеспечение возможности удобства, упрощение доступа к получению информации за счет уменьшения необходимого количества манипуляций с мышью.
Для решения поставленной задачи в известном способе перемещения объекта на экране монитора компьютера с помощью 2-D манипулятора типа компьютерной мыши, включающем формирование на экране изображения по меньшей мере трехмерного пространства при помощи аксонометрической проекции осей его системы координат, формирование изображения объекта в этом пространстве, перемещение в нем изображения объекта, согласно изобретению перемещение объекта производят путем осуществления операции "drag & drop" непосредственно над объектом, создают дополнительный объект для визуализации направления перемещения, изображение которого размещают в том же пространстве и совмещают с изображением объекта, при перемещении объекта вычисляют значения вектора элементарных перемещений компьютерной мыши, интерпретируют полученную последовательность векторов как перемещение объекта в пространстве и перемещают объект и дополнительный объект в соответствии с интерпретацией.
Возможны дополнительные варианты осуществления способа, в которых целесообразно, чтобы: в качестве объекта использовали точку; для объекта - точки в качестве дополнительного объекта использовали вспомогательную систему координат с осями, параллельными осям координат пространства, и начало которой совпадает с точкой; для объекта - точки интерпретацию осуществляли путем вычисления проекции точки на плоскость экрана, вычисления проекции осей вспомогательной системы координат на плоскость экрана, для каждой оси вспомогательной системы координат вычисляли бы по два вектора, один - вдоль направления проекции оси, а другой - в противоположном ей направлении, среди этих векторов выбирали тот, который образует наименьший угол с вектором перемещения мыши, по которому выбирали вектор направления перемещения точки в пространстве так, чтобы проекции на экран ее нового положения была ближайшей к положению мыши, а вспомогательную систему координат перемещали идентично перемещению точки; в качестве объекта использовали плоскость; для объекта - плоскости в качестве дополнительного объекта использовали вспомогательную систему координат, начало которой совпадает с точкой на плоскости, на которую указывает мышь, одна из осей перпендикулярна плоскости, а другие оси расположены в плоскости; для объекта - плоскости интерпретацию осуществляли путем вычисления проекции осей вспомогательной системы координат на плоскость экрана, для каждой оси вспомогательной системы координат вычисляли по два вектора, один - вдоль на правления проекции оси, а другой - в противоположном ей направлении, среди этих векторов выбирали тот, который образует наименьший угол с вектором перемещения мыши, если вектор с наименьшим углом соответствует оси, перпендикулярной плоскости, то плоскость перемещали бы параллельно самой себе вдоль оси, соответствующей направлению этого вектора, а если вектор с наименьшим углом соответствует оси, находящейся в плоскости, то плоскость вращали бы вокруг другой оси, находящейся в плоскости, а вспомогательную систему координат перемещали идентично перемещению плоскости.
За счет создания дополнительного объекта, изображение которого совмещают с изображением объекта, вычисления значения вектора элементарных перемещений компьютерной мыши и интерпретации последовательности векторов как перемещение объекта в пространстве, удалось произвести имитацию перемещения объекта курсором мыши в пространстве с размерностью больше двух при перемещении самой мыши по плоскости, что позволяет повысить наглядность изображения перемещения объекта в пространстве и упрощение доступа к получению информации.
Указанные преимущества, а также особенности настоящего изобретения поясняются лучшим вариантом его осуществления со ссылками на прилагаемые чертежи.
Фиг. 1 показывает функциональную схему для реализации заявленного способа при помощи компьютера, связанным с монитором и мышью; фиг. 2 - изображение трехмерного пространства на экране компьютера с перемещаемым объектом; фиг. 3 - то же, что фиг. 2, с перемещаемым объектом-точкой и сформированным дополнительным объектом; фиг. 4 - область А на фиг. 3 в укрупненном масштабе; фиг. 5 - изображение четырехмерного пространства на экране компьютера с перемещаемым объектом и сформированным дополнительным объектом; фиг. 6 - изображение трехмерного пространства на экране компьютера с перемещаемым объектом-плоскостью; фиг. 7 -то же, что фиг. 6, при перемещении плоскости вдоль оси, ортогональной ей; фиг. 8 - то же, что фиг. 7, при вращении плоскости вокруг одной из осей, находящейся в этой плоскости; фиг. 9 - то же, что фиг. 8, при вращении плоскости вокруг другой из осей, находящейся в плоскости; фиг. 10 - изображение пространства при выполнении операции зуммирования; фиг. 11 - изображение трехмерного дискретного пространства для анализа экономической информации.
Для лучшего пояснения существа предложенного способа рассмотрим функциональную схему для его реализации (фиг. 1).
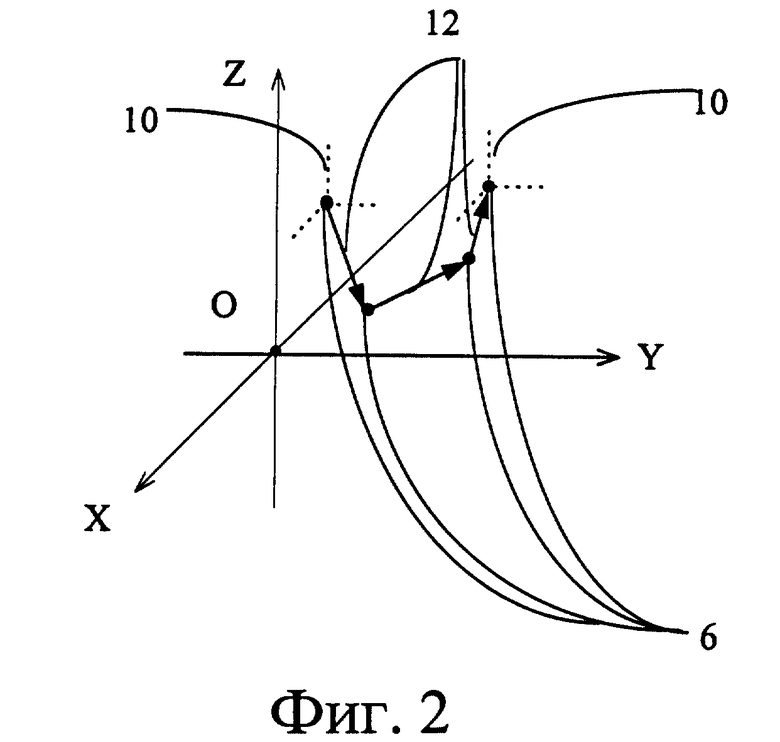
Способ включает формирование при помощи компьютера 1 на экране 2 монитора 3 посредством блока 4 формирования изображения пространства, например трехмерного. Аксонометрические проекции осей X, Y, Z системы координат этого пространства показаны на фиг. 2. Посредством блока 5 формирования изображения объекта получают изображение объекта 6 (фиг. 1, 2) в этом пространстве. В качестве объекта 6 может быть выбран любой геометрический объект, например точка, плоскость, параллелепипед, сфера и др. Для реализации перемещения объекта 6 путем операции "drag & drop" подводят курсор 7 мыши 8 (фиг. 1, 2) к объекту 6 и производят захват его путем нажатия клавиши мыши, тем самым активизируют объект 6.
После захвата объекта 6 посредством блока 9 формирования дополнительного объекта создают изображение дополнительного объекта 10 (фиг. 1, 2) для визуализации направления его перемещения и совмещают его с изображением объекта 6.
Для определения направления перемещения объекта 6 по пространству служит блок 11 определения направления перемещения (фиг. 1). В нем вычисляют значения векторов 12 (фиг. 2) элементарных перемещений мыши 8 и интерпретируют последовательность векторов 12 как задаваемое перемещение объекта 6 в пространстве.
Определение нового положения объекта 6 в пространстве осуществляют посредством блока 13 перемещения объектов, который производит построение изображений перемещенных объекта 6 и дополнительного объекта 10 на экране 2.
Далее проверяют в блоке 14 контроля, остается ли нажатой клавиша мыши 8. Если клавиша мыши 8 остается нажатой, то управление передается в блок 11 определения направления перемещения, в противном случае при отпускании клавиши мыши 8 посредством блока 15 завершения стирают с экрана 2 изображение дополнительного объекта 10.
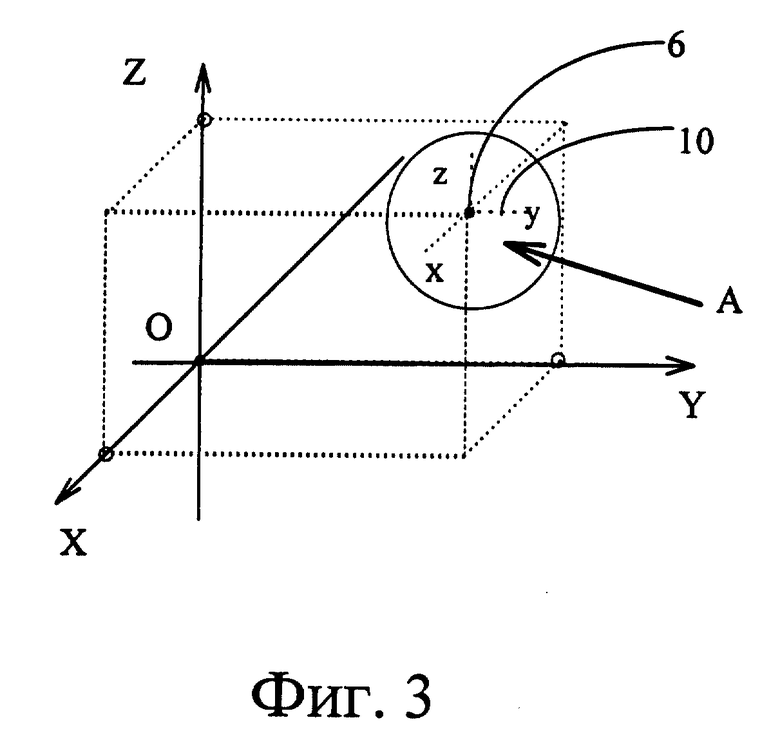
При использовании в качестве перемещаемого объекта 6 точки (фиг. 3) в качестве дополнительного объекта 10 используют вспомогательную систему координат с осями x, y, z, параллельными осям X, Y, Z пространства, и начало которой совпадает с объектом 6.
Для получения дополнительной информации о координатах точки могут быть также использованы дополнительные средства для обозначения объекта 6 и его расположения в пространстве, например: измененный цвет объекта 6; тонкие линии прямоугольного параллелепипеда, ребра которого параллельны координатным осям X, Y, Z, одна вершина которого находится в начале координат, обозначенным точкой 0, а другая совпадает с объектом 6; точки, соответствующие проекциям объекта 6 на оси X, Y, Z.
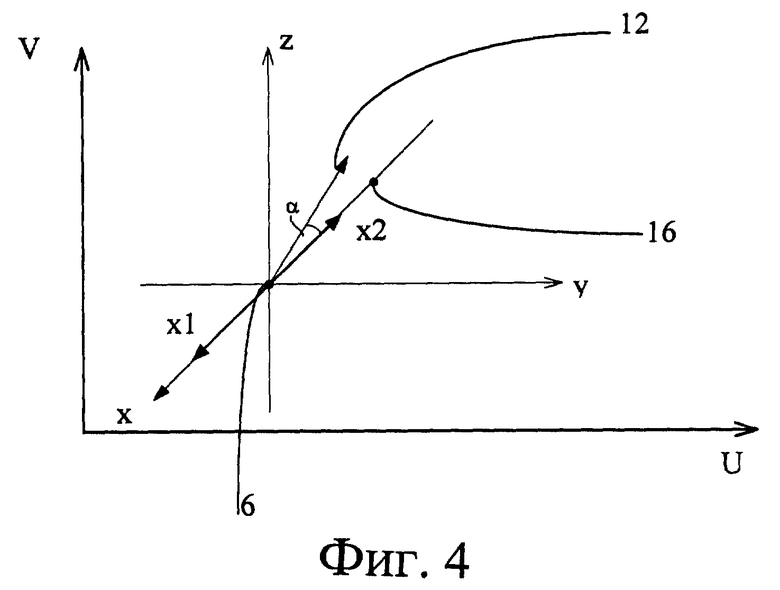
Интерпретацию осуществляют блоком 11 определения направления перемещения (фиг. 1). При этом в блоке 11 вычисляют проекции объекта 6 на плоскость экрана 2 (фиг. 4), вычисляют проекции осей x, y, z вспомогательной системы координат на плоскость экрана 2, для каждой оси x, y, z вычисляют по два вектора x1 и x2 (на фиг. 4 два вектора показаны только для оси x): один - вдоль направления проекции оси, а другой - в противоположном ей направлении. Среди этих векторов выбирают тот, который образует наименьший угол α с вектором 16 перемещения курсора 7 мыши 8 (для показанного случая это - вектор X2), и полагают его направление направлением перемещения объекта 6 в пространстве. Вычисляют новое положение 17 объекта 6 в пространстве так, чтобы проекция на экран 2 ее нового положения была ближайшей к положению вектора 16 (курсора 7). Далее вспомогательную систему координат перемещают идентично перемещению объекта 6 так, чтобы ее начало совпадало с положением 17 объекта 6.
Для упрощения рассмотрения работы блока 11 при использовании в качестве объекта 6 точки рассмотрим случай, при котором используется параллельная аксонометрическая проекция трехмерного пространства с координатами X, Y, Z, построенная на плоском экране 2, являющимся двумерным пространством с координатами U, V (фиг. 4). Объект 6 имеет координаты x0, y0, z0 в пространстве с координатами X, Y, Z, а ее проекция на экране 2 - координаты u0, v0. Все вектора x1, x2, y1, y2, z1, z2, являющиеся направляющими, задают как векторы длиной d, выходящие из объекта 6.
До проведения перемещения координаты x1, x2, y1, y2, z1, z2 на экране 2 будут:
(u0 -d•cos (π 4), v0 - d•sin (π 4)) -для вектора x1,
(u0+d, v0) - для вектора y1,
(u0, v0 + d)- для вектора z1,
(u0+d • cos (π 4), v0 + d • sin (π 4)) - для вектора x2,
(u0 - d, v0) - для вектора y2,
(u0, v0 - d) -для вектора z2.
Перемещение курсора 7 мыши 8 состоит из элементарных (малых) перемещений мыши 8, информация о каждом из которых поступает от операционной системы компьютера 1 путем передачи координат (u1, v1) курсора 7 на экране 2
Для выбора вектора, образующего наименьший угол α с вектором 16, определяют скалярное произведение вектора 16 с векторами x1, x2, y1, y2, z1, z2 в соответствиями с известными из аналитической геометрии формулами, приведенными ниже с учетом, что du=u1-u0 и dv=v1-v0.
(du•cos (π 4) + dv• sin (π 4))•d -для вектора x1,
du•d -для вектора y1,
dv•d - для вектора z1,
(du•cos (π 4) + dv• sin (π 4))•d-для вектора x2,
du•d - для вектора y2,
dv•d - для вектора z2,
Далее выбирают наибольшее из скалярных произведений и определяют вектор, задающий ось и направление, которые соответствуют ему. Для рассмотренного примера это - вектор x2.
Пусть величина скалярного произведения равна p. Тогда определяют смещение s вдоль выбранного вектора x2, как величину проекции на него вектора 16 перемещения по формуле: s = p/d.
Определяют новые координаты x*, y*, z* объекта 6 в трехмерном пространстве следующим образом: значение координаты, вдоль которой производят данное элементарное перемещение, измеряют на величину s с учетом знака: "+" для положительного направления и "-" для отрицательного, для рассмотренного примера x*=x0-s; сохраняют значения остальных координат, для рассмотренного примера y*=y0, z*=z0.
Данный способ не ограничивает свое применение в случае, когда для изображения трехмерного пространства используют аксонометрическую проекцию в традиционном виде, в котором оси Y, Z расположены параллельно плоскости UV. Расчеты проводятся по известным формулам аналитической геометрии, учитывающим углы векторов x1, x2, y1, y2 z1, z2 относительно осей U, V системы координат экрана 2. Перемещение осуществляется тем же способом.
Предлагаемый способ перемещения объекта 6 может быть реализован и для случая размерности пространства N > 3( фиг. 5).
Формируют на экране 2, описываемым в координатах U, V, N-мерное пространство в аксонометрической проекции путем изображения точки начала координат O и N координатных осей X1,...XN. Направление этих координатных осей X1, ...XN могут быть выбраны, например, по следующему правилу, хотя возможны и другие варианты.
Ось XN совпадает с осью V, положительное направление - вверх.
Ось XN-1 совпадает с осью U, положительное направление - вправо.
Для определения направления остальных осей вычисляют вспомогательные коэффициенты m1, m2:
m1 = m2 = (N-2)/2, если N - четное;
m1 = (N-1)/2, m2=m1-1, если N - нечетное.
Далее проводят в положительном направлении оси X1...Xm1, располагая их через равные углы β = (π /2) (m1+1) и отсчитывая углы β против часовой стрелки от вектора (-U), т.е. располагая оси в третьем квадранте.
Аналогичным образом проводят в положительном направлении оставшиеся оси Xm1+1. . . XN-2, располагая их через равные углы γ = (π /2) /(m2+1) и отсчитывая углы γ против часовой стрелки от вектора (-V), т.е. располагая их в четвертом квадранте.
При указанном методе построения координатные оси X1...XN-2 направлены на наблюдателя.
Изображение объекта 6 на экране 2, т.е. его проекцию на пространство UV, можно построить по известным правилам построения проекций. При захвате объекта 6 выполняют действия, аналогичные трехмерному случаю, что изображено для случая четырехмерного пространства (фиг. 5).
В качестве дополнительного объекта 10 используют вспомогательную систему координат с осями x1, x2, x3, x4, параллельными осям X1, X2, X3, X4, и начало которой совпадает с объектом 6.
Для дополнительного удобства наблюдения местоположения и направления перемещения объекта 6 могут быть построены точки, соответствующие проекциям объекта 6 на оси X1, X2, X3, X4.
Определение направления перемещения и само перемещение производят аналогично описанному случаю для трехмерного пространства.
Среди векторов выбирают тот, который образует наименьший угол α с вектором 16 перемещения курсора 7 мыши 8 и полагают его направление направлением перемещения объекта 6 в пространстве. Вычисляют новое положение 17 объекта 6 в пространстве так, чтобы проекция на экран 2 ее нового положения была ближайшей к положению вектора 16 (курсора 7). Далее вспомогательную систему координат перемещают идентично перемещению объекта 6 так, чтобы ее начало совпадало с положением 17 объекта 6.
Однако, как показали исследования, для других случаев многомерных пространств при N > 4 уменьшается сектор, отвечающий за направление по каждой из осей X1. . .XN, и ограничивается возможность пользователя перемещать мышь в заданном направлении с малым допуском. Проверка на тесте (программа, реализованная на C++ в OC Windows95) показала возможность эффективной работы при N≤7.
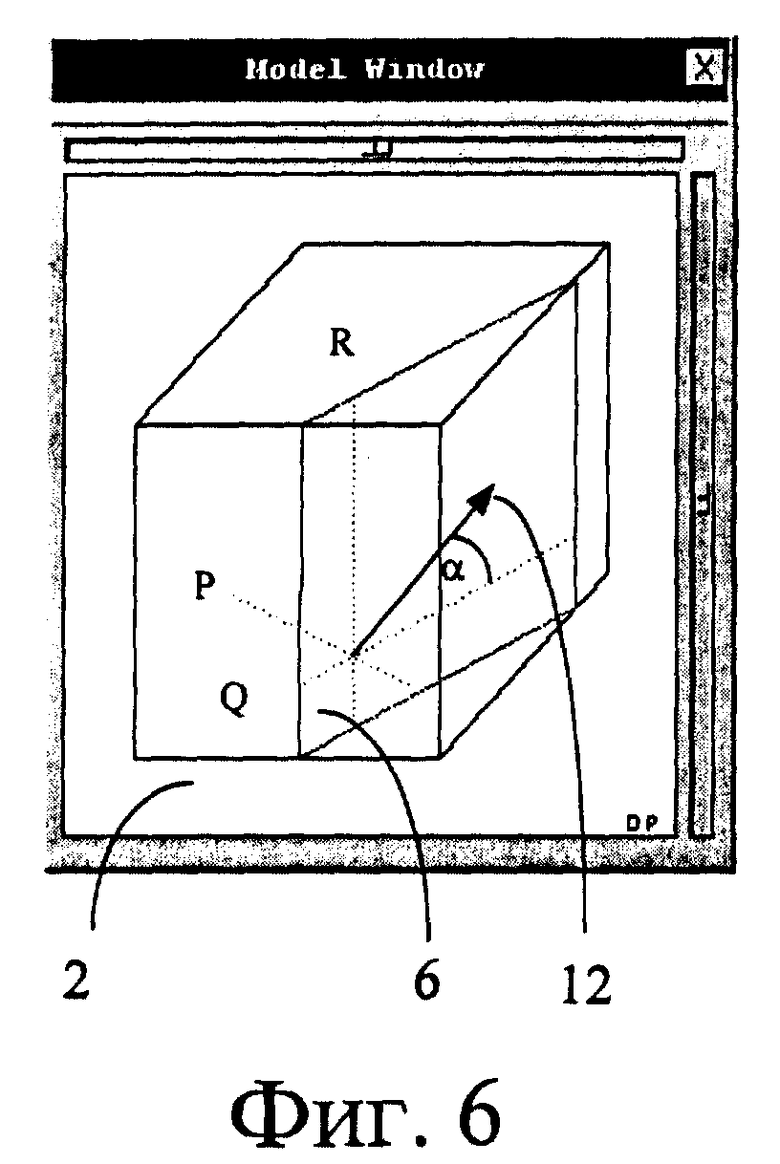
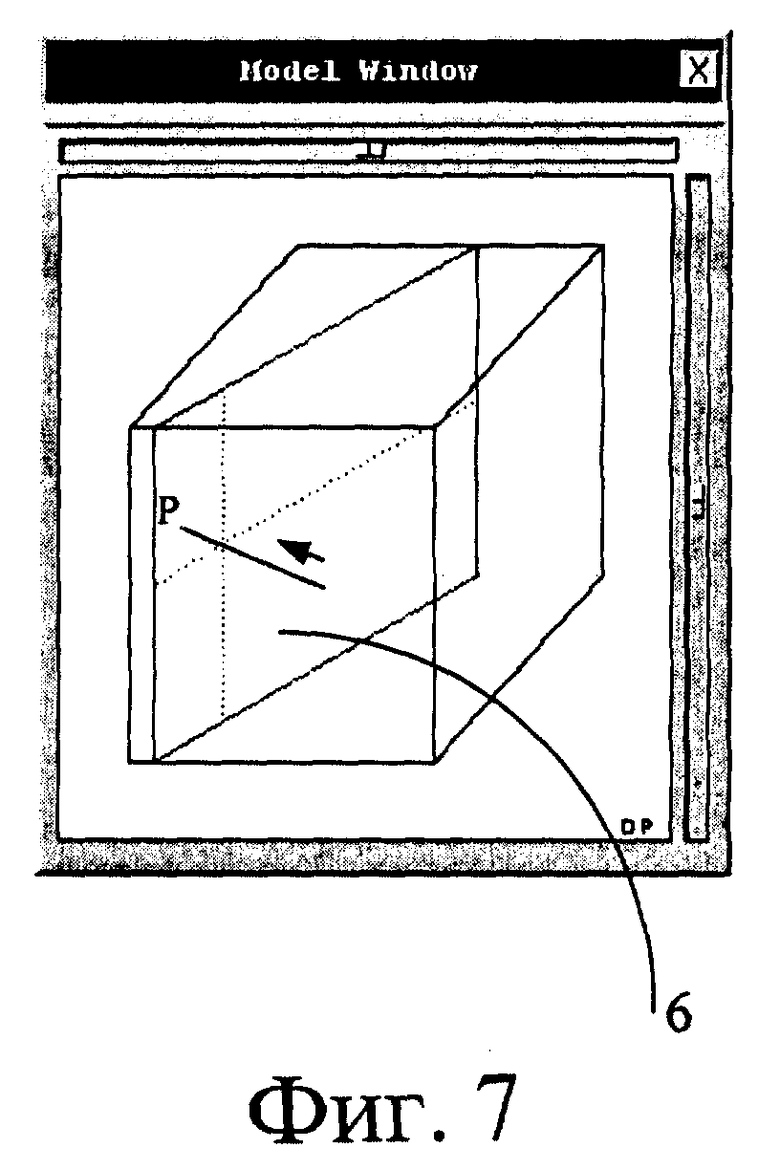
В качестве объекта 6 для его перемещения может быть выбрана плоскость (фиг. 6).
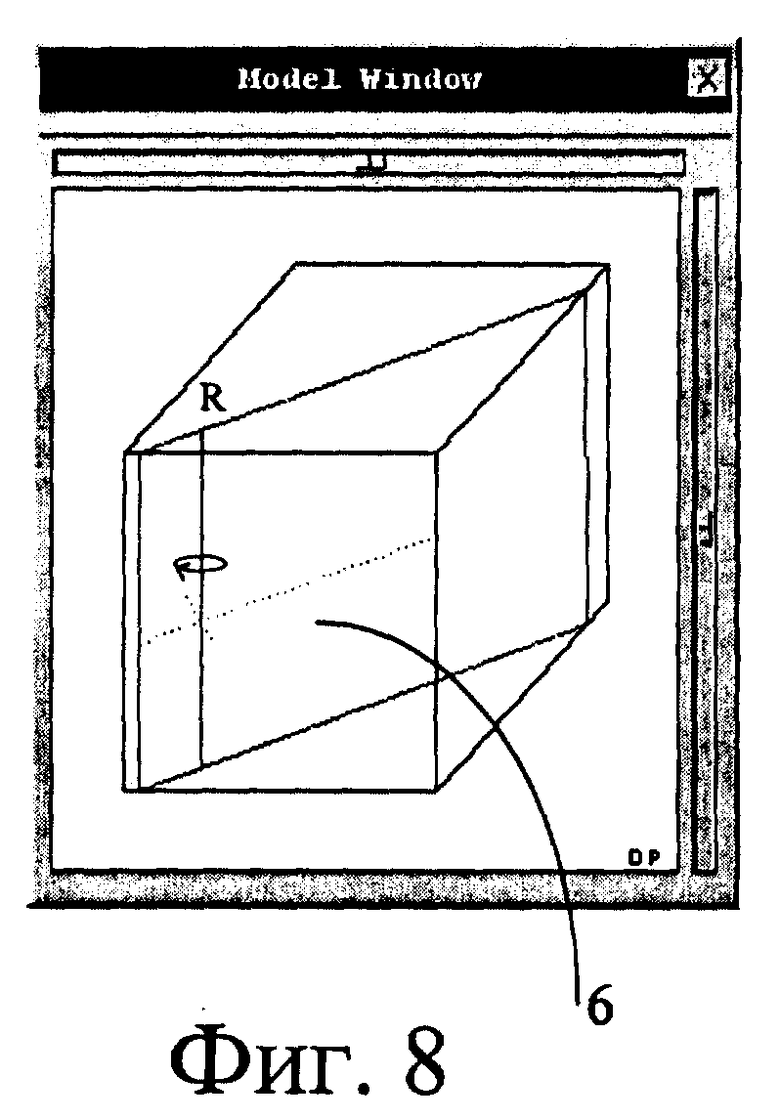
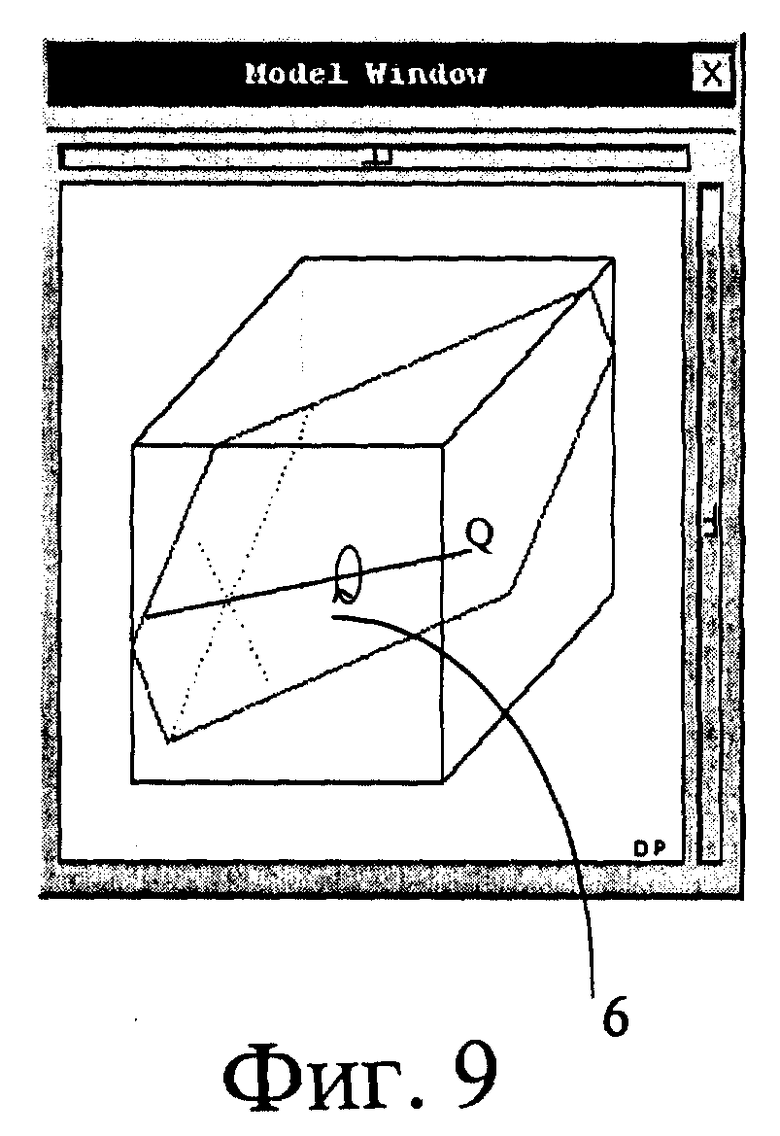
Для этого варианта в качестве дополнительного объекта 10, например, при анализе трехмерного пространства используют вспомогательную систему координат P, Q, R, начало которой совпадает с точкой на плоскости, на которую указывает курсор 7 мыши 8. Ось P перпендикулярна плоскости, а другие оси Q и R расположены в плоскости.
Блок 11 (фиг. 1) производит вычисления проекции осей P, Q, R вспомогательной системы координат на плоскость экрана 2. Для каждой оси вспомогательной системы координат вычисляют по два вектора p1, p2, q1, q2, r1, r2, один - вдоль направления проекции оси, а другой - в противоположном ей направлении. Среди этих векторов p1, p2, q1, q2, r1, r2 выбирают тот, который образует наименьший угол α с вектором 16 перемещения курсора 7. Если вектор с наименьшим углом α соответствует оси P, перпендикулярной плоскости, т.е. одному из векторов p1, p2, то плоскость перемещают параллельно самой себе вдоль оси P. Если вектор с наименьшим углом α соответствует оси Q, то плоскость вращают вокруг оси R. Если вектор с наименьшим углом α соответствует оси R, то плоскость вращают вокруг оси Q. Вспомогательную систему координат P, Q, R перемещают идентично перемещению плоскости.
Перемещение плоскости в соответствии с изложенным иллюстрируется на фиг. 7 - 9. Такое перемещение плоскости может быть использовано для изучения трехмерных объемных тел различной природы, например геологических моделей, данных медицинской томографии и т.д., поскольку такие объекты изучают посредством метода сечений (слайсов), а данный способ реализует перемещение сечений в пространстве произвольным образом по желанию потребителя, не накладывая ограничения на степень свободы перемещения.
В качестве примеров осуществления заявленного способа рассмотрим его практическую реализацию для решения различных задач.
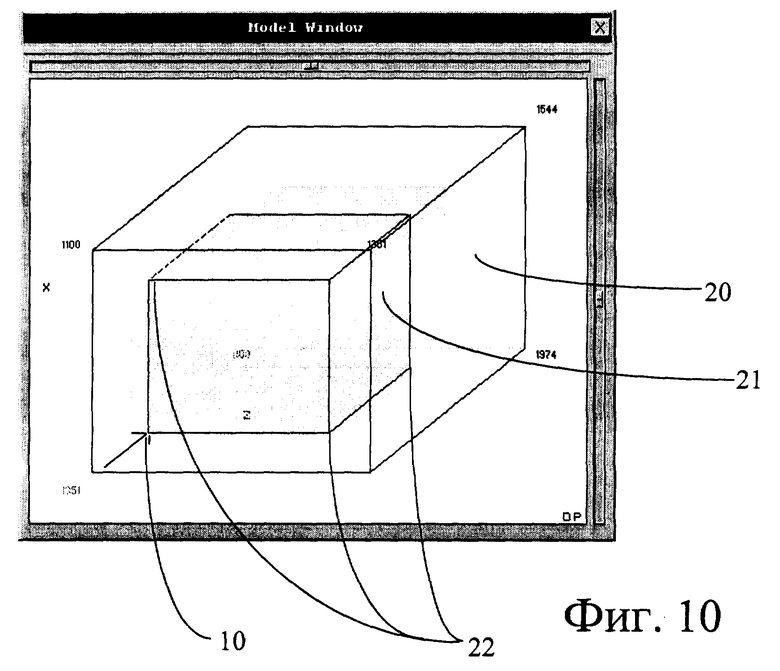
Пример 1. Использование при зуммировании трехмерного пространства.
Для изучения объекта 20 в трехмерном пространстве (фиг. 10), заданного прямоугольным параллелепипедом, ребра которого параллельны координатным осям, его изображают в аксонометрической проекции на плоском экране 2.
Данное представление часто используется в различных задачах 3D-графики. При этом внутрь объекта, называемого кубом данных, помещают различную информацию, например при помощи цветокодирования.
При изучении объекта часто возникает необходимость с целью более детального изучения выделить его часть в виде подобного ему параллелепипеда. Это производят для того, чтобы построить на экране 2 изображение выделенной части объекта в более крупном масштабе.
Для этого необходимо по каждой координатной оси X, Y, Z указать границы выделяемого параллелепипеда.
Поскольку при обычном использовании мыши 8 имеются только две степени свободы ее перемещения, то процесс выделения связан с необходимостью одновременной манипуляции с несколькими точками-объектами, например каждую грань перемещать по отдельности мышью или использовать по два слайдера на каждую грань, как в известном способе.
В соответствии с заявленным способом при зуммировании объекта 20 изображают на экране 2 в полупрозрачном или сетчатом виде параллелепипед 21, размеры и положение которого внутри объекта 20 будут изменять. Первоначально размер и положение параллелепипеда 21 совпадают с исходным.
Сразу изображают все восемь вершин 22 параллелепипеда 21, положение которых будут изменять предлагаемым способом с помощью двухмерной мыши, имитирующей трехмерную мышь. Для каждой из вершин 22 одновременно формируют дополнительные объекты 10 - вспомогательные системы координат.
Дополнительный объект 10 - вспомогательную систему координат строят в соответствии с изложенным способом, однако в одном направлении их строить не обязательно, поскольку вектора находятся на ребрах параллелепипеда 21, а в другом направлении их строят путем продолжения до пересечения с соответствующей гранью объекта 20.
Производят захват требуемой вершины 22 и перемещают ее в произвольном направлении внутри объекта 20. Одновременно перемещают три грани параллелепипеда 21, проходящие через эту вершину 22, при этом соответственно перемещаются и все вершины 22, находящиеся на этих гранях, и дополнительные объекты 10, соответствующие всеми перемещаемым вершинам 22.
Для увеличения информативности можно убирать изображения тех элементов объекта 20, которые не попадают внутрь параллелепипеда 21.
Повторяют операцию с требуемыми вершинами 22 в произвольном, определяемом пользователем порядке до тех пор, пока не будут выполнено выделение требуемого подпространства. После этого производят формирование подпространства в увеличенном масштабе. При необходимости выделенное подпространство зуммируют аналогичным образом, производя многократное вложенное зуммирование.
Пример 2. Прямой доступ к базе данных при анализе экономической информации.
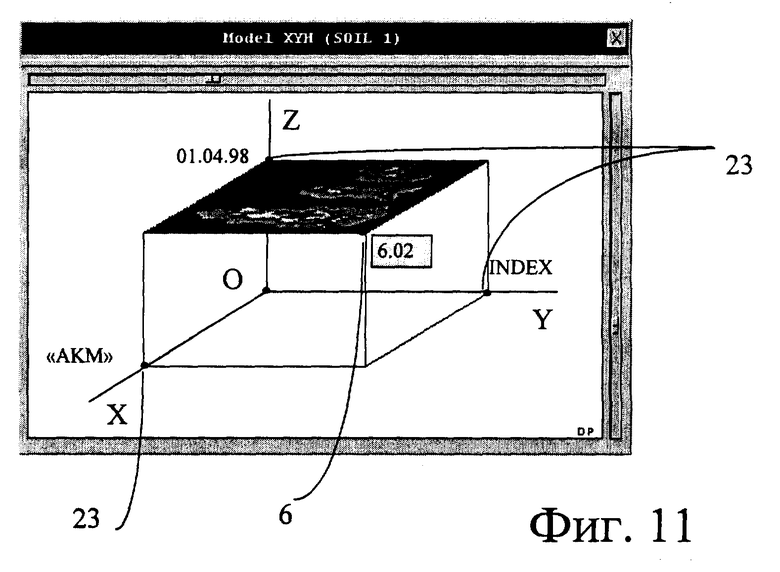
При необходимости изучения базы данных, содержащей информацию об экономических изменяющих во времени значениях показателей для совокупности предприятий, ее представляют в виде трехмерного дискретного пространства ( фиг. 11), например, следующим образом.
На первой оси X - оси предприятий откладывают точки, каждая из которых соответствует одному предприятию. Если в базе данных описаны N предприятий, то на оси X будет N делений.
На второй оси Y - оси показателей откладывают точки, каждая из которых соответствует одному показателю. Если в базе данных представлены М показателей, то на оси Y будет M делений.
На третьей оси Z - оси времени откладывают деления с шагом, соответствующим дискретности задания по времени значений показателей в базе данных. Например, если речь идет о бухгалтерских отчетах, то они могут быть заданы ежеквартально. Если в базе данных информация дана для L моментов времени, то на оси Z будет L делений.
Формируют объект 6 - точку в начальном положении, например в начале координат. Перемещают сформированную точку предложенным способом. Для получения дополнительной информации о координатах точки могут быть также использованы дополнительные средства для обозначения объекта 6 и его расположения в пространстве, например: измененный цвет объекта 6; тонкие линии прямоугольного параллелепипеда, ребра которого параллельны координатным осям X, Y, Z, одна вершина которого находится в начале координат, обозначенным точкой O, а другая совпадает с объектом 6; точки 23, соответствующие проекциям объекта 6 на оси X, Y, Z, так же, как это изображено на фиг. 3.
Рядом с каждой из точек 23 выводят информацию, расшифровывающую ее смысл, например в виде флажка с текстом. На оси X - название предприятия, на оси Y - название показателя, на оси Z - момент времени.
Кроме того, рядом с перемещаемым объектом в виде флажка выводится из базы компьютера 1 информация: значение выбранного показателя для данного предприятия в заданный момент времени.
Перемещая объект 6 по пространству, получаем первичную точечную информацию об объекте 6.
Далее, например, нажимают другой клавишей мыши 8 на объект 6 с тем, чтобы выделить ее, но не перемещать. Одновременно выделяются точки 23 - проекции объекта 6 на координатные оси X, Y, Z.
После этого осуществляют кликирование одной из точек 23. Если кликирована точка 23 на оси X, то формируют сечение, проходящее через эту точку 23 и перпендикулярное оси X, на которое выносят информацию для данного предприятия по всем показателям для всех моментов времени, любыми обычными средствами: цветокодированием или в виде графиков. Если кликирована точка на оси Y, то формируют сечение по аналогичным правилам, на которое выносят информацию для данного показателя по всем предприятиям для всех моментов времени. Наконец, если кликирована точка на оси Z, то формируют сечение (показано на фиг. 11), на которое выносят информацию для данного момента времени по всем показателям по всем предприятиям.
Построенные сечения позволяют изучать и выявлять взаимозависимости объекта 6 с элементами базы данных компьютера.
Заявленный способ в целом позволяет пользователю, благодаря принципу обратной связи через органы зрения, видеть направление перемещения курсора 7 мыши 8 и направление осей вспомогательной системы координат, что обеспечивает возможность перемещения курсора 7 по всем желаемым для него направлениям. Благодаря тому, что обеспечиваемое компьютером 1 каждое элементарное перемещение курсора 7 или мыши 8 очень мало, общее движение воспринимается непрерывным по всему пространству, а не направленным только вдоль одной оси.
Наиболее успешно заявленный способ перемещения объекта на экране монитора компьютера с помощью 2-D манипулятора типа компьютерной мыши может быть использован для анализа или изучения многомерных пространств в таких областях техники, как геофизика, медицина, экономика, управление, а также в различных компьютерных играх с объемным изображением на экране.
Источники информации:
1. Книга "X Window System Programming", Second Edition, Nabajyoti Barkakati, Samz Publishing, Indianapolis, 1994, p.509-518.
2. Патент США N 5511157, G 06 F 15/10, опубл. 23.04.96.

Изобретение относится к вычислительной технике и может быть использовано для формирования изображения на экране монитора. Техническим результатом является обеспечение удобства работы с пространством с размерностью больше двух на экране монитора и повышение информационной емкости экрана. Заявленный способ основан на формировании в изображенном пространстве на экране монитора двух объектов, которые совмещают, перемещают при помощи компьютерной мыши объекты путем приведения в соответствие перемещения компьютерной мыши с совершенным на экране перемещением объектов. 6 з.п. ф-лы, 11 ил.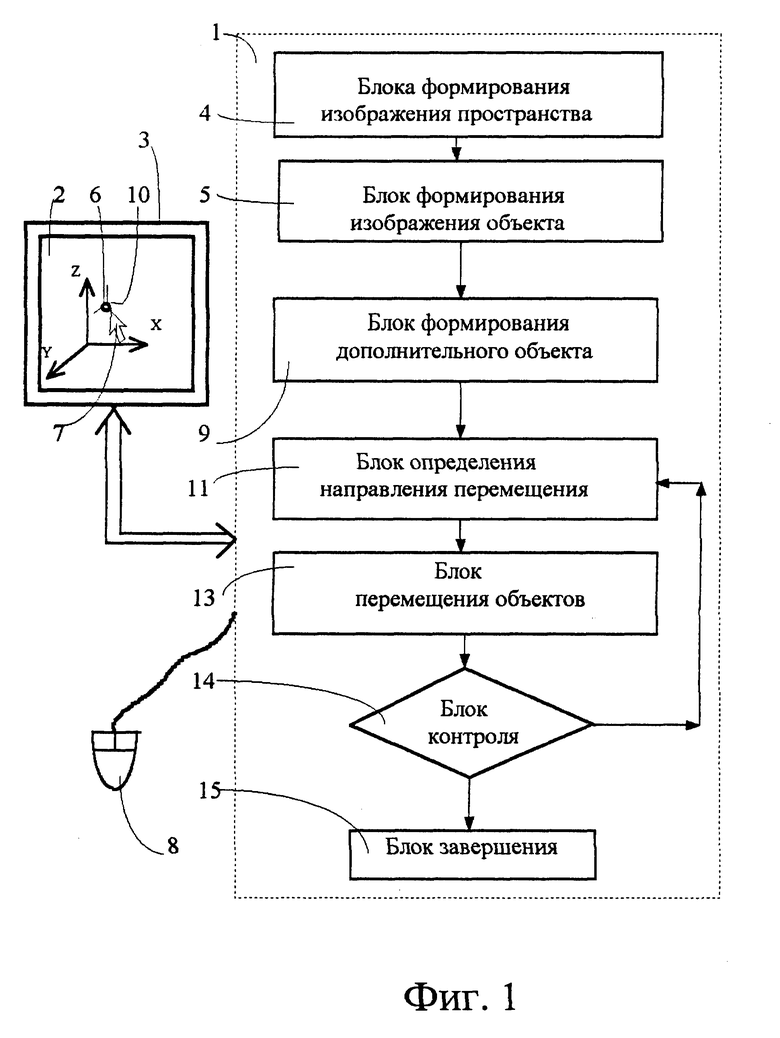
| US 5511157 A, 23.04.96 | |||
| RU 95107964 A1, 10.05.97 | |||
| Фигурнов В.Э | |||
| IBM PC для пользователя | |||
| - М.: Инфра М, 1997 с.337-338 | |||
| US 5588097 A, 24.12.96. |
Авторы
Даты
1999-06-20—Публикация
1998-09-09—Подача