Настоящее изобретение относится к области приборостроения рефлекторных систем и может быть использовано в самых различных областях техники, в частности в оптике, при создании как систем, формирующих изображение, так и систем концентрации светового потока, в рентгеновской технике и технике ускоренных микрочастиц, для обеспечения аналогичных операций, в локационной и навигационной технике и в системах самонаведения.
Распространение в среде гомоцентричных потоков частиц, в том числе и световых потоков, подчиняется фундаментальным законам физики, в частности законам отражения. При описании распространения потоков частиц лучевой моделью установлены законы отражения от зеркальных рефлекторов сферического и цилиндрического типов как для отражающих секторов, так и для отражающих сегментов, в том числе и в режиме полного внутреннего отражения (ПВО):
- Г. С. Мельников и др. "Методика лучевого описания растровых явлений в цилиндрической линзе при ее работе в области полного внутреннего отражения". Сб. тезисов докладов IV Всесоюзной конференции "Теоретическая и прикладная оптика", ГОИ, Л., 1986.
- Мельников Г.С., Ларионов С.А., Михеев П.А., Цветков Е.А. "Способ создания временных задержек светового потока". Патент РФ N 2109257 G 01 J 9/00, G 02 В 27/14 по Заявке N 95114222/25 от 07.08.1995. Официальный Бюллетень Российского Агентства по Патентам и Товарным Знакам "Изобретения" N 11 (II ч), 2108694-2109417, стр. 298 - 299, 20.04.1998г.; Патент N 2109257 зарегистрирован в Государственном реестре изобретений 20 апреля 1998 года.
Установлено также:
- Melnikov G.S. Gnosiology of fractality - fractal optics // Proc. SPIE -1997.-Vol.3010, P.58-68.,
- M. A. Gan, S.A. Larionov, G.S. Melnikov. "Elements of fractal optics for synchrogenerators and digital illumination devices", in Photonic Quantum Computing, StevenP. Hotaling, Andrew R. Pirich, Editors, Proceedings of SPIE Vol. 3076, p.207.219 (1997)"; Internet: http://www.spie.org//web/abstracts/ 3000/3076.html, page 15 (1998),
- Мельников Г. С. Поверхности текущих фокусов и семейств каустик лучей многократного отражения от рефлекторов цилиндрического и сферического типов. //Оптический журнал.- 1999- Т. 66, N 1 - C.73-79.,
- Г. С. Мельников, А.С. Попов "Каустические поверхности при отражении и преломлении сферой гомоцентрических пучков лучей". Оптический журнал" том 68, N 4, стр 84-87, С-Пб, ГОИ, 1998г,
что в меридиональном сечении сегментов сферы и цилиндра, в периферийных областях внепараксиальных лучей выделяются зоновые структуры, в которых группируются лучи, претерпевающие от криволинейной поверхности сегментов одно-, двух- или I-кратное число отражений. При этом для I-кратных отражений получены общие параметрические зависимости, точно описывающие плоские кривые сечения каустик, гомоцентричных пучков лучей, формируемых в заданных точках пространства предметов.
Все вышесказанное позволило разработать способ и устройства, имеющие существенные отличительные признаки от прототипа, используемые для построения новых анаберрационных (свободных от сферических аберраций) двухзеркальных, а в ряде случаев и апланатических систем по конструктивным схемам, аналогичным схемам прототипа. В качестве прототипа данного изобретения нами выбраны способ и устройства, описанные в монографии Г.М. Попова "Современная астрономическая оптика". М.,"Наука", ГРФМЛ, 1988г., 189с.
Возьмем также как и в прототипе систему из двух зеркал, однако в отличие от прототипа будем последовательно рассматривать не только случай падения на первое зеркало, именуемое главным, лучей света параллельными пучками, а будем отыскивать математические описания в параметрическом виде сечения каустик и профилей анаберационных асферических поверхностей вторичного зеркала, именуемого контроотражательным для гомоцентричных потоков лучей, формируемых в любой, произвольно заданной точке пространства предметов.
Г. М. Попов при описании способов построения анаберрационных систем из двух зеркал рассматривает только случай, когда предмет находится в бесконечности (т.е. описывает аналитические способы построения анаберрационных и апланатических телескопов). Из геометрических построений по вышеописанной схеме Г. М. Попов образует систему из восьми уравнений, описывающих конструктивные элементы оптической системы. Эта система уравнений учитывает отступление от условий синусов (для частного случая), общий принцип Ферма для построения анаберрационных поверхностей и дифференциальный метод определения касательной кривой, заданной в полярных координатах.
Используя методы дифференциальной геометрии и условия существования единственного решения (Коши) для диф.уравнений, Г.М. Попов находит из системы уравнений декартовы координаты вторичного зеркала, а затем уточняет параметры главного зеркала. Как правило, поверхности этих зеркал, в результате, получаются асферическими, для которых определяются радиусы кривизны и квадраты их эксцентриситетов. В отдельных частных случаях по этой методике можно получить системы, свободные от аберраций комы, т.е. апланатические системы, включая системы высокой светосилы и системы с большими углами падения на зеркала.
Недостатками указанного способа являются: отсутствие общих решений для двухзеркальных систем, формирующих изображения точки на произвольно заданном расстоянии, приближенное задание параметров асферических поверхностей отражателей, что приводит к неопределенности результатов после изготовления отражающих поверхностей. Кроме того, способ прототипа не обеспечивает возможность построения систем, близких к апланатическим, с использованием пучков лучей, претерпевших многократное отражение от главного зеркала.
Цель изобретения состояла в том, чтобы обеспечить возможность построения двухзеркальных, анаберрационных и близких к апланатическим (по крайней мере с полным устранением сферических аберраций на главном зеркале и доведением аберраций комы до пределов допуска) систем с заданной светосилой, вплоть до A= 1: 1, при этом главное зеркало в предлагаемых системах представляет собой сегменты сферы с заданным телесным углом сегментирования, в том числе большим или равным 120o, и его форма после расчетов не корректируется и остается сферической, т.е. симметричной относительно начала координат, что обеспечивает возможность создания систем с внутренним сканированием фокальными матрицами приемников излучения и оптической стабилизацией изображений. При этом ставилась задача возможности точного задания поверхностей корректирующих зеркал как в процессе расчетов схем, так и для их использования в программах для станков с числовым программным управлением в процессе изготовления рефлекторов, для всех возможных систем, таких, например, как: концентратор гомоцентричного потока частиц, телескоп, объектив, микроскоп, осветитель, в том числе для систем, использующих пучки лучей, претерпевших многократное отражение от главного зеркала. Другими словами, ставилась задача разработки способа построения анаберрационных и, по возможности, апланатических корректоров для двухкомпонентных катоптрических систем с главным зеркалом сферической формы при одно- или многократном отражении от сферы гомоцентричных потоков лучей, исходящих из любой заданной точки пространства предметов и собираемых с помощью таких контроотражателей в любую заданную точку пространства изображений безаберрационно. Форма и пространственное положение анаберрационных корректоров должна задаваться едиными для всех указанных случаев параметрическими уравнениями, а частные случаи построения систем должны задаваться рядом численных условий на дискретные параметры уравнений.
Поставленные цели и задачи решаются на основе результатов теоретических и экспериментальных исследований, изложенных в упомянутых работах, и достигаются тем, что при построении систем в качестве главного зеркала используют шаровые сегменты отражателей как пустотелые, так и заполненные материалом, с показателем преломления, большим показателя преломления окружающей среды; перед ними в вершинной части главного зеркала, за поверхностью каустик (при однократных отражениях от сферы) или в любом конструктивно удобном месте (при многократных отражениях от сферы) размещается контроотражатель, выполненный в виде усеченного тела с анаберрационной поверхностью, отражающей падающие на нее лучи в конкретную заданную точку пространства - фокус. Задание анаберрационной поверхности осуществляется в виде поверхности вращения плоской кривой, характеризуемой в меридиональном сечении сферы точными параметрическими уравнениями, представляющими собой обобщенные многопараметрические векторные уравнения с порядком ≥ 4, заданные в декартовой системе координат; а в пространстве анаберрационные поверхности представляют собой внутренние или внешние поверхности вырожденных торов, в том числе и эпициклоидных торов.
Реализация предложенного способа основана на том, что при вводе в полость отражающего сегмента сферы (шара) светового потока, имеющего некоторый угол расходимости в меридиональной плоскости S, отдельные парциальные его составляющие будут иметь в точках падения на отражающую поверхность различные углы отражения, обусловленные различием в величинах углов падения.
Лучи при многократных и, в частности, при однократных отражениях от сферического рефлектора будут образовывать фигуры концентрации энергии, которые получили название катакаустик. Для описания частных случаев кривых сечения катакаустик многократного отражения гомоцентричных пучков из бесконечности и из точки на сфере нами получены общие формулы в виде параметрических уравнений j-каустик, описывающих плоские кривые механического происхождения. При нечетных j-каустики первых, вторых, третьих и т.д. отражений формируются гомоцентричными пучками лучей, исходящими из бесконечности. При четных j-каустики первых, вторых, третьих и т.д. отражений формируются гомоцентричными пучками лучей из точки на сфере и представляют собой обыкновенные эпициклоиды. Их уравнения зависят от радиуса главного зеркала r, показателя номера каустики j, связанного с числом отражений i формулой i=floor (j+1)/2 и текущего параметра ϕ (текущая фаза)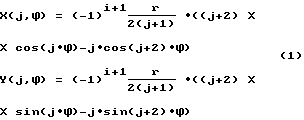
Примеры кривых сечения j-каустик лучей в сфере для j =1,2,3,4 приведены на фиг. 1. Уравнения (1) представляют собой параметрические уравнения обыкновенных эпициклоид (2) [при j=l и j=2 каустические кривые полностью совпадают с описанными ранее катакаустиками первых отражений гомоцентричных пучков лучей из точки в бесконечности и из точки на сфере соответственно (А. А. Савелов "Плоские кривые", ГИ Ф-МЛ, М.,293с.(1960г.) см. стр 117)],
x = (r0+mr0)•cos mt-mr0•cos(t+mt)
y = (r0+mr0)•sin mt-mr0•sin(t+mt) (1')
или в общем виде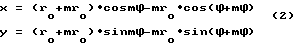
но отличающихся тем, что в (2) модуль m определяется из двух условий
rk=mr0 и 2rk+r0=r
где r - радиус окружности сечения главного зеркала;
rk - радиус "катящейся" окружности;
r0 - радиус "обкатываемой" окружности которые приводят к отношениям:
m=j/2 rk=rj/2(j+1) r0=r/(j+1)
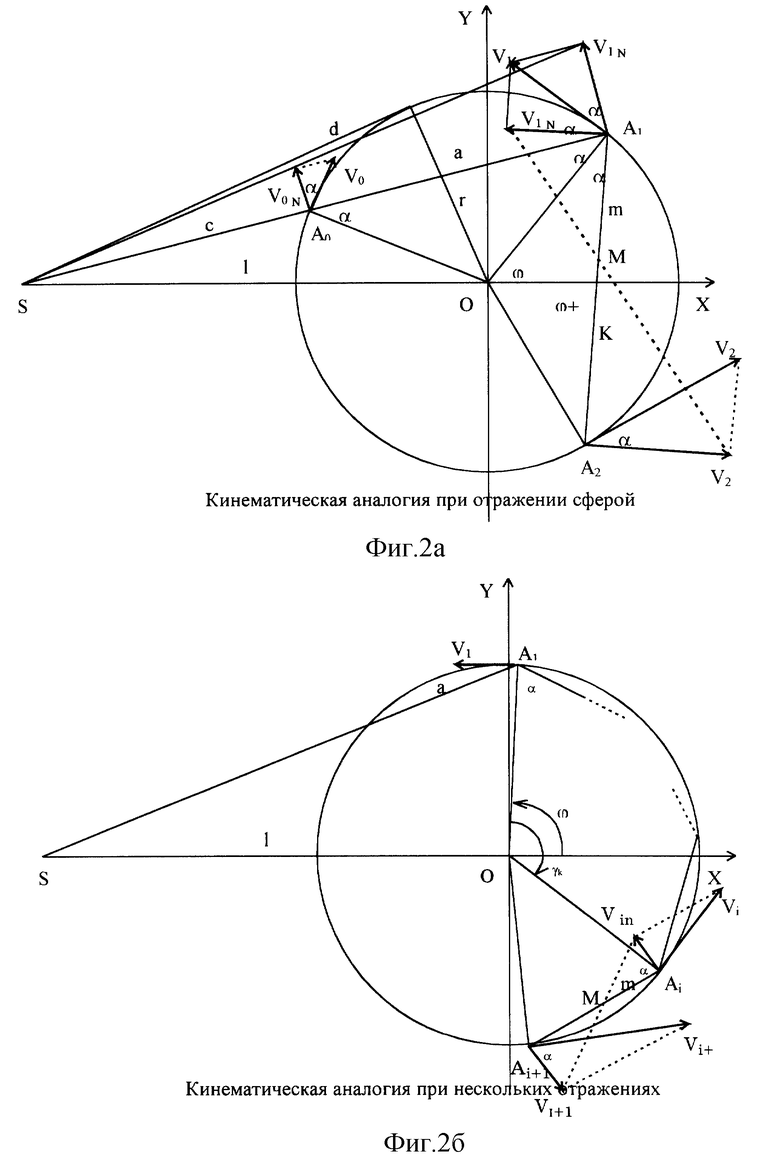
Нами, также получены выражения в общем виде, используемые для построения катакаустик гомоцентричных пучков лучей, формируемых в заданной точке пространства предметов. Из кинематической аналогии, предложенной А.С. Поповым (ОЖ том 68, N 4, стр 84-87, С-Пб, ГОИ, 1998 г.), следует, что в обобщенном виде они представляются параметрическими уравнениями
где r=r/l,
g=4+2r2 - 6r cos ϕ
ϕ угол, определяющий положение нормали OA1 в точке отражения выбранного луча (A1 лежит на отражающей сфере).
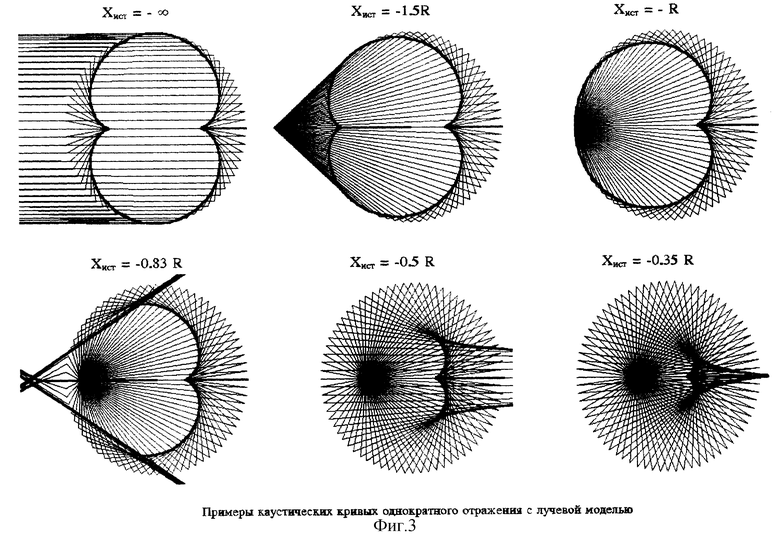
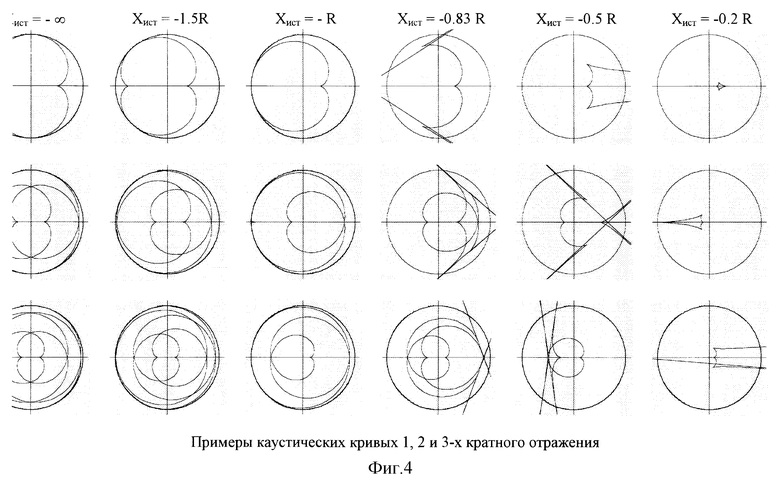
На фиг. 2 приведена схема, поясняющая вывод уравнения (3), а на фиг. 3 приведены характерные примеры каустических кривых и лучевой модели первых отражений. На фиг. 4 приведены их обобщения для катакаустик лучей первых, вторых и третьих отражений с выбранными положениями источника Xист = -∞, -1.5r, -r, - 0.83r, -0.5r, -0.2r, соответственно.
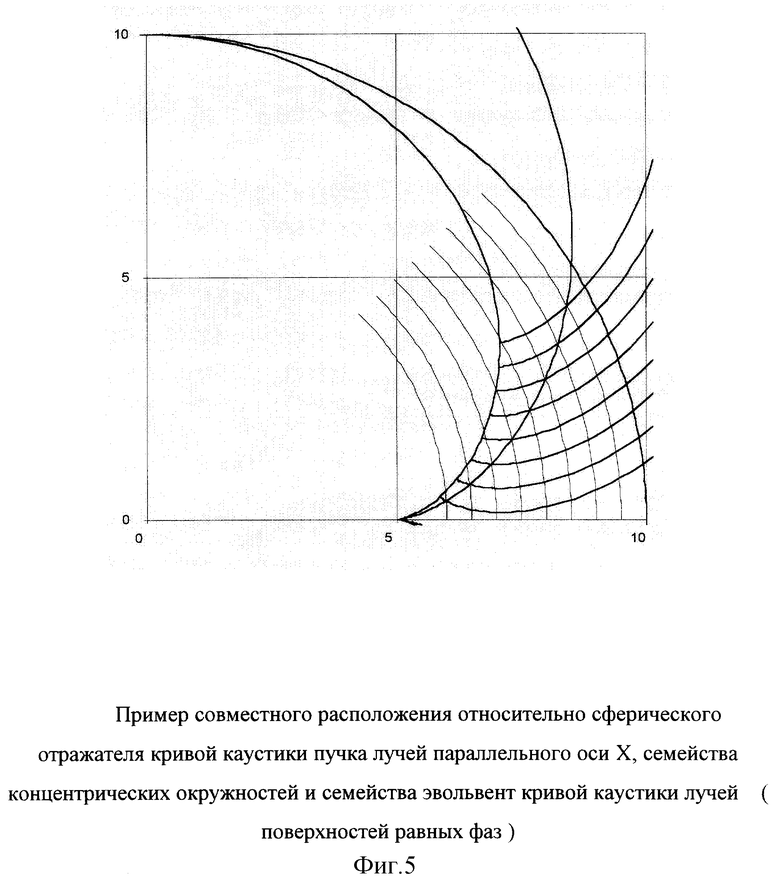
Таким образом, если известна форма кривой каустики, то из уравнения для тангенса угла наклона касательной к ней можно определить положение любого отраженного луча, а из уравнения эвольвенты к каустической поверхности - семейство поверхностей равных фаз, а по узловым точкам пересечения семейства поверхностей равных фаз и семейства окружностей, концентричных к поверхности главного зеркала, можно построить семейства анаберрационных поверхностей контроотражателей для каустик любых отражений I (фиг. 5.)
Названной последовательности операций отыскания профилей анаберрационных поверхностей контроотражательных зеркал можно избежать, используя обобщенные методы, первый этап которых изложен в статье в ОЖ том 68, N 4, стр 84-87, С-Пб, ГОИ, 1998г.
В основе обобщенного способа построения двухзеркальных систем используется математическая программа, позволяющая одновременно представлять лучевую модель отражения гомоцентричных пучков лучей от главного рефлектора и плоских кривых, описывающих сечения каустик этих потоков, формируемых в любой заданной точке пространства, расположенного перед главным зеркалом. Далее, после предварительного рассмотрения взаимного расположения каустической кривой и поверхности сегмента отражающей сферы выбирают удобное положение контроотражательного зеркала и требуемое положение точки фокуса двухзеркальной системы. На следующем этапе, другой частью подпрограммы строится лучевая модель всей системы и на нее накладывается кривая сечения контроотражательного зеркала, форма которого определяется из общего выражения (4).
Выражение (4) представляет собой аналитическое описание алгебраической плоской кривой, определяемой по точным обобщенным параметрическим уравнениям, в которых текущие координаты кривых X и Y представляются результирующим вектором в виде суммы двух векторов, один из которых неизменной длины, равной радиусу сферы r и вращающийся относительно центра сферы с текущей угловой фазой ϕ, а другой - вектор переменной длины и вращающийся относительно конца первого вектора с текущей угловой фазой (ϕ+α) , а амплитуда второго вектора изменяется пропорционально величине s, полученной из условия соблюдения принципа равенства длин пути лучей от точки источника излучения до заданного фокуса двухзеркальной системы для I-кратных отражений гомоцентричного пучка от главного сферического отражателя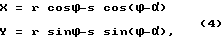
где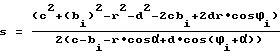
bi = b + (i -l)•a ϕi = ϕ-γi a = 2rcosα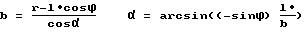
i-число отражений луча от главного зеркала. Остальные параметры ясны из фиг.2.
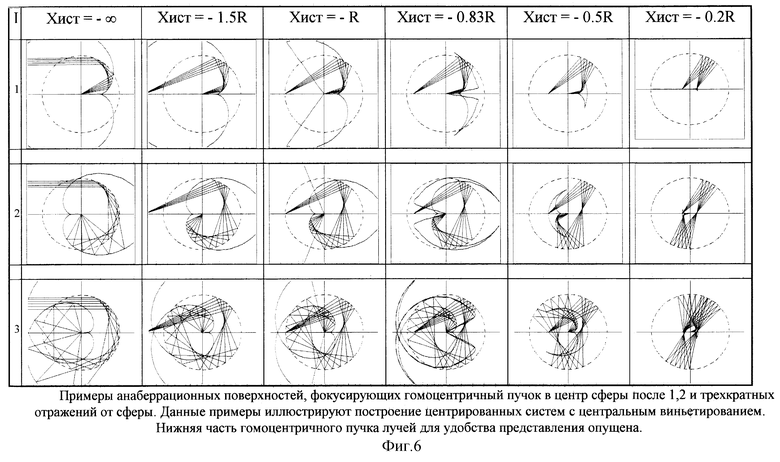
На фиг. 6 приведены кривые анаберационных поверхностей, которые получены с помощью уравнений (4) для контроотражательных зеркал, использующих каустики первых, вторых и третьих отражений соответственно, для случаев расположения источников гомоцентрических потоков в точках пространства предметной плоскости, аналогичных точкам, приведенным на фиг. 4.
Как следует из анализа выражений (4), они представляют собой обобщенные параметрические уравнения плоских кривых, имеющих в локальных областях точки возврата и точки разрыва первого и второго рода. Они получены прямым решением условия равенства геометрических длин путей для всех лучей исходного гомоцентрического потока, распространенного нами на каустики многократных отражений:
Lл = Xист+2r•i+Xиз+ΔC = const
Здесь: Lл - суммарная длина каждого парциального луча, исходящего из точки источника, расположенного на расстоянии Xист=-1 от центра сферы, отражаемого от этой сферы i-раз и один раз от анаберрационного корректора и направляемого этим корректором в точку изображения, расположенную на расстоянии Xиз= 1из, отсчитываемого от центра сферы r; ΔC - произвольная постоянная, обеспечивающая возможность получения бесконечного числа замкнутых анаберрационных кривых сечения поверхностей контроотражателей, каждый из которых удовлетворяет заданным условиям построения анаберрационных двухкомпонентных катоптрических систем по всем лучевым траекториям I-х отражений полной сферой. Для заданных параметров построения оптических систем из бесконечного числа анаберрационных корректоров выбираются конструктивно-пригодные корректоры, обеспечивающие соблюдение "обобщенного условия синусов", предложенного Давилом и Саха (Davila P.M., Saha Т.Т. //Appl. Opt.-1984 -V. 23, N. 20- P.3660-3666), которое в частном случае (при f'0=1) имеет вид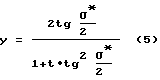
где t - параметр, определяющий величину комы, σ* - последний угол (σ*/2 - половинный угол встречи крайних лучей в точке Xиз). При t=0 это выражение принимает вид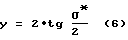
Выбирая корректор, обеспечивающий минимизацию последнего угла σ* в соответствии с (6) или (5), при заданном размере изображения "y" всегда может быть найдена схема двухзеркального апланата. В отдельных случаях возможно придется накладывать ограничения на величину рабочего телесного угла сегментирования главного зеркала. Это утверждение следует из анализа уравнения (4) с учетом всюду плотного заполнения пространства вокруг главного зеркала кривыми сечения анаберрационных корректоров за счет варьирования произвольной постоянной ΔC.
Учитывая вышесказанное, можно констатировать, что нами найден способ, при котором при заданных координатах точечного источника (Xист) и заданных координатах главного фокуса двухзеркальных систем (Xиз) относительно отражающей сферы и строятся различные рефлекторные системы с относительными отверстиями A=D/f вплоть до A = 1:1, используя участки отражающей сферы с любым телесным углом сегментирования рабочей поверхности первых отражений при затененном участке телесного угла сферы от 3...5o до 60o, используемого для размещения анаберрационного контроотражательного зеркала, приемников излучения и кардановых механизмов подвеса, гиростабилизации и совместного с контроотражательным зеркалом перемещения внутри сферы для организации режимов внутреннего сканирования входным полем зрения приемных матриц по широкому полю обзора.
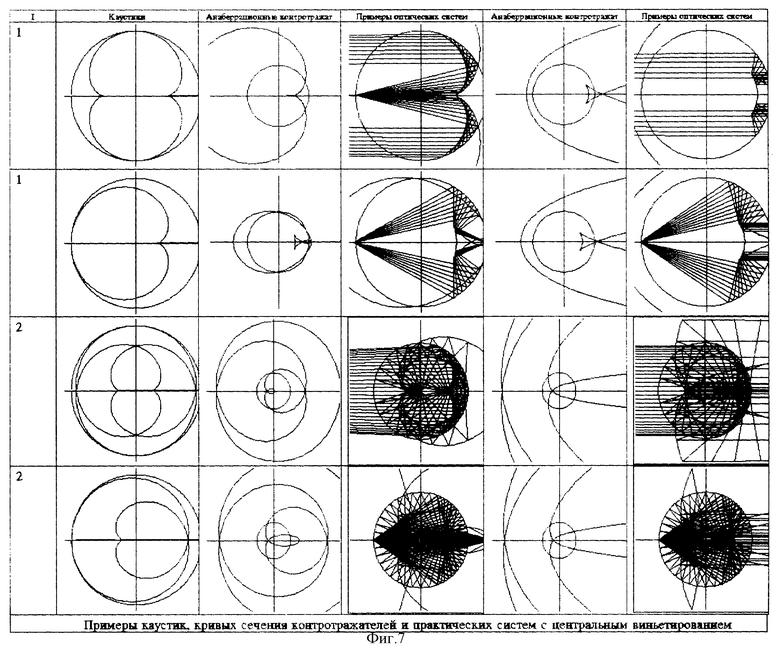
Примеры возможных схемных решений приведены на фиг. 6 и 7.
Как видно из приведенных схем, на которых также представлен геометрический ход лучей, системы состоят из главных зеркал, выполненных на сегментах сферы и контроотражательных зеркалах, представляющих собой отражающие поверхности с выведенными для них точными параметрическими уравнениями кривых их сечения в меридианальной плоскости. В силу того, что в качестве главного зеркала используются глубокие сферы, это позволяет получить оптические устройства, формирующие и не формирующие изображения с очень высокими энергетическими показателями (числовой апертурой) при существенно меньших габаритах систем по сравнению с известными аналогами на традиционных схемах, использующих только области приема лучей в центральной части отражателей сферического типа, собираемых ими в фокусе, расположенном в точке на оси на середине радиуса сферы.
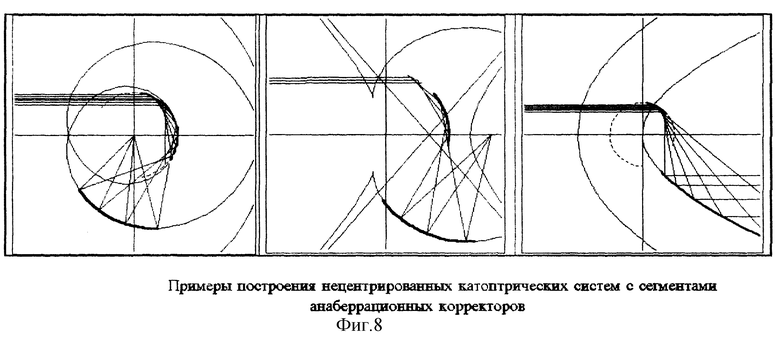
На фиг. 6 и 7 приведены центрированные оптические системы с центральным виньетированием, однако использование лучей многократного отражения обеспечивает возможность построения компактных децентрированных оптических систем без виньетирования с использованием участков главного зеркала для минимизации габаритов оптических систем и корректором лучей последнего отражения. Варианты нецентрированных оптических систем приведены на фиг. 8. По предварительной оценке, уменьшение габаритов и весов предлагаемых систем составит по отношению к аналогам экономию в 3...5 раз с учетом экономии массы и габаритов механических платформ перемещения оптических приемопередающих систем, построенных по традиционным схемам.
Предложенные схемы, в которых возможно обеспечение перемещения жесткой сборки "приемник (иточник) излучения - анаберрационное и апланатическое контроотражательное зеркало" вокруг центра сферы, позволяют обеспечивать простое сканирование оптической оси и вводить дополнительно способы оптической стабилизации.
С учетом того, что для сегментов сферы или цилиндра главого зеркала, определяемых показателем сегментирования К (где К представляет собой число, на которое делится полная окружность меридионального сечения сферы (цилиндра) при сегментировании окружности), получены общие выражения, определяющие угловые растворы зон наблюдения для систем, использующих для нецентрированных систем зоны с i-ми отражениями,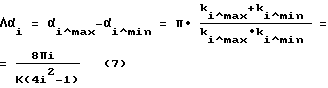
где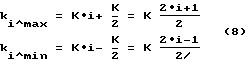
("M.A. Gan, S.A. Larionov, G.S. Melnikov. Proceedings of SPIE Vol. 3076, p. 207. . . 219 (1997)), вполне очевидно, что при использовании режимов многократного отражения мы всегда имеем дело с явлением оптической редукции.
Другими словами, переход от режима однократных отражений к режимам i-кратных отражений за счет изменения формы контроотражательного зеркала позволяет в q - раз изменять угловое увеличение зеркальных оптических систем,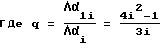 - коэффициент оптической редукции i-кратных отражений.
- коэффициент оптической редукции i-кратных отражений.
Кроме того, в оптических системах, использующих главное отражательное зеркало в виде глубокой сферы и перемещаемой внутри этого зеркала относительно центра сферы жесткой сборки "фотоприемник - контроотражательное зеркало", которые могут быть выполнены с малыми габаритами и массой, существенно облегчается задача построения систем гиростабилизации оптической оси, т.к. в них не требуется стабилизации главного зеркала.
Таким образом, устройства, реализующие заявленный способ построения двухзеркальных рефлекторов с главным сферическим зеркалом и контроотражательными зеркалами выполняемыми в виде асферических поверхностей, построенных методом создания фигур вращения профилей кривых с точным параметрическим описанием, полученным для систем с любой кратностью отражения от главного зеркала, представляют собой новый класс рефлекторных систем, который может быть реализован с помощью новых технологий изготовления, например, методом алмазного точения на станках с числовым программным управлением и аналитическим заданием профилей обрабатываемых деталей.
| название | год | авторы | номер документа |
|---|---|---|---|
| ОПТИКО-ЭЛЕКТРОННАЯ КОМПЛЕКСИРОВАННАЯ СИСТЕМА НАБЛЮДЕНИЯ И РАСПОЗНАВАНИЯ, РАБОТАЮЩАЯ В УФ, ВИДИМОЙ И ИК ОБЛАСТЯХ СПЕКТРА | 2005 |
|
RU2305303C2 |
| СПОСОБ СОЗДАНИЯ СЕМЕЙСТВА КОМПЛЕКСИРОВАННЫХ СИСТЕМ НАБЛЮДЕНИЯ, РАСПОЗНАВАНИЯ И ПРИЦЕЛИВАНИЯ НА ОСНОВЕ СЕМЕЙСТВА УНИВЕРСАЛЬНЫХ ОБЪЕКТИВОВ И КОМПЛЕКСИРОВАННАЯ СИСТЕМА | 2003 |
|
RU2273036C2 |
| ПАРАМЕТРИЧЕСКИЙ ГЕНЕРАТОР СВЕТА | 2018 |
|
RU2688860C1 |
| ЗЕРКАЛЬНО-ЛИНЗОВЫЙ ОБЪЕКТИВ | 2022 |
|
RU2798087C1 |
| Рефлектометр для вогнутых зеркал | 1991 |
|
SU1824547A1 |
| Интерферометр для контроля формы сферических поверхностей линз | 1982 |
|
SU1068699A1 |
| ОПТОЭЛЕКТРОННЫЙ ДАТЧИК ДАВЛЕНИЯ | 1990 |
|
RU2006016C1 |
| УСТРОЙСТВО ДЛЯ ИЗМЕРЕНИЯ ОБЪЕКТОВ ГЛАЗНОГО ДНА | 1997 |
|
RU2137415C1 |
| ЗЕРКАЛЬНЫЙ ОБЪЕКТИВ | 2018 |
|
RU2690034C1 |
| ПРИБОР СТАТИЧЕСКОГО ОБЗОРА | 1998 |
|
RU2147760C1 |
Способ включает определение формы вторичного зеркала, которая представляет собой асферическую зеркальную поверхность, выполненную в виде фигуры вращения алгебраической плоской кривой, определяемой по точным обобщенным параметрическим уравнениям. При этом текущие координаты кривых Х и Y представляются результирующим вектором в виде суммы двух векторов, один из которых неизменной длины, равной радиусу сферы r и вращающийся относительно центра сферы с текущей угловой фазой ϕ, а другой - вектор переменной длины и вращающийся относительно конца первого вектора с текущей угловой фазой (ϕ+α), а амплитуда второго вектора изменяется пропорционально величине s, получаемой для лучей с любой кратностью отражения от главного зеркала из условия соблюдения равенства длин пути лучей от точки источника излучения до заданного фокуса двухзеркальной системы. Обеспечивается создание двухзеркальных анаберрационных и апланатических систем с заданной светосилой вплоть до 1:1. 8 ил.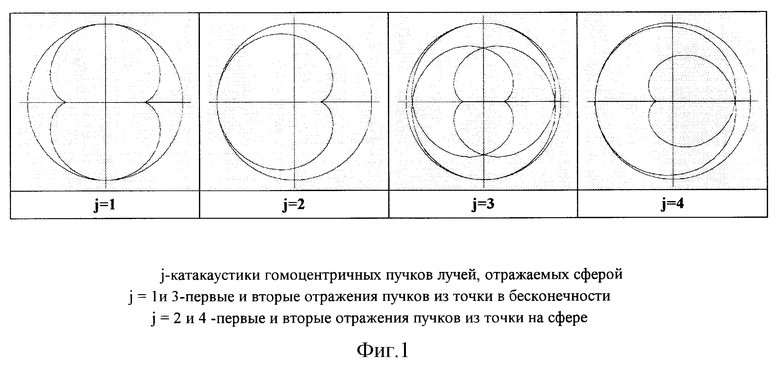
Способ создания двухзеркальных анаберрационных и апланатических систем с главным зеркалом в виде сегмента сферы, при котором определяют форму вторичного зеркала, отличающийся тем, что форма вторичного зеркала представляет собой асферическую зеркальную поверхность, выполненную в виде фигуры вращения алгебраической плоской кривой, определяемой по точным обобщенным параметрическим управлениям, в которых текущие координаты кривых X и Y представляют результирующим вектором в виде суммы двух векторов, один из которых неизменной длины, равной радиусу сферы r и вращающийся относительно центра сферы с текущей угловой фазой ϕ, а другой - вектор переменной длины и вращающийся относительно конца первого вектора с текущей угловой фазой (ϕ+α), а амплитуда второго вектора изменяется пропорционально величине s, получаемой для лучей с любой кратностью отражения от главного зеркала из условия соблюдения равенства длин пути лучей от точки источника излучения до заданного фокуса двухзеркальной системы.
| Попов Г.М | |||
| Современная астрономическая оптика | |||
| - М.: Наука, 1988 | |||
| ЛЕКАРСТВЕННОЕ СРЕДСТВО ДЛЯ ЛЕЧЕНИЯ ЖЕЛЕЗОДЕФИЦИТНОЙ АНЕМИИ | 2000 |
|
RU2197962C2 |
| US 5144497 А, 01.09.1992 | |||
| US 4033678 А, 05.07.1977 | |||
| ЗЕРКАЛЬНЫЙ ОБЪЕКТИВ ТЕЛЕСКОПА | 1992 |
|
RU2010272C1 |
Авторы
Даты
2000-09-10—Публикация
1998-07-21—Подача