Изобретение относится к области пчеловодства и может быть использовано для диагностирования состояний пчелиной семьи.
Известен способ распознавания состояний пчелиной семьи и других коллективных насекомых по издаваемому акустическому шуму путем его спектрального анализа и измерения амплитуд отдельных спектральных составляющих [1, 2]. Его основным недостатком является весьма существенные вариации результатов измерений отдельных спектральных составляющих, полученные по различным реализациям акустического сигнала. В частности, для получения приемлемой достоверности распознавания состояния пчелиной семьи по амплитудному спектру необходимо проводить усреднение измеряемых значений отдельных спектральных составляющих путем интегрирования в течение 30 с (длительность реализации звукового сигнала пчелиной семьи должна быть не меньше 30 с.). Для обработки такой реализации путем спектрального разложения (прямое преобразование Фурье) [3] потребуется значительное время для вычисления. Именно это обстоятельство препятствует использованию числового метода спектрального разложения предварительно дискретизированного акустического сигнала, что могло бы существенно повысить быстродействие и точность измерения спектральных составляющих сигнала.
Акустический сигнал пчелиной семьи не является детерменированным [1]. Его можно считать стационарным эргодическим случайным сигналом [4]. Однако для стационарного и эргодического случайного процесса амплитуды его спектрального разложения также являются случайными величинами с определенным законом распределения. Поэтому для практического использования этого способа распознавания состояний пчелиной семьи приходится находить математические ожидания амплитуд отдельных спектральных составляющих, для чего приходится усреднять спектры, полученные по многим реализациям сигнала.
Кроме того, в описываемом методе распознавание тех или иных состояний пчелиной семьи предлагалось вести по наличию (или отсутствию максимумов) спектральной плотности в определенных частотных диапазонах. Однако, как видно из представленных в [1] амплитудных спектров, измеренных при различных состояниях пчелиной семьи, такой способ распознавания не будет обладать высокой достоверностью, поскольку
а) спектры сигналов, соответствующих конкретным состояниям пчелиной семьи, могут иметь не один, а несколько максимумов спектральной плотности;
б) спектры сигналов, соответствующих различным состояниям пчелиной семьи, могут иметь локальные максимумы спектральной плотности в одних и тех же частотных полосах, только для одного состояния они будут глобальными, а для другого - локальными;
в) на относительную величину локальных максимумов спектральной плотности и их положение (на оси частот) существенно влияют время суток, календарное время, погодные условия, численность пчелиной семьи, внешние раздражители (шум, тряска, удар и т.д.) и другие факторы, соответствующие моменту измерения спектра акустического сигнала.
Поэтому для достоверного распознавания конкретных состояний пчелиной семьи необходимо не просто определить наличие максимума спектральной плотности в данной узкой полосе частот, а провести сопоставительный анализ значений спектральной плотности для нескольких наиболее характерных для распознавания данных состояний областей частот.
Величина средней мощности сигнала звуков пчел в элементарном диапазоне частот есть результат усреднения ее по множеству реализаций, и поэтому не является случайной, а определяется функцией спектральной плотности мощности, т. е. энергетическим спектром. Поэтому акустические сигналы пчелиной семьи корректно характеризовать не спектральной функцией его реализации, которая должна иметь длительность не меньше 30 с, а спектральной плотностью мощности, которую можно вычислить из автокорреляционной функции, определяемой по одной очень короткой реализации (значительно меньше 30 с) [4].
Технической задачей, на решение которой направлено предлагаемое изобретение, является обеспечение возможности достоверного распознавания состояния пчелиной семьи по одной короткой реализации акустического сигнала, создаваемого пчелиной семьей. Поэтому первой задачей, которую необходимо решить, является определение минимальной длительности реализаций, по которой можно достоверно вычислить энергетический спектр. Для этого был проведен анализ влияния длительности реализаций на вычисленный по ней энергетический спектр. Результаты этого анализа можно проиллюстрировать на примере.
Пример
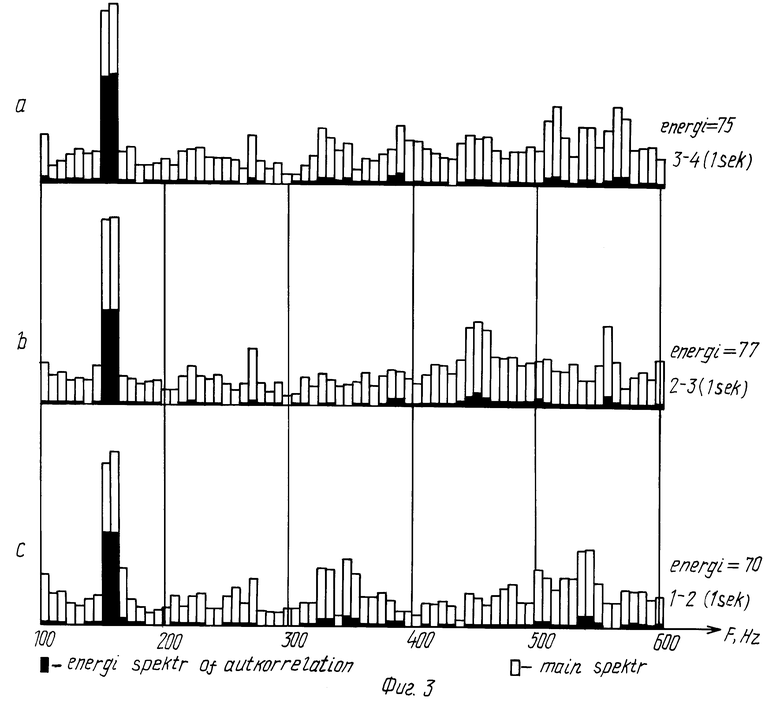
Нами были проведены три эксперимента по выбору минимальной длительности реализаций, осуществлялся анализ трех реализаций одинаковой длительности (фиг. 1 - фиг. 3), взятых из одного и того же сигнала, соответствующего случаю, когда в пчелином гнезде находятся две матки (при создании новой пчелиной семьи матка оказалась на вынутой рамке, с применением этой рамки создавался отводок, матка не была замечена пчеловодом и в новую пчелиную семью была подсажена в клетке другая матка, в итоге новая матка не принималась). Получены реализации, которые расположены друг за другом.
Из сопоставления полученных спектров сделаны следующие выводы:
1. При длительности реализаций, равной 0,2 с, амплитудные и энергетические спектры соседних реализаций существенно отличаются, причем энергетические спектры коррелируют с амплитудными (фиг. 1).
2. При последовательном увеличении длительности реализаций до 0,5 с и 1 с различия между энергетическими спектрами уменьшаются.
3. В энергетических спектрах реализаций длительностью в 1 с основная мощность сигнала локализуется в узком частотном диапазоне (140-160 Гц), в то время как амплитудные спектры хотя и имеют максимум на этих частотах, но распределены более равномерно по всему анализируемому частотному диапазону (от 100 до 600 Гц).
Однако сигналы общего шума пчел могут содержать звуки отдельных пчел (если они издают звуки в непосредственной близости от микрофона), существенно искажающие спектр сигналов. Поскольку для уменьшения времени вычислений необходимо использовать как можно более короткие реализации (порядка 1 с), то необходим выбор реализаций, свободных от доминирующего звука отдельных пчел. Отбор таких реализаций представляет вторую задачу, которую необходимо решить. Критерием отбора пригодных реализаций является идентичность их моментов распределения. Использовать для этих целей моменты первого порядка (математические ожидания) нельзя, т.к. сами сигналы являются центрированными (т.е. их математические ожидания равны нулю). Из остальных моментов наиболее просто вычисляются моменты второго порядка (т.е. дисперсия). Он и принят в качестве критерия идентичности реализаций. Практически проводится дискретизация и запись 3-5 последовательных реализаций длительностью в 1 с и вычисляются их дисперсии. Если дисперсии отдельных реализаций отличаются незначимо, то по любой из них находится автокорреляционная функция, затем проводится ее спектральное разложение, и по соотношению отдельных составляющих этого спектрального разложения судят о состоянии пчелиной семьи. Согласно [3, 4] спектральное разложение (прямое преобразование Фурье) от автокорреляционной функции имеет вид (1)
(1)
где (2)
(2)
есть автокорреляционная функция случайного сигнала и представляет собой функцию спектральной плотности мощности случайного сигнала. Для стационарных эргодических процессов эта функция не случайна и остается постоянной для любой реализации случайного сигнала. Значения отдельных спектральных составляющих этой функции, вычисленные по любой из реализаций одного и того же случайного сигнала, имеют гораздо меньшие вариации, чем амплитуды тех же спектральных составляющих исходного сигнала. Наиболее приемлемым способом определения функции спектральной плотности мощности является числовой, поскольку аналоговыми методами получить автокорреляционную функцию случайного сигнала сложно.
Однако при численном методе определения энергетического спектра случайного сигнала для очень коротких реализаций сигнала существенное значение имеют частота дискретизации исходного аналогового сигнала, величина шага квантования при расчете автокорреляционной функции и частотное разрешение при расчете по ней энергетического спектра [4]. При выборе этих величин необходимо руководствоваться необходимостью обеспечения достаточной достоверности получаемого спектра, т.е. минимальных различий спектров, получаемых по коротким реализациям одного и того же стационарного случайного процесса, и минимум затрат машинного времени, необходимого для анализа спектра.
Выбор частоты дискретизации исходного сигнала обычно осуществляют в соответствии с теоремой Котельникова. Однако поскольку наиболее информативной частью спектра акустических шумов пчелиной семьи является диапазон от 100 до 600 Гц, в то время как частотный диапазон самих сигналов простирается до десятков кГц, то выбор частоты дискретизации здесь не является тривиальным вопросом. Если выбрать частоту дискретизации, ориентируясь на верхнюю границу интересующего нас частотного диапазона (fд = 1200-1500 Гц), то наличие в сигнале частот свыше 600 Гц приведет к дополнительному разбросу спектров отдельных реализаций одного и того же сигнала. С другой стороны, увеличение частоты дискретизации будет приводить к резкому увеличению объема вычислительных работ и необходимых ресурсов оперативной памяти ЭВМ, что нежелательно. Поэтому наилучшим решением является сохранение низкой частоты дискретизации (1200-1500 Гц) при предварительной частотной фильтрации исходного аналогового сигнала с выделением из него интересующего нас частотного диапазона (100-600 Гц). При этом дополнительного разброса спектров отдельных реализаций происходить не будет.
Шаг квантования при расчете автокорреляционной функции обычно выбирается равным шагу дискретизации исходного сигнала. Шаг квантования по частоте при расчете энергетического спектра должен выбираться из следующих соображений. Для удобства анализа и надежного распознавания отдельных состояний пчелиной семьи по энергетическому спектру желательно разделить весь частотный диапазон на 10-12 полос и получать усредненные значения спектральной плотности для этих полос. В этом случае ширина каждой частотной полосы составит 40-50 Гц. Для получения достоверного усредненного значения спектральной плотности для каждой частотной полосы достаточно 5-10 значений. Отсюда, достаточное частотное разрешение при расчете энергетического спектра составляет Δf = 5 Гц.
Существенными отличительными признаками предлагаемого способа распознавания состояний пчелиной семьи по издаваемому ею акустическому шуму, использующему вычисление энергетического спектра короткой реализации сигнала, являются предварительная аналоговая частотная фильтрация анализируемого сигнала с выделением наиболее информативного частотного диапазона 100-600 Гц, что позволяет устранить дополнительный разброс спектральных составляющих, полученных по различным реализациям сигнала, при сохранении низкой частоты дискретизации; разделение всего анализируемого частотного диапазона энергетического спектра на небольшое число полос с вычислением усредненных для данных полос значений спектральной плотности, и идентификация различных состояний пчелиной семьи путем сопоставительного анализа усредненных значений спектральной плотности для этих полос. Кроме того, для повышения достоверности распознавания при очень коротких реализациях с целью исключения из анализа звуков помех, издаваемых отдельными пчелами, осуществляют выбор реализаций по критерию незначимых различий из дисперсий.
Источники информации
1. Еськов Е. К. Акустическая сигнализация общественных насекомых. М.: Наука. - 1979.
2. Еськов Е.К. Управление процессами жизнедеятельности медоносных пчел и их оптимизация. М.: Всесоюзная академия сельскохозяйственных наук имени В.И. Ленина. - 1982.
3. Баскаков С. И. Радиотехнические цепи и сигналы. М.: Высшая школа - 1983.
4. Бендат Дж., Пирсол А., Измерение и анализ случайных процессов. Пер. с англ. М.: Мир - 1971.
5. Дьяконов В.П. Справочник по алгоритмам и программам на языке бейсик для персональных ЭВМ. - М.: Наука, главная редакция физико-математической литературы. - 1987.

Изобретение предназначено для использования в пчеловодстве и состоит в том, что по издаваемому акустическому шуму пчелиной семьи вычисляют энергетический спектр реализации дискретизованного сигнала, состоящий в том, что исходный аналоговый сигнал предварительно подвергают частотной фильтрации с выделением наиболее информативного частотного диапазона, например 100-600 Гц, затем сигнал дискретизируют и из него выбирают 3-5 коротких реализаций длительностью 0,5-1,0 с, отвечающих условию незначимых различий их дисперсий, и по одной из них рассчитывают энергетический спектр, который делят на 10-12 частотных полос, для которых рассчитывают усредненные значения спектральной плотности и производят распознавание состояния пчелиной семьи путем сопоставительного анализа, усредненных значений спектральной плотности этих же полос частот для диагностируемого состояния пчелиной семьи. 3 ил.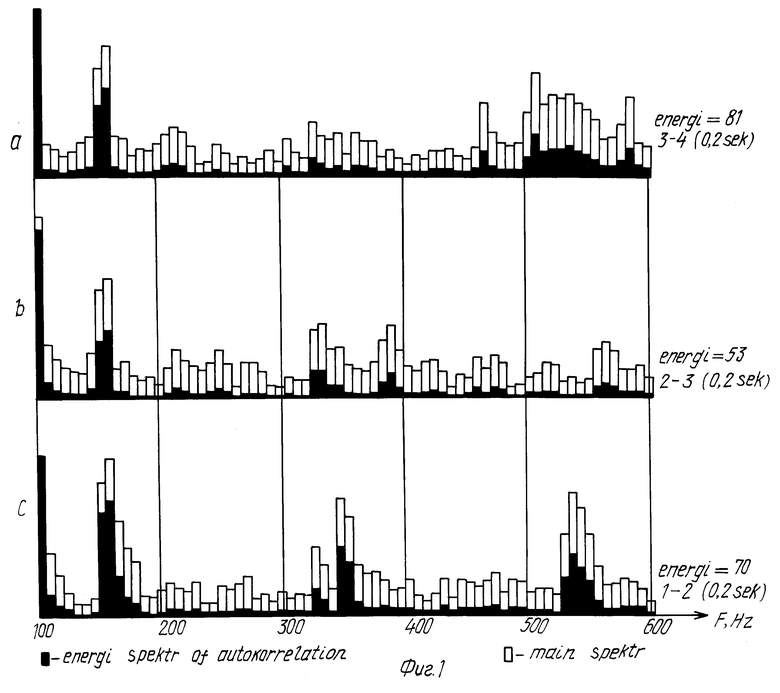
Способ диагностирования состояний пчелиной семьи по издаваемому ею акустическому шуму, использующий численное разложение акустического сигнала путем вычисления энергетического спектра по автокорреляционной функции реализации дискретизованного сигнала, отличающийся тем, что исходный аналоговый сигнал предварительно подвергают частотной фильтрации с выделением наиболее информативного частотного диапазона, например 100 - 600 Гц, затем сигнал дискретизируют и из него выбирают 3 - 5 коротких реализаций длительностью 0,5 - 1,0 с, отвечающих условию незначимых различий их дисперсий, и по одной из них рассчитывают энергетический спектр, который делят на 10 - 12 частотных полос, для которых рассчитывают усредненные значения спектральной плотности и производят распознавание состояния пчелиной семьи путем сопоставительного анализа, усредненных значений спектральной плотности этих же полос частот для диагностируемого состояния пчелиной семьи.
| АВТОМАТИЗИРОВАННАЯ СИСТЕМА ДЛЯ КРУГЛОГОДИЧНОГО СОДЕРЖАНИЯ И НАБЛЮДЕНИЯ ЗА ЖИЗНЕДЕЯТЕЛЬНОСТЬЮ ПЧЕЛИНЫХ СЕМЕЙ | 1992 |
|
RU2060653C1 |
| УСТРОЙСТВО ДЛЯ АКУСТИЧЕСКОГО КОНТРОЛЯ ЗА СОСТОЯНИЕМ ПЧЕЛИНОЙ СЕМЬИ | 1996 |
|
RU2099942C1 |
| RU 2055473 C1, 10.03.1996 | |||
| RU 2000051 C1, 07.09.1993 | |||
| Выгодский М.Я | |||
| Справочник по высшей математике | |||
| - М.: Физматлит, 1995, с | |||
| МЕТАЛЛИЧЕСКАЯ ШАРНИРНАЯ СЕТКА | 1922 |
|
SU603A1 |
Авторы
Даты
2001-01-20—Публикация
1998-07-13—Подача