Изобретение относится к области пчеловодства и может найти применение в практической работе на индивидуальных и коллективных пасеках.
Известен способ распознавания состояний пчелиной семьи по издаваемому ею акустическому шуму путем его спектрального анализа и измерения амплитуд отдельных спектральных составляющих [1, 2]. Его недостатками являются:
отсутствие четких количественных критериев распознавания конкретных состояний пчелиных семей и определенного алгоритма классификации (указываются лишь качественные отличия амплитудных спектров при различных состояниях);
большое число информативных признаков, по которым должно вестись распознавание различных состояний (этими признаками являются средние значения сигнала в узких частотных полосах шириной 25-30 Гц, причем всего таких частотных полос - 20-25 и они перекрывают диапазон частот от 60 до 600 Гц).
Эти недостатки затрудняют распознавание конкретных состояний пчелиных семей, увеличивают время анализа, не обеспечивают возможности количественной оценки достоверности распознавания и усложняют аппаратную (или программную) реализацию средств распознавания.
Технической задачей, на решение которой направлено предлагаемое изобретение, является сокращение числа информативных признаков (анализируемых узких полос частот) путем использования количественных критериев информативности этих признаков и отбора наиболее информативных, что позволит построить оптимальный классификатор (решающие правила), а также существенно упростить аппаратную (или программную) реализацию средств распознавания и сократить время анализа.
Решение указанной задачи проводится в три этапа. На первом этапе определяются коэффициенты информативности каждого информативного признака для распознавания конкретных состояний пчелиной семьи. Исходными данными для решения этой задачи являются перечень распознаваемых состояний (Sj, где j = 0, 1, 2, . , N, причем S0 - нормальное состояние) и снятые для них амплитудные или энергетические спектры акустических сигналов, представляемые средневыпрямленными значениями сигнала в узких полосах частот (шириной 25-30 Гц), перекрывающие диапазон от 60 до 600 Гц. Для каждого состояния желательно иметь не менее m = 10 реализаций сигнала (и, соответственно, их спектров), чтобы можно было оценить стабильность спектральных составляющих. Тогда усредненные по этим реализациям значения спектральных составляющих будем называть интенсивностями спектральных составляющих Iij, где i = 1, 2,.., n- порядковые номера спектральных полос, j = 0, 1, 2,.., N - распознаваемые состояния пчелиной семьи
где Iijt - измеренная интенсивность сигнала в i-ой полосе частот при j-м состоянии пчелиной семьи для t-ой реализации сигнала.
Для оценки стабильности Cij этих интенсивностей для каждого j-го состояния пчелиной семьи определяется дисперсия Dij интенсивностей по m реализациям сигнала
Далее по ним определяются коэффициенты вариаций νij как отношения среднеквадратических отклонений интенсивностей к их усредненным значениям
и уже по ним определяются стабильности
Cij = 1-νij. (4)
Чтобы устранить влияние коэффициента передачи приемного тракта (микрофона и усилителя) на измеренные значения спектральных составляющих сигнала, производится их нормирование относительно среднеквадратического значения всего сигнала в анализируемой полосе частот (60 - 600 Гц).
Проще всего нормирование осуществлять аппаратно, введя в приемный тракт АРУ (автоматическую регулировку усиления), управляющий сигнал для которой получают с выхода детектора среднеквадратического значения, на вход которого поступает выходной сигнал усилителя с полосой пропускания от 60 до 600 Гц. В этом случае выделенные с помощью узкополосных фильтров или расчетным путем (с помощью дискретного преобразования Фурье) спектральные составляющие сигнала будут пронормированы относительно среднеквадратического значения сигнала для всей анализируемой полосы частот (60 - 600 Гц).
Если используется численный метод спектрального анализа, то предпочтительней использовать не амплитудные, а энергетические спектры сигнала, поскольку они более устойчивы и могут быть определены по более коротким реализациям сигнала.
Таким образом, исходные данные представлены двумя матрицами, размерностью n•(N+1), одна из которых состоит из интенсивностей Iij, а вторая - из их стабильностей Cij.
По этим двум матрицам можно вычислить коэффициенты информативности Jjki каждой i-ой спектральной полосы для распознавания каждой из пар j и k состояний:
J
где j, k = 0, 1, 2,..., N, причем j ≠ k.
Для каждой i-ой спектральной полосы таких пар состояний будет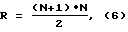
где R - число сочетаний из (N+1) по два.
Таким образом, коэффициенты информативности Jjki составляют матрицу размерностью n•R. Определим суммарные информативности каждой спектральной полосы по всем парам состояний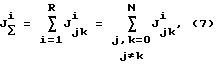
Это позволяет ранжировать спектральные полосы по их информативности для распознавания данных состояний.
Однако суммарные коэффициенты информативности характеризуют усредненную информативность данной узкой полосы частот по всем парам состояний. При этом одни пары состояний могут разделяться очень хорошо (разница между интенсивностями сигнала в данной полосе частот большая), а другие - плохо (разница между интенсивностями сигнала при соответствующих состояниях мала и находится в пределах их вариаций для различных реализаций сигналов при тех же самых состояниях). Поэтому для таких плохо различаемых пар состояний надо искать другие узкие полосы частот, для которых именно эти пары состояний хорошо различаются, т.е. имеют достаточно большие значения коэффициентов информативности (хотя суммарный коэффициент информативности по всем парам классов может быть существенно ниже). Очевидно, что чем больше будет использовано информативных признаков для распознавания (узких полос частот), тем, в принципе, надежней может быть произведено распознавание заданного множества состояний, но тем сложнее окажутся решающие правила, используемые для распознавания, а следовательно, и реализующее их распознающее устройство. Поэтому возникает задача отбора минимально необходимого количества информативных признаков (узких полос частот) для надежного распознавания заданного множества состояний. Именно эта задача и решается на втором этапе.
Ее предлагается решать следующим образом. На первом шаге выбирается узкая полоса частот, обеспечивающая максимальную суммарную информативность по всем парам классов -J
В качестве ориентировочного значения для выбора Jjk(кp) можно использовать
где R- число всех пар состояний.
Все коэффициенты информативностей для выбранной на первом шаге узкой полосы частот сравниваются с этим критическим значением и все строки матрицы коэффициентов информативностей, для которых Jjk(1) ≥ Jjk(кp) вычеркиваются. Вычеркивается и столбец, соответствующий первой выбранной узкой полосе частот Jjk(1) (здесь верхний индекс в скобках указывает номер шага).
На втором шаге по оставшейся после вычеркивания строк и столбца матрице вновь подсчитываются суммарные коэффициенты информативности по всем оставшимся узким полосам частот и выбирается полоса частот, соответствующая максимальному значению суммарной информативности. Парные коэффициенты информативности этой полосы частот Jjk(2) также сравниваются с Jjk(кp) и строки, для которых Jjk(2) превышают Jjk(кp) вычеркиваются из матрицы. Если и после этого шага не все пары состояний достаточно хорошо различаются, то процесс отбора продолжается дальше, т.е. отбирается третий информативный признак и т.д.
Если на каком-то q-ом шаге все парные коэффициенты информативности Jjk(q) выбранного столбца оказываются меньше первоначально назначенного критического значения, то его надо снизить. При этом можно воспользоваться тем же критерием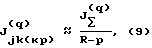
где J
Процесс отбора информативных признаков (число шагов) должен продолжаться до тех пор, пока каждая из пар распознаваемых состояний хотя бы по одному из отобранных информативных признаков будет иметь достаточно большое значение коэффициента информативности (больше критического значения).
И, наконец, третий этап заключается в построении решающих правил (классификатора), позволяющих по отобранным на предыдущем этапе информативным признакам достоверно распознавать любое из заданных возможных состояний пчелиной семьи.
Решающие правила предлагается определять в виде алгебраических уравнений, задающих границы областей в многомерном пространстве отобранных информативных признаков, соответствующих каждому распознаваемому состоянию (с учетом возможных вариаций отдельных реализаций одних и тех же состояний).
Пусть в результате выполнения второго этапа будет отобрано d < n информативных признаков (как показывает наш опыт, величина d лежит в предела от 2 до 5 в зависимости от заданного числа N распознаваемых состояний). Значениями информативных признаков являются усредненные по m реализациям нормированные значения интенсивностей шумового сигнала в отобранных узких полосах частот Iij (см. выражение (1)).
В итоге, для всех (N+1) заданных состояний будем иметь матрицу
Центры областей d - мерного пространства, соответствующих заданным (N+1) состояниям будут определяться уравнениями
Здесь: у0, y1,..., yi,... yN - выходные величины решающего устройства, соответствующие каждому из заданного множества состояний; аij - постоянные коэффициенты уравнений, которые и требуется определить.
Фактически каждое из этих уравнений преобразует d - мерное пространство информативных признаков в одномерное пространство результативного признака уi. Теперь, чтобы полностью определить решающие правила, необходимо, во-первых, определить неизвестные коэффициенты aij, а во-вторых, задать верхние и нижние границы каждого результативного признака yi, соответствующие границам распознаваемых состояний.
Постоянные коэффициенты аij должны определять удельный вклад каждого информативного признака (а ими являются измеренные значения Ii) в соответствующий результативный признак. Логично принять этот вклад пропорциональным сумме различительных способностей этого признака (способности отличать данное состояние от всех остальных заданных состояний). А они определяются соответствующими коэффициентами информативности Jiki. Следовательно, целесообразно определять весовые коэффициенты aij в виде
aij = J
где 
hi - нормирующий множитель;
Jiki - коэффициенты информативности.
Это эквивалентно общепринятому методу определения неизвестных коэффициентов в уравнениях регрессии в метрических задачах (где объект характеризуется не различными качественными состояниями, а различными значениями выходного количественного признака). Действительно, в таких задачах коэффициенты линейного уравнения регрессии (весовые коэффициенты уравнения, связывающего результативную выходную величину с информативными признаками) находят из условия их пропорциональности частным производным выходной величины по соответствующему информативному признаку.
Естественно, что в зависимости от знака приращения информативного признака ΔIjk при переходе объекта от j-ого состояния к k-му, и весовые коэффициенты aij могут иметь разные знаки. Поэтому в выражении (13) должны учитываться знаки коэффициентов информативностей, тогда как до этого нас интересовало лишь их абсолютное значение, которое и определялось в соответствии с (5). Для учета знака необходимо определять Jiki как
Jjki = (Iij -Iik) • Cij • Cik (14)
Оно отличается от (5) лишь тем, что разность (Iij-Iik) берется с учетом ее знака.
В этом случае, очевидно, и bij, находимые по (13), а следовательно, и aij, находимые по (12), могут иметь различные знаки.
Если на допустимые значения результативных признаков не накладывается никаких ограничений (что имеет место при цифровом способе реализации распознающего устройства), то нормирующий множитель hi можно принимать равным единице.
Если же на предельно допустимые значения результативного признака накладываются ограничения (что имеет место при аналоговом способе реализации распознающего устройства), то нормирующий множитель hi подбирается из условия, чтобы yjmax соответствовал (0,7 - 0,9)yjдоп. Ограничение нормирующего множителя снизу обусловлено тем, что в аналоговых устройствах при малых уровнях сигналов возрастают погрешности.
Теперь остается лишь определить границы каждого состояния по соответствующим результативным признакам уjгр. Наиболее корректным решением данной задачи в условиях, когда заданное первоначально множество состояний (N+1) далеко не исчерпывает всего множества возможных состояний пчелиной семьи, является ограничение каждого состояния двусторонними границами с центрами, определяемыми в соответствии с уравнениями (11) и шириной интервалов, зависящей от дисперсии значений интенсивностей сигналов в используемых узких полосах частот при данных состояниях для различных реализаций сигналов.
Учитывая, что при нормальном законе распределения значений информативных признаков в интервал шириной  попадает примерно 95% всех реализаций, можно рекомендовать именно таким образом определять границы состояний
попадает примерно 95% всех реализаций, можно рекомендовать именно таким образом определять границы состояний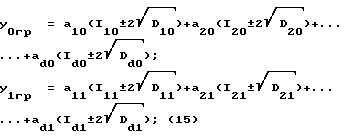
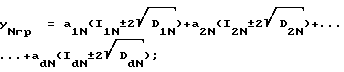
где Dij - дисперсии интенсивностей в i-м узком диапазоне частот при j-м состоянии, определяемая по m реализациям сигнала в соответствии с (2).
Очевидно, что определяемые таким образом границы отдельных состояний будут располагаться симметрично относительно их центров, заданных уравнениями (11). Поэтому более удобно определить интервалы Δyj между центром каждого j-гo состояния и его границами, которые можно находить из уравнений
и, откладывая их по обе стороны от центров состояний yj, определять границы каждого состояния. При нахождении интервалов Δyj в соответствии с (16) используются модули коэффициентов aij, т.к. в (15) в каждой скобке стоят знаки (±), а это значит, что при любом знаке соответствующего коэффициента результаты будут получаться одни и те же.
Таким образом, решающие правила полностью построены. Их можно реализовать в распознающих устройствах двух типов: цифровых и аналоговых (независимо от того, каким образом из шумового сигнала выделяются узкие полосы частот и в них измеряются интенсивности сигналов, что также может быть реализовано различными способами). Цифровой способ реализации предполагает наличие процессора, который в цифровом виде получает измеренные нормированные значения интенсивностей сигнала lij в отобранных d узких полосах частот, подставляет их в уравнения (11), вычисляет значения результативного признака y0, y1, y2, ..., yN и сопоставляет их с заранее вычисленными границами по каждому из распознаваемых состояний. При этом, в принципе, возможны три исхода:
1. Если лишь для одного из уравнений системы (11) вычисленное значение yj попадает в разрешенный интервал между верхним и нижним граничными значениями, то данная реализация сигнала соответствует именно данному j-му состоянию. 2. Если ни для одного из уравнений значение yj не попадает между границами данного состояния, то это будет свидетельствовать о том, что данная реализация сигнала соответствует состоянию, не включенному в заданное множество N. Такая ситуация вполне вероятна, поскольку реальные состояния пчелиной семьи зависят от множества факторов, которые могут накладываться друг на друга, что может приводить к практически неограниченному множеству возможных состояний, из которого мы первоначально выбираем лишь некоторые, наиболее интересующие пчеловодов состояния.
3. И, наконец, в принципе возможен и третий исход, когда одновременно опознаются более чем одно состояние. Это будет свидетельствовать о том, что границы областей, соответствующих заданным состояниям в d-мерном пространстве пересекаются, что может произойти, если разделимость данных пар состояний, определяемых соответствующими парными коэффициентами информативности, недостаточна. В этом случае необходимо увеличить мерность пространства информативных признаков, т.е. добавить еще одну узкую полосу частот, что требует полной перестройки всей системы распознавания. Чтобы этого избежать, можно попытаться сузить границы соответствующих пересекающихся состояний, т. е. в соответствующих уравнениях из системы уравнений (15) принять допустимые границы вариаций интенсивности не  а, например,
а, например, 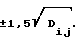 Такую перестройку распознающей системы легко осуществить при любом способе ее реализации.
Такую перестройку распознающей системы легко осуществить при любом способе ее реализации.
При аналоговом способе реализации распознающее устройство состоит из (N+1) аналоговых сумматоров с d-входами каждый, причем коэффициенты передачи по каждому из входов соответствуют значениям весовых коэффициентов аij. К выходу каждого сумматора подключено по два компаратора, настроенных соответственно на верхнюю и нижнюю границы соответствующего результативного признака yj, а выходы каждой пары компараторов подключены к логической схеме, срабатывающей в том случае, когда выходной сигнал сумматора находится в интервале между порогами срабатывания соответствующих компараторов. Выходы логических схем подключены к сигнальным светодиодам, которые зажигаются при распознавании одного из заданных состояний.
Пример:
Проиллюстрируем все изложенное конкретным примером.
Зададим следующее множество распознаваемых состояний пчелиной семьи:
S0 - нормальное;
S1 - потеря матки;
S2 - принятие новой матки;
S3 - отвергание новой матки;
S4 - предроевое состояние;
S5 - перегрев улья.
Для каждого из данных состояний было снято по m = 12 реализаций акустических сигналов и получены их амплитудные спектры, представленные нормированными значениями интенсивностей сигнала в узких частотных полосах шириной 30 Гц, равномерно распределенных в диапазоне от 60 до 570 Гц (всего n = 17 частотных полос, т. е. i = 1,2,...,17). Нормирование спектральных составляющих проводилось аппаратно, с помощью АРУ, встроенной в предварительный усилитель.
По этим нормированным значениям, определенным для каждой t-ой реализации сигнала, в соответствии с (1) находились усредненные по всем реализациям интенсивности спектральных составляющих для j-ого состояния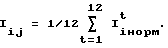
Они образуют матрицу размерностью n(N+1), т.е. 17•6 представленную табл. 1.
Далее в соответствии с (2) определялась дисперсия каждой спектральной составляющей по всем m реализациям: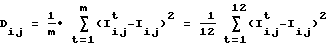
А затем по (3) определялись коэффициенты вариации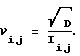
и по (4) стабильности этих спектральных составляющих:
Cij= l-νij
Имея усредненные по всем m реализациям сигналов значения интенсивностей lij и стабильностей Cij спектральных составляющих для каждой i-ой полосы частот и каждого j-ого состояния, по формуле (5) вычисляем коэффициенты информативности каждой из этих спектральных полос для различения любой j-ой пары состояний - Jjk.
В итоге получаем матрицу коэффициентов информативности размерностью n • R, т.е. в нашем случае 17 • 15. Эта матрица представлена в табл. 2.
Проведя суммирование коэффициентов информативности по каждой узкой полосе частот (согласно критерию (3)), мы получаем суммарные коэффициенты информативности этих спектральных составляющих по различению всех пар состояний. Они представлены первой из дополнительных строк табл. 2 в виде суммы ее столбцов J∑1.
На первом шаге выбираем признак, имеющий максимальное значение критерия (7). В нашем случае ему соответствует полоса частот 210-240 Гц. Вычисляем по (8) критическое значение коэффициента информативности
Затем из табл.2 вычеркиваем те строки, в которых выбранный информативный признак дает значения коэффициента информативности Jjk > Jjk(кp) = 17,6. В нашем случае будут вычеркнуты строки 2 (J02 = 23,4), 3 (J03 = 33,8), 4 (J04 = 23,7), 6 (J12= 23,4), 10 (J23 = 33,7), 11 (J24 = 32,3) и 12 (J25 = 36,7).
По оставшимся строкам для всех признаков, кроме уже отобранного, вновь подсчитываются суммарные коэффициенты информативности и следующим отбирается признак, имеющий максимальное значение этого коэффициента. Для нашего случая это будет спектральная составляющая, соответствующая полосе 420-450 Гц (J∑2 = 181). Таким образом, на втором шаге мы должны выбрать информативный признак, соответствующий полосе частот 420-450 Гц.
Далее, пользуясь тем же правилом, вычеркиваем из усеченной таблицы столбец, соответствующий этой полосе частот, и строки, где значения коэффициента информативности в данном столбце Jjk > Jjk(кp) Таких строк здесь три: третья J13 = 29,9, шестая J34 = 45,2 и седьмая J35 = 72,7. По оставшимся строкам и столбцам вновь подсчитываем суммарный коэффициент информативности. Он максимальный у столбца, соответствующего полосе частот 300-330 Гц (J∑3 = 128,5). Следовательно, на третьем шаге мы должны выбрать именно эту полосу частот.
Далее опять вычеркиваем этот столбец и строки, где Jjk в этом столбце больше Jjk(кp). Это будут строки, соответствующие J05 (26,6), J14 (37,5), J15 (47,3).
По оставшимся строкам, а их остается всего две: J01 и J45, вновь подсчитываем значения критерия J∑4 и анализируем признаки с максимальными значениями критерия J∑4. Они соответствуют частотным полосам 240-270 Гц (J4Σ = 56,4), 180-210 Гц (J4Σ = 50,2), 390-420 Гц (J4Σ = 45,9). По значениям этого критерия данные частотные полосы отличаются ненамного. Однако, поскольку в данном случае он определяет суммарную разделимость двух пар состояний, то выгодно в качестве четвертого и последнего информативного признака взять тот, который обеспечивает хорошую разделимость обеих пар состояний. Этому условию соответствует частотная полоса 390-420 Гц. Хотя по суммарной информативности он уступает первым двум, но зато каждая из оставшихся двух пар состояний им различается достаточно хорошо (J01 = 17,8 и J45 = 28,1), тогда как информативный признак, соответствующий максимуму J∑4, хорошо различая состояния 4 и 5 (J45 = 53,1), плохо различает состояния нулевое и первое (J01 = 3,3).
Итак, для распознавания указанных шести состояний оказалось достаточно четырех информативных признаков, соответствующих полосам частот 210-240 Гц, 420-450 Гц, 300-330 Гц и 390-420 Гц.
Теперь остается лишь определить оптимальные значения весовых коэффициентов в уравнениях (11), связывающих значения выходных величин, распознающих системы Yj с информативными признаками Ii. Поскольку приращения информативных признаков  при переходе пчелиной семьи от одного состояния к другому могут быть различных знаков, то и весовые коэффициенты могут иметь различные знаки, в то время как в табл. 2 знаки приращений информативных признаков не учитывались.
при переходе пчелиной семьи от одного состояния к другому могут быть различных знаков, то и весовые коэффициенты могут иметь различные знаки, в то время как в табл. 2 знаки приращений информативных признаков не учитывались.
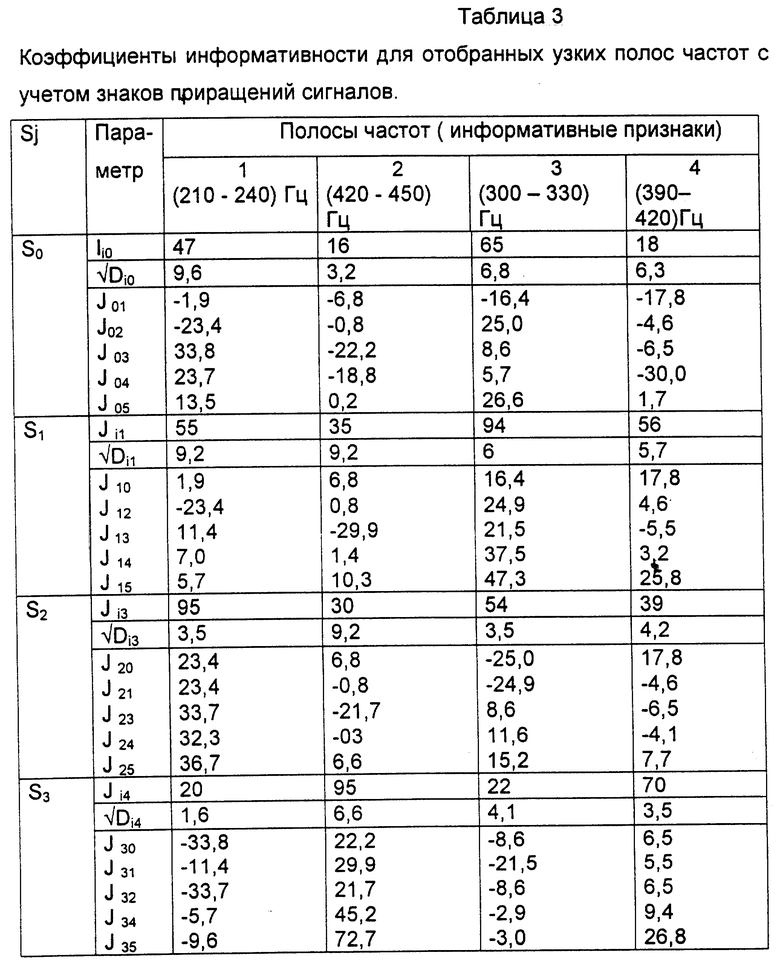
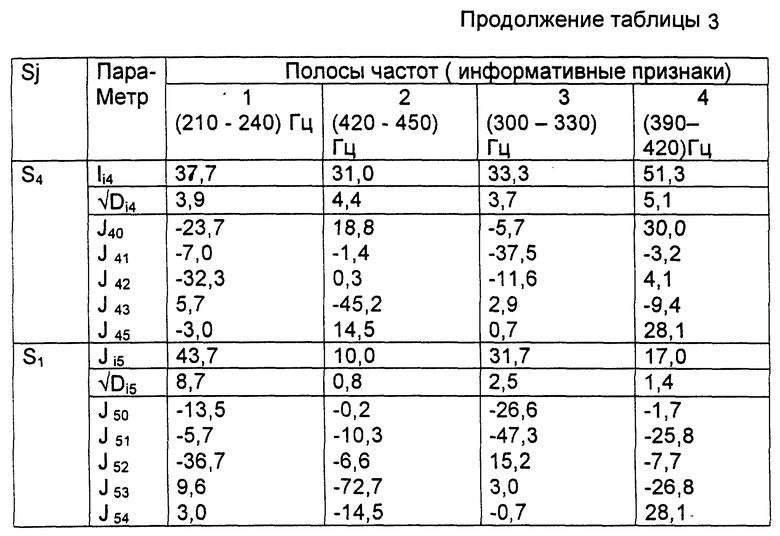
Поэтому для отобранных четырех узких полос частот приведем значения коэффициентов информативности с учетом их знака. Эти данные, а также соответствующие значения усредненных нормированных значений сигнала lij и их среднеквадратических отклонений, определяемых по m =12 реализациям спектров, представлены в табл. 3. Все эти данные необходимы для определения весовых коэффициентов аij и границ диагностируемых состояний.
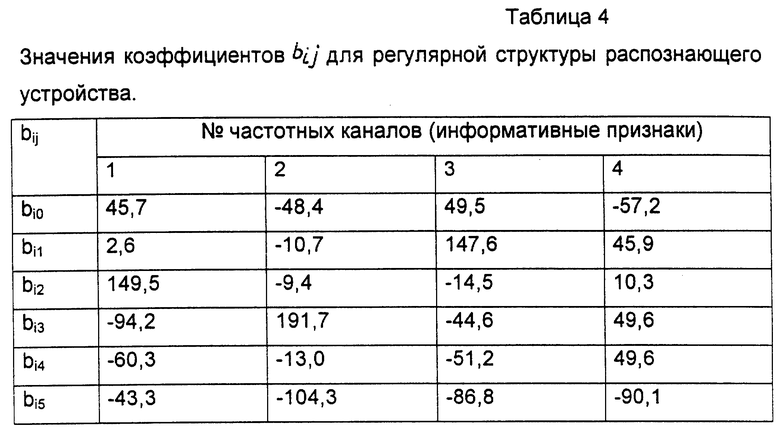
Сначала будем находить значения коэффициентов bij. В соответствии с выражением (13) они равны алгебраическим суммам коэффициентов информативностей по всем диагностируемым состояниям
Найденные значения bij представлены в табл. 4. Эти значения могут непосредственно использоваться в качестве весовых коэффициентов аij в цифровых распознающих системах (поскольку для них можно значения всех нормирующих множителей hj принять равным единице).
Для аналоговых распознающих систем этого сделать нельзя, т.к. напряжения на выходах сумматоров не должны превышать предельно допустимых значений. Кроме того, в аналоговых распознающих системах целесообразно, по возможности, провести упрощение структуры, т.е. на сумматоры, выделяющие определенные состояния заводить не все 4 сигнала (с узкополосных каналов), а лишь наиболее информативные из них (именно для выделения данного состояния), что несложно определить по соответствующим коэффициентам информативности.
В частности, на сумматор, выделяющий нулевое состояние, целесообразно завести сигналы с 1-го и 3-го частотных каналов, а со 2-го и 4-го не заводить. Действительно, по первому каналу хорошо разделяются состояния 0-2; 0-3 и 0-4 (соответствующие значения коэффициентов информативности равны 23,4; 33,8 и 23,7). Для разделения же пар состояний 0-1 и 0-5 достаточно использовать 3-й канал (соответствующие коэффициенты информативности равны 16,4 и 26,6).
Для выделения первого состояния вообще достаточно только одного 3-го канала, т.к. по данному каналу все коэффициенты информативности достаточно велики (J10 = 16,4, J12 = 24,9, J13 = 21,5, J14 = 37,5, J15= 47,3).
Для выделения второго состояния также достаточно завести сигнал лишь с одного 1-го канала (J20 = 23,4, J21 = 23,4, J23 = 33,7, J24 = 32,3, J25 = 36,7).
Для выделения третьего состояния тоже достаточно сигнала с одного 2-го канала (J30 = 22,2, J31 = 29,9, J32 = 21,7, J34 = 45,2, J35 = 72,7).
Для выделения 4-го и 5-го состояний необходимы сигналы со всех 4-х частотных каналов.
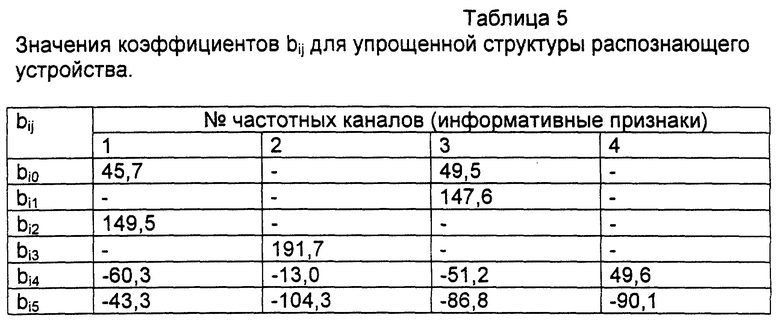
С учетом указанных упрощений распознающего устройства значения коэффициентов bij изменятся. Для упрощенной структуры эти значения приведены в табл. 5.
Теперь можно приступить к определению необходимых значений нормирующих множителей hj. Для получения числового решения зададимся значениями напряжений на выходах узкополосных каналов, равными нормированным усредненным значениям соответствующих интенсивностей, умноженным на 0,1 В. В результате получим следующую матрицу сигналов на выходах узкополосных каналов при всех диагностируемых состояниях пчелиной семьи (в вольтах).

Для нахождения масштабных коэффициентов hj используем условие, чтобы при любом из диагностируемых состояний максимальный выходной сигнал любого сумматора не превышал 0,8 Uдоп (0,8 Uдоп взято с учетом возможности превышения отдельных реализаций сигнала над усредненными значениями, приведенными в матрице (17)).
В общем случае это условие можно записать
U
Здесь U
Очевидно, что hj надо получать для такого k, при котором U
Для этого необходимо вычислить для всех значений k выражения записанные в скобках  затем взять из них максимальное значение и из него найти hj. Приняв Uдоп = 10 B, все результаты вычислений сведем в табл. 6.
затем взять из них максимальное значение и из него найти hj. Приняв Uдоп = 10 B, все результаты вычислений сведем в табл. 6.
Из этой таблицы видно, что на выходе первого сумматора максимальное напряжение будет при состоянии S1. Отсюда
Аналогично определяем остальные нормирующие множители:


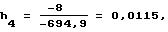

Теперь можно определить весовые коэффициенты аij = bijhj Их значения представлены матрицей (19): (19)
(19)
Коэффициенты aij представляют собой коэффициенты передачи сумматоров по каждой из суммирующих цепей.
При подаче на входы сумматоров напряжений, представленных матрицей (17), на выходах сумматоров будут сформированы напряжения, представленные табл. 7.
Теперь осталось только вычислить граничные интервалы состояний и определить их границы. Для этого воспользуемся выражением (16), но при этом надо учесть, что приведенные в табл. 3 значения среднеквадратических отклонений 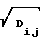 приведены в абсолютном виде, а при переходе от усредненных интенсивностей сигнала Iij к значениям сигналов, действующих на входах сумматоров мы вводим коэффициент 0,1 (В). Этот же коэффициент необходимо учитывать и в выражении (16). В итоге получаем
приведены в абсолютном виде, а при переходе от усредненных интенсивностей сигнала Iij к значениям сигналов, действующих на входах сумматоров мы вводим коэффициент 0,1 (В). Этот же коэффициент необходимо учитывать и в выражении (16). В итоге получаем
Δy0 = 0,512 • 2 • 0,96 + 0,554 • 2 • 0,68 = 1,74;
Δy1 = 0,85 • 2 • 0,6 = 1,02
Δy2 = 0,842 • 2 • 0,35 = 0,59;
Δy3 = 0,843 • 2 • 0,66 = 1,11;
Δy4 = 0,693 • 2 • 0,39 + 0,149 • 2 • 0,44 + 0,589 • 2 • 0,37 + 0,57 • 2 • 0,51 = 1,69;
Δy5 = 0,18 • 2 • 0,87 + 0,434 • 2 • 0,08 + 0,361 • 2 • 0,25 + 0,375 • 2 • 0,14 = 0,67.
Таким образом, границы состояния S0 по выходному напряжению сумматора Σ0 будут от у0н = 6,01- 1,74 = 4,27 B до Y0в = 6,01 + 1,74 = 7,75 B.
Ближайшее значение к этим границам снизу представляет сигнал при состоянии S5, равный 4,03 В, а сверху - при состоянии S2, равный 7,85 В. Как видим, до границ состояния S0 остается еще некоторый запас, т.е. по выходному сигналу сумматора Σ0 эти классы не перекрываются. Таким образом, подключаемые к выходу этого сумматора компараторы должны настраиваться на пороговые напряжения U0н ≈ 4,3 B, U0в ≈ 7,7 B
Аналогично получаем пороговые напряжения компараторов, подключаемых к выходам остальных сумматоров:
U1н= 8,00 - 1,02 ≈ 7 B, U1в = 8,00 + 1,02 ≈ 9B;
U2н= 8,00 - 0,59 ≈ 7,4 B, U2в = 8,00 + 0,59 ≈ 8,6 B;
U3н= 8,00 - 1,11 ≈ 6,9 B, U3в = 8,00 + 1,11 ≈ 9,1 B;
U4н= 8,00 - 1,69 ≈ 0,4 B, U4в = 8,00 + 1,69 ≈ 3,8 B;
U5н= 8,00 - 0,67 ≈ 2,3 B, U5в = 8,00 + 0,67 ≈ 3,7 B;
Примечание: Выходные напряжения сумматоров Σ4/ и Σ5/ в соответствии с табл. 7 для всех состояний пчелиной семьи получаются отрицательными. Поэтому их можно инвертировать и знак "минус" не учитывать, что и сделано при вычислении пороговых напряжений.
Сопоставление полученных граничных напряжений с номинальными выходными напряжениями при других состояниях пчелиной семьи (из диагностируемого множества состояний) показывает, что все остальные состояния не пересекаются с границами выделяемых состояний. Таким образом, распознавание диагностируемых состояний будет осуществляться весьма надежно (с доверительной вероятностью не хуже 0,95).
Источники информации
1. Еськов Е.К. Акустическая сигнализация общественных насекомых. - М.: Наука. 1979.
2. Еськов Е.К. Управление процессами жизнедеятельности медоносных пчел и их оптимизация. - М.: Всесоюзная академия сельскохозяйственных наук имени В. И. Ленина. - 1982.
3. Дж. Ту. Р. Гонсалес. Принципы распознавания образов. - М.: Мир, 1978, стр. 177. (Обучаемые классификаторы образов, детерминистский подход).
4. Основы метрологии и электрические измерения. Под ред. Е.М. Душина. - Л.: Энергоатомиздат, 1987.
5. Шиндовский Э. , Щурц О. Статистические методы управления качеством/Контрольные нормы и планы контроля/ Пер. с немецкого. - М.: Мир, 1976-579 с.






Изобретение может найти применение в практической работе на индивидуальных и коллективных пасеках. Способ предусматривает для каждой узкой полосы частот (25-30 Гц) помимо нормированного значения интенсивности определение стабильности, зависящей от вариации значений интенсивности для разных реализаций сигнала. Далее для каждой пары диагностируемых состояний определяют коэффициенты информативности по каждой выделенной полосе частот. Выделяют минимальную совокупность спектральных составляющих акустического сигнала пчелиных семей. Подсчитывают суммарную информативность для каждой выделенной узкой полосы частот по всем парам диагностируемых состояний, выбирают полосу частот с максимальной суммарной информативностью и выделяют те пары состояний, которые плохо разделяются данным информативным признаком. Для этих пар состояний подсчитывают суммарную информативность по всем оставшимся полосам частот. Следующей выбирается полоса, которая имеет максимальную суммарную информативность для данных пар классов. Далее отбор продолжается таким же образом, пока все пары классов не будут характеризоваться достаточными значениями коэффициентов информативности хотя бы для одной из отобранных узких полос частот. Способ позволяет упростить и оптимизировать аппаратурную реализацию средств распознавания и сократить время анализа. 2 з.п. ф-лы, 7 табл.
| Еськов Е.К | |||
| Акустическая сигнализация общественных насекомых | |||
| - М | |||
| Наука, 1979 | |||
| Еськов Е.К | |||
| Управление процессами жизнедеятельности медоносных пчел и их оптимизация | |||
| - М | |||
| Всесоюзная академия сельскохозяйственных наук имени В.И.Ленина | |||
| Устройство для видения на расстоянии | 1915 |
|
SU1982A1 |
| Гонсалес ДЖ.ТУ.Р | |||
| Принципы распознавания образцов - М.: Мир, 1978, с.177 | |||
| (Обучаемые классификаторы образцов, детерминистический подход). | |||
Авторы
Даты
2001-05-27—Публикация
1998-10-16—Подача