Изобретение относится к хронологии и вычислительной технике и может быть использовано в качестве вечного календаря для ежегодного пользования для определения в короткий промежуток времени полных календарных данных без дополнительных вычислений.
Известен календарь, содержащий закодированные цветом элементы с календарными датами - патент США N 3765111, кл. G 09 D 3/00, 16.10.1973.
Недостатком таких календарей является малые функциональные и эксплуатационные возможности при определении календарных дат и неудобство в использовании.
Известна также периодическая таблица времени в пространстве, содержащая пластину с размещенными горизонтально и вертикально соответственно кодовыми символами числовых значений годов - патент РФ N 2056063, кл. G 09 D 3/00, 10.03.1996.
Однако и эта временная таблица не обладает широкими функциональными и эксплуатационными возможностями и не позволяет определить календарные даты в широком временном диапазоне.
Задачей изобретения является создание периодической таблицы времени в пространстве, позволяющей определить любую календарную дату в широком диапазоне до и после Рождества Христова.
Указанный технический результат достигается за счет того, что в периодической таблице времени в пространстве, содержащей пластину с размещенными горизонтально и вертикально соответственно кодовыми символами числовых значений годов, последние выполнены в форме геометрических фигур - квадратов, каждый угол которых соответствует одному конкретному году, годовой календарь которого идентичен всем годам, расположенным на соответствующих углах квадратов разных периодов уходящих в бесконечность временных пространств прошлого и будущего, при этом кодовые символы - квадраты расположены рядами с образованием временной кодированной сетки, соответствующей одному большому циклу периодом в 28 лет, причем количество символов - квадратов в одном горизонтальном ряду в одном временном периоде с четырьмя годами на углах квадрата - семь, временное пространство до Рождества Христова принимается со знаком минус, а после Рождества Христова - со знаком плюс.
Указанный технический результат в другом варианте выполнения периодической временной таблицы достигается за счет того, что в ней, содержащей пластину с размещенными горизонтально и вертикально соответственно указателями наименований дней недели, начиная с понедельника до воскресенья, и кодовыми символами числовых значений годов, кодовые символы выполнены в форме геометрических фигур - квадратов и пятиугольников, таблица представлена числовыми значениями годов, расположенных на углах семи квадратов первого периода -1P до Рождества Христова и на углах семи квадратов первого периода +1P после Рождества Христова с образованием кодированной временной сетки, в которой сумма чисел годов соответствующих углов без учета знаков плюс - минус, равная 28, развернута в вертикальное положение с 28 горизонталями, соответствующими по вертикали годовым остаткам ±n от деления этих годов на 28 с расположением между ними семи граф по вертикали, каждая из которых соответствует дням недели с понедельника до воскресенья, слева направо, и заполнена комбинациями тройных пятиугольников, соответствующих кодированным январским месяцам 28 кодированных годовых календарей, при этом в кодированной временной сетке образованные два геометрических зеркально отраженных повернутых на 180o рисунка кодовых символов представлены в виде временного в 28 лет геометрического алгоритма, одиночные и двойные пятиугольники которых расположены в графах суббот, воскресений, понедельников, вторников, для одиночных пятиугольников, берущих начало с горизонтали, соответствующей остатку +n= +1 и опускающихся по воскресной вертикали с последующим расположением согласно числовым интервалам +1-7-12-7, для двойных пятиугольников, берущих начало с горизонтали, соответствующей остатку +n=+6 и опускающихся по субботней и воскресной вертикалям с последующим расположением согласно числовым интервалам +6-7-6-7, представляющих собой цифровой алгоритм, в котором +1 и +6 - номера горизонталей соответствующих остатков +n, а остальные числа - интервалы между одноименными комбинациями пятиугольников.
Указанный технический результат достигается также тем, что в периодической временной таблице, включающей скомпанованную годовую и месячную информацию о числах и днях одного наименования недели, выраженную в кодовых символах, кодовые символы информации выполнены в форме геометрических фигур, объединенных в повторяющиеся периоды, цикл которых равен 28 годам, а временная периодичность бесконечна в прошлом и будущем, при этом при замене годов числами их периодов ±P и их двухзначными годовыми остатками ±n образуется альтернативный алгоритм времени для использования в компьютерной технике.
Периодическая таблица времени в пространстве включает 28 годовых кода по январю месяцу, каждый из которых - начало годового календаря для многих столетий, соответствующих этому календарю, символы которых, проставляемые по соответствующим углам геометрических фигур, обозначают годовые кодированные календари и образуют вечный кодированный календарь.
На фиг. 1 представлена периодическая таблица времени в пространстве в двух периодах до и после Рождества Христова,
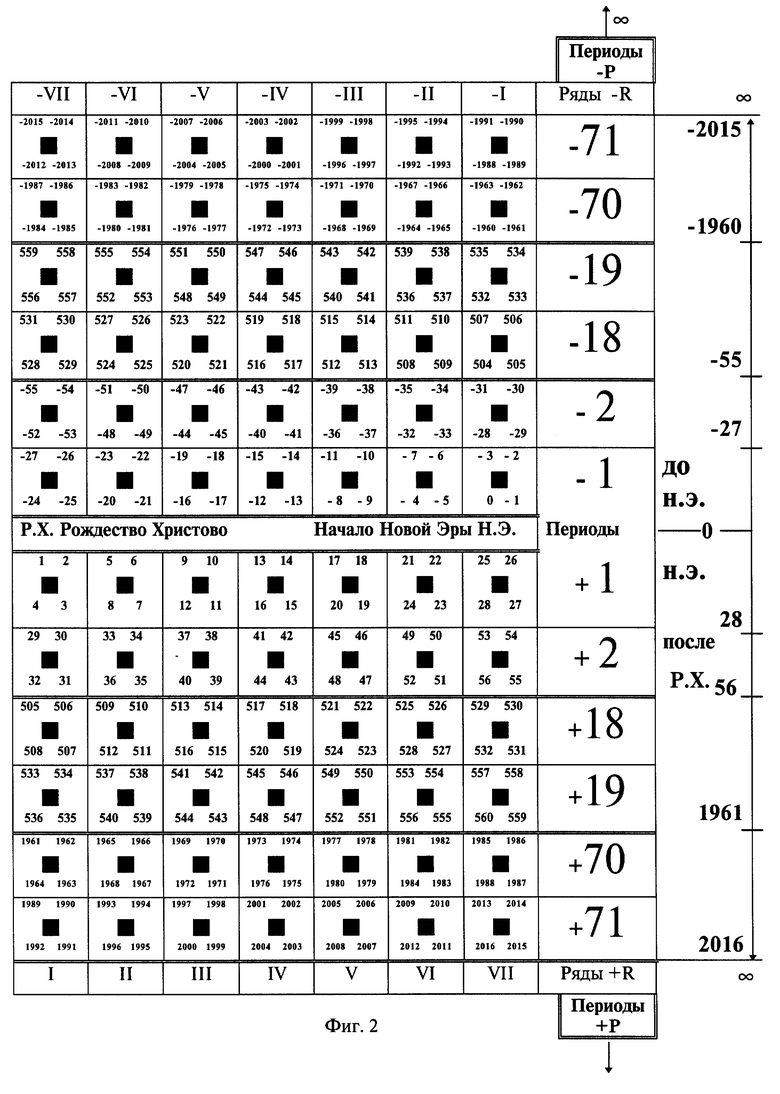
на фиг. 2 - периодическая таблица с фрагментами некоторых временных периодов,
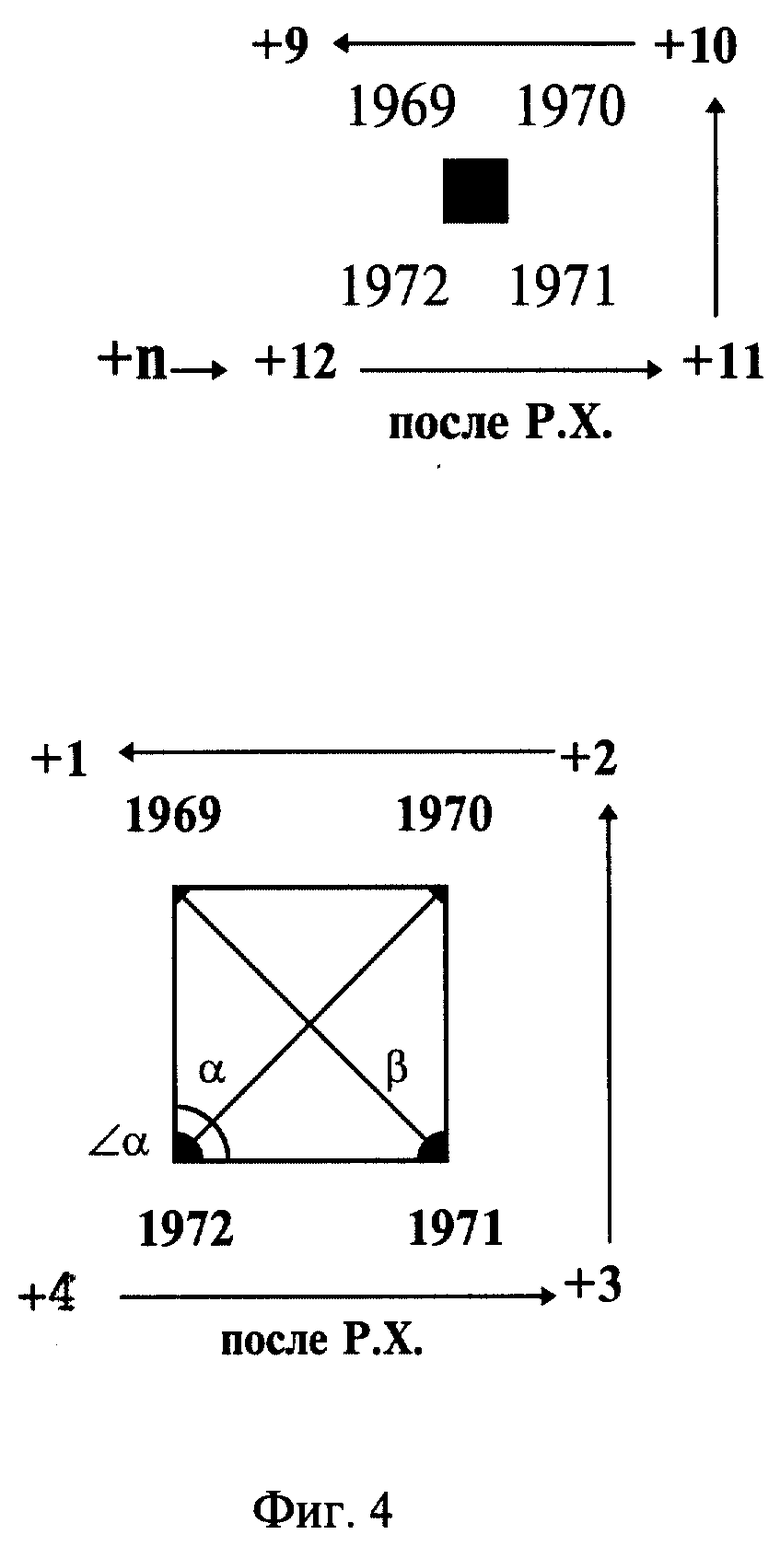
на фиг. 3 и 4 - кодированный временной квадрат до и после Рождества Христова,
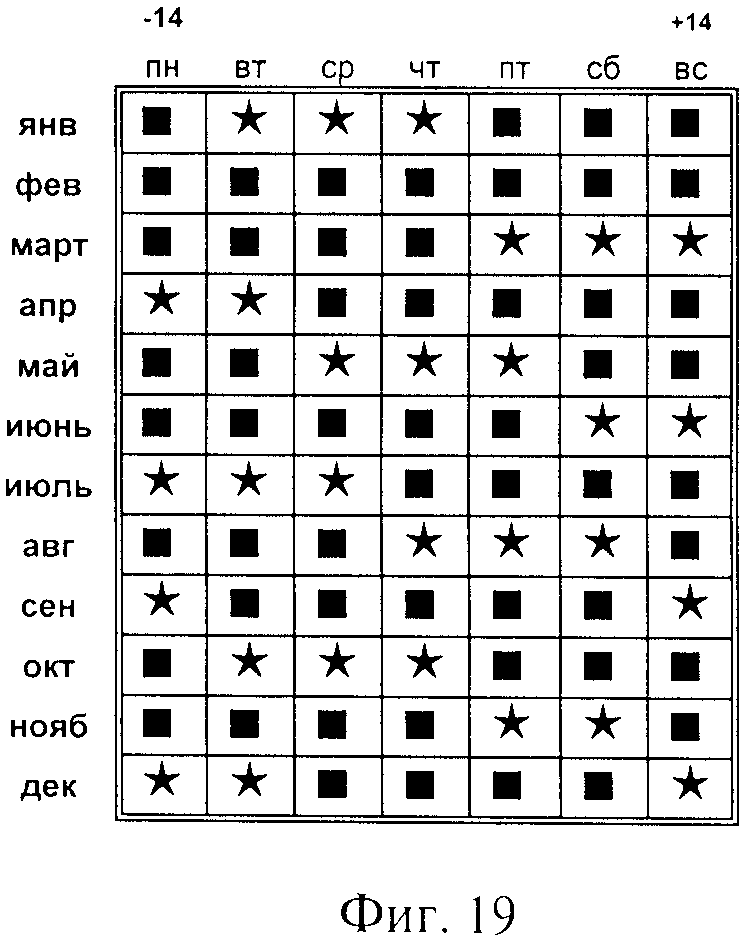
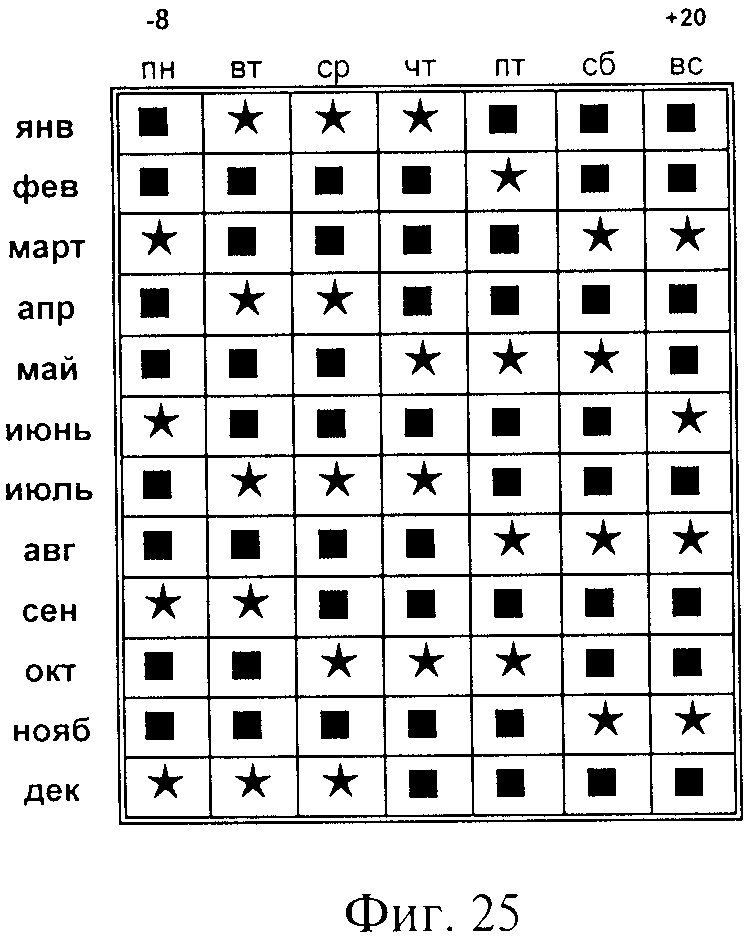
на фиг. 5-32 - двадцать восемь кодированных годовых календарей, составляющих кодированную временную сетку - временной алгоритм,
на фиг. 33 - кодированный временной квадрат с развернутым кодированным годовым календарем,
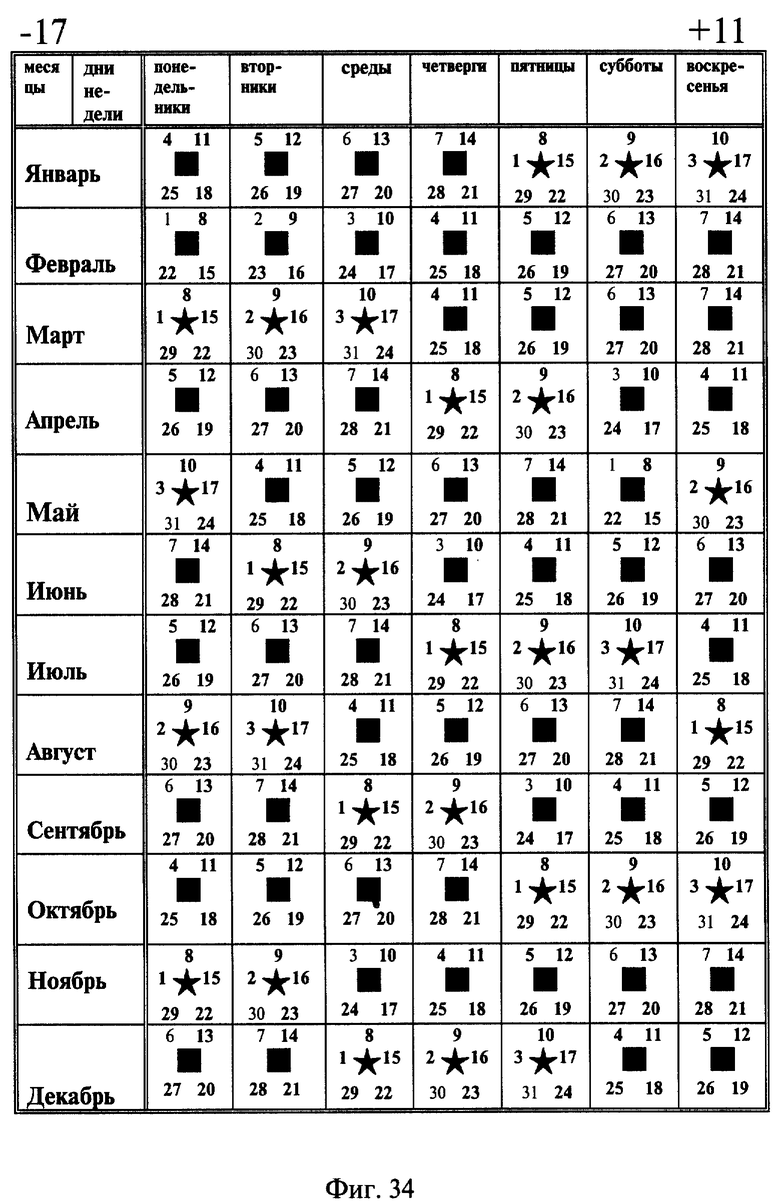
на фиг. 34 - кодированный годовой календарь на 1999 год,
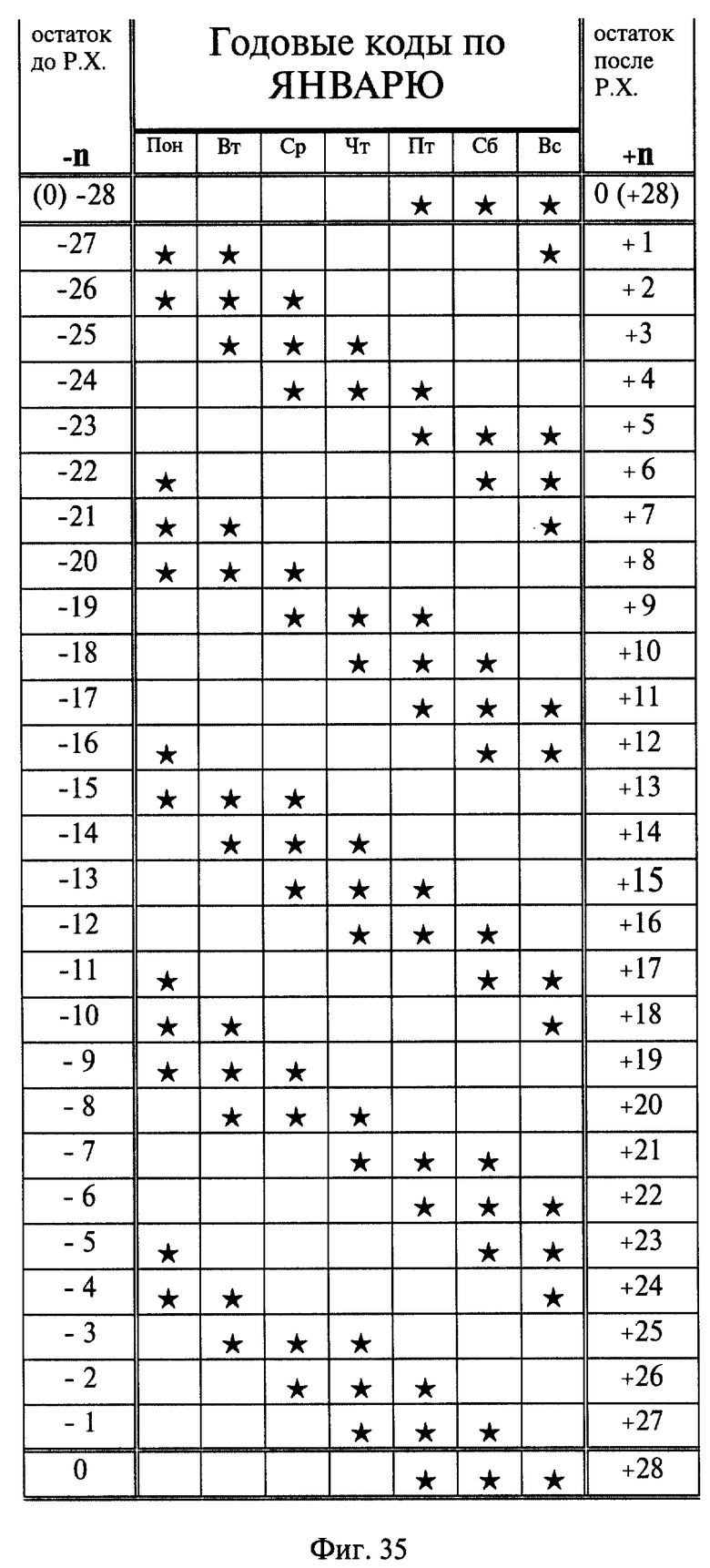
на фиг. 35 - кодированная временная сетка с годовыми кодами по январю,
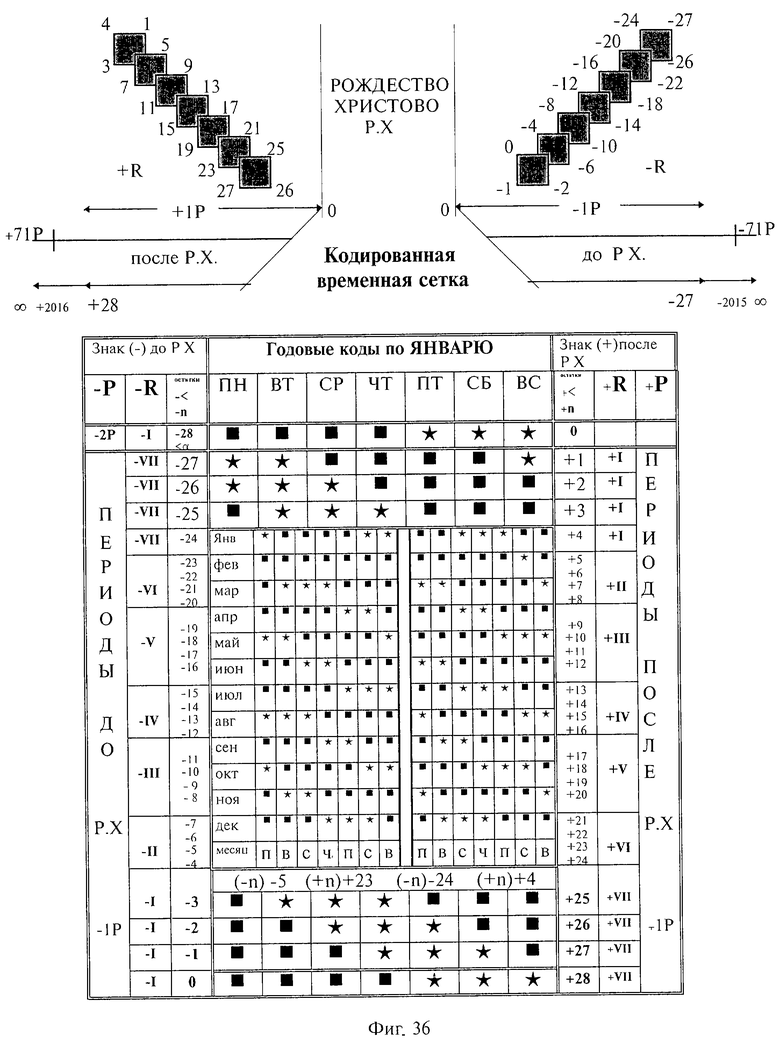
на фиг. 36 - кодированная временная сетка с годовыми кодами по январю и с фрагментами кодированных годовых календарей (-n)-5-(+n)+23, (-n)-24-(+n)+4.
Периодическая таблица времени в пространстве построена на основе двух временных периодов - малого и большого циклов времени с использованием кодовых символов числовых значений годов в форме геометрических фигур квадратов и пятиугольников, каждый угол которых соответствует одному конкретному году, и годовой календарь которого идентичен всем годам, расположенным на соответствующих углах квадратов разных периодов уходящих в бесконечность временных пространств прошлого и будущего.
Малый временной цикл составляет 4 года - между високосными годами - и назван кодированным временным квадратом. Семь таких квадратов образуют кодированную временную сетку периодом в 28 лет и равную одному большому циклу ±Р. Расположенные горизонтально один под другим периоды в вертикальном направлении образуют семь рядов ±R, при этом года в семи рядах со знаком плюс от +1 до + VII соответствуют временным периодам после Рождества Христова (Р.Х. ), т.е. новой эре и, соответственно, в семи рядах со знаком минус от -VII до -1 - временным периодам до Рождества Христова (Р.Х.), т.е. до новой эры.
Соответствующие углы кодированных временных квадратов, находящиеся в одном ряду, располагаются с интервалом в 28 лет, их годовые календари идентичны всем числовым значениям годов, уходящих в бесконечность временных пространств прошлого и будущего.
Значения этих углов в рядах таблицы до и после Р.Х. расположены таким образом, что числовые значения годов любого временного периода, разделенные на 28, дают в остатке от ±1/28 до + 27/28 лет, размещенных на соответствующих кодированных временных углах кодированного временного квадрата по обе стороны от разделительной черты 0 (фиг. 1) периодов до Р.Х. (-1P) и после Р. Х. (+1P), при этом формулы соответствия рядов и углов во временных кодированных квадратах и соответствие временных параметров в рядах таблицы представляются следующим образом:
+R=VIII-R
+n=28-n
Сумма римских числовых значений, обозначающих ряды временных периодов до (-R) и после (+R) Рождества Христова, без учета их знаков, равна VIII.
Например: (-VII+I), (-VI+II)·(-V+III), (-IV+IV), (-III+V),(-II+VI), (-I+VII).
Числовые значения остатков ±n, полученных от деления на 28 любых числовых значений годов прошлого и будущего, находящихся в соответствующих рядах +R и периодах ±P, равны величинам от 0 до -27 и от 1 до +28, что соответствует временным кодированным углам временных кодированных квадратов, во временной кодированной сетке первых временных периодов -1P и +1P периодической таблицы времени в пространстве, где между периодами -1P и +1P сумма числовых остатков ±n без учета знаков принадлежности к эпохам составляет 28:
Например: (-3+25), (-5+23), (-24+4), (-21+7), (-1+27) и т.д.
Определение остатка производится по формуле временной периодичности:
X:28=P+n,
где X - год,
P - период 28 лет,
n - остаток от деления года на 28.
Например: x= 1965 г., P=70.
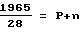
1965=28P+28n
1965-(28·70)=28n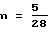
Обратное решение:
X=28(P+n),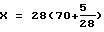
X=1965
Остатки ±n от 1/28 до 27/28 представляются в графах -n и +n своими числителями.
Результат расчета позволяет через формулы временного соответствия определить место нахождения того или иного временного периода в периодической таблице с последующим определением годового календаря.
Например:
1. 511 год до новой эры (-511),
разделив на 28, получим -P = -18 - период,
остаток - n = -7/28
+n = 28-n, +n = 28-7 - по формуле соответствия углов
+n =+21, т.е. -7 соответствует +21
2. +P =+70, +n = +21
+(28·70) + 21 = 1960 + 21 = +1981 год н.э.
3. -P = -70, -n = -7
-(28 · 70)-7 = -1960-7 = -1967 год до н.э.
4. +P = +18, + n = +21
+ (28·18) + 21 = +504 + 21 = +525 год н.э.
5. -P = -251, -n = -7
-(28·251) -7 = -7028-7 = -7035 лет до н.э.
-511; +525; -1967; +1981; -7035, - все эти года в периодической таблице занимают левый верхний угол квадрата, своего соответствующего ряда в различных временных периодах. Они - идентичны и имеют один и тот же календарь, при этом каждую из этих величин можно записать, закодировав числами периода и остатка
+1981 ---> +7021
-1981 --> -7007
+525 ---> +1821
-7035 ---> -25107
В кодированном временном квадрате, на углах которого года различных временных периодов располагаются хронологически, начиная с левого нижнего високосного угла ∠α, далее против часовой стрелки в сторону увеличения числовых значений годов, что соответствует временным периодам до Р.Х., а против часовой стрелки в сторону уменьшения числовых значений годов - для временных периодов после Р.Х.
Сокращая величины временных периодов прошлого и будущего делением на 28 с целью более детальной конкретизации места расположения в периодической таблице времени в пространстве искомых годов, месяцев, дат во временных периодах производится дальнейшее деление остатков ±n на 4 (при ± n ≥ 4), - получим целые числа со своими остатками остатков от 0 до ± 3. Это остатки остатков ± n ±∠α = 4 или 0; ± ∠1; ±∠2; ±∠3. Делением величин високосных годов, соответствующих високосным углам на 4 получим целые числа остатков ± n с нулевым остатком остатка ± n (±∠α), соответствующие левым нижним углам временных кодированных квадратов. Остальные 3 угла во временном кодированном квадрате ± ∠1; ± ∠2; ± ∠3, цифры которых соответствуют остатку остатков ± n и номерам углов в том или ином ряду ± R периодической временной таблицы.
Ряд c + ∠0 остатком остатка ± n определяется по формуле +n/4 = +R. которая применима только для годов, располагаемых на левых нижних високосных углах +∠α, кодированных временных квадратов временных периодов после Р.Х. Это целые числа с нулевыми остатками, что соответствует ряду +R, 0. Все остальные исчисления рядов, года которых находятся во временных периодах до Р. Х. и после Р.Х., определяются формулой
±(n/4+1)=±R, где ±R±∠1; ±R±∠2; ±R±∠3 и -R,0.
Для удобного и быстрого поиска временных величин в кодированном временном квадрате применим правила двух диагоналей. Диагональ α - восходящий вектор, который соединяет левый нижний угол ∠±α с противоположным четным углом и называется четной восходящей диагональю α. Диагональ, соединяющая углы ± ∠1 и ± ∠3, называется нечетной восходящей или нисходящей диагональю β.
Четная восходящая диагональ ±α для всех временных периодов до Р.Х.и после Р.Х. одна и та же и соединяет углы от 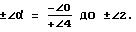
Нечетная восходящая диагональ β - для временных периодов до Р.Х. и соединяет правый нижний угол с левым верхним углом -∠1 и -∠3.
Нечетная нисходящая обратная диагональ β - вектор для временных периодов после Р.Х. Она соединяет величины левого верхнего угла с правым нижним углом +∠1 и +∠3.
Например: 1) -X= -1976 год
-1976: 28=-70P - 16
-16:4= -4,0 остаток остатка нулевой, что соответствует углу -∠α
-R=-(16:4)+1);-R=-5
-1976 год находится в -V ряду в нижнем левом углу -∠α, в -70 периоде до н.э.
2) +X=+2121 год
+2121:28=+75P+21; n=21
+R=+(21:4)+1; +R=(5+1)+∠1=6 ряд
остаток остатка +∠1, соответствует левому верхнему углу, в +VI ряду 75 периода н.э.
3) +X= +1976 год, +1976:28=+70P+n,
+n= +16; 16:4=4,0
+P= +n/4 P=4 P=IV
Остаток остатка нулевой, соответствующий високосному, левому нижнему углу ∠α, находящемуся в IV ряду 70 периода после Р.Х.
Искомый 2121 год после Р.Х., разделив на 28, получим период Р, равный 75, и остаток, равный 21, таким образом запись можно сделать -+2121, где +P = +75, +n = +21, что соответствует альтернативной записи +7521
+1981 году альтернативная запись - +7021
-1967 году альтернативная запись - -7007
+525 году альтернативная запись - +1821
-7035 году альтернативная запись - +25107
+2000 году альтернативная запись - +7112
-1976 году альтернативная запись - -7016
Результаты определения ±P периодов и ±n остатков после деления на 28 в вышеперечисленных примерах получены на основе выведенных формул временного соответствия и временной периодичности из периодической таблицы времени в пространстве. Таким образом каждую числовую величину года можно записать числами своего периода и своего остатка. Эти две величины будут соответствовать только одному году в своем временном периоде до Р.Х. со знаком /-/ и после Р.Х. со знаком /+/ со своим определенным годовым календарем. Это позволило получить альтернативную запись существующего на сегодняшний день летоисчисления, названную альтернативным алгоритмом времени.
Для использования в компьютерной технике альтернативного алгоритма времени его числовые значения необходимо увеличить дополнением цифр, соответствующих числовым значениям временных кодированных рядов и углов.
Например: -1981 альтернативная запись -7021
-702161, где -70 - период -P
-21 - остаток - n
-6 - ряд -P
-1- угол,
или +2000 альтернативная запись +7112
+711234, P = 71, +n = 12, R = +3, + ∠4;
или -2000 -.-.- -7112 -.- -711240, -P = -71, -n =-12, -R = -4, -∠0.
Периодическую таблицу времени в пространстве, развернутую в вертикальное положение, можно представить как временной алгоритм, состоящий из набора 28 строго соответствующих месячных кодов кодированных годовых календарей, повторяющихся через каждые 28 лет. Разделив любую заданную величину годов на равные в 28 лет периоды, в конечном результате получим сокращенные числа до минимума, соответствующие их годовым календарям, выразившимся числам годов первых периодов ±1P до и после Р.Х. Эти числа также называются остатками ± n от деления величин годов на 28.
Кодированная временная сетка как временной алгоритм своими годовыми кодами, например, по январю месяцу несет компактную, скрытую информацию чисел 28 кодированных январских месяцев, 28 кодированных годовых календарей, которые легко могут быть раскодированы. Аналогично начальными месячными кодами могли быть мартовские, декабрьские и др.
В кодированной временной сетке расположенные последовательно вертикально, сверху вниз, с интервалом в один год 28 январских кодов строго соответствуют своим календарям, каждый из которых служит точкой отсчета для дальнейшего быстрого построения кодированного годового календаря.
Семь граф по горизонтали отражают 7 дней недели с понедельника до воскресения, слева направо. За основу январского месячного кода взяты геометрические фигуры - пятиугольники. Три пятиугольника в месячном коде годового кодированного календаря всегда соответствуют месяцу с 31 днем. В кодированном январском месяце - 3 пятиугольника  , которые своими числами отражают первым - начало и третьим, последним - конец месяца.
, которые своими числами отражают первым - начало и третьим, последним - конец месяца.
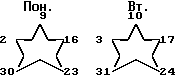



Каждый пятиугольник своими углами несет числовую информацию о 5 днях одного наименования недели в месяце. Все числа месяца располагаются на углах геометрических фигур по часовой стрелке с интервалом в 7 дней.
В кодированной временной сетке каждому январскому коду соответствуют два числа со знаками плюс и минус, сумма которых, без учета их знаков, составляет 28.
Например: (-5+23), (-8+20), (-12+16) и т.д.
Эти числа - числители дробей от ±1/28 до ±27/28 или остатки ±n от ±1 до ±28 от деления на 28 величин годов временных периодов до Р.Х. - со знаком минус, располагаемых в вертикальном ряду слева от понедельников, и после Р. Х. - со знаком плюс, располагаемых в вертикальном ряду справа от воскресений.
Первый воскресный пятиугольник  одиночный, расположен на горизонтали, соответствующей остатку +n =+1. Последующие одиночные пятиугольники во временной кодированной сетке располагаются по горизонталям, соответствующим остаткам +n=+7, +n=+18, +n=+24. Интервалы между этими горизонталями выразятся в числах +1 -7-12-7.
одиночный, расположен на горизонтали, соответствующей остатку +n =+1. Последующие одиночные пятиугольники во временной кодированной сетке располагаются по горизонталям, соответствующим остаткам +n=+7, +n=+18, +n=+24. Интервалы между этими горизонталями выразятся в числах +1 -7-12-7.
Например: 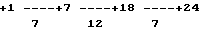
Первый двойной пятиугольник  начинающийся с субботы, соответствует горизонтали с остатком +n = +6. Последующие - соответствуют остаткам +n = 12, +n = 17, +n = +23, интервалы между которыми выразятся в числах +6-----7-----6-----7
начинающийся с субботы, соответствует горизонтали с остатком +n = +6. Последующие - соответствуют остаткам +n = 12, +n = 17, +n = +23, интервалы между которыми выразятся в числах +6-----7-----6-----7
алгоритмы интервалов: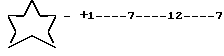 одиночного пятиугольника
одиночного пятиугольника двойного пятиугольника.
двойного пятиугольника.
Эти алгоритмы легко запоминаются и позволяют в дальнейшем легко завершить составление временного 28-летнего алгоритма установкой недостающих пятиугольников до полного количества (до 3-х), размещаемых по горизонталям от суббот, воскресений с переносом на понедельники и вторники. Смещение или движение комбинаций 3-х пятиугольников, слева направо на определенные интервалы, в определенной последовательности, при заполнении пятиугольниками граф дней недели во временной кодированной сетке строго соответствует определенному порядку и геометрическому рисунку, напрямую связанных с остатками ±n. Расставив одиночные и двойные пятиугольники согласно их алгоритмам и заполнив их горизонтали недостающими тройными пятиугольниками во временной кодированной сетке, получим два зеркально отраженных, повернутых на 180o геометрических рисунка.
Первый геометрический рисунок расположен в пределах остатков +n = +1---+n = +12, линия отражения проходит между горизонталями, соответствующими остаткам +6, +7. Второй геометрический рисунок расположен в пределах остатков +13--+28 с линией отражения --- между горизонталями, соответствующими остаткам +20 и +21. При развороте одной из двух частей одного из геометрических рисунков по линии отражения на 180o получатся два одинаковых, идентичных геометрических рисунка, с количеством горизонталей по 6. Аналогичное происходит и со вторым геометрическим рисунком, с количеством горизонталей по 8.
Для завершения составления временного 28-летнего алгоритма оставшиеся пустыми графы заполняются тройными пятиугольниками. Они располагаются по горизонтали на один интервал ниже образовавшихся от недостающих одиночных и двойных пятиугольников в графах понедельников и вторников. Начало их движения - от понедельников до воскресений последовательно с интервалом в 1 год - по вертикали и в 1 день - по горизонтали. Следующая за високосным годом горизонталь - одна имеет интервал в 2 дня. Последние во временном алгоритме - четыре тройных пятиугольника, первый из которых соответствует горизонтали остатков ±n = -3, +25, берет свое начало со вторника.
Временная кодированная сетка или временной геометрический алгоритм - это не что иное, как компактно сконцентрированные числовые значения годов, месяцев, дней недели, часовые, минутно-секундные пояса вечного временного календаря.
Для получения вечного календаря делим любые числовые значения лет разных временных периодов на 28. Полученный остаток, числовое значение которого соответствует месячному январскому коду, позволяет продолжить кодирование годового календаря по принципу: последний пятиугольник предыдущего месяца является продолжением пятиугольников, количественно соответствующих последующему месяцу, при динамике в сторону увеличения срока лет. В кодированном годовом календаре количество дней недели одного наименования либо четыре, либо пять и обозначаются или соответственно либо четырехугольником, либо пятиугольником, углы которых соответствуют числам дней недели. Последовательность заполнения числами углов кодированных символов, полученных в календарном месяце, начинается с первого пятиугольника, производится на каждой фигуре по часовой стрелке с интервалом в семь дней. Три пятиугольника в месячном коде соответствуют месяцу с 31 днем, два пятиугольника в месячном коде соответствует месяцу с 30 днями, а один пятиугольник в месячном коде соответствует месяцу февралю в високосном году с 29 днями, февраль обычного года не содержит пятиугольников. Остальные фигуры в месячном коде, а их всего семь по числу дней недели, составляют четырехугольники.
Таким образом, при наличии листка бумаги и пишущего элемента, мела, доски или любой стены, песка и веточки, хорошей памяти с воображением имеется возможность составить годовой календарь любого года временных периодов до и после Р.Х.
Временной период, равный одним суткам, также как альтернативный вариант цифровой записи, может быть представлен теми же символами с добавлением к пятиугольникам и четырехугольникам геометрических фигур - треугольников и шестиугольников, отражающих:
- шестиугольники - часовой пояс,
- пятиугольники, квадрат, треугольники, незаштрихованные - минутный пояс,
- треугольники, квадраты, звезды (пятиугольники) заштрихованные - секундный пояс.
| название | год | авторы | номер документа |
|---|---|---|---|
| ГОДОВОЙ КОДОВЫЙ КАЛЕНДАРЬ ДОКТОРА САЖНЕВА | 1999 |
|
RU2143138C1 |
| ВЕЧНЫЙ КАЛЕНДАРЬ | 2001 |
|
RU2242801C2 |
| ЧАСЫ С ИНДИКАЦИЕЙ ДАТ ПЕРЕХОДЯЩИХ ПРАЗДНИКОВ | 2014 |
|
RU2565862C1 |
| Многолетний календарь | 1978 |
|
SU780028A1 |
| МНОГОЛЕТНИЙ КАЛЕНДАРЬ | 1991 |
|
RU2016421C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ДНЯ НЕДЕЛИ И КАЛЕНДАРЬ ЯР | 1995 |
|
RU2123206C1 |
| ВЕЧНЫЙ КАЛЕНДАРЬ-АВТОРУЧКА | 1992 |
|
RU2070339C1 |
| Календарь | 1979 |
|
SU1309076A1 |
| ВЕЧНЫЙ ТАБЕЛЬ-КАЛЕНДАРЬ "ВОЛСЛОВ" | 1998 |
|
RU2128368C1 |
| Многолетний календарь | 1990 |
|
SU1737497A1 |




























Изобретение относится к хронологии, вычислительной и компьютерной технике, и обеспечивает возможность в короткий промежуток времени составить годовой календарь любых годовых периодов, уходящих в бесконечность временных пространств прошлого и будущего. Периодическая таблица времени в пространстве - это компактная информация о годах, месяцах, числах и днях одного наименования недели, представленная путем кодирования геометрическими фигурами. Информация объединена в периоды, циклы которых составляют 28 лет с повторением. На основе формул временных соответствий и временной периодичности создан альтернативный алгоритм времени, при замене числовых значений этих лет числовыми значениями их периодов и их годовыми двухзначными остатками возможно использование альтернативного алгоритма в компьютерной технике. В периодической таблице времени кодовые символы выполнены в виде квадратов, углы которых соответствуют 4 годам, один из которых -високосный. Семь таких квадратов образуют временную кодированную сетку, равную одному периоду в 28 лет. Каждый угол квадрата - это соответствующий ему год со своим кодированным годовым календарем, со своими кодовыми символами - пятиугольными и квадратами. Изобретение обеспечивает оригинальность и простоту составления временной кодированной сетки, позволяющей составить годовой календарь любого периода без сложных предварительных вычислений, а также удобство и широкие возможности использования. 3 с. и 1 з.п.ф-лы, 36 ил.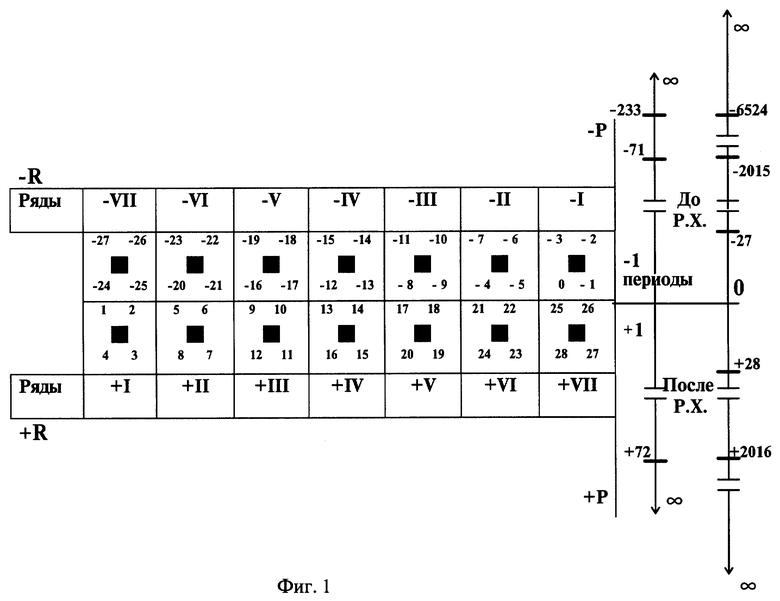
| RU 2056063 A1, 10.03.1996 | |||
| МНОГОЛЕТНИЙ КАЛЕНДАРЬ | 1991 |
|
RU2016421C1 |
| SU 1251160 A1, 15.08.1986 | |||
| Вечный календарь | 1988 |
|
SU1695369A1 |
| Многолетний календарь | 1990 |
|
SU1737497A1 |
| Многолетний перекидной календарь | 1988 |
|
SU1587570A1 |
| US 3765111 A, 16.10.1973 | |||
| FR 1542061 A1, 11.101968 | |||
| РЕКТИФИКАЦИОННАЯ КОЛОННА | 2010 |
|
RU2445996C2 |
| АНТИТЕЛА ПРОТИВ РАСТВОРИМОГО ST-2 ЧЕЛОВЕКА И СПОСОБЫ АНАЛИЗА | 2011 |
|
RU2625014C2 |
Авторы
Даты
2001-01-20—Публикация
1999-04-26—Подача