Изобретение относится к оптическим методам неразрушающего контроля структурных геометрических параметров тканых материалов любой природы и может быть использовано при создании оптических датчиков контроля этих параметров ткани в лаборатории по образцам или в процессе их производства.
В любой ткани основные и уточные нити при взаимодействии друг с другом в процессе изготовления ткани изгибаются.
Величина изгиба нити является важным технологическим параметром ткани, так как определяет поверхностную плотность ткани и расход нити.
К настоящему времени отсутствуют какие-либо неразрушающие методы измерения изгиба нити в ткани. Контроль этой величины проводится только в лаборатории на срезах ткани стандартными способами с помощью лупы или под микроскопом. Эти способы описаны, например в /1/ (Кукин Г.Н. и др. "Лабораторный практикум по текстильному материаловедению", Л.И., Москва, 1974, 260 с. - ГОСТ 3812-72) и /2/ (учебное пособие для средних профессионально- технических училищ Т.С.Грановский, А.П.Мшвениерадзе "Строение и анализ тканей". Москва, Легпромбытиздат, 1988, с. 77-78).
К основным недостаткам этих методов относятся их субъективность и трудоемкость (большое время на измерение). Методы являются разрушающими.
Наиболее близким к предлагаемому является стандартный дифракционный способ анализа, использованный, например, в /3/ (П.Г.Шляхтенко, Г.П.Мещерякова и др. "Исследование связи между коэффициентом поверхностного заполнения тканого полотна и параметрами Фраунгоферовой дифракционной картины от Не- Ne лазера". Известия вузов, ТТП- 1998- N 4, С. 45-49) для анализа геометрических структурных параметров ткани, заключающийся в том, что исследуемый участок материала освещают параллельным пучком монохроматического света перпендикулярно его поверхности и анализируют симметрию и взаимное расположение основных максимумов во фраунгоферовой дифракционной картине, образуемой светом, прошедшим сквозь исследуемый материал, и наблюдаемой на экране, который установлен за образцом в фокальной плоскости объектива, по которым судят о величине структурных параметров ткани (плотность ткани по основе и утку, перекос нитей, диаметр нитей утка и основы).
Этот метод анализа пригоден для осуществления неразрушающего дистанционного контроля структурных параметров ткани как при работе с образцами, так и в процессе движения ткани, при этом положение дифракционной картины на экране не зависит от скорости движения ткани.
К недостатку способа относится невозможность его использования для контроля изгиба нитей в материале.
Целью настоящего изобретения является расширение возможностей метода для реализации возможности контроля величины изгиба нитей утка и основы в тканых материалах.
Поставленная задача достигается за счет того, что исследуемый участок тканого материала освещают параллельным пучком монохроматического света и анализируют симметрию и взаимное расположение основных максимумов во фраунгоферовой дифракционной картине, образуемой светом, прошедшим сквозь исследуемый материал, и наблюдаемой на экране, который установлен за образцом в фокальной плоскости объектива, отличающийся тем, что освещение материала проводят под углом падения света на материал α > 0 в горизонтальной плоскости, перпендикулярной направлению исследуемой нити в ткани, а о величине изгиба этой нити δ судят по величине угла ϕ, измеренного между горизонталью и средней линией дополнительных максимумов в дифракционной картине на экране, проходящей через ее центр, появляющихся в дифракционной картине при α > 0, и известному значению угла α по формуле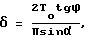
где То - период расположения нитей в ткани, обвиваемых исследуемой нитью.
Существенными отличиями заявляемого решения являются:
1. Освещение тканого материала проводят под углом падения света на материал α > 0 в горизонтальной плоскости, перпендикулярной направлению исследуемой нити в ткани.
Ранее в /3/ освещение ткани производилось параллельным пучком перпендикулярно ее поверхности. При таком падении света изгиб нитей в ткани в дифракционной картине не проявлялся.
2. О величине изгиба этой нити δ судят по величине угла ϕ, измеренного между горизонталью и средней линией дополнительных максимумов в дифракционной картине на экране, проходящей через ее центр, появляющейся в дифракционной картине при α > 0, и известному значению угла α по формуле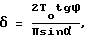
где То - период расположения нитей в ткани, обвиваемых исследуемой нитью.
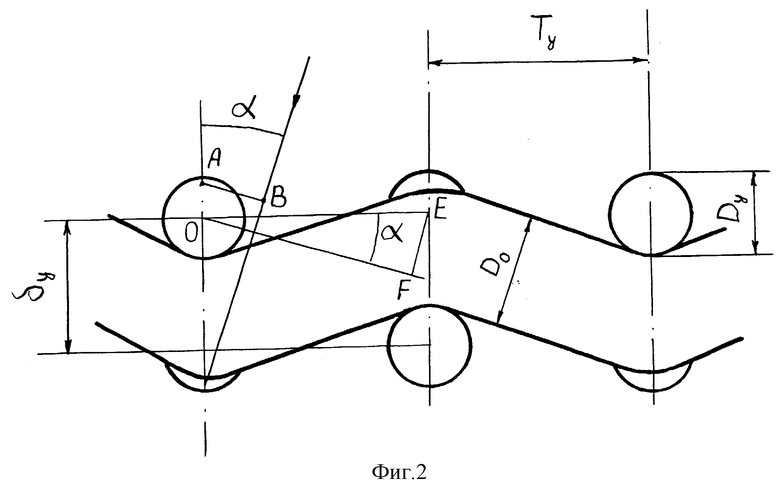
На фиг. 1, 2 приведены сечения тканого полотна соответственно по середине уточной нити, перпендикулярно направлению нитей основы (фиг. 1) и середине основной нити, перпендикулярно направлению уточной нити (фиг. 2), поясняющие суть предлагаемого решения и смысл параметров, входящих в предложенную формулу.
На фиг. 1 пунктиром показана апроксимация уточных нитей отрезками прямых. В приближении, что истинная форма границ нити хорошо описывается синусом, апроксимирующие прямые проведены, как касательные в точке перегиба синуса.
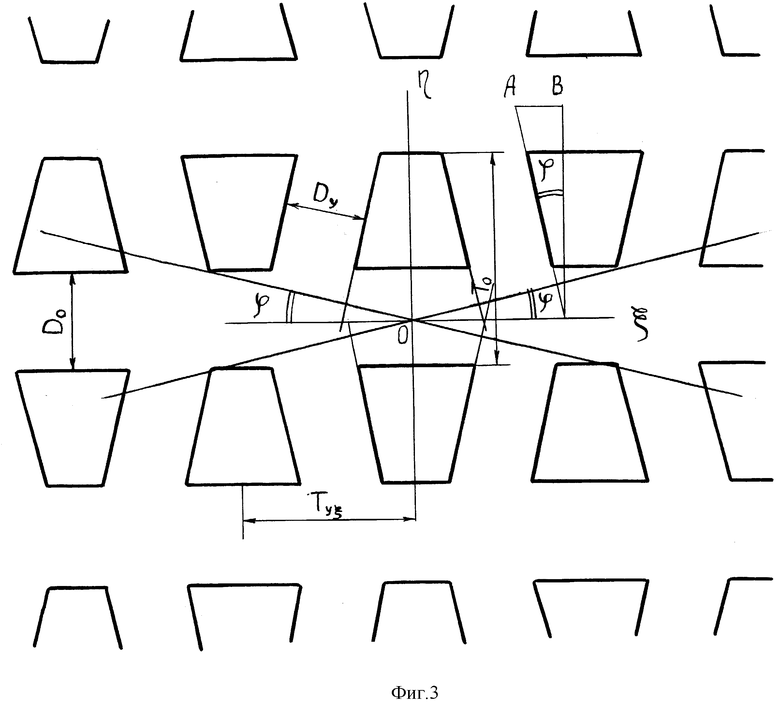
Из фиг. 2 видно, что при нормальном падении света (α = 0), когда плоскость падения света совпадает с плоскостью рисунка, в проекции ткани на плоскость, перпендикулярную плоскости падения света, изгибы нитей основы и утка не проявляются. При косом освещении ткани под углом α, в проекции на плоскость, перпендикулярную направлению падения света на поверхность ткани, изгибы нитей основы наблюдаться по-прежнему не будут, но проявятся изгибы утка. Эта проекция при линейной апроксимации нитей утка (фиг. 1) будет иметь вид, представленный на фиг. 3. Эта проекция, как показывают данные /3/ определяет вид дифракционной картины. Из симметрии фиг. 3 и данных /5/ (М.Борн, Э.Вольф "Основы оптики") в дифракционной фраунгоферовой картине в этом случае следует ожидать появления линий максимумов в направлениях, перпендикулярных апроксимационным линиям профиля нитей утка, идущим через центр дифракционной картины под углом ϕ к горизонтали (координате ζ на фиг. 3).
Из геометрии фиг. 1-3 можно получить формулу для величины изгиба утка δу, справедливой в рамках использованной линейной апроксимации
δу= 2Totgϕ/(πsinα), (1)
где То-период по основе.
Очевидно, что при повороте образца на 90o на место уточной нити встанет основная и наоборот. Поэтому все рассуждения, проведенные выше, сохранятся, как и вид формулы (1). Однако в последнем случае будет измеряться изгиб основной нити, а под То необходимо понимать величину периода по утку.
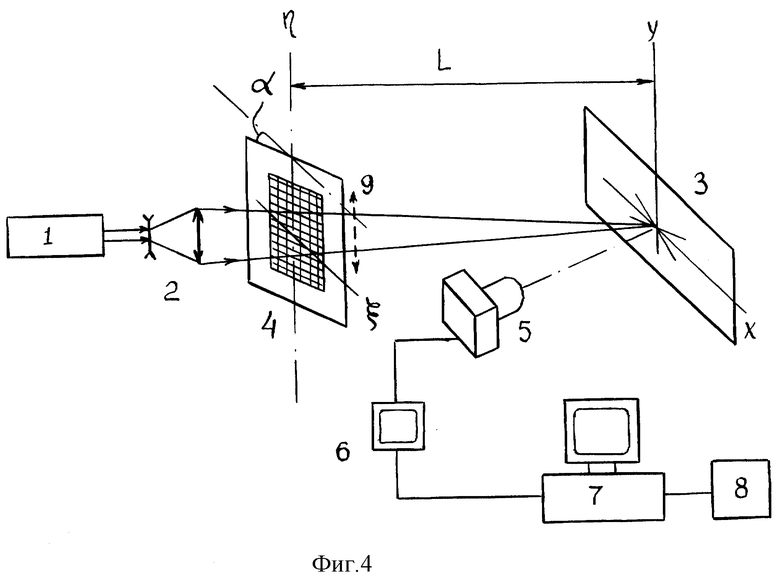
Для проверки работоспособности предложенного способа была собрана схема, приведенная на фиг. 4.
Свет от маломощного Не- Ne лазера 1 падает на телескопический объектив 2, который фокусирует свет в центре экрана 3. Непосредственно за объективом установлен держатель с исследуемой тканью 4, который можно поворачивать и устанавливать под любым углом падения света на образец α. Дифракционная картина на экране может с помощью камеры машинного видения 5 наблюдаться на мониторе 6 и записываться на компьютере 7. Стандартные программы, заложенные в компьютере, позволяют обрабатывать изображение (инверсия, изменение контраста изображения и его яркости), выводить его на дисплей и распечатывать на принтере 8. Расстояние от образца до экрана во всех измерениях было одинаковым (L = 6 м).
На фиг. 5 приведены компьютерные изображения наблюдаемых дифракционных картин от образца полотна (Dо = 0.78 мм, удвоенный уток Dу= 0.34 мм, Tо = 2.1 мм, Тут = 1.5 мм, лавсан, мононить) для нормального падения света на образец фиг. 5-а (α = 0) и при повороте образца вокруг оси, совпадающей с направлением нитей утка на угол α = 30o (фиг. 5-b).
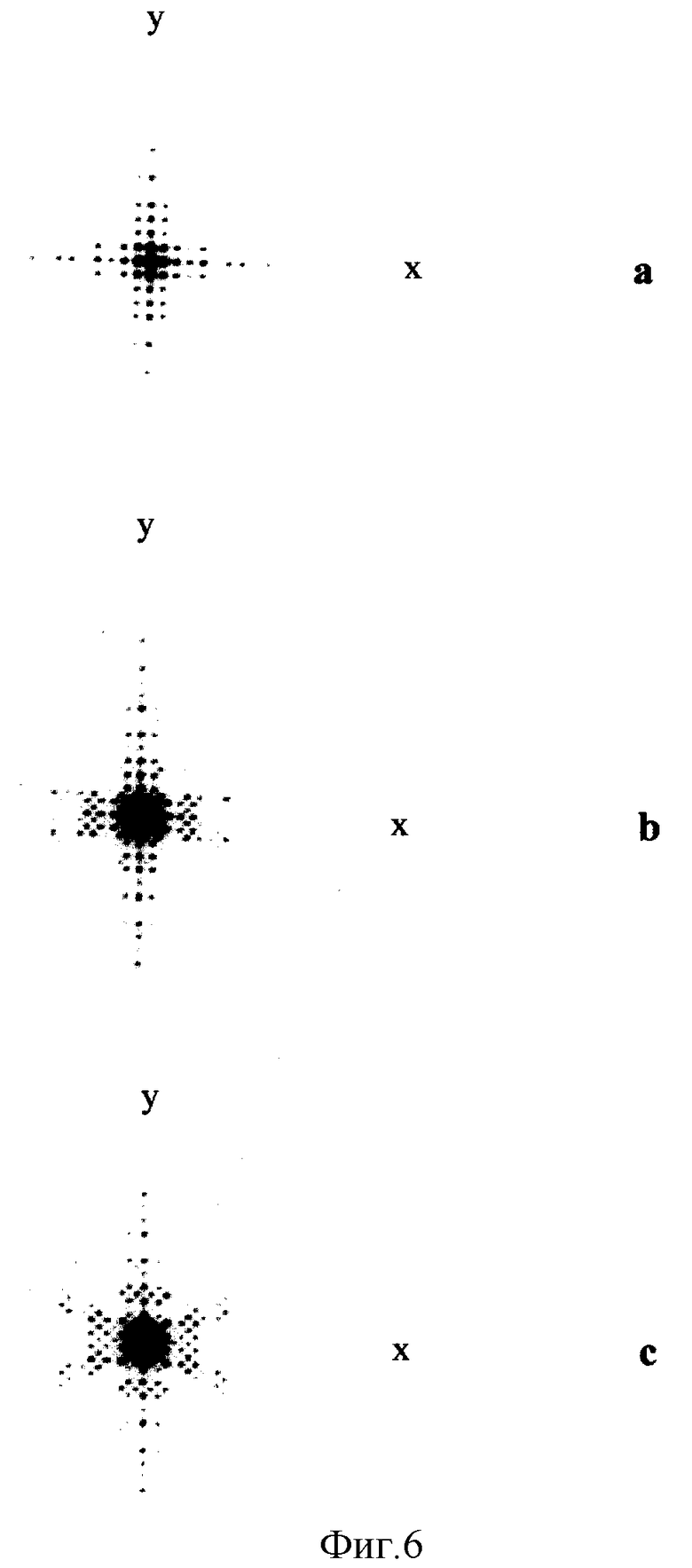
На фиг. 6-a,b,c приведены аналогичные дифракционные картины для образца тканой металлической сетки (Dyr = 0.36 мм, Тут = 0.96 мм, Dо = 0.4 мм, Tо = 1 мм), полученные с помощью установки, изображенной на фиг. 4. Фиг. 6-а соответствует случаю нормального падения света на образец (α = 0), фиг. 6-b при α = 15, фиг. 6-с при α = 30o.
Из данных фиг. 5, 6 можно сделать следующие выводы:
1. При нормальном падении света (фиг. 5,6-а) дифракционная картина обладает симметрией относительно осей х и у, параллельных осям ζ и η на фиг. 3 и аналогична картинам, исследованным ранее в работах /3/ и /4/.
2. Дифракционные картины, полученные при косом освещении образца, остаются симметричными, но в них появляются дополнительные линии максимумов, пересекающие центр картины под углами ϕ и -ϕ относительно оси x. При этом с ростом угла α угол ϕ растет (рис 6-a,Ь).
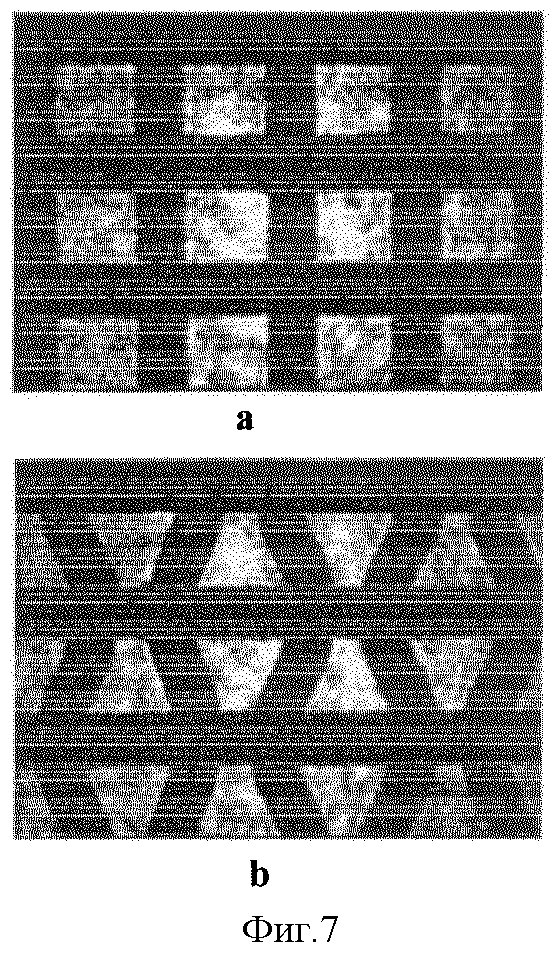
На фиг. 7-a, b приведены теневые проекции образца металлической сетки, дифракционная картина от которой приведена на фиг. 6. Для получения этих проекций в схему (фиг. 4) на оптическую ось устанавливалась собирающая линза 9 таким образом, что она на экране 3 давала увеличенное изображение исследуемой ткани 4. Фиг. 7-а получен при α = 0, фиг. 7-b получен при повороте сетки вокруг уточной нити на угол α = 30o.
Из данных этих рисунков видно, что при повороте образца проекция сетки действительно трансформируется в структуру, подобную представленной на фиг. 3, которая справедлива при линейной апроксимации изгибов уточной нити отрезками прямых. Вместе с тем видно также, что точной линейности в наклонных линиях трапеций на фиг. 7-b все же не наблюдается. Однако ясно, что, используя основную идею, заложенную в формуле предлагаемого метода, всегда можно найти более точную формулу для этой апроксимации, а следовательно, и формулу для расчета изгиба нити, уточняющую формулу (1) для любой тканой структуры.
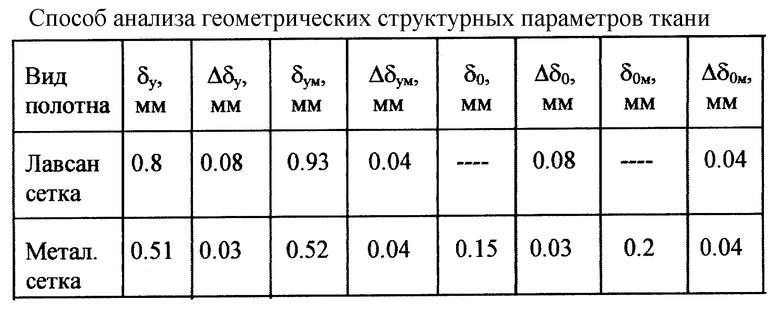
В таблице приведены результаты оценки изгибов уточной нити (δу) и основной (δ0) для образцов этих тканей, проведенные по заявляемому методу и формуле 1 при α = 30o результаты прямого измерения изгибов нитей под микроскопом (δум,δoм), а также соответствующие значения погрешностей, рассчитанных при доверительной вероятности 0.9.
Прочерки означают, что измеряемые величины меньше погрешности измерения.
Из сравнения данных Таблицы можно сделать вывод о том, что результаты прямых измерений изгибов нитей по утку и основе в пределах ошибки практически совпадают с результатами измерений этих параметров по предлагаемому методу. Максимальное отличие относится к лавсановой сетке и объясняется по-видимому тем, что в расчет не закладывалась удвоенность нити утка в этой ткани.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ КОНТРОЛЯ СТРУКТУРНЫХ ГЕОМЕТРИЧЕСКИХ ПАРАМЕТРОВ ТКАННЫХ МАТЕРИАЛОВ | 1999 |
|
RU2164679C2 |
| ДИФРАКЦИОННЫЙ СПОСОБ ОПРЕДЕЛЕНИЯ РЯДА ОСНОВНЫХ ХАРАКТЕРИСТИК ТКАНИ И ТКАНЕПОДОБНЫХ МАТЕРИАЛОВ | 2001 |
|
RU2199739C2 |
| СПОСОБ КОНТРОЛЯ ФИЗИЧЕСКИХ ПАРАМЕТРОВ ДВИЖУЩЕЙСЯ НИТИ | 1996 |
|
RU2138588C1 |
| СПОСОБ ПРИГОТОВЛЕНИЯ ОБРАЗЦОВ ДЛЯ КОНТРОЛЯ СТРУКТУРНЫХ ГЕОМЕТРИЧЕСКИХ ПАРАМЕТРОВ НЕПРОЗРАЧНЫХ МАТЕРИАЛОВ | 2001 |
|
RU2213343C2 |
| СПОСОБ КОНТРОЛЯ АНИЗОТРОПИИ УГЛОВОГО РАСПРЕДЕЛЕНИЯ ВОЛОКОН В СТРУКТУРЕ ПЛОСКОГО ВОЛОКНИСТОГО МАТЕРИАЛА | 2011 |
|
RU2463578C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ УГЛА КРУТКИ НИТИ | 2013 |
|
RU2534720C1 |
| СПОСОБ ПОЛУЧЕНИЯ ТКАНЕЙ КОМБИНИРОВАННЫХ ПЕРЕПЛЕТЕНИЙ | 1999 |
|
RU2144579C1 |
| СПОСОБ ИЗГОТОВЛЕНИЯ ИЗОЛЯЦИОННЫХ ПРОКЛАДОК | 1991 |
|
RU2047708C1 |
| СПОСОБ ИЗМЕРЕНИЯ ПОВЕРХНОСТИ ОБЪЕКТА | 1994 |
|
RU2085839C1 |
| ОПТИЧЕСКИЙ СПОСОБ КОНТРОЛЯ КРУТКИ НИТЕЙ | 2011 |
|
RU2463579C1 |

Изобретение относится к оптическим методам неразрушающего контроля параметров тканых материалов и может быть использовано при создании датчиков контроля этих параметров. Исследуемый участок материала освещают параллельным пучком монохроматического света. Освещение материала проводят под углом падения света на материал α > 0 в горизонтальной плоскости, перпендикулярной направлению исследуемой нити в ткани. О величине изгиба нити δ судят по величине угла ϕ и значению угла α по формуле 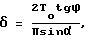 где То - период расположения нитей в ткани, обвиваемых исследуемой нитью. Угол ϕ измеряется между горизонталью и средней линией дополнительных максимумов, которые появляются в дифракционной картине при α > 0. Изобретение позволяет уменьшить время измерения параметров ткани и не разрушать структуру ткани при ее анализе. 1 табл., 7 ил.
где То - период расположения нитей в ткани, обвиваемых исследуемой нитью. Угол ϕ измеряется между горизонталью и средней линией дополнительных максимумов, которые появляются в дифракционной картине при α > 0. Изобретение позволяет уменьшить время измерения параметров ткани и не разрушать структуру ткани при ее анализе. 1 табл., 7 ил.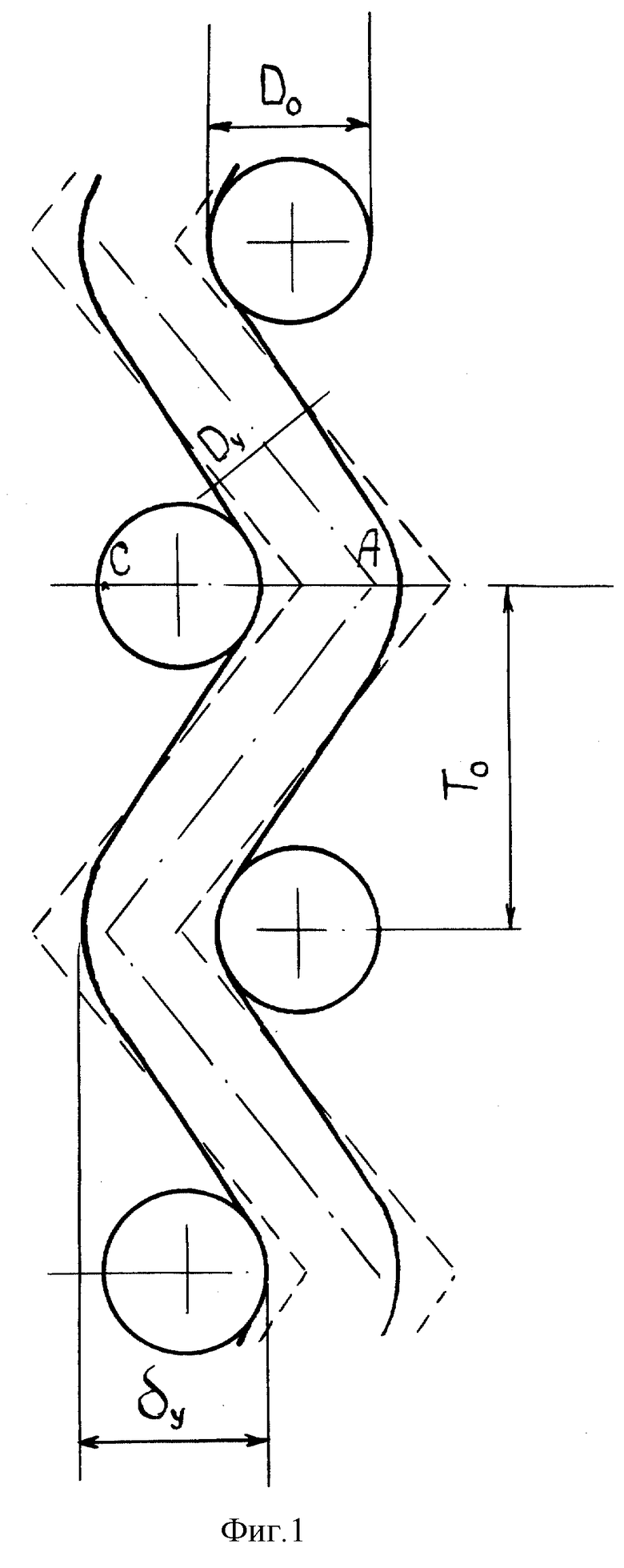
Способ анализа геометрических структурных параметров ткани, заключающийся в том, что исследуемый участок материала освещают параллельным пучком монохроматического света перпендикулярно его поверхности и анализируют симметрию и взаимное расположение основных максимумов в фраунгоферовой дифракционной картине, образуемой светом, прошедшим сквозь исследуемый материал, и наблюдаемой на экране, который установлен за образцом в фокальной плоскости объектива, отличающийся тем, что освещение материала проводят под углом падения света на материал α > 0 в горизонтальной плоскости, перпендикулярной направлению исследуемой нити в ткани, а о величине изгиба этой нити δ судят по величине угла ϕ, измеренного между горизонталью и средней линией дополнительных максимумов в дифракционной картине на экране, проходящей через ее центр, появляющихся в дифракционной картине при α > 0, и известному значению угла α по формуле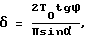
где Т0 - период расположения нитей в ткани, обвиваемых исследуемой нитью.
| ШЛЯХТЕНКО П.Г | |||
| и др | |||
| Известия вузов, ТТП, 1998, № 4, с.45-49 | |||
| RU 94044532 A, 16.12.1994 | |||
| БЕСКОНТАКТНЫЙ СПОСОБ АНАЛИЗА СТРУКТУРЫ ТКАНИ | 1998 |
|
RU2131605C1 |
Авторы
Даты
2001-03-27—Публикация
2000-03-10—Подача