Изобретение относится к измерительной технике и может быть использовано для определения параметров надводных кораблей в том или ином районе Мирового океана.
Известен способ определения размеров наземных (надводных) объектов путем их аэровизуальных наблюдений [1]. Данный способ вполне может быть применен для нахождения длины судна, движущегося в океане.
Однако известный способ требует наличия оптической аппаратуры высокого разрешения. Кроме того, само судно может быть скрыто естественным или искусственным оптически (электромагнитно) непроницаемым экраном. Скорость же судна по причине его тихоходности определить однократным пролетом над ним невозможно.
Предлагаемый способ определения параметров надводных кораблей базируется на том, что в приближении линейной теории получены теоретические спектральные оценки (ТСО) поверхностных корабельных волн, и выполнен анализ зависимости распределения энергии ТСО от параметров генератора, в качестве которых рассматриваются тонкие водоизмещающие суда.
Рассмотрим теоретическую спектральную оценку поверхностных корабельных волн, генерируемых тонким водоизмещающим судном.
Пусть к горизонтальной поверхности жидкости, занимающей пространство (-H < z < 0, -∞ < x < ∞, -∞ < y < ∞).
На вертикальной стенке y = 0 находится препятствие y = f(x,y), - моделирующее форму судна. Предполагаем, что продольный размер значительно превосходит поперечный. В момент времени t = 0 возникает поток жидкости с постоянной скоростью C в положительном направлении оси OX. Задача состоит в нахождении Фурье - спектра волн, возникающих на поверхности жидкости при обтекании препятствия. Математическая постановка задачи включает в себя уравнение Лапласа.
Δϕ = 0, (-H < Z < 0) (1)
с граничными условиями: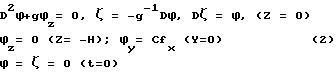
здесь ϕ - потенциал возмущенных скоростей;
g, ρ, ζ - ускорение свободного падения, плотность жидкости и отклонение свободной поверхности;
D = ∂/∂t+C∂/∂x,
подстрочный индекс означает дифференцирование по соответствующей переменной.
Применение интегральных преобразований к (1) - (2) приводит к следующей задаче: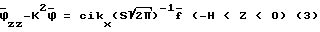
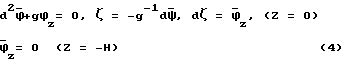
Построим функцию Грина краевой задачи (3) - (4).
Фундаментальные решения однородной задачи, соответствующей (3)-(4), имеют вид: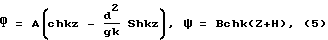
где A, B - произвольные постоянные.
Вронскиан фундаментальной системы решений определяется выражением: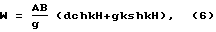
С учетом (5), (6) легко построить функцию Грина: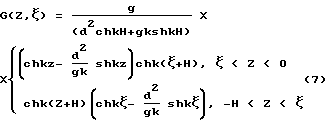
Решение однородной задачи (3)-(4) с использованием функции Грина (7) выражается следующим образом: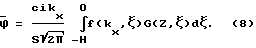
Используя выражение 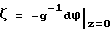 и предельную теорему Лапласа, получим выражение для трансформанты Фурье смещений свободной поверхности, вызываемых обтеканием тонкого водоизмещающего судна:
и предельную теорему Лапласа, получим выражение для трансформанты Фурье смещений свободной поверхности, вызываемых обтеканием тонкого водоизмещающего судна: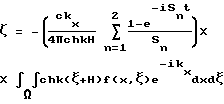
где Ω - носитель функции f(x,z).
Анализ адекватности теоретической спектральной оценки поверхностных корабельных волн на основе сопоставления теоретических и экспериментальных данных.
Для определения адекватности построенных теоретических спектральных оценок поверхностных корабельных волн рассматриваемому физическому процессу выполнено сопоставление теоретических расчетов с данными обработки реальных аэрофотоснимков.
Форма судна в расчетах моделировалась функцией вида: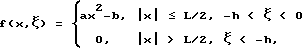
где L - длина надводного судна, h - осадка, b - ширина, 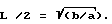
При этом для теоретических спектральных оценок поверхностных корабельных волн справедливо следующее выражение: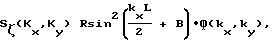
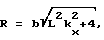
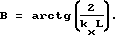
Выражение для Ф(kx,ky) не выписывается в силу его громоздкости.
Поскольку экспериментальные спектры поверхностных корабельных волн представлены в виде одномерных спектров, полученных усреднением двумерных по азимутальному углу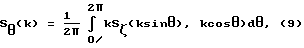
то и используемые в расчетах теоретические спектральные оценки поверхностных корабельных волн приводились к такому виду.
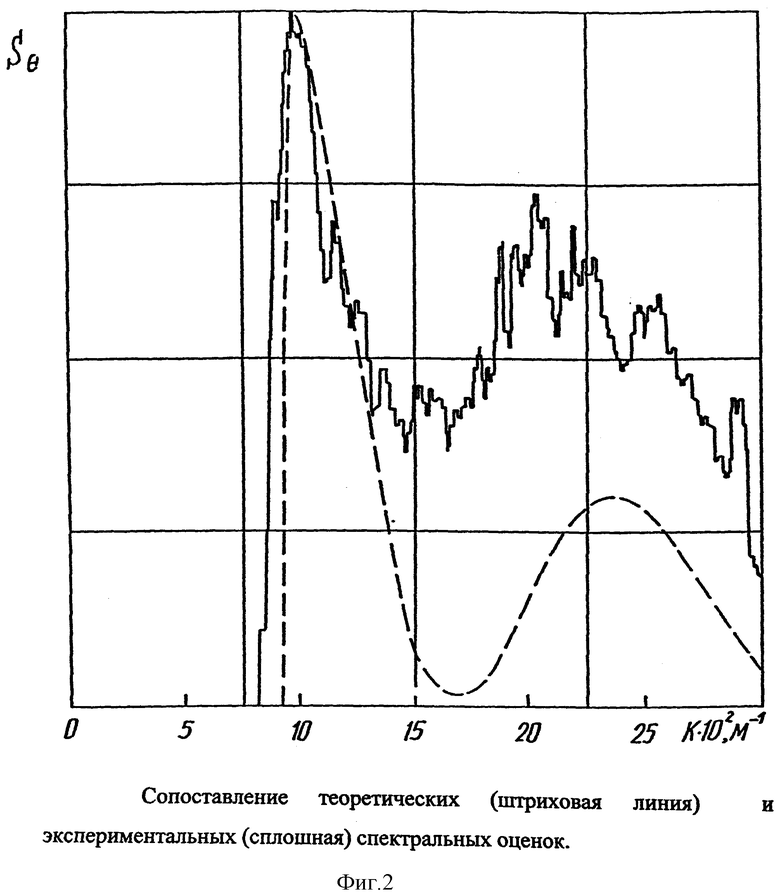
Результаты сравнения для двух объектов представлены на фиг. 1 и 2. Сплошной кривой показаны результаты эксперимента, штриховой - теоретические. Объекты различались длиной, водоизмещением и скоростью движения (фиг. 1 соответствует объекту большой длины, при этом скорость его движения меньше).
При сравнении учтено следующее:
в реальных спектрах используется только часть волнового поля, попавшего в кадр, что приводит к размыванию энергии по спектру. Действительно, пусть f(x, y) - исходное поле поверхностных корабельных волн, g(x,y) εΩ - финитная функция (окно наблюдения), F(kx, ky) - двумерный спектр f(x,y), G(kx,ky). Тогда в действительности мы получим данные о функции f1(x,y) = f(x,y) g(x, y). При этом спектр f1(x,y) имеет вид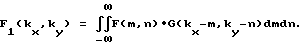
Кроме поля поверхностных корабельных волн в кадре присутствует фоновое ветровое волнение, что приводит к появлению паразитных пиков в спектре;
теоретические спектральные оценки поверхностных корабельных волн, используемые в расчетах, строились в приближении линейной теории волн.
Но даже с учетом вышесказанного, сопоставление результатов показывает, что получение оценки качественно правильно описывают распределение энергии по модулю волнового вектора, а расположение максимумов - и количественно.
Дополнительно на основании полученных оценок был проведен численный анализ зависимости спектров поверхностных корабельных волн от параметров надводных судов, таких как длина (L), ширина (b), осадка (h), скорость движения (c) для различных способов задания формы надводного судна.
Как показали численные эксперименты, энергия в спектрах поверхностных корабельных волн локализована в узкой окрестности дисперсионных кривых поверхностных корабельных волн, описываемых выражением:
c2kx2 = gkthkH. (10)
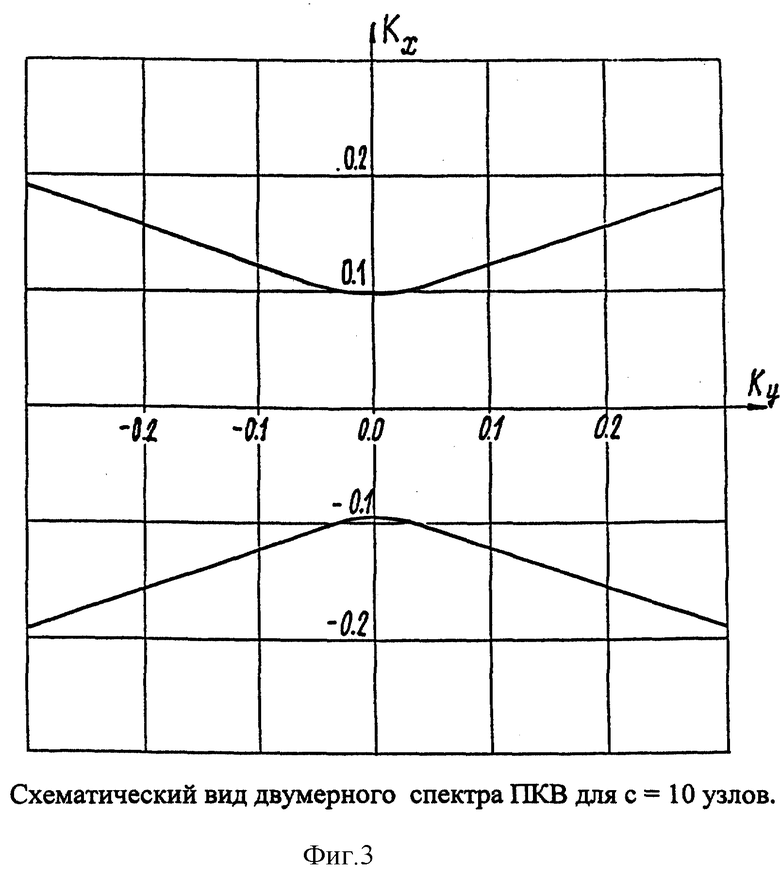
Схематический вид двумерного спектра для c = 10 узлов приведен на фиг. 3. Для заданной скорости движения изменение L, b, h приводит только к перераспределению энергии вдоль дисперсионной кривой. Как следует из (10) при ky = 0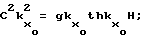
отсюда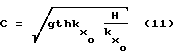
или для коротких волн 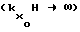 , что для поверхностных корабельных волн практически всегда справедливо:
, что для поверхностных корабельных волн практически всегда справедливо: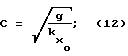
Таким образом, двумерный спектр дает возможность оценить на основании простой формулы скорость движения надводного судна. Для оценки других параметров удобнее использовать одномерные оценки типа (9).
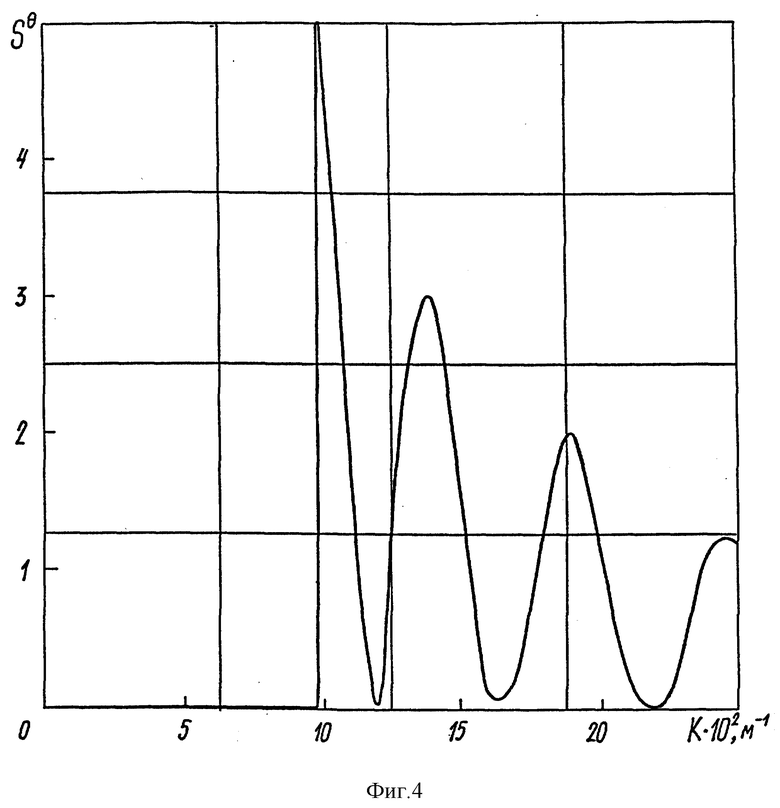
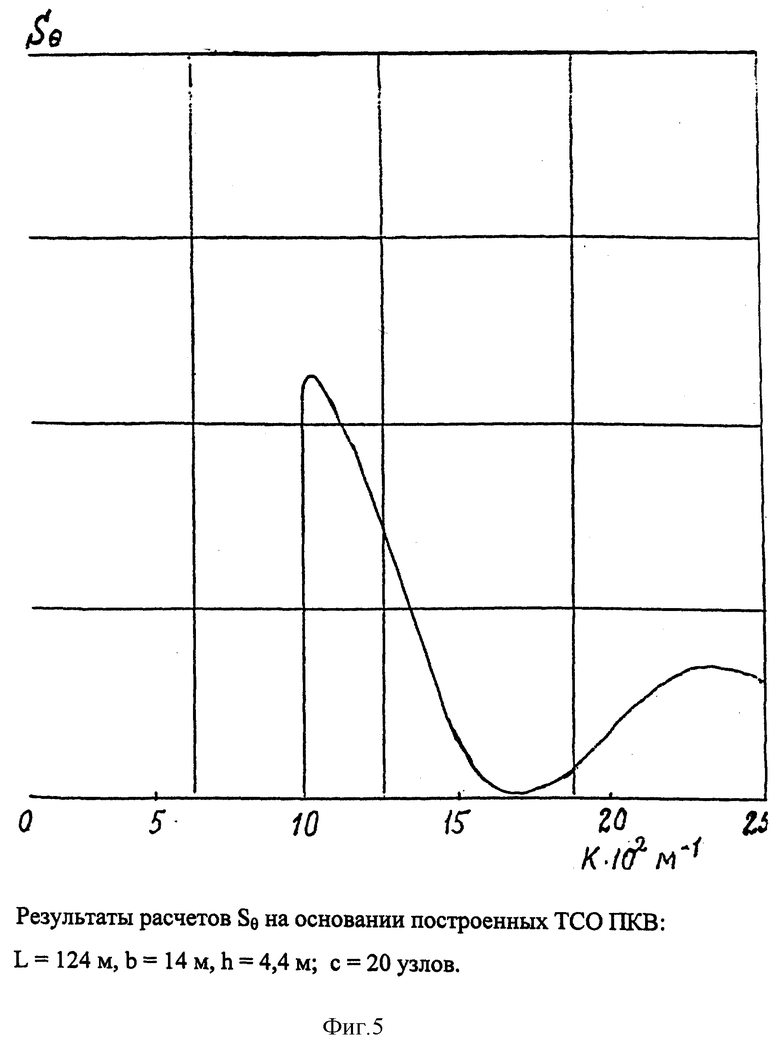
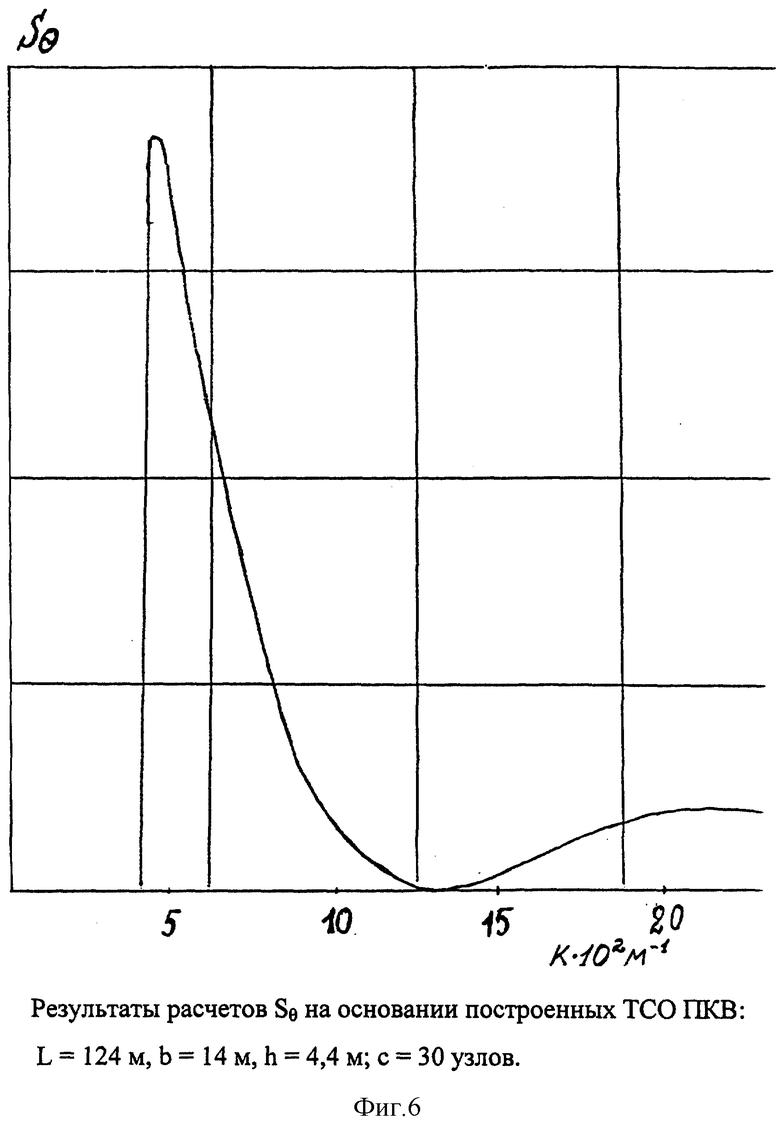
На фиг. 4, 5 и 6 представлены результаты расчетов Sθ для двух типов надводных судов и двух скоростей движения.
Фиг. 4 соответствует: L = 273 м, b = 73 м, h = 6 м, с = 20 узлам,
фиг. 5: L = 124 м, b = 14 м, h = 4,4 м, c = 20 узлам,
фиг. 6: L = 124 м, b = 14 м, h = 4,4 м, c = 30 узлам.
Видно, что при одинаковых скоростях движения частота среза для различных надводных судов одинакова, что и следует из (9) и (11). Изменение размеров надводного судна приводит к перераспределению энергии по спектру волнового числа. Для представленной модели расстояние между соседними максимумами в проекции на ось OX Δ kx связано с длиной надводного судна выражением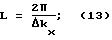
В этой связи более удобным при анализе представляется использование одномерного спектра, полученного интегрированием по ky: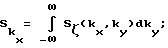
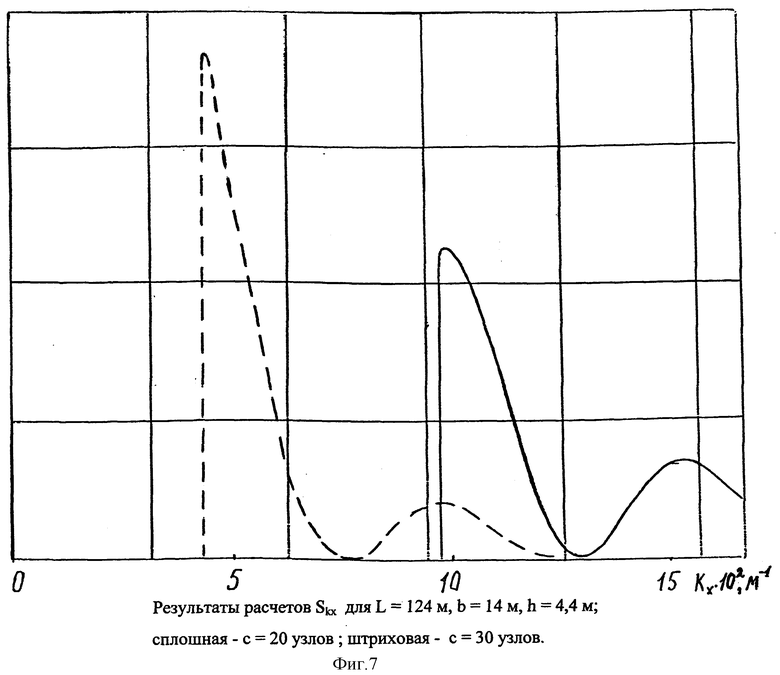
На фиг. 7 представлены оценки 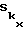 для тех же значений параметров, что и для фиг. 5 и 6.
для тех же значений параметров, что и для фиг. 5 и 6.
Расстояние между максимумами в 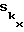 для двух объектов одинаково и определяется длиной надводного судна. Расчеты для других функций, моделирующих форму надводного судна, дали аналогичный результат.
для двух объектов одинаково и определяется длиной надводного судна. Расчеты для других функций, моделирующих форму надводного судна, дали аналогичный результат.
Использование формул (11), (13) к реальным спектрам (фиг. 1 и 2) подтвердило их работоспособность, при этом ошибка составляла 20% для длины надводного судна и 10% - для его скорости.
К настоящему времени достаточно полно отработана методика определения спектра волнения моря путем спектрального анализа аэрофотоснимков [2-5]. В работе [2] показано, что двумерный спектр флюктуаций яркости оптического изображения Sou(kx, ky), (kx,ky) - компоненты волнового вектора - связан со спектром возвышения волновой морской поверхности Sζ(kx,ky).
Таким образом можно сделать вывод: построенные теоретические спектральные оценки поверхностных корабельных волн удовлетворительно описывают распределение энергии в реальных спектрах, полученных на основании обработки аэрофотоснимков движущихся надводных судов;
частота среза в одномерных спектрах, полученных усреднением исходных по азимутальному углу, определяется скоростью надводных судов, а характерные масштабы неоднородностей - его размерами.
Предложенные формулы для определения скорости движения и длины надводного судна подтвердили свою работоспособность при анализе реальных наблюдений.
Литература
1. Большая советская энциклопедия, т. 2, с. 476.
2. Лупян Е.А., Шарков Е.А. Критерии восстановления спектральных характеристик шероховатой морской поверхности по ее оптическому изображению. Исслед. Земли из космоса. N 2, 1986, с. 68-76.
3. Лупян Е.А. Восстановление углового распределения энергии в двумерном спектре возвышения морской поверхности по ее оптическому изображению. Исслед. Земли из космоса, N 3, 1988, с. 31-35.
4. Гришин В.А., Ильин Ю.А., Лазарев А.А., Лупян Е.А., Малинников В.А., Покровская И.В., Скачков В.А., Суслов А.И., Стулов А.А., Шарков Е.А. Синхронные оптические и контактные исследования пространственно-спектральных характеристик морского волнения. Исслед. Земли из космоса, N 2, 1986, с. 57-67.
5. Большаков А. Н., Бурдюгов В.М., Гродский С.А., Кудрявцев В.Н. Определение спектра энергонесущих поверхностных волн по изображению солнечного блика. Исслед. Земли из космоса, N 5, 1988.
Изобретение относится к технологии измерений и может быть использовано при определении параметров надводных судов по данным аэрофотосъемок и спутниковых наблюдений. Способ содержит операцию наблюдения за судном в океане. Скорость и длину судна определяют по спектру возбуждаемых им поверхностных волн. Скорость судна находят по частоте среза спектральной кривой. Длину судна определяют по расстоянию между максимумами спектра. Технический результат реализации изобретения заключается в упрощении и обеспечении надежности процесса получения параметров надводных судов в океане. 7 ил.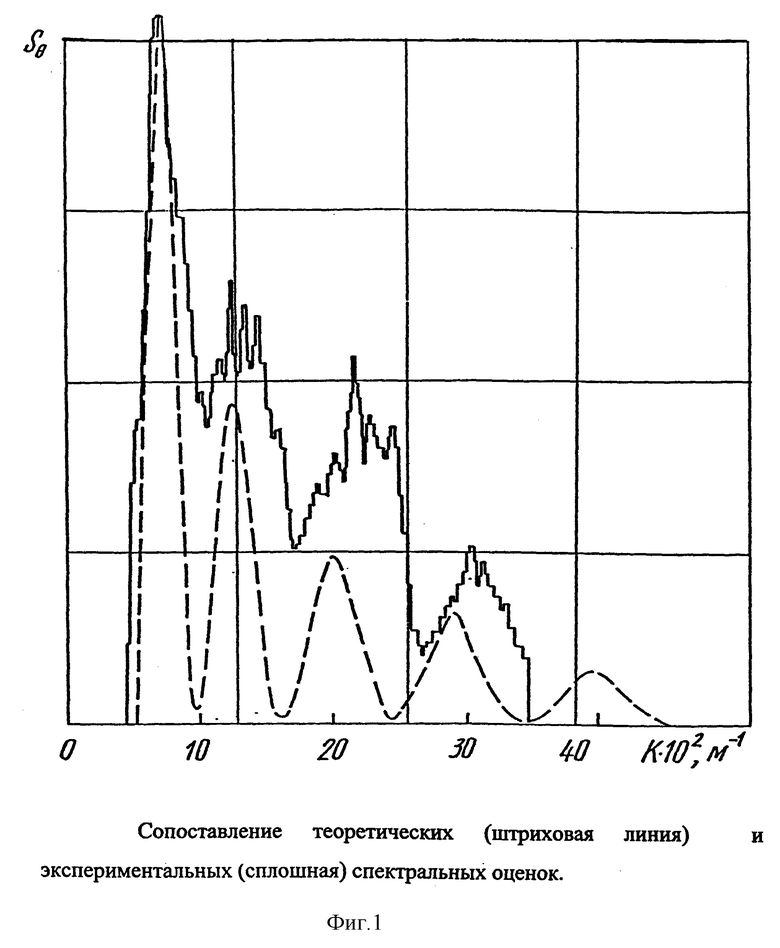
Способ определения параметров надводного судна, заключающийся в наблюдении его в океане, отличающийся тем, что скорость и длину судна определяют по спектру возбуждаемых им поверхностных волн, при этом скорость судна определяется по частоте среза спектральной кривой, а его длина - по расстоянию между максимумами спектра.
| Аэровизуальные наблюдения | |||
| Большая Советская Энциклопедия./Под ред | |||
| А.М.Прохорова, Третье издание | |||
| - М.: Советская Энциклопедия, 1970, т.2, с.476 | |||
| US 3751979 А, 14.08.1973 | |||
| РЕАГЕНТ ДЛЯ ИНВЕРТНЫХ ЭМУЛЬСИОННЫХ РАСТВОРОВ | 2001 |
|
RU2200753C1 |
Авторы
Даты
2001-04-20—Публикация
1999-04-07—Подача