Изобретение относится к области исследования физических свойств вещества, в частности к способам измерения электрических параметров плазмы в газоразрядных приборах, ионосферной плазме, в космическом пространстве.
Известен способ определения дебаевского радиуса в плазме заданной плотности n0 при измерении температуры электронов путем пропускания через плазму электромагнитной волны /1/. При этом дебаевский радиус находится путем расчета из выражения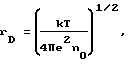
где k - постоянная Больцмана,
e - заряд электрона.
Этот способ не является способом прямого экспериментального определения дебаевского радиуса, на котором должно происходить полное разделение электрических зарядов.
Известен также расчетный способ определения дебаевского радиуса в плазме плотности n0 при измерении температуры электронов с помощью электрического ленгмюровского зонда /2/. Зонд вводится в плазму и представляет собой металлический электрод, размеры которого малы по сравнению с изучаемой областью плазмы. Получаемая с помощью зонда вольт-амперная характеристика позволяет определить температуру электронов в плазме.
К недостаткам этого способа относится необходимость измерения электронной температуры зондами, что часто оказывается невозможным, например, в отсутствие максвелловского распределения, при больших магнитных полях, в электроотрицательных газах.
Недостатком указанных расчетных способов определения дебаевского радиуса является отсутствие объективного контроля за необходимым полным разделением ионов и электронов при определении дебаевского радиуса.
Техническая задача, решаемая в предлагаемом изобретении, заключается в разработке способа экспериментального определения дебаевского радиуса в электрических колебаниях при возбуждении в плазме волн плотности и потенциала (см. /3/).
Поставленная задача достигается тем, что в плазме с известной концентрацией n0 возбуждают потенциальную волну и измеряют флуктуации электрического потенциала Φ1. При этом длина волны определяется из формулы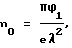
а дебаевский радиус rD находят из выражения
λ = 2πrD.
Данный способ впервые дает возможность осуществить прямое экспериментальное определение дебаевского радиуса в электрических колебаниях при объективном контроле за полным разделением заряженных частиц в волне.
Сущность способа заключается в следующем. Согласно уравнению Пуассона
▿2Φ = 4πρ. (1)
Из (1) можно получить выражение для разности концентраций ионов и электронов в волне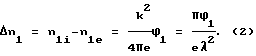
где n1i и n1e - флуктуации концентраций ионов и электронов в волне соответственно, k = 2π/λ, λ - длина волны, ρ = eΔn.
Выражение (2) связывает величину флуктуации потенциала Φ1 с возмущением зарядов в волне Δn1. Измеряя значения Φ1 в возбуждаемой в плазме волне, можно рассчитывать флуктуации неквазинейтральности Δn1. При этом длина волны λ легко определяется экспериментально /3/.
При полном разделении зарядов в волне, когда Δn1 = Δn1c = n0 при λ = λс, величина флуктуаций потенциала достигает максимального значения Φ1 = Φ1c и определяется температурой электронов, так что
Φ1c = kTe/e (3)
Подстановка (3) в (2) дает выражение для длины волны, на которой достигается полное разделение зарядов в колебаниях,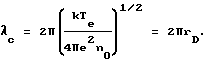
Величина λc имеет смысл дебаевского радиуса, но превышает рассчитанный по формуле rD = (kTe/4πe2n0)1/2
в 2π раз.
Схема измерений дебаевского радиуса в колебаниях показана на чертеже.
Внутри разрядной трубки 1, заполненной плазмой, помещается электрический зонд 2, измеряющий флуктуации потенциала Φ1 с помощью стандартной электрической схемы. Длину волны λ измеряют с помощью двух фотоэлектронных умножителей 3 и 4 и световодов 5 и 6. Световод 5 подвижный. С помощью световода 6 осуществляется синхронизация сигналов. Заметим, что величины Φ1 и λ могут быть измерены и другими способами. Длину волны, например, можно определить с помощью зондов.
В экспериментах газоразрядная плазма создавалась в стеклянных цилиндрических трубках, наполненных инертными газами при давлениях в диапазоне от 10-1 до 5•10-4 Торр. Испытания проводились как в магнитном поле, так и без него.
Пример 1. В гелиевой плазме при давлении 10-2 Торр и магнитном поле 2 кГс равенство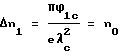
обнаруживается при стационарной концентрации электронов n0 = 6•107 см-3. При этом Φ1 = 5,75 В, длина волны λ = 1,45 см, а rD = 0,23 см. Расчет дебаевского радиуса по измеренной температуре электронов (Te = 7,9•104 К) дает rD = 0,25 см.
Пример 2. При давлении 7,6•10-3 Торр и поле 1,7 кГс равенство Δn1 = n0 выполняется при n0 = 3,5•107 см-3. При этом Φ1c = 7,8 В, длина волны λc = 2,2 см, а rD = 0,36 см. Расчет дебаевского радиуса по измеренной температуре электронов (Te = 9,5•104 К) дает rD = 0,36 см.
Таким образом, в предложенном способе впервые предложено новое решение экспериментального определения дебаевского радиуса, основанное на измерении длины возбужденной в плазме волны и флуктуаций потенциала при полном разделении заряда в электрических колебаниях. Способ позволяет установить границу между плазмой и простой совокупностью заряженных частиц (электронов и ионов), на которой достигается равенство тепловой кинетической энергии заряженных частиц и их потенциальной энергии при полном разделении зарядов.
Способ прост в осуществлении, универсален и эффективен. Его можно применять в исследованиях в лабораторной и ионосферной плазме.
Источники информации
1. Бекефи Д. Радиационные процессы в плазме. - М., "Мир", 1971, с. 230.
2. Козлов О.В. Электрический зонд в плазме. - М., "Атомиздат". 1969, с. 41.
3. Bondarenko V.E., Shvilkin B.N. J. Phys. D 29, 1996, p. 638.
Изобретение относится к газоразрядным приборам, использующим электрический разряд, и может быть применено при исследованиях плазмы. Способ экспериментального определения дебаевского радиуса в электрических колебаниях в плазме заключается в том, что в плазме с известной концентрацией n0 возбуждают волну и измеряют флуктуации потенциала Φ1. При этом длина волны λ определяется из формулы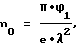
а дебаевский радиус rD находят из выражения λ = 2π•rD. Техническим результатом изобретения является простота способа и его универсальность. 1 ил.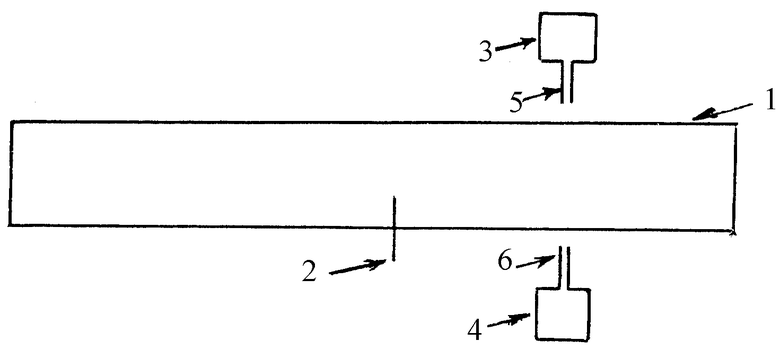
Способ экспериментального определения дебаевского радиуса в электрических колебаниях в плазме, отличающийся тем, что в плазме с известной концентрацией n0 возбуждают потенциальную волну и измеряют флуктуации потенциала Φ1, при этом длина волны λ определяется из формулы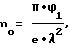
а дебаевский радиус rD находят из выражения λ = 2π•rD.
| БЕКЕФИ Д | |||
| Радиационные процессы в плазме | |||
| - М.: Мир, 1971, с.230 | |||
| RU 94025083/07 A1, 27.05.1996 | |||
| СПОСОБ ПРЕДСКАЗАНИЯ ЗЕМЛЕТРЯСЕНИЙ | 1997 |
|
RU2120647C1 |
| СПОСОБ ИМПУЛЬСНО-ПЕРИОДИЧЕСКОЙ ИОННОЙ ОБРАБОТКИ ИЗДЕЛИЯ И УСТРОЙСТВО ДЛЯ ЕГО ОСУЩЕСТВЛЕНИЯ | 1989 |
|
SU1764335A1 |
Авторы
Даты
2001-05-10—Публикация
1999-03-02—Подача