Изобретение относится к области электросвязи и вычислительной техники, а конкретнее к области способов шифрования и криптографических устройств для защиты информации, передаваемой по каналам связи или хранимой в компьютерных системах.
В совокупности признаков заявляемого способа используются следующие термины:
- секретный ключ представляет из себя двоичную информацию, известную только законному пользователю;
- подключ - часть секретного ключа;
- шифрование есть процесс преобразования информации, который зависит от секретного ключа и преобразует исходный текст в шифртекст (криптограмму), представляющий собой псевдослучайную последовательность знаков, из которой получение информации без знания секретного ключа практически неосуществимо;
- дешифрование есть процесс обратный процедуре шифрования; дешифрование обеспечивает восстановление информации по криптограмме при знании секретного ключа;
- шифр представляет собой совокупность элементарных шагов преобразования входных данных с использованием секретного ключа; шифр может быть реализован в виде программы для ЭВМ или в виде отдельного устройства;
- двоичный вектор - это некоторая последовательность нулевых и единичных битов, например (101101011); двоичный вектор интерпретируется как двоичное число, т.е. двоичному вектору может быть сопоставлено численное значение;
- криптоанализ - метод вычисления секретного ключа для получения несанкционированного доступа к зашифрованной информации;
- криптостойкость является мерой надежности защиты зашифрованной информации и представляет собой трудоемкость, измеренную в количестве элементарных операций, которые необходимо выполнить для восстановления информации по криптограмме при знании алгоритма преобразования, но без знания секретного ключа;
- одноместная операция - это операция, выполняемая над двоичным вектором; двоичный вектор, формируемый на выходе одноместной операции, зависит только от входного двоичного вектора; примером одноместных операций являются операции циклического сдвига;
- двуместная операция - это операция, выполняемая над двумя операндами; результат выполнения некоторой данной двуместной операции зависит от значения каждого операнда; примером двуместных операций являются операции сложения, вычитания, умножения и др.
- операнд - это двоичный вектор, над которым выполняется двуместная или одноместная операция;
- управляемая двуместная операция - это операция, выполняемая над двумя операндами под управлением некоторого двоичного вектора, называемого управляющим вектором; результат выполнения некоторой управляемой двуместной операции при фиксированном управляющем векторе зависит от значения каждого операнда, а при фиксированных значениях операндов - от значения управляющего вектора; примеры реализации управляемых двуместных операций описаны в патенте 2140716 [Молдовян А.А., Молдовян Н.А., Молдовян П.А. Способ криптографического преобразования блоков цифровых данных // Патент РФ 2140716, МПК6 H 04 L 9/28, БИ 30 от 27.10.1999]; в формулах управляемую двуместную операцию будем обозначать записью Z:=QV(A,B), где А, В - операнды, V - управляющий вектор, Z - двоичный вектор, являющийся результатом выполнения управляемой двуместной операции QV;
- модификация управляемой двуместной операции - двуместная операция, соответствующая преобразованию двух операндов при фиксированном значении управляющего вектора;
- управляемая перестановка - это операция, выполняемая над одним операндом под управлением некоторого двоичного вектора, называемого управляющим вектором и заключающаяся в перестановке битов операнда в зависимости от значения управляющего вектора; примеры реализации управляемых перестановок описаны в патенте 2140714 [Алексеев Л.Е., Белкин Т.Г., Молдовян А.А., Молдовян Н.А. Способ итеративного шифрования блоков данных // Патент РФ 2140714, МПК6 Н 04 L 9/20, БИ 30 от 27.10.1999]; в формулах управляемую перестановку будем обозначать записью РV, а преобразование операнда В путем выполнения над ним управляемой перестановки - записью В:=РV(В), где V - управляющий вектор; управляемая перестановка является частным случаем управляемой одноместной операции;
- модификация управляемой перестановки - фиксированная перестановка битов операнда, соответствующая заданному значению управляющего вектора;
- обратная управляемая перестановка (по отношению к некоторой данной управляемой перестановке) - это перестановка, все модификации РV -1 которой являются обратными по отношению к модификациям перестановки РV, т.е. для любого заданного значения управляющего вектора последовательное выполнение операций РV и РV -1 над двоичным вектором В не изменяют значение последнего, что аналитически можно записать в виде В=PV -1(PV(B)) или В=PV(PV -1(B)); варианты реализации двух взаимно обратных управляемых перестановок описаны в патенте РФ 2140714.
- обратная управляемая двуместная операция (по отношению к некоторой данной управляемой двуместной операции Q - это такая управляемая двуместная операция (обозначаемая как Q-1), которая для любого заданного значения управляющего вектора V и любого заданного значения операнда В удовлетворяет условию А=QV -1(Z, B), если Z=QV(A, B); варианты реализации двух взаимно обратных управляемых двуместных операций описаны в работе [Гуц Н.Д., Молдовян А. А. , Молдовян Н.А. Гибкие аппаратно-ориентированные шифры на базе управляемых сумматоров // Вопросы защиты информации, 2000, 1, с. 8-15];
- обращаемая управляемая двуместная операция Q* - это такая управляемая двуместная операция, которая контролируется специальным битом инвертирования е; разные значения е задают два разных варианта управляемой двуместной операции, причем эти варианты являются взаимно обратными; например, если при е=0 выполняется операция Q(0), а при е=1 - операция Q(1), то для этих управляемых двуместных операций имеет место соотношение Q(1)=Q(0) -1; вариант реализации обращаемой управляемой двуместной операции описан в работе [Гуц Н.Д., Молдовян А.А., Молдовян Н.А. Гибкие аппаратно-ориентированные шифры на базе управляемых сумматоров // Вопросы защиты информации, 2000, 1, с. 8-15];
- управляемая перестановочная инволюция - это операция управляемой перестановки Р, для которой обратная по отношению к ней управляемая перестановка совпадает с ней самой, т.е. РV -1=РV для всех возможных значений управляющего вектора; это означает, что для управляемой перестановочной инволюции справедливо равенство В=РV(РV(В)) при произвольном значении V.
Известны способы итеративного шифрования блоков цифровых данных, см. например, шифр DES [B. Schneier, "Applied Cryptography", Second Eddition, John Wiley & Sons, Inc., New York, 1996, p. 270-277]. В данном способе данные разбиваются на блоки, шифрование которых выполняют путем формирования секретного ключа, разбиения преобразуемого блока данных на два подблока L и R и поочередного изменения последних путем выполнения операции поразрядного суммирования по модулю два над подблоком L и двоичным вектором, который формируется как выходное значение некоторой функции Е от значения подблока R. После этого подблоки переставляются местами. Функция Е в указанном способе реализуется путем выполнения операций перестановки и подстановки, выполняемых над подблоком R. Данный способ обладает высокой скоростью преобразований при реализации в виде специализированных электронных схем. Однако известный способ-аналог использует секретный ключ малого размера (56 бит), что делает его уязвимым к криптоанализу на основе подбора ключа. Последнее связано с высокой вычислительной мощностью современных ЭВМ.
Другим известным способом итеративного шифрования блоков дискретных данных является способ, описанный в Российском стандарте криптографической защиты данных [Стандарт СССР ГОСТ 28147-89. Системы обработки информации. Защита криптографическая. Алгоритм криптографического преобразования]. Этот способ включает в себя формирование ключа шифрования в виде последовательности из 8 подключей длиной 32 бита, разбиение входной информации, представленной в виде двоичного кода, на участки длиной по 64 бит, формирование на их основе 64-битовых блоков данных и преобразование блоков под управлением ключа шифрования. Перед преобразованием каждый блок данных разбивается на два 32-битовых подблока A и В, которые поочередно преобразуются путем выполнения 32 раундов преобразования (итераций). Один раунд преобразования заключается в следующем. По подблоку А и одному из подключей вычисляется 32-битовое значение раундовой функции Е и полученное значение Е(А) накладывают на подблок В с помощью операции поразрядного суммирования по модулю два (⊕) в соответствии с формулой B := B⊕E(A). Вычисление раундовой функции осуществляется в соответствии со следующими шагами преобразования. По подблоку А формируется двоичный вектор F. Преобразуют двоичный вектор F путем наложения на него текущего подключа Ki, являющегося фиксированным для данного раунда и называемого раундовым подключом, с помощью операции сложения по модулю 232 (+) в соответствии с формулой F:=(R+Ki) mod 232, где 1≤i≤8, после чего над двоичным вектором F выполняют операцию подстановки (F:=S(F)), затем операцию циклического сдвига влево на одиннадцать бит, т.е. на одиннадцать двоичных разрядов в сторону старших разрядов (F:=F<<<11). После каждого раунда шифрования, за исключением последнего раунда, подблоки переставляются. Операция подстановки выполняется следующим образом. Двоичный вектор F разбивается на 8 двоичных векторов длиной по 4 бит. Каждый двоичный вектор заменяется двоичным вектором из таблицы подстановок. Выбранные из таблицы подстановок восемь 4-битовых векторов объединяются в преобразованный 32-битовый двоичный вектор F.
Однако способ-аналог имеет недостатки, а именно, операции подстановок выполняются над двоичными векторами малой длины (4 бита), что создает предпосылки для атаки этого шифра методом дифференциального криптоанализа [B. Schneier, "Applied Cryptography", Second Eddition, John Wiley & Sons, Inc. , New York,1996, p. 285-290]. Поэтому для обеспечения высокой стойкости к дифференциальному криптоанализу требуется выполнить большое число раундов шифрования, что снижает скоростные показатели шифра.
Наиболее близким по своей технической сущности к заявляемому способу итеративного шифрования блоков дискретных данных является способ, описанный в патенте РФ 2141729 [Молдовян А.А., Молдовян Н.А. Способ криптографического преобразования блоков двоичных данных // Патент РФ 2141729, МПК6 Н 04 L 9/00, БИ 32 от 20.11.1999]. Способ прототип включает в себя формирование секретного ключа, разбиение блока данных на два подблока А и В и преобразование подблоков под управлением ключа шифрования путем выполнения над ними 16 раундов преобразования (итераций). Каждый раунд включает поочередное преобразование подблоков, причем над каждым из них выполняются не менее двух операций. В частном случае реализации способа прототипа (см. пример 1 при r= 1 в описании патента 2141729) один раунд включает следующие шаги преобразования:
1. С помощью операции поразрядного суммирования по модулю два (⊕) на подблок А накладывается подключ К1 в соответствии с формулой A := A⊕K1.
2. С помощью операции сложения по модулю 232 (+) на подблок В накладывается подключ К2 в соответствии с формулой В:=В+К2, где знак ":=" обозначает операцию присваивания.
3. Подблок В преобразуется в соответствии с выражением В:=РV(В), где РV - модификация управляемой перестановки, V - значение управляющего вектора, формируемого в зависимости от значений подблока А и подключа К3.
4. На подблок А накладывается подблок В в соответствии с формулой: А:= А+В.
5. Над подблокoм А выполняется операция управляемой перестановки А:= РV(А), где V - значение управляющего вектора формируемого в зависимости от значений подблока В и подключа К4.
6. Преобразуется подблок В в соответствии с формулой B := B⊕A.
Однако способ прототип имеет недостатки, а именно при его реализации в виде электронных криптографических устройств для выполнения шифрования и дешифрования необходимо использовать две различные электронные схемы, что усложняет его реализацию.
В основу изобретения положена задача разработать способ итеративного шифрования блоков цифровых данных, в котором преобразование входных данных осуществлялось бы таким образом, чтобы процедуры шифрования и дешифрования могли осуществляться с помощью одной и той же электронной схемы, используя подключи в обратной очередности при выполнении дешифрования по отношению очередности использования под ключей при шифровании, что упрощает схемотехническую реализацию.
Поставленная задача достигается тем, что в способе итеративного шифрования блоков дискретных данных, включающем формирование секретного ключа, разбиение блока данных на два подблока и выполнение R≥2 раундов шифрования, включающих преобразование первого подблока путем выполнения над ним последовательности операций L1, L2, ..., Ln, где n>1, и преобразование второго подблока путем выполнения над ним последовательности операций H1, H2,..., Нm, где m>1, новым, согласно изобретению, является то, что m является четным числом, n является нечетным числом и дополнительно в первых (R-1) раундах шифрования после выполнения операций Ln и Нm осуществляют перестановку подблоков, а операции Hi являются обратными по отношению к операциям Hm-i+1, где 1≤i≤m/2, и операции Lj являются обратными по отношению к операциям Ln-j+1, где 1≤j≤(n-1)/2, причем перед выполнением операции L(n-1)/2+1 формируют управляющий вектор, а в качестве операции L(n-1)/2+1 используется обращаемая управляемая двуместная операция.
Благодаря такому решению выполнение последовательности операций L1, L2,. . ., Ln и операций Н1, H2,..., Нm, задает процедуру преобразования блока данных являющуюся инволюцией, что обеспечивает возможность осуществления дешифрования зашифрованного блока данных с помощью той же электронной схемы, которая использовалась при его шифровании. Это упрощает схемотехническую реализацию способа итеративного шифрования блоков дискретных данных.
Новым является также то, что дополнительно перед выполнением каждой операции L1, L2, ..., Ln, Н1, H2,..., Hm формируют управляющий вектор, а в качестве операций L1, L2,..., Ln, H1, H2,..., Нm используются управляемые перестановки и управляемые двуместные операции, причем в качестве операции L(n-1)/2+1 используется обращаемая управляемая двуместная операция.
Благодаря такому решению, обеспечивается повышение стойкости к дифференциальному криптоанализу.
Кроме того, новым является то, что перед выполнением операции Lj, 1≤j≤n над первым подблоком управляющий вектор формируют в зависимости от секретного ключа и от текущего значения второго подблока, а перед выполнением операции Hi, 1≤i≤m над вторым подблоком управляющий вектор формируют в зависимости от секретного ключа и от текущего значения первого подблока.
Благодаря такому решению, обеспечивается дополнительное повышение криптостойкости и возможность сокращения числа раундов шифрования, что обеспечивает повышение скорости шифрования.
Ниже сущность заявляемого изобретения более подробно разъясняется примерами его осуществления со ссылками на прилагаемые чертежи.
Обобщенная схема итеративного шифрования блоков данных на основе заявляемого способа представлена структурой раунда шифрования, показанной на фиг. 1а, где А и В - подблоки преобразуемого блока данных.
Пример 1
Данный пример показан на фиг.1б и поясняет реализацию способа для случая n= 5 и m=4. Блок данных Т имеет длину 64 бит и разбивается на два 32-битовых подблока А и В. На фиг.1б использованы следующие обозначения:
Р и Р-1 - взаимно обратные управляемые перестановки, выполняемые над 32-битовыми двоичными векторами и имеющие 64-битовый управляющий вход;
π и π-1- взаимно обратные фиксированные перестановки, т.е. такие фиксированные перестановки, последовательное выполнение которых над любым операндом не изменяют значения последнего, т.е. имеют место соотношения: π(π-1(A)) = A, и π-1(π(A)) = A. Фиксированные перестановки легко реализуются в электронных схемах и не вводят задержки в процесс преобразования данных;
Q* - обращаемая двуместная операция с 32-битовым управляющим входом;
"-" - операция вычитание по модулю 232.
Шифрование в соответствии с примером 1 осуществляется следующим образом. Формируется секретный ключ в виде следующей совокупности 32-битовых раундовых подключей: К1, К2,..., К16 и W1, W2,...., W16. Блок данных разбивается на два подблока А=Т div 232 и В=Т mod 232. Шифрование блока данных выполняется в соответствии со следующим алгоритмом.
1. Установить счетчик числа раундов шифрования r:=1 и значение е=1.
2. Наложить подключ Wr на подблок A с помощью операции суммирования по модулю 232:
A:=(A+Wr) mod 232.
3. Наложить подключ Кr на подблок В с помощью операции поразрядного суммирования по модулю 2:
B := B⊕Kr.
4. Сформировать 64-битовый управляющий вектор V:V = A|A, где знак "|" обозначает операцию конкатенации.
5. Выполнить над подблоком В операцию управляемой перестановки:
В:=РV(В).
6. Выполнить над подблоком А операцию фиксированной перестановки:
A := π(A).
7. Сформировать управляющий вектор V в зависимости от подблока A и подключей Кr и Wr:
V = A⊕Kr⊕Wr.
8. Наложить подблок A на подблок В с помощью обращаемой управляемой двуместной операции
B := Q
9. Выполнить над подблоком А операцию обратной фиксированной перестановки:
A := π-1(A).
10. Сформировать по подблоку А 64-битовый управляющий вектор V:V = A|A.
11. Выполнить над подблоком В операцию обратной управляемой перестановки:
В:=РV -1(В).
12. Наложить подключ Кr на подблок А с помощью операции вычитания по модулю 232:
А:=(A-Кr) mod 232.
13. Наложить подключ Wr на подблок В с помощью операции поразрядного суммирования по модулю 2:
B := B⊕Wr.
14. Если r<16, то прирастить r:=r+1, переставить подблоки А и В (т.е. взять двоичный вектор A в качестве двоичного вектора В, а двоичный вектор В - в качестве двоичного вектора A) и перейти к шагу 2.
15. СТОП.
Блок криптограммы С формируется путем объединения преобразованных двоичных векторов А и В: C = A|B. Дешифрование блока криптограммы осуществляется с помощью этого же алгоритма, за исключением того, что на первом шаге устанавливается значение е=0 и при выполнении шагов 2, 7 и 13 используется подключ К17-r вместо подключа Wr, а при выполнении шагов 3, 7 и 12 - подключ W17-r вместо Кr. Бит е служит для обращения управляемой двуместной операции Q* и для задания очередности использования раундовых подключей, т.е. значение этого бита задает режим шифрования (е=1) или дешифрования (е=0). Поскольку шифрование и дешифрование осуществляются с помощью одного и того же алгоритма, то обе эти процедуры могут быть выполнены с помощью одной и той же электронной схемы.
Пример 2. Шифрование 64-битового блока данных Т
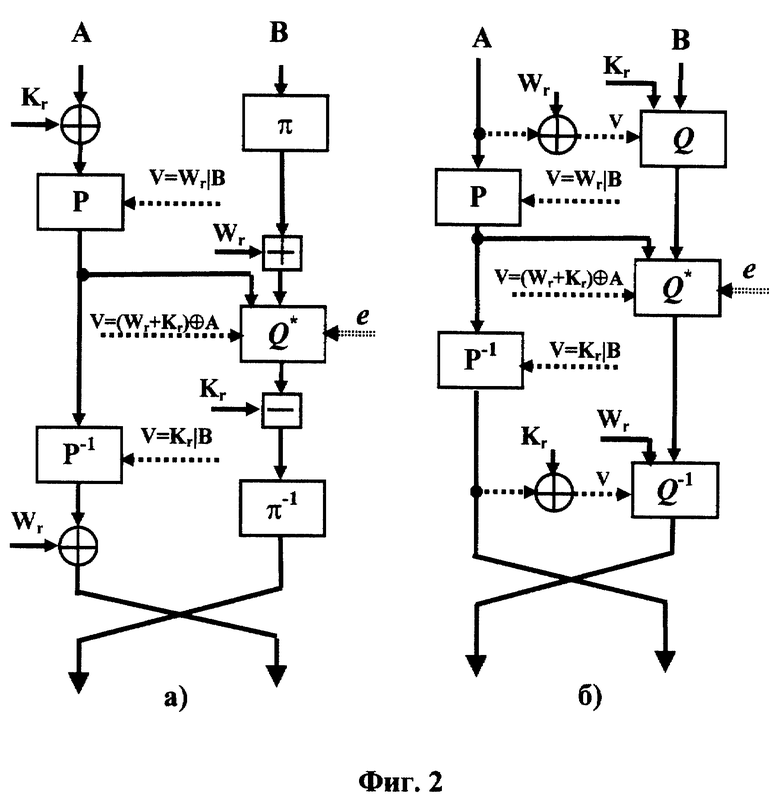
Данный пример поясняется на фиг.2а и соответствует случаю n=5 и m=4 и использованию обращаемой управляемой двуместной операции Q* в качестве операции L(n-1)/2+1. В данном примере используется обращаемая управляемая двуместная операция Q* с 32-битовым управляющим входом. Шифрование в соответствии с примером 2 осуществляется следующим образом. Формируется секретный ключ в виде следующей совокупности 32-битовых раундовых подключей: K1, K2, . . ., К8 и W1, W2,..., W8. Разбить блок данных T на два 32-битовых подблока А и В. Затем выполняется шифрование блока данных в соответствии со следующим алгоритмом.
1. Установить счетчик числа раундов шифрования r:=1 и значение бита инвертирования е=1.
2. Наложить подключ Кr на подблок A в соответствии с формулой:
A := A⊕Kr.
3. Выполнить над подблоком В операцию фиксированной перестановки:
B := π(B).
4. По подключу Wr и по подблоку В сформировать 64-битовый управляющий вектор V:V = Wr|B.
5. Выполнить над подблоком А операцию управляемой перестановки:
А:=РV(А).
6. Наложить подключ Wr на подблок В в соответствии с выражением:
В:=(В+Wr) mod 232.
7. Сформировать 32-битовый управляющий вектор V в зависимости от подблока А и подключей Кr и Wr в соответствии с выражением:
V = (Wr+Kr)⊕A.
8. Наложить подблок А на подблок В с помощью обращаемой управляемой двуместной операции:
B := Q
9. Наложить подключ Кr на подблок В в соответствии с выражением:
В:=(В-Кr) mod 232.
10. По подключу Кr и по подблоку В сформировать 64-битовый управляющий вектор V:V = Kr|B.
11. Выполнить над подблоком A операцию обратной управляемой перестановки:
А:=РV -1(А).
12. Наложить подключ Wr на подблок А в соответствии с формулой:
A := A⊕Wr.
13. Выполнить над подблоком В операцию обратной фиксированной перестановки:
B := π-1(B).
14. Если r<8, то прирастить r:=r+1, переставить подблоки A и В и перейти к шагу 2.
15. СТОП.
В результате выполнения алгоритма формируется блок криптограммы C = A|B. Дешифрование блока криптограммы осуществляется с помощью этого же алгоритма, за исключением того, что на первом шаге устанавливается значение е=0, а при выполнении шагов 4, 6, 7 и 12 используется подключ K9-r вместо подключа Wr и при выполнении шагов 2, 7, 9 и 10 - подключ W9-r вместо подключа Кr.
Пример 3
Данный пример поясняется на фиг. 2б, где Q - управляемая двуместная операция с 32-битовым управляющим входом и Q-1 - соответствующая обратная управляемая двуместная операция с 32-битовым управляющим входом. Пример 3 соответствует случаю n=3 и m=2 и использованию операций управляемых перестановок и управляемых двуместных операций в качестве операций L1, L2,..., Ln, H1, H2,..., Нm и операции Q* в качестве операции L(n-1)/2+1.
Шифрование в соответствии с примером 3 осуществляется следующим образом. Формируется секретный ключ в виде следующей совокупности 32-битовых раундовых подключей: K1, К2,..., К16 и W1, W2,...., W16. Разбить блок данных Т на два 32-битовых подблока А и В. Шифрование блока данных выполняется в соответствии со следующим алгоритмом.
1. Установить r:=1 и е=1.
2. По подключу Wr и по подблоку А сформировать 32-битовый управляющий вектор V:V = Wr⊕A.
3. Наложить подключ Кr на подблок В в соответствии с формулой:
B:=QV(B, Kr).
4. По подключу Wr и по подблоку В сформировать 64-битовый управляющий вектор V:V = Wr|B.
5. Выполнить над подблоком А операцию управляемой перестановки:
А:=РV(А).
6. Сформировать управляющий вектор V в зависимости от подблока А и подключей Кr и Wr:
V = (Wr+Kr)⊕A.
7. Наложить подблок А на подблок В с помощью обращаемой управляемой двуместной операции Q*:
B := Q
8. По подключу Кr и по подблоку В сформировать 64-битовый управляющий вектор V:V = Kr|B.
9. Выполнить над подблоком А операцию обратной управляемой перестановки:
А:=РV -1(А).
10. По подключу Кr и по подблоку А сформировать 32-битовый управляющий вектор V в соответствии с формулой: V = Kr⊕A.
11. Наложить подключ Wr на подблок В в соответствии с формулой:
В:=QV -1(B, Wr).
12. Если r<16, то прирастить r:=r+1, переставить подблоки А и В и перейти к шагу 2.
13. СТОП.
В результате выполнения алгоритма формируется блок криптограммы C = A|B. Дешифрование блока криптограммы осуществляется с помощью этого же алгоритма, за исключением того, что на первом шаге устанавливается значение бита инвертирования е= 0, а при выполнении шагов 2, 4, 6 и 11 используется подключ K17-r вместо подключа Wr, а при выполнении шагов 3, 6, 8 и 10 - подключ W17-r вместо подключа Кr. Такое изменение очередности использования подключей в электронных схемах может быть легко задано в зависимости от установки значения бита инвертирования е.
Приведенные примеры показывают, что предлагаемый способ итеративного шифрования блоков дискретных данных технически реализуем и позволяет решить поставленную задачу.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ ИТЕРАТИВНОГО ШИФРОВАНИЯ БЛОКОВ ЦИФРОВЫХ ДАННЫХ | 2000 |
|
RU2199826C2 |
| СПОСОБ БЛОЧНОГО ИТЕРАТИВНОГО ШИФРОВАНИЯ | 2000 |
|
RU2186467C2 |
| СПОСОБ ИТЕРАТИВНОГО БЛОЧНОГО ШИФРОВАНИЯ ДВОИЧНЫХ ДАННЫХ | 2001 |
|
RU2206961C2 |
| ИТЕРАТИВНЫЙ СПОСОБ БЛОЧНОГО ШИФРОВАНИЯ | 2001 |
|
RU2204212C2 |
| СПОСОБ БЛОЧНОГО ИТЕРАТИВНОГО ШИФРОВАНИЯ ЦИФРОВЫХ ДАННЫХ | 2000 |
|
RU2184423C2 |
| ИТЕРАТИВНЫЙ СПОСОБ БЛОЧНОГО ШИФРОВАНИЯ | 1999 |
|
RU2172075C1 |
| СПОСОБ ИТЕРАТИВНОГО ШИФРОВАНИЯ БЛОКОВ ДВОИЧНЫХ ДАННЫХ | 1999 |
|
RU2144268C1 |
| СПОСОБ ИТЕРАТИВНОГО ШИФРОВАНИЯ БЛОКОВ ДАННЫХ | 1999 |
|
RU2140714C1 |
| СПОСОБ БЛОЧНОГО КРИПТОГРАФИЧЕСКОГО ПРЕОБРАЗОВАНИЯ ДВОИЧНОЙ ИНФОРМАЦИИ | 1998 |
|
RU2140713C1 |
| СПОСОБ КРИПТОГРАФИЧЕСКОГО ПРЕОБРАЗОВАНИЯ БЛОКОВ ЦИФРОВЫХ ДАННЫХ | 1999 |
|
RU2140716C1 |
Изобретение относится к области электросвязи и вычислительной техники, а конкретнее к области криптографических способов для шифрования данных. Способ включает формирование секретного ключа, разбиение блока данных на два подблока и выполнение R≥2 шифрования, включающих преобразование первого подблока путем выполнения над ним последовательности операций L1, L2,..., Ln, где n>1, и преобразование второго подблока путем выполнения над ним последовательности операций H1, Н2, ..., Нm, где m>1, причем, по крайней мере, одна из операций L1, L2,..., Ln, H1, H2,..., Нm является управляемой операцией и перед выполнением этой операции формируют управляющий вектор, а при выполнении, по крайней мере, одной из операций L1, L2,..., Ln, H1, Н2..., Hm используют один из подключей, причем m является четным числом, n является нечетным числом и дополнительно во всех раундах шифрования, кроме последнего, после выполнения операций Ln и Hm осуществляют перестановку подблоков, а операции Hi являются обратными по отношению к операциям Hm-i+1, где 1≤i≤m/2, и операции Lj являются обратными по отношению к операциям Ln-j+1, где L≤j≤(n-1)/2, а в качестве операции L(n-1)/2+1 используется обращаемая управляемая двуместная операция и перед ее выполнением формируют управляющий вектор в зависимости от второго блока. Технический результат, достигаемый при реализации способа, состоит в повышении стойкости к дифференцианальному криптоанализу. 3 з.п.ф-лы, 2 ил.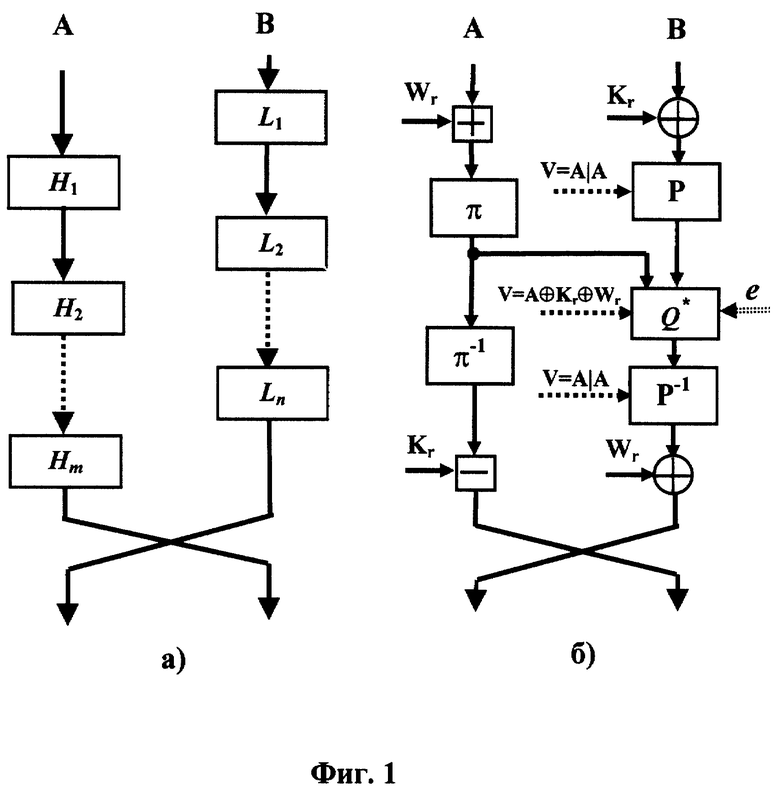
| СПОСОБ ИТЕРАТИВНОГО ШИФРОВАНИЯ БЛОКОВ ДАННЫХ | 1999 |
|
RU2140714C1 |
| WO 8907375 А, 10.08.1989 | |||
| US 5168521 А, 01.12.1992 | |||
| US 5442705 А, 15.08.1995 | |||
| DE 4016203 A1, 21.11.1991. | |||
Авторы
Даты
2002-07-27—Публикация
2000-09-25—Подача