Изобретение относится к области электросвязи и вычислительной техники, а конкретнее к области криптографических способов и устройств для шифрования сообщений (информации).
В совокупности признаков заявляемого способа используются следующие термины:
- секретный ключ представляет из себя двоичную информацию, известную только законному пользователю;
- подключ - участок секретного ключа;
- криптографическое преобразование - это преобразование цифровой информации, которое обеспечивает влияние одного бита исходных данных на многие биты выходных данных, например, с целью защиты информации от несанкционированного чтения, формирования цифровой подписи, выработки кода обнаружения модификаций; видами криптографического преобразования являются одностороннее преобразование, хэширование и шифрование;
- блок криптограммы - блок преобразованных данных, полученный в результате выполнения процедуры односторонних преобразований или шифрования;
- одностороннее преобразование - это такое преобразование m-битового входного блока данных в m-битовый выходной блок данных (блок криптограммы), которое позволяет легко вычислить блок криптограммы по входному блоку, а вычисление входного блока, который бы преобразовался в случайно выбранный блок криптограммы, является практически невыполнимой задачей;
- хэширование информации есть некоторый способ формирования так называемого хэш-кода, размер которого является фиксированным (обычно 128 бит) для сообщений любого размера; процедуры хэширования обеспечивают зависимость хэш-кода от каждого бита сообщения.
- шифрование есть процесс, преобразования информации, который зависит от секретного ключа и преобразует исходный текст (данные) в шифртекст (криптограмму), представляющий собой псевдослучайную последовательность знаков, из которой получения информации без знания секретного ключа практически неосуществимо;
- дешифрование есть процесс, обратный процедуре шифрования; дешифрование обеспечивает восстановление информации по криптограмме при знании секретного ключа;
- шифр представляет собой совокупность элементарных шагов преобразования входных данных с использованием секретного ключа; шифр может быть реализован в виде программы для ЭВМ или в виде отдельного устройства;
- двоичный вектор - это некоторая последовательность нулевых и единичных битов, например (101101011); конкретная структура двоичного вектора может быть интерпретирована как двоичное число, если считать, что позиция каждого бита соответствует двоичному разряду, т.е. двоичному вектору может быть сопоставлено численное значение, которое определяется однозначно структурой двоичного вектора;
- криптоанализ - метод вычисления секретного ключа для получения несанкционированного доступа к зашифрованной информации или разработка метода, обеспечивающего доступ к зашифрованной информации без вычисления секретного ключа;
- криптостойкость является мерой надежности защиты зашифрованной информации и представляет собой трудоемкость, измеренную в количестве элементарных операций, которые необходимо выполнить для восстановления информации по криптограмме при знании алгоритма преобразования, но без знания секретного ключа; в случае односторонних преобразований под криптостойкостью понимается сложность вычисления входного значения блока по его выходному значению;
- операции циклического сдвига, зависящие от преобразуемых данных или зависящие от двоичного вектора - это операции циклического сдвига на число бит, задаваемое значением двоичного вектора; операции циклического сдвига влево (вправо) обозначаются знаком "<<<" (>>>"), например, запись B1 <<< B2 обозначает операцию циклического сдвига влево двоичного вектора B1 на число бит, равное значению двоичного вектора B2; подобные операции являются базовыми для шифра RC5;
- одноместная операция - это операция, выполняемая над одним операндом (блоком данных или двоичным вектором); значение двоичного после выполнения некоторой данной одноместной операции зависит только от его начального значения; примером одноместных операций являются операции циклического сдвига;
- двуместная операция - это операция, выполняемая над двумя операндами; результат выполнения некоторой данной двуместной операции зависит от значения каждого операнда; примером двуместных операций являются операции сложения, вычитания, умножения и др.
- операция конкатенации - это операция объединения нескольких двоичных векторов, в результате которой формируется новый двоичный вектор, включающий все биты каждого из объединяемых двоичных векторов, причем взаимное расположение битов, соответствующих исходным двоичным векторам, не изменяется; например, конкатенация двоичных векторов W1 = (101101011) и W2 = (011101010) записывается в виде W1|W2 = (101101011011101010); данные двоичные вектора могут быть объединены операцией конкатенации еще одним способом: W2W1 = (01110101010101101011).
Известны способы блочного шифрования данных, см. например шифр DES [B. Schneier, "Applid Cryptography", Second Eddition, John Wiley & Sons, Inc., New York, 1966, pp. 336 - 339]. В данном способе шифрование 64-битовых блоков данных T выполняют путем формирования секретного ключа, формирования 32-битовых двоичных векторов L и R по блоку данных (в качестве L берутся старшие 32 бита блока данных, а в качестве R - младшие 32 бита блока данных) и выполнения 16 раундов шифрования. Один раунд шифрования заключается в формировании дополнительного двоичного вектора F путем преобразования двоичного вектора R и преобразовании двоичного вектора L в соответствии с выражением L: = L ⊕ F, где ⊕ - операция поразрядного суммирования по модулю два, ":=" - операция присваивания. Перед выполнением второго и последующих раундов двоичному вектору L присваивается значение R, а двоичному вектору R присваивается значение L, полученное сразу после выполнения предыдущего раунда. Данный способ обладает высокой скоростью преобразований при реализации в виде специализированных электронных схем. Однако известный способ-аналог использует секретный ключ малого размера (56 бит), что делает его уязвимым к криптоанализу на основе подбора ключа. Последнее связано с высокой вычислительной мощностью современных ЭВМ массового применения.
Наиболее близким по своей технической сущности к заявляемому способу криптографического преобразования блоков цифровых данных является способ, реализованный в программном шифре RC5 и описанный в монографии [B.Schneier, "Applied Cryptography", Second Eddition, John Wiley & Sons, Inc., New York, 1966, pp. 344-346]. Способ прототип включает в себя формирование секретного ключа в виде совокупности подключей, формирование по блоку данных двух n-битовых двоичных векторов (A и B) и поочередное преобразование двоичных векторов. Преобразование n-битовых, где n = 8, 16, 32, двоичных векторов A и B осуществляют путем выполнения над ними одноместных и двуместных операций. В качестве двуместных операций используются операции сложения по модуль 2n и операция поразрядного суммирования по модулю 2. В качестве одноместной операции используется операция циклического сдвига влево, причем число бит на которое сдвигается преобразуемый двоичный вектор зависит от значения другого двоичного вектора, это определяет зависимость операции циклического сдвига на текущем шаге преобразования двоичного вектора от исходного значения входного блока данных. Двуместная операция выполняется над двоичным вектором и подключом, а также над двумя двоичными векторами. Характерным для способа прототипа является использование операции циклического сдвига, зависящей от значения входного блока. Двоичный вектор, например B, преобразуют следующим путем. Выполняется операция поразрядного суммирования по модулю 2 над A и B и значение, получаемое после выполнения этой операции присваивается двоичному вектору В. Это записывается в виде соотношения B: = B ⊕ A, где знак ":=" обозначает операцию присваивания и знак "⊕" обозначает операцию поразрядного суммирования по модулю 2. После этого над B выполняют операцию циклического сдвига влево на число бит, равное значению A: B: = B <<< A. Затем над двоичным вектором и одним из подключей S выполняют операцию суммирования по модулю 2n, где n - длина двоичного вектора в битах: B: = B + S mod 2n. После этого аналогичным образом преобразуется двоичный вектор A. Выполняется несколько таких шагов преобразования обоих двоичных векторов. Завершающим шагом является формирование блока криптограммы C по значениям преобразованных двоичных векторов путем их объединения: C:= A|B, где " | " - операция конкатенации.
Данный способ обеспечивает высокую скорость шифрования при реализации в виде программы для ЭВМ. Однако способ прототип имеет недостатки, а именно, он не обеспечивает высокой стойкости криптографического преобразования данных к дифференциальному и линейному криптоанализу [Kaliski B.S., Yin Y.L. On Differential and Linear Cryptanalysis of tne RC5 Encryption Algorithm. Advances in Cryptology - CRYPTO '95 proceedings, Springer-Verlag, 1995, pp. 171-184] . Этот недостаток связан с тем, что эффективность использования операций, зависящих от преобразуемых данных, являющихся переменными параметрами шифрования, с целью усложнения известных методов криптоанализа снижается тем, что число возможных вариантов операции циклического сдвига равно числу двоичных разрядов двоичного вектора n и не превышает 32.
В основу изобретения положена задача разработать способ криптографического преобразования блоков цифровых данных, в котором преобразование входных данных осуществлялось бы таким образом, чтобы обеспечивалось повышение числа различных вариантов операции, зависящей от переменных параметров криптографического преобразования - входного блока и/или секретного ключа, благодаря чему повышает стойкость к дифференциальному и линейному криптоанализу.
Поставленная задача достигается тем, что в способе криптографического преобразования блоков цифровых данных, заключающемся в формировании по блоку данных N ≥ 2 двоичных векторов, поочередном преобразовании двоичных векторов и формировании блока криптограммы по преобразованным двоичным векторам, новым согласно изобретению является то, что дополнительно формируют управляющий код V и при преобразовании по крайней мере одного двоичного вектора над двоичным вектором выполняют по крайней мере одну управляемую двуместную операцию, зависящую от значения управляющего кода V.
Благодаря такому решению обеспечивается повышение числа возможных вариантов операции, зависящей от преобразуемого блока, что обеспечивает повышение стойкости криптографического преобразования к дифференциальному и линейному криптоанализу.
Новым является также то, что управляющий код V формируют по значению одного из двоичных векторов. Благодаря такому решению, обеспечивается дополнительное повышение стойкости к дифференциальному и линейному криптоанализу.
Новым является также то, что дополнительно формируют секретный ключ, а управляющий код V формируют по секретному ключу. Благодаря такому решению, обеспечивается повышение криптостойкости к атакам, основанным на сбоях устройства шифрования.
Новым является также то, что дополнительно формируют секретный ключ, а управляющий код V формируют по секретному ключу и по двоичному вектору.
Благодаря такому решению, обеспечивается дополнительное повышение криптостойкости к атакам, основанным на сбоях устройства шифрования.
Под формированием управляющего кода по двоичному вектору (секретному ключу) мы понимаем установление некоторой совокупности единичных и нулевых сигналов на управляющем входе управляемого операционного блока, реализующего управляемую двуместную операцию, в зависимости от значения двоичного вектора (секретного ключа). В частности, может быть сформирован управляющий код, который равен, например, подключу или одному из двоичных векторов.
Ниже сущность заявляемого изобретения более подробно разъясняется примерами его осуществления со ссылками на прилагаемые чертежи.
На фиг. 1 представлено обозначение управляемой двуместной операции (а - управляемого суммирования; б - управляемого умножения), где W1 и W2 - входные двоичные векторы длины |W1| и |W2|, над которыми выполняется управляемая двуместная операция, R - выходной двоичный вектор длины |R|, представляющий собой результат выполнения операции, V - управляющий код длины |V|, от которого зависит управляемая двуместная операция. В общем случае количество двоичных разрядов во входных двоичных векторах, управляющем коде и выходном двоичном векторе может быть произвольным, т.е. может быть использовано различное соотношение между числами |W1|, |W2|, |V| и |R|. Конкретный вариант соотношения этих чисел относится к конкретному типу управляемой двуместной операции, реализуемой с помощью специальных операционных блоков. Управляемую операцию суммирования, выполняемую над операндами W1 и W2 будем обозначать следующим образом: (W1, W2)[V] , т.е. в результате выполнения этой операции получим двоичный вектор R: R = (W1, W2)[V]. Управляемую операцию умножения обозначим как (W1 ⊕ W2)[V], т.е. в результате выполнения такой операции получим двоичный вектор R: R = (W1 ⊕ W2)[V].
Под управляемой двуместной операцией понимается операция, выполняемая над двумя операндами, в зависимости от некоторого двоичного кода, называемого управляющим кодом, и реализуемая с помощью специально сконструированного операционного блока, который не может быть представлен в виде соединения известных операционных блоков, используемых в устройствах криптографического преобразования, на вход которых подаются двоичные вектора W1, W2 и V. Таким образом, под управляемой двуместной операцией мы понимаем новый вид операции, который не может быть заменен некоторой совокупностью операций преобразования, используемых в известных способах криптографического преобразования. Рассмотрим примеры построения управляемых двуместных операций.
Пример 1: управляемая операция суммирования. Данная операция выполняется над двумя n-битовыми двоичными векторами A и B под управлением (n - 1)-битового управляющего кода V. Обозначим двоичные вектора и управляющий код в виде последовательности битов: A = (an, an-1,..., a2, a1), B (bn, bn-1,..., b2, b1) и V = (υn-1, υn-2,...υ2, υ1). Управляемое суммирование в данном примере выполняется по правилам обычного суммирования двоичных векторов по модулю 2n, за исключением того, что перенос из i-го разряда обнуляется при выполнении условия υi = 0 Таким образом, существуют 2n-1 модификаций операции управляемого суммирования, которые отличаются сочетаниями двоичных разрядов, перенос из которых игнорируется (обнуляется). Пусть A = (11011101) и B = (10010101), тогда при V = (1101011) имеем R = (A,B)[V] = (01001010) (перенос, который бы имел место из третьего в четвертый разряд при обычном суммировании по модулю 2n в случае данного варианта управляемого суммирования обнуляется, поскольку в третьем разряде управляющего кода расположен 0).
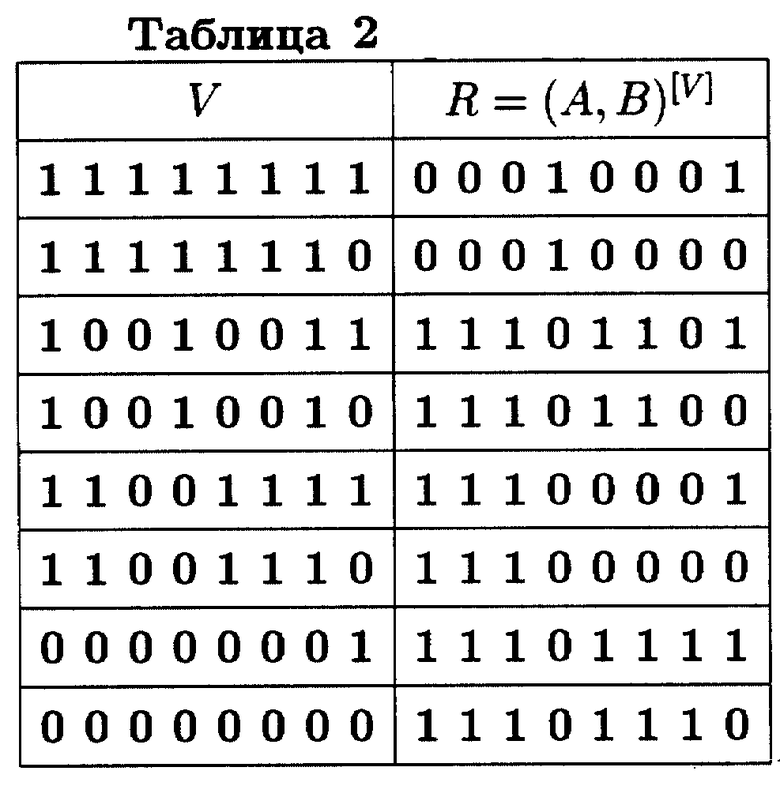
Составим для A = (10111011) и B = (01010101) таблицу значений R = (A, B)[V], получаемых в зависимости от выбора модификации управляемого суммирования, который определяется значением V.
В первой строке приведено значение R, соответствующее величине V = (1111111), для которой реализуется обычное суммирование двоичных векторов A и B по модулю 2n. В последней строке приведено значение R, соответствующее величине V = (0000000), для которой реализуется поразрядное суммирование двоичных векторов A и B по модулю 2n, обозначаемое знаком " ⊕ ". Операция " ⊕ " соответствует одной из 2n-1 модификаций операции управляемого суммирования. Результаты в промежуточных строках соответствуют ряду других модификаций, определяемых сочетаниями разрядов, перенос из которых обнуляется (см. табл. 1)
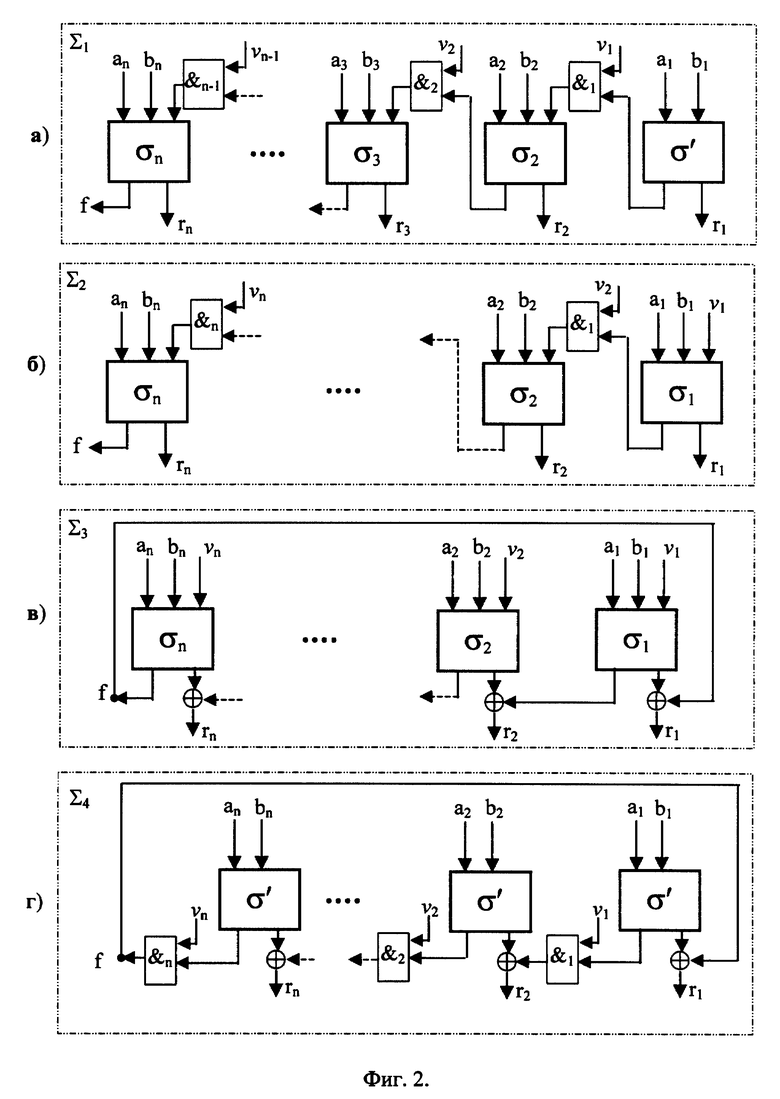
На фиг. 2а представлена структура операционного блока, реализующего операцию управляемого суммирования, описанную в примере 1. Данный операционный блок - управляемый сумматор Σ1 - состоит из полусумматора σ′ и (n-1) сумматоров σi где i = 2,..., n. На полусумматор подаются биты первого разряда a1 и b1, на i-ый сумматор - биты i-го разряда ai и bi. Правый выход полусумматора и всех сумматоров формирует значение соответствующих битов двоичного вектора R. На левом выходе этих узлов формируется бит переноса, подаваемый на один из входов логического элемента И (на схеме обозначенного знаком &). На второй вход логического элемента И, выход которого соединен с правым входом i-го сумматора подается (i-1)-й бит управляющего кода υi-1 . Благодаря тому, что бит переноса проходит через элемент И, он обнуляется при нулевом значении соответствующего управляющего бита. Бит переноса из n-го разряда f игнорируется, т.е. не используется при формировании значения R. Выходной двоичный вектор R формируется как последовательность битов (rn, rn-1, ...,r1, r1) на правом выходе сумматоров, т.е. имеем R = (rn, rn-1,..., r1, r1).
Пример 2: управляемая операция суммирования. Данная операция выполняется над двумя n-битовыми двоичными векторами A = (an, an-1,..., a2, a1) и B = (bn, bn-1, . . . , b2, b1) под управлением n-битового управляющего кода V = (υn, υn-1,...υ2, υ1) На фиг. 2б представлена структура операционного блока, реализующего операцию управляемого суммирования для примера 2. Данный операционный блок - управляемый сумматор Σ2 - состоит из n сумматоров σi где i = 1,2, ..., n. структура данного операционного блока аналогична блоку на фиг. 2а, за исключением того, что вместо полусумматора используется сумматор σ1, на правый вход которого подается управляющий бит υ1 а на верхний вход элемента &i, подается бит υi+1 вместо бита υi .
Управляемое суммирование в данном примере выполняется по правилам обычного суммирования двоичных векторов по модулю 2n, за исключением того, что перенос из i-го разряда обнуляется при выполнении условия υi+1 = 0 Бит переноса из n-го разряда f игнорируется. Бит υ1 можно рассматривать как бит переноса из управляющего кода. Поскольку существует два значения бита υ1 то в данном варианте операции управляемого суммирования существуют в два раза больше различных модификаций по сравнению с примером 1. Их число составляет 2n, т. е. каждому значению n-битового управляющего кода V соответствует уникальная модификация операции управляемого суммирования.
Составим для A = (10111011) и B = (01010101) и нескольких различных управляющих кодов V таблицу значений R = (A,B)[V], получаемых благодаря заданию различных модификаций операции управляемого суммирования (см. табл. 2).
Пример 3: управляемая операция суммирования. Данная операция выполняется над двумя n-битовыми двоичными векторами A = (an, an-1,..., a2, a1) и B = (bn, bn-1, . . . , b2, b1) под управлением n-битового управляющего кода V = (υn, υn-1,...υ2, υ1) На фиг. 2в представлена структура операционного блока, реализующего операцию управляемого суммирования для примера 3. Данный операционный блок обозначен буквой Σ3 На левый вход i-го сумматора подается бит ai; на средний вход - бит bi и на правый вход - бит υi. Левый выход i-го сумматора и правый выход (i+1)-го сумматора являются входами одноразрядного сумматора по модулю два (обозначен узлом ⊕ ), а выход этого одноразрядного сумматора является (i + 1)-м выходом управляемого операционного блока. Левый выход n-го сумматора и правый выход первого сумматора являются входами одноразрядного сумматора по модулю два, выход которого является первым выходом управляемого сумматора Σ3
Пример 4: управляемая операция суммирования. Данная операция выполняется над двумя n-битовыми двоичными векторами A и B под управлением n-битового управляющего кода V. На фиг. 2г представлена структура операционного блока, реализующего операцию управляемого суммирования для примера 4. Данный операционный блок обозначен буквой Σ4 и состоит из n полусумматоров σ На левый вход i-го полусумматора подается бит ai, на правый вход - бит bi. Левый выход i-го полусумматора и управляющий бит υi подаются на два входа элемента & i. Правый выход (i + 1)-го полусумматора и выход элемента &i являются входами одноразрядного сумматора по модулю два, а выход этого одноразрядного сумматора является (i + 1)-вым выходом управляемого операционного блока. Выход элемента & n и правый выход первого сумматора являются входами одноразрядного сумматора по модулю два, выход которого является первым выходом управляемого сумматора Σ4/
Пример 5: управляемая операция умножения. Данная операция выполняется над двумя двоичными векторами A = (an, an-1,..., a2, a1) и B = (bg, bn-1,... , b2, b1) под управлением h-битового, где h = n + g - 1, управляющего кода V = (υh, υh-1,...υ2, υ1) Осуществление управляемой операции умножения в данном примере включает следующие шаги:
1. По значению A формируется табл. 3, содержащая g строк и g + n - 1 столбцов (см. в конце описания)
Первая строка этой матрицы сформирована путем добавления g - 1 нуля слева к последовательности битов an, an-1,..., a1, a1. Каждая следующая строка получена из предыдущей путем сокращения числа нулей слева на единицу и добавления одного нуля справа. Таким образом, в каждой строке содержится участок битов an, an-1,...,a1, a1, который перемещается из крайней правого положения в верхней строке в крайнее левое положение в нижней строке.
2. Из построенной матрицы выбираются все строки, для номера которых i выполняется соотношение bi = 1. Каждая такая строка рассматривается как h-битовый двоичный вектор. Пусть имеем j таких двоичных векторов: A'1, A'2,... ,A'j.
3. Установить счетчик s: = 1 и начальное значение двоичного вектора R: = 1.
4. Выполнить операцию управляемого суммирования из примера 2:
R: = (R, A'1)[V].
5. Если s < j,то прирастить j: = j + 1 и перейти к шагу 4.
6. СТОП.
Значение R на выходе шага 6 берется в качестве результата выполнения управляемой операции умножения. Поскольку результат выполнения шага 4 зависит от значения управляющего кода V, то и результат умножения зависит от значение V. Обозначим управляемую операцию умножения как (A ⊕ B)[V]. Другие типы управляемой операции умножения могут быть получены путем выполнения шагов 1 - 6, если на шаге 4 использовать операцию управляемого суммирования, например, из примеров 1,3 и 4.
Пример 6: управляемая операция суммирования. Данная операция выполняется над двумя n-битовыми двоичными векторами A и B под управлением n-битового управляющего кода V. Обозначим двоичные вектора и управляющий код в виде последовательности битов: A = (an, an-1,...,a2, a1), B = (bn, bn-1,...,b2, b1) и V = (υn, υn-1,...υ2, υ1)
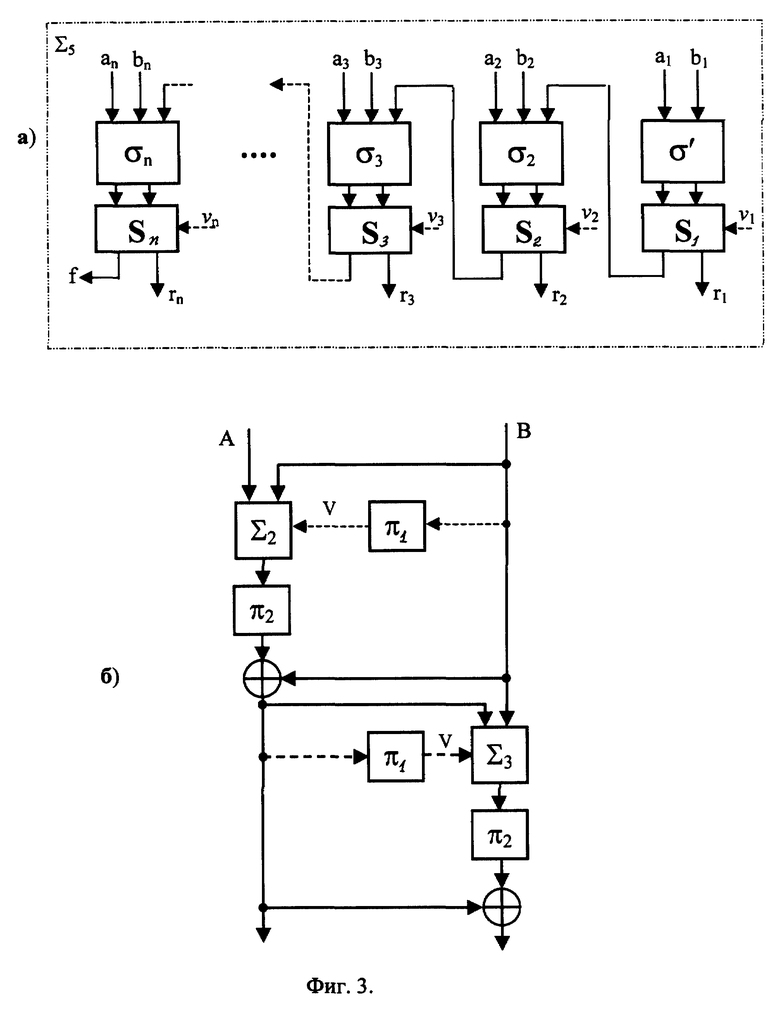
Управляемое суммирование в данном примере выполняется с помощью операционного узла (управляемого сумматора Σ5 ), представленного на фиг. 3a и состоящего из полусумматора σ′ и сумматоров σi где i = 2,..., n, (число сумматоров равно n-1). На полусумматор подаются биты первого разряда a1 и b1, не левый и средний входы i-го сумматора σi где i = 2,3,...,n, - биты i-го разряда двоичных векторов, т. е. биты ai и bi. Выход полусумматора и всех сумматоров является входом соответствующего управляемого элементарного переключателя Si, i = 1,2,3,...,n, на управляющий вход которого подается соответствующий бит υi управляющего кода. (Переключатель Si, работает следующим образом. При единичном управляющем сигнале (u1 = 1) осуществляется коммутация левого входа с левым выходом и правого входа с правым выходом. При нулевом управляющем сигнале (ui = 0) осуществляется коммутация левого входа с правым выходом и правого входа с левым выходом. Элементарный переключатель реализуется с помощью простейшей комбинационной электрической схемы, обладающей высоким быстродействием.). Левый выход переключателя Si, где i = 1,2,3, . . . ,n-1, соединен с правым входом сумматора σi+1 Сигнал f на левом выходе переключателя Sn игнорируется, т.е. не используется при формировании значения результата суммирования R. Правые выходы всех переключателей Si являются соответствующими выходами управляемого сумматора Σ5 (Выходной двоичный вектор R формируется как последовательность битов (rn, rn-1,..., r2, r1) на правом выходе переключателей Si, т.е. имеем R = (rn, rn-1,...,r2 r1).)
Данные примеры показывают реализуемость управляемых двуместных операций с большим числом возможных модификаций. Могут быть составлены и другие типы управляемых двуместных операций, которые легко реализуются в виде управляемых операционных блоков на базе стандартных узлов электронных схем.
Рассмотрим варианты заявляемого способа криптографического преобразования блоков цифровых данных.
Пример 7: одностороннее преобразование 64-битового блока данных T. Данный пример поясняется на фиг. 3б. Сформировать по блоку данных два двоичных вектора A = T div 232 и B = T mod 232, т.е. двоичный вектор A содержит старшие 32 бита блока данных, а двоичный вектор B - младшие 32 бита блока данных. Далее преобразование выполнить в соответствии со следующим алгоритмом.
1. Установить счетчик числа раундов преобразования r: = 1.
2. Сформировать по двоичному вектору B управляющий код V путем выполнения перестановки π1 над B: V = π1(B) где перестановка π1 реализуется с помощью операционного блока π1 на фиг. 3. (В электрических схемах данный операционный блок реализуется как простое переплетение проводников.)
3. В зависимости от значения V преобразовать двоичный вектор A путем выполнения управляемого суммирования из примера 2 над A и B: A: = (A,B)[V].
4. Преобразовать двоичный вектор A путем выполнения над ним операции перестановки π2: A:= π2(A)
5. Преобразовать двоичный вектор A в соответствии со следующей формулой: A: = A ⊕ B.
6. Сформировать по двоичному вектору A управляющий код V путем выполнения перестановки π1 над A: V = π1(A)
7. В зависимости от значения V преобразовать двоичный вектор B путем выполнения управляемого суммирования из примера 3 над A и B: B: = (B,A)[V] .
8. Преобразователь двоичный вектор B путем выполнения над ним операции перестановки π2: B:= π2(B)
9. Преобразовать двоичный вектор B в соответствии с формулой: B: = B ⊕ A.
10. Если r < 16, то прирастить r: = r + 1 и перейти к шагу 2.
11. СТОП.
Блок криптограммы C формируется путем объединения преобразованных двоичных векторов A и B: C = A|B.
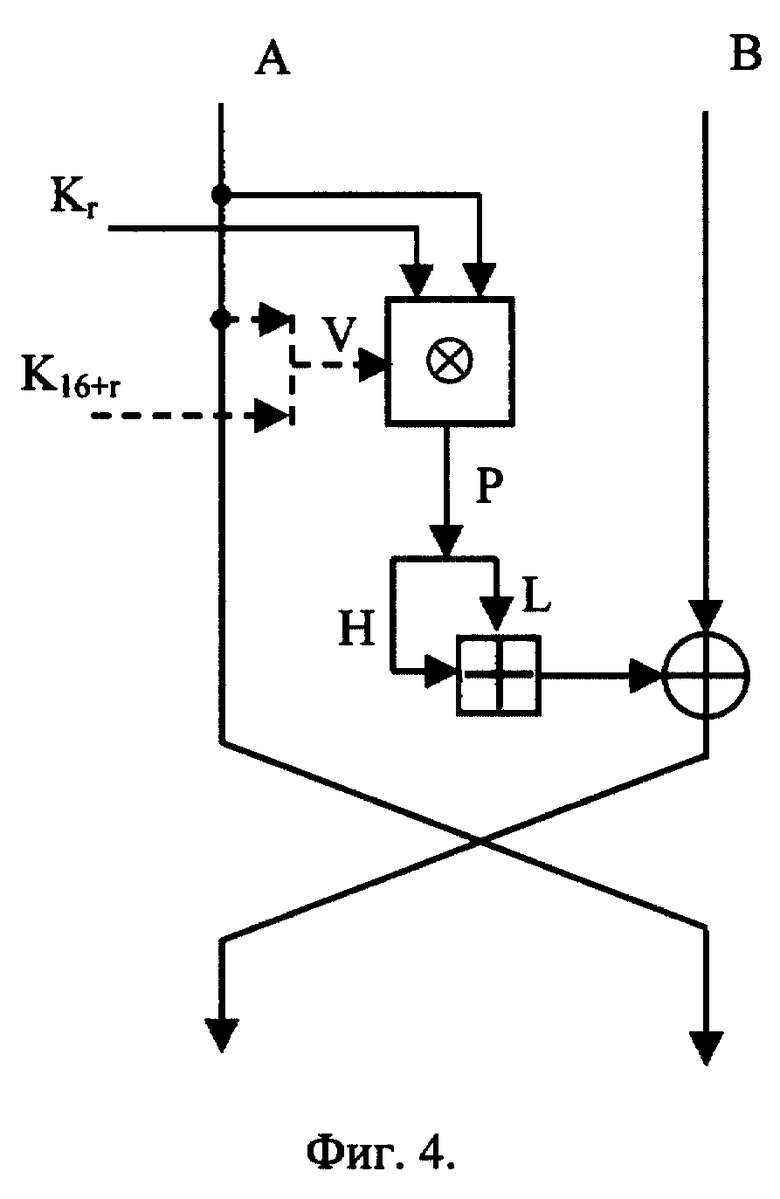
Пример 8: шифрование 64-битового блока данных T. Данный пример поясняется на фиг. 4. Сформировать секретный ключ, представленный в виде следующей совокупности n-битовых раундовых подключей: K1, K2,...,K32. Сформировать по блоку данных два двоичных вектора A = T div 232 и B = T mod 232. Шифрование блока данных выполнить в соответствии со следующим алгоритмом.
1. Установить счетчик числа раундов шифрования r: = 1.
2. Сформировать по двоичному вектору A и подключу Kr+16 управляющий код V путем объединения A и Kr+16 в соответствии с выражением: V = A|Kr+16.
3. В зависимости от значения V сформировать двоичный вектор P путем выполнения операции управляемого умножения из примера 5 над A и Kr: P: = (A ⊕ Kr)[V].
4. По значению P сформировать данных два двоичных вектора H = P div 232 и L = P mod 232.
5. Преобразовать двоичный вектор H путем выполнения над L и H операции суммирования по модулю 232: H: = (L + H) mod 232.
6. Преобразовать двоичный вектор B по формуле: B: = B ⊕ h.
7. Если r < 16, то прирастить r: = r + 1, взять двоичный вектор A в качестве двоичного вектора B, а двоичный вектор B - в качестве двоичного вектора A и перейти к шагу 2.
8. СТОП
Поясним шаг 7. Перед началом выполнения (i + 1)-го, где i = 1,2,...,15, раунда двоичному вектору A(B) присваивается значение B (A), полученное после выполнения i-го раунда. Блок криптограммы C формируется путем объединения преобразованных двоичных векторов A и B: C:= A|B. Процедура дешифрования блока криптограммы осуществляется с помощью этого же алгоритма, за исключением того, что при выполнении шага 2 используется подключ K33-r вместо подключа K16+r, а при выполнении шага 3 - подключ K17-r вместо Kr.
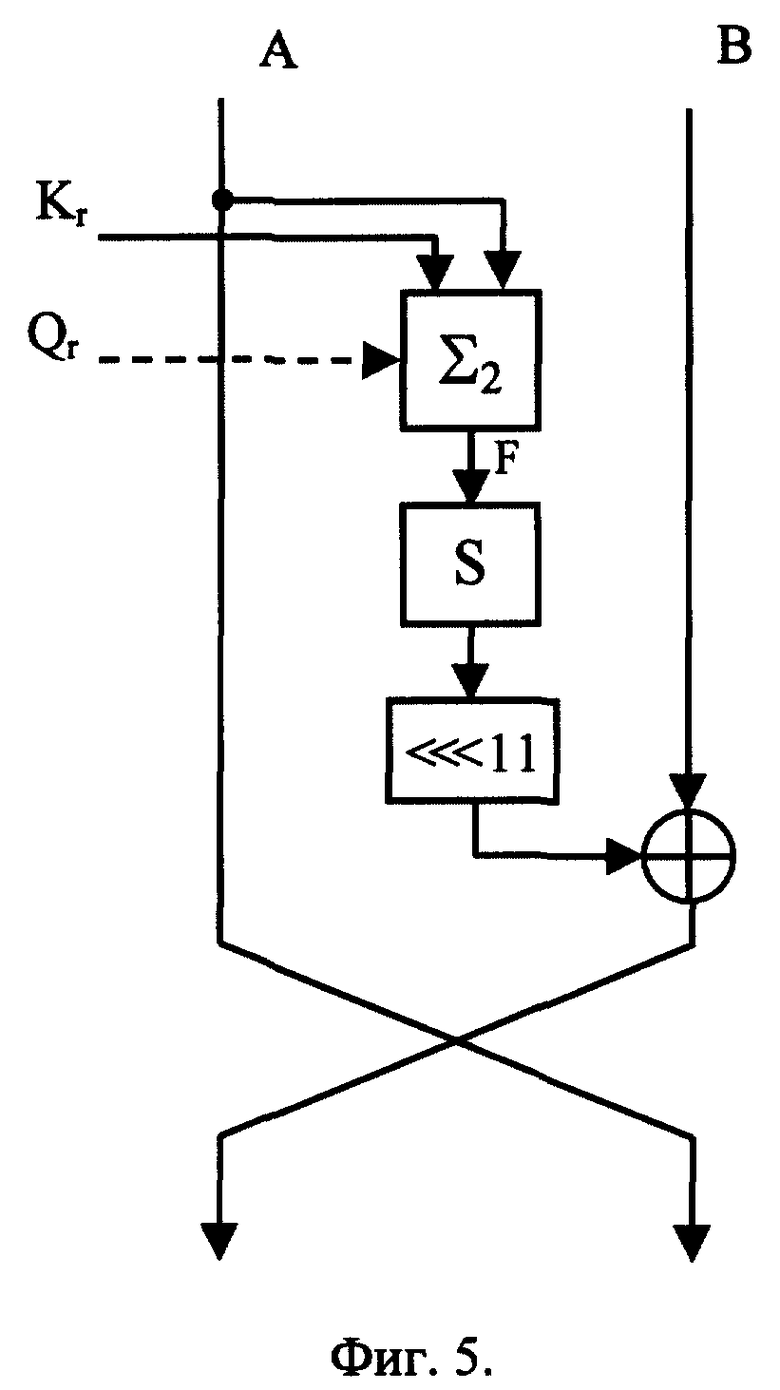
Пример 9: шифрование 64-битового блока данных T. Пример 8 поясняется на фиг. 5. Сформировать секретный ключ, представленный в виде следующей совокупности n-битовых раундовых подключей: K1, K2,..., K16 и Q1, Q1,..., Q16. Сформировать по блоку данных два двоичных вектора A = T div 232 и B = T mod 232. Шифрование блока данных выполнить в соответствии со следующим алгоритмом.
1. Установить счетчик числа раундов шифрования r: = 1.
2. Сформировать по подключу Qr управляющий код V: V: = Qr.
3. В зависимости от значения V сформировать двоичный вектор F путем выполнения операции управляемого суммирования из полимера 2 над двоичным вектором a и подключом Kr: F: = (A,Kr)[V].
4. Представить двоичный вектор F в виде конкатенации 4-битовых двоичных векторов fi: F:= f16|f15|...|f1, где i = 1,2,..., 16.
5. Преобразовать двоичный вектор F в соответствии с выражением:
F:= S(f16)|S(f15)|...|S(f1),
где "S(fi)" - обозначение операции подстановки, выполняемой над 4-битовым двоичным вектором fi, где i = 1,2,..., 16, по следующей таблице:
Выполнение операции подстановки состоит в следующем. Вычисляется значение j = i mod 4. Вместо двоичного вектора со значением fi подставляется двоичный вектор со значением стоящим на пересечении j-й строки и fj-го столбца.
6. Преобразовать двоичный вектор F путем выполнения над ним операции циклического сдвига влево на 11 бит: F: = F <<< 11.
7. Преобразовать двоичный вектор B по формуле: B: = B ⊕ F.
8. Если r < 16, то прирастить r: = r + 1, взять двоичный вектор A в качестве двоичного вектора B, а двоичный вектор B - в качестве двоичного вектора A и перейти к шагу 2.
9. СТОП.
Блок криптограммы C формируется путем объединения преобразованных двоичных векторов A и B: C = A|B. Дешифрование блока криптограммы осуществляется с помощью этого же алгоритма, за исключением того, что при выполнении шага 2 используется подключ Q17-r вместо подключа Qr, а при выполнении шага 3 - подключ K17-r вместо Kr.
Приведенные примеры показывают, что предлагаемый способ криптографических преобразований блоков цифровых данных технически реализуем и позволяет решить поставленную задачу. Управляемые двуместные операции с большим числом возможных модификаций могут быть легко реализованы в устройствах криптографического преобразования с помощью быстродействующих управляемых операционных блоков на базе стандартных узлов электронных схем.
| название | год | авторы | номер документа |
|---|---|---|---|
| ИТЕРАТИВНЫЙ СПОСОБ БЛОЧНОГО ШИФРОВАНИЯ | 1999 |
|
RU2172075C1 |
| СПОСОБ БЛОЧНОГО ИТЕРАТИВНОГО ШИФРОВАНИЯ ЦИФРОВЫХ ДАННЫХ | 2000 |
|
RU2184423C2 |
| ИТЕРАТИВНЫЙ СПОСОБ БЛОЧНОГО ШИФРОВАНИЯ | 2001 |
|
RU2204212C2 |
| СПОСОБ ИТЕРАТИВНОГО ШИФРОВАНИЯ БЛОКОВ ДИСКРЕТНЫХ ДАННЫХ | 2000 |
|
RU2186466C2 |
| СПОСОБ ИТЕРАТИВНОГО БЛОЧНОГО ШИФРОВАНИЯ ДВОИЧНЫХ ДАННЫХ | 2001 |
|
RU2206961C2 |
| СПОСОБ ИТЕРАТИВНОГО ШИФРОВАНИЯ БЛОКОВ ДАННЫХ | 1999 |
|
RU2140714C1 |
| СПОСОБ ИТЕРАТИВНОГО ШИФРОВАНИЯ БЛОКОВ ЦИФРОВЫХ ДАННЫХ | 2000 |
|
RU2199826C2 |
| СПОСОБ БЛОЧНОГО ИТЕРАТИВНОГО ШИФРОВАНИЯ | 2000 |
|
RU2186467C2 |
| СПОСОБ ИТЕРАТИВНОГО ШИФРОВАНИЯ БЛОКОВ ДВОИЧНЫХ ДАННЫХ | 1999 |
|
RU2144268C1 |
| СПОСОБ БЛОЧНОГО КРИПТОГРАФИЧЕСКОГО ПРЕОБРАЗОВАНИЯ ДВОИЧНОЙ ИНФОРМАЦИИ | 1998 |
|
RU2140713C1 |


Изобретение относится к электросвязи и вычислительной технике, а конкретнее к криптографическим способам и устройствам для шифрования данных. В основу изобретения положена задача увеличения числа различных вариантов операции, зависящей от преобразуемого блока, благодаря чему повышается стойкость криптографического преобразования, в чем и состоит технический результат, достигаемый при реализации изобретения. Способ заключается в формировании по блоку данных N ≥ 2 двоичных векторов, поочередном преобразовании двоичных векторов и формировании блока криптограммы по преобразованным двоичным векторам. Новым является то, что дополнительно формируют управляющий код V и при преобразовании по крайней мере одного двоичного вектора над двоичным вектором выполняют по крайней мере одну управляемую двуместную операцию, зависящую от значения управляющего кода V. Новым является также то, что управляющий код формируют по значению одного из двоичных векторов. Новым является также то, что дополнительно формируют секретный ключ, а управляющий код V формируют по секретному ключу. Кроме того, новым является то, что дополнительно формируют секретный ключ, а управляющий код V формируют по текущему значению преобразуемого информационного блока. 3 з.п.ф-лы, 5 ил., 3 табл.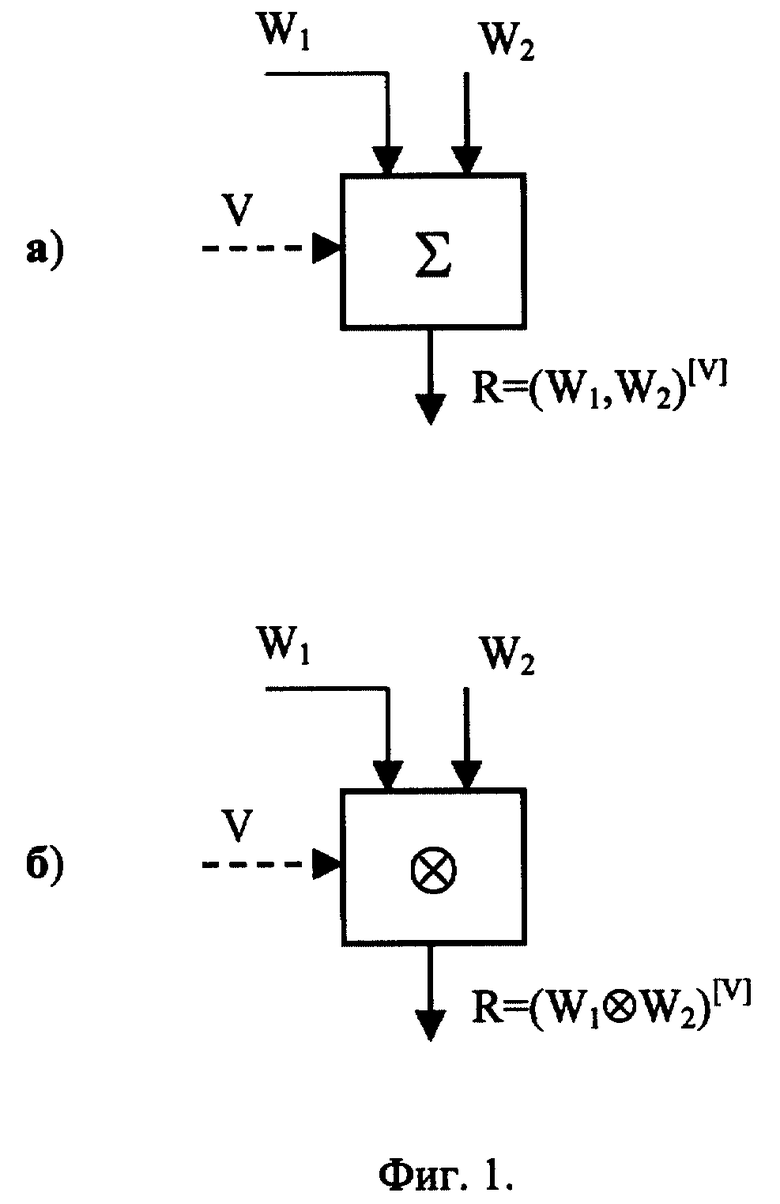
| US 5535277 A, 09.07.96 | |||
| US 5479513 A, 26.12.95 | |||
| Имитатор моментов инерции | 1977 |
|
SU720328A1 |
| БЕЗЗАЗОРНАЯ ЧЕРВЯЧНАЯ ПЕРЕДАЧА | 0 |
|
SU366288A1 |
| ТОКОПРОВОДЯЩАЯ СТРУНА ДЛЯ КРЕПЛЕНИЯ КОНТАКТНОГО ПРОВОДА НА НЕСУЩЕМ ТРОСЕ КОНТАКТНОЙ ПОДВЕСКИ | 2020 |
|
RU2739994C1 |
| СПОСОБ ШИФРОВАНИЯ ДВОИЧНОЙ ИНФОРМАЦИИ | 1992 |
|
RU2032990C1 |
| Затвор для тары | 1977 |
|
SU644676A1 |
| УСТРОЙСТВО ШИФРОВАНИЯ ДВОИЧНОЙ ИНФОРМАЦИИ "АЛБЕР" | 1991 |
|
RU2024209C1 |
Авторы
Даты
1999-10-27—Публикация
1999-01-18—Подача