СПОСОБ ПОТОЧНОГО ШИФРОВАНИЯ ДАННЫХ Российский патент 2004 года по МПК H04L9/00 H04K1/06 

Изобретение относится к области электросвязи и вычислительной техники, а конкретнее к области способов и устройств криптографического преобразования данных.

В совокупности признаков заявляемого способа, используются следующие термины:

секретный ключ (или пароль) представляет из себя комбинацию битов, известную только законному пользователю;

ключ шифрования - дешифрования (шифрключ) представляет из себя комбинацию битов, используемых при шифровании информационных сигналов; шифрключ является сменным элементом шифра и используется для преобразования данного сообщения или данной совокупности сообщений; шифрключ является известным только законному пользователю или может быть выработан по детерминированным процедурам по паролю;

шифр представляет собой совокупность элементарных шагов преобразования входных данных с использованием шифрключа; шифр может быть реализован в виде программы для ЭВМ или в виде отдельного устройства;

шифрование есть процесс криптографического преобразования данных с использованием шифрключа, переводящий данные в криптограмму, представляющую собой псевдослучайную последовательность знаков, из которой получение информации без знания ключа, практически невыполнимо;

дешифрование есть процесс, обратный процедуре шифрования; дешифрование обеспечивает восстановление информации по криптограмме при знании шифрключа;

двоичный вектор - это сигнал в виде последовательности нулевых и единичных символов, соответствующий представлению числа в двоичной системе исчисления.

Известны способы поточного шифрования данных (см., например, Российский стандарт шифрования стандарт СССР РОСТ 28147-89 [1], Британский алгоритм B-Grypt, Стандарт США DES, Японский алгоритм шифрования данных FEAL [2] стр. 48-52, а также патент Российской Федерации на изобретение №2106752, кл. Н 04 L 9/00).

В известных способах шифрование данных осуществляется путем формирования ключа шифрования, генерирования псевдослучайной последовательности двоичных символов и поблочного преобразования потока данных, включающего операции сложения символов по модулю два с операциями подстановок и перестановок символов в блоках данных.

Однако, известные способы-аналоги поточного шифрования данных имеют небольшое быстродействие, поскольку для обеспечения статистической равномерности символов шифрованного текста используется до 32 раундов перемешивания и рассеивания символов в блоках.

Наиболее близким по своей технической сущности к заявленному способу поточного шифрования данных является способ, представленный в стандарте США DES ([1] стр. 126-127 и в [3] стр. 50-51).

Способ-прототип включает в себя формирование ключа шифрования в виде двоичного вектора длиною n бит, подачу его для начального заполнения регистра сдвига с обратной связью, имеющего n разрядов и вырабатывающего псевдослучайную последовательность максимальной длины, содержащую 2ⁿ-1 двоичных символов, генерирование псевдослучайной последовательности символов, преобразование потока данных путем сложения по модулю два символов исходного текста с символами псевдослучайной последовательности и передачу зашифрованного сообщения по линии связи другому пользователю сети.

Однако способ-прототип имеет недостаток. Несмотря на то, что шифр, основанный на сложении потока псевдослучайных битов с битами исходного текста по модулю 2 является в общем случае теоретически нераспознаваемым (см. [2], стр. 128), сама криптосистема не отличается стойкостью и может быть раскрыта. Если структура регистра сдвига, имеющего n разрядов, известна, то для нахождения начального состояния регистра сдвига, надо знать n символов известного открытого текста, которые складываются по модулю 2 с соответствующими n символы шифртекста. Полученные n символов псевдослучайной последовательности определяют состояние регистра сдвига на некоторый момент времени. Моделируя работу регистра сдвига в обратном направлении, можно определить его исходное состояние, а следовательно и ключи, используемые пользователями сети при шифровании-дешифровании информации.

Если структура регистра сдвига, имеющего n-разрядов, является неизвестной, то достаточно 2· n символов известного открытого текста и им соответствующих 2· n символов шифрованного текста, чтобы сравнительно быстро (в течение нескольких секунд работы ЭВМ) определить состояние регистра сдвига и вычислить используемые ключи (см., например, [4] стр. 93). А это приводит не только к снижению стойкости шифра к атакам на основе известных и подобранных исходных текстов, но и к значительному усложнению процедуры формирования ключа шифрования-дешифрования в вычислительной сети, так как шифроключи могут использоваться только один раз и при очередном сеансе связи должны определяться по-новому.

Изобретение направлено на повышение стойкости шифра к атакам на основе известных и подобранных исходных текстов.

Это достигается тем, что в известном способе шифрования потока данных, заключающемся в формировании ключа шифрования в виде двоичного вектора, длиною n бит, подаче его для начального заполнения регистра сдвига с обратной связью, имеющего n разрядов и вырабатывающего псевдослучайную последовательность максимальной длины, содержащего 2ⁿ-1 символов, формировании псевдослучайной последовательности символов, преобразовании потока данных с использованием псевдослучайной последовательности символов в зашифрованное сообщение и передаче его по линии связи, согласно изобретению дополнительно формируют одну или несколько псевдослучайных последовательностей, при этом все псевдослучайные последовательности формируют как псевдослучайные последовательности символов конечного поля F_p с характеристикой p=257 в виде двоичных векторов длиною 8 бит путем снятия информации с восьми различных разрядов регистра, сдвига и замене символов "0" на символы "256", разбивают поток данных на блоки в виде двоичных векторов длиною 8 бит и поочередно преобразуют блоки путем использования псевдослучайных последовательностей символов конечного поля, а также линейных или нелинейных криптографических преобразований, включающих операции сложения, умножения или возведения в степень символов в конечном поле F_p.

Перечисленная совокупность существенных признаков исключает возможность определения ключей шифрования-дешифрования при использовании метода криптоанализа с известным открытым текстом и повышает стойкость шифра к атакам на основе известных и подобранных исходных текстов. В этом случае сформированные псевдослучайные последовательности символов в виде двоичных векторов длиною 8 бит являются псевдослучайной последовательностью символов {0, 1, 2, ..., 255} конечного поля F₂₅₇, имеют тот же период N=2ⁿ-1, что и псевдослучайные последовательности двоичных чисел и обеспечивают статистическую равномерность использованных символов. При замене символов "0" на символы "256" обеспечивается формирование псевдослучайных последовательностей символов мультипликативной группы конечного поля F₂₅₇ {1, 2, ..., 255}. Это позволяет формировать в поле F₂₅₇ разнообразные функции для шифрования символов исходного текста α , включающие операции сложения символов по модулю р, умножение символов по модулю р, возведение символов в степень по модулю р и их различные комбинации в отличие от поля F₂, в котором для шифрования одного двоичного символа исходного текста сложение по модулю два будет единственным способом построения обратимой функции шифрования.

Поскольку с одного регистра сдвига может сниматься несколько псевдослучайных последовательностей символов конечного поля {x, ..., y}, каждая из которых не будет являться циклически сдвинутой относительно других псевдослучайных последовательностей, то могут быть реализованы как линейные, так и нелинейные криптографические преобразования с использованием нескольких псевдослучайных последовательностей символов конечного поля F_p для получения зашифрованных символов β конечного поля F_p

α x+y≡ β (mod p), α ^x+y≡ β (mod p), α ^x·^{y=β (mod p), ...,.}

Поскольку символы псевдослучайных последовательностей x и y являются элементами мультипликативной группы конечного поля F_p, то могут быть вычислены обратные величины

x^-1≡^{xp-2(mod p), y-1≡yp-2(mod p), ...}

и сопряженные элементы

x*=p-x, y*=p-y, ...

которые позволяют реализовать криптографические преобразования для дешифрования символов шифртекста

(β +y*)x^-1≡^{α (mod p), (β +y*)x-1≡α(mod p),}

(β · y^-1)x^-1≡^{α(mod p), ...}

Выбор в качестве характеристики конечного поля числа p=257 обусловлен тем, что для воспроизведения мультимедийных данных современные вычислительные машины используют 256 символов и ближайшим простым числом к числу 256 является 257.

Поскольку псевдослучайные последовательности символов конечного поля F_p снимаются с восьми разрядов регистра сдвига, то не воспроизводится один символ конечного поля F_p, так как максимальное число, представленное 8 двоичными разрядами, составляет 255, поэтому снимаемые псевдослучайные последовательности не являются псевдослучайными последовательностями максимальной длины в конечном поле F_p, а представляют нелинейные псевдослучайные последовательности. Общее число возможных псевдослучайных последовательностей символов конечного поля будет определяться числом возможных комбинаций из восьми разрядов регистра сдвига, с которых может сниматься информация, и числом перестановок в рамках одной комбинации, каждая из которых определяет порядок считывания информации и для регистра сдвига, состоящего из n=256 разрядов, число различных псевдослучайных последовательностей символов конечного поля F₂₅₇ будет составлять Q=8!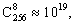 в то время как для поля F₂, с каких бы точек регистра сдвига не снимали бы информацию, псевдослучайная последовательность двоичных чисел будет лишь циклически сдвинутой относительно других псевдослучайных последовательностей двоичных чисел, снимаемых с других разрядов регистра сдвига.

Так как в криптографических преобразованиях используются две и более псевдослучайных последовательностей символов конечного поля F₂₅₇, то, при наличии сколь угодно символов исходного и им соответствующих символов шифрованного текста, исключается возможность определения символов псевдослучайных последовательностей, так как для их определения число уравнений всегда будет в два раза меньше числа неизвестных. При этом обеспечивается стойкость шифра к атакам на основе известных и подобранных исходных текстов, так как вскрытие состояния регистра сдвига в этом случае может быть обеспечено только путем тотального перебора всего множества возможных состояний регистра сдвига. Поскольку стандарт США шифрования данных DES предусматривает использование регистра сдвига, имеющего 128 разрядов (длина ключа 128 бит), мощность множества возможных состояний регистра сдвига будет составлять 10³⁸. Если вскрытие состояния регистра сдвига будет осуществляться с помощью ЭВМ, имеющей тактовую частоту 10 ГГц, то число операций, выполняемых этой ЭВМ в течение года будет составлять 3-10¹⁹, а время вскрытия составляет 10¹⁸ лет.

В соответствии с Российским стандартом ГОСТ28147-89 для регистра сдвига, имеющего 256 разрядов (длина ключа 256 бит), время вскрытия состояния регистра сдвига будет составлять 10⁵⁷ лет.

Возможность технической реализации заявленного способа шифрования потока данных поясняется следующим образом. Формирование шифрключа можно осуществлять путем ввода пароля с клавиатуры или с магнитного носителя информации в генератор псевдослучайных чисел, получая на выходе шифрключ необходимого размера (см., например, [5] стр. 87-89).

Формирование псевдослучайной последовательности максимальной длины, содержащей 2ⁿ-1 символов, можно осуществлять путем использования линейного регистра сдвига, имеющего n разрядов, обратную связь которого определяют по виду выбранного примитивного полинома степени n. Нахождение примитивных полиномов степени n изложено в [4] на стр. 74-75.

Формирование псевдослучайных последовательностей символов конечного поля F₂₅₇ в виде двоичных векторов длиною 8 бит можно осуществить путем снятия информации с восьми различных разрядов регистра сдвига, номера, которых могут определены по значению вводимого шифрключа К. Например, путем определения порождающего элемента

L₀=K(mod q), если 1₀<2, то 1₀=2,

и вычисления номера разряда регистра сдвига по формуле

1₁=1₀, l_i≡_{l0li-1(mod q), i=}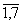

Значение q выбирается из простых чисел и для регистра сдвига, имеющего 256 разрядов, q=257, для регистра сдвига, имеющего 128 разрядов, q=127. В этом случае за счет возведения в степень порождающего числа 1₀ будем переходить от одного элемента поля F_q к другому. При этом, как показано в [4] стр. 44, если 1₀ - элемент порядка k, то все элементы 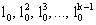будут различны. В псевдослучайных последовательностях x и y двоичных векторов осуществляют замену символов "0" на "256".

Формирование псевдослучайных последовательностей символов конечного поля F_p можно осуществить также по типу "сжимающего генератора" путем снятия информации с восьми разрядов регистра сдвига и пропуска тех тактов работы регистра сдвига, для которых хотя бы в одной из псевдослучайных последовательностей присутствует символ "0".

Преобразование потока данных в зашифрованное сообщение можно осуществить путем разбиения исходных данных на блоки в виде символов α двоичных векторов длиною 8 бит, вычисления в конечном поле F_p, (p=257) значений символов β зашифрованного текста в соответствии с выбранной функцией шифрования, например α · x+y=β (mod p), преобразования полученного числа β в двоичный вектор и передачи его по линии связи.

Могут быть использованы еще три варианта формирования псевдослучайных последовательностей символов конечного поля в виде двоичных векторов.

1. Элементы одной из выделенной и формируемой псевдослучайной последовательности символов конечного поля y в виде двоичных векторов используются как порождающие элементы y_n для дополнительной псевдослучайной последовательности z, элементы которой на каждом такте работы регистра сдвига определяются как порожденные элементы поля F_p: z≡ z· y_n(mod p)

Если в процессе вычислений на каком-то i такте работы регистра сдвига окажется, что z=1, то в этом случае меняется порождающий элемент y_n поля F_p. При этом в качестве нового порождающего элемента y_n принимается элемент, сформированный на данном такте работы регистра сдвига выделенной псевдослучайной последовательности y символов конечного поля F_p, y_n=y, если y<2, то y_n=2. Сформированная дополнительная псевдослучайная последовательность конечного поля z используется в криптографических преобразованиях при преобразовании потока данных в зашифрованное сообщение, например:

α · x+y+z=β (mod p) или α · x+z=β (mod p)

Поскольку в дополнительной псевдослучайной последовательности конечного поля элементы формируются за счет возведения в степень порождающего элемента y_n, имеющего порядок k, то все элементы 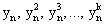будут различны на интервале k тактов работы регистра сдвига. Поскольку порождающие элементы y_n могут быть разного порядка в конечном поле F_p, то смена порождающих элементов будет осуществляться по псевдослучайному закону. При этом обеспечивается статистическая равномерность символов зашифрованного текста на интервале, равном p-1 тактам работы регистра сдвига, что исключает применение статистических методов криптоанализа для определения состояния регистра сдвига.

2. Изменяют номера разрядов регистра сдвига, с которых снимается информация для одной из псевдослучайных последовательностей символов конечного поля в соответствии с изменением порождающего элемента дополнительной псевдослучайной последовательности

l₀=y_n, l_i=y_nl_i-1(mod q),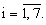

3. Изменяют порядок считывания информации для одной из формируемых псевдослучайных последовательностей символов конечного поля в соответствии с изменением поражающего элемента, дополнительной псевдослучайной последовательности символов, например, с использованием соотношений

l_i=l_k,

k≡ i+y_n(mod 8),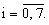

Формирование псевдослучайных последовательностей символов конечного поля по п.1, 2 и 3 повышает стойкость шифра к атакам на основе известных и подобранных исходных текстов при формировании ключа шифрования малой длины.

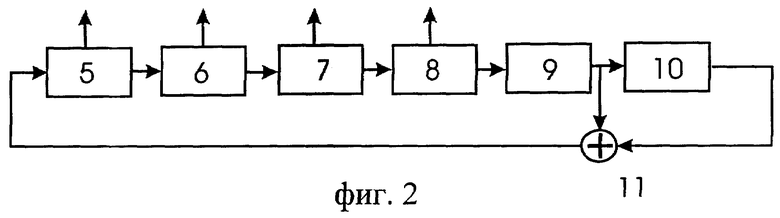
Предлагаемый способ может быть реализован с помощью ЭВМ или устройства. На фиг.1 представлена структурная схема устройства, где

блок 1 - устройство формирования ключа шифрования;

блок 2 - регистр сдвига;

блок 3 - шифрующее устройство;

блок 4 - передающее устройство.

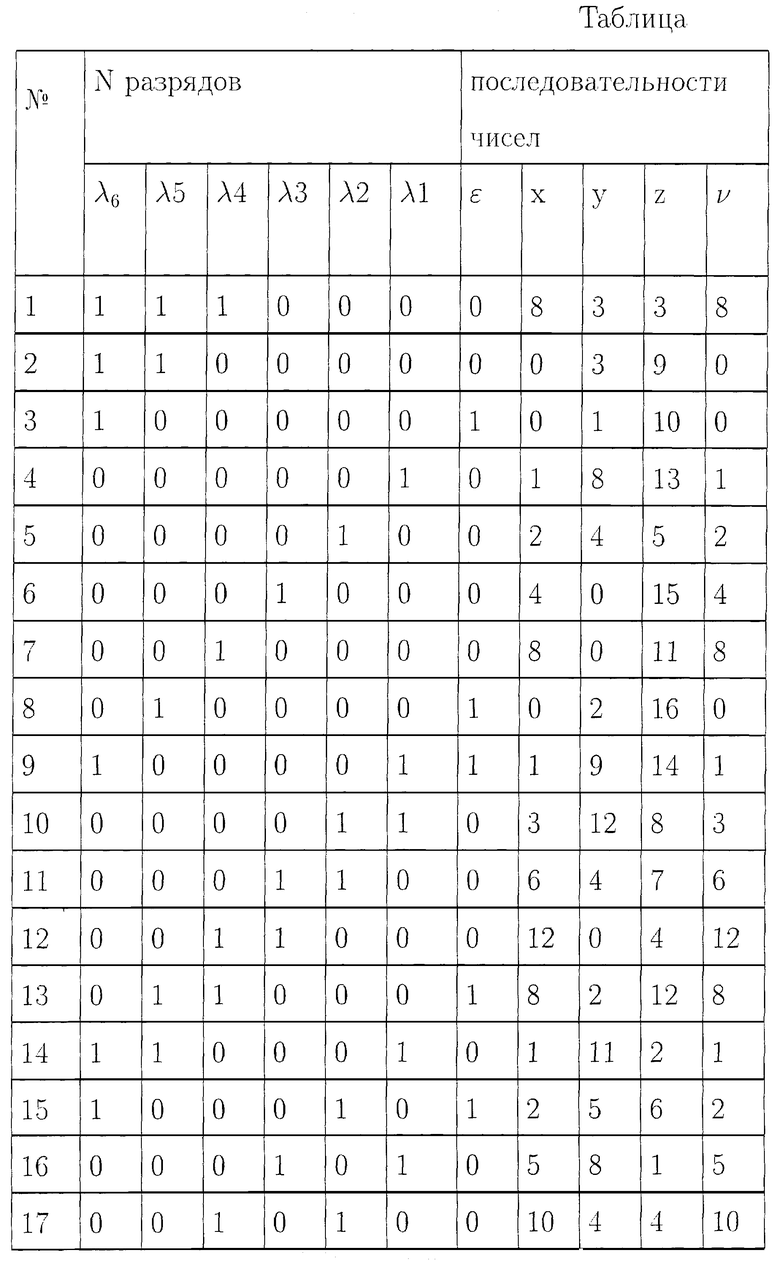
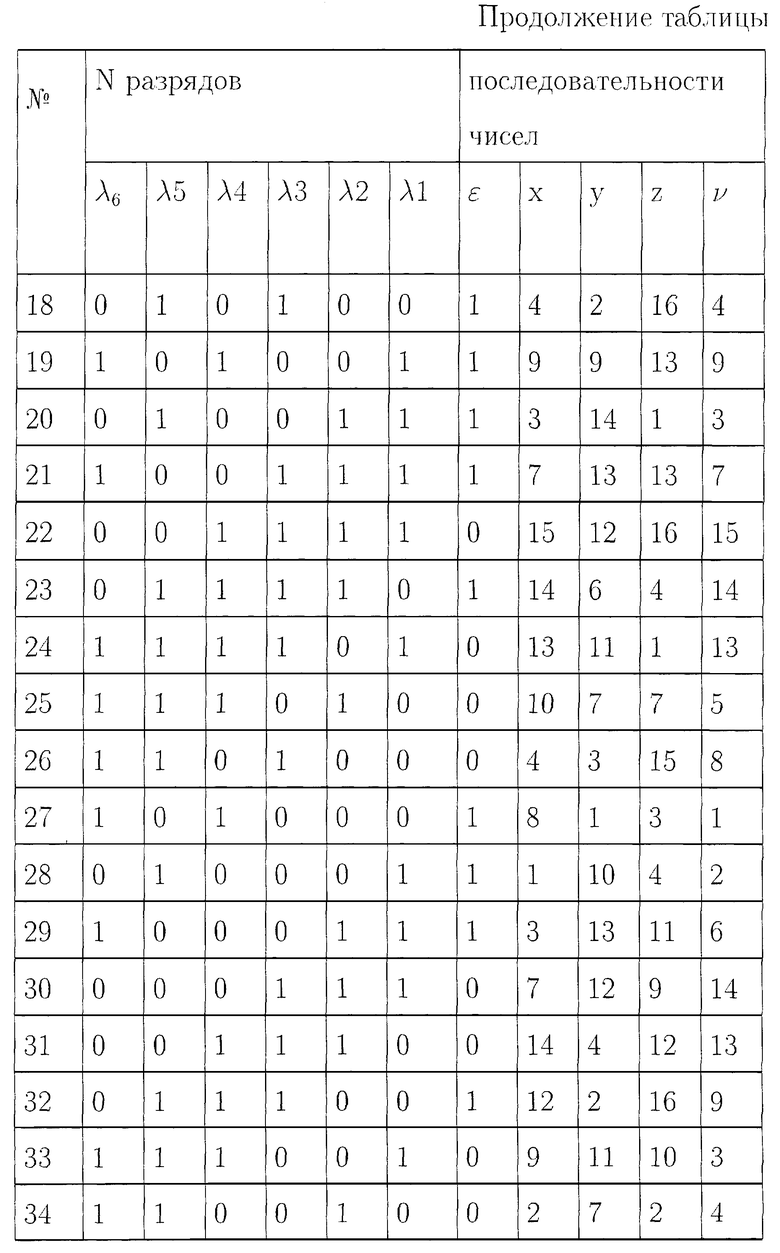
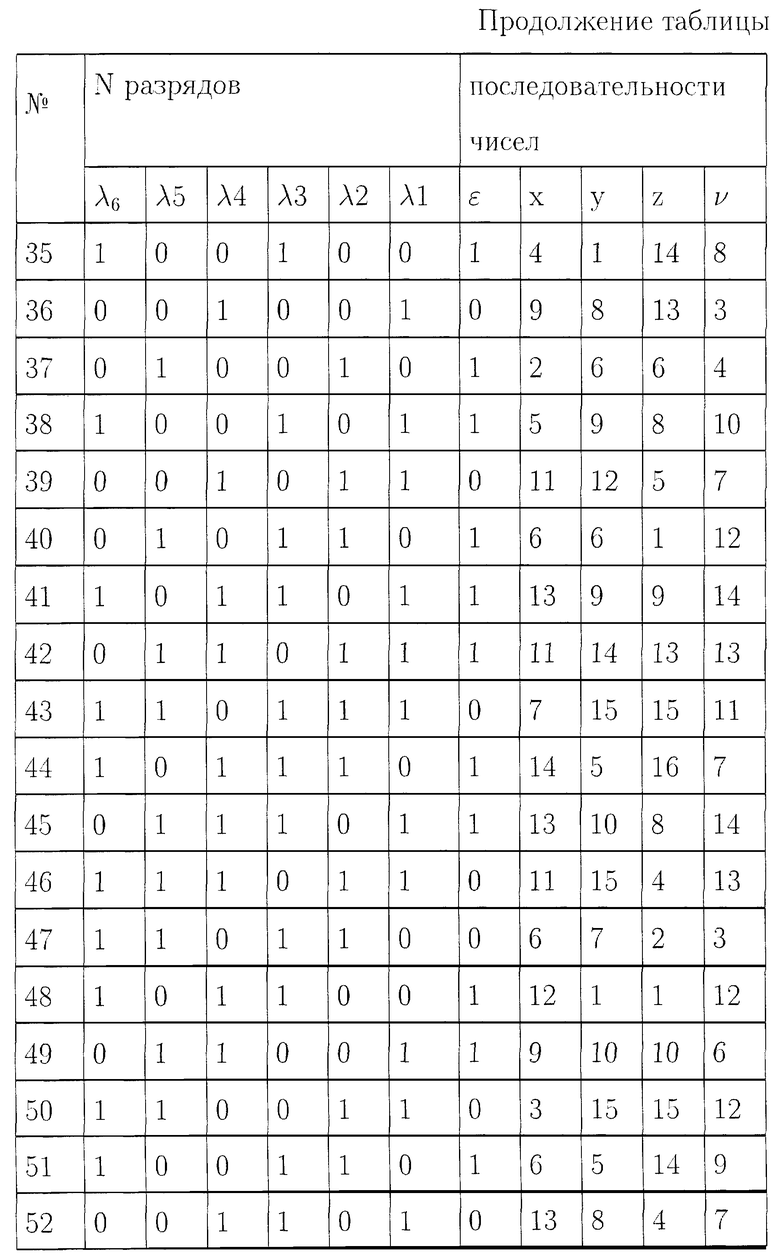
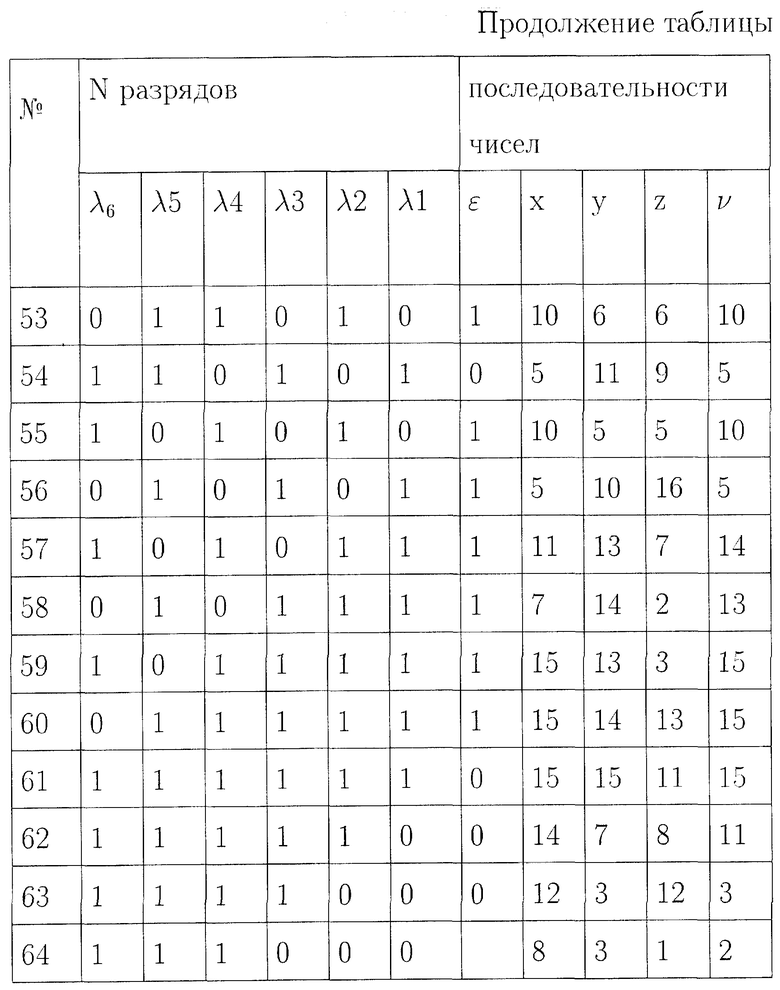
Для простоты описания работы устройства будем пользоваться малыми числами. Будем считать, что регистр сдвига имеет 6 разрядов (длина ключа 6 бит), а весь алфавит исходного текста содержит 16 символов, тогда для передачи одного символа может быть использован двоичный вектор длиною 4 бита, а, в качестве характеристики конечного поля F_p может быть выбрано число p=17.

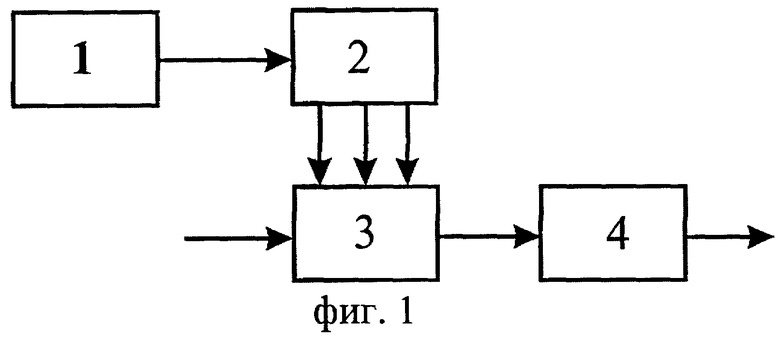
Для определения структуры регистра сдвига, выбирают примитивный многочлен шестой степени, например λ ⁶+λ ⁵+1.

Для выбранного примитивного многочлена структурная схема регистра сдвига с обратной связью будет иметь вид, представленный на фиг.2, где блоки 5-10 - разряды 1-6 регистра сдвига, а блок 11 - сумматор по модулю два.

Сформированный в блоке 1 фиг.1 с помощью генератора случайных чисел ключ шифрования длиною 6 бит

<λ ₆, λ ₅, λ ₄, λ ₃, λ ₂, λ _l >,

где λ _I=0, λ ₂=0, λ ₃=0, λ ₄=1, λ ₅=1, λ ₆=1;

поступает в регистр сдвига и используется для начального заполнения разрядов регистра сдвига. Двоичные символы с 5 и 6 разряда регистра сдвига поступают в каждом такте работы на вход сумматора 11 по модулю два, а с выхода сумматора по модулю два символы ε поступают на вход первого разряда регистра сдвига (блок 5, фиг.2). При этом состояния разрядов для каждого такта в процессе работы регистра сдвига определяются выражением

λ _I=λ _i-1 для 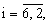λ ₁=ε

и представлены в таблице.

Если символы будут сниматься с шестого разряда λ ₆ регистра сдвига (блок 10, фиг.2), то двоичная псевдослучайная последовательность максимального периода, будет иметь вид {1110000010000110001010011110100011100100101101110110011010101111}.

Заметим, что на периоде этой последовательности любой ненулевой набор из шести знаков 0 и 1 встречается только один раз.

Если двоичные числа будем снимать с 1, 2, 3 и 4 разряда регистра сдвига, (блоки 5, 6, 7, 8, фиг.2) и на каждом такте работы регистра сдвига и с набором <λ ₁, λ ₂, λ ₃, λ ₄> будем сопоставлять двоичный вектор (число) x=λ ₁+2λ ₂+2²λ3

+2³λ4, то последовательность двоичных чисел в процессе работы регистра можно рассматривать как последовательность x чисел (символов) {0, 1, 2, ..., 15} в виде

x={8, 0, 0, 1, 2, 4, 8, 0, 1, 3, 6, 12, 8, 1, 2, 5, 10, 4, 9, 3, 7, 15, 14, 13, 10, 4, 8, 1, 3, 7, 14, 12, 9, 2, 4, 9, 2, 5, 11, 6, 13, 11, 7, 14, 13, 11, 6, 12, 9, 3, 6, 13, 10, 5, 10, 5, 11, 7, 15, 15, 15, 14, 12, ...}.

Если двоичные числа будем снимать одновременно с 1, 2, 5, 6 разряда, регистра сдвига (блоки 5, 6, 9, 10, фиг.2) и на каждом такте работы регистра сдвига с набором <λ ₆, λ ₅, λ ₂, λ ₁> будем сопоставлять число в виде y=λ ₆+2λ ₅+2²λ2

+2³λ1, то последовательность двоичных чисел в процессе работы регистра сдвига можно рассматривать как последовательность символов

y{0, 1, 2, ..., 15} в виде

y={3, 3, 1, 8, 4, 0, 0, 2, 9, 12, 4, 0, 2, 11, 5, 8, 4, 2, 9, 14, 13, 12, 6, 11, 7, 3, 1, 10, 13, 12, 4, 2, 11, 7, 1, 8, 6, 9, 12, 6, 9, 14, 15, 5, 10, 15, 7, 1, 10, 15, 5, 8, 6, 11, 5, 10, 13, 14, 13, 14, 15, 7, 3, ...}.

Анализ сформированных последовательностей x и y показывает, что на интервале, соответствующем периоду, равному 63 тактам работы регистра сдвига, каждый из символов {1, 2, ..., 15} встречается ровно четыре раза. Символ, соответствующий нулю в обеих последовательностях, встречается ровно три раза, при этом последовательности x и y не могут быть получены друг из друга, в результате циклического сдвига. В последовательностях x и y отсутствуют скрытые периодичности и обеспечивается статистическая равномерность используемых символов. Поскольку один из символов псевдослучайных последовательностей конечного поля F₁₇ не воспроизводится, то символ "0" в обеих последовательностях заменяют на символ "16".

Помимо псевдослучайных последовательностей символов x, y конечного поля F_p в таблице 1 представлено формирование дополнительной псевдослучайной последовательности z путем использования в качестве порождающих элементов символов псевдослучайной последовательности y, а также формирование псевдослучайной последовательности символов конечного поля v путем изменения порядка считывания информации для псевдослучайной последовательности символов конечного поля x в соответствии с изменением порождающего элемента дополнительной псевдослучайной последовательности z.

Сформированные псевдослучайные последовательности символов конечного поля x и y в виде двоичных векторов поступают в шифрующее устройство 3 (фиг.1), где преобразуется поступающий поток данных в зашифрованное сообщение путем использования псевдослучайных последовательностей символов x и y конечного поля F₁₇ в соответствии с выбранным криптографическим преобразованием в конечном поле F₁₇, например

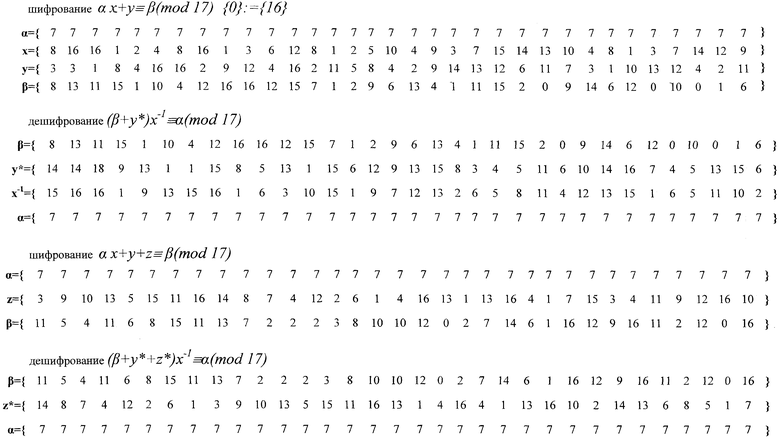
Источники информации

1. Российский стандарт шифрования стандарт СССР ГОСТ 28147-89 Системы обработки информации. Защита криптографическая. Алгоритм криптографического преобразования.

2. С.Мафтик. Механизмы защиты в сетях ЭВМ, М., 1993 г.

3. В.И. Нечаев. Элементы криптографии. Основы теории защиты информации. - М.: Высшая школа, 1999 г.

4. Б.Н. Воронков, В.И. Тупота. Методическое пособие по разработке средств защиты информации в вычислительных сетях. Воронеж: Воронежский государственный университет, 2000.

5. Э.Ф. Бикелл, Э.М. Одлижко. Криптоанализ: Обзор новейших результатов // ТИИЭР, 1988, т. 16, №5.

Изобретение относится к области электросвязи и вычислительной технике, а конкретнее к области криптографического преобразования. Сущность способа заключает в формировании ключа шифрования в виде двоичного вектора, подачи двоичного вектора для начального заполнения регистра сдвига с обратной связью, формирующего псевдослучайную последовательность (ПСП) двоичных символов, преобразовании потока данных в зашифрованное сообщение и передачи его по линии связи, отличающийся тем, что ПСП двоичных символов формируют как ПСП символов конечного поля Fp с характеристикой р=257 в виде двоичных векторов длиной 8 бит путем снятия информации с восьми различных разрядов регистра сдвига, номера которых определяют по значению вводимого ключа шифрования, пропускают те такты работы регистра сдвига, в которых хотя бы одна из формируемых ПСП символов конечного поля Fp имеет символ "0". Преобразование потока данных в зашифрованное сообщение осуществляют путем разбиения потока исходных данных на блоки в виде двоичных векторов длиною 8 бит и поочередно преобразуют блоки в двоичный вектор путем использования ПСП символов конечного поля Fp в соответствии выбранными линейным или нелинейным криптографическим преобразованиями, включающими операции сложения, умножения или возведения в степень символов в конечном поле Fp. Технический результат, достигаемый при осуществлении изобретения, состоит в повышении стойкости шифра к атакам на основе известных и подобранных исходных текстов. 3 з.п. ф-лы, 1 табл., 2 ил.

1. Способ поточного шифрования данных, заключающийся в формировании ключа шифрования в виде двоичного вектора, подачи двоичного вектора для начального заполнения регистра сдвига с обратной связью, формирующего псевдослучайную последовательность двоичных символов, преобразовании потока данных в зашифрованное сообщение и передачи его по линии связи, отличающийся тем, что псевдослучайные последовательности двоичных символов формируют как псевдослучайные последовательности символов конечного поля Fp с характеристикой р=257 в виде двоичных векторов длиной 8 бит путем снятия информации с восьми различных разрядов регистра сдвига, номера которых определяют по значению вводимого ключа шифрования, а общее число возможных псевдослучайных последовательностей символов конечного поля определяют числом возможных комбинаций из восьми разрядов регистра сдвига, с которых снимают информацию, и числом перестановок в рамках одной комбинации, пропускают те такты работы регистра сдвига, в которых хотя бы одна из формируемых псевдослучайных последовательностей символов конечного поля Fp имеет символ 0, преобразование потока данных в зашифрованное сообщение осуществляют путем разбиения потока исходных данных на блоки в виде двоичных векторов длиною 8 бит и поочередно преобразуют блоки в двоичный вектор путем использования псевдослучайных последовательностей символов конечного поля Fp в соответствии с выбранными линейным или нелинейным криптографическим преобразованиями, включающими операции сложения, умножения или возведения в степень символов в конечном поле Fp.2. Способ по п.1, отличающийся тем, что символы одной из формируемых псевдослучайных последовательностей конечного поля используют как порождающие элементы для формирования дополнительной псевдослучайной последовательности символов, которые на каждом такте работы сдвига определяют как порожденные элементы конечного поля Fp.3. Способ по п.2, отличающийся тем, что изменяют номера разрядов регистра сдвига, с которых снимается информация для одной из формируемых псевдослучайных последовательностей символов конечного поля Fp в соответствии с изменением порождающего элемента дополнительной псевдослучайной последовательности.4. Способ по п.2, отличающийся тем, что изменяют порядок считывания информации для одной из формируемых псевдослучайных последовательностей символов в соответствии с изменением порождающего элемента дополнительной псевдослучайной последовательности.