Изобретение относится к области электросвязи и вычислительной техники, а конкретнее к области способов и устройств криптографического преобразования данных.
Известны способы поточного кодирования дискретной информации (см. например, Российский стандарт шифрования стандарт СССР ГОСТ 28147-89 [1], Британский алгоритм B-Grypt, являющий дополнением к стандарту США DES [2] стр.50, 126, способ, описанный в [3] стр.50-51), а также способ, описанный в патенте на изобретение №2251816 от 10.05.2005 г. [5])
В известных способах кодирование дискретной информации осуществляется путем формирования ключа защиты, генерирования псевдослучайной последовательности двоичных символов и преобразовании потока данных, включающего операции сложения по модулю два символов потока данных с символами псевдослучайной последовательности.
Известные способы-аналоги поточного кодирования дискретной информации обеспечивают целостность передаваемой информации.
Несмотря на то, что код, основанный на сложении потока псевдослучайных битов с битами исходного текста по модулю 2, является в общем случае теоретически нераспознаваемым (см. [2], стр.128), сама система кодирования не отличается стойкостью и может быть раскрыта при наличии небольшого числа символов исходного и кодированного текста (см., например, [4] стр.92).
Наиболее близким по своей технической сущности к заявленному способу является способ, описанный в [5].
Способ-прототип включает в себя формирование ключа защиты в виде двоичного вектора длиною n бит, подачи его для начального заполнения регистра сдвига с обратной связью, имеющего n разрядов и вырабатывающего псевдослучайную последовательность максимальной длины, содержащую 2n-1 двоичных символов, формирование псевдослучайной последовательности символов конечного поля с характеристикой p=2k+1 в виде двоичных векторов длиною k бит путем снятия информации с k различных разрядов регистра сдвига с обратной связью, номера которых определяют по значению ключа защиты, при этом формируют псевдослучайную последовательность символов из нечетных значений за счет пропуска тактов работы регистра сдвига с обратной связью, для которых символы псевдослучайной последовательности принимают четные значения, разбиение потока данных исходного текста на блоки-символы в виде двоичных векторов длиною k бит, поочередное преобразование символов исходного текста в закодированное сообщение путем возведения их в степень, соответствующую символам псевдослучайной последовательности, и передачу его по линии связи.
Однако способ-прототип имеет низкую скорость декодирования данных и слабо регулируемый диапазон изменения стойкости кода к атакам на основе известных или подобранных исходных текстов. Низкая скорость декодирования данных обусловлена тем, что для обеспечения высокой стойкости кода к атакам на основе известных или подобранных исходных текстов используется операция возведения символов в конечном поле Fp, p=2k+1, k ∈ 2, 4, 8, 16. В этом случае для декодирования данных необходимо определить обратные элементы символов x псевдослучайной последовательности. Вычисление обратных элементов осуществляется путем возведения символов x псевдослучайной последовательности в степень p-2 в конечном поле Fp, x-1≡xp-2(mod)p, что представляет собой трудоемкую операцию, так как число умножений в конечном поле будет большим. Поскольку число k ограничено значениями k ∈ 2, 4, 8, 16, для которых модуль сравнения p должен быть простым числом p=2k+1, то это уменьшает регулировку диапазона изменения стойкости кода к атакам на основе известных и подобранных исходных текстов.
Изобретение направлено на повышение скорости декодирования данных и расширение диапазона изменения стойкости кода к атакам на основе известных или подобранных исходных текстов.
Это достигается тем, что в известном способе кодирования дискретной информации, заключающемся в формировании ключа защиты в виде двоичного вектора длиною n бит, подаче его для начального заполнения регистра сдвига с обратной связью, имеющего n разрядов и вырабатывающего псевдослучайную последовательность максимальной длины, содержащую 2n-1 двоичных символов, формировании псевдослучайной последовательности символов в виде двоичных векторов длиною k бит путем снятия информации с k различных разрядов регистра сдвига с обратной связью, номера которых определяют по значению ключа защиты, при этом формируют псевдослучайную последовательность символов из нечетных значений за счет пропуска тактов работы регистра сдвига с обратной связью, для которых символы псевдослучайной последовательности принимают четные значения, разбиении потока данных исходного текста на блоки-символы в виде двоичных векторов длиною k бит, поочередном преобразовании символов исходного текста в закодированное сообщение путем возведения их в степень, соответствующую символам псевдослучайной последовательности, и передачи его по линии связи, согласно изобретению преобразуют четные символы потока данных исходного текста в нечетные путем замены символа "0" на символ "1" в нулевом разряде двоичного вектора потока данных исходного текста, а возведение символов исходного текста в степень осуществляют в кольце класса вычетов по модулю p=2k, при этом двоичный вектор полученного результата возведения символов в степень для четных символов исходного текста преобразуют путем замены в нулевом разряде двоичного вектора символа "1" на символ "0".
В совокупности признаков заявляемого способа под двоичным вектором понимается сигнал в виде последовательности нулевых и единичных битов, соответствующей представлению числа в двоичной системе исчисления.
Перечисленная совокупность существенных признаков повышает скорость декодирования данных. Это обусловлено тем, что в качестве модуля сравнения используют числа вида p=2k. Для этих чисел функция Эйлера ϕ(p)=2(k-1) где k - целое число большее единицы. В этом случае по отношению к числу x в кольце класса вычетов по модулю (p/2) существуют обратные элементы х-1 только для нечетных чисел. Эти числа являются элементами мультипликативной группы кольца класса вычетов по модулю (p/2). При этом могут вычислены обратные элементы для декодирования сообщения:
х-1≡xq(mod(p/2)), где q=2(k-2)-1.
Для вычисления обратных величин число умножений в кольце класса вычетов по модулю p/2=2k-1 уменьшается более чем в четыре раза по отношению к вычислению обратных величин в конечном поле Fp, p=2k+1, для которого функция Эйлера ϕ(p)=2k. В этом случае q<2k-1 более чем в четыре раза.
Так как число k для кольца класса вычетов по модулю p не ограничивается значениями k ∈ 2, 4, 8, 16, а может принимать любые целые числа более единицы, то это увеличивает возможность регулировки диапазона изменения стойкости кода к атакам на основе известных или подобранных исходных текстов.
В этом случае сформированная псевдослучайная последовательность символов в виде двоичных векторов длиною k бит является псевдослучайной последовательностью символов {0, 1, 2,..., p-1}, имеет тот же период N=2n-1, что и псевдослучайная последовательность двоичных чисел, и обеспечивает статистическую равномерность использованных символов.
За счет пропуска тактов работы регистра сдвига, для которых символы псевдослучайной последовательности принимают четные значения, будет сформирована псевдослучайная последовательность символов x из нечетных чисел 1, 3, 5, 7,..., р-1, которую используют для кодирования символов исходного текста α за счет возведения их в степень, соответствующую символам псевдослучайной последовательности х. При этом закодированное сообщение будет представлять последовательность символов β, определяемых по формуле
β≡αx(modp)
Поскольку число p=2k является четным, то функция Эйлера ϕ(p)=(p/2) и в соответствии с теоремой Эйлера-Ферма будет иметь следующее тождество
α1+mϕ(p)=α1+m(p/2)≡α(modp).
Так как х·х-1=1+m(p/2)≡1(mod(p/2)), где
m - произвольное целое положительное число,
x-1 - символ, обратный символу x в кольце класса вычетов по модулю
(p/2),
то справедливо соотношение 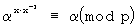 . В этом случае вычисленные на приемной стороне значения символов x-1 в кольце класса вычетов по модулю (p/2) позволяют реализовать обратные преобразования для декодирования исходного текста
. В этом случае вычисленные на приемной стороне значения символов x-1 в кольце класса вычетов по модулю (p/2) позволяют реализовать обратные преобразования для декодирования исходного текста
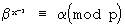 .
.
Поскольку псевдослучайная последовательность х включает только нечетные символы 1, 3, 5,..., p-1, то все они являются элементами мультипликативной группы кольца классов вычетов по модулю p/2 и будут иметь обратные величины х-1, которые могут быть определены по формуле
x-1≡xϕ(p/2)-1(mod(p/2)),
где ϕ(p/2) - функция Эйлера для числа (p/2).
Поскольку (p/2)=2k-1, то ϕ(p/2)=2k-2. В этом случае x-1 можно рассчитать по формуле
х-1≡xq(mod(p/2)),
где q=2(k-2)-1. При этом для вычисления х-1 может быть использован алгоритм быстрого возведения чисел по модулю, представленный в [4] на стр.39.
Так как в криптографических преобразованиях используются операции возведения символов в степень по модулю p, а псевдослучайная последовательность символов формируется по принципу сжимающего генератора с неравномерным движением регистра сдвига, то исключается вскрытие состояния регистра сдвига при наличии сколь угодно символов исходного и им соответствующих символов кодированного текста. Это обусловлено тем, что для определения символов псевдослучайной последовательности по известным символам исходного и кодированного текста необходимо вычисление дискретного логарифма, что может быть обеспечено только в результате тотального перебора символов этого поля, а для определения состояния регистра сдвига по вычисленным символам псевдослучайной последовательности необходимо знать символы псевдослучайной последовательности для пропускаемых тактов работы регистра сдвига, начало и число которых в процессе последовательного движения регистра сдвига меняется по псевдослучайному закону. При этом обеспечивается стойкость кода к атакам на основе известных и подобранных исходных текстов.
Возможность технической реализации заявленного способа поясняется следующим образом. Формирование ключа защиты можно осуществить путем ввода пароля с клавиатуры или с магнитного носителя информации в генератор псевдослучайных чисел, получая на выходе ключ защиты необходимого размера.
Формирование псевдослучайной последовательности максимальной длины, содержащей 2n-1 символов, можно осуществлять путем использования линейного регистра сдвига, имеющего n разрядов, обратную связь которого определяют по виду выбранного примитивного полинома степени n. Нахождение примитивных полиномов степени n изложено в [4] на стр.106-110.
Формирование псевдослучайной последовательности символов конечного поля Fp в виде двоичных векторов длиною k бит можно осуществить путем снятия информации с k различных разрядов регистра сдвига, номера которых могут определены по значению вводимого ключа защиты К. Например, путем определения порождающего элемента
l0≡K(mod q), если l0<2, то l0=2,
и вычисления номера разряда регистра сдвига по формуле
l1=l0, li≡l0li-1(mod q), 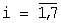 .
.
Значение q выбирают из простых чисел и для регистра сдвига, имеющего 256 разрядов, q=257, для регистра сдвига, имеющего 128 разрядов, q=127. В этом случае за счет возведения в степень порождающего числа l0 мы будем переходить от одного элемента поля Fq к другому. При этом, как показано в [4] стр.9, если l0 - элемент порядка k, то все элементы l0, 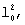
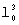 ,...,
,..., 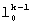 будут различны.
будут различны.
Псевдослучайную последовательность символов можно сформировать по типу "сжимающего генератора" путем снятия информации с k разрядов регистра сдвига и пропуска тех тактов работы регистра сдвига, для которых символы псевдослучайной последовательности принимают четные значения.
Сформированная псевдослучайная последовательность используют в криптографических преобразованиях при преобразовании потока данных в закодированное сообщение:
αх≡β(mod p)
Могут быть использованы еще четыре варианта формирования псевдослучайных последовательностей символов в виде двоичных векторов.
1. Псевдослучайные последовательности символов мультипликативной группы кольца класса вычетов по модулю p=2k формируют в виде двоичных векторов длиною k бит путем использования символа "1" в нулевом разряде двоичного вектора, а для остальных разрядов двоичного вектора используют символы, снимаемые с k-1 различных разрядов регистра сдвига
2. Изменяют число разрядов k, c которых снимается информация для псевдослучайной последовательности символов конечного поля Fp, p=2k+1 в соответствии с изменением начального заполнения регистра сдвига.
3. Изменяют номера разрядов регистра сдвига, с которых снимается информация для псевдослучайной последовательности символов конечного поля, в соответствии с изменением начального заполнения регистра сдвига.
4. Изменяют порядок считывания информации для псевдослучайной последовательности символов конечного поля в соответствии с изменением начального заполнения регистра сдвига.
Формирование псевдослучайной последовательности символов по п.1, 2, 3 и 4 повышает стойкость кода к атакам на основе известных и подобранных исходных текстов при формировании ключа защиты или двоичного вектора псевдослучайной последовательности малой длины.
Преобразование потока данных в закодированное сообщение осуществляют путем разбиения потока данных исходного текста на блоки в виде символов α двоичных векторов длиною k бит, преобразовании четных символов исходного текста в нечетные путем замены в нулевом разряде двоичного вектора символа "0" на символ "1", вычисляют по модулю (p=2k) значения символов β закодированного сообщения в соответствии с выбранной функцией кодирования, αx≡β(mod p), преобразуют полученное число β в двоичный вектор, при этом в нулевом разряде двоичного вектора заменяют символ "1" на символ "0" для четных символов исходного текста и передают закодированное сообщение по линии связи.
Предлагаемый способ может быть реализован с помощью ЭВМ или устройства.
На фиг.1 представлена структурная схема устройства, где
блок 1 - устройство формирования ключа защиты и исходного сигнала;
блок 2 - регистр сдвига;
блок 3 - формирователь псевдослучайной последовательности;
блок 4 - кодирующее устройство;
блок 5 - передающее устройство.
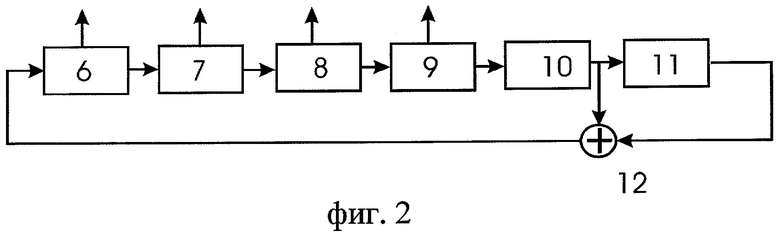
Для регистра сдвига на фиг.2 блоки 6-11 - разряды 1-6 регистра сдвига, а блок 12 - сумматор по модулю два.
Для простоты описания работы устройства будем пользоваться малыми числами. Будем считать, что регистр сдвига имеет 6 разрядов (длина ключа 6 бит), а весь алфавит исходного текста содержит 16 символов, тогда для передачи одного символа может быть использован двоичный вектор длиною 4 бита, а в качестве модуля сравнения может быть выбрано число p=16.
Для определения структуры регистра сдвига выбирают примитивный многочлен шестой степени, например
λ6+λ5+1
Для выбранного примитивного многочлена структурная схема регистра сдвига с обратной связью представлена на фиг.2.
Сформированный в блоке 1 (фиг.1) с помощью генератора случайных чисел ключ защиты длиною 6 бит
<λ6, λ5, λ4, λ3, λ2, λ1>,
где λ1=0, λ2=0, λ3=0, λ4=1, λ5=1, λ6=1;
поступает в регистр сдвига и используется для начального заполнения разрядов регистра сдвига. Двоичные символы с 5 и 6 разряда регистра сдвига поступают в каждом такте работы на вход сумматора 12 по модулю два, а с выхода сумматора по модулю два символы ε поступают на вход первого разряда регистра сдвига (блок 6, фиг.2). При этом состояния разрядов для каждого такта в процессе работы регистра сдвига определяются выражением
λi=λi-1 для 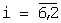 , λ1=ε
, λ1=ε
Если символы будут сниматься с шестого разряда λ6 регистра сдвига (блок 11, фиг.2), то двоичная псевдослучайная последовательность максимального периода будет иметь вид
{1110000010000110001010011110100011
100100101101110110011010101111}.
Заметим, что на периоде этой последовательности любой ненулевой набор из шести знаков 0 и 1 встречается и только один раз.
Если двоичные числа будем снимать с 1, 2, 3 и 4 разряда регистра сдвига (блоки 6, 7, 8, 9, фиг.2) и на каждом такте работы регистра сдвига с набором <λ1, λ2, λ3, λ4> будем сопоставлять двоичный вектор (число) y=λ1+2λ2+22λ3+23λ4, то последовательность двоичных чисел в процессе работы регистра можно рассматривать как последовательность y чисел (символов) {0, 1, 2,..., 15} в виде
y={8, 0, 0, 1, 2, 4, 8, 0, 1, 3, 6, 12, 8, 1, 2, 5, 10, 4, 9, 3, 7, 15, 14, 13, 10, 4, 8, 1, 3, 7, 14, 12, 9, 2, 4, 9, 2, 5, 11, 6, 13, 11, 7, 14, 13, 11, 6, 12, 9, 3, 6, 13, 10, 5, 10, 5, 11, 7, 15, 15, 15, 14, 12,...}.
Анализ сформированной последовательности y показывает, что на интервале, соответствующем периоду, равному 63 тактам работы регистра сдвига, каждый из символов {1, 2,..., 15} встречается ровно четыре раза. Символ, соответствующий нулю, встречается ровно три раза, при этом в последовательности у отсутствуют скрытые периодичности и обеспечивается статистическая равномерность используемых символов.
Поскольку в процессе работы регистра сдвига не используют такты, в которых символы y принимают четные значения, то формируется псевдослучайная последовательность чисел символов) 1, 3, 5, 7, 9, ..., 15 в виде:
x=1, 1, 3, 1, 5, 9, 3, 7, 15, 13, 1, 3, 7, 9, 9, 5, 11, 13, 11, 7, 13, 11,...
Сформированный в блоке 1 (фиг.1) ключ защиты 111000 подают в блок 2. В блоке 3 формируют псевдослучайную последовательность нечетных символов.
Сформированную псевдослучайную последовательность символов x в виде двоичных векторов подают в кодирующее устройство 4 (фиг.1), где преобразуют поступающий поток данных α в закодированное сообщение β в соответствии с выбранным криптографическим преобразованием, при этом четные символы исходного текста заменяют на нечетные, например
α=2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 11,,
α=3, 3, 5, 5, 7, 7, 9, 9, 11, 11, 13, 13, 15, 11,,
х=3, 5, 9, 7, 15, 13, 9, 11, 3, 15, 7, 9, 11, 15,,
β=11, 3, 3, 13, 7, 7, 9, 9, 3, 3, 5, 13, 1, 3,.
Для полученных значений β формируют двоичный вектор и передают с помощью устройства 5 фиг.1 на приемный конец радиолинии, при этом нечетные символы двоичного вектора β заменяют на четные для четных символов исходного текста путем замены в нулевом разряде двоичного вектора символа "1" на символ "0".
β=10, 3, 2, 13, 6, 7, 8, 9, 2, 3, 4, 13, 0, 3,.
На приемном конце радиолинии осуществляют декодирование принятой последовательности символов β в соответствии с установленным криптографическим преобразованием, при этом четные символы двоичного вектора β заменяют на нечетные путем замены в нулевом разряде двоичного вектора символа "0" на символ "1", а для найденного символа α нечетные символы заменяют на четные путем замены в нулевом разряде двоичного вектора полученного результата символа "1" на символ "0".
α≡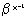 (mod16).
(mod16).
Так как p=16, k=4, то расчет х-1 осуществляют по формуле х-1≡x3(mod8). Тогда для рассмотренного примера значения соответствующих символов при декодировании сообщения будут иметь вид:
β=10, 3, 2, 13, 6, 7, 8, 9, 2, 3, 4, 13, 0, 3,.
β=11, 3, 3, 13, 7, 7, 9, 9, 3, 3, 5, 13, 1, 3,.
х=3, 5, 9, 7, 15, 13, 9, 11, 3, 15, 7, 9, 11, 15,
х-1=3, 5, 1, 7, 7, 5, 1, 3, 3, 7, 7, 1, 3, 7,
α=3, 3, 5, 5, 7, 7, 9, 9, 11, 11, 13, 13, 15, 11,,
α=2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 11,,
Реализация предлагаемого способа не вызывает затруднений, так как все блоки и узлы, входящие в устройство, реализующее способ, общеизвестны и широко описаны в технической литературе.
Источники информации
1. Российский стандарт шифрования стандарт СССР ГОСТ 28147-89 Системы обработки информации. Защита криптографическая. Алгоритм криптографического преобразования.
2. С.Мафтик. Механизмы защиты в сетях ЭВМ, М., 1993 г.
3. В.И.Нечаев. Элементы криптографии. Основы теории защиты информации, М.: Высшая школа, 1999 г.
4. В.И.Тупота. Адаптивные средства защиты информации в вычислительных сетях, - М.: Радио и связь, 2002 г.
5. Способ поточного кодирования дискретной информации. Патент на изобретение №2251816 по заявке №2003117834 от 16.06.2003 г.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ ПОТОЧНОГО КОДИРОВАНИЯ ДИСКРЕТНОЙ ИНФОРМАЦИИ | 2003 |
|
RU2251816C2 |
| СПОСОБ ПОТОЧНОГО КОДИРОВАНИЯ ДИСКРЕТНОГО СООБЩЕНИЯ | 2005 |
|
RU2281611C1 |
| СПОСОБ ПОТОЧНОГО ШИФРОВАНИЯ ДАННЫХ | 2005 |
|
RU2291578C1 |
| СПОСОБ ПОТОЧНОГО ШИФРОВАНИЯ ДАННЫХ | 2009 |
|
RU2423799C2 |
| СПОСОБ ПОТОЧНОГО КОДИРОВАНИЯ ДИСКРЕТНОЙ ИНФОРМАЦИИ | 2002 |
|
RU2205516C1 |
| СПОСОБ ПОТОЧНОГО КОДИРОВАНИЯ ДИСКРЕТНОЙ ИНФОРМАЦИИ | 2003 |
|
RU2246179C1 |
| СПОСОБ ПЕРЕДАЧИ ДИСКРЕТНОЙ ИНФОРМАЦИИ В ВЫЧИСЛИТЕЛЬНОЙ СЕТИ | 2002 |
|
RU2227375C2 |
| СПОСОБ ПОТОЧНОГО ШИФРОВАНИЯ ДАННЫХ | 2001 |
|
RU2239290C2 |
| СПОСОБ ПОТОЧНОГО КОДИРОВАНИЯ ДИСКРЕТНОЙ ИНФОРМАЦИИ | 2004 |
|
RU2270524C2 |
| СПОСОБ ПЕРЕДАЧИ ДИСКРЕТНОЙ ИНФОРМАЦИИ В РАДИОЛИНИИ С ПСЕВДОСЛУЧАЙНОЙ ПЕРЕСТРОЙКОЙ РАБОЧЕЙ ЧАСТОТЫ | 2002 |
|
RU2212105C1 |
Способ поточного кодирования дискретной информации относится к области электросвязи и вычислительной техники, а конкретнее к области способов и устройств для криптографического преобразования данных. Технический результат - повышение скорости декодирования данных и расширения диапазона изменения стойкости кода к атакам на основе известных или подобранных исходных текстов. Сущность изобретения заключается в формировании ключа защиты, подачи его для начального заполнения регистра сдвига, вырабатывающего псевдослучайную последовательность максимальной длины, формировании псевдослучайной последовательности символов, преобразовании потока данных в закодированное сообщение путем возведения символов исходного текста в степень, соответствующую символам псевдослучайной последовательности, и передачи закодированного сообщения по линии связи. В данном способе псевдослучайную последовательность формируют как псевдослучайную последовательность символов в виде двоичных векторов длиною k бит, а криптографические преобразования осуществляют в кольце класса вычетов по модулю p=2k. 1 з.п. ф-лы, 2 ил.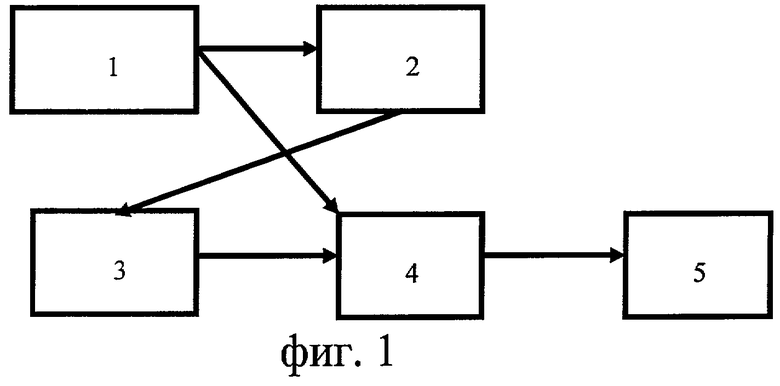
| СПОСОБ ПОТОЧНОГО КОДИРОВАНИЯ ДИСКРЕТНОЙ ИНФОРМАЦИИ | 2003 |
|
RU2251816C2 |
| СПОСОБ ПОТОЧНОГО КОДИРОВАНИЯ ДИСКРЕТНОЙ ИНФОРМАЦИИ | 2002 |
|
RU2205516C1 |
| СПОСОБ ПОТОЧНОГО КОДИРОВАНИЯ ДИСКРЕТНОЙ ИНФОРМАЦИИ | 2003 |
|
RU2246179C1 |
| US 5606616 А, 25.02.1997 | |||
| Устройство для автоматического вызова абонента | 1977 |
|
SU661843A1 |
Авторы
Даты
2007-03-27—Публикация
2005-06-29—Подача