Изобретение относится к области полупроводниковой техники и электроники, может быть использовано в научно-исследовательских институтах и технологических лабораториях.
Для измерения подвижности полупроводников в основном используется метод, основанный на эффекте Холла. Этот метод встречается с большими трудностями, когда необходимо измерять подвижность высокоомных образцов (R>107 Ом), поскольку здесь требуются очень сильные постоянные магнитные поля, а также при измерениях в магнитных материалах, так как трудно адекватно оценить, в каких реально магнитных полях происходит перемещение носителей тока в материалах со спонтанной намагниченностью. Другие непосредственные способы определения дрейфовой подвижности [1, 2], основанные на использовании световых или инжекционных зондов, от которых неравновесные неосновные носители через какое-то время доходят до запирающего контакта, что фиксируется с помощью осциллографа, как правило, требует значительно больших дрейфовых и диффузионных длин, а значит, и подвижности.
Так, в [1] описан способ определения дрейфовой подвижности, основанный на инжекции в одном конце нитевидного кристалла неосновных носителей, которые, двигаясь во внешнем электрическом поле U, доходят до коллектора, представляющего собой обратно включенный запирающий контакт. Осциллографом определяется интервал времени t между началом движения электронного пакета “наводкой от инжектирования” и приходом их к коллектору, что проявляется в виде второго пика. Зная расстояние l между точкой инжекции и коллектором определяют подвижность μ как μ=l2(tU)-1.
Для материалов с малыми подвижностями (μ<1 см2B-1с-1) приходится световой или инжекционный зонд и запирающий контакт устанавливать на очень близком расстоянии, что не исключает попадания рассеянного света в промежуток между зондом и запирающим контактом, а в случае инжекционного зонда случайных коротких замыканий.
Техническим результатом данного изобретения является разработка принципиально нового способа определения дрейфовой подвижности полупроводников, лишенного выше приведенных ограничений.
С этой целью для возбуждения неравновесных носителей была выбрана конфигурация освещения короткими импульсами из области сильного поглощения через один из электрических контактов. Схема освещения образца приведена на фиг.1а. Образец 1, к которому нанесен омический контакт 2, припаян к сапфировой пластинке 3 с нанесенным слоем индия 4. Пластинка 3 прикреплена к хладопроводу 5 оптического криостата. Прижим обеспечивался диафрагмой 6 через кварцевое стекло 7. Тонкая медная сетка 8, напыленная индием с обеих сторон, зажималась между образцом и кварцевым стеклом. Эта сетка выполняет роль прозрачного контакта. Возбуждение производилось лазером ЛГИ-21 (λ=0,337 мкм) с длительностью импульсов 10-8 с. Используя технику стробоскопического интегрирования [3], записывались формы импульсов фототока, проявляющиеся вслед за импульсами света при синхронном включении интегратора и лазера (фиг.1б). Импульсы тока имеют колоколобразную форму с резко выраженными максимальными значениями. Время tmах достижения максимального значения тока в сотни раз превышает длительность импульсов света. Как показал проведенный нами вычислительный эксперимент, это время во внешних электрических полях, приводящих к подавлению диффузионных потоков дрейфовыми, связано с подвижностью μ носителей по формуле:

где d - размер образца от контакта до контакта, U - разность потенциалов, при которой наблюдается импульс тока. Формула (1) справедлива при выполнении условия:

где lE - дрейфовая длина; lD - диффузионная длина.
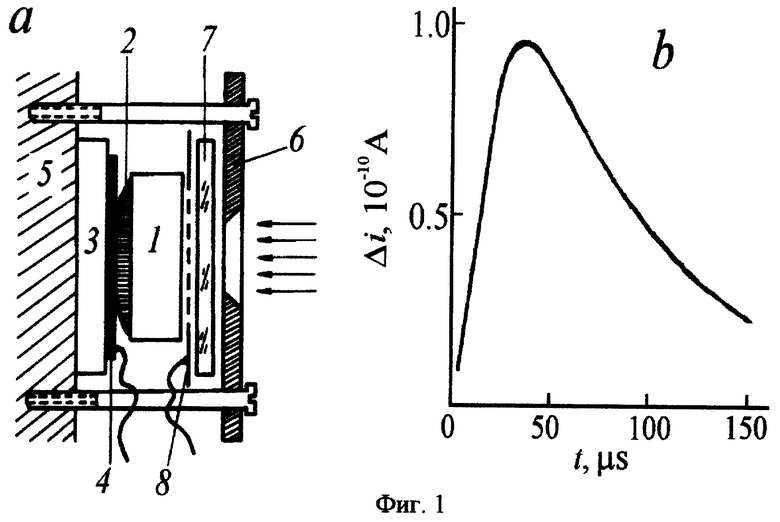
Для проведения вычислительного эксперимента формула распределения концентрации Δn неравновесных носителей при данной конфигурации и режимах возбуждения, приведенная в [4]
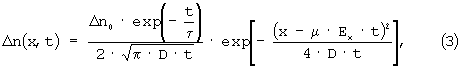
использовалась нами для нахождения тока:

где t - текущее время; х - координата, отсчитываемая от освещаемого контакта на торце образца к неосвещаемому контакту; τ - время жизни неравновесных носителей; S - площадь поперечного сечения образца; D - коэффициент диффузии; Ex - проекция напряженности электрического поля на ось x; е - величина заряда электрона.
Переходя к безразмерных величинам

выражение (4) запишем в следующем виде:

Исследовать выражение (6) аналитически не удается, так как производная от него содержит аналитически невычисляемый интеграл. Поэтому вычисления производились с использованием ЭВМ. Расчеты при дискретных значениях L и В показывают, что кривая I(T) имеет такую же форму, как и на фиг.1б, и притом зависимость времени максимума Tmax=tmax/τ от L при В≥1, то есть при условии (2), имеет линейный характер с тангенсом угла наклона 1/2:

Зависимость Tmax от В для любых L имеет форму кривой насыщения, и стационарное значение Тmax равно половине L для данной кривой.
Подставляя (5) в (7), получим выражение (1) для подвижности.
Остается выяснить, какое необходимо взять значение U, чтобы реально удовлетворялось условие (2). Для этой цели, поскольку L и В можно менять, задавая различные значения Е (5), I(Т), вычислялось при различных значениях Е, фиксировалось время Tmах и строилась зависимость Tmах(E), которая приведена на фиг.2. Здесь отметим, что μ и D задавались в соответствии с соотношением Эйнштейна:

где k - постоянная Больцмана; Θ - температура.
Основной результат вычислительного эксперимента заключался в том, что условие (2) выполняется сразу после прохождения зависимости Тmax(Е) через точку С с максимальной скоростью падения (фиг.2). Таким образом, для определения дрейфовой подвижности в реальных образцах следует записать зависимость tmax(U), выбрать значения tmах и U после самого сильного участка спада tmax(U) и по формуле (1) произвести расчет искомой величины.
На фиг.1а приведена схема ячейки для образца, используемая при освещении образца через контакт: 1 - образец, 2 - омический контакт, 3 -сапфировая пластинка, 4 - слой индия, 5 - хладопровод оптического криостата, 6 - диафрагма, 7 - кварцевое стекло, 8 - медная сетка.
На фиг.1б показана зависимость фототока от времени после попадания на образец наносекундного импульса света от лазера ЛГИ-21 при комнатной температуре.
На фиг.2 приведена зависимость безразмерного времени Tmax достижения максимального значения безразмерного тока от напряженности Е приложенного электрического поля.
Кривая, приведенная на фиг.1б, была получена для CdCr2Se4 с d=0,1 см при комнатной температуре, то есть выше точки Кюри, и при U=40 В. Максимум этой кривой приходится на tmax=36 мкс. Значение подвижности, рассчитанное по формуле (1) для этих данных, равное μ=3,47 см2В-1с-1, соответствует значению, полученному из холловских измерений μ=2,8 см2B-1c-1, что можно считать в пределах ошибок измерения достаточно хорошим совпадением.
Источники информации
1. Рывкин С.М. Фотоэлектрические явления в полупроводниках. - М.: Наука, 1963, с.347-360.
2. Haynes J.R., Shockley W. Phys. Rev., 1951, vol.81, p.835.
3. Абдуллаев А.А., Гаджиев А.З. ФТП, 1991, т.25, №1, с.30-34.
4. Зеегер К. Физика полупроводников. - М.: Мир, 1977, с.161.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ И УСТРОЙСТВО ДЛЯ ОПРЕДЕЛЕНИЯ ДЛИНЫ ДИФФУЗИИ НОСИТЕЛЕЙ ЗАРЯДА В ПОЛУПРОВОДНИКОВЫХ ПЛАСТИНКАХ | 2015 |
|
RU2578731C1 |
| ПОЛУПРОВОДНИКОВЫЙ ДЕТЕКТОР С ВНУТРЕННИМ УСИЛЕНИЕМ НА ОСНОВЕ ПОЛУИЗОЛИРУЮЩЕГО АРСЕНИДА ГАЛЛИЯ И СПОСОБ ЕГО ИЗГОТОВЛЕНИЯ | 2015 |
|
RU2586081C1 |
| Анод для фотоэлектролиза воды | 1981 |
|
SU969786A1 |
| СПОСОБ ИЗМЕРЕНИЯ ЭЛЕКТРОФИЗИЧЕСКИХ ПАРАМЕТРОВ ПОЛУПРОВОДНИКОВЫХ МАТЕРИАЛОВ | 1993 |
|
RU2079853C1 |
| Фотогальваномагнитный датчик | 1976 |
|
SU644211A2 |
| Способ измерения одномерного распределения концентрации нескомпенсированной примеси в полупроводниковом образце | 1978 |
|
SU934320A1 |
| СПОСОБ ВИЗУАЛЬНОГО ОПРЕДЕЛЕНИЯ ДРЕЙФОВОЙ ПОДВИЖНОСТИ В АЗИДАХ ТЯЖЕЛЫХ МЕТАЛЛОВ | 1993 |
|
RU2080688C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ПАРАМЕТРОВ НЕОСНОВНЫХ НОСИТЕЛЕЙ ЗАРЯДА В ПОЛУПРОВОДНИКАХ | 1989 |
|
SU1660532A1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ФОТОЭЛЕКТРИЧЕСКИХ ПАРАМЕТРОВ ВЫСОКООМНЫХ ПОЛУПРОВОДНИКОВ | 2008 |
|
RU2383081C1 |
| ОПТИЧЕСКИЙ ГЕНЕРАТОР СВЧ-ИМПУЛЬСОВ | 2009 |
|
RU2390073C1 |

Изобретение относится к области полупроводниковой техники и электроники. Предложен способ определения дрейфовой подвижности полупроводников, основанный на измерении времени достижения максимального (пикового) значения диффузионно-дрейфового тока неравновесных носителей, возбуждаемых короткими импульсами света из области сильного поглощения через один из контактов. При условии превышения дрейфового потока над диффузионным подвижность μ может быть вычислена по формуле: μ=d2(2Utmax)-1, где d - расстояние между контактами, U - приложенное напряжение, tmax - время достижения пикового значения фототока. В результате упрощаются измерения с использованием принципиально нового подхода к определению дрейфовой подвижности полупроводников. 2 ил.
Способ определения дрейфовой подвижности μЕ полупроводников, отличающийся тем, что на противоположных гранях образца в виде плоскопараллельной пластинки располагают два омических контакта, один из которых - прозрачный - выполнен в виде тонкой медной сетки, покрытой с обеих сторон слоями индия и прижатой между образцом и кварцевым стеклом с помощью диафрагмы, измеряют расстояние между контактами d (толщину образца), прилагают к контактам электрическое напряжение U, облучают образец через диафрагму и прозрачный контакт короткими (порядка 10-8 с) импульсами света из области сильного поглощения (λ=0,337 мкм), стробоскопическим методом регистрируют изменение фототока со временем, находят время tmax достижения пикового значения фототока, изменяя U строят график зависимости tmах от U до прохождения участка с максимальной скоростью его спада, выбирают выше этого участка соответствующие друг другу значения tmax и U и по формуле μЕ=d2(2Utmax)-1 вычисляют дрейфовую подвижность.
| Печь для непрерывного получения сернистого натрия | 1921 |
|
SU1A1 |
| Аппарат для очищения воды при помощи химических реактивов | 1917 |
|
SU2A1 |
| Походная разборная печь для варки пищи и печения хлеба | 1920 |
|
SU11A1 |
| Приспособление для разматывания лент с семенами при укладке их в почву | 1922 |
|
SU56A1 |
| SU 1493023, 20.01.1996 | |||
| US 5769540, 23.01.1998. | |||
Авторы
Даты
2004-11-10—Публикация
2002-08-05—Подача