Изобретение относится к области электросвязи, а именно к области систем передачи информации по цифровым каналам связи. В частности, предлагаемый способ может быть использован для передачи речевых сообщений по цифровым каналам связи со скоростью 6-16 кбит/с и может быть отнесен к классу способов кодирования формы речевого сигнала.
Известны способы кодирования речевого сигнала на основе дельта-модуляции, адаптивной дельта-модуляции, импульсно-кодовой модуляции, дифференциальной импульсно-кодовой модуляции, метода блочного кодирования с ортогональным преобразованием, см., например, книгу: М.В.Назаров, Ю.Н.Прохоров. Методы цифровой обработки и передачи цифровых сигналов. - М.: Радио и связь, 1985, с.142-160. Недостатком перечисленных выше способов-аналогов является относительно низкая информационная эффективность, под которой понимается достижение определенного качества восстановления речевой информации при заданной скорости передачи. В рассмотренных способах-аналогах приемлемое качество восстановления речевой информации достигается при скорости передачи более 16 кбит/с.
Известен также способ, описанный в патенте Великобритании №2280827 А, МПК G 10 L 3/02 от 08.02.1995, который включает дискретизацию непрерывного сигнала, квантование дискретных отсчетов, формирование матрицы квантованных отсчетов речевого сигнала, ее преобразование к цифровому виду с использованием американского стандарта сжатия JPEG, передачу цифрового потока по каналу связи, прием цифрового потока из канала связи, восстановление матрицы квантованных отсчетов речевого сигнала из цифрового потока с использованием стандарта JPEG и обратное преобразование квантованных отсчетов в непрерывный речевой сигнал. Однако недостатком этого способа является большая временная задержка речевого сигнала, что исключает возможность применения данного способа для ведения телефонных переговоров по цифровым каналам связи.
Недостатком перечисленных выше способов-аналогов также является относительно низкая устойчивость к ошибкам в цифровом канале связи. Это проявляется в существенных искажениях в восстановленном речевом сигнале при относительно малых коэффициентах ошибок, возникающих под влиянием нестабильности параметров канала связи и представляющих собой инверсию символов в передаваемых цифровых последовательностях.
Наиболее близким по своей технической сущности к заявленному способу сжатия и восстановления речевых сообщений является способ, описанный в патенте России №2152646 А, МПК G 10 L 3/02 от 10.07.2000 г.
Известный способ-прототип включает идентично выполняемую на передающей и приемной сторонах предварительную генерацию случайной квадратной матрицы размером m× m элементов, каждый элемент которой принадлежит диапазону квантованных дискретных отсчетов речевого сигнала, дискретизацию аналогового речевого сигнала, квантование дискретных отсчетов, формирование исходной матрицы размером N× N элементов, формирование прямоугольных матриц размерами N× m и m× N единичных и нулевых элементов, передачу прямоугольных матриц по каналу связи, прием их на приемной стороне из канала связи, восстановление исходной матрицы размером N× N элементов и преобразование ее в аналоговый речевой сигнал. При этом для формирования исходной матрицы ее элементам присваиваются значения квантованных дискретных отсчетов речевого сигнала.
Для формирования прямоугольных матриц размерами N× m и m× N единичных и нулевых элементов на передаче предварительно генерируют случайные прямоугольные матрицы из единичных и нулевых элементов. Затем преобразуют их. После этого вычисляют матрицу размером N× N элементов путем последовательного перемножения полученной после преобразования прямоугольной матрицы размером N× m элементов, случайной квадратной матрицы размером m× m элементов и полученной после преобразования прямоугольной матрицы размером m× N элементов. Далее вычисляют сумму квадратов разностей между элементами, полученную в результате перемножения матрицы размером N× N элементов, и элементами матрицы квантованных отсчетов речевого сигнала размером N× N элементов. Затем последовательно инвертируют каждый элемент предварительно сгенерировнных случайным образом прямоугольных матриц размером N× m и m× N элементов, выполняя при этом их преобразование, а затем перемножают полученную после преобразования прямоугольную матрицу размером N× m элементов, случайную квадратную матрицу размером m× m элементов и полученную после преобразования прямоугольную матрицу размером m× N элементов. После этого вычисляют сумму квадратов разностей между элементами полученной в результате перемножения матрицы размером N× N элементов и элементами исходной матрицы размером N× N элементов. Вычитают эту сумму от аналогичной суммы, полученной на предыдущем шаге, и в случае положительной разности сохраняют инвертированное значение элемента, а в противном случае выполняют его повторную инверсию.
Для преобразования прямоугольных матриц из единичных и нулевых элементов число элементов каждой строки прямоугольной матрицы размером N× m элементов и каждого столбца прямоугольной матрицы размером m× N элементов делят на сумму единиц соответственно в этой строке и этом столбце.
Способ-прототип позволяет при сохранении качества восстановления речевых сообщений обеспечить высокую степень сжатия передаваемой информации и снизить значение временной задержки до величины, при которой возможно ведение телефонных переговоров по низкоскоростным цифровым каналам связи.
Недостатком этого способа-прототипа является относительно низкая устойчивость к ошибкам в цифровом канале связи. Это объясняется тем, что на приемной стороне цифровые последовательности считаются принятыми без ошибок, поэтому при инверсии символов в передаваемых цифровых последовательностях под влиянием нестабильности параметров канала связи сообщения будут восстанавливаться с определенными искажениями.
Целью изобретения является разработка способа сжатия и восстановления речевых сообщений, обеспечивающего исправление ошибок, возникающих в передаваемых цифровых последовательностях под влиянием нестабильности параметров канала связи, и позволяющего осуществлять ведение телефонных переговоров по низкоскоростным цифровым каналам связи.
Поставленная цель достигается тем, что в известном способе сжатия и восстановления речевых сообщений, включающем идентично выполняемую на передающей и приемной сторонах предварительную генерацию случайной квадратной матрицы размером m× m элементов, каждый элемент которой принадлежит диапазону квантованных дискретных отсчетов речевого сигнала, дискретизацию аналогового речевого сигнала, квантование дискретных отсчетов, формирование исходной матрицы размером N× N элементов, формирование прямоугольных матриц размерами N× m и m× N единичных и нулевых элементов, передачу прямоугольных матриц по каналу связи, прием их на приемной стороне из канала связи, восстановление исходной матрицы размером N× N элементов и преобразование ее в аналоговый речевой сигнал, дополнительно предварительно на передающей и приемной сторонах идентично формируют R≥ 1 матриц разрешенных векторов размерами m2×m1 единичных и нулевых элементов, а каждую ν -ю строку, где ν =1, 2,... N, прямоугольной матрицы размером N× m элементов и каждый ν -й столбец прямоугольной матрицы размером m× N элементов формируют из значений элементов строк R матриц разрешенных векторов.
Причем формирование выполняют из условия, что длины формируемых строк 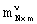 и столбцов
и столбцов  равны соответственно
равны соответственно

где номер матрицы разрешенных векторов r=1, 2,... , R;
- длина строки m1 r-й матрицы разрешенных векторов  ;
;
- количество групп элементов (далее будем называть их 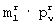 -группы) ν -й строки или ν -го столбца соответствующих матриц, формируемых из элементов строк r-й матрицы разрешенных векторов,
-группы) ν -й строки или ν -го столбца соответствующих матриц, формируемых из элементов строк r-й матрицы разрешенных векторов,  =0, 1, 2,... . При этом
=0, 1, 2,... . При этом 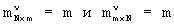 . Выбор значения
. Выбор значения  для ν -й строки прямоугольной матрицы размером N× m элементов не зависит от выбора его значения для ν -го столбца прямоугольной матрицы размером m× N элементов. На приемной стороне перед восстановлением исходной матрицы размером N× N элементов в принятых из канала связи прямоугольных матрицах размерами N× m и m× N элементов исправляют ошибки.
для ν -й строки прямоугольной матрицы размером N× m элементов не зависит от выбора его значения для ν -го столбца прямоугольной матрицы размером m× N элементов. На приемной стороне перед восстановлением исходной матрицы размером N× N элементов в принятых из канала связи прямоугольных матрицах размерами N× m и m× N элементов исправляют ошибки.
Для формирования каждой r-й матрицы разрешенных векторов размером  единичных и нулевых элементов сначала каждую i-ю строку, где i=1, 2,... ,
единичных и нулевых элементов сначала каждую i-ю строку, где i=1, 2,... ,  , r-й матрицы разрешенных векторов, формируют в виде r-й дискретной функции Уолша из упорядоченного множества
, r-й матрицы разрешенных векторов, формируют в виде r-й дискретной функции Уолша из упорядоченного множества 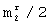 дискретных функций Уолша длины
дискретных функций Уолша длины  , где
, где  =2λ и λ =3, 4,.... В каждой сформированной строке всем элементам, равным - 1, присваивают значение 0 и затем каждую (i+
=2λ и λ =3, 4,.... В каждой сформированной строке всем элементам, равным - 1, присваивают значение 0 и затем каждую (i+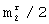 )-ю строку r-й матрицы разрешенных векторов формируют путем инверсии каждого элемента i-й строки этой же матрицы. На приемной стороне для исправления ошибок в принятых из канала связи прямоугольных матрицах размерами N× m и m× N элементов последовательно выбирают каждую
)-ю строку r-й матрицы разрешенных векторов формируют путем инверсии каждого элемента i-й строки этой же матрицы. На приемной стороне для исправления ошибок в принятых из канала связи прямоугольных матрицах размерами N× m и m× N элементов последовательно выбирают каждую 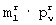 -группу элементов каждой ν -й строки принятой прямоугольной матрицы размером N× m и каждую
-группу элементов каждой ν -й строки принятой прямоугольной матрицы размером N× m и каждую  -группу элементов каждого ν -го столбца принятой прямоугольной матрицы размером m× N элементов. Затем определяют j-ю строку, где j=1, 2,... ,
-группу элементов каждого ν -го столбца принятой прямоугольной матрицы размером m× N элементов. Затем определяют j-ю строку, где j=1, 2,... ,  , r-й матрицы разрешенных векторов, у которой расстояние Хэмминга от выбранной
, r-й матрицы разрешенных векторов, у которой расстояние Хэмминга от выбранной  -группы минимально, и если минимальное расстояние Хэмминга меньше величины
-группы минимально, и если минимальное расстояние Хэмминга меньше величины  , то каждому элементу выбранной
, то каждому элементу выбранной  -группы присваивают значение соответствующего элемента j-й строки r-й матрицы разрешенных векторов, иначе выбранную
-группы присваивают значение соответствующего элемента j-й строки r-й матрицы разрешенных векторов, иначе выбранную  -группу элементов принятых из канала связи прямоугольных матриц сохраняют неизменной.
-группу элементов принятых из канала связи прямоугольных матриц сохраняют неизменной.
Для формирования прямоугольных матриц размерами N× m и m× N элементов, у которых соответственно строки и столбцы сформированы из значений элементов строк R матриц разрешенных векторов, на передающей и приемной сторонах идентично генерируют случайные ключевые матрицы размерами N× m и m× N единичных и нулевых элементов и случайный вектор из m элементов, каждый элемент которого принадлежит диапазону квантованных дискретных отсчетов речевого сигнала. Затем каждому элементу каждой  -группы каждой ν -й строки прямоугольной матрицы размером N× m элементов и каждой
-группы каждой ν -й строки прямоугольной матрицы размером N× m элементов и каждой  -группы каждого ν -го столбца прямоугольной матрицы размером mxN элементов присваивают значение соответствующего элемента первой строки r-й матрицы разрешенных векторов, после чего формируют суммарные матрицы размерами N× m и m× N элементов путем суммирования по модулю два элементов прямоугольных матриц размерами N× m и m× N элементов с соответствующими элементами ключевых матриц размерами N× m и m× N элементов соответственно. Далее преобразуют полученные суммарные матрицы размерами N× m и m× N элементов путем деления элементов каждой строки суммарной матрицы размером N× m элементов на сумму единиц соответствующей строки и деления элементов каждого столбца суммарной матрицы размером m× N элементов на сумму единиц соответствующего столбца. Затем формируют промежуточную матрицу размером N× N элементов путем перемножения диагональной матрицы, у которой каждый nn-й диагональный элемент равен сумме произведений элементов n-й строки, где n=1, 2,... , N, суммарной матрицы размером N× m элементов на соответствующие элементы случайного вектора из m элементов, а остальные элементы равны нулю, с полученной после преобразования суммарной матрицей размером N× m элементов, с ранее идентично сформированной на передающей и приемной сторонах случайной квадратной матрицей размером m× m элементов, с полученной после преобразования суммарной матрицей размером m× N элементов и с диагональной матрицей, у которой каждый nn-й диагональный элемент равен сумме произведений элементов случайного вектора из m элементов на соответствующие элементы n-го столбца суммарной матрицы размером m× N элементов, а остальные элементы равны нулю. После перемножения матриц вычисляют показатель ошибки в виде суммы квадратов разностей между элементами полученной в результате перемножения промежуточной матрицы размером N× N элементов и соответствующими элементами исходной матрицы размером N× N. Затем выполняют итерационный цикл. Для этого последовательно в каждой
-группы каждого ν -го столбца прямоугольной матрицы размером mxN элементов присваивают значение соответствующего элемента первой строки r-й матрицы разрешенных векторов, после чего формируют суммарные матрицы размерами N× m и m× N элементов путем суммирования по модулю два элементов прямоугольных матриц размерами N× m и m× N элементов с соответствующими элементами ключевых матриц размерами N× m и m× N элементов соответственно. Далее преобразуют полученные суммарные матрицы размерами N× m и m× N элементов путем деления элементов каждой строки суммарной матрицы размером N× m элементов на сумму единиц соответствующей строки и деления элементов каждого столбца суммарной матрицы размером m× N элементов на сумму единиц соответствующего столбца. Затем формируют промежуточную матрицу размером N× N элементов путем перемножения диагональной матрицы, у которой каждый nn-й диагональный элемент равен сумме произведений элементов n-й строки, где n=1, 2,... , N, суммарной матрицы размером N× m элементов на соответствующие элементы случайного вектора из m элементов, а остальные элементы равны нулю, с полученной после преобразования суммарной матрицей размером N× m элементов, с ранее идентично сформированной на передающей и приемной сторонах случайной квадратной матрицей размером m× m элементов, с полученной после преобразования суммарной матрицей размером m× N элементов и с диагональной матрицей, у которой каждый nn-й диагональный элемент равен сумме произведений элементов случайного вектора из m элементов на соответствующие элементы n-го столбца суммарной матрицы размером m× N элементов, а остальные элементы равны нулю. После перемножения матриц вычисляют показатель ошибки в виде суммы квадратов разностей между элементами полученной в результате перемножения промежуточной матрицы размером N× N элементов и соответствующими элементами исходной матрицы размером N× N. Затем выполняют итерационный цикл. Для этого последовательно в каждой  -группе элементов прямоугольных матриц одновременно всем элементам присваивают значения соответствующих элементов поочередно каждой j-и строки r-й матрицы разрешенных векторов, при этом остальные
-группе элементов прямоугольных матриц одновременно всем элементам присваивают значения соответствующих элементов поочередно каждой j-и строки r-й матрицы разрешенных векторов, при этом остальные  -группы сохраняют неизменными, и формируют суммарные матрицы размерами N× m и m× N элементов путем суммирования по модулю два элементов полученных после изменения элементов
-группы сохраняют неизменными, и формируют суммарные матрицы размерами N× m и m× N элементов путем суммирования по модулю два элементов полученных после изменения элементов 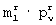 -группы прямоугольных матриц размерами N× m и m× N элементов с соответствующими элементами ключевых матриц размерами N× m и m× N элементов соответственно. Полученные суммарные матрицы размерами N× m и m× N элементов преобразуют путем деления элементов каждой строки суммарной матрицы размером N× m элементов на сумму единиц соответствующей строки и деления элементов каждого столбца суммарной матрицы размером m× N элементов на сумму единиц соответствующего столбца. Далее формируют промежуточную матрицу размером N× N элементов путем перемножения диагональной матрицы, у которой каждый nn-й диагональный элемент сумме произведений элементов n-й строки суммарной матрицы размером N× m элементов на соответствующие элементы случайного вектора из m элементов, а остальные элементы равны нулю, с полученной после преобразования суммарной матрицей размером Nxm элементов, с ранее идентично сформированной на передающей и приемной сторонах случайной квадратной матрицей размером m× m элементов, с полученной после преобразования суммарной матрицей размером m× N элементов и с диагональной матрицей, у которой каждый nn-й диагональный элемент равен сумме произведений элементов случайного вектора из m элементов на соответствующие элементы n-го столбца суммарной матрицы размером m× N элементов, а остальные элементы равны нулю. Затем вычисляют показатель ошибки в виде суммы квадратов разностей между элементами полученной в результате перемножения промежуточной матрицы размером N× N элементов и соответствующими элементами исходной матрицы размером N× N элементов и вычитают вычисленное значение показателя ошибки из его ранее вычисленного значения. Если полученная разность больше нуля, то сохраняют новые значения элементов изменяемой
-группы прямоугольных матриц размерами N× m и m× N элементов с соответствующими элементами ключевых матриц размерами N× m и m× N элементов соответственно. Полученные суммарные матрицы размерами N× m и m× N элементов преобразуют путем деления элементов каждой строки суммарной матрицы размером N× m элементов на сумму единиц соответствующей строки и деления элементов каждого столбца суммарной матрицы размером m× N элементов на сумму единиц соответствующего столбца. Далее формируют промежуточную матрицу размером N× N элементов путем перемножения диагональной матрицы, у которой каждый nn-й диагональный элемент сумме произведений элементов n-й строки суммарной матрицы размером N× m элементов на соответствующие элементы случайного вектора из m элементов, а остальные элементы равны нулю, с полученной после преобразования суммарной матрицей размером Nxm элементов, с ранее идентично сформированной на передающей и приемной сторонах случайной квадратной матрицей размером m× m элементов, с полученной после преобразования суммарной матрицей размером m× N элементов и с диагональной матрицей, у которой каждый nn-й диагональный элемент равен сумме произведений элементов случайного вектора из m элементов на соответствующие элементы n-го столбца суммарной матрицы размером m× N элементов, а остальные элементы равны нулю. Затем вычисляют показатель ошибки в виде суммы квадратов разностей между элементами полученной в результате перемножения промежуточной матрицы размером N× N элементов и соответствующими элементами исходной матрицы размером N× N элементов и вычитают вычисленное значение показателя ошибки из его ранее вычисленного значения. Если полученная разность больше нуля, то сохраняют новые значения элементов изменяемой 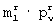 -группы и показателя ошибки, иначе сохраняют предыдущие значения элементов изменяемой
-группы и показателя ошибки, иначе сохраняют предыдущие значения элементов изменяемой 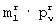 -группы прямоугольных матриц и показателя ошибки. Затем последнее сохраненное в итерационном цикле значение показателя ошибки вычитают из последнего значения показателя ошибки, полученного до начала этого итерационного цикла, и если полученная разность больше нуля, то итерационный цикл повторяют. Сформированные в результате ряда итераций прямоугольные матрицы размерами N× m и m× N элементов передаются по каналу связи. На приемной стороне для восстановления исходной матрицы размером N× N элементов формируют суммарные матрицы размерами N× m и m× N элементов путем суммирования по модулю два элементов принятых из канала связи и исправленных прямоугольных матриц размерами N× m и m× N элементов с соответствующими элементами ключевых матриц размерами N× m и m× N элементов соответственно. Затем преобразуют полученные суммарные матрицы размерами N× m и m× N элементов путем деления элементов каждой строки суммарной матрицы размером N× m элементов на сумму единиц соответствующей строки и деления элементов каждого столбца суммарной матрицы размером mxN элементов на сумму единиц соответствующего столбца. Далее перемножают диагональную матрицу, у которой каждый nn-й диагональный элемент равен сумме произведений элементов n-й строки суммарной матрицы размером N× m элементов на соответствующие элементы случайного вектора из m элементов, а остальные элементы равны нулю, с полученной после преобразования суммарной матрицей размером N× m элементов, с ранее идентично сформированной на передающей и приемной сторонах случайной квадратной матрицей размером m× m элементов, с полученной после преобразования суммарной матрицей размером m× N элементов и с диагональной матрицей, у которой каждый nn-й диагональный элемент равен сумме произведений элементов случайного вектора из m элементов на соответствующие элементы n-го столбца суммарной матрицы размером mxN элементов, а остальные элементы равны нулю.
-группы прямоугольных матриц и показателя ошибки. Затем последнее сохраненное в итерационном цикле значение показателя ошибки вычитают из последнего значения показателя ошибки, полученного до начала этого итерационного цикла, и если полученная разность больше нуля, то итерационный цикл повторяют. Сформированные в результате ряда итераций прямоугольные матрицы размерами N× m и m× N элементов передаются по каналу связи. На приемной стороне для восстановления исходной матрицы размером N× N элементов формируют суммарные матрицы размерами N× m и m× N элементов путем суммирования по модулю два элементов принятых из канала связи и исправленных прямоугольных матриц размерами N× m и m× N элементов с соответствующими элементами ключевых матриц размерами N× m и m× N элементов соответственно. Затем преобразуют полученные суммарные матрицы размерами N× m и m× N элементов путем деления элементов каждой строки суммарной матрицы размером N× m элементов на сумму единиц соответствующей строки и деления элементов каждого столбца суммарной матрицы размером mxN элементов на сумму единиц соответствующего столбца. Далее перемножают диагональную матрицу, у которой каждый nn-й диагональный элемент равен сумме произведений элементов n-й строки суммарной матрицы размером N× m элементов на соответствующие элементы случайного вектора из m элементов, а остальные элементы равны нулю, с полученной после преобразования суммарной матрицей размером N× m элементов, с ранее идентично сформированной на передающей и приемной сторонах случайной квадратной матрицей размером m× m элементов, с полученной после преобразования суммарной матрицей размером m× N элементов и с диагональной матрицей, у которой каждый nn-й диагональный элемент равен сумме произведений элементов случайного вектора из m элементов на соответствующие элементы n-го столбца суммарной матрицы размером mxN элементов, а остальные элементы равны нулю.
Для формирования исходной матрицы размером NxN элементов предварительно формируют вектор спектральных коэффициентов из z элементов, где z≥ N2, путем дискретного косинусного преобразования z квантованных дискретных отсчетов речевого сигнала и выбирают N2 элементов вектора спектральных коэффициентов, из которых формируют исходную матрицу. При этом каждому ее элементу Аkl, где k=1, 2,... , N и l=1, 2,... , N, присваивают значение h-го элемента вектора спектральных коэффициентов из z элементов, h-й номер которого определяют в соответствии с выражением: h=k+N· (l-1)+g, где g=0, 1,... , 10. На приемной стороне для преобразования восстановленной исходной матрицы размером N× N элементов в аналоговый речевой сигнал сначала преобразуют восстановленную исходную матрицу в вектор из z спектральных коэффициентов, у которого значения N2 элементов равны значениям элементов восстановленной исходной матрицы размером N× N элементов, а остальные z-N2 элементов равны нулю, и затем восстанавливают аналоговый речевой сигнал путем обратного дискретного косинусного преобразования полученного вектора из z спектральных коэффициентов.
Благодаря новой совокупности существенных признаков за счет использования при цифровом представлении речевых сообщений только разрешенных комбинаций единичных и нулевых элементов обеспечивается возможность исправления большого числа ошибок, возникающих в цифровых последовательностях под влиянием нестабильности параметров канала связи. Использование для формирования исходной матрицы N2 спектральных коэффициентов позволяет при введенных ограничениях на разрешенность комбинаций единичных и нулевых элементов обеспечить высокую степень сжатия. А за счет использования случайных ключевых матриц и диагональных матриц для формирования прямоугольных матриц, передаваемых по каналу связи, и восстановления исходной матрицы на приемной стороне при заданной пропускной способности канала связи в условиях отсутствия ошибок в принимаемых цифровых последовательностях обеспечивается минимальное снижение качества восстановленных сообщений.
Таким образом, предлагаемый способ для заданной пропускной способности канала связи позволяет исправлять возникающие ошибки и тем самым существенно повысить качество восстановленной речи при передаче цифровых последовательностей по каналу с ошибками.
Проведенный анализ уровня техники позволил установить, что аналоги, характеризующиеся совокупностью признаков, тождественными всем признакам заявленного технического решения, отсутствуют, что указывает на соответствие заявленного способа условию патентоспособности “новизна”. Результаты поиска известных решений в данной и смежных областях техники с целью выявления признаков, совпадающих с отличительными от прототипа признаками заявленного способа, показали, что они не следуют явным образом из уровня техники. Из уровня техники также не выявлена известность влияния предусматриваемых существенными признаками заявленного изобретения преобразований на достижение указанного технического результата. Следовательно, заявленное изобретение соответствует условию патентоспособности “изобретательский уровень”.
Заявленный способ поясняется чертежами:
- Фиг.1. Последовательность преобразований аналогового речевого сигнала в исходную матрицу [A]N× N;
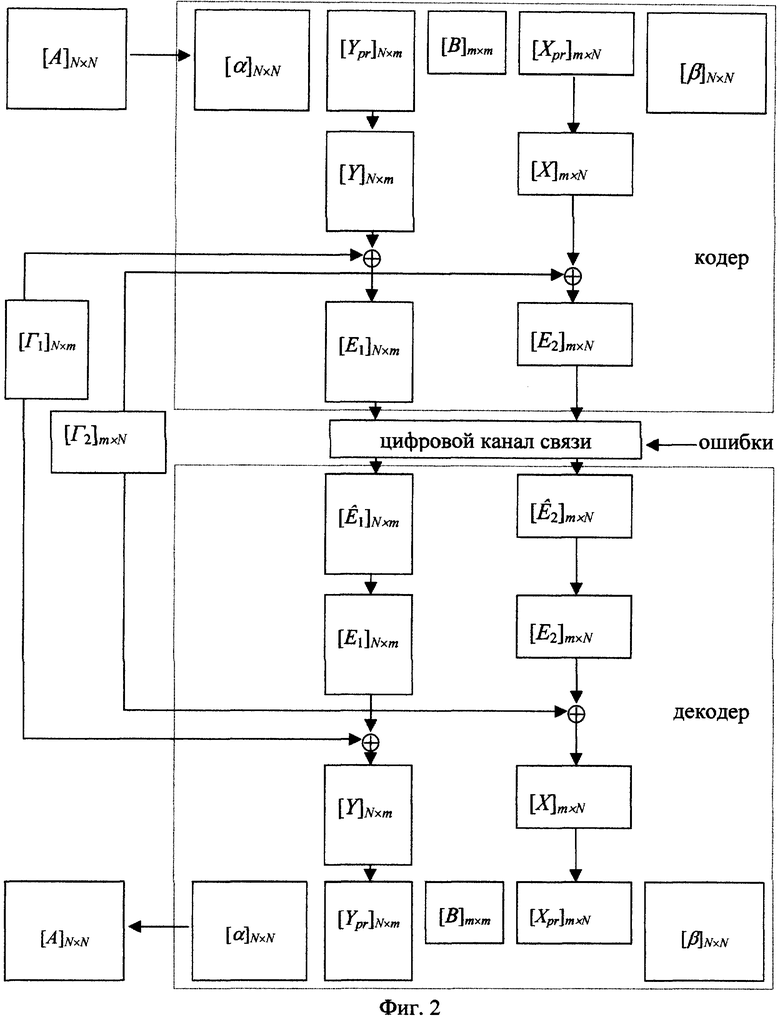
- Фиг.2. Последовательность преобразований исходной матрицы [A]N× N к цифровому виду и обратное преобразование принятого из канала связи цифрового потока в исходную матрицу;
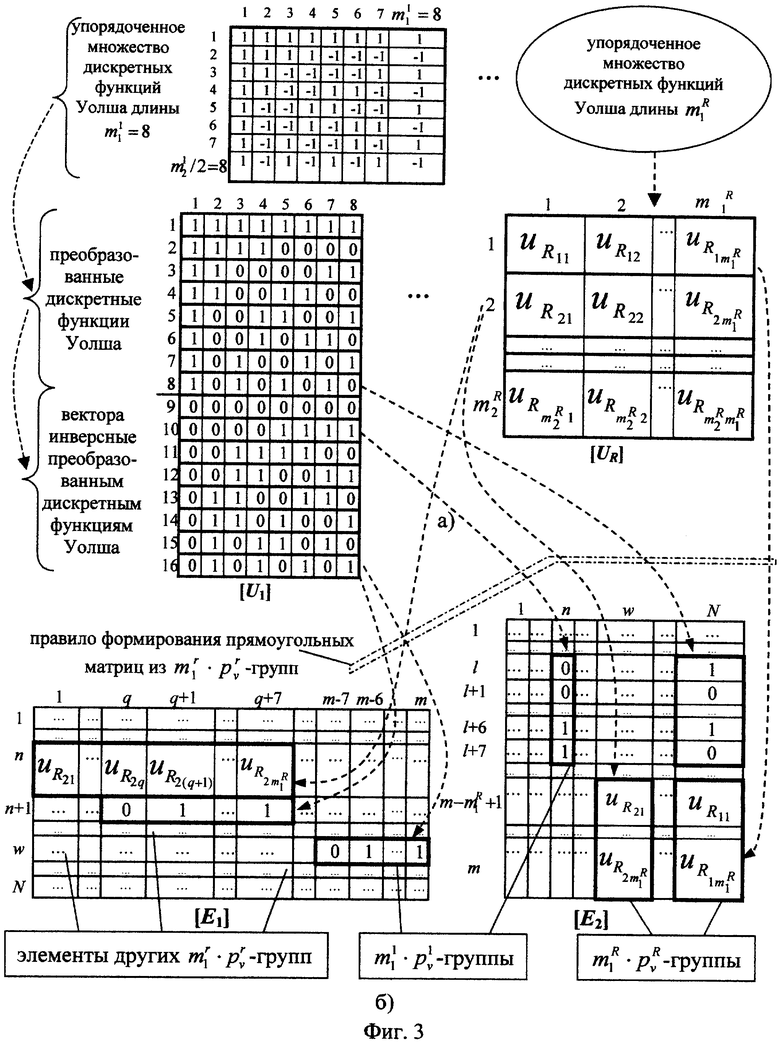
- Фиг.3. Структура матриц разрешенных векторов  и
и
прямоугольных матриц [E1]N× m и [E2]m× N;
- Фиг.4. Структура суммарных матриц [Y]N× m, [X]m× N и преобразованных суммарных матриц [Ypr]N× m, [Xpr]m× N,
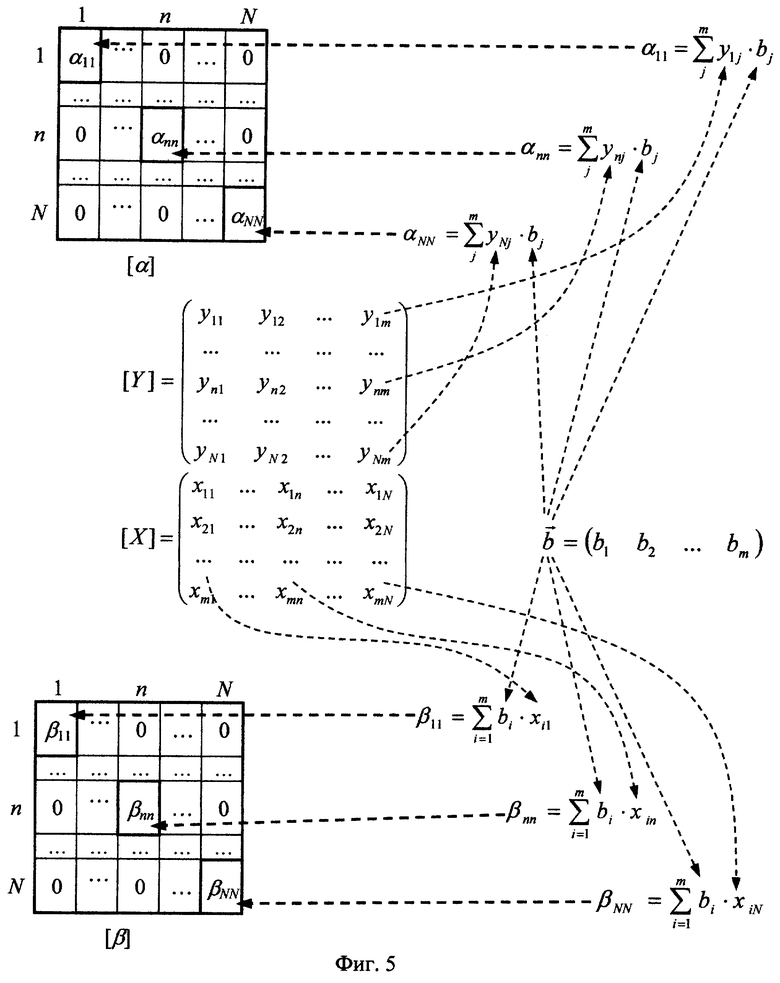
-Фиг.5. Структура диагональных матриц [α ]N× N и [β ]N× N;
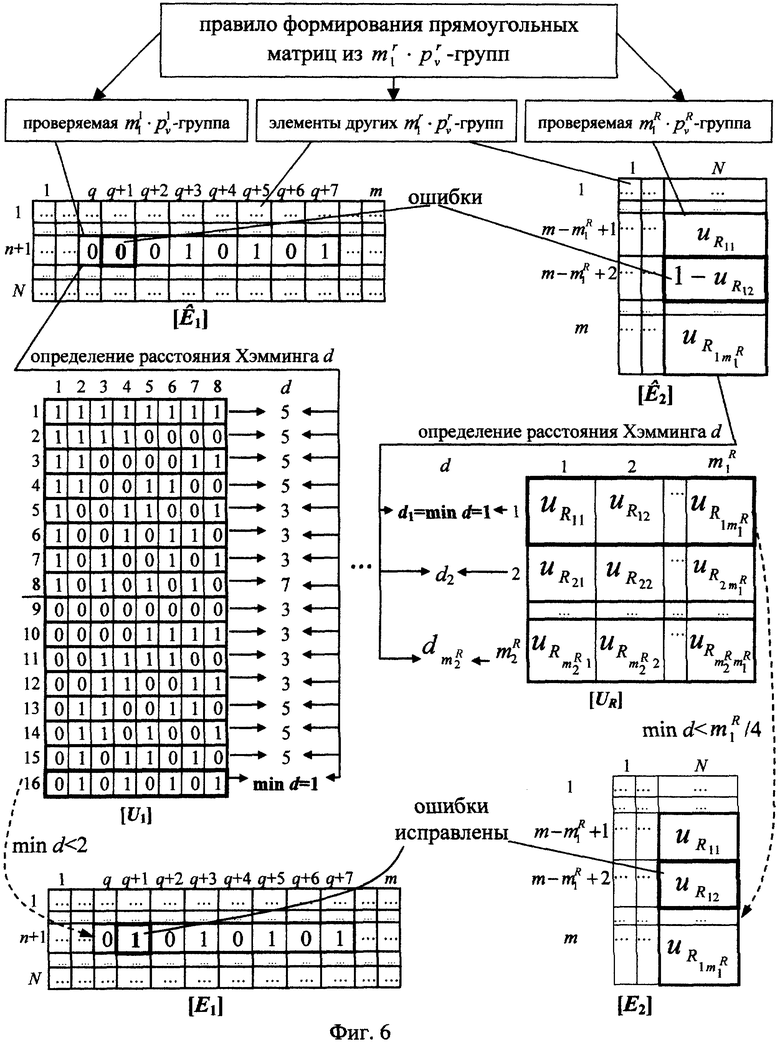
- Фиг.6. Исправление ошибок в принятых из канала связи прямоугольных матрицах;
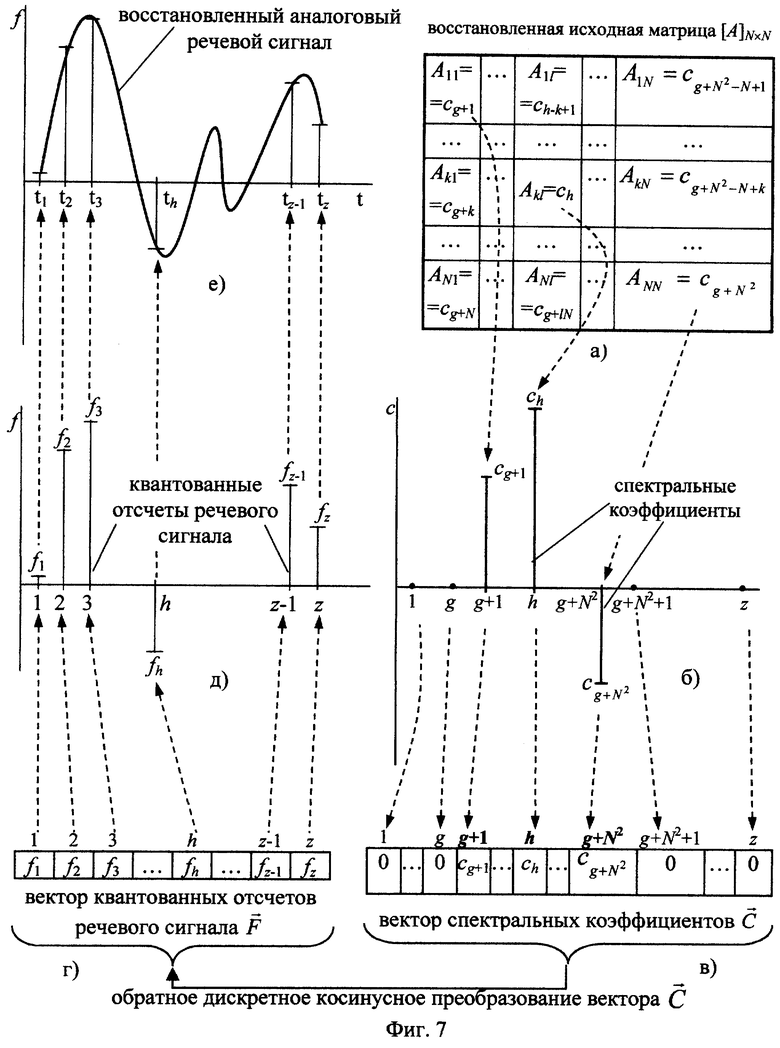
- Фиг.7. Последовательность преобразований восстановленной исходной матрицы [А]N× N в непрерывный речевой сигнал;
- Фиг.8. Последовательная оптимизация элементов прямоугольных матриц [Е1]N× m и [E2]m× N (в приложении 1).
Возможность реализации заявленного способа сжатия и восстановления речевых сообщений при сохранении хорошего качества восстановления (разборчивости и узнаваемости речи) объясняется следующим. Существует традиционный подход повышения устойчивости к ошибкам в цифровом канале связи путем использования помехоустойчивых кодов, описанных, например, в книге: У.Питерсон, Э.Уэлдон. Коды, исправляющие ошибки. - М.: Мир, 1976. Он основан на разделении всех возможных кодовых комбинаций на разрешенные и запрещенные. Такой подход предполагает введение в передаваемую цифровую последовательность дополнительных бит, и чем больше ошибок может исправлять код, тем больше вводится дополнительных бит. Это приводит к существенному снижению степени сжатия передаваемой информации и соответственно повышению требований к пропускной способности канала связи.
Однако ввиду большой избыточности речи как вида информации и адаптивного характера кодирования, используемого в предлагаемом способе, при сохранении приемлемого качества восстановленной речи возможно ввести существенные ограничения на разрешенность комбинаций элементов цифровых последовательностей с целью исправления ошибок. При этом кардинальным отличием такого подхода от помехоустойчивого кодирования является то, что дополнительные биты не вводятся и все элементы передаваемой цифровой последовательности являются информационными.
Формирование исходной матрицы размером N× N элементов возможно реализовать так же, как предлагается в способе-прототипе, где исходная матрица формируется непосредственно из квантованных речевых отсчетов. Однако в этом случае при заданном качестве восстановленной речи и отсутствии ошибок в канале связи произойдет некоторое увеличение требуемой пропускной способности канала по сравнению со способом-прототипом. Для предотвращения такого увеличения в предлагаемом способе выполняется дискретное косинусное преобразование над вектором квантованных отсчетов речевого сигнала. Это позволяет осуществить переход к представлению речевого сигнала в виде вектора спектральных коэффициентов (фиг.1,г). Для уменьшения цифрового представления речевого сигнала кодируют и передают не все, а только N2 спектральных коэффициентов, суммарная энергия которых значительно больше суммарной энергии остальных z-N2 спектральных коэффициентов (фиг.1,д).
Аналогично способу-прототипу при кодировании и восстановлении исходной матрицы возможно использовать непосредственно передаваемые по каналу связи прямоугольные матрицы размерами N× m и m× N элементов, учитывая при их формировании введенные ограничения на разрешенность комбинаций элементов. Однако при этом выравнивание требуемой пропускной способности канала связи путем использования не всех спектральных коэффициентов сохраняет некоторое снижение качества восстановленных речевых сообщений по сравнению со способом-прототипом при передаче цифровых последовательностей по каналу связи без ошибок. Это обусловлено как потерями качества при кодировании и передаче не всех спектральных коэффициентов, так и введенными ограничениями. Для минимизации снижения качества в предлагаемом способе непосредственное кодирование и восстановление исходной матрицы осуществляется не с помощью передаваемых по цифровому каналу связи прямоугольных матриц, а с помощью суммарных матриц той же размерности, полученных путем "сложения по модулю два" прямоугольных матриц и случайных ключевых матриц (фиг.2). При этом каждая суммарная матрица после преобразования умножается на соответствующую диагональную матрицу, в которой диагональные элементы имеют смысл коэффициента усиления. Это позволяет при кодировании исходной матрицы использовать в суммарных матрицах все возможные комбинации единичных и нулевых элементов.
Предлагаемый способ предполагает проведение следующих действий.
На передаче и на приеме идентично формируют R матриц разрешенных векторов [Ur] размерами 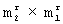 . Формирование этих матриц проиллюстрировано фиг.3,а, где в качестве примера взят случай, когда длина строк первой матрицы разрешенных векторов
. Формирование этих матриц проиллюстрировано фиг.3,а, где в качестве примера взят случай, когда длина строк первой матрицы разрешенных векторов 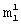 =8. Каждая i-я строка, где i=1, 2,... ,
=8. Каждая i-я строка, где i=1, 2,... ,  , r-й матрицы разрешенных векторов (для первой матрицы
, r-й матрицы разрешенных векторов (для первой матрицы  =8) является i-й дискретной функцией Уолша из упорядоченного множества дискретных функций Уолша длины
=8) является i-й дискретной функцией Уолша из упорядоченного множества дискретных функций Уолша длины 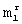 , в которой элементы, равные - 1, заменены на нулевые (преобразованные дискретные функции Уолша).
, в которой элементы, равные - 1, заменены на нулевые (преобразованные дискретные функции Уолша).  =8. Каждая (i+
=8. Каждая (i+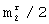 )-я строка r-й матрицы разрешенных векторов получаются инверсией элементов i-й строки этой же матрицы (вектора, инверсные преобразованным дискретным функциям Уолша).
)-я строка r-й матрицы разрешенных векторов получаются инверсией элементов i-й строки этой же матрицы (вектора, инверсные преобразованным дискретным функциям Уолша).
Используемые при формировании матриц разрешенных векторов функции Уолша, их дискретизация и упорядочение описаны, например, в книге: И.Ахмед, К.Р.Рао. Ортогональные преобразования при обработке цифровых сигналов. - М.: Радио и связь, 1980, с.86-89. Выбор одного из возможных упорядочений (например, по Уолшу, по Пэли, по Адамару) не является принципиальным. Поскольку сами функции при любом упорядочении остаются неизменными, то упорядоченность может быть любой, следовательно, в каждой r-й матрице разрешенных векторов преобразованные дискретные функции Уолша длины  могут быть заполнением любой строки из первых
могут быть заполнением любой строки из первых 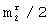 , но только одной. Соответственно значение
, но только одной. Соответственно значение 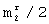 определяет общее количество всех возможных функций Уолша длины
определяет общее количество всех возможных функций Уолша длины 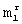 .
.
Формирование случайной квадратной матрицы [В]m× m и случайного вектора  может быть выполнено на основе датчика случайных чисел, например на основе шумового диода. Для выполнения требования идентичности матрицы [В]m× m и вектора
может быть выполнено на основе датчика случайных чисел, например на основе шумового диода. Для выполнения требования идентичности матрицы [В]m× m и вектора 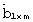 приемника, аналогичных матрице и вектору передатчика, перед началом каждого сеанса связи элементы матрицы [B]m× m и вектора
приемника, аналогичных матрице и вектору передатчика, перед началом каждого сеанса связи элементы матрицы [B]m× m и вектора 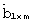 могут быть сгенерированы на передаче и переданы по цифровому каналу связи на приемную сторону, например, в составе синхропосылки.
могут быть сгенерированы на передаче и переданы по цифровому каналу связи на приемную сторону, например, в составе синхропосылки.
Дискретизацию аналогового речевого сигнала (фиг.1,а) выполняют в соответствии с теоремой Котельникова. В предлагаемом способе выбрана общепринятая частота дискретизации аналогового речевого сигнала 8 кГц. Затем выполняют квантование дискретных отсчетов (фиг.1,б). Квантование осуществляется на основе способов, описанных, например, в книге: М.В.Назаров, Ю.Н.Прохоров. Методы цифровой обработки и передачи цифровых сигналов. - М.: Радио и связь, 1985, с.142-160.
Далее на основе множества квантованных дискретных отсчетов речевого сигнала формируют вектор квантованных отсчетов речевого сигнала  (фиг.1,в) из z элементов fh, где h=1, 2, 3,... , z и fh, равно амплитуде h-го квантованного отсчета речевого сигнала. Для преобразования вектора квантованных отсчетов речевого сигнала с целью уменьшения объема информации, передаваемой по каналу связи, используют дискретное косинусное преобразование, описанное, например, в книге: Н.Ахмед, К.Р.Рао. Ортогональные преобразования при обработке цифровых сигналов. - М.: Связь, 1980, с.156-159.
(фиг.1,в) из z элементов fh, где h=1, 2, 3,... , z и fh, равно амплитуде h-го квантованного отсчета речевого сигнала. Для преобразования вектора квантованных отсчетов речевого сигнала с целью уменьшения объема информации, передаваемой по каналу связи, используют дискретное косинусное преобразование, описанное, например, в книге: Н.Ахмед, К.Р.Рао. Ортогональные преобразования при обработке цифровых сигналов. - М.: Связь, 1980, с.156-159.
В результате выполнения дискретного косинусного преобразования над вектором квантованных отсчетов речевого сигнала получают вектор квантованных спектральных коэффициентов 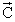 (фиг.1,г) из z элементов сh, где ch равно амплитуде h-го спектрального коэффициента. Затем выбирают N2 элементов вектора коэффициентов дискретного косинусного преобразования, суммарная энергия которых значительно больше суммарной энергии остальных z-N2 спектральных коэффициентов (фиг.1,д), и из выбранных коэффициентов формируют исходную матрицу (фиг.1,е). Поскольку амплитуды сh, распределены таким образом, что спектральные коэффициенты с наибольшей энергией расположены в основном в левой части вектора, то каждому элементу исходной матрицы Аkl, где k=1, 2,... , N и l=1, 2,... , N, присваивают значение h-го элемента вектора коэффициентов дискретно-косинусного преобразования из z элементов, h-й номер которого определяют в соответствии с выражением: h=k+N· (1-1)+g, где g=0, 1,... , 10 (фиг.1.д-е).
(фиг.1,г) из z элементов сh, где ch равно амплитуде h-го спектрального коэффициента. Затем выбирают N2 элементов вектора коэффициентов дискретного косинусного преобразования, суммарная энергия которых значительно больше суммарной энергии остальных z-N2 спектральных коэффициентов (фиг.1,д), и из выбранных коэффициентов формируют исходную матрицу (фиг.1,е). Поскольку амплитуды сh, распределены таким образом, что спектральные коэффициенты с наибольшей энергией расположены в основном в левой части вектора, то каждому элементу исходной матрицы Аkl, где k=1, 2,... , N и l=1, 2,... , N, присваивают значение h-го элемента вектора коэффициентов дискретно-косинусного преобразования из z элементов, h-й номер которого определяют в соответствии с выражением: h=k+N· (1-1)+g, где g=0, 1,... , 10 (фиг.1.д-е).
Далее (фиг.2) исходную матрицу [A]N× N кодируют, передают множество единичных и нулевых элементов прямоугольных матриц [Е1]N× m и [E2]m× N по каналу связи, на приемной стороне исправляют ошибки в принятых матрицах  и
и 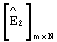 , а затем восстанавливают исходную матрицу.
, а затем восстанавливают исходную матрицу.
Для кодирования исходную матрицу [A]N× N в кодере представляют в виде произведения пяти матриц (фиг.2): диагональной матрицы [α ]N× N, преобразованной суммарной матрицы [Ypr]N× m, случайной квадратной матрицы [B]m× m, преобразованной суммарной матрицы [Xpr]m× N, диагональной матрицы [β ]N× N.При этом необходимо найти такие оптимальные матрицы [Ypr]N× m и [Xpr]m× N, которые при перемножении с матрицей [B]m× m образуют некоторую восстановленную исходную матрицу размером N× N элементов, наиболее близкую по заданному критерию к исходной матрице.
Особенностью матриц [Ypr]N× m и [Xpr]m× N является то, что они могут быть легко приведены к цифровому виду. Это достигается тем, что на элементы этих матриц накладываются следующие ограничения:
- элементы матриц [Ypr]N× m и [Xpr]m× N принимают значения в диапазоне от нуля до единицы;
- ненулевые элементы каждой строки матрицы [Ypr]N× m равны между собой и в сумме образуют единицу;
- ненулевые элементы каждого столбца матрицы [Xpr]m× N равны между собой и в сумме образуют единицу.
При таких ограничениях, если элементы каждой строки матрицы [Ypr]N× m умножить на количество ненулевых элементов в этой строке, то будет получена матрица [Y]N× m, элементы которой определены только на множестве "1" и "0". Аналогично, если элементы каждого столбца матрицы [Xpr]m× N умножить на количество ненулевых элементов в столбце, то будет получена матрица [X]m× N, элементы которой определены только на множестве "1" и "0". Следовательно, верно и обратное утверждение: элементы  , матриц [Ypr]N× m и [Xpr]m× N получаются из элементов yij, xij матриц [Ypr]N× m и [Xpr]m× N (фиг.4,б) согласно формулам:
, матриц [Ypr]N× m и [Xpr]m× N получаются из элементов yij, xij матриц [Ypr]N× m и [Xpr]m× N (фиг.4,б) согласно формулам:

При этом первый индекс показывает номер строки, а второй - номер столбца соответствующих матриц.
Диагональные матрицы [α ]N× N и [β ]N× N формируются следующим образом (фиг.5). Каждый nn-й элемент диагональной матрицы [α ]N× N, где n=1, 2,... , N, получается из элементов уnj n-й строки матрицы [Y]N× m, и элементов bj случайного вектора  по формуле:
по формуле: . Каждый nn-й элемент диагональной матрицы [β ]N× N получается из элементов bj случайного вектора
. Каждый nn-й элемент диагональной матрицы [β ]N× N получается из элементов bj случайного вектора 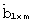 и элементов хin n-го столбца матрицы [X]m× N, по формуле:
и элементов хin n-го столбца матрицы [X]m× N, по формуле: 
Поскольку по каналу связи передаются прямоугольные матрицы [E1]N× m и [Е2]m× N, сформированные по некоторому правилу только из разрешенных комбинаций элементов (фиг.3.б, приложение 1), а не матрицы [Y]N× m и [X]m× N, которые непосредственно кодируют исходную матрицу, то взаимосвязь этих матриц осуществляют путем использования "сложения по модулю два" со случайными матрицами [Г1]N× m и [Г2]m× N, причем "сложение по модулю два" двух матриц подразумевает "сложение по модулю два" соответствующих элементов (фиг.4,а). Тогда на матрицы [Y]N× m и [X]m× N (а соответственно на [Ypr]N× m и [Xpr]m× N) накладывается дополнительное ограничение: матрицы [Ypr]N× m и [Xpr]m× N должны быть такими, чтобы при "сложении по модулю два" с матрицами [Г1]N× m и [Г2]m× N в кодере (фиг.2) соответственно получались бы прямоугольные матрицы сформированные только из разрешенных комбинаций единичных и нулевых элементов. Тогда оптимальным при наложенных ограничениях суммарным матрицам [Y]N× m и [X]m× N будут соответствовать оптимальные разрешенные комбинации элементов прямоугольных матриц [E1]N× m и [E2]m× N.
Процедура, реализующая поиск на передаче оптимальных матриц [E1]N× m и [E2]m× N (а соответственно оптимальных [Y]N× m и [X]m× N подробно описана
в приложении 1. На фиг.3,б представлен пример, когда оптимальные матрицы [E1]N× m и [E2]m× N сформированы из элементов R матриц разрешенных векторов, причем длина строк первой из матриц разрешенных векторов  =8. При этом правило формирования прямоугольных матриц предполагалось таковым, что
=8. При этом правило формирования прямоугольных матриц предполагалось таковым, что  - группы длины
- группы длины  =8 использовались:
=8 использовались:
- в строках матрицы [E1]N× m с номерами n+1 и w для элементов с номерами от q до q+7 и от m-7 до m соответственно;
- в столбцах матрицы [E2]m× N с номерами n и N для элементов с номерами от l до l+7.
А  - группы длины
- группы длины  использовались:
использовались:
- в строке матрицы [E1]N× m с номером n для элементов с номерами от 1 до 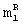 =q+7;
=q+7;
- в столбцах матрицы [E2]m× N с номерами w и N для элементов с номерами от m- +1 до m.
+1 до m.
Остальные элементы прямоугольных матриц отнесены к элементам других  -групп. При этом оптимальными для заполнения указанных
-групп. При этом оптимальными для заполнения указанных 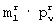 и
и  -групп показаны:
-групп показаны:
- шестнадцатая строка первой матрицы разрешенных векторов для  -групп в строках матрицы [E1]N× m с номерами n+1 и w;
-групп в строках матрицы [E1]N× m с номерами n+1 и w;
- десятая строка первой матрицы разрешенных векторов для 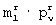 -группы в столбце матрицы [E2]m× N с номером n;
-группы в столбце матрицы [E2]m× N с номером n;
- восьмая строка первой матрицы разрешенных векторов для  -группы в столбце матрицы [E2]m× N с номером N;
-группы в столбце матрицы [E2]m× N с номером N;
- вторая строка R-й матрицы разрешенных векторов для 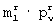 -групп в строке матрицы [E1]N× m с номером n и в столбце матрицы [E2]m× N с номером w;
-групп в строке матрицы [E1]N× m с номером n и в столбце матрицы [E2]m× N с номером w;
- первая строка R-й матрицы разрешенных векторов для  -группы в столбце матрицы [E2]m× N с номером N.
-группы в столбце матрицы [E2]m× N с номером N.
Выбор правила присвоения элементам 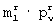 -групп значений элементов выбранной строки матрицы [Ur] не является принципиальным и может быть любым. Важным при этом является только знание этого правила декодером. В частности, для простоты в предлагаемом способе присвоение элементам любой
-групп значений элементов выбранной строки матрицы [Ur] не является принципиальным и может быть любым. Важным при этом является только знание этого правила декодером. В частности, для простоты в предлагаемом способе присвоение элементам любой  -группы прямоугольных матриц значений элементов любой j-й выбранной строки, где j=1, 2,... , m
-группы прямоугольных матриц значений элементов любой j-й выбранной строки, где j=1, 2,... , m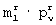 -группе ν -й строки матрицы [E1]N× m или ν -го столбца матрицы [E2]m× N определяют тот элемент, который в данной строке или в данном столбце имеет порядковый номер i, где i=1, 2,... , m, наименьший среди всех элементов этой
-группе ν -й строки матрицы [E1]N× m или ν -го столбца матрицы [E2]m× N определяют тот элемент, который в данной строке или в данном столбце имеет порядковый номер i, где i=1, 2,... , m, наименьший среди всех элементов этой  -группы i=imin. Затем ε -й номер, где ε =1, 2,...
-группы i=imin. Затем ε -й номер, где ε =1, 2,... 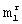 , каждого элемента в
, каждого элемента в  -группе определяют по формуле ε =i-imin+1 и каждому ε -му элементу
-группе определяют по формуле ε =i-imin+1 и каждому ε -му элементу 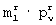 -группы присваивают значение ε -го элемента urjε ,выбранной j-й строки матрицы [Ur].
-группы присваивают значение ε -го элемента urjε ,выбранной j-й строки матрицы [Ur].
Таким образом, представление исходной матрицы [А]N× N к цифровому виду на передаче осуществляют на основе формирования прямоугольных матриц [E1]N× m и [E2]m× N. Прямоугольные матрицы передают по каналу связи с ошибками (фиг.2). В результате этого на приемной стороне принимают не матрицы [E1]N× m и [E2]m× N, а отличные от них в некоторых элементах матрицы  и
и  Для недопущения искажений при восстановлении исходной матрицы в принятых матрицах
Для недопущения искажений при восстановлении исходной матрицы в принятых матрицах  и
и  исправляют ошибки, тем самым получают прямоугольные матрицы [E1]N× m и [E2]m× N.
исправляют ошибки, тем самым получают прямоугольные матрицы [E1]N× m и [E2]m× N.
На фиг.6 показана сущность исправления ошибок на примере случая, когда передавались прямоугольные матрицы [E1]N× m и [E2]m× N, сформированные как показано на фиг.3, и при передаче по каналу связи возникла одна ошибка в 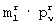 -группе в строке матрицы [E1]N× m с номером n+1 и одна ошибка в
-группе в строке матрицы [E1]N× m с номером n+1 и одна ошибка в 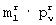 -группе в столбце матрицы [E2]m× N с номером N. Правило формирования, по которому прямоугольные матрицы разбиты кодером на
-группе в столбце матрицы [E2]m× N с номером N. Правило формирования, по которому прямоугольные матрицы разбиты кодером на  -группы, заранее известно декодеру. Информация о разбиении (правиле формирования) может быть передана в составе синхропосылки. Далее, зная местоположение различных
-группы, заранее известно декодеру. Информация о разбиении (правиле формирования) может быть передана в составе синхропосылки. Далее, зная местоположение различных  -групп в принятых из канала связи матриц
-групп в принятых из канала связи матриц  и
и 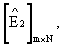 для исправления ошибок в декодере каждую
для исправления ошибок в декодере каждую  -группу элементов матриц
-группу элементов матриц  и
и  проверяют путем поэлементного сравнения поочередно со всеми строками соответствующих матриц разрешенных векторов [Ur], определяя при каждом сравнении расстояние Хэмминга d. Определение расстояния Хэмминга между двумя векторами описано, например, в книге: У.Питерсон, Э.Уэлдон. Коды, исправляющие ошибки. - М.: Мир, 1976, с.52-53. Фактически расстояние Хэмминга между двумя векторами равно количеству элементов, в которых сравниваемые вектора отличаются.
проверяют путем поэлементного сравнения поочередно со всеми строками соответствующих матриц разрешенных векторов [Ur], определяя при каждом сравнении расстояние Хэмминга d. Определение расстояния Хэмминга между двумя векторами описано, например, в книге: У.Питерсон, Э.Уэлдон. Коды, исправляющие ошибки. - М.: Мир, 1976, с.52-53. Фактически расстояние Хэмминга между двумя векторами равно количеству элементов, в которых сравниваемые вектора отличаются.
Далее для проверяемой  -группы выбирают строку соответствующей r-й матрицы разрешенных векторов [Ur], у которой расстояние Хэмминга от проверяемой
-группы выбирают строку соответствующей r-й матрицы разрешенных векторов [Ur], у которой расстояние Хэмминга от проверяемой  -группы меньше, чем у всех остальных строк, то есть равно min d. Если расстояние Хэмминга для выбранной строки меньше величины
-группы меньше, чем у всех остальных строк, то есть равно min d. Если расстояние Хэмминга для выбранной строки меньше величины  , то элементы проверяемой
, то элементы проверяемой  -группы заменяют на соответствующие элементы выбранной строки матрицы [Ur]. Иначе элементы проверяемой
-группы заменяют на соответствующие элементы выбранной строки матрицы [Ur]. Иначе элементы проверяемой  -группы оставляют неизменными.
-группы оставляют неизменными.
Так, на фиг.6 для проверяемой  -группы в матрице
-группы в матрице 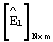 ближайшей по расстоянию Хэмминга d показана шестнадцатая строка первой матрицы разрешенных векторов. При этом min d=1. Это меньше значения,
ближайшей по расстоянию Хэмминга d показана шестнадцатая строка первой матрицы разрешенных векторов. При этом min d=1. Это меньше значения,  /4=2, поэтому элементы проверяемой
/4=2, поэтому элементы проверяемой 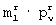 -группы заменяют на соответствующие элементы шестнадцатой строки первой матрицы разрешенных векторов. В проверяемой
-группы заменяют на соответствующие элементы шестнадцатой строки первой матрицы разрешенных векторов. В проверяемой  -группе в матрице
-группе в матрице 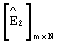 элементы заменяются на соответствующие элементы ближайшей по расстоянию Хэмминга первой строки R-й матрицы разрешенных векторов, поскольку min d=1 и это меньше, чем значение
элементы заменяются на соответствующие элементы ближайшей по расстоянию Хэмминга первой строки R-й матрицы разрешенных векторов, поскольку min d=1 и это меньше, чем значение  . Аналогичным образом исправляют ошибки в других
. Аналогичным образом исправляют ошибки в других 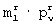 -группах. Тем самым получают истинные прямоугольные матрицы [E1]N× m и [E2]m× N.
-группах. Тем самым получают истинные прямоугольные матрицы [E1]N× m и [E2]m× N.
Значение расстояния Хэмминга меньше величины 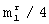 в качестве верхней границы, при которой выполняется исправление ошибок, определяется тем, что расстояние Хэмминга каждой строки матрицы [Ur] от любой другой строки той же матрицы не меньше
в качестве верхней границы, при которой выполняется исправление ошибок, определяется тем, что расстояние Хэмминга каждой строки матрицы [Ur] от любой другой строки той же матрицы не меньше  . А как известно, например, из книги: У.Питерсон, Э.Уэлдон. Коды, исправляющие ошибки. - М.: Мир, 1976, с.18, при таком минимальном расстоянии между разрешенными векторами максимально возможное число ошибок, которые могут быть гарантированно исправлены, равно
. А как известно, например, из книги: У.Питерсон, Э.Уэлдон. Коды, исправляющие ошибки. - М.: Мир, 1976, с.18, при таком минимальном расстоянии между разрешенными векторами максимально возможное число ошибок, которые могут быть гарантированно исправлены, равно 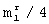 -1.
-1.
Далее определяют суммарные матрицы [Ypr]N× m и [Xpr]m× N путем "сложения по модулю два" полученных после исправления ошибок прямоугольных матриц [E1]N× m и [E2]m× N со случайными матрицами [Г1]N× m и [Г2]m× N соответственно (фиг.2, фиг.4,а).
Идентичность случайных матриц [Г1]N× m и [Г2]m× N на приемной стороне с аналогичными матрицами на передающей стороне может обеспечиваться, например, использованием на передающей и приемной сторонах генераторов с регистром сдвига одинаковой структуры, которые описаны, например, в книге: У.Питерсон, Э.Уэлдон. Коды, исправляющие ошибки. - М.: Мир, 1976, с.206-212. При этом начальное заполнение генераторов случайным образом выбирается на передающей стороне и передается на приемную сторону в составе синхропосылки.
Затем матрицы [Y]N× m и [X]m× N преобразуют в матрицы [Ypr]N× m и [Xpr]m× N соответственно. Преобразование выполняют путем деления элементов каждой строки матрицы [Y]N× m на сумму единиц соответствующей строки и деления элементов каждого столбца матрицы [Х]N× m на сумму единиц соответствующего столбца (фиг.4,б). После этого восстанавливают исходную матрицу [А]N× N (фиг.2) путем перемножения преобразованных суммарных матриц [Ypr]N× m и [Xpr]m× N, диагональных матриц [α ]N× N и [β ]N× N и ранее сформированной случайной квадратной матрицы [В]m× m, что формально соответствует выражению:
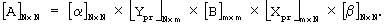
Далее из элементов Аkl восстановленной исходной матрицы (фиг.7,а) формируют вектор спектральных коэффициентов 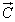 длиной z (фиг.7,б-в) путем распределения принятых N2 спектральных коэффициентов по своим местам с номерами h в соответствии с выражением: h=k+N· (l-1)+g. Остальным z-N2 спектральным коэффициентам присваивается нулевое значение. Для правильного распределения спектральных коэффициентов значение g, которое определяют на передающей стороне, можно передать на приемную сторону в составе синхропосылки.
длиной z (фиг.7,б-в) путем распределения принятых N2 спектральных коэффициентов по своим местам с номерами h в соответствии с выражением: h=k+N· (l-1)+g. Остальным z-N2 спектральным коэффициентам присваивается нулевое значение. Для правильного распределения спектральных коэффициентов значение g, которое определяют на передающей стороне, можно передать на приемную сторону в составе синхропосылки.
Затем выполняют над вектором спектральных коэффициентов длиной z операцию обратного дискретного косинусного преобразования и получают в результате этого вектор восстановленных квантованных отсчетов речевого сигнала  (фиг.7,г). Выполняют преобразование вектора восстановленных квантованных отсчетов речевого сигнала в аналоговый речевой сигнал (фиг.7,д-е).
(фиг.7,г). Выполняют преобразование вектора восстановленных квантованных отсчетов речевого сигнала в аналоговый речевой сигнал (фиг.7,д-е).
Для оценки эффективности предлагаемого способа сжатия и восстановления речевых сообщений было проведено имитационное моделирование на ПЭВМ. При кодировании речевых сообщений использовалось 8-разрядное АЦП. Моделирование проводилось для скоростей передачи по каналу связи 6, 8 и 16 кбит/с, что обеспечивалось выбором соответствующих размеров матриц m и N. При этом коэффициент сжатия равнялся соответственно 10.67, 8 и 4 раза. Достигаемый коэффициент сжатия (коэффициент уменьшения требуемой скорости передачи цифрового потока) может быть найден по формуле:

где L - число уровней квантования дискретных отсчетов речевого сигнала.
Задержка передачи речи для разных значений m и N обеспечивалась в пределах 16-256 мс, что является приемлемым для ведения телефонных переговоров (в способе-прототипе величина временной задержки речевого сигнала составляет 72 мс).
Для формирования прямоугольных матриц [E1]N× m и [E2]m× N использовались матрицы разрешенных векторов с длиной строк 8 и 16 элементов. При этом восстановленная речь сохраняет свою естественность, натуральность и обладает хорошей разборчивостью даже при вероятности ошибок в цифровом канале связи свыше 10-1.
Анализ вычислительной сложности показал, что сложность предлагаемой процедуры кодирования/декодирования пропорциональна приблизительно величине m2. Поэтому предлагаемый способ сжатия и восстановления речи может быть реализован на современных процессорах обработки сигналов.
Способ сжатия и восстановления речевых сообщений
Приложение 1.
Процедура поиска оптимальных прямоугольных матриц [E1]N× m и [E2]m× N
Процесс поиска оптимальных прямоугольных матриц [E1]N× m и [E2]m× N, определенных на множестве "1" и "0", может занимать достаточно большое время вследствие большой размерности искомых матриц, ограничений на целочисленность их элементов и разрешенность комбинаций элементов. Известно, что задачи подобного типа обладают экспоненциальной сложностью. Поэтому для сокращения времени поиска оптимальных матриц [E1]N× m и [E2]m× N в заявленном способе предлагается реализовать приближенный метод поиска. В качестве приближенного метода поиска в изобретении предложено использовать известный метод Гаусса-Зейделя для решения оптимизационных задач с большим числом неизвестных. Данный метод предполагает разбиение всего множества неизвестных на несколько подмножеств, например два, и осуществлять оптимизацию одного подмножества при фиксированном другом. Далее для найденного оптимального подмножества выполняют оптимизацию элементов другого подмножества. Данный процесс повторяется, пока изменение одного из подмножеств не будет приводить к максимизации (минимизации) выбранного критерия.
В заявленном способе предлагается разбить все множество оптимизируемых элементов на два подмножества: подмножество элементов матрицы [E1]N× m, и подмножество элементов матрицы [E2]m× N. Затем, фиксируя элементы матрицы [E1]N× m, определить оптимальные элементы матрицы [E2]m× N. Далее для найденной оптимальной матрицы и [E2]m× N определить оптимальные элементы матрицы [E1]N× m. Данный процесс повторяется, пока изменение одного из подмножеств не будет приводить к максимизации выбранного критерия. При таком подходе для оптимизации элементов матриц [E1]N× m и [E2]m× N можно воспользоваться одним и тем же алгоритмом. Это объясняется тем, что данные матрицы “меняются местами” при транспонировании исходной матрицы [А]N× N. Это показано на фиг.8. Единственное различие состоит в том, что вместо оптимальной матрицы [E1]N× m будет получена оптимальная матрица  . Однако из нее легко получить оптимальную матрицу [E1]N× m, выполняя операцию:
. Однако из нее легко получить оптимальную матрицу [E1]N× m, выполняя операцию: 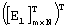 .
.
Таким образом, достаточно рассмотреть процедуру оптимизации элементов матрицы [E2]m× N. Для оптимизации элементов матрицы [E2]m× N в заявленном способе предложен эвристический метод на основе полного перебора всех разрешенных комбинаций элементов в 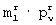 -группах.
-группах.
Возможность такого перебора определяется тем, что в каждой 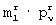 -группе, формируемой на основе использования функций Уолша, из
-группе, формируемой на основе использования функций Уолша, из 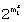 возможных используется только
возможных используется только  разрешенных комбинаций.
разрешенных комбинаций.
Сущность метода состоит в следующем. Предварительно определяют правило формирования матриц [E1]N× m и [E2]m× N. Это правило для каждой ν -й строки матрицы [E1]N× m и ν -го столбца матрицы [E2]m× N устанавливает:
- количество  групп элементов, которые имеют длину
групп элементов, которые имеют длину  ;
;
- в каком порядке располагаются различные 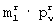 -группы, т.е. порядковый номер i каждой
-группы, т.е. порядковый номер i каждой  -группы в строке или столбце, где i=1, 2,... ,
-группы в строке или столбце, где i=1, 2,... , 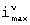 и возрастает с увеличением номера элементов данной строки или столбца, при этом максимальное значение i в ν -й строке
и возрастает с увеличением номера элементов данной строки или столбца, при этом максимальное значение i в ν -й строке

Например. Пусть m=32, количество матриц разрешенных векторов R=3, причем  =8,
=8,  =16 и
=16 и  =32. Определим, что первый столбец матрицы [E2]m× N формируется только из элементов третьей матрицы (
=32. Определим, что первый столбец матрицы [E2]m× N формируется только из элементов третьей матрицы ( -группа), т.е.
-группа), т.е.  =,
=,  . Второй столбец будем формировать из двух
. Второй столбец будем формировать из двух  -групп, т.е.
-групп, т.е. 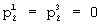 , а
, а  . Для третьего столбца пусть
. Для третьего столбца пусть 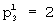 ,
,  и
и  , причем элементы столбца с номерами от 1 до 8 и от 9 до 16 образуют две
, причем элементы столбца с номерами от 1 до 8 и от 9 до 16 образуют две  -группы, которые имеют порядковые номера соответственно 1 и 2, а элементы с номерами от 17 до 32 образуют
-группы, которые имеют порядковые номера соответственно 1 и 2, а элементы с номерами от 17 до 32 образуют 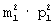 -группу с порядковым номером i=3. Для четвертого столбца пусть также
-группу с порядковым номером i=3. Для четвертого столбца пусть также  ,
, 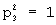 и
и 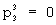 , но
, но  -группы образуются элементами столбца с номерами от 1 до 8 и от 25 до 32 и имеют порядковые номера соответственно 1 и 3, а
-группы образуются элементами столбца с номерами от 1 до 8 и от 25 до 32 и имеют порядковые номера соответственно 1 и 3, а  -группу с порядковым номером i=2 образуют элементы с номерами от 9 до 24. И т.д. для остальных столбцов матрицы [E2]m× N и строк матрицы [E1]N× m.
-группу с порядковым номером i=2 образуют элементы с номерами от 9 до 24. И т.д. для остальных столбцов матрицы [E2]m× N и строк матрицы [E1]N× m.
Чем меньше при одинаковых m и N общее число 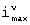
 -групп, на которые разбиваются ν -e строки матрицы [E1]N× m и ν -e столбцы матрицы [E2]m× N, тем большее количество ошибок может быть исправлено, но при этом снижается качество восстановленной речи. Поэтому выбор значений m, N и правила формирования прямоугольных матриц зависит от допустимого качества восстановленной речи и качества канала связи.
-групп, на которые разбиваются ν -e строки матрицы [E1]N× m и ν -e столбцы матрицы [E2]m× N, тем большее количество ошибок может быть исправлено, но при этом снижается качество восстановленной речи. Поэтому выбор значений m, N и правила формирования прямоугольных матриц зависит от допустимого качества восстановленной речи и качества канала связи.
После определения правила формирования прямоугольных матриц на передаче по этому правилу формируют начальные матрицы [E1]N× m и [E2]m× N, в которых каждому элементу каждой  -группы каждой ν -й строки матрицы [E1]N× m и каждой
-группы каждой ν -й строки матрицы [E1]N× m и каждой 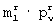 -группы каждого ν -го столбца матрицы [E2]m× N присваивают значение соответствующего (в порядке возрастания номеров) элемента первой строки r-й матрицы разрешенных векторов
-группы каждого ν -го столбца матрицы [E2]m× N присваивают значение соответствующего (в порядке возрастания номеров) элемента первой строки r-й матрицы разрешенных векторов  .
.
Далее определяют начальные суммарные матрицы [Y]N× m и [X]m× N путем "сложения по модулю два" сформированных начальных прямоугольных матриц [E1]N× m и [E2]m× N со случайными матрицами [Г1]N× m и [Г2]m× N соответственно (фиг.4,а). Затем осуществляют преобразование матрицы [Y]N× m в матрицу [Ypr]N× m путем деления элементов каждой строки матрицы [Y]N× m на сумму единиц соответствующей строки. Наглядно преобразование матрицы представлено на фиг.4,б. Затем выполняют умножение матриц [α ]N× N, [Ypr]N× m и [B]m× m, получая при этом матрицу: 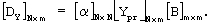
После выполнения данных подготовительных действий осуществляют оптимизацию элементов матрицы [E2]m× N путем пробной замены одновременно всех элементов каждой  -группы на значения соответствующих элементов поочередно всех строк матрицы
-группы на значения соответствующих элементов поочередно всех строк матрицы  .
.
Отметим, что замена элементов i-й  -группы ν -го столбца, где ν =1, 2,... , N, матрицы [E2]m× N приводит к изменению только элементов ν -го столбца матрицы
-группы ν -го столбца, где ν =1, 2,... , N, матрицы [E2]m× N приводит к изменению только элементов ν -го столбца матрицы 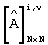 , получаемой в результате произведения
, получаемой в результате произведения

где 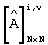 - промежуточная матрица, получаемая при замене элементов i-й
- промежуточная матрица, получаемая при замене элементов i-й
 -группы ν -го столбца матрицы [E2]m× N;
-группы ν -го столбца матрицы [E2]m× N;
 - преобразованная суммарная матрица, полученная после замены элементов i-й
- преобразованная суммарная матрица, полученная после замены элементов i-й  -группы ν -го столбца матрицы [E2]m× N, определения суммарной матрицы
-группы ν -го столбца матрицы [E2]m× N, определения суммарной матрицы 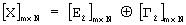 и ее последующего преобразования путем деления элементов каждого столбца на сумму единиц соответствующего столбца;
и ее последующего преобразования путем деления элементов каждого столбца на сумму единиц соответствующего столбца;
 - диагональная матрица, полученная после замены элементов i-й
- диагональная матрица, полученная после замены элементов i-й  -группы ν -го столбца матрицы [E2]m× N и определения суммарной матрицы
-группы ν -го столбца матрицы [E2]m× N и определения суммарной матрицы 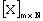 .
.
Следовательно, при поиске оптимальных элементов ν -го столбца матрицы [E2]m× N достаточно вычислить сумму квадратов разностей между элементами ν -го столбца исходной матрицы  и элементами ν -го столбца промежуточной матрицы
и элементами ν -го столбца промежуточной матрицы 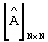 :
:

где j - номер элемента в ν -м столбце исходной и промежуточной матриц.
На основании этого можно заключить, что поиск оптимальных элементов матрицы [E2]m× N можно осуществлять последовательно по каждому ν -му столбцу, где ν =1, 2,... , N. Поэтому достаточно рассмотреть алгоритм оптимизации элементов ν -го столбца матрицы [E2]m× N.
Процесс поиска оптимальных элементов ν -го столбца матрицы [E2]m× N в заявленном способе предлагается осуществить в виде следующей последовательности действий:
1. Положить порядковый номер  -группы i=0 и номер строки матрицы разрешенных векторов
-группы i=0 и номер строки матрицы разрешенных векторов  l=0;
l=0;
2. Положить i=i+1, l=l+1 и назначить оптимальное значение lopt=l;
3. Сформировать вектор 
где 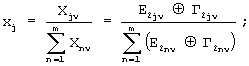
4. Если  , то вычислить ν -ый столбец промежуточной матрицы по формуле
, то вычислить ν -ый столбец промежуточной матрицы по формуле  и перейти к пункту 5, иначе перейти к пункту 2;
и перейти к пункту 5, иначе перейти к пункту 2;
5. Вычислить сумму квадратов разностей между элементами ν -го столбца исходной матрицы  и элементами ν -го столбца промежуточной матрицы
и элементами ν -го столбца промежуточной матрицы 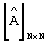 :
:
6. Положить l=l+1;
7. Если l≤ 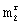 , то выполнить замену элементов i-й
, то выполнить замену элементов i-й  -группы ν -го столбца на соответствующие элементы l-й строки матрицы
-группы ν -го столбца на соответствующие элементы l-й строки матрицы  и перейти к пункту 8, иначе положить l=0 и перейти к пункту 2;
и перейти к пункту 8, иначе положить l=0 и перейти к пункту 2;
8. Аналогично пункту 3 сформировать вектор 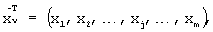
9. Если  , то аналогично пункту 4 вычислить ν -й столбец матрицы
, то аналогично пункту 4 вычислить ν -й столбец матрицы  и перейти к пункту 10, иначе перейти к пункту 6;
и перейти к пункту 10, иначе перейти к пункту 6;
10. Аналогично пункту 5 вычислить сумму квадратов разностей  между элементами ν -го столбца исходной матрицы [А]N× N и элементами ν -го столбца промежуточной матрицы
между элементами ν -го столбца исходной матрицы [А]N× N и элементами ν -го столбца промежуточной матрицы  , полученной после изменения i-й
, полученной после изменения i-й 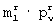 -группы;
-группы;
11. Вычислить u’=
12. Если u’>0, то значению  присвоить значение
присвоить значение  и назначить lopt=l, иначе значения
и назначить lopt=l, иначе значения 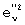 и lopt оставить без изменения;
и lopt оставить без изменения;
13. Если l<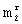 , то перейти к пункту 6, иначе перейти к пункту 14;
, то перейти к пункту 6, иначе перейти к пункту 14;
14. Если  , то назначить l=0 и перейти к пункту 2, иначе перейти к поиску оптимальных элементов следующего столбца матрицы [E2]m× N.
, то назначить l=0 и перейти к пункту 2, иначе перейти к поиску оптимальных элементов следующего столбца матрицы [E2]m× N.
В результате выполнения данных операций на передаче получают матрицу [E2]m× N, оптимальную при данной фиксированной матрице [E1]m× N. После этого на передаче кодер аналогичным образом выполняет поиск матрицы [E1]m× N, оптимальной при данной фиксированной матрице [E2]m× N.
Последовательность действий по определению оптимальной матрицы [E2]m× N при фиксированной матрице [E2]m× N и по определению оптимальной матрицы [E1]m× N при фиксированной матрице [E2]m× N назовем итерационным циклом. Итерационный цикл повторяют, пока после его очередного выполнения значение 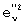 будет уменьшаться по сравнению со значением
будет уменьшаться по сравнению со значением 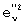 , полученным после предыдущего выполнения итерационного цикла. Иначе выполнение итерационного цикла прекращают, полученные прямоугольные матрицы [E2]m× N и [E2]m× N считают оптимальными и передают их по каналу связи.
, полученным после предыдущего выполнения итерационного цикла. Иначе выполнение итерационного цикла прекращают, полученные прямоугольные матрицы [E2]m× N и [E2]m× N считают оптимальными и передают их по каналу связи.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ СЖАТИЯ И ВОССТАНОВЛЕНИЯ РЕЧЕВЫХ СООБЩЕНИЙ | 2006 |
|
RU2343565C2 |
| СПОСОБ СЖАТИЯ И ВОССТАНОВЛЕНИЯ РЕЧЕВЫХ СООБЩЕНИЙ | 2001 |
|
RU2195715C1 |
| СПОСОБ СЖАТИЯ И ВОССТАНОВЛЕНИЯ РЕЧЕВЫХ СООБЩЕНИЙ | 2001 |
|
RU2195714C1 |
| СПОСОБ СЖАТИЯ И ВОССТАНОВЛЕНИЯ РЕЧЕВЫХ СООБЩЕНИЙ | 1998 |
|
RU2152646C1 |
| СПОСОБ СЖАТИЯ И ВОССТАНОВЛЕНИЯ СООБЩЕНИЙ | 2007 |
|
RU2374785C2 |
| СПОСОБ СЖАТИЯ И ВОССТАНОВЛЕНИЯ СООБЩЕНИЙ | 2005 |
|
RU2288547C1 |
| СПОСОБ СЖАТИЯ И ВОССТАНОВЛЕНИЯ РЕЧЕВЫХ СООБЩЕНИЙ | 2009 |
|
RU2400830C1 |
| СПОСОБ СЖАТИЯ И ВОССТАНОВЛЕНИЯ РЕЧЕВЫХ СООБЩЕНИЙ | 2002 |
|
RU2216791C1 |
| СПОСОБ СЖАТИЯ И ВОССТАНОВЛЕНИЯ СООБЩЕНИЙ | 2003 |
|
RU2246798C1 |
| СПОСОБ СЖАТИЯ И ВОССТАНОВЛЕНИЯ СООБЩЕНИЙ | 2004 |
|
RU2261532C1 |


Изобретение относится к области электросвязи, а именно к области систем передачи информации по цифровым каналам связи. Его использование позволяет получить технический результат в виде исправления ошибок, возникающих в передаваемых цифровых последовательностях под влиянием нестабильности параметров канала связи, и осуществления телефонных переговоров по низкоскоростным цифровым каналам связи. Технический результат достигается за счет того, что предварительно на передаче и приеме формируют R матриц разрешенных векторов, каждая размерами m2×m1 единичных и нулевых элементов. Затем из одномерного аналогового речевого сигнала формируют исходную матрицу размером N× N элементов и полученную матрицу преобразуют к цифровому виду. При этом прямоугольные матрицы размерами N× m и m× N единичных и нулевых элементов, являющиеся цифровым представлением исходной матрицы, формируют из элементов строк матриц разрешенных векторов. Далее элементы этих прямоугольных матриц передают по цифровому каналу связи. На приемной стороне на основе проверки соответствия групп элементов в принятых прямоугольных матрицах элементам строк предварительно сформированных матриц разрешенных векторов исправляют ошибки, а затем в обратном порядке действий производят восстановление речи. Способ особенно подходит для ведения телефонных переговоров по цифровым каналам связи со скоростью 6-16 кбит/с. 4 з.п. ф-лы, 8 ил.


где 

перед восстановлением исходной матрицы размером N× N элементов в принятых из канала связи прямоугольных матрицах размерами N× m и m× N элементов исправляют ошибки.
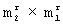 единичных и нулевых элементов сначала каждую i-ю строку, где i=1, 2,... ,
единичных и нулевых элементов сначала каждую i-ю строку, где i=1, 2,... ,  r-й матрицы разрешенных векторов формируют в виде r-й дискретной функции Уолша из упорядоченного множества
r-й матрицы разрешенных векторов формируют в виде r-й дискретной функции Уолша из упорядоченного множества 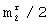 дискретных функций Уолша длины
дискретных функций Уолша длины  , где
, где  и u=3, 4,... , в каждой сформированной строке всем элементам, равным -1, присваивают значение 0 и затем каждую (i+
и u=3, 4,... , в каждой сформированной строке всем элементам, равным -1, присваивают значение 0 и затем каждую (i+ )-ю строку r-й матрицы разрешенных векторов формируют путем инверсии каждого элемента i-й строки этой же матрицы, а для исправления ошибок в принятых из канала связи прямоугольных матрицах размерами N× m и m× N элементов последовательно выбирают каждую
)-ю строку r-й матрицы разрешенных векторов формируют путем инверсии каждого элемента i-й строки этой же матрицы, а для исправления ошибок в принятых из канала связи прямоугольных матрицах размерами N× m и m× N элементов последовательно выбирают каждую 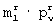 -группу элементов каждой ν -й строки принятой прямоугольной матрицы размером N× m и каждую
-группу элементов каждой ν -й строки принятой прямоугольной матрицы размером N× m и каждую 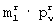 -группу элементов каждого ν -го столбца принятой прямоугольной матрицы размером mxN элементов, определяют j-ю строку, где j=1, 2,... ,
-группу элементов каждого ν -го столбца принятой прямоугольной матрицы размером mxN элементов, определяют j-ю строку, где j=1, 2,... , 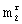 , r-й матрицы разрешенных векторов, у которой расстояние Хэмминга от выбранной
, r-й матрицы разрешенных векторов, у которой расстояние Хэмминга от выбранной 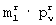 -группы минимально, и если минимальное расстояние Хэмминга меньше величины
-группы минимально, и если минимальное расстояние Хэмминга меньше величины  , то каждому элементу выбранной
, то каждому элементу выбранной 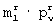 -группы присваивают значение соответствующего элемента j-й строки r-й матрицы разрешенных векторов, иначе выбранную
-группы присваивают значение соответствующего элемента j-й строки r-й матрицы разрешенных векторов, иначе выбранную  -группу элементов принятых из канала связи прямоугольных матриц сохраняют неизменной.
-группу элементов принятых из канала связи прямоугольных матриц сохраняют неизменной. -группы каждой ν -й строки прямоугольной матрицы размером Nxm элементов и каждой
-группы каждой ν -й строки прямоугольной матрицы размером Nxm элементов и каждой  -группы каждого ν -го столбца прямоугольной матрицы размером m× N элементов присваивают значение соответствующего элемента первой строки r-й матрицы разрешенных векторов, после чего формируют суммарные матрицы размерами N× m и m× N элементов путем суммирования по модулю два элементов прямоугольных матриц размерами N× m и m× N элементов с соответствующими элементами ключевых матриц размерами N× m и m× N элементов соответственно, преобразуют полученные суммарные матрицы размерами N× m и m× N элементов путем деления элементов каждой строки суммарной матрицы размером N× m элементов на сумму единиц соответствующей строки и деления элементов каждого столбца суммарной матрицы размером m× N элементов на сумму единиц соответствующего столбца, формируют промежуточную матрицу размером N× N элементов путем перемножения диагональной матрицы, у которой каждый nn-й диагональный элемент равен сумме произведений элементов n-й строки, где n=1, 2,... , N, суммарной матрицы размером N× m элементов на соответствующие элементы случайного вектора из m элементов, а остальные элементы равны нулю, с полученной после преобразования суммарной матрицей размером N× m элементов, с ранее идентично сформированной на передающей и приемной сторонах случайной квадратной матрицей размером m× m элементов, с полученной после преобразования суммарной матрицей размером m× N элементов и с диагональной матрицей, у которой каждый nn-й диагональный элемент равен сумме произведений элементов случайного вектора из m элементов на соответствующие элементы n-го столбца суммарной матрицы размером m× N элементов, а остальные элементы равны нулю, вычисляют показатель ошибки в виде суммы квадратов разностей между элементами полученной в результате перемножения промежуточной матрицы размером N× N элементов и соответствующими элементами исходной матрицы размером N× N, затем выполняют итерационный цикл, в котором последовательно в каждой
-группы каждого ν -го столбца прямоугольной матрицы размером m× N элементов присваивают значение соответствующего элемента первой строки r-й матрицы разрешенных векторов, после чего формируют суммарные матрицы размерами N× m и m× N элементов путем суммирования по модулю два элементов прямоугольных матриц размерами N× m и m× N элементов с соответствующими элементами ключевых матриц размерами N× m и m× N элементов соответственно, преобразуют полученные суммарные матрицы размерами N× m и m× N элементов путем деления элементов каждой строки суммарной матрицы размером N× m элементов на сумму единиц соответствующей строки и деления элементов каждого столбца суммарной матрицы размером m× N элементов на сумму единиц соответствующего столбца, формируют промежуточную матрицу размером N× N элементов путем перемножения диагональной матрицы, у которой каждый nn-й диагональный элемент равен сумме произведений элементов n-й строки, где n=1, 2,... , N, суммарной матрицы размером N× m элементов на соответствующие элементы случайного вектора из m элементов, а остальные элементы равны нулю, с полученной после преобразования суммарной матрицей размером N× m элементов, с ранее идентично сформированной на передающей и приемной сторонах случайной квадратной матрицей размером m× m элементов, с полученной после преобразования суммарной матрицей размером m× N элементов и с диагональной матрицей, у которой каждый nn-й диагональный элемент равен сумме произведений элементов случайного вектора из m элементов на соответствующие элементы n-го столбца суммарной матрицы размером m× N элементов, а остальные элементы равны нулю, вычисляют показатель ошибки в виде суммы квадратов разностей между элементами полученной в результате перемножения промежуточной матрицы размером N× N элементов и соответствующими элементами исходной матрицы размером N× N, затем выполняют итерационный цикл, в котором последовательно в каждой 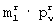 -группе элементов прямоугольных матриц одновременно всем элементам присваивают значения соответствующих элементов поочередно каждой j-й строки r-й матрицы разрешенных векторов, при этом остальные
-группе элементов прямоугольных матриц одновременно всем элементам присваивают значения соответствующих элементов поочередно каждой j-й строки r-й матрицы разрешенных векторов, при этом остальные 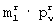 -группы сохраняют неизменными, и формируют суммарные матрицы размерами N× m и m× N элементов путем суммирования по модулю два элементов полученных после изменения элементов
-группы сохраняют неизменными, и формируют суммарные матрицы размерами N× m и m× N элементов путем суммирования по модулю два элементов полученных после изменения элементов  -группы прямоугольных матриц размерами N× m и m× N элементов с соответствующими элементами ключевых матриц размерами N× m и m× N элементов соответственно, преобразуют полученные суммарные матрицы размерами N× m и m× N элементов путем деления элементов каждой строки суммарной матрицы размером N× m элементов на сумму единиц соответствующей строки и деления элементов каждого столбца суммарной матрицы размером m× N элементов на сумму единиц соответствующего столбца, формируют промежуточную матрицу размером N× N элементов путем перемножения диагональной матрицы, у которой каждый nn-й диагональный элемент равен сумме произведений элементов n-й строки суммарной матрицы размером N× m элементов на соответствующие элементы случайного вектора из m элементов, а остальные элементы равны нулю, с полученной после преобразования суммарной матрицей размером N× m элементов, с ранее идентично сформированной на передающей и приемной сторонах случайной квадратной матрицей размером m× m элементов, с полученной после преобразования суммарной матрицей размером m× N элементов и с диагональной матрицей, у которой каждый nn-й диагональный элемент равен сумме произведений элементов случайного вектора из m элементов на соответствующие элементы n-го столбца суммарной матрицы размером m× N элементов, а остальные элементы равны нулю, вычисляют показатель ошибки в виде суммы квадратов разностей между элементами полученной в результате перемножения промежуточной матрицы размером N× N элементов и соответствующими элементами исходной матрицы размером N× N элементов и вычитают вычисленное значение показателя ошибки из его ранее вычисленного значения, если полученная разность больше нуля, то сохраняют новые значения элементов изменяемой
-группы прямоугольных матриц размерами N× m и m× N элементов с соответствующими элементами ключевых матриц размерами N× m и m× N элементов соответственно, преобразуют полученные суммарные матрицы размерами N× m и m× N элементов путем деления элементов каждой строки суммарной матрицы размером N× m элементов на сумму единиц соответствующей строки и деления элементов каждого столбца суммарной матрицы размером m× N элементов на сумму единиц соответствующего столбца, формируют промежуточную матрицу размером N× N элементов путем перемножения диагональной матрицы, у которой каждый nn-й диагональный элемент равен сумме произведений элементов n-й строки суммарной матрицы размером N× m элементов на соответствующие элементы случайного вектора из m элементов, а остальные элементы равны нулю, с полученной после преобразования суммарной матрицей размером N× m элементов, с ранее идентично сформированной на передающей и приемной сторонах случайной квадратной матрицей размером m× m элементов, с полученной после преобразования суммарной матрицей размером m× N элементов и с диагональной матрицей, у которой каждый nn-й диагональный элемент равен сумме произведений элементов случайного вектора из m элементов на соответствующие элементы n-го столбца суммарной матрицы размером m× N элементов, а остальные элементы равны нулю, вычисляют показатель ошибки в виде суммы квадратов разностей между элементами полученной в результате перемножения промежуточной матрицы размером N× N элементов и соответствующими элементами исходной матрицы размером N× N элементов и вычитают вычисленное значение показателя ошибки из его ранее вычисленного значения, если полученная разность больше нуля, то сохраняют новые значения элементов изменяемой  -группы и показателя ошибки, иначе сохраняют предыдущие значения элементов изменяемой
-группы и показателя ошибки, иначе сохраняют предыдущие значения элементов изменяемой  -группы прямоугольных матриц и показателя ошибки, затем последнее сохраненное в итерационном цикле значение показателя ошибки вычитают из последнего значения показателя ошибки, вычисленного до этого итерационного цикла, и если полученная разность больше нуля, то итерационный цикл повторяют, а для восстановления исходной матрицы размером N× N элементов на приемной стороне формируют суммарные матрицы размерами N× m и m× N элементов путем суммирования по модулю два элементов принятых из канала связи и исправленных прямоугольных матриц размерами N× m и m× N элементов с соответствующими элементами ключевых матриц размерами N× m и m× N элементов соответственно, преобразуют полученные суммарные матрицы размерами N× m и m× N элементов путем деления элементов каждой строки суммарной матрицы размером N× m элементов на сумму единиц соответствующей строки и деления элементов каждого столбца суммарной матрицы размером m× N элементов на сумму единиц соответствующего столбца, перемножают диагональную матрицу, у которой каждый nn-й диагональный элемент равен сумме произведений элементов n-й строки суммарной матрицы размером N× m элементов на соответствующие элементы случайного вектора из m элементов, а остальные элементы равны нулю, с полученной после преобразования суммарной матрицей размером N× m элементов, с ранее идентично сформированной на передающей и приемной сторонах случайной квадратной матрицей размером m× m элементов, с полученной после преобразования суммарной матрицей размером m× N элементов и с диагональной матрицей, у которой каждый nn-й диагональный элемент равен сумме произведений элементов случайного вектора из m элементов на соответствующие элементы n-го столбца суммарной матрицы размером m× N элементов, а остальные элементы равны нулю.
-группы прямоугольных матриц и показателя ошибки, затем последнее сохраненное в итерационном цикле значение показателя ошибки вычитают из последнего значения показателя ошибки, вычисленного до этого итерационного цикла, и если полученная разность больше нуля, то итерационный цикл повторяют, а для восстановления исходной матрицы размером N× N элементов на приемной стороне формируют суммарные матрицы размерами N× m и m× N элементов путем суммирования по модулю два элементов принятых из канала связи и исправленных прямоугольных матриц размерами N× m и m× N элементов с соответствующими элементами ключевых матриц размерами N× m и m× N элементов соответственно, преобразуют полученные суммарные матрицы размерами N× m и m× N элементов путем деления элементов каждой строки суммарной матрицы размером N× m элементов на сумму единиц соответствующей строки и деления элементов каждого столбца суммарной матрицы размером m× N элементов на сумму единиц соответствующего столбца, перемножают диагональную матрицу, у которой каждый nn-й диагональный элемент равен сумме произведений элементов n-й строки суммарной матрицы размером N× m элементов на соответствующие элементы случайного вектора из m элементов, а остальные элементы равны нулю, с полученной после преобразования суммарной матрицей размером N× m элементов, с ранее идентично сформированной на передающей и приемной сторонах случайной квадратной матрицей размером m× m элементов, с полученной после преобразования суммарной матрицей размером m× N элементов и с диагональной матрицей, у которой каждый nn-й диагональный элемент равен сумме произведений элементов случайного вектора из m элементов на соответствующие элементы n-го столбца суммарной матрицы размером m× N элементов, а остальные элементы равны нулю.| СПОСОБ СЖАТИЯ И ВОССТАНОВЛЕНИЯ РЕЧЕВЫХ СООБЩЕНИЙ | 2001 |
|
RU2195714C1 |
| СПОСОБ СУШКИ ПИЛОМАТЕРИАЛОВ И УСТРОЙСТВО ДЛЯ ЕГО ОСУЩЕСТВЛЕНИЯ | 2004 |
|
RU2280827C2 |
| US 5822370 А, 13.10.1998 | |||
| Установка для очистки шахтных водосборников | 1980 |
|
SU907258A1 |
| СПОСОБ ПРИЕМА И ПОИСКА СИГНАЛА, ПЕРЕДАВАЕМОГО ПАКЕТАМИ | 1996 |
|
RU2157592C2 |
Авторы
Даты
2005-01-20—Публикация
2003-07-21—Подача