Способ последовательно-параллельного вейвлетного преобразования относится к области информационных технологий и может использоваться для сжатия видеоизображений в системах обработки и передачи цифровой информации.
Вейвлетное преобразование или сокращенно ВП является перспективным методом сжатия видеоизображений, обеспечивающим высокую степень сжатия. При сжатии изображений с использованием ВП выполняют вычисления с большими массивами цифровой информации, что требует существенных затрат времени. ВП представляет собой последовательность повторяющихся вычислительных процедур, которые будем также называть итерациями ВП. Актуальной является задача разработки способа ВП, позволяющего выполнять параллельную обработку информации и использовать многопроцессорные вычислительные системы, что обеспечивает сокращение времени выполнения ВП.
Известен способ ВП, состоящий из прямого и обратного ВП, при каждом из которых входную информацию обрабатывают путем последовательных итераций. При прямом ВП входной информацией первой итерации является исходный сигнал, представленный множеством значений отсчетов сигнала. Входную информацию каждой из итераций пропускают через два фильтра: низкочастотный и высокочастотный. Значения отсчетов сигнала с выхода высокочастотного фильтра, являющиеся одновременно коэффициентами ВП, запоминают. Значения отчетов сигнала с выхода низкочастотного фильтра, прореженные через один отсчет, являются входной информацией для следующей итерации. Значения отсчетов сигнала с выхода низкочастотного фильтра последней итерации, одновременно являющиеся коэффициентами ВП, также запоминают. При обратном ВП входной информацией первой итерации являются коэффициенты ВП последней итерации прямого ВП, при этом значения низкочастотных отсчетов сигнала дополняются нулевыми значениями через один отсчет сигнала. Входную информацию каждой из итераций обратного ВП пропускают через два фильтра: низкочастотный и высокочастотный фильтр, структура этих фильтров однозначно определяется низкочастотным и высокочастотным фильтрами прямого ВП, а затем определяют выходную информацию итерации, представляющую собой разность значений отсчетов сигнала с выходов низкочастотного и высокочастотного фильтров. Выходная информация предыдущей итерации обратного ВП, дополненная нулевыми значениями через один отсчет сигнала, совместно с коэффициентами ВП предыдущей итерации прямого ВП, считая номера итераций прямого ВП с конца последовательности итераций прямого ВП, является входной информацией следующей итерации обратного ВП. Выходная информация последней итерации обратного ВП представляет собой значения отсчетов восстановленного исходного сигнала (способ Берта - Адельсона[1]).
Однако этот способ имеет низкое быстродействие, обусловленное тем, что вычисление прямого и обратного ВП осуществляется в результате последовательных итераций, и вычисления на следующей итерации можно выполнять только после окончания вычислений на предыдущей итерации.
Наиболее близким к предлагаемому способу является способ ВП (прототип), состоящий из прямого ВП и обратного ВП. При прямом ВП входная информация обрабатывается путем s последовательных итераций, причем входной информацией первой итерации является исходный сигнал, представленный множеством значений отсчетов этого сигнала. Входную информацию каждой из итераций пропускают через два фильтра: низкочастотный и высокочастотный фильтр. Значения отсчетов сигнала с выхода высокочастотного фильтра, прореженные через один отсчет сигнала, являются коэффициентами ВП, а значения отсчетов сигнала с выхода низкочастотного фильтра, прореженные через один отсчет, являются входной информацией следующей итерации прямого ВП. Значения отсчетов сигнала с выхода низкочастотного фильтра последней итерации ВП, прореженные через один отсчет сигнала, также являются коэффициентами ВП. При обратном ВП входной информацией являются коэффициенты прямого ВП, причем эти коэффициенты дополняются нулевыми значениями. Входную информацию обратного ВП пропускают через совокупность фильтров, структура которых однозначно определяется низкочастотным и высокочастотным фильтрами прямого ВП, а затем определяют выходную информацию совокупности фильтров (способ Маллата [2]).
Недостатком этого способа является низкое быстродействие, поскольку при выполнении прямого и обратного ВП требуется вычисление последовательных во времени итераций, и вычисление следующей итерации возможно лишь при наличии результатов вычислений предыдущей итерации.
Цель изобретения - повышение быстродействия ВП за счет того, что осуществляют параллельную обработку информации, поскольку обратное ВП выполняют с помощью совокупности одновременно работающих независимых друг от друга цифровых фильтров.
Для достижения цели предложен способ последовательно-параллельного ВП, состоящий из прямого и обратного ВП. При прямом ВП входная информация обрабатывается путем s последовательных итераций, причем входной информацией первой итерации является исходный сигнал, представленный множеством значений отсчетов этого сигнала. Входную информацию каждой из итераций пропускают через два фильтра: низкочастотный и высокочастотный фильтр. Значения отсчетов сигнала с выхода высокочастотного фильтра, прореженные через один отсчет сигнала, являются коэффициентами ВП, а значения отсчетов сигнала с выхода низкочастотного фильтра, прореженные через один отсчет, являются входной информацией следующей итерации прямого ВП. Значения отсчетов сигнала с выхода низкочастотного фильтра последней итерации прямого ВП, прореженные через один отсчет сигнала, также являются коэффициентами ВП. При обратном ВП входной информацией являются коэффициенты прямого ВП, причем эти коэффициенты дополняются нулевыми значениями. Входную информацию обратного ВП пропускают через совокупность фильтров, структура которых однозначно определяется низкочастотными и высокочастотными фильтрами прямого ВП, а затем определяют выходную информацию совокупности фильтров. Новым является то, что при обратном ВП коэффициенты ВП с выходов высокочастотных фильтров прямого ВП, дополненные нулевыми значениями, причем число нулевых значений равно последовательным степеням двойки, начиная с первой степени и до s-ой степени включительно, пропускают через совокупность параллельных цифровых фильтров. На выходе этих цифровых фильтров осуществляют сдвиг значений отсчетов сигнала в сторону старших разрядов на число разрядов, равное последовательным степеням двойки, начиная с первой степени и до s-ой степени включительно. Далее вычисляют сумму W полученных значений отсчетов сигнала. Одновременно коэффициенты ВП с выхода низкочастотного фильтра последней итерации прямого ВП, дополненные нулевыми значениями, причем число нулевых значений равно s-ой степени двойки, пропускают через свой цифровой фильтр. На выходе этого цифрового фильтра осуществляют сдвиг значений отсчетов сигнала в сторону старших разрядов на число разрядов, равное s-ой степени двойки, и из полученных значений отсчетов сигнала вычитают ранее вычисленную сумму W и в результате получают отсчеты восстановленного исходного сигнала.
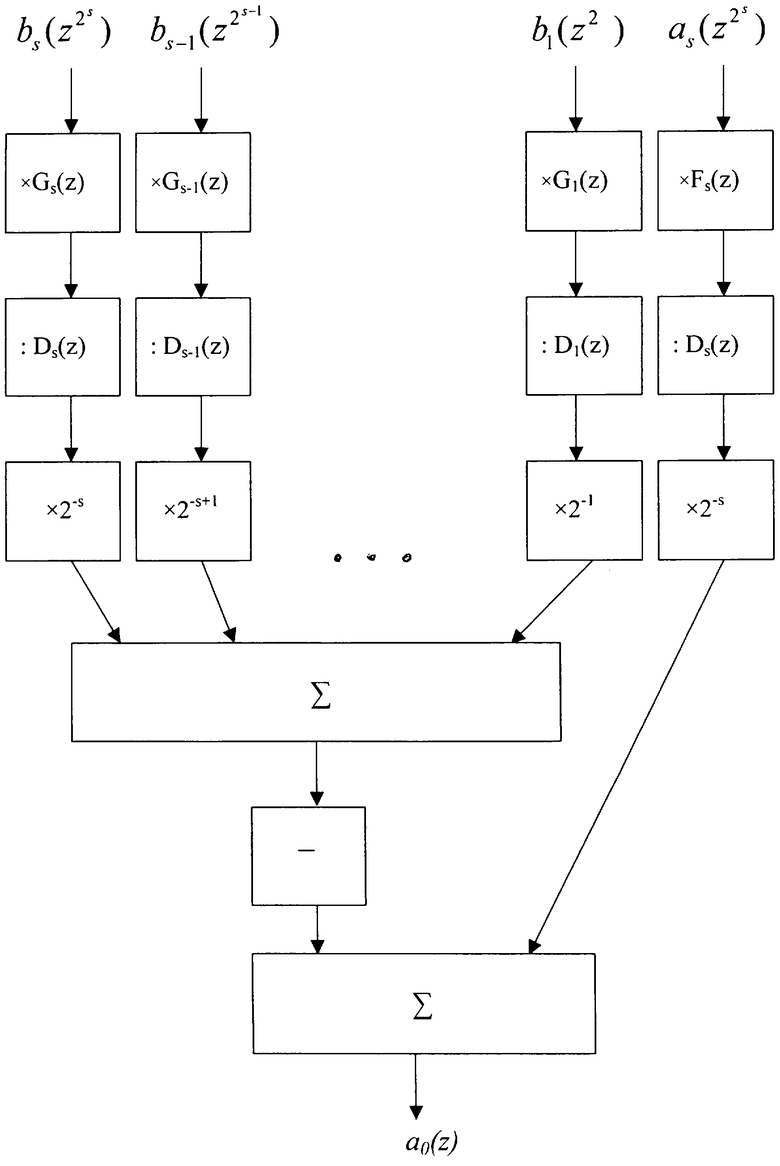
Структурная схема обратного ВП представлена на чертеже.
Рассмотрим осуществление предлагаемого способа ВП. Дискретное ВП обычно представляют на основе теории цифровой фильтрации. Для прямого ВП используют два специально подобранных фильтра: высокой и низкой частоты с передаточными функциями g(z) и f(z) соответственно. Передаточную функцию g(z) фильтра высокой частоты называют вейвлетом, а передаточную функцию f(z) низкочастотного фильтра - скейлинг-функцией. На вход этих фильтров подаются отсчеты низкочастотной составляющей, на выходе частоту дискретизации отсчетов уменьшают вдвое. Отсчеты высокочастотной составляющей с выхода фильтра высокой частоты, называемые коэффициентами ВП, запоминают, а отсчеты низкочастотной составляющей с выхода фильтра низкой частоты на следующем шаге итерации опять разделяют на высокочастотную и низкочастотную части. В терминах z -преобразования эта процедура может быть описана следующим образом.
Пусть as(z) и bs(z) - полиномы, коэффициентами которых являются отсчеты, получаемые на s-ом шаге итерации с выхода фильтра низкой и высокой частоты соответственно. Тогда a0(z) есть полином отсчетов исходного сигнала, а коэффициентами ВП будут коэффициенты полиномов b1(z), b2(z),... , bm(z) и полинома am(z), получаемого на последнем шаге итерации.
Вычисления на каждом шаге итерации при прямом ВП исходного сигнала выполняют согласно системе рекуррентных уравнений. Фильтрация есть умножение многочлена входных данных на передаточную функцию фильтра, и результат одной из итераций прямого ВП запишется в виде
as(z2)=as-1(z)f(z)/2+as-1(-z)f(-z)/2, (1)
bs(z2)=аs-1(z)g(z)/2+as-1(-z)g(-z)/2,
где s=1... m.
Эта система уравнений определяет операции фильтрации и прореживания на каждой итерации прямого ВП.
В полиномах as(z2) и bs(z2) коэффициенты при нечетных степенях z будут нулевыми, что следует из приведенной системы уравнений, поэтому каждый из этих полиномов будет иметь по крайней мере вдвое меньше значащих коэффициентов, чем исходный полином as-1(z). Степень сжатия сигнала при ВП будет определяться числом нулевых коэффициентов полиномов b1(z), b2(z),... , bm(z) и полинома am(z), получаемого на последнем шаге итерации.
В результате прямого ВП исходному сигналу, заданному в дискретные отсчеты времени, ставят в соответствие две пирамиды: пирамиду гауссианов аs(z) и пирамиду лапласианов bs(z). При этом используют два фильтра: низкочастотный для получения пирамиды гауссианов и высокочастотный для получения пирамиды лапласианов. Нулевой этаж пирамиды гауссианов - сам сигнал a0(z). Первый этаж пирамиды гауссианов a1(z) - результат фильтрации в фильтре нижних частот нулевого этажа, прореженный путем выбрасывания каждого второго коэффициента. Второй этаж a2(z) строится таким же образом из первого и т. д.
Пирамиду лапласианов строят аналогично пирамиде гауссианов, но с использованием фильтра высоких частот.
По пирамиде лапласианов и верхнему этажу пирамиды гауссианов, с точностью до величины ошибок округления, можно восстановить исходный сигнал. Для этого выполняют обратное ВП, которое получают решением предыдущей системы уравнений. Одна из итераций обратного ВП имеет вид
as-1(z)=(as(z2)g(-z)-bs(z2)f(-z))/(2· D(z)), (2)
где D(z)=(f(z)g(-z)-f(-z)g(z))/4 - определитель ВП.
Передаточные функции ВП f(z) и g(z) выбирают таким образом, чтобы определитель имел вид одночлена:
D(z)=c*zi i=1,3,5... ,
где с - константа.
При этом для обратного преобразования используют нерекурсивный фильтр, и распространение ошибок не происходит. Выбор передаточных функций ВП является наиболее ответственным моментом в реализации ВП. При этом можно пользоваться готовыми таблицами передаточных функций, например функциями Добеши.
В существующей литературе [3] приводят обычно скейлинг-функцию, на основе которой строятся подходящие вейвлеты. Наиболее распространенными являются ортогональные скейлинг-функции, к которым относятся функции Добеши, симлеты, койфлеты. Для таких функций можно построить вейвлеты следующим образом.
Пусть
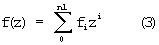
- ортогональная скейлинг-функция. Тогда соответствующий вейвлет имеет вид
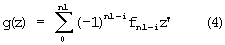
В таблице приведены ортогональные скейлинг-функции, которые можно использовать при реализации способа [3].
Пример.
Для n1=3 скейлингфункция из таблицы имеет вид
f(z)=0.34150635094622 + 0.59150635094587z+ 0.15849364905378z2 +0.09150635094587z3
Соответствующий вейвлет согласно уравнению (4) будет равен
g(z)=-0.34150635094622z3+ 0.59150635094587z2-0.15849364905378z -0.09150635094587
Использование производящих функций в рекуррентных процедурах дает возможность получения за один шаг нижнего этажа гауссианов (исходного сигнала).
Из уравнения (2) имеем
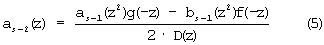
После подстановки (2) в (3) получим
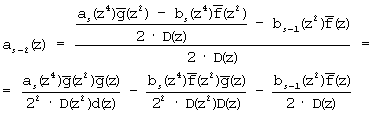
Здесь
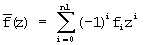
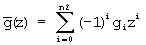
Пусть
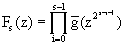
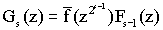
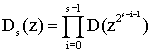
F0=1 s=1,2...
По индукции можно показать
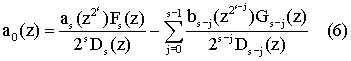
Формула (6) позволяет вычислить исходную информацию a0(z) за один шаг без вычисления промежуточных этажей пирамиды гауссианов ai(z)i=s-1... 1.
Заметим, что для ВП определитель D(z) есть одночлен и, значит, Di(z) i=s-1... 1 также будет одночленом, что позволяет существенным образом упростить реализацию способа, поскольку делению входной информации на одночлен соответствует сдвиг на определенное число разрядов.
На чертеже изображена структурная схема, отражающая последовательность действий при параллельном ВП согласно формуле (6).
Информация в виде коэффициентов лапласианов b1(z), b2(z),... , bs(z) и коэффициентов последнего гауссиана as(z), дополненная нулями, поступает на вход s+1 параллельных фильтров Fs Gs Gs-1...G1. Причем число нулей между соседними коэффициентами, как следует из формулы (6), равно последовательным степеням двойки. Далее, на выходе этих фильтров осуществляют сдвиг информации в сторону старших разрядов, причем количество разрядов соответствует степени определителя Di(z) i=s-1... 1. Выходная информация параллельного ВП получается путем поразрядного суммирования с определенными знаками сдвинутой информации. При этом отсчеты, соответствующие лапласианам, участвуют в суммировании со знаком минус, а отсчеты, соответствующие гауссиану, - со знаком плюс.
Предлагаемый способ направлен на решение актуальной задачи сокращения времени, затрачиваемого на выполнение ВП.
Данный способ может найти применение в многопроцессорных системах для увеличения скорости обработки обратного ВП путем использования s+1 параллельных фильтров Fs Gs gs-1...G1.
Достигаемым техническим результатом предлагаемого способа последовательно-параллельного ВП является сокращение времени, затрачиваемого на выполнение ВП.
Источники информации
1. Левкович Л. Дайджест вейвлет-анализа в двух формулах и 22 рисунках. Компьютерра, №8, 1998, стр.31.
2. Шаткин Я.И. Вейвлет-преобразование и сжатие изображений. Программист, №3, 2002, стр.52.
3. Добеши И. Десять лекций по вейвлетам. PXD, Москва • Ижевск, 2001 г, стр.270.

| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ ВЫПОЛНЕНИЯ ПРЯМОГО И ОБРАТНОГО ВЕЙВЛЕТ-ПРЕОБРАЗОВАНИЯ | 2013 |
|
RU2543932C2 |
| УСТРОЙСТВО ДЛЯ ВЫПОЛНЕНИЯ ДВУХМЕРНОГО ПРЯМОГО ДИСКРЕТНОГО ВЕЙВЛЕТ ПРЕОБРАЗОВАНИЯ В СИСТЕМАХ КОМПРЕССИИ ВИДЕОДАННЫХ | 2007 |
|
RU2342704C1 |
| СПОСОБ ПРЯМОГО И ОБРАТНОГО БЫСТРОГО ДВУХМЕРНОГО ВЕЙВЛЕТ-ПРЕОБРАЗОВАНИЯ | 2013 |
|
RU2540781C1 |
| СПОСОБ ОБРАБОТКИ СЕЙСМИЧЕСКИХ ДАННЫХ С ИСПОЛЬЗОВАНИЕМ ДИСКРЕТНОГО ВЕЙВЛЕТ-ПРЕОБРАЗОВАНИЯ | 2009 |
|
RU2412454C2 |
| УСТРОЙСТВО ОБНАРУЖЕНИЯ СЛОЖНЫХ ШИРОКОПОЛОСНЫХ ЧАСТОТНО-МОДУЛИРОВАННЫХ СИГНАЛОВ С ФИЛЬТРАЦИЕЙ В МАСШТАБНО-ВРЕМЕННОЙ ОБЛАСТИ НА ОСНОВЕ ДИСКРЕТНОГО ВЕЙВЛЕТ-ПРЕОБРАЗОВАНИЯ | 2010 |
|
RU2439601C1 |
| СПОСОБ ЦИФРОВОЙ ФИЛЬТРАЦИИ СИГНАЛОВ | 2009 |
|
RU2395158C1 |
| СПОСОБ ИССЛЕДОВАНИЯ ЭЛЕКТРОЭНЦЕФАЛОГРАММЫ ЧЕЛОВЕКА И ЖИВОТНЫХ | 2012 |
|
RU2543275C2 |
| УСТРОЙСТВО КОМПРЕССИИ ВИДЕОДАННЫХ | 2009 |
|
RU2416887C1 |
| СПОСОБ И УСТРОЙСТВО ОБНАРУЖЕНИЯ СЛОЖНЫХ ШИРОКОПОЛОСНЫХ ЧАСТОТНО-МОДУЛИРОВАННЫХ СИГНАЛОВ С ФИЛЬТРАЦИЕЙ В МАСШТАБНО-ВРЕМЕННОЙ ОБЛАСТИ | 2004 |
|
RU2282209C1 |
| АУТЕНТИФИКАЦИЯ ЗАЩИЩЕННЫХ ДОКУМЕНТОВ, В ЧАСТНОСТИ БАНКНОТ | 2008 |
|
RU2476936C2 |
Изобретение относится к информационным технологиям. Его использование для сжатия видеоизображений в системах обработки и передачи цифровой информации обеспечивает технический результат в виде повышения быстродействия вейвлетного преобразования (ВП). При прямом ВП входная информация в виде множества отсчетов обрабатывается в последовательных итерациях, в каждой из которых входную информацию пропускают через низкочастотный (НЧ) и высокочастотный (ВЧ) фильтры. Прореженные через один отчеты с НЧ фильтра являются входами следующей итерации, а прореженные через один отсчеты с НЧ фильтра последней итерации и с ВЧ фильтра являются коэффициентами ВП. При обратном ВП входной информацией являются коэффициенты прямого ВП, дополненные нулями через заданное число разрядов. Эту информацию пропускают через совокупность фильтров, структура которых однозначно определяется НЧ и ВЧ фильтрами прямого ВП, а по отсчетам с этих фильтров определяют выходную информацию. Технический результат достигается за счет того, что при обратном ВП коэффициенты прямого ВП, дополненные нулями через интервалы, равные степени двойки, пропускают через совокупность параллельных цифровых фильтров, на выходе которых сдвигают отсчеты на определенное число разрядов. Сумма отсчетов, взятых каждый со своим знаком, представляет собой отсчеты восстановленного исходного сигнала. 1 ил., 1 табл.
Способ последовательно-параллельного вейвлетного преобразования, заключающийся в том, что вейвлетное преобразование состоит из прямого и обратного вейвлетного преобразования, при прямом вейвлетном преобразовании входная информация обрабатывается путем s последовательных итераций, причем входной информацией первой итерации является исходный сигнал, представленный множеством значений отсчетов этого сигнала, при этом входную информацию каждой из итераций пропускают через два фильтра: низкочастотный и высокочастотный фильтр, и значения отсчетов сигнала с выхода высокочастотного фильтра, прореженные через один отсчет сигнала, являются коэффициентами вейвлетного преобразования, а значения отсчетов сигнала с выхода низкочастотного фильтра, прореженные через один отсчет, являются входной информацией следующей итерации прямого вейвлетного преобразования, значения отсчетов сигнала с выхода низкочастотного фильтра последней итерации прямого вейвлетного преобразования, прореженные через один отсчет сигнала, также являются коэффициентами вейвлетного преобразования, при обратном вейвлетном преобразовании входной информацией являются коэффициенты прямого вейвлетного преобразования, причем эти коэффициенты дополняются нулевыми значениями, при этом входную информацию обратного вейвлетного преобразования пропускают через совокупность фильтров, структура которых однозначно определяется низкочастотными и высокочастотными фильтрами прямого вейвлетного преобразования, а затем определяют выходную информацию совокупности фильтров, отличающийся тем, что при обратном вейвлетном преобразовании коэффициенты вейвлетного преобразования с выходов высокочастотных фильтров прямого вейвлетного преобразования, дополненные нулевыми значениями, число которых между соседними коэффициентами равно последовательным степеням двойки, начиная с первой степени и до s-й степени включительно, пропускают через совокупность параллельных цифровых фильтров, на выходе этих цифровых фильтров осуществляют сдвиг значений отсчетов сигнала в сторону старших разрядов на число разрядов, равное последовательным степеням двойки, начиная с первой степени и до s-й степени включительно, и далее вычисляют сумму W полученных значений отсчетов сигнала, при этом одновременно коэффициенты вейвлетного преобразования с выхода низкочастотного фильтра последней итерации прямого вейвлетного преобразования, дополненные нулевыми значениями, причем число нулевых значений равно s-й степени двойки, пропускают через свой цифровой фильтр, на выходе этого цифрового фильтра осуществляют сдвиг значений отсчетов сигнала в сторону старших разрядов на число разрядов, равное s-й степени двойки, и из полученных значений отсчетов сигнала вычитают ранее вычисленную сумму W и в результате получают отсчеты восстановленного исходного сигнала.
| ШАТКИН Я.И | |||
| Вейвлет-преобразования и сжатие изображений // Программист, № 3, 2002, стр | |||
| Устройство для устранения мешающего действия зажигательной электрической системы двигателей внутреннего сгорания на радиоприем | 1922 |
|
SU52A1 |
| УСТРОЙСТВО ДЛЯ АВТОМАТИЗИРОВАННОГО СЪЕМА И ОБРАБОТКИ ИНФОРМАЦИИ О ЭЛЕКТРОМАГНИТНОМ ПОЛЕ БИООБЪЕКТА | 2001 |
|
RU2201132C2 |
| Адаптивный компенсатор фазового дрожания | 1985 |
|
SU1298932A1 |
| US 6148111 A, 14.11.2000 | |||
| US 6134350 A, 17.10.2000 | |||
| US 5859788 A, 12.01.1999 | |||
| Перекатываемый затвор для водоемов | 1922 |
|
SU2001A1 |
| Печь для непрерывного получения сернистого натрия | 1921 |
|
SU1A1 |
| Дорожная спиртовая кухня | 1918 |
|
SU98A1 |
Авторы
Даты
2005-04-10—Публикация
2003-05-05—Подача