Предлагаемое изобретение относится к теплофизическим измерениям, в частности к измерениям теплофизических характеристик твердых материалов, и может найти широкое применение в теплоэнергетике, строительстве, химической технологии и т.д.
Известен способ определения температуропроводности твердых материалов [см., например, Кулаков М.В. Технологические измерения и приборы для химических производств. Уч. для Вузов. М.: Машиностроение, 1983, 424 с.], состоящий в воздействии от мгновенного источника тепла на исследуемый образец в виде пластины или стержня и определении момента наступления максимального значения температуры в заданных точках исследуемых образцов с последующим расчетом искомой температуропроводности по полученным соотношениям.
Основным недостатком данного способа является малая точность измерения температуропроводности, обусловленная большими динамическими погрешностями из-за влияния конечной длительности импульса, а также резко нестационарными тепловыми процессами при таком виде воздействия на исследуемый объект, большими потерями тепла из-за неучтенного теплообмена между образцом и окружающей средой, влиянием инерционности термопреобразователей (термопар), а также контактными термосопротивлениями между образцом и термопреобразователями. Кроме того, данный способ требует помещения термоприемников внутрь исследуемого образца, что нарушает его целостность.
Известен способ определения температуропроводности твердых материалов [см., например, Кондратьев Г.М. Регулярный тепловой режим / Г.М.Кондратьев. М.: Гостехиздат, 1954, 408 с.], основанный на охлаждении тела при постоянном значении температуры среды, регистрации изменения значения избыточных температур центра и поверхности исследуемого образца и вычислении искомого коэффициента температуропроводности по соотношению, учитывающему также форму и размеры исследуемого образца, координаты точек, где измеряется температура, а также интенсивность теплообмена на поверхности, соприкасающейся со средой.
Основным недостатком данного способа является необходимость тщательной реализации теоретических предпосылок о постоянстве температуры среды и коэффициента теплоотдачи на протяжении всего эксперимента, так как несоблюдение этих условий приводит к резкому увеличению погрешности измерений температуропроводности исследуемых объектов. Кроме того, недостатком этого способа является необходимость предварительного определения опытным путем коэффициента внешнего теплообмена, что существенно усложняет реализацию способа, снижает его оперативность и метрологический уровень. Существенным недостатком данного способа является также то, что при его реализации требуется помещать термоприемники внутрь исследуемого образца, что нарушает его целостность.
За прототип принят способ определения температуропроводности твердых материалов (акалориметр) [см., например, Кондратьев Г.М. Регулярный тепловой режим / Г.М. Кондратьев. М.: Гостехиздат, 1954, 408 с.], состоящий в нагреве исследуемого образца в форме пластины или параллелепипеда путем погружения его в кипящую жидкость для обеспечения бесконечно большого коэффициента теплоотдачи, т.е. создания теплообмена при граничных условиях 1-го рода, контроле изменения температуры исследуемого образца и определении наступления регулярного теплового режима по изменению натурального логарифма контролируемой избыточной температуры во времени с последующим вычислением темпа нагрева, постоянство которого характеризует наступление регулярного установившегося состояния, и определении искомого коэффициента температуропроводности как произведения значения темпа нагрева на коэффициент пропорциональности, зависящий от формы и размеров исследуемого образца.
Недостатками способа-прототипа являются:
1) необходимость проведения эксперимента в капельной среде;
2) необходимость обеспечения большой величины коэффициента теплоотдачи и поддержания его на постоянном уровне в процессе всего теплофизического эксперимента;
3) зависимость точности результатов измерения от изменения температуры окружающей среды и необходимость ее поддержания постоянной на протяжении всего эксперимента;
4) обязательная установка термопары внутри объема исследуемого образца, что нарушает его целостность;
5) во избежание смачивания образца необходимо его поверхность пассивировать (покрывать эпоксидной смолой или лаком), что, во-первых, снижает точность определения искомой температуропроводности из-за влияния защитного слоя на динамику тепловых процессов, во-вторых, усложняет условия проведения эксперимента и требует дополнительных затрат средств и времени.
Техническая задача изобретения - повышение точности определения коэффициента температуропроводности исследуемых твердых материалов без нарушения их целостности и эксплуатационных характеристик.
Поставленная техническая задача достигается тем, что в способе неразрушающего контроля температуропроводности твердых материалов, состоящем в симметричном нагреве образцов в форме призмы квадратного сечения (параллелепипеда), измерении температурно-временных изменений в фиксированных точках исследуемого образца, определении момента наступления регулярного теплового режима в исследуемом образце с последующим расчетом искомой температуропроводности на основе полученной информации, измеряют температуру на поверхности призмы в двух точках - на ребре и середине грани, определяют момент наступления упорядоченного теплового режима в исследуемом образце по динамическому критерию
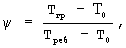
где Тгр - температура грани призмы, Треб - температура ребра призмы, Т0 - начальная температура исследуемого образца, затем после наступления упорядоченного теплового режима в два заданных момента времени τ1 и τ2 измеряют температуры Т(0, τi) и Т(R, τi) (где i=1, 2), соответственно, на ребре и в середине грани призмы, а искомый коэффициент температуропроводности определяют по соотношению
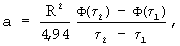
где R - расстояние между ребром и центром грани призмы (между точками контроля температуры), Ф(τi) - температурный комплекс, определяемый на основе закономерности упорядоченного теплового режима по соотношению
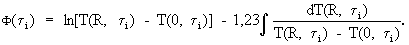
Далее нагретый образец вынимают из цилиндрической полости, охлаждают на воздухе при комнатной температуре и естественной конвекции, определяют при этом момент наступления упорядоченного теплового режима по динамическому критерию
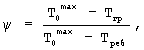
где  - максимальная температура призмы, полученная при ее нагревании до термодинамического равновесия, т.е. температура, с которой начинают охлаждение исследуемого образца, затем для заданного промежутка времени Δτ=τ2-τ1 определяют изменение температурного комплекса ΔФ(τ)=Ф(τ2)-Ф(τ1), где
- максимальная температура призмы, полученная при ее нагревании до термодинамического равновесия, т.е. температура, с которой начинают охлаждение исследуемого образца, затем для заданного промежутка времени Δτ=τ2-τ1 определяют изменение температурного комплекса ΔФ(τ)=Ф(τ2)-Ф(τ1), где
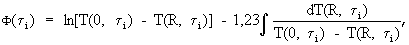 i=1,2
i=1,2
после чего вычисляют значения искомой температуропроводности а по приведенному выше соотношению, а за искомое значение температуропроводности принимают среднее значение, полученное усреднением результатов при нагреве и охлаждении исследуемого образца.
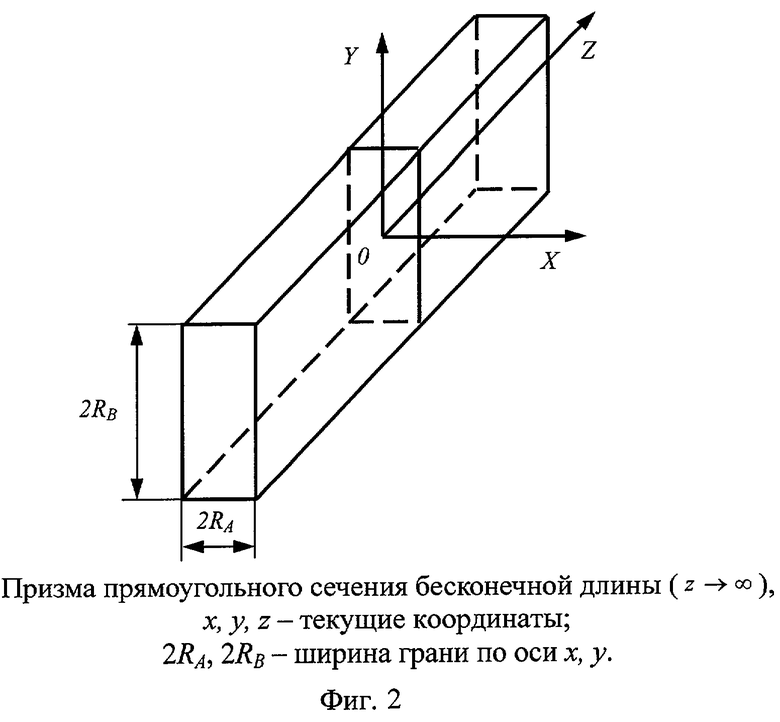
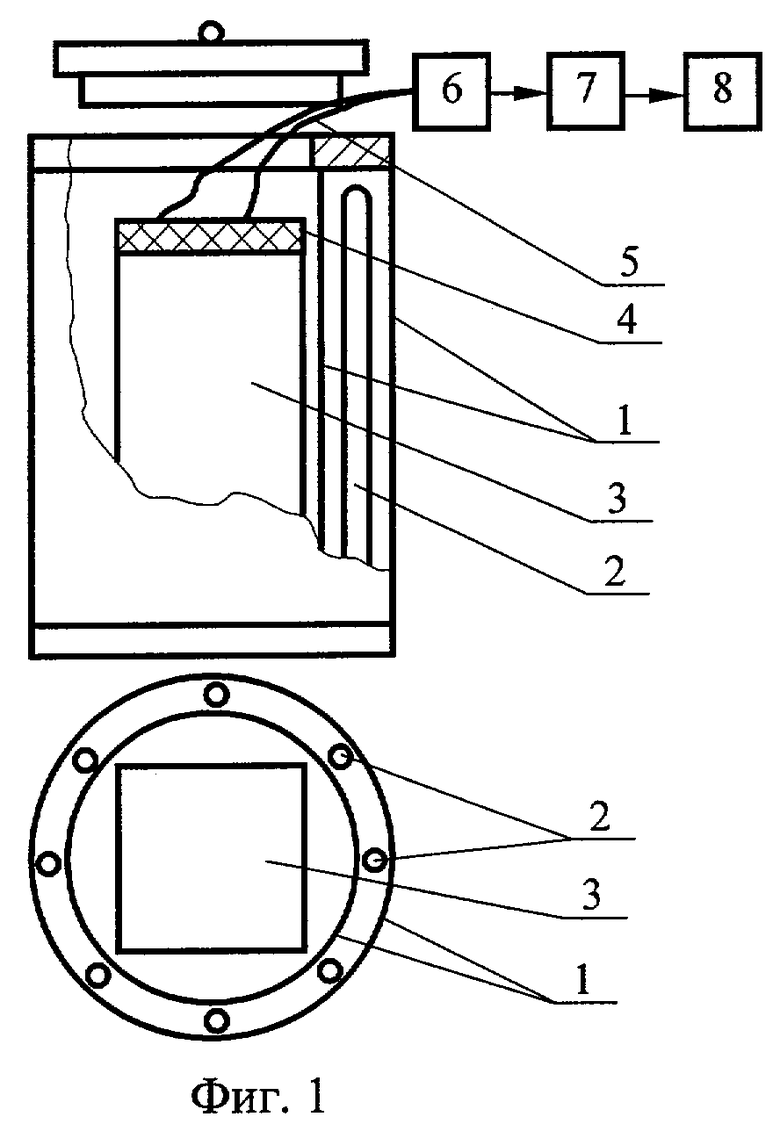
Сущность способа заключается в следующем. Исследуемый образец в форме призмы квадратного сечения, длина которой во много раз (в 6 и более) превышает ширину грани, что обеспечивает условие бесконечной длины, помещают в испытательную цилиндрическую камеру установки, схема которой приведена на фиг.1. Конструкция экспериментальной установки состоит из двух расположенных друг в друге полых цилиндров 1, служащих изотермическими поверхностями и выполненных из листового материала. В зазоре между экранами установлены коаксиальные нагреватели 2, питающиеся через стабилизатор от сети переменного тока и обеспечивающие практически симметричный нагрев исследуемого образца в виде призмы квадратного сечения 3. Нагреватель представляет собой равномерно уложенную нихромовую проволоку, помещенную в коаксиально расположенных керамических трубках, выполняющих роль электрического изолятора. Снизу камера закрыта, а сверху имеется отверстие с крышкой 4 из теплоизоляционнного материала, через которое образец помещают в установку. Измерение температур на ребре и в середине грани исследуемой призмы осуществляют термопарами 5, которые подключены к коммутатору 6 и далее через усилитель 7 и порт ввода-вывода к ЭВМ 8.
После помещения исследуемого образца в камеру установки, включают нагреватели и контролируют изменение температуры на ребре и в середине грани призмы. Расчетное соотношение для определения искомого коэффициента температуропроводности получено на основании следующих рассуждений.
При любых граничных условиях процесс симметричного нагревания призмы прямоугольного сечения (см. фиг.2), помещенной в цилиндрическую полость установки, может быть описан дифференциальным уравнением
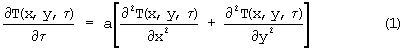
с условиями однозначности (симметрии, граничными и начальными)
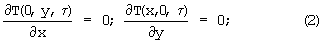
T(R,y,τ)=TП(y,τ) T(x,R,τ)=TП(x,τ); (3)
T(x,y,0)=T0. (4)
Выражение (1) можно записать в виде
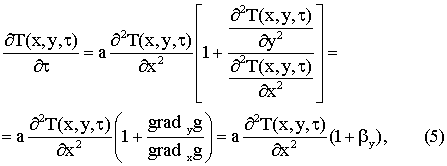
где βy - отношение составляющей градиента теплового потока в направлении y к составляющей градиента теплового потока в направлении х.
Если призму нагревать симметрично конвективным потоком тепла, то температурное поле по ее сечению можно определить по принципу перемножения температурных критериев [см. Лыков А.В. Теория теплопроводности / А.В. Лыков. М.: Высшая школа, 1967, 599 с.]:
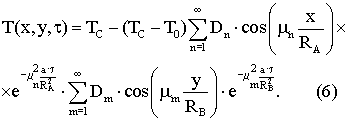
Составляющие градиента теплового потока в направлении x и y соответственно будут равны
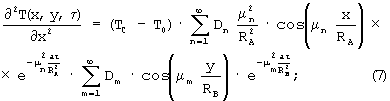
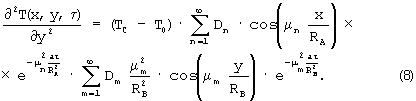
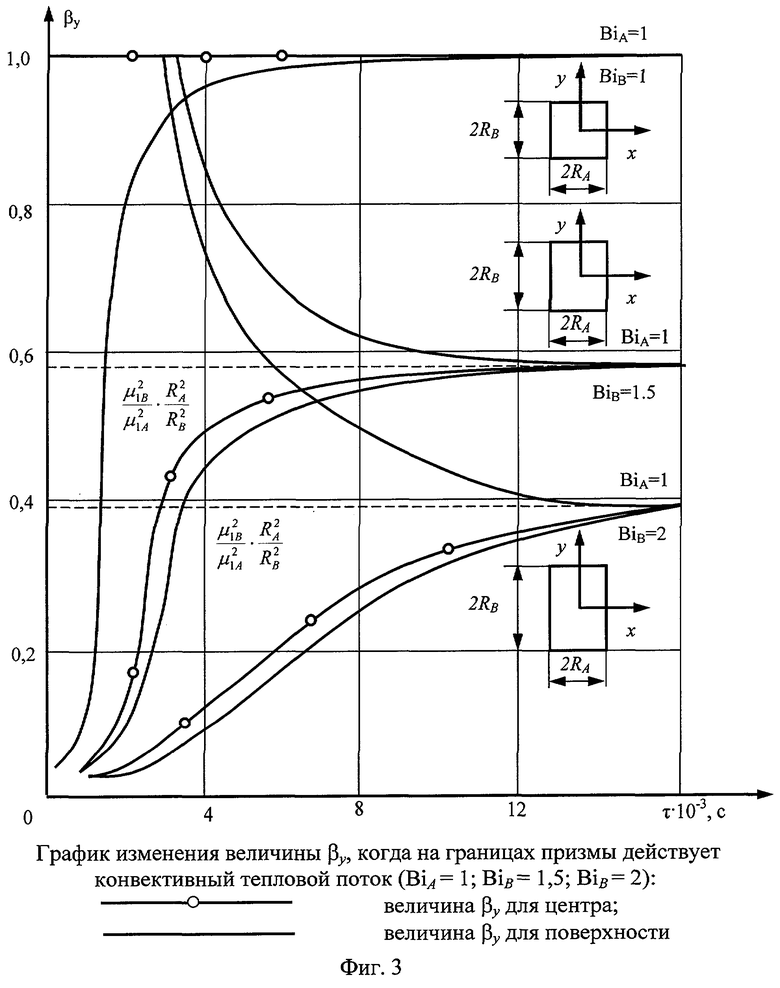
Используя решения (6)-(8), можно показать характер изменения соотношений составляющих градиента теплового потока βy для различных вариантов (см. фиг.3).
В начальном периоде теплового воздействия отношение составляющих градиента теплового потока является функцией критерия Fo, но с течением времени процесс становится автомодельным относительно аргумента τ. Это происходит потому, что в области регулярного режима (τ>τ*) выражение (6) упрощается, а кривые асимптотически стремятся к пределу
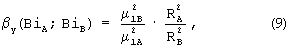
где μ1A и μ1B - первые характеристические числа, зависящие от чисел Био, определяемые по выражениям:
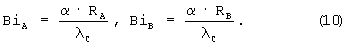
Таким образом, в регулярной стадии βy не зависит от критерия Фурье, а является функцией BiA и ВiB и отношениями между измерениями сторон призмы RA и RB во второй степени. При RB, стремящемся к RA, призма принимает форму квадратного сечения, а значение βy начинает стремиться к своему предельному значению, равному единице. Отношение составляющих градиента теплового потока βy (когда RA=RB) при лучистом нагреве призмы квадратного сечения также равно единице в области упорядоченного теплового периода. Этот же результат получается при симметричном нагреве призмы квадратного сечения и суммарным потоком тепла (одновременно конвекцией и радиацией).
Следовательно, для области упорядоченного теплового периода в призме квадратного сечения бесконечной длины условия нагревания могут быть описаны следующими зависимостями:
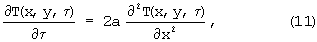
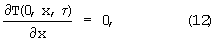
T(R,y,τ)=Tп(y,τ), (13)
T(x,y,τ*)=T*(x,y), (14)
где τ>τ*.
В процессах распространения тепла, описываемых системой уравнений (11)-(14), искомое температурное поле является функцией многих физических параметров. Поскольку любое явление природы не зависит от выбранной системы единиц и величин измерения, то наиболее целесообразно описывать его совокупностью уравнений в безразмерном виде (15)-(18). Безразмерная форма имеет ряд преимуществ и замечательна тем, что охватывает множество явлений, подобных друг другу, и, кроме того, позволяет оперировать значительно меньшим числом аргументов.
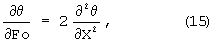
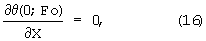
θ(1;Fo)=θП(Fo), (17)
θ(x,y,0)=θ0. (18)
где θп(Fo) - уже заданное изменение температуры поверхности тела.
Система (15)-(18) дает возможность получить решение в неявной форме [см. Видин Ю.В. Инженерные методы расчетов процессов теплопереноса / Ю.В. Видин. Красноярск, 1974, 144 с.]:
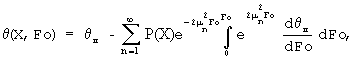
которое для упорядоченной части процесса ограничивается только первым членом ряда и имеет вид:
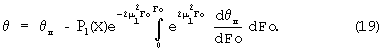
Поскольку граничные условия (17) предусматривают различные способы нагревания (или охлаждения), то решение (19) следует рассматривать как универсальное в этом отношении. Кроме того, функция Р(Х) для неограниченной пластины выражается через тригонометрическую функцию. Для призмы квадратного сечения бесконечной длины, получаемой пересечением двух неограниченных пластин, выражение (19) записывается так:
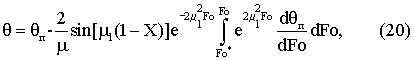
где Fo* соответствует началу упорядоченного теплового режима.
Вычислив значения относительных температур соответственно для поверхности (Х=1) и центра бруса (Х=0), определим их разность Δθ
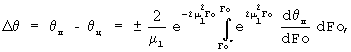
или
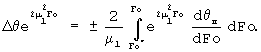
Преобразуем это выражение к виду
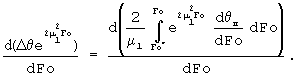
После дифференцирования получаем
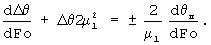
С учетом сокращения и разделения переменных
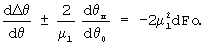
Интегрируя последнее выражение и обозначив тождество символом Ф, получим
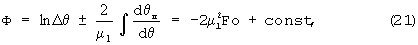
или в размерной форме
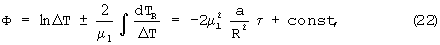
где ΔT - положительная разность температур между поверхностью и центром тела. Знак минус перед интегралом означает процесс нагревания, а знак плюс - охлаждения; R - половина ширины грани призмы; μ1=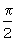 ;
;  - постоянное число, теоретически равное 1,27, что соответствует измерению температуры строго в центральной точке призмы квадратного сечения. При некотором смещении точки эта постоянная величина несколько уменьшается. С учетом объемности термопары можно рекомендовать 2/μ1=1,23.
- постоянное число, теоретически равное 1,27, что соответствует измерению температуры строго в центральной точке призмы квадратного сечения. При некотором смещении точки эта постоянная величина несколько уменьшается. С учетом объемности термопары можно рекомендовать 2/μ1=1,23.
Следовательно, математические условия (15)-(18) позволяют получить решение в неявной форме с точностью до неизвестной постоянной величины (константы)
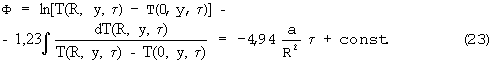
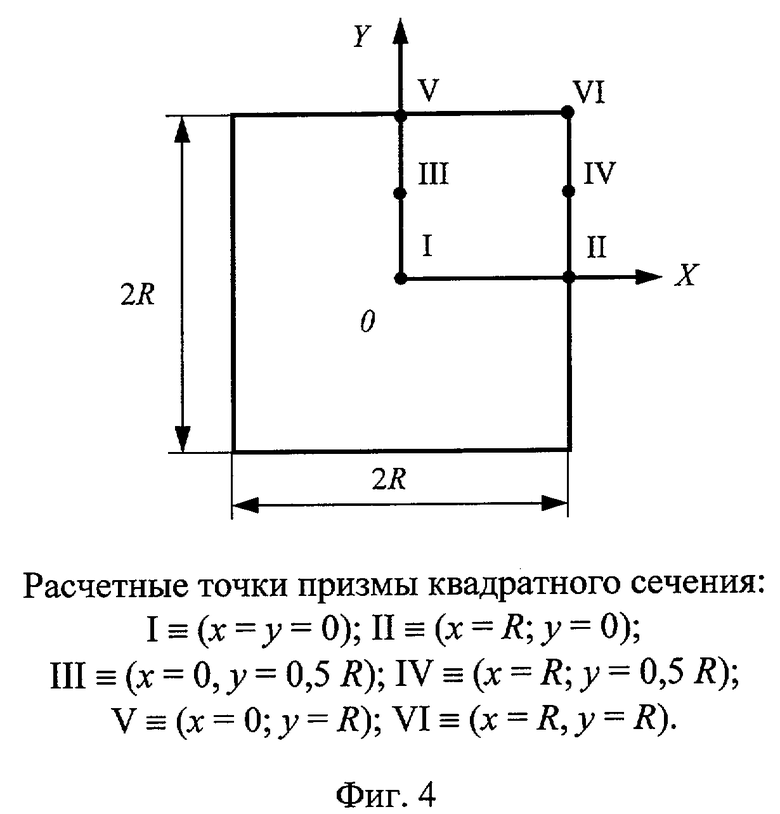
Если температуру измерять в конкретных парах точек I-II, III-IV, V-VI сечения призмы (см. фиг.4), то выражение упорядоченного теплового режима для каждой пары запишется следующим образом:
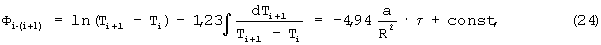
где i=1...5.
Наибольший интерес представляют точки V - середина грани призмы квадратного сечения и VI - ребра призмы, так как в этом случае все измерения температур производятся на поверхности исследуемого образца и отпадает необходимость проникать с термопарой внутрь тела образца, разрушать его, что в итоге позволяет осуществить метод неразрушающего контроля, т.е. определить искомый коэффициент температуропроводности без нарушения целостности и эксплуатационных характеристик исследуемых объектов.
Таким образом, измерив температуры в два заранее заданных момента времени τ1 и τ2 после наступления упорядоченного теплового режима, из соотношения (24) получается формула для определения коэффициента температуропроводности в следующем виде
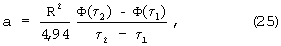
где
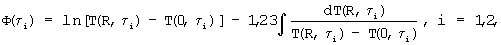
T(0,τi) и Т(R,τi) - температуры, соответственно, на ребре и в середине грани исследуемой призмы в заданные моменты времени τ1 и τ2.
Для определения начала регулярной части теплового режима используют отношение
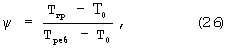
где Тгр - температура грани призмы, Треб - температура ребра призмы, Т0 - начальная температура исследуемого образца.
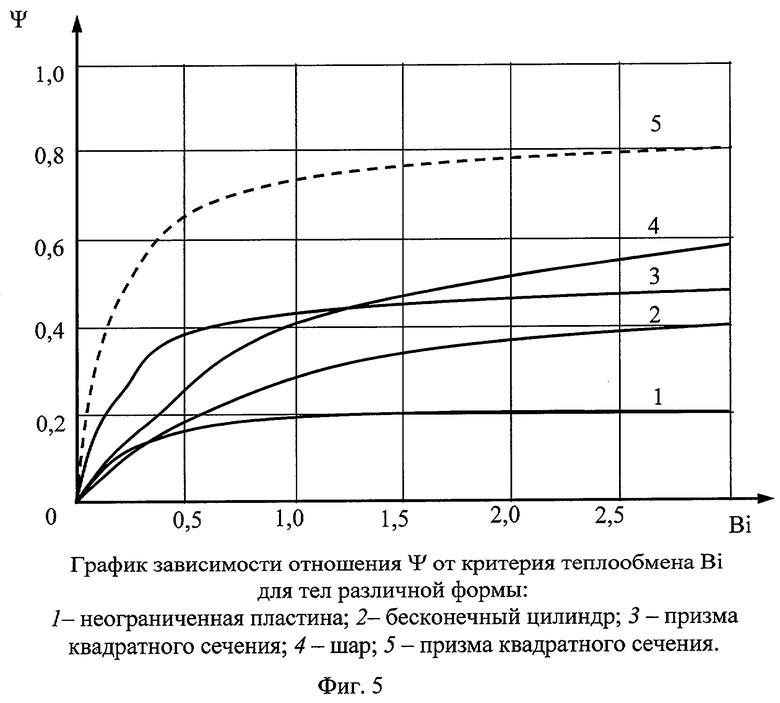
Данный динамический критерий был получен из закономерности изменения ψ в зависимости от критерия теплообмена Bi для тел различной формы.
Графики функций ψ=f(Bi) для неограниченной пластины, бесконечного цилиндра, призмы квадратного сечения и шара показаны на фиг.5.
Из графика функции ψ=f(Bi) на фиг.5 видно, что для призмы квадратного сечения наступление упорядоченного теплового режима гарантировано с погрешностью порядка 1% при ψ=0,78.
Полученная закономерность является универсальной, т.е. может быть использована при различных граничных условиях и позволяет установить наступление упорядоченного теплового режима при симметричном нагревании призмы квадратного сечения по температурам ребра, центра грани и начальной температуре без определения величины критерия Фурье.
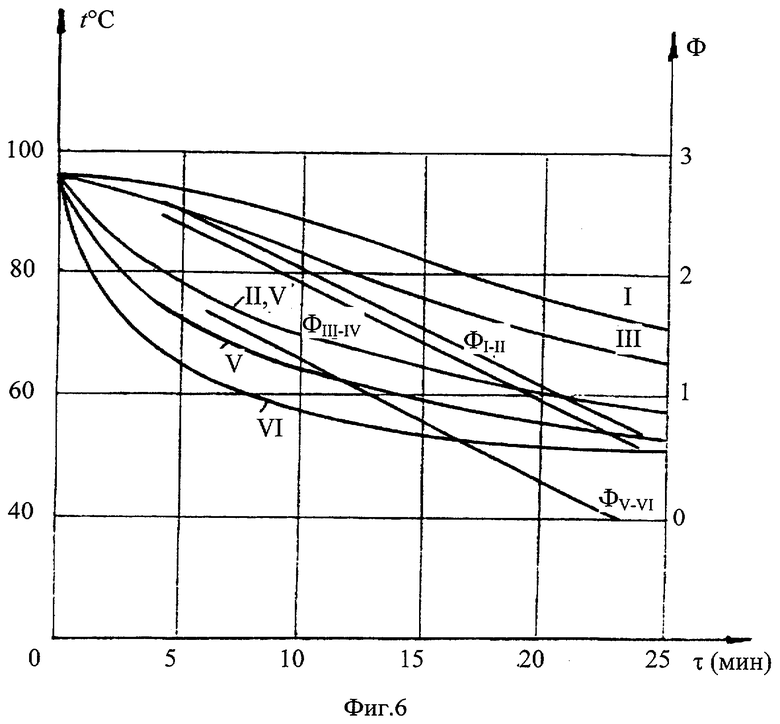
После нагрева исследуемого образца до установившегося термодинамического равновесия, снятия информации о температурно-временных изменениях в точках контроля и расчете искомой температуропроводности материала по соотношению (25) выключают нагреватели, вынимают образец из цилиндрической камеры и охлаждают на воздухе при комнатной температуре и естественной конвекции. Из экспериментальных данных и вычислений (см. фиг.6) видно, что при охлаждении призмы квадратного сечения с определенного момента времени τ* динамический критерий, определяемый по соотношению
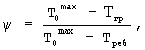
где 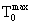 - максимальная температура призмы, полученная при ее нагревании до термодинамического равновесия, т.е. температура, с которой начинают охлаждение исследуемого образца, становится постоянным и равным для призмы ψ=0,78, после чего начинается упорядоченный тепловой режим и температурный комплекс
- максимальная температура призмы, полученная при ее нагревании до термодинамического равновесия, т.е. температура, с которой начинают охлаждение исследуемого образца, становится постоянным и равным для призмы ψ=0,78, после чего начинается упорядоченный тепловой режим и температурный комплекс
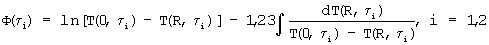
выходит на прямую линию, а угловой коэффициент ΔФ/Δτ построенной прямой линии становится постоянным. Таким образом, определив изменение температурного комплекса ΔФ за заданный интервал времени Δτ после наступления упорядоченного теплового режима, по формуле (25) рассчитывают коэффициент температуропроводности исследуемого образца при его охлаждении. За окончательное значение коэффициента температуропроводности принимают среднеарифметическое результатов измерения на стадии нагрева и охлаждения, что существенно повышает достоверность результатов и снижает случайную составляющую общей погрешности измерения искомой температуропроводности.
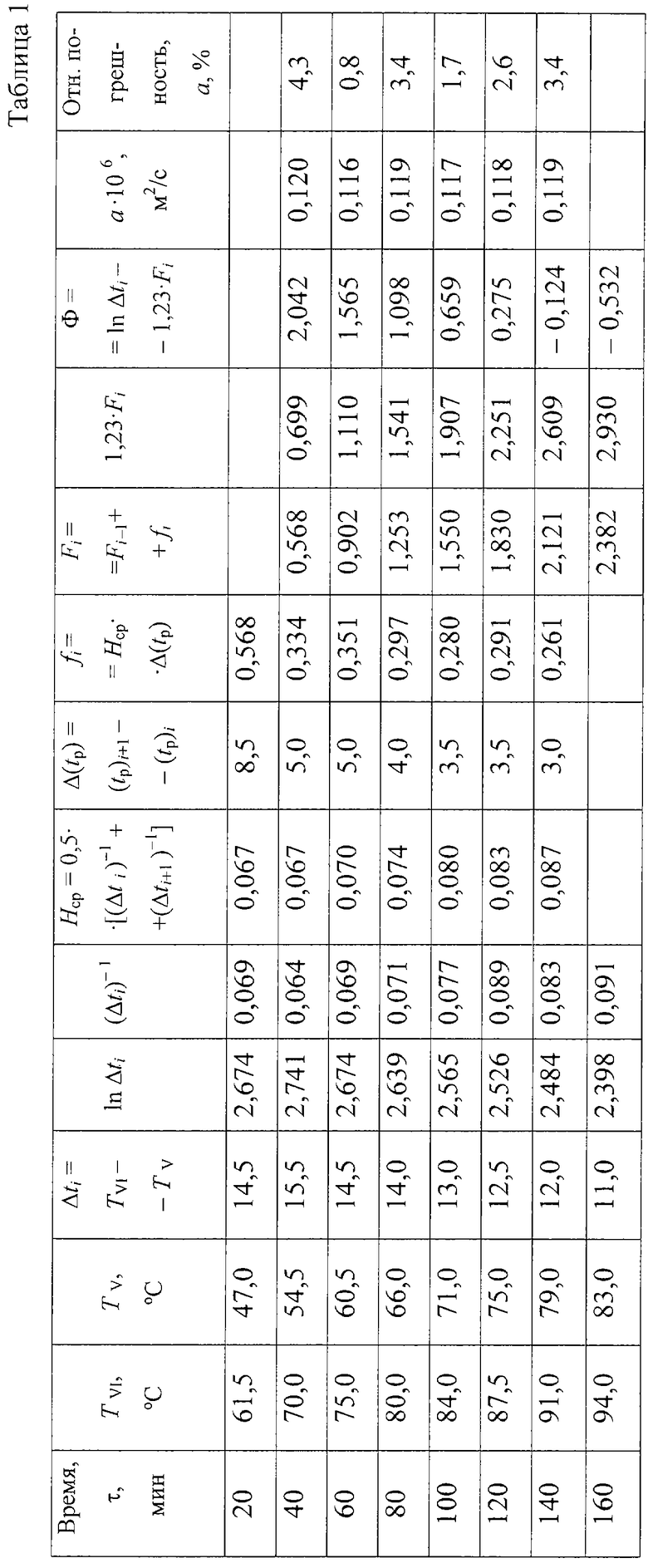
В таблице 1 представлено экспериментальное распределение температур при нагревании призмы из оргстекла и контроле температур на ребре и середине грани призмы (сечение V-VI), а также результаты расчетов температурных комплексов ФV-VI и температуропроводности.
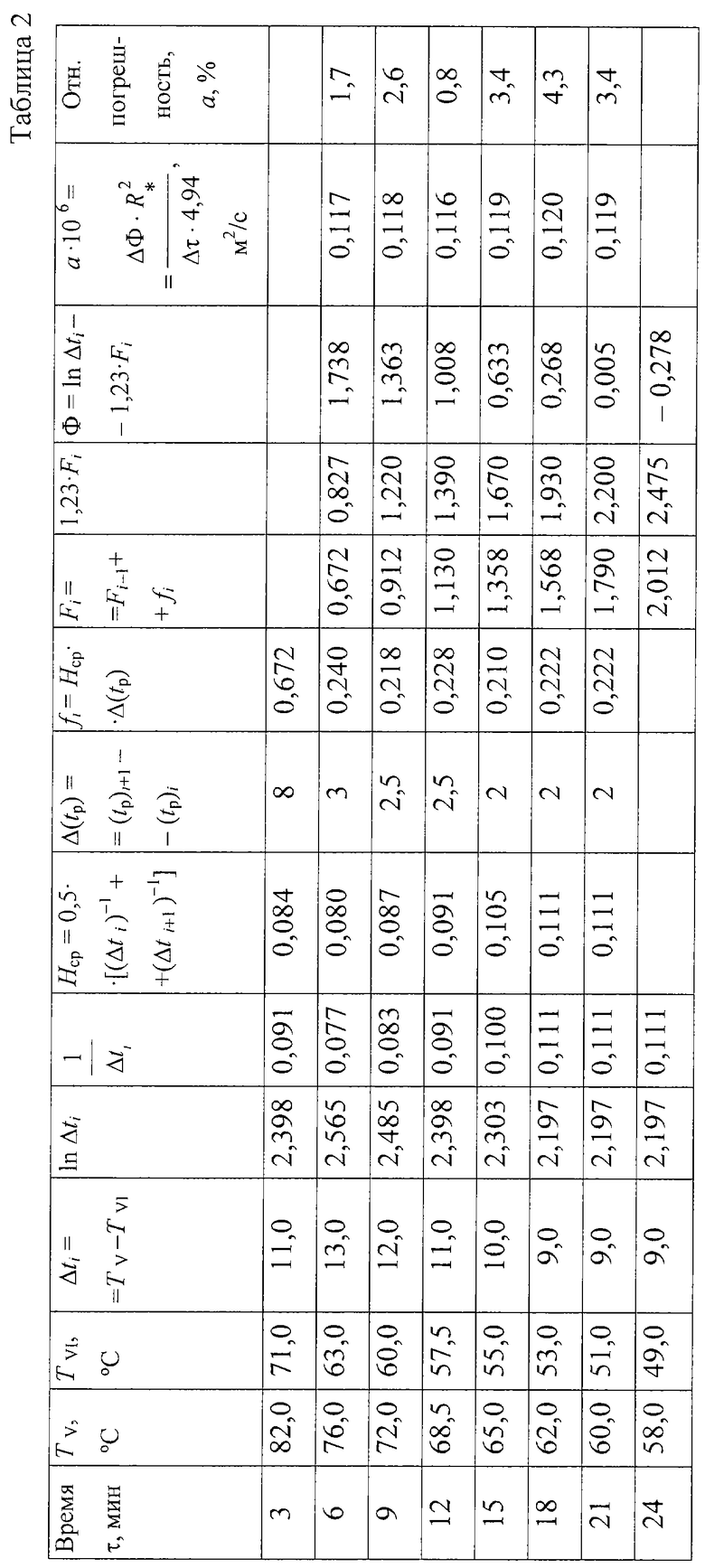
В таблице 2 представлены экспериментальные данные распределения температуры при охлаждении призмы из оргстекла и контроле температур также в сечении V-VI, а также результаты температурных комплексов ФV-VI и температуропроводности.
Из полученных экспериментальных данных следует, что относительная погрешность измерения коэффициента температуропроводности разработанным способом неразрушающего контроля, использующим упорядоченный тепловой режим в призме квадратного сечения, составляет не более 5%, тогда как в аналогах и способе-прототипе относительная погрешность определения искомой температуропроводности составляет не менее 8-10%.
Большим преимуществом разработанного способа по сравнению с известными является отсутствие необходимости в измерении в процессе эксперимента таких физических величин, как коэффициент теплообмена, температура окружающей среды, степень черноты и т.д. Кроме того, разработанный способ позволяет проводить измерения без нарушения целостности и эксплуатационных характеристик исследуемых образцов.
В заявленном техническом решении отпадает необходимость в создании чисто конвективного или чисто лучистого теплообмена, что значительно упрощает условия проведения эксперимента (экспериментальную установку) и повышает метрологический уровень результатов измерения.
Таким образом, разработанный способ неразрушающего контроля температуропроводности твердых материалов имеет ряд существенных преимуществ перед известными способами указанного назначения, что, несомненно, позволит использовать его в практике теплофизических измерений и различных отраслях народного хозяйства.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ НЕРАЗРУШАЮЩЕГО КОНТРОЛЯ КОМПЛЕКСА ТЕПЛОФИЗИЧЕСКИХ ХАРАКТЕРИСТИК ТВЕРДЫХ СТРОИТЕЛЬНЫХ МАТЕРИАЛОВ | 2004 |
|
RU2263901C1 |
| СПОСОБ НЕРАЗРУШАЮЩЕГО КОНТРОЛЯ ТЕПЛОФИЗИЧЕСКИХ ХАРАКТЕРИСТИК СТРОИТЕЛЬНЫХ МАТЕРИАЛОВ И ИЗДЕЛИЙ | 2012 |
|
RU2497105C1 |
| СПОСОБ НЕРАЗРУШАЮЩЕГО КОНТРОЛЯ КОМПЛЕКСА ТЕПЛОФИЗИЧЕСКИХ ХАРАКТЕРИСТИК ТВЕРДЫХ СТРОИТЕЛЬНЫХ МАТЕРИАЛОВ И УСТАНОВКА ДЛЯ ЕГО ОСУЩЕСТВЛЕНИЯ | 2013 |
|
RU2530441C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ТЕПЛОФИЗИЧЕСКИХ СВОЙСТВ ТВЕРДЫХ МАТЕРИАЛОВ | 2013 |
|
RU2556290C1 |
| Способ неразрушающего контроля комплекса теплофизических характеристик твердых строительных материалов и устройство для его осуществления | 2021 |
|
RU2767468C1 |
| СПОСОБ НЕРАЗРУШАЮЩЕГО КОНТРОЛЯ ТЕПЛОФИЗИЧЕСКИХ ХАРАКТЕРИСТИК СТРОИТЕЛЬНЫХ МАТЕРИАЛОВ И ИЗДЕЛИЙ | 2014 |
|
RU2570596C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ТЕПЛОФИЗИЧЕСКИХ ХАРАКТЕРИСТИК СТРОИТЕЛЬНЫХ МАТЕРИАЛОВ (ВАРИАНТЫ) | 2008 |
|
RU2399911C2 |
| Способ неразрушающего контроля теплофизических характеристик строительных материалов и изделий | 2019 |
|
RU2698947C1 |
| СПОСОБ ИДЕНТИФИКАЦИИ КОМПЛЕКСА ТЕПЛОФИЗИЧЕСКИХ СВОЙСТВ ТВЕРДЫХ МАТЕРИАЛОВ | 2006 |
|
RU2324166C1 |
| СПОСОБ ИДЕНТИФИКАЦИИ КОМПЛЕКСА ТЕПЛОФИЗИЧЕСКИХ СВОЙСТВ ТВЕРДЫХ МАТЕРИАЛОВ | 2006 |
|
RU2328724C1 |
Использование: для неразрушающего контроля теплофизических характеристик твердых материалов. Сущность заключается в том, что проводят симметричный нагрев образцов в форме призмы квадратного сечения (параллелепипеда), измерение температурно-временных изменений в фиксированных точках исследуемого образца, определение момента наступления регулярного теплового режима в исследуемом образце с последующим расчетом искомой температуропроводности на основе полученной информации, измеряют температуру на поверхности призмы в двух точках - на ребре и середине грани, определяют момент наступления упорядоченного теплового режима в исследуемом образце, затем после наступления упорядоченного теплового режима в два заданных момента времени измеряют температуры на ребре и в середине грани призмы, после чего определяют искомый коэффициент температуропроводности. Технический результат: повышение точности определения коэффициента температуропроводности исследуемых твердых материалов без нарушения их целостности и эксплуатационных характеристик. 1 з.п. ф-лы, 6 ил, 2 табл.
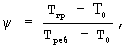
где Тгр - температура грани призмы, Треб - температура ребра призмы, Т0 - начальная температура исследуемого образца,
затем после наступления упорядоченного теплового режима в два заданных момента времени τ1 и τ2 измеряют температуры Т(0, τi) и T(R, τi) (где i=1, 2) соответственно на ребре и в середине грани призмы, а искомый коэффициент температуропроводности определяют по соотношению

где R - расстояние между ребром и центром грани призмы (между точками контроля температуры), Ф(τi) - температурный комплекс, определяемый на основе закономерности упорядоченного теплового режима по соотношению
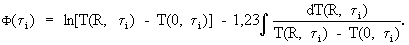
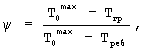
где Т
затем для заданного промежутка времени Δτ=τ2-τ1 определяют изменение температурного комплекса ΔФ(τ)=Ф(τ2)-Ф(τ1),
где 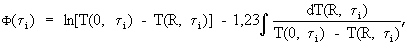 i=1,2
i=1,2
после чего вычисляют значения искомой температуропроводности а по соотношению, приведенному в п.1, и за искомое значение температуропроводности принимают среднее значение, полученное в пп.1 и 2.
| Способ определения теплофизических свойств материалов | 1972 |
|
SU458753A1 |
| Способ определения теплофизических характеристик полимерных материалов | 1979 |
|
SU934335A1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ФИЗИЧЕСКИХ СВОЙСТВ ОДНОРОДНЫХ ИЗОТРОПНЫХ УПРУГИХ МАТЕРИАЛОВ | 1993 |
|
RU2061230C1 |
| ЕР 0459036 А1, 04.12.1991 | |||
| US 4522512 A, 11.06.1985 | |||
| US 5297868 A, 29.03.1994. | |||
Авторы
Даты
2005-04-20—Публикация
2004-04-12—Подача