Предлагаемое изобретение относится к теплофизическим измерениям, в частности к измерениям теплофизических характеристик твердых материалов, и может найти широкое применение в теплоэнергетике, строительстве, химической технологии и т.д.
Известен ряд методов комплексного определения теплофизических свойств, основанных на решении задач теплопроводности при действии источника (зонда) постоянной мощности (плоского, цилиндрического, сферического) в неограниченной среде.
Известен метод комплексного определения тепловых свойств веществ [см., например, Осипова В. А. Экспериментальное исследование процессов теплообмена. М.: Энергия, 1979. 320 с], основанный на использовании регулярного теплового режима третьего рода (температурных волн) с измерением монотонного изменения средней температуры образца во времени. В методе используются два одинаковых образца с плоскими нагревателями, которые помещаются в печь, причем один образец с нагревателем является основным, второй - вспомогательным. В основном нагревателе ток изменяется по гармоническому закону, а во вспомогательном (компенсационном) нагревателе мощность задается равной средней по времени мощности основного нагревателя.
В процессе эксперимента регистрируется температура в обоих образцах в точках внутри исследуемых тел, расположенных соответственно на одинаковых расстояниях от нагревателей, а искомые коэффициенты тепло- и температуропроводности определяются по соответствующим формулам.
Основным недостатком данного способа является малая точность измерения температуропроводности и теплопроводности, обусловленная динамическими погрешностями из-за влияния значения теплоемкости и периодической составляющей мощности нагревателя, амплитудных (максимальных) периодических составляющих температур, потерями тепла за счет теплообмена с окружающей средой, а также контактным сопротивлением между образцами и нагревателем. Кроме того, метод требует помещения дифференциальных термопар внутрь исследуемого образца, что нарушает его целостность.
Известен импульсный метод линейного источника тепла [см., например, Шашков А.Г., Волохов Г.М., Абраменко Т.М. Методы определения теплопроводности и температуропроводности. М.: Энергия, 1973. с.165-178], основанный на решении двухмерного уравнения теплопроводности для неограниченного тела при действии в нем в течение короткого времени τ0 линейного источника тепла, определении максимальной избыточной температуры в фиксированной точке исследуемого тела и времени наступления максимума термограммы нагрева, расчете искомых теплофизических характеристик по соответствующим формулам.
Основным недостатком данного способа также является малая точность измерения температуропроводности и теплопроводности, обусловленная динамическими погрешностями из-за влияния теплоемкости нагревателя, амплитудных (максимальных) составляющих температур, потерями тепла за счет теплообмена с окружающей средой, а также контактным сопротивлением между образцами и нагревателем. Кроме того, метод требует помещения дифференциальных термопар внутрь исследуемого образца, что нарушает его целостность.
За прототип принят способ определения теплофизических характеристик полимерных материалов [см., например, а.с. СССР №934335, кл. G 01 N 25/18, 1982 г.], состоящий в нагреве образца в виде призмы прямоугольной формы путем возбуждения в образце вынужденных гармонических колебаний, повышении амплитуды колебаний до значения, при котором наступает изменение резонансной частоты, с последующим уменьшением ее до значения, при котором прекращается изменение резонансной частоты, измерении параметров деформирования образца, перепада температуры внутри образца и расчете по полученным соотношениям искомых теплофизических характеристик.
Недостатками способа-прототипа являются:
1) Сложность аппаратурного оснащения, необходимого для реализации вибрационного саморазогрева исследуемого образца.
2) Малая точность измерения искомых теплофизических характеристик, обусловленная необходимостью измерения большого количества таких метрологических сложных (измеряемых с большой погрешностью) параметров, как сдвиг фаз, резонансная частота, деформация, модуль упругости и т.д., а также громоздкостью и сложностью обработки результатов измерения при расчете искомых свойств, требующей использования таблиц, графиков и т.д.
3) Необходимость помещения первичных измерительных преобразователей (термопар) внутрь образца, что требует разрушения его целостности.
Техническая задача изобретения - повышение точности определения комплекса теплофизических свойств твердых строительных материалов без нарушения их целостности и эксплуатационных характеристик.
Поставленная техническая задача достигается тем, что в способе неразрушающего контроля комплекса теплофизических характеристик твердых строительных материалов, состоящем в нагреве исследуемого образца в виде призмы прямоугольного сечения подводом тепла к ее поверхности, измерении температуры и плотности теплового потока на этой же поверхности, определении искомых теплофизических характеристик по соответствующим зависимостям, исследуемый образец в виде призмы квадратного сечения помещают в цилиндрическую камеру экспериментальной установки, предварительно нагретой до температуры 80...100°С, измеряют изменение во времени температур ребра Тр и середины грани Тгр исследуемой призмы соответственно в паре точек сечения призмы, определяют наступление упорядоченного теплового режима в исследуемой призме, когда скорость изменения температурного комплекса 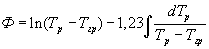 во времени достигнет постоянного значения (ΔФ/Δτ=const), а искомый коэффициент температуропроводности исследуемого материала определяют по формуле
во времени достигнет постоянного значения (ΔФ/Δτ=const), а искомый коэффициент температуропроводности исследуемого материала определяют по формуле
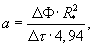
где R* - расстояние между термопарами, измеряющими температуры ребра и середины грани призмы; ΔФ=Ф(τ2)-Ф(τ1) - изменение температурного комплекса Ф за любой интервал времени Δτ=τ2-τ1 после наступления упорядоченного теплового режима, кроме того, определяют максимальный удельный тепловой поток от нагретой внутренней цилиндрической поверхности и воздуха к поверхности призмы по соотношению
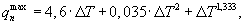
где ΔT=Тнагр-Тгр, Тнагр - начальная температура нагретой внутренней цилиндрической поверхности экспериментальной установки и воздуха внутри установки, Тгр - начальная температура середины грани на поверхности призмы квадратного сечения, а объемную теплоемкость исследуемого образца определяют по формуле
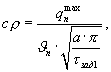
где 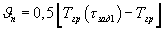 - амплитуда колебаний температурной полуволны на поверхности призмы квадратного сечения при ее нагреве, Тгр(τзад1) - температура середины грани исследуемой призмы в заданный момент времени τзад1 при наступлении упорядоченного теплового режима, определив коэффициенты температуропроводности и объемной теплоемкости исследуемого образца, коэффициент теплопроводности рассчитывают по соотношению
- амплитуда колебаний температурной полуволны на поверхности призмы квадратного сечения при ее нагреве, Тгр(τзад1) - температура середины грани исследуемой призмы в заданный момент времени τзад1 при наступлении упорядоченного теплового режима, определив коэффициенты температуропроводности и объемной теплоемкости исследуемого образца, коэффициент теплопроводности рассчитывают по соотношению
λ=а·(сρ).
Далее нагретый образец вынимают из цилиндрической камеры, охлаждают на воздухе при комнатной температуре и естественной конвекции, измеряют температуру на поверхности призмы в паре точек сечения - ребра 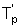 и середины грани
и середины грани 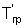 и определяют момент наступления упорядоченного теплового режима в исследуемом образце, когда скорость изменения температурного комплекса
и определяют момент наступления упорядоченного теплового режима в исследуемом образце, когда скорость изменения температурного комплекса 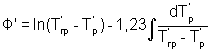 во времени достигнет постоянного неизменного значения (ΔФ'/Δτ=const), а искомый коэффициент температуропроводности исследуемого материала определяют по формуле
во времени достигнет постоянного неизменного значения (ΔФ'/Δτ=const), а искомый коэффициент температуропроводности исследуемого материала определяют по формуле
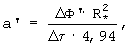
где R* - расстояние между термопарами, измеряющими температуры ребра и середины грани призмы; ΔФ'=Ф'(τ2)-Ф'(τ1) - изменение температурного комплекса Ф' за любой интервал времени Δτ=τ2-τ1 после наступления упорядоченного теплового режима остывания, определяют максимальный удельный тепловой поток от нагретой поверхности образца к окружающему воздуху по соотношению
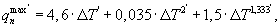
где 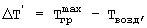
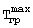 - начальная максимальная температура нагретой поверхности середины грани призмы, полученная при ее нагревании до термодинамического равновесия; Твозд - температура воздуха, а объемную теплоемкость исследуемого образца определяют по формуле
- начальная максимальная температура нагретой поверхности середины грани призмы, полученная при ее нагревании до термодинамического равновесия; Твозд - температура воздуха, а объемную теплоемкость исследуемого образца определяют по формуле
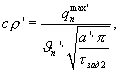
где 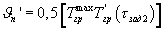 - амплитуда колебаний температурной полуволны на поверхности призмы квадратного сечения при ее охлаждении, Тгр'(τзад2) - температура середины грани призмы в заданный момент времени τзад2 при наступлении упорядоченного теплового режима в призме, далее, используя полученную информацию о температуропроводности и объемной теплоемкости, определяют теплопроводность исследуемого материала по соотношению λ'=а'·(сρ)' и за окончательные искомые теплофизические характеристики принимают средние значения, полученные на этапе нагревания и охлаждения призмы и определяемые по соотношениям:
- амплитуда колебаний температурной полуволны на поверхности призмы квадратного сечения при ее охлаждении, Тгр'(τзад2) - температура середины грани призмы в заданный момент времени τзад2 при наступлении упорядоченного теплового режима в призме, далее, используя полученную информацию о температуропроводности и объемной теплоемкости, определяют теплопроводность исследуемого материала по соотношению λ'=а'·(сρ)' и за окончательные искомые теплофизические характеристики принимают средние значения, полученные на этапе нагревания и охлаждения призмы и определяемые по соотношениям:
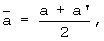
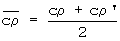 и
и 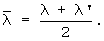
Сущность способа заключается в следующем. Исследуемый образец в форме призмы квадратного сечения, длина которой во много раз (в 6 и более) превышает ширину грани, что обеспечивает условие бесконечной длины, помещают в испытательную цилиндрическую камеру установки, схема которой приведена на фиг.1. Конструкция экспериментальной установки состоит из двух расположенных друг в друге полых цилиндров 1, служащих изотермическими поверхностями и выполненных из листового материала. В зазоре между экранами установлены коаксиальные нагреватели 2, питающиеся через стабилизатор от сети переменного тока и обеспечивающие практически симметричный нагрев исследуемого образца в виде призмы квадратного сечения 3. Нагреватель представляет собой равномерно уложенную нихромовую проволоку, помещенную в коаксиально расположенных керамических трубках, выполняющих роль электрического изолятора. Снизу камера закрыта, а сверху имеется отверстие с крышкой 4, через которое образец помещают в установку. Измерение температур на ребре и в середине грани исследуемой призмы осуществляют термопарами 5, которые подключены к коммутатору 6 и далее через усилитель 7 и порт ввода-вывода к ЭВМ 8.
После помещения исследуемого образца в камеру установки включают нагреватели и контролируют изменение температуры на ребре и в середине грани призмы. Расчетное соотношение для определения искомого коэффициента температуропроводности получено на основании следующих рассуждений.
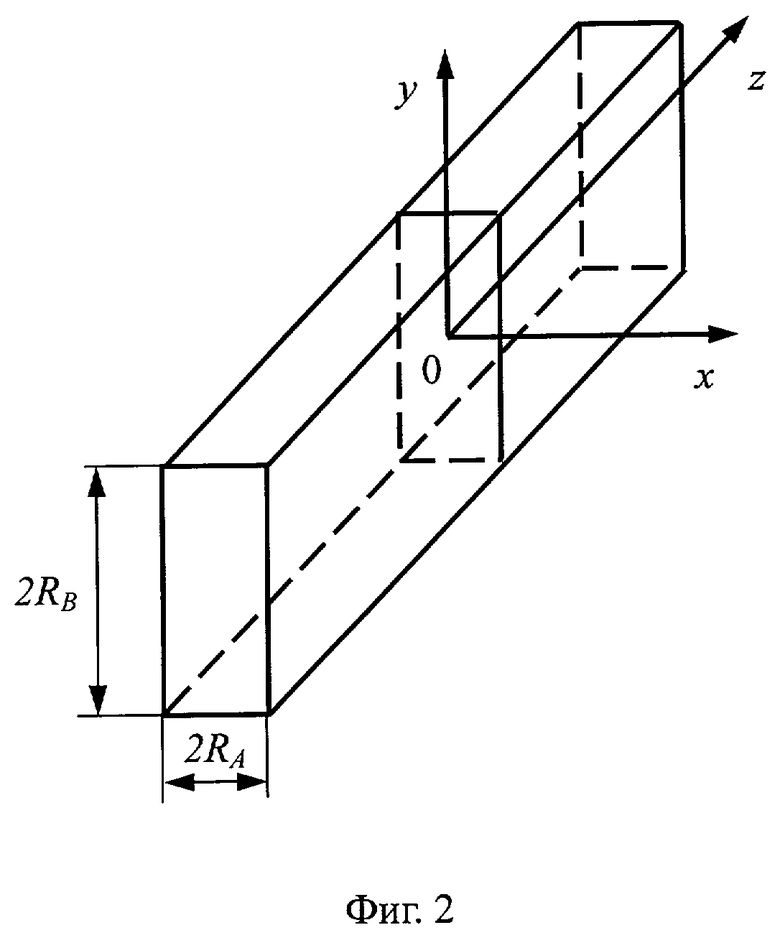
При любых граничных условиях процесс симметричного нагревания призмы прямоугольного сечения (см. фиг.2), помещенной в цилиндрическую полость установки, может быть описан дифференциальным уравнением
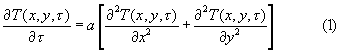
с условиями однозначности (симметрии, граничными и начальными)
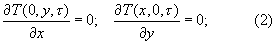
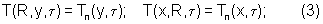
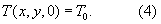
Выражение (1) можно записать в виде
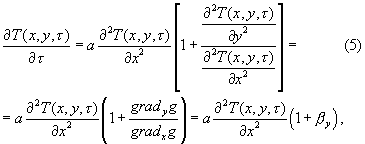
где βy - отношение составляющей градиента теплового потока в направлении y к составляющей градиента теплового потока в направлении x.
Если призму нагревать симметрично конвективным потоком тепла, то температурное поле по ее сечению можно определить по принципу перемножения температурных критериев [см. Лыков А.В. Теория теплопроводности / А.В.Лыков. М.: Высшая школа, 1967. 599 с.]:

Составляющие градиента теплового потока в направлении x и y соответственно будут равны
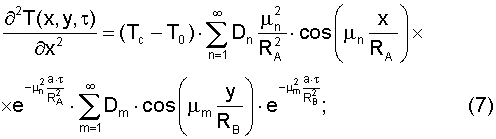
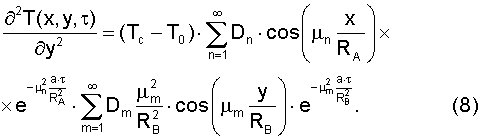
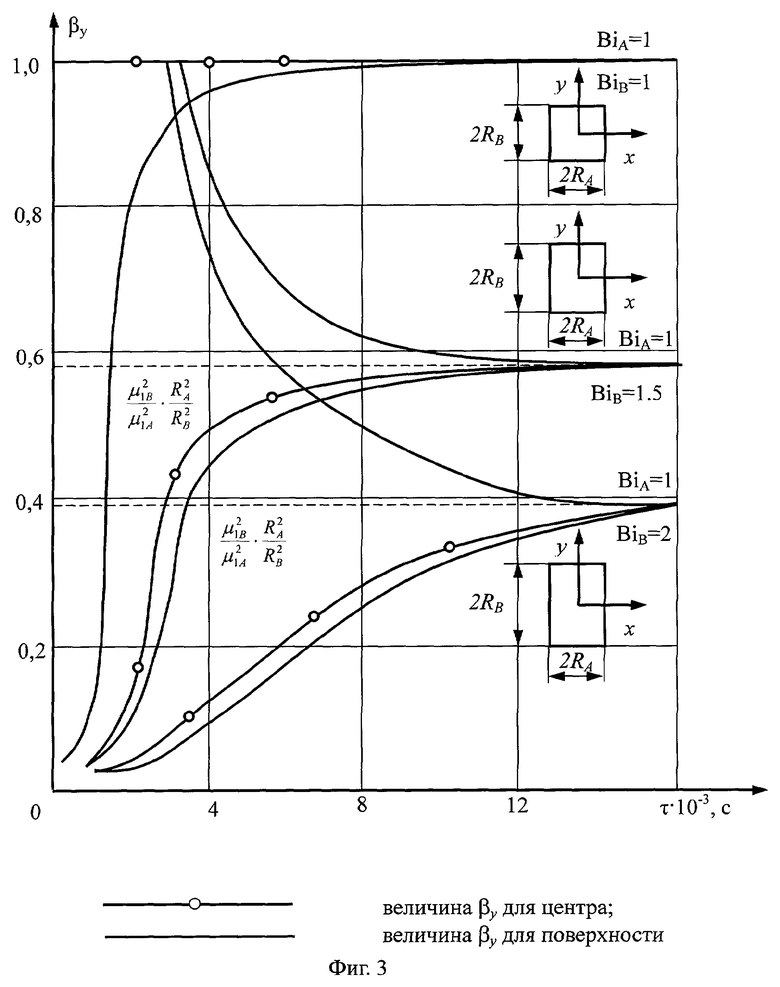
Используя решения (6) - (8), можно показать характер изменения соотношений составляющих градиента теплового потока βy для различных вариантов (см. фиг.3).
В начальном периоде теплового воздействия отношение составляющих градиента теплового потока является функцией критерия Fo, но с течением времени процесс становится автомодельным относительно аргумента τ. Это происходит потому, что в области регулярного режима (τ>τ*) выражение (6) упрощается, а кривые асимптотически стремятся к пределу
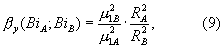
где μ1А и μ1В - первые характеристические числа, зависящие от чисел Био, определяемые по выражениям:
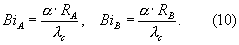
Таким образом, в регулярной стадии βy не зависит от критерия Фурье, а является функцией BiА и BiB и отношениями между измерениями сторон призмы RA и RB во второй степени. При RB, стремящемся к RA, призма принимает форму квадратного сечения, а значение βy начинает стремиться к своему предельному значению, равному единице. Отношение составляющих градиента теплового потока βy (когда RA=RB) при лучистом нагреве призмы квадратного сечения также равно единице в области упорядоченного теплового периода. Этот же результат получается при симметричном нагреве призмы квадратного сечения с суммарным потоком тепла (одновременно конвекцией и радиацией).
Следовательно, для области упорядоченного теплового периода в призме квадратного сечения бесконечной длины условия нагревания могут быть описаны следующими зависимостями:
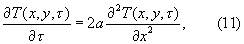
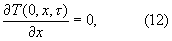
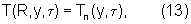
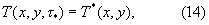
где τ>τ*.
В процессах распространения тепла, описываемых системой уравнений (11)-(14), искомое температурное поле является функцией многих физических параметров. Поскольку любое явление природы не зависит от выбранной системы единиц и величин измерения, то наиболее целесообразно описывать его совокупностью уравнений в безразмерном виде (15)-(18). Безразмерная форма имеет ряд преимуществ и замечательна тем, что охватывает множество явлений, подобных друг другу и, кроме того, позволяет оперировать значительно меньшим числом аргументов.
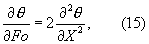
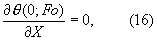
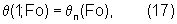
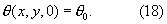
где θп(Fo) - уже заданное изменение температуры поверхности тела.
Система (15)-(18) дает возможность получить решение в неявной форме [см. Видин Ю.В. Инженерные методы расчетов процессов теплопереноса / Ю.В.Видин. Красноярск. 1974. 144 с.]:
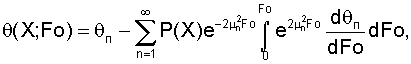
которое для упорядоченной части процесса ограничивается только первым членом ряда и имеет вид:
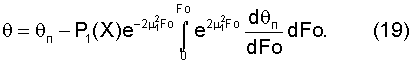
Поскольку граничные условия (17) предусматривают различные способы нагревания (или охлаждения), то решение (19) следует рассматривать как универсальное в этом отношении. Кроме того, функция Р(Х) для неограниченной пластины выражается через тригонометрическую функцию. Для призмы квадратного сечения бесконечной длины, получаемой пересечением двух неограниченных пластин, выражение (19) записывается так:
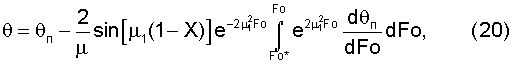
где Fo* соответствует началу упорядоченного теплового режима.
Вычислив значения относительных температур соответственно для поверхности (Х=1) и центра бруса (Х=0), определим их разность Δθ.
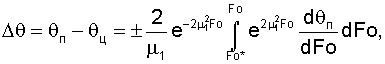
или
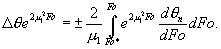
Преобразуем это выражение к виду
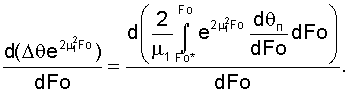
После дифференцирования получаем
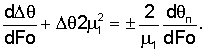
С учетом сокращения и разделения переменных
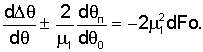
Интегрируя последнее выражение и обозначив тождество символом Ф, получим
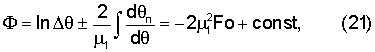
или в размерной форме
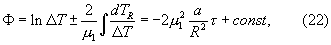
где ΔT - положительная разность температур между поверхностью и центром тела. Знак минус перед интегралом означает процесс нагревания, а знак плюс - охлаждения; R - половина ширины грани призмы; 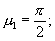 ;
; 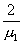 - постоянное число, теоретически равное 1,27, что соответствует измерению температуры строго в центральной точке призмы квадратного сечения. При некотором смещении точки эта постоянная величина несколько уменьшается. С учетом объемности термопары можно рекомендовать 2/μ1=1,23.
- постоянное число, теоретически равное 1,27, что соответствует измерению температуры строго в центральной точке призмы квадратного сечения. При некотором смещении точки эта постоянная величина несколько уменьшается. С учетом объемности термопары можно рекомендовать 2/μ1=1,23.
Следовательно, математические условия (15)÷(18) позволяют получить решение в неявной форме с точностью до неизвестной постоянной величины (константы)
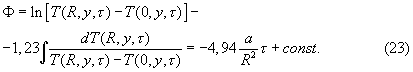
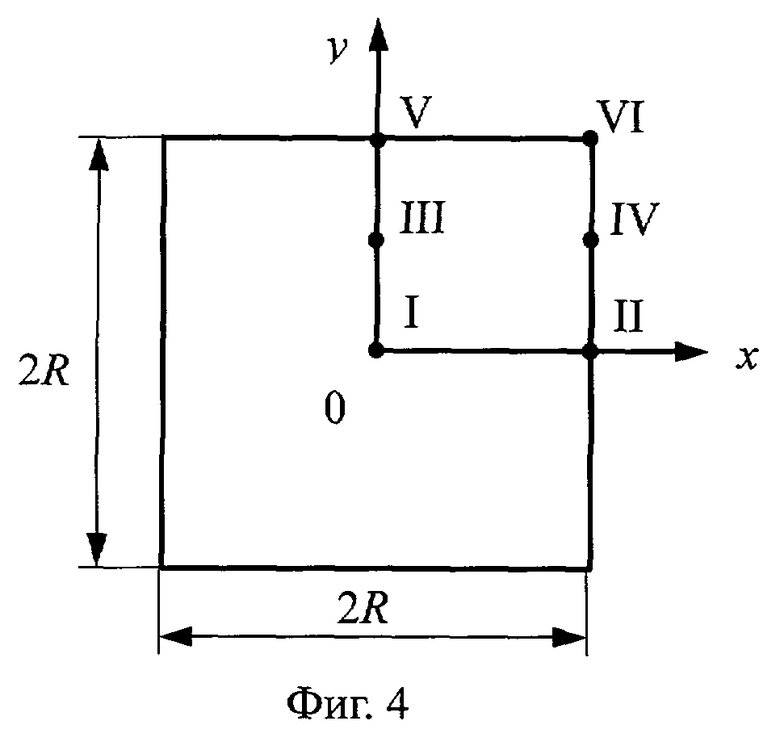
Если температуру измерять в конкретных парах точек I-II, III-IV, V-VI сечения призмы (см. фиг.4), то выражение упорядоченного теплового режима для каждой пары запишется следующим образом:
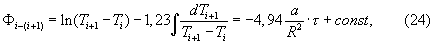
где i=1...5.
Наибольший интерес представляют точки V - середина грани призмы квадратного сечения и VI - ребра призмы, так как в этом случае все измерения температур производятся на поверхности исследуемого образца и отпадает необходимость проникать с термопарой внутрь тела образца, разрушать его, что в итоге позволяет осуществить метод неразрушающего контроля, т.е. определить искомый коэффициент температуропроводности без нарушения целостности и эксплуатационных характеристик исследуемых объектов.
Таким образом, момент наступления упорядоченного теплового режима при симметричном нагревании призмы квадратного сечения определяют, когда изменение значения температурного комплекса  во времени достигнет постоянного неизменного значения, т.е. когда скорость изменения температурного комплекса ΔФ/Δτ становится постоянной, а искомый коэффициент температуропроводности исследуемого материала определяют по формуле
во времени достигнет постоянного неизменного значения, т.е. когда скорость изменения температурного комплекса ΔФ/Δτ становится постоянной, а искомый коэффициент температуропроводности исследуемого материала определяют по формуле
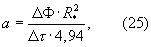
где R* - расстояние между термопарами, измеряющими температуры ребра и середины грани призмы; ΔФ=Ф(τ2)-Ф(τ1) - изменение температурного комплекса Ф за любой интервал времени Δτ=τ2-τ1 после наступления упорядоченного теплового режима.
Максимальная плотность теплового потока 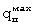 на поверхности призмы квадратного сечения при ее симметричном нагревании зависит от начальной температуры внутренней поверхности экспериментальной установки и нагретого в ней воздуха Тнагр и начальной температуры середины грани Тгр поверхности призмы.
на поверхности призмы квадратного сечения при ее симметричном нагревании зависит от начальной температуры внутренней поверхности экспериментальной установки и нагретого в ней воздуха Тнагр и начальной температуры середины грани Тгр поверхности призмы.
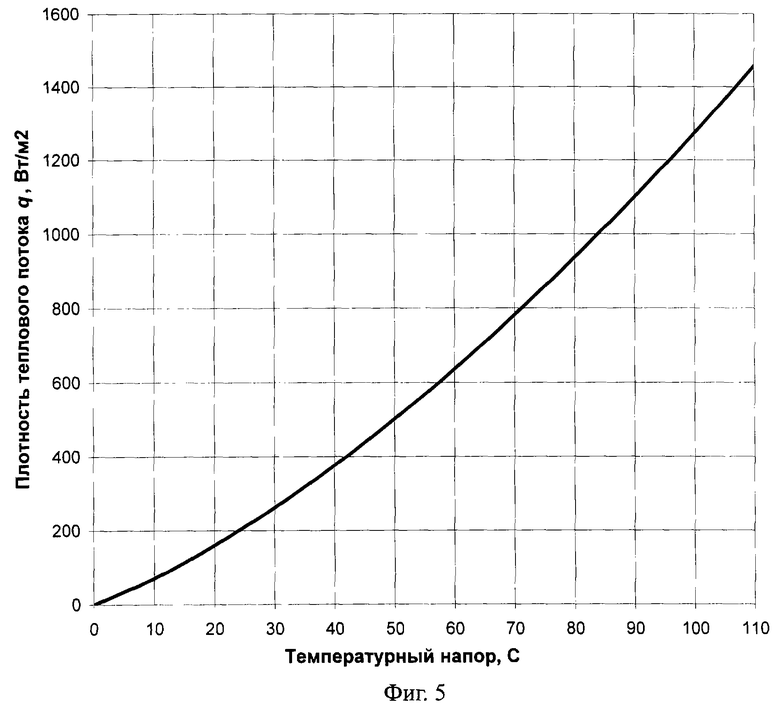
Удельный тепловой поток q, Вт/м2, от нагретой внутренней цилиндрической поверхности экспериментальной установки и воздуха (фиг.1) к поверхности призмы квадратного сечения может быть определен графически с использованием фиг.5 или может быть рассчитан с использованием трехчлена вида:
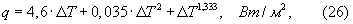
где ΔТ=Тнагр-Тгр; Тнагр - начальная температура нагретой цилиндрической поверхности экспериментальной установки и воздуха внутри установки, может изменяться до +100°С; Тгр - начальная температура середины грани на поверхности призмы квадратного сечения, может изменяться от -10 до +30°С. Удельную теплоемкость исследуемого образца далее определяют на основании следующих рассуждений.
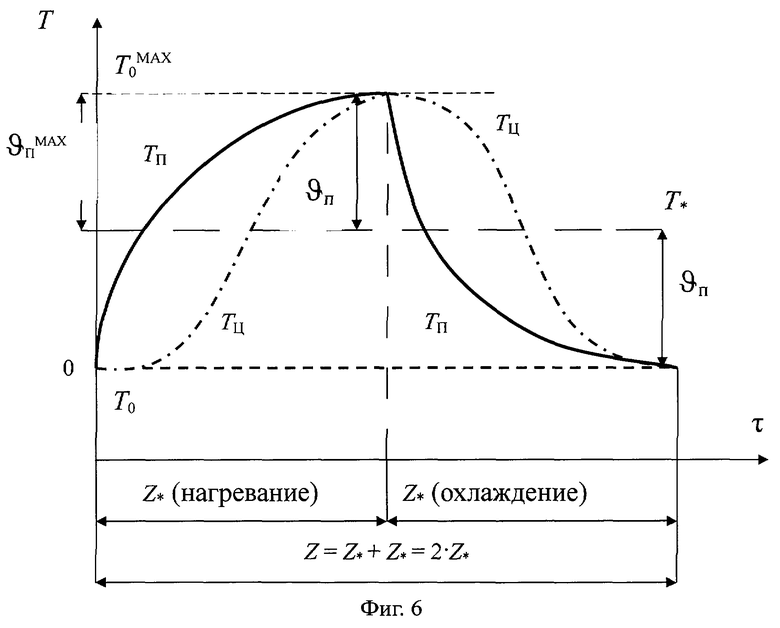
На фиг.6. показано изменение температуры (одна температурная полуволна при нагревании и одна температурная полуволна при охлаждении) при воздействии теплового потока на поверхности призмы квадратного сечения.
На представленном чертеже введены следующие обозначения: Тп - температура в середине грани поверхности призмы; Тц - температура центра; Т0 - начальная температура призмы; 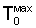 - максимальная температура призмы, полученная при ее нагревании до термодинамического равновесия; Z* - полуволна при нагревании и охлаждении призмы; Z - полный период температурной волны на поверхности призмы;
- максимальная температура призмы, полученная при ее нагревании до термодинамического равновесия; Z* - полуволна при нагревании и охлаждении призмы; Z - полный период температурной волны на поверхности призмы; 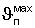 - амплитуда колебаний на поверхности или максимальное отклонение температуры на поверхности; ϑп - избыточная температура на поверхности призмы.
- амплитуда колебаний на поверхности или максимальное отклонение температуры на поверхности; ϑп - избыточная температура на поверхности призмы.
Известно [см. Бойков Г.П., Видин Ю.В., Журавлев В.М., Колосов В.В. Основы тепломассобмена. Красноярск, 2000. 272 с.], что распределение температуры в полуограниченном теле при циклическом подводе теплоты к его поверхности, максимальная плотность теплового потока на поверхности материала (массива) и его теплотехнические характеристики связаны следующей зависимостью
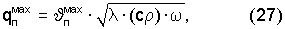
где 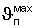 - амплитуда колебаний на поверхности (максимальное отклонение температуры на поверхности); λ - коэффициент теплопроводности материала; (сρ) - объемная теплоемкость материала;
- амплитуда колебаний на поверхности (максимальное отклонение температуры на поверхности); λ - коэффициент теплопроводности материала; (сρ) - объемная теплоемкость материала; 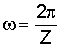 - частота колебаний; Z - полный период колебаний.
- частота колебаний; Z - полный период колебаний.
Известно [Лыков А.В. Теория теплопроводности / А.В.Лыков. М.: Высшая школа, 1967. 599 с.], что λ=а·(сρ), тогда в соответствии с формулой (27) максимальная плотность теплового потока на поверхности материала в любой момент времени нагрева или охлаждения может быть записана и в виде соотношения:
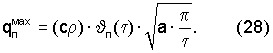
Поскольку в соответствии с фиг.6 амплитуда колебаний температурной полуволны на поверхности призмы квадратного сечения при ее нагревании и воздействии теплового потока для каждого периода времени численно равна
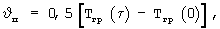
где Тгр(τ) - температура середины грани на поверхности призмы квадратного сечения в любой момент времени τ; Тгр(0) - начальная температура призмы квадратного сечения, °С.
Тогда объемную теплоемкость из формулы (28) можно рассчитать по соотношению
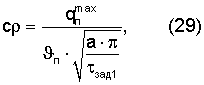
где 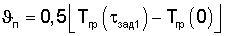 - амплитуда колебаний температурной полуволны на поверхности призмы квадратного сечения при ее нагреве, Тгр(τзад1) - температура середины грани исследуемой призмы в заданный момент времени τзад1 при наступлении упорядоченного теплового режима.
- амплитуда колебаний температурной полуволны на поверхности призмы квадратного сечения при ее нагреве, Тгр(τзад1) - температура середины грани исследуемой призмы в заданный момент времени τзад1 при наступлении упорядоченного теплового режима.
Определив коэффициент температуропроводности по формуле (25) и объемной теплоемкости исследуемого образца по формуле (29), коэффициент теплопроводности рассчитывают по соотношению
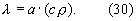
После нагрева исследуемого образца до установившегося термодинамического равновесия, снятия информации о температурно-временных изменениях в точках контроля и расчете комплекса теплофизических характеристик исследуемого материала по соотношениям (25), (29) и (30) выключают нагреватели, вынимают образец из цилиндрической камеры и охлаждают на воздухе при комнатной температуре и естественной конвекции.
Измеряют при этом также температуру на поверхности в паре точек сечения призмы - на ребре 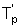 и середине грани
и середине грани 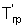 , определяют момент наступления упорядоченного теплового режима в исследуемом образце, когда скорость изменения температурного комплекса
, определяют момент наступления упорядоченного теплового режима в исследуемом образце, когда скорость изменения температурного комплекса 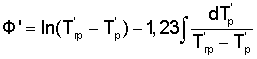 во времени достигнет постоянного неизменного значения (ΔФ'/Δτ=const), рассчитывают коэффициент температуропроводности, используя соотношение (25).
во времени достигнет постоянного неизменного значения (ΔФ'/Δτ=const), рассчитывают коэффициент температуропроводности, используя соотношение (25).
Максимальная плотность теплового потока 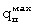 на поверхности призмы квадратного сечения при ее симметричном охлаждении на воздухе зависит от начальной температуры нагретой поверхности образца
на поверхности призмы квадратного сечения при ее симметричном охлаждении на воздухе зависит от начальной температуры нагретой поверхности образца 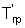 и температуры воздуха Твозд.
и температуры воздуха Твозд.
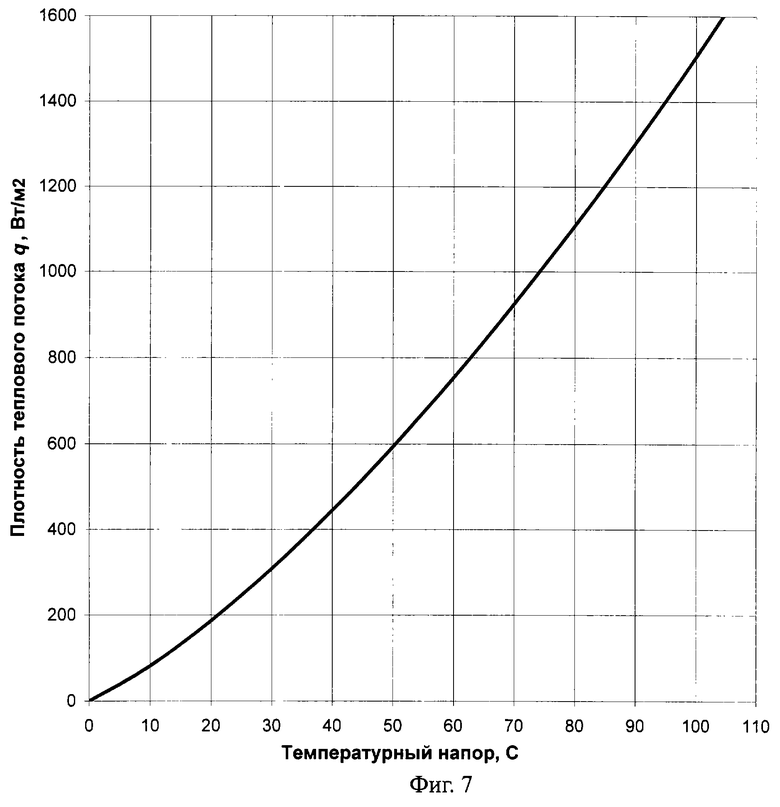
Удельный тепловой поток q, Вт/м2, от нагретой поверхности образца (призмы квадратного сечения) к воздуху может быть определен графически с использованием фиг.7 или может быть рассчитан с использованием трехчлена вида:
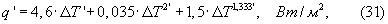
где 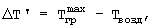
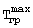 - начальная максимальная температура нагретой поверхности середины грани призмы, может изменяться до +100°С; Твозд - температура воздуха, может изменяться от -10 до +30°С.
- начальная максимальная температура нагретой поверхности середины грани призмы, может изменяться до +100°С; Твозд - температура воздуха, может изменяться от -10 до +30°С.
Поскольку в соответствии с фиг.6 амплитуда колебаний температурной полуволны на поверхности призмы квадратного сечения при ее охлаждении для каждого периода времени численно равна
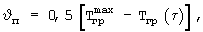
где 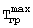 - максимальная начальная температура призмы квадратного сечения, Тгр(τ) - температура середины грани на поверхности призмы квадратного сечения в любой момент времени τ, то объемную теплоемкость исследуемого образца из формулы (28) можно рассчитать по соотношению
- максимальная начальная температура призмы квадратного сечения, Тгр(τ) - температура середины грани на поверхности призмы квадратного сечения в любой момент времени τ, то объемную теплоемкость исследуемого образца из формулы (28) можно рассчитать по соотношению
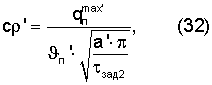
где 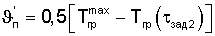 - амплитуда колебаний температурной полуволны на поверхности призмы квадратного сечения при ее охлаждении,
- амплитуда колебаний температурной полуволны на поверхности призмы квадратного сечения при ее охлаждении, 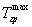 - максимальная температура призмы, полученная при ее нагревании до термодинамического равновесия;
- максимальная температура призмы, полученная при ее нагревании до термодинамического равновесия; 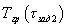 - температура середины грани призмы в заданный момент времени τзад2 при наступлении упорядоченного теплового режима в призме, далее, используя полученную информацию о температуропроводности и объемной теплоемкости, определяют теплопроводность исследуемого материала по соотношению (30): λ'=а'·(сρ)'.
- температура середины грани призмы в заданный момент времени τзад2 при наступлении упорядоченного теплового режима в призме, далее, используя полученную информацию о температуропроводности и объемной теплоемкости, определяют теплопроводность исследуемого материала по соотношению (30): λ'=а'·(сρ)'.
За окончательные искомые теплофизические характеристики принимают средние значения, полученные на стадии нагрева и охлаждения исследуемого образца: 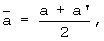
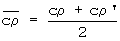 и
и 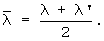
Для проверки работоспособности предлагаемого способа были проведены эксперименты с использованием установки, схема которой показана на фиг.1. Для исследования была изготовлена призма из бетона на портландцементе длиной 350 мм и шириной грани 2R = 50 мм с шамотным заполнителем (цемент - 400 кг/м3; тонкомолотая шамотная добавка - 80 кг/м3; шамотный песок - 740 кг/м3; шамотный щебень - 400 кг/м3; В/Ц = 0,6).
Для измерения температуры ребра и середины грани методом неразрушающего контроля на призме квадратного сечения закреплялись термопары с использованием контактного устройства. Расстояние между термопарами составило R=0,024 м.
Для комплексного определения теплофизических свойств бетона установку (цилиндрическую печь) вначале прогревали до того момента, пока температура среды внутри печи Тср установится постоянной. Ввиду того, что боковые экраны выполнены из листового алюминия, установка выходит в рабочий режим в течение короткого времени, не более 20...30 мин, а температура среды внутри печи Тср составила 97°С.
Подготовленная к опыту призма из бетона с установленными на ней двумя термопарами помещали в испытательную цилиндрическую камеру и симметрично нагревали от начальной комнатной температуры Т0=23°С.
В таблице 1 представлены результаты экспериментальных измерений температур ребра призмы квадратного сечения Тр и середины ее грани Тгр, а также расчеты температурного комплекса Ф, для каждого значения времени τ. Выполнены и расчеты коэффициента температуропроводности а бетона для каждого промежутка времени Δτ в течение 12 мин.
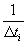
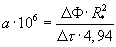 , м2/с
, м2/с
Из эксперимента и вычислений видно, что коэффициент температуропроводности бетона с шамотным заполнителем, начиная со времени τ=360 с становится равным а=0,494·10-6 м2/с и повторяет свои истинные значения для каждого последующего промежутка времени Δτ. Анализ вычислений также указывает, что до времени τ=360 с длится начальная стадия нагрева, а затем начинается упорядоченный тепловой режим.
Полученное из опыта значение коэффициента температуропроводности а=0,495·10-6 м2/c используется в дальнейшем для расчета значений объемной теплоемкости (ср) и теплопроводности λ бетона.
Плотность теплового потока 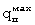 на поверхности призмы квадратного сечения из бетона в начальном периоде нагревания возможно определить графически по фиг.5 или по формуле (26) при максимальном температурном напоре на поверхности образца, когда призму помещали в прогретую установку ΔТ=Тср-Т0=97-23=74°С.
на поверхности призмы квадратного сечения из бетона в начальном периоде нагревания возможно определить графически по фиг.5 или по формуле (26) при максимальном температурном напоре на поверхности образца, когда призму помещали в прогретую установку ΔТ=Тср-Т0=97-23=74°С.
Результаты расчета объемной теплоемкости и коэффициента теплопроводности по температурному полю на поверхности при нагревании бетона при Т0=23°С, Тср=97°С, ΔТ=74°С, 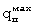 =840 Вт/м2, при коэффициенте температуропроводности а=0,495·10-6 м2/с, сведены в таблицу 2.
=840 Вт/м2, при коэффициенте температуропроводности а=0,495·10-6 м2/с, сведены в таблицу 2.
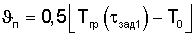
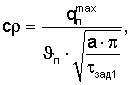
кДж/(м3·К)
Для повышения точности результатов измерения за счет уменьшения доли случайной составляющей в общей погрешности измерений был также проведен эксперимент с охлаждением бетона. Для этого призму квадратного сечения из бетона, нагретую в печи до термодинамического температурного равновесия 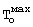 =94°С, охлаждали на воздухе при температуре Твоз=27°С и естественной конвекции.
=94°С, охлаждали на воздухе при температуре Твоз=27°С и естественной конвекции.
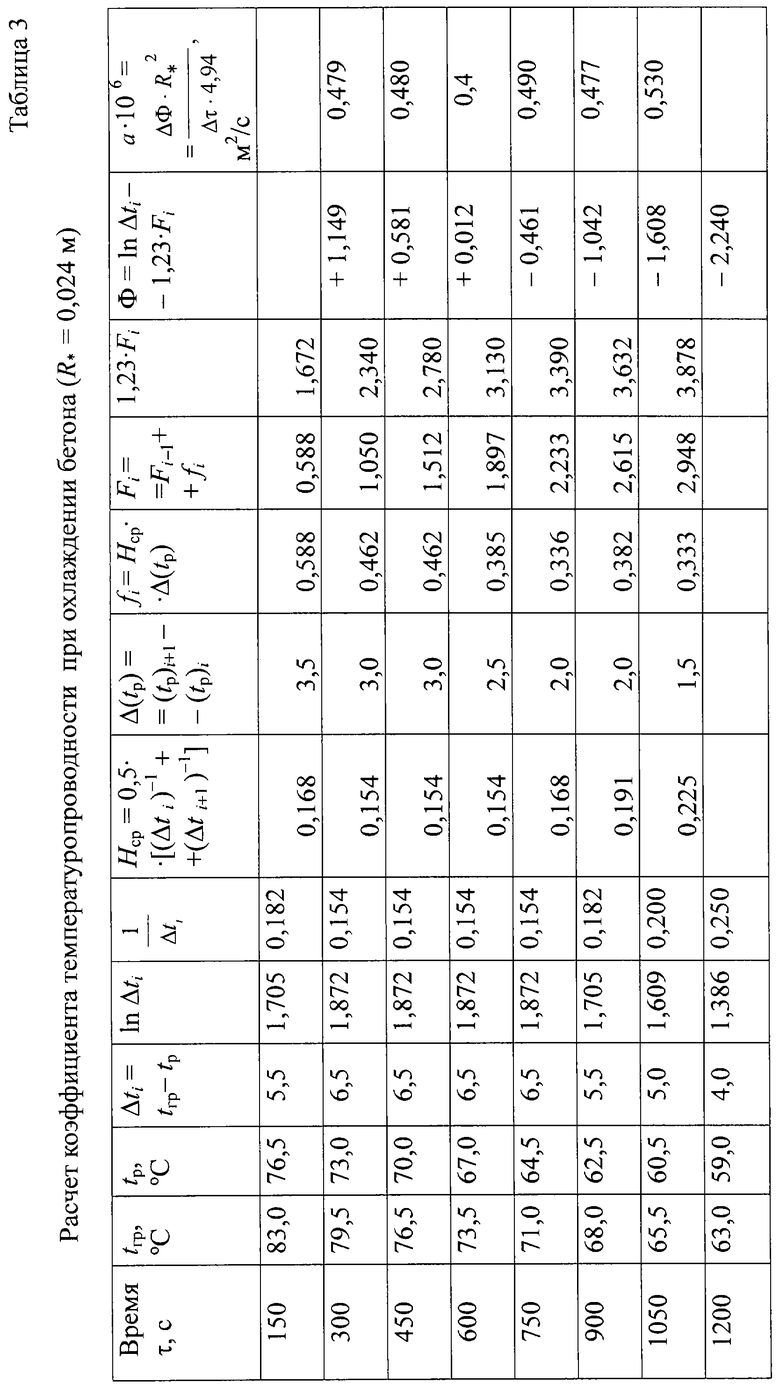
В таблице 3 представлены результаты экспериментального измерения температур ребра призмы Tр и середины ее грани Tгр, а также расчеты температурного комплекса Ф для каждого значения времени τ и расчеты коэффициента температуропроводности при охлаждении бетона для каждого промежутка времени Δτ в течение 20 мин. Полученное из опыта значение коэффициента температуропроводности а=0,465·10-6 м2/c использовалось для расчета значений объемной теплоемкости (ср) и теплопроводности λ бетона.
Плотность теплового потока 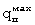 на поверхности призмы квадратного сечения из бетона в начальном периоде охлаждения определялась по формуле (31) при максимальном температурном напоре на поверхности, когда прогретая призма вынимается из нагретой установки для последующего охлаждения на воздухе при естественной конвекции, при этом ΔТ=
на поверхности призмы квадратного сечения из бетона в начальном периоде охлаждения определялась по формуле (31) при максимальном температурном напоре на поверхности, когда прогретая призма вынимается из нагретой установки для последующего охлаждения на воздухе при естественной конвекции, при этом ΔТ=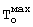 -Твоз=94-27=67°С.
-Твоз=94-27=67°С.
Результаты расчета объемной теплоемкости и коэффициента теплопроводности по температурному полю на поверхности призмы при охлаждении бетона для 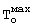 =94°С, Tж=27°С, ΔT=67°С,
=94°С, Tж=27°С, ΔT=67°С, 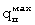 =870 Вт/м2 при коэффициенте температуропроводности а=0,465·10-6 м2/с сведены в таблицу 4.
=870 Вт/м2 при коэффициенте температуропроводности а=0,465·10-6 м2/с сведены в таблицу 4.
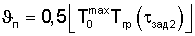
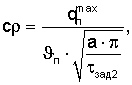
кДж/(м3·К)
Из полученных экспериментальных данных следует, что относительная погрешность измерения коэффициента температуропроводности, объемной теплоемкости и теплопроводности разработанного способа неразрушающего контроля, использующая упорядоченный тепловой режим в призме квадратного сечения, составляет не более 5%, тогда как в аналогах и способе-прототипе относительная погрешность составляет не менее 8-10%.
Большим преимуществом разработанного способа неразрушающего контроля для комплексного определения коэффициентов температуропроводности, теплопроводности и объемной теплоемкости материалов по температурным измерениям на поверхности призмы квадратного сечения по сравнению с известными является:
- отсутствие необходимости в измерении в процессе эксперимента таких физических величин, как коэффициент теплообмена, степень черноты мощности нагревателя;
- нет необходимости в создании чисто конвективной или чисто лучистой окружающей среды, что значительно упрощает экспериментальные установки;
- не требуется учета потерь тепла за счет теплообмена с окружающей средой, а также контактным сопротивлением между образцом и нагревателем;
- измерения температур производятся на поверхности призмы квадратного сечения без нарушения целостности и эксплуатационных характеристик исследуемых образцов.
Эти преимущества заявленного технического решения значительно упрощают условия проведения эксперимента (экспериментальную установку) и повышают метрологический уровень результатов измерения.
Кроме того, предлагаемый способ неразрушающего контроля комплекса теплофизических характеристик твердых материалов позволяет легко автоматизировать теплофизический эксперимент, легко реализуется на базе микропроцессорной техники и поэтому является перспективным для использования в информационно-измерительных системах неразрушающего контроля ТФХ материалов.
Таким образом, разработанный способ неразрушающего контроля для комплексного определения коэффициентов температуропроводности, теплопроводности и объемной теплоемкости материалов по температурным измерениям на поверхности призмы квадратного сечения имеет ряд существенных преимуществ перед известными способами указанного назначения, что несомненно позволит использовать его в практике теплофизических измерений, в строительной теплотехнике и различных отраслях народного хозяйства.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ НЕРАЗРУШАЮЩЕГО КОНТРОЛЯ ТЕПЛОФИЗИЧЕСКИХ ХАРАКТЕРИСТИК ТВЕРДЫХ МАТЕРИАЛОВ | 2004 |
|
RU2250454C1 |
| СПОСОБ НЕРАЗРУШАЮЩЕГО КОНТРОЛЯ КОМПЛЕКСА ТЕПЛОФИЗИЧЕСКИХ ХАРАКТЕРИСТИК ТВЕРДЫХ СТРОИТЕЛЬНЫХ МАТЕРИАЛОВ И УСТАНОВКА ДЛЯ ЕГО ОСУЩЕСТВЛЕНИЯ | 2013 |
|
RU2530441C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ КОМПЛЕКСА ТЕПЛОФИЗИЧЕСКИХ ХАРАКТЕРИСТИК ТВЕРДЫХ СТРОИТЕЛЬНЫХ МАТЕРИАЛОВ | 2022 |
|
RU2788562C1 |
| Способ неразрушающего контроля комплекса теплофизических характеристик твердых строительных материалов и устройство для его осуществления | 2021 |
|
RU2767468C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ КОМПЛЕКСА ТЕПЛОЗВУКОФИЗИЧЕСКИХ И МЕХАНИЧЕСКИХ ХАРАКТЕРИСТИК ТВЕРДЫХ МАТЕРИАЛОВ | 2023 |
|
RU2801079C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ТЕПЛОФИЗИЧЕСКИХ ХАРАКТЕРИСТИК СТРОИТЕЛЬНЫХ МАТЕРИАЛОВ (ВАРИАНТЫ) | 2008 |
|
RU2399911C2 |
| СПОСОБ НЕРАЗРУШАЮЩЕГО КОНТРОЛЯ ТЕПЛОФИЗИЧЕСКИХ ХАРАКТЕРИСТИК СТРОИТЕЛЬНЫХ МАТЕРИАЛОВ И ИЗДЕЛИЙ | 2012 |
|
RU2497105C1 |
| СПОСОБ ИЗМЕРЕНИЯ ТЕПЛОФИЗИЧЕСКИХ СВОЙСТВ АНИЗОТРОПНЫХ МАТЕРИАЛОВ МЕТОДОМ ЛИНЕЙНОГО ИМПУЛЬСНОГО ИСТОЧНИКА ТЕПЛОТЫ | 2015 |
|
RU2613194C1 |
| СПОСОБ НЕРАЗРУШАЮЩЕГО КОНТРОЛЯ ТЕПЛОФИЗИЧЕСКИХ ХАРАКТЕРИСТИК СТРОИТЕЛЬНЫХ МАТЕРИАЛОВ И ИЗДЕЛИЙ | 2014 |
|
RU2570596C1 |
| СПОСОБ КОМПЛЕКСНОГО ОПРЕДЕЛЕНИЯ ТЕПЛОФИЗИЧЕСКИХ ХАРАКТЕРИСТИК МАТЕРИАЛОВ | 2009 |
|
RU2387981C1 |
Использование: для неразрушающего контроля комплекса теплофизических характеристик твердых строительных материалов. Сущность: заключается в том, что исследуемый образец в виде призмы квадратного сечения помещают в цилиндрическую камеру экспериментальной установки, предварительно нагретой до любой произвольно выбранной температуры, например 80...100°С, измеряют изменение во времени температур ребра и середины грани исследуемой призмы соответственно в паре точек сечения призмы, определяют наступление упорядоченного теплового режима в исследуемой призме, когда скорость изменения температурного комплекса во времени достигнет постоянного значения, после чего определяют искомые теплофизические характеристики по соответствующим математическим формулам. Технический результат: повышение точности определения комплекса теплофизических свойств твердых строительных материалов без нарушения их целостности и эксплуатационных характеристик. 1 з.п. ф-лы, 7 ил., 4 табл.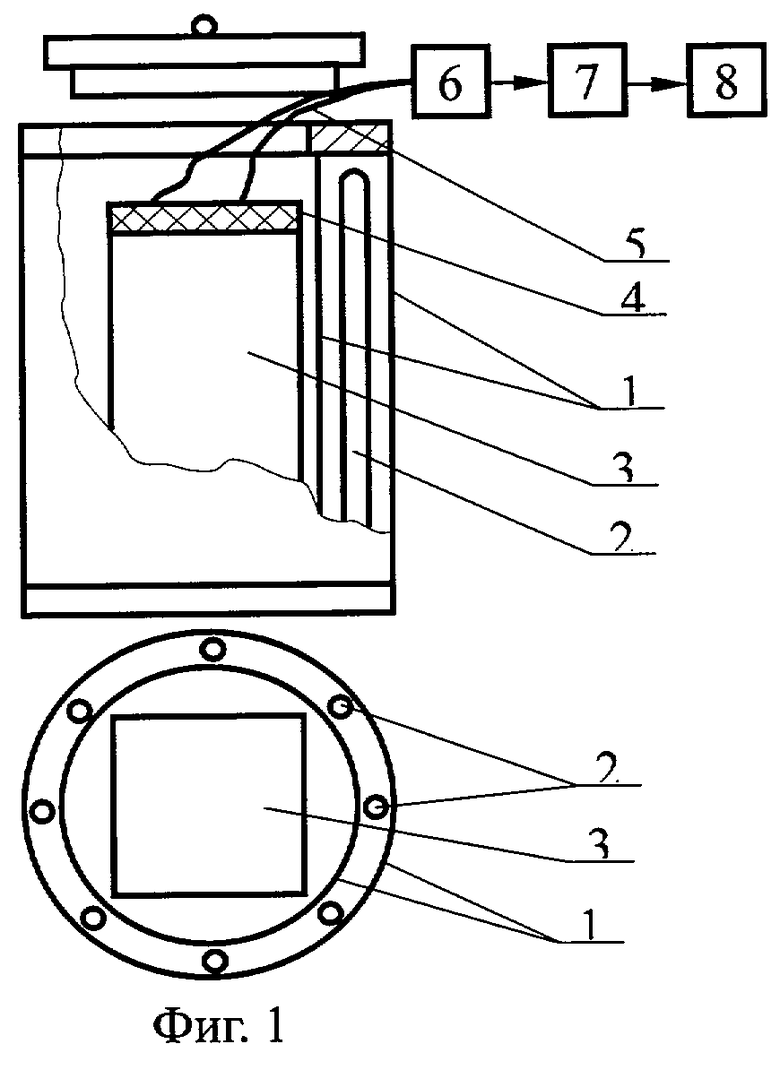
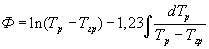 во времени достигнет постоянного значения (ΔФ/Δτ=const), а искомый коэффициент температуропроводности исследуемого материала определяют по формуле
во времени достигнет постоянного значения (ΔФ/Δτ=const), а искомый коэффициент температуропроводности исследуемого материала определяют по формуле
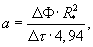
где R* - расстояние между термопарами, измеряющими температуры ребра и середины грани призмы; ΔФ=Ф(τ2)-Ф(τ1) - изменение температурного комплекса Ф за любой интервал времени Δτ=τ2-τ1 после наступления упорядоченного теплового режима, кроме того, определяют максимальный удельный тепловой поток от нагретой внутренней цилиндрической поверхности и воздуха к поверхности призмы по соотношению
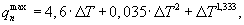
где ΔТ=Тнагр-Тгр, Тнагр - начальная температура нагретой внутренней цилиндрической поверхности экспериментальной установки и воздуха внутри установки, Тгр - начальная температура середины грани на поверхности призмы квадратного сечения, а объемную теплоемкость исследуемого образца определяют по формуле
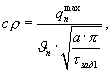
где 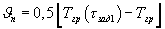 - амплитуда колебаний температурной полуволны на поверхности призмы квадратного сечения при ее нагреве, Тгр(τзад1) - температура середины грани исследуемой призмы в заданный момент времени τзад1 при наступлении упорядоченного теплового режима, определив коэффициенты температуропроводности и объемной теплоемкости исследуемого образца, коэффициент теплопроводности рассчитывают по соотношению
- амплитуда колебаний температурной полуволны на поверхности призмы квадратного сечения при ее нагреве, Тгр(τзад1) - температура середины грани исследуемой призмы в заданный момент времени τзад1 при наступлении упорядоченного теплового режима, определив коэффициенты температуропроводности и объемной теплоемкости исследуемого образца, коэффициент теплопроводности рассчитывают по соотношению
λ=а·(сρ).
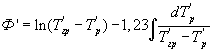 во времени достигнет постоянного неизменного значения (ΔФ'/Δτ=const), а искомый коэффициент температуропроводности исследуемого материала определяют по формуле
во времени достигнет постоянного неизменного значения (ΔФ'/Δτ=const), а искомый коэффициент температуропроводности исследуемого материала определяют по формуле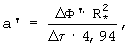
где R* - расстояние между термопарами, измеряющими температуры ребра и середины грани призмы; ΔФ'=Ф'(τ2)-Ф'(τ1) - изменение температурного комплекса Ф' за любой интервал времени Δτ=τ2-τ1 после наступления упорядоченного теплового режима остывания, определяют максимальный удельный тепловой поток от нагретой поверхности образца к окружающему воздуху по соотношению
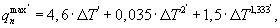
где 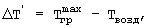
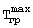 - начальная максимальная температура нагретой поверхности середины грани призмы, полученная при ее нагревании до термодинамического равновесия; Твозд - температура воздуха, а объемную теплоемкость исследуемого образца определяют по формуле
- начальная максимальная температура нагретой поверхности середины грани призмы, полученная при ее нагревании до термодинамического равновесия; Твозд - температура воздуха, а объемную теплоемкость исследуемого образца определяют по формуле
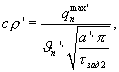
где 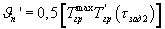 - амплитуда колебаний температурной полуволны на поверхности призмы квадратного сечения при ее охлаждении, Тгр'(τзад2) - температура середины грани призмы в заданный момент времени τзад2 при наступлении упорядоченного теплового режима в призме, далее, используя полученную информацию о температуропроводности и объемной теплоемкости, определяют теплопроводность исследуемого материала по соотношению λ'=а'·(сρ)', и за окончательные искомые теплофизические характеристики принимают средние значения, полученные на этапе нагревания и охлаждения призмы и определяемые по соотношениям
- амплитуда колебаний температурной полуволны на поверхности призмы квадратного сечения при ее охлаждении, Тгр'(τзад2) - температура середины грани призмы в заданный момент времени τзад2 при наступлении упорядоченного теплового режима в призме, далее, используя полученную информацию о температуропроводности и объемной теплоемкости, определяют теплопроводность исследуемого материала по соотношению λ'=а'·(сρ)', и за окончательные искомые теплофизические характеристики принимают средние значения, полученные на этапе нагревания и охлаждения призмы и определяемые по соотношениям
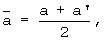
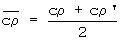 и
и 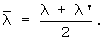
| Способ определения теплофизических характеристик полимерных материалов | 1979 |
|
SU934335A1 |
| Способ определения коэффициента температуропроводности твердых тел | 1979 |
|
SU855464A1 |
| Вычислительный томограф | 1982 |
|
SU1047283A1 |
| US 4630938 A, 23.12.1986 | |||
| US 5816706 A, 06.10.1998 | |||
| СПОСОБ ИЗВЛЕЧЕНИЯ РЕНИЯ И МОЛИБДЕНА ЖИДКОСТНОЙ ЭКСТРАКЦИЕЙ ВТОРИЧНЫМИ АМИНАМИ | 1996 |
|
RU2101371C1 |
| DE 3444383 A1, 04.07.1985. | |||
Авторы
Даты
2005-11-10—Публикация
2004-05-25—Подача