Изобретение относится к измерительной технике, а более конкретно к оптическим бесконтактным способам измерения излучательной способности и истинных температур различных объектов.
В методах оптической пирометрии результат измерений зависит не только от температуры, но и от свойств поверхности излучающего тела, пропускания промежуточной среды. Априорная информация об этих параметрах при измерении истинной температуры обычно используется в виде коэффициентов излучательной способности и пропускания промежуточной среды, табулированных в справочной литературе. Неполнота данных по этим коэффициентам, несоответствие их значений в реальных условиях табулированным, изменение свойств излучающей поверхности и промежуточной среды в процессе измерения приводят к возникновению методических погрешностей, превышающих инструментальные в десятки раз. С другой стороны, без определенной априорной информации об излучательных характеристиках объекта контроля сама задача об измерении его температуры методами оптической пирометрии оказывается беспочвенной.
Из предыдущего уровня техники известны различные варианты способов измерения излучательной способности и истинной температуры, основанные на многоволновом принципе.
Смотри, например, патент Д.Я.Света RU 2162210 C1, 7 G 01 J 5/50, недостаток описанного в нем способа заключается в невозможности его применения для полупрозрачных тел и необходимости в дополнительном двухволновом источнике излучения.
Известны также многоволновые способы спектрального отношения измерения истинных температур, например, описанные Hombeck G.A. Temperature: Its. Measurement and Control in Science and Industry, N.Y.Reinolds, 1962; Bourianes R. Morea M., Review Phys. Appl. 1977 v.42, p.893 и др., в частности, более поздний патент США 577323 Int. cl. G 01 J 5/00, G 01 J 5/08.
Все варианты способа спектрального отношения включают исключение “влияния” излучательной способности на результат измерения температуры при корректности, принятой аппроксимации зависимости спектральной излучательной способности от длины волны.
Недостатком всех способов отношения является весьма большая погрешность, за счет увеличения значения эквивалентной длины волны.
Это объясняется тем, что при расширении спектрального интервала принятая аппроксимация, например линейная, становится некорректной - теряет смысл. При сужении же спектрального интервала в методах/отношения возрастает эквивалентная длина волны, это приводит к уменьшению полезного сигнала и увеличивается погрешность измерения истинной температуры от влияния излучательной способности и пропускания промежуточной среды.
Известно, что величина логарифма сигнала InU(λ,T) в оптической пирометрии согласно закона Вина обратно пропорциональна эквивалентной длине волны, а погрешность измеряемой температуры пропорциональна величине последней.
Так, основная формула, определяющая погрешность в оптической пирометрии, гласит:
Δ Т/Т=Δ ε /ε · Λ эТ/С2
Здесь: Δ Т/Т - погрешность измерения температуры,
ε - коэффициент излучательной способности, ее произведение на коэффициент пропускания промежуточной среды,
Δ ε/ε - погрешность в значении излучательной способности (пропускания промежуточной среды),
Т - величина измеряемой температуры,
С2 - 14388 мкм град. - 2-я пирометрическая константа,
Λ экв - эквивалентная длина волны пирометрических систем.
Так, например, в способе двойного спектрального отношения при λ 1=0,72 мкм, λ 2=0,74 мкм и λ 3=0,76 мкм
Λ * экв=λ1λ 2λ 3/(2λ1λ 3-λ1λ 2-λ2λ 3)=506,6 мкм
В способе одинарного спектрального отношения (двухволновой пирометрии) величина эквивалентной длины волны также велика:
Λ **=λ1λ 2/(λ1-λ2)=0,72· 0,74/0,02=26,64
За прототип нами взят способ яркостной взаимно корреляционной пирометрии, описанной нами в авторском свидетельстве №368500 (опубликовано в Б.И. №9 за 1973 год).
Во взаимно корреляционной пирометрии температура определяется не по величине отношения, а по величине произведения спектральных интенсивностей излучения.
Так для произведения двух спектральных интенсивностей излучения: U(λ1,T) и U(λ2,T) величина логарифма их произведения будет:
lnU(λ1,T)U(λ2,T)=Inε1ε2-C2/Λ эТ
и величина эквивалентной длины волны:
Λ экв=λ1λ2/(λ1+λ2)
При весьма близких значениях λ1 и λ2, Λ э≅λ/2, т.е. при
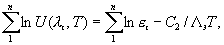 где Λ э≅λ/n
где Λ э≅λ/n
Таким образом, в методе взаимно корреляционной пирометрии эквивалентная длина волны не увеличивается с увеличением числа спектральных интенсивностей, как в методах отношения, а уменьшается, т.е. величина полезного сигнала увеличивается.
Недостаток способа взаимно корреляционной пирометрии является измерение не истинной, а взаимно корреляционной температуры.
Поставленная задача измерения истинной температуры поверхности по величине яркостных температур не менее чем на трех длинах волн решена тем, что, измеряя не менее трех компонент спектра, вычисляют логарифм произведения коэффициента спектральной излучательной способности на коэффициент пропускания промежуточной среды для каждой длины волны, при этом каждые три значения длины волны выбираются настолько близкими, что зависимость логарифма названного произведения от длины волны будет линейна; вычитают значения названного произведения из измеренных обратных значений яркостных температур, и полученные выражения суммируют для получения обратного значения искомой истинной температуры.
Таким образом, эквивалентная длина волны измеренной истинной взаимно корреляционной температуры уменьшается минимум в 3 раза. За счет чего величина полезного пирометрического сигнала увеличивается также в 3 раза.
В случае если требуемая величина погрешности не достигается из-за недостаточной величины сигнал/шум, следует увеличивать количество длин волн, сохраняя расстояние между ними, т.е. сохраняя линейность зависимости Inε (λι)=а0+а1λι на интервалах:
Inε (λ ι )=a0I+a1,Iλ ι на интервале λ1-λ3
Inε (λ ι )=а0II+a1,IIλ ι на интервале λ2-λ4
... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ...
... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ...
Inε (λ ι )=a0N+a1,Nλ ι на интервале λ N-1-λ N
Если же причиной погрешности является немонотонность спектральной зависимости произведения спектральной излучательной способности на пропускание промежуточной среды, следует сближать значения используемых длин волн, т.е. уменьшать расстояние между ними.
Рассмотрим применение предлагаемого способа при достаточно монотонном характере зависимости от длины волны произведения спектральной излучательной способности и пропускания промежуточной среды, имеющем, в частности, место в металлургии и других областях.
В этом случае каждые три значения длин волн выбираются настолько близкими, что зависимость логарифма ε (λ ) от длины волны будет линейна, т.е.:
Inε (λ )ι =a0,ι +a1,ι λ
где: a0,ι , а1,ι - коэффициенты полинома первой степени, аппроксимирующего указанную зависимость и
ε (λ )ι - произведение спектральной излучательной способности на пропускание промежуточной среды, на интервале λ 1-λ 3.
Обратные значения измеряемых трех яркостных температур запишем в обычном виде:
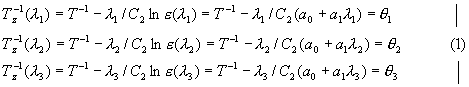
Для простоты дальнейших вычислений положим, что длины волн выбраны эквидистантно, т.е.
λ1=λ ; λ2=λ +Δλ ; λ3=λ +2Δλ , и введем следующие обозначения:
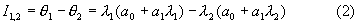
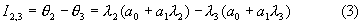
Тогда: 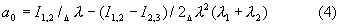
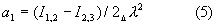
Следовательно, величина коэффициента спектральной излучательной способности (его произведения на коэффициент пропускания промежуточной среды) на длине волны λ ι будет определена как:
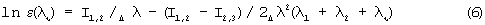
Вычитая значение Inε (λι) из соответствующего обратного значения измеренной яркостной температуры (1), (2) и (3), определим обратную величину истинной температуры на спектральном интервале λ1-λ2:
θ ι +[I1,2/Δλ -I2,3/2Δ λ (λ1+λ2+λι)]C2=Тn -1
Определяя, таким образом, Тn из θ 1, θ 2 и θ 3 и суммируя результаты, мы уменьшаем в три раза погрешность измерения истинной температуры Тn за счет укорочения эквивалентной длины волны.
Таким образом, в предлагаемом способе на спектральном интервале (λ 1-λ 3):
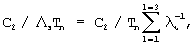 т.е. Λ э -1=1/λ 1+1/λ 2+1/λ 3
т.е. Λ э -1=1/λ 1+1/λ 2+1/λ 3
и при Δ λ <<λ , Λ э≈1/3λ 1.
Очевидно, что тоже самое мы получим, используя вместо яркостных температур спектральные интенсивности: U(λ ι ,T), т.к.
lnU(λ ι ,T)=Inξ ι +Inε (λ ι ,T)-C2/λ ι Tn
где: ξ ι - аппаратная постоянная, определяемая по градуировке.
При высоком уровне шумов, вызывающем недопустимую величину погрешности измерения истинной температуры в предлагаемом способе, следует увеличивать количество длин волн при сохранении выбранной ширины спектрального интервала (Δ λ ).
При существенной немонотонности названой зависимости количество используемых длин волн также следует увеличить, но при этом сужать величину интервала Δ λ .
Рассмотрим примеры применения предлагаемого способа.
Пример 1
Определение истинной температуры вольфрама.
Вольфрам является одним из наиболее селективных металлов. Выбираем 3 длины волны достаточно близкими: λ 1=0,9; λ 2=0,92 и λ 3=0,94.
Очевидно, что на таком узком спектральном интервале - 0,04 мкм линейная зависимость Inε (λ)w от длины волны будет вполне корректна.
С помощью таблицы из справочника “Излучательные свойства металлов” под ред. А.Е.Шейндлина, Энергия, 1974, для вольфрама разность обратных значений яркостных температур - формулы (2) и (3) при значении истинной температуры 1600К соответственно будут:
I1,2=2,337· 10-6 I3,4=2,3207· 10-6
Из формулы (4) и (5) определяем коэффициенты полинома а0 и a1. Затем по формуле (6) находим значение логарифма: Inε (0,9,Ти)=0,951. Потенцируя, находим ε (0,9)=0,386. Табличное значение ε (0,9)табл=0,399, т.е. погрешность в определении излучательной способности <Δε/ε <3,5%, и погрешность в истинной температуре на одной длине волны будет:
Δ Т/Т=Δε/ε · λ1Ти/С2=0,035· 0,9· 1600/14388≈ 0,38%
За счет определения ε (λ2,T) и ε (λ3,Т) и обратных значений: (λ2Ти)-1 и (λ3Ти)-1 на длинах волн λ2=0,92 мкм и λ3=0,94 мкм можно еще уменьшить значение эквивалентной длины волны, т.е. уменьшить погрешность определения истинной температуры еще в 3(!) раза, т.е. составит Δ Т/Т≅ 0,12%.
Пример 2
Элиминирование влияния дыма при измерении температуры в черной металлургии.
Требуется измерить температуру в условиях достаточно сильного задымления.
Положим, что пропускание дыма составляет τ (λ)=50%.
Расчет параметров дыма ведется, как обычно, по формуле Ангстрема (см., например, Ван де Хюлст “Рассеяние света малыми частицами”, М.: Иностранная литература, 1961 г.)
τ (λ )=ехр-(SI/λα )
Здесь:
SI - произведение “дисперсности” дыма на “толщу” дыма;
α =1,3 - коэффициент для “бурого” (Принятый в черной металлургии официальный термин) дыма.
(см. Velon R.G.Joul. Appi, Phys. 1962, #33, р.2140)
Так как зависимость пропускания дыма от длины волны явно нелинейная (экспоненциальная, по формуле Ангстрема), то для корректности линейной аппроксимации зависимости логарифма τ (λ 1) от длины волны, то спектральный интервал выберем более узким (чем в 1-ом примере).
Например: λ 1=0,9; λ 2=0,905 и λ 3=0,91, т.е. Δλ =0,005 мкм.
Определив для τ (λ)=50% на волне λ 1=0,9 мкм величину SI
SI=λα Inτ (λ)=0,91,3ln0,5=0,793
Элементарно найдем логарифмы пропускания дыма для трех длин волн:
In τ *(0,9)=-0,6914
In τ *(0,905)=-0,698
In τ *(0,91)=-0,7019
Определяя предлагаемым способом, коэффициент пропускания дыма на длине волны λ 1=0,9 получим:
Inτ (0,9)=-0,686
Потенцируя, имеем τ (0,9)=0,5036
И погрешность в определении коэффициента пропускания дыма будет:
[τ *(0,9)-τ (0,9)]/τ *(0,9)=0,0072=0,72%
При Т=2500K это даст погрешность в температуре:
Δ Т/Т=0,0072· 2500/14388· 0,9=0,12%
Используя еще две длины волны λ 2=0,905 и λ 3=0,91, можно получить погрешность ~0,005%.
Таким образом, в данном случае спектральный интервал Δ =0,05 можно увеличить.
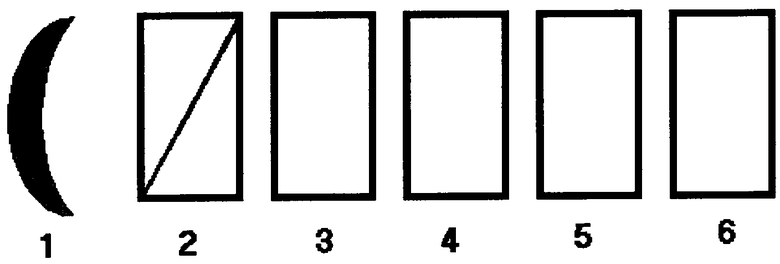
Принципиальная схема практической реализации предлагаемого способа изображена на чертеже.
Здесь:
1 - концентрирующая и визирная оптика;
2 - устройство для выделения необходимых спектральных составляющих;
3 - приемники излучения в виде отдельных элементов или линейки;
4 - усилители;
5 - аналого-цифровые преобразователи;
6 - микропроцессор или компьютер.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ ПИРОМЕТРИЧЕСКИХ ИЗМЕРЕНИЙ | 2007 |
|
RU2365883C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ СПЕКТРАЛЬНОЙ ИЗЛУЧАТЕЛЬНОЙ СПОСОБНОСТИ (ЕГО ВАРИАНТЫ) | 1999 |
|
RU2162210C1 |
| СПОСОБ ПИРОМЕТРИЧЕСКИХ ИЗМЕРЕНИЙ | 1998 |
|
RU2151382C1 |
| СПОСОБ ИЗМЕРЕНИЯ ИЗЛУЧАТЕЛЬНОЙ СПОСОБНОСТИ ОБЪЕКТА ПО ИЗМЕРЕННОЙ ТЕМПЕРАТУРЕ | 2008 |
|
RU2382994C2 |
| СПОСОБ ИЗМЕРЕНИЯ ДЕЙСТВИТЕЛЬНОЙ ТЕМПЕРАТУРЫ И СПЕКТРАЛЬНОЙ ИЗЛУЧАТЕЛЬНОЙ СПОСОБНОСТИ ОБЪЕКТА | 2019 |
|
RU2727340C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ИЗЛУЧАТЕЛЬНОЙ СПОСОБНОСТИ ТВЕРДЫХ МАТЕРИАЛОВ И УСТРОЙСТВО ДЛЯ ЕГО ОСУЩЕСТВЛЕНИЯ | 2016 |
|
RU2617725C1 |
| СПОСОБ ИЗМЕРЕНИЯ СПЕКТРАЛЬНОГО КОЭФФИЦИЕНТА ИЗЛУЧЕНИЯ ТЕЛА | 2018 |
|
RU2685548C1 |
| МНОГОКАНАЛЬНЫЙ РАДИАЦИОННЫЙ ПИРОМЕТР | 2003 |
|
RU2253845C1 |
| ПИРОМЕТР ИСТИННОЙ ТЕМПЕРАТУРЫ | 2002 |
|
RU2219504C2 |
| ПИРОМЕТРИЧЕСКИЙ СПОСОБ ОПРЕДЕЛЕНИЯ ТЕРМОДИНАМИЧЕСКОЙ ТЕМПЕРАТУРЫ МЕТАЛЛОВ И УСТРОЙСТВО ДЛЯ ЕГО ОСУЩЕСТВЛЕНИЯ | 2008 |
|
RU2381463C1 |
Изобретение относится к измерительной технике. Способ включает измерение истинной температуры поверхности по величине яркостных температур не менее чем на трех длинах волн. Измеряя не менее трех компонент спектра, вычисляют логарифм произведения коэффициента спектральной излучательной способности на коэффициент пропускания промежуточной среды для каждой длины волны, при этом каждые три значения длин волн выбираются настолько близкими, что зависимость логарифма названного произведения от длины волны будет линейна. Вычитают значения логарифма названного произведения из измеряемых обратных значений яркостных температур и полученные выражения суммируют для получения обратного значения искомой истинной температуры. Технический результат - возможность определения истинной температуры за счет увеличения полезного сигнала. 2 з.п. ф-лы, 1 ил.
| СПОСОБ ОПРЕДЕЛЕНИЯ СПЕКТРАЛЬНОЙ ИЗЛУЧАТЕЛЬНОЙ СПОСОБНОСТИ (ЕГО ВАРИАНТЫ) | 1999 |
|
RU2162210C1 |
| Способ пирометрических измерений | 1987 |
|
SU1440158A1 |
| RU 98106226 A1, 10.02.2000 | |||
| US 5029117 A, 02.07.1991. | |||
Авторы
Даты
2005-06-27—Публикация
2003-08-19—Подача