Изобретение относится к горной промышленности и может быть использовано для оптимизации объемов работ по опробованию горно-технологических и квалиметрических показателей при геометризации месторождений, разрабатываемых открытым и подземным способом.
Известен способ определения величины оптимального интервала, применяемой при составлении интервального вариационного ряда для непрерывной случайной величины горно-технологических и квалиметрических показателей свойств залежей полезного ископаемого (Ганджумян Р.А. Математическая статистика в разведочном бурении. М., Недра, 1980, с.22). При этом весь диапазон значений случайной величины разбивают на ряд интервалов, равных по величине. Оптимальная величина интервала определяется по формуле Стерджеса:
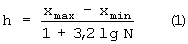
где Хmax и Хmin - соответственно максимальное и минимальное значение показателя случайной величины; N - число значений показателя.
Величина h, подсчитанная по формуле (2), соответствует приблизительно 0,5 σ (σ - среднеквадратическое отклонение показателя), т.е. условно, чтобы рассеивание значений показателя внутри интервала было несущественным. Рассмотренный способ оптимизации интервала применим для разбивки на интервалы внутри диапазона (xmax-xmin) самого показателя и не может быть использован для определения оптимального интервала опробования при изучении геометрии размещения какого-либо горно-технологического или квалиметрического показателя залежи.
Известен способ (Рыжов П.А. Геометрия недр. М., Углетехиздат, 1952, с.111) определения числа измерений какого-либо горно-технологического или квалиметрического показателя, когда задается точность, с которой необходимо получить среднюю из измерений. Необходимое число точек (скважин) опробования равно
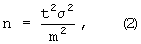
где t - коэффициент, соответствующий заданной вероятности; σ2 - дисперсия показателя; m - ср. квадратическая ошибка среднего показателя месторождения.
Однако число n, определяемое по формуле (2), обеспечивает лишь получение средней с заданной степенью точности, но ни в коей мере не обеспечивает выявление характера распределения изменения показателя.
Известен способ (Букринский В.А. Геометрия недр: Учебник для вузов. М.: Издательство Московского государственного горного университета, 2002, с.340) определения разведочного интервала через радиус корреляции. Наблюдаемая при опробовании изменчивость есть отражение природной изменчивости в нашем сознании через результаты наблюдений. По мере сгущения разведочной сети субъективное восприятие размещения показателей месторождения приближается к объективному, но полное их совпадение невозможно. Поэтому всегда при разведке месторождения существует некоторая степень неопределенности в знании размещения того или иного показателя, которая уменьшается по мере увеличения числа скважин и уменьшения расстояния между ними. Наступает такой момент, когда в результатах наблюдений за изменением показателя появляется закономерность, выявляется тренд. Разведочный интервал, при котором это происходит, называется критическим, или радиусом корреляции, пределом автокорреляции.
Опыт исследований убеждает, однако, что этот способ в практическом отношении весьма трудоемок, неудобен и не всегда однозначен при принятии окончательных решений в пользу того или иного интервала опробования. Связано это с большой чувствительностью автокорреляционных функций к эргодичности пространственных переменных.
Известен способ определения оптимального (рационального) интервала опробования (Букринский В.А. Геометрия недр: Учебник для вузов. М.: Издательство Московского государственного горного университета, 2002, с.320), принятый за прототип. Согласно этому способу на представительном участке месторождения проводят экспериментальное сплошное опробование. По результатам опробования строят кривую изменения изучаемого показателя, например, содержание полезного (вредного) компонента, вдоль линии опробования. Затем строят аналогичные графики при условии опробования через один, два, три и т.д. интервала опробования. При построении графика опробования через один интервал получают две реализации: одна реализация через интервал, начиная с первой точки опробования, другая реализация - со второй точки опробования. По этой же причине при построении графика опробования через два интервала получают три реализации, при опробовании через три интервала получаются четыре реализации и т.д. По полученным реализациям строят средние кривые Мх и определяют их изменчивость по формуле:

где К - длина соответствующей кривой Мх, мм; L - длина проекции этой кривой на горизонтальную ось, мм.
Строят зависимость изменчивости U от интервала опробования l. Интервал опробования, соответствующий перегибу кривой, является рациональным.
Однако перегиб кривой не всегда интерпретируется однозначно при сложном характере распределения показателя по линии опробования (Рылов А.П., Тимофеев Е.П. Горная геометрия. М., Недра, 1975 - рис.118 на стр.185; Букринский В.А. Геометрия недр. Учебник для вузов. - М., Недра, 1985 - рис.38 на стр.130). Как и в предыдущем способе, выбранный оптимальный (рациональный) интервал обладает недостаточной степенью достоверности и не отражает характерные признаки распределения.
Техническим результатом настоящего изобретения является повышение достоверности и надежности информации о распределении горно-геометрических показателей месторождений и оптимизация объемов работ по опробованию этих показателей.
Технический результат достигается тем, что в способе определения оптимальной длины интервала опробования при геометризации массива горных пород, заключающемся в опробовании изучаемого показателя свойств и измерении интервалов между соседними точками взятия проб на представительном участке опробования, построении графиков распределения показателей вдоль линии опробования через ноль, один, два, три и т.д. интервалы разрежения и определении оптимальной длины интервала опробования для всего массива горных пород, согласно изобретению на представительном участке измеряют показатели трещиноватости азимут и угол падения плоскостей трещин и расстояния (интервалы) между соседними трещинами строят графики азимута и угла падения плоскостей трещин вдоль линии опробования, по которым находят и строят графики вторых производных от распределения этих показателей трещиноватости при ноле, двух, трех и т.д. интервалах разрежения, по каждому из этих графиков определяют расстояние между экстремальными или нулевыми значениями вторых производных, из которых выбирают наибольший интервал разрежения, при котором расстояние между экстремальными или нулевыми значениями графиков вторых производных от распределения азимута и угла падения плоскостей трещин при различных интервалах опробования остается постоянным, и в качестве оптимального интервала принимают наименьший из полученных наибольших интервалов разряжения для азимута и угла падения плоскостей трещин.
Перечисленные отличительные признаки предлагаемого способа представляют собой новые действия и их последовательность. Эти признаки позволяют получить новый положительный эффект, заключающийся в повышении достоверности и надежности информации о распределении показателей трещиноватости массива горных пород и оптимизации объемов работ по опробованию для получения этой информации, указанные признаки, а следовательно, и предлагаемый способ в целом могут быть признаны удовлетворяющими критерию "существенные отличия".
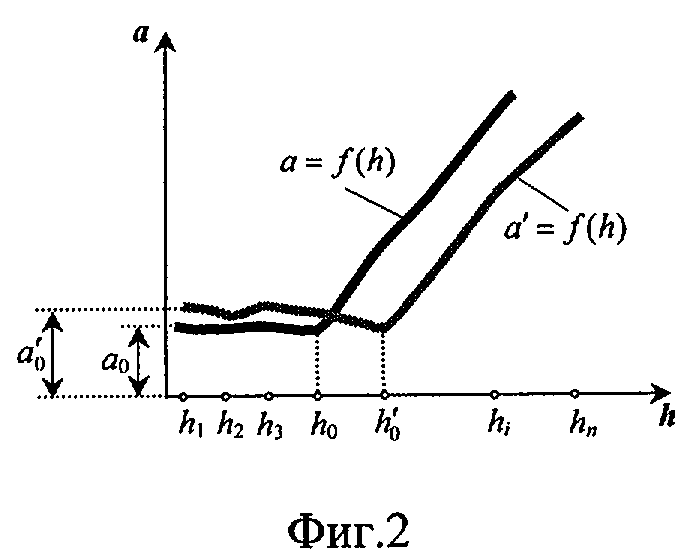
Способ поясняется чертежами, где на фиг.1 показаны графики распределения измеренного азимута и угла падения плоскостей трещин вдоль линии опробования, соответственно обозначенные как y=ƒ(x) и у=ϕ(х) и графики вторых производных от этих распределений, полученных при ноль (y1=ƒ1"(x) и y1=ϕ1"(x)), один (y2=ƒ2"(х) и y2=ϕ2"(х)), и т.д., i (yiƒi"(x) и yi=(ϕi"(x)), n (yn=ƒn"(х) и yn=ϕn"(x)) интервалах разрежения, а также расстояние между экстремальными значениями графиков вторых производных (a1, a2,..., ai, аn и а'1 a'2,..., a'i, a'n), на фиг.2 показаны графики зависимости расстояния между экстремальными значениями вторых производных (а) от интервала разрежения (h), полученные для азимута (a=ƒ(h)) и угла падения (a=ϕ(h)) плоскостей трещин.
Способ осуществляется следующим образом.
На представительном участке месторождения сначала проводится измерение показателей трещиноватости, азимута и угла падения плоскости трещин, например, горным компасом и расстояний между трещинами h1. Затем строят графики распределения измеренных азимутов и углов падения плоскостей трещин в зависимости от расстояния между соседними трещинами у=ƒ(х) и у=ϕ(х) на фиг.1.
При изучении в натурных условиях распределений различных горно-геометрических показателей трещиноватости в породах наблюдается общая тенденция периодического закономерного проявления этих показателей через определенные структурные образования (интервалы), т.е. породы проявляют свойства макроструктурной повторяемости. Исходя из того, что структурный фактор непосредственно или косвенно присутствует в получаемых функциях распределения показателей, предлагается выделить его через анализ этих функций на предмет выявления их инвариантных свойств. Инвариантность функций в этом случае будет являться инвариантностью изучаемых свойств и распределений, отражением структурных особенностей строения изучаемых пород.
Для выявления инвариантных свойств полученной функции распределения азимута трещин вдоль линии опробования y=ƒ(x) (фиг.1) необходимо сначала получить семейство подобных функций вторых производных ƒ1"(x), ƒ2"(х),... fn"(x) при интервалах между аргументами для первой функции h1 (расстояние между 1-й и 2-й, 2-й и 3-й и т.д. трещинами), для второй - h2 (расстояние между 1-й и 3-й, 3-й и 5-й и т.д. трещинами), для третьей - h3 (расстояние между 1-й и 4-й, 4-й и 7-й и т.д. трещинами) и т.д., для n-ой - hn. При этом h1<h2<...<hn (фиг.1). На практике расстояние между соседними трещинами h1 принимается как среднее из этих расстояний, тогда при получении и анализе вторых производных принимают следующие величины интервалов: h1=h1, h2=2h1, h3=3h1,..., hn=nhn. Такой подход обеспечивает подобие получаемых функций.
Вторые производные ƒ1"(x), f2 "(x),... fn"(x) представляют собой кривизну функции у=f[х), которая характеризует отклонения кривой функции распределения показателя (в малой ее части) от прямой линии. Кривизна (вторая производная) может иметь знак "+" или "-" в зависимости от направления изгиба: выпуклая часть кривой второй производной относительно оси ОХ имеет 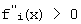 , вогнутая часть -
, вогнутая часть -  . Таким образом, кривые вторых производных состоят из набора выпуклых и вогнутых участков. Внутри этих участков можно найти точки с максимальной кривизной или с максимальным значением второй производной. С учетом этого на следующем этапе реализации предлагаемого способа производится структурный анализ полученных функций вторых производных. С этой целью для каждой из этих функций определяется структурный параметр а (фиг.1), представляющий собой либо расстояние между максимумами положительной и отрицательной кривизны, либо между соседними максимумами положительной (отрицательной) кривизны, либо между точками нулевой кривизны (точки левой кривизны (точки пересечения с осью абсцисс) и др. Затем строят график зависимости a=ƒ(h) (фиг.2).
. Таким образом, кривые вторых производных состоят из набора выпуклых и вогнутых участков. Внутри этих участков можно найти точки с максимальной кривизной или с максимальным значением второй производной. С учетом этого на следующем этапе реализации предлагаемого способа производится структурный анализ полученных функций вторых производных. С этой целью для каждой из этих функций определяется структурный параметр а (фиг.1), представляющий собой либо расстояние между максимумами положительной и отрицательной кривизны, либо между соседними максимумами положительной (отрицательной) кривизны, либо между точками нулевой кривизны (точки левой кривизны (точки пересечения с осью абсцисс) и др. Затем строят график зависимости a=ƒ(h) (фиг.2).
Результирующий график, приведенный на фиг.2, имеет 2 характерных участка: участок, в пределах которого, несмотря на увеличение интервала между трещинами, величина структурного элемента остается постоянной, и участок, где с увеличением интервала между трещинами наблюдается увеличение структурного элемента. Интервал, соответствующий точке перегиба этого графика, принимается в качестве оптимального интервала h0, через которые следует производить измерения азимута. Таким образом, оптимальным интервалом ho является интервал, до величины которого можно разрежать аргументы, сохраняя инвариантность подобных функций вторых производных, полученных при интервалах меньших, чем оптимальный интервал. Индикатором того, что функции инвариантны, является постоянство структурных элементов кривых, т.е. их равенство величине а0 (фиг.2). Аналогичным образом (фиг.1, фиг.2) производится определение оптимального интервала, через который следует измерять углы падения плоскостей трещин h'0 (фиг.2). За окончательное значение оптимального интервала опробования для двух показателей трещиноватости (азимута и угла падения) принимается наименьший из h0 и h'0 (ho на фиг.1), поскольку характерные свойства в закономерностях, отраженные в меньшем интервале опробования для одного из показателей трещиноватости, тем более будут отражены при опробовании через этот интервал другого показателя трещиноватости. В дальнейшем выявленный таким образом оптимальный интервал измерения показателей трещиноватости (h0) используется при опробовании на других участках месторождения, другими словами, распространяется на массив горных пород.
Преимуществом предлагаемого способа является существенное повышение степени однозначности, а следовательно, достоверности и надежности информации о распределении изучаемых показателей при геометризации месторождений и на этой основе оптимизация объемов работ по опробованию этих показателей за счет принятия в качестве оптимального интервала наибольшего интервала, при котором соблюдается постоянство структурного параметра а, определенного для функций вторых производных от реализации через один, два, три и т.д. интервала, т.е. соблюдается условие структурной инвариантности этих функций.
Предлагаемый способ предусматривается использовать в геолого-маркшейдерских работах по геометризации недр при разведке и эксплуатации месторождений полезных ископаемых.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ ОПРЕДЕЛЕНИЯ ЭЛЕМЕНТОВ ЗАЛЕГАНИЯ ТРЕЩИН | 2006 |
|
RU2312377C1 |
| Способ определения внутренней системы трещин массива горных пород | 2018 |
|
RU2672117C1 |
| СПОСОБ ПОСТРОЕНИЯ ГЕОЛОГО-ГИДРОДИНАМИЧЕСКИХ МОДЕЛЕЙ ДВОЙНОЙ СРЕДЫ ЗАЛЕЖЕЙ БАЖЕНОВСКОЙ СВИТЫ | 2014 |
|
RU2601733C2 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ВНУТРЕННЕЙ СИСТЕМЫ ТРЕЩИН НА ОБНАЖЕНИЯХ | 2012 |
|
RU2511422C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ПАРАМЕТРОВ СТРУКТУРЫ РАЗЛОМНОЙ ТРЕЩИНОВАТОСТИ ЛИТОСФЕРЫ | 2016 |
|
RU2625615C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ПАРАМЕТРОВ СТРУКТУРЫ РАЗЛОМНОЙ ТРЕЩИНОВАТОСТИ ЛИТОСФЕРЫ | 2018 |
|
RU2698551C1 |
| СПОСОБ БУРОВЗРЫВНОЙ ПОДГОТОВКИ ГОРНОЙ МАССЫ НА УГОЛЬНЫХ КАРЬЕРАХ | 2006 |
|
RU2319012C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ КОНТУРОВ ПРОМЫШЛЕННОГО ОРУДЕНЕНИЯ ЗОЛОТОРУДНОГО МЕСТОРОЖДЕНИЯ | 2012 |
|
RU2523766C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ТРЕЩИНОВАТОСТИ ГОРНЫХ ПОРОД В СКВАЖИНАХ | 1998 |
|
RU2150720C1 |
| СПОСОБ ПОИСКОВ СКРЫТОГО ОРУДЕНЕНИЯ | 1992 |
|
RU2056644C1 |
Изобретение относится к горной промышленности и может быть использовано при геометризации месторождений, разрабатываемых открытым и подземным способом. Способ заключается в опробовании изучаемого показателя свойств и измерении интервалов между соседними точками взятия проб на представительном участке опробования. При этом на представительном участке измеряют показатели трещиноватости - азимут и угол падения плоскостей трещин - и расстояния (интервалы) между соседними трещинами. Строят графики азимута и угла падения плоскостей трещин вдоль линии опробования, по которым находят и строят графики вторых производных от распределения этих показателей трещиноватости при ноле, двух, трех и т.д. интервалах разрежения. По каждому из этих графиков определяют расстояние между экстремальными или нулевыми значениями вторых производных, из которых выбирают наибольший интервал разрежения, при котором расстояние между экстремальными или нулевыми значениями графиков вторых производных от распределения азимута и угла падения плоскостей трещин при различных интервалах опробования остается постоянным. В качестве оптимальной длины интервала опробывания для всего массива горных пород принимают наименьший из полученных наибольших интервалов разрежения для азимута и угла падения плоскостей трещин. Изобретение направлено на повышение достоверности и надежности получаемой информации. 2 ил.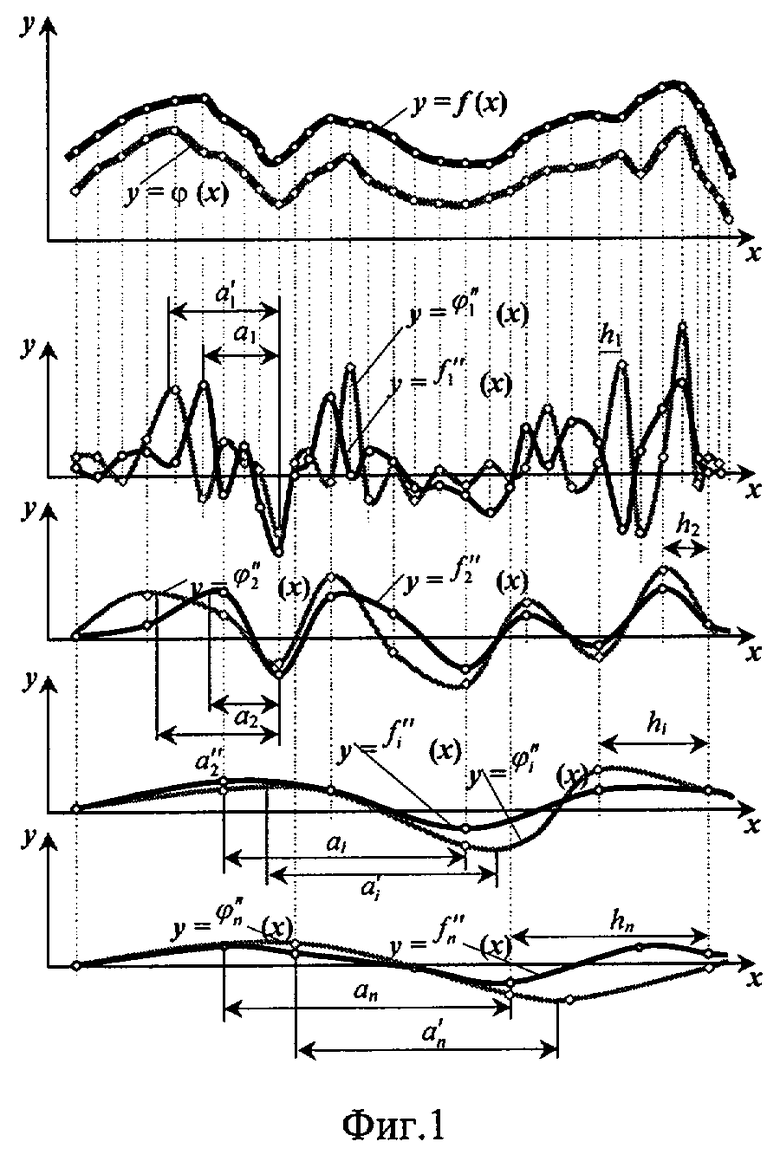
Способ определения оптимальной длины интервала опробования при геометризации массива горных пород, заключающийся в опробовании изучаемого показателя свойств и измерении интервалов между соседними точками взятия проб на представительном участке опробования, построении графиков распределения показателей вдоль линии опробования через ноль, один, два, три и т.д. интервалы разрежения и определении оптимальной длины интервала опробования для всего массива горных пород, отличающийся тем, что на представительном участке измеряют показатели трещиноватости - азимут и угол падения плоскостей трещин - и расстояния (интервалы) между соседними трещинами, строят графики азимута и угла падения плоскостей трещин вдоль линии опробования, по которым находят и строят графики вторых производных от распределения этих показателей трещиноватости при ноле, двух, трех и т.д. интервалах разрежения, по каждому из этих графиков определяют расстояние между экстремальными или нулевыми значениями вторых производных, из которых выбирают наибольший интервал разрежения, при котором расстояние между экстремальными или нулевыми значениями графиков вторых производных от распределения азимута и угла падения плоскостей трещин при различных интервалах опробования остается постоянным, и в качестве оптимального интервала принимают наименьший из полученных наибольших интервалов разрежения для азимута и угла падения плоскостей трещин.
| БУКРИНСКИЙ В.А | |||
| Геометрия недр | |||
| М.: Изд-во МГГУ, 2002, с | |||
| Способ амидирования жидких сульфохлоридов ароматического ряда | 1921 |
|
SU316A1 |
| Математическая статистика в разведочном бурении | |||
| М.: Недра, 1980, с.22. | |||
Авторы
Даты
2005-09-27—Публикация
2004-07-30—Подача