Область техники, к которой относится изобретение
Данное изобретение относится к способу формирования устойчивых состояний плотной высокотемпературной плазмы, которая может быть использована, например, для управляемого термоядерного синтеза.
Уровень техники
Из уровня техники известен сильноточный импульсный разряд, который формируется посредством цилиндрической разрядной камеры (торцы которой выполняют роль электродов), которая заполняется рабочим газом (дейтерий, водород, дейтериево-тритиевая смесь при давлении 0,5-10 мм рт.ст., либо благородные газы при давлении 0,01-0,1 мм рт.ст.). Далее через газ осуществляется разряд мощной конденсаторной батареи, с подачей напряжения на анод 20-40 кВ и достижением тока в формирующемся разряде порядка 1 МА. В экспериментах (Лукьянов С.Ю. "Горячая плазма и управляемый ядерный синтез", М., Атомиздат, 1975), наблюдали сначала первую фазу процесса - сжатие плазмы к оси магнитным полем тока с уменьшением диаметра токового канала примерно в 10 раз и образованием на оси разряда яркосветящегося плазменного шнура (z-пинч). Во второй фазе процесса наблюдали быстрое развитие неустойчивостей токового канала (изгибы, винтовые возмущения и т.д.).
Нарастание этих неустойчивостей происходит очень быстро и ведет к разрушению плазменного столба (выбрасывание плазменных струй, разрывы разряда и т.д.), что ограничивает время жизни разряда величиной порядка 10"' с. По этой причине в линейном пинче оказывается нереальным выполнение условия ядерного синтеза, определяемого критерием Лоусона nτ>1014 см-3 с, где n - концентрация плазмы, τ - время жизни разряда.
Аналогичная ситуация имеет место в Θ-пинче, когда к цилиндрической разрядной камере приложено внешнее продольное магнитное поле, индуцирующее азимутальный ток.
Известны магнитные ловушки, способные длительное время (но недостаточное для протекания ядерного синтеза) удерживать высокотемпературную плазму в ограниченном объеме (см. Арцимович Л.А. "Замкнутые плазменные конфигурации", М., Атомиздат, 1969). Существует две основные разновидности магнитных ловушек: замкнутые и открытые.
Под магнитными ловушками понимаются установки, способные достаточно длительное время удерживать высокотемпературную плазму в ограниченном объеме и которые описаны в (Арцимович Л.А. "Замкнутые плазменные конфигурации", М., Атомиздат, 1969).
К магнитным ловушкам замкнутого типа (с которьми долгое время были связаны надежды на реализацию условий управляемого ядерного синтеза (УТС)) относятся установки типа Токамак, Сферомак и Стелларатор в различных модификациях (Лукьянов С.Ю. "Горячая плазма и УТС", М., Атомиздат, 1975).
В установках типа Токамак кольцевой ток, создающий вращательное преобразование магнитных силовых линий, возбуждается в самой плазме. Компактный тор с тороидальным магнитным полем внутри плазмы представляет собой Сферомак. Вращательное преобразование магнитных силовых линий, осуществляемое без возбуждения в плазме тороидального тока, реализуется в Стеллараторах (Волков Е.Д. и др. "Стелларатор", М., Наука, 1983).
Магнитные ловушки открытого типа с линейной геометрией: пробкотрон, амбиполярная ловушка, ловушка газодинамического типа (Рютов Д.Д. "Открытые ловушки", "УФН", 1988, том 154, с.565).
Несмотря на все конструктивные отличия ловушек замкнутого и открытого типа в их основу положен один принцип - достижение состояний гидростатического равновесия плазмы в магнитном поле за счет равенства газокинетического давления плазмы и давления магнитного поля на внешней границе плазмы. Само же их разнообразие вызвано отсутствием положительных результатов.
При использовании установки типа плазменный фокус (ПФ) (так называют электроразрядную установку) получают нестационарный сгусток плотной высокотемпературной дейтериевой (как правило) плазмы (этот сгусток также называют плазменным фокусом). ПФ относится к разряду пинчей и образуется в области кумуляции токовой оболочки на оси разрядной камеры специальной конструкции, вследствие чего в отличие от прямого пинча приобретает нецилиндрическую форму (Петров Д.П. и др. "Мощный импульсный газовый разряд в камерах с проводящими стенками" в сб. "Физика плазмы и проблема управляемых термоядерных реакций", том 4, М., изд-во АН СССР, 1958).
В отличие от установок линейного пинча, где роль электродов играют торцы камеры, в ПФ роль катода выполняет корпус камеры, вследствие чего плазменный сгусток приобретает форму воронки (отсюда название установки). При тех же рабочих параметрах, что и в цилиндрическом пинче, в установке ПФ удается получить плазму с более высокими температурой, плотностью и временем жизни, однако последующее развитие неустойчивости разрушает разряд, так же как и в линейном пинче (Бурцев Б.А. и др. "Высокотемпературные плазменные образования" в кн. "Итоги науки и техники", серия "Физика плазмы", том 2, М., изд-во АН СССР, 1981) и при этом устойчивых состояний плазмы, фактически, не достигается.
Нестационарные сгустки плотной высокотемпературной плазмы получают также в газоразрядных камерах с коаксиальным расположением электродов (использование установок с коаксиальными плазменными инжекторами). Первая установка такого рода запущена в 1961 году Д.Майзером (Mather J.W., "Formation on the high-density deuterium plasma focus", Phys. Fluids, 1965, v.8, p.366). В дальнейшем она получила развитие (в частности, см. (J.Brzosko et. al "Phvs.Let.A. 192 (1994), стр.250, Phvs.Let.A. 155 (1991), стр.162)). Существенным элементом этого развития явилось использование рабочего газа с примесью многоэлектронных атомов. Инжекция плазмы в таких установках достигается за счет соосного расположения цилиндрических камер, где внутренняя камера, играющая роль анода, расположена геометрически ниже внешнего цилиндра - катода. В работах J.Brzosko было отмечено, что эффективность генерации плазменных сгустков возрастает при добавлении к водороду газов многоэлектронных атомов. Однако, и в этих установках развитие неустойчивости существенно ограничивает время жизни плазмы. В результате оно меньше, чем необходимо для достижения условий устойчивого протекания реакции ядерного синтеза. При определенных конструктивных особенностях, в частности, при использовании конических коаксиальных электродов ("Плазменные ускорители и ионные инжекторы" под ред. М.П.Козлова, А.И.Морозова, М., Наука, 1984) такие установки являются уже установками инжекции плазмы. В указанных выше установках (установки с коаксиальными цилиндрическими электродами) плазма на всех этапах, вплоть до распада, остается в области магнитного поля, хотя и имеет место ее инжекция в межэлектродное пространство. В чистом виде инжекция плазмы из межэлектродного пространства наблюдается в установках с коническими коаксиальными электродами. Область применения плазменных инжекторов рассматривается как вспомогательная: для инжекции плазмы с ее последующим использованием (например, для дополнительной накачки энергии в установке типа Токамак, лазерных устройствах и т.д.), что в свою очередь, ограничило использование этих установок не в импульсном, а в квазистационарном режиме.
Таким образом, существующий уровень техники, основанный на удержании плазмы магнитным полем, не решает задачи удержания плотной высокотемпературной плазмы в течение времени, необходимого для протекания реакций ядерного синтеза, но эффективно решает задачу нагрева плазмы до состояния, в котором эти реакции могут протекать.
Раскрытие изобретения
Таким образом, данное изобретение касается способа формирования устойчивых состояний плотной высокотемпературной плазмы, который включает следующие этапы:
a) формирование плотной высокотемпературной плазмы из водорода и его изотопов с помощью импульсных сильноточечных разрядов, при этом осуществляют подачу двухкомпонентного газа в зазор между коаксиальными коническими электродами, подачу высоковольтного напряжения 20-40 кВ на анод для создания магнитного поля;
b) инжекцию плазмы из области магнитного поля с параметрами, отвечающими условиям излучения электронов с линейчатым спектром энергии.
Причем перекачка энергии (этап с)) осуществляется путем каскадного перехода в длинноволновую область эВ-энергии до состояния запирания и усиления излучения в плазме и одновременного сжатия до состояния гидростатического равновесия, и при формировании указанных состояний в составе рабочего газа используют многоэлектронные атомы для тушения спонтанного излучения с нижних энергетических уровней электрона кэВ-области в собственном гравитационном поле.
Для получения плотной высокотемпературной плазмы используют водород и многоэлектронные атомы, такие, как криптон, ксенон и другие близкие к ним по природе (неон, аргон) элементы.
Для реализации условий
протекания реакции ядерного синтеза используют водород и углерод, причем углерод используют и для тушения спектров излучения с кэВ-энергиями и как катализатор реакции синтеза.
Заявляемый способ обеспечивает схему формирования устойчивых состояний плотной высокотемпературной плазмы, которая включает в себя устройство подачи рабочего газа, разрядную камеру, разрядный контур, камеру формирования устойчивого сгустка плазмы.
При необходимости каждый из перечисленных блоков схемы может быть оснащен соответствующей измерительной аппаратурой.
Изобретение поясняется схемой импульсного сильноточного магнитокомпрессионного разряда на многозарядных ионах с коническими коаксиальными электродами, на которой изображены:
внешний электрод;
внутренний электрод имеет сужающуюся поверхность, близкую к конической;
разрядный контур;
область сжатия магнитным полем;
область компрессии за счет тока выноса в выходящей плазменной струе и последующего сжатия.
Осуществление изобретения
Термины и определение, используемые в заявке
Определение "устойчивые состояния плотной высокотемпературной плазмы" означает состояния гидростатического равновесия плазмы, когда газокинетическое давление уравновешивается давлением магнитного поля или, в данном случае, давлением излучаемого гравитационного поля.
Определение "плотная высокотемпературная плазма" означает плазму с нижними значениями плотностей nC, ni=(1023-1025) м-3 и температур Те Ti =(107-108) К.
Определение "параметры плазмы, отвечающие гравитационному излучению электронов" (с линейчатым спектром излучения), означает параметры, которые находятся в указанном выше диапазоне плотностей и температур.
Определение "запирание гравитационного излучения в плазме" означает состояние гравитационного излучения в плазме, которое имеет место при равенстве его частоты излучения и электронной ленгмюровской частоты. В данном случае запирание излучения имеет место вследствие двух причин:
- перекачки энергии по спектру в длинноволновую область вследствие каскадных переходов с достижением частоты излучения (1013-1014) с ленгмюровской частоте плазмы, равной электронной, что и является условием запирания гравитационного излучения в плазме;
- тушением спонтанного гравитационного излучения электронов с нижних энергетических уровней ионами многоэлектронных атомов, когда энергия возбужденного электрона передается иону с соответствующими энергетическими уровнями, приводя к его ионизации.
Определение "усиление гравитационного излучения" означает усиление, которое имеет место при запирании гравитационного излучения, так как при выполнении условий запирания, оно остается в плазме с последовательным излучением полной энергии гравитационного поля, запертого в плазме.
Для лучшего понимания изобретения далее приводится описание высокотемпературных плазменных образований, имеющих место в предлагаемом способе, и описание способа формирования их устойчивых состояний как состояний гидростатического равновесия.
1. Гравитационное излучение электронов с линейчатым спектром как излучение одного уровня с электромагнитным.
Для рассматриваемой математической модели, описывающей линейчатый спектр стационарных состояний электронов в собственном гравитационном поле, существенны два момента. Первое. В полевых уравнениях Эйнштейна к - постоянная, связывающая геометрические свойства пространства-времени с распределением физической материи, так что происхождение уравнений не связано с численным ограничением величины к. Только требование соответствия с классической теорией тяготения Ньютона приводит к малому значению κ=8πG/с4, где G, с - ньютоновская гравитационная постоянная и скорость света, соответственно. Такое требование следует из первоначальной концепции эйнштейновской Общей Теории Относительности (ОТО) как релятивистского обобщения ньютоновской теории тяготения. Второе. Наиболее общей формой уравнений релятивистской гравитации являются уравнения с Λ-членом. Предельный переход к слабым полям приводит в этом случае к уравнению

где Δ - оператор Лапласа, Ф - скалярный потенциал поля, ρ - плотность источника. Это обстоятельство, в конечном счете, является решающим для отбрасывания Λ-члена, так как только в этом случае ОТО является обобщением классической теории тяготения. Таким образом, численные значения κ=8πG/с4 и Λ=0 в уравнениях ОТО не связаны с происхождением уравнений, а вытекают лишь из соответствия ОТО классической теории. Начиная с 70-х годов стало очевидным (Siravam С. and Sinha К., Phys. Res.51 (1979) 112), что в квантовой области численное значение G не совместимо с принципами квантовой механики. В ряде работ (Siravam С. and Sinha К., Phys. Res. 51 (1979) 112), в том числе и в (Fisenko S. et all, Phys. Lett. A, 148, 8, 9 (1990) 405)) было показано, что в квантовой области приемлема константа связи К, причем K≈1040 G. Это и обозначило суть проблемы обобщения релятивистских уравнений на квантовом уровне: такое обобщение должно стыковать численные значения констант в квантовой и классической областях.
В развитие этих результатов, в качестве приближения на микроуровне полевых уравнений Эйнштейна, предлагается модель, основанная на следующем предположении:
"Гравитационное поле в области локализации элементарной частицы с массой mo характеризуется такими значениями гравитационной постоянной К и постоянной Λ, которые приводят к стационарным состояниям частицы в собственном гравитационном поле, а сами стационарные состояния частиц являются источником гравитационного поля с ньютоновской гравитационной постоянной G."
Наиболее общим подходом в гравитации является подход с учетом кручения, в котором гравитационное поле выступает как калибровочное, на равных правах с другими фундаментальными полями (Иваненко Д.Д. и др. Калибровочная теория гравитации, Москва, Издательство МГУ (1985)). Такой подход лишен априорности в части геометрических свойств гравитационного поля, что не приводит к каким-либо ограничениям на микроуровне. Для элементарного спинорного источника с массой mo, система уравнений, описывающая его состояния в собственном гравитационном поле, в соответствии со сделанным предположением, будет иметь вид

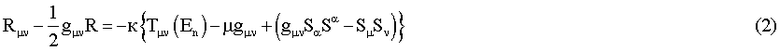

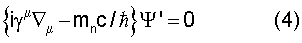
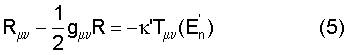
Выше впредь обозначено: κ=8πК/с4, κ'=8πG/с4, En - энергия стационарных состояний в собственном гравитационном поле с постоянной К, Λ=κμ, rn - значение координаты r, удовлетворяющей n-состоянию равновесия в собственном гравитационном поле, г, - постоянная размерности,  ▿μ - ковариантная производная со спинорной связанностью, не зависящая от кручения,
▿μ - ковариантная производная со спинорной связанностью, не зависящая от кручения, 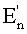 - энергетическое состояние частицы с массой mn (свободной, либо во внешнем поле), описываемой в собственном гравитационном поле с постоянной G волновой функцией Ψ'. Остальные обозначения общеприняты в теории гравитации.
- энергетическое состояние частицы с массой mn (свободной, либо во внешнем поле), описываемой в собственном гравитационном поле с постоянной G волновой функцией Ψ'. Остальные обозначения общеприняты в теории гравитации.
Уравнения (1)-(5) описывают состояния равновесия частиц (стационарные состояния) в собственном гравитационном поле и определяют область локализации поля с постоянной К, удовлетворяющую состоянию равновесия. Такие стационарные состояния являются источниками поля с постоянной G, а условие (3) является условием сшивки решения с гравитационными постоянными К, G. Предложенная модель в физическом отношении совместима с принципами квантовой механики, а гравитационное поле с постоянными К, Λ на некотором, вполне определенном расстоянии, определяемом состоянием равновесия, переходит в поле с постоянной G, где в пределе слабого поля выполняется уравнение Пуассона.
Система уравнений (1)-(5) в первую очередь представляет интерес для задачи на стационарные состояния, т.е. для задачи расчета энергетического спектра элементарного источника в собственном гравитационном поле. В этом смысле уместно воспользоваться аналогией с электродинамикой, в частности, с задачей на стационарные состояния электрона в кулоновском поле. Переход от уравнения Шредингера к релятивистскому уравнению Клейна-Гордона позволяет учесть тонкую структуру энергетического спектра электрона в кулоновском поле, а переход к уравнению Дирака позволяет учитывать тонкую структуру, обусловленную релятивизмом, и расщепление энергетических уровней, обусловленное спин-орбитальным взаимодействием. Используя такую аналогию и вид уравнения (1), можно сделать вывод о том, что решение этого уравнения без члена 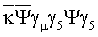 дает спектр, аналогичный спектру тонкой структуры (аналогичный в смысле релятивизма и снятия вырождения по главному квантовому числу). Учет же члена
дает спектр, аналогичный спектру тонкой структуры (аналогичный в смысле релятивизма и снятия вырождения по главному квантовому числу). Учет же члена  , как отмечено в (Siravam С. and Sinha К., Phys. Res.51 (1979) 112), аналогичен учету члена
, как отмечено в (Siravam С. and Sinha К., Phys. Res.51 (1979) 112), аналогичен учету члена 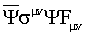 в уравнении Паули. Последнее означает, что решение задачи на стационарные состояния с учетом кручения, будет давать полный спектр энергетических состояний, в котором учитывается как тонкая структура релятивизма, так и расщепление энергетических состояний, обусловленное взаимодействием спина с кручением. Этот факт, находящийся в полном соответствии с требованиями калибровочной теории гравитации, и позволяет считать, что сделанные выше предположения о свойствах гравитационного поля в квантовой области относятся, в общем случае, именно к гравитационному полю с кручением.
в уравнении Паули. Последнее означает, что решение задачи на стационарные состояния с учетом кручения, будет давать полный спектр энергетических состояний, в котором учитывается как тонкая структура релятивизма, так и расщепление энергетических состояний, обусловленное взаимодействием спина с кручением. Этот факт, находящийся в полном соответствии с требованиями калибровочной теории гравитации, и позволяет считать, что сделанные выше предположения о свойствах гравитационного поля в квантовой области относятся, в общем случае, именно к гравитационному полю с кручением.
Сложность решения такой задачи вынуждает обратиться к более простому приближению, а именно расчету энергетического спектра только в приближении тонкой структуры, обусловленной релятивизмом. В таком приближении задача на стационарные состояния элементарного источника в собственном гравитационном поле сведется к решению следующих уравнений:
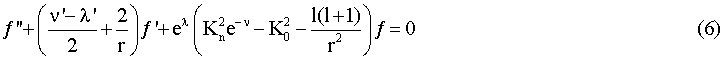
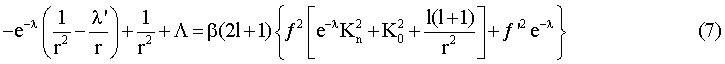
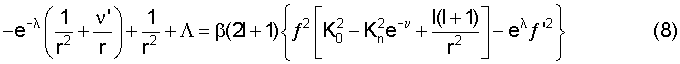
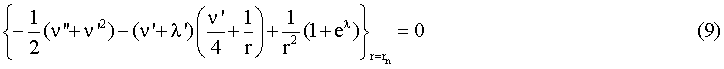




Уравнения (6)-(8) следуют из уравнений (14)-(15)


после подстановки в них Ψ в виде 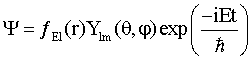 и конкретных вычислений в метрике центрально-симметричного поля, интервал в которой определяется выражением (Ландау Л.Д., Лифшиц Е.М., Теория поля, Москва, Издательство Наука (1976))
и конкретных вычислений в метрике центрально-симметричного поля, интервал в которой определяется выражением (Ландау Л.Д., Лифшиц Е.М., Теория поля, Москва, Издательство Наука (1976))

Выше обозначено: ƒEl - радиальная волновая функция, описывающая состояния с определенной энергией Е и орбитальным моментом l (далее индексы El опущены), Ylm(θ,ϕ) - сферические функции, 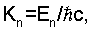

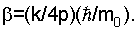
Условие (9) является условием для нахождения rn, условия (10)-(12) являются краевыми условиями и условием нормировки функции ƒ, соответственно. Условие (9) в общем случае имеет вид R(K,rn)=R(G,rn). Пренебрегая собственным гравитационным полем с постоянной G, это условие запишем в виде R(K,rn)=0, чему и соответствует равенство (9).
Правые части уравнений (7)-(8) вычислены из общего выражения для Тензора Энергии - Импульса комплексного скалярного поля:
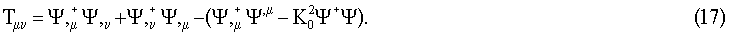
Соответствующие компоненты Тμν получены суммированием по индексу m с использованием характерных тождеств для сферических функций (Варшалович Д.А. и др. Квантовая теория углового момента, Ленинград, Издательство Наука (1975))
после подстановки в (17) 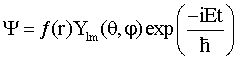 . Даже в самом простом приближении задача на стационарные состояния элементарного источника в собственном гравитационном поле является сложной математической задачей. Эта задача упрощается, если ограничиться оценкой только энергетического спектра. Уравнение (6) можно многими способами свести к уравнениям (Камке Э. Справочник по обыкновенным дифференциальным уравнениям, Москва, Издательство Наука (1976)):
. Даже в самом простом приближении задача на стационарные состояния элементарного источника в собственном гравитационном поле является сложной математической задачей. Эта задача упрощается, если ограничиться оценкой только энергетического спектра. Уравнение (6) можно многими способами свести к уравнениям (Камке Э. Справочник по обыкновенным дифференциальным уравнениям, Москва, Издательство Наука (1976)):
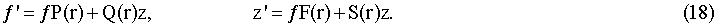
Для этого нужно выбрать Р, Q, F, S так, чтобы выполнялись условия
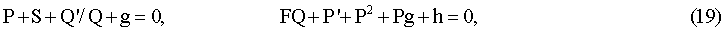
где g и h соответствуют записи уравнения (6) в виде ƒ''+gƒ'+hƒ=0. Условиям (19), в частности, удовлетворяют Р, Q, F, S в виде:
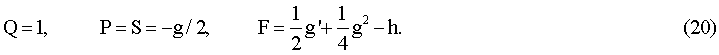
Решениями системы (18) будут функции (Камке Э. Справочник по обыкновенным дифференциальным уравнениям, Москва, Издательство Наука (1976)):

где С - произвольная постоянная, θ(r) - решение уравнения

а ρ(r) находится по формуле
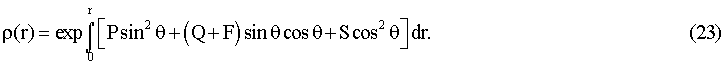
Это представление решения с помощью полярных координат в данном случае и позволяет определить нули функции ƒ(r) при r=rn, которым соответствуют значения θ=nπ (n - целое). В качестве одного из самых простых приближений для ν, λ выберем зависимость:
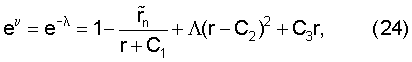 где
где
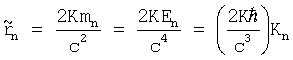
и 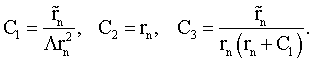
Ранее, в качестве оценки для К принималось K≈1,7×l029 Нм2кг-2. Если считать, что наблюдаемое значение массы покоя электрона m1 есть значение его массы в основном стационарном состоянии в собственном гравитационном поле, то m0=4m1/3. Из соображений размерности следует, что энергия, находящаяся в связанном состоянии, определяется выражением 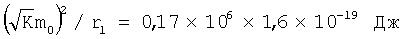 , где r1 - классический радиус электрона. Это приводит к оценке K≈5,1×1031 Нм2кг-2, которая в дальнейшем принимается за исходную. Расхождения в оценках К, полученных разными способами, вполне допустимы, тем более, что они не носят катастрофический характер. Из условия, что μ есть плотность энергии электрона, следует μ=1,1×1030 Дж/м3, Λ=κμ=4,4×1029 м-2. Из (22) следует (с учетом уравнения для ƒ(r)):
, где r1 - классический радиус электрона. Это приводит к оценке K≈5,1×1031 Нм2кг-2, которая в дальнейшем принимается за исходную. Расхождения в оценках К, полученных разными способами, вполне допустимы, тем более, что они не носят катастрофический характер. Из условия, что μ есть плотность энергии электрона, следует μ=1,1×1030 Дж/м3, Λ=κμ=4,4×1029 м-2. Из (22) следует (с учетом уравнения для ƒ(r)):

где 
Интегрирование уравнения (25) и подстановка θ=πn, r=rn дают зависимость между Kn и rn
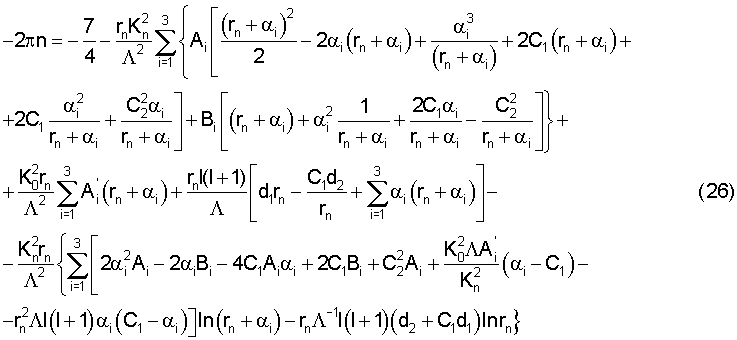
Входящие в (26) коэффициенты являются коэффициентами при простых дробях при разложении многочленов, необходимом для их интегрирования, причем 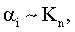
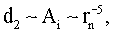
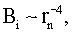
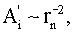

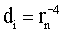 . Для исключения из (26) rn существует условие (9) (или эквивалентное ему для используемого приближения условие exp ν(K,rn)=1), однако его непосредственное использование еще более усложнит и без того громоздкое выражение (26). В то же время нетрудно заметить, что rn˜10-3 rnc, где rnc - комптоновская длина волны частицы с массой mn, и, следовательно,
. Для исключения из (26) rn существует условие (9) (или эквивалентное ему для используемого приближения условие exp ν(K,rn)=1), однако его непосредственное использование еще более усложнит и без того громоздкое выражение (26). В то же время нетрудно заметить, что rn˜10-3 rnc, где rnc - комптоновская длина волны частицы с массой mn, и, следовательно, 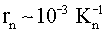 . Зависимость (26) сама по себе является весьма приближенной, но, тем не менее, ее наличие, независимо от точности приближения, означает существование спектра энергий, как следствие самодействия частицы с собственным гравитационным полем в области r≤rn, где имеет место взаимокомпенсирующее действие поля и частицы. При l=0 приближенное решение (26) с учетом связи между rn и Kn имеет вид:
. Зависимость (26) сама по себе является весьма приближенной, но, тем не менее, ее наличие, независимо от точности приближения, означает существование спектра энергий, как следствие самодействия частицы с собственным гравитационным полем в области r≤rn, где имеет место взаимокомпенсирующее действие поля и частицы. При l=0 приближенное решение (26) с учетом связи между rn и Kn имеет вид:

где α=1,65; β=1,60.
Зависимость (27) конкретизирована, исходя из того, что наблюдаемое значение массы покоя электрона является значением его массы в основном стационарном состоянии в собственном гравитационном поле, причем значения r1=2,82×10-15 м, К1=0,41×1012 м-1 дают точный нуль функции по самому определению численных значений К и Λ.
Таким образом, приведенные численные оценки для электрона показывают, что в области его локализации при численном значении К˜1031 Нм2кг-2 и Λ˜1029 м-2 существует спектр стационарных состояний в собственном гравитационном поле. Численное значение К является, разумеется, универсальным для любого элементарного источника, в то время как значение Λ определяется массой покоя элементарного источника. Расстояние, на котором локализовано гравитационное поле с постоянной К, меньше комптоновской длины волны и для электрона, например, составляет значение порядка его классического радиуса. На расстояниях, больших этого расстояния, гравитационное поле характеризуется постоянной G, т.е. имеет место правильный переход к классической ОТО.
Из (27) следуют в грубом приближении численные значения энергий стационарных состояний: Е1=0,511 МэВ, Е2=0,638 МэВ, ... Е∞=0,681 МэВ.
Квантовые переходы по стационарным состояниям должны приводить к гравитационному излучению, характеризуемому постоянной К с энергиями переходов, начиная с 127 кэВ до 170 кэВ. При этом существенны два обстоятельства. Первое. Соответствие между электромагнитным и гравитационным взаимодействием имеет место при замене электрического заряда е на гравитационный "заряд" m√K, что численное значение К ставит эффекты электромагнитного и гравитационного излучения на один уровень (например, сечения тормозного электромагнитного и тормозного гравитационного излучения будут отличаться лишь множителем 0,16 в области совпадения спектров излучения).
Второе. Естественная ширина уровней энергий в указанном выше спектре стационарных состояний электрона составит 10-9 эВ до 10-7 эВ. Малость ширин энергетических уровней по сравнению с разбросом энергии электронов в реальных условиях объясняет, почему эффекты гравитационного излучения, как массовое явление, не наблюдаются в сопутствующих явлениях, например, в процессах торможения электронных пучков на мишенях. Прямым подтверждением наличия стационарных состояний электронов в собственном гравитационном поле с постоянной К может являться наличие нижней границы β-распада ядер. Только начиная с нее может иметь место β-асимметрия, трактуемая как несохранение четности в слабых взаимодействиях, но являющаяся в действительности лишь следствием наличия возбужденных состояний электронов в собственном гравитационном поле при β-распаде. Экспериментально же β-асимметрия только и наблюдалась при β-распаде тяжелых ядер в магнитном поле (например, 27С60 в известном эксперименте Ву (Ву Ц.С., Мошковский С.А., Бета-распад, Атомиздат, Москва (1970)). На легких ядрах, например, 1Н3, где уже не должна иметь место асимметрия β-распада, аналогичные эксперименты не проводились.
2. Условия гравитационного излучения в плазме (возбуждение гравитационного излучения в плазме).
Для указанных выше энергий переходов по стационарным состояниям в собственном гравитационном поле и ширины уровней энергий единственным объектом, в котором может быть реализовано гравитационное излучение, как массовое явление, будет являться плотная высокотемпературная плазма, что следует из следующих оценок.
Используя борновское приближение для сечения тормозного излучения, выражение для энергии тормозного электромагнитного излучения единицы объема в единицу времени можно записать в виде:
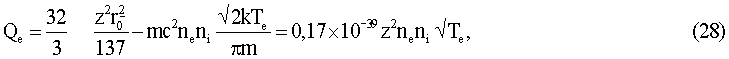
где Тe, k, ni, nе, m, z, r0 - электронная температура, постоянная Больцмана, концентрация ионной и электронной компонент, масса электрона, порядковый номер ионной компоненты, классический радиус электрона, соответственно.
Заменяя r0 на rg=2К m/с2 (что соответствует замене электрического заряда е на гравитационный заряд m√К), можно использовать для тормозного гравитационного излучения зависимость

Из (28) следует, что в плотной высокотемпературной плазме с параметрами ne=ni=1023 м-3, Те=107K удельная мощность тормозного электромагнитного излучения равна ≈0,53 1010 Дж/м3·с, а значение удельной мощности тормозного гравитационного излучения равно 0,86·109 Дж/м3·с. Эти значения параметров плазмы, по-видимому, можно принять за ориентировочные пороговые значения заметного уровня гравитационного излучения, так как относительная доля электронов, энергия которых порядка энергии переходов в собственном гравитационном поле уменьшается по экспоненте максвелловского распределения с уменьшением Те.
3. Запирание и усиление гравитационного излучения за счет каскадных переходов и тушения спонтанного излучения с нижних энергетических уровней ионами многоэлектронных атомов в плазме инжектируемой из области магнитного поля.
Для численных значений параметров плазмы Te=Ti=(107-108) K, ne=ni=(1023-1025) м-3 спектр тормозного электромагнитного излучения существенно не изменится при комптоновском рассеянии излучения электронов, а само тормозное излучение является источником радиационных потерь высокотемпературной плазмы. Частоты этого непрерывного спектра составляют порядок (1018-1020) с-1, в то время как плазменная частота для приведенных выше параметров плазмы составляет (1013-1014) с-1, или 0,1 эВ энергии излучаемых квантов.
Принципиальным отличием тормозного гравитационного излучения от тормозного электромагнитного излучения является линейчатый спектр гравитационного излучения, соответствующий спектру стационарных состояний электрона в собственном гравитационном поле.
Наличие каскадных переходов с верхних возбужденных уровней на нижние будет приводить к тому, что электроны, возбуждаясь в области энергий выше 100 кэВ, будут излучаться, в основном, в эВ-области, т.е. будет иметь место перекачка энергии по спектру в низкочастотную область. Такой механизм перекачки энергии может иметь место только при тушении спонтанного излучения с нижних энергетических уровней электрона в собственном гравитационном поле, исключающем излучение с энергией квантов в кэВ-области. Детальное описание механизма перекачки энергии по спектру в дальнейшем даст его точные численные характеристики. Тем не менее, несомненно можно утверждать о самом факте его существования, обусловленном линейчатым характером спектра тормозного гравитационного излучения. Низкочастотный характер спектра тормозного гравитационного излучения и будет приводить к его усилению в плазме в силу выполнения условия запирания ωg≤0,5√103ne.
С точки зрения практической реализации состояний высокотемпературной плазмы, сжатой излучаемым гравитационным полем, важны два обстоятельства.
Первое. Плазма должна быть двухкомпонентной, с добавкой к водороду многозарядных ионов, необходимых для тушения спонтанного излучения электронов с нижних энергетических уровней в собственном гравитационном поле. Для этого необходимо иметь ионы с энергетическими уровнями электронов, близкими к энергетическим уровням свободных возбужденных электронов. Тушение нижних возбужденных состояний электронов будет особенно эффективным при наличии резонанса между энергией возбужденного электрона и энергией возбуждения электрона в ионе (в предельном, наиболее благоприятном случае - энергией ионизации). Увеличение z увеличивает также удельную мощность тормозного гравитационного излучения, так что при выполнении условия ωg≤0,5√103ne равенство газокинетического давления и давления излучения
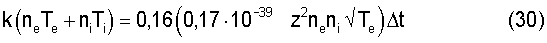
будет иметь место при Δt=(10-6-10-7)с для допустимых значений параметров сжатой плазмы nе=(1+а) ni=(1025-1026)м-3, а>2, Те≈Тi=108K, z>10.
Второе. Необходимость выброса плазмы из области магнитного поля с ориентировочными параметрами nе=(1023-1024) м-3, Те=(107-108) К с последующей накачкой энергией из области магнитного поля.
Выполнение перечисленных условий (в принципе, независимо от конкретной схемы установки, в которой реализуются эти условия) решает задачу получения состояний гидростатического равновесия плазмы, но и только. Использование в качестве добавки к водороду многоэлектронного газа (углерода) приводит к реализации условий протекания реакции ядерного синтеза, так как углерод одновременно будет выполнять роль катализатора, необходимого для реакции ядерного синтеза.
Другим вариантом ядерного синтеза в составах с многоэлектронными атомами, такими, как ксенон, криптон (и близких к ним по строению элементов), является использование в качестве легкой компоненты дейтериево-тритиевой смеси.
Анализ процессов, имеющих место в известных установках генерации устойчивых высокотемпературных состояний плазмы (а также отсутствие обнадеживающих результатов), позволяет сделать вывод о возможности использования магнитного поля только частично, на первом этапе для удержания и нагрева плазмы в процессе формирования ее высокоэнергетичного состояния. Дальнейшее наличие магнитного поля уже не удерживает плазму в ограниченном объеме, а ее же и разрушает в силу специфики характера движения заряженных частиц в магнитном поле. Принципиальным решением проблемы является способ удержания уже нагретой плазмы в излучаемом гравитационном поле, на втором этапе, после ее сжатия, нагрева и удержания в это время магнитным полем. Как следует из изложенного, при любых обстоятельствах плазма после нагрева должна быть инжектирована из области магнитного поля, но с последующей накачкой энергии из области плазмы, находящейся в магнитном поле. Именно таким условиям отвечает, в том числе, исходная схема магнитоплазменного компрессора, приведенная в описании к заявке.
Заявленный способ реализуется следующим путем: через быстродействующий клапан подается двухкомпонентный газ (водород + многоэлектронный газ) в зазор между коаксиальными коническими электродами, на которые через разрядный контур подается напряжение. Между электродами течет разряд, создающий магнитное поле. Под давлением возникающей силы ампера плазма разгоняется вдоль канала. На выходе в области компрессии поток сходится к оси, где возникает область компрессии с высокой плотностью и температурой. Формированию области компрессии способствуют токи выноса, текущие в выходящей плазменной струе. При подаче напряжения на анод (20-40) кВ и исходном давлении рабочего газа (0,5-0,8)мм рт.ст. и достижении тока в формирующемся разряде порядка 1 МА в области компрессии, будут достигаться значения параметров плазмы nе, ni=(1023-1025) м-3 и температур Те Тi=(107-108) К, необходимые для возбуждения излучения плазмы. Наличие ионов многоэлектронных атомов в составе рабочего газа, приводящих к тушению излучения с нижних энергетических уровней электронов, и каскадные переходы по уровням стационарных состояний электрона в собственном гравитационном поле будут приводить к преобразованию высокочастотного спектра излучения в низкочастотный, с частотами, соответствующими запиранию и усилению излучения плазмы. Одновременно будет расти плотность и температура плазмы вследствие ее импульсной инжекции. Таким образом, последующее сжатие плазмы после ее инжекции из области магнитного поля до состояния гидростатического равновесия имеет место за счет возбуждения, запирания и сжатия плазмодинамических разрядов (Камруков А.С. и др. "Генераторы лазерного и мощного теплового излучения на основе сильноточных плазмодинамических разрядов" в кн. "Плазменные ускорители и ионные инжекторы", М., Наука, 1984, при ее использовании в качестве квантового генератора гравитационного излучения (КГГИ) (именно КГГИ и является генератором устойчивых высокоэнергетичных состояний плотной плазмы) заключается в следующем:
1) импульсный характер разрядного контура с соответствующими плазмодинамическому разряду вольт-амперными характеристиками;
2) определенное соотношение водородной компоненты и компоненты многоэлектронного газа (примерно, 80% и 20%, соответственно), в том числе в целях достижения нужных температурных параметров плазмы;
3) близкое соотношение уровней энергии электрона в используемом многоэлектронном газе и нижних уровней энергии электрона в собственном гравитационном поле, что требует использования в качестве многоэлектронного газа таких газов, как криптон и ксенон. При этом корректируется и доля процентного содержания многоэлектронных атомов, ограниченная снизу требованием гашения возбужденных нижних энергетических состояний электрона (в собственном гравитационном поле) и сверху - требованием достижения необходимой температуры плазмы.
Специалисту должно быть понятно, что возможны различные модификации и варианты выполнения изобретения, все они включены в объем притязаний заявителя, который отражен в формуле изобретения, приведенной ниже.
| название | год | авторы | номер документа |
|---|---|---|---|
| ПЛАЗМЕННЫЙ ГЕНЕРАТОР ТОРМОЗНОГО ИЗЛУЧЕНИЯ | 2010 |
|
RU2488243C2 |
| ПАРАМЕТРИЧЕСКИЙ СИНХРОТРОННЫЙ ПРЕОБРАЗОВАТЕЛЬ | 1999 |
|
RU2165671C1 |
| СПОСОБ НАНЕСЕНИЯ НАНОПОКРЫТИЙ И УСТРОЙСТВО ДЛЯ ЕГО ОСУЩЕСТВЛЕНИЯ | 2008 |
|
RU2371379C1 |
| ГЕНЕРАТОР ЭЛЕКТРОМАГНИТНОГО ИЗЛУЧЕНИЯ С ПЕРЕСТРАИВАЕМОЙ ЧАСТОТОЙ СТИМУЛИРОВАННОГО ИЗЛУЧЕНИЯ | 2003 |
|
RU2252478C2 |
| СПОСОБ ИОННО-ПЛАЗМЕННОГО ЛЕГИРОВАНИЯ ПОВЕРХНОСТИ ИЗДЕЛИЯ | 2011 |
|
RU2479668C1 |
| СПОСОБ РАЗДЕЛЕНИЯ ИЗОТОПОВ И УСТРОЙСТВО ДЛЯ ЕГО ОСУЩЕСТВЛЕНИЯ | 2009 |
|
RU2411066C1 |
| Способ получения многозарядных ионов | 1982 |
|
SU1076982A1 |
| СПОСОБ И УСТРОЙСТВО ДЛЯ ПОЛУЧЕНИЯ ВЫСОКОТЕМПЕРАТУРНОЙ ПЛАЗМЫ С МАГНИТНОЙ СТАБИЛИЗАЦИЕЙ Z-ПИНЧА | 2020 |
|
RU2725439C1 |
| УСТРОЙСТВО ДЛЯ ПОЛУЧЕНИЯ ПЛАЗМЫ НА ОСНОВЕ СКОЛЬЗЯЩЕГО РАЗРЯДА | 1999 |
|
RU2178243C2 |
| СПОСОБ РАЗДЕЛЕНИЯ ИЗОТОПОВ И УСТРОЙСТВО ДЛЯ ЕГО ОСУЩЕСТВЛЕНИЯ | 2009 |
|
RU2405619C1 |
Изобретение относится к способу формирования устойчивых состояний плотной высокотемпературной плазмы, которая может быть использована, например, для управляемого термоядерного синтеза. Способ формирования включает формирование плотной высокотемпературной плазмы с помощью импульсных сильноточных разрядов, создающих магнитное поле, инжекцию плазмы из области магнитного поля со следующими параметрами: плотностью плазмы (1023-1025) м-3 и температурой (107-108)К, причем при формировании устойчивых состояний плазмы используют двухкомпонентный газ, состоящий из водорода (или его изотопов) и инертного газа или из водорода и углерода в соотношении компонентов 80% и 20% соответственно, а исходное давление двухкомпонентного газа составляет (0,5-0,8) мм рт. ст. Технический результат - возможность формирования и удержания плотной высокотемпературной плазмы в течение времени, необходимого для протекания реакций ядерного синтеза. 1 ил.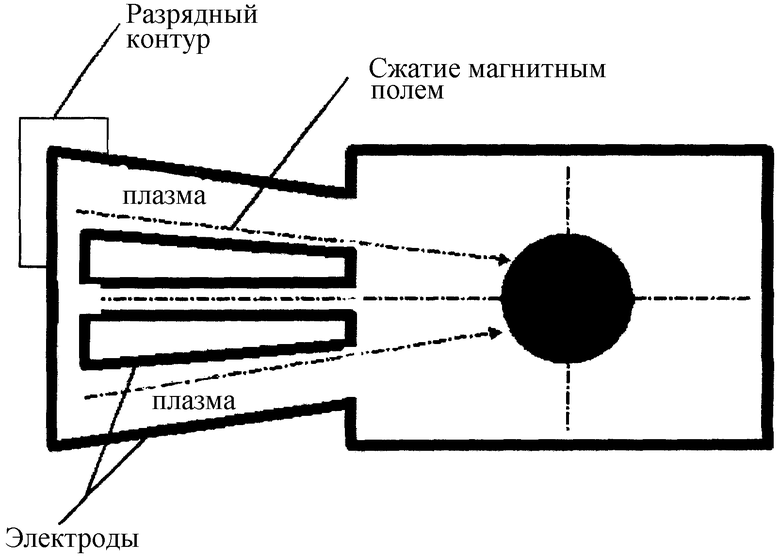
Способ формирования устойчивых состояний плотной высокотемпературной плазмы, включающий формирование плотной высокотемпературной плазмы с помощью импульсных сильноточных разрядов, создающих магнитное поле, инжекцию плазмы из области магнитного поля со следующими параметрами: плотность плазмы (1023-1025)м-3 и температура (107-108)К, причем при формировании устойчивых состояний плазмы используют двухкомпонентный газ, состоящий из водорода (или его изотопов) и инертного газа или из водорода и углерода в соотношении компонентов 80 и 20% соответственно, а исходное давление двухкомпонентного газа составляет 0,5-0,8 мм рт. ст.
| ЛУКЬЯНОВ С.Ю | |||
| Горячая плазма и управляемый ядерный синтез, Наука, Москва, 1975, с.115, 116 | |||
| СПОСОБ ПОЛУЧЕНИЯ ВЫСОКОТЕМПЕРАТУРНОЙ ПЛАЗМЫ | 1994 |
|
RU2067360C1 |
| Способ создания стационарного тока в плазме | 1984 |
|
SU1216805A1 |
| СПОСОБ ПОЛУЧЕНИЯ ВЫСОКОТЕМПЕРАТУРНОЙ ПЛАЗМЫ И ОСУЩЕСТВЛЕНИЯ ТЕРМОЯДЕРНЫХ РЕАКЦИЙ | 1995 |
|
RU2096934C1 |
| US 4292125 A, 29.09.1981. | |||
Авторы
Даты
2006-04-10—Публикация
2004-11-30—Подача