Изобретение относится к антенной технике и может быть использовано для оптимального управления взвешивающими устройствами в каналах фазированных антенных решеток (ФАР) по критерию максимума отношения сигнал/шум+помеха.
Известен способ энергетической оптимизации ФАР [1], сущность которого заключается во взвешивании сигналов, принятых каждым излучателем, с помощью весовых коэффициентов, в соответствии с которым весовые коэффициенты находят как вектор, минимизирующий функционал ошибки, при определении которого используют информацию о направлении на источник сигнала и о распределении источников помех, а в качестве максимизируемого функционала выбирают соответственно отношение мощности сигнала в заданном направлении к сумме шумов и помех, принимаемых антенной.
Недостатком известного способа энергетической оптимизации ФАР является то, что оптимизация ФАР достигается изменением весовых коэффициентов во всех элементах, причем весовые коэффициенты определяются в результате итерационной процедуры, что усложняет реализацию способа, а также затрудняет реализацию известного алгоритма в реальном масштабе времени, особенно при больших размерах ФАР.
Также известен способ энергетической оптимизации моноимпульсной антенной решетки (MAP) с совместным формированием лучей [2], сущность которого заключается во взвешивании сигналов, принятых каждым излучателем, с помощью комплексных весовых коэффициентов (КВК), разделении этих сигналов на два канала, суммировании сигналов с одноименных выходов делителей с соответствующим прогрессивно нарастающим и убывающим фазовым сдвигом, обеспечивающим отклонение каждого луча на угол ±ΔΘ, и последующем образовании суммарной и разностной диаграмм направленности (ДН). При этом КВК находят как главный вектор пучка эрмитовых форм, соответствующий максимальному характеристическому числу пучка ранга 2М+1, при определении которого используют информацию о направлении на источник сигнала и о распределении источников помех, а в качестве первой и второй эрмитовых форм пучка выбирают соответственно мощность сигнала в суммарном канале и сумму мощностей шумов и помех в лучах моноимпульсной группы, причем комплексные весовые коэффициенты части N-2M элементов MAP, где N - общее число элементов MAP, a 2М - число элементов с независимыми КВК, принимают равными произведению исходных весовых коэффициентов, обеспечивающих ориентацию равносигнального направления (РСН) на источник сигнала, на общий для этих элементов КВК Iр, определяемый из решения задачи оптимизации, после чего КВК всех элементов нормируют к значению Iр.
Недостатком известного способа [2] является невозможность его реализации применительно к ФАР, поскольку известный способ предполагает изменение комплексных весовых коэффициентов, т.е. и амплитуд и фаз токов, тогда как в ФАР изменяют только фазы токов.
Предлагаемый способ направлен на устранение указанных недостатков известных способов.
Структурная схема устройства, функционирующего по данному способу, представлена на фиг.1. На фиг.2 представлены ДН ФАР после оптимизации по способу [1] и после оптимизации по данному способу. На фиг.3 приведены отличия фазовых распределений, полученных известным и заявленным способами, от исходного фазового распределения.
Рассмотрим существо предлагаемого способа. Как и в прототипе [1], сигналы, принятые каждым излучателем, взвешивают с помощью весовых коэффициентов, которые находят как вектор, минимизирующий функционал ошибки, при определении которого используют информацию о направлении на источник сигнала и о распределении источников помех, а в качестве максимизируемого функционала выбирают соответственно отношение мощности сигнала в заданном направлении к сумме шумов и помех, принимаемых антенной. При этом весовые коэффициенты N-2M элементов фазированной антенной решетки, где N - общее число элементов фазированной антенной решетки, а 2М - число элементов с независимыми весовыми коэффициентами, принимают равными произведению исходных весовых коэффициентов, обеспечивающих ориентацию главного максимума диаграммы направленности на источник сигнала, на общий для этих элементов весовой коэффициент Х0, определяемый из решения задачи оптимизации.
Однако в отличие от прототипа порядок матриц, входящих в функционал ошибки, понижают до 2М+1, а в качестве оптимального вектора весовых коэффициентов выбирают вектор 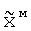 , минимизирующий функционал ошибки, который нормируют в соответствии с выражением
, минимизирующий функционал ошибки, который нормируют в соответствии с выражением 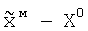 , в связи с чем весовые коэффициенты неадаптируемых N-2M элементов не изменяют.
, в связи с чем весовые коэффициенты неадаптируемых N-2M элементов не изменяют.
Проведенный сравнительный анализ заявленного способа и прототипа показывает, что в заявленном способе изменены условия выполнения операции взвешивания. При определении вектора весовых коэффициентов порядок матриц, входящих в функционал ошибки, понижают до 2М+1, а в качестве оптимального вектора весовых коэффициентов выбирают вектор  , минимизирующий функционал ошибки, который нормируют в соответствии с выражением
, минимизирующий функционал ошибки, который нормируют в соответствии с выражением 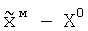 , в связи с чем весовые коэффициенты неадаптируемых N-2M элементов не изменяют.
, в связи с чем весовые коэффициенты неадаптируемых N-2M элементов не изменяют.
Рассмотрим предлагаемый способ энергетической оптимизации ФАР, полагая, что направление на источник сигнала Θ0 и распределение шумов и помех в пространстве Т(Θ) известны.
С учетом структурной схемы оптимизируемой ФАР, представленной на фиг.1, для оптимизации используем функционал вида:

где f(Θ) - диаграмма направленности линейной эквидистантной ФАР, определяемая при равномерном амплитудном распределении I=1 выражением [1]:
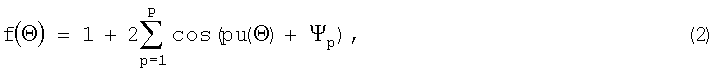
где u(Θ)=kd(sinΘ-sinΘ0); P=(N-1)/2; k - волновое число; d - шаг решетки; Ψр - фазовый сдвиг р-го элемента ФАР относительно значения, соответствующего синфазному режиму работы (в (2) учтено, что у эквидистантной ФАР с идентичными излучателями фазы элементов, расположенные симметрично относительно центра решетки, равны, но противоположны по знаку, поэтому в дальнейшем все преобразования приводятся относительно Р элементов), причем:

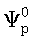 - начальная фаза р-го элемента ФАР (в случае начального синфазного возбуждения ФАР
- начальная фаза р-го элемента ФАР (в случае начального синфазного возбуждения ФАР 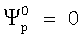 ); xр<<1 - малое возмущение фазы р-го элемента ФАР; р=1, 2,..., Р.
); xр<<1 - малое возмущение фазы р-го элемента ФАР; р=1, 2,..., Р.
Знаменатель (1) записан в предположении, что размеры излучателей вдоль оси х бесконечны, излучение происходит в полупространство z>0, а выражение (2), как и в прототипе [1], записано для случая идентичных излучателей ФАР.
Подставив (3) в (2) и далее в знаменатель (1) для выбранного функционала, получим:

где В - квадратная симметричная матрица Р-го порядка с элементами:

β - действительный Р-мерный вектор-столбец с элементами:
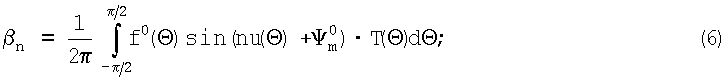
f0(Θ) - ДН невозмущенной ФАР; α - скалярная величина, определяемая выражением:

х - вектор-столбец неизвестных фазовых возмущений, которые для элементов ФАР (фиг.1) с N-P+1-го по N-й учитываются с плюсом, а для элементов ФАР с 1-го по Р-й - со знаком минус.
Выражение в знаменателе (4) представляет собой функционал ошибки.
Как показано в прототипе [1], максимум функционала (4) обеспечивает вектор xм, определяемый выражением:

при этом максимум функционала равен:

Выражение (8) определяет возмущения первого порядка относительно исходных значений  . Далее вектор Ψ0+хм трактуют как новые начальные значения и получают возмущения второго порядка. Итерационную процедуру продолжают до тех пор, пока значение максимизируемого функционала увеличивается.
. Далее вектор Ψ0+хм трактуют как новые начальные значения и получают возмущения второго порядка. Итерационную процедуру продолжают до тех пор, пока значение максимизируемого функционала увеличивается.
Проанализируем изменения в условиях взвешивания сигналов, принятых элементами ФАР, предлагаемым способом, для этого рассмотрим диаграмму направленности ФАР более подробно. Подставив (3) в (2) и раскрыв сумму аргументов косинуса, получим:

Далее учитывая, что xр<<1 и соответственно cos(xр)≈1, a sin(xp)≈xр, из (10) получим:

В соответствии с предлагаемым способом весовые коэффициенты N-2M элементов фазированной антенной решетки принимают равными произведению исходных весовых коэффициентов, обеспечивающих ориентацию главного максимума диаграммы направленности на источник сигнала, на общий для этих элементов весовой коэффициент Хо.
Далее, так же как и в прототипе [1], все преобразования приводятся для P=(N-1)/2 элементов решетки, что обусловлено принятыми допущениями по симметрии ФАР. Соответственно число элементов с независимыми весовыми коэффициентами в приводимых выражениях принято равным М. С учетом этого из (11) получим:
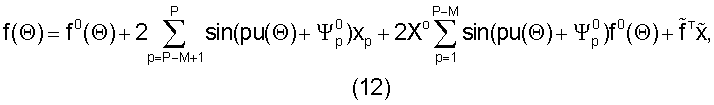
где  - мерный вектор-столбец с элементами:
- мерный вектор-столбец с элементами:

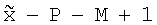 - мерный вектор-столбец неизвестных весовых коэффициентов с элементами:
- мерный вектор-столбец неизвестных весовых коэффициентов с элементами:

Таким образом, диаграмму направленности ФАР представляют функцией Р-М+1-мерного вектора неизвестных весовых коэффициентов  .
.
Подставив (12) в знаменатель (1) и выполнив преобразования, получим:

где Вd - квадратная симметричная матрица Р-М+1-го порядка с элементами:

βd - действительный P-M+1-мерный вектор-столбец с элементами:
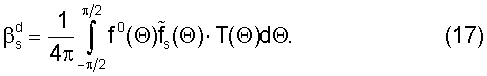
Таким образом, в результате изменения операции взвешивания предлагаемым способом порядок матриц, входящих в функционал ошибки (знаменатель (15)), понижается с Р до Р-М+1. В общем случае без учета симметрий ФАР порядок матриц, входящих в функционал ошибки, понижается с N до N-2M+1. Соответственно решением задачи оптимизации является вектор  порядка Р-М+1 (или для общего случая N-2M+1), минимизирующий функционал ошибки, входящий в знаменатель (17):
порядка Р-М+1 (или для общего случая N-2M+1), минимизирующий функционал ошибки, входящий в знаменатель (17):

Так же, как и ранее, выражение (18) определяет возмущения первого порядка, поэтому итерационную процедуру продолжают до тех пор, пока значение максимизируемого функционала увеличивается.
После определения вектора  его значения нормируют в соответствии с выражением:
его значения нормируют в соответствии с выражением:

В результате такой нормировки фазы неадаптируемых элементов не изменяются и соответствуют исходному фазовому распределению.
Работа устройства, функционирующего по предложенному способу, может быть проиллюстрирована с помощью фиг.1. Информация Θ0 о направлении на источник сигнала и о распределении источников помех Т(Θ) в пространстве поступает на входы 2 и 3 вычислителя весовых коэффициентов 3, функционирующего в соответствии с (18) и (19). Принятые первыми М и последними М элементами 1 фазированной антенной решетки сигналы взвешивают с помощью устройств взвешивания 5, на которые поступают сигналы вычислителя 3.
Сигналы, принятые неадаптируемыми элементами ФАР (с М+1 по N-M), взвешивают весовыми коэффициентами 6, обеспечивающими ориентацию максимума диаграммы направленности на источник сигнала. После этого сигналы всех элементов поступают в сумматор 7, на выходе которого 8 формируется диаграмма направленности ФАР.
На фиг.2 непрерывной линией показана ДН, соответствующая известному способу оптимизации, а штриховой линией показана диаграмма направленности ФАР, оптимизированной предложенным способом. Вертикальной линией на фиг.2 показано направление прихода помехового сигнала.
Расчеты выполнены для решетки ненаправленных излучателей с параметрами N=29, Р=14, у0=0.5λ, при Θ0=200, а также функции Т(Θ) следующего вида:

На краях ФАР выделены две подрешетки, по пять элементов в каждой (М=5), соответственно порядок матриц, входящих в функционал (4), по сравнению с известным способом с учетом допущений по симметрии решетки [1] понижен с 14 до 6, т.е. более чем в два раза (для общего случая решения задачи оптимизации с 29 до 10).
Результаты моделирования показали, что в случае воздействия помехи вида (20) отношение сигнал/шум+помеха до оптимизации составляет -0.1 дБ, а после оптимизации известным и заявленным способами соответственно 18.95 и 18.94 дБ, что свидетельствует о высокой эффективности заявленного способа, при этом полученный результат по заявленному способу достигается изменением фаз только в трети (10-ти из 29-ти) элементов ФАР при равномерном амплитудном распределении.
Представленные результаты соответствуют пятой итерации. Необходимо отметить, что процедура обращения матрицы, входящей в знаменатель максимизируемых функционалов (4) и (15), повторяется на каждой итерации, поэтому вычислительная эффективность предложенного способа возрастает с каждой итерацией, поскольку в соответствии с предложенным способом при определении весовых коэффициентов обращается матрица меньшего порядка.
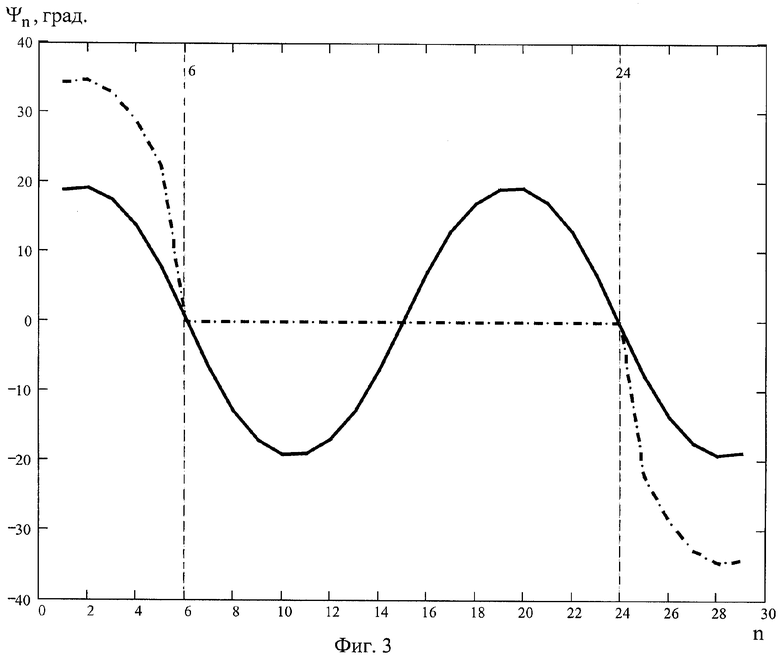
На фиг.3 сплошной линией представлена разность исходного фазового распределения и фазового распределения, соответствующего известному способу, а штриховой линией показана разность исходного фазового распределения и фазового распределения, полученного предложенным способом.
Как видно из фиг.3, в случае реализации предложенного способа фазы элементов с 6 по 24 не изменяются по отношению к исходному синфазному возбуждению, что является техническим эффектом предложенного способа, позволяющим существенно упростить дискретные схемы управления ФАР. Значения фаз (в градусах) для разных способов приведены в таблице 1.

Предлагаемый способ может быть применен также к ФАР с направленными идентичными и к ФАР с неидентичными (например, искаженными взаимными связями) излучателями.
Источник информации
1. Cheng D.K. Optimization techniques for antenna arrays // IEEE Proc. 1971. V.59. №12. P.1664.
2. Патент №2255396 РФ. Способ энергетической оптимизации моноимпульсных антенных решеток с совместным формированием лучей / Башлы П.Н., Мануилов Б.Д., Богданов В.М. // Б.И. 2005. №18.

Изобретение относится к антенной технике. Техническим результатом изобретения является повышение оперативности работы фазированной антенной решетки в условиях воздействия помех. Способ энергетической оптимизации фазированной антенной решетки основан на взвешивании сигналов, принятых каждым излучателем. Весовые коэффициенты находят как вектор, минимизирующий функционал ошибки, при определении которого используют информацию о направлении на источник сигнала и о распределении источников помех. В качестве максимизируемого функционала используют отношение мощности сигнала в заданном направлении к сумме шумов и помех. Весовые коэффициенты N-2М элементов, где N - общее число элементов фазированной антенной решетки, а 2М - число элементов с независимыми весовыми коэффициентами, принимают равными произведению исходных весовых коэффициентов на общий для этих элементов весовой коэффициент Х0, определяемый из решения задачи оптимизации. Порядок матриц, входящих в функционал ошибки, понижают до 2М+1. Вектор  нормируют в соответствии с выражением
нормируют в соответствии с выражением  , что обеспечивает неизменность весовых коэффициентов N-2М элементов антенной решетки, где вектор
, что обеспечивает неизменность весовых коэффициентов N-2М элементов антенной решетки, где вектор  - минимизирующий функционал ошибки. 3 ил., 1 табл.
- минимизирующий функционал ошибки. 3 ил., 1 табл.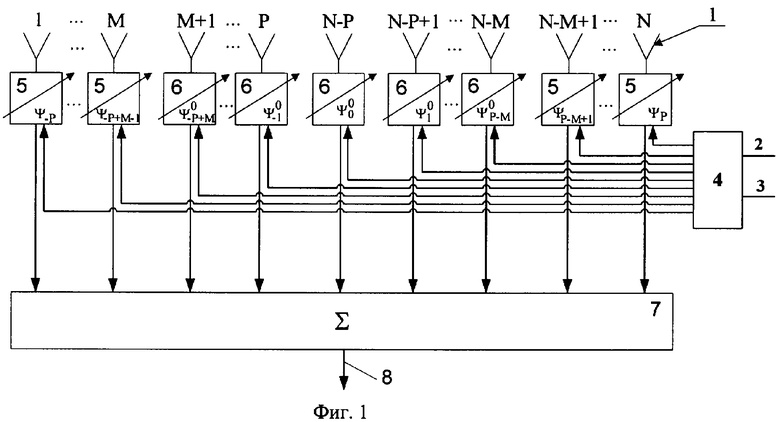
Способ энергетической оптимизации фазированной антенной решетки, основанный на взвешивании сигналов, принятых каждым излучателем, с помощью весовых коэффициентов, в соответствии с которым весовые коэффициенты находят как вектор, минимизирующий функционал ошибки, при определении которого используют информацию о направлении на источник сигнала и о распределении источников помех, а в качестве максимизируемого функционала выбирают соответственно отношение мощности сигнала в заданном направлении к сумме шумов и помех, принимаемых антенной, причем весовые коэффициенты N-2М элементов фазированной антенной решетки, где N - общее число элементов фазированной антенной решетки, а 2М - число элементов с независимыми весовыми коэффициентами, принимают равными произведению исходных весовых коэффициентов, обеспечивающих ориентацию главного максимума диаграммы направленности на источник сигнала, на общий для этих элементов весовой коэффициент Х0, определяемый из решения задачи оптимизации, отличающийся тем, что порядок матриц, входящих в функционал ошибки, понижают до 2М+1, а в качестве оптимального вектора весовых коэффициентов выбирают вектор 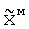 , минимизирующий функционал ошибки, который нормируют в соответствии с выражением
, минимизирующий функционал ошибки, который нормируют в соответствии с выражением  , в связи с чем весовые коэффициенты неадаптируемых N-2М элементов не изменяют.
, в связи с чем весовые коэффициенты неадаптируемых N-2М элементов не изменяют.
| RU 225596 С2, 27.06.2005 | |||
| СПОСОБ ЭНЕРГЕТИЧЕСКОЙ ОПТИМИЗАЦИИ МОНОИМПУЛЬСНЫХ АНТЕННЫХ РЕШЕТОК С СОВМЕСТНЫМ ФОРМИРОВАНИЕМ ЛУЧЕЙ | 1999 |
|
RU2169970C2 |
| АДАПТИВНАЯ АНТЕННАЯ РЕШЕТКА | 1994 |
|
RU2090960C1 |
| US 4713668 А, 15.12.1987 | |||
| УСТРОЙСТВО СТАБИЛИЗАЦИИ ИЗОБРАЖЕНИЯ | 2016 |
|
RU2631026C1 |
Авторы
Даты
2008-01-10—Публикация
2006-09-19—Подача