Область техники, к которой относится изобретение
Изобретение относится к радиотехнике, в частности к радиолокации, и может быть использовано для измерения локальных радиолокационных характеристик (РЛХ), локальных энергетических частотных спектров исследуемых объектов и для измерения радиофизических характеристик (РФХ) радиопоглощающих материалов (РПМ). В частности, может быть использовано для измерения коэффициента отражения РПМ в свободном пространстве в сверхширокой полосе частот при использовании импульсных сверхширокополосных (СШП) сигналов без несущей, у которых рабочая полоса Δf и средняя частота f0 сравнимы по величине.
Предшествующий уровень техники
Современная тенденция развития радиолокационных измерительных систем заключается в расширении полосы частот в спектре зондирующего сигнала и соответственно расширении полосы частот анализа принятого отклика от цели. Предельным случаем такого расширения полосы частот является переход к сверхширокополосной (СШП) локации, когда в сторону цели излучается последовательность коротких видеоимпульсов длительностью порядка десятков пикосекунд с частотой следования порядка нескольких мегагерц. Пространственная протяженность зондирующего импульса выбирается из условия сτ<<L0, где с - скорость света в вакууме, τ - длительность зондирующего импульса, L0 - продольный размер цели в направлении зондирования. В результате электромагнитного взаимодействия зондирующего сигнала с поверхностью радиолокационной цели формируется рассеянное электромагнитное поле, часть которого распространяется в направлении приемной антенны. Эта часть рассеянного поля несет в себе информацию об объекте, которую можно выделить с помощью соответствующей обработки принятого сигнала. Анализ отраженного сигнала производится в широком диапазоне частот от единиц мегагерц до десятков гигагерц. Исследование такого отраженного сигнала во временной области позволяет ввести понятие сложной (протяженной) цели, состоящей из отдельных элементарных отражателей (центров рассеяния), то есть представляющих собой набор из М локальных отражающих элементов («блестящих точек»), расположенных на длине цели L0 и однозначно связанных с ее геометрической формой. Теоретической основой для описания подобных экспериментов явились методы физической теории дифракции: метод геометрической теории дифракции Келлера [1. Keller J.В. Geometrical Theory of Diffraction. - J. Opt. Soc. Am., 1962, v.52,. №2, p.116-130] и метод краевых волн Уфимцева [2. Уфимцев П.Я. Метод краевых волн в физической теории дифракции. - М.: Сов. радио, 1962. - 234]. На этой теоретической основе было введено понятие локальных радиолокационных характеристик, определяющих рассеивающие свойства отдельных элементарных отражателей. СШП РЛХ (импульсные характеристики) содержат две компоненты: вынужденную (ранневременную часть реакции объекта), формирующуюся, когда падающий волновой фронт движется вдоль цели (0≤t≤2L0/c) и собственную или свободную компоненту (поздневременную частью реакции объекта), проявляющуюся, когда волновой фронт пройдет всю цель (t>2L0/c). В литературе встречаются названия этих компонент как «зеркальная» и «дифракционная». Методика выделения импульсных характеристик (ИХ) объектов в СШП радиолокационных измерениях использует ранневременную часть реакции, обладающей большей энергией по сравнению с поздневременной частью реакции объекта. [3. Беннет С.Л., Росс Дж.Ф. Времяимпульсные электромагнитные процессы и их применение. - ТИИЭР, 1978, т.66, №3, с.35-57; 4. Варганов М.Е., Зиновьев Ю.С., Астанин Л.Ю., Костылев А.А. и др. Радиолкационные характеристики летательных аппаратов / Под ред. Тучкова Л.Т. - М.: Радио и связь, 1985. - 236 с.]. При решении нестационарных электродинамических задач, связанных с применением СШП зондирующих сигналов, сформировались новые представления о механизме рассеяния электромагнитных волн радиолокационными целями, излучения и приема сигналов антеннами [5. Иммореев И.Я., Синявин A.M.: Излучение сверхширокополосных сигналов. Сборник докл. Всероссийской н.к. Сверхширокополосные сигналы в радиолокации, связи и акустике. Муром, 2003, с.88-93; 6. Астанин Л.Ю., Флерова А.А.: Характеристики антенн при формировании и излучении сверхширокополосных сигналов. Сборник докл. Всероссийской н.к. Сверхширокополосные сигналы в радиолокации, связи и акустике. Муром, 2003, с.67-73].
Использование новых методов нестационарного рассеяния и излучения электромагнитных волн, в первую очередь методов получения решений во временной области, позволило установить, что основной вклад в рассеянное целью поле вносят отдельные, локальные центры рассеяния, расположение и свойства которых определяются геометрией рассматриваемой электродинамической структуры и видом СШП сигнала. [7. Астанин Л.Ю., Костылев А.А. Методы теоретического и экспериментального исследования нестационарного рассеяния и излучения электромагнитных волн: Обзор. - Зарубежная радиоэлектроника, 1981, №9, с.3-27]. Основные результаты в прикладной нестационарной электродинамике получены с применением аппарата общей теории линейных динамических систем. Эти результаты выявили фундаментальные связи между СШП РЛХ и формой, размерами и ориентацией радиолокационного объекта, что позволило на качественно новом уровне ставить и решать обратную задачу радиолокации: определение параметров рассеивателя по измеренному полю. Импульсная характеристика, как радиолокационная характеристика объекта, описывает высокочастотные свойства рассеивателя, обусловленные наличием локальных центров рассеяния, и резонансные свойства, выявляющие взаимодействие этих центров между собой. Разрешение соответствующих элементов импульсной характеристики во времени позволяет изучать эти свойства раздельно. Дальнейшим развитием вышеперечисленных идей является создание нового математического аппарата решения обратной задачи радиолокационного зондирования и разработка методов декомпозиции и аппроксимации импульсных характеристик целей, основанных на свойствах локальности и других особенностях рассеяния нестационарных электромагнитных волн. Решение некоторых из этих вопросов представлено в настоящей заявке к патентованию.
Известен способ измерения коэффициента отражения (КО) радиопоглощающих покрытий (РПП) в свободном пространстве [8. Алимин Б.Ф. Техника измерений коэффициентов отражения поглотителей электромагнитных волн. Зарубежная радиоэлектроника, 1977, №2, с.91]. Реализация этого способа состоит в последовательном облучении узкополосным сигналом металлической пластины с нанесенным РПП и металлической пластины без РПП одинаковых размеров, приеме отраженных сигналов и вычислении КО РПП на фиксированной частоте по отношению мощностей сигналов, отраженных от металлической пластины с нанесенным РПП и металлической пластины без РПП. Недостатком данного способа является низкая точность измерений, обусловленная отражениями от стен помещения и элементов опорного устройства. Другим недостатком способа является узкая полоса частот применяемого измерительного устройства. Для исследования в широкой полосе частот требуется создание нескольких (7 и более) однотипных установок различных частотных диапазонов, что приводит к значительному увеличению времени измерений и снижению точности измерений при стыковке зарегистрированных данных, получаемых на разных измерительных установках.
Наиболее близким по технической сущности к заявляемому способу является способ измерения энергетических частотных спектров радиолокационных объектов и КО поглотителей электромагнитных волн в сверхширокой полосе частот [9. RU 2234101 Способ измерения коэффициента отражения радиоволн от радиопоглощающих покрытий. Беляев В.В., Богданов Ю.Н., Виноградов А.Д., Кирьянов О.Е., Маюнов А.Т. 10.08.2004]. Этот способ взят за прототип.
Для лучшего понимания заявляемого изобретения необходимо подробно рассмотреть сущность способа-прототипа, которая заключается в следующем. Образцы металлической пластины с нанесенным РПП и металлической пластины без РПП облучают СШП сигналом, регистрируют временные сигналы, отраженные от этих образцов, с учетом которых с помощью дискретного преобразования Фурье вычисляют спектральные плотности сигналов, отраженных от металлической пластины с нанесенным РПП Gc(fn) и металлической пластины без РПП Gm(fn). Далее разбивают диапазон рабочих частот на совокупность частотных интервалов, аппроксимируют линейными функциями фазовые характеристики спектральных плотностей Gc(fn) и Gm(fn) в каждом интервале, по наклонам которых определяют соответствующие запаздывания частотных составляющих сигналов и проводят когерентное суммирование спектральных плотностей Gc(fn) и Gm(fn) c учетом фазовых сдвигов. Затем находят их средние значения 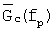 и
и 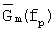 и по формуле
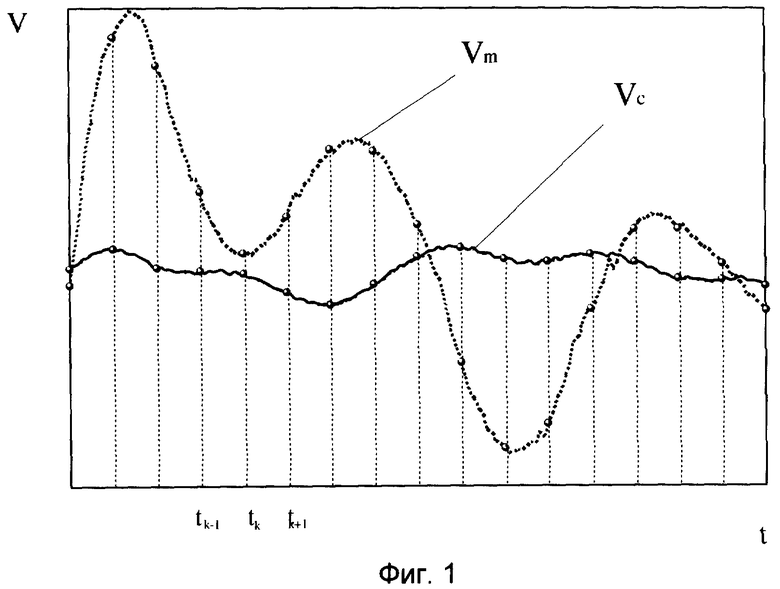
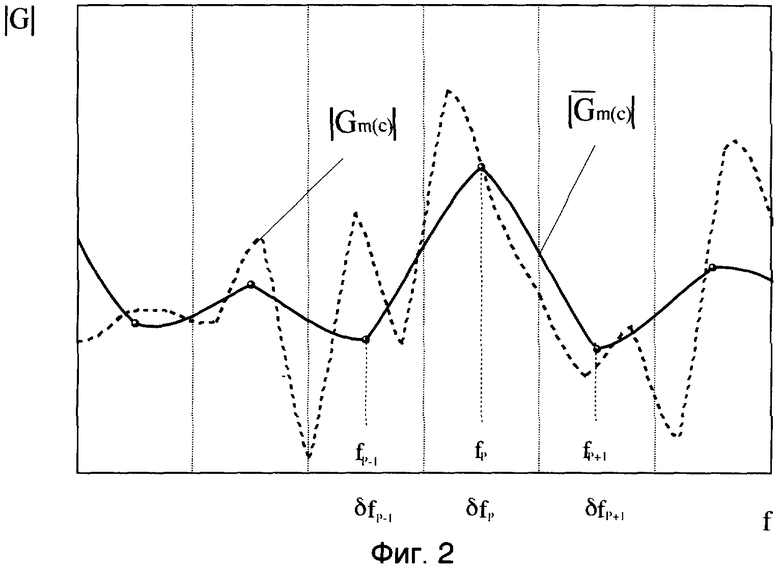
и по формуле 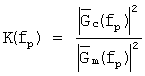 определяют коэффициент отражения радиопоглощающего покрытия в сверхширокой полосе частот как отношение энергетических спектров частот отраженных сигналов от металлической пластины с РПП и без РПП, используя классическое преобразование Фурье, не позволяющее разделять по времени спектральные компоненты. На фиг.1 приведены фрагменты регистрируемых временных сигналов, отраженных от образца металлической пластины, покрытой радиопоглощающим материалом (РПМ), Vc(t) и металлической пластины Vm(t), представляющие собой отклик всей измерительной системы вместе с измеряемым образцом на импульсное воздействие от генератора. На фиг.2 представлены рассчитанные по экспериментальным данным фиг.1 амплитудные характеристики спектральной плотности зарегистрированного сигнала Gm(c)(fn) и усредненной в интервалах δfp спектральной плотности этого же сигнала
определяют коэффициент отражения радиопоглощающего покрытия в сверхширокой полосе частот как отношение энергетических спектров частот отраженных сигналов от металлической пластины с РПП и без РПП, используя классическое преобразование Фурье, не позволяющее разделять по времени спектральные компоненты. На фиг.1 приведены фрагменты регистрируемых временных сигналов, отраженных от образца металлической пластины, покрытой радиопоглощающим материалом (РПМ), Vc(t) и металлической пластины Vm(t), представляющие собой отклик всей измерительной системы вместе с измеряемым образцом на импульсное воздействие от генератора. На фиг.2 представлены рассчитанные по экспериментальным данным фиг.1 амплитудные характеристики спектральной плотности зарегистрированного сигнала Gm(c)(fn) и усредненной в интервалах δfp спектральной плотности этого же сигнала 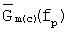 , выполненные с помощью дискретного преобразования Фурье. Способ-прототип имеет, по крайней мере, два недостатка, каждый из которых необходимо рассмотреть отдельно.
, выполненные с помощью дискретного преобразования Фурье. Способ-прототип имеет, по крайней мере, два недостатка, каждый из которых необходимо рассмотреть отдельно.
Согласно теории динамических систем нестационарного рассеяния и излучения электромагнитных волн описание преобразований сигнала во временной области при проведении измерений КО РПМ в способе-прототипе должно задаваться интегральной сверткой импульсных характеристик элементов измерительного радиолокационного канала, импульсной характеристикой цели и сигнала на выходе импульсного генератора [6]:
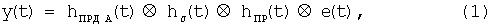
где
e(t) - зондирующий импульсный сигнал на выходе генератора;
y(t)=V(t) - принимаемый отраженный сигнал;
hПРД А - импульсная характеристика передающей антенны;
hσ(t) - импульсная характеристика цели;
hПР(t) - суммарная импульсная характеристика приемной антенны и приемника;
⊗ - операция математической свертки.
Уравнение (1) определяет связь параметров зондирующего e(t) и принимаемого у(t) сигналов при любой их широкополосности и, таким образом, являются обобщенной формой записи уравнения радиолокации. Принимаемый сигнал V(t)=у(t) (фиг.1) кроме информации об объекте содержит информацию об измерительном тракте и о форме сигнала, подаваемого с выхода генератора e(t). На практике импульсное воздействие e(t) имеет конечную длительность и определенную форму, поэтому временная зависимость реакции объекта на воздействие e(t) несет в себе не только искомую информацию об ИХ hσ(t) объекта локации, но еще и о форме возбуждающего импульсного сигнала e(t). Кроме того, сигнал, рассеянный измеряемым объектом, взаимодействует с приемной антенной и трактом приемного устройства, обладающими конечными полосами пропускания, что также необходимо учитывать. Задача определения ИХ объекта hσ(t) связана с необходимостью исключения воздействия всех внешних по отношению к радиолокационному объекту факторов. Поэтому, на наш взгляд, авторам заявки-прототипа следовало бы при вычислениях спектральных плотностей 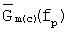 и определении коэффициента отражения радиопоглощающего покрытия в сверхширокой полосе частот оперировать не с измеренным сигналом V(t)=у(t), а рассматривать ИХ исследуемого объекта hσ(t). Для того чтобы определить ИХ объекта hσ(t) по измеренному сигналу y(t), необходимо заранее измерить сигнал, излучаемый генератором для возбуждения объекта e(t), а также, определить импульсную характеристику измерительного тракта, вычисленную по измеренному выходному сигналу при импульсном возмущении, равном e(t), но при отсутствии рассеивающего объекта. Все перечисленные выше факторы в способе-прототипе не были учтены, и это основной его недостаток, повлекший в конечном итоге неточность в вычислениях амплитудных характеристик спектральных плотностей
и определении коэффициента отражения радиопоглощающего покрытия в сверхширокой полосе частот оперировать не с измеренным сигналом V(t)=у(t), а рассматривать ИХ исследуемого объекта hσ(t). Для того чтобы определить ИХ объекта hσ(t) по измеренному сигналу y(t), необходимо заранее измерить сигнал, излучаемый генератором для возбуждения объекта e(t), а также, определить импульсную характеристику измерительного тракта, вычисленную по измеренному выходному сигналу при импульсном возмущении, равном e(t), но при отсутствии рассеивающего объекта. Все перечисленные выше факторы в способе-прототипе не были учтены, и это основной его недостаток, повлекший в конечном итоге неточность в вычислениях амплитудных характеристик спектральных плотностей 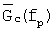 и
и 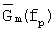 , поскольку полоса измеряемых частот в расчетах получалась значительно уже истинной, соответствующей ИХ объекта hσ(t). Вторым недостатком, повлекшим дополнительную погрешность в определении коэффициента отражения радиопоглощающего покрытия K(fp) (отношение энергетических спектров частот отраженных сигналов, полученных преобразованием Фурье), является игнорирование рассмотрения отдельно зеркальной и дифракционной компонент рассеяния отраженного электромагнитного поля. При таком подходе преобразуемый методом Фурье отраженный временной сигнал кроме короткой зеркальной компоненты в своем составе содержит относительно длительную по времени дифракционную компоненту рассеяния, вносящую значительно меньший вклад в отражательные свойства объекта, но соизмеримую в случае пластины без покрытия и пластины с покрытием. Это обстоятельство вносит дополнительную погрешность в определяемый КО РПМ. Поэтому способ-прототип может использоваться при вычислениях спектральных плотностей
, поскольку полоса измеряемых частот в расчетах получалась значительно уже истинной, соответствующей ИХ объекта hσ(t). Вторым недостатком, повлекшим дополнительную погрешность в определении коэффициента отражения радиопоглощающего покрытия K(fp) (отношение энергетических спектров частот отраженных сигналов, полученных преобразованием Фурье), является игнорирование рассмотрения отдельно зеркальной и дифракционной компонент рассеяния отраженного электромагнитного поля. При таком подходе преобразуемый методом Фурье отраженный временной сигнал кроме короткой зеркальной компоненты в своем составе содержит относительно длительную по времени дифракционную компоненту рассеяния, вносящую значительно меньший вклад в отражательные свойства объекта, но соизмеримую в случае пластины без покрытия и пластины с покрытием. Это обстоятельство вносит дополнительную погрешность в определяемый КО РПМ. Поэтому способ-прототип может использоваться при вычислениях спектральных плотностей 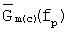 , энергетических спектров
, энергетических спектров 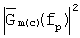 и определении коэффициента отражения K(fp) исследуемого радиопоглощающего материала только как оценочный.
и определении коэффициента отражения K(fp) исследуемого радиопоглощающего материала только как оценочный.
Предлагаемый способ измерения локальных энергетических спектров частот и коэффициента отражения радиопоглощающего материала свободен от перечисленных выше недостатков, чем выгодно отличаются от способа-прототипа. Способ позволяет проводить измерения локальных энергетических частотных спектров отраженных сигналов от радиолокационных объектов и коэффициента отражения по мощности радиопоглощающего материала при различных углах облучения в условиях изменения формы отражаемого поля. При этом локальные энергетические спектры частот находятся в соответствии с конкретной координатой поверхности объекта. Способ позволяет выделить зеркальную компоненту рассеяния электромагнитной волны с высоким разрешением по дальности.
Раскрытие изобретения
Технический результат, на получение которого направлено изобретение - измерение в свободном пространстве локальных энергетических частотных спектров, обусловленных «блестящими точками», которые, в свою очередь, однозначно связаны с геометрической формой исследуемого радиолокационного объекта, а также определение коэффициента отражения по мощности радиопоглощающего материала с повышенной точностью за счет предварительного определения локальных энергетических спектров частот импульсных характеристик объектов локации (металлической пластины без покрытия и металлической пластины с нанесенным РПМ), используя только зеркальную компоненту рассеяния электромагнитной волны в сверхширокой полосе частот.
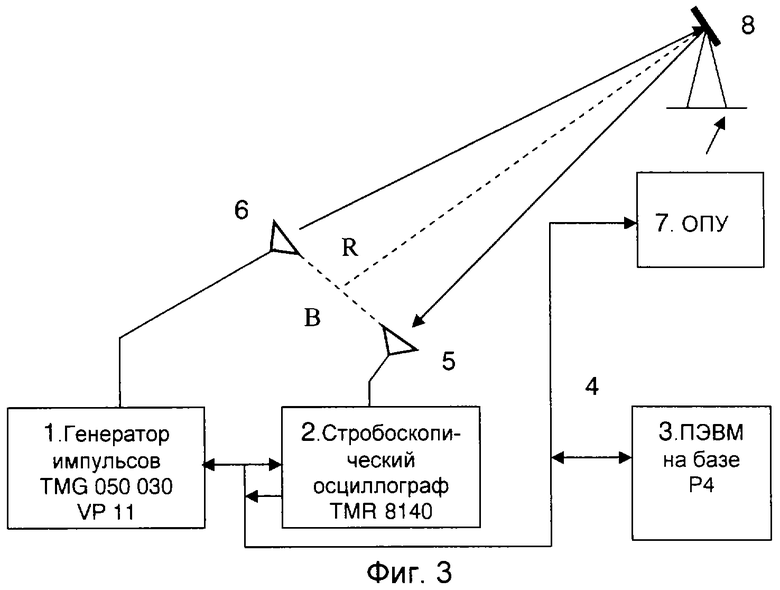
Способ нахождения локальных энергетических частотных спектров радиолокационных объектов при использовании СШП сигналов реализуется устройством, блок-схема которого приведена на фиг.3. Устройство включает: 1 - генератор сверхкоротких импульсов, 2 - стробоскопический осциллограф, 3 - персональную электронную вычислительную машину (ПЭВМ), 4 - интерфейс, 5 - приемную антенну, 6 - передающую антенну, 7 - опорно-поворотное устройство (ОПУ), управляемое ПЭВМ, 8 - объект радиолокационного наблюдения (цель). Выход генератора сверхкоротких импульсов 1 соединен со входом передающей антенны 6, которая связана с исследуемым образцом 8 посредством излучаемого сигнала. Отраженный сигнал связывает исследуемый образец 8 с приемной антенной 5 посредством отраженного сигнала. Выход антенны 5 соединен с входом сверхширокополосного стробоскопического осциллографа 2. С помощью ПЭВМ 3 через интерфейс 4 осуществляется управление ОПУ 7 и измерительными блоками 1 и 2 при использовании специального программного обеспечения. Зона целей находится на определенном расстоянии от антенн. Цели устанавливаются на изготовленном из пенопласта пилоне, ОПУ обеспечивает возможность их поворота и наклона.
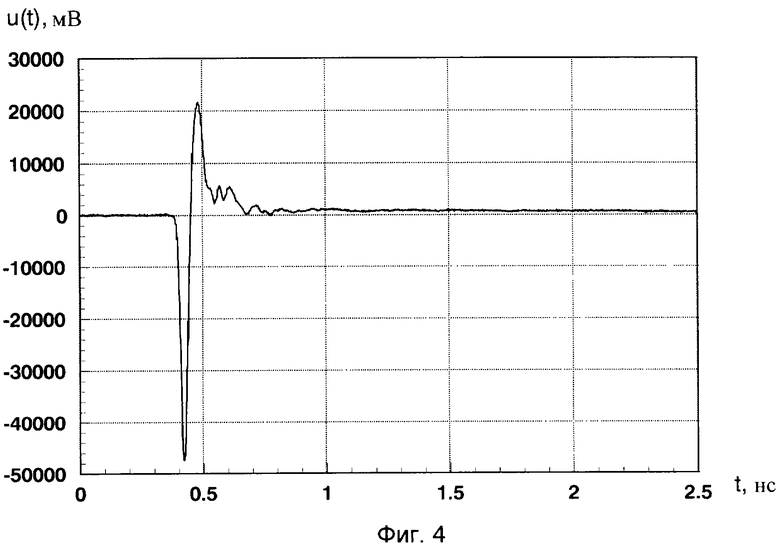
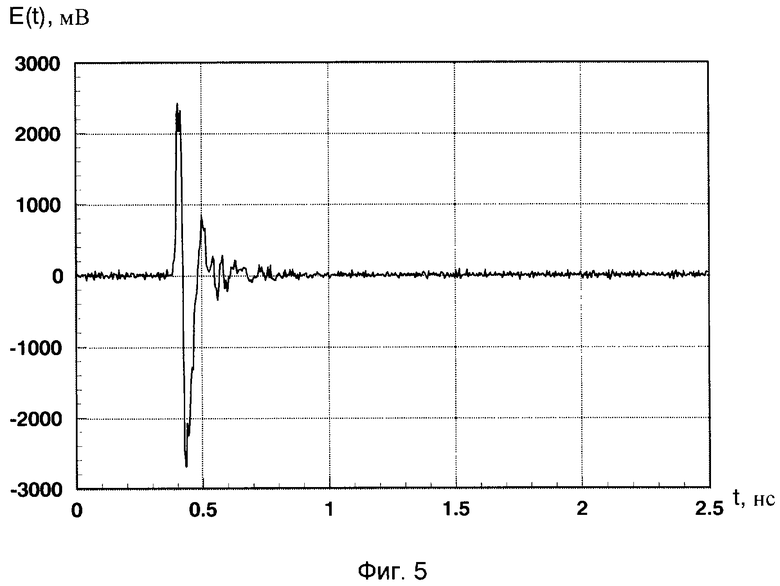
Решение поставленной задачи достигается тем, что в заявленном способе проводят облучение радиолокационных объектов временной последовательностью сверхкоротких импульсов длительностью τ≈50 пс и максимальной амплитудой 48 В (фиг.4). Форма излучаемого поля в дальней зоне приведена на фиг.5 и вычисляется согласно [10. А.В.Зайцев. Излучение наносекундных электромагнитных импульсов каноническими антеннами и их направленные свойства. В сб. Научные труды университета. Вып.8, - Смоленск, ВУ войсковой ПВО РФ, 2002, с.217-223]. Анализ РЛХ (измеренных сглаженных импульсных характеристик, несущих информацию не только об облучаемом объекте, но и о параметрах зондирующего импульса и радиолокационном тракте, и вычисленных импульсных характеристик) проводят как во временной, так и в частотной области. Отраженные от объекта сигналы, полученные в определенном импульсном объеме по времени или, что эквивалентно для СШП сигналов, в импульсном объеме по дальности, регистрируют сверхширокополосным стробоскопическим приемным устройством. С помощью вейвлет-преобразования определяют локальные центры рассеяния (блестящие точки), расположение и свойства которых определяются геометрией рассматриваемой электродинамической структуры (объектом локации) и видом СШП сигнала, и после обработки, вычисляют локальные энергетические частотные спектры.
Вопросы теории вейвлет обработки сигналов подробно изложены в источнике: [11. Малла С. Вейвлеты в обработке сигналов: Пер. с англ. - М.: Мир, 2005. - 671 с., ил.]. Для лучшего понимания сути заявленного изобретения ниже ограничимся краткими выкладками, касающимися только прямого вейвлет-преобразования, используемого в представленной заявке. В качестве зарегистрированного отраженного сигнала (фиг.6) от объекта №1 (двух проводящих сфер диаметром; ближняя сфера - 113 мм, дальняя сфера - 125 мм), разнесенных по дальности на определенное расстояние е=176 мм) рассматривается сигнал s(t). Сигнал s(t) относят к классу финитных сигналов с конечной энергией, средние значения таких сигналов, как и любых других функций из Гильбертова пространства L2(R), должны стремиться к нулю на ±∞. Вейвлеты - это математические функции из Гильбертова пространства L2(R), позволяющие анализировать различные частотные компоненты данных в нестационарных сигналах. Они обладают существенными преимуществами по сравнению с преобразованием Фурье, потому, что вейвлет-преобразование позволяют судить не только об амплитудно-частотном спектре сигнала, но также о том, в какой момент времени появилась та или иная гармоника в этом сигнале. В основе вейвлет-преобразований лежит использование двух непрерывных взаимозависимых и интегрируемых по оси времени t функций: 1) вейвлет-функции ψ(t) как psi - функции времени с нулевым значением интеграла и частотным Фурье - образом ψ(ω), который расположен вокруг некоторой ненулевой частоты ω0 - средней круговой частоты вейвлета; 2) масштабирующей функции ϕ(t) как временной скейлинг - функции phi с единичным значением интеграла, с помощью которой выполняется грубое приближение (аппроксимация) сигнала. Базисными psi - функциями пространства L2(R) могут быть самые различные функции, ограниченные по времени и местоположению на временной оси и имеющие спектральный образ, в определенной степени локализованный на частотной оси. Как и для рядов Фурье, ортонормированное базисное пространство целесообразно конструировать из одной исходной базовой функции ψ(t), норма которой должна быть равна 1. Для перекрытия локальной временной функцией вейвлета всей временной оси R(-∞,∞) пространства L2(R) используется операция сдвига (смещения по временной оси):
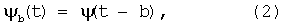
где b - параметр сдвига.
Для перекрытия всего частотного диапазона пространства L2(R) используется операция временного масштабирования вейвлета:
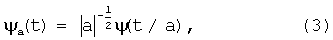
где а - параметр масштаба.
В данной заявке используется вейвлет-функция Морле (Morlet's wavelet), определяемая как:
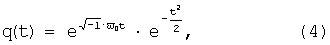
где ω0 - средняя частота вейвлета.
Можно записать:
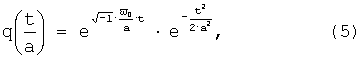
Преобразование Фурье равенства (3) является симметричной функцией относительно частоты ω0/2πа. Функция, используемая в качестве вейвлет-функции, должна удовлетворять следующему необходимому условию:
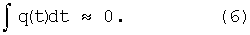
В случае вейвлет-функции Морле это условие выполнимо для широкого диапазона значений ω0. Для технических приложений используют подход, основанный на фиксации ω0 и модификации q(t) введением дополнительного параметра σ, что приводит к модифицированной вейвлет-функции:
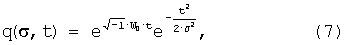
где σ=а,
W0=ω0/a.
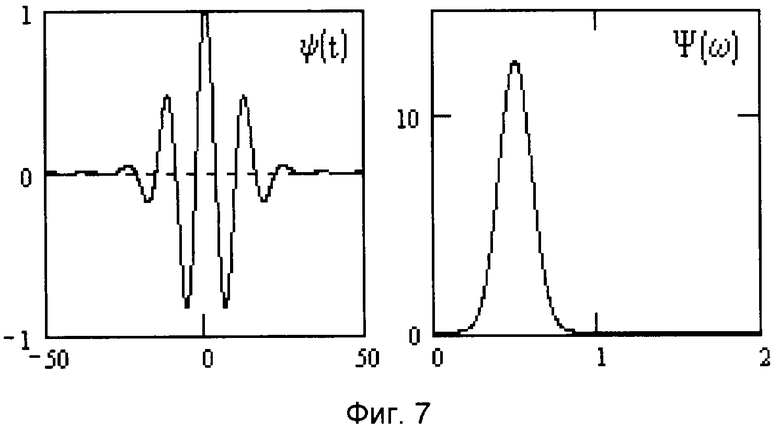
Выбирая малые значения σ=σ1, имеют высокую концентрацию энергии во временной области и получают низкое разрешение в частотной области и, наоборот, большее значения σ=σ1 приводит к более высокому разрешению в частотной области (принцип неопределенности). Изображение временного и частотного образа вейвлет-функции (вейвлет Морле) приведено на фиг.7. Из рассмотрения этих образов можно легко представить, что если временной образ вейвлета будет сужаться (при уменьшении значения параметра масштаба «а»), то его средняя частота ω0 будет повышаться, а его частотный образ перемещаться на более высокие частоты. В частотной области спектр вейвлета Морле напоминает всплеск, пик которого приходится на частоту ω0. Если приближенно трактовать вейвлет как модулированную по амплитуде синусоиду, то ее частота и будет равна средней частотой вейвлета. В том же случае, когда временная зависимость вейвлета далека от синусоидальной, определение средней частоты требует специальной, не всегда достаточно точной обработки, и реализуется итерационными методами. С использованием вейвлет операций базис функционального пространства L2(R) образуется путем масштабных преобразований и сдвигов вейвлета ψ(t) с дискретными значениями базисных параметров масштаба «а» и сдвига «b»:
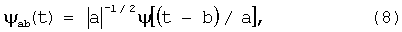
где a, b∈R,
ψ(t)∈L2(R).
Нормы вейвлетов ψab(t) равны норме ψ(t), что обеспечивает нормировочный множитель 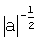 , и если базовый вейвлет ψ(t) нормировать на 1, то все функции вейвлетов также будет нормированными. Прямое интегральное вейвлет-преобразование сигнала выполняется по аналогии с преобразованием Фурье:
, и если базовый вейвлет ψ(t) нормировать на 1, то все функции вейвлетов также будет нормированными. Прямое интегральное вейвлет-преобразование сигнала выполняется по аналогии с преобразованием Фурье:
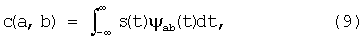
где s(t) - исследуемый сигнал,
ψab(t) - вейвлет.
Интегрирование выполняется по пространству L2(R). Так как форма базисных функций ψab(t) зафиксирована, то вся информация о сигнале переносится на значения вейвлет-коэффициентов c(a,b). Энергетический вейвлет-спектр вычисляется по формуле:
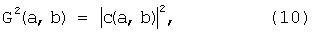
где c(a,b) - вейвлет-коэффициенты.
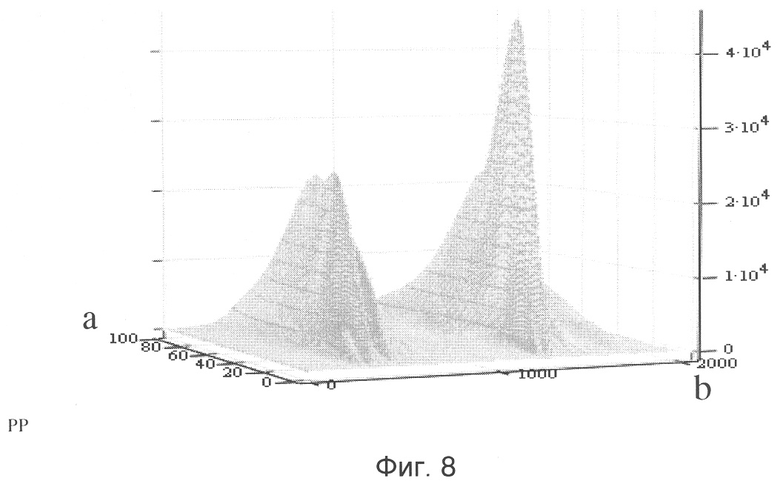
При вычислениях используют дискретные значения сигнала s(tk), где tk - интервал дискретизации сигнала. Для упрощения вычислений в рассматриваемом эксперименте ранжированные значения параметра сдвига «b» выбирают из условия b=0÷k, значение параметра масштаба «а» выбирают исходя из требуемой точности вычислений (в эксперименте: b=k=0÷2047, tk=0,001221 нс, а=1÷50). Результатом вейвлет-преобразования сигнала s(t) (9) является двумерный массив амплитуд - значений вейвлет-коэффициентов |с(а,b)|, распределение этих значений в пространстве (а,b) (а - временной масштаб, b - временная локализация) дает информацию об изменении относительного вклада вейвлетных компонент разного масштаба во времени. Такое распределение называется спектром коэффициентов вейвлет-преобразования, масштабно-временным (частотно-временным) спектром или просто вейвлет-спектром. Энергетический вейвлет-спектр отраженного сигнала от двух проводящих сфер G2(a,b) представляет собой поверхность в трехмерном пространстве, изображенную на фиг.8. Способы визуализации спектра могут быть самыми различными. Наиболее распространенный способ-проекция на плоскость «а, b» (скелетон) с изолиниями (изоуровнями) - фиг.9, что позволяет проследить изменения амплитуд на разных масштабах «а» во времени (по параметру «b»), а также выявить по амплитуде картину локальных экстремумов этих поверхностей («холмов» и «впадин»), так называемый «скелет» структуры анализируемого процесса. По сечениям сдвига параметра «b» вейвлет-спектр отражает компонентный состав энергетического вейвлет-спектра G2(a,b) (из данного комплекта вейвлетов при разных значениях параметра «а») в каждый текущий момент времени. По смыслу преобразования, как скалярного произведения исследуемого сигнала с вейвлетом, ясно, что значения коэффициентов в каждой текущей временной точке по масштабным сечениям тем больше, чем сильнее корреляция между базовым вейвлетом ψab(t) данного масштаба «аi» и поведением сигнала в окрестностях этой временной точки. Вейвлет ψab(t) локализован как во временной, так и в частотной областях и является функцией двух аргументов, первый из которых аналогичен периоду осцилляции (т.е. обратен «средней частоте ω0» разложения в спектр Фурье базисного импульса вейвлета Морле длительностью «а»), а второй - «b» смещению сигнала вдоль оси времени t.
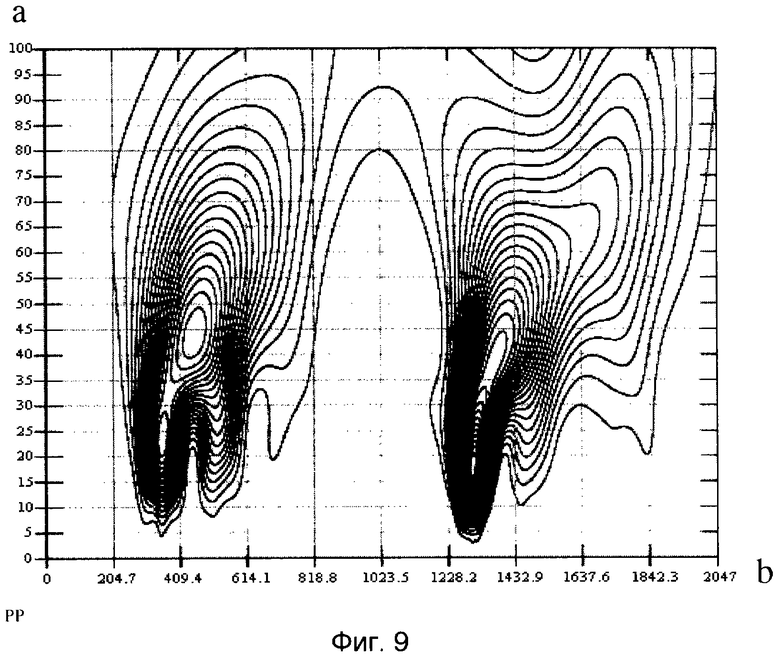
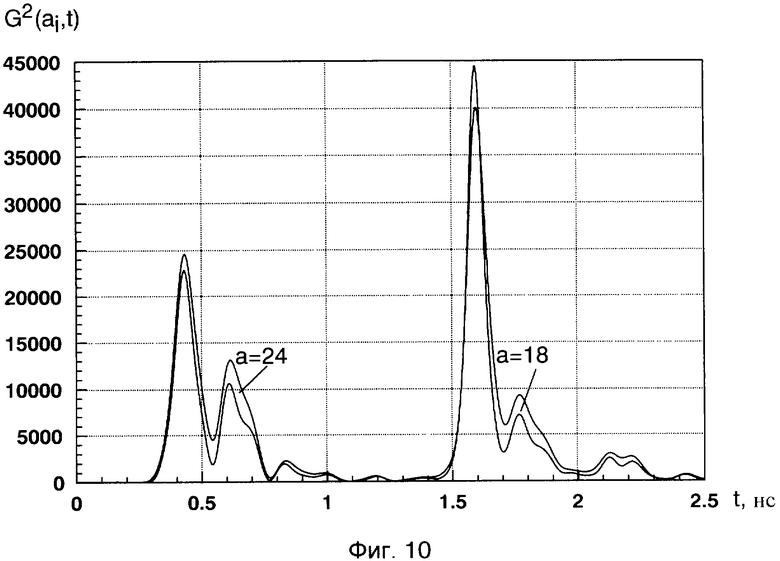
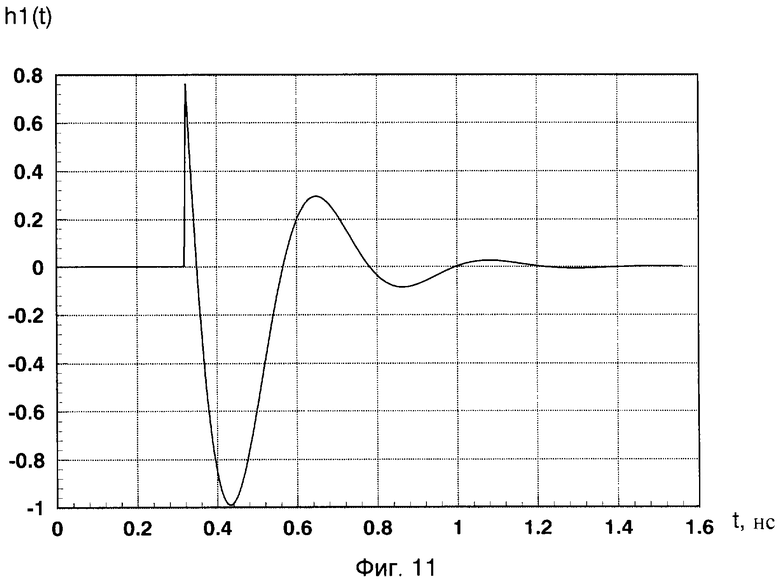
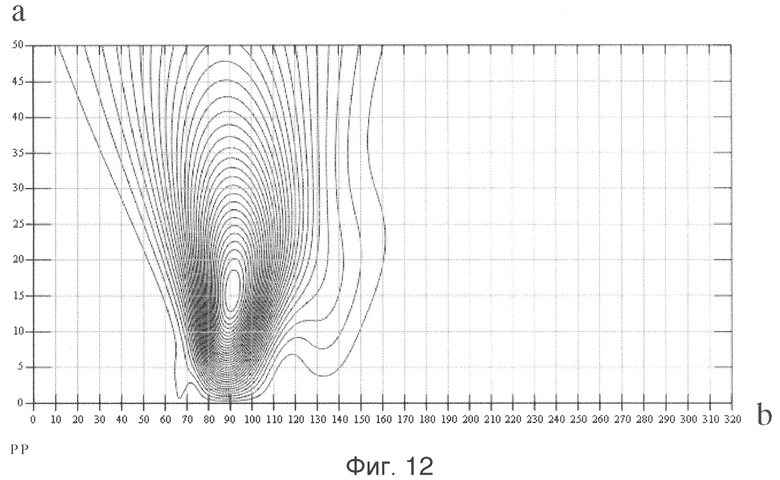
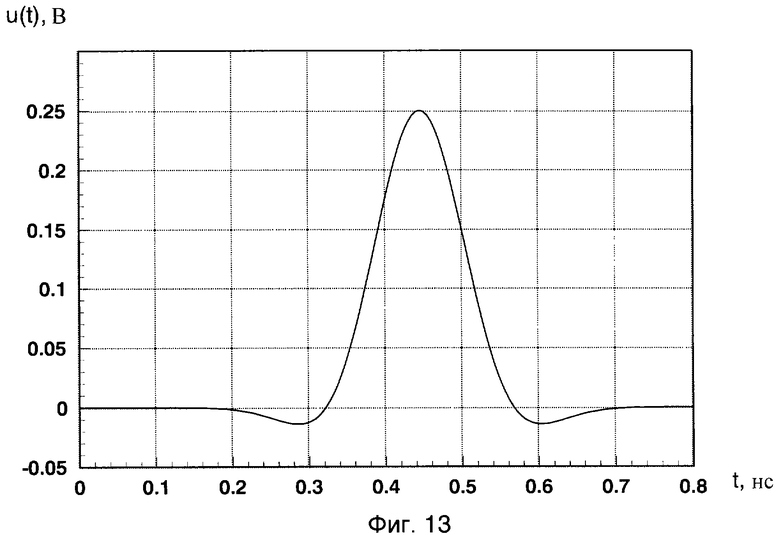
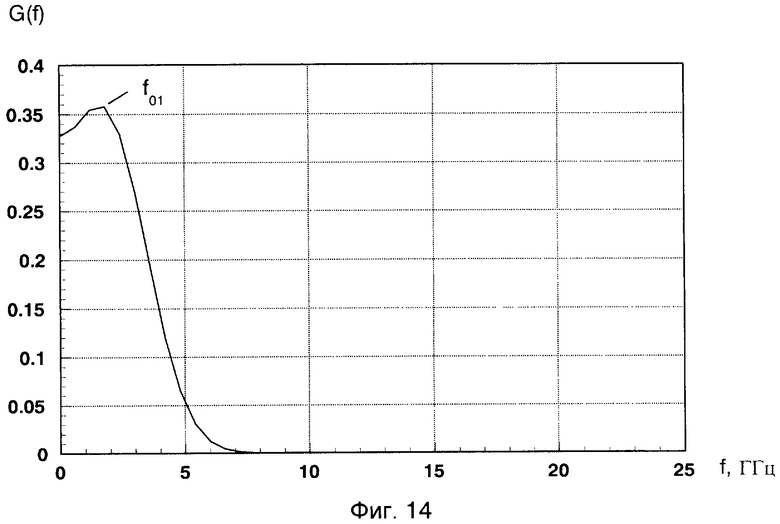
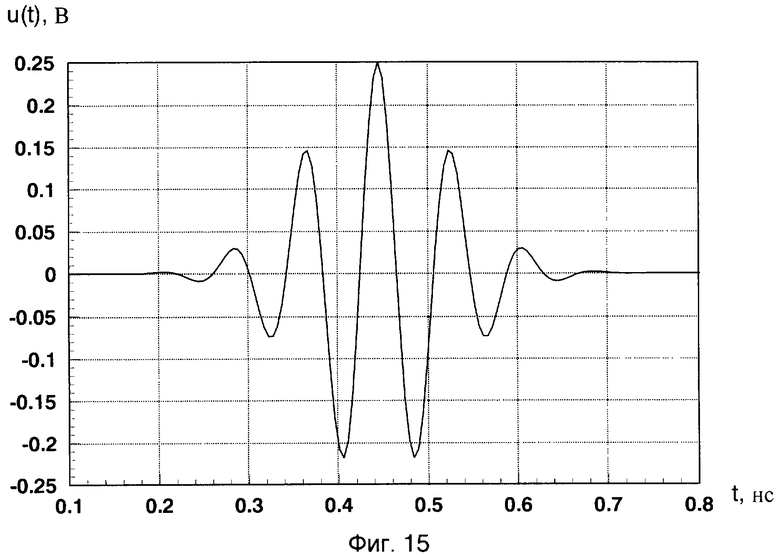
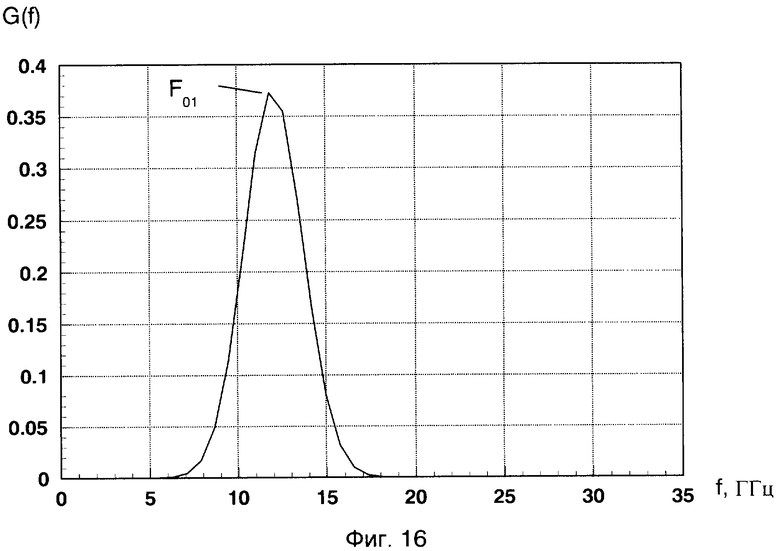
На изображении энергетического вейвлет-спектра G2(a,b)=|c(a,b)|2 отраженного сигнала от двух сфер в виде проекции на плоскость «а, b» с изоуровнями (фиг.9) хорошо различимы две «блестящие точки», обусловленные зеркальной компонентой рассеянного электромагнитного поля от этих двух сфер, с координатами (a1=24, b1=350; a2=18, b2=1300, при W0=1, σ=1,2). На фиг.10 показаны временные зависимости G2(ai,t), полученные из энергетического вейвлет-спектра |c(a,b)|2 двух сфер (сечение параллельное оси амплитуд вдоль оси b) для двух значений параметра «аi» (a1=24, a2=18), на которых также хорошо различимы два пика, разнесенные по времени на величину Δtb=1,18 не и обусловленные зеркальной компонентой рассеянного электромагнитного поля от первой и второй сфер. Соответствующее разнесение по дальности L=15·Δtb=15·1,18·10-9=17,7 см хорошо совпадает с конфигурацией исследуемого радиолокационного объекта и соответствует расстоянию между сферами е=176 мм. Координаты «блестящей точки» для дальней сферы на фиг.9 составляют a2=18, b2=1300. Положение «блестящей точки» для дальней сферы на временной оси tb2=1,58 нс (фиг.10). Для определения локального энергетического спектра сигнала, вызванного отражением именно от второй сферы радиолокационного объекта №1, необходимо принять к рассмотрению импульсную характеристику (РЛХ) этого фрагмента согласно (1). С помощью специально разработанных программ в рамках пакета System Identification системы компьютерной математики (СКМ) MATLAB 7.0.1 была получена нормированная импульсная характеристика фрагмента цели (дальней сферы) h1(t), представляющая собой реакцию исследуемой цели на δ-функцию. Нормированная импульсная характеристика h1(t) изображена на фиг.11. На фиг.12 показано соответствующее изображение энергетического вейвлет-спектра |c(a,b]|2 (при W0=1, σ=1,2) импульсной характеристики h1(t) в виде проекции на плоскость «а, b» с изоуровнями, где хорошо различима «блестящая точка», обусловленная зеркальной компонентой рассеянного электромагнитного поля, с координатой (ah1=16). Изображение коррелирующего с максимумом вейвлет-спектра импульсной характеристики h1(t) в точке (аh1) вейвлета Морле определяют согласно выражению (7) при значении параметров W0=1, σ=1,2. Это изображение приведено на фиг.13 и представляет собой выделенный по времени одиночный импульс. Этот импульс имеет определенный спектральный состав (фиг.14), включающий в качестве частоты с максимальной амплитудой частоту f01, являющуюся средней частотой данного вейвлета. Эта частота, соответственно, равна частоте с максимальной амплитудой локального энергетического спектра G2(f) в точке (ah1). Частоту f01 необходимо определить. Для определения средней частоты f01 воспользуемся следующим приемом. Изменим форму временной зависимости коррелирующего вейвлета Морле, создав вейвлет по форме, напоминающей модулированную синусоиду, для этого зададимся значением параметров W0=6, σ=1,2 (фиг.15). Средняя частота такого вейвлета составит частоту F01, увеличенную в шесть раз по отношению к f01 (фиг.16). Частота F01=11,765 ГГц может быть легко определена как величина, обратная квазипериоду (Т0=85 пс) модулированной синусоиды в изображении временной зависимости вейвлета с W0=6, σ=1,2 (фиг.16). Разделив вычисленное значение F01 на шесть, получают значение F01=1,961 ГГц, равное средней частоте коррелирующего с максимумом энергетического вейвлет-спектра импульсной характеристики h1 вейвлета, изображенного на фиг.13. Локальный энергетический частотный спектр определяют по формуле:
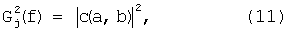
где c(a,bj) - значения вейвлет коэффициентов, полученных согласно (10) при фиксированном значении bj.
Локальный энергетический частотный спектр 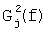 нормированной импульсной характеристики h1(t) «блестящей точки» для дальней сферы (аh1=16), (tb2=1,58 нс) в зависимости от частоты:
нормированной импульсной характеристики h1(t) «блестящей точки» для дальней сферы (аh1=16), (tb2=1,58 нс) в зависимости от частоты:
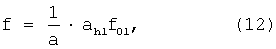
где ah1 - значение параметра масштаба «блестящей точки» энергетического вейвлет-спектра импульсной характеристики h1(t),
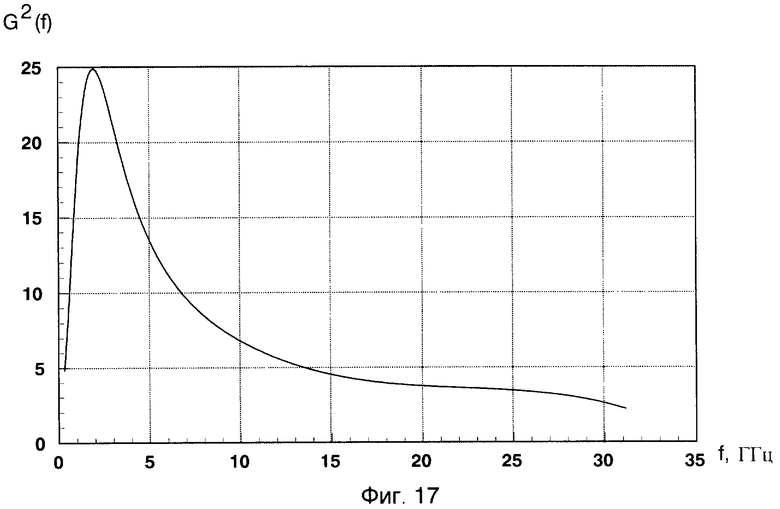
f01 - средняя частота коррелирующего с максимумом энергетического вейвлет-спектра импульсной характеристики h1(t) в точке (аh1) вейвлета Морле, измеряют 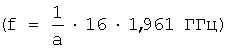 в диапазоне частот 0,5-31 ГГц при изменении масштабного коэффициента «а» от 50 до 1. Локальный энергетический частотный спектр G2(f), обусловленный «блестящей точкой» от второй сферы радиолокационного объекта №1, приведен на фиг.17 и представляет собой кривую с пиком в районе частоты f01=1,961 ГГц, с уменьшением амплитуды в области низких и высоких частот.
в диапазоне частот 0,5-31 ГГц при изменении масштабного коэффициента «а» от 50 до 1. Локальный энергетический частотный спектр G2(f), обусловленный «блестящей точкой» от второй сферы радиолокационного объекта №1, приведен на фиг.17 и представляет собой кривую с пиком в районе частоты f01=1,961 ГГц, с уменьшением амплитуды в области низких и высоких частот.
В заявленном изобретении предложен способ, позволяющий проводить измерения локальных энергетических частотных спектров, обусловленных «блестящими точками» радиолокационных объектов в импульсном объеме с высокой разрешающей способностью по дальности. Способ основан на облучении радиолокационного объекта последовательностью коротких видеоимпульсов длительностью порядка десятков пикосекунд с частотой следования порядка нескольких мегагерц и приеме отраженного сигнала от этого объекта. При обработке отраженного сигнала вычисляют энергетический спектр коэффициентов вейвлет-преобразования измеренного отраженного сигнала, выявляют значения параметров масштаба и сдвига соответствующих максимумам энергии отраженного сигнала на вейвлет-спектрограмме. Методом компьютерной обработки зондирующего и отраженного сигналов получают импульсную характеристику интересующего центра рассеяния, расположенного на фиксированном временном отрезке. Для этой импульсной характеристики вычисляют энергетический спектр коэффициентов вейвлет-преобразования, определяют значение параметра масштаба и среднюю частоту соответствующего значению параметра масштаба коррелирующего вейвлета, определяют локальный энергетический частотный спектр для данного центра рассеяния.
Осуществление изобретения
Заявляемый способ измерения локальных энергетических частотных спектров радиолокационных объектов может найти применение при исследовании радиолокационных характеристик образцов вооружения и военной техники (ВВТ) в условиях использования средств защиты в интересах снижения радиолокационной заметности при помощи радиопоглощающих материалов. Способ применим при исследовании уменьшенных и крупномасштабных моделей ВВТ на радиолокационных полигонах закрытого и открытого типа, а также для измерения важнейшей радиофизической характеристики РПМ-коэффициента отражения по мощности. Способ реализуется устройством, представляющим собой сверхширокополосный лабораторный измерительный комплекс закрытого типа (СШП ЛРИК), блок-схема которого приведена на фиг.3. Устройство включает: 1 - генератор сверхкоротких импульсов TMG 050030 VP 11, 2 - стробоскопический осциллограф TMR 8140, 3 - персональную электронную вычислительную машину (ПЭВМ) на базе процессора Р4, 4 - интерфейс RS 232, связывающий на программно-функциональном уровне блоки СШП ЛРИК, 5 - приемную антенну П6-23М, 6 - передающую антенну П6-23М, 7 - опорно-поворотное устройство (ОПУ), управляемое ПЭВМ, 8 - объект радиолокационного наблюдения (цель). В - база бистатической локации, R - расстояние от базы до цели. Зона целей находилась на расстоянии R=1,78 м от антенн. Цели устанавливались на изготовленном из специального пенопласта пилоне, ОПУ обеспечивало возможность задаваемого поворота и наклона РЛО. Рупоры антенн 5 и 6 располагались на расстоянии В=0,38 м один от другого, поляризация излучения горизонтальная (относительно пола камеры). Бистатический угол составил 12,3°.
В качестве образцов для измерения радиолокационных характеристик использовали: 1) объект №1, состоящий из двух металлических сфер разнесенных в пространстве относительно друг друга на расстояния Х=180 мм; Y=176 мм; Z=130 мм (ось Х выбиралась параллельно базе В, ось Y перпендикулярно оси Х так, что плоскость XY была параллельна горизонтальной плоскости, а ось Z ей перпендикулярна), диаметр ближней сферы составил 125 мм, дальней - 113 мм; 2) объекты №2, №3 - две одинаковые металлические пластины размерами 150×150×5 мм3, одна пластина без покрытия и другая, подобная ей металлическая пластина, с нанесенным с одной стороны на большую грань радиопоглощающим покрытием из РПМ. Объект №1 использовали в эксперименте, результаты которого приведены выше для пояснения сути настоящей заявки на изобретение. Объекты №2 и №3 - для проведения измерений КО по мощности РПМ. Для измерений, пластины устанавливали на пилон в вертикальной плоскости параллельной базе В. Результаты измерений использовали для нахождения коэффициента отражения по мощности для РПМ в сверхширокой полосе частот. Коэффициент отражения по мощности РПМ определяли по формуле:
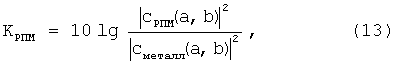
где |cРПМ(a,b)|2, |cметалл(a,b)|2 - локальные энергетические частотные спектры отраженных сигналов от пластины с РПМ и металлической пластины без покрытия.
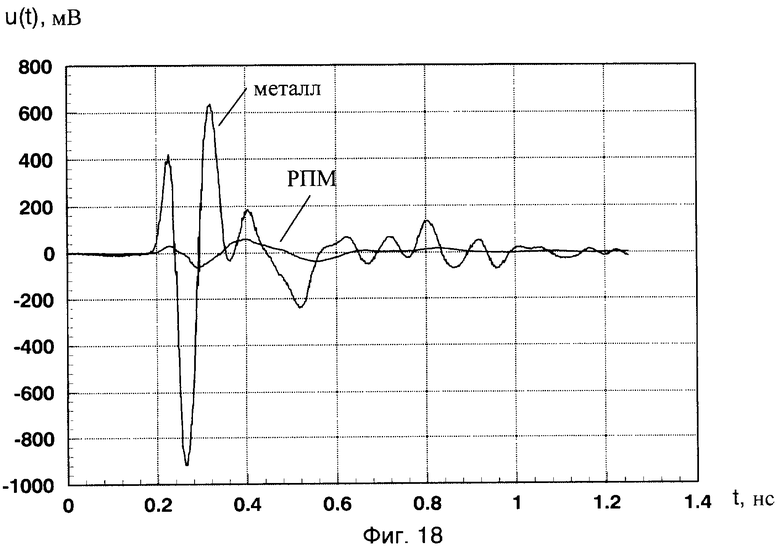
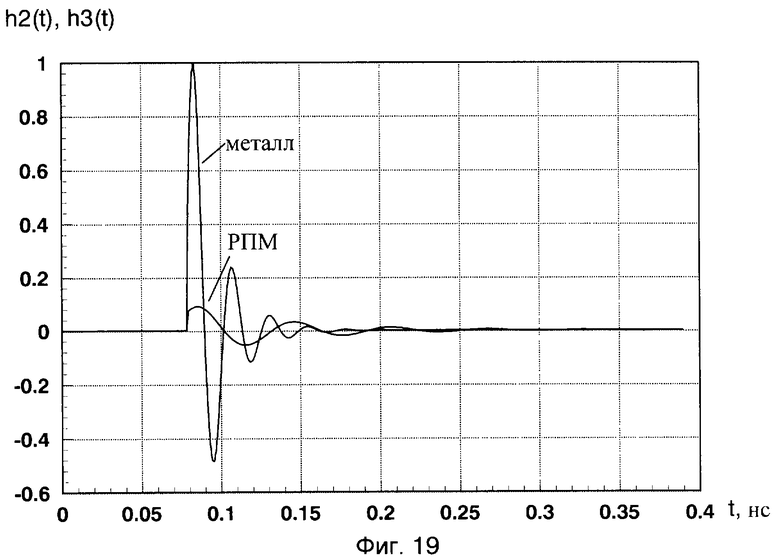
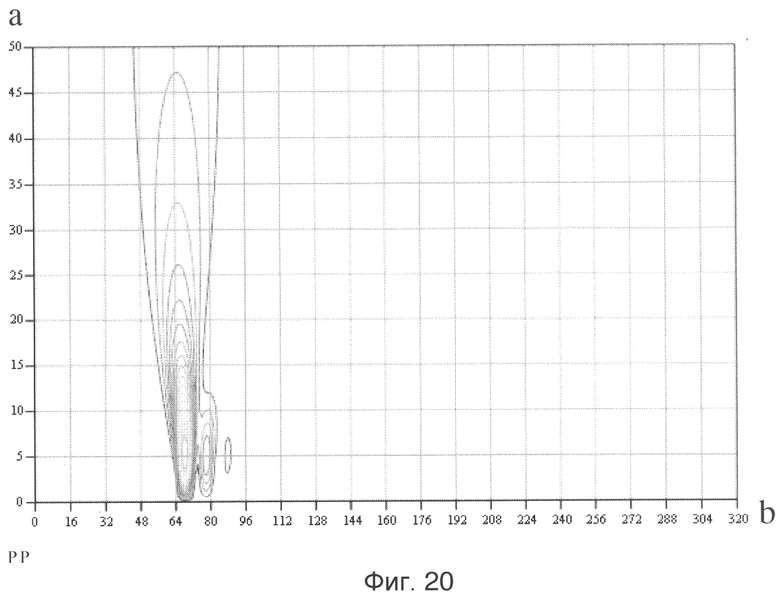
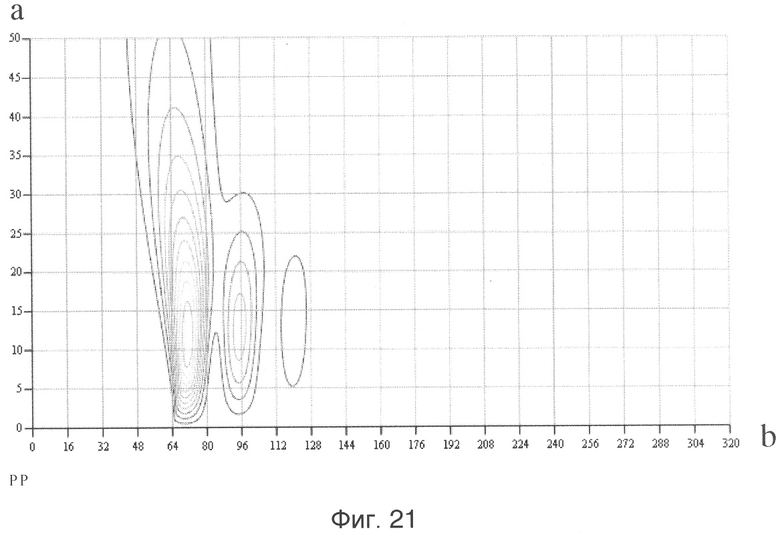
Временные зависимости отраженных сигналов от пластины с нанесенным РПМ и металлической пластины без покрытия при воздействии сверхкоротких импульсов приведены на фиг.18. В отличие от способа-прототипа при вычислении коэффициента отражения по мощности РПМ (13) использовали локальные энергетические спектры импульсных характеристик. При использовании программ в рамках пакета System Identification CKM MATLAB 7.0.1 определены нормированные импульсные характеристики h2(t), h3(t) металлической пластины без покрытия и пластины с нанесенным РПМ (фиг.19). Последовательно выполняя операции заявленного способа измерения локальных энергетических частотных спектров, были получены соответствующие изображения энергетических вейвлет-спектров G2 i(f)=|ci(a,b)|2 для нормированных к максимальной величине h2(t) импульсных характеристик h2(t), h3(t) металлической пластины без покрытия и пластины с нанесенным РПМ в виде проекций на плоскость «а, b» (фиг.20, фиг.21). На этих фигурах хорошо различимы «блестящие точки» с координатами параметров «аi, bj» (аh2=6, bh2=68; ah3=12, bh3=72). Далее были определены значения средних частот f02=5,556 ГГц, f03=2,703 ГГц соответствующих коррелирующих вейвлетов с максимумами вейвлет-спектров импульсных характеристик h2(t), h3(t) и получены соответствующие локальные энергетические частотные спектры 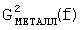 ,
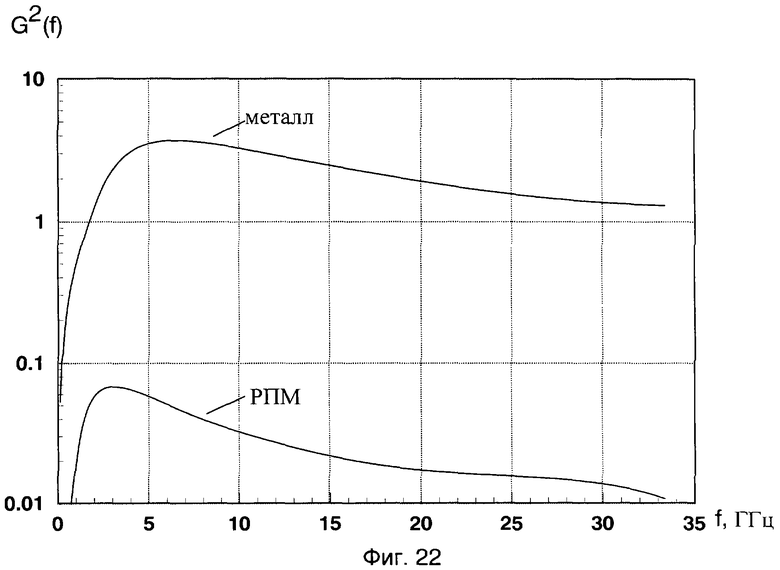
, 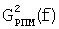 , изображенные на фиг.22. Частотная зависимость коэффициента отражения по мощности K(f) РПМ определена по формуле (13) в диапазоне частот 1-33 ГГц и представлена на фиг.23. С целью оценки погрешности измерения КО РПМ предлагаемым способом были проведены соответствующие измерения КО РПМ на аттестованном комплексе «Панорама». Результаты (фиг.23) дали расхождение порядка 4% в диапазоне рабочих частот комплекса «Панорама».
, изображенные на фиг.22. Частотная зависимость коэффициента отражения по мощности K(f) РПМ определена по формуле (13) в диапазоне частот 1-33 ГГц и представлена на фиг.23. С целью оценки погрешности измерения КО РПМ предлагаемым способом были проведены соответствующие измерения КО РПМ на аттестованном комплексе «Панорама». Результаты (фиг.23) дали расхождение порядка 4% в диапазоне рабочих частот комплекса «Панорама».
Таким образом, предложен способ измерения коэффициента отражения по мощности радиопоглощающего материала в сверхширокой полосе частот с повышенной точностью за счет предварительного определения локальных энергетических частотных спектров импульсных характеристик металлической пластины без покрытия и пластины с нанесенным РПМ.
Краткое описание чертежей
На фигурах изображено:
Фиг.1 - фрагменты регистрируемых временных сигналов, отраженных от образца РПМ Vc(t) и металлической пластины Vm(t).
Фиг.2 - рассчитанные по экспериментальным данным фиг.1 амплитудные характеристики спектральной плотности зарегистрированного сигнала Gm(c)(fn) и усредненной в интервалах δfp спектральной плотности этого же сигнала 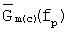 , выполненные с помощью дискретного преобразования Фурье (фиг.1, фиг.2 - прототип).
, выполненные с помощью дискретного преобразования Фурье (фиг.1, фиг.2 - прототип).
Фиг.3 - блок-схема сверхширокополосного лабораторного измерительного комплекса (СШП ЛРИК).
Фиг.4 - форма сверхкороткого импульса с выхода генератора 1.
Фиг.5 - форма излученного поля в дальней зоне.
Фиг.6 - отраженный сигнал от двух проводящих сфер диаметром (ближняя сфера - диаметром 113 мм, дальняя сфера - диаметром 125 мм), разнесенных по дальности на расстояние е=176 мм.
Фиг.7 - изображение временного и частотного образа вейвлета Морле.
Фиг.8 - энергетический вейвлет-спектр коэффициентов |с(а,b)|2 отраженного сигнала от двух проводящих сфер.
Фиг.9 - энергетический вейвлет-спектр двух проводящих сфер в виде проекции на плоскость «а, b».
Фиг.10 - временные зависимости G2(ai,t), полученные из энергетического вейвлет-спектра коэффициентов |c(ai,b)|2 двух проводящих сфер (сечение параллельное оси амплитуд вдоль оси b) для двух значений параметра a (a1=24, а2=18).
Фиг.11 - нормированная импульсная характеристика h1(t) «блестящей точки» дальней сферы.
Фиг.12 - энергетический вейвлет-спектр нормированной импульсной характеристики h1(t) виде проекции на плоскость «а, b».
Фиг.13 - изображение коррелирующего с энергетическим вейвлет-спектром импульсной характеристики h1(t) в точке (аh1) вейвлета Морле при W0=1, σ=1,2.
Фиг.14 - амплитудная характеристика G(f) спектральных плотностей коррелирующего с вейвлет-спектром импульсной характеристики h1(t) вейвлета Морле в точке (аh1) при W0=1, σ=1,2.
Фиг.15 - изображение вейвлета Морле при W0=6, σ=1,2.
Фиг.16 - амплитудная характеристика G(f) спектральных плотностей вейвлета Морле в точке (аh1) при W0=6, σ=1,2.
Фиг.17 - локальный энергетический частотный спектр G2(f) «блестящей точки» дальней сферы объекта №1 (аh1=16), (tb2=1,58 нс)) в диапазоне частот 0,5-31 ГГц при изменении масштабного коэффициента «а» от 50 до 1.
Фиг.18 - временные зависимости отраженных сигналов от пластины с нанесенным РПМ и металлической пластины без покрытия.
Фиг.19 - нормированные импульсные характеристики h2(t) и h3(t) металлической пластины без покрытия и пластины с нанесенным РПМ.
Фиг.20 - энергетический вейвлет-спектр G2(f) нормированной импульсной характеристики h2(t) металлической пластины без покрытия в виде проекции на плоскость «а, b».
Фиг.21 - энергетический вейвлет-спектр G2(f) нормированной импульсной характеристики h3(t) пластины с нанесенным РПМ в виде проекции на плоскость «а, b».
Фиг.22 - локальные энергетические частотные спектры 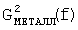 ,
, 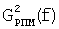 .
.
Фиг.23 - частотная зависимость коэффициента отражения по мощности K(f) РПМ в диапазоне частот 1-33 ГГц, полученная заявленным способом; частотная зависимость коэффициента отражения по мощности K(f) РПМ, полученная в диапазоне рабочих частот комплекса «Панорама».
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ ИЗМЕРЕНИЯ КОЭФФИЦИЕНТА ОТРАЖЕНИЯ ПО МОЩНОСТИ РАДИОПОГЛОЩАЮЩЕГО МАТЕРИАЛА В СВЕРХШИРОКОЙ ПОЛОСЕ ЧАСТОТ | 2007 |
|
RU2346286C1 |
| СПОСОБ ИЗМЕРЕНИЯ ЛОКАЛЬНЫХ ЭФФЕКТИВНЫХ ПОВЕРХНОСТЕЙ РАССЕЯНИЯ ОБЪЕКТОВ В СВЕРХШИРОКОЙ ПОЛОСЕ ЧАСТОТ | 2007 |
|
RU2360264C1 |
| УСТРОЙСТВО ДЛЯ ИЗМЕРЕНИЯ КОЭФФИЦИЕНТА ОТРАЖЕНИЯ РАДИОВОЛН ОТ РАДИОПОГЛОЩАЮЩИХ ПОКРЫТИЙ | 2007 |
|
RU2339048C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ЭФФЕКТИВНОЙ ПЛОЩАДИ РАССЕЯНИЯ УЧАСТКОВ КРУПНОГАБАРИТНЫХ ОБЪЕКТОВ | 2024 |
|
RU2839594C1 |
| СПОСОБ ИЗМЕРЕНИЯ КОЭФФИЦИЕНТА ОТРАЖЕНИЯ РАДИОВОЛН ОТ РАДИОПОГЛОЩАЮЩИХ ПОКРЫТИЙ | 2002 |
|
RU2234101C2 |
| СПОСОБ ИЗМЕРЕНИЯ КОЭФФИЦИЕНТА ОТРАЖЕНИЯ РАДИОПОГЛОЩАЮЩИХ МАТЕРИАЛОВ | 2016 |
|
RU2618480C1 |
| УСТРОЙСТВО ДЛЯ ДИСТАНЦИОННОГО ИЗМЕРЕНИЯ ОТРАЖАТЕЛЬНЫХ СВОЙСТВ ОБЪЕКТОВ СЛОЖНОЙ ФОРМЫ В СВЧ ДИАПАЗОНЕ РАДИОВОЛН | 1997 |
|
RU2111506C1 |
| УСТРОЙСТВО СВЕРХШИРОКОПОЛОСНОЙ РАДИОСВЯЗИ С ПОВЫШЕННОЙ ПОМЕХОЗАЩИЩЕННОСТЬЮ | 2012 |
|
RU2527487C2 |
| РАДИОПОГЛОЩАЮЩЕЕ ПОКРЫТИЕ, СПОСОБ ПОЛУЧЕНИЯ И УПРАВЛЕНИЯ ЕГО СВОЙСТВАМИ И УСТРОЙСТВО ДЛЯ ДИСТАНЦИОННОГО ИЗМЕРЕНИЯ ОТРАЖАТЕЛЬНЫХ СВОЙСТВ ПОКРЫТИЙ НА ОБЪЕКТАХ В СВЧ ДИАПАЗОНЕ РАДИОВОЛН | 2000 |
|
RU2155420C1 |
| КОМПОЗИЦОННЫЙ МАТЕРИАЛ ДЛЯ ПОГЛОЩЕНИЯ ЭЛЕКТРОМАГНИТНОГО ИЗЛУЧЕНИЯ И СПОСОБ ЕГО ПОЛУЧЕНИЯ | 2003 |
|
RU2242487C1 |


Предложенное изобретение относится к радиотехнике и может быть использовано для измерения локальных радиолокационных характеристик, локальных энергетических частотных спектров исследуемых объектов и для измерения радиофизических характеристик радиопоглощающих материалов. Предложенный способ позволяет проводить измерения искомых параметров при различных углах облучения в условиях изменения формы отражаемого поля, а также выделять зеркальную компоненту рассеяния электромагнитной волны с высоким разрешением по дальности. Способ измерения локальных энергетических частотных спектров радиолокационных объектов заключается в том, что радиолокационный объект облучают последовательностью коротких видеоимпульсов длительностью порядка десятков пикосекунд с частотой следования порядка нескольких мегагерц, вычисляют энергетический спектр коэффициентов вейвлет-преобразования этого сигнала, на вейвлет-спектрограмме определяют значения параметров масштаба и сдвига соответствующих максимумам энергии отраженного сигнала, обусловленных локальными центрами рассеяния (блестящими точками), связанными с геометрической формой исследуемого радиолокационного объекта, соответствующей обработкой зондирующего и отраженного сигналов получают импульсную характеристику интересующего локального центра рассеяния, расположенного на фиксированном временном отрезке соответствующего максимуму энергии отраженного сигнала, для этой импульсной характеристики интересующего центра рассеяния вычисляют энергетический спектр коэффициентов вейвлет-преобразования, выявляют значения параметра масштаба, определяют среднюю частоту соответствующего этому значению параметра масштаба коррелирующего вейвлета, определяют локальный энергетический частотный спектр для данного центра рассеяния. 2 н.п. ф-лы, 23 ил.
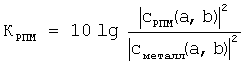 определяют коэффициент отражения радиопоглощающего материала по мощности в сверхширокой полосе частот.
определяют коэффициент отражения радиопоглощающего материала по мощности в сверхширокой полосе частот.
| СПОСОБ ИЗМЕРЕНИЯ КОЭФФИЦИЕНТА ОТРАЖЕНИЯ РАДИОВОЛН ОТ РАДИОПОГЛОЩАЮЩИХ ПОКРЫТИЙ | 2002 |
|
RU2234101C2 |
| СПОСОБ ПАНОРАМНОГО ИЗМЕРЕНИЯ МОДУЛЯ КОЭФФИЦИЕНТА ОТРАЖЕНИЯ СВЧ ДВУХПОЛЮСНИКА | 2002 |
|
RU2253874C2 |
| Способ определения коэффициента отражения радиопоглощающего материала | 1985 |
|
SU1290201A1 |
| СПОСОБ УЛАВЛИВАНИЯ РАСПЛАВЛЕННЫХ ВЫПЛЕСКОВ | 0 |
|
SU211711A1 |
| УСТАНОВКА ДЛЯ СЕПАРАЦИИ МАСЛОВОДЯНОЙ ЭМУЛЬСИИ КОАГУЛЯЦИЕЙ И ФЛОТАЦИЕЙ | 1992 |
|
RU2040478C1 |
| СПОСОБ ПРОИЗВОДСТВА АРОМАТИЗИРОВАННОГО ВАФЕЛЬНОГО ХЛЕБА | 2009 |
|
RU2409049C1 |
Авторы
Даты
2008-03-27—Публикация
2006-08-28—Подача