Область техники, к которой относится изобретение
Настоящее изобретение в общем относится к мониторингу заполненных жидкостью областей в среде и, в частности, - к обнаружению, отслеживанию развития и определению характерных размеров и свойств заполненных жидкостью областей в среде на основе граничных волн, распространяющихся по их поверхностям.
Предшествующий уровень техники
Используемый в описании термин "заполненная жидкостью область" является обобщенным понятием для любой заполненной жидкостью несплошности в сплошной среде. В частности, заполненными жидкостью областями могут быть трещины, слои, разломы, сдвиги. Используемый в описании термин "мониторинг" является обобщенным понятием для действий по обнаружению, наблюдению, прогнозированию, анализу или определению основных характеристик.
Настоящее изобретение применимо к широкому разнообразию сред (в частности, подземным формациям, элементам конструкций, костям) и жидкостей (в частности, воде, нефти).
Мониторинг заполненных жидкостью трещин имеет исключительное значение во многих областях человеческой деятельности, например в добывающей промышленности, медицине, строительстве. При этом заполненные жидкостью трещины в среде могут быть как желательными, так и нежелательными. К желательным трещинам относятся трещины, созданные искусственным путем, например трещины гидроразрыва, предназначенные для повышения эффективности нефтедобычи или предварительной обработки руды при добыче. К нежелательным заполненным жидкостью трещинам относятся, в частности, крупномасштабные естественные подземные трещины в окрестности городов и промышленных объектов, трещины в строительных конструкциях и костях.
В нефтяной промышленности формирование трещин гидроразрыва широко используется для интенсификации добычи нефти за счет формирования или расширения каналов от скважины к резервуару. Трещины гидроразрыва формируют посредством нагнетания жидкости (называемой также жидкостью разрыва) в скважину под давлением. В результате этого в подземной формации формируется и заполняется жидкостью одна или более трещин нормального отрыва, что обычно приводит к повышению интенсивности нефтедобычи.
Жидкость разрыва содержит расклинивающий наполнитель, проппант, малоразмерные частицы которого добавляют в жидкость для поддержания трещины открытой после того, как нагнетание жидкости прекращают и давление сбрасывают, для создания в формации дренирующего слоя с высокой пропускной способностью. Такими частицами являются частицы песка или керамического материала. Для эффективности использования трещина должна распространяться внутри продуктивного пласта и не выходить в прилегающие слои, а также иметь достаточные размеры. Таким образом, определение характерных размеров заполненной жидкостью трещины является важным этапом обеспечения оптимизации процесса добычи.
Иногда проппант образует непроницаемую структуру вблизи вершины трещины, в результате чего трещина прекращает расти. Обнаружение момента, когда трещина перестает расти, является важным для оператора, которому требуется определить момент остановки закачивания проппанта.
Мониторинг заполненных жидкостью областей также имеет большое значение в контексте обнаружения, отслеживания и определения характерных размеров масштабных природных трещин в подземных формациях, которые могут стать причиной эрозии земной поверхности, трещин в различных элементах строительных конструкций, таких как плиты, фундаменты зданий, различные виды опор, которые могут привести к разрушению элементов конструкций, а также разведки подземных слоев, заполненных жидкостью, и определения их характеристик.
В настоящее время характерные размеры заполненных жидкостью трещин определяют, применяя различные технологии и методики. Наиболее широко используется методика косвенного определения, основанная на анализе характеристик изменения давления в ходе разработки и добычи, которая описана, например, в публикации Reservoir Stimulation, Third Edition, M.J.Economides and K.G.Nolte (Ed.), Chichester, UK, Wiley, 2000. Более надежной методикой является методика акустического исследования трещин, применяемая в полевых условиях и основанная на локации событий с использованием пассивного акустического излучения. Такая технология описана, например, в публикации D.Barree, М.К.Fisher, R.A.Woodroof, "A practical guide to hydraulic fracture diagnostic technologies", материал SPE 77442, представленный на Ежегодной технической конференции и выставке в Сан-Антонио, штат Техас, США, 28.09.2002-02.10.2002.
Еще одной технологией оценки размеров заполненной жидкостью трещины является построение карты наклона свободной поверхности, раскрытое в публикации D.Barree, M.K.Fisher, R.A.Woodroof, "A practical guide to hydraulic fracture diagnostic technologies", упомянутой выше. Эта технология включает в себя отслеживание поля деформации породы, окружающей трещину, с использованием датчиков наклона.
Все из перечисленных технологий и методик подразумевают сложную предварительную обработку собранных данных, которая требуется для последующего определения геометрических характеристик трещины на основе моделей. В результате сложность обработки данных, характерная для упомянутых технологий и методик, не позволяет быстро интерпретировать данные измерений и сильно ограничивает возможности определения геометрических характеристик трещин в реальном масштабе времени.
Из US 5206836 известен способ определения характерных размеров подземной трещины, пересекающей имеющуюся скважину, на основе возбуждения колебаний в заполняющей трещину жидкости с резонансной частотой и определения размеров трещины на основе этой резонансной частоты, причем параметры, используемые в расчетах, зависят от динамических характеристик жидкости и подземной формации, а также от геометрических характеристик. Геометрические характеристики заполненной жидкостью подземной трещины определяют посредством обращения физических свойств трещины, полученных в результате моделирования с использованием данных наблюдений давления жидкости в скважине.
Результат, обеспечиваемый данным способом, достигается посредством интерпретации регистрируемых колебаний давления жидкости в скважине на основе волн, распространяющихся в жидкости внутри трещины. Более детальное описание преимуществ способа, соответствующего настоящему изобретению, по сравнению со способом по US 5206836 изложено ниже после подробного раскрытия способа, соответствующего настоящему изобретению.
Таким образом, в настоящее время в рассматриваемой области техники имеется потребность в быстрых надежных способах мониторинга заполненных жидкостью областей, обеспечивающих возможность выполнять мониторинг в реальном времени.
Сущность изобретения
Задачей настоящего изобретения является создание эффективного способа определения характерных размеров заполненных жидкостью трещин в среде и системы для его реализации.
Для решения этой задачи в соответствии с изобретением предложен способ определения характерных размеров, по меньшей мере, одной заполненной жидкостью трещины в среде, содержащий этапы, на которых регистрируют колебания, по меньшей мере, одной заполненной жидкостью трещины, определяют волновые характеристики стоячих граничных волн, распространяющихся вдоль поверхностей, по меньшей мере, одной заполненной жидкостью трещины, на основе зарегистрированных колебаний с учетом свойств среды и жидкости и вычисляют характерные размеры, по меньшей мере, одной заполненной жидкостью трещины на основе определенных таким образом волновых характеристик стоячих граничных волн.
В предпочтительном варианте средой является подземная формация, устье трещины примыкает к нагнетательной скважине, и ширину w трещины определяют отдельно от других ее характерных размеров. На этапе регистрации колебаний регистрируют колебания давления жидкости в нагнетательной скважине и выделяют самые низкие резонансные частоты, которые соответствуют колебаниям по меньшей мере одной заполненной жидкостью трещины. На этапе определения волновых характеристик определяют частоты ν(n) стоячих граничных волн (n - целое), распространяющихся вдоль поверхностей по меньшей мере одной заполненной жидкостью трещины, как соответствующие выделенным резонансным частотам колебаний по меньшей мере одной заполненной жидкостью трещины и вычисляют групповую скорость V(ν(n), w) граничной волны, которая зависит от свойств формации и жидкости. На этапе вычисления характерных размеров по меньшей мере одной заполненной жидкостью трещины вычисляют характерный размер L вдоль распространения стоячей граничной волны по формуле 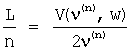 .
.
В другом предпочтительном варианте средой является погруженная в жидкость часть элемента конструкции, а по меньшей мере одна заполненная жидкостью трещина пересекает поверхность погруженной в жидкость части элемента конструкции, причем ширину w трещины измеряют непосредственно. На этапе регистрации колебаний закрепляют датчик на пересечении по меньшей мере одной заполненной жидкостью трещины с поверхностью погруженной в жидкость части элемента конструкции, регистрируют колебания посредством этого датчика и выделяют самые низкие резонансные частоты, которые соответствуют колебаниям по меньшей мере одной заполненной жидкостью трещины. На этапе определения волновых характеристик определяют частоты ν(n) стоячих граничных волн (n - целое), распространяющихся вдоль поверхностей по меньшей мере одной заполненной жидкостью трещины, как соответствующие выделенным резонансным частотам колебаний по меньшей мере одной заполненной жидкостью трещины, и вычисляют групповую скорость V(ν(n), w) граничной волны, которая зависит от свойств элемента конструкции и жидкости. На этапе вычисления характерных размеров по меньшей мере одной заполненной жидкостью трещины вычисляют характерный размер L вдоль распространения стоячей граничной волны по формуле 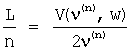 .
.
Система, предназначенная для определения характерных размеров по меньшей мере одной заполненной жидкостью трещины в подземной формации в соответствии с вышеупомянутым предпочтительным вариантом способа, соответствующего настоящему изобретению, содержит средство регистрации для регистрации колебаний давления жидкости в нагнетательной скважине, средство обработки данных для определения частот стоячих граничных волн, распространяющихся вдоль поверхностей по меньшей мере одной заполненной жидкостью трещины, вычисления групповой скорости граничной волны и вычисления характерного размера по меньшей мере одной заполненной жидкостью трещины вдоль распространения стоячей граничной волны и средство формирования сигнала для формирования сигнала, содержащего результаты вычислений.
Одним из основных отличительных признаков заявляемых способов является то, что интерпретацию регистрируемых колебаний выполняют на основе граничных волн, распространяющихся по поверхностям заполненных жидкостью областей, что, в частности, позволяет эффективно и надежно вычислять характерные размеры и свойства заполненных жидкостью областей в реальном времени.
Краткое описание чертежей
Вышеуказанные и иные признаки и преимущества настоящего изобретения раскрыты в нижеследующем описании предпочтительных вариантов его осуществления, приводимых со ссылками на чертежи, на которых
Фиг.1 - блок-схема этапов способа определения характерных размеров заполненной жидкостью трещины согласно изобретению.
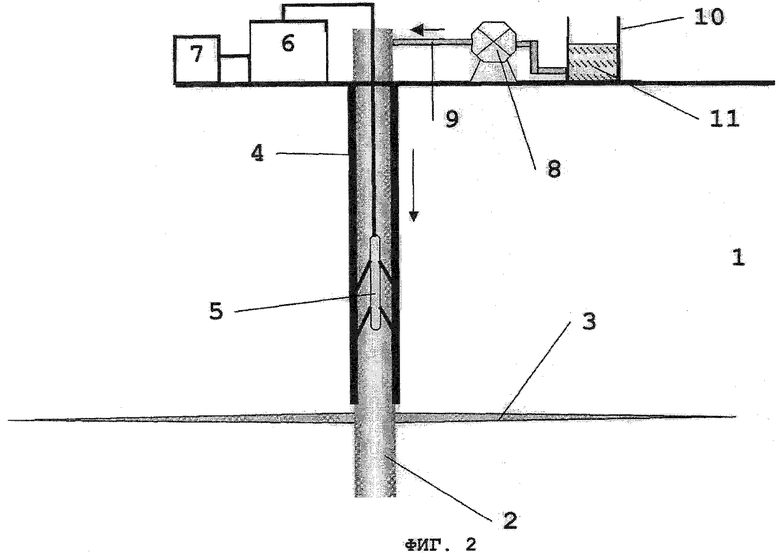
Фиг.2 - схематическое изображение системы для практической реализации предпочтительного варианта способа по фиг.1.
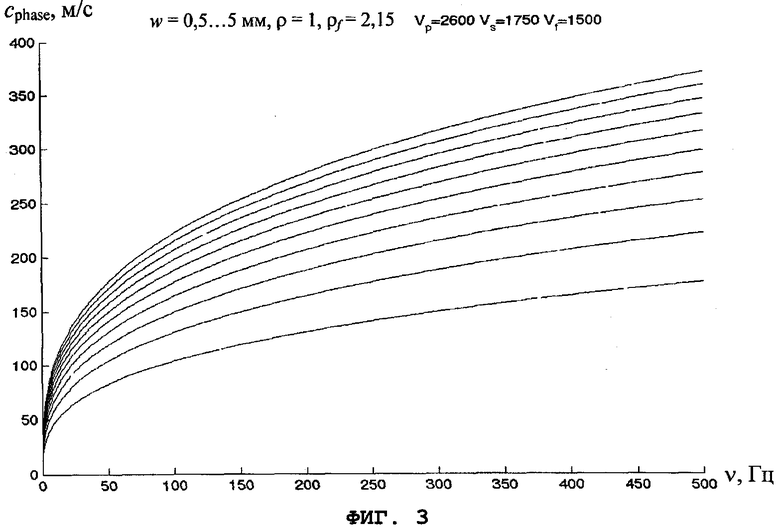
Фиг.3 - дисперсионные кривые для волн, распространяющихся вдоль трещины.
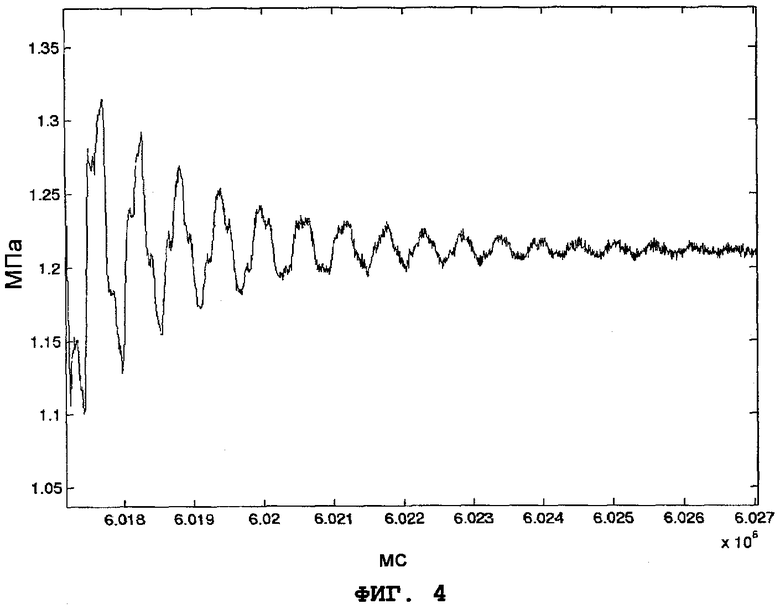
Фиг.4 - зависимость давления жидкости, регистрируемого в иллюстративном предпочтительном варианте способа по фиг.1, от времени.
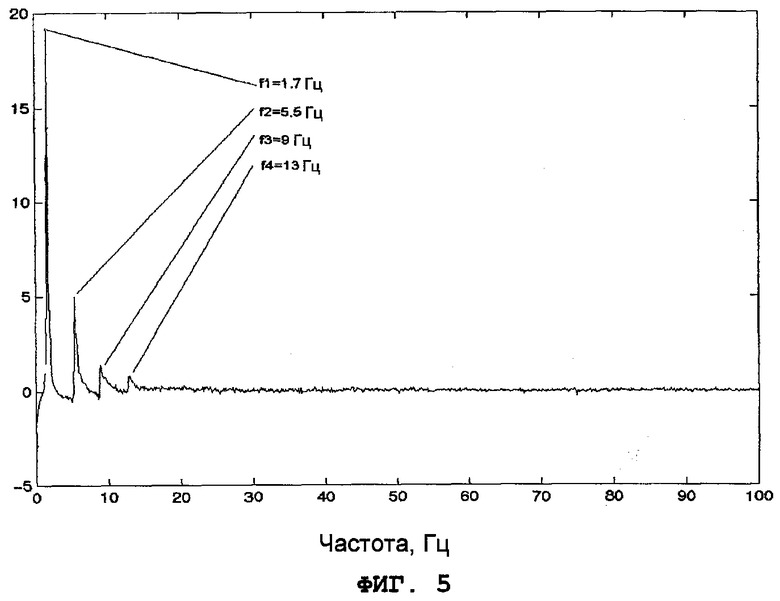
Фиг.5 - Фурье-образ зависимости по фиг.3.
Фиг.6 - схематическое изображение средства обработки данных из состава системы по фиг.2.
Описание предпочтительных вариантов осуществления изобретения
В соответствии с вышесказанным определение характерных размеров заполненных жидкостью трещин имеет большое значение в различных областях человеческой деятельности. Далее со ссылкой на фиг.1 излагается соответствующий настоящему изобретению способ, позволяющий эффективно определять характерные размеры заполненной жидкостью трещины.
На этапе 110 по фиг.1 регистрируют колебания заполненной жидкостью трещины. В частности, эти колебания могут быть возбуждены заранее с целью их последующей регистрации. Регистрацию и возбуждение колебаний трещины можно выполнить любым подходящим средством, известным из уровня техники. Ряд способов и средств возбуждения и регистрации колебаний заполненной жидкостью трещины излагается более подробно ниже. Следует отметить, что колебания трещины можно регистрировать не только непосредственным образом, но и путем регистрации колебаний или иных явлений, индуцированных колебаниями трещины.
На этапе 120 по фиг.1 зарегистрированные колебания интерпретируют на основе стоячих граничных волн, распространяющихся вдоль поверхностей заполненной жидкостью трещины. В данном описании под термином "стоячая граничная волна" понимается приближенное решение уравнений упругой среды, содержащей заполненную жидкостью трещину конечной длины L, описывающее смещение частиц в окрестности трещины как
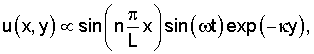
где ω - частота, κ - параметр затухания, n - целое число, при этом ось х направлена вдоль трещины в направлении распространения волны, ось z направлена вдоль трещины перпендикулярно распространению волны, а ось y направлена поперек трещины. Это решение обращается в 0 на концах трещины и гармонически меняется вдоль нее. Вследствие присутствия экспоненциального затухания поперек трещины соответствующие решения оказываются локализованными в окрестности границы раздела "жидкость-среда". Такие решения и называются стоячими граничными волнами.
На этапе 120 интерпретация включает в себя определение волновых характеристик стоячих граничных волн, распространяющихся вдоль поверхностей трещины, на основе колебаний заполненной жидкостью трещины, зарегистрированных на этапе 110. К волновым характеристикам стоячих граничных волн относятся, например, частоты, скорости, спектральная плотность и т.п. При этом определяемые волновые характеристики могут зависеть от свойств среды и жидкости (например, от их плотностей, вязкости жидкости, проницаемости среды). Свойства среды и жидкости, от которых зависят волновые характеристики стоячих граничных волн, должны быть либо известны заранее, либо определены любым известным способом независимо от этапов описываемого способа. Примеры зависимостей волновых характеристик стоячих граничных волн от свойств среды и жидкости приведены ниже при описании предпочтительных вариантов осуществления данного способа.
На этапе 130 по фиг.1 вычисляют характерные размеры заполненной жидкостью трещины на основе волновых характеристик стоячих граничных волн, определенных на этапе 120. В основе вычислений лежит соответствие между длинами стоячих граничных волн, распространяющихся вдоль поверхностей заполненной жидкостью трещины, и ее характерными размерами. Примеры выражения этого соответствия в формульном виде приведены ниже при описании предпочтительных вариантов осуществления настоящего изобретения.
Описанный способ в силу простоты соответствующей ему обработки данных, в частности вычислений, можно реализовать в реальном времени. Также с его помощью возможно определение характерных размеров более чем одной заполненной жидкостью трещины, что будет подробно изложено ниже при описании предпочтительных вариантов осуществления данного способа.
Одним из наиболее предпочтительных вариантов осуществления вышеописанного способа является определение характерных размеров заполненной жидкостью трещины в подземной формации, в которой обеспечена нагнетательная скважина. Устье трещины примыкает к нагнетательной скважине. Такая система, проиллюстрированная на фиг.2, характерна для трещин гидроразрыва, описанных выше.
При регистрации колебаний заполненной жидкостью трещины регистрируют колебания давления жидкости в нагнетательной скважине, индуцированные колебаниями трещины. Предпочтительно, перед регистрацией трещину возбуждают посредством скачкообразного изменения давления жидкости в нагнетательной скважине. Наиболее очевидным способом обеспечения скачкообразного изменения давления жидкости является остановка нагнетания жидкости на несколько секунд. Для регистрации колебаний давления жидкости в нагнетательной скважине можно использовать любую известную подходящую высокоскоростную систему сбора данных, например, позволяющую выполнять одну запись за 5 мс. В частности, регистрацию колебаний давления жидкости можно осуществить с помощью одного или нескольких датчиков, установленных вблизи заполненной жидкостью трещины, например в нагнетательной скважине.
Помимо регистрации колебаний заполненной жидкостью трещины посредством регистрации колебаний давления жидкости в нагнетательной скважине известно множество способов регистрации колебаний трещины. В частности, колебания заполненной жидкостью трещины можно регистрировать посредством регистрации любых колебаний, индуцированных колебаниями трещины. Также регистрация колебаний трещины выполняется путем наблюдения за любыми естественными явлениями, индуцированными колебаниями трещины, включая
а) гравитационные явления, приводящие к изменению ускорения свободного падения в окрестности формации за счет крупномасштабного смещения пластов (здесь имеются в виду приложения к мониторингу гигантских трещин сейсмического масштаба);
б) электромагнитные явления, приводящие к возбуждению электромагнитного поля в окрестности трещины как за счет движения существующих свободных зарядов в среде, так и за счет разделения связанных зарядов;
в) оптические явления, например генерация света в оптических волноводах, расположенных вблизи трещины и чувствительных к механическим напряжениям среды;
г) сейсмоэлектрические явления, представляющие собой генерацию электромагнитного поля в среде вследствие изменения напряженного состояния среды;
д) электрокинетические явления, представляющие собой генерацию электромагнитного поля за счет фильтрации жидкости в трещине и в порах среды;
е) термодинамические явления, такие как, например, фазовые переходы "жидкость-газ", индуцированные колебаниями давления в окрестности трещины.
Кроме того, регистрацию колебаний трещины можно осуществить путем наблюдения за любыми данными, получаемыми в процессе измерений в трещине, таких как данные о проницаемости формации, ее электрической проводимости и т.п.
Согласно одному из предположений, лежащих в основе заявляемого способа и подтверждаемого экспериментально, характерный размер L трещины делится нацело на длины λ(n) стоячих граничных волн, распространяющихся в направлении этого характерного размера. В соответствии с вышесказанным упомянутый характерный размер L можно определить по следующему уравнению:
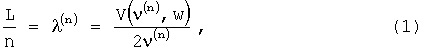
где n - целое, ν(n) - частота n-ой стоячей граничной волны, V(ν(n), w) - групповая скорость граничной волны, w - ширина заполненной жидкостью трещины. При этом уравнение (1) позволяет, определить более одного характерного размера заполненной жидкостью трещины, поскольку каждое измерение трещины (исключая ширину) характеризуется собственным набором стоячих граничных волн с соответствующими частотами ν(n).
Входящие в уравнение (1) частоты ν(n) выделяют на основе зарегистрированных колебаний давления жидкости в нагнетательной скважине, индуцированных колебаниями заполненной жидкостью трещины. Эти частоты соответствуют самым низким резонансным частотам зарегистрированных колебаний. Упоминаемый в описании термин "самые низкие резонансные частоты" соответствует наличию (например, на спектрограмме) резонансных частот, значительно меньших ожидаемых в отсутствие заполненных жидкостью трещин. При этом, как показывает моделирование, самые низкие резонансные моды колебаний трещины формируются именно стоящими граничными волнами, распространяющимися вдоль поверхностей трещины. Пример выделения самых низких резонансных частот приведен ниже.
Основной подлежащей определению волновой характеристикой стоячих граничных волн, распространяющихся по поверхностям заполненной жидкостью трещины, является групповая скорость V(ν(n), w) граничной волны, которая, помимо ширины w рассматриваемой трещины, зависит также от свойств подземной формации и жидкости.
Групповую скорость V(ν(n), w) можно получить либо в приближении невязкой жидкости, либо в приближении вязкой ньютоновской жидкости. Используемые в описании термины "невязкая жидкость" и "вязкая ньютоновская жидкость" известны из уровня техники и подробно изложены в кн.: Теоретическая физика. Т.6: Гидродинамика, Ландау Л.Д., Лифшиц Е.М., 4-е изд., "Физматлит", 1988 г., ISBN: 5-9221-0121-8, глава I, стр.13-70 для невязкой жидкости, глава II, стр.71-136 для вязкой ньютоновской жидкости.
Ниже приводится вывод соотношений для V(ν(n), w) в каждом из приближений.
Вывод соотношения для групповой скорости в приближении невязкой жидкости
Смещения частиц, соответствующие граничной волне, образуют эллиптические траектории с амплитудами, гармонически изменяющимися в продольном направлении трещины и экспоненциально затухающими в ее поперечном направлении. Скорость этой волны меньше наименьшей из скорости упругой волны в жидкости и скорости поперечной упругой волны в формации. Скорость граничной волны зависит от частоты и является очень малой при низких частотах.
Фазовую скорость сphase граничной волны, распространяющейся вдоль поверхностей трещины, для бесконечной заполненной невязкой жидкостью трещины постоянной ширины можно определить из нижеследующего дисперсионного соотношения, выведенного в работе "Slow waves trapped in a fluid-filled infinie crack: implications for volcanic tremor", V.Ferrazini и К.Aki, J. Geophys. Res., 1992, No B9, стр.9215-9223, 1987
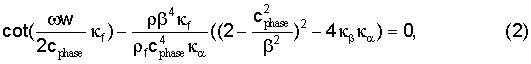
где ω - круговая частота, w - ширина трещины, ρ и ρf - плотности формации и жидкости, соответственно, а
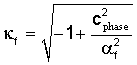
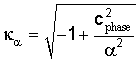
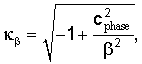
где αf - скорость упругой волны в жидкости, α - скорость продольной упругой волны в формации, β - скорость поперечной упругой волны в формации.
Здесь cphase - скорость распространения волны вдоль трещины. Сама по себе волна, распространяющаяся вдоль поверхностей трещины, представляет собой эллипсоидальное движение частиц с амплитудой, экспоненциально затухающей поперек трещины при ограничении, что перемещения частиц являются симметричными по отношению к оси трещины.
Типичные дисперсионные кривые для волн, распространяющихся вдоль трещины, представлены на фиг.3.
На этих фигурах представлены решения уравнения (2) для различных значений w (w=0,5...5 мм) и различных частот ν=ω/2π. Высокочастотная асимптота для всех кривых (скорость Шолте) близка к скорости упругой волны в жидкости. При нулевой частоте скорость равна нулю, что является главным объяснением всех основных рассматриваемых явлений.
В уравнении (2) можно использовать аппроксимацию cot(x)≈1/x, верную в случае малых х. Замена cot(х) на 1/х не вносит существенных изменений в скорость: для реальных ширин трещин (0,5-50 мм) ошибка в скорости составляет доли мм/с.
В пределе cphase<<αf, что в действительности имеет место для низких частот, можно показать, что хорошей аппроксимацией решения уравнения (2) является
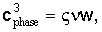
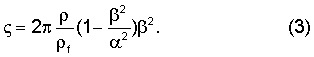
Соответствующие точным решениям кривые по фиг.3 на самом деле близки к зависимости сphase˜ν1/3.
В контексте настоящего изобретения требуется вычислить групповую скорость V граничной волны
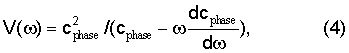
но для граничных волн, распространяющихся вдоль поверхностей трещины, есть хорошая аппроксимация, следующая из уравнений (3) и (4), а именно
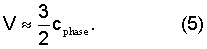
В случае прямоугольных трещин конечной длины численное моделирование показывает, что соответствующие самым низким частотам резонансные моды соответствуют граничным волнам, распространяющимся по поверхностям трещины, с дисперсионным соотношением, являющимся измененной формой уравнения (2). При этом отмечено, что упомянутое изменение становится пренебрежимо малым в пределе большого форматного отношения "длина/ширина", что всегда выполняется для трещин.
Вывод соотношения для групповой скорости в приближении вязкой ньютоновской жидкости
В этом подразделе приведено оригинальное изложение теории граничных волн, распространяющихся вдоль поверхностей трещины, в случае вязкой ньютоновской жидкости.
Для трещины, заполненной вязкой жидкостью, дисперсионное соотношение определяется следующим образом.
Вначале формулируются уравнения движения, при этом в приводимых ниже уравнениях подразумевается суммирование по повторяющимся индексам
I. Уравнения движения формации сформулированы в терминах смещений ui (i=1, 2, 3) следующим образом:
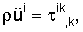
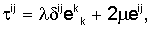
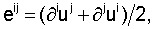
где τij и еij - тензоры напряжений и деформаций, соответственно, λ и μ - коэффициенты Ляме, ∂i - частная производная по xi, δij - символ Кронекера.
II. Уравнениями движения жидкости являются линеаризованные уравнения Навье-Стокса, сформулированные в терминах скорости νi жидкости следующим образом:
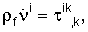
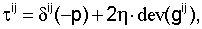
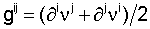
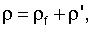
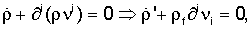
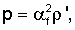
где ρ'(х) - флуктуация плотности, ρf - постоянная плотность жидкости, 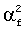 - возведенная в квадрат скорость звука, η - вязкость жидкости и dev(gij)=gij-δijgkk/3. Точка над символом означает производную соответствующей переменной по времени. Обе вышеприведенных системы приводят к уравнениям второго порядка. Например, в случае жидкости (дифференцируя уравнение
- возведенная в квадрат скорость звука, η - вязкость жидкости и dev(gij)=gij-δijgkk/3. Точка над символом означает производную соответствующей переменной по времени. Обе вышеприведенных системы приводят к уравнениям второго порядка. Например, в случае жидкости (дифференцируя уравнение 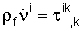 по времени и используя остальные уравнения) можно получить
по времени и используя остальные уравнения) можно получить
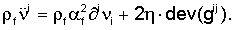
III. Граничные условия
На границе раздела "упругая среда - вязкая жидкость" должны удовлетворяться следующие граничные условия:
непрерывность скорости: 
непрерывность нормальной составляющей усилия:
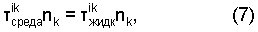
где nk - компонента вектора нормали к границе раздела "упругая среда - вязкая жидкость".
Далее приводится вывод дисперсионного соотношения. После того, как сформулированы основные уравнения, вводится представление полей векторов смещения и скорости через продольный и поперечный потенциалы следующим образом:
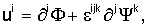
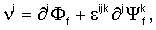
где εijk - полностью антисимметричный тензор. Далее осуществляется переход к частотной области посредством преобразования Фурье по отношению к времени. Вследствие уравнений движения потенциалы удовлетворяют следующим уравнениям:
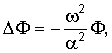
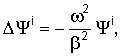
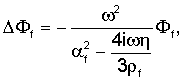
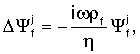
где Δ≡∂i∂i, что подразумевает, что плоские волны имеют следующую форму:
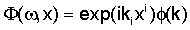



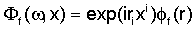
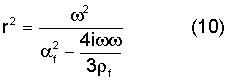
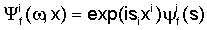
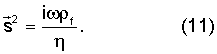
Следует отметить, что волновые векторы ki, li, ri, si являются комплексными.
В рассматриваемой ситуации решения для формации и среды строятся в качестве рядов по плоским волнам (8)-(11), при этом волновые числа ki, li, ri, si выбираются так, чтобы были удовлетворены граничные условия (6), (7).
Предполагая, что трещина распространяется только в плоскости х-y, любое решение представляет собой комбинацию плоских волн в этой плоскости; вследствие осевой симметрии в х-y достаточно изучать плоские волны при условии, что y-компонента волнового вектора обращается в нуль. Таким образом, мы ограничиваемся случаем
ky=ly=ry=sy=0; uy=νy=0; Ψx=Ψz=0,
что приводит к следующему представлению введенных выше потенциалов
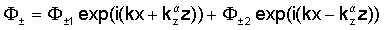
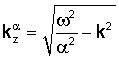
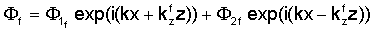
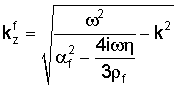
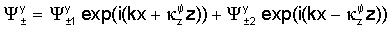
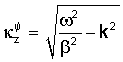
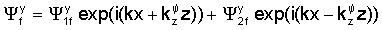
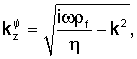
где k∈C - произвольное комплексное число (волновое число в направлении х), в то время как Ф и Ψ - комплексные константы; "±" соответствуют областям формации над трещиной (z≥w) и под трещиной (z≤w).
Мы рассматриваем случай, когда 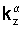 и
и 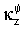 имеют ненулевые мнимые части (что для действительных ω и k будет означать
имеют ненулевые мнимые части (что для действительных ω и k будет означать 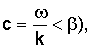 которые без ограничения общности можно считать положительными. В таком случае следует положить
которые без ограничения общности можно считать положительными. В таком случае следует положить
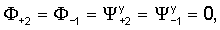
чтобы избежать решения, стремящегося к бесконечности, при бесконечном z. Граничные условия (6), (7) должны выполняться на двух плоскостях z=±w/2. В результате имеются восемь комплексных констант 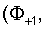
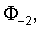
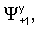
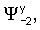
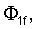
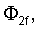
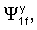
 и восемь независимых граничных условий - по четыре на каждой плоскости (два для непрерывности скорости частицы и два для непрерывности нормальной составляющей усилия). Линейная система уравнений выглядит следующим образом:
и восемь независимых граничных условий - по четыре на каждой плоскости (два для непрерывности скорости частицы и два для непрерывности нормальной составляющей усилия). Линейная система уравнений выглядит следующим образом:
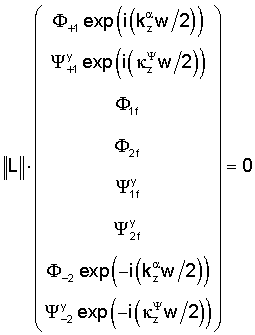
где матрица L линейной этой системы имеет следующий вид:

где
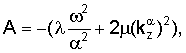
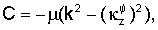
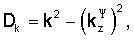
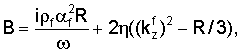
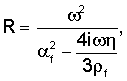
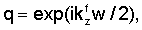
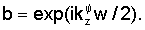
Первая и вторая строки L соответствуют непрерывности смещений по х и z на z=w/2, третья и четвертая строки соответствуют непрерывности нормальной составляющей усилия на z=w/2. Строки с пятой по восьмую представляют аналогичные уравнения на z=-w/2.
Для существования ненулевого решения определитель соответствующей линейной системы должен обращаться в нуль

что и дает дисперсионное соотношение.
В случае нулевой вязкости необходимо удалить первую и пятую строки, а также пятый и шестой столбцы матрицы L и положить η=0 в оставшейся ее части. В результате вышеприведенное уравнение для матрицы L обеспечивает два дисперсионных уравнения: одно для антисимметричной моды (когда давление жидкости антисимметрично по отношению к z) и для симметричной моды (когда давление жидкости симметрично по отношению к z). Антисимметричная мода существенно быстрее. Ее дисперсионная кривая начинается над скоростью упругой волны в жидкости при низких частотах и затем плавно спадает до скорости Шолте по мере роста частоты. Дисперсионное соотношение для симметричной моды совпадает с уравнением (2).
В случае ненулевой вязкости также существуют антисимметричная и симметричная моды. Они характеризуются требованиями в отношении того, что z-компонента смещения либо антисимметрична по отношению к оси трещины (симметричный случай), либо симметрична по отношению к оси трещины (антисимметричный случай). Эти определения согласуются с основными уравнениями в том смысле, что они извлекают независимые системы из этих уравнений. В этих подсистемах нормировочные константы потенциалов ограничены следующим образом:
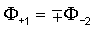
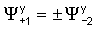
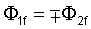
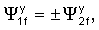
где верхний и нижний знаки относятся к симметричной и антисимметричной модам, соответственно. Эти ограничения приводят к двум следующим уравнениям:
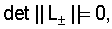
где
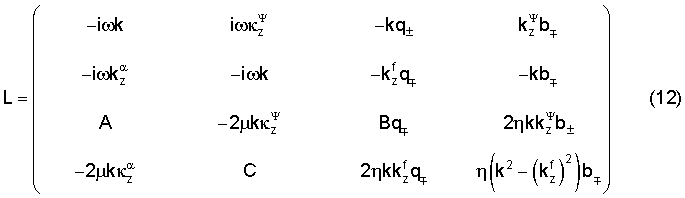
q±=q±1/q, b±=b±1/b.
Эти уравнения могут быть решены численно. Полезно использовать следующую параметризацию решения:
ω=2πν+iθ/ν, k=2πν/c-iσc/ν,
где ν - частота; с - фазовая скорость; θ - интенсивность затухания во времени, измеряемая в единицах частоты; σ - интенсивность ослабления в пространстве, измеряемая в единицах обратной длины волны, при этом все параметры действительные. На параметры θ и σ налагается ограничение, состоящее в том, что они должны быть отрицательными. Если они оказываются положительными, то соответствующие решения должны быть отброшены, так как в противном случае это приведет к экспоненциальному возрастанию либо во времени, либо в направлении распространения. Также можно рассматривать только θ и σ, которые меньше единицы или сравнимы с единицей, поскольку в противном случае затухание во времени или ослабление делает волну пренебрежимо малой для времени одного колебания. В таком случае решение уравнения (12) в случае '+' представляет собой двумерное пространство в четырехмерном пространстве (ν, с, θ, σ), которое может рассматриваться как двумерное расширение кривой c(ν) нулевой вязкости, лежащей в плоскости (ν, с, 0, 0).
Согласно вышесказанному для реальных заполненных жидкостью трещин, ширина которых много меньше 1 см, и низких (в упомянутом выше значении) частот колебаний хорошей аппроксимацией точных соотношений для групповой скорости V является следующее уравнение, получаемое объединением уравнений (3) и (5):
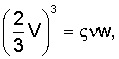
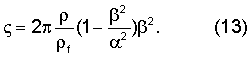
Входящие в это уравнение свойства жидкости и формации предполагаются известными.
Как следует из уравнений (1) и (13), групповая скорость граничной волны зависит также от ширины w трещины. Ширина w трещины должна быть определена отдельно от других ее характерных размеров. В частности, ширину трещины можно определить посредством измерений, выполняемых, например, с помощью одного или более датчиков наклона. Помимо этого, ширину трещины можно определить на основе любых независимых данных. Например, ширину w трещины можно оценить на основе сопоставления объема Volpumped закачанной в трещину жидкости и оценки объема трещины
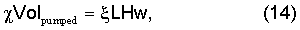
где χ - эффективность трещины, ξ - коэффициент, учитывающий геометрию трещины (выбираемый таким образом, чтобы правая часть уравнения (14) была равна объему трещины, например, ξ=1 для прямоугольной трещины и ξ=π/4 для эллиптической трещины), в то время как L и H - длина и высота трещины, соответственно. При закачивании жидкости объем Volpumped известен, а Н можно оценить либо по соотношению (1), либо посредством измерений. Таким образом, ширину трещины можно оценить посредством сопоставления абсциссы и ординаты на графике зависимости Volpumped от w.
Вводя переменную
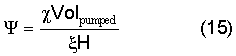
и используя уравнения (1), (13) и (14), можно получить следующие выражения для длины и ширины трещины:
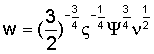
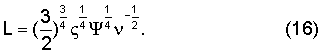
Следует отметить, что неопределенность при определении формы трещины, проявляющаяся в виде неопределенности в коэффициенте ξ, не вносит существенной ошибки при определения длины трещины. Например, отношение коэффициентов Ψ, соответствующих эллиптической и прямоугольной геометрии трещины, составляет 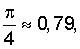 что приводит к отношению соответствующих оценок длин трещин, выполняемых по формуле (16), равному
что приводит к отношению соответствующих оценок длин трещин, выполняемых по формуле (16), равному 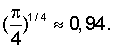 По той же самой причине даже ошибка в 50% при определении объема трещины приведет лишь к ошибке в 16% при оценке ее длины. То же самое можно сказать и о зависимости оценки длины трещины от предположений в отношении эффективности трещины χ.
По той же самой причине даже ошибка в 50% при определении объема трещины приведет лишь к ошибке в 16% при оценке ее длины. То же самое можно сказать и о зависимости оценки длины трещины от предположений в отношении эффективности трещины χ.
Рассмотрим конкретный пример применения описанного выше способа для трещины гидроразрыва, созданной в неглубокой скважине в формации, обладающей следующими упругими характеристиками:
плотность формации ρ=2700 кг/м3;
скорость продольной упругой волны в формации α=3900 м/с;
скорость поперечной упругой волны в формации β=2575 м/с.
Закачиваемой жидкостью является вода.
С помощью изображений, полученных посредством датчиков наклона, определена следующая геометрия трещины: трещина является эллиптической, субгоризонтальной, половина ее длины, то есть расстояние от нагнетательной скважины до дальнего края трещины, равна 55 м, половина ее высоты равна 46 м и ее ширина равна 2,5 мм.
Во время остановки закачивания жидкости была включена высокоскоростная система регистрации давления жидкости как на поверхности, так и внутри скважины. Зависимость регистрируемого давления жидкости от времени представлена на фиг.4.
На фиг.5 представлен Фурье-образ вышеупомянутой зависимости (для простоты изображена только его мнимая часть, действительная же часть, по существу, подобна мнимой части). На представленной спектрограмме невооруженным глазом четко видна последовательность из четырех негармонических пиков, то есть в рассматриваемом случае резонансные пики идентифицированы без какой-либо дополнительной обработки.
Согласно способу, соответствующему настоящему изобретению, вычисляется "групповая" длина граничных волн, распространяющихся по поверхностям заполненной жидкостью трещины, соответствующая частоте каждого пика, посредством деления групповой скорости граничных волн на упомянутую частоту. Для вычислений используется значение ширины трещины, измеренное посредством датчиков наклона. Ниже в Таблице приведены результаты этих вычислений.
Из Таблицы видно, что длина волны, относящаяся к наименьшей частоте (f1) равна 55 м, то есть половине длины рассматриваемой трещины. Следующая длина волны (относящаяся к f2) приближенно равна 55/2, следующая за ней длина волны (относящаяся к f3) приближенно равна 55/3, а последняя длина волны (относящаяся к f4) приближенно равна 55/4. Отсюда следует, что длина трещины делится нацело на длины стоячих граничных волн. Полученные результаты вычислений свидетельствуют о корректности подхода на основе стоячих граничных волн, распространяющихся вдоль поверхностей заполненной жидкостью трещины.
В соответствии с вышеприведенным примером и уравнением (1) в качестве характерного размера заполненной жидкостью трещины можно оценить максимальное расстояние Lmax между ее краями по формуле
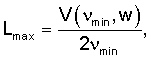
где νmin - минимальная резонансная частота колебаний трещины.
Следует отметить, что математическое моделирование показывает, что оценки характерных размеров заполненной жидкостью трещины согласно описываемому способу слабо чувствительны к профилю ширины трещины, который в общем случае является неоднородным. Таким образом, при использовании уравнений (1), (13), (14) для оценки характерных размеров трещины можно считать ширину w трещины однородной.
На основе набора резонансных частот ν(n) можно не только определять характерные размеры заполненной жидкостью трещины, но и уточнять свойства формации и жидкости. В силу того, что обычно количество отстоящих друг от друга острых пиков в каждой последовательности может быть достаточно большим (от 3 до 10 или более), дополнительные уравнения (1) можно использовать для уточнения свойств формации и жидкости, от которых зависит входящая в уравнение (1) групповая скорость V(ν(n), w) граничной волны. Эти свойства включают в себя, в частности, пористость и проницаемость формации, вязкость жидкости.
В случае существования в формации нескольких заполненных жидкостью трещин в зарегистрированных колебаниях давления жидкости в нагнетательной скважине необходимо выделять для каждой трещины соответствующую ей последовательность низкочастотных резонансных пиков, что позволяет определить характерные размеры и получить дополнительную информацию для каждой из заполненных жидкостью трещин.
Описанный предпочтительный вариант осуществления соответствующего изобретению способа в силу простоты соответствующих ему сбора и обработки данных можно реализовать в реальном масштабе времени. В применении к гидроразрыву выполнение способа "в реальном масштабе времени" означает получение требуемых выходных данных в течение процедуры гидроразрыва или быстрее.
Описанный предпочтительный вариант осуществления соответствующего изобретению способа применим как для природных трещин, так и для трещин, созданных искусственным путем. В частности, он пригоден для морских применений, когда подземной формацией является подземная формация шельфа.
Далее со ссылкой на фиг.2 описывается в общем виде система, в которой можно реализовать вышеописанный предпочтительный вариант осуществления способа определения характерных размеров заполненных жидкостью трещин.
Как следует из фиг.2, устье заполненной жидкостью трещины 3 примыкает к нагнетательной скважине 2, выполненной в подземной формации 1. Нагнетательная скважина 2 может иметь внутреннюю обсадку в виде обсадной трубы 4. Наиболее широко в качестве материала обсадной трубы используют сталь.
Описываемая система включает в себя установленное в нагнетательной скважине средство 5 регистрации, предназначенное для регистрации колебаний давления жидкости в нагнетательной скважине. Как было отмечено ранее, средством 5 регистрации может быть любое известное средство регистрации (например, датчик), способное регистрировать колебания давления с высокой скоростью (например, не менее одной записи за 5 мс) и установленное в любом подходящем месте (например, вблизи устья трещины).
Средство 5 регистрации выдает данные зарегистрированных колебаний в виде сигналов на расположенное на поверхности средство 6 обработки данных, при этом передача сигналов от средства 5 регистрации на средство 6 обработки данных осуществляется любым известным способом (проводным или беспроводным) в любой форме (аналоговой или цифровой), понятной для средства 6 обработки данных.
Средство 6 обработки данных выполняет основные этапы способа, а именно определяет частоты стоячих граничных волн, распространяющихся вдоль поверхностей заполненной жидкостью трещины 3, вычисляет групповую скорость граничной волны (например, согласно соотношениям (13)) и вычисляет характерные размеры трещины 3 вдоль распространения стоячей граничной волны согласно уравнению (1). Иллюстративный вариант осуществления средства 6 обработки данных раскрыт ниже более подробно со ссылкой на фиг.6.
Средство 6 обработки данных выдает результаты вычислений на средство 7 формирования сигнала, предназначенное для формирования сигнала, содержащего результаты вычислений, выполненных средством 6 обработки данных в соответствии с заявляемым способом. Хотя на фиг.2 средство 7 формирования сигнала показано в качестве автономного устройства, оно может входить в состав средства 6 обработки данных.
Формируемый сигнал предназначен для последующего отображения результатов вычислений на локальном или удаленном устройстве отображения (не показаны), которым может быть дисплей, принтер и т.п. В случае выдачи сформированного сигнала на локальное устройство отображения средство 7 формирования сигнала может представлять собой адаптер (например, видеоадаптер). В случае выдачи сформированного сигнала на удаленное устройство отображения или удаленное запоминающее устройство средство 7 формирования сигнала может представлять собой сетевую интерфейсную плату, модем или любое другое устройство, обеспечивающее передачу сформированного сигнала на удаленное устройство. Передача сформированного сигнала на удаленные устройства может осуществляется любым известным способом (проводным или беспроводным) в любой форме (аналоговой или цифровой), поддерживаемыми средством 7 формирования сигнала и согласующимися с доступной средой передачи. В частности, упомянутый сигнал может передаваться посредством спутниковой связи.
Предпочтительно, но не обязательно, описываемая система включает в себя расположенный на поверхности насос 8, соединенный каналом 9 со скважиной 2. Насос 8 соединен также с резервуаром 10, заполненным жидкостью 11. При работе насос 8 нагнетает жидкость в скважину 2 через канал 9. Насос 8 может иметь средство управления давлением (не показано), позволяющее непрерывно повышать и понижать давление жидкости в нагнетательной скважине 2, в частности, скачкообразно сбрасывать давление на короткое время для возбуждения колебаний трещины 3.
Далее со ссылкой на фиг.6 схематично описывается иллюстративный вариант осуществления средства 6 обработки данных. В этом иллюстративном варианте средство 6 обработки данных включает в себя процессорное устройство 61, ОЗУ 62, запоминающее устройство 63, блок 64 преобразования и (необязательно) средство 7 формирования сигнала. Блок 64 преобразования принимает данные регистрации колебаний давления в виде сигналов от средства 5 регистрации и преобразует эти сигналы в форму, пригодную для дальнейшей обработки процессорным устройством 61 и сохранения в цифровом виде в ОЗУ 62 или запоминающем устройстве 63. В запоминающем устройстве 63 хранятся машинно-исполняемые команды, реализующие вышеописанные основные этапы способа, а также данные для связанных с моделированием вычислений, в частности могут храниться данные, выдаваемые блоком 64 преобразования. Выдаваемые блоком 64 преобразования данные также могут поступать непосредственно в ОЗУ 62. В процессе работы средства 6 обработки данных упомянутые машинно-исполняемые команды и данные поступают от запоминающего устройства 62 в ОЗУ 62 для последующего их исполнения и обработки процессорным устройством 61. Далее процессорное устройство 61 выполняет вычисления и выдает их результаты на средство 7 формирования сигнала. Перед выдачей на средство 7 формирования сигнала результаты вычислений могут быть сохранены в запоминающем устройстве 63.
Средство 6 обработки данных может быть любым средством обработки данных, позволяющим выполнить этапы предпочтительного варианта способа, соответствующего настоящему изобретению, закодированные в виде машинно-исполняемых инструкций, например персональным компьютером, сервером, универсальным компьютером и т.п. Процессорное устройство 61 может представлять собой один или более процессоров общего или специального назначения. Запоминающее устройство 63 может представлять собой накопитель на жестких магнитных дисках, привод для магнитного или оптического диска с соответствующим машинно-читаемым носителем и т.п. Следует отметить, что помимо описанных блоков и устройств средство 6 обработки данных может включать в себя и другие компоненты.
Как было отмечено ранее, из US 5206836 известен способ определения характерных размеров подземной заполненной жидкостью трещины, называемый способом HIT (Hydraulic Impedance Test, испытания на основе гидравлического сопротивления). Способ HIT основывается на анализе колебаний давления жидкости в нагнетательной скважине. Ниже приводится сравнительный анализ способа, соответствующего изобретению, и способа HIT, поясняются их основные отличия и описываются преимущества способа, соответствующего изобретению.
В способе HIT система, состоящая из нагнетательной скважины и трещины гидроразрыва, рассматривается как одномерная гидродинамическая система, где параметры этой системы, такие как гидравлическое сопротивление, являются функциями динамических характеристик жидкости и формации, а также геометрических характеристик системы. Согласно способу HIT на основе наблюдений колебаний давления жидкости и предположений о геометрии трещины определяют длину, ширину и высоту трещины посредством обращения теоретически вычисленных емкости, сопротивления и коэффициента инерции. Не касаясь теоретического обоснования способа HIT, отметим, тем не менее, что данный способ основывается на ряде довольно грубых приближений реальных физических процессов.
В способе HIT отклик трещины на изменения давления жидкости в скважине (на основе чего определяют емкость трещины) полагают однородным, то есть трещина раскрывается и схлопывается без изменения формы ("дыхание трещины"), как в случае стационарного решения, определяемого зависящим от времени, но пространственно-однородным распределением давления вдоль трещины.
Также в способе HIT использование малопонятной не зависящей от частоты величины, называемой "скорость звуковой волны" (на основе которой определяют сопротивление трещины), является довольно спорным в предположении однородного распределения давления.
Предположим, что в нагнетательной скважине обеспечено скачкообразное изменение давления жидкости. Согласно способу HIT это изменение обуславливает раскрытие и схлопывание трещины без каких-либо изменений ее формы в соответствии со стационарным приближением, в котором определяющее стационарное решение распределения давления, однородное по объему трещины, считается равным давлению в устье трещины. В то же время считается, что импульсы распространяются через трещину до ее конца и обратно к устью со "скоростью звуковой волны", что является противоречием с однородным распределением давления вдоль трещины.
Далее то же самое явление рассматривается на основе подхода, соответствующего способу по настоящему изобретению, и этот способ сопоставляется со способом HIT. Согласно подходу, соответствующему изобретению, изменение давления в устье трещины приводит к распространению вдоль трещины различных упругих волн, включая волны в жидкости, продольные и поперечные волны в формации и граничные волны, распространяющиеся вдоль поверхностей трещины. Для источников колебаний давления жидкости, характеризуемых низкочастотными гармониками (в диапазоне, ограниченном кГц сверху), любое смещение трещины определяется суперпозицией вышеперечисленных упругих волн. В частности, макроскопическое раскрытие и схлопывание трещины, на котором основывается способ HIT, также представляет собой суперпозицию такого рода.
Далее приводится доказательство того, что "дыхание трещины" по способу HIT соответствует моде самой низкой частоты, формируемой стоячей граничной волной, распространяющейся вдоль поверхностей трещины. Следует отметить, что рассматриваемая здесь симметричная мода граничных волн соответствует случаю, когда смещения поперек трещины симметричны относительно ее оси.
Таким образом, для каждого конкретного положения вдоль трещины трещина либо раскрывается, либо схлопывается. Далее, поскольку длина волны, соответствующая основной моде, равна удвоенной длине трещины, в каждый конкретный момент времени амплитуда смещения в направлении, нормальном к поверхности трещины, либо положительна вдоль трещины, что соответствует раскрытию трещины, либо отрицательна, что приводит к схлопыванию трещины. В соответствии с вышесказанным скорость этой волны достаточно низка. Таким образом, основную моду также можно трактовать как "дыхание трещины". Если такая трактовка корректна, то соответствующая способу HIT независимая от частоты "скорость звуковой волны" должна быть близка к скорости граничной волны при основной частоте. Ниже показано, что это действительно выполняется.
Для эллиптической трещины квадрат соответствующей способу HIT "скорости звуковой волны" представлен следующим образом (см. US 4802144, US 4783769, US 5170378):
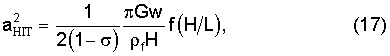
где G - модуль сдвига формации, σ - коэффициент Пуассона, ρf - плотность жидкости, w, H, L - ширина, высота и длина трещины, соответственно, f - ограниченная функция, принимающая значения между 1/2 и 1.
Согласно подходу, соответствующему настоящему изобретению, квадрат скорости определяется согласно уравнению (3) для частоты, определяемой уравнением
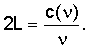
В этом случае используется фазовая, а не групповая скорость, поскольку частота известна точно. Решение уравнения (3) совместно с последним уравнением дает в результате
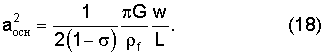
Уравнения (17) и (18) совпадают, если
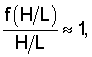
что выполняется при H/L≈1.
Таким образом, показано, что способ HIT можно трактовать как усечение способа, соответствующего настоящему изобретению, до самой низкой частоты.
Соответствующий настоящему изобретению способ подразумевает анализ всех частот отклика трещины. Высшие моды колебаний трещины обуславливают отклик в скважине аналогично основной моде, что объясняет согласно предлагаемой интерпретации наличие пиков более высокой частоты на спектрограмме колебаний давления жидкости в нагнетательной скважине. При наличии нескольких пиков имеется большее число уравнений, которые можно использовать для более точной оценки характерных размеров трещины и для уточнения свойств рассматриваемой системы.
Из US 5206836 следует, что способ HIT основывается на упругих волнах в жидкости, а не на граничных волнах, при этом подразумевается, что высшие (следующие за основной) резонансные моды являются гармоническими, поскольку дисперсия упругих волн в жидкости пренебрежимо мала в низкочастотном диапазоне. Наблюдаемые же в действительности высшие резонансные моды не являются гармоническими. Согласно подходу, соответствующему способу по настоящему изобретению, упомянутые пики интерпретируются как соответствующие высшим модам колебаний трещины. Подход же на основе HIT не обеспечивает интерпретацию упомянутых пиков.
Вариантом осуществления соответствующего изобретению способа, изложенного выше со ссылкой на фиг.1, является определение характерных размеров заполненной жидкостью трещины в погруженной в жидкость части элемента конструкции, при этом трещина пересекает поверхность этой погруженной в жидкость части элемента конструкции. Таким элементом конструкции могут быть опора моста, опора морской платформы, фундамент здания и т.п.
Поскольку трещина пересекает поверхность элемента конструкции, то ее ширину w можно измерить непосредственно. Колебания трещины регистрируют посредством датчика, закрепленного на пересечении трещины с поверхностью элемента конструкции. Предпочтительно, колебания трещины возбуждают перед регистрацией, например, посредством скачкообразной деформации края трещины.
Далее все операции по определению характерных размеров трещины аналогичны соответствующим операциям вышеописанного способа определения характерных размеров трещины в подземной формации, являющегося предпочтительным вариантом способа, соответствующего изобретению. Согласно этим операциям определяют частоты стоячих граничных волн, распространяющихся вдоль поверхностей заполненной жидкостью трещины, как соответствующие самым низким резонансным частотам зарегистрированных колебаний, вычисляют групповую скорость граничной волны, которая зависит от ширины трещины w, свойств элемента конструкции и жидкости и вычисляют характерный размер трещины вдоль распространения стоячей граничной волны по формуле (1) предпочтительно с учетом уравнений (13) и (14).
В соответствии с вышесказанным описываемый способ, соответствующий изобретению, также применим для определения более одного характерного размера заполненной жидкостью трещины, а также для определения характерных размеров нескольких заполненных жидкостью трещин.
Более того, для практической реализации этого способа, соответствующего изобретению, пригодна система, подобная описанной со ссылками на фиг.2, 6 системе, включающей в себя средство 5 регистрации, средство 6 обработки данных и средство 7 формирования сигнала. В рассматриваемом случае средство регистрации, скорее всего, будет отличаться от средства 5 регистрации по фиг.2. Тем не менее, средство 6 обработки данных и средство 7 формирования сигнала или их аналоги применимы к рассматриваемому случаю. Предпочтительно, основные связанные с моделированием и вычислениями этапы вышеописанного предпочтительного варианта способа, соответствующего изобретению, закодированы в виде машинно-исполняемых команд, исполняемых средством 6 обработки данных, и результаты вычислений передаются в виде сигнала средством 7 формирования сигнала на локальное или удаленное устройство отображения.
Описанная выше регистрация низких резонансных частот, формируемых граничными волнами, распространяющимися по поверхностям заполненных жидкостью трещин, предоставляет возможности для широкого круга вариантов применений.
Изобретение было раскрыто выше со ссылкой на конкретный вариант его осуществления. Для специалистов в данной области техники могут быть очевидны и иные варианты осуществления изобретения, не меняющие его сущности, как она раскрыта в настоящем описании. Соответственно изобретение следует считать ограниченным по объему только нижеследующей формулой изобретения.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ ОБНАРУЖЕНИЯ ЗАРОЖДЕНИЯ ИЛИ СУЩЕСТВОВАНИЯ ПО МЕНЬШЕЙ МЕРЕ ОДНОЙ ЗАПОЛНЕННОЙ ЖИДКОСТЬЮ ТРЕЩИНЫ В СРЕДЕ | 2007 |
|
RU2370791C2 |
| СПОСОБ ФОРМИРОВАНИЯ ТРЕЩИН ГИДРОРАЗРЫВА В ПОДЗЕМНОЙ ФОРМАЦИИ | 2007 |
|
RU2347218C1 |
| СПОСОБ ОБНАРУЖЕНИЯ ПРЕКРАЩЕНИЯ РАСПРОСТРАНЕНИЯ ЗАПОЛНЕННОЙ ЖИДКОСТЬЮ ТРЕЩИНЫ В СРЕДЕ | 2007 |
|
RU2347217C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ СВОЙСТВ ЖИДКОСТИ, ЗАПОЛНЯЮЩЕЙ СЛОЙ В СРЕДЕ, СРЕДЫ И СЛОЯ | 2007 |
|
RU2353917C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ЭФФЕКТИВНЫХ ГЕОМЕТРИЧЕСКИХ РАЗМЕРОВ ЗОНЫ РАЗЛОМА, ЗАПОЛНЕННОЙ ФЛЮИДАМИ | 2014 |
|
RU2570589C1 |
| СПОСОБ АКУСТИЧЕСКОГО ВЫРАВНИВАНИЯ ФРОНТА ЗАВОДНЕНИЯ НЕФТЯНОГО ПЛАСТА | 2010 |
|
RU2447273C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ПАРАМЕТРОВ СИСТЕМЫ ТРЕЩИН ГИДРОРАЗРЫВА | 2012 |
|
RU2507396C9 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ФИЗИЧЕСКИХ ХАРАКТЕРИСТИК ОДНОРОДНОЙ СРЕДЫ И ЕЕ ГРАНИЦ | 2016 |
|
RU2717162C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ СВОЙСТВ УГЛЕВОДНОГО ПЛАСТА И ДОБЫВАЕМЫХ ФЛЮИДОВ В ПРОЦЕССЕ ДОБЫЧИ | 2012 |
|
RU2505675C1 |
| СПОСОБ СНИЖЕНИЯ ЗАСОРЕНИЯ ЧАСТИЦАМИ ПРИМЕСЕЙ ПЕРФОРАЦИОННЫХ ОТВЕРСТИЙ И МАГИСТРАЛЬНЫХ ТРЕЩИН ПОРИСТОЙ МАТРИЦЫ ПЛАСТА В НАГНЕТАТЕЛЬНЫХ СКВАЖИНАХ | 2006 |
|
RU2341649C2 |

Изобретение относится к мониторингу заполненных жидкостью областей в различных средах. Сущность: регистрируют колебания трещины. Определяют частоты ν(n) стоячих граничных волн (n - целое), распространяющихся вдоль поверхностей по меньшей мере одной заполненной жидкостью трещины. Вычисляют групповую скорость V(ν(n), w) граничной волны с учетом свойств среды и жидкости и ширины трещины w. Вычисляют характерный размер L вдоль распространения стоячей граничной волны по формуле 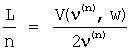 . Система содержит средство регистрации давления жидкости в нагнетательной скважине, средство обработки данных для определения частот стоячих граничных волн, вычисления групповой скорости граничной волны и вычисления характерного размера трещины вдоль распространения стоячей граничной волны, средство управления давлением жидкости, позволяющее скачкообразно сбрасывать или увеличивать давление, и средство формирования сигнала, содержащего результаты вычислений. Технический результат: обеспечение эффективного мониторинга, который можно выполнять в реальном времени. 2 н. и 11 з.п. ф-лы, 6 ил., 1 табл.
. Система содержит средство регистрации давления жидкости в нагнетательной скважине, средство обработки данных для определения частот стоячих граничных волн, вычисления групповой скорости граничной волны и вычисления характерного размера трещины вдоль распространения стоячей граничной волны, средство управления давлением жидкости, позволяющее скачкообразно сбрасывать или увеличивать давление, и средство формирования сигнала, содержащего результаты вычислений. Технический результат: обеспечение эффективного мониторинга, который можно выполнять в реальном времени. 2 н. и 11 з.п. ф-лы, 6 ил., 1 табл.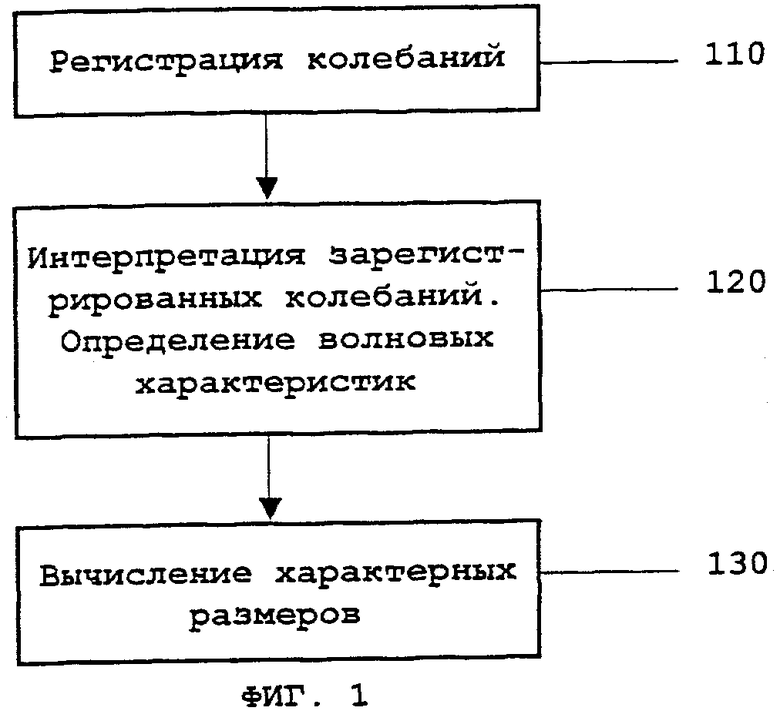
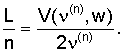
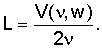
на этапе регистрации колебаний закрепляют датчик на пересечении по меньшей мере одной заполненной жидкостью трещины с поверхностью погруженной в жидкость части элемента конструкции, регистрируют колебания посредством этого датчика и выделяют самые низкие резонансные частоты, которые соответствуют колебаниям по меньшей мере одной заполненной жидкостью трещины;
на этапе определения волновых характеристик определяют частоты ν(n) стоячих граничных волн (n - целое), распространяющихся вдоль поверхностей по меньшей мере одной заполненной жидкостью трещины, как соответствующие выделенным резонансным частотам по меньшей мере одной заполненной жидкостью трещины и вычисляют групповую скорость V(ν(n), w) граничной волны, которая зависит от свойств элемента конструкции и жидкости.
| US 5206836 А, 27.04.1993 | |||
| US 4858130 А, 15.08.1989 | |||
| ДЕНЕЖНЫЙ ДОКУМЕНТ ИЛИ ДОКУМЕНТ БЕЗОПАСНОСТИ, СОДЕРЖАЩИЙ ПРИСПОСОБЛЕНИЕ, ЗАЩИЩАЮЩЕЕ ЕГО ОТ ПОДДЕЛКИ, НЕСУЩАЯ ЛЕНТА ДЛЯ ИЗГОТОВЛЕНИЯ ЗАЩИЩЕННОГО ОТ ПОДДЕЛКИ ДЕНЕЖНОГО ДОКУМЕНТА ИЛИ ДОКУМЕНТА БЕЗОПАСНОСТИ, СПОСОБ ИЗГОТОВЛЕНИЯ ДЕНЕЖНОГО ДОКУМЕНТА ИЛИ ДОКУМЕНТА БЕЗОПАСНОСТИ | 1992 |
|
RU2060903C1 |
| РЕЛЕ-РЕГУЛЯТОР | 2002 |
|
RU2231155C1 |
| Способ определения параметров расслоения кровли горных выработок | 1984 |
|
SU1232800A1 |
Авторы
Даты
2008-06-20—Публикация
2004-04-23—Подача