ОБЛАСТЬ ТЕХНИКИ
Изобретение относится к способам исследования однородных сред и может быть использовано для определения физических характеристик как самих сред, так и их границ. Так, например, в случае однородного по длине сегмента скважины, пробуренной в земле и заполненной жидкостью, можно определять скорость звука и вязкость самой жидкости, а также коэффициент продуктивности пласта, примыкающего к данному сегменту. Изобретение также применимо к исследованию сред, представляющих собой комбинацию однородных компонентов, например, таких заполненных жидкостью скважин, которые являются объединением сегментов постоянного диаметра, заполненных жидкостями с различными свойствами.
УРОВЕНЬ ТЕХНИКИ
Гармоническая волна представляет собой синусоидальное во времени и пространстве колебание определенной частоты, фазы и амплитуды. Такие возбуждения обычно возникают в физических системах, описываемых гиперболическими уравнениями, например, волны давления в жидкости, Р- или S- волны в упругих телах, электромагнитные волны, и т.д. Во многих случаях, как правило, когда длина волны значительно превосходит поперечные размеры объекта, распространение волны можно представить как одномерное. В этих случаях каждый гармонический сигнал является наложением двух волн, распространяющихся в противоположных направлениях.
Регистрация гармонической волны, распространяющейся по однородному одномерному сегменту, может дать информацию о физических характеристиках сегмента на основании фазовой скорости и коэффициента затухания волны, а также о граничных условиях на краях сегмента на основании коэффициента отражения, являющегося отношением амплитуд волн, распространяющихся в противоположных направлениях. Граничные условия могут предоставить ценную информацию об объекте, находящемся на границе, например, в случае распространения волны давления в скважине, отношение типа P=ZQ между давлением Р и дебитом Q в насосно-компрессорной трубе в непосредственной близости от продуктивного пласта может позволить судить о "входной функции пласта-коллектора" Z, предел нулевой частоты которой является не чем иным, как коэффициентом продуктивности пласта. Наличие трещины или зоны утечек жидкости будет проявляться как Z→0 на низких частотах, и т.д. При сейсмических исследованиях, т.е. при распространении упругой волны в массиве горных пород и ее отражении от очередного пласта, граничное условие оказывается чувствительно к контрасту импеданса пластов, где импеданс Z пропорционален произведению плотности пласта ρ на фазовую скорость волны с, Z~ρc, что позволяет исследовать механические характеристики пластов.
Из уровня техники известен способ определения характеристик гармонической волны, описанный в патенте США №5331604, позволяющий определить все количественные характеристики волны. В данном способе осуществляют регистрацию акустических волн посредством датчиков, размещенных на каротажном зонде, расположенном в скважине. Способ предусматривает интерпретацию гармонических волн, "волн дискретной частоты", для получения частотно-зависимых коэффициентов отражения. Вычислительные методы, описанные в данном патенте, опираются на интерпретацию набора комплексных амплитуд, являющихся коэффициентами спектрального разложения сигнала, записанного датчиками. Эти методы достаточно чувствительны к таким ошибкам при регистрации, при которых возникает погрешность определения фазы комплексных амплитуд, в частности, к ошибкам в синхронизации датчиков или в определении положения датчиков.
РАСКРЫТИЕ ИЗОБРЕТЕНИЯ
Предлагаемый способ определения физических характеристик однородной среды и ее границ является нечувствительным к произвольным фазовым сдвигам между датчиками, осуществляющими регистрацию гармонических волн, и может применяться в тех случаях, когда отсутствует точная информация о временном сдвиге между датчиками или когда временная шкала датчиков подвержена дрейфу. Фактически, предлагаемый в данной заявке способ использует только абсолютные величины (модули) комплексных амплитуд, и не использует фазы комплексных амплитуд.
В соответствии с предлагаемым способом для определения физических характеристик однородной среды и ее границ осуществляют регистрацию гармонической волны, распространяющейся в однородной среде и представляющей собой колебание физической величины вдоль одного направления распространения в однородной среде. Регистрацию осуществляют путем регистрации указанной физической величины посредством датчиков вдоль направления распространения колебания по меньшей мере в пяти точках, расположенных на равном расстоянии друг от друга. Посредством компьютерной системы методом спектрального анализа преобразуют выходные сигналы датчиков в соответствующие комплексные спектральные амплитуды, соответствующие частотному разложению выходных сигналов. Создают модель распространения гармонической волны в однородной среде, в которой для любой частоты колебаний волна представляется в виде распространяющихся в противоположные стороны нисходящей и восходящей экспоненциально затухающих гармонических волн, при этом модель зависит от комплексных амплитуд нисходящих и восходящих волн и комплексной константы распространения колебаний. Посредством компьютерной системы абсолютные величины комплексных спектральных амплитуд выходных сигналов датчиков на каждой частоте используют в качестве исходных данных для уравнений, сравнивающих абсолютные величины комплексных амплитуд с созданной моделью распространения волны в однородной среде. Путем решения полученных уравнений определяют полные комплексные амплитуды нисходящих и восходящих волн и комплексную константу распространения колебаний на каждой частоте. Полученные результаты используют для определения физических характеристик границ однородной среды на основе интерпретации отношения комплексных амплитуд нисходящих и восходящих волн, а также для определения физических характеристик самой среды на основе интерпретации компонент комплексной константы распространения, а именно, фазовой скорости и коэффициента затухания волны.
В соответствии с одним из вариантов осуществления изобретения колебания физической величины вдоль направления распространения создают в среде искусственным путем.
В соответствии с одним из вариантов осуществления изобретения однородная среда представляет собой сегмент заполненной жидкостью скважины, пробуренной в пласте, колебания физической величины создают подключенным к скважине или находящимся в ней насосом, физическими характеристиками однородной среды являются сжимаемость и вязкость заполняющей скважину жидкости, а физическими характеристиками границ однородной среды является коэффициент продуктивности пласта, примыкающего к данному сегменту.
В соответствии с другим вариантом осуществления изобретения однородная среда является носителем электромагнитных волн, а колебания физической величины создают излучателем электромагнитных колебаний.
В соответствии с еще одним вариантом осуществления изобретения преобразование выходных сигналов датчиков осуществляют при помощи дискретного преобразования Фурье.
В соответствии с одним из вариантов осуществления изобретения регистрацию физической величины по меньшей мере в пяти точках осуществляют одновременно посредством датчиков, каждый из которых установлен в соответствующей точке.
В соответствии с другим вариантом осуществления изобретения регистрацию физической величины по меньшей мере в пяти точках осуществляют последовательно путем последовательного перемещения по меньшей мере одного дачика в направлении распространения колебания физической величины.
КРАТКОЕ ОПИСАНИЕ ЧЕРТЕЖЕЙ
Изобретение поясняется чертежами, где на фиг. 1 представлен график полинома 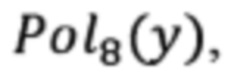 на фиг. 2 представлен график полинома
на фиг. 2 представлен график полинома 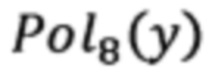 при наличии дополнительного датчика, на фиг. 3 показана общая структура решений, на фиг. 4 показан пример реализации способа.
при наличии дополнительного датчика, на фиг. 3 показана общая структура решений, на фиг. 4 показан пример реализации способа.
ПОДРОБНОЕ ОПИСАНИЕ ИЗОБРЕТЕНИЯ
Дальнейшее описание раскрывает сущность настоящего изобретения, позволяющего определить все параметры гармонической волны, опираясь лишь на абсолютные значения комплексных амплитуд.
Для группы из 2N+1 равноудаленных датчиков (N=0,1,2,…) имеем, для каждой частоты ν:
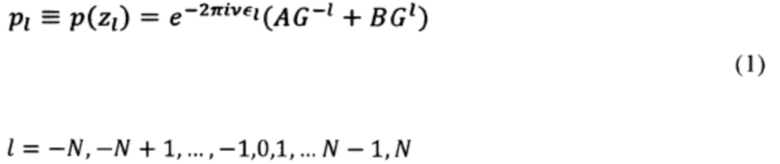
где А, В - комплексные амплитуды нисходящих и восходящих волн, G - комплексное число, «передаточная функция» антенны, 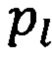 - значения измеряемой величины в точке номер
- значения измеряемой величины в точке номер 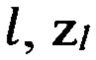 - координата точки номер
- координата точки номер 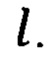 Здесь также введены неизвестные временные задержки
Здесь также введены неизвестные временные задержки 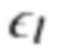 между началом отсчета времени датчиков. Данные уравнения справедливы для описания распространения волн в любой не зависящей от времени однородной среде.
между началом отсчета времени датчиков. Данные уравнения справедливы для описания распространения волн в любой не зависящей от времени однородной среде.
При помощи расчета абсолютных значений комплексных величин 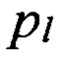 устраняется фазовая зависимость:
устраняется фазовая зависимость:
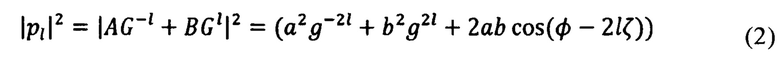
где:
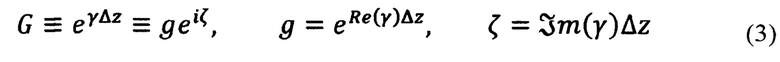
а=|А|, b=|В|, ф=arg(A) - arg(B)
и Δz - расстояние между соседними датчиками.
При N=2 имеются 5 вещественных уравнений для 5 вещественных величин: а, b, ф,  γ. Алгебраические преобразования позволяют свести эти уравнения к одному полиномиальному уравнению 8-го порядка для у=cos(2ζ). Последнее решается численно.
γ. Алгебраические преобразования позволяют свести эти уравнения к одному полиномиальному уравнению 8-го порядка для у=cos(2ζ). Последнее решается численно.
Уравнения обладают тремя дискретными симметриями:



Таким образом, во всех случаях получаются как минимум 4 решения для у из одного для у=cos(2ζ):
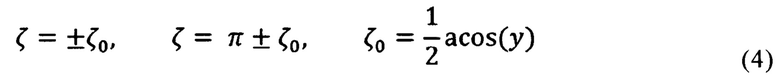
Опишем процедуру построения решения. Определяем





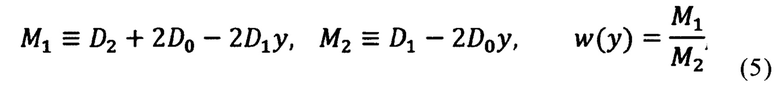
Тогда уравнение 8-го порядка на у имеет вид:


Среди его корней необходимо выбрать те, которые соответствуют условиям
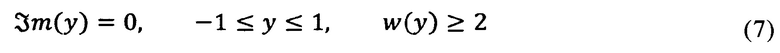
Так как аргумент передаточной функции антенны ζ восстанавливается только с точностью до дискретных симметрий (3.1-2), получаем 4 ζ из одного у. Для устранения дискретной неопределенности требуются дополнительные соображения, например, если известна оценка фазовой скорости с, можно записать

и выбрать из 4-х ζ наиболее близкий к (8).
Другие величины выражаются через у следующим образом.
Находим 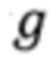 которое равно
которое равно
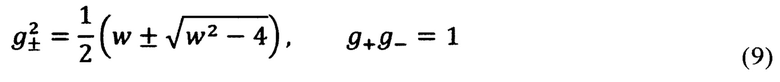
Затем находим а и b,



Последняя величина, cos(ф), равна

и она не чувствительна к неопределенности знака "±". Однако, есть еще одна простая неопределенность для получения ф,

Есть 8 различных решений на G, так как симметрии "±" по отношению к g, переводящие g в g-1, существуют наряду с "четырьмя ζ, из одного у". Есть 4 различных решения для А и В из-за симметрии "±", наряду с решением ϕ↔-ϕ. При симметрии "±" коэффициент отражения

изменяется следующим образом
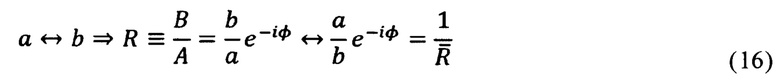
При симметрии ϕ↔-ϕ получаем

Таким образом, можно определить R с 4-кратной дискретной неопределенностью. Истинное значение R можно найти при помощи дополнительных соображений, таких, как расчеты ζ по формуле (8).
Обычно имеется больше одного корня уравнения 8-го порядка, которые отвечают необходимым ограничениям (7):
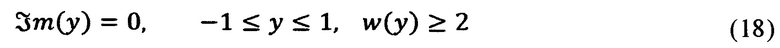
На фиг. 1 представлен график полинома 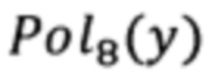 для А=1.5, В=-1+0.1i, G=1.0462+0.33992i. Крестами обозначены решения
для А=1.5, В=-1+0.1i, G=1.0462+0.33992i. Крестами обозначены решения 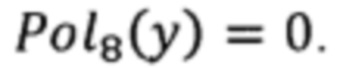 Сплошными кружками обозначено подмножество решений, выполняющих условие w(y)≥2. В квадрате показано истинное решение.
Сплошными кружками обозначено подмножество решений, выполняющих условие w(y)≥2. В квадрате показано истинное решение.
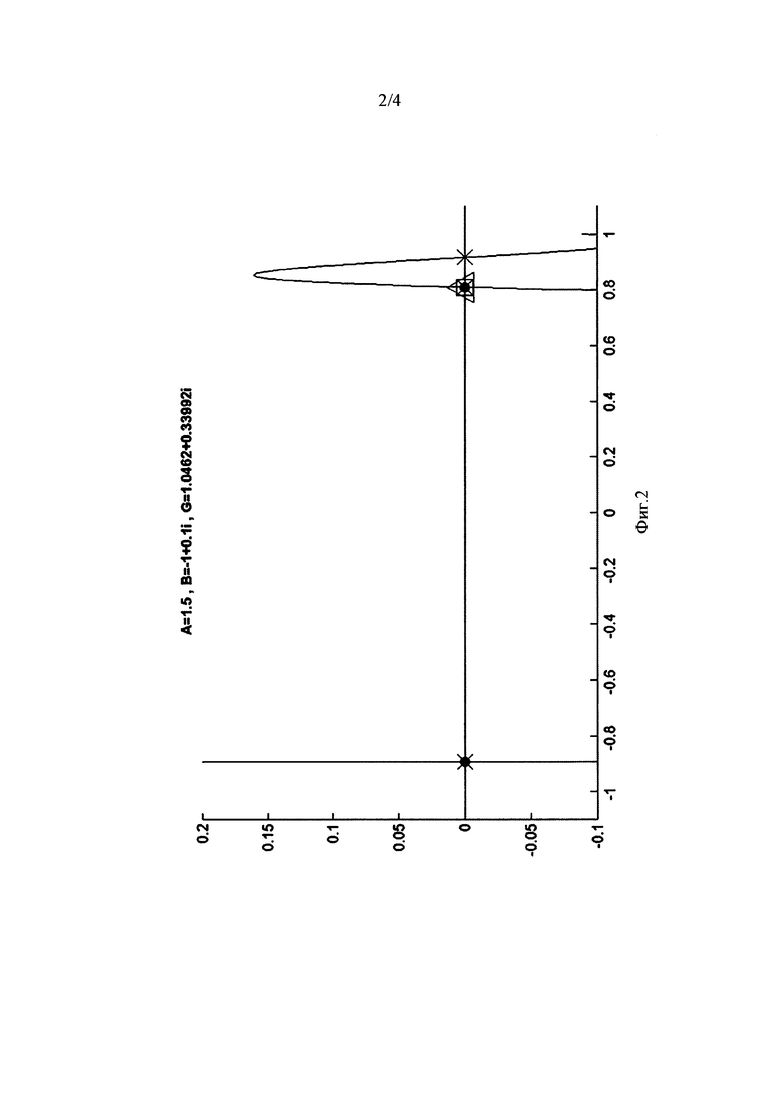
Добавление еще одного датчика позволяет устранить вышеупомянутую неопределенность и получить истинный корень для у. Покажем это на следующем примере. На Фиг. 2 представлен график полинома 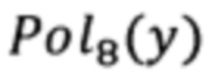 для тех же исходных данных, что и для Фиг. 1. Крестами обозначены решения
для тех же исходных данных, что и для Фиг. 1. Крестами обозначены решения 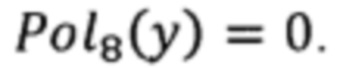 Сплошными кружками обозначено подмножество решений, выполняющих условие w(y)≥2. В квадрате показано истинное решение. Треугольником обозначено решение, остающееся при учете данных дополнительного шестого датчика.
Сплошными кружками обозначено подмножество решений, выполняющих условие w(y)≥2. В квадрате показано истинное решение. Треугольником обозначено решение, остающееся при учете данных дополнительного шестого датчика.
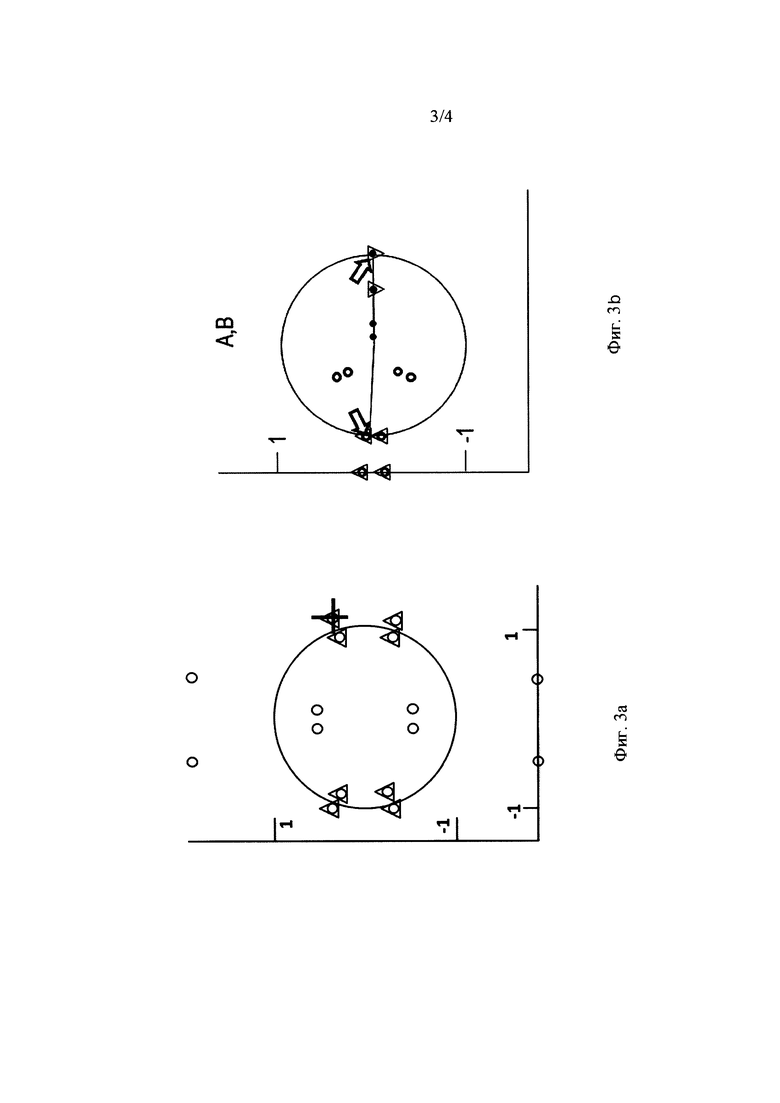
Общая структура решений показана на Фиг. 3. На Фиг. 3а показаны решения для G, а на Фиг. 3b - показаны решения для А, В. Показаны 3 набора данных: 1) G 2) А, В. Для каждого набора показано истинное решение, наряду с решениями для методов, основанных на использовании 5 сенсоров, «5s», и 6 сенсоров, «6s». График слева: G. Крест - истинное значение, круги: решения для 5 датчиков, треугольники: решения для 6 датчиков. График справа: А, В. Стрелка + линия справа: истинное А, стрелка + линия справа: истинное В, заполненные круги: А из решений для 5 датчиков, пустые круги: В из решений для 5 датчиков, треугольники, направленные вниз: А из решений для 6 датчиков, треугольники, направленные вверх: В из решений для 6 датчиков.
Решения для G разбиваются на 8-кратные множества, каждое из которых соответствует решению Р8(у)=0. Во всех случаях имеется одно решение для метода 5s или 6s, совпадающее с истинным решением, для всех величин А, В, G. Однако все 8 решений для метода 6s будут всегда соответствовать истинному значению y=cos (2γ), поэтому метод 6s является предпочтительным. Неопределенность общего временного сдвига, связанная со сдвигом начала отсчета времени истинных записей на постоянную величину, используется для задания ℑm(A)=0.
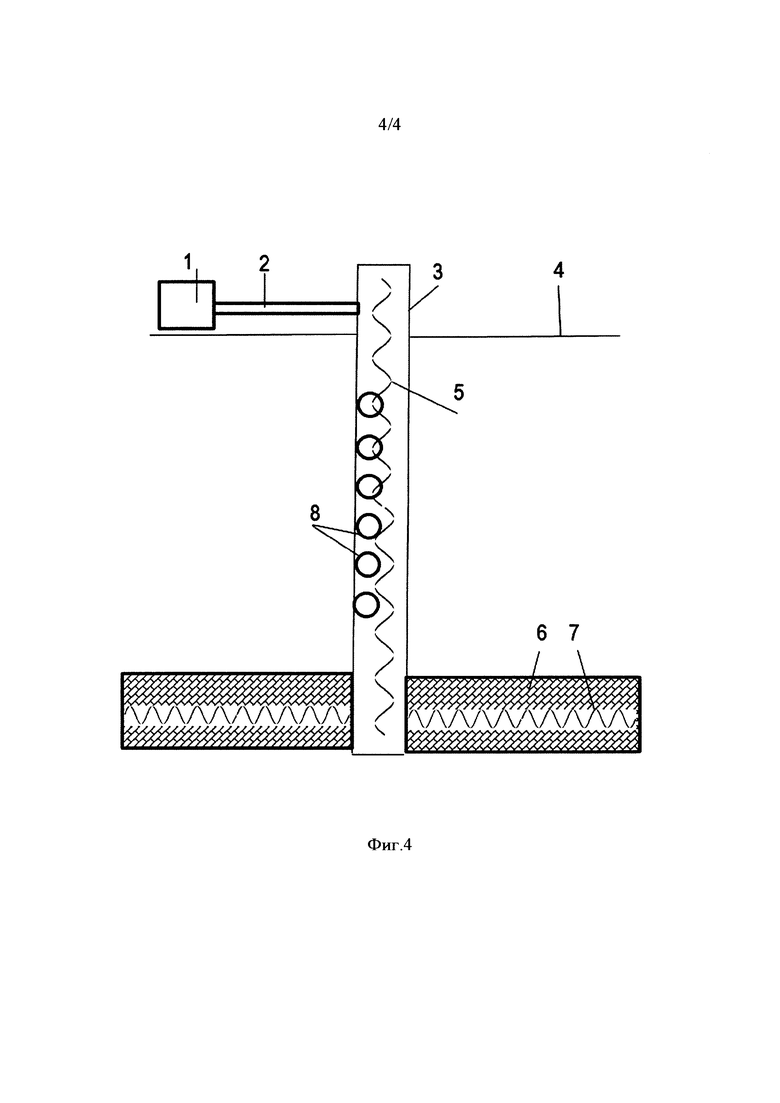
В качестве практического применения предложенного метода рассмотрим пример, приведенный на фиг. 4, где 1 - насос, 2 - труба или система труб, соединяющая насос и скважину, 3 - скважина, 4 - поверхность земли, 5 - профиль гармонической волны давления в скважине, в фиксированный момент времени и на одной из доминантных частот, 6 - пласт, 7 - профиль гармонической волны давления в пласте, в фиксированный момент времени и на одной из доминантных частот, 8 - система из шести равноудаленных датчиков. Данный пример ни в коем случае не ограничивает применение метода и приводится для иллюстрации.
Пусть имеется скважина 3, пробуренная в земле, и заполненная жидкостью, например, водой, или нефтью. Скважина 3 может сообщаться с как минимум одним проницаемым пластом 6, пересекающим ее, например нефтеносным пластом. Пусть имеется насос 1, установленный на поверхности 4, и либо закачивающий жидкость в пласт 6 посредством трубы 2, либо выкачивающим жидкость из пласта 6 через скважину 3. Как правило, насос, вне зависимости от специфики его технической реализации, создает, помимо основного квазистационароного изменения давления в скважине, периодические колебания давления в заполняющей скважину жидкости. Таким образом, скважина 3 оказывается заполненной волнами давления 7, распространяющимися в ней вверх и вниз. В скважине размещают систему 8 из шести равноудаленных датчиков давления, например высокоскоростных манометров или гидрофонов, и записываются периодические колебания давления в скважине, соответствующие работе насоса. Датчики могут записывать данные в память, а могут передавать их на поверхность сразу же после записи, если они подключены к подходящей системе передачи данных, такой, как, например, геофизический кабель. В первом случае анализ данных предполагает извлечение датчиков на поверхность и выгрузку данных в компьютер, во втором - анализ данных может происходить без извлечения датчиков из скважины. Таким образом, получают набор данных 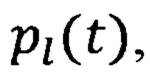 где t - время, а
где t - время, а 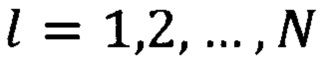 - номер датчика.
- номер датчика.
Полученные данные анализируются компьютерной программой следующим образом. Осуществляют дискретное преобразование Фурье и получают комплексные амплитуды 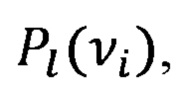 где νi - набор частот. Определяют доминантные частоты νiD, для которых модули комплексных амплитуд максимальны, для каждой из νiD решают уравнения (1), где в качестве входных данных используются
где νi - набор частот. Определяют доминантные частоты νiD, для которых модули комплексных амплитуд максимальны, для каждой из νiD решают уравнения (1), где в качестве входных данных используются 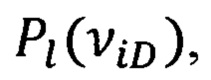 и определяют комплексные амплитуды AiD, BiD и передаточную функцию антенны GiD. GiD содержит информацию о фазовой скорости и коэффициенте затухания волн давления на доминантных частотах и, таким образом, может быть использована для определения реологии жидкости, в частности, ее сжимаемости и вязкости, в то время как отношение AiD/BiD может быть использовано для определения коэффициента продуктивности проницаемого пласта.
и определяют комплексные амплитуды AiD, BiD и передаточную функцию антенны GiD. GiD содержит информацию о фазовой скорости и коэффициенте затухания волн давления на доминантных частотах и, таким образом, может быть использована для определения реологии жидкости, в частности, ее сжимаемости и вязкости, в то время как отношение AiD/BiD может быть использовано для определения коэффициента продуктивности проницаемого пласта.
В другой модификации метода данного изобретения рассматривается та же ситуация, что описана выше, однако вместо набора из шести датчиков используется один единственный датчик, который последовательно записывает давление на шести равноудаленных глубинах. Полученные данные 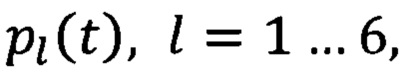 затем используются точно так же, как и в методе, описанном выше, при этом сдвиг по времени между измерениями одним датчиком на разных глубинах оказывается несущественен благодаря математической структуре метода. Единственным ограничением в данном случае является условие стабильности работы насоса и стационарности всех основных параметров скважины и пласта за все время сбора данных. Подразумевается, что предварительно была создана модель распространения волн в данной среде, в которой для каждой частоты колебаний волна представляется в виде распространяющихся в противоположные стороны нисходящей и восходящей экспоненциально затухающих гармонических волн, при этом модель зависит от комплексных амплитуд нисходящих и восходящих волн и комплексной константы распространения колебаний. Поскольку модель зависит от набора геометрических и физических параметров среды, и величины, характеризующие распространение волны являются функциями этих параметров и частоты, можно подбирать параметры среды таким образом, чтобы данные величины совпали с измеряемыми. В качестве примера можно привести распространение слабого импульса давления в заполненной жидкостью жесткой трубе постоянного диаметра, в этом случае физические параметры, определяющие фазовую скорость и коэффициент затухания на определенной частоте, это плотность, модуль объемного сжатия, вязкость, а также диаметр трубы, в то время как примером параметров, влияющих на коэффициент отражения, является отношение диаметров соседних участков трубы.
затем используются точно так же, как и в методе, описанном выше, при этом сдвиг по времени между измерениями одним датчиком на разных глубинах оказывается несущественен благодаря математической структуре метода. Единственным ограничением в данном случае является условие стабильности работы насоса и стационарности всех основных параметров скважины и пласта за все время сбора данных. Подразумевается, что предварительно была создана модель распространения волн в данной среде, в которой для каждой частоты колебаний волна представляется в виде распространяющихся в противоположные стороны нисходящей и восходящей экспоненциально затухающих гармонических волн, при этом модель зависит от комплексных амплитуд нисходящих и восходящих волн и комплексной константы распространения колебаний. Поскольку модель зависит от набора геометрических и физических параметров среды, и величины, характеризующие распространение волны являются функциями этих параметров и частоты, можно подбирать параметры среды таким образом, чтобы данные величины совпали с измеряемыми. В качестве примера можно привести распространение слабого импульса давления в заполненной жидкостью жесткой трубе постоянного диаметра, в этом случае физические параметры, определяющие фазовую скорость и коэффициент затухания на определенной частоте, это плотность, модуль объемного сжатия, вязкость, а также диаметр трубы, в то время как примером параметров, влияющих на коэффициент отражения, является отношение диаметров соседних участков трубы.
Как указано выше, полученные результаты могут быть использованы для определения физических характеристик границ однородной среды на основе интерпретации отношения комплексных амплитуд нисходящих и восходящих волн (коэффициента отражения), а также для определения физических характеристик самой среды на основе интерпретации компонент комплексной константы распространения, а именно, фазовой скорости и коэффициента затухания волны. Приведем пример.
В случае волн, распространяющихся в жесткой трубе радиуса r, заполненной вязкой жидкостью плотности ρ с фазовой скоростью объемных волн с и вязкостью η, в низкочастотном приближении выполнены следующие соотношения:
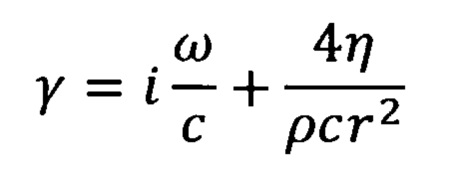
где i - мнимая единица, ω - круговая частота, а коэффициент отражения в зоне соединения труб радиусов r1 и r2
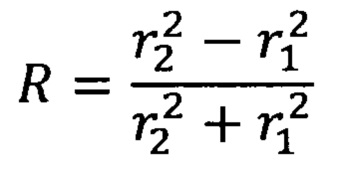
Таким образом, зная r1 и измеряя γ и R описанным выше методом, можно определить 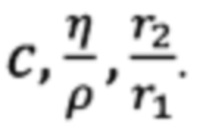
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ ОПРЕДЕЛЕНИЯ СВОЙСТВ УГЛЕВОДНОГО ПЛАСТА И ДОБЫВАЕМЫХ ФЛЮИДОВ В ПРОЦЕССЕ ДОБЫЧИ | 2012 |
|
RU2505675C1 |
| СПОСОБ И СИСТЕМА ДЛЯ МОНИТОРИНГА ЗАПОЛНЕННЫХ ЖИДКОСТЬЮ ОБЛАСТЕЙ В СРЕДЕ НА ОСНОВЕ ГРАНИЧНЫХ ВОЛН, РАСПРОСТРАНЯЮЩИХСЯ ПО ИХ ПОВЕРХНОСТЯМ | 2004 |
|
RU2327154C2 |
| СИСТЕМА И СПОСОБ ВЕРТИКАЛЬНОГО СЕЙСМИЧЕСКОГО ПРОФИЛИРОВАНИЯ С ПРЕДСТАВЛЕНИЕМ РАЗВЕДОЧНЫХ ДАННЫХ В ВИДЕ КОМБИНАЦИИ ПАРАМЕТРИЗОВАННЫХ КОМПРЕССИОННОГО, СДВИГОВОГО И ДИСПЕРСИВНОГО ВОЛНОВЫХ ПОЛЕЙ | 2012 |
|
RU2593687C2 |
| СПОСОБ ОПРЕДЕЛЕНИЯ СВОЙСТВ ПРОНИЦАЕМОГО ПЛАСТА | 2012 |
|
RU2492510C1 |
| Способ определения положения сбрасываемой цементировочной пробки в обсадной колонне | 2022 |
|
RU2805636C1 |
| ПОЛНАЯ ИНВЕРСИЯ ВОЛНОВОГО ПОЛЯ ПРИ НАЛИЧИИ ПЛОЩАДНОГО И ТОЧЕЧНОГО ИСТОЧНИКОВ | 2017 |
|
RU2706831C1 |
| СИСТЕМА МИКРОСЕЙСМИЧЕСКОГО ЗОНДИРОВАНИЯ ЗЕМНОЙ КОРЫ И ПРОВЕДЕНИЯ СЕЙСМИЧЕСКОГО МОНИТОРИНГА | 2012 |
|
RU2498357C1 |
| СПОСОБ ПРЯМОГО ПРОГНОЗА ЗАЛЕЖЕЙ УГЛЕВОДОРОДОВ | 2010 |
|
RU2454687C1 |
| Способ электрической корреляции | 1981 |
|
SU1078388A1 |
| СПОСОБ СКВАЖИННОЙ СЕЙСМОРАЗВЕДКИ | 2004 |
|
RU2302648C2 |

Изобретение относится к области геофизики и может быть использовано для определения границ однородной среды при обработке сейсмических данных. Согласно заявленному способу осуществляют регистрацию гармонической волны, представляющей собой колебание физической величины вдоль одного направления распространения в однородной среде, посредством датчиков вдоль направления распространения колебания по меньшей мере в пяти точках, расположенных на равном расстоянии друг от друга. Преобразуют выходные сигналы датчиков в соответствующие комплексные спектральные амплитуды, соответствующие частотному разложению выходных сигналов. Создают модель распространения гармонической волны в однородной среде, в которой для каждой частоты колебаний волна представляется в виде распространяющихся в противоположные стороны нисходящей и восходящей экспоненциально затухающих гармонических волн. Абсолютные величины комплексных спектральных амплитуд выходных сигналов датчиков на каждой частоте используют в качестве исходных данных для уравнений, сравнивающих абсолютные величины комплексных амплитуд с созданной моделью распространения волны. Путем решения полученных уравнений определяют полные комплексные амплитуды нисходящих и восходящих волн и комплексную константу распространения колебаний на каждой частоте и определяют характеристики границ однородной среды на основе отношения комплексных амплитуд нисходящих и восходящих волн, а характеристики однородной среды на основе фазовой скорости и коэффициента затухания волны. Технический результат – повышение точности и достоверности получаемых данных. 6 з.п. ф-лы, 4 ил.
1. Способ определения физических характеристик однородной среды и ее границ, в соответствии с которым:
- осуществляют регистрацию гармонической волны, распространяющейся в однородной среде и представляющей собой колебание физической величины вдоль одного направления распространения в однородной среде, причем регистрацию осуществляют путем регистрации указанной физической величины посредством датчиков вдоль направления распространения колебания по меньшей мере в пяти точках, расположенных на равном расстоянии друг от друга,
- посредством компьютерной системы методом спектрального анализа преобразуют выходные сигналы датчиков в соответствующие комплексные спектральные амплитуды, соответствующие частотному разложению выходных сигналов,
- создают модель распространения гармонической волны в однородной среде, в которой для каждой частоты колебаний волна представляется в виде распространяющихся в противоположные стороны нисходящей и восходящей экспоненциально затухающих гармонических волн, при этом модель зависит от комплексных амплитуд нисходящих и восходящих волн и комплексной константы распространения колебаний,
- посредством компьютерной системы абсолютные величины комплексных спектральных амплитуд выходных сигналов датчиков на каждой частоте используют в качестве исходных данных для уравнений, сравнивающих абсолютные величины комплексных амплитуд с созданной моделью распространения волны,
- путем решения полученных уравнений определяют полные комплексные амплитуды нисходящих и восходящих волн и комплексную константу распространения колебаний на каждой частоте, и
- определяют физические характеристики границ однородной среды на основе отношения комплексных амплитуд нисходящих и восходящих волн, а физические характеристики однородной среды на основе фазовой скорости и коэффициента затухания волны.
2. Способ по п. 1, в соответствии с которым колебания физической величины вдоль направления распространения создают в среде искусственным путем.
3. Способ по п. 2, в соответствии с которым однородная среда является сегментом заполненной жидкостью скважины, пробуренной в пласте, колебания физической величины создают подключенным к скважине или находящимся в ней насосом, физическими характеристиками однородной среды являются сжимаемость и вязкость заполняющей скважину жидкости, а физическими характеристиками границ однородной среды является коэффициент продуктивности пласта, примыкающего к данному сегменту.
4. Способ по п. 2, в соответствии с которым однородная среда является носителем электромагнитных волн, а колебания физической величины создают излучателем электромагнитных колебаний.
5. Способ по п. 1, в соответствии с которым преобразование выходных сигналов датчиков осуществляют при помощи дискретного преобразования Фурье.
6. Способ по п. 1, в соответствии с которым регистрацию указанной физической величины по меньшей мере в пяти точках осуществляют одновременно посредством датчиков, каждый из которых установлен в соответствующей точке.
7. Способ по п. 1, в соответствии с которым регистрацию указанной физической величины по меньшей мере в пяти точках осуществляют последовательно путем последовательного перемещения по меньшей мере одного дачика в направлении распространения колебания физической величины.
| СПОСОБ И СИСТЕМА ДЛЯ МОНИТОРИНГА ЗАПОЛНЕННЫХ ЖИДКОСТЬЮ ОБЛАСТЕЙ В СРЕДЕ НА ОСНОВЕ ГРАНИЧНЫХ ВОЛН, РАСПРОСТРАНЯЮЩИХСЯ ПО ИХ ПОВЕРХНОСТЯМ | 2004 |
|
RU2327154C2 |
| СПОСОБ ОБРАЩЕНИЯ ДЛЯ ОПРЕДЕЛЕНИЯ ДОБРОТНОСТИ ГЕОЛОГИЧЕСКОЙ СРЕДЫ | 2012 |
|
RU2579164C1 |
| US 5331604 A1 19.07.1994 | |||
| US 7376517 B2 20.05.2008 | |||
| US 20150012221 A1 08.01.2015 | |||
| WO 2013151524 A1 10.10.2013. | |||
Авторы
Даты
2020-03-18—Публикация
2016-12-01—Подача