Уровень техники изобретения
Область техники, к которой относится изобретение
Это изобретение в общем относится к области инструментов для измерений во время бурения. Более конкретно, это изобретение относится к способам обработки электромагнитных сигналов от инструмента для измерения во время бурения для моделирования и визуализации слоистых подземных формаций, окружающих инструмент.
Уровень техники
Скважины, пробуренные сквозь земные формации для добычи флюидов, таких как нефть, часто бурятся вдоль по существу горизонтальной траектории в резервуаре с целью увеличения дренажной области в резервуаре. Поскольку такие резервуары часто расположены в слоистых подземных формациях, то местоположение по существу горизонтальной скважины относительно границ слоев в земной формации часто оказывает материальный эффект на продуктивность таких скважин.
Были разработаны геонаправляющие решения для систем управления параметрами бурения, которые используют инструмент для измерения во время бурения для обеспечения в режиме реального времени предсказания и визуализации слоистой структуры подземной формации, окружающей инструмент. Такая визуализация в режиме реального времени позволяет операторам управлять направлением операций бурения скважины с целью разместить (т.е. пробурить) скважину в определенную секцию резервуара для минимизации прорыва газа или воды и максимизации рентабельной добычи из него.
Каротажные инструменты на принципе электромагнитной (ЭМ) индукции и распространения хорошо подходят для этих применений в системах управления параметрами бурения из-за их относительно большой боковой глубины исследований в подземной формации. Недавно были предложены направленные ЭМ инструменты для измерения во время бурения; см. Seydoux et al., " A Deep-Resistivity Logging-While-Drilling Device for Proactive Geosteering," The Leading Edge, Vol.23, no.6, pp 581-586, 2004; Li et al., "New Directional Electromagnetic Tool For Proactive Geosteering And Accurate Formation Evaluation While Drilling," 46th SPWLA Annual Symposium, June 26-29, 2005; и Yang et al., "Bed-Boundary Effect Removal to Aid Formation Resistivity Interpretation from LWD Propagation Measurements at All Dip Angles", SPWLA 46th Annual Logging Symposium, New Orleans, June 26-29, 2005, все включены сюда по ссылке во всей своей полноте. Такие направленные ЭМ инструменты для измерения во время бурения делают возможным различение резистивных свойств формации сверху и снизу местоположения инструмента во время бурения по существу горизонтальных или наклонных скважин. Эти инструменты для измерения во время бурения обычно оснащены как катушками с относительно коротким интервалом, чувствительными к электромагнитным свойствам слоев формации возле местоположения каротажного инструмента, так и катушками с большим интервалом, которые также чувствительны к резистивным свойствам слоев формации далеко от местоположения инструмента.
Во время бурения сквозь некоторые земные формации направленные ЭМ инструменты для измерения во время бурения являются чувствительными к свойствам формации достаточно далеко от местоположения инструмента, в то время как в других формациях инструменты чувствительны только к свойствам более близких формаций около инструмента.
Современные решения для систем управления параметрами бурения обеспечивают моделирование и визуализацию свойств формации около местоположений инструмента (см. общедоступный патент США №6594584, озаглавленный "Способ расчета расстояния между скважинным каротажным инструментом и границей формации путем инверсии обрабатываемых измерений от каротажного инструмента", включенный сюда по ссылке во всей своей полноте). Однако современные решения для систем управления параметрами бурения не обеспечивают эффективного механизма для моделирования и визуализации свойств формации на большом расстоянии от местоположений инструмента. Таким образом, в некоторых земных формациях свойства формации и границы местоположений на большом расстоянии от местоположения инструмента определяются только частично из измерений, и бывает трудно расположить (т.е. пробурить) скважину в желаемой секции резервуара, что позволило бы максимизировать рентабельность добычи без расчетов и эффективного отображения этой частичной информации.
Современные способы для отображения местоположений, в которых инвертированное удельное сопротивление является ненадежным из-за использования насыщенности цвета, были опубликованы ранее Oldenburg, et al., "Estimating depth of investigation in DC resistivity and IP Surveys," Geophysics Soc. of Expl. Geophys., Vol.64, pp 403-416, 1999, включенном сюда по ссылке во всей своей полноте. Эти способы (a) не используют неопределенности, кроме индекса "глубины исследований" (DOI), для указания того, где удельное сопротивление является неопределенным по данным и (b) применены к измерениям удельного сопротивления на поверхности. Учет неопределенности отображает частичную информацию, доступную из измерений, содержащих свойства формации на большом расстоянии от местоположений инструментов.
Более того, в некоторых случаях, земная формация может быть разведана с помощью другого средства (например, пространственной сейсморазведки) перед бурением. В таких случаях, было бы полезно провести сравнение свойств формации, визуализированных с помощью решения для системы управления параметрами бурения со свойствами формации предшествующей разведки для более информированного принятия решения относительно управления направлением буровых работ. Из-за того что современные решения для системы управления параметрами бурения не обеспечивают эффективного механизма для моделирования и визуализации свойств формации на большом расстоянии от местоположений инструмента, является затруднительным подтверждать с определенностью соответствие между текущим положением бурения и предшествующей разведкой. Это делает затруднительной эффективную интеграцию информации предшествующей разведки с информацией реального времени, генерируемой системой управления параметрами бурения, и, таким образом, ограничивает процесс принятия решения по управлению бурением.
Сущность изобретения
Следовательно, задачей изобретения является обеспечение способа для моделирования и визуализации во время бурения свойств формации в местоположениях как около инструмента, так и в местоположениях на большом расстоянии от инструмента.
Другой задачей изобретения является обеспечение способа для моделирования и визуализации во время бурения неопределенности предсказания свойств формации в местоположениях как около инструмента, так и в местоположениях на большом расстоянии от инструмента.
Дополнительной задачей изобретения является обеспечение способа для моделирования и визуализации во время бурения предсказаний свойств формации относительно следующих местоположений точке измерения таким способом, который предсказывает пространственное распределение как свойств формации, так и соответствующих им неопределенностей для следующего местоположения точки измерения на основе модели для текущего местоположения точки измерения.
В соответствии с этими задачами, которые будут подробно описаны ниже, обеспечивается компьютерный способ для моделирования и визуализации свойства подземной формации во время бурения в ней скважины. Компьютерный способ собирает множество электромагнитных сигналов, соответствующих текущему положению точки измерения инструмента для измерений во время бурения. Генерируется многослойная модель, которая соответствует множеству электромагнитных сигналов. Гистограмма, характеризующая неопределенность многослойной модели относительно значений глубины выше и ниже инструмента для измерения во время бурения, генерируется с помощью перекрывающихся частей многослойной модели. Множество значений оттенков цвета и соответствующее множество значений насыщенности генерируются на основе гистограммы. Множество значений оттенков цвета представляет предсказания свойства формации (например, удельное сопротивление) для значений глубины выше и ниже инструмента для измерения во время бурения. Множество значений насыщенности представляет неопределенности для предсказаний, из которых получены соответствующие значения оттенков цвета. Предпочтительно, значения оттенков цвета, соответствующие значениям насыщенности, получены из суммарной информации гистограммы (например, 50% кривая контура и кривая ширины). Такая суммарная информация используется в качестве индекса для карты цветов, который конвертирует суммарную информацию в соответствующие значения оттенков цветов и значения насыщенности. Генерируется и отображается экранный график. Столбцы экранного графика используют цвета для визуализации предсказаний свойства формации для значений глубины над и под инструментом для измерения во время бурения относительно следующих местоположений точки измерения. Новый столбец экранного графика генерируется для текущего местоположения точки измерения. Значения цвета нового столбца основаны на множестве значений оттенков цвета и множестве значений насыщенности, полученных из гистограммы. Уровни насыщенности значений цветов нового столбца представляют неопределенности предсказаний, из которых получены соответствующие значения цветов.
Должно быть оценено, что эта методология позволяет осуществлять улучшенные вычисления и более легкую интерпретацию неопределенностей предсказания для пользователя, особенно при описании свойств формации на большом расстоянии от местоположения точки измерения инструмента для измерения во время бурения.
Дополнительные задачи и преимущества изобретения станут очевидны специалистам в данной области техники после обращения к подробному описанию вместе с прилагающимися чертежами.
Краткое описание чертежей
Фиг.1A является блок-схемой компьютерной вычислительной системы, которая воплощает методологию настоящего изобретения.
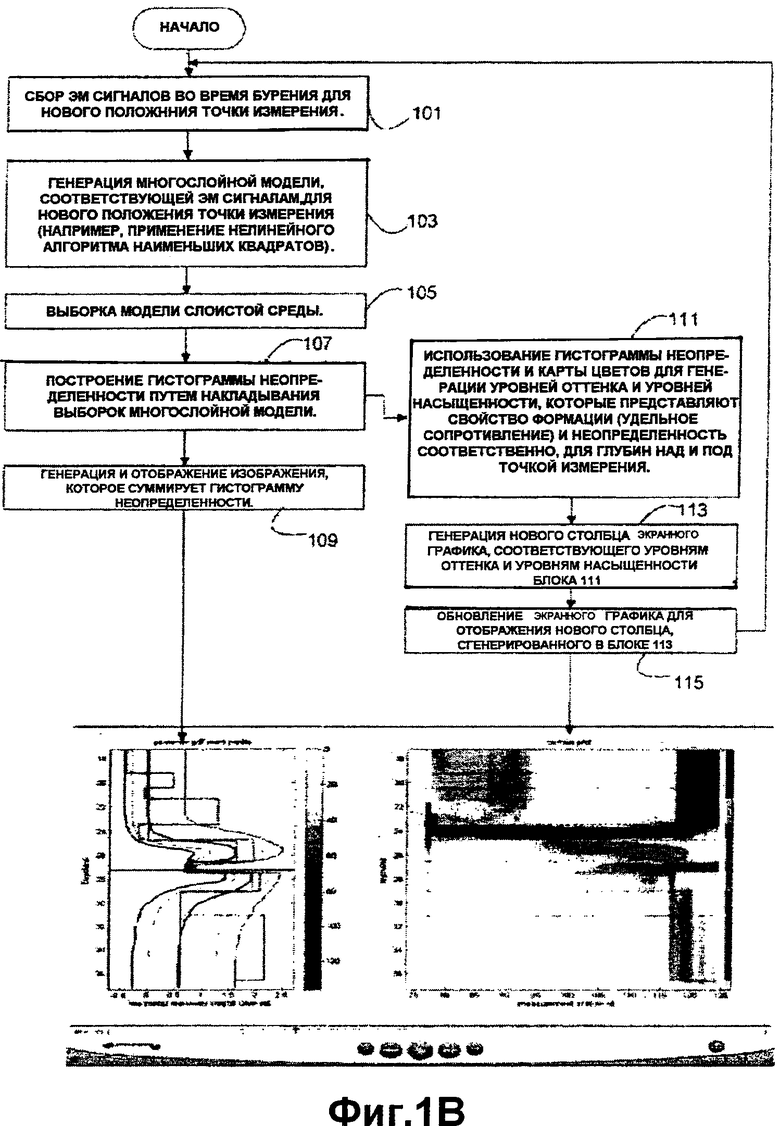
Фиг.1B является блок-схемой, иллюстрирующей последовательность процессов компьютерной методологии для моделирования и визуализации во время бурения свойств подземной формации в соответствии с настоящим изобретением.
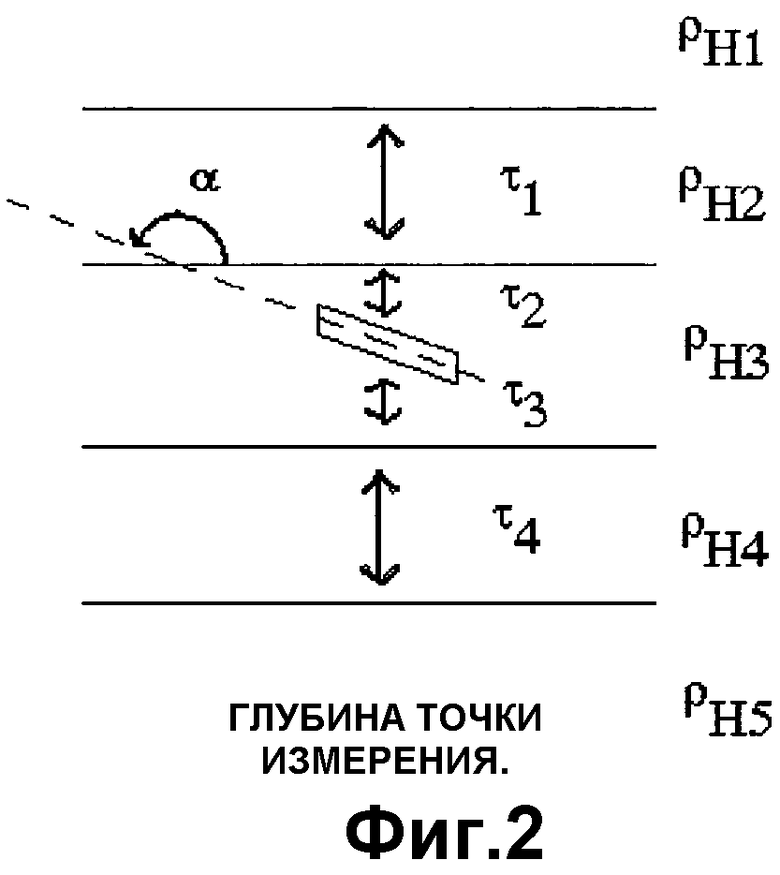
Фиг.2 является схематической иллюстрацией примерной модели в соответствии с настоящим изобретением, включающей параметры толщины слоя, свойства горизонтального удельного сопротивления слоя и параметр α относительного наклона формации.
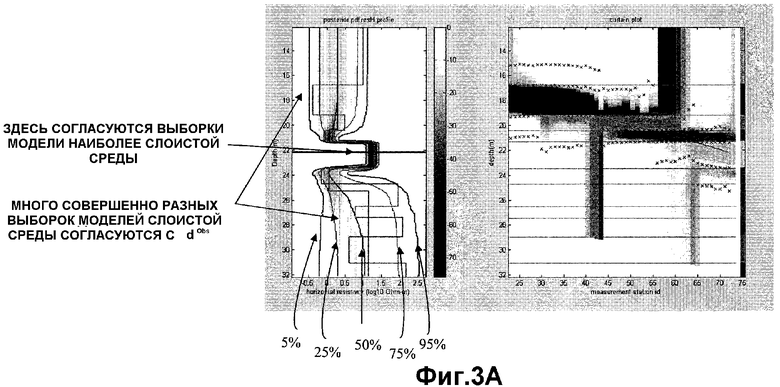
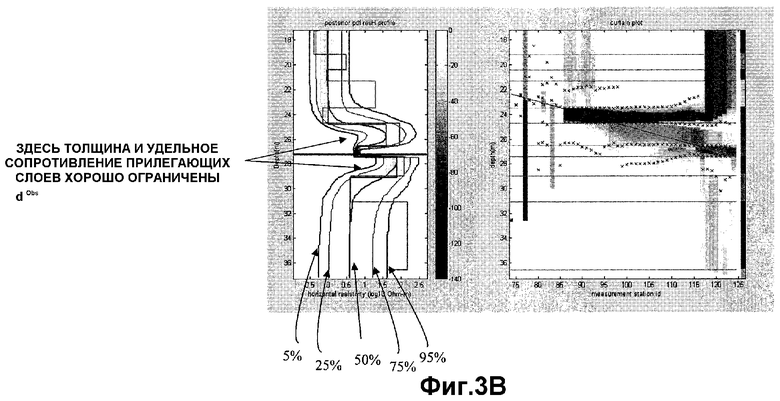
Фиг.3A и 3B иллюстрируют примерные окна отображения, сгенерированные последовательностью операций моделирования и визуализации во время бурения на Фиг.1B.
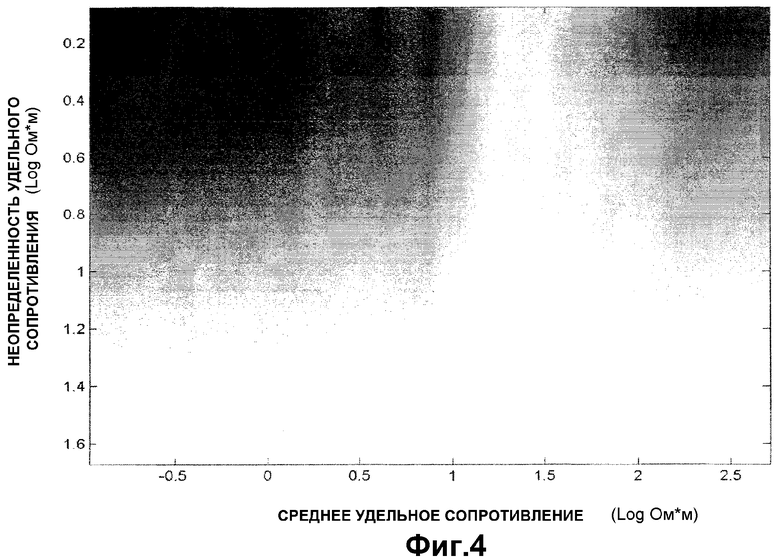
Фиг.4 является изображением примерной карты цветов, используемой в качестве части последовательности операций на Фиг.1B для конвертирования информации профиля неопределенности в новый столбец, которая добавляется в изображение экранного графика.
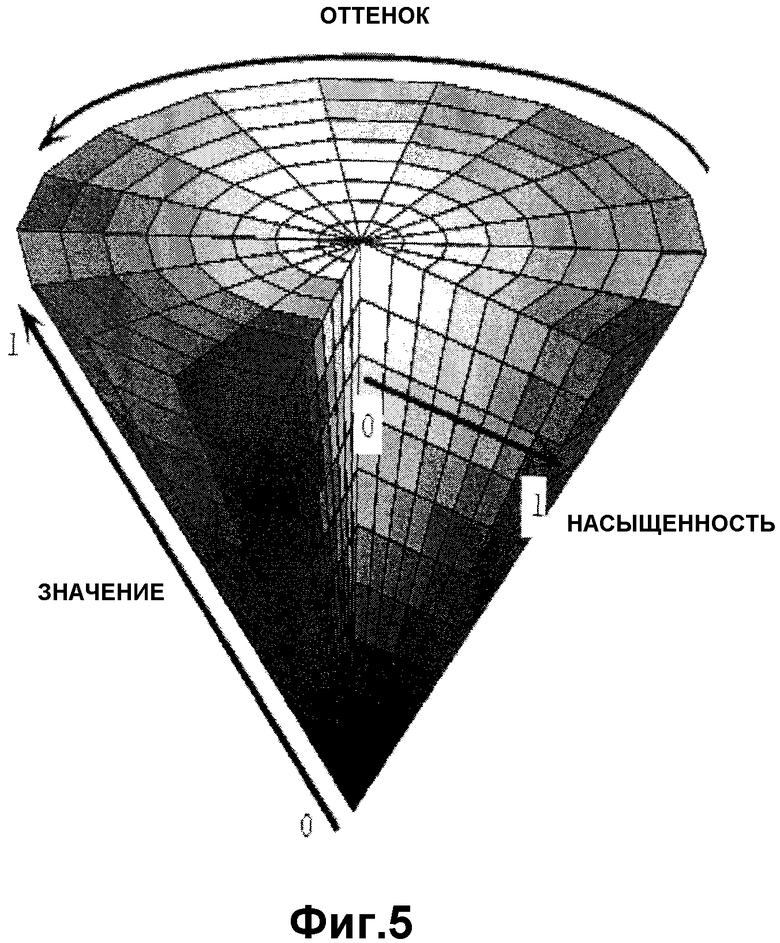
Фиг.5 является графической иллюстрацией цветового пространства HSV (ОНЯ) (оттенок-насыщенность-яркость).
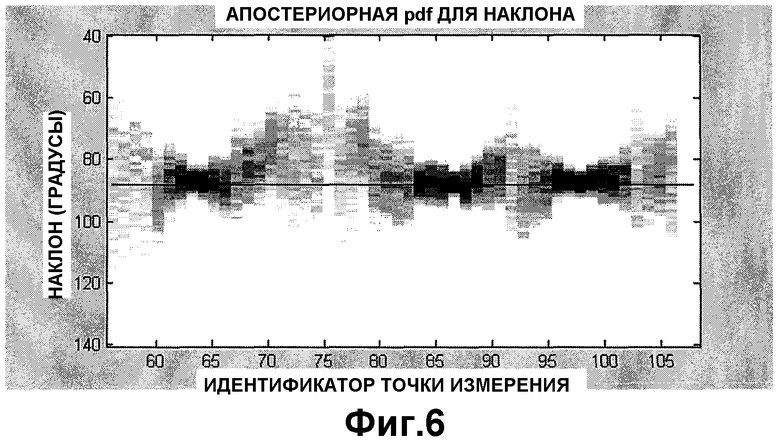
Фиг.6 является изображением, показывающим профиль параметра α наклона формации относительно множества точек измерения.
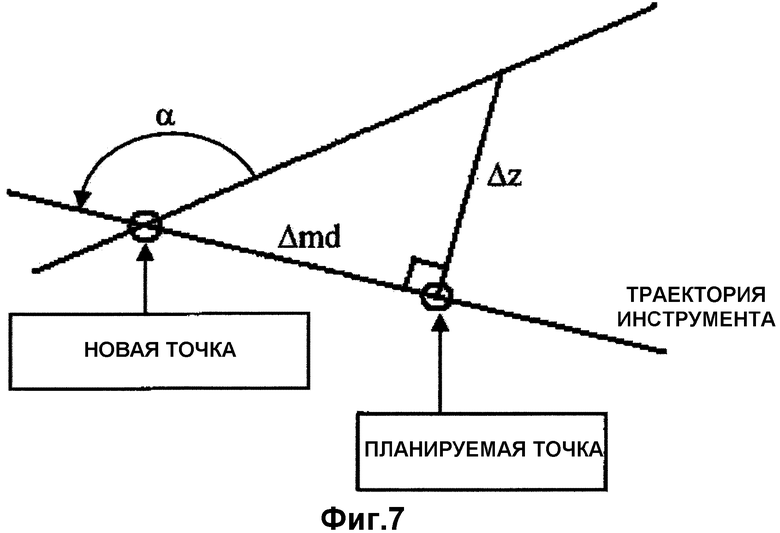
Фиг.7 является графической иллюстрацией параметра α модели наклона формации и геометрии интерполирующей текущей гистограммы удельного сопротивления формации от одной точки измерения к другой.
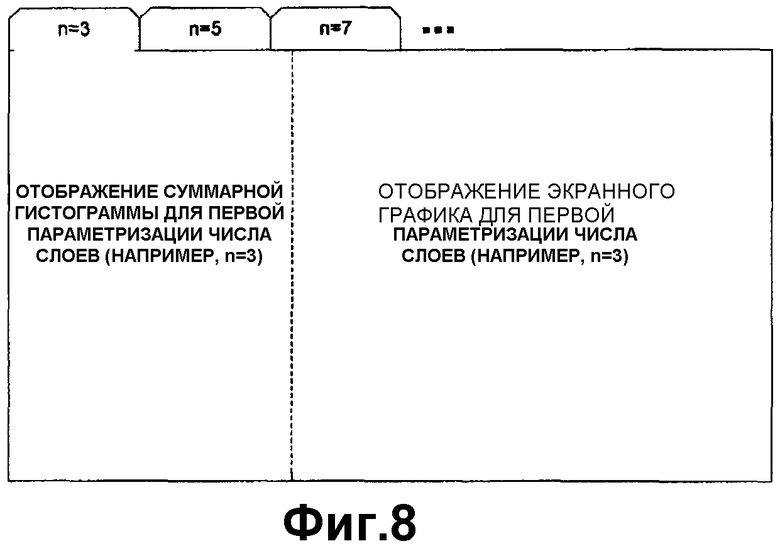
Фиг.8 является схематической иллюстрацией многооконной схемы с вкладками для отображения множества экранных графиков, отображающих изменения параметризации номера слоя.
Подробное описание предпочтительных вариантов осуществления
Фиг.1A является функциональной блок-схемой компьютерной системы 10 общего назначения, которая воплощает настоящее изобретение. Компьютерная система 10 может включать в себя рабочую станцию (или высокопроизводительный персональный компьютер), которая выполняет значимые вычисления и визуализации, как обсуждается ниже. Например, компьютерная система 10 может включать в себя устройство 12 отображения и пользовательские устройства ввода, такие как клавиатура 14 и мышь 16. Компьютерная система 10 также включает в себя память 18 (например, как постоянную память, такую как магнитный жесткий диск, так и не постоянную память, такую как один или более DRAM (динамическая память с произвольным доступом) модулей), которая хранит программные приложения, которые выполняются на процессоре 20 для выполнения значимых вычислений и визуализаций, как обсуждается ниже. Память 18 и процессор 20 могут быть реализованы с помощью однопроцессорной компьютерной системы, многопроцессорной компьютерной системы или кластера из компьютерных вычислительных систем, что является хорошо известным в области компьютерной техники. Программные приложения, хранящиеся в памяти 18, включают в себя запрограммированные последовательности инструкций и данных, которые обычно хранятся на одном или более оптических дисках и загружаются в память 18 с помощью привода оптических дисков (не показан) для постоянного в ней хранения. В качестве альтернативы, такие программные приложения могут быть загружены в память 18 через сетевое соединение (например, соединение с Интернетом) или с помощью другого подходящего средства для постоянного хранения в постоянного в ней хранения.
Фиг.1B иллюстрирует последовательность операций, которые воплощают компьютерную методологию, которая использует электромагнитные (ЭМ) сигналы от инструмента для измерения во время бурения для генерации предсказаний и визуализации в режиме реального времени, по меньшей мере, одного свойства подземной формации (например, удельного сопротивления) с количественными неопределенностями. Предсказания и визуализация в режиме реального времени обеспечивает информацию относительно свойств формации, расположенных на большом расстоянии от местоположения инструмента. Такая информация и визуализация в режиме реального времени является полезной в приложениях системы управления параметрами бурения, потому что они позволяют располагать скважину в желаемых секциях резервуара для максимизации рентабельности добычи из нее.
Методология начинается с этапа 101 сбором электромагнитных (ЭМ) сигналов, полученных от инструмента для измерения во время бурения в его новой точке измерения. В блоке 103 многослойная модель сгенерирована так, что находится в соответствии с электромагнитными (ЭМ) сигналами для новой точки измерения. В блоке 105 модель дискретизуется для получения набора моделей слоистой среды, которые приближенно согласуются с электромагнитными (ЭМ) сигналами для новой точки измерения. В предпочтительном варианте осуществления многослойная модель получается и дискретизуется с использованием нелинейного алгоритма наименьших квадратов, как описано ниже. В блоке 107 выборки модели накладываются одна на другую для построения гистограммы, которая характеризует неопределенность, по меньшей мере, в одном предсказанном свойстве формации (например, удельном сопротивлении) в местоположениях выше и ниже точки измерения. В блоке 109 изображение, которое суммирует гистограмму, генерируется и отображается как часть окна отображения (например, левая панель окна отображения на Фиг.3A или 3B). В блоке 111 применяется карта цветов для конвертирования свойства формации и информации о неопределенности, представленных гистограммой в уровни оттенка и уровни насыщенности, которые представляют, по меньшей мере, одно предсказанное свойство формации и соответствующей неопределенности для местоположения выше и ниже точки измерения. В блоке 113 уровни оттенка и уровни насыщения, сгенерированные в блоке 111, используются для генерации нового столбца экранного графика. В блоке 115 новый столбец экранного графика отображается как часть окна отображения (например, новая правая панель окна отображения на Фиг.3A или 3B). Выполнение затем возвращается обратно к блоку 101 для продолжения выполнения для измерений во время бурения для следующей точки измерения.
Основным компонентом изобретения является функция распределения вероятности (PDF), которая описывает многослойную модель свойств формации в каждой точке измерения или сегменте точек измерений вдоль траектории скважины. Эта многослойная модель проиллюстрирована на Фиг.2. Параметры многослойной модели m состоят из:
a. горизонтального и вертикального удельного сопротивления (p) слоев;
b. вертикальных глубин/толщин (r) границ слоя; и
c. относительного наклона (a) формации относительно оси измерительного устройства.
Количество слоев в модели может быть задано пользователем или программное обеспечение может оптимизировать количество слоев для модели в каждой точке измерения, как более детально описано ниже. В представленных здесь примерах модель использует 5 слоев и, таким образом, простирается на большое расстояние от местоположения инструмента, что станет очевидным из нижеследующего описания.
Параметры многослойной модели определяются на основе электромагнитных измерений, полученных в текущей точке измерения (или, возможно, из нового сегмента точек измерений). Электромагнитные измерения состоят из амплитуды и фазы измеренных электромагнитных сигналов, записанных с использованием множества приемников и передатчиков, на различных рабочих частотах и расстояниях между катушками. Эти измерения обозначены dObs. В предпочтительном варианте осуществления измерения dObs получены в режиме реального времени от направленного инструмента для измерения во время бурения распространительного типа, который способен к различению свойств формации над и под местоположением инструмента, как описывалось выше.
Основная представляющая интерес функция является апостериорной PDF неопределенных параметров модели относительно измерений dObs. Это PDF может быть записано с использованием правила Байеса.
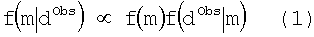
где предыдущая PDF f(m) определена на основе того, что известно об m независимо от данных измерений dObs и обычно описывается физически приемлемыми границами для параметров модели.
Вероятностная функция f(dObs|m) измеряет, насколько вероятными являются полученные значения данных для заданного значения параметров многослойной модели m. Из предшествующего уровня техники известно много способов вычисления этого апостериорного распределения. Предпочтительный вариант осуществления изобретения использует нелинейный алгоритм наименьших квадратов, как описано ниже, для получения апостериорного среднего m и ковариационной матрицы 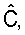 которая может быть использована для определения нормального распределения
которая может быть использована для определения нормального распределения 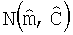 , которое аппроксимирует апостериорное распределение f(m|dObs). Могут быть использованы дополнительные способы, когда нелинейный алгоритм наименьших квадратов не сходится. Такие дополнительные способы включают в себя метод выборки цепи Маркова-Монте-Карло, как описано ниже.
, которое аппроксимирует апостериорное распределение f(m|dObs). Могут быть использованы дополнительные способы, когда нелинейный алгоритм наименьших квадратов не сходится. Такие дополнительные способы включают в себя метод выборки цепи Маркова-Монте-Карло, как описано ниже.
Путем выборки из этого нормального распределения 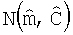 (блок 105) можно получить набор моделей слоистой среды, которые приблизительно согласуются с измерениями dObs. Путем наложения большого количества таких выборок (блок 107) генерируется профиль неопределенности предсказанного удельного сопротивления формации выше и ниже точки измерения. В общем, около точки измерения по вертикальной глубине многие из профилей удельного сопротивления будут относительно похожими, и будет существовать небольшая определенность в изображении профиля неопределенности. На большом расстоянии от точки измерения по вертикальной глубине измерения обычно обеспечивают только неопределенные ограничения, и имеются большие вариации в моделях удельного сопротивления слоистой среды. В этих удаленных регионах неопределенность в профилях удельного сопротивления будет большой. Эта изменчивость неопределенности в профилях удельного сопротивления зависит как от реальных удельных сопротивлений формации, так и расстояний, частот и других характеристик измерительного устройства. В предпочтительном варианте осуществления профиль неопределенности является набором контурных кривых (например, 5%, 25%, 50%, 75%, 95% контуры) гистограммы предсказаний горизонтального удельного сопротивления, которые выбираются из многослойной модели. Изображения таких профилей неопределенности для двух примерных множеств данных отображены в левой панели окна отображения на Фиг.3A и 3B соответственно.
(блок 105) можно получить набор моделей слоистой среды, которые приблизительно согласуются с измерениями dObs. Путем наложения большого количества таких выборок (блок 107) генерируется профиль неопределенности предсказанного удельного сопротивления формации выше и ниже точки измерения. В общем, около точки измерения по вертикальной глубине многие из профилей удельного сопротивления будут относительно похожими, и будет существовать небольшая определенность в изображении профиля неопределенности. На большом расстоянии от точки измерения по вертикальной глубине измерения обычно обеспечивают только неопределенные ограничения, и имеются большие вариации в моделях удельного сопротивления слоистой среды. В этих удаленных регионах неопределенность в профилях удельного сопротивления будет большой. Эта изменчивость неопределенности в профилях удельного сопротивления зависит как от реальных удельных сопротивлений формации, так и расстояний, частот и других характеристик измерительного устройства. В предпочтительном варианте осуществления профиль неопределенности является набором контурных кривых (например, 5%, 25%, 50%, 75%, 95% контуры) гистограммы предсказаний горизонтального удельного сопротивления, которые выбираются из многослойной модели. Изображения таких профилей неопределенности для двух примерных множеств данных отображены в левой панели окна отображения на Фиг.3A и 3B соответственно.
Следует отметить, что левая панель окна на Фиг.3A показывает изображение профиля неопределенности, где большинство моделей слоистой среды имеет относительно похожий профиль около глубины точки измерения (отмеченный горизонтальной красной линией). Однако имеется относительно большая вариация в описании соседних слоев на глубинах, сильно удаленных от точки измерения. Измерения в основном ограничивают толщину и удельные сопротивления слоя, содержащего измерительное устройство, и удельное сопротивление слоев над и под измерительным устройством, в то время как о толщине прилегающих слоев является доступной только неопределенная информация. Эта большая вариация в удельном сопротивлении формации на большом расстоянии от измерительного устройства является по существу неопределенностью предшествующего распределения, так что это изображение профиля апостериорной неопределенности показывает, где измерения ограничивают удельное сопротивление формации относительно предшествующего распределения.
В отличие от этого, левая панель окна отображения на Фиг.3B показывает профиль неопределенности, где многие из моделей слоистой среды имеют прилегающие слои, чьи толщина и удельные сопротивления хорошо ограничены измерениями. Другими словами, имеется относительно маленькая вариация в описании прилегающих слоев на глубинах, сильно удаленных от точки измерения.
Следует отметить, что, несмотря на то что и в Фиг.3A и 3B используется пятислойная модель, гистограммы выбранных моделей слоистой среды из апостериорного распределения ясно показывают глубину разведки и разрешение измерительного устройства для двух соответствующих множеств данных.
Профиль неопределенности для предсказанного удельного сопротивления формации выше и ниже точки измерения может быть суммирован, и такая суммарная информация включается в виде последнего столбца в специально построенный экранный график (блоки 111-115). Экранный график суммирует и предсказанное удельное сопротивление формации, и соответствующую ему неопределенность для всех доступных точек измерений. В предпочтительном варианте осуществления изобретения новый столбец для экранного графика строится путем первого извлечения 50% кривой контура и кривой ширины из профиля неопределенности. Кривая ширины определяется как половина разности между 95 и 5 процентильными кривыми профиля неопределенности. Извлеченная 50% кривая контура и кривая ширины оцифровываются в два вектора, чьи элементы соответствуют значениям вертикальной глубины. Карта цветов применяется для конвертирования элементов двух векторов во множество соответствующих уровней оттенков и уровней насыщенности (блок 111). Значения цвета для нового столбца на экранном графике генерируются с использованием этих уровней оттенка и уровней насыщенности (блок 113), и новая колонка добавляется к отображению экранного графика (блок 115). Следует отметить, что оттенок на отображении экранного графика передает локализованную информацию об удельном сопротивлении, в то время как уровень насыщенности отображения экранного графика передает неопределенность соответствующей локализованной информации об удельном сопротивлении. Таким образом, уровни насыщенности цветов на экранном графике предоставляют информацию, такую как неопределенность предсказаний удельного сопротивления формации, где предсказания удельного сопротивления с более высокой определенностью имеют более высокие уровни насыщенности по сравнению с предсказаниями удельного сопротивления формации с меньшей определенностью.
Цветовая карта является двумерным массивом, где каждый элемент массива содержит данные, которые представляют конкретный оттенок и конкретное насыщение. В предпочтительном варианте осуществления каждый элемент массива содержит триплет в соответствии с хорошо известным цветовым пространством HSV, состоящий из значения оттенка, значения насыщенности и значения яркости (Фиг.5). Эти три значения определяют конкретный оттенок и конкретное насыщение. Также может быть использовано RGB пространство цветов. Элементы карты цветов расположены таким образом, что оттенки, определяемые элементами, являются постоянными для заданного столбца массива и изменяются по заданной строке массива. Точно так же, уровни насыщения, определенные элементами массива, являются постоянными для заданной строки и изменяются по заданному столбцу массива. Примерная карта цветов показана на Фиг.4. Для заданного значения реальной глубины значение 50% кривой контура (которая соответствует среднему предсказанному горизонтальному удельному сопротивлению) определяет индекс столбца (оттенок) в карте цветов, в то время как значение контура ширины на той же глубине определяет индекс строки (насыщенность) в карте цветов. Пара индексов столбца и строки указывает на элемент в таблице цветов, который определяет конкретный оттенок и конкретную насыщенность. Таким образом, оттенок элемента соответствует среднему предсказанному горизонтальному удельному сопротивлению профиля неопределенности и насыщенность элемента соответствует ширине профиля неопределенности. Значение цвета, определенное элементом, используется в заданной точке на реальной глубине в последнем столбце экранного графика. Результатом кодирования карты цветов является создание столбца на изображении экранного графика, где более насыщенные цвета описывают, где удельные сопротивления формации являются лучше определенными (большая определенность) и где более размытые цвета (менее насыщенные цвета) показывают, где удельное сопротивление формации является хуже ограниченным измерениями (меньшая определенность).
Следует отметить, что верхняя граница для оси неопределенности карты цветов (вертикальная ось) определяется из предшествующего распределения, так что когда измерения ограничивают удельное сопротивление относительно предшествующего, насыщенность назначенного цвета является большей. Это позволяет визуализации неопределенности быть относительно свободной от эффектов выбора предшествующего распределения.
Экранный график обеспечивает практическое средство для улучшения решений для систем управления параметрами бурения и оценки формации во время бурения путем указания значений удельного сопротивления формации выше и ниже глубины точки измерения и путем описания неопределенности этих предсказаний удельного сопротивления.
В предпочтительном варианте осуществления изобретения модель удельного сопротивления слоистой среды параметризируется с использованием толщины слоя (вместо реальных вертикальных глубин) границ слоя. Нелинейный алгоритм наименьших квадратов является обычно более устойчивым при таком выборе параметризации модели. Также начальное предположение для итеративной нелинейной процедуры наименьших квадратов обычно дается с помощью апостериорного среднего, вычисленного на предшествующей точке измерения. Эта операция является по существу приложением фильтра Кальмана и выгодно предоставляет эффективное и стабильное средство для конвертирования апостериорной модельной PDF от одной точки измерения к другой.
Параметризация модели
В предпочтительном варианте осуществления настоящего изобретения модель удельного сопротивления параметризируется с n слоями, как показано на Фиг.2, следующим образом. Сначала логарифм горизонтальных удельных сопротивлений параметризируется:
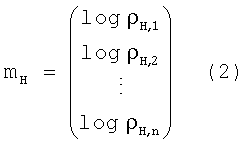
Параметризация логарифма горизонтальных удельных сопротивлений гарантирует, что эти величины будут всегда положительными.
Далее, вертикальные удельные сопротивления слоев параметризируются с использованием логарифма отношения вертикального удельного сопротивления к горизонтальному:
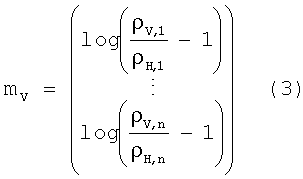
Использование этой параметризации гарантирует, что отношение вертикального удельного сопротивления к горизонтальному удельному сопротивлению (отношение, называемое анизотропией) является больше 1 и тем самым делает результаты моделирования физически более реалистичными. Также может быть использована альтернативная параметризация для вертикального удельного сопротивления, использующая то же анизотропное отношение, a, для каждого слоя.

В этом случае вертикальные удельные сопротивления слоев модели моделируются как
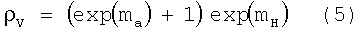
так что опять вертикальное удельное сопротивление ограничено снизу горизонтальным удельным сопротивлением. Использование анизотропного отношения уменьшает размер модели и может сделать процедуру выборки Монте-Карло более эффективной.
Далее, позиции слоя параметризируются относительно вертикальной высоты измерительного устройства, tvd(l), где l является индексом текущей точки измерения.
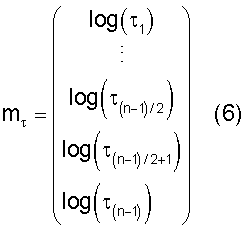
Здесь τk является толщиной kго слоя, за исключением выражений τ(n-1)/2 и τ(n-q)/2-1, которые описывают расстояние между измерительным устройством и двумя внутренними границами слоя.
Модель параметризации при использовании нелинейного алгоритма наименьших квадратов описывается с помощью
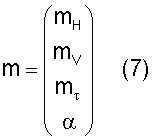
где α является относительным наклоном между осью инструмента и локальной слоистостью формации.
Нелинейный алгоритм наименьших квадратов
Нелинейный алгоритм наименьших квадратов является итеративным методом, который производит последовательность векторов 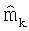 модели, которые сходятся к апостериорному среднему
модели, которые сходятся к апостериорному среднему 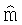 функции распределения вероятности (PDF) f(m|dObs). Нелинейный алгоритм наименьших квадратов подробно описан в Tarantola et al., "Generalized Nonlinear Inverse Problems Solved using the Least Squares Criterion," Reviews of Geophysics and Space Physics, Vol.20, No.2, pp.219-232, 1982, который включен сюда по ссылке во всей своей полноте. Нелинейный метод наименьших квадратов включает в себя:
функции распределения вероятности (PDF) f(m|dObs). Нелинейный алгоритм наименьших квадратов подробно описан в Tarantola et al., "Generalized Nonlinear Inverse Problems Solved using the Least Squares Criterion," Reviews of Geophysics and Space Physics, Vol.20, No.2, pp.219-232, 1982, который включен сюда по ссылке во всей своей полноте. Нелинейный метод наименьших квадратов включает в себя:
(1) способ вычисления предсказанного отклика dk Pred измерительного инструмента для последовательности векторов 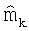 модели, где dk Pred=g(
модели, где dk Pred=g(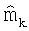 ); предсказанный отклик dk Pred рассчитывается с использованием методологии опережающего моделирования на пространственном распределении электрических и магнитных полей, которые генерируются передатчиками измерительного устройства; в предпочтительном варианте изобретения такое опережающее моделирование основывается на преобразовании Фурье-Хенкеля для анизотропной слоистой среды; также могут быть использованы и другие методологии моделирования;
); предсказанный отклик dk Pred рассчитывается с использованием методологии опережающего моделирования на пространственном распределении электрических и магнитных полей, которые генерируются передатчиками измерительного устройства; в предпочтительном варианте изобретения такое опережающее моделирование основывается на преобразовании Фурье-Хенкеля для анизотропной слоистой среды; также могут быть использованы и другие методологии моделирования;
(2) способ для вычисления чувствительностей измерительного отклика относительно изменений в заданной модели слоистой среды m, которая задается матрицей Якоби частных производных
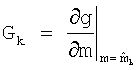 .
.
Предпочтительно, что конечно-разностное приближение используется для вычисления матрицы Gk чувствительностей, как описано в Bjorck et al., "Numerical Methods", Prentice-Hall, Inc, Englewood Cliffs, New Jersey, 1974;
(3) определение функции F(m) предшествующего распределения в уравнении 1 выше; и
(4) оценка ошибок измерений в модели слоистой среды m (например, dObs-g(m)).
Функция f(m) предшествующего распределения определяется на основании того, что известно о модели слоистой среды m независимо от данных измерений dObs и обычно описывает физически приемлемые границы для параметров модели. Предпочтительно функция f(m) предшествующего распределения определяется как нормальная случайная переменная 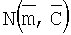 , где
, где 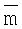 является предшествующим средним вектором и
является предшествующим средним вектором и 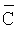 является предшествующей ковариантной матрицей следующего вида.
является предшествующей ковариантной матрицей следующего вида.
Первое, элементы предшествующего среднего вектора 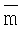 , относящиеся к горизонтальным удельным сопротивлениям модели слоистой среды, определяются следующим образом:
, относящиеся к горизонтальным удельным сопротивлениям модели слоистой среды, определяются следующим образом:
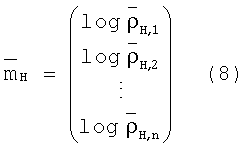
Обычными значениями для предшествующего среднего горизонтального сопротивления являются 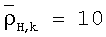 Ом·м для всех слоев k.
Ом·м для всех слоев k.
Далее, элементы предшествующего среднего вектора, относящиеся к вертикальным удельным сопротивлениям модели слоистой среды, определяются следующим образом:
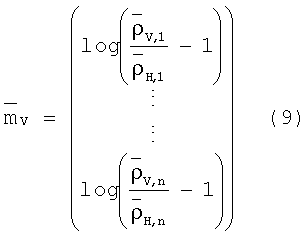
Обычными значениями для предшествующего среднего горизонтального сопротивления являются 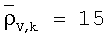 Ом·м для всех слоев k.
Ом·м для всех слоев k.
Далее, элементы предшествующего среднего вектора 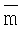 , относящиеся к толщинам модели слоистой среды, определяются следующим образом:
, относящиеся к толщинам модели слоистой среды, определяются следующим образом:
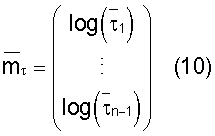
Обычные значения для 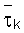 задаются:
задаются:
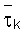 =(полная толщина модели)/(количество слоев), (11)
=(полная толщина модели)/(количество слоев), (11)
где «полная толщина модели» означает двойную ожидаемую глубину разведки измерительного устройства и обычно равно максимальному расстоянию между катушками измерительного устройства.
И наконец, элементы предшествующего среднего вектора, относящиеся к параметру α наклона, обычно устанавливаются как наклон 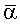 инструмента относительно поверхности земли и обеспечиваются измерениями во время бурения.
инструмента относительно поверхности земли и обеспечиваются измерениями во время бурения.
Таким образом, предшествующий средний вектор 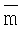 модели слоистой среды описывается
модели слоистой среды описывается
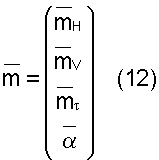
Предшествующая ковариационная матрица 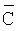 является диагональной матрицей, чьи элементы задаются предшествующими расхождениями для параметров модели. Эти предшествующие расхождения описывают диапазон физически приемлемых значений для удельного сопротивления, толщины слоя и наклона. Значения предшествующей ковариационной матрицы
является диагональной матрицей, чьи элементы задаются предшествующими расхождениями для параметров модели. Эти предшествующие расхождения описывают диапазон физически приемлемых значений для удельного сопротивления, толщины слоя и наклона. Значения предшествующей ковариационной матрицы 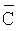 описываются ниже начиная с левого верхнего угла и заканчивая правым нижним. Первый (левый верхний) блок значений является расхождениями параметров горизонтального удельного сопротивления, заданными уравнением (2),
описываются ниже начиная с левого верхнего угла и заканчивая правым нижним. Первый (левый верхний) блок значений является расхождениями параметров горизонтального удельного сопротивления, заданными уравнением (2), 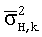 ,
, 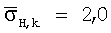 для всех k. Следующий блок элементов соответствует расхождениям для логарифма отношения вертикального удельного сопротивления к горизонтальному, как описывается в уравнении (3),
для всех k. Следующий блок элементов соответствует расхождениям для логарифма отношения вертикального удельного сопротивления к горизонтальному, как описывается в уравнении (3), 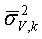 ,
, 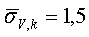 для всех k. Следующий блок элементов соответствует расхождениям для логарифма параметров толщины слоя модели, описанным в уравнении (6),
для всех k. Следующий блок элементов соответствует расхождениям для логарифма параметров толщины слоя модели, описанным в уравнении (6), 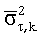 ,
, 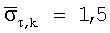 для всех k. В заключение, последний (левый нижний) элемент является расхождением параметра
для всех k. В заключение, последний (левый нижний) элемент является расхождением параметра 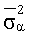 наклона, где
наклона, где 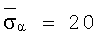 для всех k.
для всех k.
Предшествующая функция распределения вероятности f(m), описанная в уравнении (1), задается как:
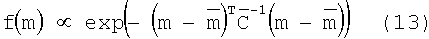
И, наконец, ошибки измерений в модели слоистой среды оцениваются разностью между наблюдениями dObs и данными, предсказанными для заданного значения параметра вектора m. Здесь допускается, что эти ошибки являются нормально распределенными и могут, таким образом, быть описаны нормальной случайной переменной со средним 0 и ковариационной матрицей Cε, которая является диагональной матрицей, чьи элементы описывают ожидаемое расхождение в предсказанных измерениях. Обычные значения элементов этой матрицы зависят от типа катушки, расстояния между катушками, частоты измерения и так далее. С этими допущениями относительно ошибок измерения вероятностная функция в уравнении (1) выглядит как
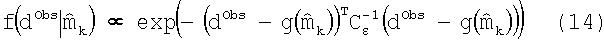
С элементами (1)-(4) как описано выше, реализация нелинейного алгоритма наименьших квадратов задается как

Когда алгоритм сходится, апостериорная PDF f(m|dObs) уравнения 1 может быть аппроксимирована нормальной случайной переменной 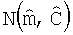 с апостериорным средним
с апостериорным средним 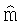 и ковариационной матрицей
и ковариационной матрицей 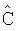 , вычисленной во время последней итерации алгоритма. Начальное предположение для нелинейного алгоритма наименьших квадратов
, вычисленной во время последней итерации алгоритма. Начальное предположение для нелинейного алгоритма наименьших квадратов 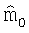 может быть предшествующим средним
может быть предшествующим средним 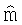 или апостериорным средним
или апостериорным средним 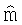 , вычисленным во время нового успешного запуска нелинейного алгоритма наименьших квадратов. Использование апостериорного среднего из предшествующей точки измерения эквивалентно использованию фильтра Кальмана для конвертирования апостериорной модельной PDF в одной точке измерения в PDF в следующей точке измерения. Фильтр Кальмана описывается в Welch et al., "An Introduction to the Kalman Filter, " Technical Report TR 95-041, Department of Computer Science, University of North Carolina at Chapel Hill, 2002, доступном по адресу Интернет http://www.cs.unc.edu/welch и включенном сюда по ссылке во всей своей полноте.
, вычисленным во время нового успешного запуска нелинейного алгоритма наименьших квадратов. Использование апостериорного среднего из предшествующей точки измерения эквивалентно использованию фильтра Кальмана для конвертирования апостериорной модельной PDF в одной точке измерения в PDF в следующей точке измерения. Фильтр Кальмана описывается в Welch et al., "An Introduction to the Kalman Filter, " Technical Report TR 95-041, Department of Computer Science, University of North Carolina at Chapel Hill, 2002, доступном по адресу Интернет http://www.cs.unc.edu/welch и включенном сюда по ссылке во всей своей полноте.
В предпочтительном варианте осуществления алгоритм наименьших квадратов выполняется до тех пор, пока ошибки предсказанных измерений являются относительно меленькими (например, меньше 1,0), как измеряется с помощью следующего логарифма вероятностной функции:
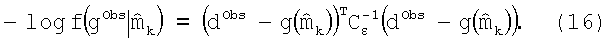
Алгоритм наименьших квадратов также останавливается, когда не может сойтись (например, по окончании 25-й итерации и когда логарифм вероятности больше, чем 100).
Визуализация апостериорной функции распределения вероятности
а. Гистограмма моделей слоистой среды
Для описания и визуализации неопределенности набора моделей слоистой среды, описанных с помощью апостериорной PDF f(m|dObs), выборки из этого распределения складываются в двумерную гистограмму. Первым этапом в построении гистограммы является собирание вместе выборок из f(m|dObs). Когда нелинейный алгоритм наименьших квадратов успешно выдает нормальную PDF 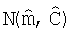 , большое количество выборок набираются из
, большое количество выборок набираются из 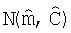 для гистограммы следующим образом:
для гистограммы следующим образом:
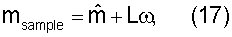
где L является разложением Холецкого апостериорной ковариационной матрицы 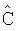 и ω является вектором идентично и независимо распределенных выборок из стандартной нормальной случайной переменной.
и ω является вектором идентично и независимо распределенных выборок из стандартной нормальной случайной переменной.
Эти выборки соответствуют набору моделей слоистой среды.
Вторым этапом в построении гистограммы является подготовка матрицы H гистограммы, которая обеспечивает профиль неопределенности набора моделей слоистой среды. В предпочтительном варианте осуществления горизонтальная ось матрицы H гистограммы будет описывать горизонтальное удельное сопротивление слоев, в то время как вертикальная ось будет описывать реальную вертикальную глубину слоев. Относительная степень детализации матрицы H гистограммы определяется количеством строк и столбцов в матрице H гистограммы, N и M, которые обычно равны 500 и 200 соответственно, и физическими размерами осей гистограммы. Физические границы горизонтальной оси гистограммы определяются ρMIN и ρMAX, которые описывают наименьшее и наибольшее удельные сопротивления слоя, ожидаемые как результат процесса выборки. Обычные значения для этих параметров являются ρMIN=0.1 Ом·м и ρMAX=500 Ом·м. Физические границы вертикальной оси гистограммы задаются величиной histogramHeight, которая определяет вертикальный размер гистограммы в единицах реальной вертикальной глубины. Типичное значение величины histogramHeight является большим, чем удвоенная полная толщина модели, определенная в предыдущем разделе.
Координаты для отдельных столбцов (j) гистограммы вводятся сначала определением их физического размера:
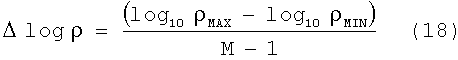
и затем определением горизонтальных координат отдельных ячеек сетки гистограммы:
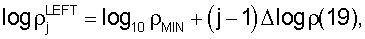
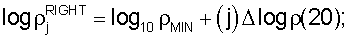
Координаты для отдельных строк (i) гистограммы вводятся сначала определением их физического размера Δd:
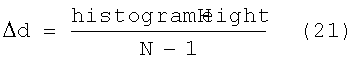
и затем определением вертикальных координат отдельных ячеек сетки гистограммы:
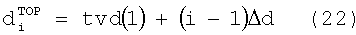
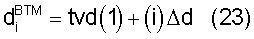
где tvd(1) является реальной вертикальной глубиной инструмента в первой точке измерения, i является целым случайным от 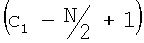 до
до 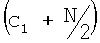 , и cl является индексом ячейки гистограммы, ассоциированной с реальной вертикальной глубиной текущей точки измерения (tvd(l)), которая задается
, и cl является индексом ячейки гистограммы, ассоциированной с реальной вертикальной глубиной текущей точки измерения (tvd(l)), которая задается
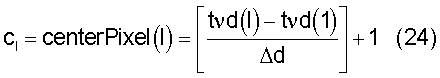
Построение матрицы H гистограммы продолжается затем следующим образом. Для каждой модели слоистой среды в наборе, горизонтальное удельное сопротивление ρH модели слоистой среды вычисляется в каждом интервале глубин 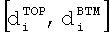 для
для 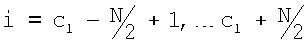 . Затем определяется индекс столбца, соответствующий ρН, и увеличивается соответствующий элемент гистограммы. H затем может быть отображена в виде изображения в градациях серого на левой панели окна отображения на Фиг.3A. Эта процедура представлена следующим псевдокодом
. Затем определяется индекс столбца, соответствующий ρН, и увеличивается соответствующий элемент гистограммы. H затем может быть отображена в виде изображения в градациях серого на левой панели окна отображения на Фиг.3A. Эта процедура представлена следующим псевдокодом
//псевдокод для построения гистограммы H удельного сопротивления моделей слоистой среды
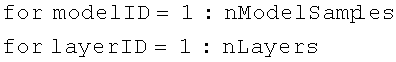 //вычислим диапазон строк, соответствующих этому слою
//вычислим диапазон строк, соответствующих этому слою
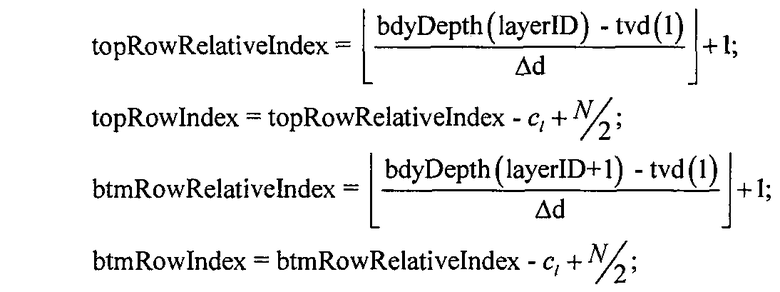
//вычислим индекс столбца, соответствующий горизонтальному удельному сопротивлению слоя
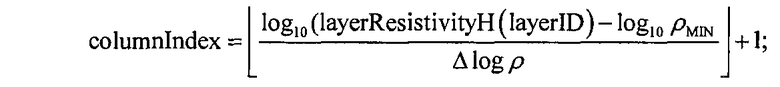
//увеличим элементы H

Набор вертикальных контурных кривых вычисляется для матрицы H гистограммы. В предпочтительном варианте осуществления, как проиллюстрировано в левых панелях окон отображения на Фиг.3A и 3B, пять вертикальных контурных кривых (5, 25, 50, 75 и 95% - три синих и две красных) вычисляются следующим образом. В каждой строке i матрицы H гистограммы вычисляется сумма Si элементов в iй строке H. Для вычисления 5% контурной кривой вычисляется 0.05·Si, затем вычисляется первый столбец j iй строки, где сумма первых j элементов iй строки H превышает 0,05·Si. Повторение этой процедуры для каждой строки i идентифицирует вертикальную кривую, описывающую 5% контур. Подобные процедуры могут быть выполнены для остальных четырех контурных кривых предпочтительного варианта осуществления. Этот процесс обобщен в виде следующего псевдокода.
//псевдокод для вычисления гистограммных контурных кривых
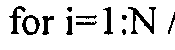 //индексы для строк гистограммы H
//индексы для строк гистограммы H
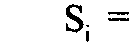 сумма элементов в iй строке гистограммы H
сумма элементов в iй строке гистограммы H
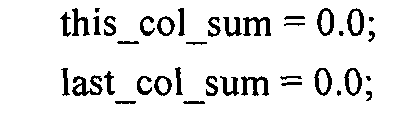
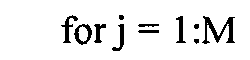 //индексы столбцов и M является числом столбцов
//индексы столбцов и M является числом столбцов
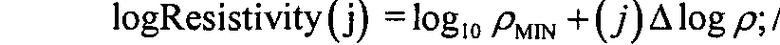 //логарифм удельного сопротивления в jм столбце
//логарифм удельного сопротивления в jм столбце

//подобный код для 25 и 75% кривых
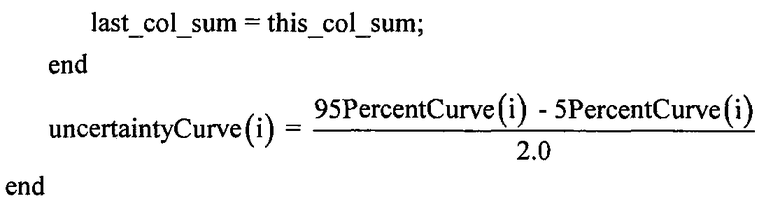
b. Кодирование предсказаний удельного сопротивления формации и соответствующей неопределенности с использованием карты цветов переменной насыщенности
Профиль неопределенности набора слоев модели суммируется с помощью одной или более вертикальных контурных кривых набора. В предпочтительном варианте осуществления, как проиллюстрировано на правой панели Фиг.3A и 3B, 50% контурная кривая (обозначенная как 50PercentCurve(i)) и кривая ширины неопределенности (которая определяется как половина разности между 95 и 5 процентными контурными кривыми) кодируются с использованием карты цветов и размещаются на экранном графике. Карта цветов использует 50% контурную кривую и значение ширины неопределенности для определения соответствующего оттенка цвета и уровня насыщенности.
В предпочтительном варианте осуществления карта цветов (обозначенная как C) является массивом P на M, где M является количеством столбцов в двухмерной гистограмме H модели слоистой среды и P является количеством строк в массиве, которое будет использоваться для индексирования логарифма неопределенности удельного сопротивления (обычно 64 или 128). Каждый элемент массива содержит триплет в соответствии с хорошо известным пространством цветов HSV, состоящим из значения цвета, значения насыщенности и значения яркости. В пространстве цветов HSV, при изменении оттенка от 0 до 1.0, соответствующие цвета меняются от красного через желтый, зеленый, голубой, синий, фиолетовый и обратно к красному, имеется два актуальных красных значения при 0 и 1.0. При изменении насыщенности от 0 до 1.0 соответствующие оттенки изменяются от ненасыщенного (градации серого) до полностью насыщенного (без белой составляющей). При изменении значения, или яркости, от 0 до 1,0 соответствующие цвета становятся более яркими. Фиг.5 иллюстрирует пространство цветов HSV. Следует отметить, что значения яркости для элементов массива карты цветов могут быть пропущены, так как приняты постоянными со значением 1,0 для всех элементов массива. Фиг.4 иллюстрирует изображение примерной карты цветов, использующей пространство цветов HSV, где значения насыщенностей С(i,j,2) элементов массива вычисляются как C(i,j,2)=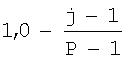 и значения оттенков C(i,j,1) элементов массива вычисляются как C(i,j,2)=
и значения оттенков C(i,j,1) элементов массива вычисляются как C(i,j,2)=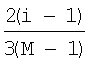 . Значения яркостей C(i,j,3) элементов массива являются постоянными C(i,j,3)=1,0. В этой примерной карте цветов уменьшение насыщенности увеличивает белую составляющую цвета и, таким образом, карта цветов постепенно становится совершенно ненасыщенной и полностью белой.
. Значения яркостей C(i,j,3) элементов массива являются постоянными C(i,j,3)=1,0. В этой примерной карте цветов уменьшение насыщенности увеличивает белую составляющую цвета и, таким образом, карта цветов постепенно становится совершенно ненасыщенной и полностью белой.
Столбцы массива карты цветов индексированы теми же координатами, что и матрица H гистограммы логарифма удельного сопротивления модели слоистой среды, т.е. с использованием 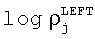 и
и 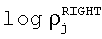 уравнений 19 и 20. Минимальные и максимальные значения ширины неопределенности для P строк массива карты цветов вычисляются с помощью
уравнений 19 и 20. Минимальные и максимальные значения ширины неопределенности для P строк массива карты цветов вычисляются с помощью
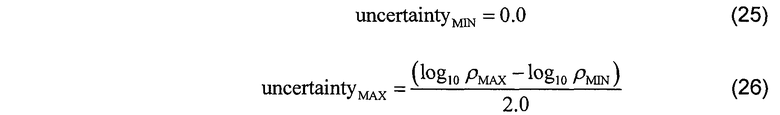
и отдельные строки массива карты цветов имеют физический размер, задаваемый
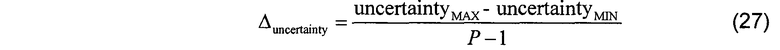
так что строки массива индексируются координатами, задаваемыми
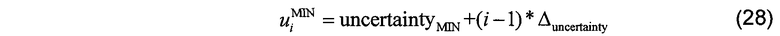
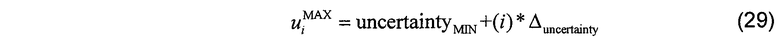
50% контурный вектор и вектор ширины неопределенности кодируются для столбца P экранного графика путем использования 50% контурной кривой (50PercentIndex) для индексирования первой координаты карты цветом C и контур ширины неопределенности (uncertaintyCurve) для индексирования координаты насыщенности карты цветов C в соответствии с псевдокодом, представленным ниже.
//Псевдокод для задания значения HSV света для значений среднего удельного сопротивления и неопределенности
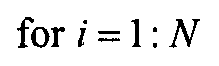 //индексирует строки изображения H гистограммы
//индексирует строки изображения H гистограммы

Результатом является массив размером N на 3 из значений оттенка/насыщенности/яркости, заданный картой C цветов, который суммирует апостериорный профиль удельного сопротивления над и под измерительным устройством в текущей точке измерения. Новый столбец предпочтительно добавляется как новый столбец (I) к экранному графику, как описано ниже.
c. Построение и отображение экранного графика
Изображение экранного графика строится с использованием массива, обозначенного как "curtainPlotCompacted" и предназначен для суммирования информации, извлеченной из апостериорных профилей неопределенности удельного сопротивления, вычисленных на новых точках измерения. Предпочтительно пользователь задает размеры массива curtainPlot изображения экранного графика с использованием переменных windowWidth и windowHeight. Переменная windowHeight имеет предпочтительно значение N, которое является количеством строк в изображении профиля неопределенности удельного сопротивления. Это позволяет отображать изображение гистограммы моделей слоистой среды и экранный график рядом, в одном окне, как показано на Фиг.3A и 3B. Предпочтительно переменная windowWidth выбирается пользователем и изменяется между 50 и 500 или более, в зависимости от приложения.
Построение изображения экранного графика требует размещения столбцов массива curtainPlotCompacted в необходимый набор строк в массиве curtainPlot в соответствии с реальной вертикальной глубиной соответствующих точек измерения. Вертикальное размещение этих столбцов определяется элементами вектора centerPixel в приведенном выше уравнении 24. Обычно столбец, рассчитанный из новой точки измерения, центрируется в последнем столбце массива экранного графика и остальные столбцы размещаются относительно вертикальной позиции последнего столбца, как это описывается ниже в псевдокоде.
//псевдокод для построения изображения экранного графика из набора слоев
//информация о среднем и неопределенности модели из новых точек измерения
//массив curtainPlot имеет размеры windowWidth * windowHeight * 3
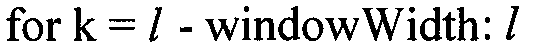
//центральный пиксель для нового столбца, l, назначается
//(windowHeight / 2)-й строке массива curtainPlot
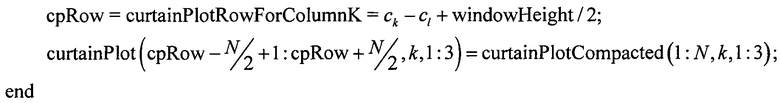
Следует отметить, что значения цветов, используемые для отображения экранного графика, обычно определяются в пространстве цветов RGB. В этом случае значения оттенка, насыщенности и яркости, которые определяют цвет для нового столбца экранного графика в пространстве цветов HSV, могут быть преобразованы в соответствующие значения RGB, как это хорошо известно в данной области техники. В качестве альтернативы при необходимости могут быть применены другие подходящие преобразования цвета.
d. Отображение диаграммы наклона
Осуществление выборки коллекции модели слоистой среды, как описано выше (например, отбор уравнения 17), включает в себя выборки параметра α относительного наклона. Эти выборки могут быть собраны в гистограмму, обозначенную как "dipHistogram". Изображение dipHistogram может быть отображено для пользователя, так что можно наблюдать ограничения, накладываемые на параметр α относительного наклона измерениями в последующих точках измерения. Изображение примерной dipHistogram показано на Фиг.6.
Число строк в dipHistogram равно величине nDip, которая обычно составляет 100, и столбцы индексируются по точкам измерения. Физическими границами для вертикальной оси dipHistogram являются 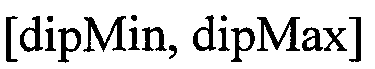 , и обычные значения равны 40 и 140 градусов при бурении искривленной скважины. Следующий псевдокод реализует построение нового столбца изображения dipHistogram, например, lго столбца.
, и обычные значения равны 40 и 140 градусов при бурении искривленной скважины. Следующий псевдокод реализует построение нового столбца изображения dipHistogram, например, lго столбца.
//псевдокод для построение lго столбца изображения dipHistogram
//dipHistogram имеет nDip строк.
//физические размеры вертикальной оси dipHistogram равны
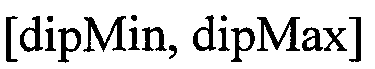
 //вертикальный размер пикселей в dipHistogram
//вертикальный размер пикселей в dipHistogram
//горизонтальная ось изображения dipHistogram является индексом станции измерения

e. Использование наклона формации для предсказания удельного сопротивления перед буровой коронкой.
Выборка параметра α относительного наклона в новой точке измерения может быть использована для предсказания распределения параметров удельного сопротивления формации для будущих точек измерения. Взаимосвязь между относительным наклоном α формации и траекторией инструмента проиллюстрирована на Фиг.7. Относительное вертикальное смещение между траекторией инструмента и формацией в планируемой точке измерения является  и может быть вычислено как
и может быть вычислено как
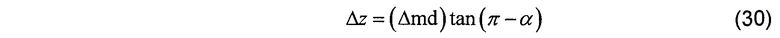
где Δmd является изменением в измеренной глубине между точками измерения.
Заданный размер пикселя для вертикальной оси в экранном графике, Δd из уравнения 21, количество вертикальных пикселей, на которое должен быть смещен новый столбец экранного графика для согласования с параметром α относительного наклона является
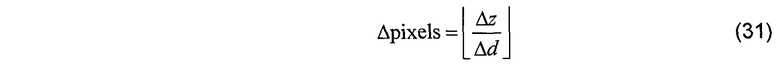
Новый столбец экранного графика может быть затем извлечен в столбцы для планируемых точек измерения следующим образом:
//псевдокод для экстраполяции нового столбца экранного графика в планируемые
//точки измерения с использованием апостериорной оценки для наклона α в новой точке
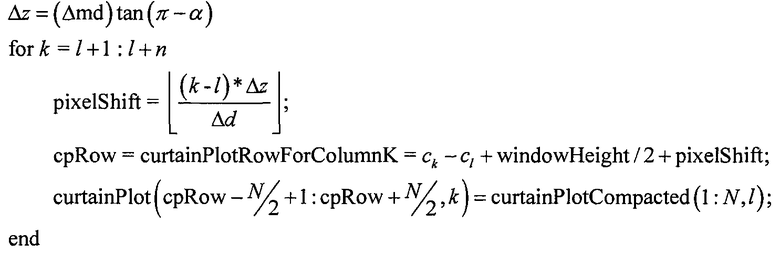
Расширения
a. Выборка по методу Монте-Карло
Способ, описанный выше для вычисления апостериорного профиля моделей слоистой среды удельного сопротивления может быть реализован с использованием выборки Монте-Карло моделей формации вместо использования нелинейного алгоритма наименьших квадратов. Нелинейный алгоритм наименьших квадратов используется в основном для удобства вычисления, как реализующий прямую модель, которая отображает значения модели в предсказанные измерения много раз, не является вычислительно осуществимым для некоторых сценариев бурения в режиме реального времени.
При использовании выборки Монте-Карло может быть полезным использовать более компактную параметризацию для уменьшения вычислительных расходов процедуры выборки Монте-Карло. Пример такой компактной параметризации использует главный анизотропный параметр a как замену вертикального удельного сопротивления следующим образом:
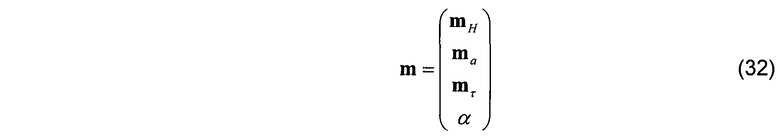
Для этой альтернативной параметризации модели элементы предшествующего среднего вектора 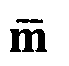 , относящегося к общему параметру а анизотропии модели слоистой среды, определяются следующим образом:
, относящегося к общему параметру а анизотропии модели слоистой среды, определяются следующим образом:
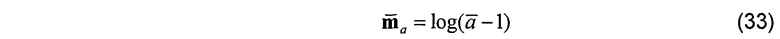
Обычным значением для параметра 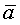 =1,5 для всех слоев k. Предшествующее расхождение для логарифма анизотропии
=1,5 для всех слоев k. Предшествующее расхождение для логарифма анизотропии 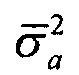 имеет
имеет 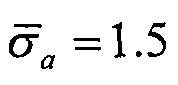 .
.
Могут быть использованы много других алгоритмов Монте-Карло. Например, может быть использован алгоритм цепи Маркова Монте-Карло (MCMC) для непосредственно выборки апостериорного распределения 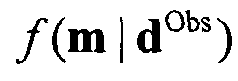 . Алгоритм MCMC является хорошо известным в данной области техники. Например, алгоритмы MCMC описаны в Sen et al. "Global optimization methods in Geophysical Inversion," Elsevier, Amsterdam, 1995, включенном сюда по ссылке во всей своей полноте.
. Алгоритм MCMC является хорошо известным в данной области техники. Например, алгоритмы MCMC описаны в Sen et al. "Global optimization methods in Geophysical Inversion," Elsevier, Amsterdam, 1995, включенном сюда по ссылке во всей своей полноте.
Одна возможная реализация может быть простой бракующей выборкой моделей формации, как описано в Press et al. "Numerical Recipes in C: The Art of Scientific Computing," Cambridge University Press, New York, 2nd Edition, 1992, Section 7.3, включенном сюда по ссылке во всей своей полноте. Другая возможная реализация основывается на технике, описанной в Malinverno et al., "Bayesian Inversion of DC electrical measurements with uncertainties for reservoir monitoring", Inverse Problems, Vol.16, pp.1343-1356, 2000, включенном сюда по ссылке во всей своей полноте. Таким образом, реализация начинается в выбора начальной выборки из предшествующей PDF, описанной в уравнении 13 или с выборки из нормальной случайной переменной 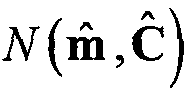 , вычисленной во время нового успешного запуска нелинейного алгоритма наименьших квадратов. Во время процесса выборки текущее значение вектора m параметра модели изменяется случайным образом для получения кандидата вектора
, вычисленной во время нового успешного запуска нелинейного алгоритма наименьших квадратов. Во время процесса выборки текущее значение вектора m параметра модели изменяется случайным образом для получения кандидата вектора 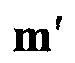 модели. Этот кандидат извлекается из предполагаемой функции распределения вероятности (PDF)
модели. Этот кандидат извлекается из предполагаемой функции распределения вероятности (PDF) 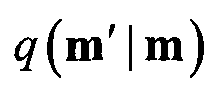 .
.
Эта предполагаемая PDF может быть также и предшествующей PDF
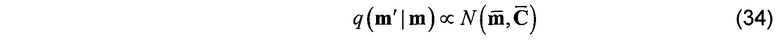
или предполагаемая PDF может быть апостериорной PDF, вычисленной во время последнего успешного запуска нелинейного алгоритма наименьших квадратов.
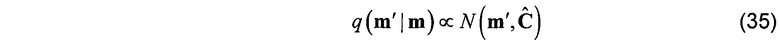
Это кандидат m' принимается с принятой вероятностью, заданной
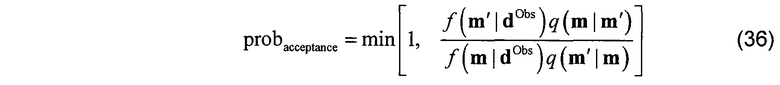
где 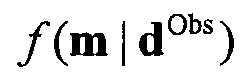 вычисляется непосредственно с использованием уравнений 1, 13 и 14 как
вычисляется непосредственно с использованием уравнений 1, 13 и 14 как
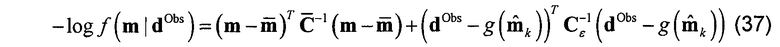
На каждом этапе в процедуре выборки собирается параметр новой принятой модели. Этот сбор выборок фактически выбирает апостериорное распределение 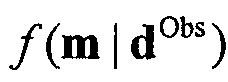 . В предшествующем варианте осуществления процесс выборки запускается 10 раз и каждый осуществляет 100 итераций.
. В предшествующем варианте осуществления процесс выборки запускается 10 раз и каждый осуществляет 100 итераций.
b. Выбор количества слоев модели
В предпочтительном варианте осуществления количество слоев, n, в параметризации модели является свободным параметром, устанавливаемым пользователем или в качестве параметра по умолчанию в программном обеспечении.
В качестве альтернативы количество слоев в параметризации модели может изменяться от одной точки измерения к другой. В каждой точке измерения можно сгенерировать пространственную гистограмму удельного сопротивления формации и соответствующие колонки экранного графика для конкретного выбора количества слоев. В этом примере количество слоев в параметризации модели в заданной точке измерения может быть определено с использованием маргинального правдоподобия следующим образом
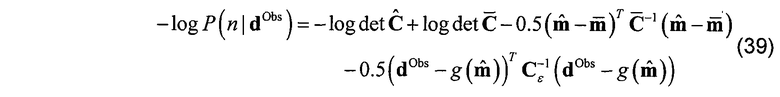
Такой анализ маргинального правдоподобия подробно описан в Malinverno et al. "Expanded uncertainty quantification in inverse problems: Hierarchical Bayes and Empirical Bayes," Geophys. Soc. of Expl. Geophys., Vol.69, pp.1005-1016, 2004, включенном сюда по ссылке во всей своей полноте.
В еще одной альтернативной методологии окно отображения на Фиг.3A и 3B может быть представлено с вкладками, как изображено на Фиг.8. В этой схеме отображения с вкладками вкладки показывают результат обработки для разных параметризаций количества слоев (например, вкладки для 3, 5, 7 слоев и, возможно, вкладка для оптимального количества слоев). Это позволит иметь лучшее понимание роли количества слоев в пространственной гистограмме и изображениях экранного графика.
В качестве альтернативы может использоваться техника обратимых скачков цепи Маркова Монте-Карло для вычисления апостериорного профиля удельного сопротивления, который рассчитывается для неопределенности при выборе числа слоев в модели, как описано в Malinverno, A., "Parsimonious Bayesian Markov chain Monte Carlo inversion in a nonlinear geophysical problem", Geophys. J. Int., Vol.151, pp.675, 2002, включенном сюда по ссылке во всей своей полноте.
c. Отображение гистограммы анизотропии
При использовании параметризации модели в уравнении 32, выборка набора моделей слоистой среды, как описано выше (например, в выборке уравнения 17), включает в себя выборки параметров a анизотропии формации. Эти выборки могут быть собраны в гистограмму, обозначенную "anisotropyHistogram". Изображение гистограммы может быть отображено так, чтобы видеть ограничения, наложенные на параметр анизотропии измерениями в предыдущих точках измерения.
Построение anisotropyHistogram осуществляется полностью аналогичным образом, что и построение dipHistogram, описанное выше. Количество строк в anisotropyHistogram может быть 100 и точки измерения могут быть индексами столбцов. Физические границы вертикальной оси могут быть 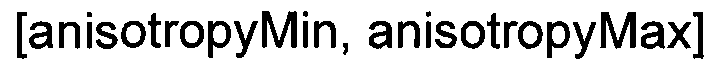 , обычные значения которых могут быть 1 и 10. Псевдокод, аналогичный описанному выше для построения dipHistogram на Фиг.6, может быть использован для выполнения построения и отображения нового столбца в anisotropyHistogram.
, обычные значения которых могут быть 1 и 10. Псевдокод, аналогичный описанному выше для построения dipHistogram на Фиг.6, может быть использован для выполнения построения и отображения нового столбца в anisotropyHistogram.
d. Использование других каротажных измерений и проводных приложений
Описанная здесь компьютерная методология может также быть расширена для использования других измерений во время бурения, таких как звуковые и сейсмические измерения во время бурения. Эти приложения могут потребовать введения других свойств слоя, таких как скорость продольной волны или акустическое сопротивление. Пространственные гистограммы, аналогичные созданным для горизонтального удельного сопротивления и отображенным в левой панели окна отображения на Фиг.3A и 3B, могут быть созданы для этих дополнительных свойств с использованием процедур выборки с помощью уравнения 17 или с использованием выборки Монте-Карло. Затем аналогичным образом для этих свойств могут быть созданы соответствующие экранные графики. Эти экранные графики для различных свойств формации могут быть размещены один рядом с другим в новом отображении для того, чтобы показать взаимосвязь этих свойств формации и точек слоя. Общая вероятностная структура и структура отображения могут остаться в большей части неизменными.
В дополнение, компьютерная методология может быть применена для измерений, полученных в искривленных или горизонтальных скважинах с использованием проводных измерений.
Здесь были описаны и проиллюстрированы несколько вариантов осуществления компьютерного способа для моделирования и визуализации во время бурения подземных формаций. Несмотря на то что были описаны конкретные варианты осуществления изобретения, это не означает, что изобретение ограничено ими, но это означает, что изобретение имеет настолько широкий объем, насколько это позволяет уровень техники, и что описание должно интерпретироваться подобным образом. Таким образом, в то время как были раскрыты конкретные параметры модели, следует понимать, что могут также быть использованы и другие параметры модели. В дополнение, в то время как были раскрыты конкретные типы инверсного анализа модели, следует понимать, что могут быть использованы и другие типы инверсного анализа модели. Также, в то время как предпочтительными для моделирования и визуализации является удельное сопротивление формации, следует понимать, что могут быть смоделированы и визуализированы и другие свойства формации. Более того, в то время как были раскрыты конкретные структуры данных для гистограммы неопределенности и карты цветов, следует понимать, что точно так же могут быть использованы и другие структуры данных. Поэтому специалистам в данной области техники следует понимать, что могут быть сделаны и другие изменения представленного изобретения без отклонения от сущности и объема формулы изобретения.
| название | год | авторы | номер документа |
|---|---|---|---|
| СИСТЕМА И СПОСОБ ДЛЯ ПОЛУЧЕНИЯ ОПЕРЕЖАЮЩИХ ИЗМЕРЕНИЙ В ПРОЦЕССЕ ОПЕРАЦИИ БУРЕНИЯ | 2012 |
|
RU2576043C1 |
| УСТРОЙСТВО, СПОСОБ И СИСТЕМА СТОХАСТИЧЕСКОГО ИЗУЧЕНИЯ ПЛАСТА ПРИ НЕФТЕПРОМЫСЛОВЫХ ОПЕРАЦИЯХ | 2008 |
|
RU2496972C2 |
| СПОСОБ ПОЛУЧЕНИЯ ХАРАКТЕРИСТИК ГЕОЛОГИЧЕСКОЙ ФОРМАЦИИ, ПЕРЕСЕКАЕМОЙ СКВАЖИНОЙ | 2009 |
|
RU2440591C2 |
| ПРЯМЫЕ МОДЕЛИ ДЛЯ АНАЛИЗА ПОДЗЕМНЫХ ФОРМАЦИЙ С ПОМОЩЬЮ ИЗМЕРЕНИЯ ГАММА-ИЗЛУЧЕНИЯ | 2009 |
|
RU2464593C1 |
| УСТРОЙСТВА И СПОСОБЫ ВИЗУАЛЬНОГО ОТОБРАЖЕНИЯ ОТНОСЯЩИХСЯ К ПЛАСТАМ ОСОБЕННОСТЕЙ | 2013 |
|
RU2635848C2 |
| СИСТЕМА И СПОСОБЫ ПОЛУЧЕНИЯ СВОЙСТВ СКВАЖИННЫХ ФЛЮИДОВ И ИХ НЕОПРЕДЕЛЕННОСТИ | 2006 |
|
RU2435030C2 |
| УСОВЕРШЕНСТВОВАННОЕ КОДИРОВАНИЕ СОДЕРЖИМОГО ЭКРАНА С УЛУЧШЕННЫМИ СПОСОБАМИ КОДИРОВАНИЯ ТАБЛИЦЫ ПАЛИТРЫ И ИНДЕКСНОЙ КАРТЫ | 2015 |
|
RU2654200C1 |
| УСТРОЙСТВО ДЛЯ ЭКСПЕРТИЗЫ, ОЦЕНКИ И КЛАССИФИКАЦИИ ДРАГОЦЕННЫХ КАМНЕЙ | 2008 |
|
RU2476862C2 |
| СПОСОБ УСТРАНЕНИЯ ВЛИЯНИЯ ПРИЛЕГАЮЩИХ СЛОЕВ (ВАРИАНТЫ) | 2006 |
|
RU2413070C2 |
| СПОСОБ И СИСТЕМА ПРОВЕДЕНИЯ АНАЛИЗА ГЕОЛОГИЧЕСКОГО БАССЕЙНА | 2010 |
|
RU2491579C2 |
Изобретение относится к способам обработки электромагнитных сигналов от инструмента для моделирования и визуализации слоистых подземных формаций, окружающих инструмент. Техническим результатом является моделирование и визуализация свойств подземной формации во время бурения в ней скважины. Для этого получают электромагнитные сигналы, соответствующие текущему положению точки измерения инструмента для измерения во время бурения, и генерируют многослойную модель, соответствующую таким электромагнитным сигналам. Гистограмма, описывающая неопределенность многослойной модели, используется для генерации множества значений оттенка цвета, которое представляет предсказания свойства формации для значений глубины выше/ниже инструмента, и соответствующее множество значений насыщенности. Генерируют и отображают экранный график. Экранный график использует цвета для визуализации предсказаний свойства формации для значений глубины над и под инструментом для последующих положений точки измерения. Генерируют новый столбец для экранного графика для текущего положения точки измерения. Значения цвета нового столбца основаны на множестве значений оттенка цвета и множестве значений насыщенности, полученных из гистограммы. Значения насыщенности нового столбца представляют неопределенности для соответствующих предсказаний. 24 з.п. ф-лы, 10 ил.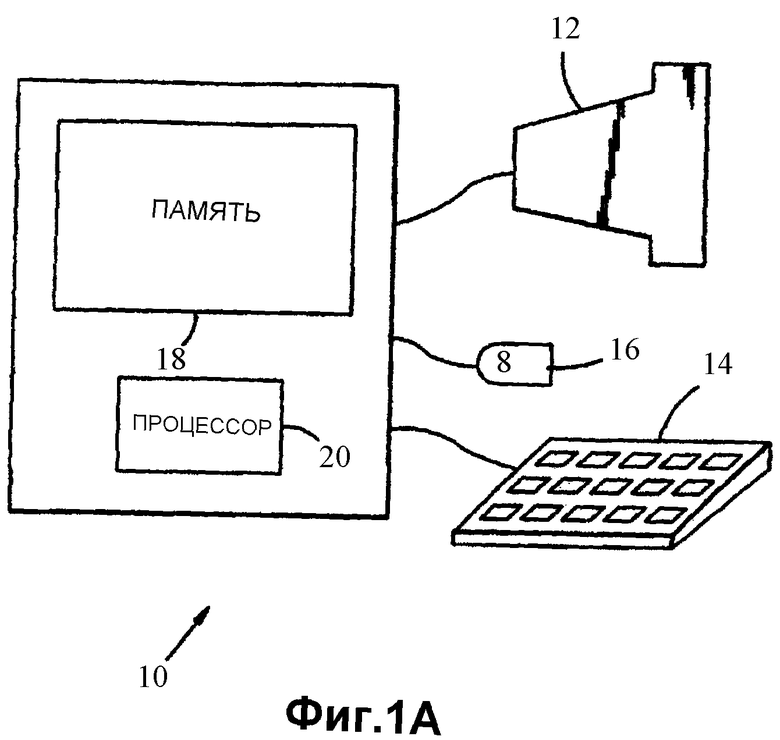
получают множество электромагнитных сигналов, соответствующих местоположению текущей точки измерения инструмента для измерения во время бурения;
генерируют многослойную модель, соответствующую множеству электромагнитных сигналов;
генерируют гистограмму, описывающую неопределенность многослойной модели относительно значений глубины над и под инструментом для измерения во время бурения путем осуществления выборки упомянутой многослойной модели и наложения выборки упомянутой многослойной модели;
генерируют множество значений оттенков цветов на основании упомянутой гистограммы, при этом упомянутое множество оттенков цветов представляет предсказания свойств земной формации для значений глубины над и под инструментом для измерения во время бурения;
генерируют множество значений насыщенности на основании упомянутой гистограммы, при этом упомянутое множество значений насыщенности соответствует упомянутому множеству значений оттенков цветов и представляет неопределенности для предсказаний, из которых выводятся соответствующие значения оттенков цветов;
генерируют и отображают экранный график, чьи столбцы используют цвета для изображения предсказаний свойств подземной формации для значений глубины над и под инструментом для измерения во время бурения для следующих положений точек измерения, где каждый столбец экранного графика соответствует заданному положению точки измерения; и
генерируют новый столбец экранного графика для текущего положения точки измерения, где значения цвета нового столбца основываются на множестве значений оттенков цветов и множестве значений насыщенности, полученных из упомянутой гистограммы, где значения насыщенности значений цвета нового столбца представляют неопределенности для предсказаний, из которых выводятся соответствующие значения цвета.
отображают изображение, включающее в себя множество контурных кривых, которые суммируют упомянутую гистограмму.
упомянутое изображение и упомянутый экранный график отображаются рядом друг с другом как часть окна отображения.
многослойная модель получается в результате работы нелинейного алгоритма наименьших квадратов.
начальное предположение для нелинейного алгоритма наименьших квадратов является одним из:
i) предшествующее среднее, вычисленное во время последнего успешного выполнения нелинейного алгоритма наименьших квадратов, и
ii) апостериорное среднее, вычисленное во время последнего успешного выполнения нелинейного алгоритма наименьших квадратов.
выборка осуществляется с помощью одного из
i) выборки апостериорной функции распределения вероятности многослойной модели, и
ii) выборки цепи Маркова-Монте-Карло апостериорного распределения многослойной модели.
свойство содержит удельное сопротивление земной формации.
многослойная модель включает в себя, по меньшей мере, один из:
i) параметр, представляющий горизонтальное удельное сопротивление земной формации на протяжении N слоев модели;
ii) параметр, представляющий вертикальное удельное сопротивление земной формации на протяжении N слоев модели;
iii) параметр, представляющий общую анизотропию земной формации на протяжении N слоев модели;
iv) параметр, представляющий толщину земной формации на протяжении N слоев модели; и
v) параметр, представляющий относительный наклон формации относительно оси инструмента для измерения во время бурения.
число N является большим, чем 3.
гистограмма применяет горизонтальную ось, описывающую горизонтальное сопротивление, и вертикальную ось, описывающую вертикальную глубину слоев упомянутой многослойной модели;
физические границы горизонтальной оси гистограммы определяются ρMIN и ρMAX, которые описывают наименьшее и наибольшее горизонтальные удельные сопротивления, которые ожидаются в результате этапа выборки;
горизонтальные координаты для отдельного столбца гистограммы определяются вычислением физического размера отдельного столбца гистограммы как
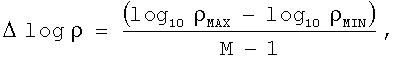
и, затем, определением горизонтальных координат отдельных ячеек сетки гистограммы как
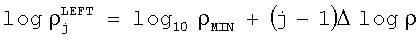 ,
,
и
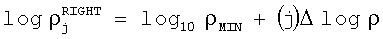 ;
;
физические границы вертикальной оси гистограммы определяются параметром histogramHeight; и
вертикальные координаты для отдельных строк гистограммы определяются путем вычисления физического размера отдельных строк гистограммы как
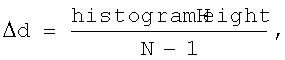
и, затем, определением вертикальных координат отдельных ячеек сетки гистограммы как
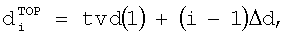
и
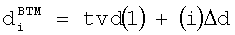 ,
,
где tvd(1) является реальной вертикальной глубиной устройства в первой точке измерения, i является целым числом в диапазоне от 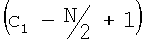 до
до 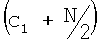 , и сl является индексом ячейки гистограммы, ассоциированной с реальной вертикальной глубиной текущей точки измерения (tvd(l)), которая задается с помощью
, и сl является индексом ячейки гистограммы, ассоциированной с реальной вертикальной глубиной текущей точки измерения (tvd(l)), которая задается с помощью
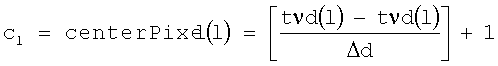 .
.
гистограмма строится для каждой модели слоистой среды в наборе моделей слоистой среды следующим образом:
i) вычисляют горизонтальное удельное сопротивление модели слоистой среды для каждого интервала глубины 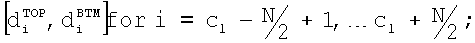 , и
, и
ii) определяют индекс j столбца, соответствующий каждому вычисленному горизонтальному удельному сопротивлению, и увеличивают соответствующий элемент гистограммы.
множество значений оттенка цвета получается из первой контурной кривой гистограммы; и
множество значений насыщенности получается из второй и третьей контурных кривых гистограммы.
множество значений оттенка цвета получается из 50% контурной кривой гистограммы; и
множество значений насыщенности получается из разности между 95% контурной кривой и 5% контурной кривой гистограммы.
карта цветов хранит массив элементов, который определяет цвет с использованием цветового пространства HSV (оттенок, насыщенность, яркость), где значения насыщенности C(i,j,2) элементов вычисляются как C(i,j,2)=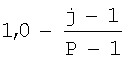 , значения оттенка C(i,j,1) элементов вычисляются как C(i,j,2)=
, значения оттенка C(i,j,1) элементов вычисляются как C(i,j,2)=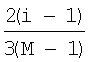 и значения яркости C(i,j,3) элементов являются постоянными C(i,j,3)=1,0.
и значения яркости C(i,j,3) элементов являются постоянными C(i,j,3)=1,0.
упомянутая карта цветов использует горизонтальную ось, описывающую предсказанные горизонтальные сопротивления, и вертикальную ось, описывающую неопределенность,
физические границы горизонтальной оси карты цветов определяются ρMIN и ρMAX, которые описывают наименьшее и наибольшее горизонтальные удельные сопротивления, ожидаемые в результате этапа выборки;
горизонтальные координаты для отдельных столбцов карты цветов определяются вычислением физических размеров отдельных столбцов карты цветов как
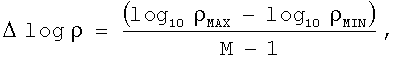
и, затем, определением горизонтальных координат отдельных ячеек сетки карты цветов как
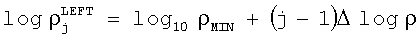 ,
,
и
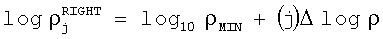 ;
;
физические границы вертикальной оси карты цветов определяются как
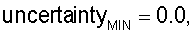
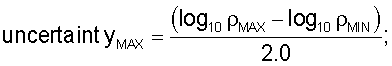
вертикальные координаты для отдельных строк карты цветов определяются вычислением физических размеров отдельных строк карты цветов как
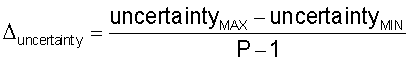
и, затем, определением вертикальных координат отдельных ячеек сетки карты цветов как
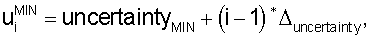
и
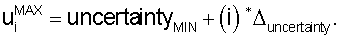 .
.
генерируют гистограмму наклона, описывающую предсказания наклона формации для последующих положений точки измерения; и
отображают изображение на основании гистограммы наклона.
генерируют предсказания анизотропии формации для последующих точек измерения; и
отображают изображение на основании гистограммы анизотропии.
генерируют предполагаемый параметр α наклона для текущего положения точки измерения; и
используют предполагаемый параметр α наклона и траекторию инструмента для предсказания пространственного распределения свойств удельного сопротивления формации, по меньшей мере, для одного будущего положения точки измерения.
многослойная модель имеет множество слоев n, имеющее, по меньшей мере, одно из перечисленных свойств:
i) n является свободным параметром, устанавливаемым пользователем;
ii) n может изменяться между положениями точки измерения; и
iii) n оптимизируется с использованием анализа маргинального правдоподобия.
генерируют множество экранных графиков, каждый из которых имеет различную параметризацию множества слоев для многослойной модели, из которой это множество получается.
отображают упомянутое множество экранных графиков в различных окнах отображения.
упомянутые различные окна отображения могут быть представлены в виде вкладок.
электромагнитные сигналы получаются в режиме реального времени от направленного электромагнитного инструмента для измерения во время бурения, который способен разведывать свойства формации выше и ниже положения инструмента.
многослойная модель соответствует другим измерениям во время бурения.
другие измерения во время бурения содержат, по меньшей мере, измерения во время бурения акустического типа и сейсмического типа.
| US 6950751 B2, 27.09.2005 | |||
| RU 96106756 A, 10.07.1998 | |||
| СПОСОБ И УСТРОЙСТВО ДЛЯ СОЗДАНИЯ, ПРОВЕРКИ И МОДИФИКАЦИИ ГЕОЛОГИЧЕСКИХ МОДЕЛЕЙ ПОДПОВЕРХНОСТНЫХ ЗОН | 1998 |
|
RU2223521C2 |
| СПОСОБ ДИНАМИЧЕСКОЙ ВИЗУАЛИЗАЦИИ ДАННЫХ ОБ ОБЪЕКТЕ | 1998 |
|
RU2142162C1 |
| Ванная стекловаренная печь | 1977 |
|
SU745870A1 |
| Роторно-лопастной двигатель внутреннего сгорания | 2019 |
|
RU2734069C1 |
| US 4340934 A, 20.07.1982 | |||
| МАДАТОВ А.Г | |||
| и др | |||
| Численное моделирование трехмерных геофизических полей по данным скважинных наблюдений | |||
| Секция "Исследование геофизических процессов в Арктике". | |||
Авторы
Даты
2008-10-27—Публикация
2007-01-12—Подача