Изобретение относится к измерительной технике и может быть использовано при физических исследованиях поведения микрочастиц вещества, помещенных в вакуум и находящихся в состоянии невесомости, в частности, для обнаружения броуновского движения микрочастиц.
Броуновское движение (Б.д.) - беспорядочное движение малых частиц, взвешенных в жидкости или газе, происходящее под действием ударов молекул окружающей среды. Исследовано в 1827 Р.Броуном (Браун; R. Brown), который наблюдал в микроскоп движение цветочной пыльцы, взвешенной в воде. Наблюдаемые частицы (броуновские) размером ˜1 мкм и менее совершают неупорядоченные независимые движения, описывая сложные зигзагообразные траектории. Интенсивность Б.д. не зависит от времени, но возрастает с ростом температуры среды, уменьшением ее вязкости и размеров частиц (независимо от их хим. природы). Полная теория Б.д. была дана А.Эйнштейном (A. Einstein) и М.Смолуховским (М.Smoluchowski) в 1905-06. Причины Б.д. - тепловое движение молекул среды и отсутствие точной компенсации ударов, испытываемых частицей со стороны окружающих ее молекул, т.е. Б.д. обусловлено флуктуациями давления. Удары молекул среды приводят частицу в беспорядочное движение: скорость ее быстро меняется по величине и направлению. Если фиксировать положение частиц через небольшие равные промежутки времени, то построенная таким методом траектория оказывается чрезвычайно сложной и запутанной.
Б.д. - наиболее наглядное экспериментальное подтверждение представлений молекулярно-кинетической теории о хаотическом тепловом движении атомов и молекул. Если промежуток наблюдения τ достаточно велик, чтобы силы, действующие на частицу со стороны молекул среды, много раз меняли свое направление, то средний квадрат проекции ее смещения на какую-либо ось (в отсутствие других внешних сил) пропорционален времени τ (закон Эйнштейна):
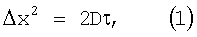
где D - коэффициент диффузии броуновской частицы. Для сферических частиц радиусом r: D=kT/6πηr3 (Т - абсолютная температура, η- динамическая вязкость среды). При выводе закона Эйнштейна предполагается, что смещения частицы в любом направлении равновероятны и что можно пренебречь инерцией броуновской частицы по сравнению с влиянием сил трения (это допустимо для достаточно больших τ). Формула для коэффициента D основана на применении закона Стокса для гидродинамического сопротивления движению сферы радиусом r в вязкой жидкости. Соотношения для Δх2 и D были экспериментально подтверждены измерениями Ж.Перрена (J.Perrin) и Т.Сведберга (T.Svedberg). Из этих измерений экспериментально определены постоянная Больцмана k и постоянная Авогадро NA.
Кроме поступательного Б.д., существует также вращательное Б.д. - беспорядочное вращение броуновской частицы под влиянием ударов молекул среды. Для вращательного Б.д. среднеквадратичное угловое смещение частицы пропорционально времени наблюдения
Δϕ2=2Dврτ,
где Dвр - коэффициент диффузии вращательного Б.д., равный для сферической частицы: Dвр=kT/8πηr3. Эти соотношения были также подтверждены опытами Перрена, хотя этот эффект гораздо труднее наблюдать, чем поступательное Б.д.
Теория Б.д. [1-9] исходит из представления о движении частицы под влиянием "случайной" обобщенной силы f(t), которая описывает влияние ударов молекул и в среднем равна нулю, систематической внешней силы X, которая может зависеть от времени, и силы трения - h(dx/dt), возникающей при движении частицы в среде со скоростью dx/dt. Уравнение случайного движения броуновской частицы - уравнение Ланжевена - имеет вид:
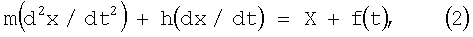
где m - масса частицы (или, если х - угол, ее момент инерции), h - коэффициент трения при движении частицы в среде. Для достаточно больших промежутков времени (τ>>m/h) инерцией частицы (то есть членом m(d2x/dt2)) можно пренебречь и, проинтегрировав уравнение Ланжевена при условии, что среднее произведение импульсов случайной силы для неперекрывающихся промежутков времени равно нулю, найти средний квадрат флуктуации Δх2, т.е. вывести соотношение Эйнштейна. В более общей задаче теории Б. д. последовательность значений координат и импульсов частиц через равные промежутки времени рассматривается как марковский случайный процесс, что является другой формулировкой предположения о независимости толчков, испытываемых частицами в разные неперекрывающиеся промежутки времени. В этом случае вероятность состояния х в момент t полностью определяется вероятностью состояния х0 в момент t0, и можно ввести функцию w(t0, х0, t, х) - плотность вероятности перехода из состояния x0 в состояние, для которого х лежит в пределах х, x+dx в момент времени t. Плотность вероятности удовлетворяет интегральному уравнению Смолуховского, которое выражает отсутствие "памяти" о начальном состоянии для случайного марковского процесса. Это уравнение для многих задач теории Б. д. можно свести к дифференциальному уравнению Фоккера-Планка в частных производных - обобщенному уравнению диффузии в фазовом пространстве. Поэтому решение задач теории Б.д. можно свести к интегрированию уравнения Фоккера-Планка при определенных граничных и начальных условиях. Математической моделью Б.д. является винеровский случайный процесс.
В том случае когда микрочастицы (броуновские частицы) находятся в вакуумной среде и в состоянии невесомости (например, в космическом аппарате), силовое влияние на них движущихся атомов и молекул внешней среды (жидкости или газа) полностью отсутствует. Однако при заданной температуре микрочастиц неуравновешенное колебательное хаотическое движение молекул этих микрочастиц оказывает на них такое же действие, какое оказывали на них движущиеся атомы и молекулы внешней среды. Это указывает на возможность наблюдения броуновского движения микрочастиц в вакууме под действием неуравновешенных импульсов хаотически колеблющихся молекул. При этом скачки Δxj микрочастиц в произвольных направлениях растут с уменьшением радиуса r микрочастиц (dΔxj/dr<0).
Возможность наблюдения броуновского движения в вакууме связана с разработкой соответствующего устройства, аналоги которого в настоящее время отсутствуют.
Заявляемое техническое решение - прибор для наблюдения броуновского движения в вакууме, отличающийся тем, что включает прозрачную вакуумную колбу с помещенным в нее управляемым по положению предметным столиком, на котором размещена группа броуновских микрочастиц, направленный на группу броуновских микрочастиц микроскоп с устройством подсветки, совмещенный со съемочной камерой, а весь прибор установлен, например, на космическом аппарате (то есть находится в состоянии невесомости), причем наблюдение броуновского движения в группе броуновских микрочастиц происходит путем удаления предметного столика электромеханическим устройством с соленоидом.
Поставленная в заявляемом устройстве цель - наблюдение Б.д. в вакууме - достигается помещением в свободное вакуумное пространство группы броуновских микрочастиц, находящихся в состоянии невесомости, после удаления предметного столика электромагнитным тяговым устройством с соленоидом. Движение микрочастиц объясняется неуравновешенными импульсами сил, возникающими из-за хаотического колебательного движения молекул этих микрочастиц, которое обусловлено их тепловым движением. Тепловая энергия микрочастиц определяет кинетическую энергию их молекул. При этом чем меньше радиус броуновских микрочастиц, тем больше вероятность неуравновешенности импульсов их движущихся молекул, следовательно, тем большие по величине скачки микрочастиц в целом наблюдаются, что полностью согласуется с законом сохранения центра инерции (законом сохранения импульса). Подобно тому, как тепловая энергия - функция температуры - определяет кинетическую энергию или импульс отдельной молекулы, то есть скорость колебательного движения ее массы, тепловая энергия является также и причиной Б.д. микрочастиц.
Упрощенная схема заявляемого устройства представлена на чертеже и включает следующие элементы:
1 - прозрачную вакуумную колбу,
2 - предметный столик,
3 - соленоид,
4 - группу броуновских микрочастиц,
5 - микроскоп, установленный снаружи или внутри прозрачной вакуумной колбы,
6 - съемочную камеру,
7 - устройство подсветки,
8 - источник питания подсветки,
9 - источник питания соленоида,
10 - пружину предметного столика (разжимающую),
11 - ферромагнитный стержень,
12 - направляющую стержня предметного столика.
Рассмотрим работу заявляемого технического решения.
Прибор помещают в состояние невесомости, например, в центр инерции космического аппарата для полного исключения гравитационного взаимодействия группы броуновских микрочастиц (ГБМ) со стороны самого космического аппарата. После этого подают постоянный электрический ток от источника питания соленоида 9, и ферромагнитный стержень 11 втягивается соленоидом 3 в направляющую стержня 12 предметного столика 2, преодолевая силу разжимающей пружины 10. При этом ГБМ находится на том же месте, где она находилась на поверхности предметного столика 2 до его перемещения с помощью соленоида. В результате ГБМ оказывается в свободном полете (невесомости) и на нее не оказывается какая-либо внешняя сила, кроме собственных сил гравитационного притяжения, которые, во-первых, чрезвычайно малы из-за очень малой массы элементов ГБМ, во-вторых, эти силы приводят к однонаправленным перемещениям элементов ГБМ к их общему центру тяжести, что легко различается от движений хаотических, свойственных Б.д.
ГБМ подсвечивают устройством подсветки 7 от источника подсветки 8 и наблюдают Б.д. с помощью микроскопа 5, связанного оптически со съемочной камерой 6, в которой производится экспозиция пространственного расположения ГБМ через определенные промежутки времени, например через одну минуту. Сопоставлением серии снимков можно сделать вывод о наличии Б.д. ГБМ в вакууме и о параметрах такого движения, обусловленного тепловым хаотическим движением молекул (атомов) вещества ГБМ. Количество микрочастиц в ГБМ не должно быть очень большим, чтобы упростить процедуру различения одних и тех же микрочастиц в составе ГБМ, либо следует уменьшить временной интервал между последовательными съемками.
Представляет интерес рассмотреть теоретические аспекты Б.д. в вакууме.
Как отмечалось выше, Б.д. возникает из-за неуравновешенности действующих на микрочастицу импульсов силы от хаотического движения n молекул, из числа которых имеется S неуравновешенных импульсов, алгебраическая сумма которых действует на массу m броуновской микрочастицы, приводя ее в движение со скоростью vк в течение некоторого интервала времени Δtk, при этом микросдвиг броуновской частицы равен Δхк=vkΔtk, где j=1, 2, 3, ...,к, где к - число опытно нефиксируемых (в силу их малости) микросдвигов между последовательными съемками пространственного положения данной броуновской микрочастицы. Нетрудно показать, что скорость vк броуновской микрочастицы находится из выражения:
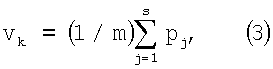
где pj - вектор-импульс молекулы из числа неуравновешенных вектор-импульсов S, величина которого определяется температурой Т согласно выражению pj=(3kTmjмол)-1/2, где mjмол - масса j-ой молекулы (здесь k=1,38·10-23 Дж/град. - постоянная Больцмана). При этом смещение броуновской микрочастицы Δх за интервал наблюдения τ между последовательными съемками подчиняется выражению (1), где 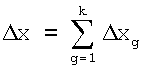 (смещения Δxg - суть проекции на ось, совпадающую с направлением перемещения микрочастицы из одного ее пространственного положения в другое за время τ между последовательными съемками), если на микрочастицу действуют импульсы молекул внешней среды - жидкой или газообразной. Однако для Б.д. в вакууме внешнее воздействие на броуновские микрочастицы отсутствует и соответственно не работает уравнение движения (2), так как отсутствует трение среды (h=0).
(смещения Δxg - суть проекции на ось, совпадающую с направлением перемещения микрочастицы из одного ее пространственного положения в другое за время τ между последовательными съемками), если на микрочастицу действуют импульсы молекул внешней среды - жидкой или газообразной. Однако для Б.д. в вакууме внешнее воздействие на броуновские микрочастицы отсутствует и соответственно не работает уравнение движения (2), так как отсутствует трение среды (h=0).
Стохастическое колебательное движение молекул микрочастиц вызывает Б.д. последних, и это движение может быть описано винеровским случайным процессом [10-11] - нормальным марковским случайным процессом x(t) с независимыми приращениями. В любой момент времени t распределение вероятностей винеровского случайного процесса в одномерном случае равна P(x,t)=(2πDt)-1/2 ехр(-x2/2Dt), где D - коэффициент диффузии. Плотность распределения приращений Δх=x(t2) - x(t1) за время Δt=t2-t1 равна Р(Δх, (t)=(2πDt)-3/2·exp[-(Δx)2/2DΔt)]. Распределение вероятностей винеровского случайного процесса изучено Н.Винером в 1923 году. Среднее значение (математическое ожидание) процесса равно нулю<x(t)>=0, а дисперсия линейно растет со временем σ2=Dt, корреляционная функция винеровского случайного процесса определяется выражением<x(t) x(t')>=D min (t, t').
Траектории винеровского случайного процесса непрерывны, но нигде не дифференцируемы. Производная процесса - обобщенный случайный процесс n(t), называемый белым шумом (стационарный нормальный случайный процесс с независимыми значениями, нулевым средним значением и дельтаобразной корреляционной функцией<n(t) n(t')>=D b(t-t').
Среднестатистическая частота соударений молекул Fм определяется их концентрацией в микрочастицах и скоростью хаотического колебательного движения молекул в функции температуры и может быть представлена выражением:
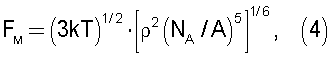
где ρ - плотность вещества, NA=6,02·1023 моль-1 - число Авогадро, А - молекулярный (атомный) вес вещества.
Число молекул в микрочастице n=4πr3ρNa/3А так велико, несмотря на их малые размеры, что их импульсы pj практически взаимно уравновешивают друг друга за достаточно большой промежуток времени (математическое ожидание суммарного импульса силы равно нулю), однако в каждый произвольный момент времени среди чисел n находится s молекул с неуравновешенными импульсами и движущимися в одном каком-либо направлении. Если ввести квантование такого движения по направлениям в телесном угле 4π стерадиан, учитывая размеры поверхности микрочастицы и поперечное сечение молекулы (атома), то можно показать, что вероятность движения s молекул в заданном направлении Θj равна P(Θj)={4πr2·[(ρNA/A)2]1/3}-1, а при этом само число s=r(ρNA/А)1/3/3, то есть линейно растет с увеличением радиуса микрочастицы. Однако масса последней возрастает пропорционально кубу радиуса, следовательно, микроскачки микрочастиц имеют порядок Δxj=А/4πr2ρNA, то есть растут обратно пропорционально квадрату радиуса микрочастиц. Это согласуется с опытными данными по Б.д. - чем меньше микрочастицы, тем большие сдвиги их регистрируются за единицу времени или интервал отсчета τ.
Весьма высокая средняя частота соударения молекул микрочастицы Fм согласно (4) и ничтожно малые микроскачки Δxj как результат этих соударений приводят к квазинепрерывному и хаотическому движению микрочастицы, перемещающейся по криволинейной траектории, длина которой ΔхΣ(τ) за время τ равна:
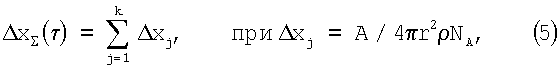
где к=Fм τ=τ·(3kT)1/2*·[ρ2(NA/А)5]1/6 - число микроскачков микрочастицы за интервал отсчета положения микрочастиц τ.
Если экспозицию положения помеченных микрочастиц производить через время τ, то окажется, что расстояние по прямой между начальным положением данной микрочастицы в момент времени t1 и конечным в момент времени t2=t1+τ, обозначаемым как Δх, будет значительно короче величины действительного отрезка траектории данной микрочастицы ΔхΣ(τ)>>Δх, что связано со стохастизмом направлений Θj в микроскачках микрочастицы. Можно показать, что набор микроскачков Δх1, Δх2, Δх3, ...,Δхк с соответствующим набором направлений Θ1, Θ2, Θ3, ...,Θк-1 этих микроскачков удовлетворяет рекуррентному соотношению вида:
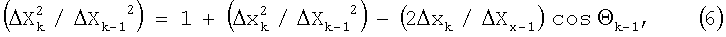
где ΔХк - расстояние между начальным и конечным положениями данной микрочастицы (ΔХк=Δх), ΔХк-1 - это же расстояние, но в предыдущем микроскачке. Подставляя в (6) различные значения индекса к, можно задать положение микрочастицы в любом j-ом состоянии (здесь Δх1, Δх2, Δх3, ...,Δхк - текущие величины микроскачков микрочастицы в пределах отсчетного интервала τ), однако при этом надо знать величины микроскачков Δхj и направления Θj, которые в общем случае произвольны и носят стохастический характер. Стохастизм проявляется и в выборе числа s неуравновешенных молекул для каждого из микроскачков, так что задача предсказания траектории движения микрочастицы становится неопределенной, имеет характер белого шума.
Теория Б. д. имеет принципиальное значение, она проясняет статистическую природу второго начала термодинамики и показывает границы его применимости. Она позволила уточнить критерии обратимости или необратимости молекулярных процессов и показать, что различие между ними не носит абсолютного характера. По Смолуховскому, процесс является необратимым, если переход из рассматриваемого состояния в исходное требует большого времени, и обратимым, если время возврата невелико. Смолуховскому удалось оценить время возврата, которое относится к экспериментально наблюдаемому параметру, т.е. является характеристикой макросостояния, а не микросостояния.
Модификацией заявляемого технического решения является замена прозрачной вакуумной колбы с предметным столиком и устройством его перемещения с помощью соленоида на прозрачную капсулу с броуновскими микрочастицами, причем из капсулы откачен воздух с помощью паромасляного насоса до получения глубокого вакуума. В состоянии невесомости в такой капсуле броуновские микрочастицы приходят в Б.д., не слипаясь между собой за счет самогравитационных сил, поскольку гравитационные силы между микрочастицами на много порядков меньше сил Б.д. При этом микрочастицы в такой вакуумной капсуле в состоянии невесомости (внутри космического аппарата) будут находиться в безразличном пространственном положении и в состоянии постоянного хаотического движения.
Сила гравитационного взаимодействия Fграв двух микрочастиц сферической формы с радиусом сферы r и с плотностью вещества ρ микрочастиц находится из выражения:

где γ=6,67·10-11 кг-1 м3 с-2 - гравитационная постоянная, 2r - расстояние между центрами соприкасающихся микрочастиц. Так, при ρ=2,5·103 кг/м3, r=0,5 мкм сила гравитационного притяжения микрочастиц равна Fграв=1,14·10-29 Н. С учетом массы микрочастицы m=0, 98·10-15 кг ее ускорение под действием силы гравитации Fграв было бы равным а=Fграв/m=1,16·10-14 м/с2. За интервал времени τ=60 сек броуновские микрочастицы под действием силы гравитации прошли бы путь h(τ)=аτ2/2=2,05·10-11 м=2·10-5 мкм. При этом реально проходимый путь броуновской частицей может достигать единиц микрон, то есть на пять порядков больший, чем h(τ). В том случае, когда микрочастицы удалены друг от друга, гравитационные силы их стягивания еще гораздо меньше, чем сила, указанная в (7). Это и является основанием считать, что в вакуумной капсуле броуновские микрочастицы НИКОГДА не будут стягиваться между собой гравитационными силами, а будут пространственно разделены между собой и находиться в состоянии Б.д. Использование в заявляемом приборе вакуумной капсулы с ГБМ позволяет эксперимент по наблюдению Б.д. в вакууме и в состоянии невесомости проводить более качественно, поскольку при этом на микрочастицы не действует магнитное поле соленоида (хотя последний экранируется магнитным экраном от предметного столика, и эти компоненты экранировки для простоты не представлены на чертеже). Всякие вещества являются теоретически магнитовосприимчивыми, и магнитное поле, даже и ослабленное магнитным экраном, может частично изменить характер Б.д. наложением сил магнитного тяготения, которые могут оказаться больше сил гравитационного стягивания микрочастиц.
Следует, однако, отметить, что заявляемое техническое решение с соленоидом, магнитное действие которого приводит к однонаправленному дрейфу броуновских микрочастиц в направлении соленоида (для парамагнитных веществ) или в противоположном к нему направлению (для диамагнитных веществ), не препятствует использованию его для наблюдения Б.д. в вакууме. При использовании парамагнитного вещества для приготовления ГБМ наблюдение Б.д. в условиях дрейфа ГБМ к соленоиду может быть продолжено поднятием предметного столика при отключении соленоида от его источника питания и под действием растягивающей пружины с последующим включением соленоида. При использовании броуновских микрочастиц из диамагнитного вещества можно использовать встречный компенсирующий магнитный поток от противоположно установленного дополнительного соленоида, согласовав величину этого компенсирующего магнитного потока с потоком от соленоида, входящего в состав устройства управления положением предметного столика. Наконец, следует отметить, что броуновские микрочастицы не должны содержать какие-либо электрические заряды.
Фиксация Б.д. в вакууме на основе заявляемого технического решения в начале XX века не представлялась возможной, поскольку в то время космонавтика еще не существовала и состояние невесомости могло быть получено лишь на короткое время при падении исследующего прибора. Поэтому в то время Б.д. связывалось только с неуравновешенными соударениями молекул внешней среды (жидкой или газообразной) о микрочастицу. Наличие Б.д. в вакууме поэтому представляет новый физический результат, причиной которого являются хаотические колебательные движения молекул самих микрочастиц при ненулевой температуре этих микрочастиц. Возможность Б.д. полностью согласуется с фундаментальным законом физики - законом сохранения импульса (центра инерции). При этом ясно, что чем меньше масса микрочастиц, тем большие отклонения Δxj будет испытывать микрочастица. Математическое ожидание смещения центра инерции микрочастицы за достаточно большой промежуток времени равно нулю, хотя дисперсия растет пропорционально времени. Поэтому мы никогда не наблюдаем колебательного хаотического движения макротел, и Б.д. проявляется лишь для микрочастиц малой массы.
Теория Б. д. находит приложение в физической химии дисперсных систем, на ней основаны кинетическая теория коагуляции растворов (М.Смолуховский, 1916), теория седиментационного равновесия (равновесия дисперсных систем в поле тяготения или в поле центробежной силы). В метрологии Б.д. рассматривают как основной фактор, ограничивающий точность чувствительных измерительных приборов. Предел точности измерений оказывается достигнутым, когда флуктуационное (броуновское) смещение подвижных частей измерительного прибора по порядку величины совпадет со смещением, вызванным измеряемым эффектом.
Б.д. микрочастиц в вакууме в условиях отсутствия действующих на них внешних сил (при проведении эксперимента в условиях невесомости) указывает на необходимость уточнения этого классического феномена с учетом также и движущих сил, возникающих вследствие хаотического колебательного движения молекул (атомов) самих микрочастиц, хотя эти силы и оказываются существенно меньшими тех внешних сил, которые принимались в расчет при описании Б.д. для микрочастиц, помещенных в жидкости или газы.
Заявляемое устройство может быть изготовлено в институте физических проблем РАН и испытано в соответствующем космическом полете.
Источники информации
1. Эйнштейн А., Смолуховский М., Броуновское движение. Сб. ст., [пер. с нем. и франц.], М. - Л., 1936.
2. Чандрасекар С., Стохастические проблемы в физике и астрономии, пер. с англ., М., 1947.
3. Исихара А., Статистическая физика, пер. с англ., М., 1973.
4. Хир К., Статистическая механика, кинетическая теория и стохастические процессы, пер. с англ., М., 1978, гл. 10.
5. Lax М., Fluctuations from the no equilibrium steady state, "Revs Mod. Phys.", 1960, v. 32, p.25.
6. Kirkwood J. G., The statistical mechanical theory of transport processes. I, "J. Chem. Phys", 1946, v.14, p.180.
7. Lebowitz J.L., Rubin E., Dynamical study of Brownian motion, "Phys. Rev.", 1963. v.l 31, p.2381.
8. Green М. S., Markoff random processes and the statistical mechanics of time dependent phenomena. I-II.
9. "J. Chem. Phys.", 1952, v. 20, p.1281; 1954, v. 22, p.398. Д.Н.Зубарев.
10. Кац М., Вероятность и смежные вопросы в физике, пер. с англ., М., 1965.
11. Ахманов С.А., Дьяков Ю.Е., Чиркин А.С., Введение в статистическую радиофизику и оптику, М., 1981.
| название | год | авторы | номер документа |
|---|---|---|---|
| УСТРОЙСТВО ДЛЯ ОБНАРУЖЕНИЯ ТЕРМОДИНАМИЧЕСКОГО ВОЗМУЩЕНИЯ СОСТОЯНИЯ МИКРОЧАСТИЦ В ВАКУУМЕ | 2009 |
|
RU2402077C1 |
| ПРИБОР ДЛЯ РЕГИСТРАЦИИ ХАОТИЧЕСКОГО ДВИЖЕНИЯ ФЕРРОМИКРОЧАСТИЦ В ВАКУУМЕ В СОСТОЯНИИ НЕВЕСОМОСТИ | 2007 |
|
RU2359249C1 |
| МАГНИТНЫЙ ДВИГАТЕЛЬ | 2005 |
|
RU2310265C2 |
| СПОСОБ ПОЛУЧЕНИЯ ЭНЕРГИИ И УСТРОЙСТВО ДЛЯ ЕГО РЕАЛИЗАЦИИ | 2006 |
|
RU2332778C1 |
| МАГНИТОВЯЗКИЙ РОТАТОР | 2006 |
|
RU2325754C1 |
| ФЕРРОМАГНИТОВЯЗКИЙ РОТАТОР | 2005 |
|
RU2309527C2 |
| УСТРОЙСТВО ДЛЯ ПРОВЕРКИ ГИПОТЕЗЫ СИЛОВОЙ ОТДАЧИ НА ИСТОЧНИК ЗВУКОВОГО ВОЛНОВОГО ПОЛЯ | 2010 |
|
RU2439840C1 |
| УСТРОЙСТВО КОМПЕНСАЦИИ ФАРАДЕЕВСКОГО ВРАЩЕНИЯ ПЛОСКОСТИ ПОЛЯРИЗАЦИИ СВЕТА | 2008 |
|
RU2365957C1 |
| СПОСОБ ПОЛУЧЕНИЯ ЭНЕРГИИ И УСТРОЙСТВО ДЛЯ ЕГО РЕАЛИЗАЦИИ | 2010 |
|
RU2452074C1 |
| МАГНИТОВЯЗКИЙ МАЯТНИК | 2005 |
|
RU2291546C1 |
Изобретение относится к области физического приборостроения и может быть использовано при проведении научного эксперимента в космосе. Прибор для наблюдения броуновского движения микрочастиц включает прозрачную вакуумную колбу с помещенным в нее управляемым по положению предметным столиком, на котором размещена группа броуновских микрочастиц, направленный на группу броуновских микрочастиц микроскоп с устройством подсветки, совмещенный со съемочной камерой. Прибор установлен, например, в космическом аппарате. Наблюдение броуновского движения в группе броуновских микрочастиц происходит путем удаления предметного столика электромеханическим устройством с соленоидом.1 ил.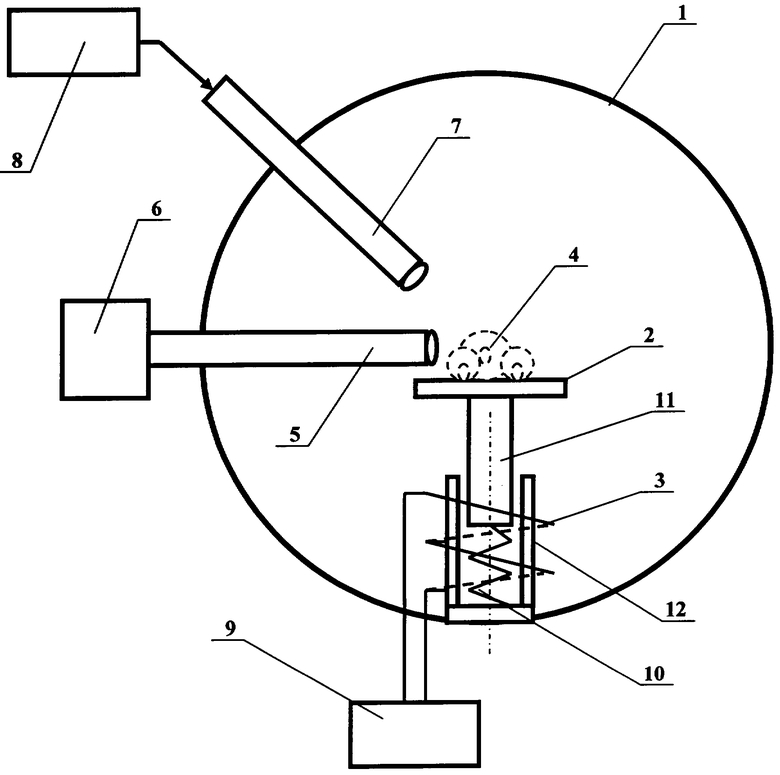
Прибор для наблюдения броуновского движения в вакууме, отличающийся тем, что включает прозрачную вакуумную колбу с помещенным в нее управляемым по положению предметным столиком, на котором размещена группа броуновских микрочастиц, направленный на группу броуновских микрочастиц микроскоп с устройством подсветки, совмещенный со съемочной камерой, а весь прибор установлен, например, в космическом аппарате (то есть находится в состоянии невесомости), причем наблюдение броуновского движения в группе броуновских микрочастиц происходит путем удаления предметного столика электромеханическим устройством с соленоидом.
| Устройство для наблюдения броуновского движения | 1990 |
|
SU1797142A1 |
| Устройство для демонстрации броуновского движения | 1991 |
|
SU1818628A1 |
| Учебный прибор по физике для демонстрации броуновского движения | 1981 |
|
SU1020855A1 |
Авторы
Даты
2009-01-10—Публикация
2007-04-19—Подача