Изобретение относится к области приборостроения, и в частности к физике магнетизма, и может быть использовано в качестве устройства преобразования магнитного поля в механическое вращательное движение.
Магнетизм - особая форма взаимодействия электрических токов и магнитов (тел с магнитным моментом) между собой и одних магнитов с другими магнитными материалами. Магнитное взаимодействие пространственно разнесенных тел осуществляется через магнитное поле Н, которое, как и электрическое поле Е, представляет собой проявление электромагнитной формы движения материи. Между магнитными и электрическими полями нет полной симметрии, так как источниками электрических полей являются электрические заряды, а магнитные заряды - монополя пока не обнаружены, хотя теория предсказывает их существование. Источник магнитного поля - движущийся электрический заряд, то есть электрический ток. В атомных масштабах движение электронов и протонов создает орбитальные микротоки, связанные с переносным движением этих частиц в атомах или атомных ядрах, кроме того, наличие у микрочастиц спина обусловливает существование у них спинового магнитного момента. Поскольку электроны, протоны и нейтроны, образующие атомные ядра, атомы, молекулы и все макротела (газы, жидкости, кристаллические и аморфные твердые тела) имеют собственный магнитный момент, то, в принципе, все вещества подвержены влиянию магнитного поля - обладают магнитными свойствами, то есть являются магнетиками. Магнетики подразделяются на диамагнетики, парамагнетики и ферромагнетики. Последние имеют наибольшую магнитную восприимчивость и используются в технике в качестве эффективных магнитов. В них атомные магнитные моменты спонтанно коллинеарно самоориентируются, образуя аномально большие магнитные моменты. У лучших современных магнитных материалов энергетическое произведение (ВН)max достигает величины 320 Т·кА/м (40 млн Гс·Э), например, у материала с высокой коэрцитивной силой SmCo3 (см., напр., Преображенский А.А., Биширд Е.Г., Магнитные материалы и элементы, 3 изд., М., 1986; Февралева И.Е., Магнитотвердые материалы и постоянные магниты. К., 1969; Постоянные магниты. Справочник, М., 1971).
Сложность атомной структуры веществ, построенных из огромного числа микрочастиц, дает практически неисчерпаемое разнообразие их магнитных свойств, связь которых с немагнитными свойствами (электрическими, механическими, оптическими и др.) позволяет использовать исследования магнитных свойств для получения информации о внутренней структуре и других свойствах микрочастиц и макротел. Отметим, что магниты обладают внутренней энергией. В случае однородного магнитного поля в объеме магнита V энергия запасенного магнитного поля W˜μ0H2V/2, где μ0=1,256·10-6 Гн/м - абсолютная магнитная проницаемость. Причем эта величина энергии практически не расходуется при силовых взаимодействиях с другими магнетиками и сохраняется благодаря постоянному движению заряженных микрочастиц вещества.
Источником является вещество магнитов, обладающее запасом магнитной энергии, который за счет процессов, происходящих на микроуровне (атомов и молекул вещества), непрерывно восполняется, а точнее, поддерживается на неизменном уровне, если не считать факторов, приводящих к так называемому старению магнитов.
Известный принцип возрастания энтропии и первое и второе начала термодинамики оперируют с теплоэнергетическими преобразованиями, которые всегда (кроме состояния равновесия) идут с затратой энергии при совершении какой-либо работы, большей той, которая составляет саму проделанную работу, а часть затраченной энергии безвозвратно превращается в тепловую. Поэтому кпд всех известных преобразователей энергии всегда меньше единицы. Однако в микромире действует иной процесс: движение микрочастиц обусловлено тепловой энергией - импульс р движения микрочастиц массой m1 определяется как р2/2m1=(3/2)kT0, где k - постоянная Больцмана, Т0 - температура по шкале Кельвина, а соударения микрочастиц между собой вызывают тепловые процессы - среда нагревается, то есть происходит самовоспроизводящийся обмен энергией, при котором беспредметно говорить о тепловых потерях, поскольку тепловая энергия и является источником движения микрочастиц, а это движение порождает саму тепловую энергию. На поддержание хаотического движения микрочастиц и, следовательно, хаотического распределения магнитных моментов (спинов) в веществе, при котором оно не обнаруживает ощутимых магнитных свойств, затрачивается, по-видимому, больше энергии, чем для тех микрочастиц, которые имеют упорядоченное расположение их магнитных моментов. Поэтому высвободившаяся в результате упорядочения микрочастиц (доменов) часть энергии как раз и составляет энергию магнитного поля. Эта энергия самовосполняемая, определяемая природой процессов превращения энергии на микроуровне.
Для ферромагнетиков, подчиняющихся закону Кюри, существует так называемая критическая температура Θ, при которой магнитная восприимчивость становится сравнимой с единицей или даже становится меньшей единицы, и вещество становится из парамагнитного диамагнитным (закон Кюри-Вейсса), то есть магнитная восприимчивость зависит от действия различных факторов - температуры, величины напряженности магнитного поля, механического напряжения и некоторых других.
Одним из интересных свойств ферромагнитных материалов является их так называемая магнитная вязкость, магнитное последействие - отставание по времени намагниченности ферромагнетика от изменения напряженности магнитного поля. В наиболее простых случаях изменение намагниченности ΔJ в зависимости от времени t описывается формулой
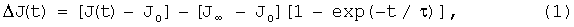
где J0 и J∞ - соответственно значения намагниченности непосредственно после изменения напряженности Н магнитного поля в момент t=0 и после установления нового равновесного состояния, τ - константа, характеризующая скорость процесса и называемая постоянной времени релаксации. Значение τ зависит от природы магнитной вязкости и в различных материалах может изменяться от 10-9 с до нескольких десятков часов. В общем случае для описания процесса последействия одного значения τ недостаточно.
Различают два вида магнитной вязкости: диффузионный (рихтеровский) и термофлук-туационный (иордановский). В первом из них магнитная вязкость определяется диффузией примесных атомов или дефектов кристаллической структуры. Объяснение роли примесей было дано J.Snock, а более строгая теория построена L.Neel и базируется на предположении о преимущественной диффузии примесных атомов в те межатомные промежутки кристалла, которые определенным образом ориентированы относительно направления спонтанной намагниченности. Это создает локальную наведенную анизотропию, приводящую к стабилизации доменной структуры. Поэтому после изменения магнитного поля новая доменная структура устанавливается не сразу, а после диффузного перераспределения примеси, что и является причиной магнитной вязкости.
Второй вид магнитной вязкости более универсален и наблюдается практически во всех ферромагнетиках, особенно в области магнитных полей, сравнимых с коэрцитивной силой. Неелем был предложен термофлуктуационный механизм для объяснения этого вида магнитной вязкости. Тепловые флуктуации способствуют преодолению доменными стенками энергетических барьеров в магнитных полях, меньших критического поля. В высококоэрцитивных сплавах, состоящих из однодоменных областей, наблюдается особенно большая магнитная вязкость, так как в этом случае термические флуктуации сообщают дополнительную энергию для необратимого вращения спонтанной намагниченности тех частиц, потенциальная энергия которых во внешнем магнитном поле недостаточна для их перемагничивания.
Кроме этих основных механизмов магнитной вязкости, существуют и другие. Например, в некоторых ферритах вклад магнитной вязкости дает перераспределение электронной плотности (диффузия электронов между ионами разной валентности). С магнитной вязкостью тесно связаны такие явления в ферромагнетиках, как потери на перемагничивание, временной спад относительной магнитной проницаемости μ и ее частотная зависимость (см., напр., Kronmuller H., Nachwirkung in Ferromsgnetika, 1068; С.В.Вонсовский, Магнетизм, М., 1971; Д.Д.Мишин, Магнитные материалы, М., 1981).
Известное свойство магнитной вязкости ферромагнетиков использовано в заявляемом техническом решении. В качестве ближайшего аналога (прототипа) заявляемому техническому решению является устройство «Магнитовязкий маятник», известное из заявки того же автора №2005111823/28 (013701) от 20.04.2005, по которой отделом измерительной техники и приборостроения ФИПС 06.09.2006 вынесено решение о выдаче патента РФ на изобретение.
В устройстве-прототипе использован постоянный магнит с насыщающим магнитным полем для ферромагнитного тела из магнитовязкого материала, подвешенного на пружине и совершающего колебательное движение относительно магнитного зазора постоянного магнита, причем постоянная релаксации магнитной вязкости тела из ферромагнитного материала выбрана соизмеримой, например, с одной десятой периода свободных колебаний этого тела.
Недостатком известного устройства является относительно малая его энергетическая эффективность, обусловленная низкочастотностью механических колебаний.
Указанный недостаток устранен в заявляемом техническом решении.
Целью изобретения является повышение частоты вращательного движения насыщающегося магнитовязкого ферромагнитного диска (кольца) в поле постоянного магнита.
Указанная цель достигается в устройстве - магнитовязком ротаторе, содержащем постоянный магнит и связанное с ним ферромагнитное тело, отличающемся тем, что ферромагнитное тело выполнено в виде вращающегося на оси диска (кольца) между полюсами постоянного магнита и состоит из ферромагнитного материала с магнитной вязкостью, постоянная релаксации τ которой по отношению к периоду Т вращения ферромагнитного диска (кольца) выбрана, например, из условия τ˜ТХ0/4,4πR, где Х0 - длина магнитного зазора между полюсами постоянного магнита (с однородным или неоднородным магнитным полем в зазоре), в который помещен край ферромагнитного диска (кольца) радиуса R, при этом напряженность магнитного поля в зазоре постоянного магнита выбрана насыщающей для материала ферромагнитного диска (кольца).
Поставленная цель в заявляемом техническом решении достигается благодаря замене колебательного движения некоторой массы ферромагнитного тела на ее вращательное движение и отставанию в динамике вращательного движения ферромагнитного диска (кольца) его магнитного «центра тяжести» размещенной в поле постоянного магнита части ферромагнитного диска (кольца) от центра притяжения постоянного магнита, что создает тангенциальную силу тяготения со стороны постоянного магнита, приложенную к краевой части ферромагнитного диска (кольца), в результате чего возникает вращательный момент, поддерживающий вращательное движение ферромагнитного диска (кольца) с угловой скоростью, определяемой постоянной релаксации магнитной вязкости ферромагнитного материала диска (кольца). В случае однородного магнитного поля в зазоре между полюсами постоянного магнита реализуется так называемый «жесткий режим» самовозбуждения вращательного движения, при котором необходимо принудительно (под действием внешних сил) привести ферромагнитный диск (кольцо) во вращательное движение с необходимой угловой скоростью. В случае неоднородного магнитного поля с заданным градиентом вдоль касательной к краевой части ферромагнитного диска (кольца), находящейся в магнитном зазоре, реализуется так называемый «мягкий режим» самовозбуждения, при котором ферромагнитный диск (кольцо) постоянно испытывает втягивающее усилие со стороны магнитного поля постоянного магнита в направлении градиента напряженности этого поля и поэтому приходит в ускоренное вращательное движение в переходном процессе, доводя угловую скорость вращения до некоторой величины, определяемой постоянной релаксации магнитной вязкости выбранного ферромагнитного материала. По мере достижения указанной угловой скорости магнитный «центр тяжести» части ферромагнитного диска (кольца), связанной с магнитным полем постоянного магнита, смещен относительно центра тяготения поля постоянного магнита, и эта величина смещения между указанными центрами определяет постоянно действующий вращательный момент, уравновешиваемый величиной момента трения (нагрузочного момента) в ротаторе, пропорционально возрастающего с увеличением угловой скорости вращения ферромагнитного диска (кольца). Отставание магнитного «центра тяжести» вышеуказанной части ферромагнитного диска (кольца) от центра притяжения магнитного поля постоянного магнита определяется магнитной вязкостью, при которой дифференциальные объемы указанной части ферромагнитного диска (кольца), более длительное время находящиеся в насыщающем магнитном поле постоянного магнита, в большей степени уменьшают свою магнитную восприимчивость, чем дифференциальные объемы, магнитное насыщение в которых еще не наступило. Это создает перераспределение в указанной части ферромагнитного диска (кольца) величин магнитной восприимчивости, градиент которой направлен противоположно к вектору действующей на ферромагнитный диск (кольцо) силы со стороны магнитного поля постоянного магнита. В такой системе магнитное поле постоянного магнита является статическим, а роль его временного изменения в тангенциальном направлении выполняют краевые участки ферромагнитного диска (кольца) с переменными параметрами магнитной восприимчивости, то есть система является параметрическим генератором вращательного движения. Замена колебательного движения ферромагнитной массы на ее вращательное движение в заявляемом техническом решении энергетически более эффективно, так как можно использовать достаточно быстрое вращение этой массы.
Заявляемое техническое решение будет понятно из представленных чертежей.
На фиг.1 приведено одно из возможных конструктивных решений поставленной задачи. Устройство состоит из ферромагнитного диска 1 с осью его вращения 2, краевая часть диска помещена в магнитный зазор постоянного магнита 3, образованный между полюсами 4 и 5 магнита. При этом рассматривается вариант неоднородного магнитного поля в зазоре.
Ниже на фиг.1 изображена схема взаимного расположения части ферромагнитного диска 1 в магнитном зазоре между полюсами 4 и 5 магнита 3, которые развернуты друг по отношению к другу на некоторый угол, в результате чего в зазоре образуется неоднородное магнитное поле Н(х), изменение которого вдоль оси х показано на графике внизу фиг.1. Штрихпунктирной линией на этом графике показано изменение магнитной восприимчивости J(x) в статике, как если бы диск 1 не вращался, обусловленное действием на ферромагнетик разного по напряженности магнитного поля.
Зависимость магнитной индукции В в ферромагнетике от величины напряженности магнитного поля Н приведена на фиг.2. При этом полагаем, что с правого края магнитного зазора на фиг.1 напряженность магнитного поля выбрана равной Нmin, как указано на фиг.2, а на левом краю этого магнитного зазора она равна максимальному значению Нмах. Кривая намагничивания ферромагнетика определяется по формуле В(Н)=μ0μ(Н)Н.
В соответствии с указанной на фиг.2 характеристикой В(Н) статическая характеристика зависимости удельной магнитной восприимчивости χ=J/ρ(ρ - плотность ферромагнитного вещества) приведена на фиг.3, из которой видно, что ферромагнитное вещество, входящее в магнитный зазор с его правого края, имеет максимальное значение относительной магнитной проницаемости μмах, а выходящее с его левого края - минимальное μmin. При этом из графика фиг.1 видно, что внутри зазора в статическом режиме (без вращения ферромагнитного диска) происходит насыщение ферромагнитного материала, что смещает вправо (относительно выбранной оси X) его магнитный «центр тяжести» относительно центра тяготения магнитного поля магнита 3. Положение последнего в случае однородного магнитного поля в магнитном зазоре находится посередине магнитного зазора (х=Х0/2), а в случае неоднородного поля (как на фиг.1) центр тяготения смещен влево от середины магнитного зазора и имеет координату х=X*>Х0/2, где Х0 - длина магнитного зазора. Кривая удельной магнитной восприимчивости χ(Н)=(В-μ0Н)/μ0Нρ=[μ(Н)-1]/ρ с ее рабочим участком в форме спадающей квазилинейной функции с отрицательной производной, где частная производная для относительной магнитной проницаемости ферромагнитного материала отрицательна (∂μ(Н)/∂Н<0) в заданной области магнитного поля и характеризуется для выбранного ферромагнитного вещества его отношением минимальной к максимальной относительной магнитной проницаемости, равным β= =μmin/μmax<1, соответственно для магнитного поля в конце и в начале магнитной системы с зазором длиной Х0. При этом градиент для величины относительной магнитной проницаемости ферромагнитного вещества grad[μ(H)]=∂μ(Н)/∂Н=-(1-β)μmax/Х0<0.
На фиг.4 представлен график для определения относительного положения центра тяготения магнитного поля постоянного магнита при неоднородном магнитном поле в зазоре, обозначаемый как ξ=Х*/Х0, в функции перепада напряженностей магнитного поля по краям магнитного зазора α=Нмах/Hmin на его длине Х0. При этом градиент магнитного поля в зазоре направлен вдоль оси х и равен

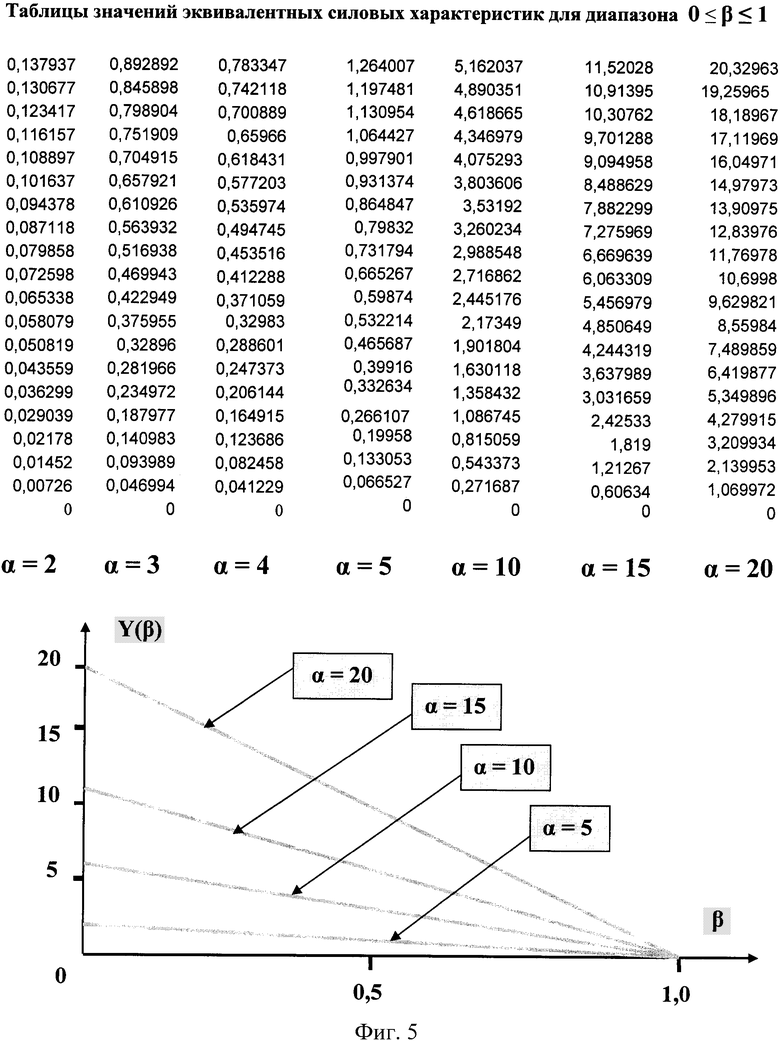
На фиг.5 приведены расчетная таблица эквивалентных силовых характеристик Y(β) для различных значений перепада α напряженности магнитного поля в зазоре магнита, а также графики к этим таблицам для нескольких значений α. О значении функции Y(β), где 0<β=μmin/μmax<1, будет указано ниже.
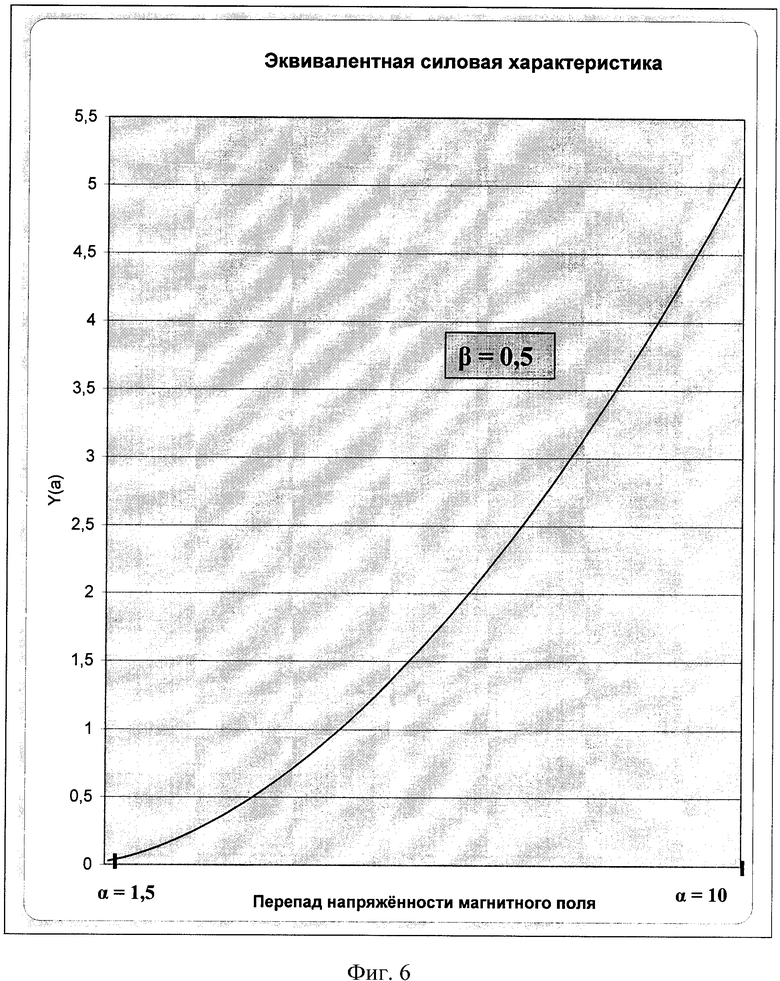
Зависимость Y(α) при фиксированном значении β=0,5 графически представлена на фиг.6, что указывает на нелинейный характер эквивалентной силовой характеристики от величины перепада α напряженности магнитного поля в зазоре постоянного магнита.
На фиг.7 представлена схема магнитовязкого ротатора, краевая часть ферромагнитного диска (кольца) которого размещена в зазоре постоянного магнита с однородным магнитным полем (gradH(х)=0).
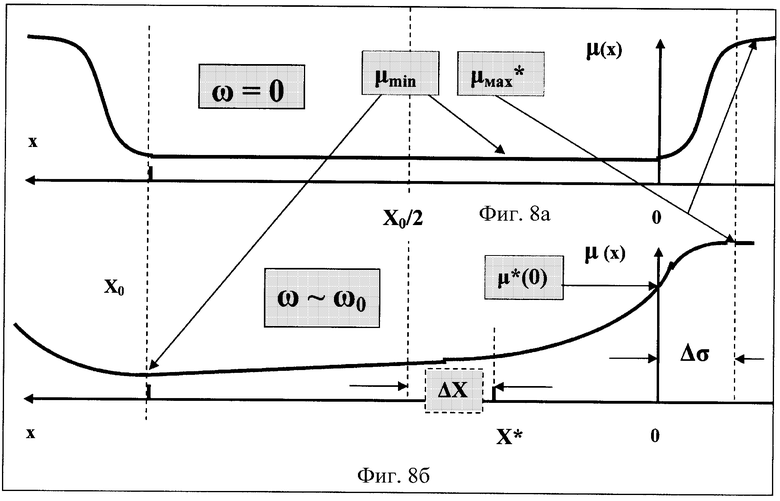
На фиг.8а представлен график функции μ(х) при неподвижном ферромагнитном диске (кольце) при ω=0, а на фиг.8б - график μ(x) при условии вращения ферритового диска (кольца) с угловой скоростью ω=ω0, согласующейся с постоянной релаксации магнитовязкого ферромагнетика τ с учетом (1).
На фиг.9 приведена модификация заявляемого технического решения для повышения эффективности его действия.
Рассмотрим действие заявляемого технического решения, представленного на фиг.1.
Рассмотрим на первом этапе относительное положение центра тяготения магнитной системы, например, в магнитном зазоре (на фиг.1), то есть найдем величину ξ(α)=Х*/Х0. Пусть пунктирная линия, восстановленная по координате х=X*, определяет поперечное сечение магнитного зазора, совпадающее с центром тяготения магнитной системы. Для нахождения этого значения X* вычислим интегралы для энергий магнитного поля в объемах зазора в интервале [0-X*] и в интервале [X*-Х0]. Приравняв значения полученных интегралов, найдем искомую величину X*:

с учетом заданного распределения напряженности магнитного поля вдоль координаты х интегрирования, например, линейного с градиентом gradH(х)=∂H/∂х=(Нmax-Hmin)/Х0 с крутизной α=Нmax/Hmin>1, где минимальная напряженность магнитного поля Нmin соответствует координате х=0, а максимальная Нmax - координате х=Х0.
Вычислив интегралы (3), находим относительную величину центра тяготения магнитной системы по формуле:
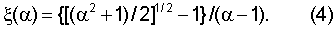
Расчет по этой формуле при различных значениях аргумента α (от 1 до 30) приведен в таблице на фиг.4, согласно таблице построен график этой функции (значение ее для аргумента α=1 вычислялось по правилу Лопиталя). Из приведенных расчетов видно, что в сильно неоднородном поле значение ξ(α) асимптотически приближается к значению 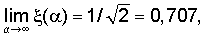 и притом достаточно быстро. Так, если перепад напряженности магнитного поля на концах магнитного зазора равен α=10, то при длине зазора Х0=10 см положение центра тяготения магнитной системы расположено от правого края зазора на расстоянии X*=67,85 мм.
и притом достаточно быстро. Так, если перепад напряженности магнитного поля на концах магнитного зазора равен α=10, то при длине зазора Х0=10 см положение центра тяготения магнитной системы расположено от правого края зазора на расстоянии X*=67,85 мм.
Из теории магнитостатики известно, что сила магнитного тяготения магнитного тела с магнитным моментом М в неоднородном магнитном поле с градиентом вдоль оси х, равным gradH(х)=∂H/∂x=Нmin(α-1)/Х0, вычисляется согласно выражению:


где величина магнитного момента М=JV=(В-μ0Н)V=(μ-1)μ0HV (здесь V - объем магнитного тела, J - его намагниченность).
С учетом неоднородности магнитного поля Н(х)=Нmin[1+(α-1)х/Х0] и неоднородности относительной магнитной проницаемости ферромагнитного вещества, находящегося в магнитном зазоре с неоднородным магнитным полем, μ[Н(х)]=μ(х)=μmax[1-(1-β/)x/Х0], где μmax - начальное значение относительной магнитной проницаемости ферритового вещества в начале магнитного зазора при х=0, для дифференциала силы dF(x), действующей на заданный дифференциальный объем ферромагнитного вещества dv со стороны магнитного поля, согласно (5) и с учетом того, что имеем ферромагнитное вещество, для которого μ(Н) в заданном диапазоне напряженностей магнитного поля существенно больше единицы, что позволяет в расчетах вместо μ-1 использовать величину μ, получаем общее выражение:
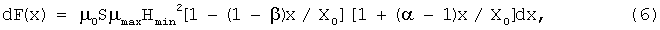
где S=dv/dx - сечение краевой части ферромагнитного диска в магнитном зазоре.
Выражение (6) учитывает как изменение напряженности магнитного поля Н(х), так и изменение относительной магнитной проницаемости μ(Н) ферромагнитного вещества в зазоре постоянного магнита 3 (фиг.1) по координате х. Будем для простоты расчета полагать, что величины α и β являются постоянными, не зависящими от координаты х, то есть работа устройства происходит на линейных участках: gradH(х)=const и gradμ(х)=const. Тогда можно вычислить интегралы действующих встречно сил:
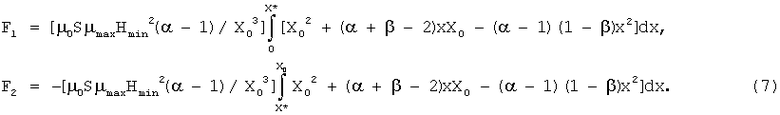
Равнодействующую силу ΔF=F1+F2 согласно выражениям (7) получим несложным вычислением:
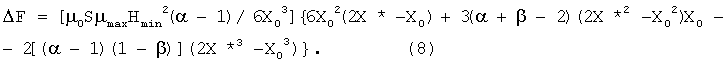
Учитывая выражение (4), для выражения (8) получаем:

Поскольку, как мы выяснили выше, величина ξ(α)≤(2)-1/2=0,707, то выражение (9) удобнее записать в форме:

Величина μ0SμmaxНmin 2/6, вообще говоря, является известной, параметр α также является известным для конкретной конструкции устройства, поэтому выражение (10) с учетом уравнения (4) полностью определяют значения β (в форме неравенства), при которых равнодействующая сила ΔF>0, и ферромагнитный диск (фиг.1) испытывает вращательный момент.
Найдем граничные значения β0, при которых ΔF=0, и решим (10) относительно этой граничной величины β0, полагая величины α и ξ(α) известными заданными числами. Поскольку μ0SμmaxHmin 2(α-1)/6>0 при α>1 - есть общий множитель выражения (10), то соответствующее уравнение для β0 имеет вид:
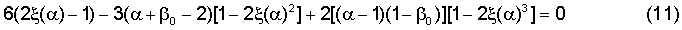
откуда находим значение β0 в явном виде:

и при этом выражение (12) обозначает условие в форме соотношения между величинами α и β0, при выполнении которого равнодействующая сила ΔF=0. Из таблицы на фиг.4 для значения α=10 имеем ξ(а)=0,6785. Подставляя эти значения в (12), получим для значения β0=1. Аналогичный результат для величины β0 получается при любых других значениях α, что усматривается из исследования зависимости β0(α) на основе (12) и (4) при расчете по программе на Microsoft Excel, и при этом величина β0(α)=const(α)=1.
Величина самой силы ΔF>0, естественно, определяется как напряженностью магнитного поля Hmin, ее перепадом α, максимальным значением относительной магнитной проницаемости μmax в начале магнитного зазора ферромагнитного диска (при х=0), так и значением β применяемого для диска ферромагнитного материала (чем меньше величина β, тем большая возникает сила втягивания диска в магнитный зазор). Эта сила рассчитывается по формуле (10), которую целесообразно переписать в более удобном для анализа виде:
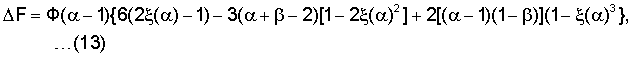
где Ф=μ0SμmaxНmin 2/6=const(α, β) - некоторая постоянная величина, определяемая начальными конструктивными параметрами устройства (магнитной системы и ферромагнитного диска).
Найдем зависимость ΔF как функцию β<1 при каком-либо заданном значении параметра α, например, для α=10. Так, для данного параметра перепада напряженности магнитного поля в зазоре магнитной системы имеем следующие значения множителей выражения (13):
2ξ(α)-1=0,35403; 1-2ξ(α)2=0,07933; 1-ξ(α)3=0,37534. Тогда при β=0,5 получаем выражение ΔF(10; 0,5)=1,5 μ0SμmaxНmin 2[6·0,35403-3·8,5·0,07933+2·4,5·0,37534]=5,21899μ0SμmaxHmin 2.
Построим семейство функций Y(β)=ΔF/μ0SμmaxHmin 2 при различных значениях параметра α по соответствующей программе Microsoft Excel (см. фиг.5). Эти функции Y(β) являются эквивалентными силовыми характеристиками (ЭСХ) рассматриваемого преобразователя энергии. Проведенные расчеты показали, что ЭСХ являются линейными функциями относительно β, сходящиеся в одной точке на оси абсцисс β=1, как это следовало из таблицы для функции (10). С увеличением параметра α неоднородности магнитного поля наклон ЭСХ также возрастает, хотя и нелинейно, что усматривается из семейства ЭСХ на фиг.6. Это означает, что для увеличения мощности преобразователя следует выбирать ферромагнитные вещества с малым значением β, а также возможно большее значение неоднородности магнитного поля α. Как и следовало ожидать, при значении β=1 никакого вращательного момента ферромагнитному диску не сообщается. Также не возникает вращающий момент в ферромагнитном диске при α=1, когда магнитное поле в магнитном зазоре однородно, но только если не учитывать магнитную вязкость, о чем будет сказано ниже. Кроме указанного, мощность ротатора определяется согласно (13) квадратом Нmin 2 минимальной напряженности магнитного поля в начале магнитного зазора и наибольшей величиной относительной магнитной проницаемости ферромагнитного материала диска μмах. При этом желательно выбирать значение Нmin такой величины, при которой относительная магнитная проницаемость μ˜μмах, как показано на фиг.4 (вблизи максимума кривой Столетова), а величина Нмах должна выбираться так, чтобы происходило насыщение ферромагнитного вещества вблизи сечения магнитного зазора на расстоянии X*, то есть вблизи центра тяготения магнитной системы (см. фиг.1) и далее за ним по ходу вращения диска.
Из таблицы на фиг.5 видно, что имеет место нелинейная зависимость ЭСХ по параметру неоднородности магнитного поля α, поэтому представляет интерес исследовать функцию Y(β) по параметру α. Зададимся каким-либо промежуточным значением β, например β=0,5, и найдем по ранее составленной программе значения Y(α)|β. Результат вычислений приведен на графике фиг.6, который указывает на наличие нелинейности ЭСХ по параметру α.
Если говорить о коэффициенте полезного действия данного устройства, имея в виду то, как тратится энергия магнитного поля на создание вращающего момента в ферромагнитном диске, то можно принять значение кпд как отношение разностной силы ΔF, производящей механическую работу, к сумме ее составляющих F1+F2, указанных в (7), определяемых полной энергией магнитного поля, то есть кпд преобразователя можно считать равным η=[(F1-|F2|)/(F1+|F2|)]*100%. Нетрудно понять, что сумма модулей указанных сил (направленных взаимно встречно) определяется интегралом типа (7), взятым по полному пределу от х=0 до х=X0. Соответствующее интегрирование приводит к результату вида:
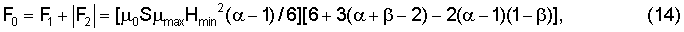
так что с учетом (10) для кпд получаем выражение:

Например, для α=10 имеем значения величин 2ξ(α)-1=0,35696, 1-2ξ(α)2=0,07933 и 1-2ξ(α)3=0,37534, так что при задании величины β=0,1 получим значение кпд такого устройства η=[6·0,35696-3·8,1·0,07933+16,2·0,37534]//(6+3·8,1-16,2)-6,2946/14,1=0,4464=44,6%. Для сравнения при α=2 и β=0,5 (соответствующие значения 2ξ(α)-1=0,16228, 1-2ξ(α)2=0,32456, 1-2ξ(α)3=0,60747) для кпд получим η=(6·0,16228-3·0,5·0,32456+2·0,5·0,60747)/(6+1,5-1)=1,1043/6,5=0,1699=17%. Таким образом, кпд устройства или, как более правильно сказать, коэффициент использования энергии магнитного поля растет с увеличением степени неоднородности поля в зазоре и при применении ферромагнитных материалов с большим отношением максимальной и минимальной относительной магнитной проницаемости (по кривой Столетова на фиг.4), то есть с ростом отношения α/β.
Коэффициент использования энергии (КИЭ) магнитного поля не подменяет понятия кпд, принятого в физике как отношения полезной работы к затраченной, поскольку получение механической работы от вращения ферромагнитного диска не связано с какими-либо внешне (макроскопически) проявляемыми затратами энергии (тепловой, электрической, химической, оптической и др. видов энергии). Поставщиком энергии выступает магнитное поле, возникающее вследствие процессов взаимодействия микрочастиц магнитного вещества на молекулярном и (или) доменном уровне, внешне феноменологически никак не проявляемых, скрытых от непосредственного наблюдения и измерения.
Согласно (10) можно рассчитать конкретную силу ΔF, создающую вращающий момент m=ΔF×r в диске радиуса r. Пусть имеем магнитное поле Нmin=6 кА/м, ферромагнитный материал с μмах=1000, сечение кромки ферромагнитного диска в магнитном зазоре S=50 мм2=5·10-5 м2, α=10 и β=0,1. Воспользовавшись полученными при расчете данными, получим ΔF=21,34 Н. При радиусе диска r=0,1 м момент вращения диска будет m=2,134 Н·м. Задавшись величиной момента трения в механическом приводе диска mтр=0,1 Н·м, получим полезную мощность в нагрузке Nн=(m-mтр)ω, где ω - угловая скорость вращения диска. При скорости вращения диска n=ω/2π=50 с-1 снимаемая мощность в нагрузке будет Nн=638,68 Вт. В качестве нагрузки может быть использован электрический генератор с кпд порядка 80%, что определит полезную выходную электрическую мощность Рэл=500 Вт.
В проведенном анализе втягивающего действия неоднородного магнитного поля на ферромагнитный диск (кольцо) с изменяющейся в функции магнитного поля относительной магнитной проницаемостью (фиг.3) при работе на падающем участке характеристики μ(Н), на котором dμ/dH<0, не использовалось свойство магнитной вязкости ферромагнетика. При этом было указано выше, что при однородном магнитном поле в зазоре постоянного магнита (α=1) никакого вращения ферромагнитного диска (кольца) производиться не будет. Иначе обстоит дело при учете магнитной вязкости ферромагнитного материала.
Обратимся к рассмотрению работы ротатора по схеме фиг.7. В однородном магнитном поле в зазоре постоянного магнита между полюсами 4 и 5 (как на фиг.1) Н(х)=const(х) на участке 0≤x≤X0 и достаточно резко падает вне этого участка по квазиэкспоненциальному закону. Это изображено на графике фиг.7. В соответствии с таким распределением напряженности магнитного поля участок ферромагнитного диска (кольца), связанный с этим полем, будет иметь относительную магнитную проницаемость μ(х) в виде функций, изображенных на фиг.8а - для неподвижного (ω=0) диска (кольца) и на фиг.8б - для вращающегося диска (кольца) с угловой скоростью ω˜ω0, где ω0 - согласованная с постоянной релаксации τ магнитной вязкости ферромагнетика диска (кольца) 1 и моментом трения (нагрузки) установившаяся угловая скорость ротатора. Согласование ω0 с постоянной τ означает следующее. Пусть радиус диска (кольца) 1 равен R, тогда при угловой скорости ω0 край диска (кольца) в магнитном зазоре длиной Х0 имеет линейную скорость V=ω0R, и каждая точка радиального кольца ферромагнетика пробегает длину магнитного зазора за время Δt=Х0/ω0R. Полагая, что за время Δt относительная магнитная проницаемость ферромагнетика в магнитном зазоре успевает снизиться с некоторой величины μ*(0), соответствующей моменту времени t=0, в который рассматриваемая точка кромки ферромагнитного диска (кольца) начинает входить в магнитный зазор и ее координата х=0, до минимальной величины μmin под действием магнитного поля напряженностью Н0, можно найти связь между величинами ω0 и τ на основании известного приближения, что Δt=2,2τ, откуда получаем ω0=Х0/2,2Rτ. Период вращения Т=2π/ω0 диска (кольца) при этом равен Т=4,4πRτ/Х0. При этом под величиной R следует понимать средний радиус кольцевой кромки диска (кольца), ширина которой равна ширине h магнитного зазора постоянного магнита 3 (фиг.1). Полагая, что R>>h, в расчетах можно, в первом приближении, брать величину R соответствующей полному радиусу ферромагнитного диска (кольца). Тогда окончательно получаем для значения выбираемой постоянной релаксации τ магнитной вязкости ферромагнитного материала формулу τ=(X0/4,4πR)T. При задании соотношения размеров R/Х0=р>>1, имеем связь вида τ=Т/4,4πр<<Т.
Так, при R=0,5 м, Х0=0,05 м получаем для отношения τ/Т=1/44π=0,00724. Это соотношение отражено в редакции формулы изобретения.
Функция относительной магнитной проницаемости μ(x) для неподвижного ферромагнитного диска (кольца) изображена на фиг.8а, и из ее рассмотрения видно, что центр притяжения магнитного поля, имеющий по оси х координату х=X0/2, точно совпадает с «центром тяжести» находящейся в магнитном зазоре части (кромки) ферромагнитного диска (кольца) X*. Это объясняет невозможность самовращения ферромагнитного диска (кольца), поскольку на диск (кольцо) со стороны магнитного поля не действует какая-либо сила.
Указанная кривая симметрична относительно центра тяготения, что и обеспечивает равенство X*=Х0/2, при соблюдении которого отсутствует вращающий момент в ферромагнитном диске(кольце).
В динамике вращения ферромагнитного диска (кольца), совмещенного с магнитным зазором длиной Х0, из-за запаздывания в установлении относительной магнитной проницаемости различных дифференциальных объемов dv=Sdx, находящихся в магнитном зазоре постоянного магнита, относительно той ее величины, какая была бы в установившемся режиме (при t→∞), а именно от величины μmin, кривая распределения μ(х) становится существенно несимметричной относительно центра тяготения магнитного поля с той же координатой х=X0/2, как показано на фиг.8б. Легко понять, что при этом «центр тяжести» краевой части ферромагнитного диска (кольца), находящейся как внутри магнитного зазора, так и по его краям, оказывается смещенным вправо на фиг.8б, то есть в сторону от центра тяготения магнитного поля, противоположную направлению вращения ферромагнитного диска (кольца), и имеет координату х=X*, отстоящую от координаты центра тяготения магнитного поля Х=Х0/2 на величину ΔХ=(Х0/2)-X*, как это показано на фиг.8б. Наличие смещения ΔХ>0 указывает на возникновение постоянно действующей на ферромагнитный диск (кольцо) силы со стороны магнитного поля постоянного магнита, что и поддерживает вращательное движение диска (кольца), если при этом момент трения может быть преодолен вращающим моментом m=ΔF×R. Вращение происходит с угловой скоростью, приблизительно равной ω0, или несколько меньшей ее из-за действия момента трения (внешней нагрузки), что связано с неточным выполнением требования подбора постоянной релаксации τ магнитной вязкости выбираемого для диска (кольца) ферроматериала, что, впрочем, может быть скорректировано изменением геометрии устройства (радиуса диска R, длины магнитного зазора Х0), чтобы обеспечить соблюдение условия, указанного в формуле изобретения. Отметим, что, вместо физического изменения радиуса ферромагнитного диска (кольца), добиться того же изменения геометрии можно смещением вдоль радиуса диска 1 (кольца) постоянного магнита 3 (фиг.1), что эквивалентно изменению параметра R.
Для определения координаты X* «центра тяжести» краевой части ферромагнитного диска (кольца) в заданном магнитном зазоре постоянного магнита при условии вращения диска (фиг.8б) с угловой скоростью ω0, необходимо решить интегральное уравнение вида
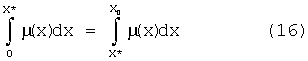
относительно неизвестной величины X* с учетом вида функции μ(x), которая является в данном случае однородного магнитного поля в зазоре постоянного магнита экспоненциальной функцией типа (1). В момент времени t=0, как уже было указано выше, дифференциальный объем ферромагнитного диска (кольца) с координатой x=0 имеет относительную магнитную проницаемость, обозначенную как μ*(0), численное значение которой достаточно близко к максимальному значению относительной магнитной проницаемости ферромагнетика μ*мах в отсутствии магнитного поля (Н=0). Величина μ*(0)<μ*мах на некоторую незначительную величину за счет того, что на отрезке Δσ, указанном на фиг.8б, действие магнитного поля вне магнитного зазора несколько уменьшит относительную магнитную проницаемость за короткий отрезок времени Δσ/ω0R<Δt=Х0/ω0R, поскольку Х0 существенно больше величины отрезка Δσ, внутри которого имеется квазиэкспоненциально изменяющееся магнитное поле (см. фиг.7). Строго говоря, с учетом фиг.2 и фиг.3 можно утверждать, что начальное действие краевого магнитного поля на участке Δσ сначала будет увеличивать относительную магнитную проницаемость выше величины, соответствующей отсутствующему магнитному полю, - стремить ее к значению μмах по экспоненциальному закону, и лишь затем вблизи правого края магнитного зазора постоянного магнита, когда напряженность магнитного поля станет выше НC (фиг.3), относительная магнитная проницаемость станет снижаться до величины μ*(0)˜μмах>μ*мах.
Полагая, в первом приближении, что μ*(0)˜μмах, можно записать уравнение для распределения μ(х) внутри магнитного зазора (на отрезке 0≤х≤Х0) в виде


Тогда при подстановке (17) в (16) и замене переменной (при ξ=Х*/Х0) получим

откуда находим вычислением интегралов (18) относительное положение «центра тяжести» ξ=Х*/Х0=0,38. Таким образом, смещение вправо на фиг.8б «центра тяжести» от центра тяготения магнитного поля составляет относительную величину

что и доказывает наличие постоянно действующей силы, оказываемой магнитным полем на вращающийся ферромагнитный диск (кольцо) с угловой скоростью ˜ω0.
Для коррекции начальной величины входящей в магнитный зазор части ферромагнетика относительной магнитной проницаемости (доведения ее до величины μмах) может быть несколько увеличена длина магнитного зазора X0, что следует из рассмотрения фиг.3.
Интересно отметить, что выходящие из магнитного зазора части ферромагнитного диска (кольца) имеют минимальную величину относительной магнитной проницаемости μmin и, двигаясь достаточно быстро, не успевают в ослабевающем магнитном поле восстановить свою относительную магнитную проницаемость до уровня μ*(0), поэтому эффект торможения ферромагнитного диска (кольца) обратным втягиванием ферроматериала к центру тяготения магнитного поля оказывается незначительным, притом меньшим, чем эффект втягивания с правого края магнитного зазора, что дополнительно увеличивает результирующую силу в направлении вращения диска (кольца).
Полное восстановление относительной магнитной проницаемости этих вышедших из магнитного зазора частей ферромагнитного диска (кольца) происходит по мере движения этих частей вне магнитного поля за время Т-2,2τ=2,2τ[(27πR/X0)-1]>>Δt.
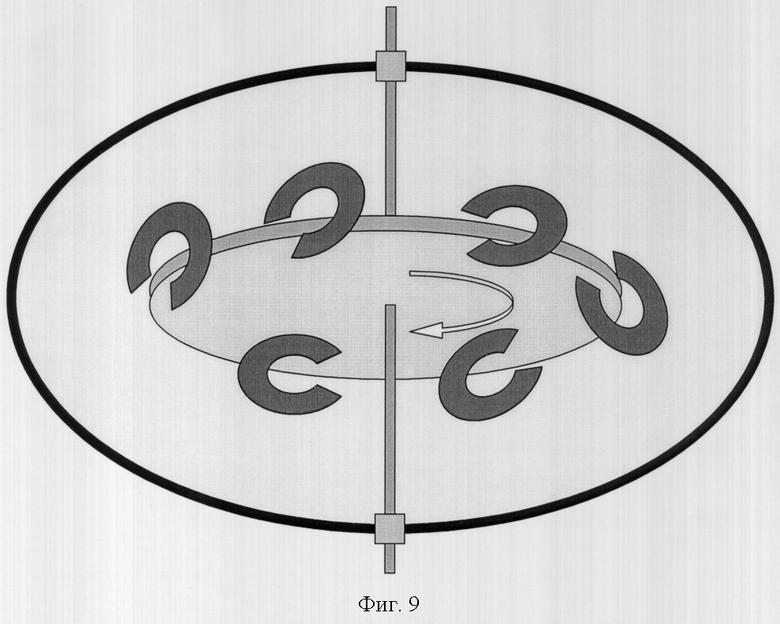
Учитывая последнее неравенство, с целью увеличения вращающего момента ферромагнитного диска (кольца) можно рекомендовать использование в заявляемом техническом решении нескольких идентичных постоянных магнитов, рассредоточенных симметрично по окружности ферромагнитного диска (кольца) так, чтобы сохранялось неравенство 2πR/N>>Х0, где N - число постоянных магнитов, допускающее восстановление в ферромагнетике исходного значения относительной магнитной проницаемости μmin→μmax* за время перехода фиксированного дифференциального объема ферромагнетика от одного магнита к другому, как это схематически представлено на фиг.9.
Идея расчета конкретной величины силы ΔF, действующей со стороны магнитного поля на вращающийся ферромагнитный диск (кольцо) и определяющей вращательный момент m=ΔF×R, аналогична ранее приведенным выражениям (6)-(10), но с учетом однородности магнитного поля (α=1) и магнитной вязкости с постоянной релаксации τ. Весь объем ферромагнитного тела, находящийся в любой момент времени в магнитном поле магнитного зазора и на его краях V=S (Х0+2Δσ) разбивают на дифференциальные объемы dv=Sdx для интервала - Δσ≤х≤Х0+Δσ, определяют в этом интервале дифференциалы сил dF(x), действующих на соответствующие дифференциальные объемы dv(x), вычисляют соответствующие интегралы сил I1 и I2 соответственно для участков от - Δσ до X* и от X* до X0, вычитают эти интегралы для получения равнодействующей силы ΔF=I1-I2. С учетом того, что для однородного магнитного поля α=1 нельзя пользоваться выражениями, содержащими множитель (α-1), обращающий в ноль результат, а следует их видоизменить с учетом динамики изменения относительной магнитной проницаемости ферромагнитного вещества в каждом дифференциальном объеме его, связанном с магнитным полем. Удобно при этом начало отсчета выбрать в центре тяготения магнитного поля с координатой х=Х0/2 и интегрирование для I1 и I2 производить по обе стороны от этого центра, полагая, что дифференциал силы dF(x)˜Н(х)2 *μ(x)/(х-Х0/2)2 при известных распределениях напряженности магнитного поля и относительной магнитной проницаемости ферромагнетика в заданном интервале по координате x. Распределение μ(х) определяется параметрами ω0 и τ и имеет вид, указанный на фиг.8б. Внутри магнитного зазора магнитное поле однородно и равно Н0, а по краям считается квазиэкспоненциально спадающим по мере удаления от краев магнитного зазора на интервалах, соизмеримых с Δσ. Конкретные значения указанных распределений могут вычисляться и измеряться в каждом отдельном случае исполнения устройства, поэтому аналитический расчет для силы ΔF в данной заявке не приводится. Достаточно лишь указать, что в динамике вращательного движения ферромагнитного диска (кольца) с учетом магнитной вязкости и правильного выбора угловой скорости вращения ω0, а также в предположении, что за краями магнитного зазора напряженность магнитного поля убывает обратно пропорционально квадрату расстояния от центра тяготения, всегда будет соблюдаться неравенство вида
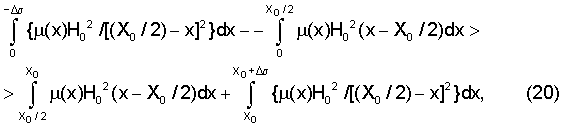
определяющее выполнение неравенства ΔF>0, что вытекает из симметричности распределения магнитного поля Н(х) относительно центра тяготения магнитного поля х=Х0/2, равенства интервалов интегрирования и сильной асимметричности распределения μ(х) из-за влияния магнитной вязкости ферромагнетика и его свойства изменять свою относительную магнитную проницаемость в функции напряженности действующего на него магнитного поля, и поэтому равнодействующая сила ΔF определяется с точностью до постоянного множителя разностью пар определенных интегралов, указанных в неравенстве (20).
Большой интерес представляет соединение обоих рассмотренных выше механизмов возбуждения вращательного движения ферромагнитного диска (кольца) - механизма втягивания ферроматериала диска (кольца) в неоднородное магнитное поле постоянного магнита и механизма динамического втягивания за счет эффекта магнитной вязкости (что отражено в формуле изобретения ссылкой на использование как однородного, так и неоднородного магнитного поля). При применении неоднородного магнитного поля центр тяготения в предельном случае имеет относительную величину смещения ξ*=0,707 (вместо 0,5, как в случае использования однородного магнитного поля). Здесь уместно отметить, что ранее полученное относительное положение «центра тяжести» ξ=0,38 справедливо в случае однородного магнитного поля в зазоре постоянного магнита. Если это поле неоднородно с градиентом, направленным в сторону вращения ферромагнитного диска (кольца), то относительное положение «центра тяжести» ξ<0,38 из-за уменьшения абсолютной величины производной dμ(x)/dx на начальном участке вхождения ферромагнетика в магнитный зазор переменной высоты (х˜0), что дополнительно увеличивает силу ΔF. Схема построения такого устройства соответствует фиг.1, а кривая распределения μ(х) при этом становится еще более асимметричной относительно центра тяготения магнитного поля, чем в случае, указанном на фиг.8б. Таким образом, использование совместно обоих механизмов втягивания ферромагнитной массы диска (кольца) в направлении к центру тяготения магнитного поля приводит к дополнительному увеличению вращательного момента.
Разработка конкретных энергетических установок бытового и промышленного применения на основе заявляемого технического решения будет инициировать поиск технологии создания ферромагнитных материалов с требуемыми свойствами по их магнитной вязкости, например вариацией различных примесей в ферромагнитном материале, и по зависимости μ(Н) в области насыщения. Так, для вращения ферромагнитного диска (кольца) радиуса R=0,5 м с длиной магнитного зазора X0=0,05 м со скоростью 50 об/с потребуется иметь ферромагнетик с постоянной релаксации τ=0,02·0,1/4,4·3,14=1,45·10-4с=145 мкс, что вполне реально осуществимо. Для гироскопических систем с частотой вращения 500 об/с при соотношении X0/R=0,1 постоянная релаксации должна быть снижена до ˜15 мкс.
Увеличение скорости вращения относительно частоты ω0 сдерживается автоматически (даже при существенно малых моменте трения и (или) моменте нагрузки) за счет снижения асимметрии в распределении μ(х), так как при сокращении времени пребывания ферромагнитного материала в насыщающем магнитном поле соответственно уменьшается перепад относительной магнитной проницаемости ферромагнетика на краях магнитного зазора.
Таким образом, можно констатировать, что постоянные магниты потенциально являются источниками энергии, своеобразными неистощимыми аккумуляторами, «подзаряд» которых осуществляется непрерывно во времени за счет происходящих процессов превращения энергии на молекулярном уровне. «Запуск» в работу таких «аккумуляторов» как толчок к началу осуществления указанных молекулярных процессов производится от внешних источников однократно на этапе создания постоянных магнитов путем доведения специальных ферромагнитных материалов с высокой коэрцитивной силой до их насыщения в магнитном поле соленоидов с электрическим током намагничивания и последующей необходимой технологической тренировкой магнитов по известной методике.
Заявляемое техническое решение может быть изготовлено и апробировано на предприятиях Министерства промышленности РФ, в физических институтах РАЕН и других организациях, занимающихся разработкой энергетических устройств.
Предложение представляет также и чисто научный интерес для проведения фундаментальных исследований физики магнетизма в ферромагнитных веществах, с целью теоретической интерпретации феномена восполняемой аккумуляции энергии за счет процессов, возможно, происходящих на уровне молекулярной магнитохимии.
| название | год | авторы | номер документа |
|---|---|---|---|
| ФЕРРОМАГНИТОВЯЗКИЙ РОТАТОР | 2005 |
|
RU2309527C2 |
| ПРИБОР ДЛЯ ИЗМЕРЕНИЯ МАГНИТНОЙ ВЯЗКОСТИ ФЕРРОМАГНЕТИКОВ | 2007 |
|
RU2338216C1 |
| СПОСОБ ПОЛУЧЕНИЯ ЭНЕРГИИ И УСТРОЙСТВО ДЛЯ ЕГО РЕАЛИЗАЦИИ | 2006 |
|
RU2332778C1 |
| МАГНИТОВЯЗКИЙ МАЯТНИК | 2005 |
|
RU2291546C1 |
| СПОСОБ ПОЛУЧЕНИЯ ЭНЕРГИИ И УСТРОЙСТВО ДЛЯ ЕГО РЕАЛИЗАЦИИ | 2010 |
|
RU2452074C1 |
| ФЕРРОМАГНИТОВЯЗКИЙ ДВИГАТЕЛЬ | 2007 |
|
RU2359398C1 |
| УСТРОЙСТВО АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ ЭЛЕКТРОГЕНЕРАТОРОМ | 2013 |
|
RU2537394C1 |
| СТАБИЛИЗИРОВАННЫЙ ГЕНЕРАТОР ПЕРЕМЕННОГО ТОКА | 2013 |
|
RU2542711C1 |
| УСТРОЙСТВО ВИЗУАЛИЗАЦИИ ТЕПЛОПРОВОДНОСТИ ФЕРРОМАГНЕТИКОВ | 2007 |
|
RU2359336C1 |
| УСТРОЙСТВО СТАБИЛИЗАЦИИ ЧАСТОТЫ ГЕНЕРАТОРА | 2007 |
|
RU2368073C2 |




Изобретение относится к физике магнетизма и может быть использовано в качестве устройства преобразования энергии магнитного поля в механическое вращательное движение. Технический результат состоит в повышении энергетической эффективности. Магнитовязкий ротатор содержит связанные между собой постоянный магнит с однородным или неоднородным магнитным полем между его полюсами и ферромагнитный диск (кольцо) с осью вращения. Ферромагнитный диск выполнен из ферромагнитного материала с магнитной вязкостью, постоянная релаксации τ которой по отношению к периоду Т вращения ферромагнитного диска (кольца) выбрана, например, согласно условию: τ˜TX0/4,47πR, где Х0 - длина магнитного зазора между полюсами постоянного магнита. В указанный магнитный зазор помещен край ферромагнитного диска (кольца) радиуса R. Напряженность магнитного поля в зазоре постоянного магнита выбрана насыщающей для материала ферромагнитного диска(кольца). 9 ил.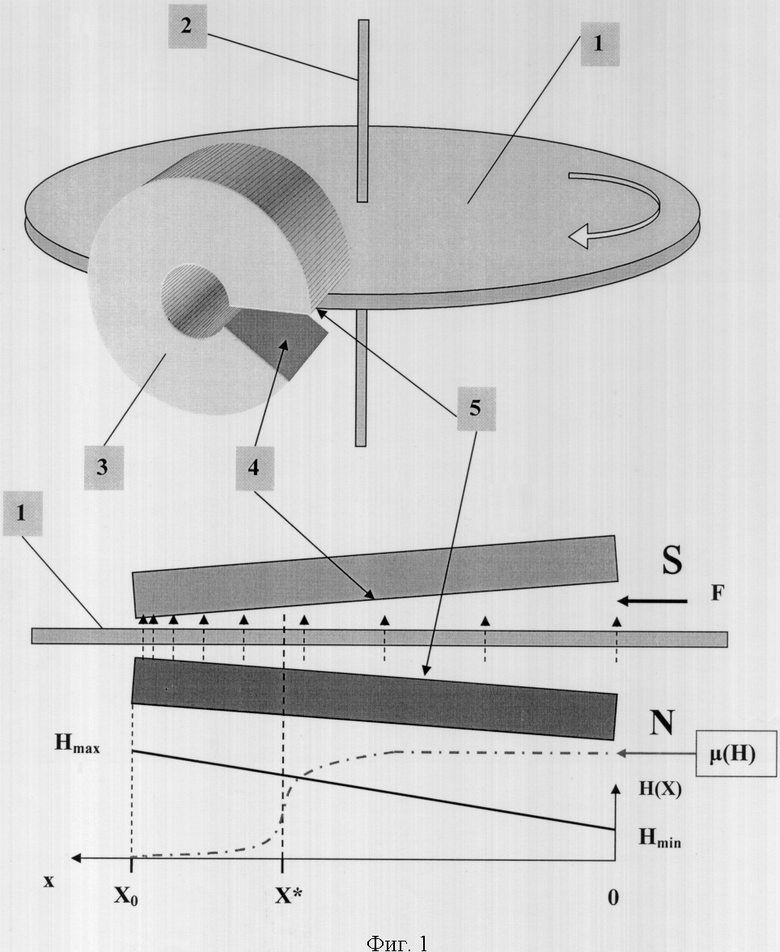
Магнитовязкий ротатор, содержащий постоянный магнит и связанное с ним ферромагнитное тело, отличающийся тем, что ферромагнитное тело выполнено в виде вращающегося на оси диска (кольца) между полюсами постоянного магнита и состоит из ферромагнитного материала с магнитной вязкостью, постоянная релаксации τ которой по отношению к периоду Т вращения ферромагнитного диска (кольца) выбрана, например, из условия τ˜TX0/4,47πR, где Х0 - длина магнитного зазора между полюсами постоянного магнита (с однородным или неоднородным магнитным полем в зазоре), в который помещен край ферромагнитного диска (кольца) радиуса R, при этом напряженность магнитного поля в зазоре постоянного магнита выбрана насыщающей для материала ферромагнитного диска (кольца).
| Однофазный электрический двигатель | 1989 |
|
SU1685271A3 |
| УСТРОЙСТВО ОПОРЫ РОТАТОРА В УСТРОЙСТВЕ ВРАЩЕНИЯ | 2001 |
|
RU2249732C2 |
| Способ регулирования вязкости жидкости в магнитном поле | 1985 |
|
SU1318844A1 |
| JP 55144784 А, 11.11.1980 | |||
| JP 2000228865 А, 15.08.2000 | |||
| US 5138207 А, 11.08.1992. | |||
Авторы
Даты
2008-05-27—Публикация
2006-10-02—Подача