Изобретение относится к вычислительной технике и может быть использовано для определения коэффициента радиальной дисторсии оптических подсистем при настройке и в процессе функционирования систем технического зрения.
Известен способ калибровки коэффициента радиальной дисторсии (De Xu, You Fu Li, Min Tan, Method for calibrating cameras with large lens distortion. Optical Engineering 45(4), 043602, April 2006), согласно которому коэффициент радиальной дисторсии определяется итерационно, путем подбора такой его величины, при которой искаженное изображение будет более всего похоже на истинное. Первоначально коэффициент радиальной дисторсии приравнивают к нулю, затем, итерационно прибавляя к нему некоторую величину, искажают кривую на изображении, используя этот коэффициент и координаты точек, принадлежащих этой кривой, вычисляют степень дисторсии и, если степень дисторсии визуально достаточно мала, то итерации прекращают и искомым коэффициентом считают тот, который был использован последним.
Недостатком этого способа является необходимость визуальной оценки степени дисторсии на изображении, что требует участия при определении величины коэффициента оператора и увеличивает время, затрачиваемое на процесс определения.
Наиболее близким к предлагаемому является способ автоматической калибровки дисторсии (патент №2289111 «Способ адаптивной калибровки радиальной дисторсии оптической подсистемы системы технического зрения» от 10.12.2006), в котором выполняют шаги: ввод изображения в ЭВМ, определение радиальной дисторсии линз по формуле
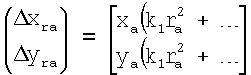 ,
,
где k1, ... - коэффициенты радиальной дисторсии, rа=(xa 2+yа 2)1/2 - радиальное расстояние, (Δxra, Δyra) - отклонение точки изображения от ее истинного положения - положения, которое занимала бы точка при отсутствии дисторсии, выделение контуров и бинаризация изображения, выбор калибровочного объекта из объектов рабочей сцены на основе математического аппарата нечеткой логики, определение центральной точки калибровочного объекта как среднего арифметического всех точек объекта, позиционирование видеокамеры СТЗ в n направлениях наблюдения (горизонтальном или вертикальном) при постоянно находящемся в кадре калибровочном объекте, определение координат центральной точки калибровочного объекта на изображении для n разных направлений наблюдения (горизонтального или вертикального) и определение коэффициентов радиальной дисторсии.
Недостатками этого способа является смещение ОЭД только в заданных направлениях - вертикальном или горизонтальном, что на практике требует специально подготовленного устройства для реализации этого способа, за счет чего область применения сужается.
Технической задачей изобретения является расширение области применения способа за счет смещения ОЭД в произвольном направлении вдоль прямой линии и повышение точности вследствие исключения ошибок, связанных с необходимостью обеспечения строго горизонтального (или вертикального) смещения ОЭД.
Задача решается тем, что в известный способ адаптивной калибровки радиальной дисторсии оптической подсистемы системы технического зрения, включающий ввод изображения в ЭВМ, определение радиальной дисторсии линз по формуле
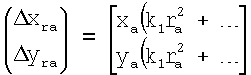 ,
,
где k1, ... - коэффициенты радиальной дисторсии, ra=(xа 2+yа 2)1/2 - радиальное расстояние, (Δxra, Δyra) - отклонение точки изображения от ее истинного положения - положения, которое занимала бы точка при отсутствии дисторсии, выделение контуров и бинаризацию изображения, выбор калибровочного объекта из объектов рабочей сцены на основе математического аппарата нечеткой логики, определение центральной точки калибровочного объекта как среднего арифметического всех точек объекта, определение координат центральной точки калибровочного объекта на изображении для n направлений наблюдения и определение коэффициентов радиальной дисторсии, добавляют произвольное смещение направления наблюдения ОЭД, сохраняя калибровочный объект в кадре, таким образом, чтобы главные оптические оси после каждого смещения находились в одной плоскости между собой и с главной оптической осью первоначального направления.
Изобретение может быть использовано для определения коэффициента радиальной дисторсии оптических подсистем при настройке и функционировании систем технического зрения и соответствует критерию «промышленная применимость».
Сущность изобретения поясняется чертежами, где на фиг.1 изображен алгоритм калибровки радиальной дисторсии, на фиг.2 и фиг.4 показаны рисунки, поясняющие процесс определения коэффициента радиальной дисторсии, на фиг.3 представлен рисунок, поясняющий процесс идентификации контуров на разных изображениях.
Искажения, вызванные радиальной дисторсией, определяются [R.Y.Tsai. «A versatile camera calibration technique for high-accuracy 3D machine vision metrology using off-the-shelf TV cameras and lenses», IEEE Trans. Rob. Autom, RA-3(4), p.323-344, 1987] по формуле:

где (Δxr, Δyr) - отклонение точки изображения от ее истинного положения - положения, которое занимала бы точка при отсутствии радиальной дисторсии, k1, k2, ... kn - коэффициенты радиальной дисторсии, r=(x2+y2)1/2 - расстояние от центра кадра до точки с координатами (x, y).
Согласно [Vark Reeves, Andrew J. Moore, Duncan P. Hand, Julian D.C.Jones. "Dynamic shape measurement system for laser materials processing", Opt. Eng. 42(10), p.2923-2929, 2003 (стр.2926, текст между 4 и 5 формулами)] для практического применения достаточно определять только коэффициент k1.
Блок-схема алгоритма калибровки радиальной дисторсии представлена на фиг.1.
В блоке 1 (фиг.1) вводят цифровое изображение в контроллер. Изображение получают с помощью оптико-электронного датчика (ОЭД). Получение происходит путем аналого-цифрового преобразования сигнала, характеризующего изображение, и сохранения изображения в цифровой форме.
Под изображением понимают матрицу значений яркостей пикселей цифрового изображения:
I=I(x,y),

где x, y - координаты пикселя изображения по горизонтали и вертикали, соответственно,
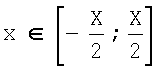 ,
,  ,
,
Х, Y - размерность изображения по горизонтали и вертикали, соответственно.
В блоке 2 (фиг.1) производят выделение контуров объектов на изображении стандартным оператором, например, оператором Лапласа [Методы компьютерной обработки изображений / Под. ред. В.А.Сойфера. - М.: Физматлит, 2001], и бинаризация. Это действие выполняет контроллер автоматически. Из выделенных контуров формируют множество K.
Множество контуров K, состоит из элементов (контуров) Kl.
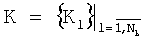 ,
,
где Nk - количество контуров.
Под контуром Kl понимают совокупность отличных от фона изображения точек, таких, что для каждой точки (xi, yi) найдется не менее одной соседней точки (xj, yj), расположенной на расстоянии 1 пиксель:
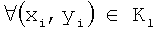 ,
, 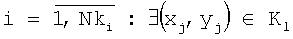 ,
, 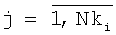 ,
, 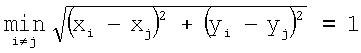 .
.
Каждый контур описывается множеством из Nkl пар координат точек (хi, yi):
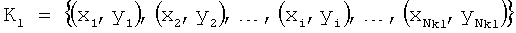 ,
,
где Nkl - количество пар координат точек, составляющих контур.
После выделения контуров осуществляется переход к выбору калибровочного контура. В блоке 3 (фиг.1) производится выбор калибровочного объекта (контура) из объектов рабочей сцены на основе математического аппарата нечеткой логики [Алтунин А.Е., Семухин М.В. Модели и алгоритмы принятия решений в нечетких условиях: Монография. Тюмень: Издательство Тюменского государственного университета, 2000].
Введем лингвистическую переменную (ЛП) «калибровочный контур» для выбора калибровочного контура из множества контуров на изображении. Калибровочный контур должен удовлетворять следующим условиям:
- иметь оптимальную площадь и размер, определяемый размером описанного вокруг объекта прямоугольника;
- находиться на оптимальном расстоянии от края кадра изображения.
Функция принадлежности ЛП «калибровочный контур» μkk равна:
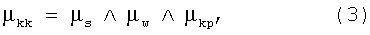
где
μs - функция принадлежности терму «оптимальная площадь»,
μw - функция принадлежности терму «оптимальное окно»,
μkp - функция принадлежности терму «оптимальное положение в кадре».
Функция принадлежности μs терма «оптимальная площадь», зависящая от площади контура S, равна:
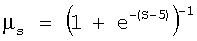 ,
,
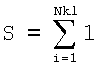 ,
,
Функция принадлежности μw терму «оптимальное окно» определяют размерами по горизонтали и вертикали описанного вокруг объекта прямоугольника:
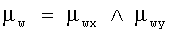 ,
,
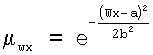 , при а=6.8, b=1.5,
, при а=6.8, b=1.5,
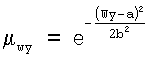 ,
,
где Wx, Wy - размеры описанного вокруг контура прямоугольника по горизонтали и вертикали, соответственно, параметры а, b подобраны экспериментально.
ФП μkp терму «оптимальное положение в кадре» позволяет выбрать контуры, расположенные близко к краю кадра, и равна:
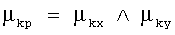 ,
,
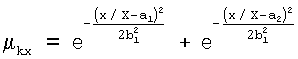 ,
,
 ,
,
при
а1=0.2,
b1=0.05,
a2=0.8,
b2=0.07,
где (x, y) - координаты центра описанного вокруг контура прямоугольника, параметры а, b подобраны экспериментально.
В блоке 4 (фиг.1) производят определение центральной точки (ЦТ) калибровочного контура. В качестве ЦТ выбирается точка изображения, являющаяся центром тяжести [Дегтярев С.В., Садыков С.С., Тевс С.С., Ширабакина Т.А. Методы цифровой обработки изображений: Учебное пособие. Ч.1 / Курск. Гос. Техн. Ун-т. Курск, 2001] калибровочного контура и определяемая средними координатами всех точек калибровочного контура по горизонтали и вертикали. Действия, представленные в блоках 3, 4 (фиг.1), выполняет контроллер.
В блоке 5 (фиг.1) дважды производят смещение направления наблюдения ОЭД, сохраняя калибровочный объект в кадре, таким образом, чтобы главные оптические оси после каждого смещения находились в одной плоскости между собой и с главной оптической осью первоначального направления. После каждого смещения получают изображения.
При этом для идентификации калибровочного объекта после смещения введена ЛП «идентичность смещенного объекта»
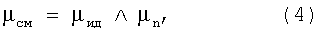
где
μид - функция принадлежности терму «идентичность объекта»,
μn - функция принадлежности терму «ожидаемое положение», характеризующая полученное положение калибровочного объекта после смещения и ожидаемое положение калибровочного объекта.
Для описания контура Kl определяется множество векторов νij с i-й точки Ti(xi,yi) контура на j-ю точку Tj(xj,yj) этого же контура:
νij={dij,dij},
i=1...Nkl,
j=1...Nkl,
i≠j,
где dij - расстояние между точками Тi и Tj, αij - направление с i-й точки контура на j-ю точку.
Расстояние dij равно:
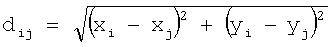 .
.
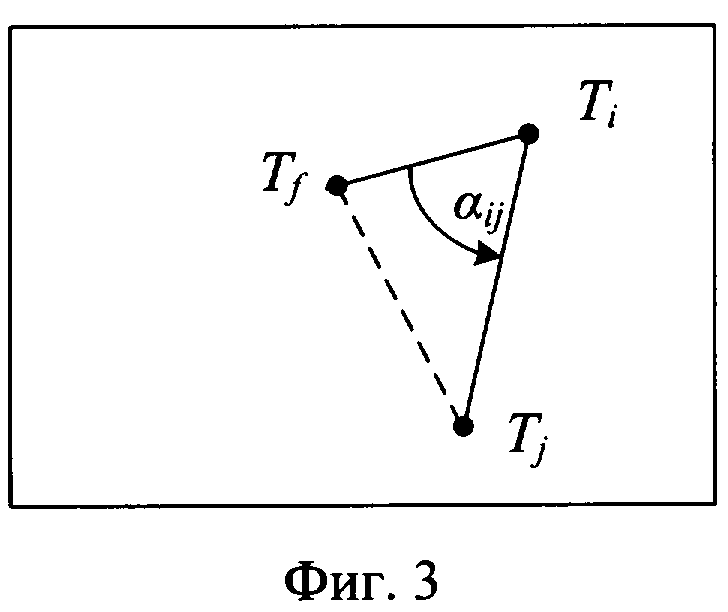
Углом с i-ой точки объекта на j-ую точку считается угол между вертикальной осью кадра и направлением на j-ую точку (фиг.3). По теореме косинусов из треугольника ΔТfTiTj
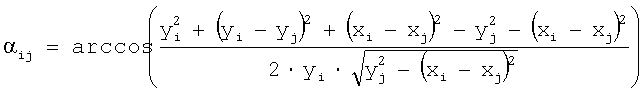 .
.
Функция принадлежности терму «идентичность объекта» μид определяется как идентичность расстояний dij между i-й j-й точками и идентичность углов αij:
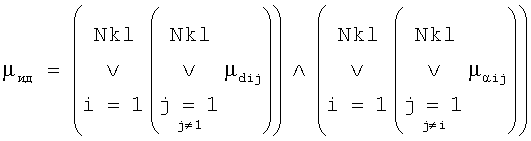 ,
,
где
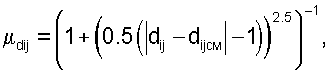
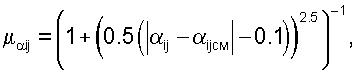
|dij-dijсм| - разность расстояний между точками до смещения и после смещения в пикселях,
|αij-αijсм| - разность величин углов между точками до смещения и после смещения в радианах.
Функция принадлежности μn терму «ожидаемое положение» характеризуется разностью ожидаемого и фактического положения калибровочного объекта:
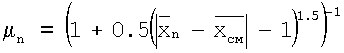 ,
,
где 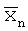 - предполагаемое среднее значение горизонтальных координат множества составляющих контур точек;
- предполагаемое среднее значение горизонтальных координат множества составляющих контур точек; 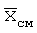 - фактическое среднее значение горизонтальных координат множества составляющих контур точек.
- фактическое среднее значение горизонтальных координат множества составляющих контур точек.
Расчет xn производится на основе информации об угловой скорости Vx смещения направления наблюдения и времени смещения t:
 .
.
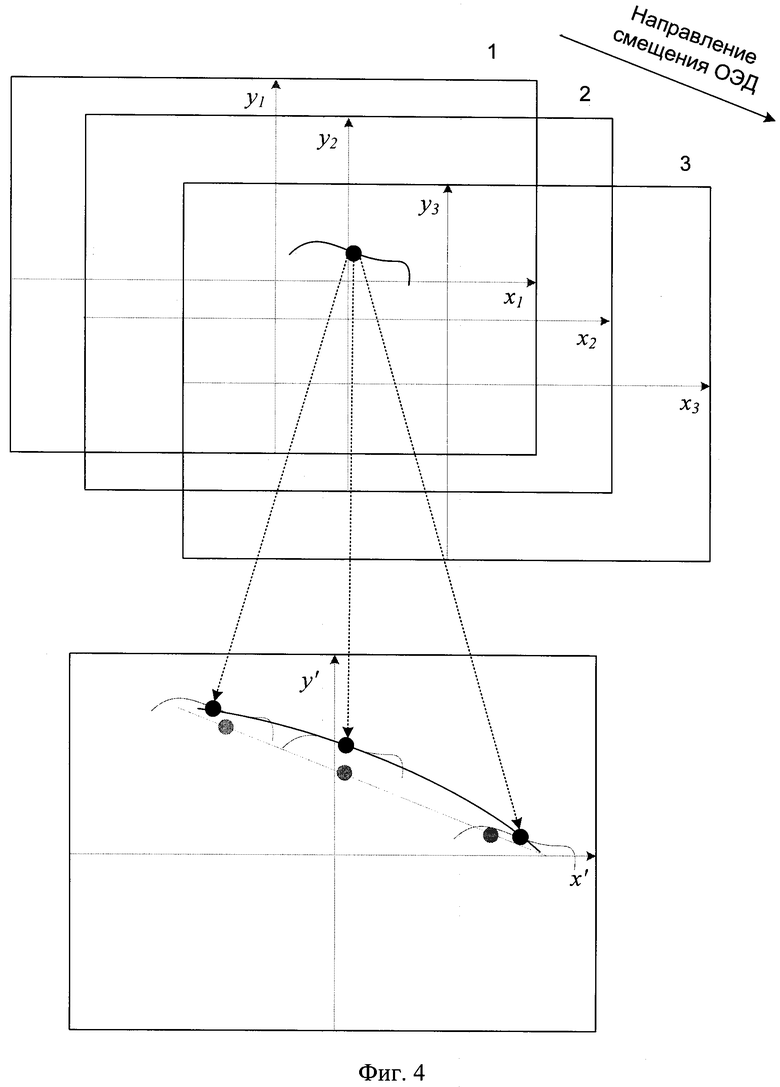
В блоке 6 (фиг.1) производят определение координат (x/, y/) ЦТ на изображениях после смещений ОЭД. Т.к. главные оптические оси в первоначальном направлении наблюдения и после каждого смещения направления наблюдения находятся в одной плоскости, то пересечение этой плоскости с картинной плоскостью будет иметь вид прямой, это означает, что если перенести на одно изображение все три полученные центральные точки, то они должны лежать на одной прямой (фиг.4). Основываясь на этом, в блоке 7 (фиг.1) вычисляют коэффициент радиальной дисторсии, путем решения системы уравнений.
Искажения, вызванные радиальной дисторсией в декартовой системе координат, исходя из (1) определяют по формулам:
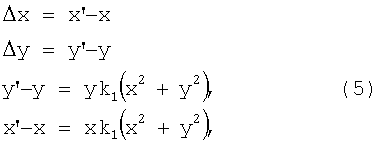
где (х',y') - координаты точки, измеряемые по изображению.
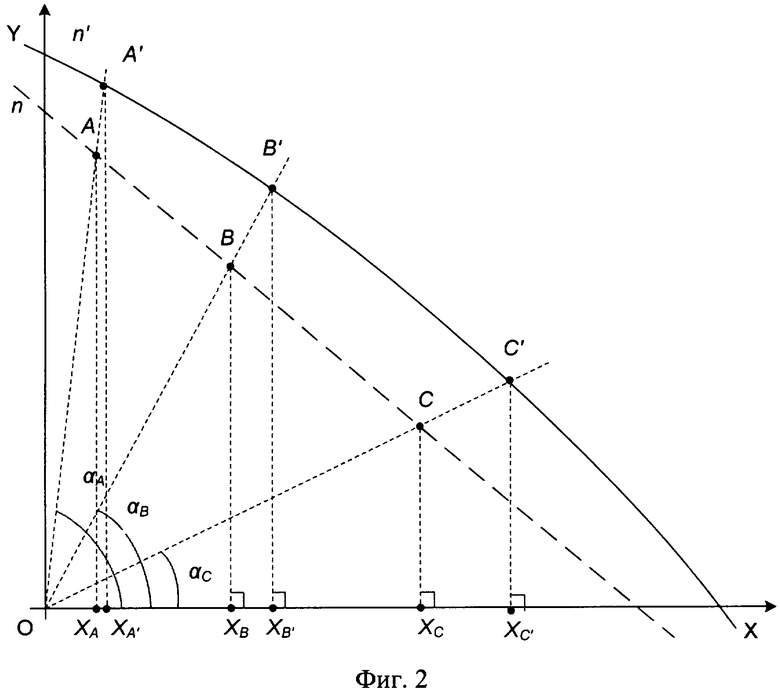
Обозначим центральную точку калибровочного контура при первоначальном направлении наблюдения А(хA, yA), после первого смещения направления наблюдения - В(хB, yB), после второго - С(хC, yC). При отсутствии радиальной дисторсии на изображении точки лежат на одной прямой (фиг.4).
Условие принадлежности одной прямой для трех точек в декартовой системе координат записывают:
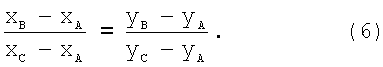
Под влиянием радиальной дисторсии положения точек А, В и С будут искажены, обозначим их положение на изображении А', В' и С'. Связь истинных абсцисс точек А, В и C с абсциссами точек А', В' и С' на изображении (фиг.2) с учетом формулы (5) выражают:
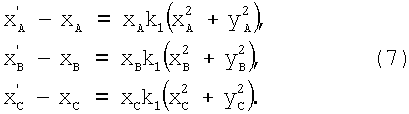
Т.к. ΔОВХB и ΔОСХC - прямоугольные (фиг.2), то:
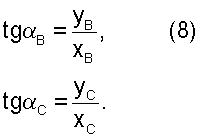
Из(8)следует:
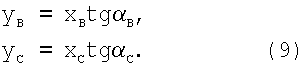
Выполнив подстановку (9) в (7) и (6), составим систему уравнений:
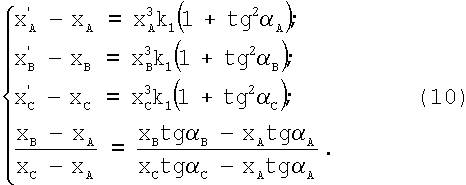
Первые три уравнения из системы (10) являются кубическими уравнениями (если их решать относительно xA, xB, xC соответственно) и имеют по одному корню [И.Н.Бронштейн, К.А.Семендяев. Справочник по математике, издание седьмое, стереотипное. М.: Гос. изд-во технико-теоретической лит-ры, 1957, с.138]. Корни вычисляют:

Полученные корни xA, xB, xC подставляют в четвертое уравнение системы (10) и получают уравнение с одной неизвестной k1, которое решают с использованием численных методов [Демидович Б.П., Марон И.А. Основы вычислительной математики. - М.: Наука. Гл. ред. физ.-мат.лит., 1966].
Исходя из того, что контроллер выполняет вычислительные операции, он может быть реализован на базе микроконтроллера, описанного в справочнике «Системы технического зрения» [Системы технического зрения: Справочник / В.И.Сырямкин, B.C.Титов., Ю.Г.Якушенков и др. // Под общей редакцией В.И.Сырямкина, B.C.Титова. Томск: МГП «РАСКО», 1992. 367 с.: ил.] на с.93-100 в главе 3.6.
В результате выполнения последовательности действий, рассмотренных в рамках предложенного способа, выполняют калибровку радиальной дисторсии. Точность калибровки можно повысить за счет увеличения числа смещений ОЭД.
Таким образом, изобретение позволяет расширить область применения способа за счет смещения ОЭД в произвольном направлении вдоль прямой линии и повысить точность вследствие исключения ошибок, связанных с необходимостью обеспечения строго горизонтального (или вертикального) смещения ОЭД.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ АДАПТИВНОЙ КАЛИБРОВКИ РАДИАЛЬНОЙ ДИСТОРСИИ ОПТИЧЕСКОЙ ПОДСИСТЕМЫ СИСТЕМЫ ТЕХНИЧЕСКОГО ЗРЕНИЯ | 2004 |
|
RU2289111C2 |
| СПОСОБ ФОРМИРОВАНИЯ ПАНОРАМНЫХ ИЗОБРАЖЕНИЙ | 2006 |
|
RU2365998C2 |
| СПОСОБ АВТОМАТИЧЕСКОГО ОПРЕДЕЛЕНИЯ И КОРРЕКЦИИ РАДИАЛЬНОЙ ДИСТОРСИИ НА ЦИФРОВОМ ИЗОБРАЖЕНИИ | 2006 |
|
RU2351091C2 |
| УСТРОЙСТВО КОРРЕКЦИИ СФЕРИЧЕСКОЙ АБЕРРАЦИИ | 2005 |
|
RU2295713C2 |
| СПОСОБ ОПТИКО-ЭЛЕКТРОННОЙ ДИАГНОСТИКИ ТРОМБОЗА ГЛУБОКИХ ВЕН ГОЛЕНИ | 2006 |
|
RU2314026C2 |
| СПОСОБ ИЗМЕРЕНИЯ ПАРАМЕТРОВ ОПТИЧЕСКИХ СИСТЕМ | 2005 |
|
RU2315965C2 |
| СПОСОБ ОПРЕДЕЛЕНИЯ КОЭФФИЦИЕНТОВ СФЕРИЧЕСКОЙ АБЕРРАЦИИ | 2005 |
|
RU2295712C2 |
| СПОСОБ КАЛИБРОВКИ СИСТЕМЫ ТЕХНИЧЕСКОГО ЗРЕНИЯ ИЗ ТРЕХ ВИДЕОКАМЕР И УСТРОЙСТВО ДЛЯ ЕГО РЕАЛИЗАЦИИ | 2008 |
|
RU2382515C1 |
| СПОСОБ ВНЕШНЕЙ КАЛИБРОВКИ БИНОКУЛЯРНОЙ СИСТЕМЫ ТЕХНИЧЕСКОГО ЗРЕНИЯ | 2005 |
|
RU2286598C1 |
| УСТРОЙСТВО ПОЛУЧЕНИЯ ИЗОБРАЖЕНИЯ С КОРРЕКЦИЕЙ ХРОМАТИЧЕСКОЙ АБЕРРАЦИИ | 2007 |
|
RU2352987C1 |
Изобретение относится к вычислительной технике и может быть использовано для определения коэффициента радиальной дисторсии оптических подсистем при настройке и функционировании систем технического зрения. Техническим результатом является расширение области применения способа за счет смещения ОЭД в произвольном направлении вдоль прямой линии и повышение точности вследствие исключения ошибок, связанных с необходимостью обеспечения строго горизонтального (или вертикального) смещения ОЭД. Это достигается тем, что способ адаптивной калибровки радиальной дисторсии оптической подсистемы системы технического зрения, включающий ввод изображения в ЭВМ, определение радиальной дисторсии линз по формуле 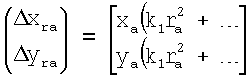 ,
,
выделение контуров и бинаризацию изображения, выбор калибровочного объекта из объектов рабочей сцены на основе математического аппарата нечеткой логики, определение центральной точки калибровочного объекта как среднего арифметического всех точек объекта, определение координат центральной точки калибровочного объекта на изображении для n направлений наблюдения и определение коэффициентов радиальной дисторсии, дополняют произвольным смещением направления наблюдения ОЭД. При этом сохраняет калибровочный объект в кадре, таким образом, чтобы главные оптические оси после каждого смещения находились в одной плоскости между собой и с главной оптической осью первоначального направления. 4 ил.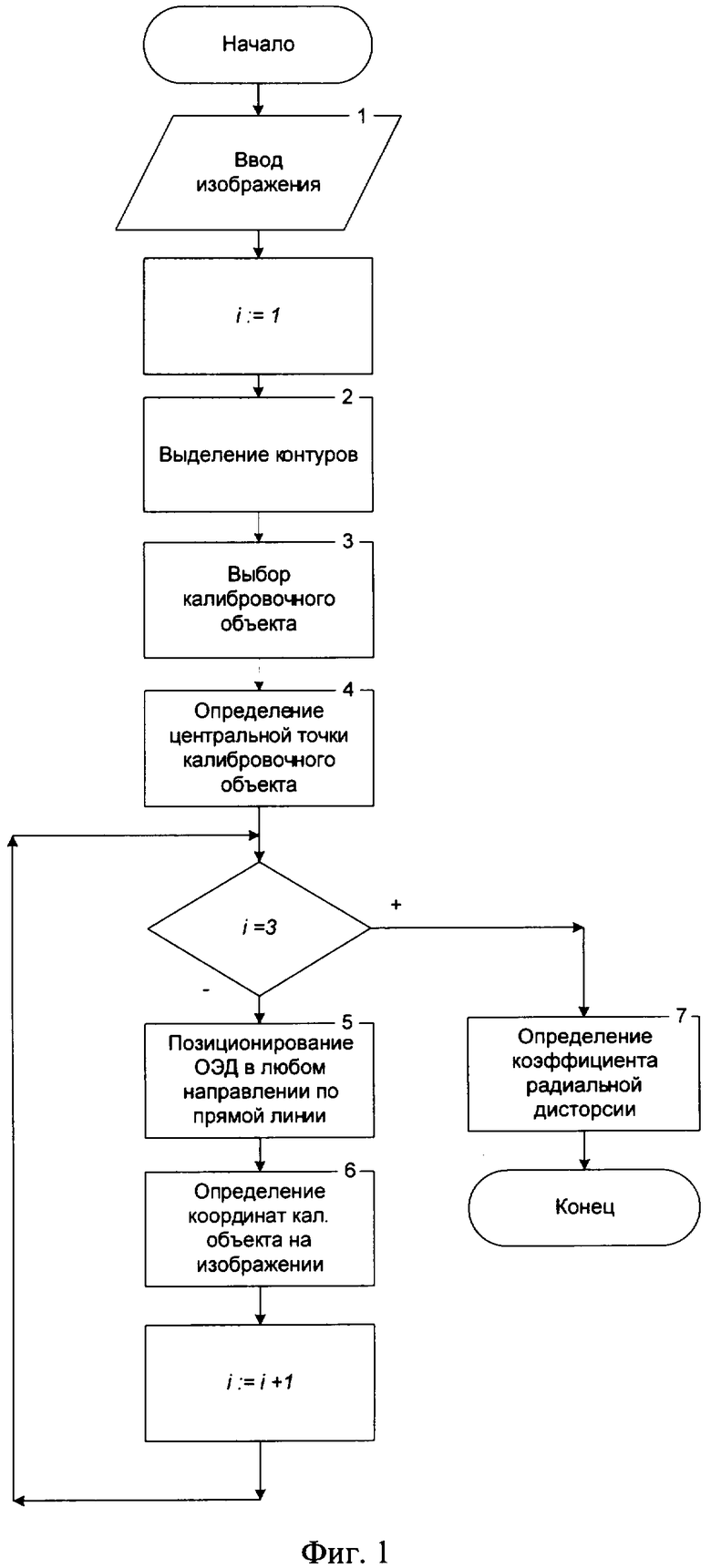
Способ калибровки радиальной дисторсии оптической подсистемы системы технического зрения, включающий ввод изображения в ЭВМ, определение радиальной дисторсии линз по формуле
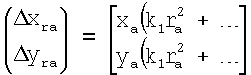 ,
,
где k1, ... - коэффициенты радиальной дисторсии, rа=(xa 2+yа 2)1/2 - радиальное расстояние, (Δxra, Δyra) - отклонение точки изображения от ее истинного положения - положения, которое занимала бы точка при отсутствии дисторсии, выделение контуров и бинаризацию изображения, выбор калибровочного объекта из объектов рабочей сцены на основе математического аппарата нечеткой логики, определение центральной точки калибровочного объекта как среднего арифметического всех точек объекта, определение координат центральной точки калибровочного объекта на изображении для n направлений наблюдения и определение коэффициентов радиальной дисторсии, отличающийся тем, что произвольно смещают направление наблюдения ОЭД, сохраняя калибровочный объект в кадре, таким образом, чтобы главные оптические оси после каждого смещения находились в одной плоскости между собой и с главной оптической осью первоначального направления, вычисляют дисторсии k1 посредством решения системы уравнений
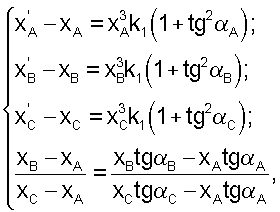
где (xA, yA), (хB, yB), (хC, yС) - координаты центральных точек А, В и С калибровочных контуров при первоначальном направлении наблюдения, после первого смещения направления наблюдения, после второго соответственно, (xA', yA'), (хB', yB'), (хC', yС') - координаты этих точек на изображении, искаженном радиальной дисторсией, αA, αB, αС - углы между осью абсцисс и прямыми, образованными точкой начала отсчета координат и точками А, В и С соответственно.
| Способ измерения дисторсии оптических систем | 1984 |
|
SU1275248A1 |
| СПОСОБ АДАПТИВНОЙ КАЛИБРОВКИ РАДИАЛЬНОЙ ДИСТОРСИИ ОПТИЧЕСКОЙ ПОДСИСТЕМЫ СИСТЕМЫ ТЕХНИЧЕСКОГО ЗРЕНИЯ | 2004 |
|
RU2289111C2 |
| US 6002525 A, 14.12.1999. | |||
Авторы
Даты
2009-02-10—Публикация
2007-03-01—Подача