Изобретение относится к вычислительной технике и может быть использовано для определения и коррекции радиальной дисторсии на изображениях, полученных цифровыми фото-, видеокамерами и системами технического зрения, использующих в качестве приемников изображения матричные приемники изображения.
Известен способ коррекции дисторсии на фотографических изображениях с использованием структурного (текстурированного) отображения (патент США №5878174, G06K 9/00, от 02.03.1999), в котором коррекция искаженного изображения основана на использовании кривой коррекции дисторсии. Способ включает в себя следующие шаги: формирование множества точек на шаблоне - предопределенной двухмерной физической плоскости, определение радиальных расстояний для каждой точки этой плоскости, получение тестовой фотографии данной плоскости с использованием фотоустройства, преобразование изображения в цифровое, определение радиальных расстояний для множества точек изображения, определение функциональной зависимости (кривой) радиальных расстояний на шаблоне от соответствующих радиальных расстояний тестового изображения и восстановление на изображении истинных положений множества точек изображения с использованием полученной кривой.
Недостатком этого способа является использование для определения дисторсии тестового изображения, для получения которого необходимо подготовить шаблон, что усложняет процесс коррекции и исключает возможность определения коэффициента дисторсии и коррекции для уже существующих изображений.
Наиболее близким к предлагаемому является способ калибровки коэффициента радиальной дисторсии (De Xu, You Fu Li, Min Tan. Method for calibrating cameras with large lens distortion. Optical Engineering 45(4), 043602, April 2006), в котором коэффициент радиальной дисторсии определяется итерационно, путем подбора такой его величины, при которой искаженное изображение будет более всего похоже на истинное. Сначала коэффициент радиальной дисторсии приравнивают к нулю, затем, итерационно прибавляя к нему некоторую величину, искажают кривую на изображении, используя этот коэффициент и координаты точек, принадлежащих этой кривой, вычисляют степень дисторсии и, если степень дисторсии визуально достаточно мала, то итерации прекращают и искомым коэффициентом считают тот, который был использован последним.
Недостатком этого способа является необходимость визуальной оценки степени дисторсии на изображении, что требует участия при определении величины коэффициента оператора и увеличивает время, затрачиваемое на сам процесс определения.
Технической задачей изобретения является увеличение скорости определения коэффициента радиальной дисторсии, повышение точности коррекции искажений, вызванных радиальной дисторсией, а также расширение области применения способа.
Задача решается тем, что в известный способ калибровки коэффициентов радиальной дисторсии, включающий определение коэффициента дисторсии, добавляют автоматическое выделение на изображении контуров, их анализ и отбор наиболее подходящих, выбор трех точек на каждом контуре и расчет коэффициентов радиальной дисторсии для каждого контура с использованием координат этих точек, составление гистограммы зависимости частот повторяемости найденных коэффициентов от их величин, определение по гистограмме значения коэффициента, используемого для последующей коррекции как среднего в окрестности значения коэффициента с максимальной частотой повторения, автоматическую коррекцию искажений, вызванных радиальной дисторсией.
Изобретение может быть использовано для коррекции дисторсии на изображениях, полученных фотоаппаратурой различного назначения и соответствует критерию «промышленная применимость».
Сущность изобретения поясняется чертежами, где на фиг.1 изображен общий алгоритм определения коэффициента дисторсии и коррекции изображений, на фиг.2 представлен алгоритм определения множества коэффициентов дисторсии для различных контуров, на фиг.3 изображена прямая линия, искаженная радиальной дисторсией, фиг.4 и 5 поясняют процесс определения коэффициента дисторсии.
Искажения, вызванные радиальной дисторсией линз, определяются [R.Y.Tsai. «A versatile camera calibration technique for high-accuracy 3D machine vision metrology using off-the-shelf TV cameras and lenses», IEEE Trans. Rob. Autom, RA-3(4), pp.323-344, 1987] по формуле:
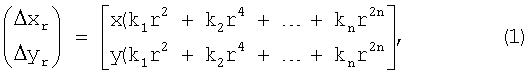
где (Δхr, Δyr) - отклонение точки изображения от ее истинного положения - положения, которое занимала бы точка при отсутствии радиальной дисторсии; k1, k2, ... kn - коэффициенты радиальной дисторсии; r=(х2+y2)1/2 - расстояние от центра кадра до точки с координатами (х, y).
Согласно [Vark Reeves, Andrew J.Moore, Duncan P.Hand, Julian D.C.Jones. "Dynamic shape measurement system for laser materials processing", Opt. Eng. 42(10), pp.2923-2929, 2003 (стр.2926)] для практического применения достаточно определять только коэффициент k1.
Блок-схема общего алгоритма определения коэффициента радиальной дисторсии и коррекции изображения представлена на фиг.1.
Входными данными является цифровое изображение (блок 1, фиг.1). Под изображением понимают матрицу значений яркостей пикселей оцифрованного изображения:
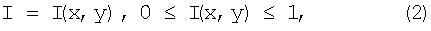
где х, y - координаты пикселя изображения по горизонтали и вертикали, соответственно,  ,
, 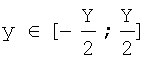 , X, Y - размерность изображения по горизонтали и вертикали, соответственно.
, X, Y - размерность изображения по горизонтали и вертикали, соответственно.
В блоке 2 (фиг.1) производится выделение контуров объектов на изображении стандартным оператором, например оператором Лапласа [Методы компьютерной обработки изображений. / Под. ред. В.А.Сойфера. - М.: Физматлит, 2001], и бинаризация. Согласно оператору Лапласа для дискретной функции яркости вычисляются вторые производные по горизонтальному и вертикальному направлениям изображения, аппроксимируемые вторыми разностями:
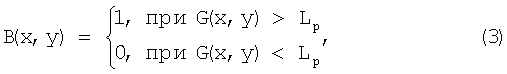
где G(x, y)=|I(x+1, y)+I(х-1, y)+I(x, y+1)+I(х, y-1)-4·I(x, y)|,
В - контурное изображение, определяемое множеством значений яркостей в точках с координатами (х, y),
Lp - пороговое значение изменения яркости, по которому определяют принадлежность точки изображения фону или контуру.
Порог Lp рассчитывают по формуле
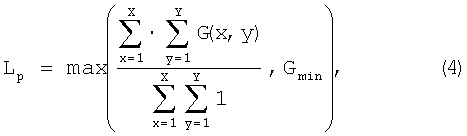
где Gmin - параметр, определяющий минимальное изменение яркости и задаваемый для всего изображения:

Так же в блоке 3 (фиг.1) рассчитывают радиусы кривизны выявленных контуров.
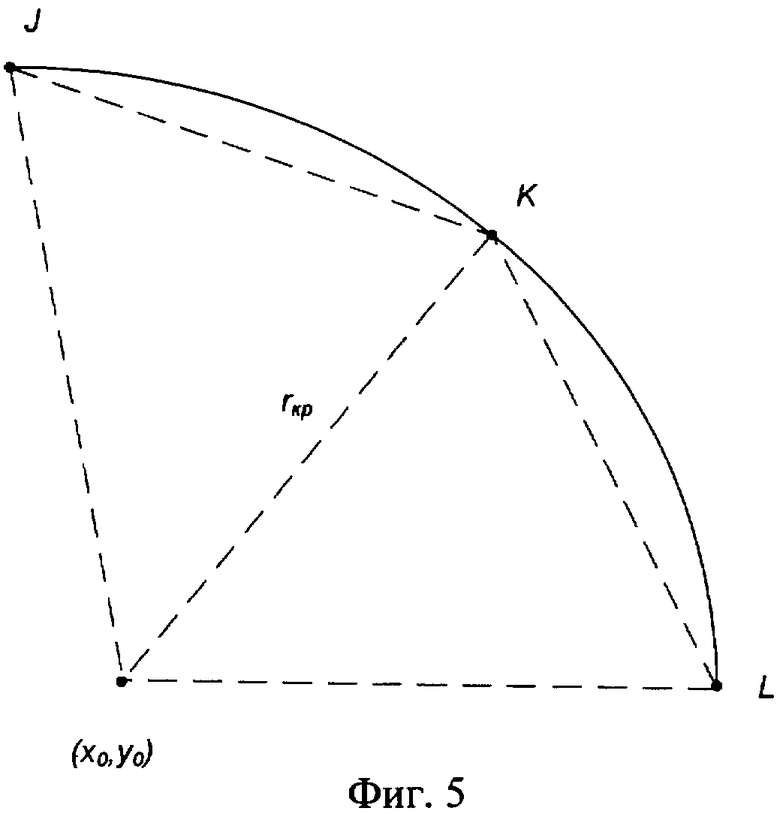
На каждом контуре определяют координаты трех точек: начальной, конечной и средней. На фиг.5 точки обозначены J(x1, y1), K(x2, y2) и L(х3, y3). При этом считают, что контур представляет собой часть окружности с центром в точке с координатами (х0, y0) и радиусом rкр. Для определения радиуса rкр составляют систему уравнений:

После решения системы уравнений получают:
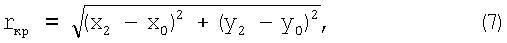
где
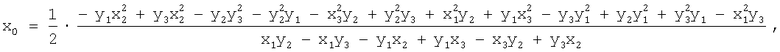
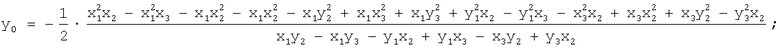
Затем, используя формулу (7), производят расчет радиусов кривизны для каждого контура.
Анализ полученных радиусов позволяет исключить из рассмотрения контуры, радиусы кривизны которых вследствие их больших значений не могут быть вызваны только дисторсией (т.е. контуров, уже не прямых до искажения, и которые не могут быть использованы для определения величины дисторсии) и контуров, лежащих на прямых, проходящих через центр кадра (т.к. согласно предлагаемому способу данные контура не могут быть использованы для определения коэффициента дисторсии).
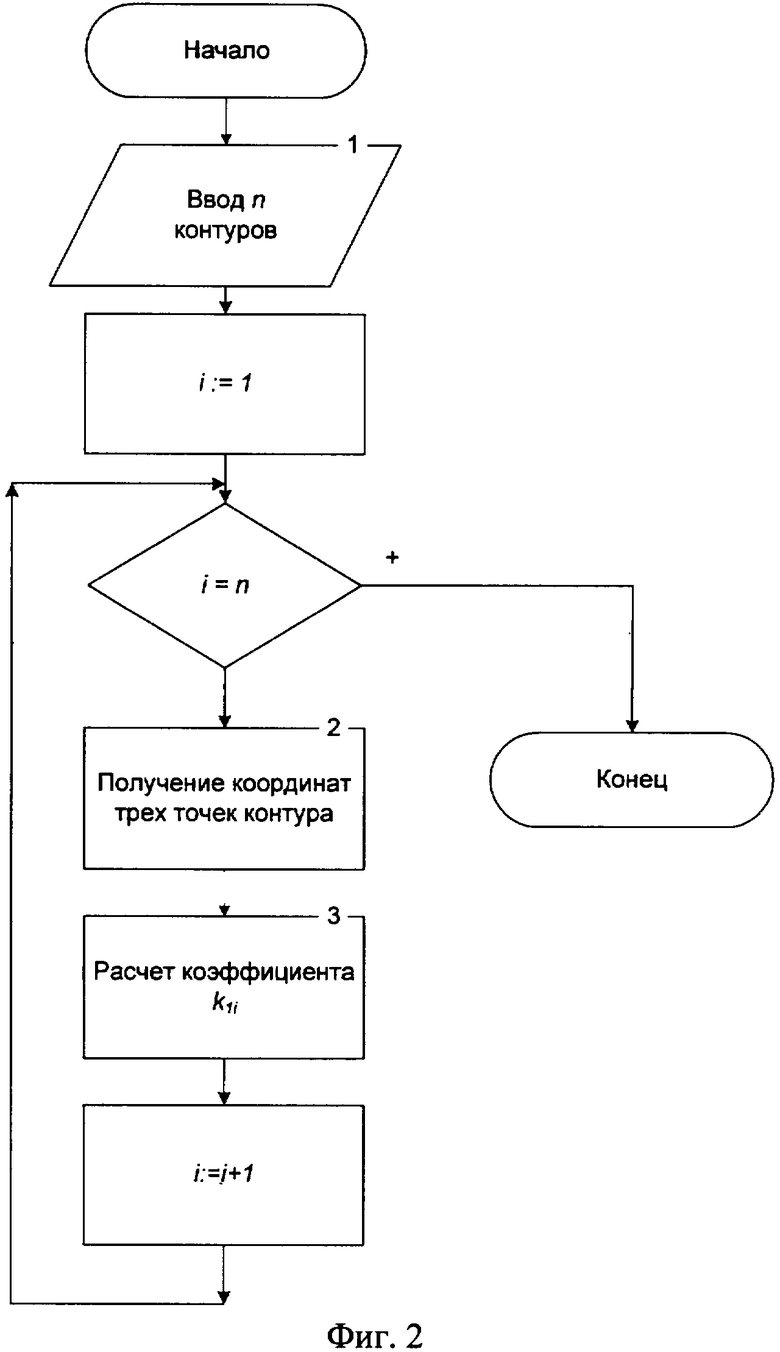
После выбора контуров осуществляют определение множества коэффициентов k1i радиальной дисторсии (блок 4, фиг.1), где i=1...n, n - количество используемых контуров. Для этого считают, что каждый контур до искажения был прямой, а его искажение обусловлено только влиянием дисторсии.
Для каждого контура производят последовательность действий, изображенную на алгоритме (фиг.2).
Входными данными (блок 1, фиг.2) являются координаты начала, конца и точки, принадлежащей контуру и равноудаленной от его концов, для каждого контура в декартовой системе координат, а также количество контуров. Начало системы координат совпадает с центром кадра, ось абсцисс параллельна верхнему краю кадра, а ординат правому краю.
Для каждого контура берут три точки (блок 2, фиг.2), т.е. используют для определения коэффициента k1i координаты начала контура, его конца и точки, принадлежащей контуру и равноудаленной от его концов.
Рассмотрим расчет коэффициента радиальной дисторсии (блок 3, фиг.2).
Каждый из контуров на изображении до искажения представлял собой прямую линию, которая вследствие искажения стала кривой.
Как известно из геометрии, уравнение прямой имеет вид:

где q, w - постоянные коэффициенты.
Обозначим начало контура точкой 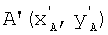 , среднюю точку -
, среднюю точку - 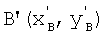 , конечную -
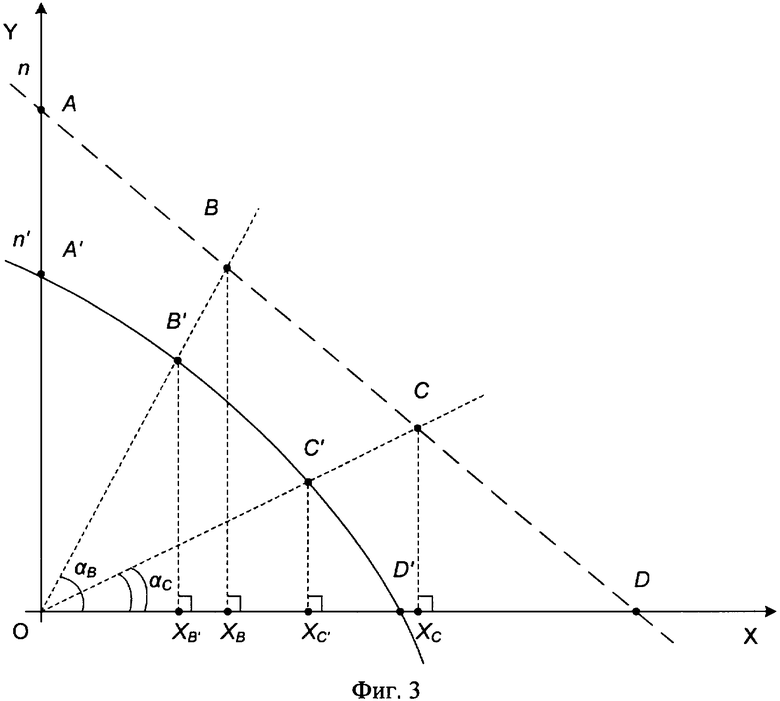
, конечную - 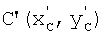 и введем точку D', которая является точкой пересечения прямой, на которой лежит контур, с осью абсцисс (фиг.3). Точка D' - вспомогательная и используется для составления системы уравнений, необходимой для вычисления коэффициента дисторсии. До искажения перечисленные точки имели иное расположение, на фиг.3 обозначено их истинное положение точками А(хA, yA), В(хB, yB), С(хC, yC), D(xD, yD) соответственно.
и введем точку D', которая является точкой пересечения прямой, на которой лежит контур, с осью абсцисс (фиг.3). Точка D' - вспомогательная и используется для составления системы уравнений, необходимой для вычисления коэффициента дисторсии. До искажения перечисленные точки имели иное расположение, на фиг.3 обозначено их истинное положение точками А(хA, yA), В(хB, yB), С(хC, yC), D(xD, yD) соответственно.
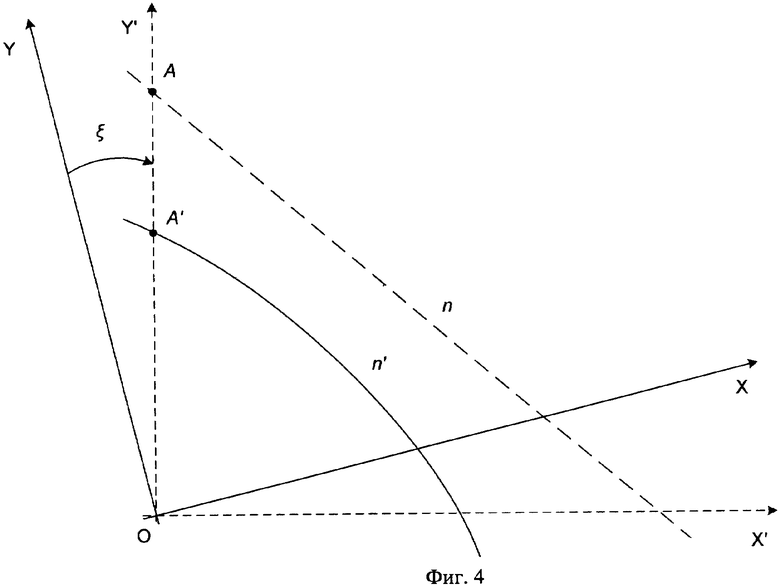
Для определения коэффициента радиальной дисторсии одна из трех точек должна располагаться на оси ординат. Если ни одна из точек не расположена на оси ординат, тогда изображение поворачивают таким образом, чтобы указанное условие выполнялось. Радиальная дисторсия не зависит от угла наклона к осям абсцисс и ординат. Используя формулы аффинного преобразования в плоскости, а именно поворота относительно начала координат на угол ξ, координаты точек преобразуют:
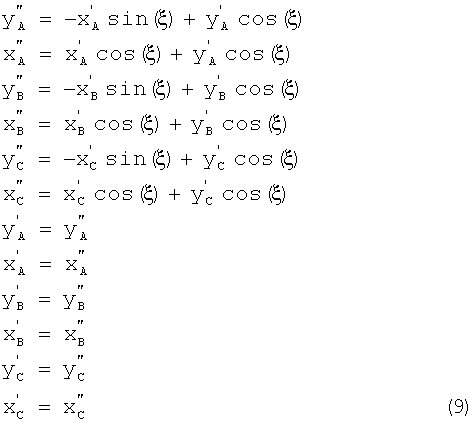
где  ,
, 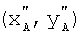 ,
, 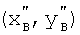 ,
, 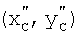 - координаты точек А', В', С' после преобразования.
- координаты точек А', В', С' после преобразования.
Для точек А, В, С, D уравнение (8) выглядит следующим образом:

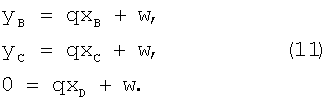
После подстановки уравнения (10) в уравнения (11)
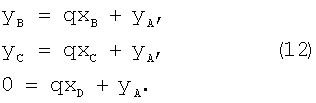
Так как ΔОВХB и ΔОСХC - прямоугольные (фиг.3), то
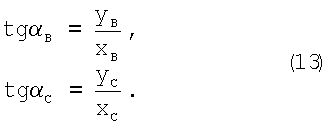
Из (14) следует

Выполнив подстановку (14) в (12), уравнения примут вид:
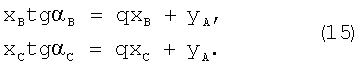
Искажения, вызванные радиальной дисторсией в декартовой системе координат, исходя из (1) определяют по формулам
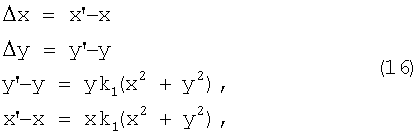
где (х', y') - координаты точки, измеряемые по изображению.
Для точек А, В и С выражения (16) записывают следующим образом:
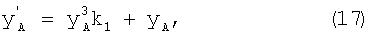
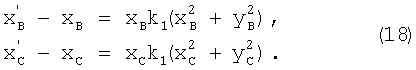
После подстановки выражения (14) в выражение (18) получают
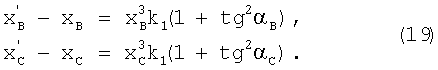
Если правые и левые части каждого из выражений (19) равны, то и отношение правых частей будет равно отношению левых частей этих выражений, при этом коэффициент k1 сократится:

Взаимосвязь истинного положения точки и ее положения на искаженном изображении в полярной системе координат определяют формулой
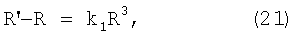
где R, R' - расстояния от центра координат до истинного положения точки и ее положения на искаженном изображении соответственно.
Для точки С выражение (21) примет вид
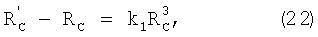
где RC, 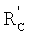 - расстояния от центра координат до точки С и до точки С' соответственно.
- расстояния от центра координат до точки С и до точки С' соответственно.
Так как ΔОСХC' - прямоугольный (фиг.3):
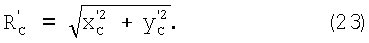
Используя выражение (14) и то, что ΔОСХC - прямоугольный (фиг.3), формула расчета его гипотенузы примет вид
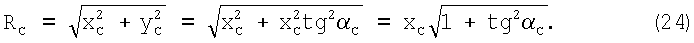
Выполнив подстановку выражения (24) в (22), получают

Используют замену
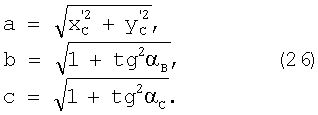
Подставив выражения (26) в выражение (25), получают
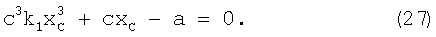
Для определения коэффициента радиальной дисторсии составляют систему уравнений, используя выражения (12), (15), (17), (20), (27):
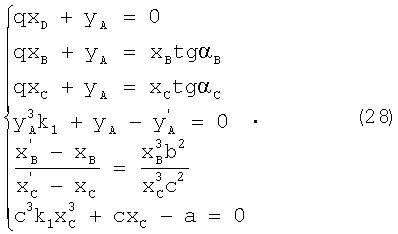
В результате решения системы уравнений (28) получают уравнение
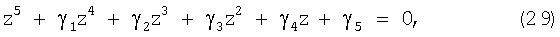
где 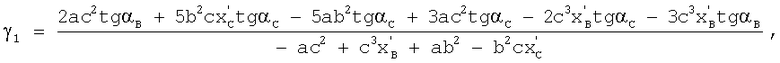
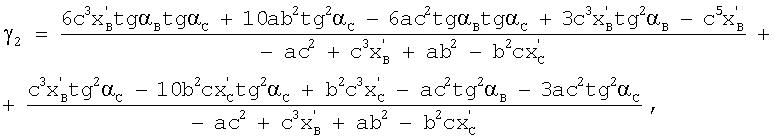
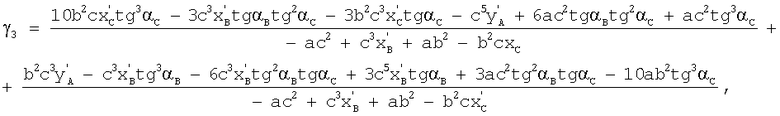
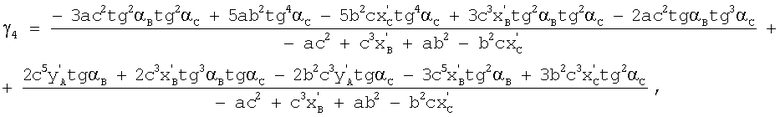
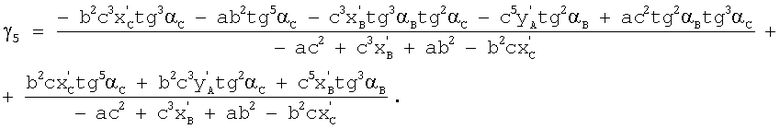
Корни уравнения (29) являются значениями q. Известно, что многочлен пятой степени имеет не более пяти действительных корней
Нахождение корней производят численными методами [Демидович Б.П., Марон И.А. Основы вычислительной математики. - М.: Наука. Гл. ред. физ.-мат. лит., 1966] автоматически с заданной точностью.
Рассматривают только действительные корни. После их нахождения рассчитывают для каждого из них yA по формуле, полученной в результате решения системы уравнений (28):
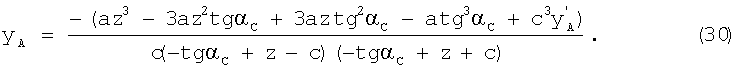
В результате находят пять либо три, либо одно возможное значение истинной ординаты точки А. Если значение одно, значит, оно и есть искомое, иначе производят отбор искомого значения ординаты точки А из полученных. Для осуществления отбора применяют несколько критериев:
- ордината точки А после выполнения преобразования поворота на угол -ξ относительно начала координат не может численно превосходить половины ширины изображения;
- ордината точки не может быть другого знака, т.е. истинное положение точки должно быть в той же четверти, в которой расположено и искаженное;
- при подстановке значений q и yA в систему уравнений (28) рассчитанные координаты абсцисс и ординат точек В и С также не могут численно превосходить половины длины и ширины изображения соответственно и должны быть одинакового знака с искаженными координатами.
После проведения анализа возможных вариантов остается значение, удовлетворяющее критериям. Используя это значение и формулу, полученную из системы уравнений (28), вычисляют
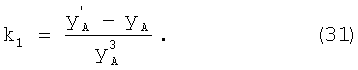
После расчета коэффициентов для каждого контура производят анализ частоты встречаемости коэффициентов (блок 5, фиг.1). Для этого строят гистограмму зависимости величины коэффициента от частот его повторяемости и определяют по гистограмме значение k1, используемого для последующей коррекции как среднего в окрестности значения k1i с максимальной частотой повторения.
После нахождения коэффициента k1 в блоке 6 (фиг.1) по известным искаженным координатам (x', y') на изображении определяют истинное положение точки (х, y), используя формулу (1).
Предложенный способ обеспечивает определение коэффициента и проведение коррекции радиальной дисторсии на цифровом изображении, используя только информацию, которую содержит само изображение независимо от параметров фото-, видеокамеры, в которой оно было получено.
Примером применения предложенного способа определения и коррекции радиальной дисторсии может быть его реализация в цифровом фотоаппарате с матричным приемником изображений, который после получения изображения, его аналого-цифрового преобразования и занесения изображения в память, при помощи встроенного вычислительного устройства выполняет действия, описанные в данном способе, и сохраняет в своей памяти уже скорректированное изображение.
Таким образом, изобретение позволяет увеличить скорость и точность определения коэффициента радиальной дисторсии и коррекции изображения за счет автоматизации этих процессов, отсутствия подбора величин и исключения визуальной оценки, а также расширить область применения изобретения путем его использования независимо от параметров фото-, видеокамеры, в которой изображение было получено, на основе информации, содержащейся в самом изображении.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ АДАПТИВНОЙ КАЛИБРОВКИ РАДИАЛЬНОЙ ДИСТОРСИИ ОПТИЧЕСКОЙ ПОДСИСТЕМЫ СИСТЕМЫ ТЕХНИЧЕСКОГО ЗРЕНИЯ | 2004 |
|
RU2289111C2 |
| СПОСОБ ФОРМИРОВАНИЯ ПАНОРАМНЫХ ИЗОБРАЖЕНИЙ | 2006 |
|
RU2365998C2 |
| СПОСОБ ОЦЕНКИ СОДЕРЖАНИЯ АПОЛЯРНЫХ ФЛОТОРЕАГЕНТОВ В ПУЛЬПЕ ПО ЦИФРОВОМУ ИЗОБРАЖЕНИЮ ПУЗЫРЬКА ГАЗА | 2005 |
|
RU2292033C2 |
| СПОСОБ КАЛИБРОВКИ РАДИАЛЬНОЙ ДИСТОРСИИ ОПТИЧЕСКОЙ ПОДСИСТЕМЫ СИСТЕМЫ ТЕХНИЧЕСКОГО ЗРЕНИЯ | 2007 |
|
RU2346326C2 |
| СПОСОБ КАЛИБРОВКИ ДИСТОРСИИ ОПТИКО-ЭЛЕКТРОННОГО УСТРОЙСТВА | 2006 |
|
RU2321888C1 |
| СПОСОБ КОРРЕКЦИИ ХРОМАТИЧЕСКОЙ АБЕРРАЦИИ ОПТИЧЕСКОЙ ПОДСИСТЕМЫ СИСТЕМЫ ТЕХНИЧЕСКОГО ЗРЕНИЯ | 2007 |
|
RU2352988C1 |
| СПОСОБ КОМПЕНСАЦИИ ДИСТОРСИИ ОБЪЕКТИВА | 2022 |
|
RU2790055C1 |
| УСТРОЙСТВО ОБЪЕДИНЕНИЯ ИЗОБРАЖЕНИЙ В ЕДИНУЮ КОМПОЗИЦИЮ СЦЕНЫ | 2013 |
|
RU2536675C1 |
| СПОСОБ И СИСТЕМА КАЛИБРОВКИ КАМЕРЫ | 2012 |
|
RU2601421C2 |
| СПОСОБ ОПРЕДЕЛЕНИЯ КООРДИНАТ ОБЪЕКТОВ ПО ИХ ЦИФРОВЫМ ИЗОБРАЖЕНИЯМ | 2018 |
|
RU2697822C2 |
Изобретение относится к вычислительной технике и может быть использовано для определения и коррекции радиальной дисторсии на изображениях, полученных цифровыми фото-, видеокамерами и системами технического зрения, использующих в качестве приемников изображения матричные приемники изображения. Техническим результатом изобретения является увеличение скорости определения коэффициента радиальной дисторсии, повышение точности коррекции искажений, вызванных радиальной дисторсией, а также расширение области применения за счет использования способа независимо от параметров аппаратуры, в которой получено изображение, на основе информации, содержащейся в самом изображении. В способе определяют коэффициент дисторсии, выделяют изображения контуров, анализируют их, выбирают три точки на каждом контуре и рассчитывают коэффициенты радиальной дисторсии, составляют гистограммы зависимости частот повторяемости найденных коэффициентов от их величин, определяют значение коэффициента как среднего в окрестности значения коэффициента с максимальной частотой повторения, корректируют искажения, вызванные радиальной дисторсией. 5 ил.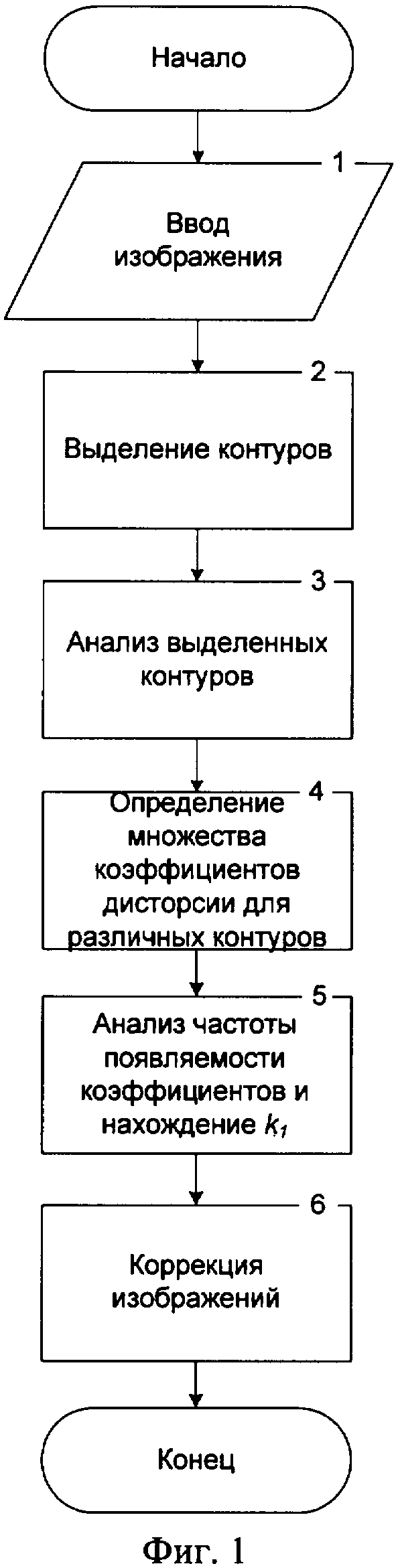
Способ определения и коррекции радиальной дисторсии на цифровом изображении, заключающийся в том, что выделяют контуры объектов на изображении, представляющем матрицу значений яркости пикселей изображения, точки на котором имеют координаты по горизонтали и вертикали, для чего используют пороговое значение изменения указанной яркости, по которому определяют принадлежность указанных точек указанному контуру объекта, на каждом контуре объекта,
представленном как часть окружности, определяют координаты трех точек, по которым рассчитывают радиусы, исключают из рассмотрения контуры, кривизна которых не может быть вызвана только влиянием радиальной дисторсии, для каждого из оставшихся контуров объектов изображения определяют коэффициент радиальной дисторсии,
составляют гистограмму зависимости частоты повторяемости указанных коэффициентов радиальной дисторсии от их величин, определяют по гистограмме значения коэффициента радиальной дисторсии, как среднего в окрестности значения указанного коэффициента с максимальной частотой повторения, которое используют для последующей коррекции искажения, вызванного радиальной дисторсией с определением истинного положения указанных точек.
| RU 2004104494 А, 10.08.2005 | |||
| US 2005018175 А, 27.01.2005 | |||
| JP 8287243, 01.11.1996 | |||
| US 5878174, 02.03.1999 | |||
| JP 9056662, 04.03.1997. |
Авторы
Даты
2009-03-27—Публикация
2006-12-04—Подача