Предлагаемое изобретение относится к медицине, в частности к кардиологии, и может быть использовано как неинвазивный способ определения электрической активности сердца (ЭАС) и наглядного, реалистичного представления «электрического портрета» сердца пациента. Под «электрическим портретом» сердца понимается распределение или топика ЭАС. Исследования ученых показывают трудности моделирования работы сердца и определения ЭАС. Так, реализация модели требует больших вычислительных затрат: «для того, чтобы рассчитать секунду работы сердца требуются сутки работы мощного компьютера» [13]. На современном уровне развития вычислительной техники невозможно полностью исключить человека из процесса анализа кардиографической информации. С другой стороны, очевидна невозможность освоения человеком всего объема кардиографической информации. Во избежание «информационного паралича» необходимо создать такие условия для функциональной диагностики, при которых лечащий врач максимально концентрировался бы на постановке диагноза.
Предлагаемое изобретение относится к решению обратной задачи электрокардиографии, когда по результатам анализа электрокардиограммы (ЭКГ) определяется ЭАС, эквивалентная сторонним (мембранным) токам в представлении Нобла [16], формирующим трансмембранный потенциал действия (ТМПД).
Известно, что решение обратных задач сложнее решения прямых задач и всегда неоднозначно, то есть результат можно получить множеством способов [9].
Известен неинвазивный способ ультразвуковой эхокардиографии [7], основанный на регистрации отраженных от лоцируемого объекта ультразвуковых волн и дающий возможность визуализации сердечных структур в реальном масштабе времени. Эхокардиографический метод позволяет определить функциональное состояние сердца, однако требует участия при диагностике высококвалифицированного специалиста, использования дорогостоящей аппаратуры и значительных затрат времени на проведение одного исследования. Кроме того, при эхокардиографическом методе невозможно получить диагностическую информацию об ЭАС и наглядную реалистичную картину топики ЭАС.
Наиболее близким по достигаемому результату к предлагаемому изобретению является неинвазивный способ определения основных функциональных показателей миогемодинамики сердца [3], заключающийся в регистрации и анализе кардиографической информации, синтезе реалистичного трехмерного изображения модели сердца пациента и вычислении основных объемно-функциональных показателей миогемодинамики сердца по оригинальным математическим формулам.
В известном способе определения основных функциональных показателей миогемодинамики сердца с помощью классических способов регистрации и анализа кардиографической информации осуществляется только определение «геометрии» и информационных параметров миогемодинамики сердца пациента. Это является принципиальной отличительной особенностью известного способа. Очевидно, что такого представления результатов анализа кардиографической информации недостаточно для постановки диагноза. Необходимо расширить диагностические возможности анализа кардиографической информации.
К недостаткам известного способа определения основных функциональных показателей миогемодинамики сердца относится то, что результаты анализа ЭКГ и флюорографии не используются для определения ЭАС и наглядного представления распределения ЭАС, а также не рассматривается динамика показателей миогемодинамики сердца пациента в течение кардиоцикла.
Предлагаемый способ определения электрической активности сердца является неинвазивным и позволяет расширить диагностические возможности путем представления «электрического портрета» сердца. ЭКГ является ценным диагностическим инструментом. По ней можно оценить источник ритма, регулярность сердечных сокращений, их частоту. Все это имеет большое значение для диагностики различных патологий. По продолжительности различных интервалов и зубцов ЭКГ можно судить об изменениях сердечной проводимости. Изменения конечной части желудочкового комплекса (интервал ST и зубец Т) позволяют врачу определить наличие или отсутствие ишемических изменений в сердце.
Иными словами, путем анализа ЭКГ врач на основании имеющихся знаний и опыта определяет топику ЭАС и нарушение кровоснабжения. Формализации этого процесса посвящен предлагаемый способ определения ЭАС.
Изобретение направлено на расширение функциональных возможностей электрокардиологического исследования за счет наглядного представления изменения распределения ЭАС на модели реалистичного изображения сердца пациента.
Это достигается тем, что в способ определения основных функциональных показателей миогемодинамики сердца, заключающийся в том, что регистрируют электрокардиограмму и определяют конечный диастолический радиус (КДР) и конечный систолический радиус (КСР) полости ЛЖ, конечный диастолический объем (КДО) и конечный систолический объем (КСО) ЛЖ, которые рассчитываются по данным электрокардиограммы в одном из следующих отведений: 4, 5, 6-м грудном (по Вильсону) или 11 стандартном (по Эйнтховену), выбранном соответственно направлению электрической оси сердца, а при невозможности их регистрации - в отведении А (по Небу), измеряют при отсутствии блокад ножек пучка Гиса продолжительности интервалов QR, RS, QRS, ST-T, R-R и дополнительно при блокаде левой ножки пучка Гиса - продолжительности интервала R1R2, а при блокаде правой ножки пучка Гиса - продолжительности интервала S1S2, и при синусовом и других наджелудочковых ритмах сердца в состоянии физического покоя определяют по формулам: КДР=(44,5-100*tRS)*(tQR+tRS)-11*tRS, где tQR - время от начала зубца Q до вершины зубца R при отсутствии блокады левой ножки пучка Гиса, а при наличии блокады левой ножки пучка Гиса - до первой вершины раздвоенного зубца R(R1), то есть tQR=tQR, с; tRS - время от вершины зубца R
до конца зубца S - при отсутствии блокад ножек пучка Гиса, а при блокаде левой ножки пучка Гиса вместо tRS - разность временных интервалов от первой вершины раздвоенного зубца R до конца зубца S (R1 S) и от первой вершины раздвоенного зубца R до его второй вершины (R1R2), то есть  , с;
, с; 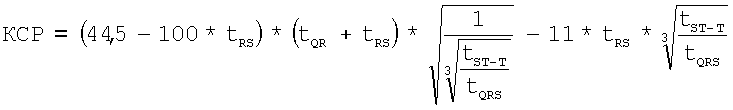 ,
,
где tQRS - время комплекса QRS, с; tST-T - время от конца зубца S до конца зубца Т - при отсутствии блокад ножек пучка Гиса, а при блокаде левой ножки пучка Гиса вместо tST-T - сумма 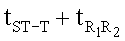 и при блокаде правой ножки пучка Гиса вместо tST-T сумма
и при блокаде правой ножки пучка Гиса вместо tST-T сумма 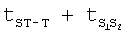 , с;
, с; 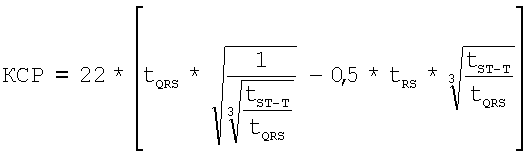 ,
,
и далее вычисляют при всех указанных видах сердечного ритма КДО=(4/3)*π*КДР3 и КСО=(4/3)*π*КСР3, а также регистрируют фронтальный и левобоковой флюорографические снимки сердца пациента, определяют по снимкам геометрические параметры сердца пациента, синтезируют реалистичное трехмерное изображение сердца пациента, значения КДР и КСР заменяют реальными эквивалентными геометрическими параметрами модели ЛЖ сердца пациента, значения которых определяют по формулам Ri_КДРЛЖ=ККДР*Ri_модели; Ri_КСРЛЖ=ККСР*Ri_модели;
ККДР=КДР3/R3 ср_модели; ККСР=КСР3/R3 ср_модели, где Ri_КДРЛЖ - конечное диастолическое расстояние от центра геометрического места точек поверхности модели ЛЖ сердца пациента до i-й точки поверхности модели ЛЖ сердца пациента;
Ri_КСРЛЖ - конечное систолическое расстояние от центра геометрического места точек поверхности модели ЛЖ сердца пациента до i-й точки поверхности модели ЛЖ сердца пациента; Ri_модели - расстояние от центра геометрического места точек поверхности модели ЛЖ сердца пациента до i-й точки поверхности модели ЛЖ сердца пациента;
Rсф_модели - радиус сферы, объем которой равен объему модели ЛЖ сердца пациента;
ККДР, ККСР - коэффициенты пропорциональности объема модели ЛЖ сердца пациента соответственно диастолическому и систолическому объему ЛЖ сердца пациента Введены действия, в результате которых определяются координаты точек (xj, yj, zj) отведений (j=1÷12) на поверхности торса пациента в правой системе координат, начало которой совпадает с центром трансверсального сечения грудной клетки; характеристика электрической активности i-й точки на поверхности модели сердца пациента Ji, эквивалентной сторонним токам; показатели миогемодинамики сердца в процессе изменения электрической активности соответствующей анатомической части сердца.
Координаты точек (xj, yj, zj) отведений (j=1÷12) на поверхности торса пациента определяются следующим образом. Сначала вычисляются параметры трансверсального сечения грудной клетки пациента (трансверсальный и сагиттальный диаметры) по формулам:
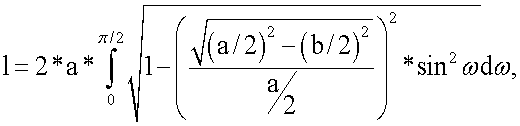
 ,
,
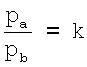 ,
,
где l - длина обхвата груди; а - большая ось трансверсального сечения грудной клетки пациента (трансверсальный диаметр); b - малая ось трансверсального сечения грудной клетки пациента (сагиттальный диаметр); ω - переменная интегрирования; pa - количество пикселей на флюорографическом снимке, принадлежащих торсу пациента, по оси абсцисс; pb, - количество пикселей на флюорографическом снимке, принадлежащих торсу пациента, по оси аппликат.
Затем определяется смещение геометрического центра сердца относительно центра трансверсального сечения грудной клетки по формулам
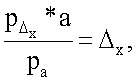
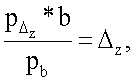
где 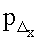 - количество пикселей на флюорографическом снимке, определяемое от центра грудной клетки до центра сердца по оси абсцисс;
- количество пикселей на флюорографическом снимке, определяемое от центра грудной клетки до центра сердца по оси абсцисс;
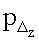 - количество пикселей на флюорографическом снимке, определяемое от центра грудной клетки до центра сердца по оси аппликат;
- количество пикселей на флюорографическом снимке, определяемое от центра грудной клетки до центра сердца по оси аппликат;
Δx - смещение геометрического центра сердца относительно центра трансверсального сечения грудной клетки по оси абсцисс;
Δz - смещение геометрического центра сердца относительно центра трансверсального сечения грудной клетки по оси аппликат.
Координаты точек (xj, yj, zj) отведений (j=1÷12) на поверхности торса пациента определяются:
- для стандартных отведений I, II, III по формулам:
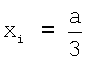 ,
,
yI=0,
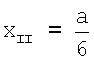 ,
,
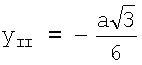 ,
,
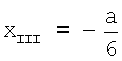 ,
,
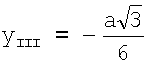 ,
,
zI,II,III=0.
- для усиленных отведений от конечностей aVR, aVL, aVF по формулам:
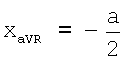 ,
,
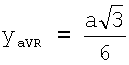 ,
,
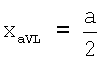 ,
,
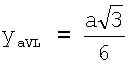 ,
,
xaVF=0,
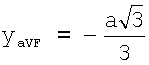 ,
,
zaVR,aVL,aVF=0.
- для грудных отведений V1÷V6:
координаты (xV1÷V6, zV1÷V6) определяют из системы уравнений:
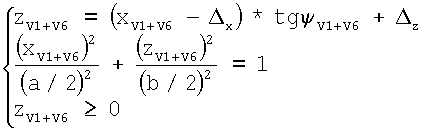 ,
,
где ψV1+V6 - угол между осью абсцисс и отрезком, соединяющим точку соответствующего стандартного грудного отведения с геометрическим центром сердца;
координаты yV1÷V6 определяют по формулам:
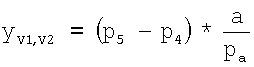 ,
,
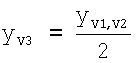 ,
,
yV4,V5,V6=0,
где yV1,V2 - координаты точек грудных отведений V1-V2 на поверхности торса пациента по оси ординат;
yV3 - координата точки грудного отведения V3 на поверхности торса пациента по оси ординат;
yV4,V5,V6 - координаты точек грудных отведений V4-V6 на поверхности торса пациента по оси ординат;
p5 - количество пикселей на флюорографическом снимке до 5 межреберья;
р4 - количество пикселей на флюорографическом снимке до 4 межреберья.
Характеристику электрической активности Ji i-й точки на поверхности модели сердца пациента, эквивалентную сторонним токам, определяют из решения СЛАУ:
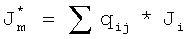 ,
,
qij=cosλ,
m=1÷M,
i=1÷I,
где М - число возможных электрически активных областей на поверхности модели сердца пациента, равное числу электрически активных точек I на поверхности модели сердца пациента;
qij - коэффициент пропорциональности;
λ - угол между вектором направления от i-й точки на поверхности модели сердца пациента к j-й точке отведения и нормалью в i-й точке поверхности сердца пациента;
J* m - характеристика электрической активности Sm-й области на поверхности модели сердца пациента, содержащая i-ю точку, которую определяют из решения 1/12 систем уравнений размерностью 12х12:
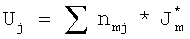 ,
,
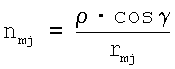 ,
,
где Uj - значение регистрируемого по данным электрокардиограммы напряжения в j-й точке отведения;
nmj - коэффициент пропорциональности;
ρ - удельное сопротивление;
γ - угол между вектором направления от m-й области на поверхности сердца пациента к j-й точке отведения и нормалью в m-й области на поверхности сердца пациента;
rmj - расстояние от точки j-го отведения до области Sm находится как среднее арифметическое расстояний от точки j-го отведения до точек, входящих в область Sm. Размеры области Sm на поверхности модели сердца пациента определяются следующим образом:
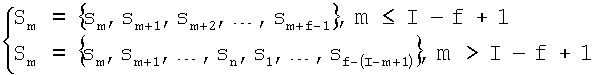
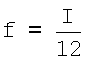 ,
,
где sm - обозначение точки, принадлежащей области Sm;
f - число точек в каждой области;
I - число электрически активных точек.
Показатели миогемодинамики сердца в процессе изменения электрической активности соответствующей анатомической части сердца определяются по формуле:
Vtime,part=КДОpart-(КДОpart-КСОpart)*ψtime,part,
где Vtime,part - объем полости анатомической части сердца part в момент времени time процесса изменения электрической активности сердца; КДОpart - конечный диастолический объем полости анатомической части сердца part; KCOpart - конечный систолический объем полости анатомической части сердца part; ψtime,part - характеристика процесса изменения электрической активности анатомической части сердца, вычисляемая по формуле:
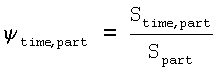 ,
,
где Stime,part - площадь возбужденного участка поверхности анатомической части сердца part в момент времени time; Spart - общая площадь поверхности анатомической части сердца part.
Введенные действия с их связями проявляют новые свойства, которые позволяют определить электрическую активность участка поверхности сердца. По мнению авторов, определение и наглядное представление «электрического портрета» сердца по результатам анализа его электрической активности является принципиальной отличительной особенностью предлагаемого способа. Известно, что графическую информацию человек воспринимает лучше «из-за большей пропускной способности зрительного канала» [12], поэтому в предлагаемом способе на реалистичной модели сердца пациента осуществляется отображение полученной электрической активности участка поверхности сердца, то есть отображение топики ЭАС на реалистичном изображении модели сердца пациента.
На фигуре 1 приведена блок-схема алгоритма, реализующего известный способ определения основных показателей миогемодинамики сердца. На блок-схеме приняты следующие обозначения:
1 - регистрация ЭКГ;
2 - анализ информационных показателей ЭКГ;
3 - синтез модели сердца человека;
4 - определение показателей миогемодинамики сердца;
5 - регистрация флюорографии;
6 - анализ информационных показателей флюорографии.
На фигуре 2 приведена блок-схема алгоритма, реализующего предлагаемый способ определения электрической активности сердца. На блок-схеме приняты следующие обозначения:
1 - регистрация ЭКГ;
2 - анализ информационных показателей ЭКГ;
3 - синтез модели сердца пациента;
4 - определение электрической активности сердца;
5 - определение показателей миогемодинамики сердца;
6 - регистрация флюорографии;
7 - анализ информационных показателей флюорографии.
На фигуре 3 приведен алгоритм работы блока определения электрической активности сердца.
На фигуре 4 приведено изображение сердца в модели торса пациента с расположением на модели торса 12 точек стандартных отведений.
На фигуре 5 приведено изображение треугольника Эйнтховена с расположением шести точек стандартных отведений (I, II, III, aVR, aVL, aVF).
На фигуре 6 приведено изображение трансверсального сечения торса пациента с расположением точек грудных отведений (V1, V2, V3, V4, V5, V6).
На фигуре 7 приведена схема модели ЭАС [2].
На фигуре 8 приведено изображение поля напряженности сердца.
На фигуре 9 изображена поверхность сердца, аппроксимированная плоскими треугольными гранями.
На фигуре 10 приведено изображение сердца с нормалями, проведенными к плоскостям.
На фигуре 11 приведено изображение поверхности модели сердца пациента с выделенными электрически активными областями.
На фигуре 12 приведено изображение электрически активной области Sm поверхности модели сердца пациента, содержащей электрически активные точки сердца.
На фигуре 13 приведена схема группировки точек на смежные непересекающиеся области.
На фигуре 14 приведена схема процесса составления СЛАУ для определения электрической активности области.
На фигуре 15 приведено изображение проводящей системы сердца.
На фигуре 16 приведена схема генезиса ЭКГ [2].
Суть предлагаемого способа заключается в следующем: поверхность модели сердца задается опорными точками. Чем больше опорных точек, тем точнее модель аппроксимирует сердце пациента. Для аппроксимации поверхности модели сердца используется триангуляция Делоне. Для построения триангуляции точки поверхности соединяют прямыми так, чтобы каждая точка стала вершиной треугольника, а каждый отрезок прямой - стороной треугольника (см. фигуру 9). Таким образом, поверхность модели сердца человека изображается в виде совокупности плоских треугольных граней.
Можно считать, что ЭАС пациента определяется электрической активностью опорных точек модели сердца. Если число отведений равно числу опорных точек, то определение электрической активности опорных точек не затруднительно: необходимо составить и решить соответствующую СЛАУ. В случае стандартных отведений возможно определение электрической активности 12 областей. По сути, так дело и обстоит: каждое из 12 стандартных отведений позволяет регистрировать изменения электрической активности определенного отдела сердца, осуществлять топическую диагностику одной из областей сердца (см. таблицу 1) [4].
Так как число опорных точек модели сердца пациента во много раз больше числа стандартных отведений, то непосредственное, «лобовое» построение и решение СЛАУ не позволит определить электрическую активность всех опорных точек модели сердца пациента. Определение ЭАС заключается в построении СЛАУ, число неизвестных которой равно количеству опорных точек модели сердца пациента.
Возможно увеличение количества отведений. Метод ЭКГ-картирования сердца [15, 10] использует большое число отведений (до 90÷192), располагающихся на всей поверхности грудной клетки, что обеспечивает получение максимальной информации об особенностях структуры электрического поля сердца; поэтому помимо прочих своих достоинств (предоставления возможности синхронизации всех электрокардиосигналов и представление данных не в традиционной (аналоговой) форме, а в виде последовательных (моментных), интегральных и изоинтегральных картограмм распределения потенциалов) позволяет определить динамику процессов де- и реполяризации до 90÷192 областей миокарда. Поскольку число опорных точек модели сердца пациента превышает минимум на порядок число отведений в методе ЭКГ-картирования сердца, то получается, что метод ЭКГ-картирования непосредственно не позволяет определить электрическую активность всех опорных точек модели сердца пациента.
В предлагаемом способе нахождение ЭАС осуществляется путем построения определенным образом и решения ряда СЛАУ. При этом количество СЛАУ обусловлено числом опорных точек модели сердца пациента, электрическую активность которых необходимо определить.
Первоначально в предлагаемом способе определения ЭАС осуществляется (см. фигуру 2) регистрация электрокардиографических и флюорографических данных. Затем по данным ЭКГ определяются КСР, КДР, КСО и КДО сердца пациента. Данные флюорографии «накладываются» на модель сердца и путем совмещения и нелинейного масштабирования осуществляется «подгонка» данных модели сердца к данным флюорографии. В результате определяется «геометрия» сердца пациента.
Далее осуществляется поэтапное определение электрической активности каждой точки сердца (см. фигуру 3). Для определения электрической активности необходимо вычислить расстояния от точек на поверхности модели сердца человека до точек стандартных 12 отведений. Координаты точек поверхности модели сердца получены из блока определения «геометрии» сердца человека. По флюорографическим и антропологическим данным осуществляется определение параметров трансверсального сечения грудной клетки (трансверсальный и сагиттальный диаметры). В качестве упрощенной модели грудной клетки (см. фигура 4) используется осредненная структура в виде эллиптического цилиндра, имеющей три параметра а, b и h, которые соответствуют основным антропометрическим параметрам груди - трансверсальному диаметру, сагиттальному диаметру и высоте. Согласно общепринятому правилу, трансверсальный и сагиттальный диаметры измеряются на уровне между 4-м и 5-м межреберьями у края грудины; высота или длина туловища измеряется как расстояние между уровнями гребня лопатки и верхней части подвздошной ости. Внутри модели грудной клетки задается геометрический центр сердца с координатами xс, yс, zc в системе координат xyz с началом в центре модели грудной клетки [10].
Окружность грудной клетки равняется полной дуге эллипса. Полная дуга эллипса с осями а и b выражается через полный эллиптический интеграл второго рода по формуле  , где
, где 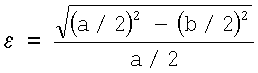 [11]. Следовательно, для определения параметров трансверсального сечения грудной клетки (трансверсальный и сагиттальный диаметры или большая и малая оси эллипса соответственно) необходимо, чтобы в процессе их перебора с заданной точностью выполнялись равенства
[11]. Следовательно, для определения параметров трансверсального сечения грудной клетки (трансверсальный и сагиттальный диаметры или большая и малая оси эллипса соответственно) необходимо, чтобы в процессе их перебора с заданной точностью выполнялись равенства 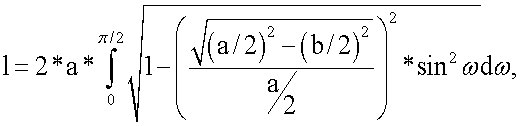
 ,
, 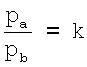 .
.
Далее происходит определение смещений геометрического центра сердца относительно центра грудной клетки. При определении смещений (Δx, Δz) геометрического центра сердца относительно центра трансверсального сечения грудной клетки необходимо воспользоваться данными, полученными из флюорографии: количество пикселей на флюорографическом снимке, определяемое от центра грудной клетки до центра сердца по оси абсцисс (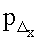 ), количество пикселей на флюорографическом снимке, определяемое от центра грудной клетки до центра сердца по оси аппликат (
), количество пикселей на флюорографическом снимке, определяемое от центра грудной клетки до центра сердца по оси аппликат (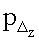 ), количество пикселей на флюорографическом снимке, принадлежащих торсу пациента, по оси абсцисс (ра), количество пикселей на флюорографическом снимке, принадлежащих торсу пациента, по оси аппликат (рb) а также значениями параметров транрверсального сечения грудной клетки пациента (трансверсальный а и сагиттальный b диаметры). Смещения геометрического центра сердца относительно центра трансверсального сечения грудной клетки (Δx, Δz) вычисляются по формулам:
), количество пикселей на флюорографическом снимке, принадлежащих торсу пациента, по оси абсцисс (ра), количество пикселей на флюорографическом снимке, принадлежащих торсу пациента, по оси аппликат (рb) а также значениями параметров транрверсального сечения грудной клетки пациента (трансверсальный а и сагиттальный b диаметры). Смещения геометрического центра сердца относительно центра трансверсального сечения грудной клетки (Δx, Δz) вычисляются по формулам: 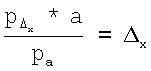 ,
, 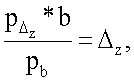 где отношения
где отношения 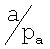 и
и 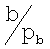 используются в качестве коэффициентов масштабирования.
используются в качестве коэффициентов масштабирования.
На основе полученных данных осуществляется определение координат точек стандартных отведений (I, II, III), усиленных отведений от конечностей (aVR, aVL, aVF) и грудных отведений (V1, V2, V3, V4, V5, V6), представленных на фигуре 4.
Координаты точек (xj, yj, zj) стандартных отведений (I, II, III) и усиленных отведений от конечностей (aVR, aVL, aVF) на поверхности торса пациента определяются из треугольника Эйнтховена, центром которого является центр сердца (см. фигура 4). Зная значение большой оси эллипса (трансверсального диаметра грудной клетки - а), которое будет равно длине стороны треугольника Эйнтховена, и, учитывая, что треугольник равносторонний, находятся координаты шести точек отведений.
Обратимся к фигуре 5, на которой представлен треугольник Эйнтховена с точками шести стандартных отведений (I, II, III, aVR, aVL, aVF).
Точки отведений I и II делят сторону ВС треугольника Эйнтховена на три равные части. Треугольники ΔCFB и ΔCOD являются подобными, так как ∠C - общий, ∠FBC=∠ODC - как соответствующие углы при параллельных прямых FB и OD. Коэффициент подобия треугольников ΔCFB и ΔCOD составляет 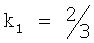 , следовательно,
, следовательно, 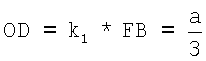 .
.
Значит координата х отведения I равна 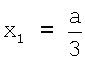 . Координата y отведения I равна 0, так как точка отведения принадлежит оси Ох.
. Координата y отведения I равна 0, так как точка отведения принадлежит оси Ох.
Для определения координаты х для отведения II рассматриваются подобные треугольники ΔCFB и ΔCHE (∠C - общий, ∠FBC=∠HEC - как соответствующие углы при параллельных прямых FB и НЕ). Коэффициент подобия треугольников ΔCFB и ΔCHE составляет 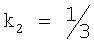 , следовательно,
, следовательно, 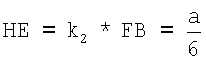 . Значит координата х отведения II равна
. Значит координата х отведения II равна 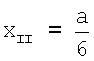 . Координата y для отведения II определяется следующим образом: yII=-ОН=-(ОС-НС). Угол ∠C в треугольнике ΔCHE равен 30°, отсюда
. Координата y для отведения II определяется следующим образом: yII=-ОН=-(ОС-НС). Угол ∠C в треугольнике ΔCHE равен 30°, отсюда 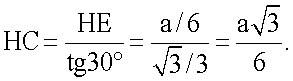
Отрезок ОС определяется из треугольника ΔCOD: 
Значит
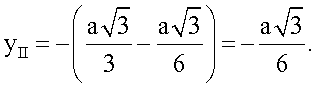
Для отведения III координата x определяется также как для отведения II и равна 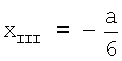 . Координата y для отведения III равна
. Координата y для отведения III равна 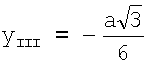 , так как точка отведения III находится на одной горизонтальной прямой с точкой отведения II.
, так как точка отведения III находится на одной горизонтальной прямой с точкой отведения II.
Координата z для отведений I, II, III равна 0, так как треугольник Эйнтховена располагается во фронтальной плоскости.
Точки усиленных отведений aVR и aVL находятся на одной горизонтальной прямой АВ (следовательно yaVL=yaVR) и равноудалены от оси Oy на расстояние 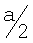 , следовательно, координаты x этих отведений равны хaVR=-а/2, хaVL=а/2. Координата у усиленных отведений aVR и aVL определяется следующим образом: yaVL=yaVR=CF-OC. Отрезок CF определяется из прямоугольного треугольника ΔCFB:
, следовательно, координаты x этих отведений равны хaVR=-а/2, хaVL=а/2. Координата у усиленных отведений aVR и aVL определяется следующим образом: yaVL=yaVR=CF-OC. Отрезок CF определяется из прямоугольного треугольника ΔCFB: 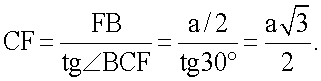 Отрезок
Отрезок 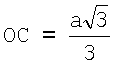 был вычислен выше. Итак,
был вычислен выше. Итак, 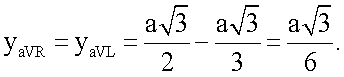
Координата х для усиленного отведения aVF равна 0, так как точка отведения принадлежит оси Оy. Координата у отведения aVF равна 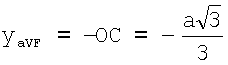 ,
,
так как точка отведения располагается на отрицательном луче оси Оy.
Координата z для усиленных отведений от конечностей aVR, aVL, aVF равна 0, т.к. треугольник Эйнтховена располагается во фронтальной плоскости.
На фигуре 6 представлено трансверсальное сечение грудной клетки пациента (эллипс 7), центром которого является центр грудной клетки, и смещенный эллипс по осям Ох и Oz (на величины Δх и Δz соответственно) с центром в геометрическом центре сердца (эллипс 2). Эллипс 1 и эллипс 2 имеют одинаковые параметры: значения осей а и b. Оси грудных отведений расположены в горизонтальной плоскости. Ось каждого грудного отведения представляет собой линию, соединяющую место расположения активного электрода на грудной стенке с электрическим центром сердца. Оси грудных отведений расположены в горизонтальной плоскости приблизительно под следующими углами к оси Ох: ψV1+V6: V1+115°, V2+94°, V3+58°, V4+47°, V5+22° и V6+0° [8].
Каждая точка, принадлежащая эллипсу 7, удовлетворяет уравнению эллипса 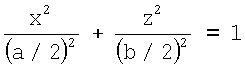 . Принимая во внимание значения смещений (Δx и Δz) от центра грудной клетки до центра сердца, уравнения осей отведений имеют вид zV1+V6=(xV1+V6-Δx)*tgψV1+V6+Δz. Таким образом, координаты х и z определяют из решения системы уравнений
. Принимая во внимание значения смещений (Δx и Δz) от центра грудной клетки до центра сердца, уравнения осей отведений имеют вид zV1+V6=(xV1+V6-Δx)*tgψV1+V6+Δz. Таким образом, координаты х и z определяют из решения системы уравнений  .
.
Для определения координаты у для грудных отведений V1-V6 необходимо воспользоваться следующими данными, полученными из флюорографии: количество пикселей на флюорографическом снимке до 5 межреберья (p5), количество пикселей на флюорографическом снимке до 4 межреберья (р4).
Центр сердца и точки грудных отведений V4-V6 находятся в одной плоскости (трансверсальное сечение грудной клетки), а по отношению к торсу - это пятое межреберье. Поэтому координата у для отведений V4-V6 равна 0. Точки грудных отведений V1-V2 располагаются в четвертом межреберье и поэтому координата у для этих отведений вычисляется по формуле 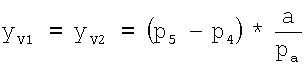 , а точка V3 располагается на половине расстояния между электродами V2 и V4, т.е. на половине расстояния между 5-м и 4-м межреберьем. Соответственно, координата у для отведения V3 определяется по формуле
, а точка V3 располагается на половине расстояния между электродами V2 и V4, т.е. на половине расстояния между 5-м и 4-м межреберьем. Соответственно, координата у для отведения V3 определяется по формуле 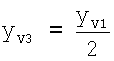 .
.
По этим координатам и координатам точек на поверхности модели сердца пациента вычисляются расстояния от каждой точки сердца до точек отведений. Для определения расстояния от двух точек в пространстве (от выбранной i-й точки на поверхности сердца пациента до точки j-го отведения) используется формула 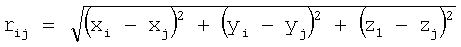 .
.
ЭАС определяется с учетом модели эквивалентного электрического генератора сердца (ЭЭГС) [2, 10]. Модель ЭЭГС рассматривает сердце в виде двойного электрического слоя (см. фигуру 7) по поверхности электрически активного миокарда [2]. Теоретическую основу модели составляют дифференциальные уравнения для потенциала электрического поля стационарных токов, создаваемого сердцем в теле как в объемном проводнике [6]:
rot H=J,
rot E=0,
J=σ(E+E*),
где Е и Н - векторы напряженности электрического и магнитного полей соответственно, σ - удельная электропроводность, J - вектор объемной плотности тока, Е* - вектор напряженности стороннего электрического поля.
В последнее уравнение вводится обозначение J*=σЕ* - плотность стороннего тока, порождаемого внешними электродвижущими силами биохимического происхождения. Она не равна 0 только в области мембран возбудимых клеток миокарда и фактически характеризует истинный или первичный генератор. Таким образом, ЭАС определяется сторонним (мембранным в представлении Нобла [16]) током J*, который, в свою очередь, формирует трансмембранный потенциал действия (ТМПД).
Очевидно, что Е и J* - основные векторные поля, исследуемые в электрокардиографии.
Электрическое поле Е выражается через скалярный потенциал:
Е=-gradφ.
Применение операции дивергенции к обеим частям первого уравнения приводит к выражению:
divJ=0.
Подстановка в это уравнение соотношений
Е=-gradφ и J=σ(Е+Е*)
приводит к выражению:
 ,
,
где Δ - оператор Лапласа.
Внутри однородной области среды gradσ=0. Кроме того, вне области мембран сторонние токи отсутствуют (J*=0). Тогда последнее уравнение сводится к уравнению Лапласа:
Δφ=0.
В основе предлагаемого способа определения ЭАС лежит электродинамическое представление о генезисе ЭКГ [6, 8, 10] (см. фигуру 7). Генезис ЭКГ определяется процессами деполяризации (возбуждения) и реполяризации (расслабления или восстановления исходного состояния) в клетках миокарда [8]. Процесс возбуждения сначала распространяется по проводящей системе сердца (см. фигуру 15), затем по миокарду предсердий и желудочков. Процесс расслабления происходит в обратном порядке: сначала восстанавливается исходное состояние предсердий, затем - желудочков. В норме единственным водителем ритма является синусовый или синоатриальный (СА) узел, который подавляет автоматическую активность остальных (эктопических) водителей ритма. Наглядно процесс генезиса ЭКГ можно представить в виде условной схемы (см. фигуру 16) [2]. Чем больше площадь элемента ΔS и чем меньше расстояние r от него до точки отведения и угол между r и нормалью N к ΔS (что эквивалентно условию: «чем больше телесный угол W»), тем больше потенциал Δφ, создаваемый этим элементом в точке отведения. Знак Δφ, плюс или минус, зависит от того, какая сторона элемента двойного слоя видна из точки наблюдения (точки отведения). Для равномерно заряженного двойного слоя S произвольной формы величина потенциала определяется телесным углом, под которым из точки отведения виден край слоя, т.е. контур, на который этот двойной слой натянут.
С учетом изложенного в основе разработанного способа определения ЭАС лежит следующее выражение для определения потенциала φj(t) в j-й точке стандартного отведения:
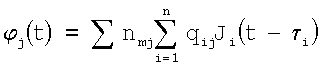
Учитывая то, что количество стандартных отведений равно 12 (j=1÷12), а количество электрически активных точек сердца из модели сердца равно I (I>>12), то выражение 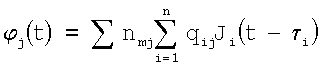 представляет собой запись системы диофантовых уравнений (системы алгебраических уравнений, у которых число неизвестных превосходит число уравнений). Доказано, что не существует единого алгоритма, позволяющего за конечное число шагов решать в целых числах произвольные диофантовы уравнения. Системы диофантовых уравнений имеют, как правило, бесконечное число решений [14].
представляет собой запись системы диофантовых уравнений (системы алгебраических уравнений, у которых число неизвестных превосходит число уравнений). Доказано, что не существует единого алгоритма, позволяющего за конечное число шагов решать в целых числах произвольные диофантовы уравнения. Системы диофантовых уравнений имеют, как правило, бесконечное число решений [14].
Для определения электрической активности точки сердца, по мнению авторов предполагаемого изобретения, необходимо представить выражение 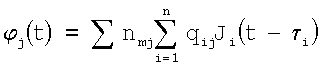 в виде СЛАУ, в которых число неизвестных равно числу уравнений.
в виде СЛАУ, в которых число неизвестных равно числу уравнений.
Для этого поверхность сердца разбивается на смежные непересекающиеся области (см. фигуру 11), в каждой из которых находятся точки сердца, электрическую активность которых необходимо определить. Число этих областей равно числу отведений, то есть 12. Каждая область содержит 1/12 электрически активных точек сердца. На рисунке 12 приведено изображение электрически активной области Sm поверхности модели сердца пациента, содержащей электрически активные точки сердца. Затем осуществляются последовательные смещения этих областей (схематично данная процедура представлена на фигуре 13, где I=9, а количество отведений равно 3), в результате которых образуются новые смежные непересекающиеся области. При этом каждая из областей содержит другую совокупность точек. Возможные электрически активные области Sm на поверхности модели сердца пациента выбираются согласно системе:
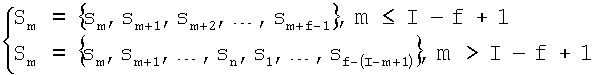 .
.
В результате количество возможных различных областей М становится равным количеству электрически активных точек сердца I. Для полученных таким образом областей составляются 1/12 СЛАУ вида 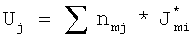 размерностью 12×12, где
размерностью 12×12, где
Uj - значение регистрируемого по данным электрокардиограммы напряжения в j-й точке отведения, nmj - коэффициент пропорциональности, 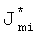 - характеристика электрической активности Sm-й области на поверхности модели сердца пациента (схематично данная процедура для вышеупомянутого примера представлена на фигуре 14). Коэффициент пропорциональности nmj прямо пропорционален удельному сопротивлению ρ, косинусу угла γ между вектором направления от m-й области на поверхности сердца пациента к j-й точке отведения и нормалью к m-й области на поверхности сердца пациента (см. фигуру 10), и обратно пропорционален расстоянию от точки j-го отведения до области Sm - rmj. Коэффициент пропорциональности nmj вычисляется по формуле
- характеристика электрической активности Sm-й области на поверхности модели сердца пациента (схематично данная процедура для вышеупомянутого примера представлена на фигуре 14). Коэффициент пропорциональности nmj прямо пропорционален удельному сопротивлению ρ, косинусу угла γ между вектором направления от m-й области на поверхности сердца пациента к j-й точке отведения и нормалью к m-й области на поверхности сердца пациента (см. фигуру 10), и обратно пропорционален расстоянию от точки j-го отведения до области Sm - rmj. Коэффициент пропорциональности nmj вычисляется по формуле 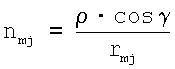 . В результате решения полученных СЛАУ определяется электрическая активность М областей.
. В результате решения полученных СЛАУ определяется электрическая активность М областей.
Из вышесказанного следует, что каждая точка принадлежит 1/12 областям и ее электрическая активность определяется из СЛАУ вида 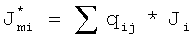 ,
,
где Ji - характеристика электрической активности i-й точки на поверхности сердца пациента, эквивалентная сторонним токам, формирующим ТМПД, qij - коэффициент пропорциональности, который вычисляется по формуле qij=cosλ, где λ - угол между вектором направления от i-й точки на поверхности сердца пациента к j-й точке отведения и нормалью, проведенной к поверхности сердца в точке i. В полученной СЛАУ число неизвестных (в нашем случае, это электрические активности точек поверхности сердца) становится равным числу уравнений. При этом исчезает неразрешимость исходной системы диофантовых уравнений.
Таким образом, определяется электрическая активность каждой точки на поверхности модели сердца пациента, необходимая для определения ЭАС в целом.
При определении показателей миогемодинамики соответствующей анатомической части сердца в процессе распространения волны возбуждения в миокарде рассматривается отношение площади поверхности возбужденного участка анатомической части сердца к общей площади поверхности анатомической части сердца. Общая площадь поверхности анатомической части сердца определяется как сумма площадей треугольников модели сердца человека, вершины которых принадлежат данной анатомической части сердца. Под площадью возбужденного участка анатомической части сердца понимается сумма площадей треугольников модели сердца человека, принадлежащих данной анатомической части модели сердца человека, причем вершинами треугольников являются электрически активные точки, находящиеся в возбужденном состоянии.
Для определения площади треугольника применяется следующий метод. Треугольники в модели сердца человека заданы координатами вершин в трехмерной декартовой системе координат: А(ах, ay, аz), B(bx, by, bz), С(сх, сy, сz). Координаты векторов 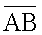 и
и 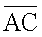 определяются следующим образом:
определяются следующим образом:
 ;
;
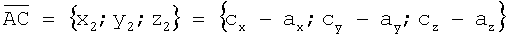 .
.
Площадь треугольника АВС равна половине площади параллелограмма, построенного на векторах 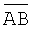 и
и 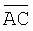 , поэтому находим векторное произведение этих векторов [5]
, поэтому находим векторное произведение этих векторов [5]
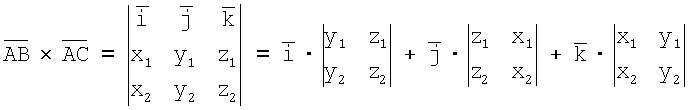
Здесь 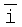 ,
, 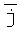 и
и 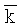 - основные векторы или орты.
- основные векторы или орты.
Следовательно,
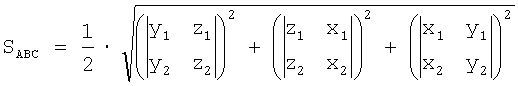
или
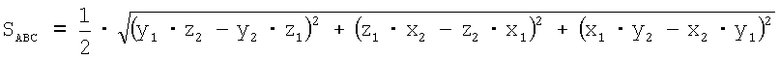
Определение показателей миогемодинамики сердца в процессе изменения электрической активности соответствующей анатомической части сердца осуществляется по формуле:
Vtime,part=КДОpart-(КДОpart-КСОpart)*ψtime,part,
где Vtime,part - объем полости анатомической части сердца part в момент времени time процесса изменения электрической активности сердца, КДОpart - конечный диастолический объем полости анатомической части сердца part, KCOpart - конечный систолический объем полости анатомической части сердца part, ψtime,part - характеристика процесса изменения электрической активности анатомической части сердца, вычисляемая по формуле:
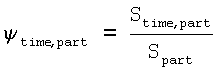 ,
,
где Stime,part - площадь возбужденного участка поверхности анатомической части сердца part в момент времени time, Spart - общая площадь поверхности анатомической части сердца part.
Таким образом, в предлагаемом способе по данным, полученным с помощью электрокардиографии и флюорографии, осуществляется создание модели сердца пациента и определение его координат, а также определение электрической активности сердца (см. фигуру 2) и параметров миогемодинамики в течение кардиоцикла.
При этом модель сердца пациента представлена в виде реалистичного трехмерного изображения, исходные точки которого получены из флюорографических снимков путем совмещения и нелинейного масштабирования, и реализована средствами компьютерной графики.
Компьютерная диагностическая система (КДС) «Кардиовид», разработанная авторами на основе предлагаемого способа, определяет электрическую активность участка поверхности сердца и показатели миогемодинамики в течение кардиоцикла. По мнению авторов, аналогов КДС «Кардиовид» с подобными функциональными возможностями не существует.
Новые методы обработки и наглядного представления результатов анализа кардиографической информации, по мнению авторов, повышают возможности функциональной диагностики.
При этом сохраняются достоинства известного способа по исходной точности анализа ЭКГ и флюорографии при определении основных функциональных показателей миогемодинамики сердца и его наглядного представления.
Литература
1. Амиров Р.З. Интегральные топограммы потенциалов сердца. М.: Наука. - 1973. - 108 с.
2. Баум О.В., Попов Л.А., Волошин В.И., Муромцева Г.А. QT-дисперсия: модели и измерения // Вестник аритмологии, №20, 2000, с.6-17.
3. Бодин О.Н. и др. Способ определения основных функциональных показателей миогемодинамики сердца. Патент РФ №2264786, МПК А61В 5/0402, 2005.
4. Зудбинов Ю.И. Азбука ЭКГ. Изд. 4-е, испр. и доп., Ростов н/Д: Феникс, 2003,
240 с.
5. Корн Г., Корн Т. Справочник по математике для научных работников и инженеров. - М.: Наука. Главная редакция физико-математической литературы, 1974, 832 с.
6. Ландау Л.Д., Лившиц Е.М. Теоретическая физика: Теория поля. Т.2 М.: Наука, 1988, 509 с.
7. Мухарлямов Н.М., Беленков Ю.Н. Ультразвуковая диагностика в кардиологии. - М.: Медицина, 1981, 160 с.
8. Орлов В.Н. Руководство по электрокардиографии. - М.: Медицина, 1984, 528 с.
9. Петров Ю.П., Сизиков B.C. Корректные, некорректные и промежуточные задачи с приложениями: Учебное пособие для вузов. - СПб: Политехника, 2003, 261 с.
10. Титомир Л.И., Трунов В.Г., Айду Э.А.И. Неинвазивная электрокардиотопография. - М.: Наука, 2003, 198 с.
11. Фильчаков П.Ф. Справочник по высшей математике. - Киев: Наукова Думка, 1974.
12. Эйнджел Э. Интерактивная компьютерная графика. Вводный курс на базе OpenGL, 2 изд.: Пер. с англ. - М.: Изд. Дом «Вильяме», 2001, 592 с.
13. http://news.bbc.co.uk/2/hi/health/1775853.stm
14. http://math.ournet.md/krujok/diofantr/diofantr.html
15. Kienle F.A.N. Grudzuge der Funtionselektrokardiographie. - Karlsruhe, 1955. - 211 p.
16. Noble D.A modification of the Hodjkin-Huxley equations applicable to Purkinje fibre action and pacemaker potentials. - J. Physiol, Lond. 160 (1962) p.317-352
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ НЕИНВАЗИВНОГО ОПРЕДЕЛЕНИЯ ЭЛЕКТРОФИЗИОЛОГИЧЕСКИХ ХАРАКТЕРИСТИК СЕРДЦА | 2011 |
|
RU2489083C2 |
| СПОСОБ МОДЕЛИРОВАНИЯ И ВИЗУАЛИЗАЦИИ РАСПРОСТРАНЕНИЯ ВОЗБУЖДЕНИЯ В МИОКАРДЕ | 2007 |
|
RU2358646C2 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ОСНОВНЫХ ФУНКЦИОНАЛЬНЫХ ПОКАЗАТЕЛЕЙ МИОГЕМОДИНАМИКИ СЕРДЦА | 2004 |
|
RU2264786C1 |
| СПОСОБ АВТОМАТИЧЕСКОГО ОПРЕДЕЛЕНИЯ ГЕОМЕТРИЧЕСКИХ ПАРАМЕТРОВ СЕРДЦА И ТОРСА ПАЦИЕНТА ПО ФЛЮОРОГРАФИЧЕСКИМ СНИМКАМ И ИХ ВИЗУАЛИЗАЦИИ | 2016 |
|
RU2639018C2 |
| СПОСОБ ПРОГНОЗИРОВАНИЯ АВ-БЛОКАДЫ II СТЕПЕНИ | 2009 |
|
RU2410022C2 |
| СПОСОБ НЕИНВАЗИВНОГО ОПРЕДЕЛЕНИЯ ЭЛЕКТРОФИЗИОЛОГИЧЕСКИХ ХАРАКТЕРИСТИК СЕРДЦА | 2017 |
|
RU2651068C1 |
| СПОСОБ АВТОМАТИЧЕСКОГО ОПРЕДЕЛЕНИЯ РАЗМЕРОВ И ПОЛОЖЕНИЯ СЕРДЦА ПАЦИЕНТА ПО ФЛЮОРОГРАФИЧЕСКИМ СНИМКАМ | 2008 |
|
RU2372844C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ КОНТУРА СЕРДЦА НА ФЛЮОРОГРАФИЧЕСКИХ СНИМКАХ | 2011 |
|
RU2478337C2 |
| СПОСОБ И УСТРОЙСТВО РЕГИСТРАЦИИ МНОЖЕСТВЕННЫХ ОТВЕДЕНИЙ ЭЛЕКТРОКАРДИОСИГНАЛА | 2020 |
|
RU2764498C2 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ОСНОВНЫХ ФУНКЦИОНАЛЬНЫХ ПОКАЗАТЕЛЕЙ МИОГЕМОДИНАМИКИ ЛЕВОГО ЖЕЛУДОЧКА СЕРДЦА | 1997 |
|
RU2107457C1 |
Изобретение относится к медицине и предназначено для определения электрической активности сердца. Регистрируют электрокардиограмму и определяют конечный диастолический радиус (КДР), конечный систолический радиус (КСР) полости ЛЖ, конечный диастолический объем (КДО), конечный систолический объем (КСО) ЛЖ. Регистрируют фронтальный и левобоковой флюорографические снимки сердца пациента. Определяют по снимкам геометрические параметры сердца пациента. Синтезируют реалистичное трехмерное изображение сердца пациента. Значения КДР и КСР заменяют реальными эквивалентными геометрическими параметрами модели ЛЖ сердца пациента. Определяют координаты точек отведений на поверхности торса пациента в правой системе координат, начало которой совпадает с центром трансверсального сечения грудной клетки, а также характеристику электрической активности Ji i-й точки на поверхности модели сердца пациента. Рассчитывают показатели миогемодинамики сердца в процессе изменения электрической активности соответствующей анатомической части сердца. Предлагаемый способ позволяет визуализировать распространение возбуждения в миокарде, а также определить показатели миогемодинамики сердца в процессе распространения волны возбуждения в миокарде. 3 з.п. ф-лы, 16 ил., 1 табл.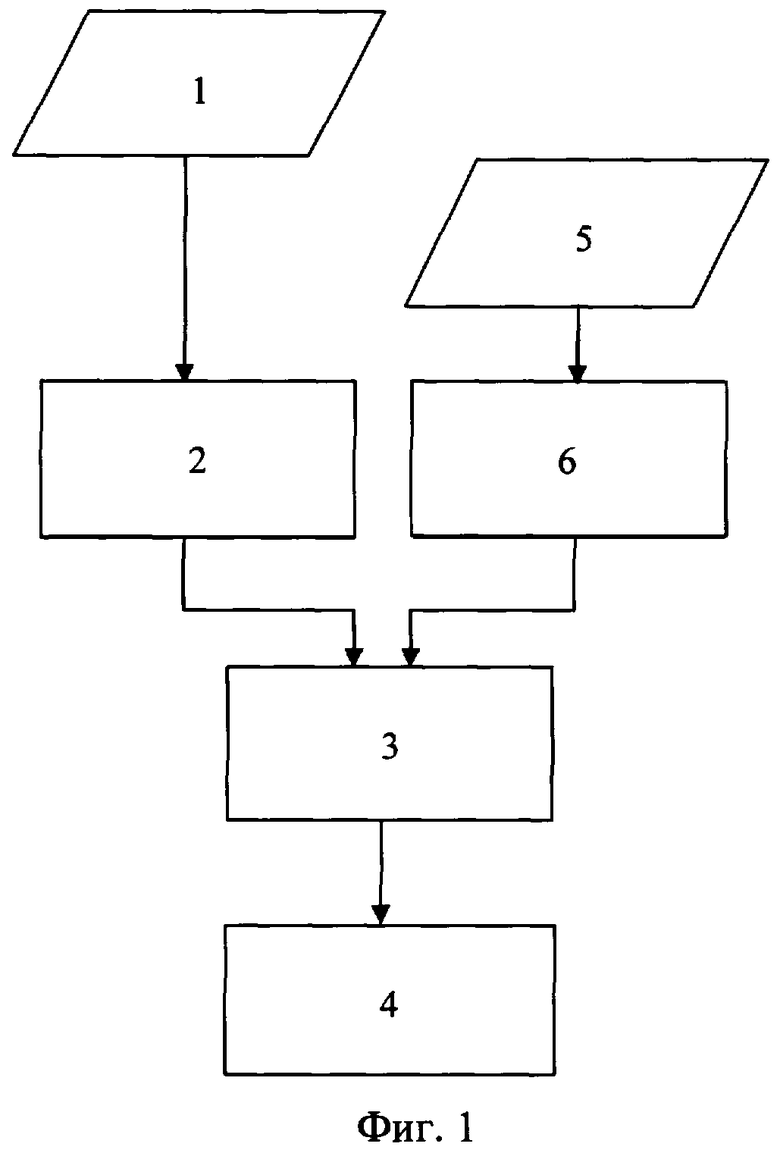
1. Способ определения электрической активности сердца, заключающийся в том, что регистрируют электрокардиограмму и определяют конечный диастолический радиус (КДР) и конечный систолический радиус (КСР) полости ЛЖ, конечный диастолический объем (КДО) и конечный систолический объем (КСО) ЛЖ, которые рассчитываются по данным электрокардиограммы в одном из следующих отведений: 4, 5, 6-м грудном (по Вильсону), или 11 стандартном (по Эйнтховену), выбранном соответственно направлению электрической оси сердца, а при невозможности их регистрации - в отведении А (по Небу), измеряют при отсутствии блокад ножек пучка Гиса продолжительности интервалов QR, RS, QRS, ST-T, R-R и дополнительно при блокаде левой ножки пучка Гиса - продолжительности интервала 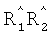 , а при блокаде правой ножки пучка Гиса - продолжительности интервала
, а при блокаде правой ножки пучка Гиса - продолжительности интервала 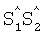 , и при синусовом и других наджелудочковых ритмах сердца в состоянии физического покоя определяют по формулам
, и при синусовом и других наджелудочковых ритмах сердца в состоянии физического покоя определяют по формулам
КДР=(44,5-100·tRS)·(tQR+tRS) -11·tRS,
где tQR - время от начала зубца Q до вершины зубца R при отсутствии блокады левой ножки пучка Гиса, а при наличии блокады левой ножки пучка Гиса - до первой вершины раздвоенного зубца R(R1), то есть tQR=tQR, с; tRs - время от вершины зубца R до конца зубца S - при отсутствии блокад ножек пучка Гиса, а при блокаде левой ножки пучка Гиса вместо tRs - разность временных интервалов от первой вершины раздвоенного зубца R до конца зубца S(R1 S) и от первой вершины раздвоенного зубца R до его второй вершины (R1 R2), то есть 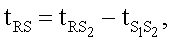
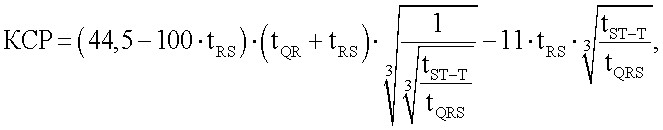
где tQRS - время комплекса QRS, с; tST-T - время от конца зубца S до конца зубц0а Т - при отсутствии блокад ножек пучка Гиса, а при блокаде левой ножки пучка Гиса вместо 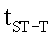 - сумма
- сумма  и при блокаде правой ножки пучка Гиса вместо
и при блокаде правой ножки пучка Гиса вместо 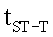 - сумма
- сумма 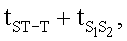 с;
с;
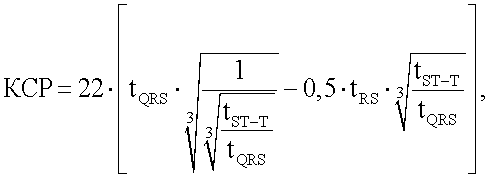
и далее вычисляют при всех указанных видах сердечного ритма КДО=(4/3)·π·КДР3 и КСО=(4/3)·π·КСР3, а также регистрируют фронтальный и левобоковой флюорографические снимки сердца пациента, определяют по снимкам геометрические параметры сердца пациента, синтезируют реалистичное трехмерное изображение сердца пациента, значения КДР и КСР заменяют реальными эквивалентными геометрическими параметрами модели ЛЖ сердца пациента, значения которых определяют по формулам Ri_КДРЛЖ=ККДР·Ri_модели; Ri_КСРЛЖ=ККСР·Ri_модели; ККДР=КДР3/R3 сф_модели; ККСР=КСР3/R3 сф_модели, где Ri_КДРЛЖ - конечное диастолическое расстояние от центра геометрического места точек поверхности модели ЛЖ сердца пациента до i-й точки поверхности модели ЛЖ сердца пациента; Кi-КСРЛЖ - конечное систолическое расстояние от центра геометрического места точек поверхности модели ЛЖ сердца пациента до i-й точки поверхности модели ЛЖ сердца пациента; Ri_модели - расстояние от центра геометрического места точек поверхности модели ЛЖ сердца пациента до i-й точки поверхности модели ЛЖ сердца пациента; Rсф_модели - радиус сферы, объем которой равен объему модели ЛЖ сердца пациента; ККДР, ККСР - коэффициенты пропорциональности объема модели ЛЖ сердца пациента соответственно диастолическому и систолическому объему ЛЖ сердца пациента, отличающийся тем, что определяют координаты точек (xj, yj, zj) отведений (j=1-12) на поверхности торса пациента в правой системе координат, начало которой совпадает с центром трансверсального сечения грудной клетки; характеристику электрической активности Ji i-й точки на поверхности модели сердца пациента; показатели миогемодинамики сердца в процессе изменения электрической активности соответствующей анатомической части сердца.
2. Способ по п.1, отличающийся тем, что координаты точек (xj, yj, zj) отведений
(j=1-12) на поверхности торса пациента определяются следующим образом:
сначала вычисляются параметры трансверсального сечения грудной клетки пациента (трансверсальный и сагиттальный диаметры) по формулам
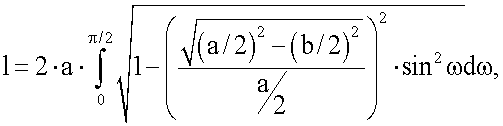
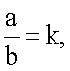
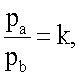
где l - длина обхвата груди; а - большая ось трансверсального сечения грудной клетки пациента (трансверсальный диаметр); b - малая ось трансверсального сечения грудной клетки пациента (сагиттальный диаметр); ω - переменная интегрирования; pa - количество пикселей на флюорографическом снимке, принадлежащих торсу пациента, по оси абсцисс; pb - количество пикселей на флюорографическом снимке, принадлежащих торсу пациента, по оси аппликат,
затем определяется смещение геометрического центра сердца относительно центра трансверсального сечения грудной клетки по формулам
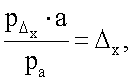
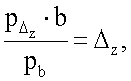
где PΔx - количество пикселей на флюорографическом снимке, определяемое от центра грудной клетки до центра сердца по оси абсцисс;
PΔz - количество пикселей на флюорографическом снимке, определяемое от центра грудной клетки до центра сердца по оси аппликат;
Δx - смещение геометрического центра сердца относительно центра трансверсального сечения грудной клетки по оси абсцисс;
Δz - смещение геометрического центра сердца относительно центра трансверсального сечения грудной клетки по оси аппликат;
координаты точек (xj, yj, zj) отведений (j=1-12) на поверхности торса пациента определяются
для стандартных отведений I, II, III по формулам
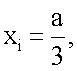
yI=0,
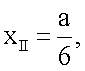
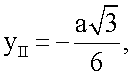
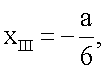
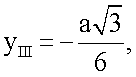
zI,II,III=0,
для усиленных отведений от конечностей aVR, aVL, aVF no формулам
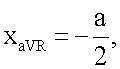
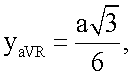
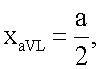
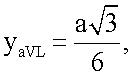
xaVF=0,
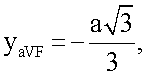
zaVR,aVL,aVF=0,
для грудных отведений V1-V6: координаты (xV1-V6, zv1-V6) определяют из системы уравнений

где Ψv1-v6 - угол между осью абсцисс и отрезком, соединяющим точку соответствующего стандартного грудного отведения с геометрическим центром сердца;
координаты yv1-V6 определяют по формулам
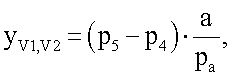

yV4,V5,V6=0,
где yV1,V2 - координаты точек грудных отведений V1-V2 на поверхности торса пациента по оси ординат;
yV3 - координата точки грудного отведения V3 на поверхности торса пациента по оси ординат;
yzv4,v5,v6 - координаты точек грудных отведений V4-V6 на поверхности торса пациента по оси ординат;
р5 - количество пикселей на флюорографическом снимке до 5 межреберья;
р4 - количество пикселей на флюорографическом снимке до 4 межреберья.
3. Способ по п.1, отличающийся тем, что характеристику электрической активности Ji i-й точки на поверхности модели сердца пациента определяют из решения СЛАУ
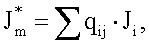
qij=cosλ,
где М - число возможных электрически активных областей на поверхности модели сердца пациента, равное числу электрически активных точек I на поверхности модели сердца пациента;
qij - коэффициент пропорциональности;
λ - угол между вектором направления от i-й точки на поверхности модели сердца пациента к j-й точке отведения и нормалью в i-й точке поверхности сердца пациента.
J*m - характеристика электрической активности Sm-й области на поверхности модели сердца пациента, содержащая i-ю точку, которую определяют из решения 1/12 систем уравнений размерностью 12×12
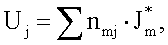
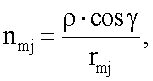
где Uj - значение регистрируемого по данным электрокардиограммы напряжения в j-й точке отведения;
nmj - коэффициент пропорциональности;
ρ - удельное сопротивление в направлении от m-й области на поверхности сердца пациента к j-й точке отведения;
γ - угол между вектором направления от i-й области на поверхности сердца пациента к j-й точке отведения и нормалью в i-й области на поверхности сердца пациента;
rmj - расстояние от точки j-го отведения до области Sm находится как среднее арифметическое расстояний от точки j-го отведения до точек, входящих в область Sm, размеры области Sm на поверхности модели сердца пациента определяются следующим образом
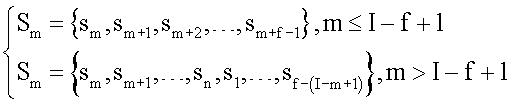

где Sm - обозначение точки, принадлежащей области Sm;
f - число точек в каждой области;
I - число электрически активных точек.
4. Способ по п.1, отличающийся тем, что показатели миогемодинамики сердца в процессе изменения электрической активности соответствующей анатомической части сердца определяются по формуле
Vtime,part=КДОpart-(КДОpart-КСОpart)·ψtime,part,
где Vtime,part - объем полости анатомической части сердца part в момент времени time процесса изменения электрической активности сердца;
КДОpart - конечный диастолический объем полости анатомической части сердца part;
KCOpart - конечный систолический объем полости анатомической части сердца part;
ψtime,part - характеристика процесса изменения электрической активности анатомической части сердца, вычисляемая по формуле
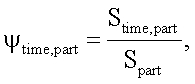
где Stime,part - площадь возбужденного участка поверхности анатомической части сердца part в момент времени time;
Spart - общая площадь поверхности анатомической части сердца part.
| СПОСОБ ОПРЕДЕЛЕНИЯ ОСНОВНЫХ ФУНКЦИОНАЛЬНЫХ ПОКАЗАТЕЛЕЙ МИОГЕМОДИНАМИКИ СЕРДЦА | 2004 |
|
RU2264786C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ОСНОВНЫХ ФУНКЦИОНАЛЬНЫХ ПОКАЗАТЕЛЕЙ МИОГЕМОДИНАМИКИ ЛЕВОГО ЖЕЛУДОЧКА СЕРДЦА | 1997 |
|
RU2107457C1 |
| МЕДВИНСКИЙ А.Б | |||
| и др | |||
| Исследование автоволновых механизмов вариабельности электрокардиограмм во время высокочастотных аритмий: результат математического моделирования | |||
| - Биофизика, 2003, т.48, вып.2, с.314-323 | |||
| ALIEV R.R | |||
| et al | |||
| A simple model of cardiac excitation | |||
| - Chaos, Soliton & Fractals, 1996, №3, p.293-301. | |||
Авторы
Даты
2009-07-10—Публикация
2007-04-02—Подача