Предлагаемое изобретение относится к медицине, в частности, к кардиологии и может быть использовано как электрокардиографический способ диагностики состояния сердца. В результате неинвазивного ЭКГ-обследования и последующей обработки данных определяются изменяющиеся со временем пространственные распределения электрофизиологических характеристик сердца. Предлагаемое изобретение относится к решению обратной задачи электрокардиографии [1, 2], когда по результатам анализа электрокардиосигналов (ЭКС) реконструируется электрическая активность сердца (ЭАС) на «портрете» эпикарда.
Известен способ исследования ЭАС путем реконструкции эквивалентного электрического генератора сердца (ЭЭГС) дипольного типа и исследования пространственно-временных характеристик этого ЭЭГС [3]. В этом способе по измеренным ЭКС, снятым в определенных токах на поверхности торса человека, вычисляются координаты, ориентация и модуль дипольного момента (интенсивность) ЭЭГС дипольного типа. Однако недостатком этого подхода является отсутствие механизма регуляризации при синтезе ЭГС, приводящее к возможным неустойчивостям в поведении координат и вектора дипольного момента этого ЭГС. Кроме того, в этом способе не предусмотрена реконструкция ЭГС поверхностного типа, важная для диагностики нарушений процессов проводимости в сердце.
Известен способ неинвазивного электрофизиологического исследования сердца [4]. В этом способе на основе аппаратных измерений проводится оцифровка поверхности торса и поверхности эпикарда, после чего по ЭКС, снятым в определенных точках на поверхности торса человека, реконструируется распределение электрического потенциала на поверхности эпикарда. Недостатком этого способа являются существенные аппаратные затраты, ориентированные на использование в узкоспециализированных центрах и не позволяющие проводить диагностику ЭАС в широких масштабах. Так, в этом способе необходимо использование компьютерного томографа или МРТ-томографа; кроме того требуется использовать значительное количество измерительных электродов (до 240). Кроме аппаратных затрат, при этом также существенно возрастает время проведения обследования.
Наиболее близким по достигаемому результату к предлагаемому изобретению является способ неинвазивного определения электрофизиологических характеристик сердца, заключающийся в том, что осуществляют регистрацию электрокардиосигналов (ЭКС), предварительную обработку ЭКС и выделение временных отсчетов элементов кардиоцикла, определение антропометрических параметров торса пациента, отображение электрофизиологических характеристик сердца [5].
На фигуре 1 приведена схема алгоритма известного способа неинвазивного определения электрофизиологических характеристик сердца.
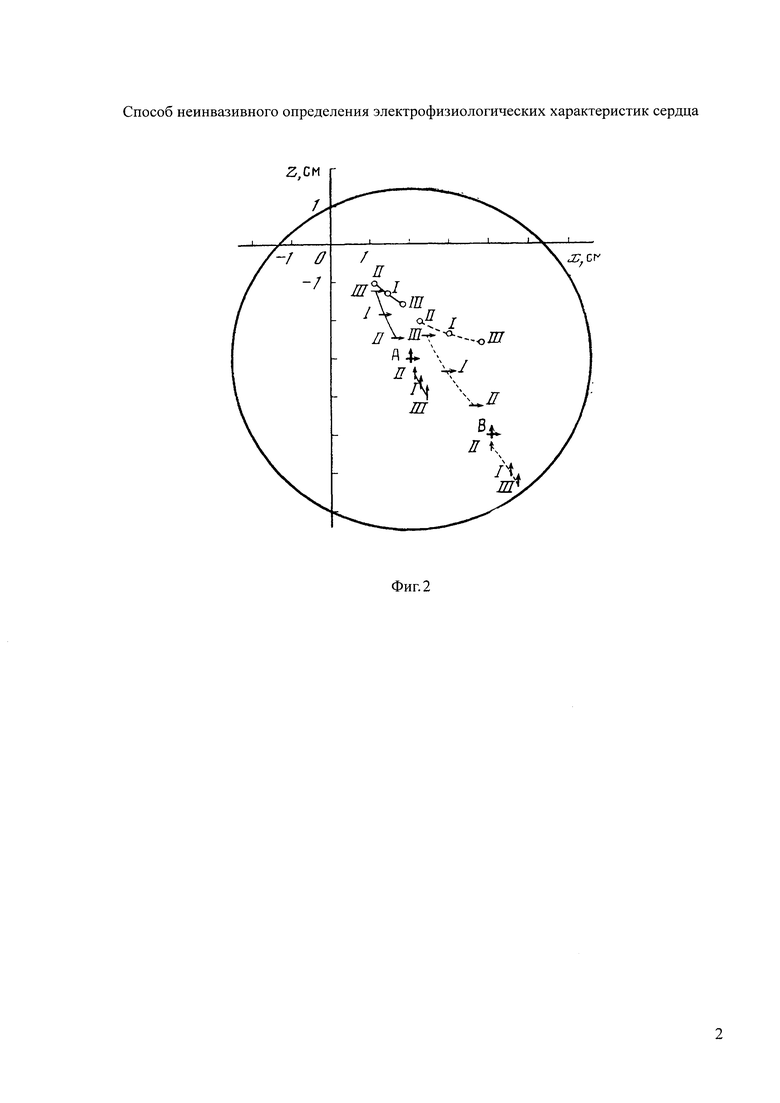
На фигуре 2 представлены ошибки в определении координат дипольного ЭЭГС при допущении о наличии неограниченной проводящей среды, окружающей ЭЭГС.
В известном способе неинвазивного определения электрофизиологических характеристик сердца в блоке измерения проводят регистрацию ЭКС в 12 стандартных отведениях, измерение потенциалов, генерируемых сердцем путем предварительной обработки измеренных ЭКС, включающей подавление помех, выделение кардиоцикла. Далее регистрируют флюорограмму пациента с целью определения положения и размеров сердца и определяют антропометрические параметры торса пациента.
Затем проводят синтез модели сердца пациента, при этом по сигналам ЭКС определяются параметры сердца человека: конечный диастолический радиус (КДР), конечный систолический радиус (КСР), конечный диастолический объем (КДО), конечный систолический объем (КСО). Далее формируется реалистическая компьютерная модель сердца человека, синхронизированная по положению и размерам с флюорографическими снимками и найденными по сигналам ЭКС конечными систолическими и диастолическими радиусами и объемами, повторяющая сердце человека в положении систолы и диастолы.
Затем рассчитывают потенциалы, генерируемые сердцем на поверхности торса пациента. Для этого по ЭКС стандартных отведений определяют проекции вектора дипольного момента сердца, далее рассчитывают координаты N точек дополнительных отведений, расположенных равномерно (с одинаковым углом между векторами отведений) на поверхности торса. По проекциям дипольного момента и координатам точек дополнительных отведений рассчитывают потенциалы в этих точках.
Далее рассматривают многодипольную модель, согласно которой в N точках на поверхности эпикарда находится элементарный диполь, ориентированный перпендикулярно этой поверхности. Определяют дипольные моменты элементарных диполей путем решения системы линейных алгебраических уравнений, связывающих потенциалы в N точках поверхности торса с дипольными моментами элементарных диполей.
Затем проводят моделирование распространения волны возбуждения в миокарде с использованием двухкомпонентной сеточной модели Алиева-Панфилова, основываясь на распределении трансмембранного потенциала (ТМП) в начальный момент времени моделирования. Моделирование осуществляется на плоской развертке модели поверхности эпикарда, проводимой с помощью цилиндрической проекции. Результатом моделирования является распределение трансмембранного потенциала на поверхности эпикарда для временных отсчетов кардиоцикла.
Далее проводят синтез модельного ЭКС в точках стандартных грудных отведений V1-V6. Для синтеза ЭКС в каждой точке грудного отведения проводят суммирование по N элементам поверхности эпикарда, причем каждый элемент поверхности рассматривается как элементарный диполь с моментом, равным произведению площади элемента поверхности на величину ТМП для данного элемента в текущий момент времени.
В блоке проверки синтезированные ЭКС сравниваются с зарегистрированными ЭКС. По результатам анализа расхождения этих ЭКС при необходимости проводится коррекция параметров модели Алиева-Панфилова и повторяется расчет электрической активности на эпикарде.
В блоке выдачи результатов проводится отображение электрофизиологических характеристик на синтезированной трехмерной модели поверхности сердца.
Недостатком известного способа неинвазивного определения электрофизиологических характеристик сердца является недостаточно высокая достоверность диагностики состояния сердца, связанная с тем, что из-за небольшого числа электродов (стандартная методика 12 общепринятых отведений) потенциалы на поверхности торса рассчитываются приближенно, через приближенную дипольную модель ЭЭГС в неограниченной проводящей среде; в формулах для усиленных и конечностных отведений не учитывается различие в расстояниях от дипольного ЭГС до электродов. Так, в работе [1] представлены ошибки в определении координат дипольного ЭЭГС при допущении о наличии неограниченной проводящей среды, окружающей ЭЭГС (см. фигуру 2). Здесь истинный диполь располагается в точках А и В, а стрелками или кружками показано положение «кажущихся» (см. [1]) диполей, найденных в предположении о неограниченной окружающей среде. При этом горизонтальные стрелки соответствуют ориентации истинного диполя вдоль линии плеч, вертикальные - по направлению от груди к спине, а кружки - по направлению от головы к ногам; сплошные линии соединяют положение «кажущихся» диполей при различной форме поперечного сечения торса (символы I, II и III) для истинного диполя, расположенного в точке А, а штриховые - для диполя, расположенного в точке В. Получается, что неучет электрической изоляции торса на границе с окружающим воздухом, приводит к ошибкам в определении расстояния между дипольным источником и точками на поверхности торса порядка 2-3 см.
Кроме того, имеются затруднения в оперативном использовании способа, так как требуется дополнительно фронтальная и левобоковая цифровые флюорограммы грудной клетки.
Методически волновая модель Алимова-Панфилова затруднена в использовании для определения локализации нарушений процессов проводимости, так как привязана к ЭКС, который интегрально связан с процессами электрической активности в различных участках миокарда; использование модели ограничено достаточно большим числом подбираемых параметров (реально четыре) и необходимостью задания формы границ предсердий и желудочков.
По мнению авторов, повышение достоверности определения электрофизиологических характеристик сердца должно обеспечиваться:
- расчетом потенциалов на поверхности торса путем интерполирования по непосредственно измеренным однополярным ЭКС;
- увеличением количества измерительных электродов до 30-36;
- привязкой опорных точек эталонной модели эпикарда к центру модели эпикарда пациента;
- учетом граничного условия электрической изоляции на поверхности торса;
- контролем параметров реконструированных ЭЭГС поверхностного и дипольного типа путем сравнения модельных потенциалов на поверхности торса с исходными потенциалами для каждого временного отсчета кардиоцикла;
- расширением перечня электрофизиологических характеристик путем добавления параметров ЭЭГС дипольного типа; применением алгоритма регуляризации при реконструкции ЭЭГС поверхностного и дипольного типа.
При этом расширение области применения обеспечивается тем, что в рамках одного обследования представляются пространственно-временные характеристики как ЭЭГС поверхностного типа для диагностики нарушения процессов проводимости, так и характеристики ЭЭГС дипольного типа для диагностики ишемии; кроме того, для обследования не требуются цифровые фронтальная и левобоковая флюорограммы грудной клетки. В то же время в отличие от способа [4] не требуются существенные аппаратные затраты, связанные с использованием компьютерного томографа или МРТ, а также с большим количеством измерительных электродов (до 240).
Важной методологической отличительной особенностью предлагаемого метода в отношении получения новой диагностической информации является представление кардиологам пространственно-временных характеристик как ЭЭГС поверхностного типа -для диагностики нарушения процессов проводимости, так и ЭЭГС дипольного типа - для диагностики ишемии.
Целью предлагаемого изобретения является расширение функциональных возможностей оценки состояния сердца.
Для этого предлагается способ неинвазивного определения электрофизиологических характеристик сердца, заключающийся в том, что осуществляют регистрацию электрокардиосигналов (ЭКС), предварительную обработку ЭКС и выделение временных отсчетов элементов кардиоцикла, определение антропометрических параметров торса пациента, отображение электрофизиологических характеристик сердца, отличающийся тем, что дополнительно осуществляют:
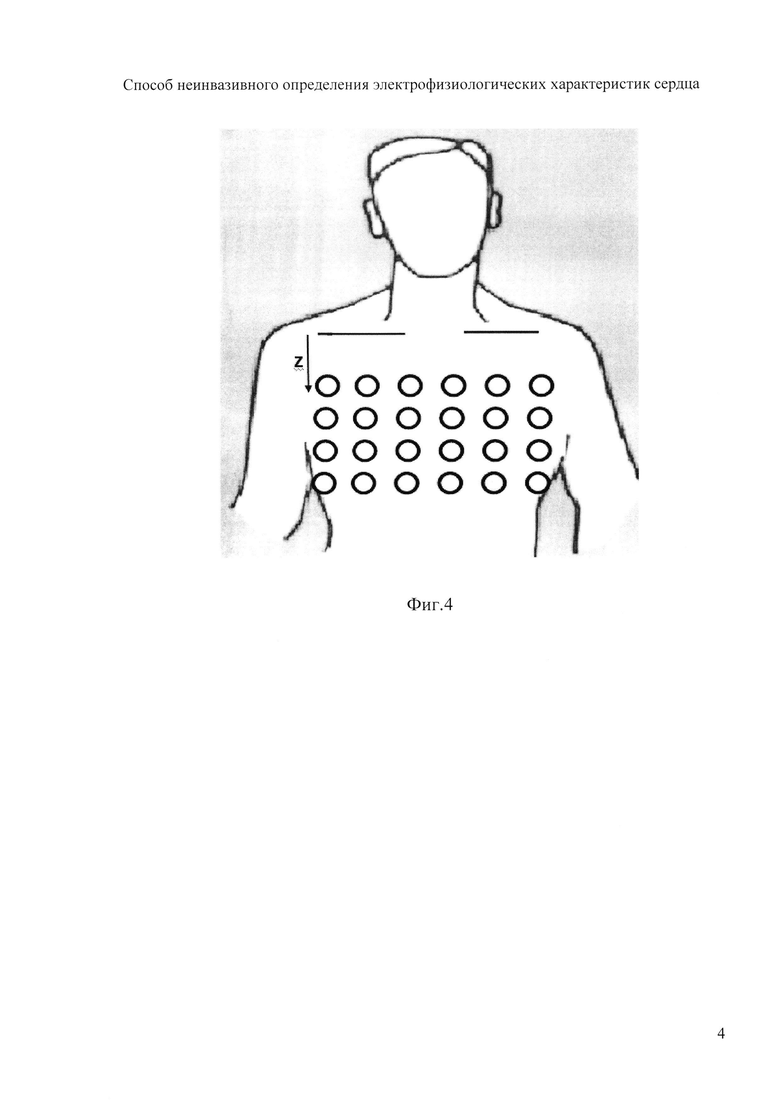
- установку электродов в количестве не менее 30, расположенных по поперечному сечению торса в 4 ряда;
- определение координат x и y электродов путем:
- измерения длины l контура поперечного сечения торса с помощью измерительной ленты;
- решения трансцендентного уравнения l=аЕ(ϕ,е) относительно угла ϕ, где 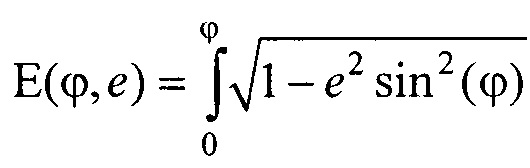 - нормальный эллиптический интеграл Лежандра второго рода;
- нормальный эллиптический интеграл Лежандра второго рода; 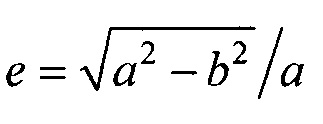 - эксцентриситет поперечного сечения торса, а и b - антропометрические параметры торса пациента; ϕ - угол между прямой, соединяющей подмышечные впадины, и направлением на текущий электрод,
- эксцентриситет поперечного сечения торса, а и b - антропометрические параметры торса пациента; ϕ - угол между прямой, соединяющей подмышечные впадины, и направлением на текущий электрод,
- определения координат x и у электродов по формулам х=r sin(ϕ); у=-r cos(ϕ), где r - расстояние от центра поперечного сечения торса до электрода определяется по формуле 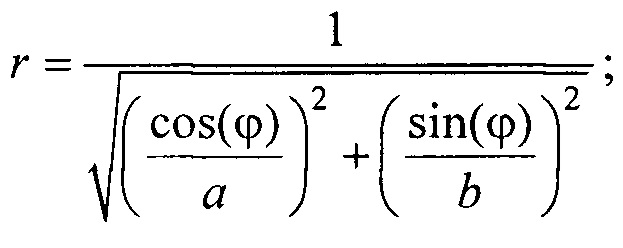
- интерполяцию потенциалов φ на поверхности торса по формуле
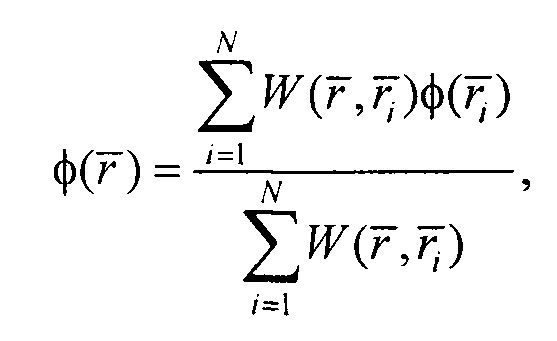
где 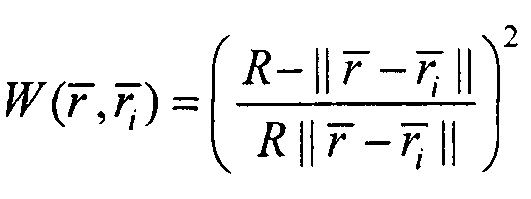 - весовая функция по Шепарду,
- весовая функция по Шепарду, 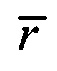 - радиус-вектор пространственного положения текущей точки интерполяции,
- радиус-вектор пространственного положения текущей точки интерполяции, 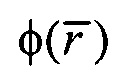 - искомое значение потенциала в этой точке,
- искомое значение потенциала в этой точке, 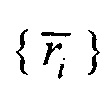 - множество точек поверхности с известными значениями потенциалов
- множество точек поверхности с известными значениями потенциалов 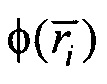 , R - радиус сферы с центром в точке
, R - радиус сферы с центром в точке 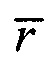 , ограничивающей число точек N, используемых для интерполяции;
, ограничивающей число точек N, используемых для интерполяции;
- реконструкцию модели эпикарда путем:
- построения поверхности вспомогательного внутреннего эллиптического цилиндра, расположенного внутри торса и окружающего эпикард, по формуле
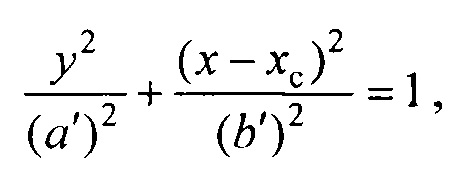
где 2a'=DH+8 см; 2b'=DH+4 см; DH=12 см - размер эпикарда; yc=b-b'-Δy, b - полуось поперечного сечения торса в направлении от спины к груди; Δу=2 см - расстояние между торсом и внутренним цилиндром в направлении от спины к груди,
- расчета распределения потенциала φ и его нормальной производной 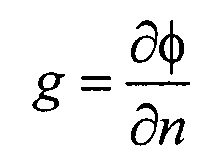 на поверхности внутреннего эллиптического цилиндра для временных отсчетов от начала Р-зубца до конца Т-зубца кардиоцикла путем решения итерационным методом Зейделя системы линейных матричных уравнений:
на поверхности внутреннего эллиптического цилиндра для временных отсчетов от начала Р-зубца до конца Т-зубца кардиоцикла путем решения итерационным методом Зейделя системы линейных матричных уравнений:
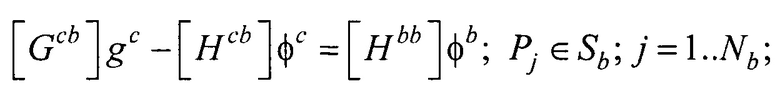
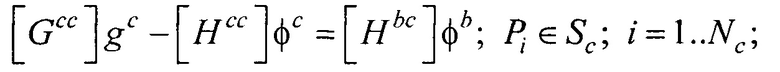
где Pj - точка на поверхности торса Sb; Pi - точка на поверхности внутреннего эллиптического цилиндра Sc; 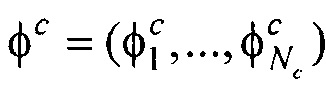 ,
, 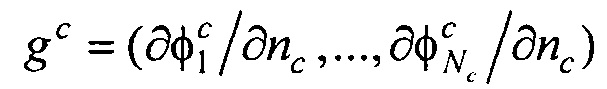 - векторы потенциалов поверхности внутреннего эллиптического цилиндра и производных потенциалов по направлению нормали к поверхности внутреннего эллиптического цилиндра, при этом нормаль берется внешняя по отношению к области между торсом и внутренним цилиндром;
- векторы потенциалов поверхности внутреннего эллиптического цилиндра и производных потенциалов по направлению нормали к поверхности внутреннего эллиптического цилиндра, при этом нормаль берется внешняя по отношению к области между торсом и внутренним цилиндром; 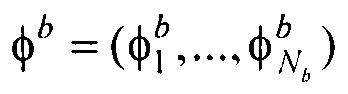 - вектор потенциалов на поверхности торса;
- вектор потенциалов на поверхности торса; 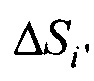 ,
, 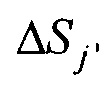 - площади элементов поверхности внутреннего эллиптического цилиндра и торса соответственно;
- площади элементов поверхности внутреннего эллиптического цилиндра и торса соответственно; 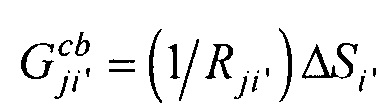 ;
; 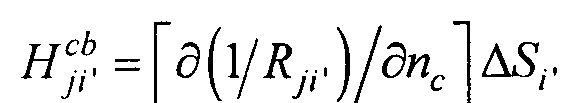 ;
; 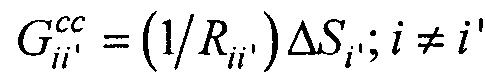 ;
; 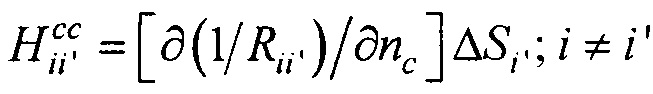 ;
;  ;
; 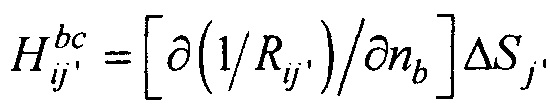 ;
; 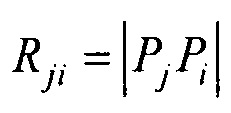 - элементы матриц, входящих в систему линейных матричных уравнений,
- элементы матриц, входящих в систему линейных матричных уравнений,
- определения пространственного распределения электрической активности сердца, суммарного по всему кардиоциклу Ψ0(z,l) и по интервалу Р-зубца Ψat(z,l) с использованием формул
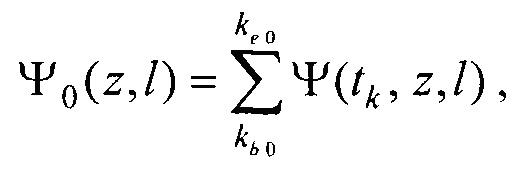
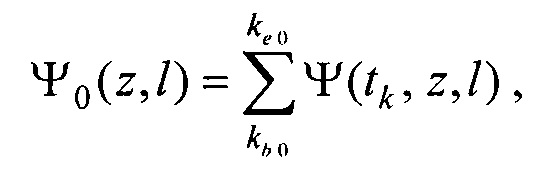
где 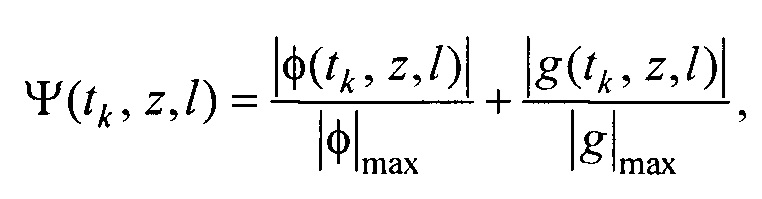 kb 0, ke 0, ke at - номера временных отсчетов кардиоцикла, соответствующих началу Р-зубца, окончанию Т-зубца и окончанию Р-зубца,
kb 0, ke 0, ke at - номера временных отсчетов кардиоцикла, соответствующих началу Р-зубца, окончанию Т-зубца и окончанию Р-зубца,
- определения координат центра модели эпикарда пациента хсе, усе, zce и центра модели предсердий пациента xc at, yc at, zc at, по распределениям Ψ0(z,l) и Ψat(z,l) соответственно по формулам:
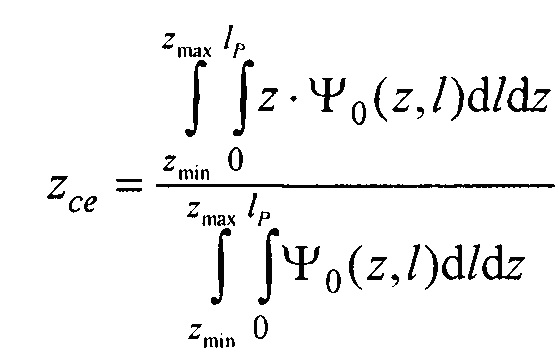 ,
, 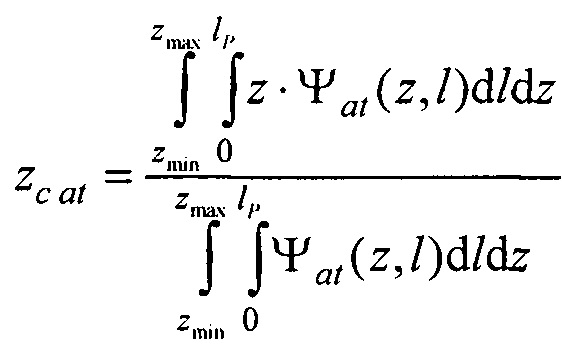 ,
,
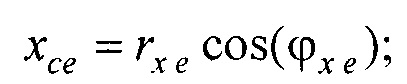
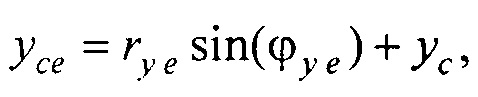
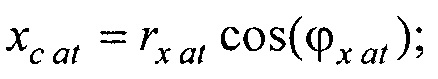
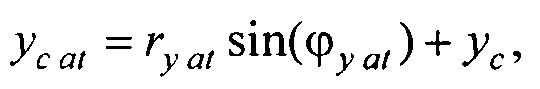
где 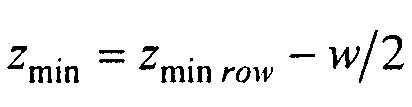 ;
; 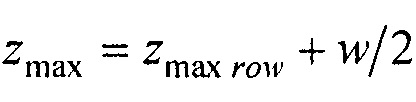 ;
; 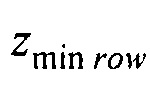 - вертикальная координата нижнего ряда электродов; zmax row - вертикальная координата верхнего ряда электродов; w - расстояние между соседними рядами электродов;
- вертикальная координата нижнего ряда электродов; zmax row - вертикальная координата верхнего ряда электродов; w - расстояние между соседними рядами электродов; 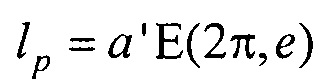 - периметр внутреннего цилиндра, ϕх е, ϕу е ϕх at и ϕу at - решения трансцендентных уравнений
- периметр внутреннего цилиндра, ϕх е, ϕу е ϕх at и ϕу at - решения трансцендентных уравнений 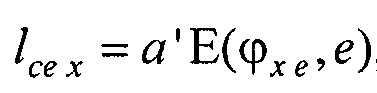 ,
, 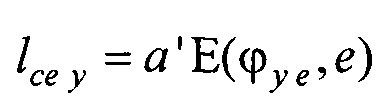 ,
, 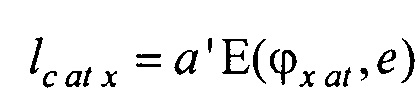 ,
, 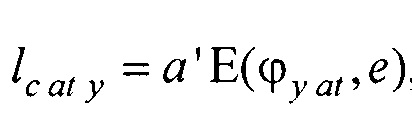 ,
, 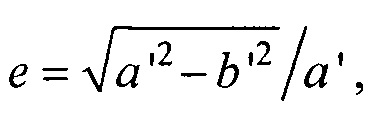
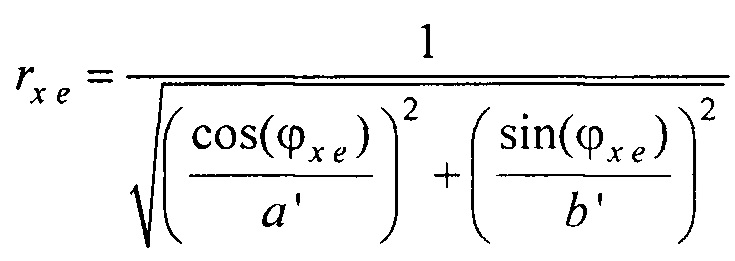 ,
, 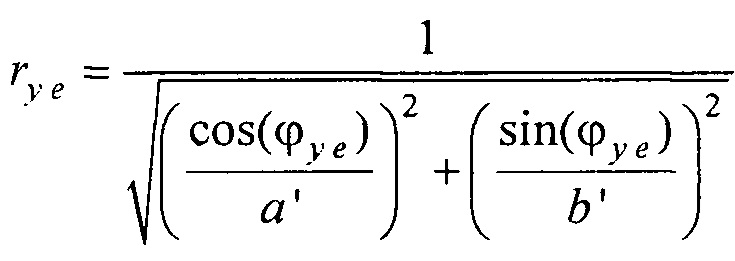 ,
,
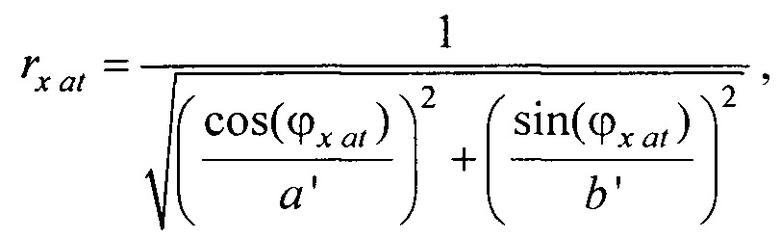
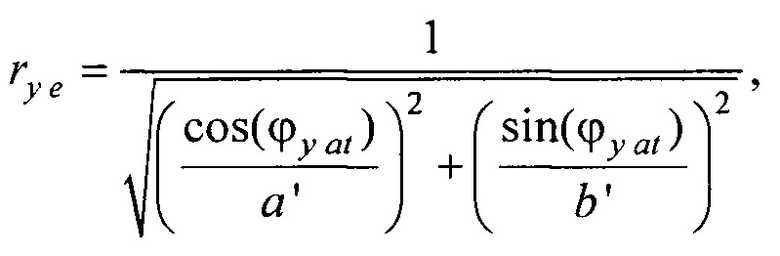
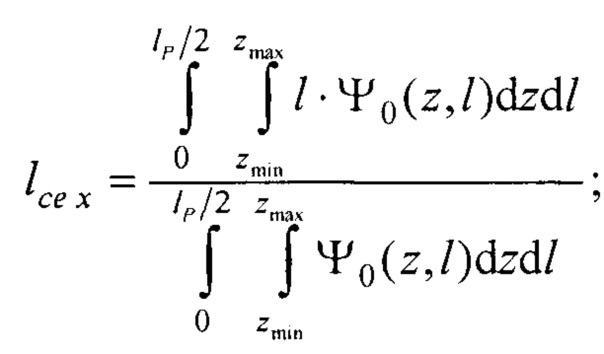
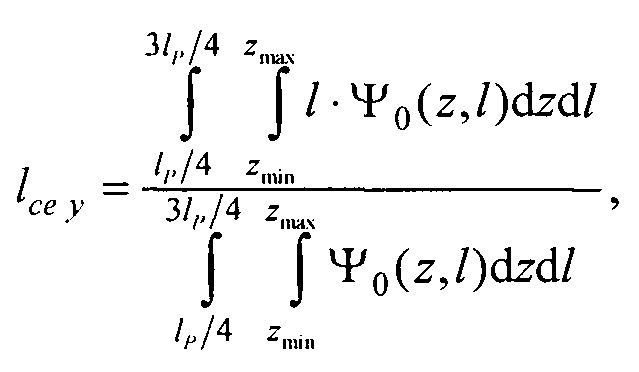

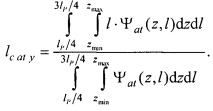
- определения на эталонной модели эпикарда координат центра эталонной модели эпикарда xM e, yM e, zM e и координат центра эталонной модели предсердий xM at, yM at, zM at, по формулам
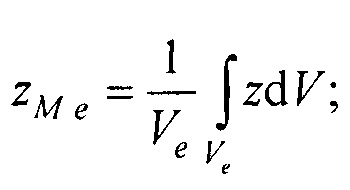
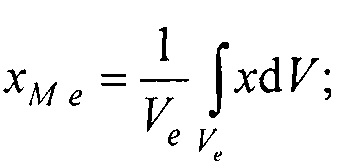
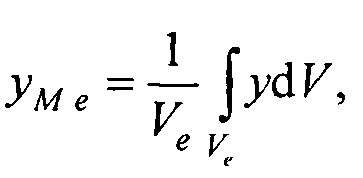
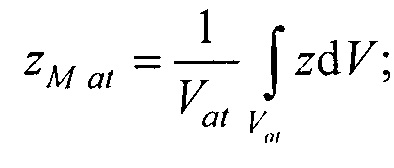
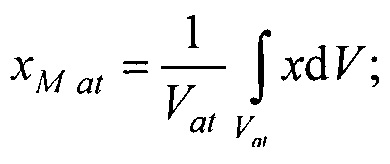
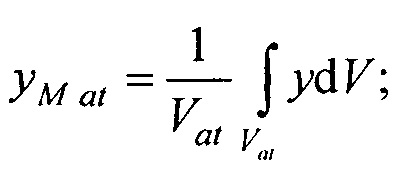
- аффинного преобразования (перемещения, масштабирования и поворота) координат эталонной модели эпикарда до совмещения координат центра эпикарда CMe(xMe, yMe, zMe) и центра предсердий CM at(xM at, yM at, zM at) с рассчитанными соответствующими координатами центра эпикарда пациента Се(хсе, усе, zce) и центра предсердий пациента Cat(xc at, yc at, zc at), по формуле
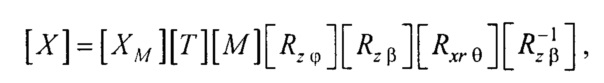
где 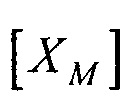 - координатная матрица для точек поверхности эталонной модели эпикарда;
- координатная матрица для точек поверхности эталонной модели эпикарда; 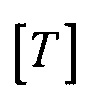 - матрица переноса центра эпикарда эталонной модели в центр модели эпикарда пациента; [М] - матрица масштабирования, обеспечивающая перевод расстояния
- матрица переноса центра эпикарда эталонной модели в центр модели эпикарда пациента; [М] - матрица масштабирования, обеспечивающая перевод расстояния 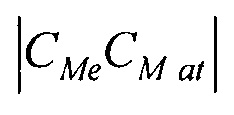 между опорными точками в эталонной модели эпикарда в расстояние
между опорными точками в эталонной модели эпикарда в расстояние 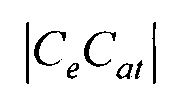 между опорными точками в модели эпикарда пациента;
между опорными точками в модели эпикарда пациента;  - матрица поворота вокруг оси z на угол ϕ0 для совмещения проекций единичных векторов
- матрица поворота вокруг оси z на угол ϕ0 для совмещения проекций единичных векторов 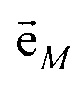 и
и 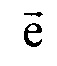 на плоскость XOY;
на плоскость XOY; 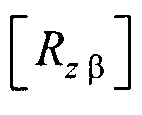 - матрица поворота вокруг оси z на угол β для совмещения вектора
- матрица поворота вокруг оси z на угол β для совмещения вектора 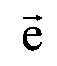 с плоскостью ZOX;
с плоскостью ZOX; 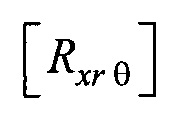 - матрица поворота вокруг нормали к плоскости
- матрица поворота вокруг нормали к плоскости  на угол θ для совмещения
на угол θ для совмещения 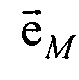 и
и 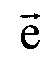 ;
; 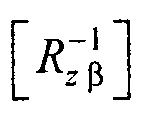 - матрица обратного поворота вокруг оси z на угол (-β);
- матрица обратного поворота вокруг оси z на угол (-β); 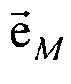 - единичный вектор, направленный из точки CMe в точку СМ at;
- единичный вектор, направленный из точки CMe в точку СМ at; 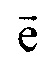 - единичный вектор, направленный из точки Се в точку Cat;
- единичный вектор, направленный из точки Се в точку Cat; 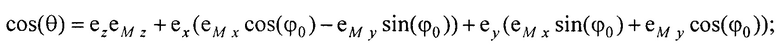
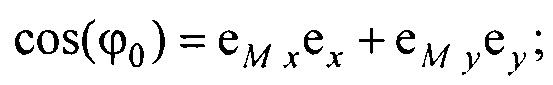

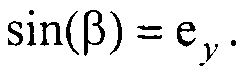
- реконструкцию эквивалентного электрического генератора сердца (ЭЭГС) поверхностного типа путем:
- расчета распределения потенциала и его нормальной производной на поверхности реконструированной модели эпикарда пациента для временных отсчетов кардиоцикла от начала Р-зубца до конца Т-зубца итерационным методом Зейделя по формулам:
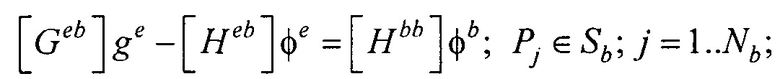
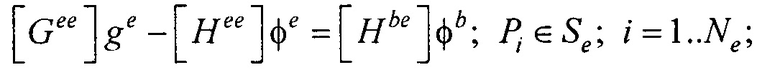
где Pj - точка на поверхности торса Sb; Pi - точка на поверхности модели эпикарда Se; 
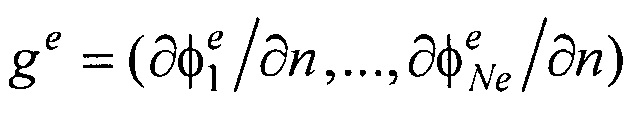 - векторы потенциалов поверхности модели эпикарда и производных потенциалов по направлению нормали к поверхности модели эпикарда пациента;
- векторы потенциалов поверхности модели эпикарда и производных потенциалов по направлению нормали к поверхности модели эпикарда пациента; 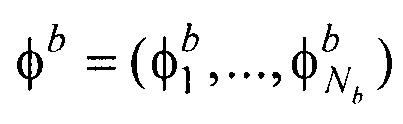 - вектор потенциалов на поверхности торса;
- вектор потенциалов на поверхности торса;
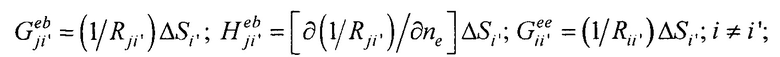

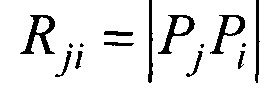 - элементы матриц, входящих в систему линейных матричных уравнений,
- элементы матриц, входящих в систему линейных матричных уравнений,
- контроля сходимости итерационного процесса при расчете распределения потенциала на эпикарде и точности аппроксимации потенциалов на торсе для m-ой итерации по формуле
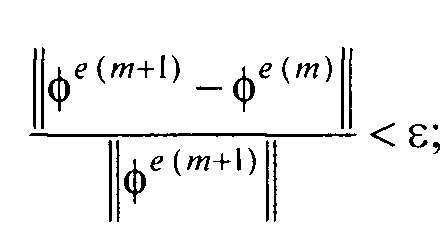
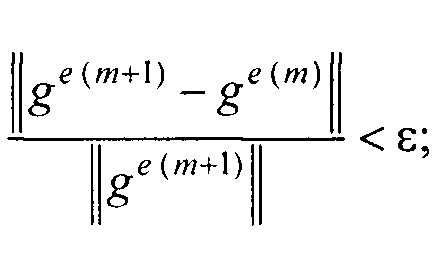
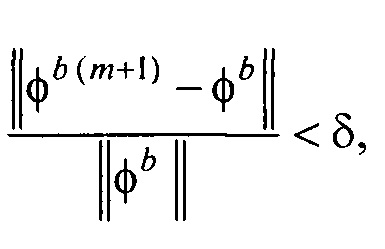
где ε и δ - малые положительные безразмерные величины;
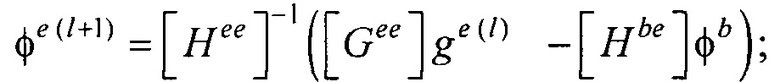
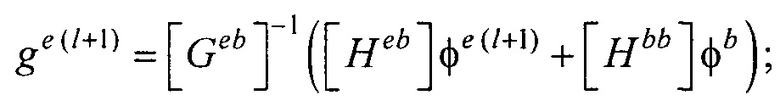

- реконструкцию ЭЭГС дипольного типа, путем:
- получения для всех временных отсчетов кардиоцикла  предварительной оценки массива параметров ЭЭГС
предварительной оценки массива параметров ЭЭГС 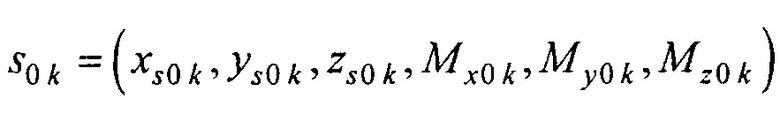 , где
, где 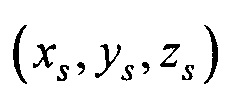 - координаты ЭЭГС,
- координаты ЭЭГС, 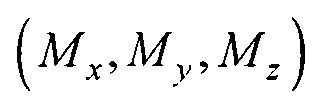 - проекции вектора дипольного момента ЭЭГС
- проекции вектора дипольного момента ЭЭГС 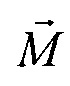 , путем поиска минимума функционала
, путем поиска минимума функционала 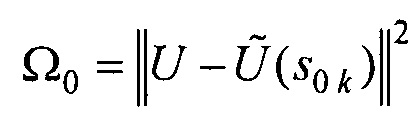 , где
, где 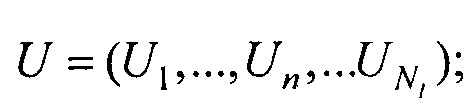 Un - ЭКС, снимаемый с n-го электрода;
Un - ЭКС, снимаемый с n-го электрода; 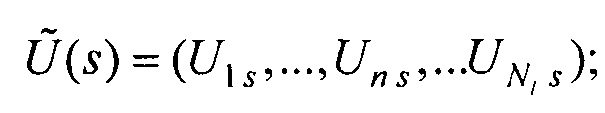 Un s - сигнал дипольного ЭЭГС с параметрами s0 k, рассчитанный для n-го электрода;
Un s - сигнал дипольного ЭЭГС с параметрами s0 k, рассчитанный для n-го электрода;
- получения оценки коэффициента регуляризации αk для каждого момента времени tk по формуле
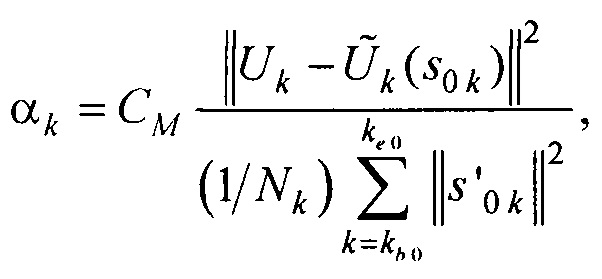
где CM - масштабный коэффициент регуляризации 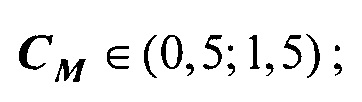
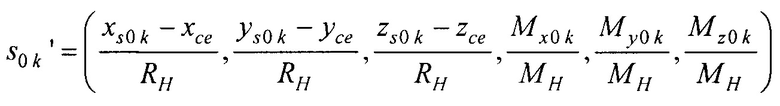 - нормированный массив оценок параметров ЭЭГС;
- нормированный массив оценок параметров ЭЭГС; 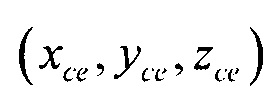 - координаты центра модели эпикарда пациента; RH=6 см - усредненный радиус эпикарда;
- координаты центра модели эпикарда пациента; RH=6 см - усредненный радиус эпикарда; 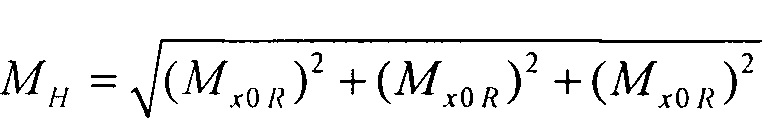 ,
, 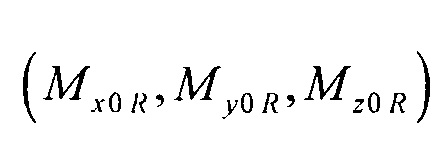 - соответственно модуль и проекции вектора дипольного момента ЭЭГС дипольного типа для временного отсчета максимума R-зубца кардиоцикла;
- соответственно модуль и проекции вектора дипольного момента ЭЭГС дипольного типа для временного отсчета максимума R-зубца кардиоцикла;
- поиска параметров ЭЭГС дипольного типа 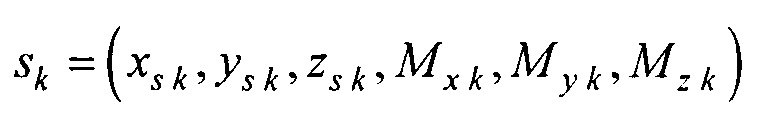 для каждого момента времени tk путем минимизации функционала
для каждого момента времени tk путем минимизации функционала
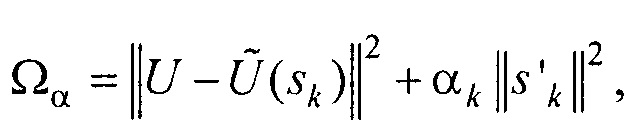
где 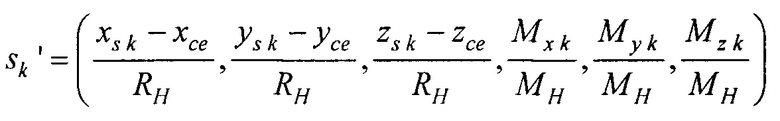 - нормированный массив параметров ЭЭГС дипольного типа;
- нормированный массив параметров ЭЭГС дипольного типа;
- контроля результатов поиска параметров ЭЭГС дипольного типа путем проверки сходимости параметров ЭЭГС и близости массива отсчетов ЭКС для ЭЭГС дипольного типа к массиву отсчетов измеренных ЭКС по формулам:
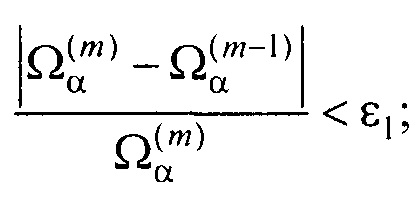

где m - номер итерации в процессе поиска минимума функционала Ωα; ε1 и δ1 - малые положительные безразмерные величины.
На фигуре 3 приведена схема предлагаемого алгоритма, реализующего предлагаемый способ неинвазивного определения электрофизиологических характеристик сердца.
На фигуре 4 представлены модель торса пациента и схема наложения электродов.
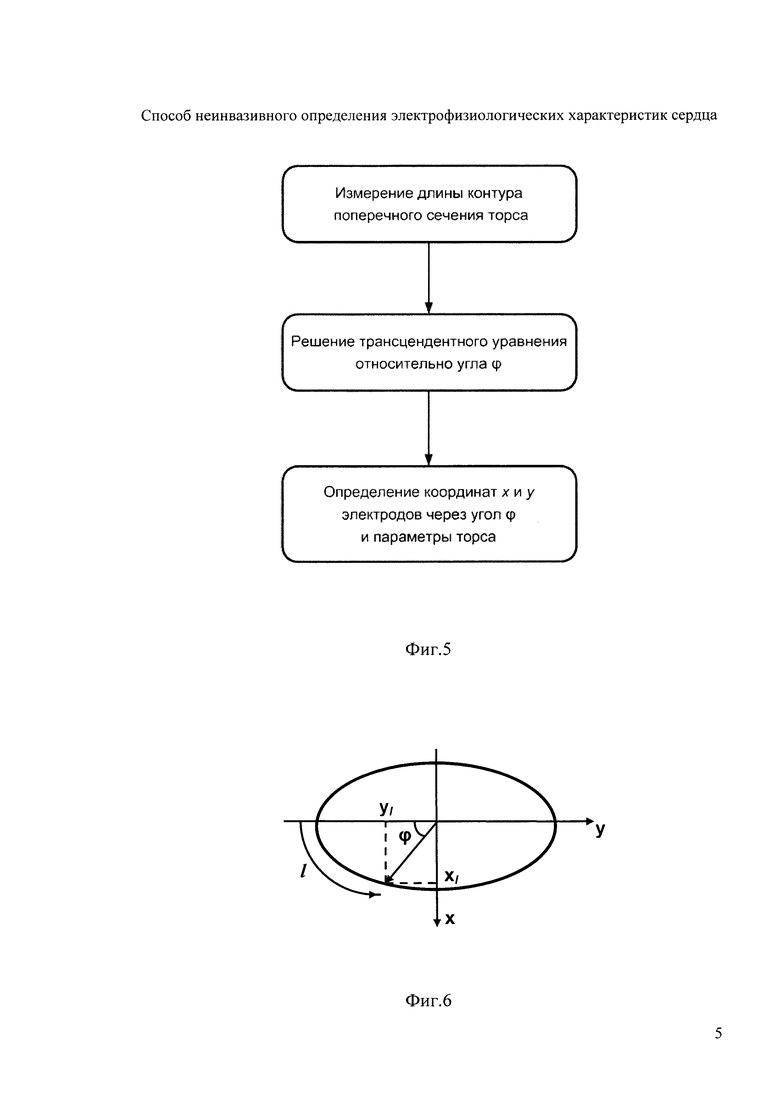
На фигуре 5 представлены этапы определения координат электродов.
Фигура 6 иллюстрирует определение угла положения электрода.
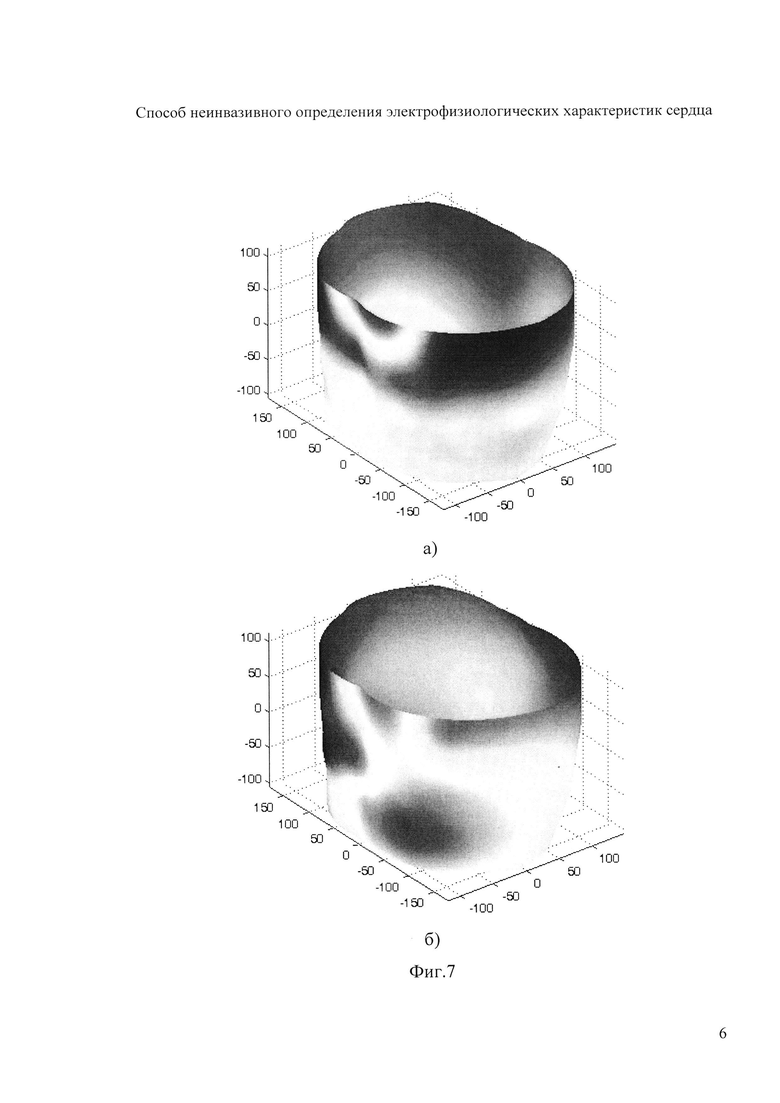
На фигуре 7 представлены карты потенциалов на поверхности торса.
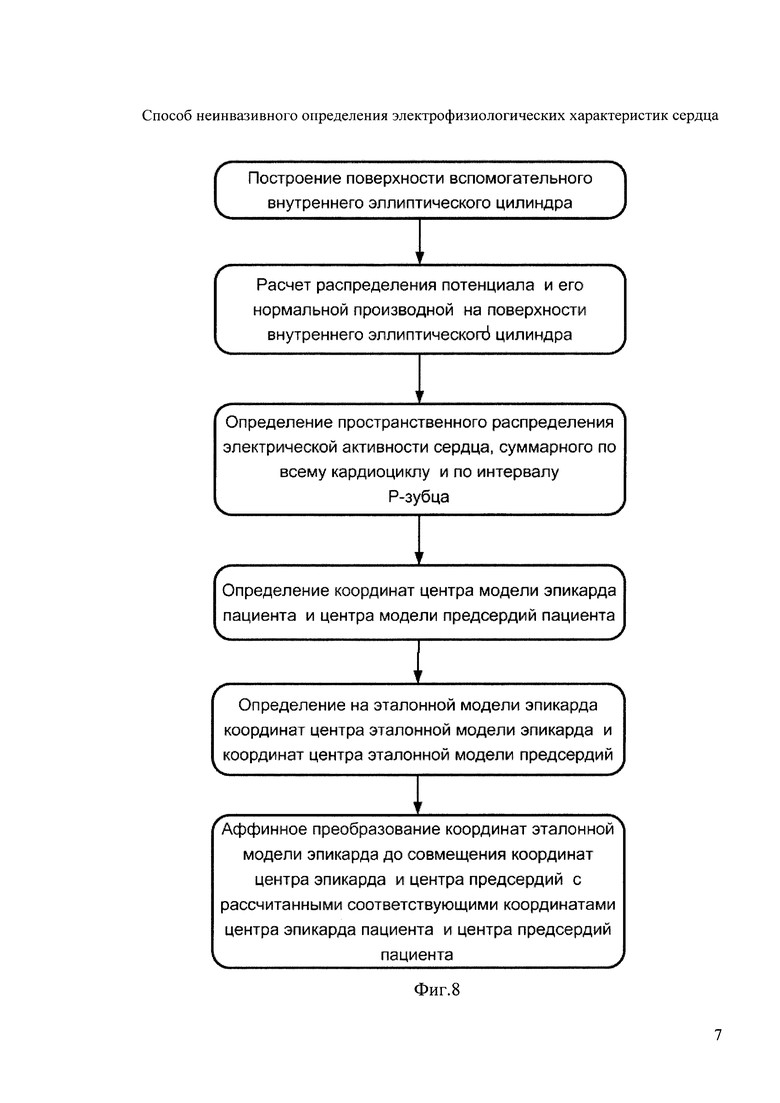
На фигуре 8 представлены этапы реконструкции модели эпикарда.
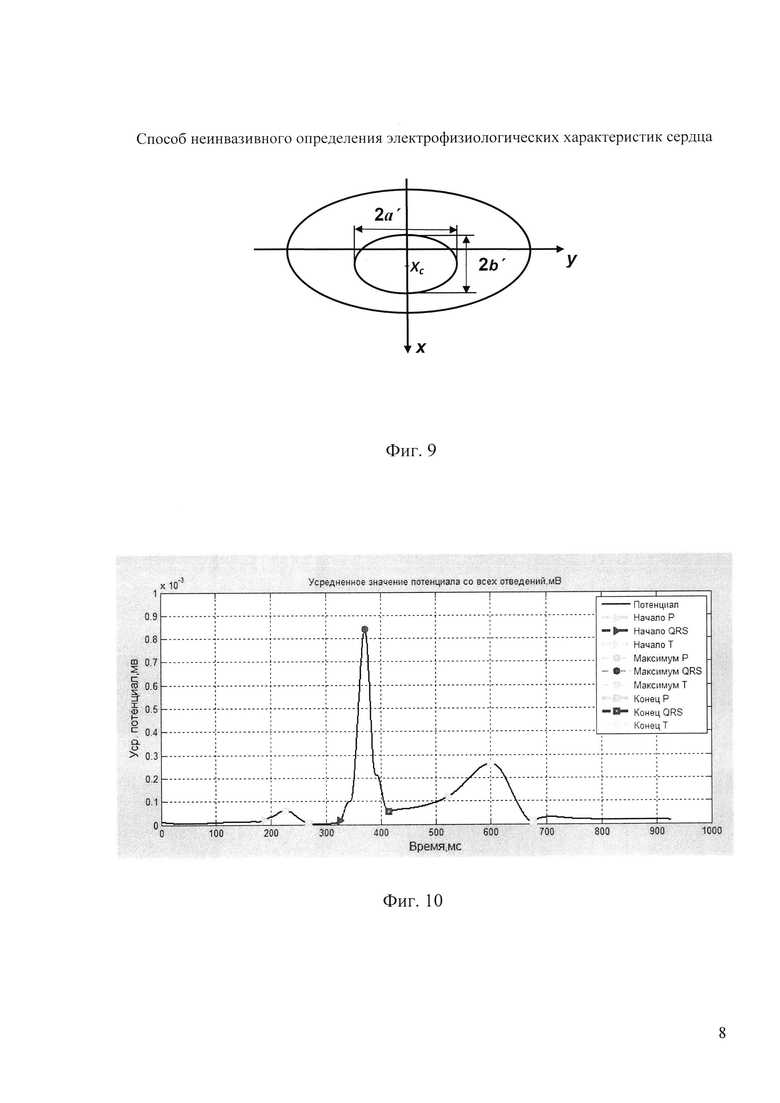
На фигуре 9 представлена внутренняя вспомогательная поверхность для реконструкции модели эпикарда.
На фигуре 10 представлен среднеквадратический ЭКС.
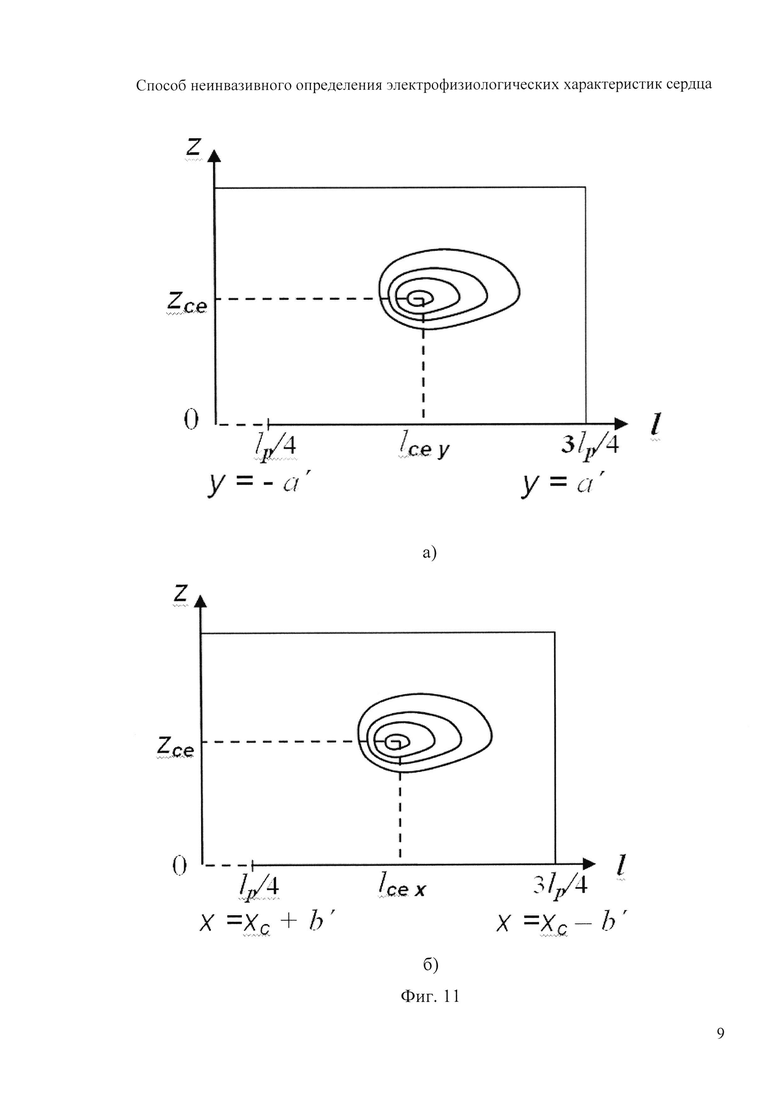
На фигуре 11 представлена иллюстрация определения опорных точек эпикарда.
На фигуре 12 показана эталонная модель эпикарда.
На фигуре 13 представлены этапы реконструкции эквивалентного электрического генератора сердца (ЭЭГС) поверхностного типа.
На фигуре 14 показано распределение потенциала на поверхности эпикарда.
На фигуре 15 представлены этапы реконструкции ЭЭГС дипольного типа.
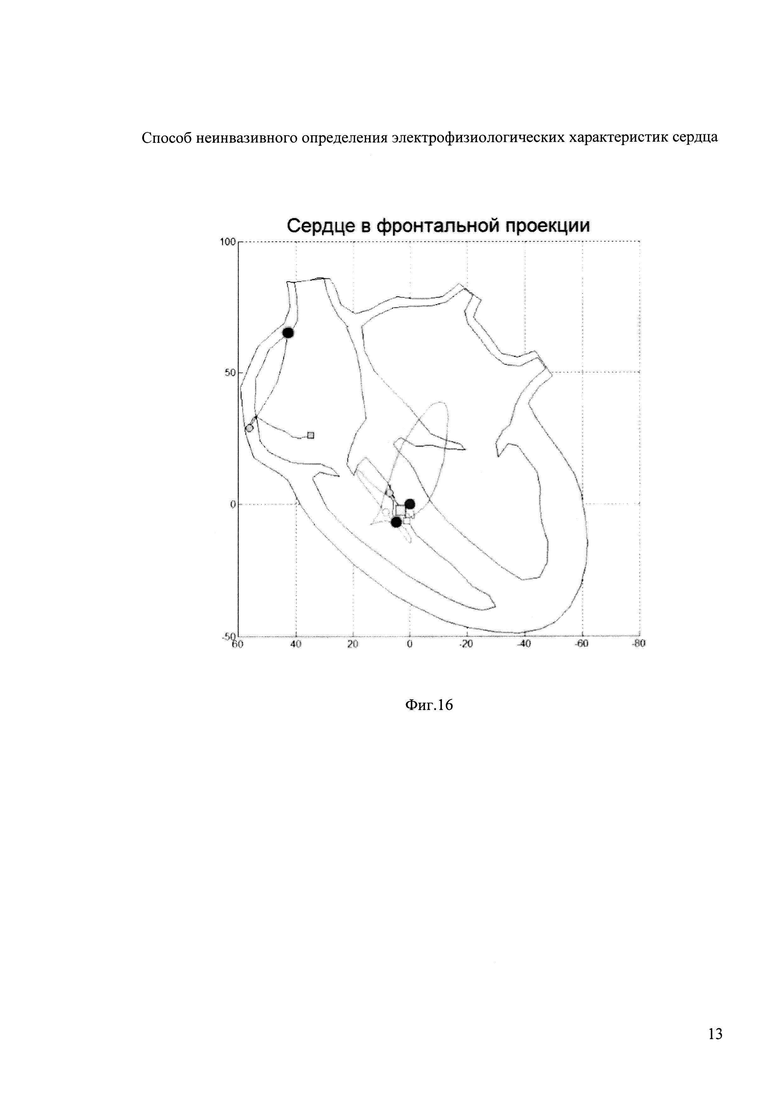
На фигуре 16 показаны треки движения ЭЭГС дипольного типа во фронтальной плоскости на портрете контуров эпикарда и миокарда для Р-зубца, QRS-комплекса и Т-зубца.
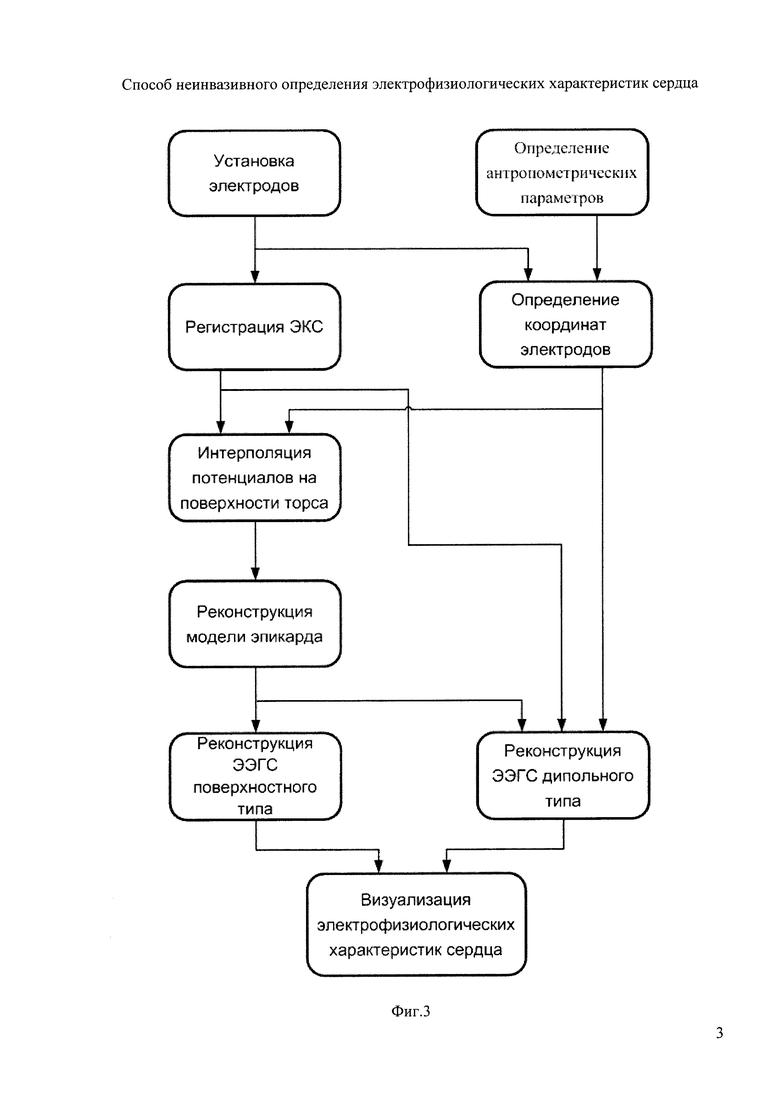
Из анализа фигуры 3 следует, что суть предлагаемого изобретения заключается в получении пространственных распределений параметров ЭЭГС. Для этого после установки электродов и определения антропометрических параметров торса пациента проводятся регистрация ЭКС и определение координат электродов, затем начинается этап основной обработки полученных данных, который включает интерполяцию потенциалов на поверхности торса, реконструкцию модели эпикарда пациента, реконструкцию ЭЭГС поверхностного типа и реконструкцию ЭЭГС дипольного типа [6-8]. Полученные пространственные распределения параметров ЭЭГС представляются функциями времени, что используется в отображении этих распределений в блоке визуализации электрофизиологических характеристик сердца.
Поясним особенности выполнения введенных действий.
Устанавливают электроды в количестве не менее 30, располагая их по поперечному сечению торса в 4 ряда (фигура 4). Далее определяют координаты электродов (фигура 5). Координату z электродов отсчитывают от акромиального конца ключицы до текущего горизонтального ряда электродов с помощью измерительной ленты с нанесенными на нее делениями (цена деления 1 мм). Для определения координат х и у электродов предварительно с помощью измерительной ленты измеряют длину дуги l, отсчитываемую по контуру поперечного сечения торса от прямой, соединяющей подмышечные впадины, до текущего электрода (фигура 6). Решают трансцендентное уравнение l=аЕ(ϕ,е), относительно угла ϕ, где 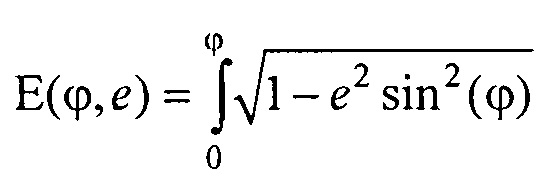 - нормальный эллиптический интеграл Лежандра второго рода;
- нормальный эллиптический интеграл Лежандра второго рода; 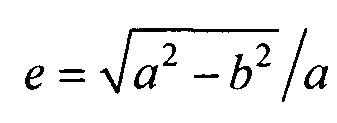 - эксцентриситет поперечного сечения торса, а и b - антропометрические параметры торса пациента; ϕ - угол между прямой, соединяющей подмышечные впадины и направлением на текущий электрод. Координаты электродов х и у определяют по формулам х=r sin(ϕ); у=-rcos(ϕ), где r - расстояние от центра поперечного сечения торса до электрода, которое определяется по формуле
- эксцентриситет поперечного сечения торса, а и b - антропометрические параметры торса пациента; ϕ - угол между прямой, соединяющей подмышечные впадины и направлением на текущий электрод. Координаты электродов х и у определяют по формулам х=r sin(ϕ); у=-rcos(ϕ), где r - расстояние от центра поперечного сечения торса до электрода, которое определяется по формуле 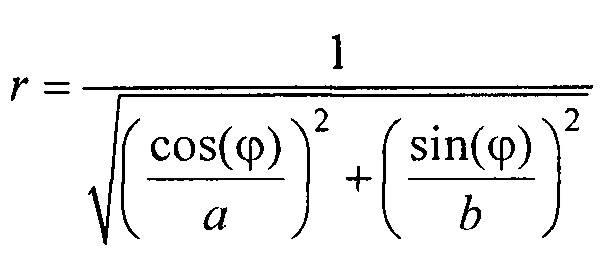 .
.
Интерполяцию потенциалов на поверхности торса проводят по формуле:
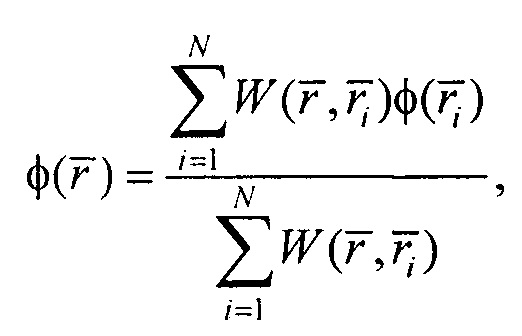
где 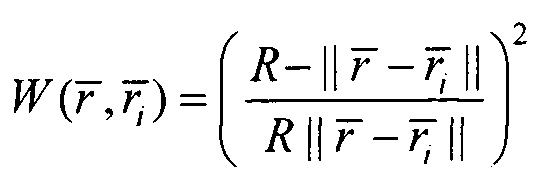 - весовая функция по Шепарду,
- весовая функция по Шепарду, 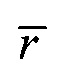 - радиус-вектор пространственного положения текущей точки интерполяции,
- радиус-вектор пространственного положения текущей точки интерполяции, 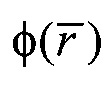 - искомое значение потенциала в этой точке,
- искомое значение потенциала в этой точке, 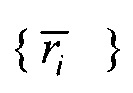 - множество точек поверхности с известными значениями потенциалов, R - радиус сферы с центром в точке
- множество точек поверхности с известными значениями потенциалов, R - радиус сферы с центром в точке 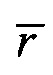 , ограничивающей число точек N, используемых для интерполяции. На фигуре 7 представлены карты поверхностных потенциалов для моментов времени, соответствующих вершинам Р и R-зубцов кардиоцикла.
, ограничивающей число точек N, используемых для интерполяции. На фигуре 7 представлены карты поверхностных потенциалов для моментов времени, соответствующих вершинам Р и R-зубцов кардиоцикла.
Так как целью обработки является реконструкция пространственно-временных характеристик ЭЭГС на поверхности эпикарда, то вначале необходимо найти модель поверхности эпикарда (фигура 8). Для этого на первом этапе находят положение опорных точек модели эпикарда. С данной целью вводят вспомогательный эллиптический цилиндр (фигура 9), расположенный внутри торса и окружающий эпикард, поверхность которого описывается уравнением:
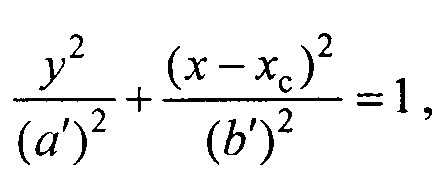
где 2а'=DH+8 см; 2b'=DH+4 см; DH=12 см - размер эпикарда; yc=b-b'-Δу, b - полуось поперечного сечения торса в направлении от спины к груди; Δу=2 см - расстояние между торсом и внутренним цилиндром в направлении от спины к груди. Далее вычисляют среднеквадратический электрокардиосигнал всех электродов (фигура 10) по формуле
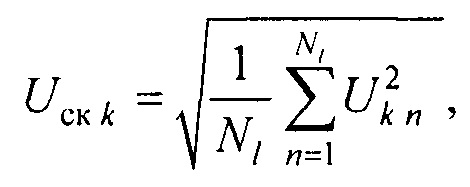
где k - номер отсчета по времени, n - номер электрода, Nl - количество отведений (измерительных электродов). По значениям Uск k определяются номера временных отсчетов, соответствующих началу Р-зубца и окончаниям Р-зубца и Т-зубца. Для временных отсчетов в диапазоне от начала Р-зубца до конца Т-зубца выполняют следующие действия.
Рассчитывают распределения потенциала φ и его нормальной производной 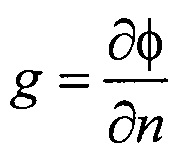 на поверхности внутреннего эллиптического цилиндра для временных отсчетов от начала Р-зубца до конца Т-зубца кардиоцикла (фигура 10) путем решения итерационным методом Зейделя системы линейных матричных уравнений:
на поверхности внутреннего эллиптического цилиндра для временных отсчетов от начала Р-зубца до конца Т-зубца кардиоцикла (фигура 10) путем решения итерационным методом Зейделя системы линейных матричных уравнений:
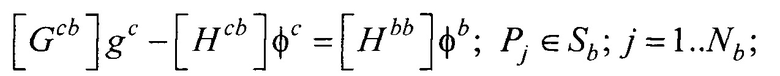
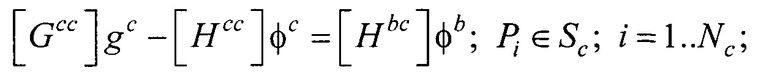
где Pj - точка на поверхности торса Sb; Pi - точка на поверхности внутреннего эллиптического цилиндра Sc; 
 - векторы потенциалов поверхности внутреннего эллиптического цилиндра и производных потенциалов по направлению нормали к поверхности внутреннего эллиптического цилиндра, при этом нормаль берется внешняя по отношению к области между торсом и внутренним цилиндром;
- векторы потенциалов поверхности внутреннего эллиптического цилиндра и производных потенциалов по направлению нормали к поверхности внутреннего эллиптического цилиндра, при этом нормаль берется внешняя по отношению к области между торсом и внутренним цилиндром; 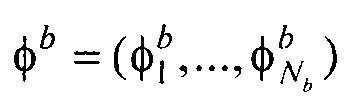 - вектор потенциалов на поверхности торса;
- вектор потенциалов на поверхности торса;  ,
,  - площади элементов поверхности внутреннего эллиптического цилиндра и торса соответственно;
- площади элементов поверхности внутреннего эллиптического цилиндра и торса соответственно; 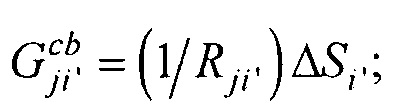
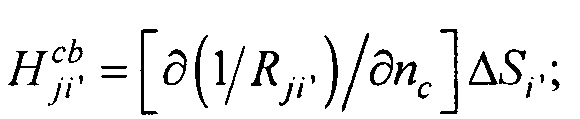
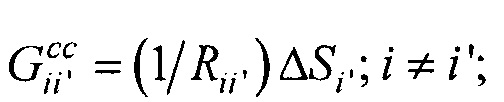
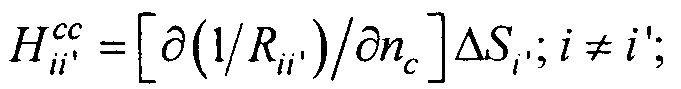
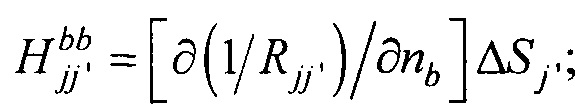
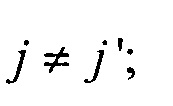
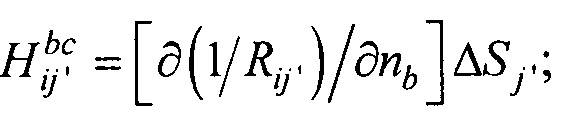
 - элементы матриц, входящих в систему линейных матричных уравнений.
- элементы матриц, входящих в систему линейных матричных уравнений.
В качестве опорных точек модели эпикарда принимают координаты центра модели эпикарда пациента хсе, усе, zce и центра модели предсердий пациента xc at, yc at, zc at, которые определяют с помощью характеристик ЭЭГС на поверхности эпикарда φ и 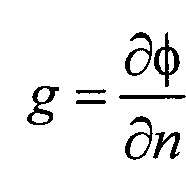 , найденных на предыдущем этапе. Для этого вначале вычисляют пространственные распределения электрической активности сердца, суммарной по всему кардиоциклу
, найденных на предыдущем этапе. Для этого вначале вычисляют пространственные распределения электрической активности сердца, суммарной по всему кардиоциклу 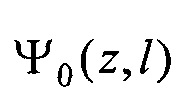 и по интервалу Р-зубца
и по интервалу Р-зубца 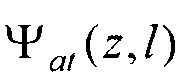 с использованием формул:
с использованием формул:
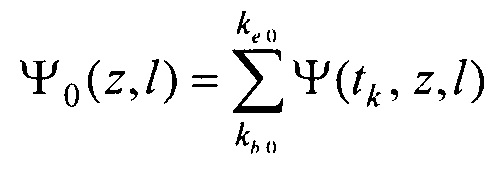 ,
, 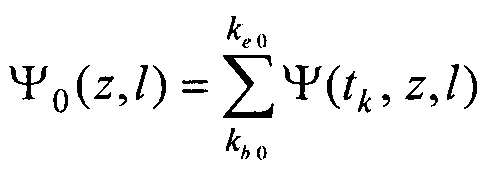 ,
,
где 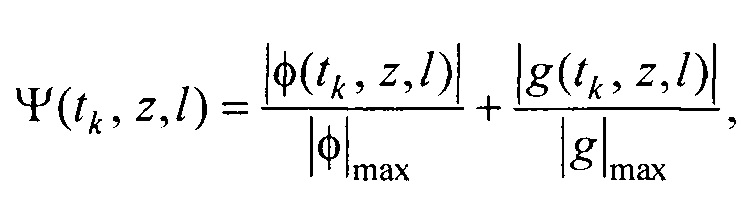 kb 0, ke 0 ke at - номера временных отсчетов кардиоцикла, соответствующих началу Р-зубца, окончанию Т-зубца и окончанию Р-зубца. Затем находят координаты опорных точек по формулам:
kb 0, ke 0 ke at - номера временных отсчетов кардиоцикла, соответствующих началу Р-зубца, окончанию Т-зубца и окончанию Р-зубца. Затем находят координаты опорных точек по формулам:
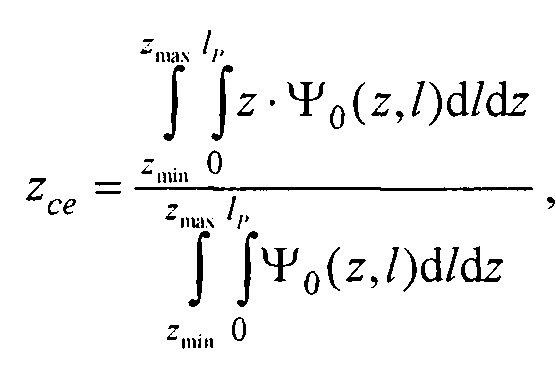

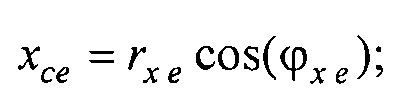
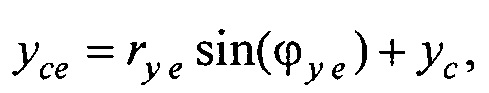
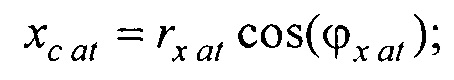
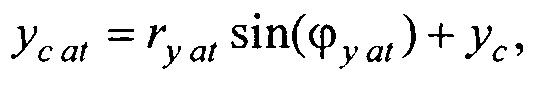
где 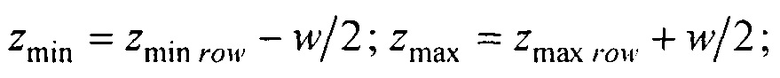
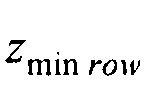 - вертикальная координата нижнего ряда электродов;
- вертикальная координата нижнего ряда электродов; 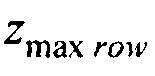 - вертикальная координата верхнего ряда электродов; w - расстояние между соседними рядами электродов;
- вертикальная координата верхнего ряда электродов; w - расстояние между соседними рядами электродов; 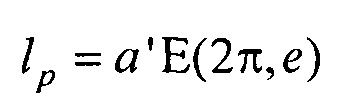 - периметр внутреннего цилиндра,
- периметр внутреннего цилиндра, 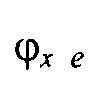 ,
, 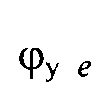 ,
, 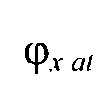 и
и 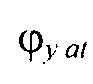 - решения трансцендентных уравнений
- решения трансцендентных уравнений 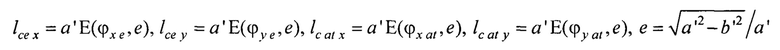 (фигура 11, а и б),
(фигура 11, а и б),
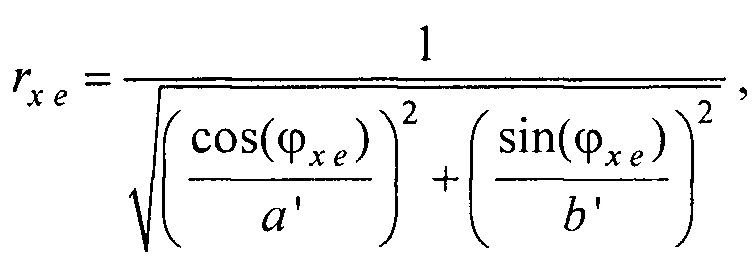
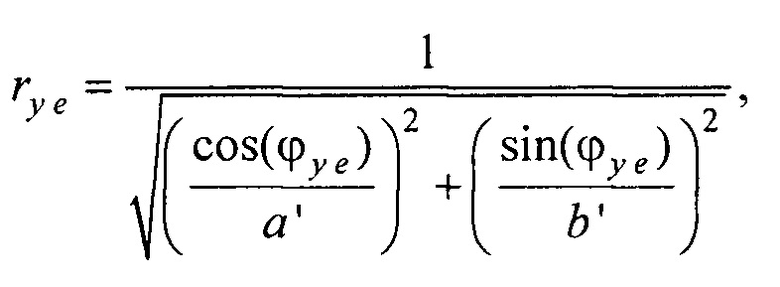
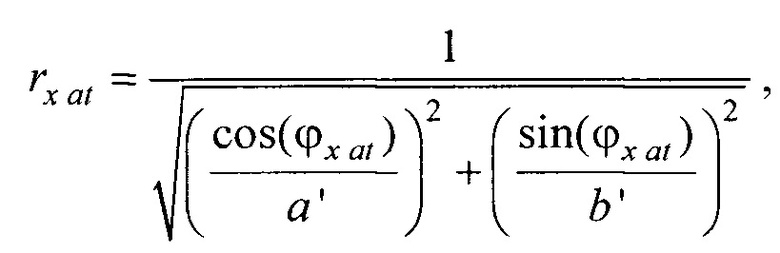
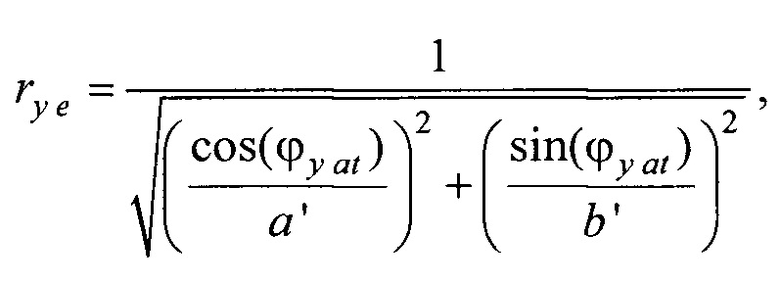
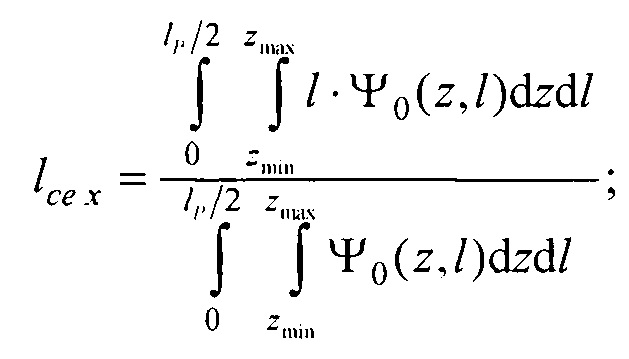
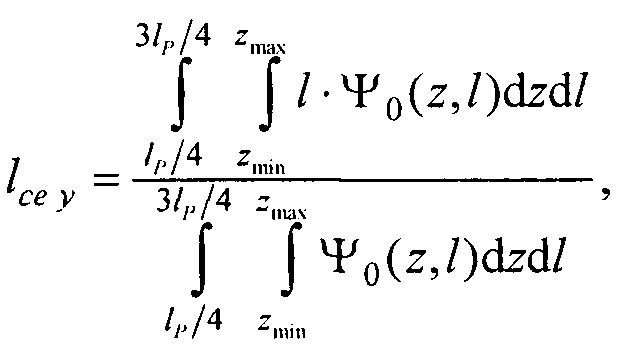
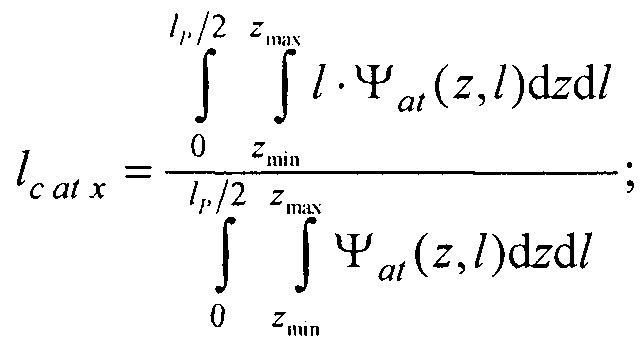
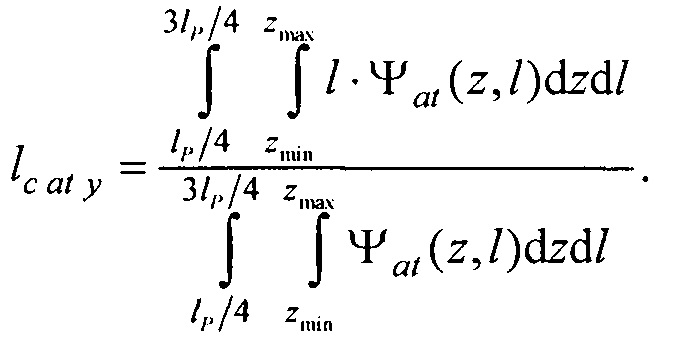
Модель эпикарда пациента получают на базе эталонной модели эпикарда (фигура 12), которая является реалистическим анатомическим отображением эпикарда. Для привязки эталонной модели к модели эпикарда пациента, находят координаты центра эталонной модели эпикарда 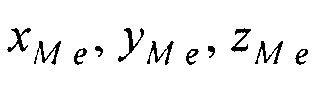 и координаты центра эталонной модели предсердий
и координаты центра эталонной модели предсердий 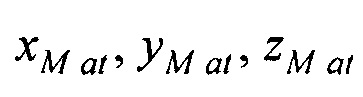 , по формулам:
, по формулам:
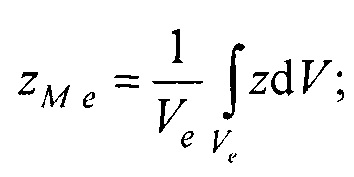
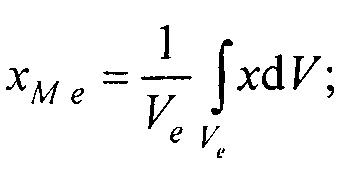
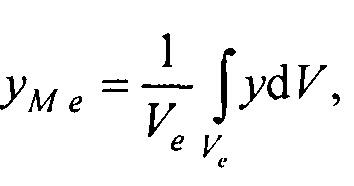
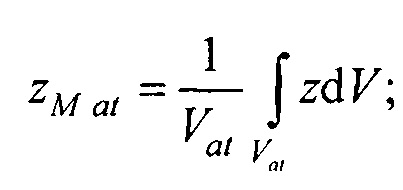
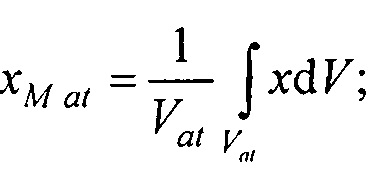
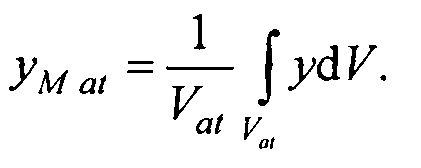
Координаты точек поверхности модели эпикарда пациента получают с помощью аффинного преобразования (перемещения, масштабирования и поворота) координат эталонной модели эпикарда до совмещения координат центра эпикарда 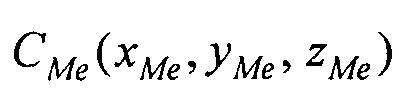 и центра предсердий
и центра предсердий 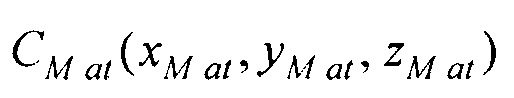 с рассчитанными соответствующими координатами центра эпикарда пациента
с рассчитанными соответствующими координатами центра эпикарда пациента 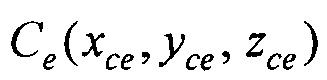 и центра предсердий пациента
и центра предсердий пациента 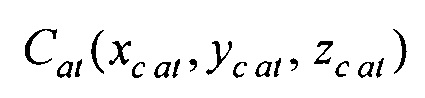 , по формуле:
, по формуле:
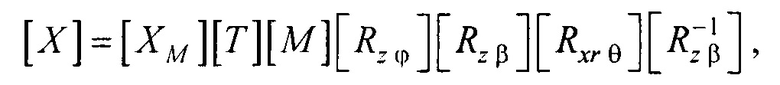
где 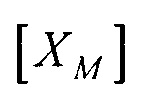 - координатная матрица для точек поверхности эталонной модели эпикарда;
- координатная матрица для точек поверхности эталонной модели эпикарда; 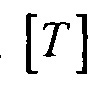 - матрица переноса центра эпикарда эталонной модели в центр модели эпикарда пациента;
- матрица переноса центра эпикарда эталонной модели в центр модели эпикарда пациента; 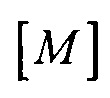 - матрица масштабирования, обеспечивающая перевод расстояния
- матрица масштабирования, обеспечивающая перевод расстояния 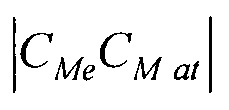 между опорными точками в эталонной модели эпикарда в расстояние
между опорными точками в эталонной модели эпикарда в расстояние 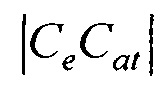 между опорными точками в модели эпикарда пациента;
между опорными точками в модели эпикарда пациента; 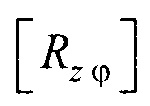 - матрица поворота вокруг оси z на угол ϕ0 для совмещения проекций единичных векторов
- матрица поворота вокруг оси z на угол ϕ0 для совмещения проекций единичных векторов 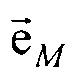 и
и 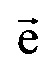 на плоскость XOY;
на плоскость XOY; 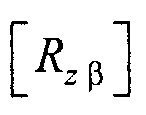 - матрица поворота вокруг оси z на угол β для совмещения вектора
- матрица поворота вокруг оси z на угол β для совмещения вектора 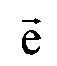 с плоскостью ZOX;
с плоскостью ZOX; 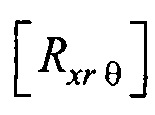 - матрица поворота вокруг нормали к плоскости
- матрица поворота вокруг нормали к плоскости 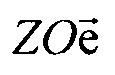 на угол θ для совмещения
на угол θ для совмещения 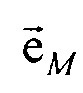 и
и 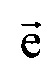 ;
; 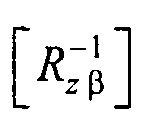 - матрица обратного поворота вокруг оси z на угол (-β);
- матрица обратного поворота вокруг оси z на угол (-β); 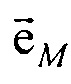 - единичный вектор, направленный из точки СМе в точку CM at;
- единичный вектор, направленный из точки СМе в точку CM at; 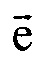 - единичный вектор, направленный из точки Се в точку Cat;
- единичный вектор, направленный из точки Се в точку Cat;
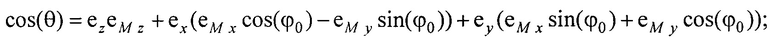
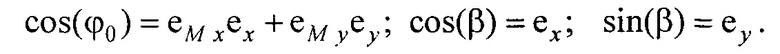
Располагая моделью эпикарда, проводят реконструкцию ЭЭГС поверхностного типа на поверхности эпикарда (фигура 13). Для этого рассчитывают распределения потенциала и его нормальной производной на поверхности реконструированной модели эпикарда пациента для временных отсчетов кардиоцикла от начала Р-зубца до конца Т-зубца итерационным методом Зейделя по формулам:
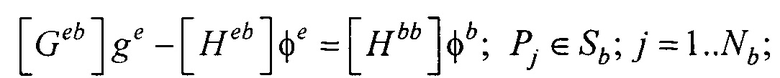
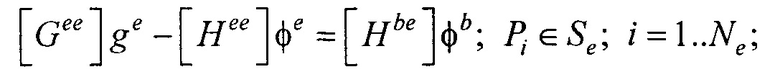
где Pj - точка на поверхности торса Sb; Pi - точка на поверхности модели эпикарда Se; 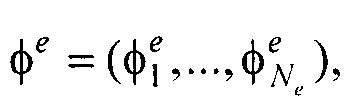
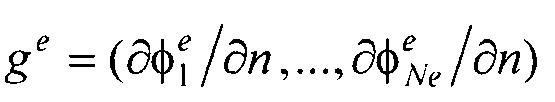 - векторы потенциалов поверхности модели эпикарда и производных потенциалов по направлению нормали к поверхности модели эпикарда пациента;
- векторы потенциалов поверхности модели эпикарда и производных потенциалов по направлению нормали к поверхности модели эпикарда пациента; 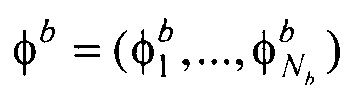 - вектор потенциалов на поверхности торса;
- вектор потенциалов на поверхности торса;
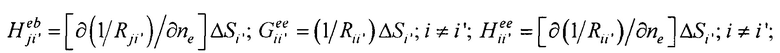
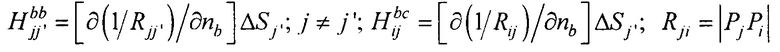 - элементы матриц, входящих в систему линейных матричных уравнений. В ходе итерационного процесса реконструкции осуществляют контроль сходимости итерационного процесса при расчете распределения потенциала на эпикарде и контроль точности аппроксимации потенциалов на торсе для m-ой итерации по формуле:
- элементы матриц, входящих в систему линейных матричных уравнений. В ходе итерационного процесса реконструкции осуществляют контроль сходимости итерационного процесса при расчете распределения потенциала на эпикарде и контроль точности аппроксимации потенциалов на торсе для m-ой итерации по формуле:
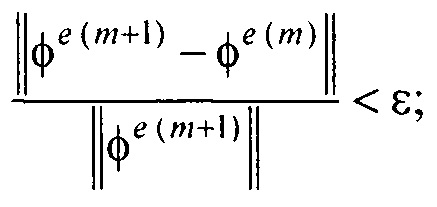
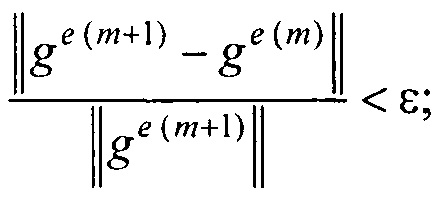
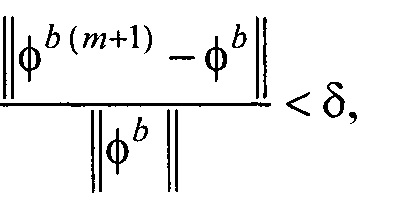
где ε и δ - малые положительные безразмерные величины;
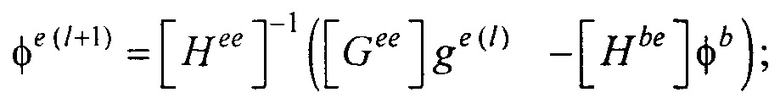
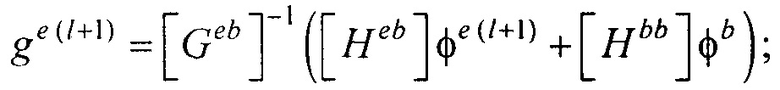
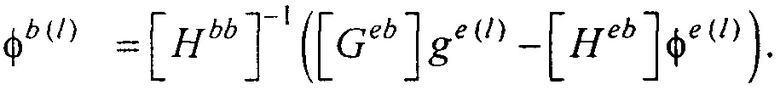
На фигуре 14 показано распределение потенциала на поверхности эпикарда в фазе возбуждения желудочков (R-зубец).
С целью расширения диагностических возможностей электрокардиологии пространственно-временные характеристики электрической активности сердца на поверхности эпикарда (ЭЭГС поверхностного типа) целесообразно дополнить пространственно-временными характеристиками электрической активности в объеме сердца. Для этого предлагается проводить дополнительно реконструкцию ЭЭГС дипольного типа (фигура 15), который для всех временных отсчетов кардиоцикла tk характеризуется вектором параметров 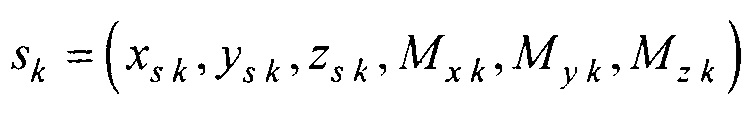 , где
, где  - координаты ЭЭГС,
- координаты ЭЭГС,  - проекции вектора дипольного момента ЭЭГС. Поскольку задача реконструкции относится к классу математически некорректных задач [9], то для ее решения решают оптимизационную задачу - ищут вектор sk параметров ЭЭГС, при котором достигается минимум функционала
- проекции вектора дипольного момента ЭЭГС. Поскольку задача реконструкции относится к классу математически некорректных задач [9], то для ее решения решают оптимизационную задачу - ищут вектор sk параметров ЭЭГС, при котором достигается минимум функционала
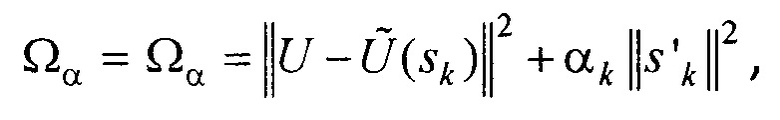
где 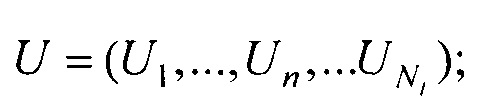 Un - ЭКС, снимаемый с n-го электрода;
Un - ЭКС, снимаемый с n-го электрода; 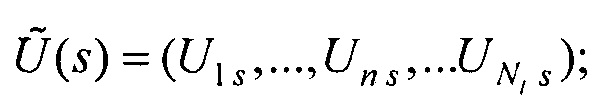 Un s - сигнал дипольного ЭЭГС с параметрами sk, рассчитанный для n-го электрода;
Un s - сигнал дипольного ЭЭГС с параметрами sk, рассчитанный для n-го электрода; 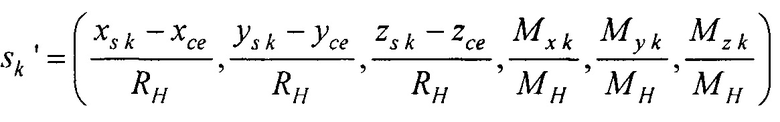 - нормированный вектор параметров ЭЭГС; (xce, yce, zce) - координаты центра модели эпикарда пациента; RH=6 см - усредненный радиус эпикарда; МН - модуль вектора дипольного момента ЭЭГС дипольного типа для временного отсчета максимума R-зубца кардиоцикла; αk - коэффициент регуляризации для момента времени tk. Для поиска MH и αk проводят предварительную оценку параметров ЭЭГС
- нормированный вектор параметров ЭЭГС; (xce, yce, zce) - координаты центра модели эпикарда пациента; RH=6 см - усредненный радиус эпикарда; МН - модуль вектора дипольного момента ЭЭГС дипольного типа для временного отсчета максимума R-зубца кардиоцикла; αk - коэффициент регуляризации для момента времени tk. Для поиска MH и αk проводят предварительную оценку параметров ЭЭГС 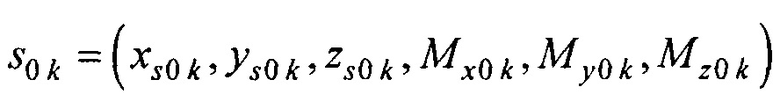 путем поиска минимума функционала
путем поиска минимума функционала 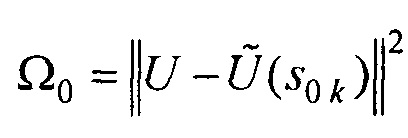 , после чего находят
, после чего находят
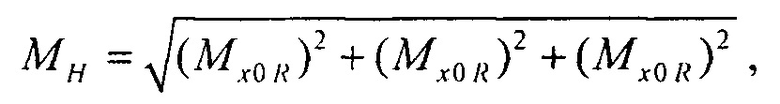
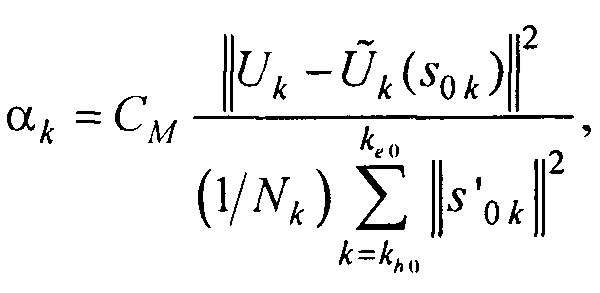
где CM - масштабный коэффициент регуляризации, CM ∈ (0,5; 1,5); 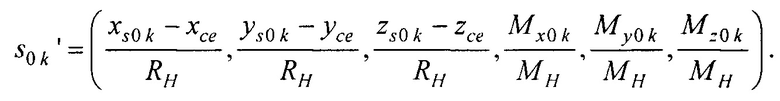 В ходе процесса поиска параметров ЭЭГС дипольного типа осуществляют контроль результатов поиска путем проверки сходимости параметров ЭЭГС и близости массива отсчетов ЭКС ЭЭГС дипольного типа к массиву отсчетов измеренных ЭКС по формулам:
В ходе процесса поиска параметров ЭЭГС дипольного типа осуществляют контроль результатов поиска путем проверки сходимости параметров ЭЭГС и близости массива отсчетов ЭКС ЭЭГС дипольного типа к массиву отсчетов измеренных ЭКС по формулам:
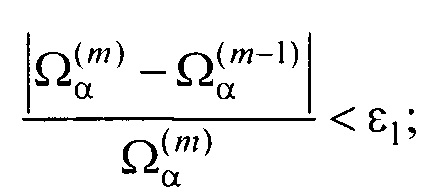
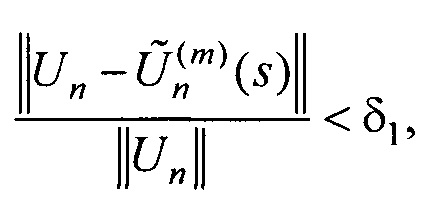
где m - номер итерации в процессе поиска минимума функционала Ωα; ε1 и δ1 - малые положительные безразмерные величины. На фигуре 16 показаны треки движения ЭЭГС дипольного типа во фронтальной плоскости на портрете контуров эпикарда и миокарда для Р-зубца, QRS-комплекса и Т-зубца.
Таким образом, предлагаемое изобретение позволяет получать изменяющиеся во времени в течение кардиоцикла картины изменения электрического потенциала на поверхности эпикарда для диагностики нарушений процессов проводимости, а также картины изменения координат и вектора дипольного момента ЭЭГС дипольного типа - для диагностики ишемии.
Источники информации
1. Титомир Л.И., Кнеппо П. Математическое моделирование биоэлектрического генератора сердца. - М.: Наука. Физматлит, 1999, - 447 с.
2. Титомир Л.И., Трунов В.Г., Айду Э.А.И. Неинвазивная электрокардиотопография. - М.: Наука, 2003, - 198 с.
3. Пат. №2448643, Российская Федерация, МПК А61В 5/02, А61В 5/0402. Электрокардиограф с измерением координат и параметров источника электрической активности сердца / Лебедев В.В., Крамм М.Н., Жихарева Г.В., Винокуров Д.С., Филонов Д.В., Стрелков Н.О. // Опубл. 27.04.2012, Бюл. №12, - 12 с.
4. Патент №2435518, Российская Федерация, МПК А61В 5/0402. Способ неинвазивного электрофизиологического исследования сердца / Ревишвили А.Ш., Калинин В.В., Калинин А.В. // Опубл. 27.04.2012, Бюл. №12, - 12 с.
5. Патент №2360597, Российская Федерация, МПК А61В 5/0402, Способ определения электрической активности сердца / Бодин О.Н., Гладкова Е.А., Кузьмин А.В., Митрохина Н.Ю., Мулюкина Л.А. // Опубл. 27.04.2012, Бюл. №12, - 12 с.
6. Винокуров Д.С., Крамм М.Н., Лебедев В.В., Попов Ю.Б. Реконструкция токового источника в области миокарда. - Медицинская техника. 2008. №4. С. 7-11.
7. Филонов Д.В., Винокуров Д.С., Жихарева Г.В., Крамм М.Н. Реконструкция токовых источников в области миокарда по измеренным поверхностным потенциалам. - Измерительная техника. 2009. №9. С. 61-64.
8. M.N. Kramm, G.V. Zhikhareva, D.V. Filonov, N.A. Zhuravleva. Reconstruction of equivalent current sources on quasi-epicardium, Proceedings of the Russian-German Conference on Biomedical Engineering RGC'2013, October 23-26, 2013, Hanover, Germany, p. 77.
9. Тихонов A.H., Арсенин В.Я. Методы решения некорректных задач. - М.: Наука. Гл. ред. физ.-мат. лит., 1986, - 288 с.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ И УСТРОЙСТВО РЕГИСТРАЦИИ МНОЖЕСТВЕННЫХ ОТВЕДЕНИЙ ЭЛЕКТРОКАРДИОСИГНАЛА | 2020 |
|
RU2764498C2 |
| СПОСОБ ПОВЫШЕНИЯ ДИАГНОСТИЧЕСКОЙ ТОЧНОСТИ НАГРУЗОЧНОГО ЭКГ ТЕСТА ДЛЯ ВЫЯВЛЕНИЯ ПРИЗНАКОВ ПРЕХОДЯЩЕЙ ИШЕМИИ МИОКАРДА | 2017 |
|
RU2676625C1 |
| СПОСОБ НЕИНВАЗИВНОГО ОПРЕДЕЛЕНИЯ ЭЛЕКТРОФИЗИОЛОГИЧЕСКИХ ХАРАКТЕРИСТИК СЕРДЦА | 2011 |
|
RU2489083C2 |
| СПОСОБ НЕИНВАЗИВНОГО ОПРЕДЕЛЕНИЯ ЭЛЕКТРОФИЗИОЛОГИЧЕСКИХ ХАРАКТЕРИСТИК СЕРДЦА | 2016 |
|
RU2615286C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ЭЛЕКТРИЧЕСКОЙ АКТИВНОСТИ СЕРДЦА | 2007 |
|
RU2360597C2 |
| СПОСОБ ОБРАБОТКИ ЭЛЕКТРОКАРДИОСИГНАЛА ДЛЯ ДИАГНОСТИКИ ИНФАРКТА МИОКАРДА | 2008 |
|
RU2383295C1 |
| ЭЛЕКТРОКАРДИОГРАФ С ИЗМЕРЕНИЕМ КООРДИНАТ И ПАРАМЕТРОВ ИСТОЧНИКА ЭЛЕКТРИЧЕСКОЙ АКТИВНОСТИ СЕРДЦА | 2010 |
|
RU2448643C2 |
| СПОСОБ ПОВЫШЕНИЯ ТОЧНОСТИ ПРИ ИЗМЕРЕНИИ КООРДИНАТ СИГНАЛОВ МИОКАРДА И УСТРОЙСТВО ЕГО РЕАЛИЗАЦИИ | 2012 |
|
RU2535439C2 |
| СПОСОБ НЕЙРОСЕТЕВОГО АНАЛИЗА СОСТОЯНИЯ СЕРДЦА | 2011 |
|
RU2461877C1 |
| СПОСОБ ВЫДЕЛЕНИЯ НАЧАЛА КАРДИОЦИКЛА | 2007 |
|
RU2359606C2 |



Изобретение относится к медицине, в частности к кардиологии, и может быть использовано как электрокардиографический способ диагностики состояния сердца. Устанавливают электроды, регистрируют электрокардиосигналы. Определяют антропометрические параметры торса, определяют координаты электродов. Проводят интерполяцию потенциалов на поверхности торса. Рассчитывают распределения потенциала и его нормальной производной на поверхности вспомогательного внутреннего эллиптического цилиндра. Определяют пространственные распределения электрической активности сердца, суммарного по всему кардиоциклу и по интервалу Р-зубца. Вычисляют координаты центра модели эпикарда пациента и центра модели предсердий пациента. Проводят реконструкцию модели эпикарда пациента путем аффинного преобразования координат поверхности эталонной модели эпикарда. Проводят реконструкцию эквивалентного электрического генератора сердца (ЭЭГС) поверхностного типа. Получают оценку коэффициента регуляризации для временных отсчетов кардиоцикла. Осуществляют реконструкцию ЭЭГС дипольного типа. Проводят визуализацию изменяющихся во времени в течение кардиоцикла картин распределения электрического потенциала на поверхности эпикарда, а также картин изменения координат и вектора дипольного момента ЭЭГС дипольного типа. Способ позволяет повысить достоверность диагностики состояния сердца. 16 ил.
Способ неинвазиного определения электрофизиологических характеристик сердца, заключающийся в том, что осуществляют регистрацию электрокардиосигналов (ЭКС), предварительную обработку ЭКС и выделение временных отсчетов элементов кардиоцикла, определение антропометрических параметров торса пациента, отображение электрофизиологических характеристик сердца, отличающийся тем, что дополнительно осуществляют:
- установку электродов в количестве не менее 30, расположенных по поперечному сечению торса в 4 ряда;
- определение координат х и у электродов путем:
- измерения длины l контура поперечного сечения торса с помощью измерительной ленты;
- решения трансцендентного уравнения 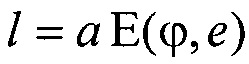 относительно угла ϕ, где
относительно угла ϕ, где 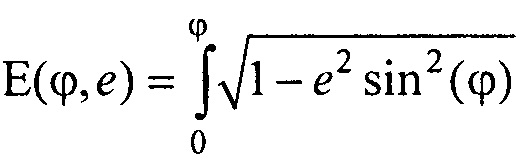 - нормальный эллиптический интеграл Лежандра второго рода;
- нормальный эллиптический интеграл Лежандра второго рода; 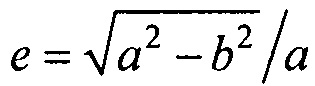 - эксцентриситет поперечного сечения торса, а и b - антропометрические параметры торса пациента; ϕ - угол между прямой, соединяющей подмышечные впадины, и направлением на текущий электрод,
- эксцентриситет поперечного сечения торса, а и b - антропометрические параметры торса пациента; ϕ - угол между прямой, соединяющей подмышечные впадины, и направлением на текущий электрод,
- определения координат х и у электродов по формулам х=r sin(ϕ); у=-r соs(ϕ), где r - расстояние от центра поперечного сечения торса до электрода, определяется по формуле 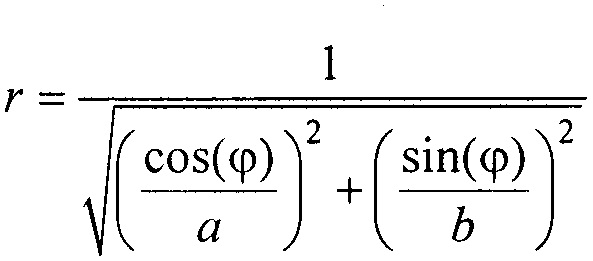 ;
;
- интерполяцию потенциалов φ на поверхности торса по формуле
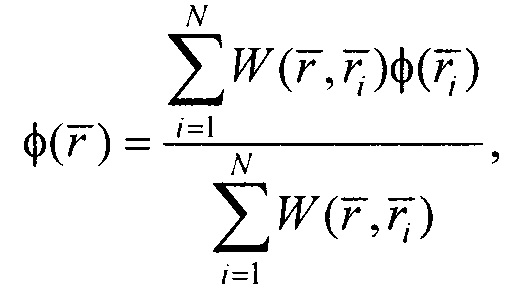
где  - весовая функция по Шепарду,
- весовая функция по Шепарду, 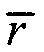 - радиус-вектор пространственного положения текущей точки интерполяции,
- радиус-вектор пространственного положения текущей точки интерполяции,  - искомое значение потенциала в этой точке,
- искомое значение потенциала в этой точке, 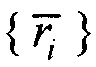 - множество точек поверхности с известными значениями потенциалов
- множество точек поверхности с известными значениями потенциалов 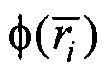 , R - радиус сферы с центром в точке
, R - радиус сферы с центром в точке 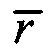 , ограничивающей число точек N, используемых для интерполяции;
, ограничивающей число точек N, используемых для интерполяции;
- реконструкцию модели эпикарда путем:
- построения поверхности вспомогательного внутреннего эллиптического цилиндра, расположенного внутри торса и окружающего эпикард, по формуле
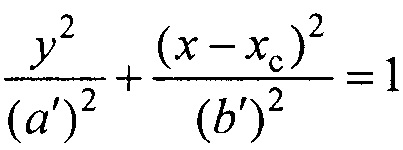 ,
,
где 2а'=DH+8 см; 2b'=DH+4 см; DH=12 см - размер эпикарда; ус=b-b'-Δу, b - полуось поперечного сечения торса в направлении от спины к груди; Δу=2 см - расстояние между торсом и внутренним цилиндром в направлении от спины к груди,
- расчета распределения потенциала φ и его нормальной производной 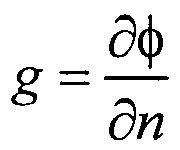 на поверхности внутреннего эллиптического цилиндра для временных отсчетов от начала Р-зубца до конца Т-зубца кардиоцикла путем решения итерационным методом Зейделя системы линейных матричных уравнений:
на поверхности внутреннего эллиптического цилиндра для временных отсчетов от начала Р-зубца до конца Т-зубца кардиоцикла путем решения итерационным методом Зейделя системы линейных матричных уравнений:
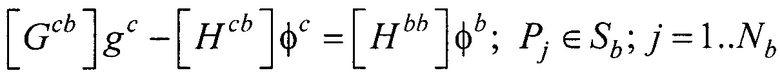 ;
;
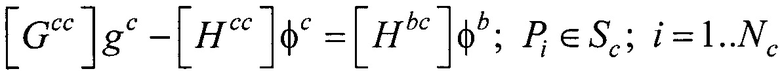 ;
;
где Pj - точка на поверхности торса Sb; Pi - точка на поверхности внутреннего эллиптического цилиндра Sc; 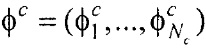 ,
, 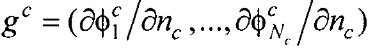 - векторы потенциалов поверхности внутреннего эллиптического цилиндра и производных потенциалов по направлению нормали к поверхности внутреннего эллиптического цилиндра, при этом нормаль берется внешняя по отношению к области между торсом и внутренним цилиндром;
- векторы потенциалов поверхности внутреннего эллиптического цилиндра и производных потенциалов по направлению нормали к поверхности внутреннего эллиптического цилиндра, при этом нормаль берется внешняя по отношению к области между торсом и внутренним цилиндром;  - вектор потенциалов на поверхности торса;
- вектор потенциалов на поверхности торса; 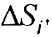 ,
,  - площади элементов поверхности внутреннего эллиптического цилиндра и торса соответственно;
- площади элементов поверхности внутреннего эллиптического цилиндра и торса соответственно; 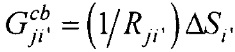 ;
;  ;
; 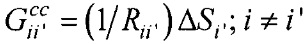 ;
; 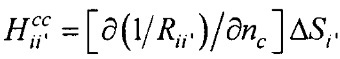 ; i≠i';
; i≠i'; 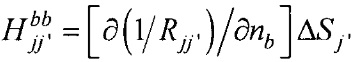 ; j≠j';
; j≠j'; 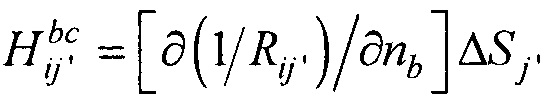 ; Rji=|PjPi| - элементы матриц, входящих в систему линейных матричных уравнений,
; Rji=|PjPi| - элементы матриц, входящих в систему линейных матричных уравнений,
- определения пространственного распределения электрической активности сердца, суммарного по всему кардиоциклу Ψ0(z,  ) и по интервалу Р-зубца Ψat(z,
) и по интервалу Р-зубца Ψat(z,  ) с использованием формул
) с использованием формул
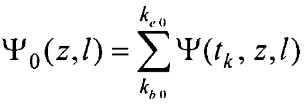 ,
, 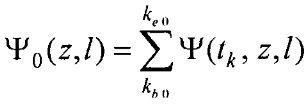 ,
,
где 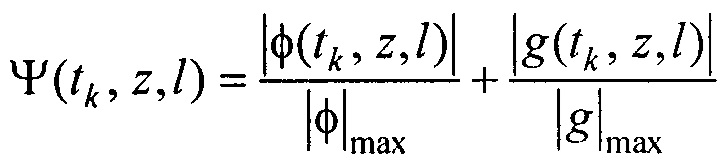 , kb0, kе0, kе аt - номера временных отсчетов кардиоцикла, соответствующих началу Р-зубца, окончанию Т-зубца и окончанию Р-зубца,
, kb0, kе0, kе аt - номера временных отсчетов кардиоцикла, соответствующих началу Р-зубца, окончанию Т-зубца и окончанию Р-зубца,
- определения координат центра модели эпикарда пациента xce, yce, zce и центра модели предсердий пациента xc at, yc at, zc at, по распределениям Ψ0(z,  ) и Ψat(z,
) и Ψat(z,  ) соответственно по формулам:
) соответственно по формулам:
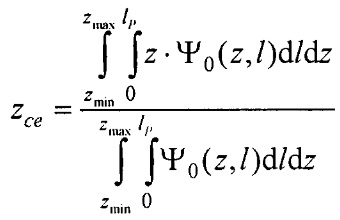 ,
, 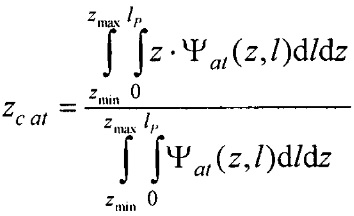 ,
,
xсе=rх еcos(ϕx е); yсе=rу еsin(ϕy е)+yс,
xс at=rх atcos(ϕx at); yс аt=rу at sin(ϕy аt)+yс,
где zmin=zmin row - w/2; zmax=zmax row+w/2; zmin row - вертикальная координата нижнего ряда электродов; zmax row - вертикальная координата верхнего ряда электродов; w - расстояние между соседними рядами электродов;  p=а'Е(2π,е) - периметр внутреннего цилиндра, ϕх е, ϕу е ϕх at и ϕу at - решения трансцендентных уравнений
p=а'Е(2π,е) - периметр внутреннего цилиндра, ϕх е, ϕу е ϕх at и ϕу at - решения трансцендентных уравнений  се х=а'Е(ϕx е, е),
се х=а'Е(ϕx е, е),  се у=а'Е(ϕу е, е),
се у=а'Е(ϕу е, е), 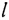 с аt х=а'Е(ϕх аt, е),
с аt х=а'Е(ϕх аt, е), 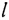 с аt у=а'Е(ϕу аt, e),
с аt у=а'Е(ϕу аt, e), 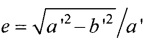 ,
,
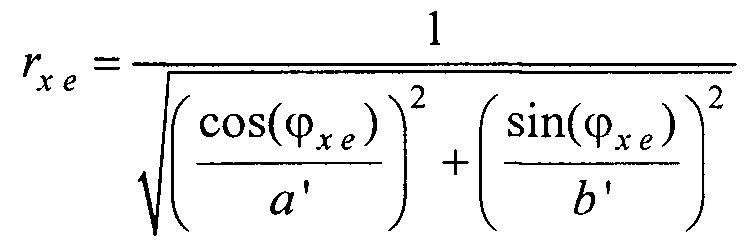 ,
, 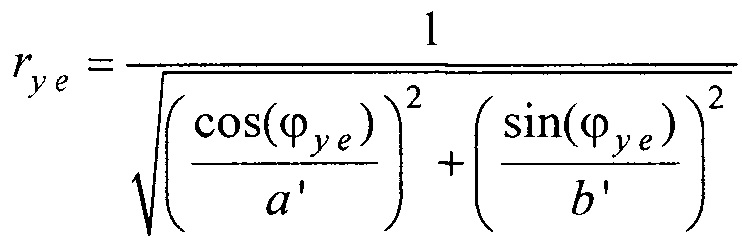 ,
,
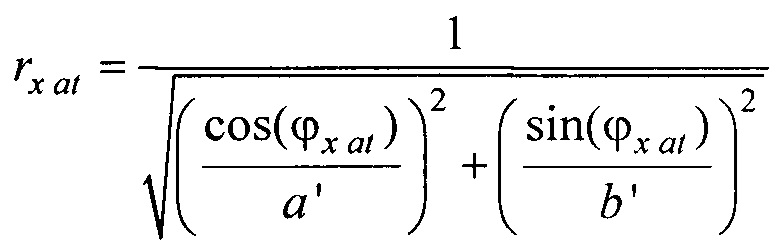 ,
, 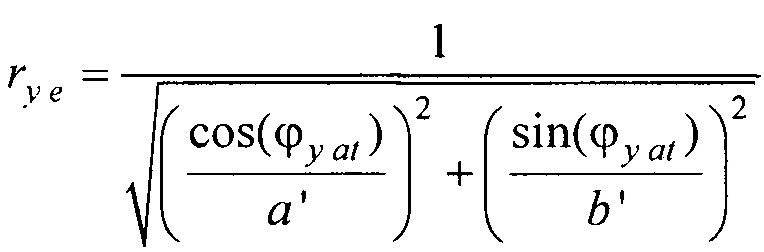 ,
,
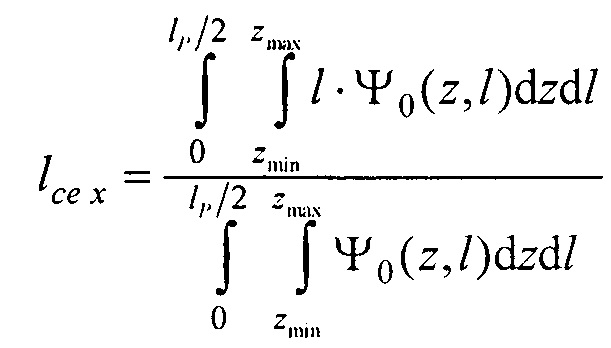 ;
; 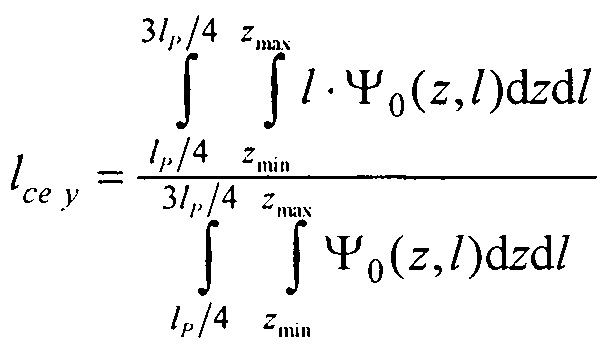 ,
,
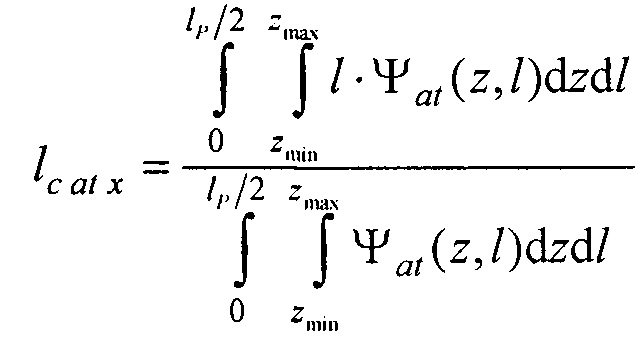 ;
; 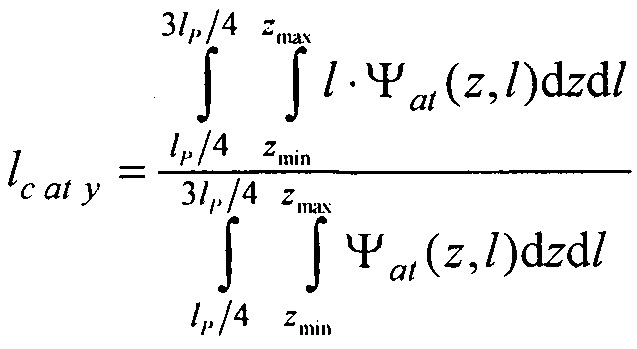 .
.
- определения на эталонной модели эпикарда координат центра эталонной модели эпикарда xM e, yM e, zM e и координат центра эталонной модели предсердий xМ аt, yМ at, zM at, по формулам
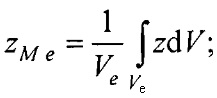
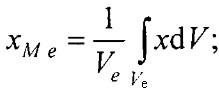
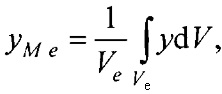
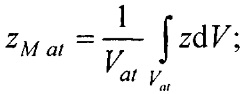
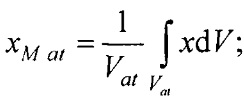
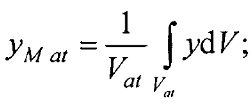
- аффинного преобразования (перемещения, масштабирования и поворота) координат эталонной модели эпикарда до совмещения координат центра эпикарда СМе(хМе, yMе, zMе) и центра предсердий CM at(xM at, yM at, zM at) с рассчитанными соответствующими координатами центра эпикарда пациента Се(хсе, усе, zce) и центра предсердий пациента Саt (хс at, ус at, zc at), по формуле
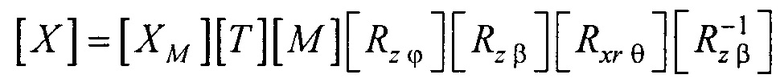 ,
,
где [XM] - координатная матрица для точек поверхности эталонной модели эпикарда; [T] - матрица переноса центра эпикарда эталонной модели в центр модели эпикарда пациента; [М] - матрица масштабирования, обеспечивающая перевод расстояния |СМеСМ аt| между опорными точками в эталонной модели эпикарда в расстояние |СеСat| между опорными точками в модели эпикарда пациента; [Rz ϕ] - матрица поворота вокруг оси z на угол ϕ0 для совмещения проекций единичных векторов 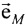 и
и 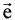 на плоскость XOY; [Rz β] - матрица поворота вокруг оси z на угол β для совмещения вектора
на плоскость XOY; [Rz β] - матрица поворота вокруг оси z на угол β для совмещения вектора 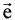 с плоскостью ZOX; [Rxr θ] - матрица поворота вокруг нормали к плоскости ZO
с плоскостью ZOX; [Rxr θ] - матрица поворота вокруг нормали к плоскости ZO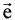 на угол θ для совмещения
на угол θ для совмещения 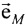 и
и 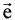 ;
; 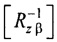 - матрица обратного поворота вокруг оси z на угол (-β);
- матрица обратного поворота вокруг оси z на угол (-β); 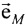 - единичный вектор, направленный из точки СМ е в точку СМ аt;
- единичный вектор, направленный из точки СМ е в точку СМ аt; 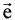 - единичный вектор, направленный из точки Се в точку Саt; cos(θ)=е2еМ z + еx(еM xсos(ϕ0)-еM y sin(ϕ0))+еy(еM xsin(ϕ0)+еM усоs(ϕ0)); cos(ϕ0)=eM xex+eM yey; cos(β)=ex; sin(β)=ey;
- единичный вектор, направленный из точки Се в точку Саt; cos(θ)=е2еМ z + еx(еM xсos(ϕ0)-еM y sin(ϕ0))+еy(еM xsin(ϕ0)+еM усоs(ϕ0)); cos(ϕ0)=eM xex+eM yey; cos(β)=ex; sin(β)=ey;
- реконструкцию эквивалентного электрического генератора сердца (ЭЭГС) поверхностного типа путем:
- расчета распределения потенциала и его нормальной производной на поверхности реконструированной модели эпикарда пациента для временных отсчетов кардиоцикла от начала Р-зубца до конца Т-зубца итерационным методом Зейделя по формулам:
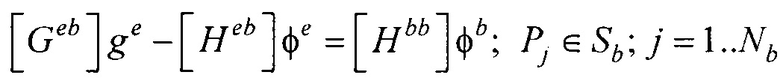 ;
;
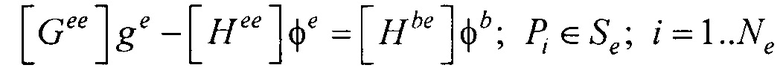 ;
;
где Pj - точка на поверхности торса Sb; Pi - точка на поверхности модели эпикарда Se;  ,
, 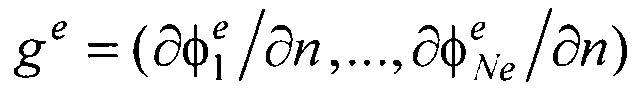 - векторы потенциалов поверхности модели эпикарда и производных потенциалов по направлению нормали к поверхности модели эпикарда пациента;
- векторы потенциалов поверхности модели эпикарда и производных потенциалов по направлению нормали к поверхности модели эпикарда пациента;
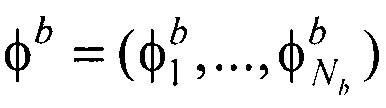 - вектор потенциалов на поверхности торса;
- вектор потенциалов на поверхности торса;
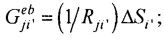
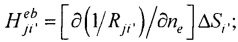
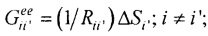
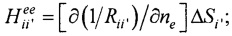 i≠i';
i≠i'; 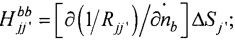 j≠j';
j≠j';  Rji=|PjPi| - элементы матриц, входящих в систему линейных матричных уравнений,
Rji=|PjPi| - элементы матриц, входящих в систему линейных матричных уравнений,
- контроля сходимости итерационного процесса при расчете распределения потенциала на эпикарде и точности аппроксимации потенциалов на торсе для m-й итерации по формуле
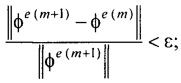
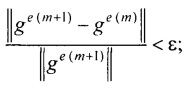
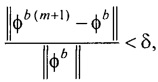
где ε и δ - малые положительные безразмерные величины;



- реконструкцию ЭЭГС дипольного типа путем:
- получения для всех временных отсчетов кардиоцикла tk(k∈(kb0..ke0)) предварительной оценки массива параметров ЭЭГС s0k=(xs0k, ys0k, zs0k, Мх0k, Му0k, Mz0k), где (xs, ys, zs) - координаты ЭЭГС, (Мх, Му, Мz) - проекции вектора дипольного момента ЭЭГС  , путем поиска минимума функционала
, путем поиска минимума функционала 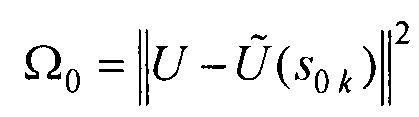 , где
, где  ; Un - ЭКС, снимаемый с n-го электрода;
; Un - ЭКС, снимаемый с n-го электрода;  ; Un s - сигнал дипольного ЭЭГС с параметрами s0 k, рассчитанный для n-го электрода;
; Un s - сигнал дипольного ЭЭГС с параметрами s0 k, рассчитанный для n-го электрода;
- получения оценки коэффициента регуляризации αk для каждого момента времени tk по формуле
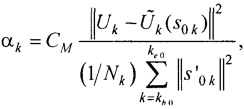
где СM - масштабный коэффициент регуляризации СM ∈ (0,5; 1,5); 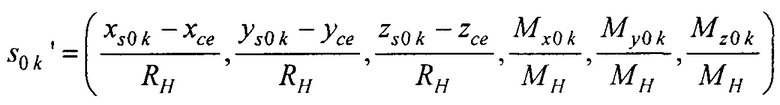 - нормированный массив оценок параметров ЭЭГС; (xce, yce, zce) - координаты центра модели эпикарда пациента; RH
- нормированный массив оценок параметров ЭЭГС; (xce, yce, zce) - координаты центра модели эпикарда пациента; RH 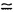 6 см - усредненный радиус эпикарда;
6 см - усредненный радиус эпикарда; 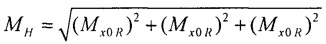 , (Мх0R, Му0R, Мz0R) - соответственно модуль и проекции вектора дипольного момента ЭЭГС дипольного типа для временного отсчета максимума R-зубца кардиоцикла;
, (Мх0R, Му0R, Мz0R) - соответственно модуль и проекции вектора дипольного момента ЭЭГС дипольного типа для временного отсчета максимума R-зубца кардиоцикла;
- поиска параметров ЭЭГС дипольного типа sk=(xs k, ys k, zs k, Mx k, My k, Mz k) для каждого момента времени tk путем минимизации функционала
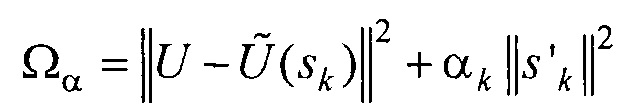
где 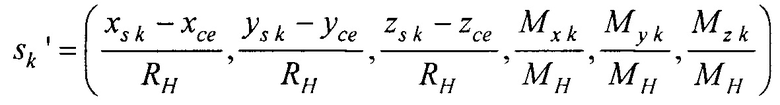 - нормированный массив параметров ЭЭГС дипольного типа;
- нормированный массив параметров ЭЭГС дипольного типа;
- контроля результатов поиска параметров ЭЭГС дипольного типа путем проверки сходимости параметров ЭЭГС и близости массива отсчетов ЭКС для ЭЭГС дипольного типа к массиву отсчетов измеренных ЭКС по формулам:
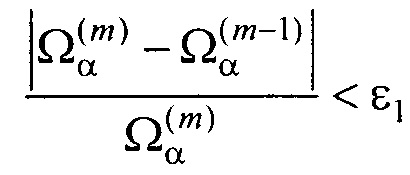 ;
; 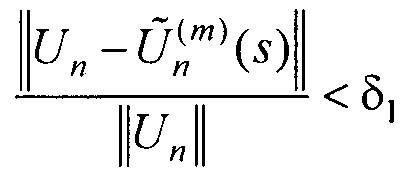 ,
,
где m - номер итерации в процессе поиска минимума функционала Ωα; ε1 и δ1 - малые положительные безразмерные величины.
| СПОСОБ ОПРЕДЕЛЕНИЯ ЭЛЕКТРИЧЕСКОЙ АКТИВНОСТИ СЕРДЦА | 2007 |
|
RU2360597C2 |
| СПОСОБ НЕИНВАЗИВНОГО ОПРЕДЕЛЕНИЯ ЭЛЕКТРОФИЗИОЛОГИЧЕСКИХ ХАРАКТЕРИСТИК СЕРДЦА | 2011 |
|
RU2489083C2 |
| БОДИН О.Н., Построение компьютерной модели торса и сердца пациента в компьютерной диагностической системе "КАРДИОВИД", Приборы и системы | |||
| управление, контроль, диагностика, Издательство: Издательство "Научтехлитиздат", 2015, cc | |||
| Прибор для равномерного смешения зерна и одновременного отбирания нескольких одинаковых по объему проб | 1921 |
|
SU23A1 |
| РЯБЧИКОВ Р.В., Cовершенствование систем обработки кардиографической информации для диагностики инфаркта миокарда, Диссертация на соискание ученой степени кандидата технических наук, Пенза, 2014, cc | |||
| Способ образования коричневых окрасок на волокне из кашу кубической и подобных производных кашевого ряда | 1922 |
|
SU32A1 |
Авторы
Даты
2018-04-18—Публикация
2017-07-05—Подача