Изобретение относится к отрасли машиностроения, в частности к резьбам, как составному элементу разъемных и не разъемных резьбовых соединений.
В зависимости от формы сечения резьбы, которая определяет профиль витка резьбы, резьба называется прямоугольной, треугольной, трапецеидальной, пилообразной, круглой и т.п.
Стандартом регламентирован радиус округления резьбы на внутреннем диаметре винта, который находится в пределах одной шестой части от высоты выступа профиля и существенно влияет на усталостную прочность резьбового соединения.
Основные размеры профиля резьбы определяют в долях от шага. Поэтому с изменением шага резьбы изменяются и размеры профиля по геометрическому подобию.
Стандартом предусмотрены резьбы с различными шагами при одинаковом наружном диаметре резьбы.
Недостатком указанных резьб является наличие концентраторов напряжений во впадинах резьбы, поэтому для их уменьшения вершина и впадина профиля закругляются [1].
Вопрос повышения усталостной прочности и долговечности путем создания переменной площади контактной поверхности между витками резьбы болта и гайки решается в изобретении резьбового соединения тем, что резьбу на болте выполняют со срезом на конус при радиусе впадин резьбы болта, равном 0,144-0,18. Такое резьбовое соединение довольно сложно в изготовлении, но проблема снижения концентраторов напряжения в нем не решена [2].
Наиболее близкой к заявленной является резьба круглая. Профиль этой резьбы образуется дугами круга, связанными между собой участками прямых линий, которые образуют угол 30°. Вследствие больших радиусов закруглений круглые резьбы имеют уменьшенную концентрацию напряжений и используются при значительных переменных и ударных нагрузках, а также в случаях частого завинчивания и отвинчивания в условиях воздействия абразивной среды [3].
Недостатком круглой резьбы является то, что контакт в резьбовом соединении винт-гайка рабочих поверхностей происходит по прямолинейному участку под углом 30°, а наличие больших радиусов закруглений r=0,2385s не решает должным образом проблему снижения до минимума концентрации напряжений.
В основу настоящего изобретения поставлена задача посредством увеличения площади контакта сопрягаемых поверхностей резьбового соединения создать профиль резьбы без концентраторов напряжений.
Поставленная задача решается тем, что резьба эллиптическая содержит чередующиеся выступы и впадины на поверхности тела вращения, расположенные по винтовой линии, образованной шагом и углом подъема. Новым в изобретении является то, что выступ и впадина образованы в осевом сечении сопрягающимися по среднему диаметру резьбы двумя полуокружностями, радиусы которых составляют одну четвертую часть осевого шага резьбы, центры их полуокружностей смещены относительно друг друга на величину полушага резьбы, а в нормальном сечении выступы и впадины образованы сопрягающимися полуэллипсами с радиально расположенными большими полуосями, равными радиусу упомянутой полуокружности, тангенс угла подъема винтовой линии в осевом сечении определяется отношением осевого шага к длине окружности среднего диаметра резьбы, размер малой полуоси эллипса равен произведению радиуса упомянутой полуокружности на косинус угла подъема винтовой линии.
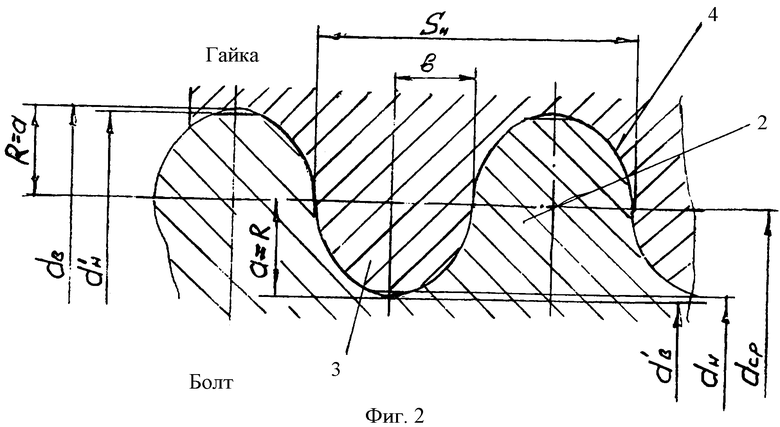
Профиль эллиптической резьбы поясняется чертежом. На фиг.1 изображена резьбовая пара винт-гайка в осевом сечении профиля; на фиг.2 - то же, но в нормальном сечении профиля отражающего его эллиптичность.
Резьба эллиптическая содержит чередующиеся на поверхности тела вращения 1, расположенные но винтовой линии выступы 2 и впадины 3. Выступ 2 включает элементы - головку 4 и ножку 5, находящиеся соответственно над средним диаметром резьбы dcp и ниже.
Эллиптический профиль винтового выступа 2 характеризуется формами в зависимости от положения секущих плоскостей. В нормальном сечении витка (фиг.2), когда секущая плоскость проходит под углом наклона к продольной оси тела вращения, мы имеем в сечении два полуэллипса, сопрягающихся по среднему диаметру dcp резьбы, при этом один полуэллипс образует головку 4 выступа 2 профиля резьбы, а другой со смещением - ножку 5 и впадину 3. Центр пересечения осей эллипса находится на среднем диаметре резьбы. Малая полуось «b» равна одной четвертой шага в нормальном сечении Sн, именуемым в дальнейшем нормальный шаг. Большая полуось эллипса «а» равна радиусу R полуокружностей, определяющих профиль резьбы в осевом сечении плоскостью, проходящей через продольную ось тела вращения (фиг.1).
В сечении витка резьбы плоскостью, проходящей через ось тела вращения, так называемое осевое сечение, мы имеем в сечении две полуокружности. Эти полуокружности сопрягаются по среднему диаметру резьбы, при этом одна полуокружность образует головку 4 и выступ 2, а другая - впадину 3 с радиусами R, равными одной четвертой длины осевого шага So резьбы. Центры выступов смещены но среднему диаметру резьбы относительно центров впадин на величину полушага резьбы. Тангенс угла подъема винтовой линии в осевом сечении определяется отношением осевого шага So к длине окружности среднего диаметра резьбы π·dсp. Размер малой полуоси эллипса «b» равен произведению радиуса R полуокружности на косинус угла подъема винтовой линии, т.е.: Cosα=b/а=b/R отсюда b=R·Cosα.
Если взять пруток эллиптического профиля и рассечь плоскостью под определенным углом по большой оси эллипса, то в сечении получится окружность радиусом R, равным длине большой полуоси эллипса «а». В то же время, идя от обратного, если рассечем резьбу под определенным углом в нормальном сечении мы получим тот же результат, когда большая полуось «а» эллипса будет равна радиусу R полуокружности, а малая полуось «b» эллипса будет равна одной четверти осевого шага So, то в этом случае эллиптический профиль резьбы преобразуется в круговой.
В связи с тем, что образующей фигурой для этой резьбы является в осевом сечении полуокружность, а в нормальном - полуэллипс, сопрягаемые по среднему диаметру, то угол профиля резьбы будет равен нулю.
Чтобы изготовить резьбовое соединение с эллиптическим профилем резьбы Андросова - Гребенюка достаточно задаться следующими исходными данными:
So - шаг резьбы в осевом сечении;
dcp - средний диаметр резьбы, определяемый по формуле
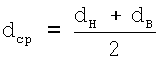
dH - наружный диаметр резьбы гайки;
d'H - внутренний диаметр резьбы болта;
dB - внутренний диаметр резьбы гайки;
d'B - внутренний диаметр резьбы болта.
Угол подъема винтовой линии α в осевом сечении для эллиптический резьбы определяется отношением шага резьбы в осевом сечении к длине окружности по среднему диаметру резьбы и выражается формулой
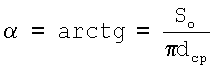 откуда
откуда 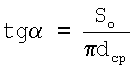
Задавшись шагом резьбы в осевом сечении So и исходя из определения, что So=4R, то tgα определится по формуле 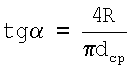
Эллиптическая резьба из-за отсутствия прямолинейного участка на боковой поверхности профиля имеет большую площадь контакта сопрягаемых поверхностей винта и гайки и соответственно обеспечивает большую несущую нагрузку.
Другим преимуществом эллиптической резьбы является то, что она значительно меньше изнашивается при частом завинчивании и отвинчивании, поэтому такая резьба найдет широкое применение при работе в условиях воздействия абразивной среды.
Резьба технологически легко выполнима на универсальном оборудовании, а так же методом накатывания.
Источники информации
1. В.А.Добровольский. Детали машин. ГИТЛ УССР Киев - 1954. Стр.132…135; 141, рис.170.
2. Патент РФ №1807755, F16B 29/00, F16B 33/04, 1990.
3. То же, что и п.1. Стр.141, рис.170.
| название | год | авторы | номер документа |
|---|---|---|---|
| РОТОРНЫЙ ПОДШИПНИК КАЧЕНИЯ | 2008 |
|
RU2387892C2 |
| ЗУБЧАТАЯ ПЕРЕДАЧА | 1993 |
|
RU2057267C1 |
| САМОСМАЗЫВАЮЩАЯСЯ ЗУБЧАТАЯ ПЕРЕДАЧА | 2008 |
|
RU2376516C1 |
| ГИДРОМОТОР КИРМАК | 2008 |
|
RU2405968C2 |
| ЧЕРВЯЧНАЯ ЗУБОРЕЗНАЯ ФРЕЗА ГРЕБЕНЮКА | 2009 |
|
RU2429952C2 |
| ГИДРОМАШИНА | 2007 |
|
RU2347122C1 |
| УСТРОЙСТВО ДЛЯ ПОЛУЧЕНИЯ ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ АБРАМОВА В. А. | 2016 |
|
RU2686648C9 |
| Устройство для получения вращательного движения Абрамова Валентина Алексеевича (Абрамова В.А.) | 2016 |
|
RU2654690C9 |
| РЕЗЬБОВОЕ СОЕДИНЕНИЕ БУРИЛЬНЫХ ТРУБ | 2012 |
|
RU2508491C1 |
| КАМЕРНЫЙ ДВИГАТЕЛЬ МАГ | 2008 |
|
RU2396445C2 |
Изобретение относится к резьбовым крепежным элементам. Резьба эллиптическая содержит чередующиеся на цилиндрической поверхности тела вращения выступы и впадины, расположенные по винтовой линии, образованной шагом и углом подъема. Выступ и впадина образованы в осевом сечении сопрягающимися по среднему диаметру резьбы двумя полуокружностями, радиусы которых составляют одну четвертую часть осевого шага резьбы, центры их полуокружностей смещены относительно друг друга на величину полушага резьбы. В нормальном сечении выступы и впадины образованы сопрягающимися полуэллипсами с радиально расположенными большими полуосями, равными радиусу упомянутой полуокружности. Тангенс угла подъема винтовой линии в осевом сечении определяется отношением осевого шага к длине окружности среднего диаметра резьбы. Размер малой полуоси эллипса равен произведению радиуса упомянутой полуокружности на косинус угла подъема винтовой линии. В результате, в резьбе отсутствуют концентраторы напряжений. 2 ил.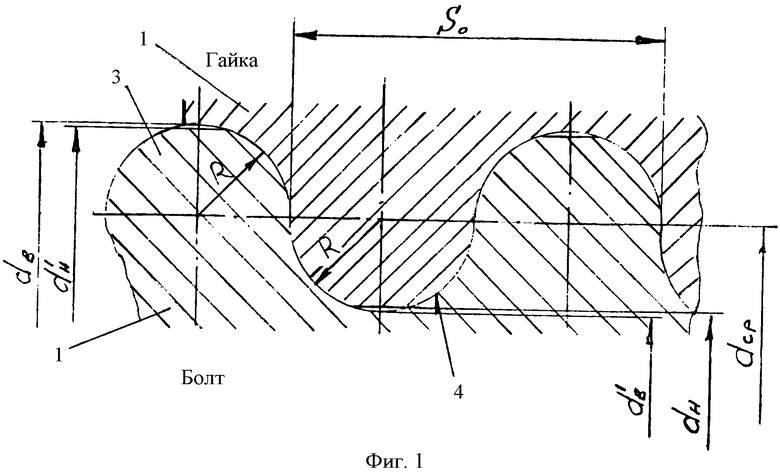
Резьба эллиптическая, содержащая чередующиеся на цилиндрической поверхности тела вращения выступы и впадины, расположенные по винтовой линии, образованной шагом и углом подъема, отличающаяся тем, что выступ и впадина образованы в осевом сечении сопрягающимися по среднему диаметру резьбы двумя полуокружностями, радиусы которых составляют одну четвертую часть осевого шага резьбы, центры их полуокружностей смещены относительно друг друга на величину полушага резьбы, а в нормальном сечении выступы и впадины образованы сопрягающимися полуэллипсами с радиально расположенными большими полуосями, равными радиусу упомянутой полуокружности, тангенс угла подъема винтовой линии в осевом сечении определяется отношением осевого шага к длине окружности среднего диаметра резьбы, размер малой полуоси эллипса равен произведению радиуса упомянутой полуокружности на косинус угла подъема винтовой линии.
| Устройство для защиты конической резьбы | 1987 |
|
SU1530531A1 |
| ПРЕДОХРАНИТЕЛЬНЫЙ КЛАПАН С СЕРВОДЕЙСТВИЕМ | 0 |
|
SU324442A1 |
| Коммутируемый фильтр | 1984 |
|
SU1317651A1 |
| 0 |
|
SU158454A1 |
Авторы
Даты
2010-05-20—Публикация
2007-09-17—Подача