Изобретение относится к методам определения коэффициента диффузии примесных атомов в полупроводнике и позволяет по данным вольт-фарадной характеристики p-n перехода и математической модели процесса диффузии, в результате которого создан p-n переход, определять концентрационные профили введенной в полупроводник примеси. Метод может применяться для неразрушающего контроля концентрационных профилей приборных структур с одним или несколькими р-n переходами, созданными с применением диффузионных процессов, к которым относится также постимплантационный отжиг.
Известен способ определения коэффициента диффузии примеси в субмикронных структурах, основанный на определении концентрационного профиля примеси методом послойного анализа и последующем расчете коэффициента диффузии по известной термодинамической модели, (см. R.Ghez, G.S.Oehlein, Sedwick. Exact description and data fitting of ion-implanted dopant profile evolution during anneling/ //. Appl. Phys. Lett., 45 (8), 1984, pp.881-883). Недостатком такого метода является необходимость послойного удаления материала. Изменение примесного состава по глубине при послойном удалении приводит к изменению скорости травления и, как следствие, - к погрешности в определении толщины снятого слоя. Количественный состав примесных атомов в поверхностном слое также существенно изменяется при травлении за счет сегрегации на границе травитель-полупроводник, что приводит к возникновению погрешности также в определении абсолютного значения концентрации примеси и, как следствие, - к увеличению погрешности в определении коэффициента диффузии. Кроме того, необходимость многократного повторения операций травления и анализа поверхности ведет к увеличению суммарной погрешности за счет накопления ошибок на каждом этапе. Операции послойного анализа достаточно трудоемки, для их проведения требуется дорогостоящее оборудование.
Известен также наиболее близкий к предлагаемому способ определения коэффициента диффузии по концентрационным профилям, рассчитанным из вольт-фарадных характеристик емкости барьера Шотки, изготовленного на поверхности полупроводниковой структуры (см. Ардышев В.М., Ардышев М.В. Активация и распределение кремния, имплантированного в арсенид галлия, при изотермическом радиационном отжиге // ФТП, 1998, том 32, выпуск 10, с.1153). К недостаткам метода следует отнести ограниченность участка профиля концентрации, о котором получается информация и необходимость создания образца-спутника с барьером Шоттки, либо барьера на специально введенном участке рабочей приборной структуры, что не всегда возможно.
Задачей, решаемой при использовании предлагаемого способа, является неразрушающий контроль диффузионных концентрационных профилей, техническим результатом является уменьшение стоимости и трудоемкости контроля технологических процессов и разработки технологии изготовления полупроводниковых приборов с одним или несколькими p-n переходами.
Указанный технический результат достигается предлагаемым способом определения коэффициента диффузии примесных атомов в полупроводнике, который заключается в том, что в слаболегированном полупроводнике при заданных условиях диффузии, имеющих математическую модель процесса, на основе которой определено математическое выражение концентрационного профиля распределения примесных атомов с коэффициентом диффузии в качестве аргумента, создают p-n переход, при двух значениях обратного напряжения на р-n переходе Um и Un, причем Um больше Un, измеряют значения его емкости, определяют параметр модуляции ширины области пространственного заряда (ОПЗ) p-n перехода n по формуле:
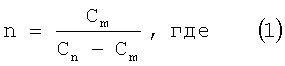
Cm и Cn - измеренные емкости p-n перехода для значений Um и Un соответственно,
также производят расчет численной зависимости того же параметра модуляции n, определяемого в данном случае как
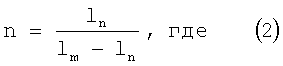
lm, ln - ширина ОПЗ p-n перехода при напряжении на p-n переходе Um и Un соответственно, от параметра диффузии Dt, являющегося произведением коэффициента диффузии D на продолжительность процесса диффузии t, решением системы двух уравнений:
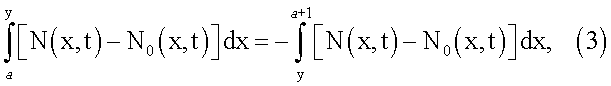
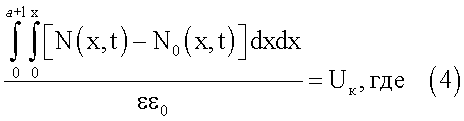
x - координата вглубь образца в направлении диффузии;
N(x,t) - профиль распределения концентрации примеси после диффузии;
N0(x,t) - профиль распределения концентрации примеси исходного кристалла;
a - координата границы области пространственного заряда, при условии, что начало отсчета совпадает с границей раздела образец-среда;
y - глубина залегания p-n перехода;
е - элементарный заряд;
ε - диэлектрическая проницаемость области пространственного заряда;
ε0 - электрическая постоянная;
Uк=U0+UB - напряжение на p-n переходе, равное сумме контактной разности потенциалов (U0), которая является напряжением отсечки (напряжение отсечки соответствует напряжению начала резкого возрастания тока) на прямой ветви вольт-амперной характеристики (ВАХ) p-n перехода, и приложенного напряжения (UB), после подстановки в них выражений N0(x,t) для выбранного полупроводника и N(x,t) для выбранных условий диффузии и затем по значению параметра модуляции n, полученному из емкостных измерений, из рассчитанной зависимости параметра модуляции n от параметра диффузии Dt, определяют значение параметра диффузии Dt, соответствующее эксперименту, из которого делением на продолжительность процесса диффузии t определяют коэффициент диффузии D. В частном случае, с целью достижения наибольшей точности определения коэффициента диффузии, значения напряжений на p-n переходе Um и Un, при которых измеряют значения емкости сформированного p-n перехода, выбирают на краях участка вольт-фарадной характеристики p-n перехода с наибольшей крутизной. Также частными случаями выполнения способа являются следующие различные условия диффузии для создания p-n перехода, имеющие математические модели и выражения для концентрационного профиля распределения примесных атомов с коэффициентом диффузии в качестве аргумента:
- диффузия из неограниченного источника (загонка), когда

где N0 - концентрация примеси на поверхности;
- диффузия из ограниченного источника (разгонка), когда
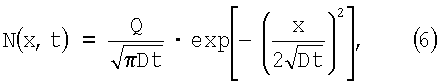
где Q - доза легирования;
- диффузия из ограниченного источника, созданного ионной имплантацией, когда
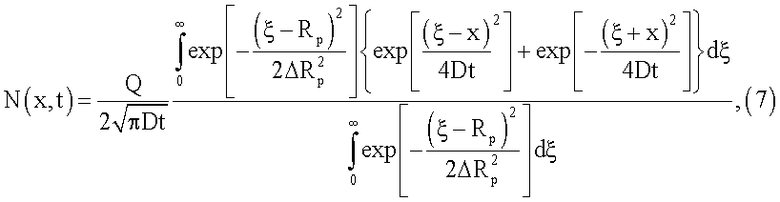
где
Q - доза имплантации;
Rp - средний проецированный пробег имплантированных атомов;
ΔRp - дисперсия пробега;
ξ - переменная интегрирования.
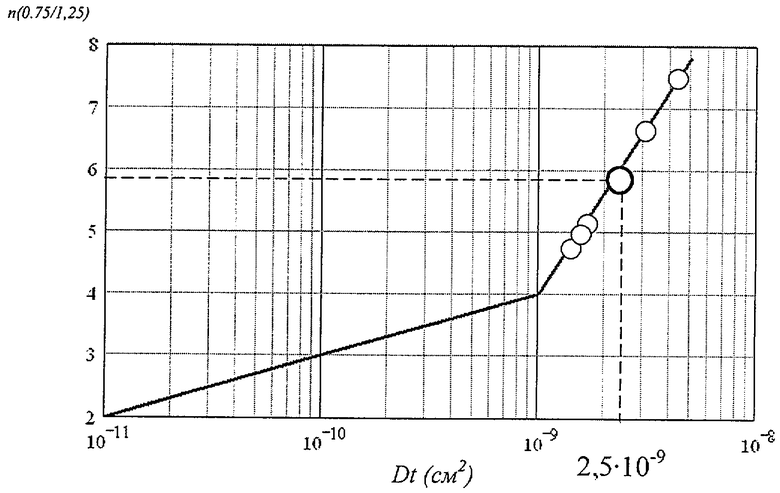
Предлагаемое техническое решение поясняется чертежом, на котором графически (сплошная линия) представлена зависимость параметра модуляции ширины ОПЗ p-n перехода для значений обратного напряжения на p-n переходе 0,75 и 1,25 В n(0.75/1,25) от параметра диффузии Dt.
Если в исходный полупроводниковый образец производится диффузионное введение примесных атомов, изменяющих тип проводимости полупроводника, то в глубине полупроводника в точке концентрационного профиля распределения примесных атомов, в которой концентрации диффундирующих и исходных примесных атомов равны, возникает p-n переход. Ширина ОПЗ p-n перехода при фиксированном напряжении смещения l зависит от сформированного при диффузии концентрационного профиля и для заданного напряжения на p-n переходе она определяется из решения системы уравнений (3)-(4). Уравнение (3) получено из условия равенства объемных зарядов в обеих областях полупроводника, прилегающих к р-n переходу. Уравнение (4) - решение уравнения Пуассона для ОПЗ, созданного контактом сильно- и слаболегированного полупроводников, который практически всегда образуется при легировании методами диффузии.
При известных функциях N(x,t) и N0(x,t) решение системы уравнений (3)-(4) позволяет получить зависимость параметра модуляции n, определяемого выражением (2), от параметра диффузии Dt. Для удобства расчетов выбирают диапазон значений Dt, например, исходя из известной продолжительности процесса диффузии t и выбранного на основе известных из литературных источников для аналогичных или близких условий диффузии, значения D.
Следует отметить, что введение параметра модуляции n позволяет произвести нормировку, исключающую ошибку, связанную с необходимостью знания точных значений диэлектрической проницаемости ОПЗ и площади измеряемой структуры, которая в большинстве практических случаев, например при применении прижимных и ртутных зондов к легированным областям, является неопределенной. Влияние нормировки и идентичность значений n, определяемых выражениями (1) и (2), следует из преобразований
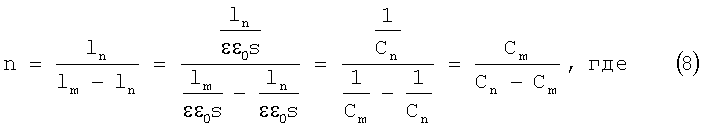
s - площадь измеряемого p-n перехода.
Подстановкой фиксированного значения параметра Dt из выбранного диапазона в выражение N(x,t) определяется глубина залегания p-n перехода y. Из системы уравнений (3)-(4), в которую подставлена функция N(x,t) и N0(x,t), которая как правило является постоянной величиной, определяемой концентрацией примеси в исходном кристалле, рассчитывается ширина ОПЗ p-n перехода для выбранных напряжений на p-n переходе lm, ln и по формуле (2) вычисляется параметр модуляции n. Аналогичные вычисления производятся для остальных выбранных значений параметра Dt. Таким образом получается зависимость n от Dt, которая может быть представлена графически. Из этой зависимости по значению n, рассчитанному по формуле (1) на основе результатов, полученных из измерений емкости на экспериментальном образце, определяют значение параметра Dt, соответствующее эксперименту. Значение коэффициента диффузии D получается делением параметра Dt на известную продолжительность процесса t.
Предлагаемый способ применялся для определения коэффициента диффузии атомов бора, имплантированных в кремний n-типа при последующем отжиге. Функция, задающая зависимость концентрации имплантированной примеси N(x,t) от координаты x и времени отжига t для случая полностью отражающей поверхности кристалла и отсутствия концентрационной зависимости коэффициента диффузии имеет вид (7) (см. Справочник по точным решениям уравнений тепло- и массопереноса. А.Д.Полянин, А.В.Вязьмин, А.И.Журов, Д.А.Казенин. М., Факториал, 1998, 229 с.). Как видно из выражения (7), при известных параметрах имплантации концентрация примеси в любой точке кристалла, а следовательно, и ширина ОПЗ при различных напряжениях смещения, определяются только параметром диффузии Dt.
Далее, подставляя выражение (7) в систему уравнений (3)-(4) определяем ширину ОПЗ p-n перехода lm и ln для выбранных обратных напряжений на p-n переходе 0,75 и 1,25 В и по формуле (2) вычисляем параметр модуляции n(0,75/1,25) для выбранных значений параметра диффузии Dt.
На чертеже сплошной линией представлена рассчитанная таким образом графическая зависимость параметра n(0.75/1,25) от Dt для атомов бора, имплантированных в кремний в условиях эксперимента: энергия 70 кэВ и доза 2·1013 см-2 после отжига в атмосфере азота при температуре 1050°С в течение 8 часов. Средние значения проекции пробега и нормальное отклонение проекции пробега при данной энергии имплантации для бора соответственно равны 283 и 76 нм (см. Готра З.Ю. Технология микроэлектронных устройств. М.: Радио и связь, 1991, 528 с.). Исходная концентрация примеси n-типа N0(x,f) имеет величину 5·1015 см-3. Расчеты производились по формулам (2), (3) и (4) для диапазона значений параметра Dt от 10-11 см2 до 10-8 см2. Этот диапазон определен на основе продолжительности процесса диффузии 3·104 с (8 часов) и данных по параметру D для температуры 1050°С, представленных в той же работе, диапазон значений которых расширен до 4·10-14 - 10-12 см2/с.
В экспериментах использовались пластины кремния n-типа проводимости, на которых изготавливалась транзисторная структура n++(эмиттер)-p+(база)-n(коллектор)-n+-типа сначала имплантацией и диффузионной разгонкой атомов бора, затем имплантацией и диффузионной разгонкой атомов фосфора в соответствии с последовательностью технологических операций и их режимами, представленными в таблице 1. Из данных таблицы 1 следует, что атомы бора подвергались разгонке и после имплантации бора, и после имплантации фосфора, продолжительность которых в сумме составляет ~8 часов. Омический контакт к обратной стороне пластины создавался имплантацией фосфора и последующим отжигом при температуре значительно ниже, чем на предыдущих стадиях изготовления структуры, поэтому влиянием этой операции на профиль распределения атомов бора можно пренебречь. Легирование ионами Р+ и В+ проводили на установке "Везувий-5". Все термические операции производили в диффузионных печах типа СДОМ-3.
Образцы имели контакты к эмиттеру и коллектору. Зависимость емкости такой структуры от приложенного к p-n переходу напряжения Uk при полярности, соответствующей обратному смещению коллекторного перехода, измерялась цифровым RLC-метром Е7-20 (погрешность измерения емкости ±1%) на частоте 250 кГц. В этом случае измеряется фактически только емкость p+-n перехода, созданного диффундирующими атомами бора, поскольку вклад емкости прямосмещенного последовательно включенного эмиттерного n++-p+ перехода пренебрежимо мал и его влиянием можно пренебречь. Значения Uk определялись в соответствии с выражением (4), куда подставлялось значение контакной разности потенциалов U0=0,75 В, измеренное как напряжение отсечки на прямой ветви ВАХ коллекторного p-n перехода. Таким образом, значения Uk=0,75 и 1,25 В соответствуют приложенному к структуре напряжению UB=0 и 0,5 В. Значения емкости при двух выбранных значениях напряжения Uk для пяти образцов представлены в таблице 2.
Для экспериментального определения глубины залегания p-n-перехода применялись метод окрашивания поверхности полупроводника после формирования шарового шлифа и метод сканирующей контрастной электронной микроскопии при наблюдении плоскости разлома кристалла. По данным метода шарового шлифа глубина залегания составила 3,0 мкм. По данным сканирующей электронной микроскопии - 2,55 мкм.
В таблице 3 представлены результаты расчетов параметра модуляции n(0.75/1,25) для каждого образца, среднее значение nср и наибольшие абсолютное и относительное отклонения от средней величины этого параметра для 5 образцов по данным таблицы 2.
На чертеже проиллюстрировано определение значения параметра Dt по расчетной зависимости n(0.75/1,25) от Dt, где сплошная линия - расчетная зависимость n, О - экспериментальные значения параметра модуляции n из таблицы 3, О - среднее значение параметра модуляции n. Как видно из данных чертежа, среднему значению параметра модуляции n(0.75/1,25)=6 на графической расчетной зависимости соответствует величина параметра диффузии Dt=1.5·10-9 см2.
Исходя из этой величины среднее значение коэффициента диффузии атомов бора, имплантированных в кремний, для температуры отжига 1050°С составляет:
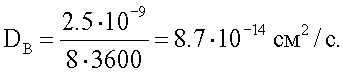
При этом за величину t принята суммарная продолжительность процессов разгонки бора и фосфора при температуре 1050°С.
Расчетная глубина залегания, соответствующая параметру Dt=2.5·10-9 см2 и исходной концентрации примеси N0(x,t)=5·1015 см-3 составила 3,1 мкм, что фактически совпадает со значением, полученным методом сферического шлифа, и на 20% превышает значение, полученное методом электронной микроскопии. Такое отличие находится в пределах ошибки, вносимой неортогональностью плоскостей разлома и поверхности пластины при электронно-микроскопических измерениях.
Коэффициент объемной диффузии бора по вакансиям в кремнии, рассчитанный из соотношения
DB=0,76·ехр(-3,46 эВ/kT), см2/с
для температуры 1050°С составляет 5,15·10-14 см2/с. Несколько большее значение коэффициента диффузии бора в нашем случае можно объяснить специфическим для биполярной технологии эффектом эмиттерного выдавливания базовой области n-p-n транзистора под эмиттером при его формировании путем диффузии фосфора. Таким образом, значения D, определенные по предлагаемому техническому решению, соответствуют экспериментальным данным, полученным методом сферического шлифа и сканирующей электронной микроскопии.
В целом все представленные результаты позволяют сделать вывод о том, что применение разработанного неразрушающего метода позволяет существенно снизить трудоемкость и себестоимость методов контроля концентрационных профилей диодных и транзисторных структур, созданных по диффузионной технологии.
| название | год | авторы | номер документа |
|---|---|---|---|
| Способ изготовления многоплощадочного кремниевого pin-фоточувствительного элемента | 2017 |
|
RU2654998C1 |
| ВАРАКТОР | 1994 |
|
RU2102819C1 |
| ВАРИКАП | 1994 |
|
RU2086045C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ЭЛЕКТРОФИЗИЧЕСКИХ ХАРАКТЕРИСТИК ЛЕГИРОВАННЫХ СЛОЁВ КРЕМНИЕВЫХ ПЛАСТИН | 2022 |
|
RU2785802C1 |
| СПОСОБ ЛЕГИРОВАНИЯ ПОЛУПРОВОДНИКОВЫХ ПЛАСТИН | 1995 |
|
RU2111575C1 |
| ВАРИКАП | 1995 |
|
RU2119698C1 |
| Способ изготовления многоплощадочного быстродействующего кремниевого pin-фоточувствительного элемента | 2017 |
|
RU2654961C1 |
| ВАРАКТОР | 1994 |
|
RU2086044C1 |
| ПОЛУПРОВОДНИКОВЫЙ ПРИБОР | 1996 |
|
RU2139599C1 |
| СПОСОБ СОЗДАНИЯ ОМИЧЕСКИХ КОНТАКТОВ В ТОНКОПЛЕНОЧНЫХ УСТРОЙСТВАХ НА АМОРФНЫХ НЕЛЕГИРОВАННЫХ ПОЛУПРОВОДНИКАХ | 2009 |
|
RU2392688C1 |
Изобретение относится к методам определения коэффициента диффузии примесных атомов в полупроводнике и позволяет по данным вольт-фарадной характеристики p-n перехода и математической модели процесса диффузии, в результате которого создан p-n переход, определять концентрационные профили введенной в полупроводник примеси. Техническим результатом является уменьшение стоимости и трудоемкости контроля технологических процессов и разработки технологии изготовления полупроводниковых приборов с одним или несколькими p-n переходами. Сущность изобретения: способ определения коэффициента диффузии примесных атомов в полупроводнике заключается в том, что в слаболегированном полупроводнике при заданных условиях диффузии, для которых определено математическое выражение концентрационного профиля распределения примесных атомов с коэффициентом диффузии в качестве аргумента, создают p-n переход, при двух значениях обратного напряжения на p-n переходе измеряют значения его емкости, определяют параметр модуляции ширины области пространственного заряда p-n перехода n, также производят расчет численной зависимости того же параметра модуляции от параметра диффузии Dt, являющегося произведением коэффициента диффузии D на продолжительность процесса диффузии t, решением системы уравнений, определяют значение параметра диффузии Dt, соответствующее эксперименту, из которого делением на продолжительность процесса диффузии t определяют коэффициент диффузии D. 4 з.п. ф-лы, 1 ил, 3 табл.
1. Способ определения коэффициента диффузии примесных атомов в полупроводнике, заключающийся в том, что в слаболегированном полупроводнике при заданных условиях диффузии, для которых определено математическое выражение концентрационного профиля распределения примесных атомов с коэффициентом диффузии в качестве аргумента, создают p-n переход, при двух значениях обратного напряжения на p-n переходе Um и Un, причем Um больше Un, измеряют значения его емкости, определяют параметр модуляции ширины области пространственного заряда p-n перехода n по формуле:
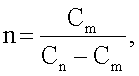
где Cm и Cn - измеренные емкости p-n перехода для значений Um и Un соответственно,
также производят расчет численной зависимости того же параметра модуляции n, определяемого в данном случае как
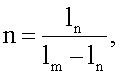
где lm, ln - ширина области пространственного заряда p-n перехода при напряжении смещения Um и Un соответственно,
от параметра диффузии Dt, являющегося произведением коэффициента диффузии D на продолжительность процесса диффузии t, решением системы двух уравнений:
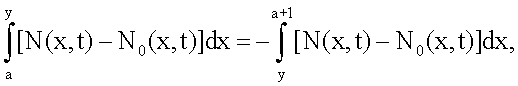
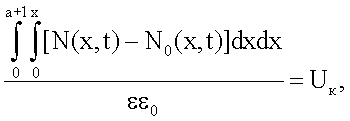
где x - координата вглубь образца в направлении диффузии;
N(x,t) - концентрационный профиль распределения примесных атомов после диффузии;
N0(x,t) - концентрационный профиль распределения примесных атомов в исходном полупроводнике;
а - координата границы области пространственного заряда при условии, что начало отсчета совпадает с границей раздела образец-среда;
у - глубина залегания p-n перехода;
е - элементарный заряд;
ε - диэлектрическая проницаемость области пространственного заряда;
ε0 - электрическая постоянная;
Uк=U0+UB - напряжение на p-n переходе, равное сумме контактной разности потенциалов (U0), которая является напряжением отсечки на прямой ветви вольт-амперной характеристики p-n перехода, и приложенного напряжения (UB),
после подстановки в них выражений N0(x,t) для исходного полупроводника и N(x,t) для заданных условий диффузии и затем по значению параметра модуляции n, полученному из емкостных измерений, из рассчитанной зависимости параметра модуляции n от параметра диффузии Dt, определяют значение параметра диффузии Dt, соответствующее эксперименту, из которого делением на продолжительность процесса диффузии t определяют коэффициент диффузии D.
2. Способ определения коэффициента диффузии примесных атомов в полупроводнике по п.1, отличающийся тем, что значения напряжений на p-n переходе Um и Un, при которых измеряют значения емкости сформированного p-n перехода, выбирают на краях участка вольт-фарадной характеристики p-n перехода с наибольшей крутизной.
3. Способ определения коэффициента диффузии примесных атомов в полупроводнике по п.1 или 2, отличающийся тем, что p-n переход создают при условии диффузии из неограниченного источника, когда
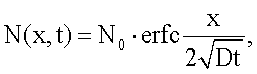
где N0 - концентрация примеси на поверхности.
4. Способ определения коэффициента диффузии примесных атомов в полупроводнике по п.1 или 2, отличающийся тем, что p-n переход создают при условии диффузии из ограниченного источника, когда
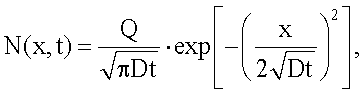
где Q - доза легирования.
5. Способ определения коэффициента диффузии примесных атомов в полупроводнике по п.1 или 2, отличающийся тем, что p-n переход создают при условии диффузии из ограниченного источника, созданного ионной имплантацией, когда
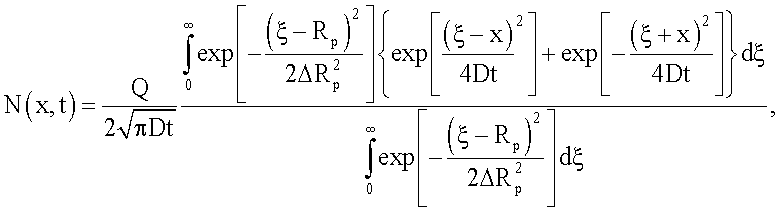
где Q - доза имплантации;
Rp - средний проецированный пробег имплантированных атомов;
ΔRp - дисперсия пробега;
ξ - переменная интегрирования.
| Ардышев В.М., Ардышев М.В | |||
| Активация и распределение кремния, имплантированного в арсенид галлия, при изотермическом радиационном отжиге | |||
| ФТП, 1998, т.32, вып.10, стр.1153 | |||
| R.Ghez, et all | |||
| Exact description and data fitting of ion-implanted dopant profile evolution during anneling | |||
| Appl | |||
| Phys | |||
| Lett., 45 (8), 1984, pp.881-883 | |||
| Способ определения коэффициента диффузии в полупроводниках | 1982 |
|
SU1053189A1 |
Авторы
Даты
2011-01-10—Публикация
2009-12-04—Подача