Изобретение относится к механическим передачам для преобразования вращательного движения во вращательное или возвратно-поступательное, использующим зубчатое зацепление профилей, и может найти применение в цилиндрических, конических или планетарных редукторах, в реечных передачах, обладающих высоким передаточным отношением, малыми габаритами и высокой нагрузочной способностью.
Широко применяемое в зубчатых передачах эвольвентное зацепление колес при всех его достоинствах обладает невысокой несущей способностью, определяемой размерами зубьев, а также имеет ограничения по величине передаточного отношения для одной ступени. На практике передаточное отношение одноступенчатого редуктора редко превышает 7. Для увеличения нагрузочной способности эвольвентного зацепления необходимо увеличивать модуль зубьев, что ведет к неоправданному увеличению габаритов передачи.
Известно косозубое зацепление Новикова (А.Ф.Крайнев. Словарь-справочник по механизмам. М.: Машиностроение, 1987, с.242). Зубчатые профили его имеют точку контакта, которая во время работы перемещается по линии, параллельной осям колес. У зубчатых колес выпуклые поверхности начальных головок зубьев взаимодействуют с вогнутыми поверхностями начальных ножек зубьев. Для этого профили в торцовом сечении очерчиваются дугами окружностей с кривизной разных знаков. Коэффициент торцового перекрытия зацепления равен или близок к нулю. Плавность работы достигается за счет осевого перекрытия, коэффициент которого выбирают больше 1. Зацепление Новикова по сравнению с эвольвентным имеет в два раза более высокую нагрузочную способность и обладает повышенным КПД, но в отличие от эвольвентного очень чувствительно к изменению межосевого расстояния. Поэтому для него требуются высокая точность изготовления и повышенная жесткость валов и опор.
Известно эксцентриково-циклоидальное зацепление колес с криволинейными зубьями (см. Становской В.В., Казакявичюс С.М. и др. Новый вид зацепления колес с криволинейными зубьями. Справочник. Инженерный журнал №9, 2008. С.34-39). Меньшее его колесо имеет всего один винтовой зуб, зубчатый профиль которого в торцовом сечении представляет собой окружность, эксцентрично смещенную относительно оси вращения колеса. Криволинейный винтовой профиль колеса образован последовательным и непрерывным смещением этой окружности вдоль оси колеса с одновременным поворотом ее вокруг этой же оси. Профиль зуба большего колеса в торцовом сечении сопрягается с эксцентрично смещенной окружностью меньшего колеса. Профиль построен как огибающая семейства эксцентриковых окружностей в разных фазах зацепления и представляет собой циклоидальную кривую, являющуюся для внешнего зацепления эквидистантой эпитрохоиды. Винтовая криволинейная поверхность зубьев второго колеса образуется аналогично последовательным и непрерывным поворотом циклоидальных торцовых сечений вокруг оси колеса. Зацепление может использоваться для цилиндрических или конических колес или в реечной передаче. В случае зацепления конических колес зубья будут иметь вышеописанную форму в сечениях дополнительным конусом или в сферических сечениях с центром сферы в точке пересечения осей колес. Сечение дополнительным конусом для конических колес и торцовое сечение для цилиндрических колес можно определить одним обобщенным понятием - главное сечение.
Профили зубьев колес сопрягаются в каждом торцовом сечении и имеют одновременно множество точек контакта. Эти точки образуют непрерывную винтовую линию контакта. В любом торцовом сечении зацепления силовой контакт профилей будет осуществляться на участке, меньшем половины оборота винтового эксцентрика. Следовательно, коэффициент торцового перекрытия меньше или равен 1/2, и для плавной работы передачи коэффициент осевого перекрытия выбирается больше 1/2. Эти значения справедливы для идеального зацепления. На практике же из-за погрешностей в изготовлении коэффициент осевого перекрытия выбирают равным или большим 1, и угол осевого перекрытия составляет 360 градусов. Зацепление обладает высоким передаточным отношением, высоким КПД и нагрузочной способностью. Зацепление менее чувствительно к изменению межосевого расстояния, чем даже эвольвентное, так как при одинаковых с ним передаточном отношении и габаритах имеет большую высоту зуба.
Поскольку зацепление косозубое, то для него существуют ограничения на максимальный угол наклона зубьев, определяемый ГОСТом в 45 градусов. При таком угле наклона для получения угла осевого перекрытия в 360 градусов необходимо увеличивать осевые габариты передачи, что не всегда допустимо. Указанное зацепление выбираем за прототип.
Таким образом, задачей изобретения является создание малогабаритной передачи с высокой нагрузочной способностью и высоким КПД, мало чувствительной к неточностям межцентрового расстояния.
Техническим результатом является уменьшение угла осевого перекрытия и осевых размеров зацепления.
Дополнительным техническим результатом, достигаемым в некоторых вариантах выполнения зацепления, является уменьшение площади поверхности, требующей точной обработки.
Для достижения указанного результата в эксцентриково-циклоидальном зацеплении зубчатых профилей с криволинейными зубьями один из профилей представляет собой зубчатое колесо, по меньшей мере, с двумя винтовыми зубьями. Рабочие боковые участки поверхности каждого зуба этого колеса в любом главном сечении очерчены дугами эксцентрично смещенной окружности. Рабочая поверхность зубьев второго профиля в том же главном сечении очерчена участками фронтов циклоидальных кривых, сопрягающихся с зубьями колеса первого профиля. Вершины и впадины между зубьями обоих профилей могут иметь любую форму с единственным условием их не пересечения во время работы.
В частности, винтовые зубья первого профиля в главном сечении могут быть полностью очерчены эксцентрично смещенными окружностями. Тогда зубья второго профиля в том же главном сечении будут очерчены участками пересекающихся циклоидальных кривых, сопрягающихся с зубьями первого колеса. Эти циклоидальные кривые представляют собой эквидистанты циклоид, повернутых относительно друг друга на угол, равный шагу циклоиды, деленному на число зубьев колеса. Следует отметить, что зацепление, зубья которого полностью очерчены дугами эксцентричной окружности и пересекающимися циклоидальными кривыми, требует гораздо больших затрат времени на обработку, так как значительно увеличивается площадь поверхности, имеющей сложную геометрическую форму.
Указанное зацепление может быть реализовано в зацеплениях различных типов (внешнее и внутреннее), для колес различной формы (цилиндрические и конические), а также в качестве реечного зацепления.
Для зацепления цилиндрических колес главными сечениями колес являются их торцовые сечения. Для реечного зацепления главным сечением является сечение плоскостью, перпендикулярной оси колеса и параллельной рейке. Для зацепления конических колес главными сечениями являются сечения дополнительным конусом.
Но для конического зацепления возможна и другая модификация зацепления, когда зубья имеют описанную выше форму в сечениях сферой с центром в точке пересечения осей колес. Т.е. рабочие участки каждого зуба первого колеса в этом сферическом сечении очерчены дугами эксцентрично смещенных окружностей, а поверхность зубьев второго профиля в этом же сферическом сечении очерчена участками циклоидальных кривых, сопрягающихся с зубьями колеса. Или, другими словами, профилями зубьев в главном сечении зацепления колес являются дуги эксцентрических окружностей, выполненных на сфере, и участки сферических циклоидальных кривых.
Если радиус эксцентрической окружности, образующей зубья первого колеса, больше, чем ее эксцентриситет, то тело колеса образовано пересечением этих окружностей. Если же эксцентричное смещение окружности становится больше ее радиуса, то телом колеса является цилиндр определенного радиуса, величина которого выбирается исходя из требуемой нагрузочной способности колеса. В этом случае в профиле второго колеса вершины винтовых зубьев, образуемые участками циклоидальных кривых, должны быть срезаны до величины, обеспечивающей не пересечение зубьев с телом колеса.
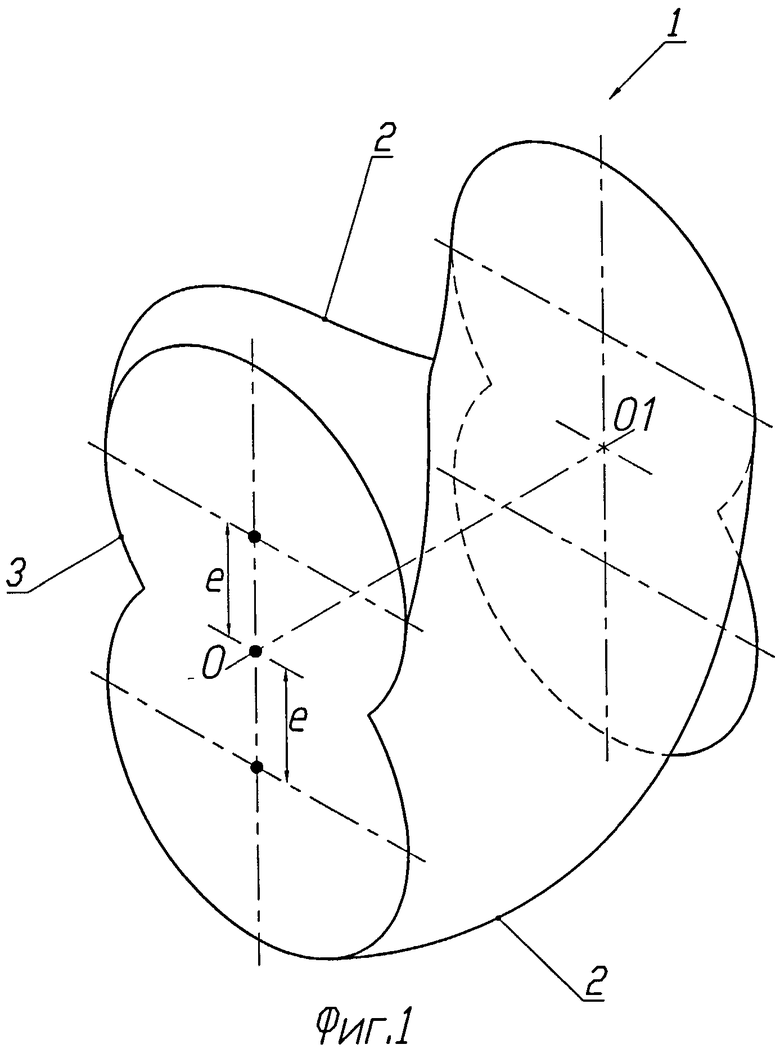
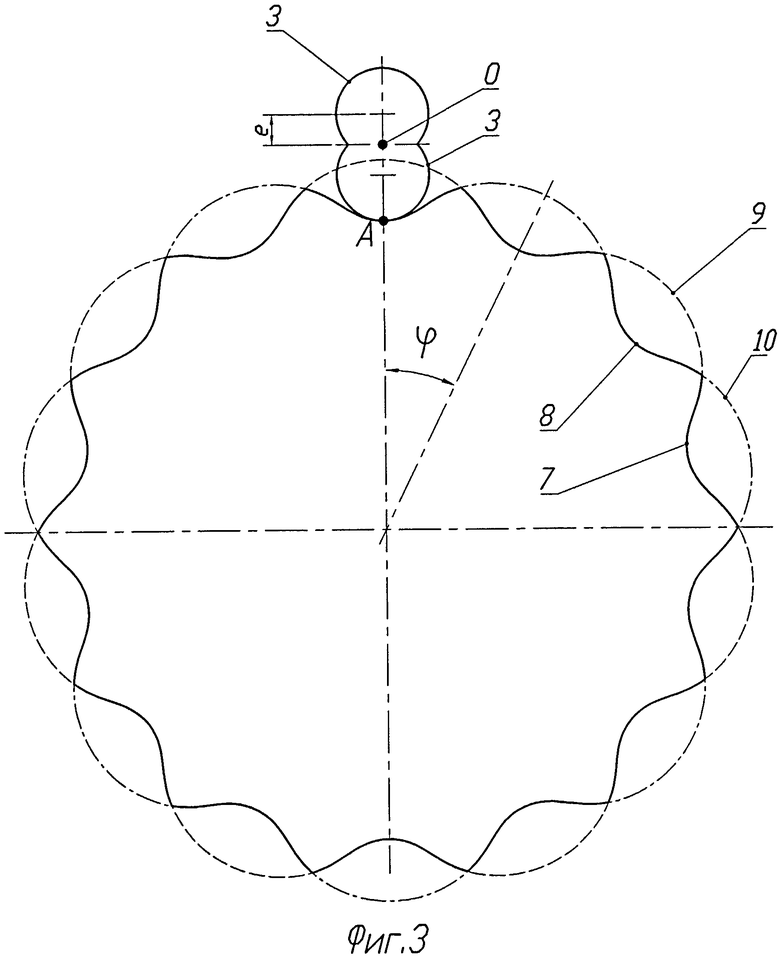
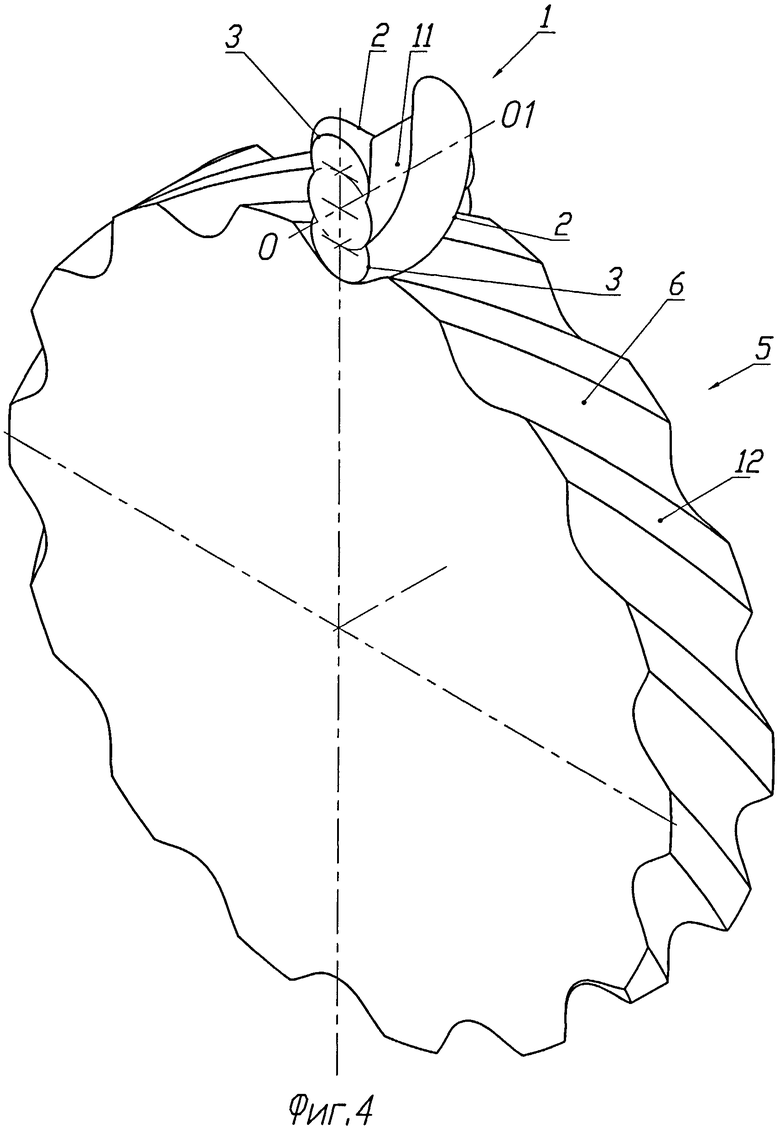
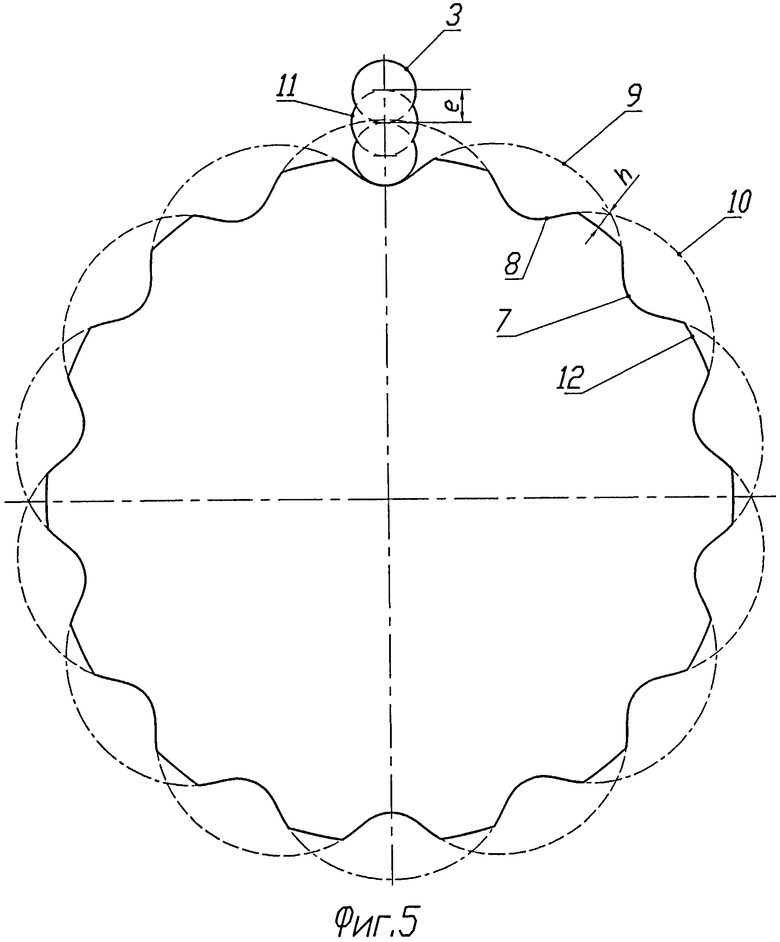
Изобретение иллюстрируется графическими материалами. На фиг.1 показан общий вид цилиндрического колеса с двумя винтовыми эксцентриковыми зубьями, причем эксцентриситет е окружности, образующей зубья, меньше, чем ее радиус. На фиг.2 дан общий вид внешнего зацепления, образуемого этим колесом, а на фиг.3 - торцовое сечение этого зацепления. На фиг.4 и 5 показаны общий вид и торцовое сечение внешнего цилиндрического зацепления двузубого колеса с винтовыми эксцентриковыми зубьями, у которого окружности, образующие эти зубья, имеют эксцентриситет, равный ее радиусу. Фиг.6 и 7 показывают зацепление таких же колес, у которых определенную в соответствии с изобретением форму имеют только рабочие участки зубьев. На фиг.8 приведен общий вид цилиндрического колеса с тремя эксцентриковыми зубьями, а на фиг.9 показано торцовое сечение внешнего зацепления колес, образуемое этим колесом. На фиг.10 показан общий вид зацепления цилиндрического колеса с тремя зубьями, у которого форму эксцентрично смещенных окружностей имеют только боковые рабочие участки зубьев, а вершины и впадины образованы цилиндрическими поверхностями различного радиуса с осями, совпадающими с осью вращения колеса. На фиг.11 дано торцевое сечение внешнего зацепления с этим колесом. На фиг 12 представлен общий вид предлагаемого зацепления для варианта конических колес, а на фиг.13 приведена схема образования зубчатых профилей для конических колес в сферическом сечении зацепления.
На чертежах не показаны варианты внутреннего зацепления цилиндрических колес и реечного зацепления, которые также могут быть выполнены в соответствии с предлагаемым изобретением. Внутреннее зацепление отличается от внешнего только тем, что зубья циклоидального профиля формируются на внутренней цилиндрической поверхности. Реечное зацепление является частным случаем зацепления цилиндрических колес, когда радиус большего колеса становится бесконечно большим.
Рассмотрим зацепление зубчатых профилей, изображенное на фиг.1, 2 и 3. Один из профилей представляет собой колесо 1 с двумя винтовыми зубьями 2. Каждый из зубьев в любом главном сечении, которым для цилиндрических колес является торцовое сечение, очерчен окружностью 3, эксцентрично смещенной относительно оси вращения колеса ОО1 на величину е. Винтовые зубья 2 колеса 1 образованы непрерывным поворотом этих окружностей относительно оси ОО1, с одновременным непрерывным смещением их вдоль этой оси. Тело колеса образуется пересечением этих двух винтовых эксцентриков. По сравнению с прототипом - однозубым винтовым эксцентриком и по аналогии с червячной передачей можно сказать, что зубья этого колеса выполнены двухзаходным винтовым эксцентриком. Второй зубчатый профиль в зацеплении представляет собой колесо 5 с винтовыми зубьями 6. Зубья 6 в торцовых сечениях очерчены участками 7 и 8 циклоидальных кривых 9 и 10, сопрягающихся с зубьями колеса 1. Циклоидальные кривые 9 и 10 представляют собой эквидистанту одной и той же циклоиды, но повернутой относительно друг друга на угол, равный угловому шагу циклоиды, деленному на число зубьев меньшего колеса 1. В данном случае угловой шаг равен 360/7 градусов, и кривые 9 и 10 смещены относительно друг друга на угол φ=360/7/2≈25,7 градуса.
По условию образования винтовых зубьев 2 и 6 в каждом торцовом сечении они будут иметь точку контакта, образующую по винтовому зубу непрерывную линию контакта АВ. Здесь следует отметить, что именно непрерывная линия контакта в идеальном теоретическом зацеплении и является принципиальным отличием предлагаемого зацепления от зацепления Новикова, у которого в теории профили имеют единственную точку контакта. Как показали наши исследования, в реальном выполнении предлагаемого зацепления с отклонениями межцентрового расстояния от расчетного линия контакта превращается в точку контакта, которая во время работы зацепления перемещается вдоль прямой линии, параллельной оси колеса. Причем в зависимости от величины отклонения межцентрового расстояния от расчетного эта линия перемещается по высоте циклоидального зуба на относительно небольшую величину. В результате предлагаемое зацепление зависит от неточностей межцентрового расстояния даже меньше, чем эвольвентное, так как высота зуба у предлагаемого зацепления больше. По сравнению с прототипом - однозубым эксцентриково-циклоидальным зацеплением, при одном и том же угле наклона винтового зуба предлагаемое зацепление будет иметь в два раза меньшую его длину и, следовательно, в два раза меньшие осевые размеры передачи. Действительно, для равномерной и непрерывной работы в прототипе угол осевого перекрытия должен быть больше 180 градусов. У описываемого зацепления этот угол будет меньше во столько раз, сколько зубьев имеет колесо с винтовыми эксцентриковыми зубьями. Для зацепления с двумя зубьями на фиг.1, 2 и 3 осевая длина передачи будет в два раза меньше, чем у прототипа. Правда, при этом для достижения того же передаточного отношения необходимо будет в два раза увеличить число циклоидальных зубьев второго профиля, что несколько увеличит радиальные размеры передачи.
Обратимся теперь к фиг.4 и 5, на которых изображено зацепление, у которого эксцентриситет е окружности 3, образующей зубья колеса 1, равен ее радиусу. В этом случае телом колеса служит цилиндрическая поверхность 11, радиус которой выбирают исходя из требований прочности. На чертежах радиус цилиндрической поверхности 11 выбран равным радиусу эксцентрической окружности 3, образующей зубья первого профиля. Винтовые зубья 6 второго профиля 5 образованы также участками 7 и 8 двух циклоидальных кривых 9 и 10. Однако для того, чтобы не происходило пересечения с поверхностью цилиндра 11, образующего тело колеса 1, вершины каждого винтового циклоидального зуба 6 срезаны, образуя винтовые участки 12 цилиндрической поверхности. Высота h среза выбирается такой, чтобы во время работы зацепления не происходило пересечения профиля зуба с цилиндрической поверхностью 11 тела колеса 1.
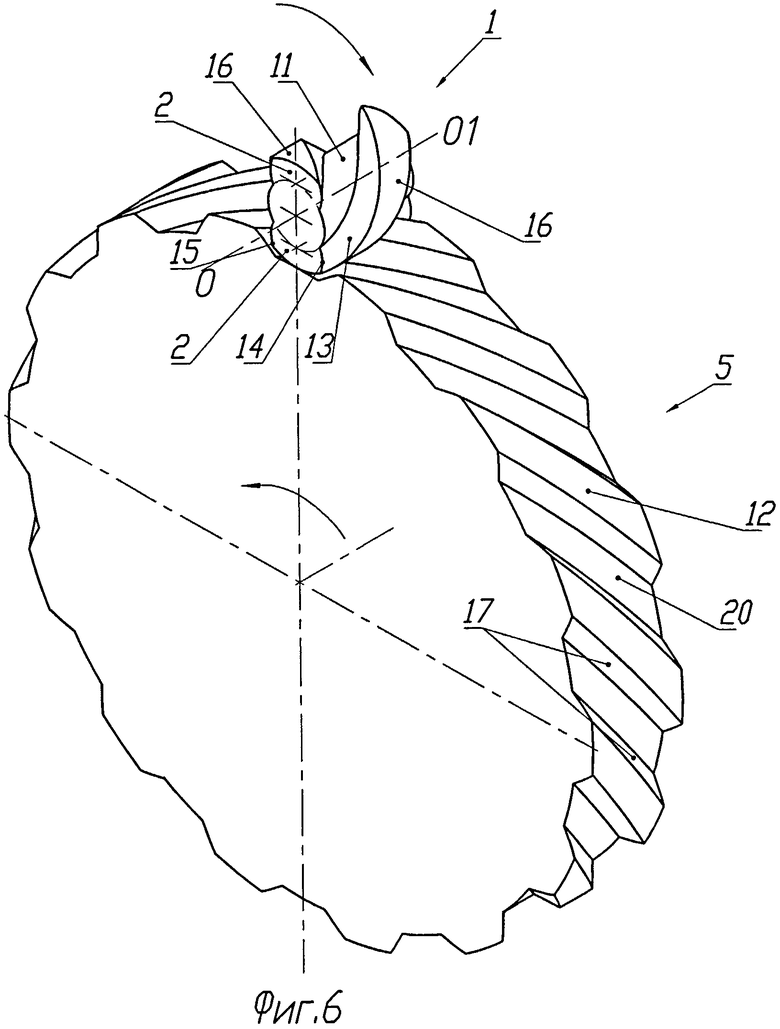
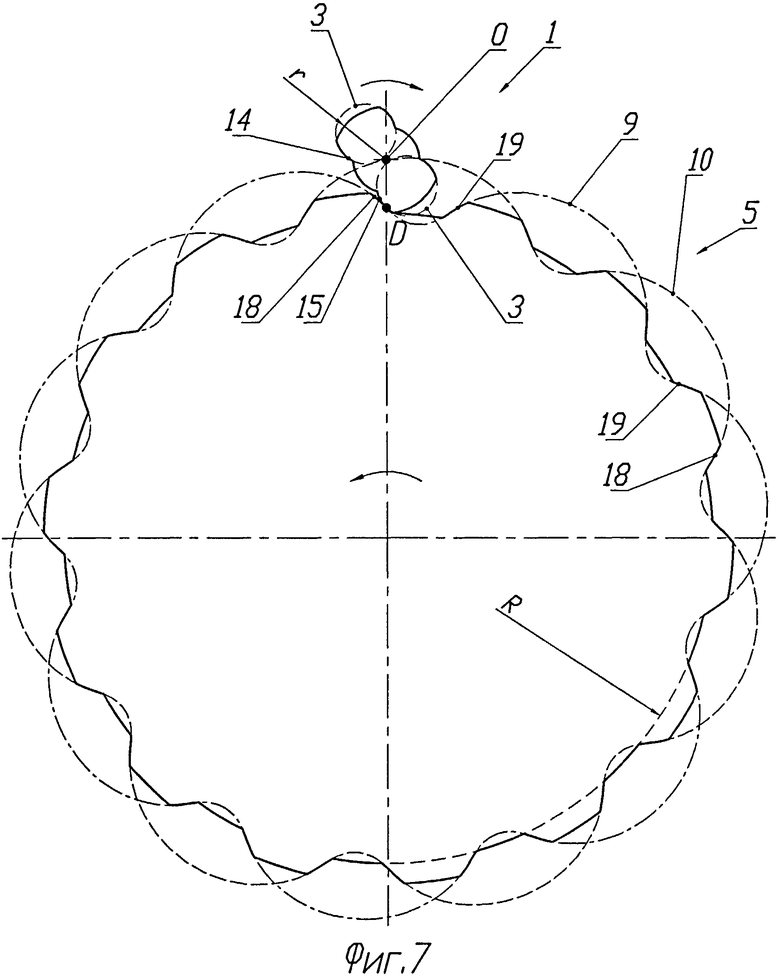
Как показало компьютерное математическое моделирование предлагаемого зацепления, силовой контакт в зацеплении происходит только на участках фронтов циклоидальной кривой. При этом изменение межцентрового расстояния колес в пределах, регламентируемых ГОСТом для эвольвентного зацепления, очень мало влияет на положение точки контакта на участке этого фронта. Линия зацепления перемещается по высоте зуба всего на несколько процентов относительно его высоты. Отсюда был сделан вывод, что остальные участки профилей колес могут иметь любую непересекающуюся друг с другом форму. Этот факт позволяет значительно упростить и удешевить технологию изготовления колес, так как точной обработке должны подвергаться только небольшие по площади участки. Вариант такого зацепления приведен на фиг.6 и 7. Зубчатое колесо 1 первого профиля имеет два винтовых зуба 2. Боковые рабочие участки 13 каждого из этих зубьев в торцовом сечении очерчены дугами 14 и 15 эксцентрической окружности 3. Наиболее удаленные от центра вращения колеса дуги этих окружностей срезаны с образованием в пространственных винтовых зубьях винтовых участков 16, имеющих форму цилиндрической поверхности радиуса r. Тело колеса 1, как и в предыдущем случае, образует цилиндрическая поверхность 11.
Колесо 5 второго профиля имеет винтовые зубья, рабочие участки 17 которых в торцовом сечении очерчены фронтами 18 и 19 циклоидальных кривых 9 и 10. Впадины между зубьями представляют собой винтовые участки 20 цилиндрической поверхности радиуса R. Радиусы R и r выбираются такими, чтобы их сумма была меньше межцентрового расстояния колес. В этом случае не будет происходить пересечения профилей. Как и в предыдущем варианте, для обеспечения не пересечения зубьев с телом колеса 1 вершины циклоидальных зубьев также срезаны, образуя винтовые участки цилиндрической поверхности 12. В результате такой модификации профилей точной и финишной обработки требуют только рабочие участки 13 зубьев колеса 1 и участки 17 колеса 5. Здесь следует отметить, что поверхности вершин и впадин зубьев сопряженных профилей могут иметь любую непересекающуюся друг с другом форму. В частности, это могут быть поверхности, образованные эксцентрическими окружностями для колеса 1 и циклоидальными кривыми для колеса 5. Т.е. в главных сечениях профили сопрягающихся зубьев полностью очерчены эксцентрическими окружностями и участками пересекающихся циклоидальных кривых.
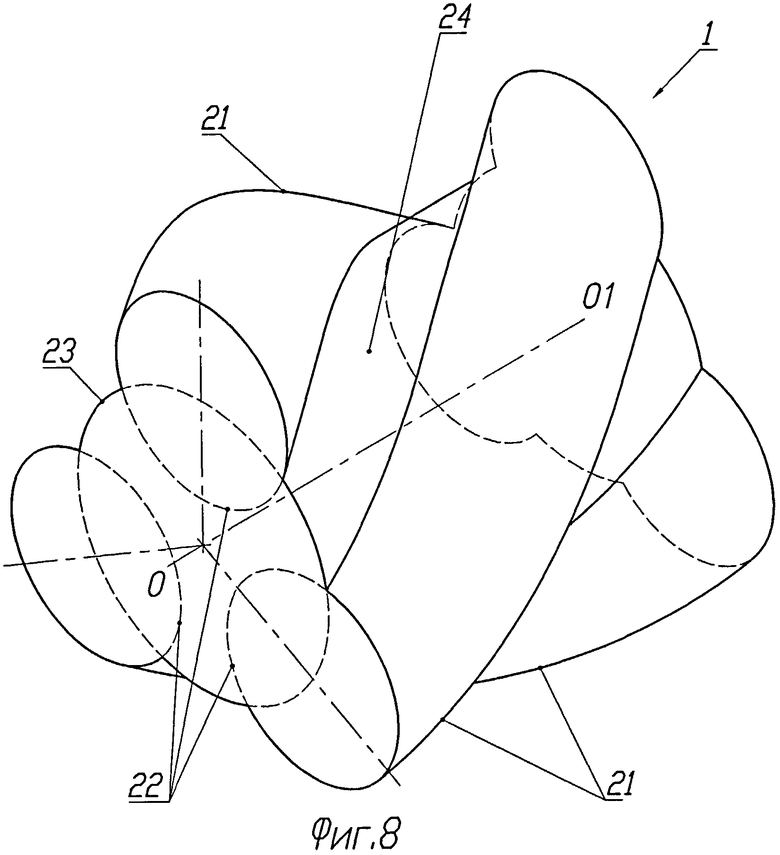
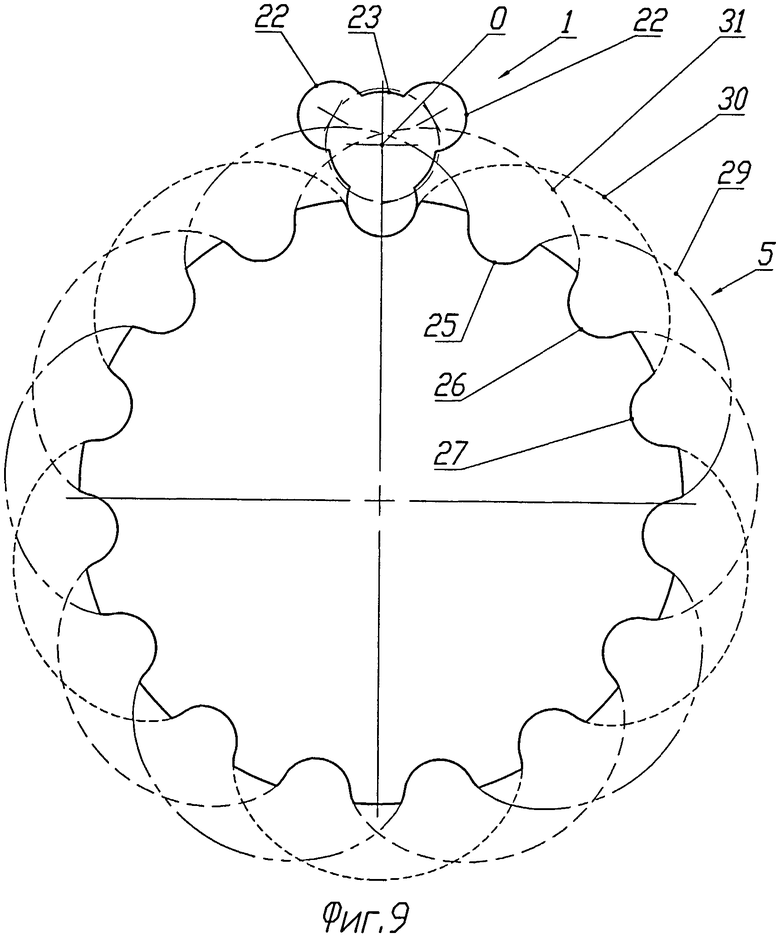
Обратимся теперь к зацеплению, в котором зубчатое колесо 1 первого профиля имеет три винтовых зуба 21 (см. фиг.8 и 9). Эти зубья в торцевом сечении колеса очерчены тремя эксцентрично смещенными от оси вращения колеса окружностями 22. На фигурах показан случай, когда эксцентриситет окружностей 22 больше их радиуса. В торцовом сечении окружности соединены дугами окружности 23, образующей цилиндрическое тело 24 колеса 1. Радиус этого цилиндра 24 выбирается из условий прочности колеса 1.
Второй зацепляющийся профиль представляет собой колесо 5. Его винтовые зубья в торцовом сечении очерчены участками 25, 26 и 27 циклоидальных кривых 29, 30 и 31 соответственно. Кривые 29-31, по сути, представляют собой эквидистанту одной и той же циклоиды, смещенной на фазовые углы, равные угловому шагу циклоиды, деленному на число зубьев эксцентрикового колеса 1. Вершины циклоидальных зубьев срезаны на величину, обеспечивающую непересечение с телом 24 колеса 1.
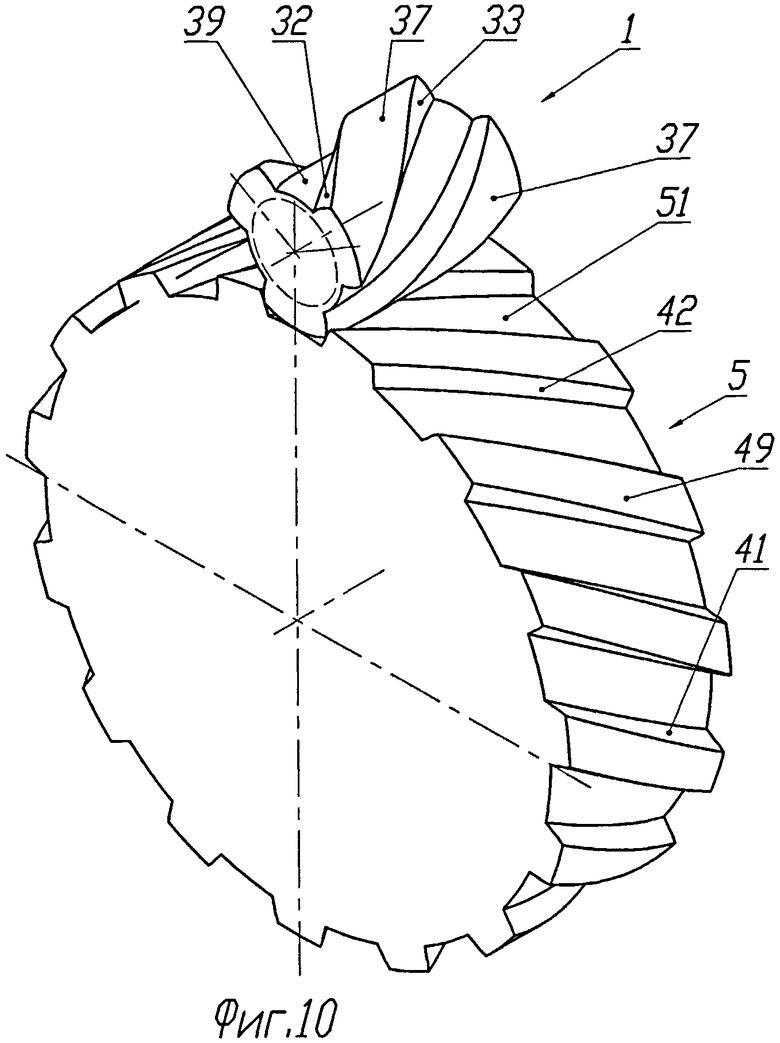
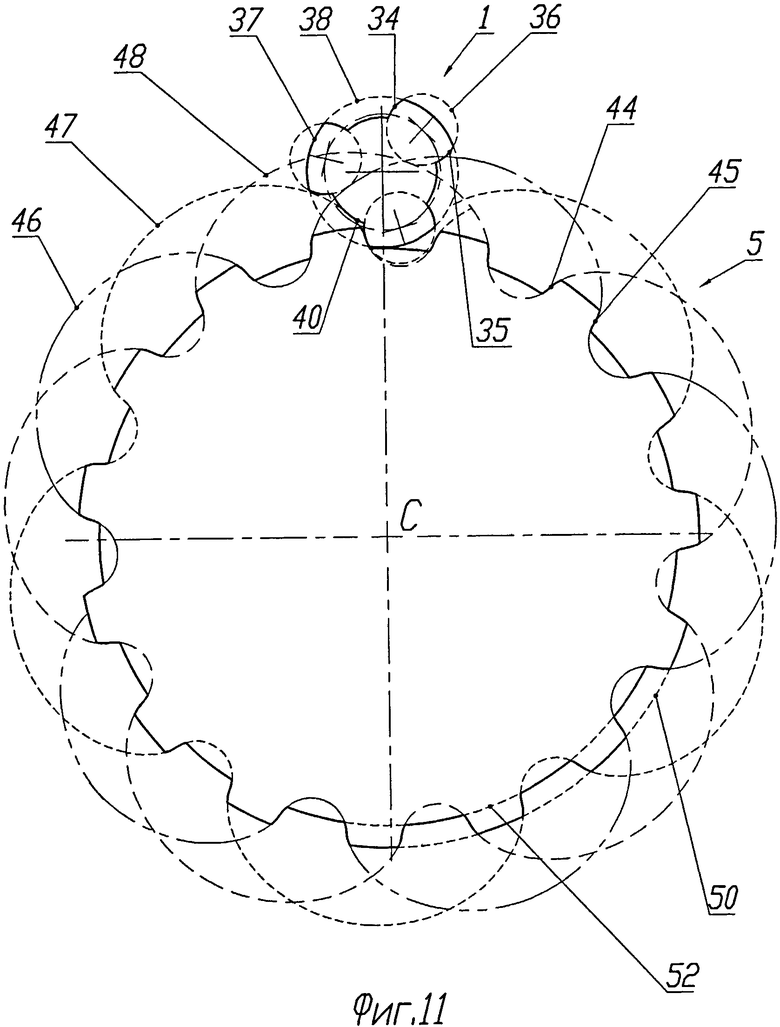
В зубчатом зацеплении, изображенном на фиг.10 и 11, зубчатое колесо 1 первого профиля имеет также три винтовых зуба. В отличие от зацепления на предыдущих фигурах зубья этого зацепления модифицированы следующим образом. Боковые рабочие участки 32 и 33 каждого зуба в главном сечении, являющемся в настоящем зацеплении цилиндрических колес торцовым, очерчены дугами 34 и 35 окружностей 36, эксцентрично смещенных относительно оси вращения колеса 1. Вершины 37 зубьев имеют форму винтовых участков цилиндрической поверхности, в торцовом сечение представленной окружностью 38. Впадины между зубьями также представляют собой винтовые участки 39 цилиндрической поверхности, в торцовом сечении представленной окружностью 40.
Зубчатое колесо 5 имеет винтовые зубья, винтовые рабочие поверхности которых 41 и 42 в торцовом сечении очерчены участками фронтов 44 и 45 циклоидальных кривых 46, 47 и 48. Эти кривые являются эквидистантами циклоид, повернутых относительно друг друга на угол, равный угловому шагу колеса 5, деленному на число зубьев колеса 1. В данном случае этот угол составляет примерно 5,71 градуса. Вершинами зубьев колеса 5 являются винтовые участки 49 цилиндрической поверхности, представленной в торцовом сечении окружностью 50. Соответственно впадины между зубьями представляют собой винтовые участки 51 цилиндрической поверхности, представленной в торцовом сечении окружностью 52. Здесь следует отметить, что, как и в двузубом зацеплении на фиг.6 и 7, поверхности вершин и впадин зубьев сопряженных профилей могут иметь любую непересекающуюся друг с другом форму. В частности, это могут быть поверхности, образованные эксцентрическими окружностями для колеса 1 и циклоидальными кривыми для колеса 5.
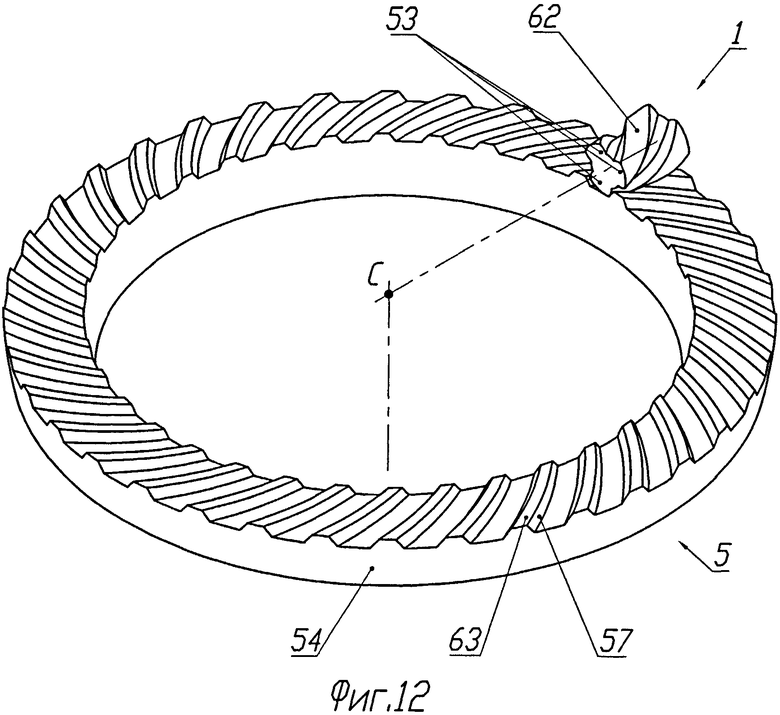
Рассмотрим теперь варианты зацепления конических колес. В одном из вариантов профили зацепления образуются точно так же, как было описано выше для цилиндрических колес, только главным сечением в этом случае будет сечение дополнительным конусом. И именно в этом сечении профили зубьев одного колеса очерчены дугами эксцентрических окружностей, а профили зубьев другого колеса очерчены участками циклоидальных кривых. Такое зацепление по аналогии с эвольвентным можно назвать квази-ЭЦ зацеплением конических колес (см. Крайнев А.Ф. Словарь-справочник по механизмам. М.: Машиностроение, 1987, стр.166). На чертежах этот вариант зацепления не приведен в виду того, что его построение мало чем отличается от построения профилей цилиндрических колес. Для более строгого построения профилей зубьев зацепления конических колес соответственные профили должны строиться в сечении колес сферической поверхностью, как это показано на фиг.12 и 13 (сферическое ЭЦ-зацепление).
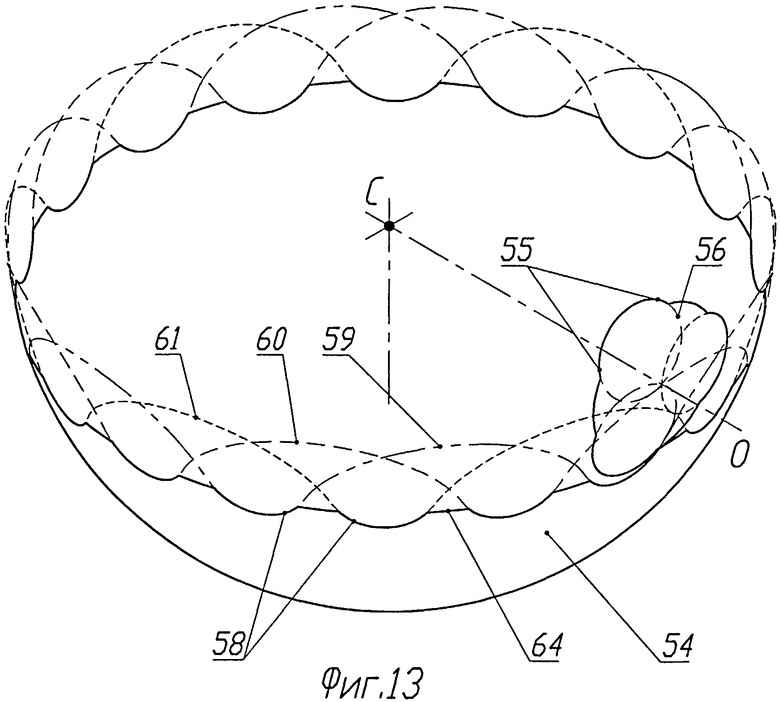
Здесь коническое колесо 1 имеет три винтовых зуба 53. Профили каждого из зубьев образуются следующим образом. Строится сферическая поверхность 54 с центром С в точке пресечения осей конических колес 1 и 5. В любом сечении колеса 1 такой сферой рабочие участки профилей зубьев очерчены дугами 55 окружностей 56, эксцентрично смещенных от оси вращения колеса 1. Винтовые зубья колеса 5 имеют рабочие участки 57, которые в сечении любой такой же сферой очерчены участками фронтов циклоидальных кривых 59, 60, 61, лежащих на этой сфере, в частности на сфере 54. Вершины зубьев колес 1 и 5 могут быть срезаны, образуя винтовые поверхности 62 и 63, как это показано на фиг.12. Эти поверхности в сферических сечениях очерчены дугами 64 концентрических окружностей, лежащих на сфере 54. Следует отметить, что на фиг.13 показана схема образования профилей конических колес зацепления, у которого срезаны вершины только циклоидальных зубьев, в то время как на фиг.12 показано зацепление конических колес, у которого срезаны вершины зубьев обоих профилей. Как уже было отмечено выше, форма зуба на участках вне рабочих поверхностей, т.е. форма вершины зуба и впадины между зубьями, не имеет значения и может быть любой.
Рассмотрим работу предлагаемого зацепления на примере зацепления цилиндрических колес, изображенного на фиг.6 и 7. Один из винтовых зубьев колеса 1 имеет точку контакта D с винтовым профилем колеса 5, показанную в торцовом сечении колес. Пусть колесо 1 вращается вокруг оси ОО1, например, по часовой стрелке. При повороте колеса 1 взаимодействующие рабочие участки 15 и 18 профилей зубьев вызовут поворот колеса 5 в противоположную сторону. В дальнейшем зубья профилей выйдут из зацепления в показанном на фиг.7 сечении, но точка контакта профилей переместится в следующее сечение, где и будет передаваться вращение. После поворота колеса 1 на половину оборота первый зуб колеса 1 выйдет из зацепления, и в зацепление с этим же зубом колеса 5 войдет второй зуб. Т.е. угол осевого перекрытия можно сделать в два раза меньше, чем для колеса с одним зубом. При повороте колеса 1 на полный оборот колесо 5 повернется на угол, равный 360°/(Z5/Z1), где Z5 и Z1 - число зубьев колеса 5 и 1 соответственно. Передаточное отношение будет определяться как Z5/Z1 и для данного зацепления составит Z5/2. Для реального зацепления, т.е. для зацепления с отклонениями межцентрового расстояния от расчетного, точка контакта профилей колес 1 и 5 будет существовать всегда, она только может сместиться по высоте зуба и по положению вдоль оси колеса.
Все вышесказанное в равной мере относится и к работе других вариантов зацепления колес. В случае реечной передачи второй профиль будет не вращаться, а линейно перемещаться с линейной скоростью, определяемой скоростью вращения колеса и передаточным отношением.
| название | год | авторы | номер документа |
|---|---|---|---|
| ЭКСЦЕНТРИКОВО-ЦИКЛОИДАЛЬНОЕ ЗАЦЕПЛЕНИЕ ЗУБЧАТЫХ ПРОФИЛЕЙ (ВАРИАНТЫ) | 2010 |
|
RU2439401C2 |
| ЗАЦЕПЛЕНИЕ КОЛЕС С КРИВОЛИНЕЙНЫМИ ЗУБЬЯМИ (ВАРИАНТЫ) И ПЛАНЕТАРНАЯ ПЕРЕДАЧА НА ЕГО ОСНОВЕ | 2007 |
|
RU2338105C1 |
| ШЕСТЕРЕННАЯ МАШИНА | 2014 |
|
RU2553848C1 |
| УСТРОЙСТВО ДЛЯ ПРЕОБРАЗОВАНИЯ ЭНЕРГИИ ВОДЫ В МЕХАНИЧЕСКУЮ ЭНЕРГИЮ ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ | 2014 |
|
RU2570959C1 |
| ЭКСЦЕНТРИКОВО-ЦИКЛОИДАЛЬНОЕ ЗАЦЕПЛЕНИЕ СОСТАВНЫХ ЗУБЧАТЫХ ПРОФИЛЕЙ | 2008 |
|
RU2385435C1 |
| РЕЕЧНОЕ ЗАЦЕПЛЕНИЕ ДЛЯ ЛИНЕЙНОГО ПРИВОДА (ВАРИАНТЫ) | 2008 |
|
RU2362925C1 |
| РАБОЧИЙ ОРГАН ВИНТОВОЙ РОТОРНОЙ МАШИНЫ | 2013 |
|
RU2534657C1 |
| ЭКСЦЕНТРИКОВЫЙ ЦИКЛОИДАЛЬНЫЙ РЕДУКТОР С ПРЕДВАРИТЕЛЬНОЙ СТУПЕНЬЮ | 2007 |
|
RU2338103C1 |
| ЦИКЛОИДАЛЬНО-ЦЕВОЧНАЯ ПЕРЕДАЧА | 2007 |
|
RU2338102C1 |
| ЭКСЦЕНТРИКОВАЯ ПЛАНЕТАРНАЯ ПЕРЕДАЧА ВНУТРЕННЕГО ЗАЦЕПЛЕНИЯ | 2008 |
|
RU2360160C1 |
Изобретение относится к механическим передачам для преобразования вращательного движения во вращательное или возвратно-поступательное, использующим зубчатое зацепление профилей, и может найти применение в цилиндрических, конических или планетарных редукторах, в реечных передачах. Один из зацепляющихся профилей представляет собой колесо (1), имеющее, по меньшей мере, два винтовых зуба (2). Боковые рабочие участки поверхности каждого зуба в главных сечениях этого колеса очерчены дугами эксцентрично смещенной относительно центра вращения колеса окружности (3). Сопрягающиеся винтовые зубья (6) второго профиля (5) в этих же сечениях очерчены участками фронтов циклоидальных кривых. Вершины и впадины между зубьями (6) могут иметь любую форму, не пересекающуюся с зубьями колеса (1). Изобретение позволяет создать передачи с высоким передаточным отношением, малыми габаритами и высокой нагрузочной способностью. 1 з.п. ф-лы, 13 ил.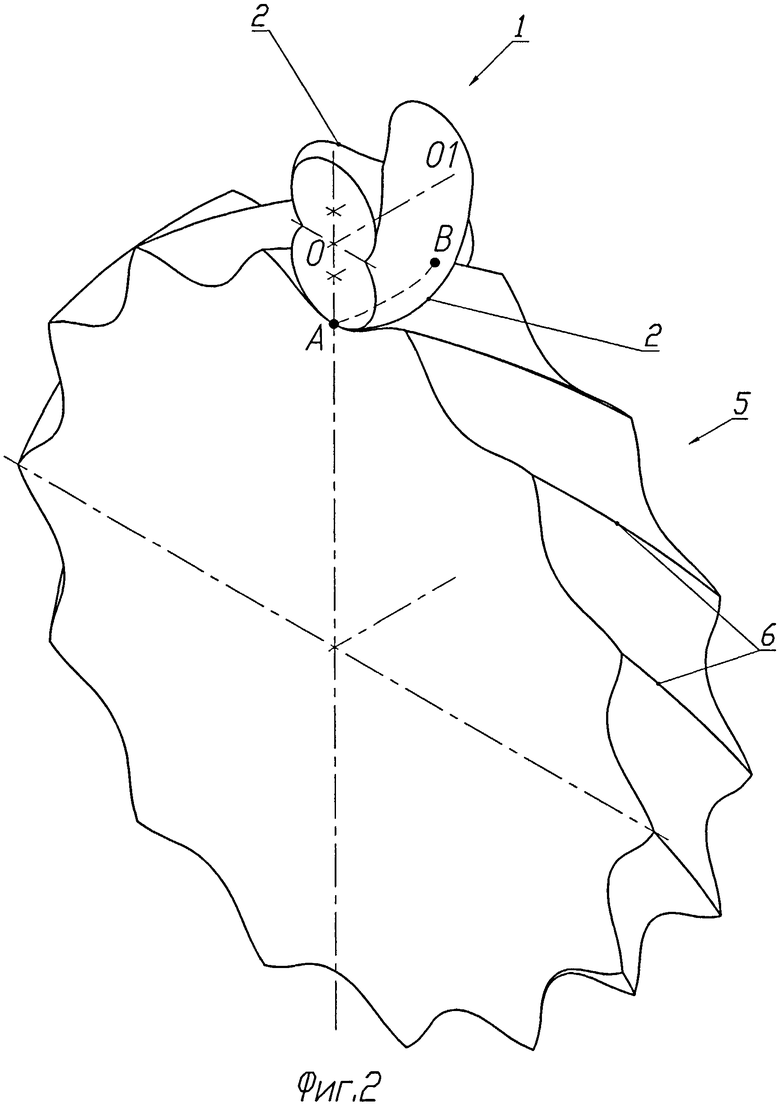
1. Эксцентриково-циклоидальное зацепление зубчатых профилей с криволинейными зубьями, один из которых представляет собой колесо, выполненное с, по меньшей мере, двумя винтовыми зубьями, боковые рабочие участки поверхности каждого зуба в главных или сферических сечениях этого колеса очерчены дугами эксцентрично смещенной относительно центра вращения колеса окружности, а зубья другого профиля в этих же сечениях очерчены участками фронтов пересекающихся циклоидальных кривых, сопрягающихся с зубьями колеса.
2. Эксцентриково-циклоидальное зацепление профилей по п.1, отличающееся тем, что эксцентриситет смещенных окружностей, образующих форму зуба колеса, больше или равен радиусу этих окружностей, и вершины винтовых циклоидальных зубьев второго профиля срезаны на величину, обеспечивающую не пересечение его с телом первого колеса.
| ЗАЦЕПЛЕНИЕ КОЛЕС С КРИВОЛИНЕЙНЫМИ ЗУБЬЯМИ (ВАРИАНТЫ) И ПЛАНЕТАРНАЯ ПЕРЕДАЧА НА ЕГО ОСНОВЕ | 2007 |
|
RU2338105C1 |
| Матричное устройство для умножения и сложения | 1977 |
|
SU657434A2 |
| US 4858487 А, 22.08.1989. | |||
Авторы
Даты
2011-04-20—Публикация
2010-02-01—Подача