Изобретение относится к исследованию процессов многофазной фильтрации жидкостей и газов в пористой среде, в частности к вытеснению нефти водой, и может быть использовано для нахождения относительных фазовых проницаемостей (ОФП) и функции Баклея.
В нефтяной промышленности нахождение ОФП осуществляется как нестационарными методами, так и лабораторным моделированием стационарной фильтрации. К нестационарным методам относится способ определения относительных фазовых проницаемостей [1], состоящий из проведения исследований на эталонных образцах пористых сред со сходными физико-химическими свойствами и снятием эталонных кривых относительных фазовых проницаемостей с представлением полученных кривых через аналитические выражения. Недостатком данного способа является использование априорной информации о форме зависимостей ОФП и трудоемкость обработки полученных результатов.
Определение относительных фазовых проницаемостей пористой среды методом стационарных состояний основано на измерении фазовых насыщенностей и градиента давления в установившемся режиме фильтрации в образце (керне) при заданном расходе каждой из фаз.
Известен способ определения относительных фазовых проницаемостей пористой среды в лабораторных условиях при совместной стационарной многофазной фильтрации нефти и воды [2], состоящий из вытеснения резидентного агента (нефти) из образца пористой среды вытесняющим агентом (водой) и проведения измерений по достижению установившейся стационарной фильтрации, которая фиксируется по стабилизации показаний дифференциального манометра, подключенного к торцам образца пористой среды, и измерения на рабочем участке параметров пористой среды. Измерения проводятся при заданном соотношении «вода-нефть» только при достижении установившегося стационарного течения, при этом фиксируется только один отсчет насыщенности. Для построения кривой насыщенности проводят несколько измерений при разных соотношениях объемов «вода-нефть» строго после достижения установившегося стационарного течения, что значительно увеличивает длительность получения искомых результатов. Для нахождения ОФП проводится обработка полученных результатов стандартными методами согласно известным специалисту формулам. Существенным недостатком известного способа является то, что при проведении стационарных исследований для получения экспериментальных данных процесс нахождения кривой насыщенности трудоемок, т.к. необходимо значительное время для стабилизации процесса.
Наиболее близким к предлагаемому техническому решению является способ определения относительных фазовых проницаемостей [3], состоящий из вытеснения вытесняющим агентом резидентного агента из образца пористой среды с торцовыми и боковой поверхностями, определения насыщенности пористой среды при достижении стационарного течения и вычисления ОФП. Недостатком данного способа является то, что стационарность распределения насыщенности достигается при времени t→∞ и даже время достижения квазистационарного состояния может оказаться весьма большим. Для нахождения каждого отсчета при измерении насыщенности требуется отдельный эксперимент, а это трудоемкий процесс, требующий значительных затрат времени.
Задачей технического решения является сокращение времени получения результатов для определения ОФП в образце пористой среды и упрощение обработки параметров.
Технический результат достигается путем сокращения времени установления стационарного течения двухфазной среды (жидкость-жидкость, жидкость-газ, газ-жидкость) и одновременного измерения стационарного распределения насыщенности пористой среды (за один эксперимент).
Поставленная задача решается следующим образом. В известном способе определения относительных фазовых проницаемостей, состоящем из вытеснения вытесняющим агентом резидентного агента из образца пористой среды с торцевыми и боковой поверхностями, определения насыщенности пористой среды после достижения стационарного течения и вычисления относительных фазовых проницаемостей, согласно изобретению, одновременно с вытесняющим агентом в пористую среду через боковую поверхность образца дополнительно подают резидентный агент, распределенный по произвольному закону с заданным расходом на единицу длины образца.
При этом вытесняющий и резидентный агенты имеют газовую или жидкую фазу.
Причем время достижения стационарного течения определяют по формуле

где ϕ - пористость, V - объем образца, Q2 - расход резидентного агента через боковую поверхность образца пористой среды, n - показатель степени.
Техническая сущность предложенного решения поясняется чертежом, где представлено условное изображение испытываемого образца в процессе осуществления предложенного способа: исследуемый образец 1 с торцевыми 2 и боковыми 3 поверхностями; вытесняющий агент 4; резидентный агент 5; вытесняемая смесь 6, состоящая из вытесняющего агента 4 и резидентного агента 5; радиоактивный источник 7 томографа (не показан) с коллимированным пучком 8 излучения; экран 9 томографа; кривая 10 распределения стационарной насыщенности S по длине образца 1 вдоль координаты x.
Предлагаемый способ состоит из последовательности следующих операций. Из исследуемого образца 1 через торцевую поверхность 2 осуществляют вытеснение вытесняющим агентом 4 резидентного агента 5, одновременно через боковую поверхность 3 дополнительно подается резидентный агент 5, распределенный вдоль образца по произвольному закону с заданным расходом на единицу длины образца. Вытесняемая смесь 6 выходит через противоположную торцевую поверхность 2 образца 1. Радиоактивный источник 7 томографа пучком 8 сканирует образец 1 и на экране 9 томографа отображается кривая 10 распределения стационарной насыщенности S по длине образца 1 вдоль координаты x, стрелка на чертеже у радиоактивного источника 7 показывает направление сканирования.
Пример конкретного выполнения способа определения ОФП. Пусть на торцевую поверхность 2 образца 1 пористой среды, насыщенной резидентным агентом 5 (нефтью), поступает вытесняющий агент 4 (вода) и начинает закачиваться в пористую среду с некоторым расходом. Распределение содержания воды в пористой среде (характеризуемое зависимостью насыщенности от координаты x) в каждый момент времени имеет область с большим значением градиента на фронте обводнения. В этой области происходит скачкообразное изменение насыщенности от нуля до некоторого конечного значения. С физической точки зрения это происходит потому, что вода смачивает скелет пористого образца 1 и стремится занять наиболее мелкие поры (поэтому вода при малой насыщенности малоподвижна). Данное скачкообразное изменение насыщенности на фронте обводнения происходит в пределах некоторой зоны, ширина которой зависит от капиллярных явлений. В данном примере ширина этой зоны для получения искомых результатов никакого значения не имеет. Найдем долю вытесняющего агента 4 в двухфазном течении в пористой среде, заполненной резидентным агентом 5, как функцию насыщенности S, полученную в результате измерения стационарного распределения насыщенности вдоль координаты x исследуемого образца 1 (керна) с пористой средой при заданном расходе дополнительного резидентного агента 5, нагнетаемого через боковую 3 поверхность образца 1 при заданном расходе вытесняющего агента 4 через торец 2 образца 1 и измеренном градиенте давления. При этом функцию Баклея b(S) можно найти из соотношений:
b(S)=W0/(Q(x)+W0),
S=S(x),
где S(x) - измеренное во время лабораторных исследований распределение насыщенности вдоль x (вдоль исследуемого образца 1 с пористой средой), Q(x) - измеренное (или заданное) распределение расхода резидентного 5 агента до сечения, соответствующего координате xn (где n - 1, 2, …, k места измерения, для сканирования томографом xn - координата сканирования вдоль образца), W0 - объемный расход вытесняющего агента 4 через торец 2 исследуемого образца. Функция Баклея показывает связь между относительными фазовыми проницаемостями:

где f1(S) - ОФП вытесняющего агента (например, воды), f2(S) - ОФП резидентного агента (например, нефти), µ0=µ1/µ2 - отношение вязкостей.
Отношение расходов, при котором стационарное распределение насыщенности реализуется в момент прихода скачка насыщенности на выходной торец 2 образца 1, определяют по формуле:

где Q2 - расход резидентного агента 5 через боковую поверхность 3 пористого образца 1,
Q1 - расход вытесняющего агента 4 через торец 2 пористого образца 1,
µ1 - вязкость вытесняющего агента,
µ2 - вязкость резидентного агента,
n - показатель степени (показывает зависимость относительной фазовой проницаемости от насыщенности и выбирается априорно).
Для времени, необходимого для создания стационарного распределения насыщенности указанным способом, справедлива оценка

где ϕ - пористость,
V - объем пористого образца 1.
Введение дополнительного резидентного агента 5 (расход распределен вдоль длины образца) позволяет вычислить время t установления (в сторону уменьшения) вплоть до реализации стационарного течения за скачком насыщенности на фронте вытеснения. В отличие от традиционных стационарных методов, в результате единичного эксперимента мы получаем кривую стационарной насыщенности во всем измеряемом диапазоне насыщенности по длине образца, а не отдельную точку, как в прототипе.
Сведения, подтверждающие возможность осуществления изобретения. Теоретическое исследование вопроса на основе решения задачи вытеснения с распределенным дополнительным резидентным агентом показало, что управление таким параметром как количество дополнительного распределенного резидентного агента, подаваемого через боковую поверхность образца, позволяет уменьшить время установления стационарного двухфазного течения. Эта возможность связана с поведением характеристик дифференциального уравнения, описывающего процесс фильтрации в плоскости (x, t) при введении дополнительного распределенного резидентного агента с регулируемым расходом. В данной задаче характеристическим инвариантом является поток вытесняющего агента, а замыкающая характеристика, соответствующая установившемуся течению, при выполнении определенных условий, зависящих от расхода распределенного резидентного агента, приходит на скачок насыщенности. Это означает, что стационарное распределение насыщенности в образце реализуется непосредственно за фронтом скачка насыщенности.
Таким образом, подача в пористую среду через боковую поверхность образца дополнительного резидентного агента, распределенного по произвольному закону с заданным расходом на единицу длины образца, позволяет непосредственно за время одного эксперимента измерять насыщенность, что существенно ускоряет нахождение ОФП.
То, что вытесняющий и резидентный агенты имеют газовую или жидкую фазу, позволяет вычислять ОФП в двухфазной среде («жидкость-жидкость», «жидкость-газ», «газ-жидкость») применительно к нефтедобыче.
То, что время достижения стационарного течения определяют по формуле

показывает, за какой срок наступит установившийся режим, т.е. доказывает, что время нахождения ОФП за один эксперимент будет существенно меньше, чем при нескольких лабораторных исследованиях, как в прототипе.
Таким образом, в данном способе дается новая взаимосвязь при вытеснении резидентного агента из пористой среды вытесняющим агентом, что достигается при дополнительном воздействии резидентного агента (при соблюдении определенных режимов) через боковые поверхности образца. Это позволяет создать условия, при которых возможно быстро достичь стационарного течения, чем значительно сократить время получения ОФП. Заявляемый способ позволяет упростить и ускорить обработку полученных результатов для определения ОФП.
Существуют экспериментальные установки [1, 2, 3], которые позволяют осуществить предлагаемый способ. Различные методы измерения насыщенности пористой среды в лабораторных условиях приведены в [5].
Источники информации
1. Патент РФ №2097740. Способ определения относительных фазовых проницаемостей. Хасанов М.М., Телин А.Г., Хисамутдинов Н.И., Кондаратцев С.А., Латыпов А.Р., Карачурин Н.Т.
2. ОСТ 39-235-89. Нефть. Метод определения фазовых проницаемостей в лабораторных условиях при совместной стационарной фильтрации.
3. Abaci S. and. Edwards J.S. RELATIVE PERMEABILITY MEASUREMENTS FOR TWO PHASE FLOW IN UNCONSOLIDATED SANDS, Mine Water and The Environment (Formerly International Journal of Mine Water), VoU1, No.2, June 1992, pp.11-26.
4. Баренблатт Г.И., Ентов B.M., Рыжик B.M. Движение жидкостей и газов в природных пластах. М., Недра, 1984.
5. Скрипкин А.Г. Повышение точности определения водо- и нефтенасыщенности образцов горных пород рентгеновским методом. Докторская диссертация. Новосибирск, 2008. (Приводится анализ методов измерения насыщенности пород в лабораторных условиях).
ПРИЛОЖЕНИЕ 1
Пример конкретного осуществления предложенного способа
Конкретное осуществление предложенного способа определения относительных фазовых проницаемостей при фильтрации двухфазных потоков «вода-нефть» в пластовых условиях с использованием рентгеновского томографа, предназначенного для исследования фильтрационно-емкостных свойств кернов рентгенографическим методом.
На торцевую поверхность исследуемого образца (керн), расположенного горизонтально при длине образца 35÷1000 мм, диаметре 30 мм, температуре образца 20÷150°C, содержащего резидентный агент (нефть), воздействовали вытесняющим агентом (вода) при давлениях, близких к забойному 30÷100 атм. При этом давление в порах образца равно 1÷50 атм, скорости вытеснения 0,0001÷20 см3/мин. Одновременно вдоль образца от регулируемого источника дополнительного резидентного агента (нефть) через кольцевые форсунки дополнительно подавалась нефть с расходом 0,0001÷20 см3/мин и под давлением 30÷100 атм. Для измерения насыщенности в воду или нефть добавлялось рентгеноконтрастное вещество. При достижении установившегося равновесия (стационарное течение), определяемого расчетным путем, рентгеновский сканер (размер кадра 103×130 мм) начинал сканировать образец по всей его длине с получением разрешения на экране 0,1 мм, при этом точность измерения расхода составляла 0,1 см3. Полученная информация о распределении насыщенности во всех точках образца по всей его длине отображалась на экране приемника рентгеновского изображения и фиксировалась в электронном виде.
Снятие информации в каждой точке образца позволило минимизировать ошибки измерения, связанные с локальными неоднородностями керна (кавернами, трещинами, непроницаемыми включениями).

Расчет ОФП проводят по известной методике. Чтобы определить относительные фазовые проницаемости, необходимо дополнительно измерить распределение среднего порового давления Р(x) вдоль образца или измерить поровое давление одного из агентов и использовать определенный вид зависимости капиллярного давления от насыщенности Рс(S)1 (1см. [4] стр.125 формула (IV.16)).
Для нахождения ОФП введем функцию φ(S)=f1(S)+µ0f2(S), аналогично F(S), зависимость φ(S) определяеют из эксперимента.

S=S(x)
где µ1 - вязкость вытесняющего агента (воды); k - абсолютная проницаемость;
Р'(x)=dP/dx; Q(x) - поток резидентного агента через боковую поверхность до сечения с координатой x; S(x) - измеренное распределение насыщенности вдоль образца.
ОФП определяют по формулам:

ПРИЛОЖЕНИЕ 2
Вытеснение жидкости в пористой среде при наличии распределенного дополнительного агента
Введение
Исследуется одномерный нестационарный процесс вытеснения жидкости, насыщающей пористую среду, другой несмешивающейся жидкостью. Жидкости считаются несжимаемыми. Индекс α=1 соответствует вытесняющему флюиду (воде), α=2 - резидентному флюиду (нефти). Скелет предполагается однородным, изотропным, недеформируемым, поэтому пористость ϕ и проницаемость k - постоянные величины. Вязкости флюидов µα для простоты также считаются постоянными, причем µ1<µ2. Задача рассматривается в квазистатическом приближении (число Эйлера мало и можно пренебречь инерционными силами). Давление флюидов считается одинаковым, т.е. капиллярным давлением пренебрегается. Однако скорости флюидов различны, что приводит к перемешиванию жидкостей. Поэтому насыщенность S (доля объема порового пространства, занятая вытесняющей жидкостью) становится функцией координат и времени.
Рассматривается одномерное движение в тонком слое с непроницаемыми границами. Изменением давления и скорости в сечении слоя пренебрегается вследствие малости толщины слоя по сравнению с его длиной. В начальный момент времени слой целиком заполнен резидентным флюидом (агентом, например нефтью). При времени t≥0 на границе x=0 задается постоянная скорость фильтрации W0 вытесняющего флюида, который полностью заполняет все сечение.
В отличие от классической модели, называемой обычно задачей Баклея-Леверетта [Backley, Leverett, 1942, Coussy, 2004], в которой рассматривается поступление жидкости в слой только через входное сечение x=0, в данном случае предполагается, что в слое действует с интенсивностью q(x) источник дополнительного агента, распределенного в пористой среде. Введение распределенного дополнительного агента схематически отражает высвобождение нефти при термическом воздействии горячей вытесняющей жидкости на содержащуюся в скелете пористой среды нефтематеринскую органику типа керогена [Шишкин, 2009]. Изменение температуры не рассматривается.
Другой аспект введения распределенного дополнительного агента связан с построением стационарной картины течения, которая позволяет проводить измерение насыщенности и относительных фазовых проницаемостей пористой среды более просто по сравнению со стандартными методами [Abaci, Edwards, 1992], основанными на использовании квазистационарного приближения, которое достигается при длительной прокачке смеси жидкостей через пористый образец.
Основные уравнения
Требуется найти зависящие от координаты x и времени t скорости фильтрации флюидов Wα(х,t), поровое давление р(х,t) и насыщенность S(x,t). Поведение среды в рассматриваемом изотермическом приближении описывается уравнениями неразрывности и законом Дарси. Уравнения неразрывности для несжимаемых флюидов и недеформируемого скелета записываются в форме

где W1=ϕSν1 и W2=ϕ(1-S)ν2 - парциальные скорости фильтрации, q(x)>0 - источник резидентного флюида (нефти). Если перекрестные члены в законе многофазной фильтрации отсутствуют [Кондауров, 2009], поровые давления флюидов равны, а процесс - квазистатический, то закон Дарси записывается в виде

Здесь и далее fα(S) - относительные фазовые проницаемости.
Складывая уравнения неразрывности (1), получим

Величина W - скорость суммарной фильтрации. Из уравнения (1, 2, 3) и граничного условия W(0, t)=W0 следует

где Q(x) - объем резидентного флюида (нефти), выделяющегося за единицу времени на интервале 0≤s≤x.
Выражая из закона Дарси (2) парциальные скорости фильтрации Wα через градиент давления и подставляя в (3), приходим к уравнению для давления

При известной насыщенности S(x, f) это уравнение эллиптического типа с соответствующими граничными условиями служит для определения поля давлений.
Чтобы сформулировать уравнение для насыщенности, исключим градиент давления из уравнений (2). В результате придем к соотношению k2W1-k1W2=0. Вместе с определением W=W1+W2 скорости суммарной фильтрации это соотношение дает систему двух уравнений, которая позволяет выразить парциальные скорости через суммарную скорость фильтрации

где

- функция Баклея. Из соотношения (5) видно, что в отсутствие силы тяжести эта функция представляет собой долю воды в общем потоке.
Для относительных проницаемостей вида f1(S)=Sn, f2(S)=(1-S)n характерный вид функции Баклея b(S) и ее производной b'(S) изображен на рис.1. Видно, что при S→0 функция b(S) вместе со своей производной стремятся к нулю. При S→1 имеет место b(S)→1, b'(S)→0. При малой насыщенности

функция b(S) (сплошная кривая) выпукла вниз.
Подставляя первое из соотношений (5) в уравнение неразрывности (1) для вытесняющего флюида (воды) и переходя к безразмерным переменным
 ,
,  ,
, 
получим дивергентную форму уравнения, которое вместе с уравнением (3) определяет эволюцию насыщенности (черта над безразмерными переменными далее опущена)

Здесь и далее F(S,x) - поток вытесняющей жидкости. Функции b(S) и W(x) таковы, что

Краевые условия для уравнения (1,6)


Соотношение (8) - условие отсутствия вытесняющей жидкости (воды) в слое в начальный момент времени, соотношение (9) - условие, что все сечение x=0 занято водой.
Умножая уравнение (6) на производную ∂F(S,х)/∂S и учитывая, что
∂F(S,x)/∂t=FS(S,x)∂S/∂t, FS(S,x)=∂F/∂S
приходим к уравнению в характеристической форме

Отсюда следует уравнение для характеристик

из которого видно, что наклон характеристик уравнения (10) на плоскости (t,х) определяется не только производной b'(S) функции Баклея, как это имеет место в классической постановке задачи Баклея-Леверетта [Backley, Leverett, 1942], но и скоростью суммарной фильтрации W(x). Изменение насыщенности вдоль характеристики определяется условием постоянства потока вытесняющей жидкости

Поэтому насыщенность порового пространства вытесняющей фазой вдоль характеристики меняется по закону
S(x,t(x))=σ(x;F0), σ(x;F0)≡b-1[F0/W(x)]
где F0 - значение потока, различное для разных характеристик, b-1(y) - функция, обратная функции Баклея y=b(S), которая определена на отрезке 0≤S≤1.
Решение задачи (6)-(9)
Из соотношений (11), (12) следует, что уравнение выходящей из точки (x=0, t=0) характеристики имеет вид
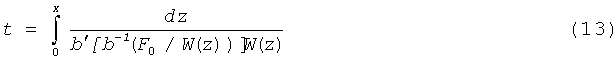
Справа (рис.1.2) семейство характеристик ограничено сильным разрывом X(t), который выходит из точки (t=0, х=0). Образование сильных разрывов насыщенности в задаче (6)-(9) связано с разрывом краевых условий (8)-(9). Поскольку на выпуклом вниз участке кривой b(S) большие значения насыщенности в силу уравнения (11) распространяются быстрее малых насыщенностей, то разрыв не распадается, по крайней мере, в окрестности t>0.
Пусть характеристический инвариант F0=1-ε, 0≤ε≤1. В случае ε=0 величине F0=1 соответствует насыщенность S=1, производная функции Баклея b'(1)=0 и подынтегральное выражение в уравнении (13) имеет особенность при z=0. Переходя к переменной S и учитывая, что в силу (12) справедливо соотношение
b(S)W'(z)dz=-b'(S)W(z)dS, находим, что при ε→0 подынтегральное выражение в интеграле (13) ограничено.
Уравнение tc=t(x) предельной характеристики, выходящей из точки (x=0, t=0), определяется выражением
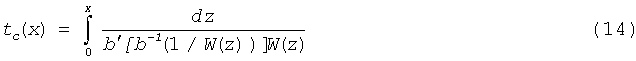
Пусть t* - момент пересечения предельной характеристики с разрывом, координата которого в этот момент равна X*. Решение в области t>t*(x) определяется стационарным потоком F(x)=1, которому соответствует стационарное распределение насыщенности S(x)=b-1(1/W(x)). Для определения точки X* воспользуемся интегральным соотношением


которое выражает баланс вытесняющей фазы в момент времени t. Учитывая, что при t≥t* насыщенность не зависит от времени, получим при учете формулы (15)
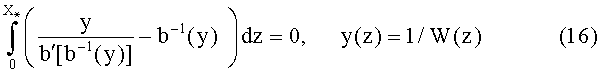
Для существования корня этого уравнения необходимо, чтобы подынтегральное выражение обращалось в нуль при некотором значении у>0, то есть должно выполняться равенство
b-1(y)b'[b-1(y)]=y, y=1/W(z), 0<y≤1
Подстановка y=b(S) приводит к условию Sb'(S)=b(S), которое означает, что в некоторой точке интервала 0<S<1 существует проведенная из точки S=0, b=0 прямая линия, которая является касательной к кривой b(S). Это условие совпадает с условием существования устойчивого разрыва в классической задаче Баклея.
Характеристики, выходящие из точек оси t, задаются уравнением

Пересечение этой характеристики с сильным разрывом определяет координату X(t) разрыва, для которой имеет место уравнение

Величина насыщенности непосредственно за фронтом разрыва при t≥t* равна
S(X(t))=b-1(1/W(X(t))), t≥t*
Поскольку распределение насыщенности для предельной характеристики и характеристики (17) при x≤X* совпадают, a W(z) - неубывающая при q≥0 функция, то координата разрыва X(t)>X* - также монотонно растущая функция, а амплитуда сильного разрыва S(X(t)) убывает при t≥t*

Таким образом, решение задачи (6)-(9) в областях 1-3, изображенных на рис.2, можно записать в виде:
в области 1 (х≥X(t), t>0)

в области 2 (x(tc)<x<X(t), 0≤t≤t*)
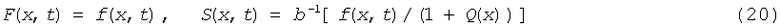
в области 3 (x≤X(t), t≥t* или 0≤x≤(tc), 0≤t≤t*)

где x(tc) - координата предельной характеристики,

- время прихода предельной характеристики на разрыв, f(x,t) - корень уравнения, определяющего значение потока на семействе характеристик

Постоянный источник дополнительного резидентного агента (q=const)
Пусть через границу х=0 слоя с единичной скоростью поступает вытесняющая жидкость (вода), присутствие которой приводит к появлению в рассматриваемой точке источника резидентного флюида (агента, например нефти). Тогда при постоянном источнике функция W(x)=1+qx. Пренебрегая остаточными насыщенностями и используя степенные зависимости для относительных фазовых проницаемостей f1(S)=Sn, f2(S)=(1-S)n, придем к функции Баклея


Используя соотношение (21), стационарное распределение насыщенности за движущимся разрывом при времени t≥t* можно записать в виде
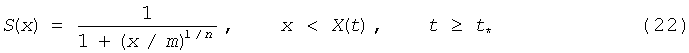
где X(t) - координата разрыва при t≥t*. Уравнение для координаты разрыва в рассматриваемом случае записывается так

Здесь 2F1(a,b,c,z) - гипергеометрическая функция Гаусса [5]. Координата X* находится из соотношения (16), которое дает


где несобственный интеграл в левой части сходится при любом n>1. Единственное решение этого уравнения X*=m1/(1-n). В размерном виде это дает

Для момента времени t* справедлива оценка t*<n/(n-1), поскольку

Нестационарное распределение насыщенности при малых временах t<t* для значений параметров m=0.2, n=3 представлено на рис.3 кривыми 1-4, которые соответствуют моментам времени 102t=1.87, 3.74, 5.61, 7.48. Пунктирная кривая - распределение насыщенности при t>t*.
Полученное решение показывает, что стационарное распределение насыщенности за разрывом достигается тем быстрее, чем больше интенсивность источника и отношение вязкостей и чем меньше скорость нагнетания воды. Стационарное распределение насыщенности за сильными разрывами 1-5 в моменты времени t=0.187, 0.374, 0.561, 0.748, 0.935 представлено на рис.4.

Наличие стационарного распределения насыщенности может быть использовано для более эффективного по сравнению со стандартным способом [Abaci, Edwards, 1992]
экспериментального определения функции Баклея и относительных фазовых проницаемостей двухфазного течения. Этот способ основан на измерении распределения насыщенности, которое является стационарным только в асимптотическом смысле и достигается при времени t→∞. Время установления такого «квазистационарного состояния» может оказаться весьма большим.
В данном случае, когда подвижная вытесняющая фаза (вода) поступает с заданным расходом W0 через один из торцов трубы, а резидентная жидкость (резидентный агент) дополнительно подается через боковую поверхность с заданным расходом на единицу длины q(x), то стационарное распределение насыщенности S(x) реализуется непосредственно за распространяющимся по трубе разрывом насыщенности, определяемым соотношениями (23)-(24).
Литература
1. Backley S.E., Leverett M.C. Mechanism of Fluid Displacement in Sands // Trans. AIME. 1942. V.146. P.107-116.
2. Coussy O. Poromechanics. Wiley, New York. 2004. 298 p.
3. Шишкин Ю.Л. Определение количества и качества органического вещества пород, генетического потенциала керогена термическими, оптическими и механическими методами // Геология, геофизика и разработка нефтяных и газовых месторождений. 2009. №3.
4. Abaci S., Edwards J.S. Relative permeability measurements for two phase flow in unconsolidated sands // Mine Water and the Environment. 1992. V.11. No.2. PP.11-26.
5. Янке Е., Эмде Ф., Леш Ф. Специальные функции (Формулы, графики, таблицы). М.: Наука. 1968. 344 с.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ ОПРЕДЕЛЕНИЯ ОТНОСИТЕЛЬНЫХ ФАЗОВЫХ ПРОНИЦАЕМОСТЕЙ | 1994 |
|
RU2097740C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ МОДИФИЦИРОВАННЫХ ФУНКЦИЙ ОТНОСИТЕЛЬНЫХ ФАЗОВЫХ ПРОНИЦАЕМОСТЕЙ ДЛЯ СЛОИСТО-НЕОДНОРОДНЫХ ПОРИСТЫХ СРЕД | 1994 |
|
RU2061221C1 |
| СПОСОБ КОНТРОЛЯ ФИЛЬТРАЦИОННЫХ ПОТОКОВ, ФОРМИРУЮЩИХСЯ ПРИ РАЗРАБОТКЕ НЕФТЯНЫХ МЕСТОРОЖДЕНИЙ СО СЛОИСТО-НЕОДНОРОДНЫМИ ПЛАСТАМИ | 1995 |
|
RU2092691C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ТЕКУЩИХ НЕФТЕНАСЫЩЕННОСТЕЙ ОТДЕЛЬНЫХ ПРОПЛАСТКОВ СЛОИСТО-НЕОДНОРОДНОГО ПЛАСТА ПО ОБВОДНЕННОСТИ ПРОДУКЦИИ | 1994 |
|
RU2061220C1 |
| СПОСОБ КОНТРОЛЯ ЗА РАЗРАБОТКОЙ НЕФТЯНОГО МЕСТОРОЖДЕНИЯ | 1999 |
|
RU2166630C1 |
| СПОСОБ КОНТРОЛЯ ЗА РАЗРАБОТКОЙ НЕФТЯНОГО МЕСТОРОЖДЕНИЯ СО СЛОИСТО-НЕОДНОРОДНЫМИ ПЛАСТАМИ | 1998 |
|
RU2148169C1 |
| СПОСОБ КОНТРОЛЯ ЗА РАЗРАБОТКОЙ НЕФТЯНОГО МЕСТОРОЖДЕНИЯ СО СЛОИСТО-НЕОДНОРОДНЫМИ ПЛАСТАМИ | 2000 |
|
RU2183268C2 |
| Способ контроля разработки месторождений с оценкой выработки запасов вязкопластичной нефти на стадии обводнения пласта | 2017 |
|
RU2682830C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ТЕКУЩЕЙ СРЕДНЕЙ НЕФТЕНАСЫЩЕННОСТИ СЛОИСТОНЕОДНОРОДНОГО ПЛАСТА ПО ВЕЛИЧИНЕ ОБВОДНЕННОСТИ ПРОДУКЦИИ | 1994 |
|
RU2061222C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ГЕОЛОГО-ФИЗИЧЕСКИХ СВОЙСТВ ПЛАСТА И ЗАПАСОВ НЕФТИ | 2022 |
|
RU2789872C1 |
Изобретение относится к исследованию процессов многофазной фильтрации жидкостей и газов в пористой среде, в частности к вытеснению нефти водой, и может быть использовано для нахождения относительных фазовых проницаемостей (ОФП) и функции Баклея. Способ определения относительных фазовых проницаемостей в пористой среде состоит из вытеснения вытесняющим агентом резидентного агента из образца пористой среды с торцовыми и боковой поверхностями. Затем осуществляют определение насыщенности пористой среды после достижения стационарного течения и вычисляют относительную фазовую проницаемость. При этом одновременно с вытесняющим агентом в пористую среду через боковую поверхность образца дополнительно подают резидентный агент, распределенный по произвольному закону с заданным расходом на единицу длины образца. Причем вытесняющий и резидентный агенты имеют газовую или жидкую фазу. При этом время достижения стационарного течения определяют по формуле  , где ϕ - пористость, V - объем пористого образца, Q2 - расход резидентного агента через боковую поверхность пористого образца, n - показатель степени. Технический результат изобретения - сокращение времени установления стационарного течения двухфазной среды (жидкость-жидкость, жидкость-газ, газ-жидкость) и одновременное измерение стационарного распределения насыщенности пористой среды (за один эксперимент). 2 з.п. ф-лы, 1 ил.
, где ϕ - пористость, V - объем пористого образца, Q2 - расход резидентного агента через боковую поверхность пористого образца, n - показатель степени. Технический результат изобретения - сокращение времени установления стационарного течения двухфазной среды (жидкость-жидкость, жидкость-газ, газ-жидкость) и одновременное измерение стационарного распределения насыщенности пористой среды (за один эксперимент). 2 з.п. ф-лы, 1 ил.
1. Способ определения относительных фазовых проницаемостей в пористой среде, состоящий из вытеснения вытесняющим агентом резидентного агента из образца пористой среды с торцовыми и боковой поверхностями, определения насыщенности пористой среды после достижения стационарного течения и вычисления относительных фазовых проницаемостей, отличающийся тем, что одновременно с вытесняющим агентом в пористую среду через боковую поверхность образца дополнительно подают резидентный агент, распределенный по произвольному закону с заданным расходом на единицу длины образца.
2. Способ по п.1, отличающийся тем, что вытесняющий и резидентный агенты имеют газовую или жидкую фазу.
3. Способ по п.1, отличающийся тем, что время достижения стационарного течения определяют по формуле  ,
,
где ϕ - пористость;
V - объем пористого образца;
Q2 - расход резидентного агента через боковую поверхность пористого образца;
n - показатель степени.
| Abaci S | |||
| and | |||
| Edwards J.S, RELATIVE PERMEABILITY MEASUREMENTS FOR TWO PHASE FLOW IN UNCONSOLIDATED SANDS, Mine Water and The Environment, (Formerly International Journal of Mine Water) V.1, №2, с.11-26 | |||
| ОПОРА КАЧЕНИЯ ВАЛА | 1992 |
|
RU2006702C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ОТНОСИТЕЛЬНЫХ ФАЗОВЫХ ПРОНИЦАЕМОСТЕЙ | 1994 |
|
RU2097740C1 |
| RU 23663845 C1, 10.08.2009 | |||
| US 5269180 A, 14.12.1993. | |||
Авторы
Даты
2012-02-10—Публикация
2010-12-09—Подача