УРОВЕНЬ ТЕХНИКИ
Область техники, к которой относится изобретение
Изобретение в общем относится к способу, в котором используют основополагающий алгоритм Многоточечной статистики (MPS) для генерирования численных псевдокернов из цифровых образов пород или кернов и диаграмм изображений скважин. Более конкретно, настоящее описание изобретения относится к созданию трехмерных (3D) численных кернов по данным компьютерной рентгеновской томографии (СТ-сканов, СТ-томограмм) и формированию микроизображений (FMI) геологического разреза скважины, и выполнению моделирования потока в этих численных кернах для понимания маршрутов потока текучих сред и коэффициентов отдачи в выбранном коллекторе.
Уровень техники
Электрические и акустические приборы для построения изображения скважины широко применяются для геофизических исследований в подземных скважинах, чтобы обозначить и картографировать границы между слоями породы, например границы пластов, и для визуализации и ориентирования разломов и сдвигов. Поскольку электрические приборы для геофизических исследований представляют собой устройства башмачного типа с фиксированной расстановкой электродов, общим местом оказываются пробелы с отсутствием информации между измерительными башмаками. Электрические и акустические диаграммы обычно имеют интервалы с низким качеством данных вследствие нефункционирующих электродов, недостаточного давления прижима башмаков, неоднородностей скважины, обломков выбуренной породы, отклонений от центрирования приборного оборудования или плохих акустических отражений.
Цифровые модели породы выстраивают из двумерных (2D) тонких секций, изображений, полученных с использованием сканирующего электронного микроскопа (SEM), генерированных на компьютере упаковок сфер, изображений, полученных с помощью сканирующего лазерного конфокального микроскопа, и разнообразных типов изображений, полученных при компьютеризованной томографии (СТ), например традиционных компьютерных микротомограмм и синхротронных компьютерных микротомограмм. Изображения, полученные с помощью компьютерной томографии (СТ, рентгеновские томограммы), представляют собой наиболее широко распространенный подход. Компьютерные рентгеновские томограммы представляют собой двумерные (2D) поперечные сечения, полученные с помощью источника рентгеновского излучения, который вращается вокруг образца. Плотность рассчитывают по коэффициентам затухания рентгеновского излучения. Томограммы из серии поперечных сечений используют для построения трехмерных (3D) изображений образца. Ввиду высокого контраста плотности между породой и порами, заполненными текучей средой, изображения компьютерных томограмм могут быть использованы для визуализации системы «порода-пора». Разрешение варьирует от субмиллиметрового до микронного масштаба, в зависимости от применяемого устройства.
Методы многоточечной статистики (MPS) применяются для создания модельных имитаций пространственных полей свойств геологических структур и коллекторов для моделирования подземного коллектора. Эти методы представляют собой условное моделирование, для которого используют известные результаты, такие как измеренные в скважинах и называемые фиксированными или «твердыми» данными, которым отдается абсолютное предпочтение при моделировании. В многоточечной статистике (MPS) применяют одномерные (1D), двумерные (2D) или трехмерные (3D) «тренировочные образы» в качестве количественных шаблонов для моделирования полей свойств подземного объекта. Моделирование с помощью многоточечной статистики (MPS) извлекает геологические структуры из тренировочных образов и привязывает их к местам расположения данных. Эти структуры либо a priori могут представлять собой геологические интерпретации, либо могут быть концептуальными моделями.
Многоточечная геостатистика (MPS) представляет собой новый прогрессивный геостатистический подход. Он позволяет специалистам, моделирующим коллектор, вводить их предшествующий опыт, интерпретации или концептуальные модели в процесс моделирования коллектора с помощью тренировочных образов. Эти тренировочные образы представляют собой численные образы структур/признаков, которые представляются существующими в исследуемом коллекторе. Когда в распоряжении имеются тренировочные образы, многоточечная геостатистика (MPS) может извлекать криволинейные структуры или комплексные признаки из тренировочных образов и привязывать их к местам расположения коллекторов, где собраны образцы/наблюдения, приводя к более реалистическим моделям коллекторов. Введение тренировочных образов в моделирование коллекторов является контрольной точкой процесса проектирования. Следует отметить, что есть две составных части в применении многоточечной геостатистики (MPS): тренировочные образы (концептуальные модели) и реальные данные (наблюдения). Эти две части типично являются разделенными. Однако в практическом приложении генерирование показательных тренировочных образов, в особенности в трехмерном (3D) представлении, оказалось узким местом в реализации методов многоточечной геостатистики (MPS). Генерирование непрерывно переменного тренировочного образа является даже более затруднительным, чем создание однозначного тренировочного образа.
Существуют различные типы электрических и акустических приборов для сканирования скважины, применяемые для геофизического исследования скважин, чтобы определить местоположение и картографировать границы между слоями породы, например, границы слоев, и для визуализации и ориентирования разломов и складок.
Например, электрическое сканирование скважины может быть проведено в буровом растворе на водной основе (электропроводном), к примеру, с помощью пластового микросканера (FMI) фирмы «Шлюмберже» (Schlumberger), который основан на технологии инклинометрии, которая стала коммерчески доступной с конца 1950-х годов. Оборудование для электрического сканирования скважин по существу представляет собой скважинные наклономеры сложной конструкции. Приборы для сканирования имеют микрорезистивные электроды, размещенные по периметру скважины на башмаках, которые прижаты к стенке скважины. Тенденция эволюционного развития от пластовых наклономеров до изображений скважин проявилась в переходе от нескольких электродов до сложной компоновки электродов на многочисленных башмаках. Смотри работу автора Hurley, N.F., 2004, Borehole Images (Изображения скважин), в книге авторов Asquith, G. и Krygowski, D.: и смотри Basic Well Log Analysis (Основы анализа каротажных диаграмм), 2-е издание, AAPG Methods in Exploration Series (Методы Американской ассоциации геологов-нефтяников в изыскательской работе), №16, стр.151-164. Инструменты сначала опускают в скважину с закрытыми башмаками. В начале каротажного зондирования либо четыре, шесть, либо восемь башмаков прижимают к стенке скважины. Число башмаков зависит от устройства для каротажного зондирования. Электрический ток посылается в породу через электроды, и датчики измеряют ток после его взаимодействия с формацией. Необработанные данные включают многообразные показания с электродов, показания каверномера от отдельных башмаков или пар башмаков, и показания акселерометра и магнитометра по осям х, y и z. Угол наклона ствола скважины и ориентация башмака 1 (прибора) определяются по магнитометрам. Частота выборки для электрода и показаний акселерометра очень высока, как правило, 120 отсчетов/фут (400 отсчетов/метр).
Площадь охвата поверхности скважины является функцией ширины электродных блоков, количества башмаков и диаметра скважины. В общем, в типичных скважинах показания снимаются для получения изображения от 40 до 80% поверхности скважины. Не попавшие на изображения части скважины выглядят как белые полосы между башмаками.
Изображения скважин создаются путем соотнесения цветных карт к различным глубинным площадкам или диапазонам значений удельного сопротивления. Затем цветные пиксели располагают в их надлежащем геометрическом положении вокруг скважины. По договоренности, участки с низким удельным сопротивлением, такие как глинистые сланцы или заполненные текучей средой трещины, изображают темными цветами. Участки с высоким удельным сопротивлением, такие как песчаники и известняки, показывают как оттенки коричневого, желтого и белого цвета.
В распоряжении имеются два основных типа обработанных изображений скважин: статические и динамические. Статическими изображениями являются таковые, которые имеют одну настройку контраста, применимую ко всей скважине. Они дают информативные представления об относительных изменениях в удельном сопротивлении пород на протяжении скважины. Динамические изображения, которые имеют переменный контраст, вынесенный в подвижное окно программы, обеспечивают улучшенный обзор таких особенностей, как каверны, трещины и границы слоев. Динамические изображения позволяют выявить малозаметные структурные особенности породы, которые имеют очень низкие значения удельного сопротивления, такие как глинистые сланцы, и очень высокие значения удельного сопротивления, такие как карбонаты и кристаллические породы.
Еще один пример электрических изображений скважин может быть реализован в буровом растворе на нефтяной основе (неэлектропроводном), в частности, когда высокие значения удельного сопротивления буровых растворов (выше, чем 50 ом·м), типичные для буровых растворов на нефтяной основе, непригодны для многих электрических изображений скважин. С 2001 года для буровых растворов на нефтяной основе на рынке имеется в продаже Микроимиджер скважин, заполненных растворами на нефтяной основе (OBMI) фирмы Schlumberger. Этот прибор генерирует изображения скважины пропусканием электрического тока в формацию из двух крупных электродов на каждом башмаке, который имеет высокое напряжение (около 300 Вольт). На каждом из 4 башмаков размещена серия близко расположенных дисковых электродов, установленных в два ряда по пять штук. Изображения скважины генерируются из разности потенциалов (падения напряжения) между близко расположенными электродами. Широкие промежутки, соответствующие несканированным участкам скважины, являются обычными между башмаками. Еще один аспект изображений скважины может быть реализован во время бурения, например, «каротаж в процессе бурения», или далее обозначаемый как “LWD”. Примеры каротажного оборудования фирмы Schlumberger представляют приборы GeoVision Resistivity (GVR) и Azimuthal Density Neutron (ADN) (нейтронный датчик азимутальной плотности). В резистивном приборе GVR используют вращающиеся электроды, и работу производят в буровом растворе на водной основе. Прибор AND генерирует изображения по показаниям азимутальной плотности и работает в любом буровом растворе. Когда прибор вращается во время бурения, получается полное сканирование всей поверхности скважины, без пробелов.
Еще один аспект изображений скважин может представлять собой акустические изображения скважин, также известные как скважинные телевизионные камеры, которые основываются на технологии, впервые разработанной в 1960-х годах. Смотри статью авторов Zemanek, J., Glenn, E.E., Norton, L.J., и Caldwell, R.L., 1970, Formation evaluation by inspection with borehole televiewer (Оценка формации путем исследования с помощью скважиной телевизионной камеры): Geophysics, том 35, стр.254-269.
Ультразвуковой скважинный сканер (UBI) является главным акустическим инструментом фирмы Schlumberger для применения в необсаженной скважине. Прибор UBI, который размещают центрированно по оси скважины, имеет вращающийся преобразователь, который испускает и регистрирует звуковые волны, которые отражаются от стенки скважины. Изображение формируется путем регистрации и обработки как амплитуды, так и времени прохождения акустического сигнала. Как правило, охват поверхности скважины достигает 100%, без пробелов в изображениях. Однако могут получаться изображения плохого качества, когда прибор не центрирован, или же стенка скважины не является однородной.
В качестве характеристических показателей на картинах изображений скважин, помимо всего прочего, могут проявляться петрофизические фации, такие как пустоты, и пятна резистивности и проводимости. В частности, авторы Dehghani et al. в обзоре 1999 года предполагают, что вблизи каверн существуют зоны повышенной пористости и проницаемости. Смотри статью авторов Dehghani, K., Harris, P.M., Edwards, K.A. и Dees, W.T., 1999, Modeling a vuggy carbonate reservoir (Моделирование кавернозного карбонатного коллектора): AAPG Bulletin, том 83, стр.19-42.
Авторы Dehghani et al. (1999) для подтверждения своей концепции использовали тонкие срезы, изображения, полученные с использованием сканирующего электронного микроскопа (SEM), и измерения мини-проницаемости породы. Авторы Schindler (2005) и Tanprasat (2005) использовали анализ изображений с фотографий кернов, изготовленных с помощью флуоресцентных красок, чтобы показать, что скопления мелких каверн преимущественно существуют вблизи крупных полостей. Смотри работы авторов Schindler, J., 2005, Quantification of vuggy porosity, Indian Basin field, New Mexico (Количественный анализ кавернозной пористости, месторождение бассейна Indian, Нью-Мексико): неопубликованная магистерская диссертация, Colorado School of Mines (Колорадская горная школа), Голден, Колорадо; и Tanprasat, S., 2005, Petrophysical analysis of vuggy porosity in the Shu'aiba Formation of the United Arab Emirates (Петрофизический анализ кавернозной пористости в формации Шуайба в Объединенных Арабских Эмиратах): неопубликованная магистерская диссертация, Колорадская горная школа, Голден, Колорадо. Такие мелкие каверны оказываются ниже уровня разрешения прибора для создания изображений скважины, так что они появляются скорее в затемненных областях, нежели в виде дискретных полостей в картине геологического разреза. Если это является общим местом для кавернозных карбонатных пород, то электрические и акустические изображения скважин должны иметь зоны или ореолы высокой проводимости или низкой амплитуды (темные) вблизи полостей. Действительно, эта особенность обычно наблюдается, например, как показано в ФИГ.3. Зоны высокой проводимости, окружающие каверны и области повышенной мелкомасштабной пористости, известные как пятна проводимости, создают основу для части пакета программ BorTex фирмы Schlumberger, цитированных в работах авторов Russel et al. (2002) и Hassall et al. (2004). Смотри работу авторов Russell, S.D., Akbar, M., Vissapragada, B., и Walkden, G.M., 2002, Rock types and permeability prediction from dipmeter and image logs: Shuaiba reservoir (Aptian), Abu Dhabi (Типы породы и прогнозирование проницаемости по показаниям наклономера и картинам геологического разреза: месторождение Шуайба (Аптиан), Абу Даби): AAPG Bulletin, том 86, стр.1709-1732; и смотри работу авторов Hassall, J.K., Ferraris, P., Al-Raisi, M., Hurley, N.F., Boyd, A. и Allen, D.F., 2004, Comparison of permeability predictors from NMR, formation image and other logs in a carbonate reservoir (Сравнение прогнозов проницаемости по данным ядерного магнитного резонанса, формированию изображений и прочих кернограмм в карбонатном коллекторе): препринт 88683 Общества инженеров-нефтяников (SPE), представленный на 11-й Международной Нефтяной выставке и конференции, Абу Даби, ОАЭ, 10-13 октября.
Автор Delhomme (1992) продемонстрировал важность картографирования электрически резистивных и нерезистивных участков в изображениях скважин. Смотри работу автора Delhomme, J.P., 1992, A quantitative characterization of formation heterogeneities based on borehole image analysis (Количественное охарактеризование неоднородностей формации на основе анализа изображений скважины): Trans. 33rd Symposium SPWLA (Труды 33-его Симпозиума Общества профессиональных аналитиков скважинных каротажных диаграмм), статья Т. Однако его подход действовал неудовлетворительно вследствие промежутков между башмаками. Он был не в состоянии очертить четкие контуры вокруг областей с высоким или низким удельным сопротивлением ввиду неопределенности профилей. Полные круговые изображения стенки скважины (ФИГ.4) позволили авторам настоящего изобретения очертить четкие контуры вокруг резистивных и/или нерезистивных областей в изображениях скважин. Такие области дали важные меры гетерогенности, в особенности в карбонатных коллекторах. Эти области в общем являются гораздо большими, чем цифровые образы породы или кернов, которые авторы настоящего изобретения генерировали, например, из СТ-томограмм пород. Вследствие этого авторам настоящего изобретения потребовались изображения скважин для выяснения, могут ли они рассчитывать на обнаружение неоднородностей от дециметрового до метрового масштаба в своих моделях потока.
Области с характеристическими особенностями на изображениях геологического разреза скважины, такими как каверны, и пятнами резистивности и проводимости здесь называются как петрофизические фации. Другие авторы, такие как Leduc et al. (2002) и Mathis et al. (2003), называют такие относящиеся к структуре области электрофациями. Смотри работу авторов Leduc, J.P., Delhaye-Prat, V., Zaugg, P., и смотри работу автора Mathis, B., 2002, FMI* based sedimentary facies modelling, Surmont Lease (Athabasca, Canada) (abs.) (Моделирование осадочных фаций на основе показаний пластового электрического микросканера, месторождение Surmont Lease (озеро Атабаска, Канада) (реферат): CSPG Annual Convention, Калгари, Альберта, Канада, 10 стр.; и смотри работу авторов Mathis, B., Leduc, J.P. и Vandenabeele, T., 2003, From the geologist's eyes to synthetic core descriptions: Geological log modeling using well-log data (abs.) (Описания синтетических кернов с точки зрения геолога: моделирование геологического разреза с использованием данных каротажа скважин (реферат)): AAPG Annual Meeting (Ежегодный семинар Американской Ассоциации геологов-нефтяников (AAPG), Солт-Лейк-Сити, Юта, 7 стр.
Для определения петрофизических фаций могли бы быть использованы структурные особенности, представленные различными цветами, например, черным, коричневым и белым (ФИГ.4). Такие фации имеют сложные трехмерные (3D) формы. Пятна проводимости, если таковые представляют собой зоны с повышенной пористостью и проницаемостью, и формируют области непрерывного потока между кавернами.
В опубликованной литературе есть много примеров численных образов пород, построенных с использованием способов (или цифровых моделей пород для пород и пор), которые включают реконструкции, выполненные из двумерных (2D) тонких срезов или изображений, полученных с помощью сканирующего электронного микроскопа (SEM), электрофаций, выведенных из каротажных диаграмм, сгенерированных на компьютере сферических упаковок, данных лазерной сканирующей конфокальной микроскопии и разнообразных типов СТ-томограмм (традиционных, микро-СТ-томограмм и синхротронных компьютеризованных микротомограмм).
Авторы Bakke и Oren (1997), Oren et al. (1998) и Oren и Bakke (2002) разработали способ, которым из тонких двумерных (2D) срезов конструируются трехмерные (3D) сетчатые структуры. Методом “Numerical Rocks” («Численные образы пород») (смотри веб-сайт http://www.numericalrocks.com/) рассчитываются трехмерные (3D) модели пор из тонких двумерных (2D) срезов. Смотри работы авторов Bakke, S., и Oren, P.-E., 1997, 3-D pore-scale modeling of sandstones and flow simulations in the pore networks (Трехмерное моделирование порового масштаба в песчаниках и имитации потока в поровых сетевых структурах): препринт 35,479 Общества инженеров-нефтяников (SPE), European 3-D Reservoir Modeling Conference (Европейская конференция по трехмерному моделированию коллекторов), Ставангер, Норвегия, 16-17 апреля, стр.136-149; Oren, P.-E., Bakke, S., и Arntzen, O.J., 1998, Extending predictive capabilities to network models (Распространение прогностического потенциала на моделирование скважинных сетей): SPE Journal, том 3, стр.324; и Oren, P.-E. и Bakke, S., 2002, Process based reconstruction of sandstones and prediction of transport properties (Базовый способ реконструкции песчаников и прогнозирование транспортных характеристик): Transport in Porous Media, том 46, стр.311-343. Эта компания также использует поровые модели, построенные из микро-СТ-томограмм. Авторы Bakke et al. (2002) успешно применили этот способ для белых кристаллических доломитов. Статьи авторов Duey (2008) и Suicmez и Touati (2008) обобщают результаты разнообразных поровых сетевых структур в песчаниках, обработанные с использованием метода Numerical Rocks. Смотри работу автора Duey, R., 2008, Quick analysis answers Heidrun question (Быстрый анализ отвечает на вопросы месторождения Хейдрун): издательство Hart Energy Publishing, LP, доступную в интернете на веб-сайте http://www.eandp.info/index2.php?area=article&articleId=767, 27 марта 2008 года; и авторов Suicmez, V.S. и Touati, M., 2008, Pore network modeling: A new technology for SCAL predictions and interpretations (Моделирование поровых сетевых структур: новый подход для прогнозирования и интерпретаций с использованием интерактивной программы анализа керна (SCAL)): Saudi Arabia Oil and Gas, выпуск 5, стр.64-70. Авторы Wu et al. (2006) представили метод генерирования трехмерных (3D) численных моделей пород из двумерных (2D) тонких срезов с использованием сети Маркова третьего порядка. Смотри статью авторов Wu, K., Van Dijke, M.I.J., Couples, G.D., Jiang, Z., Ma, J., Sorbie, K.S., Crawford, J., Young, I. и Zhang, X., 2006, 3D stochastic modelling of heterogeneous porous media - Applications to reservoir rocks (Трехмерное стохастическое моделирование неоднородной пористой среды - Применение к породам коллекторов): Transport in Porous Media, том 65, стр.443-467. Автор Awwiller (2007) разработал метод, который моделирует более сложные песчаники, чем таковые, описанные авторами Oren и Bakke (2002). Патентная заявка US 2007/0203677 А1 (ниже) автора Awwiller (2007) относится к этой работе. Авторы Okabe и Blunt (2004, 2005) генерировали трехмерные (3D) изображения из двумерных (2D) тонких срезов с использованием многоточечной статистики. Смотри работу авторов Okabe, H. и Blunt, M.J., 2004, Prediction of permeability for porous media reconstructed using multiple-point statistics (Прогнозирование проницаемости пористой среды, воспроизведенной с использованием многоточечной статистики): Physical Review E, том 70, стр.066135-1-10; и смотри статью авторов Okabe, H. и Blunt, M.J., 2005, Pore space reconstruction using multiple-point statistics (Воспроизведение порового пространства с использованием многоточечной статистики): Journal of Petroleum Science and Engineering, том 46, стр.121-137. Авторы Tomutsa и Radmilovic (2003) использовали выклинивание ионным пучком для создания множественных двумерных (2D) последовательных срезов, которые они применяли для построения трехмерных (3D) моделей пор субмикронного масштаба. Смотри работу авторов Tomutsa, L. и Radmilovic, V., 2003, Focused ion beam assisted three-dimensional rock imaging at submicron scale (Построение трехмерных изображений пород в субмикронном масштабе с помощью фокусированного ионного пучка): International Symposium of the Soc. of Core Analysis, По, Франция, 21-24 сентября, статья SCA2003-47.
Авторы Dvorkin et al. (2003) описали технологию Digital Rock Physics («Цифровая физика горных пород»), которая состоит из численных моделей в масштабе пор, выведенных из: (а) двумерных (2D) тонких срезов и модели статистических показателей, или (b) СТ-томограмм. Смотри работу авторов Dvorkin, J., Kameda, A., Nur, A., Mese, A. и Tutuncu, A.N., 2003, Real time monitoring of permeability, elastic moduli and strength in sands and shales using Digital Rock Physics (Мониторинг в реальном масштабе времени проницаемости, модуля упругости и прочности в песках и глинистых сланцах с использованием Цифровой Физики Горных Пород): препринт 82246 Общества инженеров-нефтяников (SPE), представленный на Европейской конференции Общества инженеров-нефтяников (SPE) по нарушениям эксплуатационных качеств продуктивных пластов, Гаага, Нидерланды, 13-14 мая, 7 стр. Они построили трехмерные (3D) модели гипотетической породы и провели моделирование потоков с использованием метода решеточных уравнений Больцмана. К этой работе относится Патент США 6516080 (ниже).
Авторы Leduc et al. (2002) и Mathis et al. (2003) (оба цитированы выше) генерировали «синтетические керны» из ограниченного числа описанных кернов, традиционных каротажных диаграмм необсаженных скважин и изображений геологических разрезов скважин. В традиционных каротажных диаграммах необсаженных скважин использовали кластерный анализ. «Электрофации», которые представляют собой основанные на каротажных диаграммах интервалы глубин со сходной литологией, определены с использованием традиционных каротажных диаграмм необсаженных скважин и структурного анализа изображений скважин. Гипотетические керны рассчитаны на компьютере для скважин, из которых керны не отбирались, с использованием «факторных таблиц». К этой работе относится Патент США 6011557 (ниже).
Авторы Vahrenkamp et al. (2008) описали мини-модели, то есть модели коллекторов, размеры которых составляют менее, чем 1,0 м3, и дают псевдосвойства для датчиков объема в моделях в масштабе коллекторов. Смотри работу авторов Vahrenkamp, V.C., Creusen, A., Tull, S., Farmer, A., Mookerjee, A. и Al Bahry, A, 2008, Multi-scale heterogeneity modelling in giant carbonate field, northern Oman (abs.) (Мультимасштабное моделирование неоднородности в гигантском карбонатном месторождении, северный Оман (реферат): GeoArabia, том 13, №1, стр.248. Мини-модели наполняются с использованием «основополагающих типов пород» (PRT), которые «охватывают и классифицируют весь диапазон типов пор, размеров пор, распределения пор по величине, давлений заполнения капилляров, относительных величин проницаемости и т.д.». Основополагающие типы пород (PRT) организованы в «ассоциации типов пород» (RTA), которые основываются на «осадочной ткани», определяемой из изображений геологического разреза скважины. Ассоциации типов пород (RTA) распределены в коллекторе с использованием изображений геологического разреза скважины и наблюдаемой слоистости, моделей фаций и сейсмических данных.
Авторы Bryant et al. (1993) и Behseresht et al. (2007) описали цифровые модели пород, которые представляют собой генерированные на компьютере плотные упаковки сфер с хаотичной периодичностью. Смотри работу авторов Bryant, S., Mellor, D. и Cade, C., 1993, Physically representative network models of transport in porous media (Физически репрезентативные сетевые модели транспорта в пористой среде): American Institute of Chemical Engineers Journal, том 39, №3, стр.387-396; и смотри работу авторов Behseresht, J., Bryant, S.L. и Sepehrnoori, K., 2007, Infinite-acting physically representative networks for capillarity-controlled displacements (Неограниченно действующие физически репрезентативные сети для контролируемых капиллярностью смещений): препринт 110581 Общества инженеров-нефтяников (SPE), представленный на Ежегодной Технической Конференции и Выставке Общества инженеров-нефтяников (SPE), Анахайм, Калифорния, 11-14 ноября, 15 стр. Другие авторы, такие как Bosl et al. (1998) и Holt (2001), генерировали подобные цифровые модели пород для экспериментов с потоком. Смотри работу авторов Bosl, W.J., Dvorkin, J. и Nur, A., 1998, A study of porosity and permeability using lattice Boltzmann simulation (Исследование пористости и проницаемости с использованием моделирования на основе решеточных уравнений Больцмана): Geophysical Research Letters, том 25, стр.1475-1478; и смотри работу автора Holt, R.M., 2001, Particle vs. laboratory modelling in in situ compaction (Поведение частиц при in situ уплотнении сравнительно с лабораторным моделированием): Physics and Chemistry of the Earth, Part А: Solid Earth and Geodesy, том 26, выпуск 1-2, стр.89-93.
Авторы Fredrich et al. (1995) и Fredrich (1999) создали трехмерные (3D) изображения пород с использованием лазерной сканирующей конфокальной микроскопии. Смотри работу авторов Fredrich, J.T., Menendez, B. и Wong, T.F., 1995, Imaging the pore structure of geomaterials (Построение изображений пористой структуры геологических материалов): Science, том 268, стр.276-279; и смотри работу автора Fredrich, J.T., 1999, 3D imaging of porous media using laser scanning confocal microscopy with application to microscale transport processes (Построение трехмерных изображений пористой среды с использованием лазерной сканирующей конфокальной микроскопии в приложении к транспортным процессам микроскопического масштаба): Physics and Chemistry of the Earth, Part A: Solid Earth and Geodesy, том 24, выпуск 7, стр.551-561. Авторы O'Connor и Fredrich (1999) провели эксперименты с потоком на этих численных образах пород с использованием методов решеточных уравнений Больцмана. Смотри работу авторов O'Connor, R.M. и Fredrich, J.T., 1999, Microscale flow modeling in geologic materials (Моделирование потока в микромасштабе в геологических материалах): Physics and Chemistry of the Earth, Part A: Solid Earth and Geodesy, том 24, выпуск 7, стр.611-616.
В наиболее общепринятом подходе для генерирования поровых сетевых структур используют разнообразные типы СТ-томограмм. Авторы Vinegar (1986), Wellington и Vinegar (1987) и Withjack et al. (2003) обобщили методологию и обсудили разнообразные варианты применения рентгеновской компьютерной томографии. Смотри работу автора Vinegar, H.J., 1986, X-ray CT and NMR imaging of rocks (Построение изображений пород с помощью методов рентгеновской компьютерной томографии и ядерного магнитного резонанса): JPT (Journal of Petroleum Technology), стр.257-259; смотри работу авторов Wellington, S.L. и Vinegar, H.J., 1987, X-ray computerized tomography (Рентгеновская компьютерная томография): JPT, стр.885-898; и смотри работу авторов Withjack, E.M., Devier, C. и Michael, G., 2003, The role of X-ray computed tomography in core analysis (Роль рентгеновской компьютерной томографии в анализе кернов): препринт 83467 Общества инженеров-нефтяников (SPE), представленный на Объединенной сессии Западной региональной секции Общества инженеров-нефтяников (SPE) и Тихоокеанской секции Американской Ассоциации геологов-нефтяников (AAPG), Лонг Бич, Калифорния, 19-24 мая 2003 года, 12 стр. Авторы Siddiqui и Khamees (2005) и Siddiqui et al. (2005) акцентировали применение трехмерных (3D) изображений кернов и обломков выбуренной породы, полученных с помощью традиционных и микро-СТ-томограмм. Смотри работу авторов Siddiqui, S. и Khamees, A.A., 2005, Data visualization challenges for displaying laboratory core and flow data in three-dimensions (Проблемы визуализации в экранном отображении лабораторных данных по кернам и потокам в трех измерениях): препринт 106334 Общества инженеров-нефтяников (SPE), представленный на Техническом Симпозиуме Общества инженеров-нефтяников (SPE) в Саудовской Аравии, 14-16 мая, 9 стр.; и смотри работу авторов Siddiqui, S. и Khamees, A.A., 2005, Data visualization challenges for displaying laboratory core and flow data in three-dimensions (Проблемы визуализации в экранном отображении лабораторных данных по кернам и потокам в трех измерениях): препринт 106334 Общества инженеров-нефтяников (SPE), представленный на Техническом Симпозиуме Общества инженеров-нефтяников (SPE) в Саудовской Аравии, 14-16 мая, 9 стр. Авторы Coles et al. (1996), Fredrich et al. (2006) и Fredrich et al. (2007) использовали синхротронную компьютерную микротомографию для построения численных трехмерных (3D) моделей поровых сетевых структур в натуральных и синтетических песчаниках. Смотри работы авторов Coles, M.Е., Hazlett, R.D., Muegge, R.L., Jones, K.W., Andrews, B., Dowd, B., Siddons, P., Peskin, A., Spanne, P. и Soll, W.E., 1996, Developments in synchrotron X-ray microtomography with applications to flow in porous media (Развитие синхротронной компьютерной томографии применительно к потоку в пористой среде): препринт 36531 Общества инженеров-нефтяников (SPE), представленный на Ежегодной Технической Конференции и Выставке Общества инженеров-нефтяников (SPE), Денвер, Колорадо, стр.413-424; смотри работу авторов Fredrich, J.T., DiGiovanni, A.A. и Noble, D.R., 2006, Predicting macroscopic transport properties using microscopic image data (Прогнозирование макроскопических характеристик транспорта с использованием данных микроскопических изображений): Journal of Geophysical Research B: Solid Earth, том 111, выпуск 3; и смотри работу авторов Fredrich, J.T., Haney, M.M. и White, J.A., 2007, Predicting petrophysical properties using 3D image data (abs.) (Прогнозирование петрофизических свойств с использованием данных трехмерных изображений) (реферат): материалы Ежегодной конференции Американской Ассоциации геологов-нефтяников (AAPG), выложенные в интернет на веб-сайт http://www.aapg.org. Для моделирования проницаемости они использовали методы решеточных уравнений Больцмана.
Методы многоточечной (или множественно-точечной) статистики (MPS) представляют собой новое семейство алгоритмов пространственной статистической интерполяции, предложенных в 1990-х годах, которые используются для генерирования условных моделей полей дискретных переменных, таких как геологические фации. Смотри работу авторов Guardiano, F. и Srivastava, R.M., 1993, Multivariate geostatistics: beyond bivariate moments (Мультивариантная геостатистика: за пределами двумерных моментов): Geostatistics-Troia, под редакцией A. Soares. Дордрехт, Нидерданды, издательство Kluwer Academic Publications, том 1, стр.133-144. Тренировочный образ представляет собой численную модель прежде геологической структуры, которая содержит структуры фаций и взаимосвязи, которые, как предполагается, существуют в реальных коллекторах. Тренировочные образы являются концептуальными по своей природе и могут быть простыми, как вычерченная от руки карта, или же они могут быть созданы с помощью компьютерного оборудования. Исходный алгоритм многоточечной статистики (MPS), предложенный авторами Guardiano и Srivastava (1993), строит многоточечную функцию распределения условной вероятности (CPDF) сканированием тренировочного образа вновь и вновь для каждой узловой точки модели. Ввиду ограничений, обусловленных центральным процессором компьютера (CPU), этот требующий большого расхода времени алгоритм сейчас не практикуется.
Автор Strebelle (2002) ввел концепцию дерева перебора, которая сохраняет все реплики картин, найденных в пределах шаблона по всему тренировочному образу. Смотри работу автора Strebelle, S., 2002, Conditional simulation of complex geological structures using multiple point statistics (Условное моделирование сложных геологических структур с использованием многоточечной статистики). Mathematical Geology, том 34, стр.1-22. Основополагающий алгоритм многоточечной статистики (MPS), предложенный автором Strebelle (2002), называемый SNESIM, был применен во многих случаях для моделирования коллекторов и стал своего рода справочным аппаратом для моделирования речных канальных отложений, будучи скомбинированным с ротационными и аффинными преобразованиями (Zhang, 2002; Caers и Zhang, 2004; Strebelle и Zhang, 2004). Смотри работу автора Zhang, T., 2002, Multiple-point simulation of multiple reservoir facies (Многоточечное моделирование фаций множественных коллекторов): неопубликованная магистерская диссертация, Стэнфордский университет, Калифорния, 163 стр.; смотри работу авторов Caers, J. и Zhang, T., 2004, Multiple-point geostatistics: A quantitative vehicle for integration of geologic analogs into multiple reservoir models (Количественный инструмент для внедрения геологических аналогов в модели множественных коллекторов), в книге Integration of Outcrop and Modern Analogs in Reservoir Modeling (Введение обнажений и современных аналогов в моделирование коллекторов), под редакцией M. Grammer, P.M. Harris и G.P. Eberli, издательство AAPG, статья 80, стр.383-394; и смотри работу авторов Strebelle, S. и Zhang, T., 2004, Non-stationary multiple-point geostatistical models (Нестационарные многоточечные геостатистические модели), в книге Geostatistics (Геостатистика), под редакцией Leuangthong, O. и Deutsch, C.V., том 1, стр.235-244.
Основополагающий алгоритм многоточечной статистики (MPS) представляет собой порядки величины, более быстрый, чем первоначальный алгоритм авторов Guardiano и Srivastava (1993), но он требует применения большого объема оперативной памяти (RAM) компьютера, в особенности в трехмерном (3D) представлении для крупного тренировочного образа. Смотри работу авторов Guardiano, F. и Srivastava, R.M., 1993, Multivariate geostatistics: beyond bivariate moments (Мультивариантная геостатистика: за пределами двумерных моментов): Geostatistics-Troia, под редакцией A. Soares. Дордрехт, Нидерданды, издательство Kluwer Academic Publications, том 1, стр.133-144. Это ограничение в плане оперативной памяти (RAM) в трехмерных (3D) представлениях требует компромиссного решения, что может привести к ненадлежащему воспроизведению формы трехмерных (3D) объектов. Ограничение оперативной памяти (RAM) также не позволяет авторам настоящего изобретения рассматривать слишком много категорий или классов одновременно, тем самым ограничивая основополагающий алгоритм многоточечной статистики (MPS) моделированием однозначных переменных.
Чтобы обращаться как с однозначно, так и непрерывно переменными тренировочными образами, и снизить расход оперативной памяти (RAM) и улучшить воспроизведение формы в трехмерных (3D) приложениях, создан такой алгоритм многоточечной статистики (MPS), как FILTERSIM (Zhang 2006a). Смотри работу автора Zhang, T., 2006a, Filter-based training image pattern classification for spatial pattern simulation (Сортировка картин тренировочных образов на основе цифрового фильтра для моделирования пространственного образа): неопубликованная магистерская диссертация, Стэнфордский университет, Калифорния, 153 стр. Алгоритм FILTERSIM применяет набор локальных фильтров к тренировочному образу, который может быть либо однозначным, либо непрерывным, для группирования локальных изображений в классы изображений. Затем производится моделирование изображений на основе этой классификации. Фильтр представляет собой локальный шаблон (окно) с набором плотностей, связанных с местоположением на шаблоне каждого пикселя. Приложение фильтра к локальному изображению имеет результатом оценочный показатель фильтра, оценочный показатель выглядит как численное резюме этого локального изображения. Набор фильтров по умолчанию или заданных пользователем формируют так, что каждый фильтр может регистрировать различные аспекты тренировочного образа, видимые в пределах шаблона. Эти фильтры используют для трансформирования тренировочного образа в пространство оценочных показателей фильтра. Эта количественная оценка изображения обеспечивает сокращение размеров изображений. Путем подразделения этого оценочного пространства с ограниченной величиной сходные инструктивные картины отсортировываются на основании их фильтровых оценочных показателей.
Основополагающий алгоритм многоточечной статистики (MPS) представляет собой порядки величины, более быстрый, чем первоначальный алгоритм авторов Guardiano и Srivastava (1993), но он требует применения большого объема оперативной памяти (RAM) компьютера, в особенности в трехмерном (3D) представлении для крупного тренировочного образа. Это ограничение в плане оперативной памяти (RAM) в трехмерных (3D) представлениях требует компромиссного решения, что может привести к ненадлежащему воспроизведению формы трехмерных (3D) объектов. Ограничение оперативной памяти (RAM) также не позволяет авторам настоящего изобретения рассматривать слишком много категорий или классов одновременно, тем самым ограничивая основополагающий алгоритм многоточечной статистики (MPS) моделированием однозначных переменных. Основополагающий алгоритм многоточечной статистики (MPS) выявляет точные реплики события преобразования данных, строит модель коллектора по одному пикселю за раз, преобразует в событие многоточечных данных и не позволяет никакой фильтрации или усреднения картинок, выявленных в тренировочном образе.
Чтобы обращаться как с однозначно, так и непрерывно переменными тренировочными образами, и снизить расход оперативной памяти (RAM) и улучшить воспроизведение формы в трехмерных (3D) приложениях, создан такой алгоритм многоточечной статистики (MPS), как FILTERSIM (Zhang 2006a). Алгоритм FILTERSIM применяет набор локальных фильтров к тренировочному образу, который может быть либо однозначным, либо непрерывным, для группирования локальных изображений в классы изображений. Затем производится моделирование изображений на основе этой классификации. Фильтр представляет собой локальный шаблон (окно) с набором плотностей, связанных с местоположением на шаблоне каждого пикселя. Приложение фильтра к локальному изображению имеет результатом оценочный показатель фильтра, оценочный показатель выглядит как численное резюме этого локального изображения. Набор фильтров по умолчанию или заданных пользователем формируют так, что каждый фильтр может регистрировать различные аспекты тренировочного образа, видимые в пределах шаблона. Эти фильтры используют для трансформирования тренировочного образа в пространство оценочных показателей фильтра. Эта количественная оценка изображения обеспечивает сокращение размеров изображений. Путем подразделения этого оценочного пространства с ограниченной величиной сходные тренировочные шаблоны отсортировываются на основании их фильтровых оценочных показателей.
Алгоритм FILTERSIM стартует с сортировки локальных тренировочных образов в фильтровом оценочном пространстве сокращенной величины. Моделирование выполняется по последовательной траектории в пространстве моделирования путем определения, какой класс изображений наиболее подобен локальному событию преобразования данных, извлечения конкретного изображения из класса изображений и затем патчингом квантованной картинки в изображение на сайтах моделирования. Случайная траектория моделирования и выборка классов изображений обеспечивает возможность различных модельных реализаций, тем не менее все они обусловлены одними и теми же исходными данными. Благодаря сокращению величины, обеспеченному фильтровым резюмированием каждого изображения, и благодаря группированию изображений в классы алгоритм является быстрым и рациональным в плане условий оперативной памяти (RAM).
Основополагающий алгоритм многоточечной статистики (MPS) и алгоритм FILTERSIM способны принимать на обработку абсолютные, или так называемые «твердые» граничные условия из данных, полученных в скважинах или обнажениях пород, и условные, или «мягкие» граничные условия из сейсмических данных, полей фациальных вероятностей и ротационных и аффинных (или масштабных) преобразований условных координатных сеток. Все эти данные используются в процессе стохастического моделирования для генерирования одномерных (1D), двумерных (2D) или трехмерных (3D) карт геологических фаций или характеристик пород. Поскольку есть случайный компонент, включенный в многоточечное статистическое (MPS) моделирование, индивидуальные реализации полей свойств, созданных алгоритмами многоточечной статистики (MPS), различаются, но множество реализаций предоставляет ученым-геологам и инженерам-разработчикам нефтяных и газовых месторождений улучшенные количественные оценки пространственного распределения и неопределенности геологических фаций в моделируемом объеме коллектора. Более того, эти алгоритмы принимают на обработку как жесткие, так и мягкие входные граничные условия (Zhang, 2006a). Смотри работу авторов Zhang, T., Switzer, P. и Journel A., 2006b, Filter-based classification of training image patterns for spatial pattern simulation (Фильтровая сортировка картин тренировочных образов для моделирования пространственных образов): Mathematical Geology, том 38, стр.63-80.
Есть шесть направленных двумерных (2D) фильтров по умолчанию, которые обычно используются в алгоритме FILTERSIM (Zhang, 2006a; Zhang et al., 2006b) (обе работы цитированы выше). Есть три типа фильтров: усредняющий фильтр, градиентный фильтр и фильтр кривизны, и каждый тип фильтра употребляется как для горизонтального, так и для вертикального направления. Усредняющие фильтры ориентированы на локализацию признаков; градиентные фильтры используются для выявления границ признаков выделением контраста различных признаков (разность первого порядка); фильтры кривизны выявляют разность второго порядка признаков.
Чтобы отразить крупномасштабную структуру, используют многосеточное моделирование. Таковое постепенно моделирует каждый уровень множественной сетки от более крупного до более мелкого разрешения с более мелкой модельной сеткой, ограниченной предшествующими модельными значениями, полученными для более огрубленных сеток. На каждом уровне моделирования используются фильтры с измененным масштабом, налагаемые на соответственную сетку (Zhang, 2006b).
Есть два типа тренировочных образов: один с очень ограниченным числом категорий, и еще один с непрерывными переменными, такими как петрофизические характеристики коллектора. Многоточечные геостатистические методы требуют применения одномерных (1D), двумерных (2D) и трехмерных (3D) сеток тренировочных образов в качестве первичных концептуальных геологических моделей, которые содержат картины исследуемых пространственных параметров. Формы различных структурных особенностей, проявляющиеся в изображениях, как предполагается, представляют модель реальных геологических структур, с каждой категорией, типично представляющей различные геологические фации или различные типы геологического тела. Обычно требуется, чтобы тренировочные образы содержали «стационарные» картины, то есть картины должны быть независимыми от их местоположения в пространстве (инвариантными относительно любого перемещения) и должны быть периодически повторяющимися в пространстве тренировочного образа. В случае тренировочных образов, употребляемых для геологического моделирования, эта стационарность может состоять, но не ограничивается таковой, в стационарности ориентации геологического объекта (где направленные объекты/структурные особенности не поворачиваются в пределах изображения) и стационарности геологического масштаба (где размер объектов/признаков на изображении не изменяется в пределах изображения) (Caers и Zhang, 2004). Смотри работу авторов Caers, J. и Zhang, T., 2004, Multiple-point geostatistics: A quantitative vehicle for integration of geologic analogs into multiple reservoir models (Количественный инструмент для внедрения геологических аналогов в модели множественных коллекторов), в книге Integration of Outcrop and Modern Analogs in Reservoir Modeling (Введение обнажений и современных аналогов в моделирование коллекторов), под редакцией M. Grammer, P.M. Harris и G.P. Eberli, издательство AAPG, статья 80, стр.383-394.
Проблема, неявным образом связанная с настоящими алгоритмами многоточечной статистики (MPS), состоит в том, каким образом генерировать тренировочные образы. Как предполагается, тренировочные образы моделируют или воспроизводят реальные геологические структурные особенности и должны быть настолько, насколько это возможно, выведены из существующих геологических поддающихся интерпретации изображений. Это требует исследования методами статистики и обработки изображений, которые позволили бы использовать изображения из любого источника, например вычерченных от руки набросков, фотографий воздушной разведки, спутниковых фотографий, сейсмических объемов, моделей геологических объектов, физических масштабных моделей или моделей развивающихся геологических процессов. Сравнительно с созданием непрерывно переменных тренировочных образов, генерирование однозначно (категорийно) переменных тренировочных образов является более простым. Для генерирования тренировочных образов с однозначными переменными обычно употребляется основанный на реальных объектах подход. Подход, основанный на характеристиках региона, в сочетании с добавленными желательными граничными условиями, может быть использован для генерирования тренировочных образов с непрерывными переменными (Zhang et al., 2005). Смотри работу авторов Zhang, T., Nair, N., Jennings, J.W. и Bryant, S.L., 2005, Models and methods for determining transport properties of touching-vug carbonates (Модели и методы определения транспортных характеристик кавернозных карбонатов): препринт 96027 Общества инженеров-нефтяников (SPE), представленный на Ежегодной Технической Конференции и Выставке Общества инженеров-нефтяников (SPE), Даллас, Техас, 9-12 октября, 9 стр.
Чтобы выполнить моделирование с использованием многоточечной статистики (MPS), тренировочные образы должны быть стационарными. Однако во многих вариантах применения моделирования коллекторов геологические отложения не проявляют стационарности картин/признаков, которые отражают неоднородности коллекторов и анизотропию осаждения.
СУЩНОСТЬ ИЗОБРЕТЕНИЯ
Задачей настоящего изобретения является создание способа генерирования численных (цифровых) псевдокернов с использованием изображений скважины, цифровых образов породы и многоточечной статистики.
Настоящее изобретение относится к способу генерирования трехмерных (3D) компьютерных моделей пород и пор, известных как численные псевдокерны. В способе используются полные круговые изображения стенки скважины, цифровые образы пород и многоточечная статистика (MPS) для воспроизведения трехмерного (3D) псевдокерна для интервала каротажа, где реальный керн не был взят, но имеются полученные с помощью каротажа изображения скважины. Цифровые образы кернов используют как инструкцию для воспроизведения трехмерных (3D) признаков псевдокернов с помощью многоточечной геостатистики, и конечные псевдокерны ограничены полными круговыми изображениями стенки скважины.
Прочие признаки и преимущества изобретения станут более понятными из нижеследующего подробного описания в сочетании с сопроводительными чертежами.
КРАТКОЕ ОПИСАНИЕ ЧЕРТЕЖЕЙ
Настоящее изобретение далее показано в нижеследующем подробном описании, со ссылкой на многочисленные чертежи в качестве неограничивающих примеров показательных вариантов осуществления настоящего изобретения, в котором сходные ссылочные позиции обозначают подобные части на чертежах, на которых:
ФИГ.1а показывает тренировочный образ, представленный как трехфутовый (или однометровый) интервал диаграммы изображения скважины, в частности, за один проход пластового микросканера (FMI) в кавернозной карбонатной формации, согласно по меньшей мере одному варианту осуществления изобретения;
ФИГ.1b иллюстрирует результат Многоточечного Статистического Моделирования (MPS) с использованием алгоритма FILTERSIM для того же тренировочного образа из ФИГ.1а, согласно по меньшей мере одному варианту осуществления изобретения;
ФИГ.2а показывает тот же самый тренировочный образ из ФИГ.1, согласно по меньшей мере одному варианту осуществления изобретения;
ФИГ.2b иллюстрирует результат первой реализации тренировочного образа из ФИГ.1а и согласуется с оригинальными данными измерения кавернозной формации Фигуры 1 таким образом, что данные измерений приняты на обработку в первой (ФИГ.2а), второй (ФИГ.2b) и третьей (ФИГ.2с) реализации, которые представляют тонкие вариации моделированных участков, согласно по меньшей мере одному варианту осуществления изобретения;
ФИГ.2с иллюстрирует результат второй реализации тренировочного образа из ФИГ.1а и соответствует оригинальным данным измерений кавернозной формации из ФИГ.1а, согласно по меньшей мере одному варианту осуществления изобретения;
ФИГ.2d иллюстрирует результат третьей реализации тренировочного образа из ФИГ.1а и соответствует оригинальным данным измерений кавернозной формации из ФИГ.1а, согласно по меньшей мере одному варианту осуществления изобретения;
ФИГ.3а показывает статическое изображение каверн, проявляющихся как темные участки в изображениях, полученных при каротаже в ходе бурения (LWD) кавернозного карбоната, таким образом, что пятна проводимости показаны коричневым цветом, и непроводящие участки изображены белым цветом, согласно по меньшей мере одному варианту осуществления изобретения;
ФИГ.3b показывает динамическое изображение пустот, проявляющихся как темные участки в изображениях, полученных при каротаже в ходе бурения (LWD) кавернозного карбоната, таким образом, что пятна проводимости показаны коричневым цветом, и непроводящие участки изображены белым цветом, согласно по меньшей мере одному варианту осуществления изобретения;
ФИГ.4 показывает полное круговое изображение стенки скважины с кавернозной пористостью из ФИГ.1а, которое показывает контуры (зеленые линии), которые очерчивают области с меньшим удельным сопротивлением на электрическом изображении, согласно по меньшей мере одному варианту осуществления изобретения;
ФИГ.5а и 5b показывают вид блок-схемы способа генерирования численных псевдокернов с использованием изображений скважины, цифровых образов породы и многоточечной статистики, согласно по меньшей мере одному варианту осуществления изобретения;
ФИГ.6 показывает тренировочный образ из ФИГ.1а в полупрозрачном трехмерном (3D) виде рентгеновской компьютерной (СТ) томограммы пластинчатого образца кавернозного карбоната (приблизительно 6 дюймов (152,4 мм) высотой и 4 дюйма (101,6 мм) в диаметре), таким образом, что каверны проявляются цветом от красного до серого, и скелет породы иллюстрирован голубым цветом, согласно варианту осуществления изобретения;
ФИГ.7 показывает изображения скважины, свернутые в цилиндрическую форму, соответственно диаметру скважины (диаметр скважины приблизительно 8,5 дюйма (215,9 мм), и длина интервала приблизительно 3 фута, или 1 метр), на конкретной глубине. Тренировочный образ из СТ-томограмм ФИГ.6 выполнен в надлежащем масштабе и правильно позиционирован на своей должной глубине в центре изображений скважины; в котором каверны иллюстрированы красным цветом, и скелет породы показан светло-голубым цветом, согласно вариантам осуществления изобретения.
ФИГ.8 иллюстрирует результат генерирования численного двухфациального псевдокерна из тренировочного образа и полного кругового изображения стенки скважины, который соответствует ФИГ.7 таким образом, что каверны иллюстрированы красным цветом, и скелет породы иллюстрирован темно-синим цветом, согласно вариантам осуществления изобретения;
ФИГ.9 иллюстрирует результат генерирования численного псевдокерна из тренировочного образа и полного кругового изображения стенки скважины, который соответствует ФИГ.7 таким образом, что каверны невидимы, и скелет породы иллюстрирован серым цветом. Произвольно выделенный срез (смотри верхнюю часть ФИГ.9) показывает, что это представляет собой трехмерную (3D) модель, с множеством пор в каждом срезе (приблизительная длина интервала составляет 1 фут, или 0,3 метра, и диаметр скважины составляет приблизительно 8,5 дюйма (215,9 мм)), согласно вариантам осуществления изобретения;
ФИГ.10 иллюстрирует результат генерирования численного псевдокерна из тренировочного образа и полного кругового изображения стенки скважины, который соответствует ФИГ.6. Пятна проводимости (иллюстрированные красным цветом) напоминают контуры вокруг пятен проводимости, как показанных в ФИГ.4. Следует отметить, что показаны три петрофизических фации: поры, или каверны (иллюстрированные зеленым цветом), пятна проводимости (иллюстрированные красным цветом) и скелет породы (иллюстрированный голубым цветом), согласно вариантам осуществления изобретения;
ФИГ.11 показывает численный псевдокерн, как в ФИГ.10, с невидимым скелетом породы, который выделяет трехмерную (3D) взаимосвязанную природу пор или каверн (иллюстрированных зеленым цветом) и пятен проводимости (иллюстрированных красным цветом).
ФИГ.12 показывает численный псевдокерн, как в ФИГ.10, и сложную трехмерную (3D) форму пор или каверн (иллюстрированных зеленым цветом), и как пятна проводимости, так и скелет породы являются невидимыми, согласно вариантам осуществления изобретения;
ФИГ.13 показывает численные псевдокерны, которые могут быть подвергнуты повторной выборке или преобразованию координатной сетки в радиальные координатные сетки, в которых радиальные сетки могут быть разделены на слои, основываясь на слоях, наблюдаемых в изображениях скважины или других диаграммах скважины, согласно вариантам осуществления изобретения;
ФИГ.14а показывает кривую относительной проницаемости, которая используется для пятна проводимости в моделировании потока; в которой есть три различных кривых относительной проницаемости для каждого из трех типов пород в модели псевдокерна: таких как каверны, пятна проводимости и непроницаемый скелет породы, согласно вариантам осуществления изобретения; и
ФИГ.14b показывает результат моделирования потока через численный псевдокерн, таким образом, что ряд микроинжекторов воды окружает наружный диаметр, ряд микропродуцентов окружает внутренний диаметр псевдокерна: цвета представляют нефтенасыщенность (So), где в этой модели потока показано образование неоднородных языков и прорывов, согласно вариантам осуществления изобретения.
ПОДРОБНОЕ ОПИСАНИЕ ПРЕДПОЧТИТЕЛЬНЫХ ВАРИАНТОВ
ОСУЩЕСТВЛЕНИЯ ИЗОБРЕТЕНИЯ
Показанные здесь подробности приведены только в качестве примера и для целей иллюстративного обсуждения вариантов осуществления настоящего изобретения, и представлены в таком плане, каковой предполагается наиболее полезным и легко понимаемым описанием принципов и концептуальных аспектов настоящего изобретения. В этом отношении не предпринималось никаких попыток показать структурные детали настоящего изобретения более подробно, чем это необходимо для фундаментального понимания настоящего изобретения. Описание совместно с чертежами делает очевидным для специалистов в этой области техники, каким образом некоторые формы настоящего изобретения могут быть реализованы на практике.
Настоящее изобретение относится к способу генерирования трехмерных (3D) компьютерных моделей пород и пор, известных как численные псевдокерны. В способе используются полные круговые изображения стенки скважины, цифровые образы пород и многоточечная статистика (MPS) для воспроизведения трехмерного (3D) псевдокерна для интервала каротажа, где реальный керн не был взят, но имеются полученные с помощью каротажа изображения скважины. Цифровые образы пород используют как инструкцию для воспроизведения трехмерных (3D) признаков псевдокернов с помощью многоточечной геостатистики, и конечные псевдокерны обусловлены полными круговыми изображениями стенки скважины.
Согласно аспекту изобретения, основополагающая идея состоит в применении тренировочного образа: авторы настоящего изобретения непосредственно употребляют сами данные [в создании полной круговой картины это исходное двумерное (2D) неполное изображение (тренировочный образ с непрерывными переменными), которое охватывает >60% всей области, тогда как в воспроизведении псевдокерна подход CatScan (computerized axial tomographic scan, компьютерная аксиальная томографическая развертка) цифрового керна непосредственно применяют в качестве трехмерного (3D) тренировочного образа, который впоследствии комбинируют с данными полного кругового изображения стенки скважины]. Таким образом, весь процесс применения многоточечной статистики (MPS) в целом становится компьютерно-управляемым. Это преимущество должно быть подчеркнуто в нашей патентной заявке и условиях.
Изображения скважин формируют ориентированные электрические и акустические карты пород и текучих сред, с которыми встречается скважина. Полные круговые изображения стенки скважины представляют собой полные, охватывающие 360 градусов виды стенки скважины. По своей конструкции большинство акустических устройств и приборов для каротажа во время бурения создают полные круговые изображения стенки скважины. Многие картины геологических разрезов, построенные на данных удельного сопротивления, нуждаются в наличии моделированных полных круговых изображений стенки скважины, поскольку между башмаками существуют промежутки, и может иметь место повреждение каких-то электродов или башмаков. В процессе моделирования используют алгоритмы с непрерывными переменными, разработанные в пределах многоточечной статистики (MPS). Полные круговые изображения стенки скважины предоставляют данные о физическом местоположении структурных особенностей, таких как границы слоев, поры и пятна проводимости и резистивности внутри породы на стенке скважины. Таковые очерчивают сложные трехмерные объемы, известные как петрофизические фации.
Цифровые образы пород или кернов могут быть генерированы из двумерных (2D) тонких срезов, изображений, полученных с помощью сканирующего электронного микроскопа, изображений, полученных с использованием конфокального микроскопа, или генерированных на компьютере упаковок сфер. Однако многие цифровые образы пород или кернов генерируют из компьютерных томограмм (СТ-сканов) пород и текучих сред. Томографические изображения создаются, когда сканер пропускает рентгеновские лучи под различными углами через породу к приемнику. Ослабление рентгеновского излучения преобразуется в плотность, и из последовательных срезов строятся трехмерные (3D) образы пород и пор. Согласно аспекту изобретения, каждый цифровой образ керна, например, СТ-томограмма, непосредственно воспринимается как тренировочный образ. Таковые представляют собой дискретные переменные тренировочные образы с характерными признаками породы (белый цвет) или поры (черный цвет) в каждом пикселе изображения. Тренировочный образ может иметь любую форму границ или содержать любое количество хаотичных полостей.
Численные псевдокерны создаются с использованием алгоритма с дискретными переменными в пределах многоточечной статистики (MPS). Каждой петрофизической фации приписывают целочисленные значения, такие как порода (0), поры (1) и пятна проводимости (2). Цифровые образы породы или керна используют в качестве тренировочных образов, то есть количественных шаблонов, употребляемых для моделирования полей свойств. Полные круговые изображения стенки скважины охватывают численный псевдокерн с цилиндрическими очертаниями для модифицирования моделей. Каждый численный псевдокерн полностью следует цифровым образам породы или керна и полным круговым изображениям стенки скважины. Численные псевдокерны могут иметь координатную привязку с образованием моделей, пригодных для имитаций потока текучих сред. Кривые капиллярного давления и относительной проницаемости выводятся из концептуальных моделей, специального анализа керна или испытанной методики тонко масштабированного моделирования сети пор.
ФИГ.1а представляет собой тренировочный образ, определенный трехфутовым (однометровым) интервалом диаграммы изображения скважины, полученный при одном проходе пластового микросканера (FMI) в кавернозной карбонатной формации. Каверны представляют собой поры, которые заполнены буровым раствором на водной основе, и они проявляются как темные пятна с низким удельным сопротивлением. Примечательны промежутки между башмаками в ФИГ.1а. Для иллюстрации, пикселированный, заданный пользователем 3×3-шаблон (внизу) перемещается по тренировочному образу, детектируя картины и формируя фильтровые оценочные показатели для областей, составляющих ближайшее окружение каждого измеренного пикселя. Это создает основу для многоточечного статистического (MPS) моделирования с использованием алгоритма FILTERSIM. Полное круговое изображение стенки скважины в ФИГ.1b показывает реализацию алгоритма FILTERSIM, в которой используют все изображение ФИГ.1а целиком в качестве тренировочного образа. Реализация обусловлена так, что она в совершенстве согласуется с оригинальными данными измерений. Ориентации показаны вдоль вершин изображений. Сокращения: N = север; Е = восток; S = юг; и W = запад. Нет никаких вертикальных преувеличений. Диаметр долота составляет 8,5 дюйма (21,5 см). В частности, ФИГ.1b иллюстрирует результат Многоточечной Статистики (MPS) с использованием алгоритма FILTERSIM для того же самого тренировочного образа из ФИГ.1а. Таким образом, при использовании алгоритма FILTERSIM авторы настоящего изобретения определяют фильтровые оценочные показатели для каждого тренировочного образа с использованием пригодного пикселированного шаблона. Эти оценочные показатели оцифровывают картины и их вероятности как наблюдаемые в данных измерений, затем генерируют реализации полных круговых изображений стенки скважины с использованием алгоритма FILTERSIM многоточечной статистики (ФИГ.1а).
ФИГ.2b, 2c и 2d показывают три реализации полного кругового изображения стенки скважины в кавернозной карбонатной формации, в которых ФИГ.2а показывает тот же самый тренировочный образ из ФИГ.1а. Следует отметить, что данные измерений являются первоочередными в каждой реализации, и имеются тонкие вариации в моделируемых областях. ФИГ.2b иллюстрирует результат первой реализации тренировочного образа из ФИГ.2а и согласуется с оригинальными данными измерений кавернозной формации из ФИГ.1а. ФИГ.2с иллюстрирует результат второй реализации тренировочного образа и согласуется с оригинальными данными измерений кавернозной формации из ФИГ.1а. ФИГ.3d иллюстрирует результат третьей реализации тренировочного образа из ФИГ.2а и согласуется с оригинальными данными измерений кавернозной формации из ФИГ.1а.
ФИГ.3а показывает статическое изображение каверн, проявляющихся как темные структурные признаки в изображениях каротажа во время бурения (LWD) (смотри работу авторов Xiao, L., Jun, C., Duo, Y.S., Han, S.Y., Xia, W.H. и Xi, W.Y., 2007: Fully integrated solution for LWD resistivity image application a case study from Beibu Gulf, China (Полностью интегрированное решение для применения картины резистивности в каротаже во время бурения в конкретном случае залива Бэйбу, Китай): Первая Индийская региональная конференция Общества профессиональных аналитиков скважинных каротажных диаграмм (SPWLA), Оценка формаций в горизонтальных скважинах, Мумбаи, 19-20 марта, 10 стр.), таким образом, что пятна проводимости иллюстрированы коричневым цветом, и непроводящие участки показаны белым цветом. ФИГ.3b показывает динамическое изображение пустот, проявляющихся как темные участки в изображениях, полученных при каротаже в ходе бурения (LWD) кавернозного карбоната, таким образом, что пятна проводимости показаны коричневым цветом, и непроводящие участки изображены белым цветом. Авторы Dehghani et al. (1999) предполагают, что вблизи каверн существуют зоны повышенной пористости и проницаемости. Смотри статью авторов Dehghani, K., Harris, P.M., Edwards, K.A. и Dees, W.T., 1999, Modeling a vuggy carbonate reservoir (Моделирование кавернозного карбонатного коллектора): AAPG Bulletin, том 83, стр.19-42.
ФИГ.4 полного кругового изображения стенки скважины с кавернозной пористостью (того же, как Фигуры 1 и 2) показывает контуры (зеленые линии), которые очерчивают области с меньшим удельным сопротивлением на электрическом изображении. Ориентации показаны вдоль верхних частей изображения. Сокращения: N = север; Е = восток; S = юг; и W = запад. Нет никаких вертикальных преувеличений. Диаметр долота составляет 8,5 дюйма (21,5 см).
ФИГ.5 показывают вид блок-схемы способа генерирования численных псевдокернов с использованием изображений скважины, цифровых образов породы и многоточечной статистики. Этап 100 включает в себя сбор глубинных интервалов диаграмм изображений скважины из коллектора, которые могут быть использованы в качестве тренировочных образов. Тренировочные образы ориентированы; двумерные (2D) скалярные массивы непрерывно переменных численных значений, с промежутками между башмаками и/или областями, которые требуют восстановления, таким образом, что башмаки представляют измеренные значения, и промежутки представляют собой не отраженные в изображениях части скважины.
Вновь с привлечением этапа 100 в ФИГ.5, оригинальные полные круговые изображения стенки скважины генерированы с помощью определенных каротажных приборов, таких как акустические устройства и устройств для каротажа во время бурения. В других случаях должны быть генерированы полные круговые изображения стенки скважины. Это в особенности справедливо для диаграмм на основе удельного сопротивления, которые обычно имеют промежутки между башмаками.
Опять с привлечением этапа 100 в ФИГ.5, согласно аспекту изобретения, для выбора глубинного интервала диаграммы изображения скважины, например, интервал может иметь глубину измерения 1, 3 или 10 футов (0,3, 1 или 3 метра). Пользователь может пожелать выбрать толстый или тонкий интервал, в зависимости от наблюдаемой степени слоистости, трещиноватости и прочих факторов неоднородности.
Полные круговые изображения стенки скважины могут быть генерированы с использованием алгоритма FILTERSIM в пределах многоточечной статистики (MPS), как отмечено в этапе 100 в ФИГ.5. В алгоритме FILTERSIM употребляются фильтровые оценочные показатели для группирования и затем моделирования картин в промежутках между башмаками, где отсутствуют данные измерений. Метод одиночной реализации сводится к случайным образом занятым положениям пикселей, и выводимым из набора фильтровых оценочных показателей для выбора пригодной картины для произвольного сайта. Данные измерений имеют первоочередную важность, поскольку таковые представляют условное моделирование. Картины, соседствующие с краями башмаков, согласуются с картинами, наблюдаемыми на реальных башмаках. Частотное распределение цветов моделированных пикселей, являющееся непрерывной переменной, в точности согласуется с частотным распределением измеренных цветов.
Этап 200 в ФИГ.5 включает получение по меньшей мере одного образца керна из коллектора и затем генерирование цифрового образа керна из полученного образца керна. Полученный керн адекватно отражает показательные признаки и/или структуру одного или более глубинных интервалов скважины и/или коллектора. Например, цифровые образы пород или керна, такие как СТ-томограммы, могут быть использованы в качестве тренировочных образов. Тренировочные образы представляют собой трехмерные (3D) массивы дискретных численных значений. Например, в двухфациальной модели порода имеет численное значение 0, и поры имеют численное значение 1. В трехфациальной модели порода имеет численное значение 0, поры имеют численное значение 1, и пятна проводимости имеют численное значение 2. Нет никаких ограничений в отношении числа фаций. Контуры отдельных фациальных тел (объемов) могут иметь любые формы или размер.
Этап 300 в ФИГ.5 включает предварительное моделирование собранных данных диаграммы изображения скважины, таких как генерированные полные круговые изображения стенки скважины.
Этап 300а в ФИГ.5 представляет выбор глубинного интервала диаграммы изображения скважины. Полные круговые изображения стенки скважины генерируют с использованием алгоритма FILTERSIM в пределах Многоточечной Статистики (MPS), в которой MPS-моделирование извлекает геологические структуры из тренировочных образов и привязывает их к местам расположения данных. В алгоритме FILTERSIM используются фильтровые оценочные показатели для группирования и затем моделирования картин в промежутках между башмаками, где данные измерений отсутствуют.
Этап 300b в ФИГ.5 представляет округление в петрологические фации, которые идентифицируют, например: поры или каверны; пятна проводимости или резистивности в породе на стенке скважины; и границы слоев или скелет породы. Метод одиночной реализации сводится к случайным образом занятым положениям пикселей, и выводимым из набора фильтровых оценочных показателей для выбора пригодной картины для произвольного сайта. Данные измерений имеют первоочередную важность, поскольку таковые представляют условное моделирование. Картины, соседствующие с краями башмаков, согласуются с картинами, наблюдаемыми на реальных башмаках. Частотное распределение цветов моделированных пикселей, являющееся непрерывной переменной, и в точности согласуется с частотным распределением измеренных цветов.
Этап 300с в ФИГ.5 представляет сворачивание полных круговых изображений стенки скважины в Масштабированные Цилиндрические Формы. В частности, для текущих интерпретаций затруднительно исследовать изображения скважины в трехмерном (3D) представлении. Поэтому обычным является рассечение скважины вдоль географического севера и затем развертка цилиндра с получением двумерного (2D) изображения. В сильно искривленных и горизонтальных скважинах обычной практикой является рассечение изображения скважины вдоль верха скважины. Планарные структурные признаки, которые разделяют цилиндрическую скважину на части, проявляются как синусоидальные волны в двумерном (2D) виде. Для генерирования трехмерных (3D) численных псевдокернов авторам настоящего изобретения нужно свернуть двумерные (2D) изображения скважины до их оригинальной трехмерной (3D) формы. Чтобы сделать это, авторы настоящего изобретения должны знать диаметр скважины. Авторы настоящего изобретения могут без труда определить это из диаграмм диаметра скважины, которые считываются с оригинального изображения скважины. Изображения должны быть в масштабе 1:1, то есть нет никакого вертикального преувеличения.
Этап 400 в ФИГ.5 представляет предварительное моделирование полученного цифрового образа керна. В этапе 400а производят преобразование из 2 фаций в 3 фации так, чтобы были идентифицированы поры или каверны, пятна проводимости и скелет породы в цифровом образе породы. Например, если пятна проводимости не были идентифицированы в цифровом образе породы (тренировочном образе), то они могут быть смоделированы подобным преобразованием поровых фаций при фиксированном числе элементов объемного изображения (вокселов). Этим способом в численном псевдокерне может быть извлечена крупномасштабная неоднородность. Типично разрешение элементов объемного изображения цифрового образа породы или тренировочного образа керна является более мелким, чем разрешение полного кругового изображения стенки скважины. Для обеспечения того, что полученная модель псевдокерна будет иметь признаки в масштабах, согласующихся с полным круговым изображением стенки скважины, тренировочный образ отбирают приблизительно в соответствии с отношением разрешения цифрового образа породы к разрешению полного кругового изображения стенки скважины.
Этап 500 в ФИГ.5 представляет генерирование реализаций численных псевдокернов путем объединения структур, заимствованных из собранных цифровых данных кернового анализа и собранных данных диаграммы изображений скважины. Этап 500а представляет применение алгоритма MPS SNESIN для генерирования реализаций численных псевдокернов для 2 или более фаций так, чтобы модифицировать реализации для согласования с размерами и формами фаций, наблюдаемыми в тренировочных образах цифрового образа породы и полных круговых изображениях стенки скважины. Более чем 2 фации могут быть смоделированы в случаях, где пятна проводимости были картографированы (Фигуры 3 и 4) в полных круговых изображениях стенки скважины и цифровых образах пород. Если пятна проводимости не были идентифицированы в цифровом образе породы (тренировочном образе), то они могут быть смоделированы подобным преобразованием поровых фаций при фиксированном числе элементов объемного изображения (вокселов). Этим способом в численном псевдокерне может быть извлечена крупномасштабная неоднородность. Радиальный размер и высота численного псевдокерна ограничены только объемом доступной для использования памяти компьютера.
Этап 600 в ФИГ.5 представляет повторную выборку численных псевдокернов для радиальной координатной сетки. Для проведения исследования потока в численном псевдокерне производят преобразование декартовой (прямоугольной) координатной сетки численной модели псевдокерна, генерированной в процессе предшествующих этапов, в радиальную координатную сетку в форме цилиндрических координат. Каждому декартову элементу объемного изображения приписывают постоянную пористость или проницаемость согласно его типу породы (скелет, каверна или пятно проводимости). Для каждой декартовой ячейки в радиальной координатной сети, поскольку она состоит из многих декартовых элементов объемного изображения, генерируют усредненные значения пористости и проницаемости. Усредненная пористость получается путем арифметического усреднения всей пористости декартовых элементов трехмерного изображения внутри ячейки; проницаемость получают выполнением геометрического усреднения.
Этап 700 в ФИГ.5 представляет выполнение моделирований потока в области, приближенной к скважине. Численные моделирования потока текучих сред, например, заводнения, проводят на построенном псевдокерне для оценки важных параметров, таких как обводненность пласта, коэффициент нефтеотдачи и коэффициент извлечения. Справочная таблица капиллярного давления и относительной проницаемости для различных фаций в численном псевдокерне дает значения, которые вводят в программу имитации потока, например, пакет Ecllipse. Это является ключевым этапом для количественной оценки влияния гетерогенности карбонатной породы на поток текучих сред, основываясь на модели псевдокерна. Капиллярное давление и относительная проницаемость могут быть получены из данных интерактивной программы кернового анализа (SCAL) или значений капиллярного давления при нагнетании ртути (MICP, Mercury Injection Capillary Pressure) (при доступности таковых) для кернов такого же типа породы. Более обобщенно, способ моделирования поровой сетевой структуры может быть использован для оценки вышеупомянутых параметров различных типов пород.
Этап 800 в ФИГ.5 представляет определение процесса улучшения эффектов смачиваемости в параметрах оценки, таких как обводненность пласта, коэффициенты нефтеотдачи и коэффициент извлечения.
ФИГ.6 показывает тренировочный образ из ФИГ.1а в полупрозрачном трехмерном (3D) виде СТ-томограммы пластинчатого образца кавернозного карбоната (приблизительно 6 дюймов (152,4 мм) высотой и 4 дюйма (101,6 мм) в диаметре), таким образом, что каверны проявляются цветом от красного до серого, и скелет породы иллюстрирован голубым цветом. ФИГ.6 также показывает выбранный тренировочный образ, СТ-томограмму кавернозного карбоната (автор Gowelly, S., 2003, 3-D analysis of vug connectivity, Indian Basin field, New Mexico (Трехмерный анализ связности кавернозных структур, месторождение бассейна Indian, Нью-Мексико): неопубликованная магистерская диссертация, Colorado School of Mines (Колорадская горная школа), Голден, Колорадо). Следует отметить, что ФИГ.1а показывает трехфутовый (однометровый) интервал диаграммы изображения скважины, с такой же глубины и в такой же формации, и что каверны представляют собой крупные беспорядочные поры, видимые невооруженным глазом. Более того, в диаграмме изображения скважины каверны проявляются как темные пятна, поскольку они заполнены буровым раствором на водной основе, и они являются электропроводными.
ФИГ.7 показывает изображения скважины, свернутые в цилиндрическую форму соответственно диаметру скважины (диаметр скважины приблизительно 8,5 дюйма (215,9 мм), и длина интервала приблизительно 3 фута, или 1 метр), на конкретной глубине. Тренировочный образ из СТ-томограмм ФИГ.6 выполнен в надлежащем масштабе и правильно позиционирован на своей должной глубине в центре изображений скважины, в котором каверны иллюстрированы красным цветом, и скелет породы показан светло-синим цветом. Как отмечено выше, изображения скважины свернуты в трехмерную (3D) цилиндрическую форму так, что полные круговые изображения стенки скважины не показаны, поскольку это позволяет представить вид относительных масштабов тренировочного образа (СТ-томограммы) (в центре цилиндра) и изображения диаграммы. Для картины модели численного псевдокерна (смотри ниже ФИГ.8) будет отмечено, что используют тренировочный образ и полные круговые изображения стенки скважины.
ФИГ.8 иллюстрирует результат генерирования численного псевдокерна из тренировочного образа и полного кругового изображения стенки скважины, который соответствует ФИГ.7 таким образом, что каверны иллюстрированы красным цветом, и скелет породы иллюстрирован темно-синим цветом. Следует отметить, что длина интервала может составлять 3 фута (1 метр), и диаметр скважины может составлять 8,5 дюйма (22 см).
ФИГ.9 иллюстрирует результат генерирования численного псевдокерна из тренировочного образа и полного кругового изображения стенки скважины, который соответствует ФИГ.7 таким образом, что каверны невидимы, и скелет породы иллюстрирован серым цветом. Далее, произвольно выделенный срез (смотри верхнюю часть ФИГ.9) показывает, что это представляет собой трехмерную (3D) модель, с множеством пор в каждом срезе (приблизительная длина интервала составляет 1 фут, или 0,3 метра, и диаметр скважины составляет приблизительно 8,5 дюйма (215,9 мм)).
ФИГ.10 иллюстрирует результат генерирования численного псевдокерна из тренировочного образа и полного кругового изображения стенки скважины, который соответствует ФИГ.6. Численный псевдокерн (смотри ФИГ.9) показывает применение кругового подобного преобразования с 8-пиксельным радиусом вокруг каждой поры. Пятна проводимости (иллюстрированные красным цветом) похожи на контуры вокруг пятен проводимости, как показано в ФИГ.4. Поэтому данная модель имеет 3 петрофизических фации: поры или каверны (иллюстрированные зеленым цветом), пятна проводимости (иллюстрированные красным цветом) и скелет породы (иллюстрированный голубым цветом). Пятна проводимости создают трехмерную (3D) связность между порами или кавернами, и позволяют выявить гетерогенность, каковая изначально присуща большинству карбонатных пород.
ФИГ.11 показывает численный псевдокерн, как в ФИГ.10, с невидимым скелетом породы, который выделяет трехмерную (3D) взаимосвязанную природу пор или каверн (иллюстрированных зеленым цветом) и пятен проводимости (иллюстрированных красным цветом). Следует отметить, что длина интервала может составлять 3 фута (1 метр), и диаметр скважины может составлять 8,5 дюйма (22 см).
ФИГ.12 показывает численный псевдокерн, как в ФИГ.10, и сложную трехмерную (3D) форму пор или каверн (иллюстрированных зеленым цветом), и как пятна проводимости, так и скелет породы являются невидимыми. Следует отметить, что длина интервала может составлять 3 фута (1 метр), и диаметр скважины может составлять 8,5 дюйма (22 см).
ФИГ.13 показывает численные псевдокерны, которые могут быть подвергнуты повторной выборке или преобразованию координатной сетки в радиальные координатные сетки, в которых радиальные сетки могут быть разделены на слои, основываясь на слоях, наблюдаемых в изображениях скважины или других геологических разрезах скважины. ФИГ.13 также показывает радиальную координатную сетку, которая генерирована для исследования характеристик потока в численной модели псевдокерна. Следует отметить, что внутренняя часть (приблизительно 4 дюйма (101,6 мм) в диаметре) оригинального численного псевдокерна была выбурена, чтобы обеспечить возможность размещения микропродуцентов. Микроинжекторы могут быть размещены вокруг наружной границы псевдокерна.
ФИГ.14а показывает кривую относительной проницаемости, которая используется для пятна проводимости в моделировании потока; в которой есть три различных кривых относительной проницаемости для каждого из трех типов пород в модели псевдокерна: таких как каверны, пятна проводимости и непроницаемый скелет породы. В частности, ФИГ.14а показывает кривую относительной проницаемости, которая была использована для пятна проводимости в моделировании потока. Следует отметить, что псевдокерн как для ФИГ.14а, так и для ФИГ.14b может иметь высоту приблизительно 1 фут (0,3 метра), с наружным диаметром приблизительно 8,5 дюйма (22 см) (или ширина керна составляет 8,5 дюйма (22 см), и внутренний диаметр составляет приблизительно 4 дюйма (101,6 мм)).
ФИГ.14b показывает результат моделирования потока через численный псевдокерн, таким образом, что ряд микроинжекторов воды окружает наружный диаметр, ряд микропродуцентов окружает внутренний диаметр псевдокерна: цвета представляют нефтенасыщенность (So), где в этой модели потока показано образование неоднородных языков и прорывов, согласно вариантам осуществления изобретения. Следует отметить, что ФИГ.14b показывает профиль нефтенасыщенности заводненного численного псевдокерна.
Далее, в то время как настоящее изобретение было описано со ссылкой на примерные варианты осуществления, понятно, что термины, которые были здесь использованы, представляют собой скорее описательные и иллюстративные термины, нежели ограничительные термины. Изменения могут быть сделаны в пределах содержания прилагаемых пунктов формулы изобретения, как теперь заявленных и как измененных, без выхода за рамки области и смысла настоящего изобретения в его аспектах. Хотя настоящее изобретение было описано здесь со ссылкой на конкретные средства, материалы и варианты осуществления, настоящее изобретение не предполагается быть ограниченным раскрытыми здесь подробностями; скорее настоящее изобретение распространяется на все функционально эквивалентные структуры, способы и варианты применения, такие как находящиеся в пределах области прилагаемых пунктов формулы изобретения.
| название | год | авторы | номер документа |
|---|---|---|---|
| МНОГОМАСШТАБНОЕ ЦИФРОВОЕ МОДЕЛИРОВАНИЕ ПОРОДЫ ДЛЯ МОДЕЛИРОВАНИЯ ПЛАСТА | 2012 |
|
RU2573739C2 |
| СПОСОБ ПОЛУЧЕНИЯ ХАРАКТЕРИСТИК ГЕОЛОГИЧЕСКОЙ ФОРМАЦИИ, ПЕРЕСЕКАЕМОЙ СКВАЖИНОЙ | 2009 |
|
RU2440591C2 |
| СПОСОБ ОПРЕДЕЛЕНИЯ РЕПРЕЗЕНТАТИВНЫХ ЭЛЕМЕНТОВ ПЛОЩАДЕЙ И ОБЪЕМОВ В ПОРИСТОЙ СРЕДЕ | 2012 |
|
RU2544884C1 |
| СПОСОБЫ ПОСТРОЕНИЯ 3-МЕРНЫХ ЦИФРОВЫХ МОДЕЛЕЙ ПОРИСТОЙ СРЕДЫ С ИСПОЛЬЗОВАНИЕМ КОМБИНАЦИИ ДАННЫХ ВЫСОКОГО И НИЗКОГО РАЗРЕШЕНИЯ И МНОГОТОЧЕЧНОЙ СТАТИСТИКИ | 2012 |
|
RU2576501C2 |
| СПОСОБ ПОСТРОЕНИЯ ГЕОЛОГИЧЕСКОЙ И ГИДРОДИНАМИЧЕСКОЙ МОДЕЛЕЙ МЕСТОРОЖДЕНИЙ НЕФТИ И ГАЗА | 2011 |
|
RU2475646C1 |
| СПОСОБ И СИСТЕМА ОЦЕНИВАНИЯ ЗАПАСОВ УГЛЕВОДОРОДОВ В НЕОДНОРОДНОМ ПЛАСТЕ | 2018 |
|
RU2778354C1 |
| СПОСОБ АВТОМАТИЗИРОВАННОГО ПОСТРОЕНИЯ ГЕОЛОГИЧЕСКОЙ МОДЕЛИ ЗАЛЕЖИ | 2020 |
|
RU2799775C2 |
| СПОСОБ РЕКОНСТРУКЦИИ ТОНКОЙ СТРУКТУРЫ ГЕОЛОГИЧЕСКОГО ОБЪЕКТА И ПРОГНОЗА ЕГО ФЛЮИДОНАСЫЩЕНИЯ | 2014 |
|
RU2563323C1 |
| СПОСОБ ПОСТРОЕНИЯ ГЕОЛОГИЧЕСКОЙ МОДЕЛИ МЕСТОРОЖДЕНИЙ НЕФТИ И ГАЗА | 2014 |
|
RU2541348C1 |
| Способ отбора и реконструкции структуры шлама для определения коллекторских свойств и моделирования фильтрационных и петрофизических характеристик пород - технология "Псевдокерн" | 2022 |
|
RU2784104C1 |
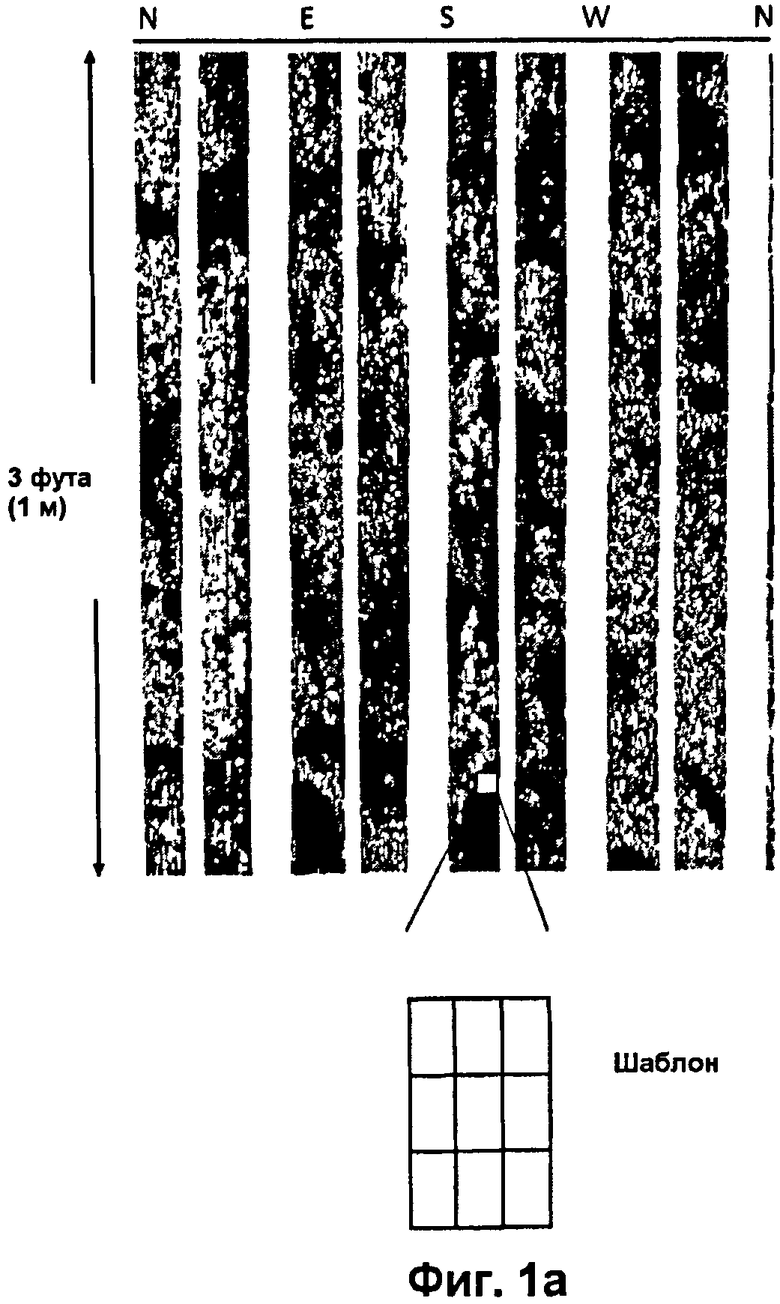

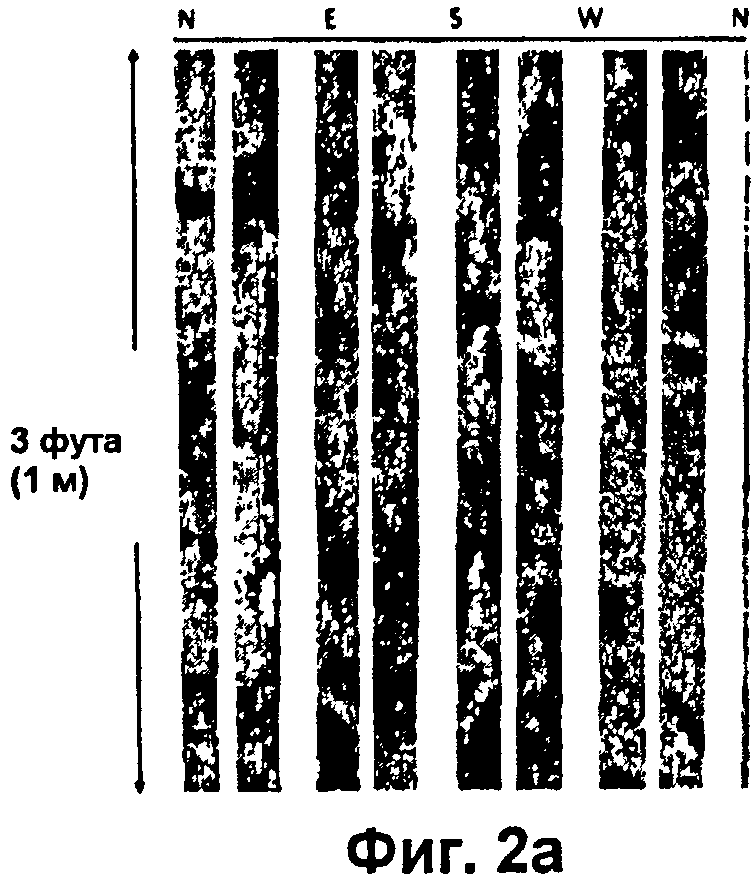



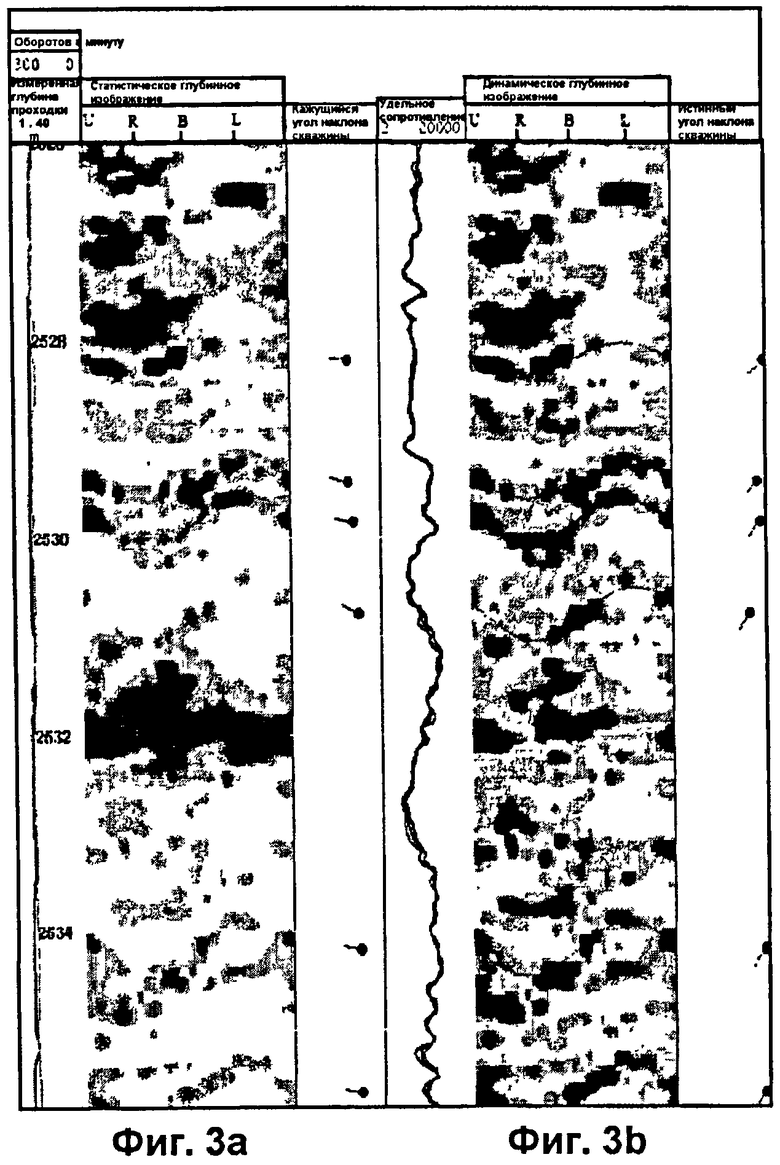
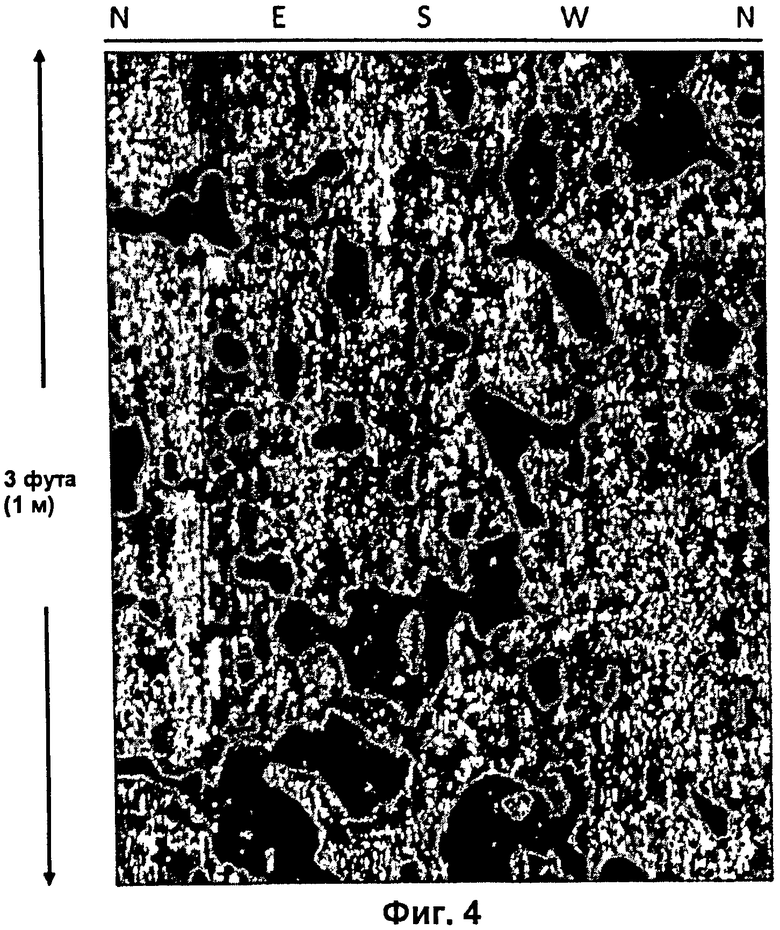


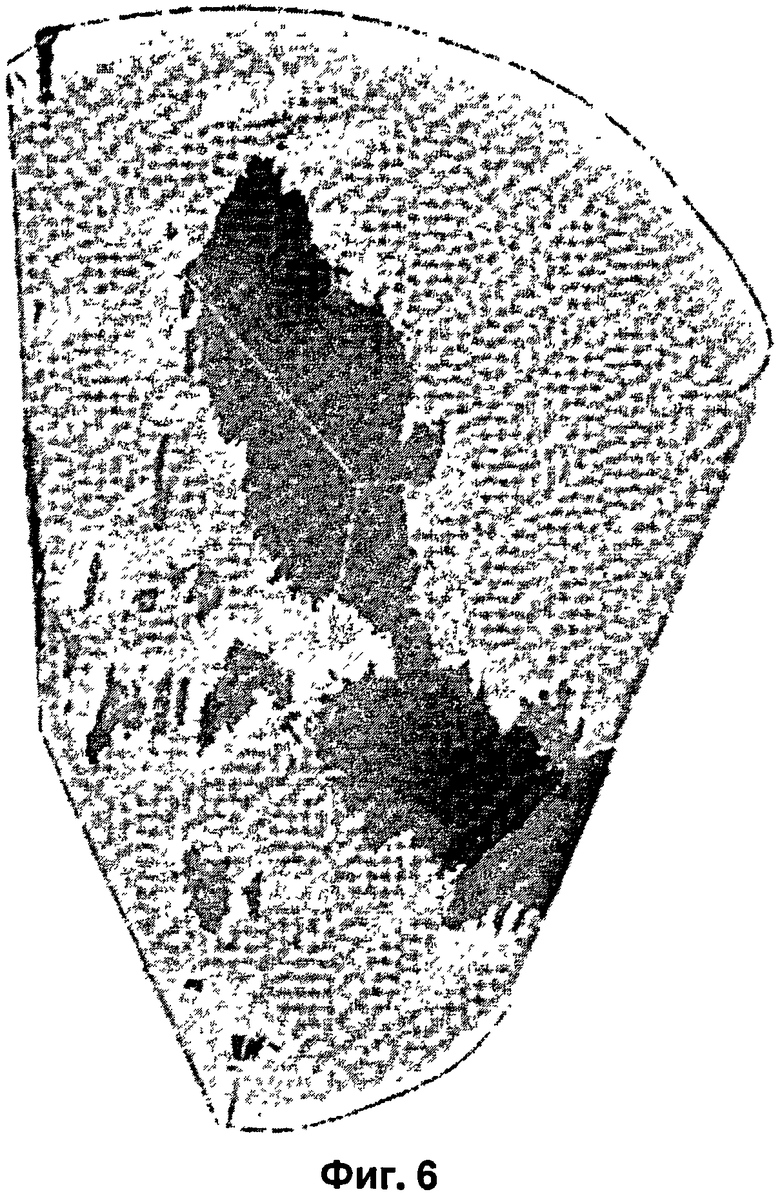





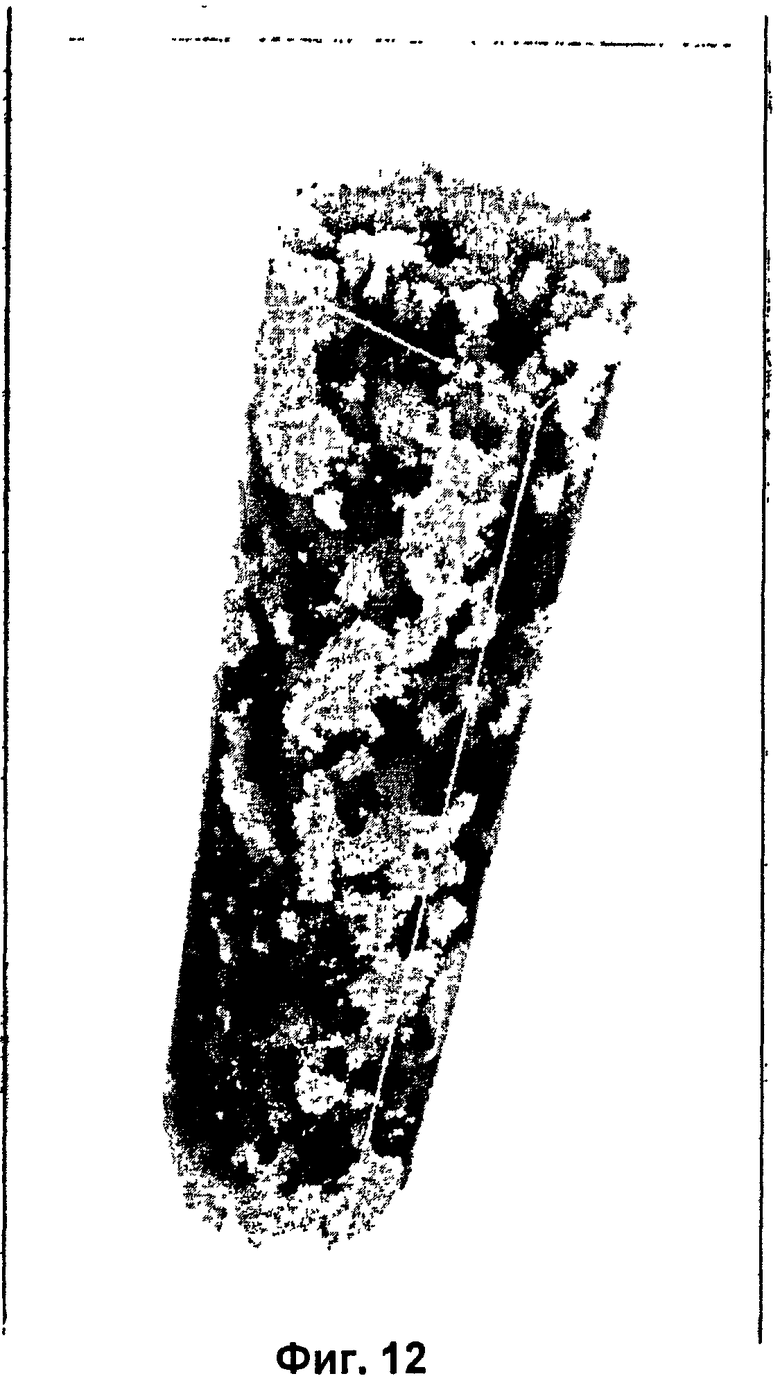

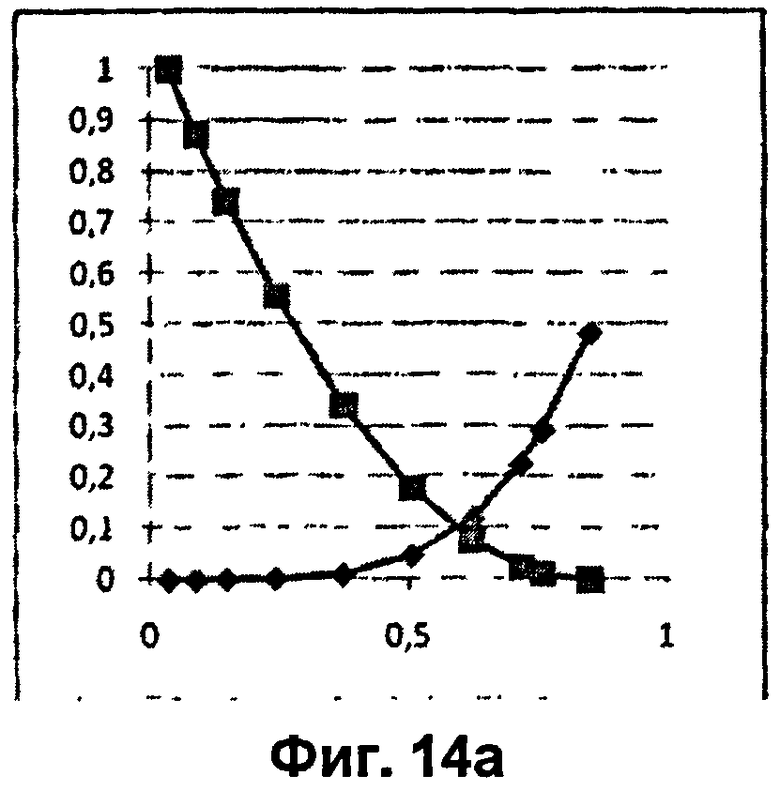
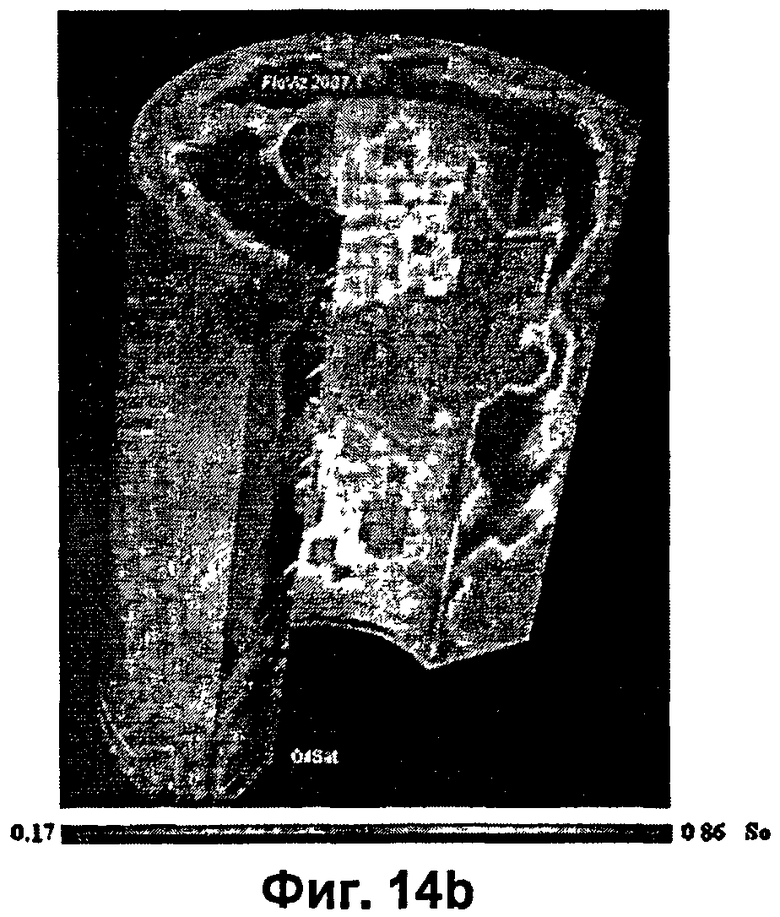
Заявленный способ относится к области геофизических исследований в подземных скважинах, а именно для обозначения и картографирования границы между слоями породы, например границы пластов, и для визуализации и ориентирования разломов и сдвигов. Способы формирования численной модели псевдокерна, содержащие этапы, на которых: a) получают каротажные данные из коллектора, которые включают в себя глубинные интервалы коллектора, и обрабатывают каротажные данные в часть данных, по меньшей мере, одного интерпретируемого изображения скважины, имеющего неидентифицированные данные изображения скважины; b) исследуют одну из частей данных, по меньшей мере, одного интерпретируемого изображения скважины, другие обработанные каротажные данные или и те и другие для генерирования неидентифицированных данных изображения скважины, затем обрабатывают генерированные неидентифицированные данные изображения скважины в часть данных, по меньшей мере, одного интерпретируемого изображения скважины так, чтобы генерировать данные, по меньшей мере, одного свернутого полного кругового изображения стенки скважины; c) получают один из, по меньшей мере, одного керна из коллектора, часть каротажных данных или и то и другое, и генерируют цифровые данные керна из одного из полученного по меньшей мере одного керна, часть каротажных данных или и того и другого, так что сгенерированные цифровые данные керна представляют один из признаков или структур одного или более глубинных интервалов коллектора; и d) обрабатывают часть сгенерированных цифровых данных керна, часть данных, по меньшей мере, одного интерпретируемого изображения скважины или часть каротажных данных для генерирования реализации численной модели псевдокерна. Технический результат заключается в создании трехмерных (3D) численных кернов по данным компьютерной рентгеновской томографии (СТ-сканов, СТ-томограмм) и формированию микроизображений (FMI) геологического разреза скважины, и выполнению моделирования потока в этих численных кернах для понимания маршрутов потока текучих сред и коэффициентов отдачи в выбранном коллекторе. 2 н. и 30 з.п. ф-лы, 21 ил.
1. Способ формирования численной модели псевдокерна, содержащий этапы, на которых:
a) получают каротажные данные из коллектора, которые включают в себя глубинные интервалы коллектора, и обрабатывают каротажные данные в часть данных, по меньшей мере, одного интерпретируемого изображения скважины, имеющего неидентифицированные данные изображения скважины;
b) исследуют одну из частей данных, по меньшей мере, одного интерпретируемого изображения скважины, другие обработанные каротажные данные или и те и другие для генерирования неидентифицированных данных изображения скважины, затем обрабатывают генерированные неидентифицированные данные изображения скважины в часть данных, по меньшей мере, одного интерпретируемого изображения скважины так, чтобы генерировать данные, по меньшей мере, одного свернутого полного кругового изображения стенки скважины;
c) получают один из, по меньшей мере, одного керна из коллектора, часть каротажных данных или и то и другое и генерируют цифровые данные керна из одного из полученного по меньшей мере одного керна, часть каротажных данных или и того и другого, так что сгенерированные цифровые данные керна представляют один из признаков или структур одного или более глубинных интервалов коллектора; и
d) обрабатывают часть сгенерированных цифровых данных керна, часть данных, по меньшей мере, одного интерпретируемого изображения скважины или часть каротажных данных для генерирования реализации численной модели псевдокерна.
2. Способ по п.1, в котором часть данных, по меньшей мере, одного интерпретируемого изображения скважины представляет собой тренировочный образ, который представляет собой двумерные (2D) скалярные массивы непрерывно изменяемых численных значений.
3. Способ по п.1, в котором часть данных, по меньшей мере, одного интерпретируемого изображения скважины состоит из обработанных исходных данных, которые состоят из измеренных значений и неизмеренных значений.
4. Способ по п.1, в котором неидентифицированные данные изображения скважины представляют одно из неизмеренных значений части данных, по меньшей мере, одного интерпретируемого изображения скважины или пробелы данных в части данных, по меньшей мере, одного интерпретируемого изображения скважины.
5. Способ по п.4, в котором пробелы данных выбраны из группы, состоящей из одного из, по меньшей мере: одного поврежденного башмака в коллекторе, по меньшей мере, одной поврежденной области в коллекторе, по меньшей мере, одного башмака с ненадлежащим давлением прижима башмака к стенке скважины в коллекторе, по меньшей мере, одного башмака с затрудненным контактом со стенкой скважины в коллекторе или, по меньшей мере, одного неработающего башмака в коллекторе.
6. Способ по п.1, в котором другие обработанные каротажные данные выбраны из группы, состоящей из одного из наборов данных каротажа во время бурения или данных каротажной диаграммы, зарегистрированных прибором, опускаемым в скважину на кабеле, или их комбинации.
7. Способ по п.6, в котором данные каротажной диаграммы, зарегистрированные прибором, опускаемым в скважину на кабеле, включают в себя, по меньшей мере, одну из каротажных диаграмм, полученных с использованием гамма-излучения, плотностного, акустического, нейтронного каротажа, кавернограммы или каротажа сопротивления.
8. Способ по п.1, в котором данные, по меньшей мере, одного свернутого полного кругового изображения стенки скважины представляют собой одно из двумерного (2D), трехмерного (3D) представления или их совместно.
9. Способ по п.1, в котором генерирование, по меньшей мере, одного полного кругового изображения стенки скважины содержит этапы, на которых:
1) выбирают глубинный интервал диаграммы изображения скважины из глубинных интервалов коллектора, обрабатывают глубинный интервал диаграммы изображения скважины с использованием алгоритма многоточечной статистики (MPS), в котором алгоритм многоточечной статистики (MPS) предусматривает моделирование, извлекающее неидентифицированные геологические структуры из части данных, по меньшей мере, одного интерпретируемого изображения скважины, чтобы идентифицировать места расположений данных в части данных, по меньшей мере, одного интерпретируемого изображения скважины;
2) обрабатывают идентифицированные места расположений данных с использованием фильтровых оценочных показателей для группирования и затем моделирования картин в неидентифицированных данных изображения скважины, в результате чего неидентифицированные данные изображения скважины представляют одно из неизмеренных значений части, по меньшей мере, одного интерпретируемого изображения скважины или пробелы данных в части, по меньшей мере, одного интерпретируемого изображения скважины;
3) идентифицируют петрофизические фации коллектора, причем петрофизические фации выбраны из группы, состоящей из трещин, пор, каверн, пятен проводимости в породах в стенке скважины коллектора, резистивных участков пород в стенке скважины коллектора, границ слоев или скелета породы; и
4) обрабатывают неидентифицированные данные изображения скважины в часть, по меньшей мере, одного интерпретируемого изображения скважины, чтобы генерировать, по меньшей мере, одно полное круговое изображение стенки скважины, затем при известном диаметре скважины сворачивают, по меньшей мере, одно полное круговое изображение стенки скважины в исходную трехмерную (3D) форму, в результате чего численный псевдокерн модифицируется так, чтобы соответствовать одной из свернутых частей полного кругового изображения стенки скважины или части, по меньшей мере, одного интерпретируемого изображения скважины.
10. Способ по п.1, в котором каротажные данные выбирают из группы, состоящей из одного набора каротажных данных, имеющего множественные глубины исследования, аналоговых моделей данных кернового анализа из одного или более коллекторов, или их комбинации.
11. Способ по п.1, в котором генерирование цифровых данных керна состоит в идентификации петрофизических фаций из одного из собранного, по меньшей мере, одного керна или части каротажных данных, причем петрофизические фации выбирают из группы, состоящей из трещин, пор, каверн, пятен проводимости в породах в стенке скважины коллектора, резистивных участков пород в стенке скважины коллектора, границ слоев или скелета породы.
12. Способ по п.11, в котором идентификация петрофизических фаций включает в себя моделирование путем подобного преобразования других петрофизических фаций собранного, по меньшей мере, одного керна посредством фиксированного числа элементов объемного изображения.
13. Способ по п.1, в котором, по меньшей мере, один керн получают, по меньшей мере, из одного другого коллектора.
14. Способ по п.1, в котором второй керн, по меньшей мере, из одного керна получают из одного или более коллекторов.
15. Способ по п.1, в котором этап (d) включает в себя построение графика цифрового файла генерированных реализаций численной модели псевдокерна в виде одного из цифрового носителя или бумажного носителя.
16. Способ по п.1, в котором генерирование реализации численной модели псевдокерна на этапе (d) включает в себя использование алгоритма многоточечной статистики (MPS) для генерирования реализации численных псевдокернов для двух или более петрофизических фаций, чтобы модифицировать реализации для соответствия размерам и формам фаций, наблюдаемых в части, по меньшей мере, одного интерпретируемого изображения скважины, части генерированных цифровых данных керна и генерированным данным, по меньшей мере, одного свернутого полного кругового изображения стенки скважины.
17. Способ по п.16, в котором две или более петрофизических фаций выбраны из группы, состоящей из собранного, по меньшей мере, одного керна, части каротажных данных или и то и другое, в котором петрофизические фации выбраны из группы, состоящей из трещин, пор, каверн, пятен проводимости в породах в стенке скважины коллектора, резистивных участков пород в стенке скважины коллектора, границ слоев или скелета породы.
18. Способ по п.15, дополнительно содержащий этап, на котором:
е) производят повторную выборку численных псевдокернов этапа (d) с преобразованием в радиальную координатную сетку.
19. Способ по п.18, в котором радиальная координатная сетка предусмотрена для исследования потока в численной модели псевдокерна и включает в себя этапы, на которых:
1) строят цилиндрическую координатную сетку, имеющую одну или более форм или один или более слоев;
2) производят повторную выборку с преобразованием численной модели псевдокерна из декартовых координат, каждый элемент объемного изображения которого имеет постоянную пористость или постоянную проницаемость в соответствии со связанным с типом породы элемента объемного изображения, в цилиндрические координаты, в которых каждая ячейка цилиндрической координатной сетки включает в себя множество декартовых элементов объемного изображения численной модели псевдокерна;
3) назначают каждой цилиндрической ячейке среднюю пористость и среднюю проницаемость на основании включенных множественных декартовых элементов объемного изображения; и
4) назначают каждой цилиндрической ячейке кривых относительную проницаемость и капиллярное давление на основании доминантного типа породы включенных множественных декартовых элементов объемного изображения с использованием справочной таблицы для одного из значений капиллярного давления, относительной проницаемости или их обоих, для различных фаций в численном псевдокерне, которое вводят в программу моделирования потока, тем самым для оцифровывания влияния гетерогенности породы на поток текучей среды на основании модели псевдокерна, с привлечением одного из данных программы специального кернового анализа (SCAL), значений капиллярного давления при нагнетании ртути (MICP), моделирования поровой сетевой структуры или их комбинации, одного или более кернов, имеющих тот же тип породы.
20. Способ по п.19, в котором связанный тип породы выбирают из группы, состоящей из трещин, пор, каверн, пятен проводимости в породах в стенке скважины коллектора, резистивных участков пород в стенке скважины коллектора, границ слоев или скелета породы.
21. Способ по п.18, дополнительно содержащий этап, на котором:
f) выполняют моделирование потока для одного или более географически связанных коллекторов, такого как область вблизи скважины.
22. Способ по п.21, в котором выполнение моделирований потока включает в себя одно из однофазного или многофазного потока так, что моделирование потока выполняют на расчетной численной модели псевдокерна этапа (е), чтобы оценить один или более параметров.
23. Способ по п.22, в котором один или более параметров выбирают из группы, состоящей из пористости, проницаемости, капиллярного давления, относительной проницаемости, обводненности пласта, коэффициента нефтеотдачи или коэффициента извлечения.
24. Способ по п.21, дополнительно содержащий этап, на котором:
g) проводят анализ чувствительности к относящимся к потоку параметрам, чтобы определить процесс для одного из заводнения, нагнетания газа в пласт, нагнетания пара в пласт или добычи нефти с увеличенной нефтеотдачей пласта (EOR).
25. Способ по п.24, в котором относящиеся к потоку параметры выбирают из группы, состоящей из пористости, проницаемости, капиллярного давления, относительной проницаемости, обводненности пласта, коэффициента нефтеотдачи или коэффициента извлечения.
26. Способ по п.21, дополнительно содержащий этап, на котором:
g) определяют процесс для оценки эффектов смачиваемости в оцениваемых параметрах, в котором оцениваемые параметры включают в себя один из: капиллярного давления, относительной проницаемости, обводненности пласта, коэффициента нефтеотдачи или коэффициента извлечения.
27. Способ получения численной модели псевдокерна, содержащий этапы, на которых:
а) получают каротажные данные из коллектора, который включает в себя глубинные интервалы коллектора, и обрабатывают каротажные данные в часть данных, по меньшей мере, одного интерпретируемого изображения скважины;
b) исследуют одну из частей данных, по меньшей мере, одного интерпретируемого изображения скважины, другие обработанные каротажные данные или и то и другое для генерирования, по меньшей мере, одного свернутого полного кругового изображения стенки скважины;
c) получают одно из, по меньшей мере, одного керна из коллектора, части каротажных данных или и то и другое и генерируют цифровые данные керна из одного из полученного, по меньшей мере, одного керна, из части каротажных данных или и того и другого, так что генерированные цифровые данные керна представляют один из признаков или структур одного или более глубинных интервалов коллектора; и
d) обрабатывают часть сгенерированных цифровых данных керна, часть данных, по меньшей мере, одного интерпретируемого изображения скважины, часть каротажных данных или комбинации таковых для генерирования реализации численной модели псевдокерна.
28. Способ по п.27, в котором часть интерпретируемых данных, по меньшей мере, одного изображения скважины представляет собой тренировочный образ, который представляет собой двумерный (2D) скалярный массив непрерывно изменяемых численных значений.
29. Способ по п.27, в котором другие обработанные каротажные данные выбирают из группы, состоящей из наборов данных каротажа во время бурения или данных каротажной диаграммы, зарегистрированных прибором, опускаемым в скважину на кабеле, или их комбинации.
30. Способ по п.27, в котором каротажные данные выбирают из группы, состоящей из наборов каротажных данных, имеющих множественные глубины исследования, или аналоговых моделей данных керна из одного или более коллекторов или некоторой комбинации таковых.
31. Способ по п.27, в котором генерирование цифровых данных керна состоит в идентификации петрофизических фаций из одного из собранного, по меньшей мере, одного керна или части каротажных данных, причем петрофизические фации выбирают из группы, состоящей из трещин, пор, каверн, пятен проводимости в породах в стенке скважины коллектора, резистивных участков пород в стенке скважины коллектора, границ слоев или скелета породы.
32. Способ по п.31, в котором идентификация петрофизических фаций включает в себя моделирование путем подобного преобразования других петрофизических фаций собранного, по меньшей мере, одного керна посредством фиксированного числа элементов объемного изображения.
| US 2007239359 A1, 11.10.2007 | |||
| US 5838634 A, 17.11.1998 | |||
| US 4821164 A, 11.04.1989. |
Авторы
Даты
2012-02-27—Публикация
2009-04-10—Подача