Ссылка на родственные заявки
Данная заявка притязает на приоритет предварительной заявки США № 60/823,753, поданной 28 августа 2006 г., под названием WET GAS MEASUREMENT SYSTEM, которая включена в полном объеме посредством ссылки. Предварительная заявка США № 60/913,148, поданная 20 апреля 2007 г. под названием WET GAS CALCULATIONS, включена в полном объеме посредством ссылки.
Область техники, к которой относится изобретение
Данное описание относится к расходомерам.
Уровень техники
Расходомеры обеспечивают информацию о материалах, транспортируемых по трубопроводу. Например, массовые расходомеры обеспечивают прямое указание массы материала, транспортируемого по трубопроводу. Аналогично, плотностные расходомеры или денситометры обеспечивают указание плотности материала, текущего через трубопровод. Массовые расходомеры также могут обеспечивать указание плотности материала.
Массовые расходомеры кориолисова типа базируются на общеизвестном эффекте Кориолиса, в котором материал, текущий через вращающийся трубопровод, становится радиально перемещающейся массой, которая подвергается действию силы Кориолиса и потому испытывает ускорение. Многие массовые расходомеры кориолисова типа порождают силу Кориолиса за счет синусоидального колебания трубопровода относительно оси поворота, перпендикулярной длине трубопровода. В таких массовых расходомерах, сила реакции Кориолиса, действующая на массу движущейся текучей среды, переносится на сам трубопровод и проявляется как отклонение или смещение трубопровода в направлении вектора силы Кориолиса в плоскости вращения.
Энергия подается на трубопровод механизмом возбуждения, который прилагает периодическую силу для колебания трубопровода. Один тип механизма возбуждения представляет собой электромеханический возбудитель, который прилагает силу, пропорциональную приложенному напряжению. В колебательном расходомере, приложенное напряжение является периодическим и, в общем случае, синусоидальным. Период входного напряжения выбирается так, чтобы движение трубопровода соответствовало резонансному режиму колебаний трубопровода. Это снижает энергию, необходимую для поддержания колебаний. Колебательный расходомер может использовать контур обратной связи, в котором сигнал датчика, который переносит информацию мгновенных частоты и фазы, связанных с колебанием трубопровода, усиливается и поступает обратно на трубопровод с использованием электромеханического возбудителя.
Сущность изобретения
В одном общем аспекте, многофазная рабочая текучая среда пропускается через вибрационную трубку Вентури. В вибрационной трубке Вентури создается движение. Первое наблюдаемое свойство многофазной рабочей текучей среды определяется на основании движения вибрационной трубки Вентури, и наблюдаемое промежуточное значение, связанное с многофазной рабочей текучей средой, определяется на основании первого наблюдаемого свойства. Скорректированное промежуточное значение определяется на основании отображения между наблюдаемым промежуточным значением и скорректированным промежуточным значением. Зависящее от фазы свойство фазы многофазной рабочей текучей среды определяется на основании скорректированного промежуточного значения.
Варианты реализации могут включать в себя один или несколько из следующих признаков. Отображение может представлять собой нейронную сеть, способную определять ошибку в промежуточном значении, обусловленную наличием многофазной рабочей текучей среды. Наблюдаемое промежуточное значение можно определить как находящееся в первой заданной области значений до определения скорректированного промежуточного значения, и скорректированное промежуточное значение можно определить как находящееся во второй заданной области значений до определения зависящего от фазы свойства фазы многофазной рабочей текучей среды.
Многофазная рабочая текучая среда может представлять собой влажный газ. Многофазная рабочая текучая среда может включать в себя первую фазу и вторую фазу, первая фаза может включать в себя негазообразную текучую среду, и вторая фаза может включать в себя газ. Многофазная рабочая текучая среда может включать в себя первую фазу, включающую в себя первую негазообразную текучую среду, и вторую фазу, включающую в себя вторую негазообразную текучую среду, и третью фазу, включающую в себя газ.
Этап определения первого наблюдаемого свойства многофазной рабочей текучей среды может включать в себя определение второго наблюдаемого свойства многофазной рабочей текучей среды. Первое наблюдаемое свойство многофазной рабочей текучей среды может представлять собой массовый расход, и второе наблюдаемое свойство может представлять собой плотность.
Можно принимать одно или несколько измерений, соответствующих дополнительному свойству рабочей текучей среды. Дополнительное свойство многофазной текучей среды может включать в себя одно или несколько из температуры многофазной текучей среды, давления, связанного с многофазной текучей средой, и обводненности многофазной текучей среды, и определение наблюдаемого промежуточного значения, связанного с многофазной рабочей текучей средой, на основании первого наблюдаемого свойства может включать в себя определение промежуточного значения на основании первого наблюдаемого свойства и дополнительного свойства.
Определение наблюдаемого промежуточного значения, связанного с многофазной рабочей текучей средой, на основании первого наблюдаемого свойства может включать в себя определение объемной доли, связанной с количеством негазообразной текучей среды в многофазной рабочей текучей среде, и объемного расхода многофазной текучей среды. Определение наблюдаемого промежуточного значения, связанного с многофазной рабочей текучей средой, на основании первого наблюдаемого свойства может включать в себя определение первого числа Фруда, соответствующего негазовой фазе многофазной текучей среды, и второго числа Фруда, соответствующего газовой фазе многофазной текучей среды.
Определение зависящего от фазы свойства фазы многофазной рабочей текучей среды на основании скорректированного промежуточного значения может включать в себя определение массового расхода негазовой фазы многофазной текучей среды.
Варианты реализации любых вышеописанных способов могут включать в себя способ или процесс, систему, расходомер, или инструкции, хранящиеся в запоминающем устройстве передатчика расходомера. Детали конкретных вариантов реализации представлены в прилагаемых чертежах и нижеследующем описании. Другие признаки явствуют из нижеследующего описания, включающего в себя чертежи, и формулы изобретения.
Варианты реализации любых вышеописанных способов могут включать в себя способ или процесс, систему, расходомер, или инструкции, хранящиеся в запоминающем устройстве передатчика расходомера. Детали конкретных вариантов реализации представлены в прилагаемых чертежах и нижеследующем описании. Другие признаки явствуют из нижеследующего описания, включающего в себя чертежи, и формулы изобретения.
Краткое описание чертежей
Фиг.1 - блок-схема цифрового массового расходомера.
Фиг.2A и 2B - виды в перспективе и сбоку механических компонентов массового расходомера.
Фиг.3A-3C - схемы трех режимов движения расходомера, показанного на фиг.1.
Фиг.4 - блок-схема аналоговой схемы управления и измерения.
Фиг.5 - блок-схема цифрового массового расходомера.
Фиг.6 - логическая блок-схема, демонстрирующая работу измерителя, показанного на фиг.5.
Фиг.7A и 7B - графики, демонстрирующие данные датчиков.
Фиг.8A и 8B - графики напряжения датчика относительно времени.
Фиг.9 - логическая блок-схема процедуры аппроксимации кривой.
Фиг.10 - логическая блок-схема процедуры генерации разностей фаз.
Фиг.11A-11D, 12A-12D и 13A-13D - напряжения возбудителя и датчика при пуске системы.
Фиг.14 - логическая блок-схема процедуры измерения частоты, амплитуды и фазы данных датчиков с использованием метода синхронной модуляции.
Фиг.15A и 15B - блок-схемы массового расходомера.
Фиг.16 - логическая блок-схема процедуры, реализованной измерителем, показанным на фиг.15A и 15B.
Фиг.17 - управление логарифма амплитуды передаточной функции.
Фиг.18 - диаграмма корневого годографа.
Фиг.19A-19D - графики производительности аналого-цифрового преобразователя относительно температуры.
Фиг.20A-20C - графики измерений фазы.
Фиг.21A и 21B - графики измерений фазы.
Фиг.22 - логическая блок-схема процедуры компенсации смещения нуля.
Фиг.23A-23C, 24A и 24B - графики измерений фазы.
Фиг.25 - график напряжения датчика.
Фиг.26 - логическая блок-схема процедуры компенсации динамических эффектов.
Фиг.27A-35E - графики, демонстрирующие применение процедуры, показанной на фиг.29.
Фиг.36A-36L - графики, демонстрирующие измерение фазы.
Фиг.37A - график напряжений датчиков.
Фиг.37B и 37C - графики измерений фазы и частоты, соответствующих напряжениям датчиков, показанным на фиг.37A.
Фиг.37D и 37E - графики параметров коррекции для измерений фазы и частоты, показанных на фиг.37B и 37C.
Фиг.38A-38H - графики необработанных измерений.
Фиг.39A-39H - графики скорректированных измерений.
Фиг.40A-40H - графики, демонстрирующие поправку на аэрацию.
Фиг.41 - блок-схема, демонстрирующая эффект аэрации в трубопроводе.
Фиг.42 - логическая блок-схема процедуры регулировки настройки.
Фиг.43A-43C - графики, демонстрирующие применение процедуры, показанной на фиг.41.
Фиг.44 - график, позволяющий сравнить производительность цифрового и аналогового расходомеров.
Фиг.45 - логическая блок-схема, демонстрирующая работу измерителя с автоматической проверкой.
Фиг.46 - блок-схема двухпроводного цифрового массового расходомера.
Фиг.47A-47C - графики, демонстрирующие отклик цифрового массового расходомера в условиях влажности и пустоты.
Фиг.48A - диаграмма, демонстрирующая результаты испытаний дозирования из пустого состояния.
Фиг.48B - схема экспериментальной гидродинамической установки.
Фиг.49 - график, демонстрирующий ошибки массового расхода относительно перепада наблюдаемой плотности.
Фиг.50 - график, демонстрирующий остаточные ошибки массового расхода после применения поправок.
Фиг.51 - график, демонстрирующий оперативный отклик цифрового массового расходомера с автоматической проверкой на наступление двухфазного потока.
Фиг.52 - блок-схема цифрового контроллера, реализующего процессор нейронной сети, который можно использовать с цифровым массовым расходомером.
Фиг.53 - логическая блок-схема метода реализации нейронной сети для прогнозирования ошибки массового расхода и генерации коэффициента коррекции ошибок для коррекции сигнала измерения массового расхода при обнаружении двухфазного потока.
Фиг.54 - трехмерный график, демонстрирующий изменения затухания в условиях двухфазного потока.
Фиг.55 - компьютерный интерфейс экспериментальной гидродинамической установки.
Фиг.56 - трехмерный график, демонстрирующий истинную ошибку массового расхода в условиях двухфазного потока.
Фиг.57 - трехмерный график, демонстрирующий скорректированную ошибку массового расхода в условиях двухфазного потока.
Фиг.58 - график, позволяющий сравнить нескорректированный сигнал измерения массового расхода с сигналом измерения массового расхода, скорректированным нейронной сетью.
Фиг.59 - логическая блок-схема процедуры компенсации ошибки в условиях многофазного потока.
Фиг.60 - блок-схема цифрового контроллера, реализующего процессор нейронной сети, который можно использовать с цифровым массовым расходомером для потоков многофазной текучей среды.
Фиг.61 - логическая блок-схема способа реализации нейронной сети для прогнозирования ошибки массового расхода и генерации коэффициента коррекции ошибок для коррекции сигнала измерения массового расхода, при ожидании и/или обнаружении многофазных потоков.
Фиг.62 - графическое представление таблицы испытаний для устий скважины, испытываемых на основании фактических испытаний при различных давлениях в скважине и скоростях газа.
Фиг.63 - графическое представление необработанных ошибок плотности при различных процентах жидкостной пустотной доли и для скважин при различных скоростях и давлениях.
Фиг.64 - графическое представление необработанных ошибок массового расхода при различных процентах жидкостной пустотной доли и для скважин при различных скоростях и давлениях.
Фиг.65 - графическое представление необработанной жидкостной пустотной доли ошибки для скважин при различных скоростях и давлениях.
Фиг.66 - графическое представление необработанного объемного расхода ошибки для скважин при различных скоростях и давлениях.
Фиг.67 - графическое представление скорректированных жидкостных пустотных долей для скважин при различных скоростях и давлениях.
Фиг.68 - графическое представление скорректированного объемного расхода смеси для скважин при различных скоростях и давлениях.
Фиг.69 - графическое представление скорректированного массового расхода газа для скважин при различных скоростях и давлениях.
Фиг.70 - графическое представление скорректированной интегральной вероятности газа испытуемого цифрового расходомера.
Фиг.71 - графическое представление скорректированной ошибки массового расхода жидкости для скважин при различных скоростях и давлениях.
Фиг.72 - графическое представление скорректированной интегральной вероятности газа испытуемого цифрового расходомера.
Осуществление изобретения
Обеспечены методы учета эффектов многофазного потока, например, в цифровом расходомере. Многофазный поток может представлять собой, например, двухфазный поток или трехфазный поток. В общем случае, двухфазный поток представляет собой текучую среду, который включает в себя две(а) фазы или компонента. Например, двухфазный поток может включать в себя фазу, которая включает в себя негазообразную текучую среду (например, жидкость) и фазу, которая включает в себя газ. Трехфазный поток представляет собой текучую среду, которая включает в себя три фазы. Например, трехфазный поток может представлять собой текучую среду с газовой фазой и двумя негазообразными жидкостями. Например, трехфазный поток может включать в себя природный газ, нефть и воду. Двухфазный поток может включать в себя, например, природный газ и нефть.
Хотя цифровой расходомер продолжает работать при наличии многофазной текучей среды, любые свойства (например, массовый расход и плотность многофазной текучей среды), определяемые цифровым расходомером, могут быть неточными, поскольку определение этих свойств с использованием традиционных методов, в общем случае, основано на предположении, что текучая среда, текущая через расходомер, является однофазный. Таким образом, даже если текучая среда не является однофазной текучей средой, расходомер может продолжать работать и генерировать наблюдаемые значения свойств, например, массового расхода и плотности многофазной текучей среды. Как описано ниже согласно фиг.59-72, в одном варианте реализации, параметры, например, массовый расход и плотность каждой фазы многофазного потока можно определить из наблюдаемого массового расхода и наблюдаемой плотности многофазной текучей среды. В частности, как рассмотрено более подробно ниже, в одном варианте реализации, одно или несколько промежуточных значений, например, объемной доли жидкости и объемного расхода или газовое и негазовое числа Фруда, определяются из наблюдаемого массового расхода и наблюдаемой плотности многофазной текучей среды, и промежуточное(ые) значение(я) можно корректировать с учетом наличия множественных фаз в текучей среде с использованием нейронной сети или другого отображения. Массовый расход и плотность каждой фазы многофазной текучей среды можно определить из скорректированного(ых) промежуточного(ых) значения(й). Использование промежуточного(ых) значения(й) вместо массового расхода и плотности многофазной текучей среды позволяет повысить точность определения массового расхода и плотности каждой фазы многофазной текучей среды.
Прежде, чем начать описывать методы со ссылкой на фиг.59, рассмотрим цифровые расходомеры со ссылкой на фиг.1-39. Различные методы учета эффектов многофазного потока, например, в цифровом расходомере рассматриваются, начиная с фиг.40.
Согласно фиг.1, цифровой массовый расходомер 100 включает в себя цифровой контроллер 105, один или несколько датчиков движения 110, один или несколько возбудителей 115, трубопровод 120 (также именуемый трубкой Вентури) и датчик температуры 125. Цифровой контроллер 105 можно реализовать с использованием одного или нескольких из, например, процессора, вентильной матрицы, программируемой пользователем, ASIC, другой программируемой логики или вентильной матрицы, или программируемой логики с ядром процессора. Цифровой контроллер генерирует измерение массового расхода через трубопровод 120 на основании, по меньшей мере, сигналов, принятых от датчиков движения 110. Цифровой контроллер также предписывает возбудителям 115 создавать движение в трубопроводе 120. Это движение воспринимается датчиками движения 110.
Массовый расход через трубопровод 120 связан с движением, возбуждаемым в трубопроводе вследствие приложения движущей силы, вырабатываемой возбудителями 115. В частности, массовый расход связан с фазой и частотой движения, а также с температурой трубопровода. Цифровой массовый расходомер также может обеспечивать измерение плотности материала, текущего через трубопровод. Плотность связана с частотой движения и температурой трубопровода. Многие из описанных методов применимы к денситометру, который обеспечивает измерение плотности, а не измерение массового расхода.
Температура в трубопроводе, которая измеряется с использованием датчика 125 температуры, влияет на некоторые свойства трубопровода, например, его жесткость и размеры. Цифровой контроллер компенсирует эти температурные эффекты. Температура цифрового контроллера 105 влияет, например, на рабочую частоту цифрового контроллера. В общем случае, эффекты температуры контроллера достаточно малы, поэтому ими можно пренебречь. Однако, в ряде случаев, цифровой контроллер может измерять температуру контроллера с использованием полупроводникового устройства и может компенсировать эффекты температуры контроллера.
A. Механическая конструкция
В одном варианте реализации, который показан на фиг.2A и 2B, трубопровод 120 имеет конструкцию, позволяющую вставлять его в магистральную трубу (не показана), небольшая часть которой удалена или зарезервирована для размещения трубопровода. Трубопровод 120 включает в себя монтажные фланцы 12 для подключения к магистральной трубе и центральный коллекторный блок 16, поддерживающий два параллельных плоских контура 18 и 20, которые ориентированы перпендикулярно магистральной трубе. Электромагнитные возбудители 46 и датчики 48 присоединены между концами обоих контуров 18 и 20. Каждый из двух возбудителей 46 соответствует возбудителю 115, показанному на фиг.1, и каждый из двух датчиков 48 соответствует датчику 110, показанному на фиг.1.
Возбудители 46 на противоположных концах контуров питаются током равной амплитуды, но противоположного знака (т.е., токами, сдвинутыми по фазе на 180°), что заставляет прямолинейные участки 26 контуров 18, 20 поворачиваться относительно компланарного им перпендикулярного бисектора 56, который пересекается с трубой в точке P (фиг.2B). Повторяющееся обращение (например, по синусоидальному закону) тока питания, подаваемого на возбудители, заставляет каждый прямолинейный участок 26 совершать колебательное движение, заметая фигуру в виде галстука-бабочки в горизонтальной плоскости вокруг линии 56-56, которая является осью симметрии контура. Полный поперечный размах контуров на нижних закругленных витках 38 и 40 невелик, порядка 1/16 дюйма для двухфутового прямолинейного участка 26 трубы, имеющей диаметр один дюйм. Частота колебаний обычно составляет примерно от 80 до 90 Гц.
B. Движение трубопровода
Движение прямолинейных участков контуров 18 и 20 показано в трех режимах на фиг.3A, 3B и 3C. В режиме возбуждения, показанном на фиг.3B, контуры возбуждаются со сдвигом фазы 180° относительно их соответствующих точек P, в результате чего два контура поворачиваются синхронно, но в противоположном направлении. Поэтому, соответствующие концы, например A и C периодически сближаются и отдаляются.
Возбуждающее движение, показанное на фиг.3B, порождает движение в кориолисовом режиме, показанное на фиг.3A, которое осуществляется в противоположных направлениях между контурами и, в результате которого, прямолинейные участки 26 слегка перемещаются друг к другу (или друг от друга). Эффект Кориолиса непосредственно связан с mvW, где m - масса материала в поперечном сечении контура, v - скорость, с которой движется масса (объемный расход), W - угловая скорость контура (W = W 0sinωt), и mv - массовый расход. Эффект Кориолиса максимален, когда два прямолинейных участка возбуждаются синусоидально и имеют синусоидально изменяющуюся угловую скорость. При этих условиях, эффект Кориолиса сдвинут по фазе на 90° относительно сигнала возбуждения.
На фиг.3C показано движение в нежелательном общем режиме, при котором контуры отклоняются в одном и том же направлении. Этот тип движения может порождаться осевой вибрацией в магистральной трубе в примере, показанном на фиг.2A и 2B, поскольку контуры перпендикулярны магистральной трубе.
Тип колебаний, показанный на фиг.3B, называется антисимметричным режимом, а кориолисов режим, показанный на фиг.3A, называется симметричным режимом. Собственная частота колебаний в антисимметричном режиме зависит от торсионной упругости отводов. Обычно резонансная частота антисимметричного режима для трубопроводов, форма которых показана на фиг.2A и 2B, выше резонансной частоты симметричного режима. Для снижения чувствительности к шуму при измерении массового расхода, желательно довести до максимума силу Кориолиса при данном массовом расходе. Как отмечено выше, контуры возбуждаются на своей резонансной частоте, а сила Кориолиса непосредственно связана с частотой, на которой колеблются контуры (т.е., угловой скоростью контуров). Соответственно, контуры возбуждаются в антисимметричном режиме, который обычно имеет более высокую резонансную частоту.
Другие варианты реализации могут включать в себя другие конструкции трубопровода. Например, в качестве трубопровода можно применять единичный контур или отрезок прямой трубы.
C. Электронная конструкция
Цифровой контроллер 105 определяет массовый расход путем обработки сигналов, вырабатываемых датчиками 48 (т.е., датчиками движения 110), расположенными на противоположных концах контуров. Сигнал, вырабатываемый каждым датчиком, включает в себя компонент, соответствующий относительной скорости, на которой контуры возбуждаются возбудителем, расположенным после датчика, и компонент, соответствующий относительной скорости контуров, обусловленной силами Кориолиса, создаваемыми в контурах. Контуры возбуждаются в антисимметричном режиме, поэтому компоненты сигналов датчиков, соответствующие скорости возбуждения, равны по величине, но противоположны по знаку. Результирующая сила Кориолиса действует в симметричном режиме, поэтому компоненты сигналов датчиков, соответствующие кориолисовой скорости, равны по величине и знаку. Таким образом, вычитание сигналов нейтрализует компоненты кориолисовой скорости и дает разность, которая пропорциональна скорости возбуждения. Аналогично, суммирование сигналов нейтрализует компоненты скорости возбуждения и дает сумму, которая пропорциональна кориолисовой скорости, которая, в свою очередь, пропорциональна силе Кориолиса. Затем эту сумму можно использовать для определения массового расхода.
1. Аналоговая система управления
Цифровой массовый расходомер 100 обеспечивает значительные преимущества над традиционными, аналоговыми массовыми расходомерами. Для использования в дальнейшем рассмотрении, на фиг.4 показана аналоговая система 400 управления традиционного массового расходомера. Каждый датчик 48 выдает сигнал напряжения, причем сигнал VA0 создается датчиком 48a, и сигнал VB0 создается датчиком 48b. VA0 и VB0 соответствуют скорости контуров относительно друг друга в положениях датчиков. До обработки, сигналы VA0 и VB0 усиливаются на соответствующих входных усилителях 405 и 410 для создания сигналов VA1 и VB1. Для коррекции дисбаланса на усилителях и датчиках, входной усилитель 410 имеет переменный коэффициент усиления, который регулируется сигналом баланса, поступающим из контура обратной связи, который содержит синхронный демодулятор 415 и интегратор 420.
На выходе усилителя 405, сигнал VA1 имеет вид:
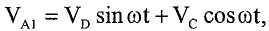
и, на выходе усилителя 410, сигнал VB1 имеет вид:
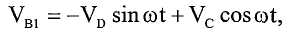
где VD и VC являются, соответственно, напряжением возбуждения и кориолисовым напряжением, и ω - круговая частота режима возбуждения.
Напряжения VA1 и VB1 дифференцируются операционным усилителем 425 для создания сигнала
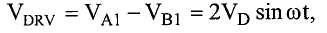
где VDRV соответствует возбуждающему движению и используется для питания возбудителей. Помимо питания возбудителей, VDRV поступает на детектор 430 пересечения нуля в положительном направлении, который создает выходную прямоугольную волну FDRV, частота которой соответствует частоте сигнала VDRV (ω = 2FDRV). FDRV используется в качестве входного сигнала цифровой схемы 435 фазовой автоподстройки частоты. FDRV также поступает на процессор 440.
Напряжения VA1 и VB1 суммируются операционным усилителем 445 для создания сигнала
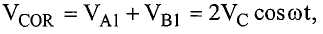
где VCOR связан с возбуждаемым кориолисовым движением.
VCOR поступает на синхронный демодулятор 450, который создает выходное напряжение VM, которое прямо пропорционально массе, отбрасывая компоненты VCOR, которые не имеют той же частоты, что и стробирующий сигнал Q, и не синфазны с ним. Схема 435 фазовой автоподстройки частоты создает Q, который является квадратурным опорным сигналом, имеющим такую же частоту (ω), как VDRV, и на 90° сдвинут по фазе относительно VDRV (т.е., синфазен с VCOR). Соответственно, синхронный демодулятор 450 отбрасывает частоты, отличные от ω, поэтому VM соответствует амплитуде VCOR на ω. Эта амплитуда прямо пропорциональна массе в трубопроводе.
VM поступает на преобразователь 455 напряжения в частоту, который создает сигнал FM прямоугольной волны, частота которого соответствует амплитуде сигнала VM. Затем процессор 440 делит FM на FDRV для создания измерения массового расхода.
Цифровая схема 435 фазовой автоподстройки частоты также создает опорный сигнал I, синфазный с VDRV и используемый для стробирования синхронного демодулятора 415 в контуре обратной связи, управляющем усилителем 410. Когда коэффициенты усиления входных усилителей 405 и 410, умноженные на компоненты возбуждения соответствующих входных сигналов, равны, операция суммирования на операционном усилителе 445 создает нулевой компонент возбуждения в сигнале VCOR (т.е., не существует сигнала синфазного с VDRV). Когда коэффициенты усиления входных усилителей 405 и 410 не равны, компонент возбуждения существует в VCOR. Этот компонент возбуждения извлекается синхронным демодулятором 415 и интегрируется интегратором 420 для генерации напряжения ошибки, которое корректирует коэффициент усиления входного усилителя 410. Когда коэффициент усиления слишком высок или слишком низок, синхронный демодулятор 415 создает выходное напряжение, в соответствии с которым интегратор изменяет напряжение ошибки, которое изменяет коэффициент усиления. Когда коэффициент усиления достигает желаемого значения, выходной сигнал синхронного модулятора достигает нуля, и напряжение ошибки перестает изменяться для поддержания желаемого значения коэффициента усиления.
2. Цифровая система управления
На фиг.5 показана блок-схема варианта реализации 500 цифрового массового расходомера 100, который включает в себя трубопровод 120, возбудители 46 и датчики 48, показанные на фиг.2A и 2B, совместно с цифровым контроллером 505. Аналоговые сигналы от датчиков 48 преобразуются в цифровые сигналы аналого-цифровыми ("А/Ц") преобразователями 510 и поступают на контроллер 505. А/Ц преобразователи можно реализовать в виде отдельных преобразователей или в виде отдельных каналов единого преобразователя.
Цифроаналоговые ("Ц/А") преобразователи 515 преобразуют цифровые сигналы управления от контроллера 505 в аналоговые сигналы для возбуждения возбудителей 46. Использование отдельного сигнала возбуждения для каждого возбудителя имеет ряд преимуществ. Например, система может легко переключаться между симметричным и антисимметричным режимами возбуждения в целях диагностики. В других вариантах реализации, сигналы, вырабатываемые преобразователями 515, можно усиливать с помощью усилителей до подачи на возбудители 46. В еще других вариантах реализации возможно использование единого Ц/А преобразователя для создания сигнала возбуждения, подаваемого на оба возбудителя, причем сигнал возбуждения инвертируется до подачи на один из возбудителей для возбуждения трубопровода 120 в антисимметричном режиме.
Высокоточные резисторы 520 и усилители 525 используются для измерения тока, подаваемого на каждый возбудитель 46. А/Ц преобразователи 530 преобразуют измеренный ток в цифровые сигналы и выдают цифровые сигналы на контроллер 505. Контроллер 505 использует измеренные токи при генерации сигналов возбуждения.
Датчики 535 температуры и датчики 540 давления измеряют, соответственно, температуру и давление на входе 545 и выходе 550 трубопровода. А/Ц преобразователи 555 преобразуют измеренные значения в цифровые сигналы и выдают цифровые сигналы на контроллер 505. Контроллер 505 использует измеренные значения по-разному. Например, разность между измеренными давлениями можно использовать для определения противодавления в трубопроводе. Поскольку жесткость трубопровода изменяется в зависимости от противодавления, контроллер может учитывать жесткость трубопровода на основании определяемого противодавления.
Дополнительный датчик температуры 560 измеряет температуру кварцевого генератора 565, используемого А/Ц преобразователями. А/Ц преобразователь 570 преобразует это измерение температуры в цифровой сигнал для использования контроллером 505. Соотношение между входом и выходом А/Ц преобразователей изменяется в зависимости от рабочей частоты преобразователей, и рабочая частота изменяется в зависимости от температуры кварцевого генератора. Соответственно, контроллер использует измерение температуры для регулировки данных, обеспеченных А/Ц преобразователями, или при калибровке системы.
В варианте реализации, показанном на фиг.5, цифровой контроллер 505 обрабатывает оцифрованные сигналы датчиков, вырабатываемые А/Ц преобразователями 510 согласно процедуре 600, показанной на фиг.6, для генерации измерения массового расхода и сигнала возбуждения, подаваемого на возбудители 46. Первоначально, контроллер собирает данные от датчиков (этап 605). С использованием этих данных, контроллер определяет частоту сигналов датчиков (этап 610), устраняет смещение нуля из сигналов датчиков (этап 615) и определяет амплитуду (этап 620) и фазу (этап 625) сигналов датчиков. Контроллер использует эти вычисленные значения для генерации сигнала возбуждения (этап 630) и для генерации массового расхода и других измерений (этап 635). После генерации сигналов возбуждения и измерений, контроллер собирает новый набор данных и повторяет процедуру. Этапы процедуры 600 можно осуществлять последовательно или параллельно и можно осуществлять в изменяющемся порядке.
Вследствие соотношений между частотой, смещением нуля, амплитудой и фазой, оценку одного можно использовать для вычисления другого. Благодаря этому повторение вычислений повышает точность. Например, первоначальное определение частоты, используемое при определении смещения нуля в сигналах датчиков, можно уточнить с использованием сигналов датчиков с устраненным смещением. Кроме того, при необходимости, значения, генерируемые для периода, можно использовать в качестве начальных оценок для следующего периода.
a. Сбор данных
Для простоты рассмотрения, оцифрованные сигналы от двух датчиков будем обозначать как сигналы SV1 и SV2, причем сигнал SV1 поступает от датчика 48a, а сигнал SV2 поступает от датчика 48b. Хотя новые данные генерируются постоянно, предполагается, что вычисления основаны на данных, соответствующих одному полному периоду обоих датчиков. При значительной буферизации данных, это условие будет выполняться, пока среднее время обработки данных меньше времени на сбор данных. Задачи, подлежащие выполнению в течение периода, включают в себя принятие решения, что период завершен, вычисление частоты периода (или частот SV1 и SV2), вычисление амплитуд SV1 и SV2 и вычисление разности фаз между SV1 и SV2. В некоторых вариантах реализации, эти вычисления повторяются для каждого периода с использованием конечной точки предыдущего периода в качестве начала следующего периода. В других вариантах реализации, периоды перекрываются на 180° или в другой степени (например, 90°), в связи с чем период пересекается с предыдущим или следующим периодом.
На фиг.7A и 7B показаны два вектора выборочных данных из сигналов SV1 и SV2, которые обозначены, соответственно, sv1_in и sv2_in. Первая выборочная точка каждого вектора известна и соответствует пересечению нуля синусоидальной волной, представленной вектором. Для sv1_in, первая выборочная точка является пересечением нуля от отрицательного значения к положительному значению, тогда как для sv2_in первая выборочная точка является пересечением нуля от положительного значения к отрицательному значению.
Фактическая начальная точка периода (т.е., фактическое пересечение нуля) редко будет в точности совпадать с выборочной точкой. По этой причине, начальные выборочные точки (start_sample_SV1 и start_sample_SV2) являются выборочными точками, возникающими непосредственно до начала периода. Для учета разности между первой выборочной точкой и фактическим началом периода, подход также использует позицию (start_offset_SV1 или start_offset_SV2) между начальной выборкой и следующей выборкой, с которой фактически начинается период.
Поскольку существует сдвиг фазы между сигналами SV1 и SV2, sv1_in и sv2_in могут начинаться в разных выборочных точках. Если частота дискретизации и разность фаз велики, может существовать разность в несколько выборок между началом sv1_in и началом sv2_in. Эта разность обеспечивает грубую оценку сдвига фазы, и ее можно использовать для проверки вычисленного сдвига фазы, что рассмотрено ниже. Например, при дискретизации на частоте 55 кГц, одна выборка соответствует сдвигу фазы около 0,5 градусов, и один период соответствует примерно 800 выборочным точкам.
Когда контроллер использует функции, например, сумму (A+B) и разность (A-B), где B взвешена так, чтобы иметь ту же амплитуду, что и A, дополнительные переменные (например, start_sample_sum и start_offset_sum) отслеживают начало периода для каждой функции. Функции суммы и разности имеют сдвиг фазы наполовину между SV1 и SV2.
В одном варианте реализации, структура данных, используемая для хранения данных от датчиков, представляет собой циклический список для каждого датчика, емкость которого, по меньшей мере, вдвое превышает максимальное количество выборок в периоде. Благодаря этой структуре данных, обработка может осуществляться на данных для текущего периода, тогда как прерывания или другие методы используются для добавления данных для следующего периода к спискам.
Обработка осуществляется на данных, соответствующих полному периоду во избежание ошибок при использовании подходов на основе синусоидальных волн. Соответственно, первая задача при сборе данных в течение периода состоит в определении начала и конца периода. При использовании неперекрывающихся периодов, начало периода можно идентифицировать как конец предыдущего периода. При использовании перекрывающихся периодов, и когда периоды перекрываются на 180°, начало периода можно идентифицировать как среднюю точку предыдущего периода или как конечную точку периода, предшествующего предыдущему периоду.
Конец периода можно первоначально оценить на основании параметров предыдущего периода и исходя из того, что параметры не будут изменяться более чем на заранее определенную величину от периода к периоду. Например, пять процентов можно использовать как максимально допустимое изменение от значения последнего периода, что разумно, поскольку, при частотах дискретизации 55 кГц, повторяющееся возрастание или убывание на пять процентов в амплитуде или частоте на протяжении последовательных периодов приведет к изменениям около 5,000 процентов за одну секунду.
При назначении процентов в качестве максимально допустимого увеличения амплитуды и частоты и допущении максимального изменения фазы в 5° для последовательных периодов, консервативную оценку для верхнего предела на конце периода для сигнала SV1 можно определить как:
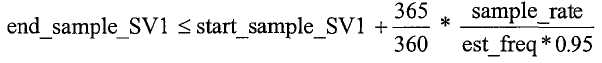 ,
,
где start_sample_SV1 это первая выборка sv1_in, sample_rate это частота дискретизации, и est_freq это частота из предыдущего периода. Аналогично можно определить верхний предел на конце периода для сигнала SV2 (end_sample_SV2).
После идентификации конца периода, можно произвести простые проверки, правильно ли обрабатывается период. Период может неправильно обрабатываться, когда, например, трубопровод блокируется, или колебательные сигналы датчиков сильно искажаются. Обработка только пригодных периодов обеспечивает значительное сокращение вычислений.
Один способ определения пригодности периода состоит в проверке определенных точек периода для подтверждения ожидаемого поведения. Как отмечено выше, амплитуды и частота последнего периода дают полезные начальные оценки соответствующих значений для текущего периода. С использованием этих значений, можно проверять точки, соответствующие 30°, 150°, 210° и 330° периода. Если амплитуда и частота в точности совпадают с амплитудой и частотой для предыдущего периода, эти точки будут иметь значения, соответствующие est_amp/2, est_amp/2, -est_amp/2 и -est_amp/2, соответственно, где est_amp - оценочная амплитуда сигнала (т.е., амплитуда из предыдущего периода). Вследствие того, что допустимо пятипроцентное изменение амплитуды и частоты, для каждой четверти периода могут генерироваться неравенства. Для точки 30°, неравенство имеет вид:
Неравенства для других точек имеют тот же вид, где градус члена смещения (x/360) и знак члена est_amp_SV1 имеют соответствующие значения. Эти неравенства можно использовать для проверки, что трубопровод вибрирует надлежащим образом.
Обработка измерений осуществляется на векторах sv1_in (start:end) и sv2_in (start:end), где:
start = min (start_sample_SV1, start_sample_SV2), и
end = max (end_sample_SV1, end_sample_SV2).
Разность между начальной и конечной точками для сигнала указывает частоту сигнала.
b. Определение частоты
Частоту дискретизируемой строго синусоидальной волны можно вычислять путем обнаружения перехода между периодами (т.е., путем обнаружения положительных или отрицательных пересечений нуля) и подсчета количества выборок в каждом период. С использованием этого метода, дискретизация, например, синусоидальной волны частоты 82,2 Гц с частотой 55 кГц будет обеспечивать оценку частоты с максимальной ошибкой 0,15 процента. Более высокой точности можно добиться, оценивая дробную часть выборки, на которой фактически происходит пересечение нуля, с использованием, например, start_offset_SV1 и start_offset_SV2. Случайный шум и смещение нуля могут снижать точность этого подхода.
Согласно фиг.8A и 8B, уточненный метод определения частоты использует квадратичную интерполяцию квадрата синусоидальной волны. Согласно этому методу, вычисляется квадрат синусоидальной волны, производится аппроксимация квадратичной функцией, минимум которой совпадает с точкой минимума возведенной в квадрат синусоидальной волны, и зоны квадратичной функции используются для определения частоты. Если
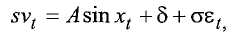
где sv t - напряжение датчика во время t, A - амплитуда колебаний, x t - угол в радианах во время t (т.е., x t = 2πft), δ - смещение нуля, εt - случайная переменная с распределением N(0,1) и σ - дисперсия шума, то функция, возведенная в квадрат, задается следующим образом:
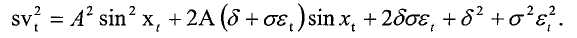
Когда x t близок к 2π, sinx t и sin2 x t можно аппроксимировать функциями x 0t = x t-2π и x 0t 2, соответственно. Соответственно, для значений x t, близких к 2π, a t можно аппроксимировать следующим образом:
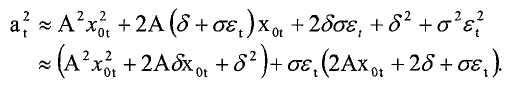
Это строго квадратичная функция (с ненулевым минимумом, предполагая δ=0) плюс шум, причем амплитуда шума зависит от σ и δ. Также можно использовать линейную интерполяцию.
Источники ошибок, связанные с этим методом аппроксимации кривой, представляют собой случайный шум, смещение нуля и отклонение от истинно квадратичной функции. Аппроксимация кривой весьма чувствительна к уровню случайного шума. Смещение нуля в напряжении датчика увеличивает амплитуду шума в функции квадрата синуса и иллюстрирует важность устранения смещения нуля (рассмотренного ниже). При удалении от минимума, квадрат даже строго синусоидальной волны не является строго квадратичным. Наиболее значимым дополнительным членом является член четвертого порядка. Напротив, наиболее значимым дополнительным членом для линейной интерполяции является член третьего порядка.
Степени свободы, связанные с этим методом аппроксимации кривой, связаны с тем, сколько и какие точки данных используются. Минимальное количество равно трем, но можно использовать больше (при более высоких вычислительных затратах) с использованием аппроксимации методом наименьших квадратов. Такая аппроксимация в меньшей степени подвержена случайному шуму. На фиг.8A показано, что квадратичная аппроксимация хороша в пределах около 20° от точки минимума. Использование точек данных, более удаленных от минимума, будет снижать влияние случайного шума, но будет увеличивать ошибки, обусловленные неквадратичными членами (т.е., четвертого порядка и выше) в функции квадрата синуса.
На фиг.9 показана процедура 900 для осуществления метода аппроксимации кривой. На первом этапе, контроллер инициализирует переменные (этап 905). Эти переменные включают в себя end_point, наилучшую оценку точки пересечения нуля; ep_int, целочисленное значение, ближайшее к end_point; s[0..i], множество всех выборочных точек; z[k], квадрат выборочной точки, ближайшей к end_point; z[0..n-1], множество квадратов выборочных точек, используемых для вычисления end_point; n, количество выборочных точек, используемых для вычисления end_point (n = 2k + 1); step_length, количество выборок в s между последовательными значениями в z; и iteration_count, счетчик итераций, произведенных контроллером.
Затем контроллер генерирует первую оценку end_point (этап 910). Контроллер генерирует эту оценку путем вычисления оценочной точки пересечения нуля на основании оценочной частоты из предыдущего периода и поиска вокруг оценочной точки пересечения (вперед и назад) для отыскания ближайшей истинной точки пересечения (т.е., появления последовательных выборок с разными знаками). Затем контроллер задает end_point равной выборочной точке, имеющей меньшую величину, чем у выборок, окружающих истинную точку пересечения.
Затем контроллер задает n, количество точек для аппроксимации кривой (этап 915). Контроллер задает n равным 5 для частоты дискретизации 11 кГц и равным 21 для частоты дискретизации 44 кГц. Затем контроллер задает iteration_count равным 0 (этап 920) и увеличивает iteration_count (этап 925), чтобы начать итерационную часть процедуры.
На первом этапе в итерационной части процедуры, контроллер выбирает step_length (этап 930) на основании значения iteration_count. Контроллер задает step_length равной 6, 3 или 1 в зависимости от того, равен ли iteration_count, соответственно, 1, 2 или 3.
Затем контроллер определяет ep_int как целую часть суммы end_point и 0.5 (этап 935) и заполняет массив z (этап 940). Например, когда n равно 5, z[0] = s[ep_int-2*step_length]2, z[1] = s[ep_int-step_length]2, z[2] = s[ep_int]2, z[3] = s[ep_int+step_length]2 и z[4] = s[ep_int+2*step_length]2.
Затем контроллер использует фильтр, например фильтр Савицкого-Голея, для вычисления сглаженных значений z[k-1], z[k] и z[k+1] (этап 945). Сглаживающие фильтры Савицкого-Голея рассмотрены Прессом (Press) и др. в Numerical Recipes in C, стр. 650-655 (2-е изд., Cambridge University Press, 1995), которая включена посредством ссылки. Затем контроллер осуществляет квадратичную интерполяцию между z[k-1], z[k] и z[k+1] (этап 950) и вычисляет минимальное значение квадратичной функции (z*) и соответствующую позицию (x*) (этап 955).
Если x* находится между точками, соответствующими k-1 и k+1 (этап 960), то контроллер задает end_point равной x (этап 965). Затем, если iteration_count меньше 3 (этап 970), то контроллер увеличивает iteration_count (этап 925) и повторяет итерационную часть процедуры.
Если x* не находится между точками, соответствующими k-1 и k+1 (этап 960), или если iteration_count равен 3 (этап 970), то контроллер выходит из итерационной части процедуры. Затем контроллер вычисляет частоту на основании разности между конечной точкой и начальной точкой для периода, которая известна (этап 975).
В сущности, процедура 900 предписывает контроллеру сделать три попытки нацеливания на end_point, с уменьшением step_length при каждой следующей попытке. Если результирующий минимум для какой-либо попытки оказывается за пределами точек, используемых для аппроксимации кривой (т.е. при наличии экстраполяции вместо интерполяции), это говорит о негодности предыдущей или новой оценки и о том, что сокращение размера шага неуместно.
Процедуру 900 можно применять, по меньшей мере, к трем разным синусоидальным волнам, вырабатываемым датчиками. Они включают в себя сигналы SV1 и SV2 и их взвешенную сумму. Кроме того, исходя из того, что смещение нуля устранено, оценки частоты, создаваемые для этих сигналов, являются независимыми. Это справедливо для сигналов SV1 и SV2, поскольку ошибки на каждом из них являются независимыми. Однако это также справедливо для взвешенной суммы, при условии, что массовый расход и соответствующая разность фаз между сигналами SV1 и SV2 достаточно велики для вычисления частоты, чтобы в каждом отдельном случае опираться на разные выборки. Когда это справедливо, случайные ошибки в оценках частоты также будут независимыми.
Три независимые оценки частоты можно комбинировать для обеспечения улучшенной оценки. Эта комбинированная оценка просто является средним трех оценок частоты.
c. Компенсация смещения нуля
Важным источником ошибок в кориолисовом передатчике является смещение нуля в напряжении каждого из датчиков. Смещение нуля вносится в сигнал напряжения датчика за счет дрейфа в схеме предварительного усиления и аналого-цифровом преобразователе. Эффект смещения нуля может ухудшаться за счет небольших различий в коэффициентах усиления предусилителя для положительного и отрицательного напряжений вследствие использования дифференциальных схем. Каждый источник ошибок изменяется между передатчиками и будет изменяться с температурой передатчика и, в более общем случае, со временем за счет износа компонента.
Ниже подробно рассмотрен иллюстративный метод компенсации смещения нуля, применяемый контроллером. В общем случае, контроллер использует оценку частоты и метод интегрирования для определения смещения нуля в каждом из сигналов датчиков. Затем контроллер устраняет смещение нуля из этих сигналов. После устранения смещения нуля из сигналов SV1 и SV2, контроллер может повторно вычислять частоту этих сигналов для обеспечения улучшенной оценки частоты.
d. Определение амплитуды
Амплитуду колебаний можно использовать во многих случаях. Они включают в себя регулирование колебаний трубопровода посредством обратной связи, балансирование вкладов напряжений датчиков при синтезе колебательных сигналов возбудителя, вычисление сумм и разностей для измерения фазы и вычисление скорости изменения амплитуды в целях коррекции измерений.
В одной реализации, контроллер использует оценочные амплитуды сигналов SV1 и SV2 для вычисления суммы и разности сигналов SV1 и SV2 и произведение суммы и разности. До определения суммы и разности, контроллер компенсирует один из сигналов для учета разностей между коэффициентами усиления двух датчиков. Например, контроллер может компенсировать данные для сигнала SV2 на основании отношения амплитуды сигнала SV1 к амплитуде сигнала SV2, чтобы оба сигнала имели одинаковую амплитуду.
Контроллер может вырабатывать дополнительную оценку частоты на основании вычисленной суммы. Эту оценку можно усреднять с предыдущими оценками частоты для создания уточненной оценки частоты сигналов, или ею можно заменять предыдущие оценки.
Контроллер может вычислять амплитуду согласно методу Фурье для устранения эффектов высших гармоник. Напряжение датчика x(t) в течение периода T (установленного с использованием методов пересечения нуля) можно представить в виде смещения и ряда гармонических членов следующим образом:
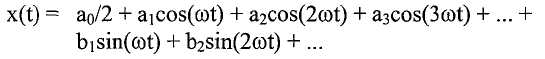
В этом представлении, ненулевое смещение a 0 порождает ненулевые косинусные члены a n. Хотя интересующая нас амплитуда является амплитудой основного компонента (т.е. амплитудой на частоте ω), отслеживание амплитуд высших гармонических компонентов (т.е. на частотах kω, где k больше 1) может иметь значение для диагностики. Значения a n и b n можно вычислять следующим образом:
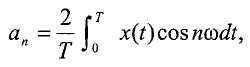
и
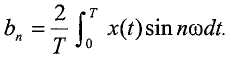
Амплитуда A n каждой гармоники задается следующим образом:
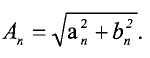
Интегралы вычисляются с использованием метода Симпсона с квадратичной поправкой (описанный ниже). Основные вычислительные затраты метода сводятся к вычислению строго синусоидальных и косинусоидальных функций.
e. Определение фазы
Контроллер может использовать несколько подходов для вычисления разности фаз между сигналами SV1 и SV2. Например, контроллер может определять сдвиг фазы каждой гармоники относительно начала отсчета времени t=0 в виде:
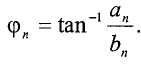
Сдвиг фазы интерпретируется применительно к единичному колебательному сигналу как разность между началом периода (т.е. точкой пересечения нуля) и точкой нулевой фазы для компонента SV(t) частоты ω. Поскольку сдвиг фазы является средним по всему колебательному сигналу, его можно использовать как сдвиг фазы от средней точки периода. В идеале, в отсутствие смещения нуля и при постоянной амплитуде колебаний, сдвиг фазы должен быть нулевым для каждого периода. Контроллер может определять разность фаз путем сравнения сдвига фазы каждого напряжения датчика по одному и тому же периоду времени.
Амплитуда и фаза могут генерироваться с использованием метода Фурье, который устраняет эффекты высших гармоник. Этот способ имеет преимущество в том, что он не предполагает, что оба конца трубопроводов колеблются на одной и той же частоте. На первом этапе способа создается оценка частоты с использованием пересечений нуля для измерения времени между началом и концом периода. Если предполагается линейное изменение частоты, эта оценка равна частоте, усредненной по времени в течение периода. С использованием оценочной, предположительно, инвариантной по времени, частоты ω для периода, контроллер вычисляет:
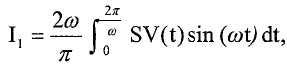 и
и
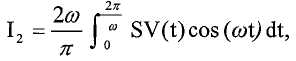
где SV(t) это колебательный сигнал напряжения датчика (т.е. SV1(t) или SV2(t)). Затем контроллер определяет оценки амплитуды и фазы:
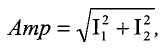 и
и
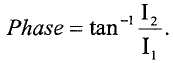
Затем контроллер вычисляет разность фаз, исходя из того, что средняя фаза и частота каждого сигнала датчика представляет весь колебательный сигнал. Поскольку эти частоты различны для SV1 и SV2, соответствующие фазы масштабируются к средней частоте. Кроме того, фазы сдвигаются к одной и той же начальной точке (т.е. средней точке периода на SV1). После масштабирования, они вычитаются для обеспечения разности фаз:
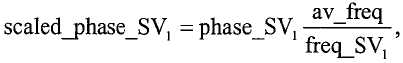
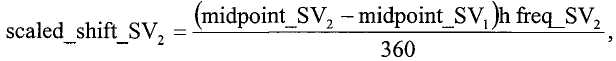 и
и
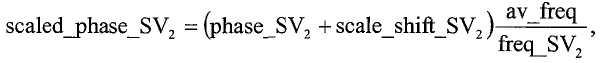
где h - длина выборки, и средние точки заданы через выборки:
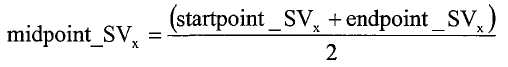
В общем случае, фаза и амплитуда не вычисляются по одному и тому же интервалу времени для двух датчиков. Когда расход равен нулю, две средние точки периода совпадают. Однако они расходятся при высоких расходах, поэтому вычисления базируются на наборах выборок, которые не совпадают по времени. Это приводит к повышению фазового шума в условиях изменения массового расхода. При полном расходе, сдвиг фазы в 4° (из 360°) означает, что только 99% выборок в наборах данных SV1 и SV2 совпадают. Еще большие сдвиги фазы можно наблюдать в условиях аэрации, что может приводить к еще большим степеням перекрытия.
На фиг.10 представлен видоизмененный подход 1000, который решает этот вопрос. Сначала контроллер находит частоты (f1, f2) и средние точки (m1, m2) наборов данных (d1, d2) SV1 и SV2 (этап 1005). Предполагая линейный сдвиг по частоте от последнего периода, контроллер вычисляет частоту SV2 в средней точке SV1 (f2m1) и частоту SV1 в средней точке SV2 (f1m2) (этап 1010).
Затем контроллер вычисляет начальные и конечные точки новых наборов данных (d1m2 и d2m1) со средними точками m2 и m1 соответственно, с предполагаемыми частотами f1m2 и f2m1 (этап 1015). Эти конечные точки не обязаны совпадать с точками пересечения нуля. Однако это не требуется для вычислений на основе Фурье-анализа.
Затем контроллер осуществляет вычисления методом Фурье фазы и амплитуды на наборах d1 и d2m1, и вышеописанные вычисления разности фаз (этап 1020). Поскольку средние точки d1 и d2m1 идентичны, scale_shift_SV2 всегда равен нулю, и его можно игнорировать. Контроллер повторяет эти вычисления для наборов данных d2 и d1m2 (этап 1025). Затем контроллер генерирует средние значения вычисленной амплитуды и разности фаз для использования при генерации измерений (этап 1030). При наличии достаточного разделения между средними точками m1 и m2, контроллер также может использовать два набора результатов для обеспечения локальных оценок отношений изменения фазы и амплитуды.
Контроллер также может использовать разностно-амплитудный метод, который предусматривает вычисление разности между SV1 и SV2, возведение в квадрат вычисленной разности и интегрирование результата. Согласно другому подходу, контроллер синтезирует синусоидальную волну, умножает синусоидальную волну на разность сигналов SV1 и SV2 и интегрирует результат. Контроллер также может интегрировать произведение сигналов SV1 и SV2, которое является синусоидальной волной, имеющей частоту 2f (где f это средняя частота сигналов SV1 и SV2), или может возводить в квадрат произведение и интегрировать результат. Контроллер также может синтезировать косинусоидальную волну, сравниваемую с синусоидальной волной произведения, и умножать синтезированную косинусоидальную волну на синусоидальную волну произведения для создания синусоидальной волны частоты 4f, которую контроллер затем интегрирует. Контроллер также может использовать несколько из этих подходов для создания отдельных измерений фазы и затем может вычислять среднее значение отдельных измерений в качестве окончательного измерения фазы.
Разностно-амплитудный метод начинается с:
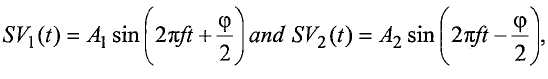
где φ это разность фаз между датчиками. Основные тригонометрические тождества можно использовать для задания суммы (Sum) и разности (Diff) между сигналами следующим образом:
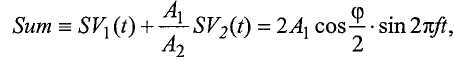 и
и
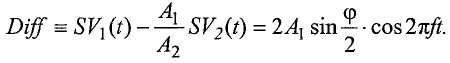
Эти функции имеют амплитуды 2A1cos(φ/2) и 2A1sin(φ/2), соответственно. Контроллер вычисляет наборы данных для Sum и Diff из данных для SV1 и SV2 и затем использует один или несколько вышеописанных методов для вычисления амплитуды сигналов, представленных этими наборами данных. Затем контроллер использует вычисленные амплитуды для вычисления разности фаз φ.
Альтернативно, разность фаз можно вычислять с использованием функции Prod, заданной в виде:
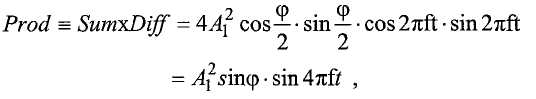
которая является функцией с амплитудой A2sinφ и частотой 2f. Prod можно генерировать выборка за выборкой, и φ можно вычислять из амплитуды результирующей синусоидальной волны.
Вычисление фазы, в частности, зависит от точности предыдущих вычислений (т.е. вычисления частот и амплитуд SV1 и SV2). Контроллер может использовать несколько методов для обеспечения отдельных (если не полностью независимых) оценок фазы, которые можно комбинировать для получения улучшенной оценки.
f. Генерация сигнала возбуждения
Контроллер генерирует сигнал возбуждения путем применения коэффициента усиления к разности сигналов SV1 и SV2. Контроллер может применять либо положительный коэффициент усиления (обеспечивающий положительную обратную связь) или отрицательный коэффициент усиления (обеспечивающий отрицательную обратную связь).
В общем случае, Q трубопровода достаточно высока, благодаря чему трубопровод будет резонировать только на определенных дискретных частотах. Например, самая низкая резонансная частота для некоторых трубопроводов составляет от 65 Гц до 95 Гц, в зависимости от плотности рабочей текучей среды, и независимо от частоты возбуждения. Поэтому желательно возбуждать трубопровод на резонансной частоте для минимизации потери энергии от периода к периоду. Обратная подача напряжения датчика на возбудители позволяет частоте возбуждения перемещаться к резонансной частоте.
Альтернативно использованию обратной связи для генерации сигнала возбуждения, строго синусоидальные волны, имеющие фазы и частоты, определяемые, как описано выше, можно синтезировать и подавать на возбудители. Этот подход обеспечивает преимущества устранения нежелательных высокочастотных компонентов, например, гармоник резонансной частоты. Этот подход также позволяет компенсировать задержки по времени, вносимые аналого-цифровыми преобразователями, обработкой и цифроаналоговыми преобразователями, чтобы гарантировать, что фаза сигнала возбуждения соответствует средней точке фаз сигналов датчиков. Эту компенсацию можно обеспечивать путем определения задержки по времени компонентов системы и внесения сдвига фазы, соответствующего задержке по времени.
Другой подход к возбуждению трубопровода состоит в использовании прямоугольных импульсов. Это другой метод синтеза, причем фиксированные (положительные и отрицательные) источники постоянного тока включаются и выключаются с заданными временными интервалами для обеспечения необходимой энергии. Переключение синхронизируется с фазой напряжения датчика. Преимущество состоит в том, что этот подход не требует цифроаналоговых преобразователей.
В общем случае, амплитуда колебаний трубопровода должна быстро достигнуть желаемого значения при пуске, чтобы быстро обеспечить функцию измерения, но должна сделать это без значительного выброса, который может повредить измеритель. Нужного быстрого пуска можно добиться за счет задания очень высокого коэффициента усиления, чтобы наличие случайного шума и высокого Q трубопровода было достаточным для инициирования движения трубопровода. В одной реализации, высокий коэффициент усиления и положительная обратная связь используются для инициирования движения трубопровода. По достижении стабильной работы, система переходит к режиму синтеза для генерации сигналов возбуждения.
Согласно фиг.11A-13D, методы синтеза также можно использовать для инициирования движения трубопровода, когда высокого коэффициента усиления недостаточно для этого. Например, если смещение напряжения постоянного тока напряжения датчиков значительно превышает случайный шум, применение высокого коэффициента усиления не будет порождать колебательное движение. Это состояние показано на фиг.11A-11D, согласно которым высокий коэффициент усиления применяется в течение приблизительно 0.3 секунды. Согласно фиг.11A и 11B, благодаря применению высокого коэффициента усиления один из сигналов возбуждения принимает большое положительное значение (фиг.11A), и другой принимает большое отрицательное значение (фиг.11B). Величины сигналов возбуждения изменяются с шумом в сигналах датчиков (фиг.11C и 11D). Однако усиленного шума недостаточно для изменения знака сигналов возбуждения для генерации колебаний.
На фиг.12A-12D показано, что наложение прямоугольной волны по нескольким периодам может надежно обеспечить быстрый запуск колебаний. Колебания трубопровода, имеющего диаметр два дюйма, могут устанавливаться приблизительно за две секунды. Об установлении колебаний трубопровода свидетельствует снижение амплитуды сигналов возбуждения, показанное на фиг.12A и 12B. На фиг.13A-13D показано, что колебания однодюймового трубопровода могут устанавливаться приблизительно за половину секунды.
Прямоугольную волну также можно использовать в ходе работы для решения проблем колебаний трубопровода. Например, в ряде случаев, известно, что трубопроводы расходомера начинают колебаться на гармониках резонансной частоты трубопровода, например, частотах порядка 1,5 кГц. При обнаружении колебаний такой высокой частоты, прямоугольную волну, имеющую более желательную частоту, можно использовать для возврата колебаний трубопровода к резонансной частоте.
g. Генерация измерения
Контроллер генерирует цифровым методом измерение массового расхода по аналогии с подходом, используемым аналоговым контроллером. Контроллер также может генерировать другие измерения, например плотность.
В одной реализации, контроллер вычисляет массовый расход на основании разности фаз в градусах между двумя сигналами датчиков (phase_diff), частоты колебаний трубопровода (freq) и температуры процесса (temp):
Tz = temp - Tc,
noneu_mf = tan(π * phase_diff/180), и
massflow = 16(MF1*Tz 2 + MF2*Tz + MF3) * noneu_mf/freq,
где Tc - калибровочная температура, MF1-MF3 - калибровочные постоянные, вычисленные в процедуре калибровки, и noneu_mf - массовый расход в безразмерных единицах.
Контроллер вычисляет плотность на основании частоты колебаний трубопровода и температуры процесса:
Tz = temp - Tc,
c2 = freq2, и
плотность = (D1*Tz 2 + D2*Tz + D3)/c2 + D4*Tz 2,
где D1-D4 - калибровочные постоянные, генерируемые в процедуре калибровки.
D. Методы интегрирования
Существуют многие методы интегрирования, причем разные методы требуют разных уровней вычислительной нагрузки и обеспечивают разные уровни точности. В описанной реализации используются варианты метода Симпсона. Основной метод можно выразить в виде:
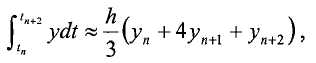
где tk - время взятия выборки k, yk - соответствующее значение функции и h - длина шага. Это правило можно повторно применять к любому вектору данных с нечетным количеством точек данных (т.е., тремя или более точками), что эквивалентно подгонке и интегрированию кубического сплайна к точкам данных. Если количество точек данных оказывается четным, то можно применять так называемое правило 3/8 на одном конце интервала:
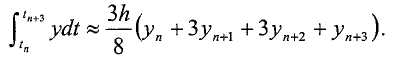
Как указано выше, каждый период начинается и заканчивается при одном и том же смещении (например, start_offset_SV1) от выборочной точки. Точность методов интегрирования значительно повышается при учете этих смещений. Например, при интегрировании полупериода синусоидальной волны, области, соответствующие частичным выборкам, нужно включить в вычисления во избежание существенного занижения оценки в результате.
В описанных вычислениях интегрируется два типа функций: либо функция синуса, либо функция квадрата синуса. Обе легко аппроксимируются вблизи нуля, где находятся конечные точки. В конечных точках, синусоидальная волна является приблизительно линейной, и функция квадрата синуса является приблизительно квадратичной.
Ввиду этих двух типов функций, были оценены три разных метода интегрирования. Это метод Симпсона без краевой поправки, метод Симпсона с линейной краевой поправкой и метод Симпсона с квадратичной поправкой.
Методы интегрирования были протестированы путем генерации и дискретизации строгих функций синуса и квадрата синуса, без моделирования какой-либо ошибки аналого-цифрового усечения. Интегралы были вычислены и результаты были сравнены с истинными амплитудами сигналов. Единственный источник ошибки в этих вычислениях был обусловлен методами интегрирования. Полученные результаты представлены в Таблицах A и B.
Для синусоидальных функций, метод Симпсона с линейной поправкой не имел смещения с наименьшим стандартным отклонением, тогда как метод Симпсона без поправки имел смещение к отрицательной ошибке, и метод Симпсона с квадратичной поправкой имел относительно высокое стандартное отклонение. Для функций квадрата синуса, ошибки, в общем случае, уменьшаются, причем квадратичная коррекция обеспечивает наилучший результат. На основании эти оценок, линейная коррекция используется при интегрировании синусоидальных функций и квадратичная коррекция используется при интегрировании функций квадрата синуса.
E. Метод синхронной модуляции
На фиг.14 показана альтернативная процедура 1400 обработки сигналов датчиков. Процедура 1400 базируется на синхронной модуляции, например, описанной Денисом (Denys) и др., в "Measurement of Voltage Phase for the French Future Defence Plan Against Losses of Synchronism", IEEE Transactions on Power Delivery, 7(1), 62-69, 1992 и Беговичем (Begovic) и др. в "Frequency Tracking in Power Networks in the Presence of Harmonics", IEEE Transactions on Power Delivery, 8(2), 480-486, 1993, которые обе включены посредством ссылки.
Сначала контроллер генерирует начальную оценку номинальной рабочей частоты системы (этап 1405). Затем контроллер пытается измерить отклонение частоты сигнала x[k] (например, SV1) из этой номинальной частоты:
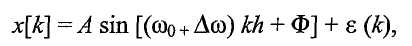
где A - амплитуда синусоидальной части сигнала, ω0 - номинальная частота (например, 88 Гц), Δω - отклонение от номинальной частоты, h - интервал дискретизации, Ф - сдвиг фазы, и ε(k) соответствует добавленным шумам и гармоникам.
Для генерации этого измерения, контроллер синтезирует два сигнала, которые колеблются на номинальной частоте (этап 1410). Сигналы сдвинуты по фазе на 0 и π/2 и имеют единичную амплитуду. Контроллер умножает каждый из этих сигналов на исходный сигнал для создания сигналов y 1 и y 2 (этап 1415):
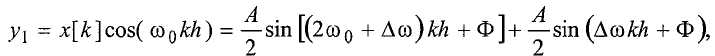 и
и
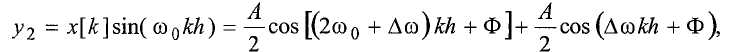
где первые члены y 1 и y 2 являются высокочастотными (например, 176 Гц) компонентами, и вторые члены являются низкочастотными (например, 0 Гц) компонентами. Затем контроллер устраняет высокочастотные компоненты с использованием фильтра низких частот (этап 1420):
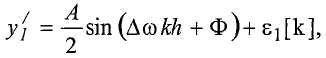 и
и
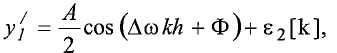
где ε1[k] и ε2[k] представляют фильтрованный шум из исходных сигналов. Контроллер объединяет эти сигналы для создания u[k] (этап 1425):
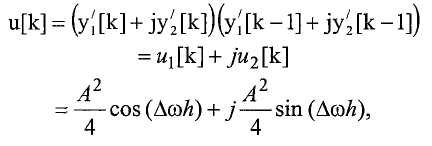
который переносит существенную информацию об отклонении частоты. Как показано, u 1[k] представляет действительную составляющую u[k], а u 2[k] представляет мнимую составляющую.
Контроллер использует действительные и мнимые составляющие u[k] для вычисления отклонения частоты, Δf (этап 1430):
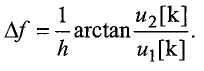
Затем контроллер прибавляет отклонение частоты к номинальной частоте (этап 1435) для получения фактической частоты:
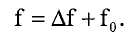
Контроллер также использует действительные и мнимые составляющие u[k] для определения амплитуды исходного сигнала. В частности, контроллер определяет амплитуду как (этап 1440):
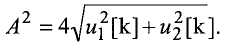
Затем контроллер определяет разность фаз между двумя сигналами датчиков (этап 1445). Исходя из того, что любой шум (ε1[k] и ε2[k]), оставшийся после применения описанного ниже фильтра низких частот, будет пренебрежимо мал, бесшумные версии y 1'[k] и y 2'[k] (y 1 *[k] и y 2 *[k]) можно выразить в виде:
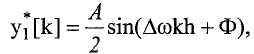 и
и
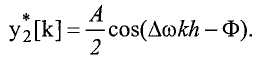
Перемножение этих сигналов дает:
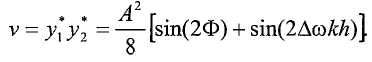
Фильтрация этого сигнала фильтром низких частот, имеющим частоту среза вблизи 0 Гц, удаляет нежелательный компонент и оставляет:
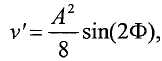
откуда можно вычислить разность фаз:
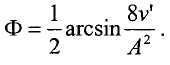
Эта процедура опирается на точность, с которой первоначально оценена рабочая частота, поскольку процедура измеряет только отклонения от этой частоты. Если обеспеченная оценка хороша, можно использовать очень узкополосный фильтр, что делает процедуру очень точной. Для типичных расходомеров, рабочие частоты составляют около 95 Гц (пустой) и 82 Гц (полный). Используется первое определение половины диапазона (88 Гц), что допускает срез фильтра низких частот 13 Гц. Нужно тщательно выбирать частоту среза, поскольку очень малая частота среза может снижать амплитуду синусоидальной волны.
Точность измерения также зависит от применяемых характеристик фильтрации. Ослабление фильтра в мертвой зоне определяет степень режекции гармоник, тогда как уменьшенная частота среза повышает режекцию шума.
F. Измеритель с PI управлением
На фиг.15A и 15B показан измеритель 1500, имеющий контроллер 1505, который использует другой метод для генерации сигналов, подаваемых на возбудители. Аналого-цифровые преобразователи 1510 цифруют сигналы от датчиков 48 и выдают оцифрованные сигналы на контроллер 1505. Контроллер 1505 использует оцифрованные сигналы для вычисления коэффициентов усиления для каждого возбудителя, причем коэффициенты усиления пригодны для генерации нужных колебаний в трубопроводе. Коэффициенты усиления могут быть либо положительными, либо отрицательными. Затем контроллер 1505 выдает коэффициенты усиления на умножающие цифроаналоговые преобразователи 1515. В других реализациях, два или более умножающих цифроаналоговых преобразователей, расположенных в ряд, можно использовать для реализации одного, более чувствительного умножающего цифроаналогового преобразователя.
Контроллер 1505 также генерирует сигналы возбуждения с использованием оцифрованных сигналов датчиков. Контроллер 1505 выдает эти сигналы возбуждения на цифроаналоговые преобразователи 1520, которые преобразуют сигналы в аналоговые сигналы, которые затем поступают на умножающие цифроаналоговые преобразователи 1515.
Умножающие цифроаналоговые преобразователи 1515 умножают аналоговые сигналы на коэффициенты усиления из контроллера 1505 для создания сигналов для возбуждения трубопровода. Затем усилители 1525 усиливают эти сигналы и подают их на возбудители 46. Аналогичные результаты можно получить с помощью контроллера 1505, осуществляющего умножение на умножающем цифроаналоговом преобразователе, причем умножающий цифроаналоговый преобразователь можно заменить стандартным цифроаналоговым преобразователем.
На фиг.15B более подробно показан подход к управлению. В контроллере 1505 оцифрованные сигналы датчиков поступают на амплитудный детектор 1550, который определяет измерение, a(t), амплитуды движения трубопровода с использованием, например, вышеописанного метода. Затем сумматор 1555 использует амплитуду a(t) и желаемую амплитуду a 0 для вычисления ошибки e(t) следующим образом:
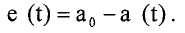
Ошибка e(t) используется блоком 1560 пропорционально-интегрального ("PI") управления для генерации коэффициента усиления K 0(t). Этот коэффициент усиления умножается на разность сигналов датчиков для генерации сигнала возбуждения. Блок PI управления допускает высокоскоростной отклик на изменение условий. Амплитудный детектор 1550, сумматор 1555 и блок 1560 PI управления можно реализовать в виде программного обеспечения, выполняемого контроллером 1505, или в виде отдельной схемы.
1. Процедура управления
Измеритель 1500 действует согласно процедуре 1600, показанной на фиг.16. Первоначально, контроллер принимает оцифрованные данные от датчиков (этап 1605). Затем, процедура 1600 включает в себя три параллельных ответвления: ответвление 1610 измерения, ответвление 1615 генерации сигнала возбуждения и ответвление 1620 генерации коэффициента усиления.
В ответвлении 1610 измерения, оцифрованные данные датчиков используются для генерации измерений амплитуды, частоты и фазы, как описано выше (этап 1625). Затем эти измерения используются для вычисления массового расхода (этап 1630) и других переменных процесса. В общем случае, контроллер 1505 реализует ответвление 1610 измерения.
В ответвлении 1615 генерации сигнала возбуждения, оцифрованные сигналы от двух датчиков дифференцируются для генерации сигнала (этап 1635), который умножается на коэффициент усиления для создания сигнала возбуждения. Как описано выше, эта операция дифференцирования осуществляется контроллером 1505. В общем случае, операция дифференцирования создает взвешенную разность, которая учитывает различия в амплитуде между сигналами датчиков.
В ответвлении 1620 генерации коэффициента усиления, коэффициент усиления вычисляется с использованием блока пропорционально-интегрального управления. Как отмечено выше, определяется амплитуда, a(t), движения трубопровода (этап 1640) и вычитается из желаемой амплитуды a 0 (этап 1645) для вычисления ошибки e(t). Генерация амплитуды, a(t), хотя и показана в виде отдельного этапа, может соответствовать генерации амплитуды на этапе 1625 генерации измерения. Наконец, блок PI управления использует ошибку e(t) для вычисления коэффициента усиления (этап 1650).
Вычисленный коэффициент усиления умножается на сигнал разности для генерации сигнала возбуждения, поступающего на возбудители (этап 1655). Как описано выше, эта операция умножения осуществляется умножающим Ц/А преобразователем или моет осуществляться контроллером.
2. PI Блок управления
Задачей блока PI управления является поддержание в трубопроводе строго синусоидальных колебаний, имеющих амплитуду a 0. Трубопровод можно моделировать в виде простой системы груза-пружины, поведение которой можно выразить в виде:
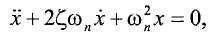
где x - функция времени и выражает смещение груза от точки равновесия, ωn - собственная частота и ζ - коэффициент затухания, который предполагается малым (например, 0.001). Решение этого уравнения движения в виде функции выхода y(t) и входа i(t) аналогично решению для электрической цепи, в которой передаточная функция между подаваемым током, i(s), и воспринимаемым выходным напряжением, y(s), имеет вид:
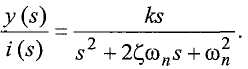
Для достижения нужных колебаний в трубопроводе, контур положительной обратной связи, имеющий коэффициент усиления K 0(t), автоматически регулируется «медленным» внешним контуром для получения:
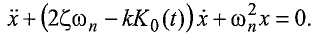
Предполагается, что система имеет свойство "две шкалы времени", что означает, что изменения в K 0(t) происходят настолько медленно, что решения уравнения относительно x, представленного выше, можно получить, предполагая постоянное затухание.
Двучленный блок PI управления, который обеспечивает нулевая ошибка стационарного состояния, можно выразить в виде:
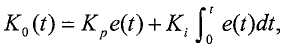
где ошибка, e(t) (т.е., a 0-a(t)), является входом в блок PI управления, и K p и K i - постоянные. В одной реализации, при a 0 = 10, постоянные контроллера K p = 0,02 и K i = 0,0005 обеспечивают отклик, в котором колебания быстро устанавливаются. Однако этот блок PI управления нелинеен, что может приводить к конструкционным и эксплуатационным трудностям.
Линейную модель поведения амплитуды колебаний можно вывести исходя из того, что x(t) равно Aεjωt, что дает:
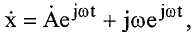 и
и
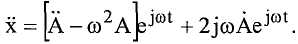
Подставляя эти выражения в выражение для колебаний контура и разделяя его на действительные и мнимые члены, получаем:
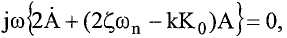 и
и
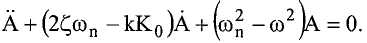
A(t) также можно выразить в виде:
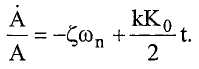
Решение этого уравнения имеет вид:
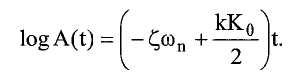
Преобразуя переменные путем задания a(t) равной logA(t), уравнение для A(t) можно переписать в виде:
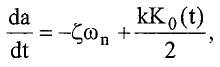
где K 0 теперь в явном виде зависит от времени. Применяя лапласово преобразование, получаем:
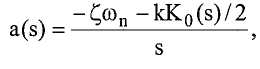
что можно интерпретировать применительно к передаточным функциям, показанным на фиг.17. Эта фигура особенно важна для конструкции контроллеров, поскольку она линейна для всех K 0 и a, с единственным предположением наличия свойства двух шкал времени. Производительность замкнутого контура устойчива согласно этому предположению, благодаря чему можно легко обеспечить быстрые отклики, достижимые на практике.
Согласно фиг.17, член ζωn выражает "возмущение нагрузки", которое должно быть устранено контроллером (т.е. kK 0/2 должно быть равно ζωn, чтобы a(t) была постоянной). Для нулевой ошибки стационарного состояния это подразумевает, что контроллер внешнего контура должен иметь интегратор (или очень большой коэффициент усиления). Поэтому можно предположить, что правильный PI контроллер, C(s), должен иметь вид K p(1+1/sT i), где T i - постоянная. Пропорциональный член необходим для стабильности. Однако член ζωn не влияет на стабильность или конструкцию контроллера, который, вместо этого, основан на передаточной функции открытого контура:
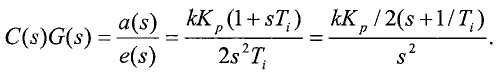
На фиг.18 показан корневой годограф для изменяющегося K p. Для малого K p, это корни с медленным докритическим затуханием. При возрастании K p, корни становятся действительными в точке P, в которой коэффициент усиления контроллера равен K p=8/(kT i). Заметим, в частности, что теория не налагает никаких ограничений на выбор T i. Следовательно, отклик, в принципе, можно сделать критически затухающим и сколь угодно быстрым, надлежащим образом выбирая K p и T i.
Хотя полюсы в точке P являются чисто действительными, это не означает, что в ступенчатом отклике замкнутого контура не происходит выброса. Это проще всего увидеть, рассмотрев передаточную функцию между желаемым значением a 0 и ошибкой e:
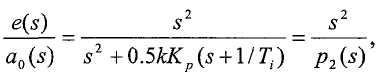
где p 2 - многочлен второго порядка. При ступенчатом входе, a 0(s)= α/s, отклик можно выразить как αp'(t), где p(t) - обратное преобразование 1/p 2(s) и равно a 1exp(-λ1 t)+a 2exp(-λ2 t). Сигнал p(t) возрастает и затем убывает до нуля, поэтому e(t), которая пропорциональна p', должна изменить знак, подразумевая выброс в a(t). Настройку a 0 можно предварительно фильтровать для получения псевдонастройки a 0 *:
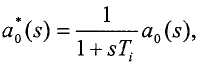
где T i это известный параметр контроллера. Благодаря этому предварительному фильтру, действительные полюсы контроллера должны обеспечивать ступенчатые отклики, свободные от выброса. Этот признак полезен, поскольку могут существовать физические ограничения на выброс (например, механическая помеха или перегрузка компонентов).
Корневой годограф, показанный на фиг.18, предполагает, что динамика обусловлена только передаточной функцией коэффициента усиления/логарифма амплитуды внутреннего контура (фиг.16) и PI контроллера C(s) внешнего контура (т.е. что логарифм амплитуды a = logA измеряется мгновенно). Однако A это амплитуда колебаний, которая может расти или убывать и, следовательно, не может, в общем случае, быть измерена без учета лежащей в основе синусоиды. Существует несколько методов измерения A, помимо рассмотренных выше. Некоторые из них более пригодны для использования в квазистационарных условиях. Например, можно применять контур фазовой автоподстройки частоты, в котором синусоидальный сигнал s(t) = sin(ωn t+Ф0) синхронизируется по фазе с измеренным колебательным сигналом y(t) = A(t)sin(ωn t+Ф1). Таким образом, мера амплитуды a = logA задается путем деления этих сигналов (с надлежащими предохранителями и фильтрами). Этот метод, возможно, удовлетворителен вблизи стационарного состояния, но не в условиях установления до синхронизации.
Другой подход использует блок отслеживания пиков, который включает в себя детектор пересечения нуля совместно с алгоритмом отслеживания пиков, реализованного в контроллере. Однако методы пересечения нуля могут быть подвержены шуму. Кроме того, результаты блока отслеживания пиков доступны только раз в полупериод, что определяет интервал выборки для обновлений контроллера.
Наконец, можно применять AM детектор. При наличии синусоидальной волны y(t) = Asinωn
t, оценку A можно получить из 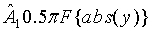 , где F{} - это подходящий фильтр низких частот с единичным коэффициентом усиления постоянного тока. AM детектор является простейшим подходом. Кроме того, он не требует наличия колебаний на любой конкретной частоте и, следовательно, полезен в условиях пуска. Он страдает тем недостатком, что существует утечка гармоник во внутренний контур, что будет влиять на спектр результирующих колебаний. Кроме того, фильтр добавляет дополнительную динамику во внешний контур, что требует нахождения компромисса между скоростью отклика и спектральной чистотой. В частности, эффект фильтра состоит в ограничении выбора наилучшего T
i.
, где F{} - это подходящий фильтр низких частот с единичным коэффициентом усиления постоянного тока. AM детектор является простейшим подходом. Кроме того, он не требует наличия колебаний на любой конкретной частоте и, следовательно, полезен в условиях пуска. Он страдает тем недостатком, что существует утечка гармоник во внутренний контур, что будет влиять на спектр результирующих колебаний. Кроме того, фильтр добавляет дополнительную динамику во внешний контур, что требует нахождения компромисса между скоростью отклика и спектральной чистотой. В частности, эффект фильтра состоит в ограничении выбора наилучшего T
i.
Ряд Фурье для abs(y) имеет известный вид:
Поэтому выходной сигнал нужно масштабировать на n/2 для обеспечения правильного выходного сигнала постоянного тока A, и (четные) гармонические члены a kcos2kωn t нужно отфильтровывать. Поскольку все, что должен сделать фильтр, это пропустить компонент постоянного тока и ослабить все остальные частоты, достаточно фильтра "кирпичная стена" с отсечкой ниже 2ωn. Однако динамика фильтра будет влиять на поведение замкнутого контура. Обычно выбирают фильтр Баттеруорта. Например, фильтр низких частот третьего порядка с конструкцией критической частоты ωb выражается в виде:
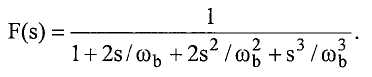
При конструктивной частоте отклик на 3 дБ ниже; на 2ωb он равен -18 дБ (0,12), и на 4ωb он равен -36 дБ (0,015). Фильтры Баттеруорта более высокого порядка имеют более крутую характеристику, но большинство их полюсов являются комплексными и могут негативно влиять на корневой годограф контура управления.
G. Компенсация смещения нуля
Как отмечено выше, смещение нуля может вноситься в сигнал напряжения датчика за счет дрейфа в схеме предварительного усиления и аналого-цифровым преобразователем. Небольшие различия в коэффициентах усиления предусилителя для положительного и отрицательного напряжений вследствие использования дифференциальных схем могут ухудшать эффект смещения нуля. Ошибки изменяются между передатчиками и с температурой передатчика и износом компонента.
Аналого-цифровые преобразователи аудио-качества (т.е. относительно низкой стоимости) можно применять по экономическим причинам. Эти устройства не имеют стабильности смещения постоянного тока и амплитуды в числе высоких приоритетов. На фиг.19A-19D показано, как изменяются смещение и положительный и отрицательный коэффициенты усиления в зависимости от рабочей температуры микросхемы для одного такого преобразователя (преобразователя AD1879). Повторяемость показанных тенденций ненадежна, и даже при обеспечении температурной компенсации на основании тенденций, остаются остаточное смещение нуля и рассогласование положительных/отрицательных коэффициентов усиления.
Если фаза вычисляется с использованием разности по времени между точками пересечения нуля для двух напряжений датчиков, смещение постоянного тока может приводить к фазовым ошибкам. Этот эффект продемонстрирован на фиг.20A-20C. На каждом графике показан вычисленный сдвиг фазы, который измеряется цифровым передатчиком, когда истинный сдвиг фазы равен нулю (т.е. при нулевом расходе).
На фиг.20A показана фаза, вычисленная на основании полных периодов, начинающихся с положительных пересечений нуля. Среднее значение равно 0,00627 градуса.
На фиг.20B показана фаза, вычисленная начиная с отрицательных пересечений нуля. Среднее значение равно 0,0109 градуса.
На фиг.20C показана фаза, вычисленная для каждого полупериода. На фиг.20C данные из фиг.20A и 20B перемежаются. Средняя фаза (-0,00234) ближе к нулю, чем на фиг.20A и 20B, но стандартное отклонение сигнала примерно в шесть раз больше.
Более усовершенствованные методы измерения фазы, например, основанные на методах Фурье, устойчивы к смещению постоянного тока. Однако желательно устранять смещение нуля, даже когда используются эти методы, поскольку данные обрабатываются в пакетах полного периода, разделенных точками пересечения нуля. Это позволяет упростить анализ эффектов, например, амплитудной модуляции, на наблюдаемых фазе и частоте. Кроме того, рассогласование коэффициентов усиления между положительными и отрицательными напряжениями будет вносить ошибки в любой метод измерения.
Метод пересечения нуля для определения фазы можно использовать, чтобы продемонстрировать влияние смещения нуля и ошибки рассогласования коэффициентов усиления, и их последующего удаления. На фиг.21A и 21B показан долговременный дрейф, синхронизированный по фазе с нулевым расходом. Каждая точка представляет среднее значение оперативных данных за одну минуту. На фиг.21A показана средняя фаза, и на фиг.21B показано стандартное отклонение фазы. За несколько часов дрейф становится заметным. Таким образом, даже если обнулять измеритель каждый день, что во многих приложениях считается чрезмерным требованием к обслуживанию, все же будет оставаться значительный дрейф фазы.
1. Метод компенсации
Метод компенсации смещения напряжения и рассогласования коэффициентов усиления использует вычислительные возможности цифрового передатчика и не требует условия нулевого расхода. Метод использует набор вычислений в каждом периоде, который, при усреднении по разумному периоду (например, 10,000 периодам) и исключении областей сильного изменения (например, изменения настройки, наступления аэрации), сходится к желаемым компенсациям смещения нуля и рассогласования коэффициентов усиления.
Предполагая наличие до трех высших гармоник, нужный колебательный сигнал напряжения датчика SV(t) можно выразить в виде:
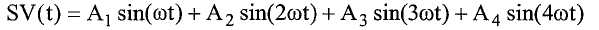 ,
,
где A1 обозначает амплитуду основного частотного компонента и A2-A4 обозначают амплитуды трех гармонических компонентов. Однако, на практике, фактический колебательный сигнал нарушается смещением нуля Z0 (которое имеет значение, близкое к нулю) и рассогласованием между отрицательным и положительным коэффициентами усиления Gn и Gp. Без потери общности, можно предположить, что Gp равен единице, и что Gn задается следующим образом:
где εG представляет рассогласование коэффициентов усиления.
Метод предполагает, что амплитуды Ai и частота ω постоянны. Это правомерно, поскольку оценки Z0 и εG базируются на средних значениях, взятых по большому количеству периодов (например, 10,000 перемежающимся периодам, происходящим в течение примерно 1 минуты работы). При реализации метода, контроллер осуществляет проверку на наличие значительных изменений в частоте и амплитуде, чтобы гарантировать правильность анализа. Наличие высших гармоник обуславливает использование методов Фурье для извлечения информации фазы и амплитуды для конкретных гармоник. Это предусматривает интегрирование SV(t) и умножение на модулирующую функцию синуса или косинуса.
Смещение нуля влияет на пределы интегрирования, а также на вид функции. Поскольку существует смещение нуля, начальная точка для вычисления амплитуды и фазы не совпадает с точкой нулевой фазы периодического колебательного сигнала SV(t). Для смещения нуля Z0, соответствующий сдвиг фазы приблизительно равен
Для малой фазы, 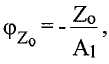 с соответствующей задержкой по времени
с соответствующей задержкой по времени 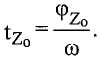
Интегралы масштабируются так, чтобы граничное значение (т.е., когда Z0 и ωG приближаются к нулю) было равно амплитуде соответствующей гармоники. Первые два интеграла, представляющие интерес, таковы:
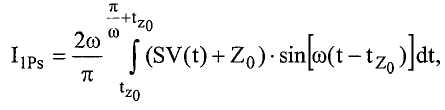 и
и
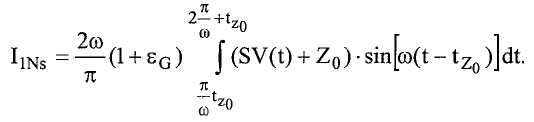
Эти интегралы представляют то, что на практике вычисляется в ходе нормального Фурье-анализа данных напряжения датчика. Нижний индекс 1 указывает первую гармонику, N и P указывают, соответственно, отрицательный или положительный полупериод, и s и c указывают, соответственно, используется ли синус или косинус в качестве модулирующей функции.
Строго говоря, средняя точка пересечения нуля и, следовательно, соответствующие пределы интегрирования должны быть заданы равными π/ω - tz0, а не π/ω + tz0. Однако использование точной средней точки вместо точной точки пересечения нуля позволяет упростить анализ и улучшить численное поведение (в принципе, вследствие ошибок в положении точки пересечения нуля). Единственная ошибка, вносимая при использовании точной средней точки, состоит в том, что малая часть каждого из вышеприведенных интегралов умножается на неверный коэффициент усиления (1 вместо 1 + εG и наоборот). Однако эти ошибки имеют порядок Z0 2εG и считаются пренебрежимо малыми.
Используя компьютерную алгебру и предполагая малыми Z0 и εG, оценки первого порядка для интегралов можно вывести в виде:
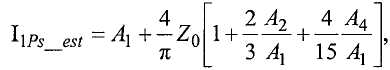 и
и
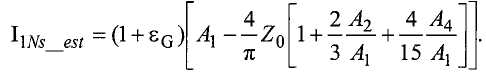
Можно определить связанные с ними полезные функции, включающие в себя сумму, разность и отношение интегралов и их оценок. Сумму интегралов можно выразить в виде:
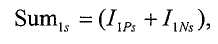
а сумма оценок равна:
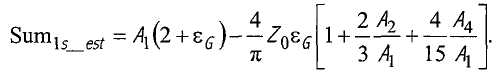
Аналогично, разность интегралов можно выразить в виде:
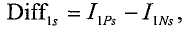
а разность оценок равна:
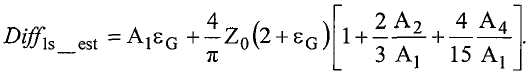
Наконец, отношение интегралов равно:
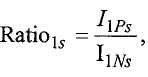
а отношение оценок равно:
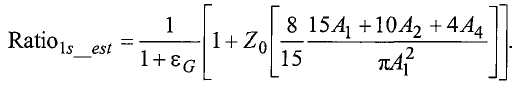
Соответствующие интегралы от косинуса задаются в виде:
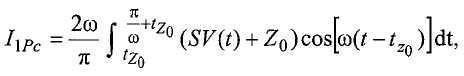 и
и
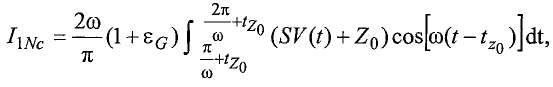
с оценками:
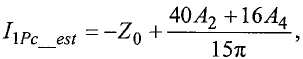 и
и
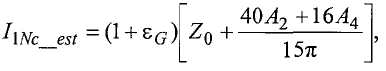
и суммами:
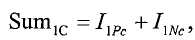 и
и
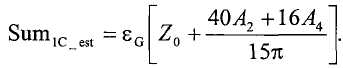
Интегралы второй гармоники выражаются в виде:
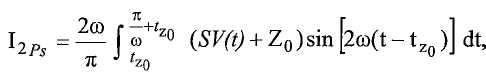 и
и
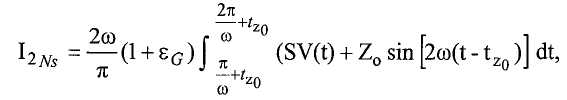
с оценками: 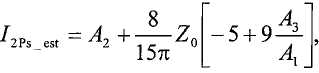 и
и
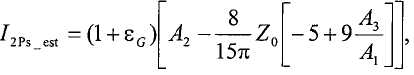
и суммами:
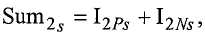 и
и
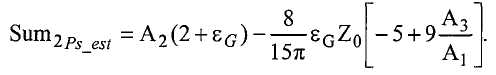
Интегралы можно вычислять численными методами для каждого периода. Как рассмотрено ниже, уравнения, позволяющие оценить значения интегралов на основании различных амплитуд и значений смещения нуля и коэффициента усиления, можно преобразовать для получения оценок смещения нуля и коэффициента усиления на основании вычисленных интегралов.
2. Пример
Точность оценочных уравнений можно проиллюстрировать на примере. Для каждого основного интеграла предусмотрено три значения: значение "истина" интеграла (вычисленного в Mathcad с использованием интегрирования по Ромбергу), значение, использующее оценочное уравнение, и значение, вычисленное цифровым передатчиком, работающим в режиме моделирования, с использованием метода Симпсона с краевой поправкой.
Таким образом, например, значение I1Ps, вычисленное согласно
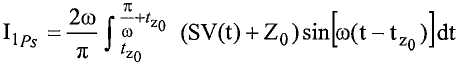 ,
,
равно 0,101353, тогда как оценочное значение (I1Ps_est), вычисленное как
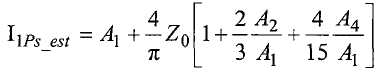 ,
,
равно 0,101358. Значение, вычисленное с использованием цифрового передатчика в режиме моделирования, равно 0,101340. Эти вычисления используют значения параметров, приведенные в Таблице C.
Точные, оценочные и модельные результаты, полученные с использованием этих значений параметров, приведены в Таблице D.
Таким образом, по меньшей мере, для конкретных выбранных значений, оценки, полученные из уравнений первого порядка, чрезвычайно точны. Когда Z0 и εG приближаются к нулю, ошибки в оценке и моделировании приближаются к нулю.
3. Реализация
Оценки первого порядка для интегралов задают ряд нелинейных уравнений относительно амплитуд гармоник, смещения нуля и рассогласования коэффициентов усиления. Поскольку уравнения нелинейны, точное решение получить невозможно. Однако аппроксимация, сопровождаемая корректирующими итерациями, обеспечивает достаточную сходимость при ограниченной вычислительной нагрузке.
Для A1-A4 можно предусмотреть отношения, зависящие от трубопровода. Поэтому, не делается попыток вычисления всех амплитуд A1-A4. Вместо этого, только A1 и A2 оцениваются с использованием заданных выше интегральных уравнений. На основании поведения относительных амплитуд, A3 можно приближенно выразить как A2/2, и A4 можно приближенно выразить как A2/10.
Метод компенсации смещения нуля можно реализовать согласно процедуре 2200, показанной на фиг.22. В течение каждого периода, контроллер вычисляет интегралы I1Ps, I1Ns, I1Pc I1Nc, I2Ns и связанные с ними функции sum1s, ratio1s, sum1c и sum2s (этап 2205). Для этого требуется минимальная дополнительная вычислительная нагрузка сверх традиционных вычислений методом Фурье, используемых для определения частоты, амплитуды и фазы.
Каждые 10,000 периодов контроллер проверяет наклон амплитуды напряжение датчика A1 с использованием традиционного метода оценки скорости изменения (этап 2210). Если амплитуда постоянна (этап 2215), то контроллер переходит к вычислениям смещения нуля и рассогласования коэффициентов усиления. Эту проверку можно распространить на тестирование стабильности частоты.
Для осуществления вычислений, контроллер генерирует средние значения функций (например, sum1s) по последним 10,000 периодам. Затем контроллер определяет первую оценку смещения нуля и рассогласования коэффициентов усиления (этап 2225):
Z0 = -Sum1c/2, и
εG = 1/Ratio1s - 1
С использованием этих значений, контроллер вычисляет обратный коэффициент усиления (k) и коэффициент амплитуды (amp_factor) (этап 2230):
k = 1,0/(1,0 + 0,5*εG), и
amp_factor = 1 + 50/75*Sum2s/Sum1s
Контроллер использует обратный коэффициент усиления и коэффициент амплитуды для выработки первой оценки амплитуды (этап 2235):
A1 = k * [Sum1s/2 + 2/π * Z0 * εG * amp_factor], и
A2 = k * [Sum2s/2 - 4/(3 * π) * Z0 * εG]
Затем контроллер улучшает оценку посредством следующих вычислений, при необходимости, повторяемых (этап 2240):
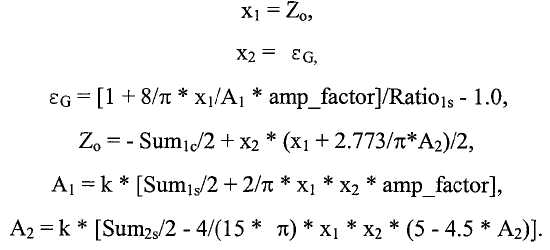
Контроллер использует стандартные методы проверки на сходимость значений Z0 εG. На практике поправки оказываются малыми после первой итерации, и из практики следует, что достаточно трех итераций.
Наконец, контроллер регулирует необработанные данные для исключения Z0 и εG (этап 2245). Затем контроллер повторяет процедуру. После устранения смещения нуля и рассогласования коэффициентов усиления из необработанных данных, функции (т.е. sum1s), используемые при генерации последующих значений Z0 и εG, базируются на скорректированных данных. Соответственно, эти последующие значения Z0 и εG отражают остаточные смещение нуля и рассогласование коэффициентов усиления, и суммируются с ранее сгенерированными значениями для создания фактических смещения нуля и рассогласования коэффициентов усиления. Согласно одному подходу к регулировке необработанных данных, контроллер генерирует регулировочные параметры (например, S1_off и S2_off), которые используются при преобразовании аналоговых сигналов от датчиков в цифровые данные.
На фиг.23A-23C, 24A и 24B показаны результаты, полученные с использованием процедуры 2200. Краткосрочное поведение проиллюстрировано на фиг.23A-23C. Здесь показаны последовательные оценки фазы, полученные через пять минут после пуска, предусмотренные, чтобы дать процедуре время начать оказывать влияние на выходной сигнал. Фаза показана на основании положительных пересечений нуля, отрицательных пересечений нуля и их обоих.
Разность между положительным и отрицательным средними значениями снижена с коэффициентом 20, при соответствующем снижении среднего смещения нуля в перемеженном наборе данных. Соответствующее стандартное отклонение снижено с коэффициентом приблизительно 6.
Более долгосрочное поведение показано на фиг.24A и 24B. Первоначально большое смещение нуля быстро корректируется, и затем сдвиг фазы остается вблизи нуля в течение многих часов. Среднее смещение фазы, за исключением нескольких первых значений, составляет 6,14e-6, что явно указывает на то, что процедура успешно компенсирует изменения в смещении напряжения и дисбалансе коэффициентов усиления.
Типичные значения Z0 и εG для цифрового кориолисова измерителя составляют Z0 = -7,923e-4 и εG = -1,754e-5 для сигнала SV1, и Z0 = -8,038e-4 и εG = +6,93e-4 для сигнала SV2.
H. Динамический анализ
В общем случае, традиционные вычисления измерения для кориолисовых измерителей предполагают, что частота и амплитуда колебаний на каждой стороне трубопровода постоянны, и что частота на каждой стороне трубопровода одинакова и равна так называемой резонансной частоте. Фазы, в общем случае, не измеряются отдельно на каждой стороне трубопровода, и разность фаз между двумя сторонами предполагается постоянной на протяжении процесса измерения. Точные измерения частоты, фазы и амплитуды в каждый полупериод с использованием цифрового измерителя демонстрируют, что эти предположения справедливы только, когда значения параметров усредняются по периоду времени порядка секунд. При наблюдении на 100 Гц или более высоких частотах, эти параметры демонстрируют заметное изменение. Например, в ходе нормальной работы, значения частоты и амплитуды SV1 могут демонстрировать сильную отрицательную корреляцию с соответствующими значениями SV2. Соответственно, традиционные алгоритмы измерения подвержены шуму, обусловленному этими динамическими изменениями. Шум повышается при возрастании скорости вычисления измерений. Другие шумовые члены могут обуславливаться физическими факторами, например, динамикой трубки Вентури, динамическими нелинейностями (например, изменением жесткости трубки Вентури с амплитудой), или динамическими последствиями напряжений датчиков, обеспечивающих данные скорости вместо данных абсолютного положения.
Описанные методы используют высокую точность цифрового измерителя для отслеживания и компенсации динамического поведения трубопровода для снижения шума с целью обеспечения более точных измерений переменных процесса, например, массового расхода и плотности. Это достигается за счет мониторинга и компенсации таких эффектов, как скоростей изменения частоты, фазы и амплитуды, динамики трубки Вентури и динамических физических неидеальностей. Вычисление разности фаз, при котором не предполагается одна и та же частота на каждой стороне, уже описано выше. Другие методы компенсации описаны ниже.
Мониторинг и компенсация динамических эффектов может осуществляться на уровне отдельных датчиков для обеспечения скорректированных оценок фазы, частоты, амплитуды или других параметров. Дополнительная компенсация также может осуществляться на уровне трубопровода, где данные от обоих датчиков объединяются, например, при вычислении разности фаз и средней частоты. Эти два уровня можно использовать совместно для обеспечения полной компенсации.
Таким образом, измерения мгновенного массового расхода и плотности расходомером можно усовершенствовать путем моделирования и учета динамических эффектов работы расходомера. В общем случае, 80% или более фазового шума в кориолисовом расходомере можно приписать динамике трубки Вентури (иногда именуемой "звоном"), а не измеряемым условиям процесса. Применение динамической модели может снижать фазовый шум с коэффициентом от 4 до 10, приводя к значительному повышению производительности измерения расхода. Единая модель эффективна для всех расходов и амплитуд колебаний. В общем случае, вычислительные требования пренебрежимо малы.
Динамический анализ можно осуществлять на каждом из сигналов датчиков отдельно друг от друга. Это позволяет избежать или, по меньшей мере, задержать моделирование динамического взаимодействия между двумя сторонами трубопровода, которое, вероятно, значительно сложнее, чем динамика на каждом датчике. Кроме того, анализ отдельных сигналов датчиков, скорее всего, приведет к успеху в условиях, например порционного пуска и аэрации, когда две стороны трубопровода подвергаются действию разных сил со стороны рабочей текучей среды.
В общем случае, при динамическом анализе рассматривается влияние изменения со временем амплитуды, частоты и фазы на вычисленные значения этих параметров. Хотя частоту и амплитуду легко задать для отдельных напряжений датчиков, фаза традиционно задается применительно к разности между напряжениями датчиков. Однако при использовании Фурье-анализа, фазу для отдельного датчика можно задавать применительно к разности между средней точкой периода и средней 180° фазовой точкой.
Три типа динамических эффектов представляют собой ошибку измерения и так называемые эффекты "обратной связи" и "скорости". Ошибка измерения обусловлена тем, что алгоритмы для вычисления амплитуды и фазы предполагают, что частота, амплитуда и фаза постоянны в течение интервала времени, представляющего интерес. Производительность алгоритмов измерения можно повысить, внося поправки в изменения этих параметров.
Эффект обратной связи обусловлен подводом энергии к трубопроводу, при котором, с учетом утечки энергии из трубопровода, поддерживается постоянная амплитуда колебаний. Необходимость в дополнительном подводе энергии к трубопроводу выявляется только, когда амплитуда колебаний начинает отклоняться от желаемой настройки. В результате, член затухания в уравнении движения для колеблющегося трубопровода отличен от нуля и постоянно колеблется вокруг нуля. Хотя собственная частота трубопровода не изменяется, она маскируется сдвигами в пересечениях нуля (т.е. изменениями фазы), связанными с этими малыми изменениями амплитуды.
Эффект скорости обусловлен тем, что напряжения датчиков отражают скорость трубопровода, но анализируются, как будто они представляют позицию трубопровода. Следствием этого является то, что скорость изменения амплитуды оказывает влияние на наблюдаемые частоту и фазу, даже если истинные значения этих параметров постоянны.
1. Компенсация для амплитудной модуляции на уровне датчиков
Один подход к коррекции динамических эффектов предусматривает мониторинг амплитуд сигналов датчиков и производство регулировок на основании изменений в амплитудах. В целях анализа динамических эффектов, предполагается, что оценки фазы, частоты и амплитуды можно определить для каждого напряжения датчика в течение каждого периода. Как показано на фиг.25, вычисления базируются на полных, но перекрывающихся периодах. Каждый период начинается в точке пересечения нуля, посередине предыдущего периода. Положительные периоды начинаются с положительных напряжений сразу же после начального пересечения нуля, тогда как отрицательные периоды начинаются с отрицательных напряжений. Таким образом, период n является положительным, а периоды n-1 и n+1 являются отрицательными. Предполагается, что коррекция смещения нуля произведена так, чтобы смещение нуля было пренебрежимо малым. Предполагается также, что высшие гармоники могут присутствовать.
Предполагается линейное изменение амплитуды, частоты и фазы. Исходя из этого предположения, среднее значение каждого параметра в течение периода равно мгновенному значению параметра в средней точке периода. Поскольку периоды перекрываются на 180 градусов, среднее значение для периода равно начальному значению для следующего периода.
Например, период n представляет собой интервал времени от 0 до 2π/ω. Средние значения амплитуды, частоты и фазы равны мгновенным значениям в средней точке, π/ω, которая также является начальной точкой для периода n+1, который представляет собой интервал времени от π/ω до 3π/ω. Конечно, эти временные границы являются приближенными, поскольку ω также изменяется со временем.
a. Процедура компенсации динамических эффектов
Контроллер учитывает динамические эффекты согласно процедуре 2600, представленной на фиг.26. Сначала контроллер создает оценку частоты (этап 2605) с использованием пересечений нуля для измерения времени между началом и концом периода, как описано выше. Исходя из того, что частота изменяется линейно, эта оценка равна частоте, усредненной по времени в течение периода.
Затем контроллер использует оценочную частоту для генерации первой оценки амплитуды и фазы с использованием вышеописанного метода Фурье (этап 2610). Как отмечено выше, этот метод устраняет эффекты высших гармоник.
Фаза интерпретируется применительно к единичному колебательному сигналу как разность между началом периода (т.е. точкой пересечения нуля) и точкой нулевой фазы для компонента SV(t) частоты ω, выражаемая как сдвиг фазы. Поскольку сдвиг фазы является средним по всему колебательному сигналу, его можно использовать как сдвиг фазы от средней точки периода. В идеале, в отсутствие смещения нуля и при постоянной амплитуде колебаний, сдвиг фазы должен быть нулевым для каждого периода. Однако на практике он демонстрирует высокий уровень изменения и обеспечивает хорошую основу для коррекции массового расхода с учетом динамических изменений амплитуды.
Затем контроллер вычисляет разность фаз (этап 2615). Хотя возможны различные определения разности фаз, анализ предполагает, что средняя фаза и частота каждого сигнала датчика представляет весь колебательный сигнал. Поскольку эти частоты различны для SV1 и SV2, соответствующие фазы масштабируются к средней частоте. Кроме того, фазы сдвигаются к одной и той же начальной точке (т.е. средней точке периода на SV1). После масштабирования, они вычитаются для обеспечения разности фаз.
Затем контроллер определяет скорость изменения амплитуды для периода n (этап 2620):
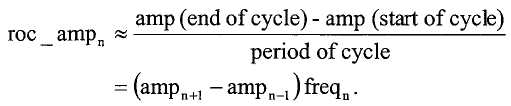
Это вычисление предполагает, что амплитуда из периода n+1 доступна при вычислении скорости изменения периода n. Это возможно, если поправки делаются спустя один период после получения необработанных вычислений амплитуды. Преимущество наличия точной оценки скорости изменения и, следовательно, хорошей коррекции измерения, перевешивает задержку в обеспечении скорректированных измерений, которая, в одной реализации, составляет порядка 5 миллисекунд. Наиболее недавно сгенерированная информация всегда используется для управления трубопроводом (т.е. для генерации сигнала возбуждения).
При желании, уточненную оценку скорости изменения можно вычислять после применения коррекции амплитуды (как описано ниже). В итоге, итерация сходится к наилучшим значениям амплитуды и скорости изменения.
b. Частотная компенсация эффектов обратной связи и скорости
Как отмечено выше, динамические аспекты контура обратной связи вносят зависящие от времени сдвиги в фазу вследствие малых отклонений амплитуды от настройки. В результате, измеренная частота, которая базируется на пересечениях нуля, отличается от собственной частоты трубопровода. Если используются датчики скорости, возникает дополнительный сдвиг по фазе. Этот дополнительный сдвиг также связан с изменениями в амплитуде позиции трубопровода. Динамический анализ позволяет отслеживать и компенсировать эти эффекты. Соответственно, контроллер использует вычисленную скорость изменения амплитуды для корректировки оценки частоты (этап 2625).
Позицию колеблющегося трубопровода в контуре обратной связи, который применяется для поддержания постоянной амплитуды колебаний трубопровода, можно выразить в виде:
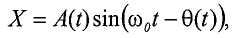
где θ(t) - фазовая задержка, обусловленная эффектом обратной связи. Механическая Q колеблющегося трубопровода обычно составляет порядка 1000, что предусматривает малые отклонения амплитуды и фазы. При этих условиях, θ(t) задается следующим образом:
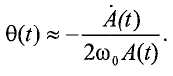
Поскольку каждый датчик измеряет скорость:
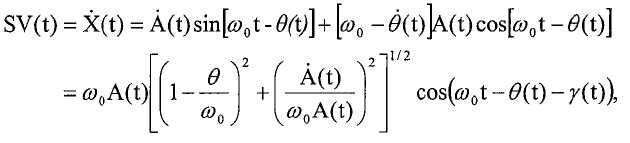
где γ(t) - фазовая задержка, обусловленная эффектом скорости:
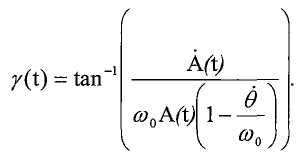
Поскольку механическая Q трубопровода обычно составляет порядка 1000, и, следовательно, изменения в амплитуде и фазе малы, резонно предположить:
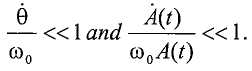
Это означает, что выражение для SV(t) можно упростить до:
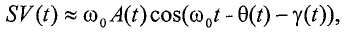
и, по некоторым причинам, выражение для фазовой задержки из-за смещения скорости можно упростить до:
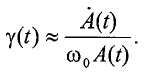
Суммирование фазовых задержек вследствие эффектов обратной связи и скорости дает полную фазовую задержку:
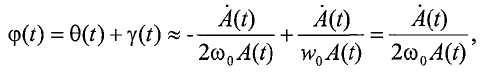
и следующее выражение для SV(t):
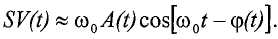
Это позволяет отличить фактическую частоту колебаний от собственной частоты колебаний. Хотя первая является наблюдаемой, последняя полезна для вычислений плотности. В течение любого разумного периода времени и предполагая надлежащее управление амплитудой, средние значения этих двух частот будут совпадать (поскольку средняя скорость изменения амплитуды должна быть равна нулю). Однако, для усовершенствованного измерения мгновенной плотности, желательно вносить поправки в фактическую частоту колебаний на динамические эффекты для получения собственной частоты. Это особенно полезно при работе с аэрированными текучими средами, мгновенная плотность которых может быстро меняться со временем.
Наблюдаемая частота, отслеживаемая в течение периода n, ограничивается пересечениями нуля, происходящими в средних точках периодов n-1 и n+1. Фазовая задержка, обусловленная изменением скорости, будет оказывать влияние на наблюдаемые начало и конец периода:
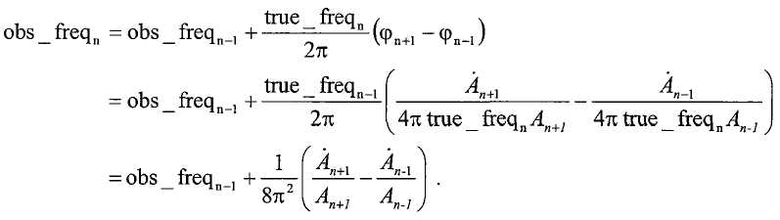
На основании этого анализа, коррекцию можно применять с использованием интегрированного ошибочного члена:
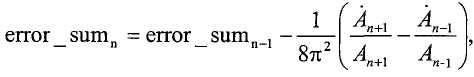 и
и
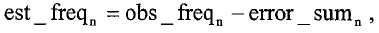
где значение error_summ при пуске (т.е. значение в нулевом периоде) равно:
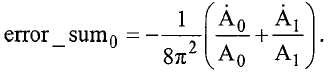
Хотя эти уравнения включают в себя постоянный член, имеющий значение 1/8π2, фактические данные говорят о том, что более пригоден постоянный член 1/8π. Это различие можно объяснить несмоделированной динамикой, которую можно определить путем дополнительного анализа.
Рассмотренные выше вычисления предполагают, что истинная амплитуда колебаний, A, доступна. Однако, на практике, можно наблюдать только напряжение датчика SV. Это напряжение датчика можно выразить в виде:
 .
.
Амплитуда, amp_SV(t), в этом выражении равна:
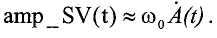
Скорость изменения этой амплитуды равна:
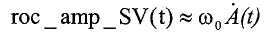
поэтому можно использовать следующую оценку:
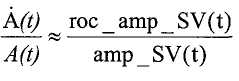 .
.
c. Применение частотной компенсации эффектов обратной связи и скорости
На фиг.27A-32B показано, как применение процедуры 2600 улучшает оценку собственной частоты и, следовательно, плотности процесса, для реальных данных из измерителя, имеющего трубопровод диаметром один дюйм. На каждой из фигур показано 10,000 выборок, собранных в течение всего лишь 1 минуты.
На фиг.27A и 27B показаны амплитудные и частотные данные из SV1, полученные посредством применения случайных изменений к настройке амплитуды. Поскольку трубопровод наполнен водой и поток отсутствует, собственная частота постоянна. Однако наблюдаемая частота существенно изменяется при изменении амплитуды. Среднее значение частоты равно 81,41 Гц, со стандартным отклонением 0,057 Гц.
На фиг.28A и 28B показаны, соответственно, отклонение частоты от среднего значения и корректирующий член, генерируемый согласно процедуре 2600. Грубые отклонения очень хорошо согласуются. Однако существует дополнительное изменение частоты, не связанное с изменениями амплитуды. Другая важная особенность, показанная на фиг.28B, состоит в том, что среднее близко к нулю в результате правильной инициализации вышеописанного ошибочного члена.
На фиг.29A и 29B необработанные частотные данные (фиг.29A) сравниваются с результатами применения корректирующей функции (фиг.29B). Сдвиг в средней частоте пренебрежимо мал, а стандартное отклонение снизилось с коэффициентом 4,4. Из фиг.29B следует, что в скорректированных частотных данных существует остаточная структура. Предполагается, что дополнительный анализ, на основании изменения фазы в течение периода и его влияния на наблюдаемую частоту, позволит дополнительно понизить шум.
На фиг.30A и 30B показано соответствующее влияние на среднюю частоту, полученную усреднением мгновенных частот напряжения датчика. Поскольку средняя частота используется для вычисления плотности рабочей текучей среды, понижение шума (здесь, с коэффициентом 5,2) скажется на вычислении плотности.
На фиг.31A и 31B показаны необработанная и скорректированная средние частоты для трубопровода диаметром 2 дюйма, настройка амплитуды которого является случайной величиной. 2" трубка Вентури демонстрирует меньшее изменение частоты, чем 1", как для необработанных, так и для скорректированных данных. Коэффициент понижения шума равен 4,0.
На фиг.32A и 32B показаны более типичные результаты с реальными данными потока для однодюймовой трубки Вентури. Алгоритм произвольной настройки заменен нормальной постоянной настройкой. В результате, изменение амплитуды оказывается меньше, чем в предыдущих примерах, что приводит к меньшему коэффициенту понижения шума 1,5.
d. Компенсация измерения фазы для амплитудной модуляции
Согласно фиг.26, контроллер затем компенсирует измерение фазы с учетом амплитудной модуляции, предполагая обеспеченное выше вычисление фазы (этап 2630). В описанных выше вычислениях фазы методом Фурье предполагается, что амплитуда колебаний постоянна на протяжении периода данных, на котором производятся вычисления. В этом разделе описана коррекция, которая предполагает линейное изменение амплитуды на протяжении периода данных.
Игнорируя высшие гармоники и исходя из того, что любое смещение нуля устранено, выражение для напряжения датчика задается следующим образом:
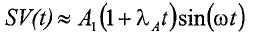 ,
,
где λA - постоянная, соответствующая относительному изменению амплитуды со временем. Как рассмотрено выше, интегралы I1 и I2 можно выразить в виде:
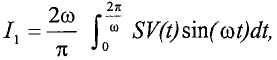 и
и
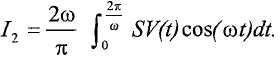
Оценивая эти интегралы, получаем:
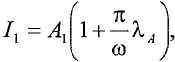 и
и
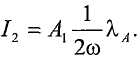
Подставляя эти выражения в вычисление амплитуды и разлагая в ряд по λA, получаем:
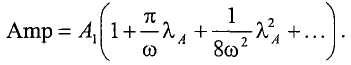
Предполагая λA малым и пренебрегая всеми членами после члена первого порядка, это выражение можно свести к:
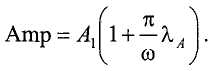
Это равно амплитуде SV(t) в средней точке периода (t = π/ω). Соответственно, вычисление амплитуды обеспечивает необходимый результат без коррекции.
Для вычисления фазы, предполагается, что истинные разность фаз и частота постоянны, и что смещения напряжения не существует, что означает, что значение фазы должно быть равно нулю. Однако, в результате амплитудной модуляции, коррекция, подлежащая применению к необработанным данным фазы для компенсации амплитудной модуляции, имеет вид:
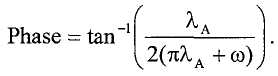
Исходя из того, что выражение в скобках мало, функцию арктангенса можно игнорировать.
Более детальный анализ учитывает эффекты высших гармоник. Исходя из того, что напряжение датчика можно выразить в виде:
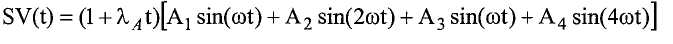 ,
,
в соответствии с чем амплитуды всех гармоник возрастают с одинаковой относительной скоростью в течение периода, результирующие интегралы можно выразить в виде:
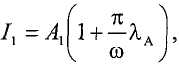
и
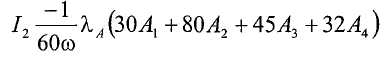
для положительных периодов, и
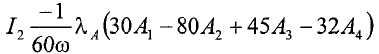
для отрицательных периодов.
Для амплитуды, подставляя эти выражения в вычисления, получаем, что на вычисление амплитуды влияют только члены второго порядка и выше, поэтому для аппроксимации первого порядка для амплитуды коррекция не требуется. Для фазы, корректирующий член имеет вид:
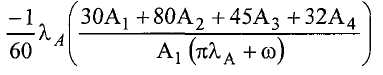
для положительных периодов, и
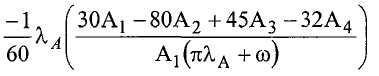
для отрицательных периодов. Эти корректирующие члены предполагают, что известны амплитуды высших гармоник. Хотя их можно вычислить с использованием обычного метода Фурье, можно также аппроксимировать некоторые или все из них с использованием предполагаемых отношений между гармониками. Например, для одной реализации трубопровода диаметром один дюйм, типичные отношения амплитуд составляют A1 = 1,0, A2 = 0,01, A3 = 0,005 и A4 = 0,001.
e. Применение компенсации амплитудной модуляции к фазе
Моделирование производилось с использованием цифрового передатчика, включающего в себя моделирование высших гармоник и амплитудной модуляции. В одном примере используются f = 80 Гц, A1(t=0) = 0.3, A2 = 0, A3 = 0, A4 = 0, X A = 1e-5 * 48 кГц (частота дискретизации) = 0,47622, что соответствует высокой скорости изменения амплитуды, но без высших гармоник. Теория прогнозирует сдвиг фазы -0,02706 градуса, при моделировании по 1000 периодов среднее смещение составляет -0,02714 градуса, со стандартным отклонением лишь 2,17e-6. Различие между моделью и теорией (прибл. 0,3% ошибки моделирование) обусловлено тем, что теория предполагает линейное изменение амплитуды по каждому периоду, тогда как при моделировании генерируется экспоненциальное изменение амплитуды.
Второй пример включает в себя вторую гармонику и имеет параметры f = 80 Гц, A1(t=0) = 0,3, A2(t=0) = 0,003, A3 = 0, A4 = 0, λA = -1e-6 * 48 кГц (частота дискретизации) = -0,047622. В этом примере, теория прогнозирует сдвиг фазы, равный +2,706e-3, ±2.66% для положительных или отрицательных периодов. Моделирование дает 2,714e-3±2,66%, т.е., опять же, хорошее совпадение.
На фиг.33A-34B приведены примеры того, как эта коррекция улучшает реальные данные расходомера. На фиг.33A показаны необработанные данные фазы из SV1, собранные из трубопровода диаметром 1", в котором низкий расход резонно предполагается постоянным. На фиг.33B показан коэффициент коррекции, вычисленный с использованием вышеописанной формулы, а на фиг.33C показана результирующая скорректированная фаза. Наиболее заметная особенность состоит в том, что коррекция повысила дисперсию фазового сигнала, хотя и произвела общее снижение стандартного отклонения разности фаз (т.е., SV2 - SV1) с коэффициентом 1,26, как показано на фиг.34A и 34B. Повышение производительности обусловлено тем, что эта коррекция улучшает корреляцию между двумя фазами, приводя к снижению измененной разности фаз. Метод столь же хорошо работает в других состояниях потока и при других размерах трубопровода.
f. Компенсация эффекта скорости для измерения фазы
На вычисление измерения фазы также влияет эффект скорости. Весьма эффективный и простой коэффициент коррекции, в радианах, имеет вид
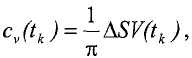
где ΔSV(t k) это относительная скорость изменения амплитуды, которую можно выразить в виде:
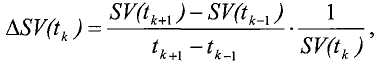
где t k это время завершения периода, для которого определяется ΔSV(t k), t k+1 это время завершения следующего периода, и t k-1 это время завершения предыдущего периода. ΔSV это оценка скорости изменения SV, масштабированная его абсолютным значением, которая также именуется пропорциональной скоростью изменения SV.
На фиг.35A-35E показан этот метод. На фиг.35A показаны необработанные данные фазы от одного датчика (SV1), после применения вышеописанных поправок на амплитудную модуляцию. На фиг.35B показан коэффициент коррекции в градусах, вычисленный с использованием вышеприведенного уравнения, а на фиг.35C показана результирующая скорректированная фаза. Заметим, что стандартное отклонение скорректированной фазы фактически увеличилось относительно необработанных данных. Однако, когда соответствующие вычисления производятся на другом датчике (SV2), наблюдается увеличение отрицательной корреляции (от -0.8 до -0.9) между фазами двух сигналов. В результате, вычисления разности фаз на основании необработанных измерениях фазы (фиг.35D) имеют значительно больший шум, чем скорректированные измерения фазы (фиг.35E).
Сравнение фиг.35D и 35E демонстрирует преимущество этого метода понижения шума. Из фиг.35E сразу видно, что переменная процесса уменьшается, и что измерение обладает заметной периодичностью, причем периоды характерны, возможно, для плохо отрегулированного насоса. Ничего подобного нельзя различить в нескорректированных данных разности фаз, представленных на фиг.35D.
g. Применение понижения шума на уровне датчиков
Комбинация вышеописанных методов понижения фазового шума позволяет значительно улучшить измерение мгновенной разности фаз в различных состояниях потока, проиллюстрированных на фиг.36A-36L. На каждом графике показано три измерения разности фаз, вычисляемые одновременно в реальном времени цифровым кориолисовым передатчиком, работающим на однодюймовом трубопроводе. Средняя полоса 3600 показывает данные фазы, вычисленные с использованием простого метода разницы по времени. Внешняя полоса 3605 показывает данные фазы, вычисленные с использованием вышеописанного метода Фурье.
Возможно, неожиданно, что метод Фурье, который использует гораздо больше данных, более сложный анализ и значительно более высокую вычислительную нагрузку, дает более шумное вычисление. Это можно объяснить чувствительностью метода Фурье к вышеописанным динамическим эффектам. Внутренняя полоса данных 3610 показывает те же данные Фурье после применения методов понижения шума на уровне датчиков. Можно видеть, что в каждом случае происходит существенное понижение шума, о чем свидетельствуют значения стандартного отклонения, представленные на каждом графике.
На фиг.36A показаны измерения в отсутствие потока, при полном трубопроводе и в отсутствие шума насоса. На фиг.36B показаны измерения в отсутствие потока, при полном трубопроводе и при включенных насосах. На фиг.36C показаны измерения при пустом, влажном трубопроводе. На фиг.36D показаны измерения при низком расходе. На фиг.36E показаны измерения при высоком расходе. На фиг.36F показаны измерения при высоком расходе и амплитуде колебаний 0,03 В. На фиг.36G показаны измерения при низком расходе с низкой аэрацией. На фиг.36H показаны измерения при низком расходе с высокой аэрацией. На фиг.36I показаны измерения при высоком расходе с низкой аэрацией. На фиг.36J показаны измерения при высоком расходе с высокой аэрацией. На фиг.36K показаны измерения при переходе от пустого состояния к высокому расходу. На фиг.36L показаны измерения при переходе от высокого расхода к пустому состоянию.
2. Динамическое моделирование на уровне трубки Вентури
Динамическую модель можно внедрять на двух основных стадиях. На первой стадии, модель создается с использованием методов идентификации системы. Трубка Вентури "стимулируется" для проявления своей динамики, при этом истинные значения массового расхода и плотности поддерживаются постоянными. Отклик трубки Вентури измеряется и используется при генерации динамической модели. На второй стадии, модель применяется к нормальным данным потока. Эффекты динамики трубки Вентури прогнозируются для фазы и частоты. Затем прогнозируемые значения вычитаются из наблюдаемых данных с образованием остаточной фазы и частоты, которые должны определяться только процессом. Каждая стадия более подробно описана ниже.
a. Идентификация системы
Идентификация системы начинается с состояния, когда трубка Вентури наполнена водой, в отсутствие потока. Амплитуду колебаний, которая обычно поддерживается постоянной, изменяют, назначая произвольную настройку между 0,05 В и 0,3 В, где 0.3 В является обычным значением. Результирующие напряжения датчиков показаны на фиг.37A, а на фиг.37B и 37C показаны, соответственно, соответствующие вычисленные значения фазы и частоты. Эти значения вычисляются один раз за период. Показано, что фаза и частота в высокой степени "структурированы". Поскольку фаза и частота, соответствующие массовому расходу, постоянны, эта структура, скорее всего, связана с динамикой трубки Вентури. Наблюдаемые переменные, которые будут предсказывать эту структуру, когда не известно, постоянны ли истинные фаза и частота, можно выразить в виде, представленном ниже.
Прежде всего, как отмечено выше, ΔSV(t k) можно выразить в виде:
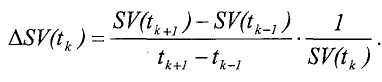
Это выражение можно использовать для определения ΔSV1 и ΔSV2.
Фаза трубки Вентури связана с Δ-, что выражается как ΔSV1 - ΔSV2, а частота связана с Δ+, что выражается как ΔSV1 + ΔSV2. Эти параметры показаны на фиг.37D и 37E. Сравнивая фиг.37B с фиг.37D и фиг.37C с фиг.37E, можно видеть необычное соотношение между Δ- и фазой и между Δ+ и частотой.
Некоторую поправку на динамику трубки Вентури можно получить, вычитая кратное соответствующей функции предсказания из фазы и/или частоты. Улучшенные результаты можно получить с использованием модели в виде:
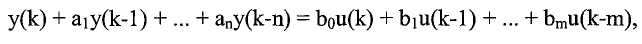
где y(k) - выходной сигнал (т.е. фаза или частота) и u - функция предсказания (т.е., Δ- или Δ+). Метод идентификации системы предусматривает значения для порядков n и m, и коэффициенты a i и b j, образующие многочлены, зависящие от времени. Значение y(k) можно вычислять каждый период и вычитать из наблюдаемой фазы или частоты для получения остаточного значения процесса.
Следует понимать, что, даже в отсутствие динамических поправок, цифровой расходомер дает очень хорошую точность на протяжении длительного периода времени. Например, при объединении порции в 200 кг, устройство легко достигает повторяемости менее 0,03%. Целью динамического моделирования является повышение динамической точности. Таким образом, необработанные и скомпенсированные значения должны иметь близкие средние значения, но пониженную "дисперсию" или "стандартное отклонение".
На фиг.38A и 39A показаны необработанные и скорректированные значения частоты. Средние значения сходны, но стандартное отклонение снижено с коэффициентом 3,25. Хотя резкие отклонения по частоте устранены, в остаточном шуме остается заметная "структура". Эта структура выглядит не связанной с функцией Δ+. Используемая модель является простой моделью первого порядка, где m = n = 1.
На фиг.38B и 39B показана соответствующая коррекция фазы. Среднее значение подвергается минимальному влиянию, тогда как стандартное отклонение снижается с коэффициентом 7,9. Порядки модели n = 2 и m = 10. Создается впечатление, что в остаточном шуме сохранилась некоторая структура. Предполагается, что эта структура обусловлена недостаточным возбуждением фазовой динамики изменениями настройки.
Более эффективная идентификация фазы была достигнута путем дополнительного моделирования динамики трубки Вентури путем непрерывного встряхивания трубки Вентури в ходе сбора данных (изменения настройки по-прежнему производятся). На фиг.38C и 39C показаны эффекты коррекции при этих условиях. Показано, что стандартное отклонение снизилось с коэффициентом 31. Эта более эффективная модель используется в дальнейших рассмотрениях.
b. Применение к данным потока
Реальное испытание идентифицированной модели заключается в усовершенствованиях, которые она обеспечивает для новых данных. Вначале полезно сделать несколько наблюдений. Прежде всего, средняя фаза, усредненная по, например, десяти секундам или более, дает достаточную точность. В показанных примерах, значения фазы отмечены на графике при частоте 82 Гц или близкой к ней. Зарегистрированное стандартное отклонение будет составлять примерно 1/3 от показанных значений при усреднении до 10 Гц и 1/9 при усреднении до 1 Гц. Для справки, на однодюймовой трубке Вентури, разность фаз в один градус соответствует расходу около 1 кг/с.
Предполагаемое преимущество метода состоит в обеспечении значительно лучшего динамического отклика на истинный процесс изменения, а не в повышении средней точности. Поэтому, в нижеследующих примерах, где расход не равен нулю, малые ступенчатые изменения расхода вносятся каждые десять секунд или около того, в ожидании, что скорректированная фаза более отчетливо продемонстрирует ступенчатые изменения.
На фиг.38D и 39D показана коррекция, применяемая к полной трубке Вентури при нулевом расходе, как после пуска. Эффект занавеса, характерный для пуска, отчетливо наблюдается в необработанных данных (фиг.38D), но устраняется коррекцией (фиг.39D), что приводит к снижению стандартного отклонения с коэффициентом 23 по всему набору данных. Заметим, что скорректированное измерение сильно напоминает белый шум, и это свидетельствует о том, что динамика трубки Вентури в основном понята.
На фиг.38E и 39E показана результирующая поправка на "осушенную" трубку Вентури. Шум снизился с коэффициентом 6.5 или около того. Заметим, однако, что в шуме, похоже, присутствует некоторая остаточная структура.
Проиллюстрированы также эффекты метода при низком (фиг.38F и 39F), среднем (фиг.38G и 39G) и высоком (фиг.38H и 39H) расходах, каждый со ступенчатыми изменениями расхода каждые десять секунд. В каждом случае, схема такая же: скорректированные средние расходы (фиг.39F-39H) идентичны необработанным средним расходам (фиг.38F-38H), но динамический шум значительно снижается. На фиг.39H, это приводит к проявлению ступенчатых изменений, которые прежде утопали в шуме (фиг.38H).
3. Развитие методов динамического мониторинга и компенсации
В предыдущих разделах были описаны различные методы (физическое моделирование, идентификация системы, гистерезис), используемые для мониторинга и компенсации различных аспектов динамического поведения (частотного и фазового шума, обусловленного амплитудной модуляцией, эффектом скорости, динамикой трубки Вентури на уровне датчиков и на уровне трубки Вентури). Путем естественного развития, аналогичные методы, хорошо известные практическим специалистам по управлению и/или оборудованию, в том числе, специалистам по искусственному интеллекту, нейронным сетям, нечеткой логике и генетическим алгоритмам, а также классическим методам моделирования и идентификации, можно применять к этим и другим аспектам динамической производительности измерителя. В частности, они могут включать в себя мониторинг и компенсацию изменения частоты, амплитуды и/или фазы на уровне датчиков, а также средней частоты и разности фаз на уровне трубки Вентури, поскольку эти изменения происходят в каждом интервале измерения, равно, как и во время между интервалами измерения (когда интервалы измерения не перекрываются).
Этот метод является новым при обеспечении снижения шума и улучшения динамического отклика для обработки изменений измерения. Поэтому метод, предположительно, будет весьма ценным применительно к измерению расхода.
I. Аэрация (двухфазный поток)
Цифровой расходомер обеспечивает повышенную производительность при наличии аэрации (также известной как двухфазный поток) в трубопроводе. Аэрация приводит к потерям энергии в трубопроводе, которые могут оказывать существенное отрицательное влияние на измерения, производимые массовым расходомером, и могут привести к блокировке трубопровода. Эксперименты показали, что цифровой расходомер имеет существенно повышенную производительность при наличии аэрации относительно традиционных, аналоговых расходомеров. Это повышение производительности можно объяснить способностью измерителя обеспечивать очень широкий диапазон коэффициента усиления, для использования отрицательной обратной связи, для точного вычисления измерений на очень низких уровнях амплитуды и для компенсации динамических эффектов, например, скорости изменения амплитуды и динамики трубки Вентури. Повышение производительности также можно объяснить тем, что измеритель использует алгоритм точного цифрового управления амплитудой.
Цифровой расходомер обнаруживает наступление аэрации, когда необходимый коэффициент усиления возбудителя растет одновременно с падением наблюдаемой плотности текучей среды. Затем цифровой расходомер может непосредственно реагировать на обнаруженную аэрацию. В общем случае, измеритель отслеживает наличие аэрации, сравнивая наблюдаемую плотность материала, текущего через трубопровод (т.е., измерение плотности, полученное нормальными методами измерения), с известной плотностью материала без аэрации. Контроллер определяет уровень аэрации на основании любого различия между наблюдаемой и фактической плотностями. Затем контроллер соответственно корректирует измерение массового расхода.
Контроллер определяет плотность материала без аэрации путем мониторинга плотности по периодам времени, в течение которых аэрация отсутствует (т.е., периодам, в течение которых плотность имеет стабильное значение). Альтернативно, система управления, к которой подключен контроллер, может обеспечивать плотность без аэрации в качестве параметра инициализации.
В одной реализации, контроллер использует три поправки для учета эффектов аэрации: поправку на пузырьковый эффект, поправку на эффект затухания и поправку на дисбаланс датчиков. На фиг.40A-40H показаны эффекты процедуры коррекции.
На фиг.40A показана ошибка в измерении фазы при снижении измеренной плотности (т.е., с ростом аэрации) для разных массовых расходов, в отсутствие коррекции аэрация. Показано, что фазовая ошибка отрицательна, и его величина возрастает при увеличении аэрации. На фиг.40B показано, что результирующая ошибка массового расхода также отрицательна. Также важно отметить, что цифровой расходомер работает на высоких уровнях аэрации. Напротив, как указано вертикальной линией 4000, традиционные аналоговые измерители имеют тенденцию к блокировке при наличии низких уровней аэрации.
Блокировка происходит, когда расходомер неспособен обеспечивать существенно большой коэффициент усиления возбудителя для обеспечения большого тока возбуждения при низких амплитудах колебаний. Если уровень затухания требует более высокого коэффициента усиления возбудителя, чем может обеспечить трубка Вентури для поддержания колебаний с определенной амплитудой, то недостаточная энергия возбуждения поступает на трубопровод. Это приводит к падению амплитуды колебаний, что, в свою очередь, приводит к подаче еще меньшей энергии возбуждения вследствие ограничения по максимальному коэффициенту усиления. В результате, происходит катастрофический коллапс, и колебание трубки Вентури оказывается невозможным, пока затухание не снизится до уровня, при котором расходомер сможет выдать соответствующее требование к коэффициенту усиления возбудителя.
Поправка на пузырьковый эффект базируется на предположении, что массовый расход снижается по мере того, как уровень аэрации, также именуемый пустотной долей, возрастает. Не пытаясь прогнозировать фактическое соотношение между пустотной долей и пузырьковым эффектом, эта коррекция предполагает, с хорошим теоретическим обоснованием, что влияние на наблюдаемый массовый расход будет таким же, как влияние на наблюдаемую плотность. Поскольку истинная плотность текучей среды известна, поправка на пузырьковый эффект корректирует массовый расход в той же пропорции. Эта коррекция является линейной регулировкой, которая одинакова для всех расходов. На фиг.40C и 40D показаны, соответственно, остаточная фаза и ошибки массового расхода после поправки на пузырьковый эффект. Показано, что остаточные ошибки теперь положительны и существенно меньше по величине, чем исходные ошибки.
Поправка на коэффициент затухания учитывает затухание движения трубопровода вследствие аэрации. В общем случае, поправка на коэффициент затухания базируется на следующем соотношении между наблюдаемой фазой, φobs, и фактической фазой, φtrue:
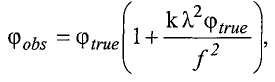
где λ - коэффициент затухания и k - постоянная. На фиг.40E показана поправка на затухание для разных массовых расходов и разных уровней аэрации. На фиг.40F показана остаточная фазовая ошибка после поправки на затухание. Показано, что фазовая ошибка существенно снижается относительно фазовой ошибки, оставшейся после поправки на пузырьковый эффект.
Коррекция баланса датчиков базируется на различиях в плотности между разными концами трубопровода. Согласно фиг.41, перепад давления между входом и выходом трубопровода приводит к увеличению размера пузырька от входа к выходу. Поскольку материал течет последовательно через два контура трубопровода, пузырьки на входной стороне трубопровода (т.е. стороне, соседствующей с первой парой датчик/возбудитель) будут меньше пузырьков на выходной стороне трубопровода (т.е. стороне, соседствующей со второй парой датчик/возбудитель). Это различие в размере пузырька приводит к различию в массе и плотности между двумя концами трубопровода. Это различие отражается в сигналах датчиков (SV1 и SV2). Соответственно, коррекция баланса датчиков базируется на отношении двух сигналов датчиков.
На фиг.40G показана коррекция баланса датчиков для разных массовых расходов и разных уровней аэрации. На фиг.40H показана остаточная фазовая ошибка после применения коррекции баланса датчиков. При низких расходах и низких уровнях аэрации, фазовая ошибка улучшается относительно фазовой ошибки, оставшейся после поправки на затухание.
Также можно использовать другие коэффициенты коррекции. Например, можно отслеживать фазовый угол каждого сигнала датчика. В общем случае, средний фазовый угол для сигнала должен быть равен нулю. Однако средний фазовый угол имеет тенденцию к увеличению при увеличении аэрации. Соответственно, коэффициент коррекции можно генерировать на основании значения среднего фазового угла. Другой коэффициент коррекции может быть основан на температуре трубопровода. В общем случае, вследствие применения коэффициентов коррекции ошибки массового расхода поддерживаются на уровне одного процента или менее. Кроме того, предполагается, что эти коэффициенты коррекции применимы в широком диапазоне расходов и уровней аэрации.
J. Регулировка настройки
Цифровой расходомер обеспечивает улучшенную регулировку настройки для амплитуды колебаний трубопровода. В аналоговом измерителе, управление посредством обратной связи используется для поддержания амплитуды колебаний трубопровода на фиксированном уровне, соответствующем нужному пиковому напряжению датчика (например, 0,3 В). Стабильная амплитуда колебаний приводит к уменьшению дисперсии частоты и измерений фазы.
В общем случае, желательна большая амплитуда колебаний, поскольку такая большая амплитуда обеспечивает большой кориолисов сигнал в целях измерения. Большая амплитуда колебаний также приводит к сохранению более высокого уровня энергии в трубопроводе, что обеспечивает повышенную устойчивость к внешним вибрациям.
Могут возникать обстоятельства, при которых невозможно поддерживать большую амплитуду колебаний вследствие ограничений по току, подаваемому на возбудители. Например, в одной реализации аналогового передатчика, ток ограничивается величиной 100 мА в целях безопасности. Это обычно в 5-10 раз меньше тока, необходимого для поддержания желаемой амплитуды колебаний. Однако если рабочая текучая среда обеспечивает значительное дополнительное затухание (например, посредством двухфазного потока), то оптимальная амплитуда уже может не быть устойчивой.
Аналогично, маломощный расходомер, например двухпроводный измеритель, описанный ниже, может иметь в своем распоряжении значительно меньшую мощность для возбуждения трубопровода. Кроме того, уровень мощности может изменяться, когда трубопровод возбуждается разрядом конденсатора.
Согласно фиг.42, процедуру управления 4200, реализованную контроллером цифрового расходомера, можно использовать для выбора наивысшей устойчивой настройки при данном максимально допустимом уровне тока. В общем случае, процедура осуществляется каждый раз при выборе желаемого выходного тока возбуждения, что обычно происходит один раз за период или один раз за полупериод, если используются перемежающиеся периоды.
Контроллер начинает с установления настройки, равной значению по умолчанию (например, 0,3 В), и инициализации фильтрованных представлений напряжения датчика (filtered_SV) и тока возбуждения (filtered_DC) (этап 4205). Каждый раз при осуществлении процедуры, контроллер обновляет фильтрованные значения на основании текущих значений напряжения датчика (SV) и тока возбуждения (DC) (этап 4210). Например, контроллер может генерировать новое значение для filtered_SV как сумму девяноста девяти процентов от filtered_SV и одного процента от SV.
Затем контроллер определяет, приостановлена ли процедура для обеспечения времени на вступление в силу предыдущих регулировок настройки (этап 4215). Приостановка процедуры указывается счетчиком периодов приостановки, имеющим значение большее нуля. Если процедура приостановлена, контроллер не осуществляет других действий в течение периода и уменьшает счетчик периодов приостановки (этап 4220).
Если процедура не приостановлена, контроллер определяет, превышает ли фильтрованный ток возбуждения пороговый уровень (этап 4225). В одной реализации, пороговый уровень составляет девяносто пять процентов от максимально допустимого тока. Если ток превышает порог, контроллер уменьшает настройку (этап 4230). Чтобы дать время измерителю стабилизироваться после изменения настройки, контроллер затем реализует приостановку процедуры, устанавливая счетчик периодов приостановки равным соответствующему значению (например, 100) (этап 4235).
Если процедура не приостановлена, контроллер определяет, меньше ли фильтрованный ток возбуждения, чем пороговый уровень (этап 4240), и меньше ли настройка, чем максимальная разрешенная настройка (этап 4245). В одной реализации, пороговый уровень равен семидесяти процентам максимально допустимого тока. При выполнении обоих условий, контроллер определяет возможную новую настройку (этап 4250). В одной реализации, контроллер определяет новую настройку как восемьдесят процентов максимально допустимого тока, умноженные на отношение filtered_SV к filtered_DC. Во избежание малых изменений (т.е. дрожания) настройки, контроллер затем определяет, на достаточную ли величину возможная новая настройка превышает текущую настройку (этап 4255). В одной реализации, возможная новая настройка должна превышать текущую настройку на 0,02 В и на десять процентов.
Если возможная новая настройка достаточно велика, контроллер определяет, превышает ли она максимальную разрешенную настройку (этап 4260). Если да, контроллер задает настройку равной максимальной разрешенной настройке (этап 4265). В противном случае, контроллер задает настройку равной возможной новой настройке (этап 4270). Контроллер затем реализует приостановку процедуры, устанавливая счетчик периодов приостановки равным соответствующему значению (этап 4235).
На фиг.43A-43C показано выполнение процедуры регулировки настройки. Согласно фиг.43C, система начинает с настройки 0,3 В. Примерно на восьмой секунде работы, аэрация приводит к падению наблюдаемой плотности материала в трубопроводе (фиг.43A). Увеличенное затухание, сопровождающее аэрацию, приводит к увеличению тока возбуждения (фиг.43B) и увеличению шума в напряжении датчика (фиг.43C). В это время не происходит никаких изменений, поскольку измеритель способен поддерживать желаемую настройку.
Примерно на пятнадцатой секунде работы, аэрация возрастает, и наблюдаемая плотность дополнительно снижается (фиг.43A). При этом уровне аэрации, ток возбудителя (фиг.43B) достигает максимального значения, которого недостаточно для поддержания настройки 0,3 В. Соответственно, напряжение датчика падает до 0,26 В (фиг.43C), уровня напряжения, который позволяет поддерживать максимальный ток возбудителя. В связи с этим, контроллер регулирует настройку (примерно на 28 секунде работы) до уровня (0,23 В), который не требует генерации максимального тока возбудителя.
Примерно на 38 секунде работы, уровень аэрации снижается, и наблюдаемая плотность возрастает (фиг.43A). Это приводит к снижению тока возбуждения (фиг.43B). На 40 секунде работы, контроллер реагирует на это условие, увеличивая настройку (фиг.43C). Уровень аэрации снижается, и наблюдаемая плотность снова возрастает примерно на 48 секунде работы, и контроллер реагирует увеличением настройки до 0,3 В.
K. Результаты производительности
Цифровой расходомер продемонстрировал заметное повышение производительности относительно традиционных аналоговых расходомеров. В одном эксперименте проверяли способность двух типов измерителей точно измерять порцию материала. В каждом случае, порцию пропускали через соответствующий расходомер в бак, где порцию взвешивали. Для порций весом 1200 и 2400 фунтов, аналоговый измеритель обеспечил среднее смещение 500 фунтов, с повторяемостью в 200 фунтов. Напротив, цифровой измеритель обеспечил среднее смещение 40 фунтов, с повторяемостью два фунта, что, очевидно, является существенным улучшением.
В каждом случае, трубопровод и окружающие трубы были пусты в начале порции. Это важно во многих порционных приложениях, где не практично начинать порцию с полным трубопроводом. Порции заканчивались с полной трубкой Вентури. Ожидается некоторое положительное смещение, поскольку расходомер измеряет материал, которым нужно заполнить трубу до начала наполнения бака взвешивания. Задержки в пуске, или смещения, обусловленные аэрацией потока или низкими амплитудами колебаний, скорее всего, вносят отрицательные смещения. Для реальных порционных приложений, самым важным вопросом является повторяемость измерения.
Результаты показывают, что с аналоговым расходомером существуют большие отрицательные смещения и повторяемость только 200 фунтов. Это объясняется наличием периода времени до пуска после наступления потока (в течение которого расход не измеряется) и ошибками измерения, пока не будет достигнута полная амплитуда колебаний. В отличие от него, цифровой расходомер достигает положительного смещения, что объясняется наполнением пустой трубы, и повторяемости в два фунта.
В другом эксперименте сравнивали общую точность измерения для двух типов измерителей. На фиг.44 показана точность и соответствующая недостоверность измерений, производимых двумя типами измерителей на разных процентах максимального рекомендованного расхода измерителей. На высоких расходах (т.е., расходах в 25% или более от максимального расхода), аналоговый измеритель создает измерения, которые соответствуют фактическим значениям в пределах 0,15% или менее, по сравнению с 0,005% или менее для цифрового измерителя. На более низких расходах, смещение аналогового измерителя составляет порядка 1,5%, по сравнению с 0,25% для цифрового измерителя.
L. Измеритель с автоматической проверкой
Цифровой расходомер можно использовать в системе управления, которая включает в себя датчики с автоматической проверкой. Для этого, цифровой расходомер можно реализовать в виде измерителя с автоматической проверкой. Измерители и другие датчики с автоматической проверкой описаны в патенте США № 5570300 под названием "SELF-VALIDATING SENSORS", которая включена посредством ссылки.
В общем случае, измеритель с автоматической проверкой обеспечивает, на основании всей информации, доступной измерителю, наилучшую оценку значения отслеживаемого параметра (например, массового расхода). Поскольку наилучшая оценка базируется, отчасти, на неизмерительных данных, наилучшая оценка не всегда согласуется со значением, указанным данными текущего, возможно, сбойного, измерения. Измеритель с автоматической проверкой также обеспечивает информацию о недостоверности и надежности наилучшей оценки, а также информацию о рабочем состоянии датчика. Информация недостоверности выводится из известного анализа недостоверности и обеспечивается даже в отсутствие сбоев.
В общем случае, измеритель с автоматической проверкой обеспечивает четыре основных параметра: проверенное значение измерения (VMV), проверенная недостоверность (VU), указание (статус MV) состояния, в котором было произведено измерение, и состояние устройства. VMV это наилучшая оценка измерителя для значения измеренного параметра. VU и статус MV связаны с VMV. Измеритель создает отдельные VMV, VU и статус MV для каждого измерения. Состояние устройства указывает рабочее состояние измерителя.
Измеритель также может обеспечивать другую информацию. Например, по запросу от системы управления, измеритель может обеспечивать детальную диагностическую информацию о состоянии измерителя. Кроме того, когда измерение превышает заранее определенный предел или близко к его превышению, измеритель может выдавать сигнал тревоги на систему управления. Разные уровни тревоги можно использовать для указания степени, в которой измерение отклонилось от заранее определенного значения.
VMV и VU являются численными значениями. Например, VMV может быть измерением температуры, оцениваемым при 200°С, и VU, недостоверность VMV, может составлять 9°. В этом случае, существует высокая вероятность (обычно 95%) того, что фактическая измеряемая температура оказывается в пределах огибающей VMV и определяется VU (т.е., от 191 до 209°С).
Контроллер генерирует VMV на основании лежащих в основе данных от датчиков. Сначала контроллер выводит необработанное значение измерения (RMV), которое базируется на сигналах от датчиков. В общем случае, когда контроллер не обнаруживает аномалий, контроллер имеет номинальную доверительность в RMV и задает VMV равным RMV. Когда контроллер обнаруживает аномалию в датчике, контроллер не задает VMV равным RMV. Вместо этого, контроллер задает VMV равным значению, которое контроллер считает лучшей оценкой, чем RMV фактического параметра.
Контроллер генерирует VU на основании необработанного сигнала недостоверности (RU), который является результатом динамического анализа недостоверности RMV. Контроллер осуществляет этот анализ недостоверности в течение каждого периода дискретизации. Анализ недостоверности, первоначально описанный в "Describing Uncertainties in Single Sample Experiments", S.J. Kline & F.A. McClintock, Mech. Eng., 75, 3-8 (1953), широко применяется и достиг статуса международного стандарта калибровки. В сущности, анализ недостоверности обеспечивает указание "качества" измерения. Каждое измерение сопряжено с ошибкой, которая, конечно, неизвестна. Однако разумный предел этой ошибки часто может выражаться одним числом недостоверности (ANSI/ASME PTC 19.1-1985 Часть 1, Недостоверность измерений: инструменты и оборудование).
Согласно описанию, приведенному Kline & McClintock, для любого наблюдаемого измерения M, недостоверность M, w M, можно определить следующим образом:
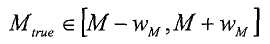 ,
,
где M истинно (M true) при определенном уровне доверительности (обычно 95%). Эту недостоверность легко выразить в относительной форме как пропорцию измерения (т.е. w M/M).
В общем случае, VU имеет ненулевое значение даже в идеальных условиях (т.е. безотказная работа датчика в контролируемых, лабораторных условиях). Причина в том, что измерение, производимое датчиком, никогда не бывает абсолютно достоверным, и всегда существует возможность ошибки. Как и с VMV, когда контроллер не обнаруживает аномалий, контроллер задает VU равной RU. Когда контроллер обнаруживает отказ, который лишь частично влияет на надежность RMV, контроллер обычно осуществляет новый анализ недостоверности, который учитывает эффекты отказа, и задает VU равной результатам этого анализа. Контроллер задает VU равной значению на основании предыдущей производительности, когда контроллер определяет, что RMV не опирается на фактическое измеренное значение.
Чтобы гарантировать, что система управления правильно использует VMV и VU, статус MV обеспечивает информацию о том, как они вычислены. Контроллер создает VMV и VU во всех условиях - даже когда датчики бездействуют. Системе управления нужно знать, базируются ли VMV и VU на "живых" или исторических данных. Например, если система управления использует VMV и VU в управлении посредством обратной связи, и датчики бездействуют, система управления должна знать, что VMV и VU определены на основании прошлой производительности.
Статус MV базируется на ожидаемой устойчивости любого аномального состояния и на уверенности контроллера в RMV. Четыре основных состояния для состояния MV генерируются согласно Таблице 1.
Статус MV CLEAR возникает, когда RMV находится в нормальном диапазоне для данных условий процесса. Статус MV DAZZLED указывает, что RMV совершенно ненормальное, но предполагается, что аномалия имеет короткую длительность. Обычно контроллер задает статус MV равным DAZZLED, когда происходит внезапное изменение сигнала от одного из датчиков, и контроллер не способен отчетливо установить, обусловлено ли это изменение еще не продиагностированным отказом датчика или же резким изменением измеряемой переменной. Статус MV BLURRED указывает, что RMV ненормально, но разумно связано с измеряемым параметром. Например, контроллер может задать статус MV равным BLURRED, когда RMV является зашумленным сигналом. Статус MV BLIND указывает, что RMV совершенно ненадежно, и что отказ, предположительно, является устойчивым.
Два дополнительных состояния для статуса MV является UNVALIDATED и SECURE. Статус MV является UNVALIDATED, когда контроллер не осуществляет проверку VMV. Статус MV является SECURE, когда VMV генерируется из избыточных измерений, в которых контроллер имеет номинальную доверительность.
Состояние устройства представляет собой общее, дискретное значение, выражающее исправность измерителя. Оно используется, прежде всего, процедурами обнаружения и устранения отказов в системе управления. Обычно состояние 32 устройства представляет собой одно из шести состояний, каждое из которых указывает то или иное рабочее состояние измерителя. Эти состояния таковы: GOOD, TESTING, SUSPECT, IMPAIRED, BAD или CRITICAL. Состояние устройства GOOD означает, что измеритель находится в нормальном состоянии. Состояние устройства TESTING означает, что измеритель осуществляет самопроверку, и что эта самопроверка может отвечать за любое временное снижение качества измерения. Состояние устройства SUSPECT означает, что измеритель выдал аномальный отклик, но контроллер не имеет детального диагноза отказа. Состояние устройства IMPAIRED означает, что измеритель испытал диагностированный отказ, который оказал незначительное влияние на производительность. Состояние устройства BAD означает, что измеритель серьезно поврежден и требует ремонта. Наконец, состояние устройства CRITICAL означает, что измеритель поврежден до такой степени, что измеритель может вызвать (или уже вызвал) риск, например, утечки, возгорания или взрыва.
На фиг.45 показана процедура 4500, согласно которой контроллер измерителя с автоматической проверкой обрабатывает оцифрованные сигналы датчиков для генерации сигналов возбуждения и проверенного измерения массового расхода совместно с недостоверностью и состоянием измерения. Первоначально, контроллер собирает данные от датчиков (этап 4505). С использованием этих данных, контроллер определяет частоту сигналов датчиков (этап 4510). Если частота попадает в ожидаемый диапазон (этап 4515), контроллер устраняет смещение нуля из сигналов датчиков (этап 4520) и определяет амплитуду (этап 4525) и фазу (этап 4530) сигналов датчиков. Контроллер использует эти вычисленные значения для генерации сигнала возбуждения (этап 4535) и для генерации необработанного измерения массового расхода и других измерений (этап 4540).
Если частота не попадает в ожидаемый диапазон (этап 4515), то контроллер реализует процедуру блокировки (этап 4545) для определения, застопорился ли трубопровод, и соответствующего реагирования. В процедуре блокировки, контроллер максимизирует коэффициент усиления возбудителя и осуществляет расширенный поиск пересечений нуля для определения, колеблется ли вообще трубопровод.
Если трубопровод не колеблется правильно (т.е., если он не колеблется или колеблется на неприемлемо высокой частоте (например, на высшей гармонике резонансной частоты)) (этап 4550), контроллер пытается восстановить нормальное колебательное движение (этап 4555) трубопровода, например, подавая на возбудители прямоугольную волну. Попытавшись восстановить колебательное движение, контроллер задает статус MV, равный DAZZLED (этап 4560), и генерирует пустые необработанные значения измерения (этап 4565). Если трубопровод колеблется правильно (этап 4550), контроллер устраняет смещение нуля (этап 4520) и переходит к рассмотренным выше действиям.
После генерации необработанных значений измерения (этапы 4540 или 4565), контроллер осуществляет диагностику (этап 4570) для определения, правильно ли работает измеритель (этап 4575). (Заметим, что контроллер не обязан осуществлять эту диагностику в течение каждого периода.)
Затем контроллер осуществляет анализ недостоверности (этап 4580) для генерации необработанного значения недостоверности. С использованием необработанных измерений, результатов диагностики и другой информации, контроллер генерирует VMV, VU, статус MV и состояние устройства (этап 4585). Затем контроллер собирает новый набор данных и повторяет процедуру. Этапы процедуры 4500 можно осуществлять последовательно или параллельно и можно осуществлять в изменяющемся порядке.
В другом примере, при обнаружении аэрации, поправки массового расхода применяются, как описано выше, статус MV получает значение BLURRED, и недостоверность увеличивается, чтобы отражать вероятную ошибку метода коррекции. Например, для трубки Вентури, работающей на 50% расхода, в нормальных условиях эксплуатации, недостоверность должна составлять порядка 0,1 - 0,2% расхода. Если аэрация происходит и корректируется с использованием вышеописанных методов, недостоверность должна увеличиваться, возможно, до 2% показания. Значения недостоверности должны снижаться при улучшении понимания эффектов аэрации и повышении способности компенсировать аэрацию. В порционных случаях, когда недостоверность расхода является переменной (например, высокой в начале/конце при дозировании из/в пустое состояние, или в ходе временных инцидентов аэрации или кавитации), недостоверность полной порции будет отражать взвешенную важность периодов высокой недостоверности относительно остатка порции с номинальной низкой недостоверностью. Это весьма полезная метрика качества в фискальных и других измерительных приложениях.
M. Двухпроводный расходомер
Согласно фиг.46, вышеописанные методы можно использовать для реализации "двухпроводного" кориолисова расходомера 4600, который осуществляет двустороннюю связь по паре проводов 4605. Схема питания 4610 принимает мощность для работы цифрового контроллера 4615 и для питания возбудителя(ей) 4620, создающих вибрацию трубопровода 4625. Например, схема питания может включать в себя схему постоянного выхода 4630, которая выдает рабочую мощность на контроллер и конденсатор возбуждения 4635, который заряжается с использованием избыточной мощности. Схема питания может принимать мощность по проводам 4605 или по второй паре проводов. Цифровой контроллер принимает сигналы от одного или нескольких датчиков 4640.
Когда конденсатор возбуждения достаточно заряжен, контроллер 4615 разряжает конденсатор 4635 для возбуждения трубопровода 4625. Например, контроллер может возбуждать трубопровод через каждые 10 периодов. Контроллер 4615 принимает и анализирует сигналы от датчиков 4640 для создания измерения массового расхода, которое контроллер затем передает по проводам 4605.
N. Дозирование из пустого состояния
Цифровой массовый расходомер 100 обеспечивает повышенную производительность при работе в условиях вызывающего применения, которое называется дозированием из пустого состояния. Существует много способов, в частности в пищевой и нефтехимической промышленности, где высокая точность и прямое измерение массового расхода, обеспечиваемые кориолисовой технологией, имеет преимущество в измерении порций материала. Однако, во многих случаях, гарантировать, что расходомер остается заполненным текучей средой от начала до конца порции, непрактично и весьма неэффективно. Например, при наполнении и опустошении танкера трудно избежать увлечения воздуха. При обработке пищи, гигиенические правила могут требовать очистки труб между порциями.
В традиционных кориолисовых измерителях, дозирование из пустого состояния может приводить к большим ошибкам. Например, гидравлический удар и требование высокого коэффициента усиления могут быть обусловлены наступлением потока в пустой трубке Вентури, что приводит к большим ошибкам измерения и блокировке.
Цифровой массовый расходомер 100 устойчив к условиям, возникающим при дозировании из пустого состояния. В частности, контроллер амплитуды имеет быстрый отклик; высокий диапазон коэффициента усиления предотвращает блокировку трубки Вентури; данные измерения можно вычислять вплоть до 0,1% нормальной амплитуды колебаний; и существует поправка на скорость изменения амплитуды.
Эти характеристики представлены на фиг.47A-47C, где показан отклик цифрового массового расходомера 100, возбуждающего влажную и пустую 25 мм трубку Вентури в течение первых секунд наступления полного потока. Согласно фиг.47A, коэффициент усиления возбуждения, необходимый для возбуждения влажной и пустой трубки до наступления потока (примерно за 4,0 секунды), имеет значение около 0,1, которое выше, чем значение около 0,034, необходимое для полной трубки Вентури. Наступление потока характеризуется существенным увеличением коэффициента усиления и соответствующим падением амплитуды колебаний. Согласно фиг.47B, примерно через 1,0 секунду после инициирования, выбор сниженной настройки способствует стабилизации амплитуды при установлении режима полного потока. Спустя примерно 2,75 секунды, последние остатки увлеченного воздуха удаляются, традиционная настройка восстанавливается, и коэффициент усиления возбуждения предполагает номинальное значение 0,034. Поведение необработанной и скорректированной разности фаз показано на фиг.47C.
Согласно фиг.47A-47C, данные фазы непрерывно задаются на протяжении перехода. В подобных обстоятельствах, аналоговая система управления блокируется и не способна обеспечивать данные измерения, пока необходимый коэффициент усиления возбуждения не возвратится к значению, близкому к номиналу, и длительная процедура пуска не завершится. Также показано, что поправка на скорость изменения амплитуды отчетливо демонстрирует преимущество, особенно спустя 1,0 секунду. Колебания в амплитуде приводят к существенным отклонениям в вычислениях фазы в частотном и временном измерениях, но они существенно снижаются в скорректированном измерении фазы. Даже в самой трудной части перехода, от 0,4 до 1,0 секунды, коррекция обеспечивает некоторое понижение шума.
Конечно, все еще существуют ошибочные данные в этом интервале. Например, поток, генерирующий разность фаз свыше около 5°, физически невозможен. Однако, с точки зрения датчика с автоматической проверкой, например, рассмотренного выше, это измерение фазы все еще составляет необработанные данные, которые можно корректировать. В некоторых реализациях, процесс проверки более высокого уровня может идентифицировать данные из интервала 0,4-1,0 секунд как не представляющие истинное значение процесса (на основании коэффициента усиления, амплитуды и других внутренних параметров) и может генерировать массовый расход DAZZLED для подавления экстремальных значений измерения.
Согласно фиг.48A, отклик цифрового массового расходомера 100 на наступление потока приводит к повышению точности и повторяемости. На фиг.48B показана иллюстративная гидродинамическая установка 4800. При получении результатов, показанных на фиг.48A, как и при получении результатов, показанных на фиг.44, текучую среду прокачивали через магнитный расходомер 4810 и кориолисов расходомер 4820 в бак взвешивания 4830, при этом кориолисов расходомер представляет собой цифровой расходомер или традиционный аналоговый расходомер. Клапаны 4840 и 4860 использовали, чтобы гарантировать, что магнитный расходомер 4810 всегда полон, тогда как трубка Вентури кориолисова расходомер 4820 в начале каждой порции пуста. В начале порции, сумматоры в магнитном расходомере 4810 и в кориолисовом расходомере 4820 сбрасывали, и поток начинался. В конце порции, запорный клапан 4850 закрывали и суммы замораживали (следовательно, кориолисов расходомер 4820 был полон в конце порции). Регистрировали три суммы, одну от магнитного расходомера 4810, одну от кориолисова расходомера 4820 и одну от весов, связанных с баком взвешивания 4830. Не предполагается, что эти суммы согласуются, поскольку существует конечная задержка по времени до кориолисова расходомера 4820, и затем, наконец, бак взвешивания 4830 наблюдает поток текучей среды. Таким образом, можно ожидать, что магнитный расходомер 4810 зарегистрирует наивысший суммарный расход, кориолисов расходомер 4820 зарегистрирует второй после наивысшего суммарного расхода, и бак взвешивания 4830 зарегистрирует наименьший суммарный расход.
На фиг.48A показаны результаты, полученные из ряда пробных прогонов с использованием гидродинамической установки 4800, показанной на фиг.48B, причем при каждом пробном прогоне через гидродинамическую установку проходит около 550 кг материала. Показанное отслеживаемое значение представляет собой смещение, наблюдаемое между весами и магнитным расходомером 4810 или кориолисовым расходомером 4820. Как объяснено выше, предполагается, что от обоих инструментов поступают положительные смещения. Магнитный расходомер 4810 (всегда полный) выдает согласованно положительное смещение, с повторяемостью (определенной здесь как максимальная разность в зарегистрированных значениях для идентичных экспериментов) 4.0 кг. Аналоговая система управления, связанная с магнитным расходомером 4810, генерирует большие отрицательные смещения, со средним значением -164,2 кг и повторяемостью 87,7 кг. Эта низкая производительность объясняется неспособностью аналоговой системы управления работать с наступлением потока и изменяющимся временем, необходимым для перезапуска трубки Вентури. Напротив, цифровой кориолисов массовый расходомер 4820 демонстрирует среднее значение положительного смещения 25,6 кг и повторяемость 0,6 кг.
Было бы трудно оценить истинный массовый расход через трубку Вентури, при условии, что она первоначально находится в пустом состоянии. Как и ожидалось, зарегистрированная суммарная масса оказывается между массой, определенной магнитным расходомером 4810, и массой, определенной с помощью весов. В промышленном применении, вопрос повторяемости часто имеет более важное значение, поскольку рецепты порции часто регулируются в соответствии со смещениями. Конечно, повторяемость процесса наполнения находится на нижней границе повторяемости суммарной массы, определенной кориолисовым расходомером. Сходной повторяемости можно добиться в произвольном промышленном способе серийного производства. Кроме того, как показано, цифровой массовый расходомер 100 обеспечивает существенное повышение производительности над его аналоговым эквивалентом (магнитным расходомером 4810) в тех же условиях. Опять же, можно заключить, что цифровой массовый расходомер 100 в этих условиях не является значительным источником ошибки измерения.
O. Двухфазный поток
Как рассмотрено выше со ссылкой на фиг.40A, двухфазный поток, обусловленный аэрацией, является другим состоянием потока, которое создает трудности для аналоговых систем управления и аналоговых массовых расходомеров. Двухфазный поток может быть спорадическим или непрерывным и возникает, когда материал в расходомере включает в себя газовый компонент и жидкостный компонент, перемещающиеся по трубке Вентури. Базовые механизмы весьма сходны со случаем дозирования из пустого состояния тем, что динамика двухфазного газожидкостного потока вызывает высокое затухание. Для поддержания колебаний требуется высокий коэффициент усиления возбуждения. Однако максимальный коэффициент усиления возбуждения аналоговой системы управления обычно достигается на низких уровнях доли газа в двухфазном материале, в результате чего трубка Вентури блокируется.
Цифровой массовый расходомер 100 способен поддерживать колебания при наличии двухфазного потока. В итоге, ни в одном из проведенных до сих пор лабораторных экспериментов не удалось заблокировать трубку любого размера ни при каком уровне газовой фазы под управлением цифрового контроллера 105. Напротив, типичная аналоговая система управления блокируется при доле газовой фазы около 2%.
Поддержание колебаний это только первый шаг в получении удовлетворительной производительности измерения от расходомера. Как было кратко рассмотрено выше, простая модель, именуемая "пузырьковой" моделью, была построена в качестве одного метода прогнозирования ошибки массового расхода.
В модели "пузырьков" или "эффективной массы", сфера или пузырек газа низкой плотности окружается текучей средой более высокой плотности. Если оба подлежат ускорению (например, в вибрирующей трубке), то пузырек движется в текучей среде, приводя к спаду наблюдаемой инерции системы в целом. Определив пустотную долю α как объемную долю газа, получаем, что эффективная масса падает с коэффициентом R, где
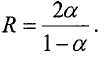
Применительно к кориолисову расходомеру, модель прогнозирует, что наблюдаемый массовый расход будет меньше истинного массового расхода с коэффициентом R, как и, в более общем случае, наблюдаемая плотность. На фиг.49 показаны наблюдаемые ошибки массового расхода для ряда прогонов на разных расходах, все с использованием 25 мм трубки Вентури с горизонтальным выравниванием, и для смеси воды и воздуха при температуре окружающей среды. По оси x отложен наблюдаемый спад плотности, а не пустотная доля. В лабораторных условиях можно вычислить пустотную долю, например, измерив давление и расход газа до его смешивания с текучей средой, совместно с давлением двухфазной смеси. Однако в заводских условиях доступен лишь наблюдаемый спад плотности, а истинная пустотная доля недоступна. Заметим, что с аналоговым расходомером, воздушно-водные смеси со спадом плотности свыше 5% вызывают заглушение трубки Вентури, что не позволяет собирать данные.
Пунктирная линия 4910 показывает соотношение между ошибкой массового расхода и спадом плотности, прогнозируемое пузырьковой моделью. Экспериментальные данные следуют аналогичному набору кривых, хотя модель почти всегда прогнозирует более отрицательную ошибку массового расхода. Как рассмотрено выше согласно фиг.40A, можно вывести эмпирические поправки массового расхода на основании наблюдаемой плотности, а также некоторых других внутренне наблюдаемых переменных, например, коэффициента усиления возбуждения и отношения напряжений датчиков. Разумно предположить, что плотность чистой жидкости известна или выводима. Например, во многих приложениях плотность текучей среды относительно постоянна (в особенности, если температурный коэффициент заложен в программное обеспечение контроллера).
На фиг.50 показаны скорректированные измерения массового расхода. Коррекция базируется на аппроксимации методом наименьших квадратов нескольких внутренних переменных, а также самой пузырьковой модели. Процесс коррекции ограничен только применимостью и менее пригоден для пониженных расходов (наибольшие ошибки наблюдаются для 1,5-1,6 кг/с). При горизонтальной ориентации, газовая и жидкая фазы начинают разделяться при пониженных расходах, и наблюдаются значительно более высокие ошибки массового расхода. В этих обстоятельствах, предположения пузырьковой модели уже не верны. Однако коррекция справедлива для более высоких расходов. В ходе оперативных экспериментальных испытаний, аналогичный алгоритм коррекции ограничивался ошибками массового расхода в пределах около 2,5% показания массового расхода.
На фиг.51 показано, как цифровой массовый расходомер 100 с автоматической проверкой реагирует на наступление двухфазного потока при измерении массового расхода. Нижний колебательный сигнал 5110 демонстрирует нескорректированное измерение массового расхода в состоянии двухфазного потока, и верхний колебательный сигнал 5120 демонстрирует скорректированное измерение массового расхода и границу недостоверности в том же состоянии двухфазного потока. При однофазном потоке (до t = 7 с), измерение массового расхода находится в состоянии CLEAR и имеет малую недостоверность около 0,2% показания массового расхода. При наступлении двухфазного потока активируется ряд процессов. Во-первых, двухфазный поток обнаруживается на основании поведения внутренних наблюдаемых параметров. Во-вторых, применяется способ коррекции измерения, и выходное состояние измерения совместно со скорректированным измерением задается равным BLURRED. В-третьих, недостоверность массового расхода возрастает с уровнем пустотной доли до максимума, составляющего около 2,3% показания массового расхода. Для сравнения, нескорректированное измерение массового расхода 5110 показано сразу под скорректированным измерением массового расхода 5120. Таким образом, пользователь имеет возможность продолжить работу со сниженным качеством скорректированного массового расхода, переключившись на альтернативное измерение, если доступно, или остановив процесс.
P. Применение нейронных сетей
Другой метод повышения точности измерения массового расхода в условиях двухфазного потока предусматривает использование нейронной сети для прогнозирования ошибки массового расхода и для генерации коэффициента коррекции ошибок для коррекции любой ошибки в измерении массового расхода, обусловленной эффектами двухфазного потока. Коэффициент коррекции генерируется с использованием внутренних наблюдаемых параметров, подаваемых на цифровой сигнальный процессор и нейронную сеть, и демонстрирует сохранение ошибок в пределах 2%. Внутренние наблюдаемые параметры могут включать в себя температуру, давление, коэффициент усиления, спад плотности и наблюдаемый расход.
На фиг.52 показан цифровой контроллер 5200, который можно использовать вместо цифрового контроллера 105 или 505 цифровых массовых расходомеров 100, 500, показанных на фиг.1 и 5. В этой реализации цифрового контроллера 5200, датчики 5204 процесса, подключенные к трубке Вентури, генерируют сигналы процесса, включающие в себя один или несколько сигналов датчиков, сигнал температуры и один или несколько сигналов давления (как описано выше). Аналоговые сигналы процесса преобразуются в цифровые данные сигналов А/Ц преобразователями 5206 и сохраняются в буферах памяти 5208 данных сигналов датчиков и возбудителей для использования цифровым контроллером 5200. Возбудители 5245, подключенные к трубке Вентури, генерируют сигнал тока возбуждения и могут передавать этот сигнал на А/Ц преобразователи 5206. Затем сигнал тока возбуждения преобразуется в цифровые данные и сохраняется в буферах памяти 5208 данных сигналов датчиков и возбудителей. Альтернативно, цифровой сигнал коэффициента усиления возбуждения и цифровой сигнал тока возбуждения могут генерироваться модулем 5235 регулировки амплитуды и передаваться в буферы памяти 5208 данных сигналов датчиков и возбудителей для сохранения и использования цифровым контроллером 5200.
Цифровые данные сигналов датчиков и возбудителей процесса дополнительно анализируются и обрабатываются модулем 5210 обработки параметров датчиков и возбудителей, который генерирует физические параметры, включающие в себя частоту, фазу, ток, затухание и амплитуду колебаний. Модуль 5212 вычисления необработанного измерения массового расхода генерирует необработанный сигнал измерения массового расхода с использованием методов, рассмотренных выше применительно к расходомеру 500.
Конечный автомат 5215 состояний потока принимает в качестве входных сигналов физические параметры от модуля 5210 обработки параметров датчиков и возбудителей, необработанный сигнал измерения массового расхода и измерение плотности 5214, которое вычисляется, как описано выше. Затем конечный автомат 5215 состояний потока обнаруживает состояние потока материала, проходящего через цифровой массовый расходомер 100. В частности, конечный автомат 5215 состояний потока определяет, находится ли материал в состоянии однофазного потока или в состоянии двухфазного потока. Конечный автомат состояний потока 5215 также вводит необработанный сигнал измерения массового расхода в блок 5230 вывода измерения массового расхода.
При обнаружении состояния однофазного потока, выходной блок 5230 проверяет необработанный сигнал измерения массового расхода и может осуществлять анализ недостоверности для генерации параметра недостоверности, связанного с проверенным измерением массового расхода. В частности, когда конечный автомат 5215 обнаруживает наличие состояния однофазного потока, коэффициент коррекции не применяется к необработанному измерению массового расхода, и выходной блок 5230 проверяет измерение массового расхода. Если контроллер 5200 не обнаруживает ошибки при производстве измерения, выходной блок 5230 может присвоить измерению традиционный параметр недостоверности, связанный с безотказным измерением, и может задать флаг состояния, связанный с измерением, равным CLEAR. Если контроллер 5200 обнаруживает ошибки при производстве измерения, выходной блок 5230 может изменить параметр недостоверности, придав ему более высокое значение недостоверности, и может задать флаг состояния равным другому значению, например BLURRED.
Когда конечный автомат состояний потока 5215 обнаруживает наличие состояния двухфазного потока, модуль 5220 коррекции ошибок двухфазного потока принимает необработанный сигнал измерения массового расхода. Модуль 5220 коррекции ошибок двухфазного потока включает в себя процессор нейронной сети для прогнозирования ошибки массового расхода и для вычисления коэффициента коррекции ошибок. Процессор нейронной сети можно реализовать в программной процедуре или, альтернативно, можно реализовать как отдельный программируемый аппаратный процессор. Работа процессора нейронной сети более подробно описана ниже.
Модуль 5225 коэффициентов и обучения нейронной сети сохраняет заранее определенный набор коэффициентов нейронной сети, которые используются процессором нейронной сети. Модуль 5225 коэффициентов и обучения нейронной сети также может осуществлять функцию оперативного обучения с использованием обучающих данных, что позволяет вычислять обновленный набор коэффициентов для использования нейронной сетью. Хотя заранее определенный набор коэффициентов нейронной сети генерируется в ходе обширных лабораторных испытаний и экспериментов на основании известных двухфазных массовых расходов, функция оперативного обучения, осуществляемая модулем 5225, может применяться на начальной стадии ввода расходомера в эксплуатацию или каждый раз при инициализации расходомера.
Коэффициент коррекции ошибок, генерируемый модулем 5220 коррекции ошибок, поступает на блок 5230 вывода измерения массового расхода. С использованием необработанного измерения массового расхода и коэффициента коррекции ошибок (если, будучи принято от модуля коррекции ошибок 5220, он указывает двухфазный поток), блок 5230 вывода измерения массового расхода применяет коэффициент коррекции ошибок к необработанному измерению массового расхода для генерации скорректированного измерения массового расхода. Затем блок 5230 вывода измерения массового расхода проверяет скорректированное измерение массового расхода и может осуществлять анализ недостоверности для генерации параметра недостоверности, связанного с проверенным измерением массового расхода. Таким образом, блок 5230 вывода измерения массового расхода генерирует проверенный сигнал измерения массового расхода, который может включать в себя недостоверность и состояние, связанные с каждым проверенным измерением массового расхода, и состояние устройства.
Модуль 5210 обработки параметров датчика также вводит параметр затухания и параметр амплитуды колебаний (описанные выше) в модуль 5235 регулировки амплитуды. Модуль 5235 регулировки амплитуды дополнительно обрабатывает параметр затухания и параметр амплитуды колебаний и генерирует цифровые сигналы возбуждения. Цифровые сигналы возбуждения преобразуются в аналоговые сигналы возбуждения Ц/А преобразователями 5240 для оперирования возбудителями 5245, подключенными к трубке Вентури цифрового расходомера. В альтернативной реализации, модуль 5235 регулировки амплитуды может обрабатывать параметр затухания и параметр амплитуды колебаний и генерировать аналоговые сигналы возбуждения для оперирования возбудителями 5245 напрямую.
На фиг.53 показана процедура 5250, осуществляемая цифровым контроллером 5200. После начала обработки (этап 5251), сигналы измерения, генерируемые датчиками процесса 5204 и возбудителями 5245, количественно оцениваются в процессе аналого-цифрового преобразования (как описано выше), и буферы памяти 5208 заполняются цифровыми данными датчиков и возбудителей (этап 5252). Для каждого нового цикла обработки, модуль 5210 обработки параметров датчиков и возбудителей извлекает данные датчиков и возбудителей из буферов 5208 и вычисляет переменные датчиков и возбудителей из данных датчиков (этап 5254). В частности, модуль 5210 обработки параметров датчиков и возбудителей вычисляет напряжения датчиков, частоты датчиков, ток возбуждения и коэффициент усиления возбуждения.
Модуль 5210 обработки параметров датчиков и возбудителей выполняет процедуру обработки diagnose_flow_condition (этап 5256) для вычисления статистических значений, включающих в себя среднее значение, стандартное отклонение и наклон для каждой из переменных датчиков и возбудителей. На основании статистики, вычисленной для каждой из переменных датчиков и возбудителей, конечный автомат 5215 состояний потока обнаруживает переходы между любыми тремя пригодными состояниями потока: FLOW_CONDITION_SHOCK, FLOW_CONDITION_HOMOGENEOUS и FLOW_CONDITION_MIXED.
Если обнаружено состояние FLOW_CONDITION_SHOCK (этап 5258), процесс анализа измерения массового расхода не осуществляется по причине нерегулярности входных сигналов датчика. По выходу из этого состояния, процедура обработки начинает новый цикл (этап 5251). Затем процедура обработки ищет новый синусоидальный сигнал для отслеживания в данных сигналов датчиков и возобновляет обработку. В порядке этого процесса слежения, процедура обработки должна найти начало и конец синусоидальной волны с использованием вышеописанного метода пересечения нуля. Если состояние FLOW_CONDITION_SHOCK не обнаружено, процедура обработки вычисляет необработанное измерение массового расхода материала, текущего через расходомер 100 (этап 5260).
Если двухфазный поток не обнаружен (т.е. обнаружено состояние FLOW_CONDITION_HOMOGENOUS) (этап 5270), материал, текущий через расходомер 100, считается однофазным материалом. При этом проверенный массовый расход генерируется из необработанного измерения массового расхода (этап 5272) блоком 5230 вывода измерения массового расхода. В этот момент, проверенный массовый расход совместно с его параметром недостоверности и флагом состояния можно передавать на другой контроллер процесса. Затем начинается новый цикл обработки (этап 5251).
Если обнаружен двухфазный поток (т.е. обнаружено состояние FLOW_CONDITION_MIXED) (этап 5270), материал, текущий через расходомер 100, считается двухфазным материалом. В этом случае, модуль 5220 коррекции ошибок двухфазного потока прогнозирует ошибку массового расхода и генерирует коэффициент коррекции ошибок с использованием процессора нейронной сети (этап 5274). Скорректированный массовый расход генерируется блоком 5230 вывода измерения массового расхода с использованием коэффициента коррекции ошибок (этап 5276). Затем проверенный массовый расход может генерироваться из скорректированного массового расхода. В этот момент, проверенный массовый расход совместно с его параметром недостоверности и флагом состояния можно передавать на другой контроллер процесса. Затем начинается новый цикл обработки (этап 5251).
Согласно фиг.52, процессор нейронной сети, образующий часть модуля 5220 коррекции ошибок двухфазного потока, представляет собой нейронную сеть с прямой связью, которая обеспечивает непараметрическую инфраструктуру для представления нелинейного функционального отображения между входным и выходным пространствами. Нейронная сеть применяется для прогнозирования ошибок массового расхода в состояниях двухфазного потока в цифровом массовом расходомере. Когда ошибка предсказана нейронной сетью, коэффициент коррекции ошибок применяется к двухфазному измерению массового расхода для коррекции ошибок. Таким образом, система позволяет оперативно прогнозировать ошибки посредством нейронной сети с использованием только внутренних наблюдаемых параметров, выводимых из сигнала датчика, переменных датчика и статистики датчика.
Из различных доступных моделей нейронной сети, для реализации цифрового расходомера использовались сети на основе многоуровневого перцептрона (MLP) и радиальных базисных функций (RBF). MLP с одним скрытым уровнем (каждый блок имеет сигмоидальную функцию активации) может одинаково хорошо аппроксимировать любое непрерывное отображение. Поэтому, этот тип нейронной сети пригоден для моделирования нелинейного соотношения между ошибкой массового расхода расходомера в условиях двухфазного потока и некоторыми внутренними параметрами расходомера.
Весовые коэффициенты сети, необходимые для осуществления нужного отображения, определяются в процессе обучения или оптимизации. В ходе контролируемого обучения, нейронная сеть повторно представляется обучающей последовательностью (множеством входных примеров x i и соответствующих нужных выходов d i), и весовые коэффициенты обновляются таким образом, чтобы минимизировать функцию ошибок. Для задачи интерполяции, связанной с настоящим методом, подходящей функцией ошибок является ошибка суммы квадратов, которую, для MLP с одним выходом, можно представить в виде:
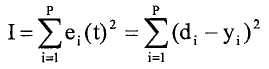 ,
,
где d i - цель, соответствующая входу x i; y i - фактический отклик нейронной сети на x i и P - количество примеров в обучающей последовательности.
Альтернативная архитектура нейронной сети, которая использовалась, представляет собой сеть RBF. Методы RBF основаны на методах осуществления точных интерполяций множества точек данных в многомерном пространстве. Сеть RBF, в общем случае, имеет простую архитектуру из двух уровней весовых коэффициентов, в которой первый уровень содержит параметры базисных функций, и второй уровень образует линейные комбинации активации базисных функций для генерации выходов. Это достигается путем представления выхода сети линейной суперпозицией базисных функций, по одной для каждой точки данных в обучающей последовательности. В этой форме, обучение проходит быстрее, чем для сети MLP.
Внутренние параметры датчика, представляющие интерес, включают в себя наблюдаемую плотность, затухание, наблюдаемый расход и температуру. Ниже рассмотрен каждый из этих параметров.
1. Наблюдаемая плотность
Наиболее распространенная метрика двухфазного потока представляет собой пустотную (или газовую) долю, определенную как объемная доля газа. Уравнение
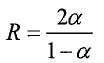
моделирует ошибку массового расхода при данной пустотной доле. Для кориолисова массового расходомера, регистрируемая плотность рабочей текучей среды обеспечивает косвенную меру пустотной доли, исходя из того, что "истинная" плотность жидкости известна. Эта регистрируемая плотность процесса подвержена ошибкам, сходным с ошибками в измерении массового расхода при наличии двухфазного потока. Эти ошибки имеют высокую повторяемость, и спад плотности является достаточно монотонным, но нелинейным индикатором пустотной доли, который можно оперативно отслеживать в расходомере. Заметим, что за пределами лабораторных условий, истинную пустотную долю невозможно независимо оценивать, напротив, ее нужно моделировать, как описано выше.
Информацию об "истинной" плотности однофазной жидкости (возможно, включающую в себя температурный коэффициент) можно получить оперативно или ее может задавать пользователь. Оба подхода были реализованы и показали хорошие результаты.
В целях этих описаний, спад плотности будет использоваться в качестве параметра оси x на графиках, показывающих поведение двухфазного потока. Заметим, что в 3D графиках, показанных на фиг.54 и 56-57, которые отражают результаты 134 оперативных экспериментов, полный диапазон точек спада плотности невозможен при высоких расходах в силу ограничений на давление воздуха в гидродинамической установке. Кроме того, эффекты температуры, хотя и не показанные на графиках, были определены экспериментально.
2. Затухание
Большинство кориолисовых расходомеров использует положительную обратную связь для поддержания колебаний трубки Вентури. Сигналы датчиков обеспечивают частоту и фазу колебания трубки Вентури, которые умножаются на коэффициент усиления возбуждения K0 для обеспечения токов, поступающих на возбудители 5245:
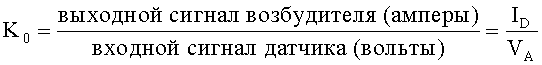
Обычно коэффициент усиления возбуждения модифицируется, чтобы гарантировать постоянную амплитуду колебаний, и он примерно пропорционален коэффициенту затухания трубки Вентури.
Одним из наиболее характерных признаков двухфазного потока является быстрый рост затухания. Например, нормально работающая 25 мм трубка Вентури имеет VA = 0,3 В, ID = 10 мА и, следовательно, K0 = 0,033. При двухфазном потоке, значения могут достигать экстремальных значений VA = 0,03 В, ID = 100 мА и K0 = 3,3, со стократным увеличеним. На фиг.54 показано, как изменяется затухание при двухфазном потоке.
3. Наблюдаемые расход и температура
Согласно фиг.49, ошибка массового расхода изменяется с истинным расходом. Также наблюдается изменение температуры. Однако истинный массовый расход недоступен в самом передатчике (или цифровом контроллере), когда расходомер используется в двухфазном потоке. Однако наблюдаемый (ошибочный) расход, равно, как и температура, можно использовать в качестве входных параметров процессора нейронной сети.
Q. Сетевое обучение и оперативная коррекция ошибок массового расхода
Реализация нейронно-сетевого анализа для прогнозирования ошибок измерения массового расхода включает в себя обучение процессора нейронной сети распознавать шаблон ошибок массового расхода в обучающих экспериментальных данных, тестирование производительности процессора нейронной сети на новом наборе экспериментальных данных и оперативную реализацию процессора нейронной сети для прогнозирования и коррекции ошибок измерения.
Качество прогнозирования процессора нейронной сети зависит от богатства обучающих данных. Для сбора данных нейронной сети, был проведен ряд экспериментов на двухфазной воздушно-водной смеси с использованием экспериментальной гидродинамической установки 5500, показанной на фиг.55. Контур потока включает в себя главный измеритель 5510, кориолисов расходомер SEVA® 100 с автоматической проверкой и ответвитель 5520 для переноса материала из трубки Вентури на весы 5530. Кориолисов расходомер 100 имеет функцию суммирования, которая может запускаться внешними сигналами. Управление гидродинамической установкой устроено так, что ответвитель потока 5520 (подающий поток на весы) и кориолисово суммирование запускаются главным измерителем 5510 в начале эксперимента, и, опять же, после того, как главный измеритель 5510 зарегистрирует 100 кг потока. Суммарное показание весов используется как опорная точка для вычисления ошибки массового расхода путем сравнения с суммированным потоком из цифрового расходомера 100, когда главный измеритель 5510 действует как дополнительная проверка. Недостоверность экспериментальной установки оценивается примерно на 0,1% типичных размеров порции в 100 кг. Для однофазных экспериментов, цифровой расходомер 100 доставляет суммарный массовый расход в пределах 0,2% суммарного показания весов. Для экспериментов с двухфазным потоком, воздух впрыскивается в поток после главного измерителя 5510 и до кориолисова расходомера 100. При низких расходах, достигаются спады плотности до 30%. При более высоких расходах достигаются, по меньшей мере, 15% спады плотности.
В конце каждой порции, кориолисов расходомер 100 выдает среднее по порции для каждого из следующих параметров: температуры, затухания, плотности, расхода и суммарного (нескорректированного) потока. Эти параметры, таким образом, доступны для использования в качестве входных данных процессора нейронной сети.
Выход или цель нейронной сети является ошибкой массового расхода в процентах:
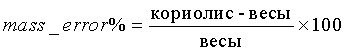
На фиг.56 показано, как ошибка массового расхода изменяется в зависимости от расхода и спада плотности. Хотя общая тенденция соответствует пузырьковой модели, существуют дополнительные признаки, представляющие интерес. Например, при высоких расходах и низких спадах плотности, ошибка массового расхода становится немного положительной (примерно на 1%), тогда как пузырьковая модель предсказывает только отрицательную ошибку. Из фиг.56 следует, что в этой области экспериментального пространства и для этой конструкции трубки Вентури происходит какой-то другой физический процесс для преодоления эффектов пропадающей массы двухфазного потока.
Наилучшие результаты были получены с использованием только четырех входных параметров нейронной сети: температуры, затухания, спада плотности и наблюдаемого расхода. Возможно, менее удовлетворительным является результат, что наилучшая аппроксимация была достигнута с использованием нейронной сети самой по себе, а не коррекции пузырьковой модели или упрощенной аппроксимации кривой.
Как часть реализации, нейронную сеть MLP использовали для оперативной реализации. Сравнения между сетями RBF и MLP с одинаковыми наборами данных и вводами показали, в целом, близкую производительность на испытательном наборе. Таким образом, резонно предположить, что входной набор, обеспечивающий наилучшую конструкцию RBF, также будет обеспечивать хорошую (если не лучшую) конструкцию MLP. Нейронные сети MLP обучали с использованием алгоритма масштабированного сопряженного градиента. Возможности Neural Network Toolbox программного пакета MATLAB® использовали для обучения нейронной сети. После исследования дополнительных вариантов конструкции, наивысшая производительность обеспечивается сетью MLP 4-9-1, имеющей в качестве входов температуру, затухание, спад плотности и расход, совместно с ошибкой массового расхода в качестве выхода.
Согласно проверочному набору, наилучшая нейронная сеть обеспечивала предсказания массового расхода в пределах 2% истинного значения. Процедуры для обнаружения и коррекции двухфазного потока были закодированы и включены в цифровой кориолисов передатчик. На фиг.57 показана остаточная ошибка массового расхода при оперативной коррекции по 134 новым экспериментам. Все ошибки ограничены 2%, и большинство из них значительно меньше. Случайный разброс обусловлен, главным образом, остаточной ошибкой в алгоритме коррекции нейронной сети (как указано выше, недостоверность гидродинамической установки составляет 0,1%). Любая очевидная тенденция в данных предусматривает объем дополнительной коррекции. Эти ошибки, конечно, относятся к среднему скорректированному массовому расходу (т.е. по порции).
На фиг.58 показано, как оперативные обнаружение и коррекция двухфазного потока отражается в интерфейсе с автоматической проверкой, генерируемом для измерения массового расхода. На графике, нижняя, непрерывная линия 5810 представляет необработанный массовый расход. Верхняя линия 5820 представляет измерение, окруженное полосой недостоверности, и представляет скорректированный или проверенный массовый расход. Пунктирная линия 5830 представляет массовый расход из главного измерителя, который расположен до точки впрыска воздуха (фиг.55).
Для однофазного потока (до t = 5 с), измерение массового расхода имеет состояние значения измерения CLEAR и малую недостоверность около 0,2% показания. Когда обнаружен двухфазный поток, коррекция нейронной сети применяется каждый перемеженный период (т.е. с частотой 180 Гц), на основании значений внутренних параметров, усредненных (с использованием движущегося окна) по последней секунде. При наличии двухфазного потока, состояние значения измерения задается равным BLURRED, и недостоверность возрастает для отражения снижения точности скорректированного измерения. Нескорректированное измерение (нижняя толстая линия) демонстрирует большую ошибку смещения около 30%.
Показание главного измерителя согласуется в первом приближении со скорректированным измерением массового расхода. Наблюдаемая задержка в его отклике на наступление двухфазного потока объясняется задержками связи в системе управления установки, и его отклик, напоминающий квадратную волну, обусловлен частотой обновления системы управления только один раз в секунду. Необработанное и скорректированное измерения от цифрового передатчика демонстрируют более высокую степень изменения, чем при однофазном потоке. Показание главного измерителя обеспечивает полезную меру водной фазы, входящей в двухфазную зону, и существует отчетливое подобие между показанием главного измерителя и 'средним' скорректированным показанием. Однако пробковый режим и сжимаемость воздуха в сложной трехмерной геометрии трубки Вентури могут приводить не только к изменениям расхода, но при этом мгновенный массовый расход в систему отличается от массового расхода из системы.
С использованием подхода обработки датчика с автоматической проверкой, измерение не просто помечается датчиком как хорошее или плохое. Вместо этого, если происходит отказ, по возможности применяется коррекция, и качество результирующего измерения указывается посредством состояния BLURRED и повышенной недостоверности. Таким образом, пользователь оценивает требования и варианты, зависящие от применения, для принятия решения, продолжать ли работу со сниженным качеством скорректированного массового расхода, переключиться ли на альтернативное измерение, если доступно, или остановить процесс. Если двухфазный поток присутствует только в течение части пропускаемой порции (например, в начале или конце), будет пропорциональное взвешивание в зависимости от недостоверности суммарной массы порции.
Многофазные потоки
На фиг.59 показан иллюстративный процесс 5900, используемый для определения зависящего от фазы свойства фазы, включенной в многофазную рабочую текучую среду. Например, способ 5900 можно использовать для определения массового расхода и плотности каждой фазы многофазной рабочей текучей среды.
Как описано ниже, наблюдаемое промежуточное значение определяется на основании, например, массового расхода и плотности многофазной рабочей текучей среды (также именуемых совокупным массовым расходом и совокупной плотностью, соответственно), определяемых, например, кориолисовым измерителем. Хотя кориолисов измеритель продолжает работать при наличии многофазной рабочей текучей среды, наличие многофазной текучей среды оказывает влияние на движение трубки Вентури (или трубопровода), которая входит в состав кориолисова измерителя. Таким образом, выходные сигналы, определяемые измерителем, могут быть неточными, поскольку измеритель работает исходя из того, что рабочая текучая среда включает в себя одну фазу. Эти выходные сигналы можно называть наблюдаемыми свойствами или необработанными свойствами многофазной текучей среды. Таким образом, в одной реализации, наблюдаемое промежуточное значение определяется на основании наблюдаемых или необработанных свойств многофазной текучей среды. Другие реализации могут определять промежуточное значение на основании скорректированной формы наблюдаемого свойства(-ств). Для коррекции неточностей, наблюдаемое промежуточное значение вводится, например, в нейронную сеть для создания скорректированного промежуточного значения, которое учитывает эффекты использования многофазной рабочей текучей среды. Скорректированное промежуточное значение используется для определения массового расхода и плотности каждой фазы многофазной рабочей текучей среды. Использование промежуточного значения вместо наблюдаемого массового расхода и плотности многофазной рабочей текучей среды может способствовать повышению точности определения массового расхода и плотности каждой фазы многофазной рабочей текучей среды.
Многофазная рабочая текучая среда пропускается через вибрационную трубку Вентури (5905). В вибрационной трубке Вентури создается движение (5910). Вибрационная трубка Вентури может представлять собой, например, трубопровод 120, рассмотренный выше согласно фиг.1. Многофазную рабочую текучую среду также можно называть многофазным потоком. Многофазная текучая среда может быть двухфазной текучей средой, трехфазной текучей средой или текучей средой, которая включает в себя более трех фаз. В общем случае, каждую фазу многофазной текучей среды можно рассматривать как составляющую или компонент многофазной текучей среды. Например, двухфазная текучая среда может включать в себя негазовую фазу и газовую фазу. Негазовая фаза может быть жидкостью, например, нефтью, и газовая фаза может быть газом, например, воздухом. Трехфазная текучая среда может включать в себя две негазовые фазы и одну газовую фазу или одну негазовую фазу и две газовые фазы. Например, трехфазная текучая среда может включать в себя газ и две жидкости, например, воду и нефть. В другом примере, трехфазная текучая среда может включать в себя газ, жидкость и твердое тело (например, песок). Дополнительно, многофазная текучая среда может представлять собой влажный газ. Хотя влажный газ может быть любой из вышеописанных многофазных текучих сред, влажный газ, в общем случае, состоит из более 95% газовой фазы по объему. Способ 5900 можно применять к любой многофазной текучей среде.
Первое свойство многофазной текучей среды можно определить на основании движения вибрационной трубки Вентури (5915). Первым свойством многофазной текучей среды может быть наблюдаемый массовый расход и/или наблюдаемая плотность текучей среды, текущей через вибрационную трубку Вентури. Таким образом, в иллюстративном способе 5900, первым свойством может быть массовый расход или плотность многофазной текучей среды. Свойства, определяемые из многофазной текучей среды, можно называть наблюдаемыми, или необработанными, свойствами в отличие от истинных (или, по меньшей мере, скорректированных) свойств многофазной текучей среды. Наблюдаемые массовый расход и плотность многофазной текучей среды, в общем случае, не согласуются с массовым расходом и плотностью каждой из отдельных фаз многофазной текучей среды вследствие воздействия многофазной текучей среды на движение трубки Вентури. Например, если многофазная текучая среда имеет сравнительно низкую объемную долю газа (например, многофазная текучая среда включает в себя больше жидкости, чем газа), наблюдаемая плотность и наблюдаемый массовый расход многофазной текучей среды, полученные из трубки Вентури, имеют тенденцию быть ниже, чем фактические плотность и массовый расход негазовой фазы. Хотя первое свойство, в общем случае, является наблюдаемым свойством, в некоторых реализациях, первое свойство может быть скорректированным или фактическим свойством. Скорректированное или фактическое свойство можно получить, например, из модели или отображения.
Как рассмотрено согласно фиг.1, массовый расход связан с движением, возбуждаемым в вибрационной трубке Вентури. В частности, массовый расход связан с фазовым и частотным поведением движения трубки Вентури и температурой трубки Вентури. Дополнительно, плотность текучей среды связана с частотой движения и температурой трубки Вентури. Таким образом, поскольку текучая среда, текущая через трубку Вентури, включает в себя более одной фазы, вибрационная трубка Вентури обеспечивает массовый расход и плотность многофазной текучей среды, а не массовый расход и плотность каждой фазы многофазной текучей среды. Как более подробно описано ниже, способ 5900 можно использовать для определения свойств каждой фазы многофазной текучей среды.
В общем случае, для определения свойств отдельных фаз в многофазной текучей среде, временами может требоваться дополнительная информация (например, известные плотности материалов в отдельных фазах) или дополнительные измерения (например, давление многофазной текучей среды или обводненность многофазной текучей среды). Однако свойства многофазной текучей среды, измеренные измерителем, обычно определяются модификацией или коррекцией традиционных методов однофазных измерений вследствие влияния многофазного потока на трубку Вентури по сравнению с однофазным потоком.
Таким образом, в некоторых реализациях, помимо свойства, определяемого на основании движения трубопровода, например первого свойства, рассмотренного выше, дополнительные или "внешние" свойства многофазной текучей среды, например, температура, давление и обводненность, можно измерять и использовать в способе 5900, например, в качестве дополнительных входов отображения или для помощи в определении расходов отдельных компонентов многофазной текучей среды. Дополнительные свойства можно измерять устройством, отличным от расходомера. Например, обводненность многофазной текучей среды, которая представляет часть многофазной текучей среды, т.е. воду, можно определять с помощью измерителя обводненности. Дополнительное свойство также может включать в себя давление, связанное с трубкой Вентури. Давление, связанное с трубкой Вентури, может представлять собой, например, давление многофазной рабочей текучей среды на входе трубки Вентури и/или перепад давлений на трубке Вентури.
Наблюдаемое промежуточное значение, связанное с многофазной рабочей текучей средой, определяется на основании первого свойства (5920). В некоторых реализациях, второе свойство многофазной текучей среды также можно определить на основании движения трубопровода. Например, в такой реализации, наблюдаемый массовый расход многофазной текучей среды и наблюдаемую плотность многофазной текучей среды можно определить на основании движения трубопровода, и оба эти наблюдаемые свойства можно использовать для определения одного или нескольких наблюдаемых промежуточных значений (например, объемной доли жидкости и объемного расхода или газового числа Фруда и негазового числа Фруда, как описано ниже). В некоторых реализациях, наблюдаемые промежуточные значения могут быть промежуточными значениями на основании одного или нескольких скорректированных или фактических свойств.
В общем случае, наблюдаемое промежуточное значение (или значения) - это значение, связанное с многофазной текучей средой, которое отражает неточности, обусловленные включением более чем одной фазы в многофазной текучей среде. Наблюдаемое промежуточное значение может быть, например, объемной долей многофазной рабочей текучей среды. Объемная доля может быть объемной долей жидкости, которая задает часть многофазной текучей среды, которая не является газом. Объемная доля также может быть объемной долей газа, которая задает часть многофазной текучей среды, которая является газом. В общем случае, объемная доля является безразмерной величиной, которую можно выразить в процентах. Объемную долю газа также можно называть пустотной долей. Если многофазная текучая среда включает в себя жидкости и газы, сумма объемных долей жидкости и газа равна 100%. В других реализациях, наблюдаемое промежуточное значение может быть объемным расходом многофазной текучей среды.
В другой реализации, наблюдаемые промежуточные значения могут включать в себя негазовое число Фруда и газовое число Фруда. Числа Фруда представляют собой безразмерные величины, которые могут представлять сопротивление объекта, движущегося через текучую среду, и которые можно использовать для описания многофазных текучих сред. В этой реализации, наблюдаемое промежуточное значение может быть негазовым числом Фруда и/или газовым числом Фруда. Наблюдаемое газовое число Фруда можно вычислять с использованием следующего уравнения, где m a g - наблюдаемый массовый расход газа, ρg - оценка плотности газовой фазы на основании законов идеального газа, ρl - оценка плотности жидкости в негазовой фазе многофазной текучей среды, A - площадь поперечного сечения трубки Вентури, D - диаметр трубки Вентури и g - ускорение свободного падения:
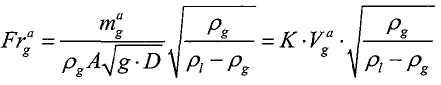 ,
,
где 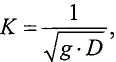 наблюдаемая скорость газа
наблюдаемая скорость газа 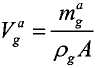 .
.
Аналогично, негазовое число Фруда (которое может быть жидкостным числом Фруда) можно вычислять с использованием следующего уравнения, где m a l - наблюдаемый массовый расход жидкости:
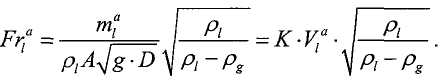
Как рассмотрено более подробно ниже, наблюдаемое промежуточное значение вводится в отображение, которое задает соотношение между наблюдаемым промежуточным значением и скорректированным промежуточным значением. Отображение может представлять собой, например, нейронную сеть, многочлен, функцию, или любой другой тип отображения. До ввода наблюдаемого промежуточного значения в отображение, наблюдаемое промежуточное значение можно фильтровать или преобразовывать для снижения шума измерения и процесса. Например, линейные фильтры можно применять к наблюдаемому промежуточному значению для снижения шума измерения. Временную постоянную линейного фильтра можно задать равным значению, которое отражает время отклика измерительных приборов (например, 1 секунду), чтобы фильтр оставался устойчивым к фактическим изменениям в текучей среде, текущей через трубку Вентури (например, осадкам негазообразной текучей среды), и в то же время был способен снижать шум измерения.
Построение отображения для коррекции или улучшения многофазного измерения предусматривает сбор данных в условиях эксперимента, где истинные или опорные измерения обеспечиваются дополнительным калиброванным оборудованием. В общем случае, непрактично проводить эксперименты, охватывающие все мыслимые многофазные условия, вследствие ограничений испытательного оборудования и/или стоимости и времени, связанных с производством, возможно, тысяч экспериментов. Дополнительно, вряд ли возможно поддерживать условия многофазного потока в точности постоянными в течение сколько-нибудь продолжительного периода времени, вследствие внутренне нестабильных состояний потока, которые имеют место в многофазных условиях. Соответственно, обычно требуется вычислять средние значения любых относящихся к делу параметров, включая наблюдаемые и истинные или опорные значения параметров, на протяжении каждого эксперимента, длительность которого обычно может составлять от 30 с до 120 с. Таким образом, отображение можно построить из экспериментальных данных, где каждая точка данных выводится из среднего значения данных по периоду, например, от 30 с до 120 с.
Трудности могут возникать при применении результирующего отображения в измерителе в ходе многофазного потока в реальном времени, благодаря чему конкретные значения параметров, наблюдаемых в измерителе, не включаются в отображение, полученное из ранее собранных экспериментальных данных. Это может происходить двумя основными путями. В первом варианте, хотя условия, в которых находится измеритель, усредненные по временной шкале примерно от 15 до 120 секунд, соответствуют условиям, охватываемым отображением, мгновенные значения параметров могут выпадать из области, вследствие шума измерения и/или мгновенных изменений фактических условий вследствие нестабильностей, присущих многофазному потоку. Как описано выше, этот эффект можно до некоторой степени ослабить усреднением по времени или фильтрацией параметров, используемых в качестве входов в функцию отображения, хотя существует компромисс между эффектами понижения шума такой фильтрации и реактивностью измерителя к фактическим изменениям условий в многофазном потоке. Альтернативно, усредненные значения параметров могут выпадать из отображения, поскольку, например, не было экономически оправдано охватывать все возможные многофазные условия на стадии эксперимента.
Может быть не выгодно применять функцию отображения (нейронную сеть, многочлен или другую функцию) к данным, которые выпадают из области, для которой предназначено отображение. Применение отображения к таким данным может приводить к генерации низкокачественных измерений. Соответственно, можно применять процедуры покрытия оболочкой, чтобы гарантировать, что поведение процедуры отображения пригодно для значений параметров вне отображаемой области, независимо от причин, по которым параметры оказываются вне отображаемой области. Данные, которые включены в область, можно называть пригодными данными.
Таким образом, наблюдаемое промежуточное значение можно "покрывать оболочкой" до ввода наблюдаемого промежуточного значения в отображение. Для реализаций, которые включают в себя отображения с одним входом, область подходящих данных можно задать посредством одного или нескольких пределов, диапазона или порога. В других реализациях, могут существовать отображения с более чем одним входом. В этих реализациях, область подходящих данных можно задать рядом линий, кривых поверхностей. Соответственно, с возрастанием количества входов отображения, задание области подходящих данных усложняется. Таким образом, может быть желательно использовать отображения с меньшим числом входов. Вышеописанные газовое и жидкостное числа Фруда являются примерами наблюдаемых промежуточных значений, которые можно подавать в отображение без дополнительных входов. Таким образом, использование газового и негазового чисел Фруда может способствовать сокращению количества входов в отображение, что также может способствовать упрощению процесса покрытия оболочкой. Дополнительно, использование меньшего числа входов отображения может приводить к упрощению отображения, что может способствовать снижению вычислительных ресурсов, используемых отображением, и способствовать повышению скорости определения скорректированных промежуточных значений на основании отображения.
Наблюдаемое промежуточное значение, имеющее значение, находящееся вне заданной области, можно определить как непригодное для ввода в отображение. В общем случае, заданы правила коррекции наблюдаемого промежуточного значения, которое определено как находящееся вне заданной области. Например, наблюдаемое промежуточное значение, которое находится вне заданной области, может игнорироваться отображением (например, наблюдаемое промежуточное значение, не скорректированное посредством отображения), наблюдаемое промежуточное значение может вовсе не вводиться в отображение, к наблюдаемому промежуточному значению можно применять фиксированную коррекцию, а не коррекцию, определяемую отображением, или можно применять коррекцию, соответствующую коррекции, которая будет применяться к значению, ближайшему к наблюдаемому промежуточному значению. Можно реализовать другие правила коррекции наблюдаемого промежуточного значения, которое находится вне заданной области. В общем случае, покрытие оболочкой относится к конкретному отображению и определяется для каждого отображения.
Скорректированное промежуточное значение определяется на основании отображения между наблюдаемым промежуточным значением и скорректированным промежуточным значением (5925). Отображение может представлять собой нейронную сеть, статистическую модель, многочлен, функцию, или любой другой тип отображения. Нейронную сеть или другое отображение можно обучать данными, полученными из многофазной текучей среды, для которой значения составляющих фаз известны. Аналогично покрытию оболочкой, описанному выше согласно (5920), скорректированное наблюдаемое значение можно покрывать оболочкой, или иначе проверять, до его использования в дальнейшей обработке. Зависящее от фазы свойство многофазной рабочей текучей среды можно определить на основании скорректированного промежуточного значения (5930). С использованием одного или нескольких из наблюдаемых промежуточных значений, рассмотренных выше, а не значения, непосредственно из трубки Вентури (например, массового расхода многофазной жидкости) можно повысить точность способа 5900. Зависящее от фазы свойство может быть, например, массовым расходом и/или плотностью негазовой и газовой фаз многофазной текучей среды.
Иллюстративный способ, описанный согласно фиг.59, можно реализовать программными или аппаратными средствами. На фиг.60 и 61 описан пример реализации. Согласно фиг.60 и 61, необязательные компоненты обозначены пунктиром. В частности, на фиг.60 и 61 показано применение цифрового расходомера к текучей среде, имеющей множественные фазы, которые предполагаются часто встречающимися (например, в вышеописанном способе серийного производства), или к потоку текучей среды, имеющей неоднородную смесь составляющих (одну или несколько газовых составляющих и/или одну или несколько жидкостных составляющих).
На фиг.60 показан цифровой контроллер 6200, который можно использовать вместо цифрового контроллера 105 или 505 цифровых массовых расходомеров 100, 500, показанных на фиг.1 и 5. В этой реализации цифрового контроллера 6200, датчики способа 6204, подключенные к трубке Вентури, генерируют сигналы способа, включающие в себя один или несколько сигналов датчиков, сигнал температуры и один или несколько сигналов давления (как описано выше). Аналоговые сигналы способа преобразуются в цифровые данные сигналов А/Ц преобразователями 6206 и сохраняются в буферах памяти 6208 данных сигналов датчиков и возбудителей для использования цифровым контроллером 6200. Возбудители 6245, подключенные к трубке Вентури, генерируют сигнал тока возбуждения и могут передавать этот сигнал на А/Ц преобразователи 6206. Затем сигнал тока возбуждения преобразуется в цифровые данные и сохраняется в буферах памяти 6208 данных сигналов датчиков и возбудителей. Альтернативно, цифровой сигнал коэффициента усиления возбуждения и цифровой сигнал тока возбуждения могут генерироваться модулем регулировки амплитуды 6235 и передаваться в буферы памяти 6208 данных сигналов датчиков и возбудителей для сохранения и использования цифровым контроллером 6200.
Цифровые данные сигналов датчиков и возбудителей способа дополнительно анализируются и обрабатываются модулем 6210 обработки параметров датчиков и возбудителей, который генерирует физические параметры, включающие в себя частоту, фазу, ток, затухание и амплитуду колебаний. Модуль 6212 вычисления необработанного измерения массового расхода генерирует необработанный сигнал измерения массового расхода с использованием методов, рассмотренных выше применительно к расходомеру 500.
Вместо того, чтобы включать в себя специализированный конечный автомат состояний потока, например 5215, рассмотренный в связи с расходомером 5200, модуль коррекции ошибок многофазного потока с одной или несколькими нейронными сетями принимает, в качестве входа, физические параметры от модуля 6210 обработки параметров датчиков и возбудителей, необработанный сигнал измерения массового расхода и измерение плотности 6214, которое вычисляется, как описано выше. Например, если рабочая текучая среда представляет собой известный двухфазный (например, газовую и жидкостную составляющие), трехфазный (например, газовую и две жидкостные составляющие) или другой многофазный поток (например, одну или несколько газовых и одну или несколько жидкостных составляющих), определение состояния потока может не потребоваться. В этом примере, рабочая текучая среда может быть влажным газом, про который известно, что он включают в себя объемную долю газа (gvf) и объемную долю жидкости (lvf). Влажный газ может включать в себя, например, природный газ, жидкий нефтепродукт и воду. Соответственно, измерение массового расхода, рассмотренное ниже, может автоматически определять измерение массового расхода каждой фазы многофазной рабочей текучей среды. Специализированную нейронную сеть для каждого состояния многофазного потока можно использовать в модуле 6220 коррекции ошибок многофазного потока. Альтернативно или дополнительно, можно использовать единую нейронную сеть, которая распознает двухфазный и/или трехфазный (или состоящий из большего количества фаз) поток и применяет коэффициенты коррекции на основании фактического состояния многофазного потока.
В условиях многофазного потока, модуль 6220 коррекции ошибок многофазного потока принимает необработанный (или наблюдаемый) сигнал измерения массового расхода и необработанный сигнал плотности. Наблюдаемые сигналы измерения массового расхода и плотности отражают массовый расход и плотность многофазной рабочей текучей среды, а не массовый расход и плотность каждой фазы, включенной в многофазную рабочую текучую среду. Модуль 6220 коррекции ошибок многофазного потока включает в себя процессор нейронной сети для прогнозирования ошибки массового расхода, что обусловлено наличием многофазной рабочей текучей среды. Процессор нейронной сети можно реализовать в программной процедуре или, альтернативно, можно реализовать как отдельный программируемый аппаратный процессор. Работа процессора нейронной сети более подробно описана ниже.
Входными сигналами процессора нейронной сети могут быть наблюдаемые промежуточные значения, определяемые из необработанных сигналов измерения массового расхода и измерения плотности. В этой реализации, модуль 6220 коррекции ошибок многофазного потока определяет наблюдаемые промежуточные значения, например, наблюдаемые промежуточные значения, рассмотренные выше согласно фиг.59, из необработанных (или наблюдаемых) значений массового расхода и плотности многофазной рабочей текучей среды. Наблюдаемые промежуточные значения вводятся в процессор нейронной сети и корректируются. Скорректированные наблюдаемые промежуточные значения выводятся на блок 6230 вывода измерения массового расхода. В других реализациях, наблюдаемые (или необработанные) измерение массового расхода и плотность можно вводить в нейронную сеть.
Модуль 6225 коэффициентов и обучения нейронной сети сохраняет заранее определенный набор или наборы коэффициентов нейронной сети, которые используются процессором нейронной сети для каждого состояния многофазного потока. Модуль 6225 коэффициентов и обучения нейронной сети также может осуществлять функцию оперативного обучения с использованием обучающих данных, что позволяет вычислять обновленный набор коэффициентов для использования нейронной сетью. Хотя заранее определенный набор коэффициентов нейронной сети генерируется в ходе обширных лабораторных испытаний и экспериментов на основании известных двухфазного, трехфазного или многофазного массовых расходов, функция оперативного обучения, осуществляемая модулем 6225, может применяться на начальной стадии ввода расходомера в эксплуатацию или каждый раз при инициализации расходомера.
Скорректированные промежуточные значения из нейронной сети поступают на блок 6230 вывода измерения массового расхода. С использованием скорректированных промежуточных значений, блок 6230 вывода измерения массового расхода определяет массовый расход каждой фазы многофазной рабочей текучей среды. В некоторых реализациях, блок 6230 вывода измерения массового расхода проверяет измерения массового расхода для фаз и может осуществлять анализ недостоверности для генерации параметра недостоверности, связанного с проверкой.
Модуль 6210 обработки параметров датчика также вводит параметр затухания и параметр амплитуды колебаний (описанные выше) в модуль 6235 регулировки амплитуды. Модуль 6235 регулировки амплитуды дополнительно обрабатывает параметр затухания и параметр амплитуды колебаний и генерирует цифровые сигналы возбуждения. Цифровые сигналы возбуждения преобразуются в аналоговые сигналы возбуждения Ц/А преобразователями 6240 для оперирования возбудителями 6245, подключенными к трубке Вентури цифрового расходомера. В некоторых реализациях, модуль 6235 регулировки амплитуды может обрабатывать параметр затухания и параметр амплитуды колебаний и генерировать аналоговые сигналы возбуждения для оперирования возбудителями 6245 напрямую.
На фиг.61 показана процедура 6250, осуществляемая цифровым контроллером 6200. После начала обработки (6251), сигналы измерения, генерируемые датчиками процесса 6204 и возбудителями 6245, количественно оцениваются в процессе аналого-цифрового преобразования (как описано выше), и буферы памяти 6208 заполняются цифровыми данными датчиков и возбудителей (6252). Для каждого нового периода обработки, модуль 6210 обработки параметров датчиков и возбудителей извлекает данные датчиков и возбудителей из буферов 6208 и вычисляет переменные датчиков и возбудителей из данных датчиков (6254). В частности, модуль 6210 обработки параметров датчиков и возбудителей вычисляет напряжения датчиков, частоты датчиков, ток возбуждения и коэффициент усиления возбуждения.
Модуль 6210 обработки параметров датчиков и возбудителей выполняет необязательную процедуру обработки diagnose_flow_condition (6256) для вычисления статистических значений, включающих в себя среднее значение, стандартное отклонение и наклон для каждой из переменных датчиков и возбудителей. Необязательную процедуру обработки diagnose_flow_condition ( 6256) можно использовать, например, для идентификации состояния двухфазного потока и/или для определения, включает ли в себя жидкостный компонент двухфазного потока отдельные жидкостные составляющие, например, нефть и воду. На основании статистики, вычисленной для каждой из переменных датчиков и возбудителей, можно использовать необязательный конечный автомат состояний потока (6258) для обнаружения переходов между любыми тремя пригодными состояниями потока: FLOW_CONDITION_SHOCK, FLOW_CONDITION_HOMOGENEOUS и FLOW_CONDITION_MIXED. Однако, если известно, что рабочая текучая среда уже включают в себя неоднородную смесь, способ может автоматически переходить от этапа 6254 к вычислению необработанного измерения массового расхода 6260.
Если обнаружено состояние FLOW_CONDITION_SHOCK (6258), способ анализа измерения массового расхода не осуществляется по причине нерегулярности входных сигналов датчика. По выходу из этого состояния, процедура обработки начинает новый цикл (6251). Затем процедура обработки ищет новый синусоидальный сигнал для отслеживания в данных сигналов датчиков и возобновляет обработку. В порядке этого способа слежения, процедура обработки должна найти начало и конец синусоидальной волны с использованием вышеописанного метода пересечения нуля. Если состояние FLOW_CONDITION_SHOCK не обнаружено, процедура обработки вычисляет необработанное измерение массового расхода материала, текущего через расходомер 100 (6260).
Если заранее известно, что многофазный поток существует в отслеживаемом способе, материал, текущий через расходомер 100, считается, например, двухфазным или трехфазным материалом. Например, материал, текущий через расходомер 100, может быть многофазной рабочей текучей средой, например, влажным газом. В этом случае, модуль 6220 коррекции ошибок многофазного потока определяет наблюдаемое промежуточное значение и, с использованием процессора(ов) нейронной сети, корректирует наблюдаемое промежуточное значение с использованием (6274). Зависящие от фазы свойства каждой фазы многофазной текучей среды определяются блоком 6230 вывода измерения массового расхода с использованием скорректированного промежуточного значения (6276). Затем начинается новый цикл обработки (6251).
Согласно фиг.60, процессор нейронной сети, образующий часть модуля 6220 коррекции ошибок двухфазного потока, может представлять собой нейронную сеть с прямой связью, которая обеспечивает непараметрическую инфраструктуру для представления нелинейного функционального отображения между входным и выходным пространствами. Из различных доступных моделей нейронной сети, для реализации цифрового расходомера использовались сети на основе многоуровневого перцептрона (MLP) и радиальных базисных функций (RBF). MLP с одним скрытым уровнем (каждый блок имеет сигмоидальную функцию активации) может одинаково хорошо аппроксимировать любое непрерывное отображение.
В одном примере, цифровой расходомер 6200 может обрабатывать поток, про который известно, что он является трехфазной текучей средой. Например, трехфазный поток может быть, в основном, природным газом, с жидкостной составляющей, которая включает в себя смесь нефти и воды. В других примерах, такой же или аналогичный способ можно применять к двухфазной текучей среде или текучей среде, содержащей более трех составляющих в смешанной текучей среде.
В частности, действие трубки Вентури поддержано в трехфазном потоке. Основные измерения частоты и фазы, амплитуды и коэффициенты усиления возбуждения датчиков получаются из сигналов датчиков и необходимого тока. Основные измерения используются, с использованием любых доступных внешних входов и информации, зависящей от способа или применения, для генерации оценок текучей среды в целом и многокомпонентного массового и объемного расходов.
Например, оценки текучей среды в целом и многокомпонентного массового и объемного расходов могут генерироваться следующим образом. Оценки частоты, фазы и/или амплитуды можно улучшить с использованием известных корреляций между значениями, например, скорость изменения амплитудной коррекции. Необработанные оценки массового расхода и плотности смеси можно получить из наилучших оценок частоты, фазы, температуры трубки Вентури и калибровочных постоянных. Простая линейная коррекция применяется к измерению плотности для наблюдаемого давления текучей среды. В некоторых реализациях, наблюдаемое давление текучей среды можно получить из внешнего входа. Поскольку давление расширяет и усиливает трубку Вентури, что может привести к ошибке в необработанной плотности, простое переменное смещение может хорошо работать, если плотности газа, ожидаемые в повторяемом способе или смешанной текучей среде, в то время, как более полная коррекция может включать в себя дополнительные члены для переменной плотности текучей среды, если изменения в концентрациях жидкостной и/или газовой составляющей предусмотрены в способе. Передатчик может включать в себя параметры конфигурации, задающие ожидаемые плотности жидкости (с температурной компенсаций) и опорную плотность газа.
В трехфазной смеси текучей среды, фиксированную обводненность (WC) можно предполагать или можно измерять. Обводненность определяется как доля воды в смеси. Температура текучей среды измеряется для вычисления оценки истинной плотности текучей среды (D1) из обводненности и плотности чистой нефти (Doil) и плотности воды (Dwater). Оценка истинной плотности текучей среды учитывает известное изменение Doil и Dwater в зависимости от температуры текучей среды и давления текучей среды.
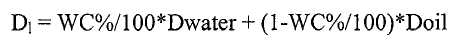
Предусмотрена модель (на основании, например, модели идеального газа) для изменения плотности газа (Dg) в зависимости от наблюдаемого давления текучей среды и температуры текучей среды, которые можно получить из внешних входов, и необработанная объемная доля жидкости (raw_LVF) из необработанной плотности смеси (raw_Dm) вычисляется с использованием
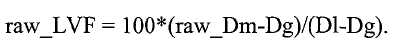
Необработанные объемные расходы смеси из необработанной смеси вычисляются с использованием
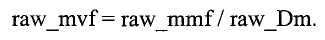
Нейронная сеть, обученная с помощью экспериментальных данных, используется для генерации скорректированных оценок необработанной объемной доли жидкости и необработанных объемных расходов, как показано ниже. В нижеприведенных уравнениях, переменная "nnfunction" представляет нейронную сеть.

Необработанная объемная доля жидкости (raw_LVF) равна 100 - объемная доля газа (GVF). Дополнительно, необработанная объемная доля жидкости тесно связана со спадом плотности. Необработанный объемный расход можно масштабировать как скорость, например, в рамках того же подхода, нейронные сети можно комбинировать, но можно использовать разные вводы.
Расходы жидкости и газа вычисляются с использованием следующих соотношений:
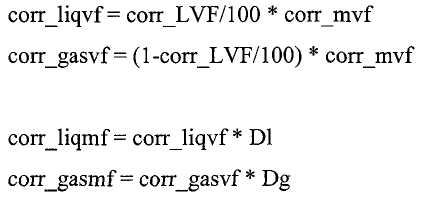
Измеритель обводненности можно использовать для обеспечения измерения, используемого в качестве дополнительного ввода в нейронную(ые) сеть(и), и для помощи в точном разделении потока жидкости на составные части. Для помощи в точном разделении потока жидкости, можно использовать следующие соотношения:
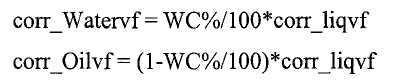
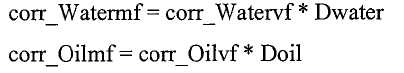
Альтернативно или дополнительно, можно определить наблюдаемые газовое и негазовое числа Фруда, скорректированные с использованием нейронной сети, и затем использовать их при определении массовых расходов компонентов многофазной текучей среды. Например, газовое число Фруда можно определить на основании следующего уравнения, где m a g - наблюдаемый массовый расход газа, ρg - оценка плотности газовой фазы многофазной текучей среды на основании законов идеального газа, ρl - оценка плотности жидкости в негазовой фазе многофазной текучей среды, A - площадь поперечного сечения трубки Вентури, D - диаметр трубки Вентури и g - ускорение свободного падения. Наблюдаемый массовый расход газа является функцией известной или предполагаемой плотности компонентов в многофазном потоке, наблюдаемой плотности многофазной текучей среды (наблюдаемой совокупной плотности) и наблюдаемого массового расхода многофазной текучей среды (наблюдаемого совокупного массового расхода).
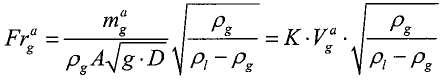 ,
,
где 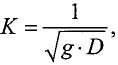 наблюдаемая скорость газа
наблюдаемая скорость газа 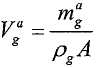
Аналогично, наблюдаемое негазовое число Фруда (которое может быть жидкостным числом Фруда) можно вычислять с использованием следующего уравнения, где m a l - наблюдаемый массовый расход жидкости, K - постоянная, заданная выше согласно газовому числу Фруда, и V a l - наблюдаемая скорость жидкости, определяемая аналогично наблюдаемой скорости газа, как показано выше:
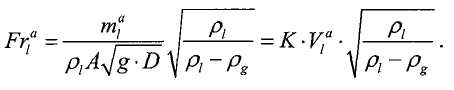
Наблюдаемые газовое и негазовое числа Фруда затем корректируются с использованием нейронной сети:
Скорректированное газовое число Фруда = nnflinction (наблюдаемое газовое число Фруда, наблюдаемое негазовое число Фруда)
Скорректированное негазовое число Фруда = nnflinction (наблюдаемое газовое число Фруда, наблюдаемое негазовое число Фруда)
Определив скорректированные газовое и негазовое числа Фруда, можно определить массовый расход для газового и негазового компонентов многофазной текучей среды. В частности, после получения скорректированных значений газового и негазового чисел Фруда, значения всех параметров для негазовых и газовых компонентов многофазной текучей среды, кроме массового расхода известны. Таким образом, скорректированный массовый расход негазовых и газовых компонентов многофазной текучей среды можно определить на основании вышеприведенных уравнений, которые используются для определения наблюдаемых чисел Фруда.
Дополнительно, как и в реализации с использованием объемной доли жидкости и объемного расхода в качестве входных сигналов нейронной сети, измеритель обводненности можно использовать в помощь разделению многофазной текучей среды на составные части. Например, измеритель обводненности может обеспечивать обводненность (WC) многофазной текучей среды, которая указывает долю воды в многофазной текучей среде, и WC можно использовать в помощь разделению многофазной текучей среды на составные части с использованием следующих уравнений:
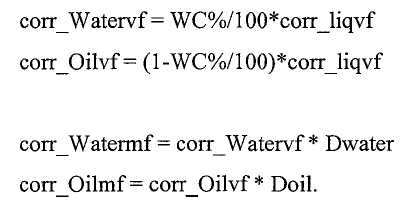
Как рассмотрено согласно фиг.59, в ряде случаев, нейронная сеть может вырабатывать более точные поправки наблюдаемых газового и негазового чисел Фруда, чем других наблюдаемых промежуточных значений. Таким образом, использование наблюдаемых газового и негазового чисел Фруда в качестве входов в нейронную сеть может давать более точное определение свойств компонентов потока, образующих многофазную текучую среду.
Вышеприведенное описание обеспечивает обзор различных цифровых кориолисовых массовых расходомеров, описывающий предпосылки, реализацию, примеры их работы и сравнение с предыдущими аналоговыми контроллерами и передатчиками. Было получено несколько усовершенствований по сравнению с аналоговым контроллером в отношении производительности, включающие в себя: высокоточное управление действием трубки Вентури, даже при работе на очень низких амплитудах; поддержание действия трубки Вентури даже в условиях сильного затухания; высокую точность и высокую скорость измерения; компенсацию динамических изменений амплитуды; компенсацию двухфазного потока и дозирование в/из пустого состояния. Это сочетание преимуществ предполагает, что цифровой массовый расходомер представляет значительный шаг вперед, а не просто постепенная эволюция аналоговой технологии. Способность работать с двухфазным потоком и внешней вибрацией означает, что цифровой массовый расходомер 100 дает повышенную производительность в традиционных кориолисовых приложениях, в то же время расширяя диапазон применений, к которым можно применять потоковую технологию. Цифровая платформа также является полезным и гибким средством для осуществления исследований путем кориолисова измерения, поскольку она дает высокие точность, вычислительную мощность и скорости передачи данных.
Дополнительное применение цифрового расходомера 6200 к трехфазной текучей среде, например, влажному газу, содержащему газовый (метан) и жидкостный компонент (нефть и воду), описано и показано со ссылкой на фиг.62-72. На фиг.62 показано графическое представление таблицы испытаний для устий скважины, испытываемых на основании фактических испытаний при различных давлениях в скважине и скоростях газа. На фиг.62 показано графическое представление необработанных ошибок плотности при различных процентах жидкостной пустотной доли и для скважин при различных скоростях и давлениях. На фиг.64 показано графическое представление необработанных ошибок массового расхода при различных процентах жидкостной пустотной доли и для скважин при различных скоростях и давлениях. На фиг.65 показано графическое представление необработанной жидкостной пустотной доли ошибки для скважин при различных скоростях и давлениях. На фиг.66 показано графическое представление необработанного объемного расхода ошибки для скважин при различных скоростях и давлениях. На фиг.67 показано графическое представление скорректированных жидкостных пустотных долей для скважин при различных скоростях и давлениях. На фиг.68 показано графическое представление скорректированного объемного расхода смеси для скважин при различных скоростях и давлениях. На фиг.69 показано графическое представление скорректированного массового расхода газа для скважин при различных скоростях и давлениях. На фиг.70 показано графическое представление скорректированной интегральной вероятности газа испытуемого цифрового расходомера. На фиг.71 показано графическое представление скорректированной ошибки массового расхода жидкости для скважин при различных скоростях и давлениях. На фиг.72 показано графическое представление скорректированной интегральной вероятности газа испытуемого цифрового расходомера.
Согласно фиг.62-72, тестовые испытания на влажном газе, содержащем воду и воздух, охватывают параметры испытательной скважины для разнообразных измерителей. Охваченные точки объемного расхода жидкостной фракции (LVF = 100% - GVF), включают в себя: 0,0; 0,2; 0,4; 0,6; 0,8; 1,0; 1,5; 2,0; 3,0; 4,0; 5,0%. В отношении обнаруженных ошибок массового расхода и плотности, ошибки массового расхода и плотности газожидкостной смеси, предположительно, без объёмного содержания жидкости, статический миксер для управления стабильного профиля потока в условиях эксплуатации и положительные ошибки плотности вследствие объёмного содержания жидкости в измерителе. Положительные ошибки плотности вследствие объемного содержания жидкости в измерителе максимальны при низких расходах и при низких плотностях газа. Отрицательные ошибки массового расхода аналогичны откликам двухфазного кориолисова измерителя.
Применимые стратегии моделирования используют наблюдаемый массовый расход и наблюдаемую плотность для применения коэффициентов коррекции или аппроксимацию кривой для собранных данных для создания реальных измерений, например, измерения плотности в реальной плотности. Однако широкий диапазон плотности газа, например 175-900 psi (12-62 бар), способствует также дополнительным подходам. Например, были идентифицированы альтернативные параметры, включающие в себя параметры модели, которые включают в себя два основных параметра ошибок. В частности, объемный расход смеси (предположительно, без скольжения между фазами) - на основании отношения масса/плотность и объемной доли жидкости (LVF), т.е. 100% - GVF. Поправки для каждого из них обеспечиваются с использованием их необработанных значений и дополнительных данных давления (только). На основании скорректированных значений LVF и объемного расхода, массовые расходы газового и жидкостного компонентов можно вычислить следующим образом:
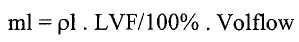
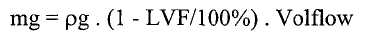
Результирующие ошибки показаны на фиг.69-72. Модель охватывает широкий диапазон условий, включающий в себя различные давления и расходы. Более ограниченный набор условий может обеспечивать улучшенные результаты, например, более высокое давление, приводящее к меньшим необработанным ошибкам, "естественному" рабочему диапазону для измерителя, очень высоким перепадам давления с высокими LVF и скоростью и/или необходимости в анализе калибровки измерителя для влажного газа.
Модель можно расширить или модифицировать так, чтобы основные "поправки" давления, которые могут включать в себя подгонку необработанных данных посредством аппроксимации кривой к непосредственно выводимым фактическим измерениям, например, без истинного коэффициента коррекции, и применяются к плотности до применения к нейронной сети. Текущие входы зависят от текучей среды, например, объемный расход зависит от фактической плотности текучей среды. Размерность входов можно уменьшить, например, путем преобразования объемного расхода в скорость, затем выразить скорость как процент от максимальной скорости, на которой может работать трубопровод, с последующей нормализацией данных для определения составляющих. Рабочие давления могут включать в себя давление потока 60 бар, с перепадом 2-3 бар, и будут поддерживать более высокие рабочие давления в диапазоне от 150 psi (10,34 бар) до 1000 psi (68,94 бар). Испытания калибровки детальной модели, приведенные на фиг.62-72, используют природный газ в диапазоне приблизительно 375 psi (25,86 бар) от устья скважины. Калибровку трубки Вентури также можно определять на основании перепада давления.
R. Текст исходного кода
Следующий исходный код, который настоящим включен в эту заявку, используется для реализации процедуры обработки массового расхода в соответствии с одной реализацией расходомера. Очевидно, что можно реализовать процедуру обработки массового расхода с использованием другого компьютерного кода, не отклоняясь от объема описанных методов. Таким образом, ни вышеприведенное описание, ни следующий текст исходного кода не призваны ограничивать описанные методы.
Текст исходного кода

/* вычисление массового расхода в безразмерных единицах */
/* преобразование к техническим единицам */

/* применение коррекции двухфазного потока при необходимости */
/* вызов нейронной сети для вычисления коррекции массового расхода */
t = VMV_temp_stats.mean; // средняя температура VMV
x = RMV_dens_stats.mean; // средняя плотность RMV
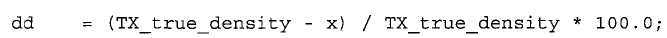
m = RMV_mass_stats.mean; // средний массовый расход RMV;
g = коэффициент усиления_stats.mean; // средний коэффициент усиления;

S. Примечание относительно авторских прав
Часть раскрытия этого патентного документа содержит материал, подлежащий защите авторских прав. Владелец авторских прав не возражает против факсимильного воспроизведения патентного документа или раскрытия патента, когда он имеет вид файла или записей патента в Патентном ведомстве США, но в противном случае сохраняет за собой все авторские права.
Другие реализации находятся в объеме нижеприведенной формулы изобретения.
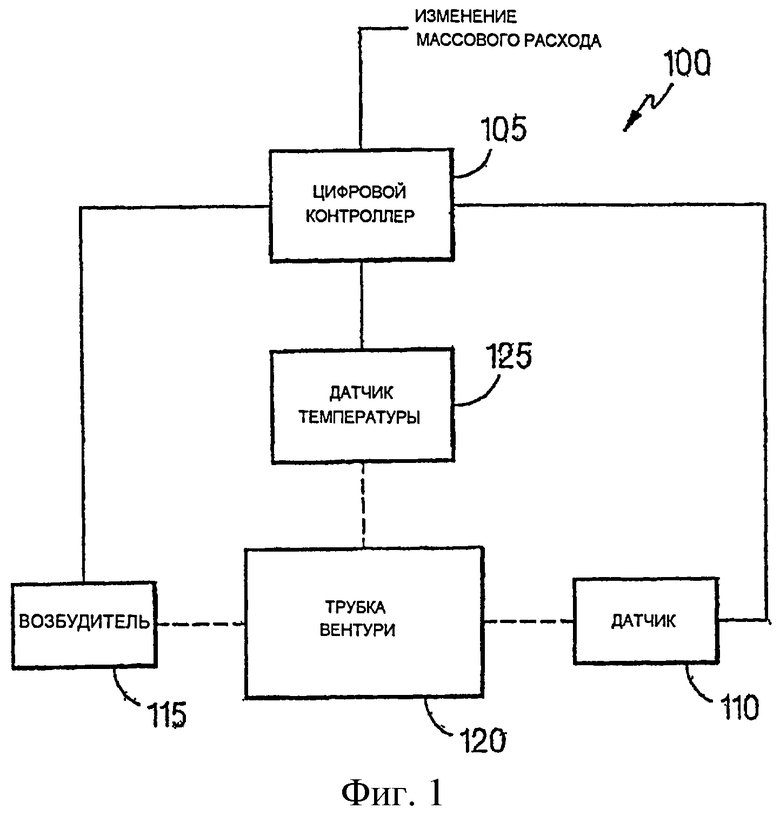
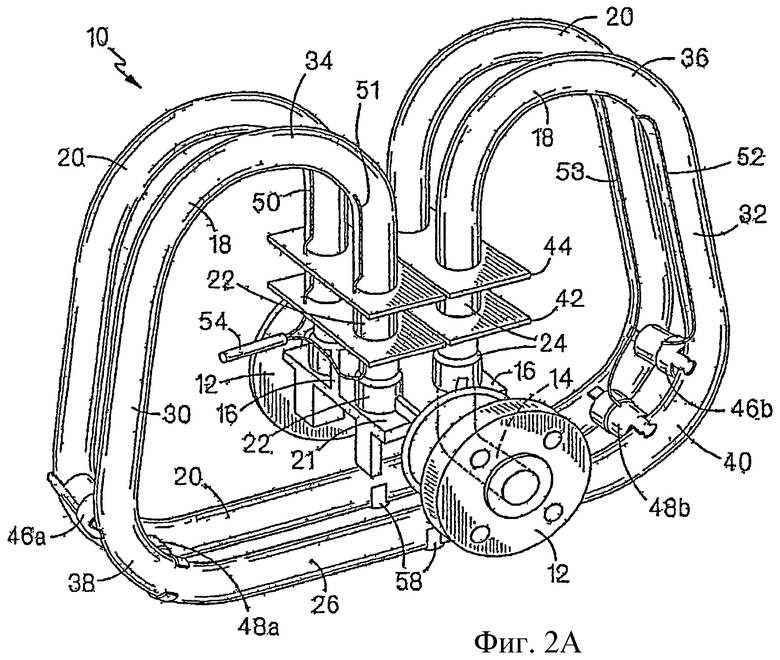

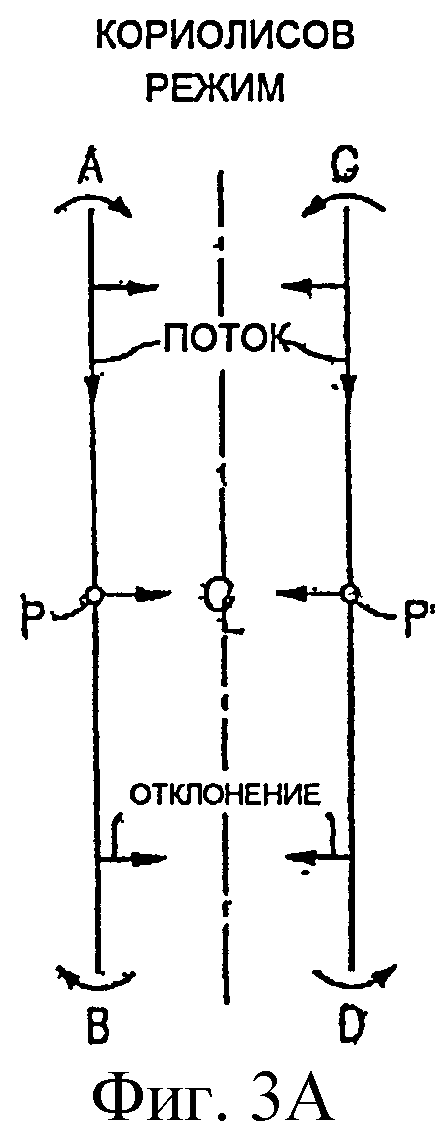

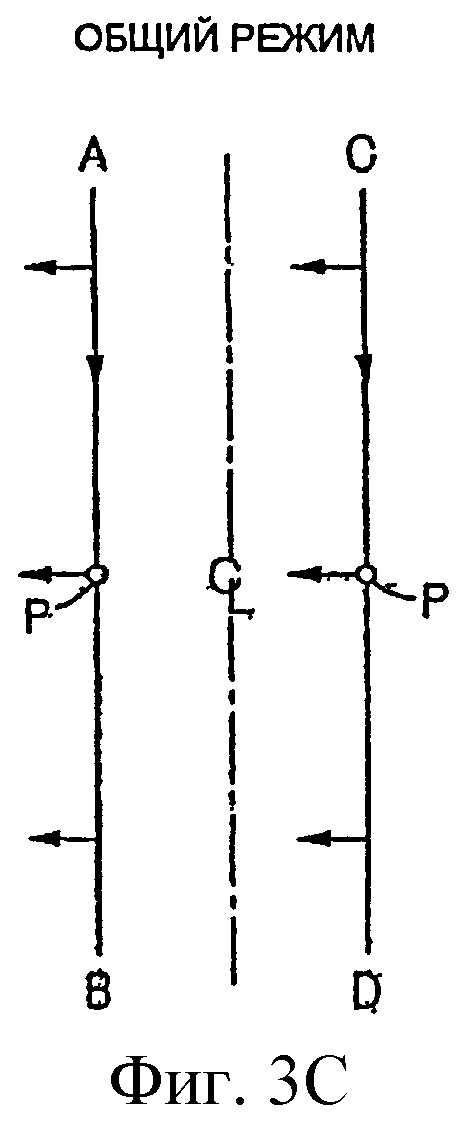
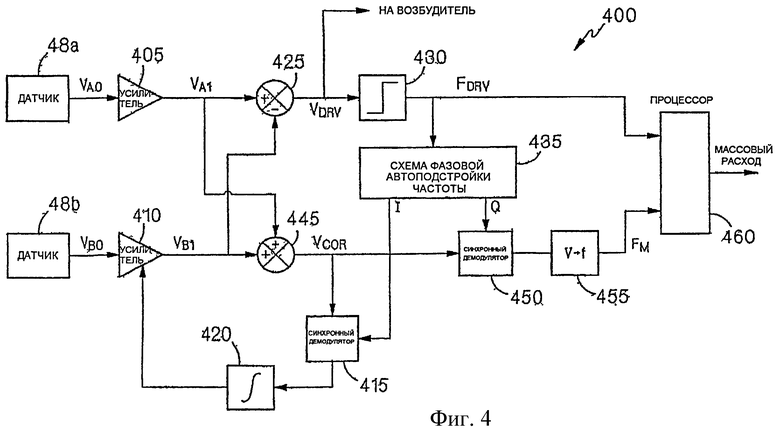
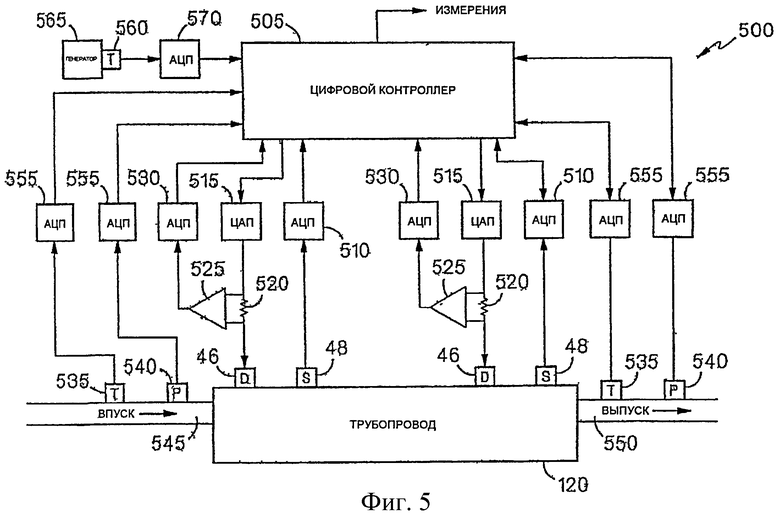
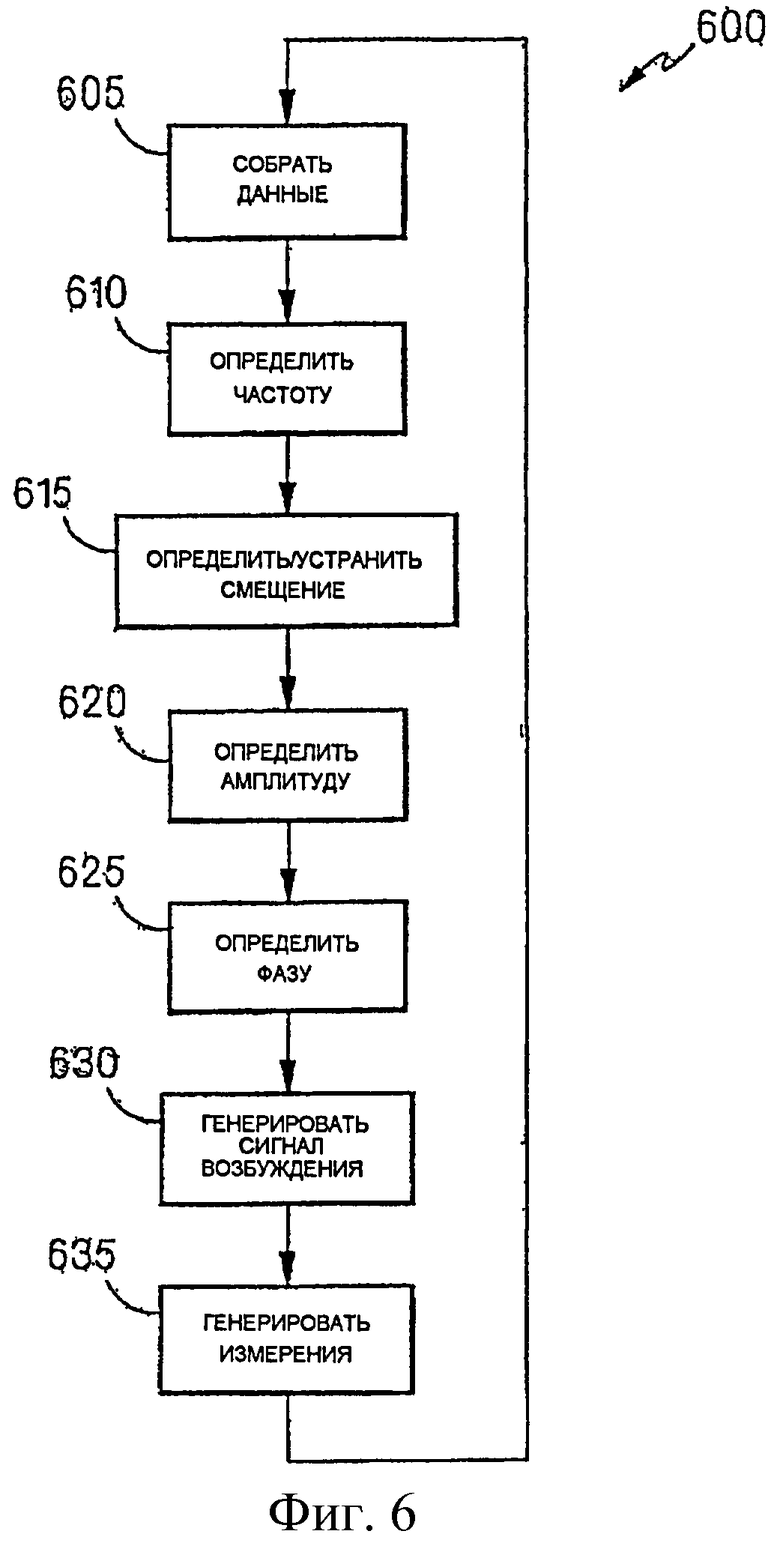
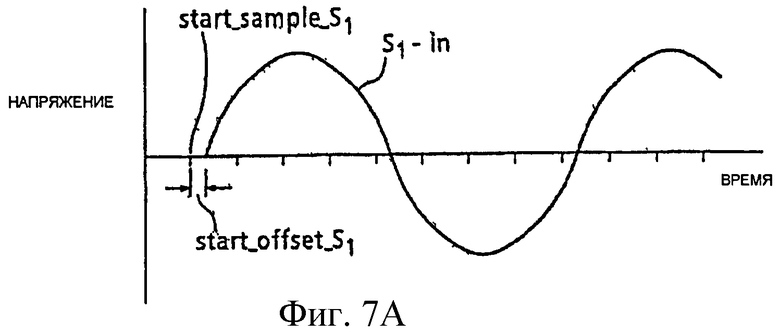
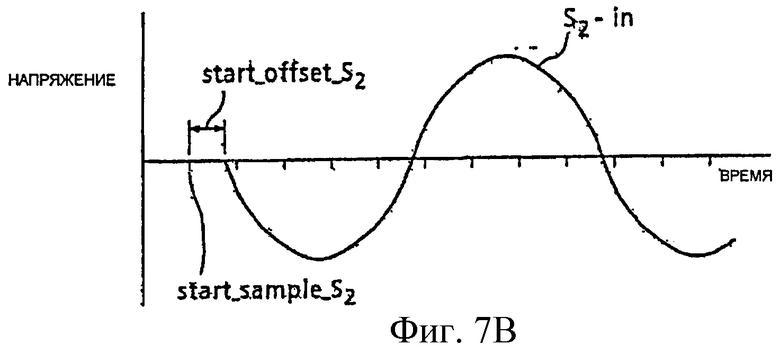
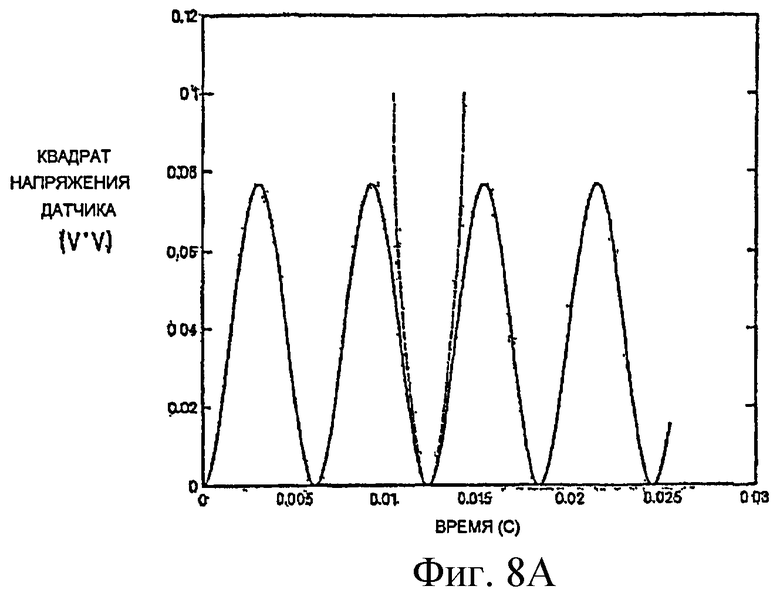
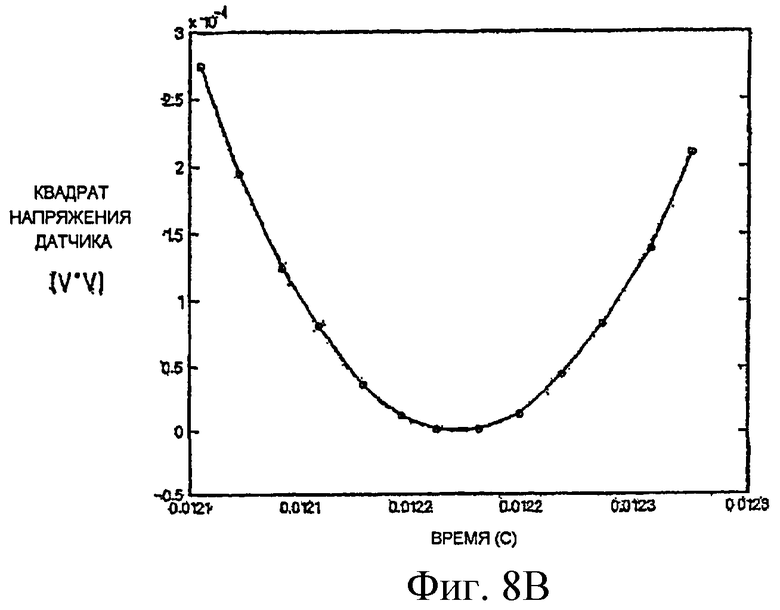
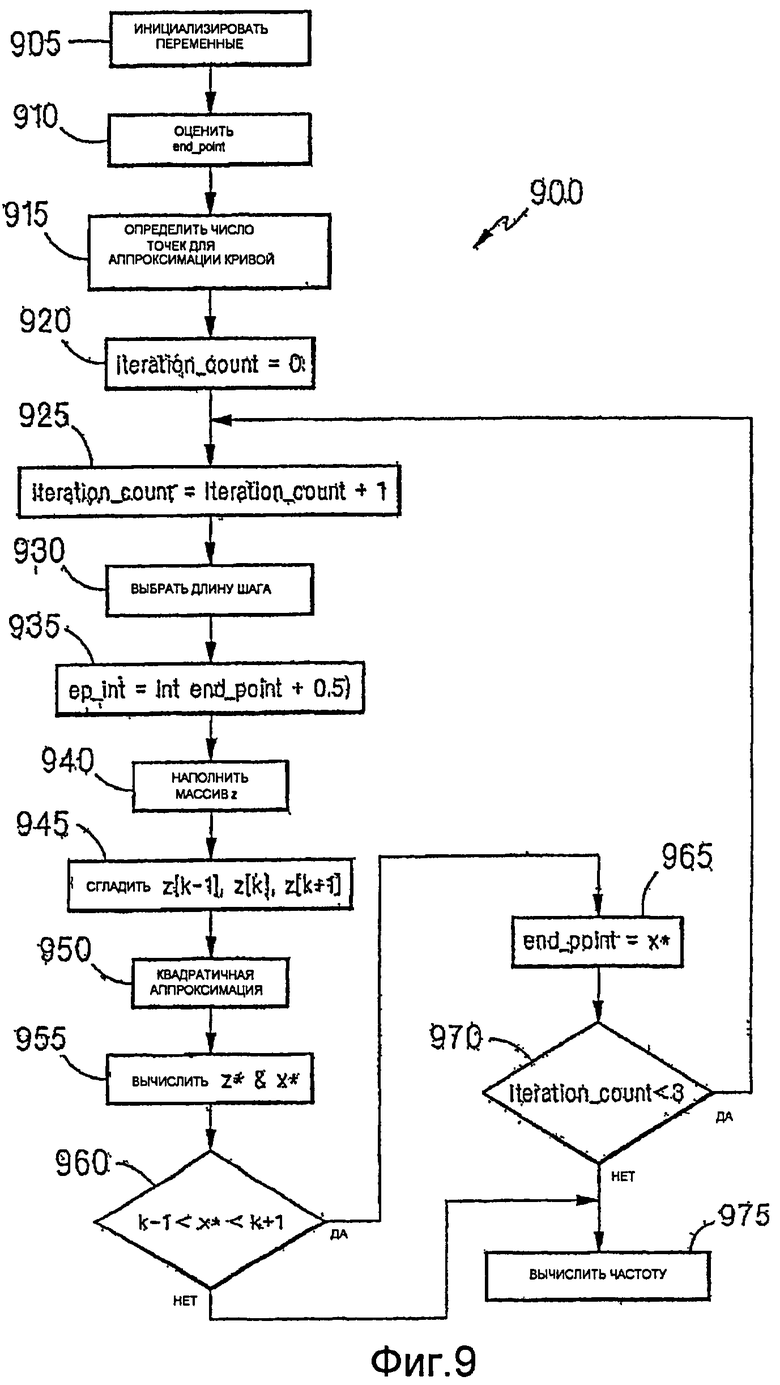
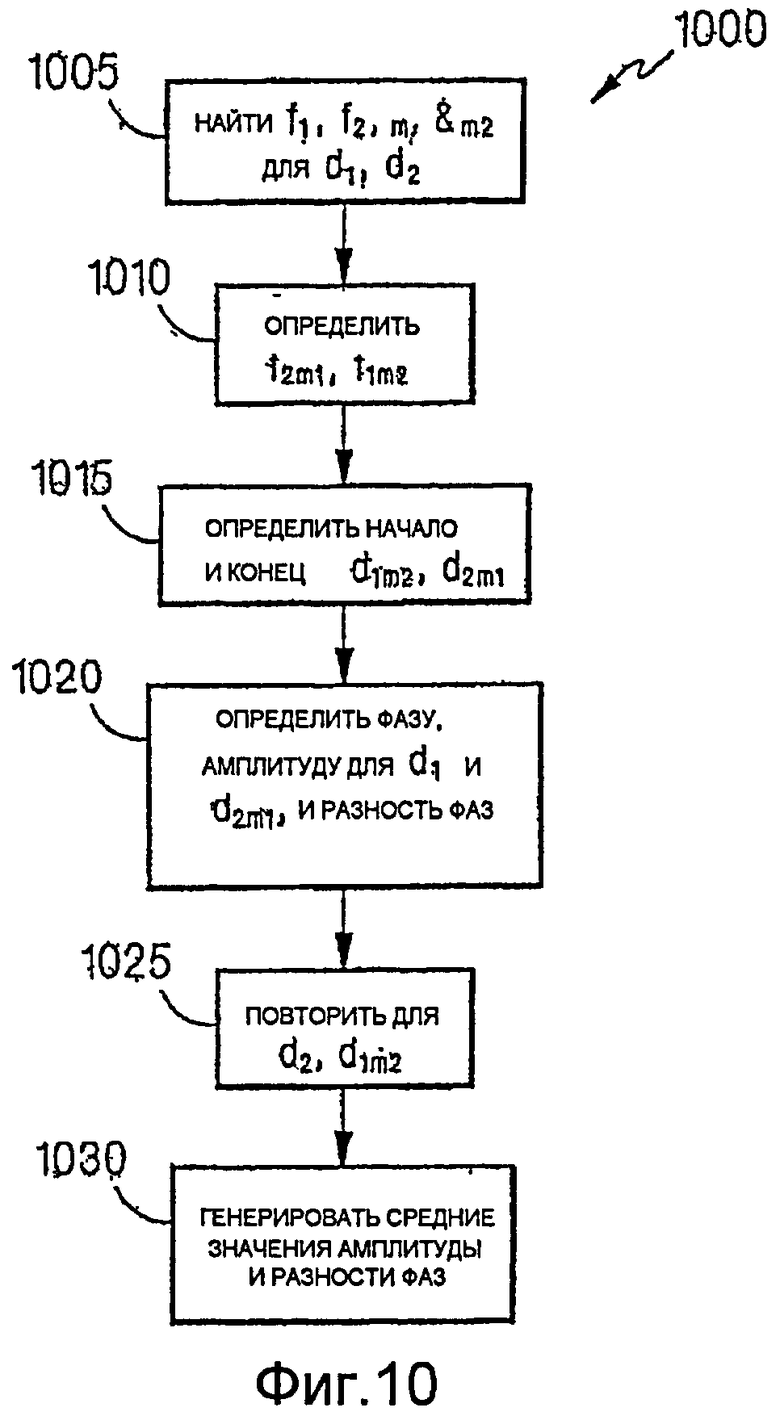

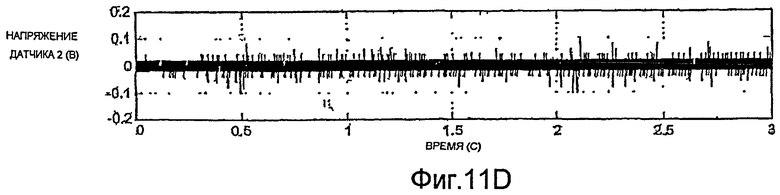

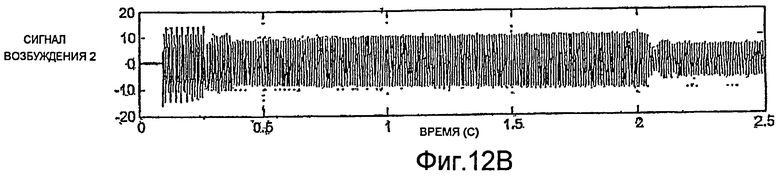
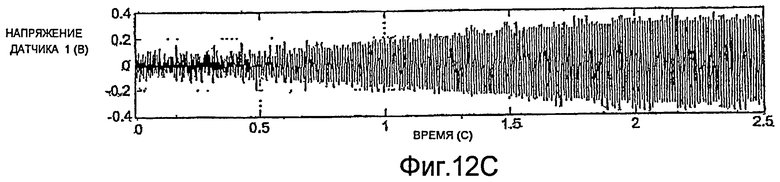
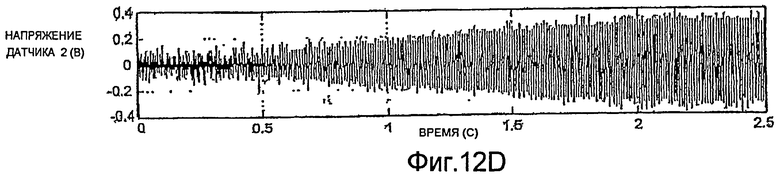
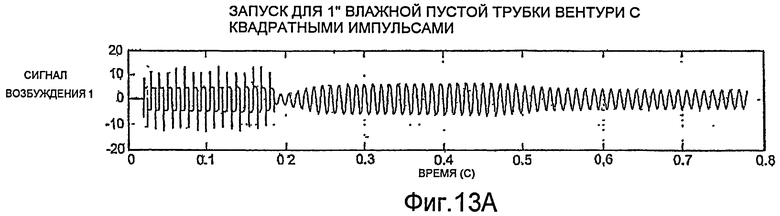
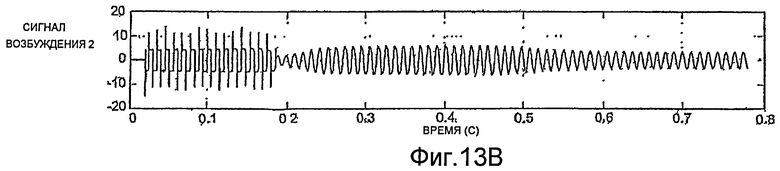
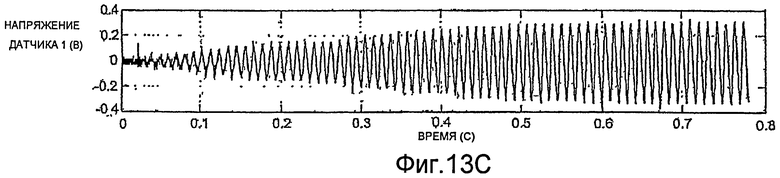
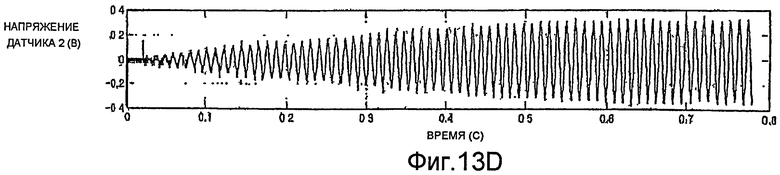
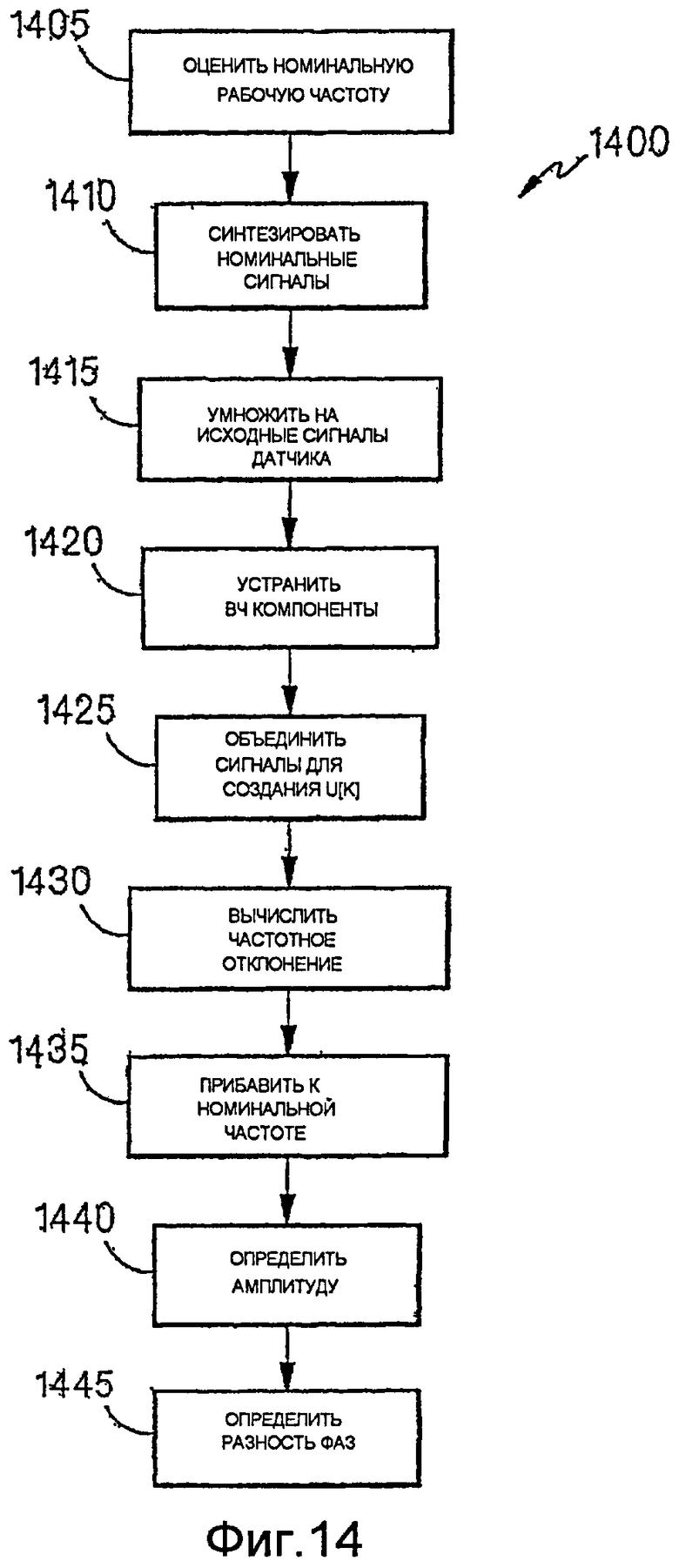
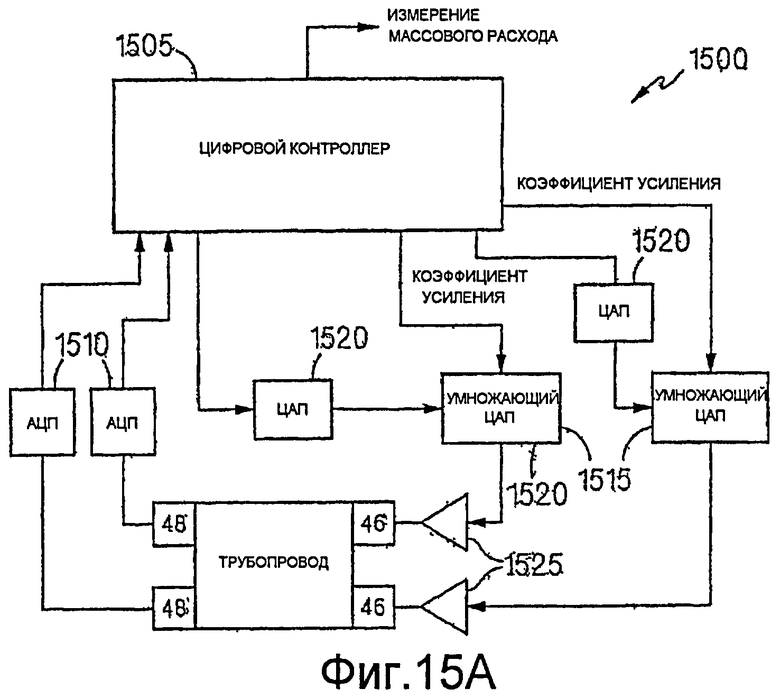
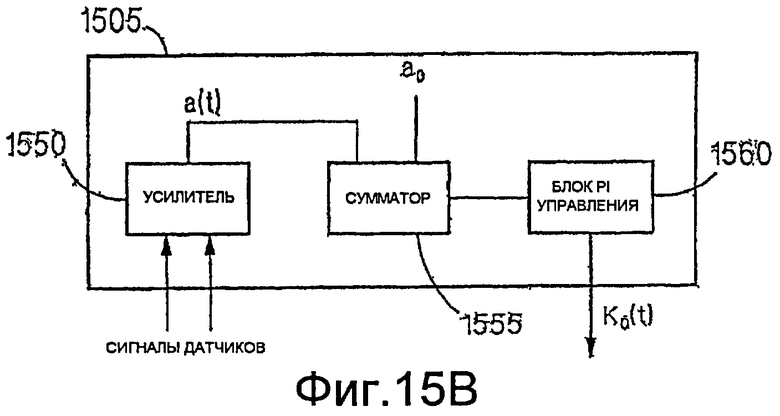
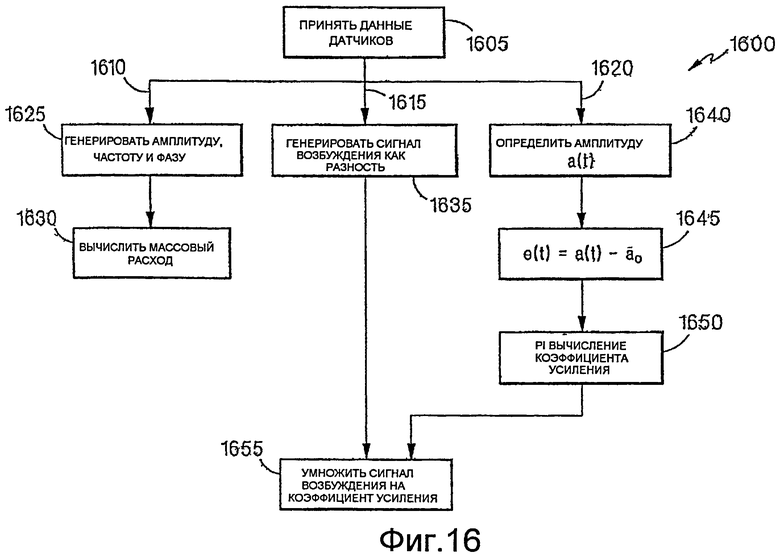
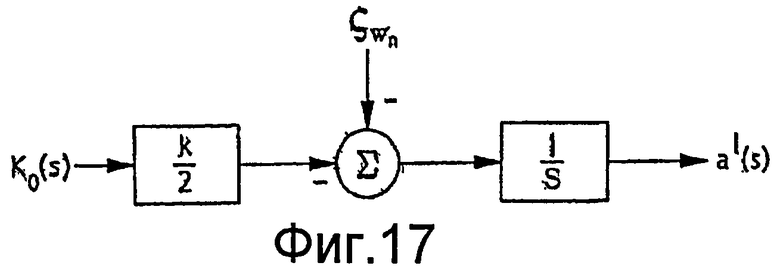
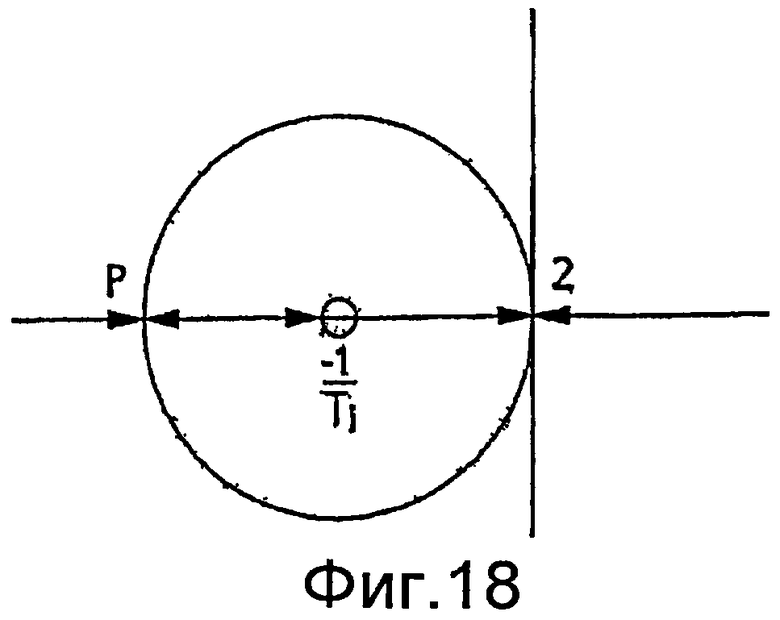
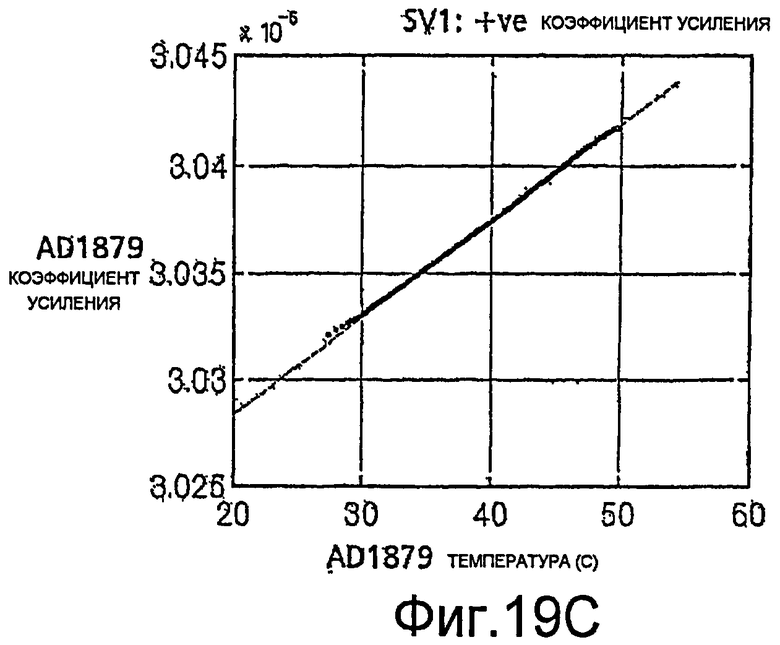
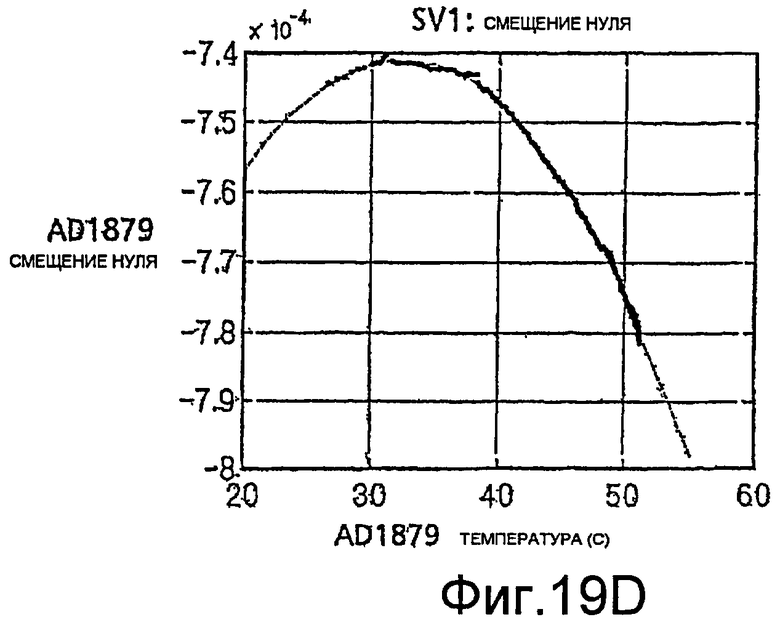
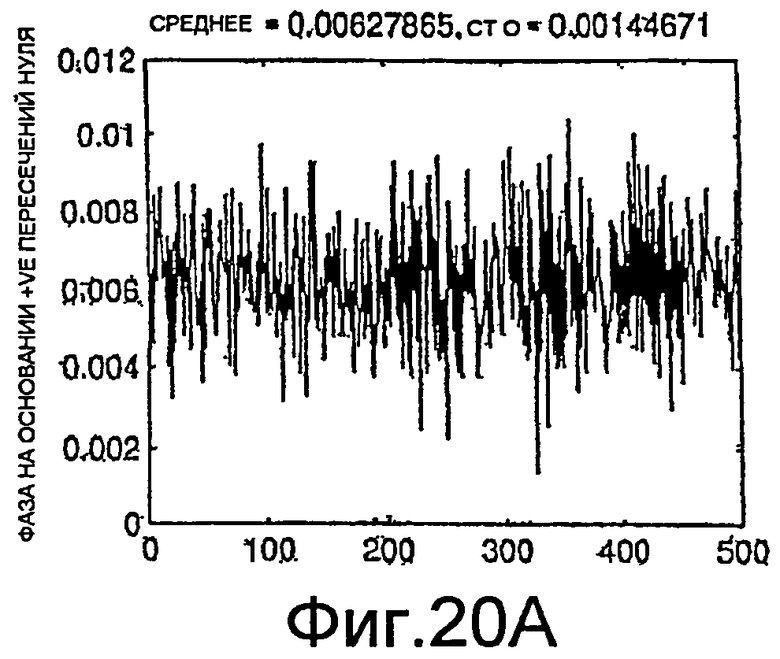
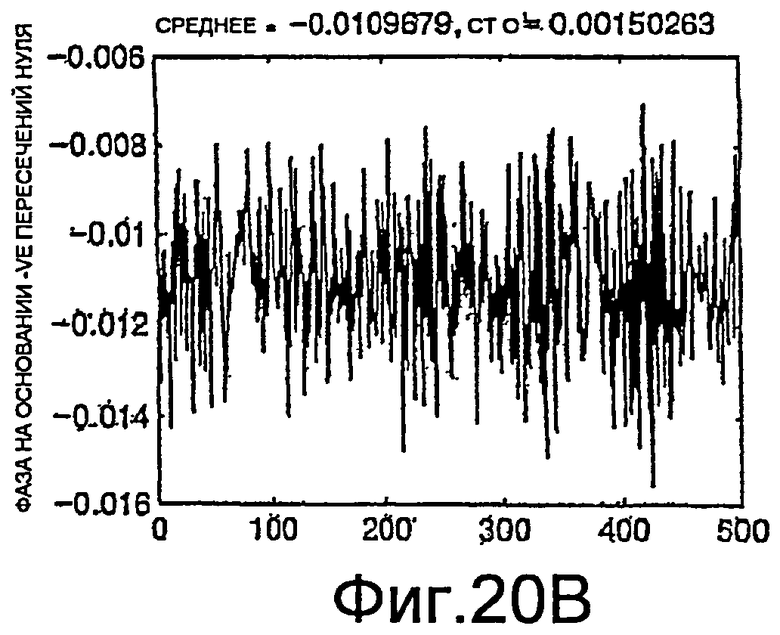
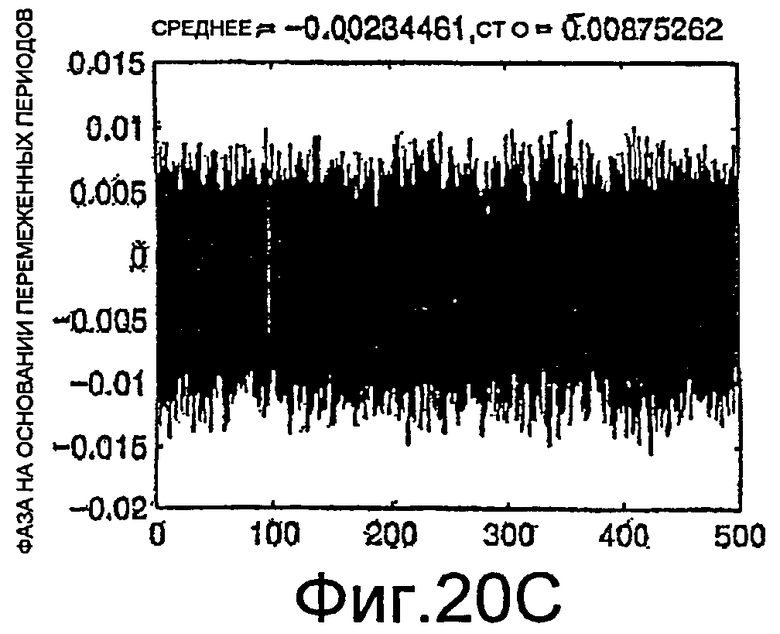
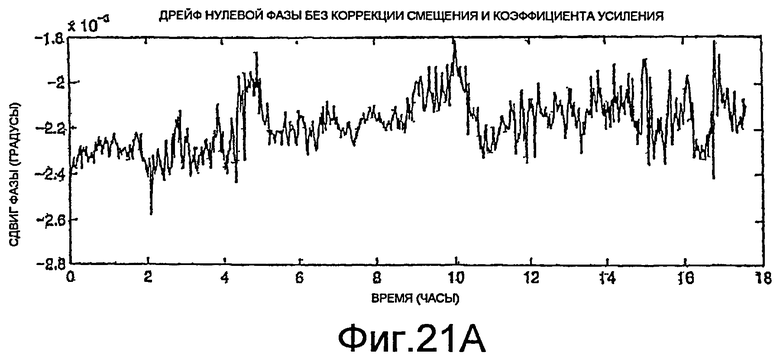
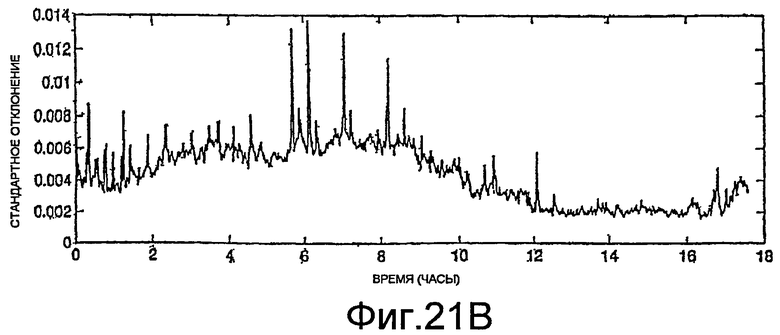
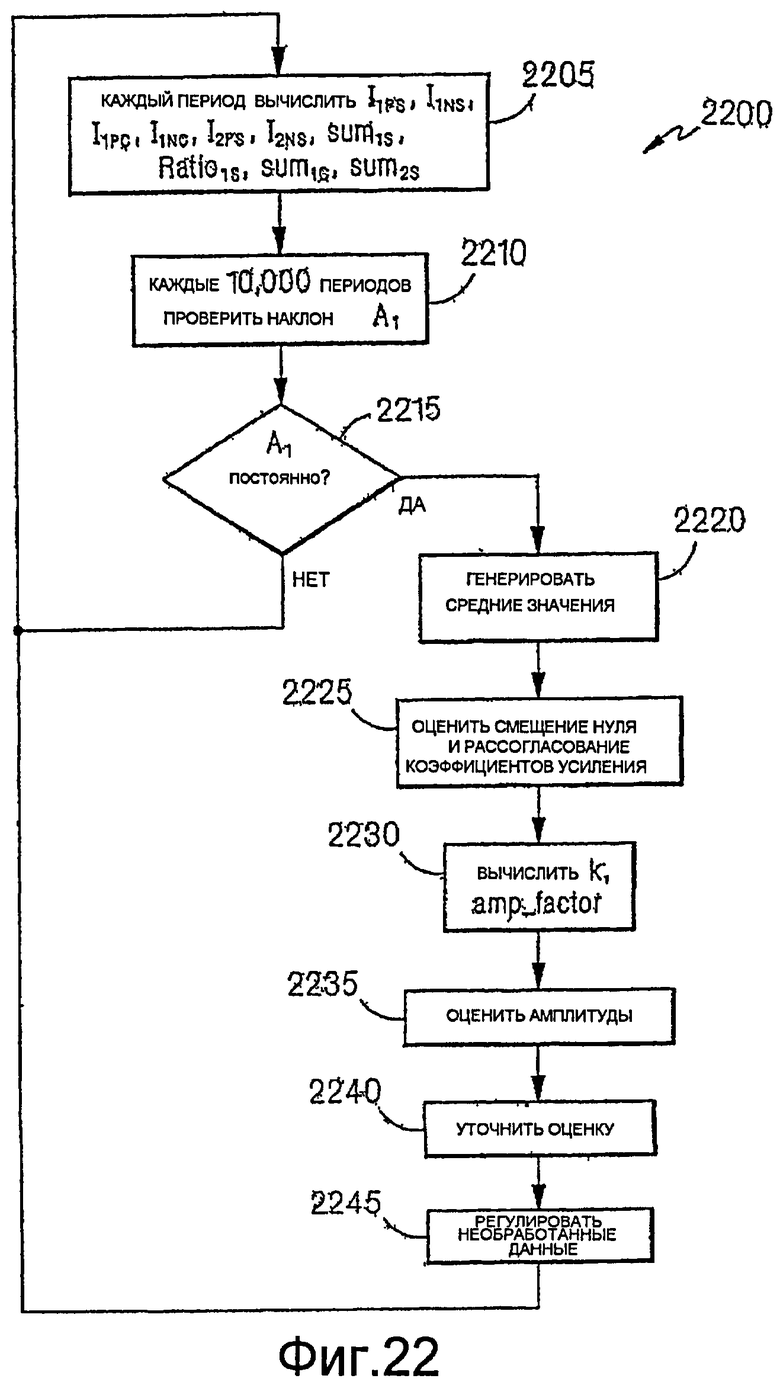
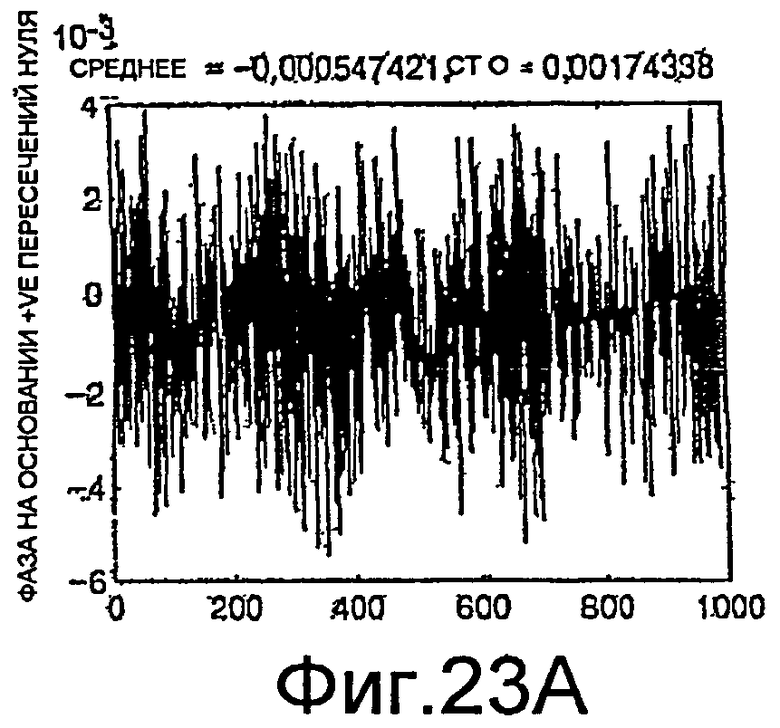
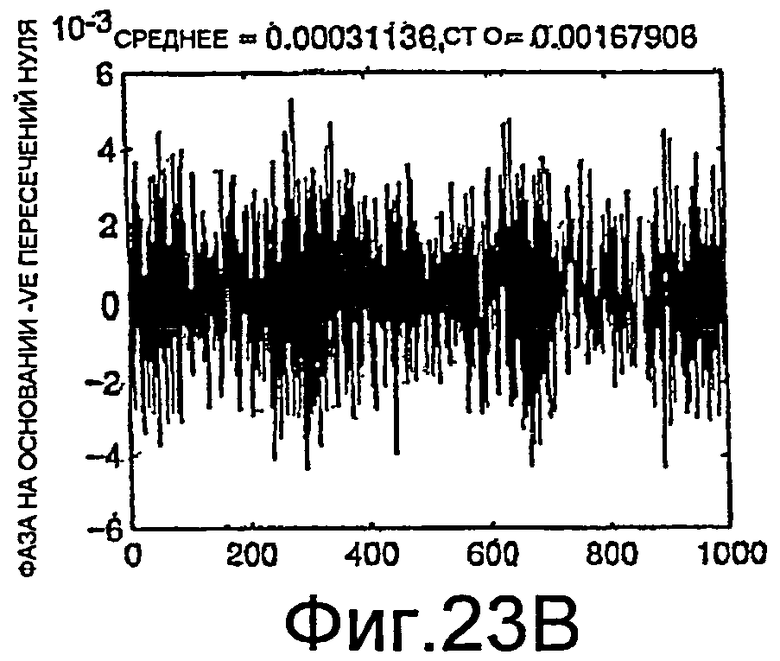
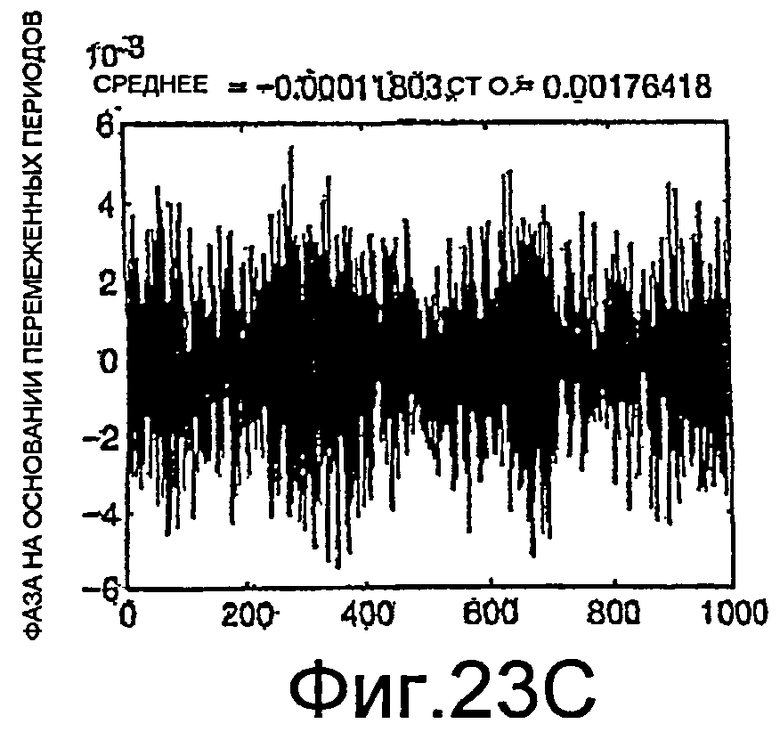
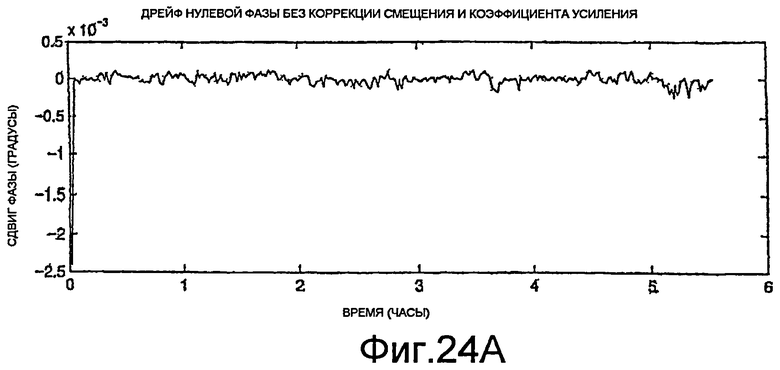
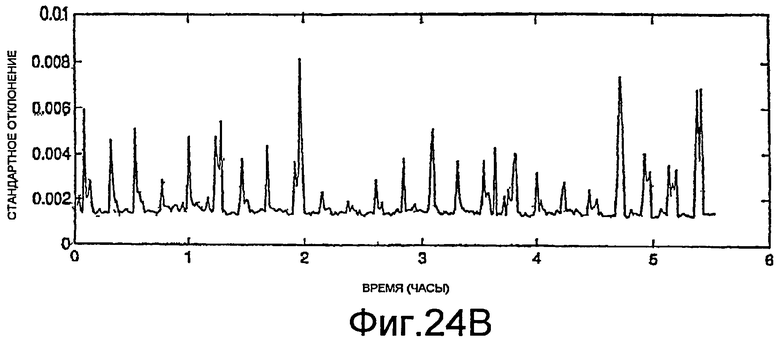
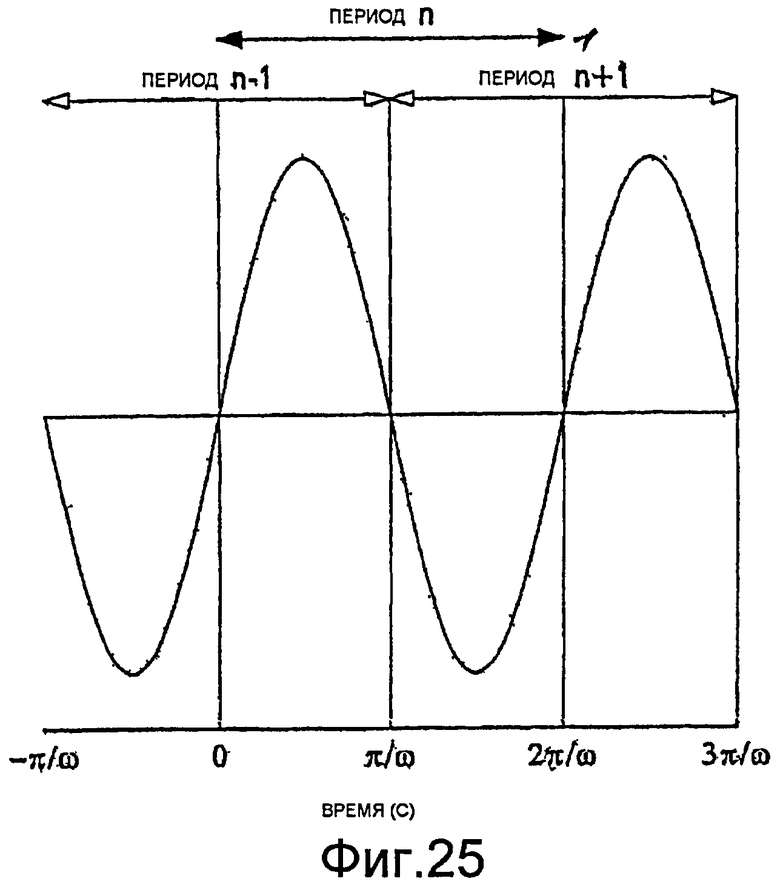
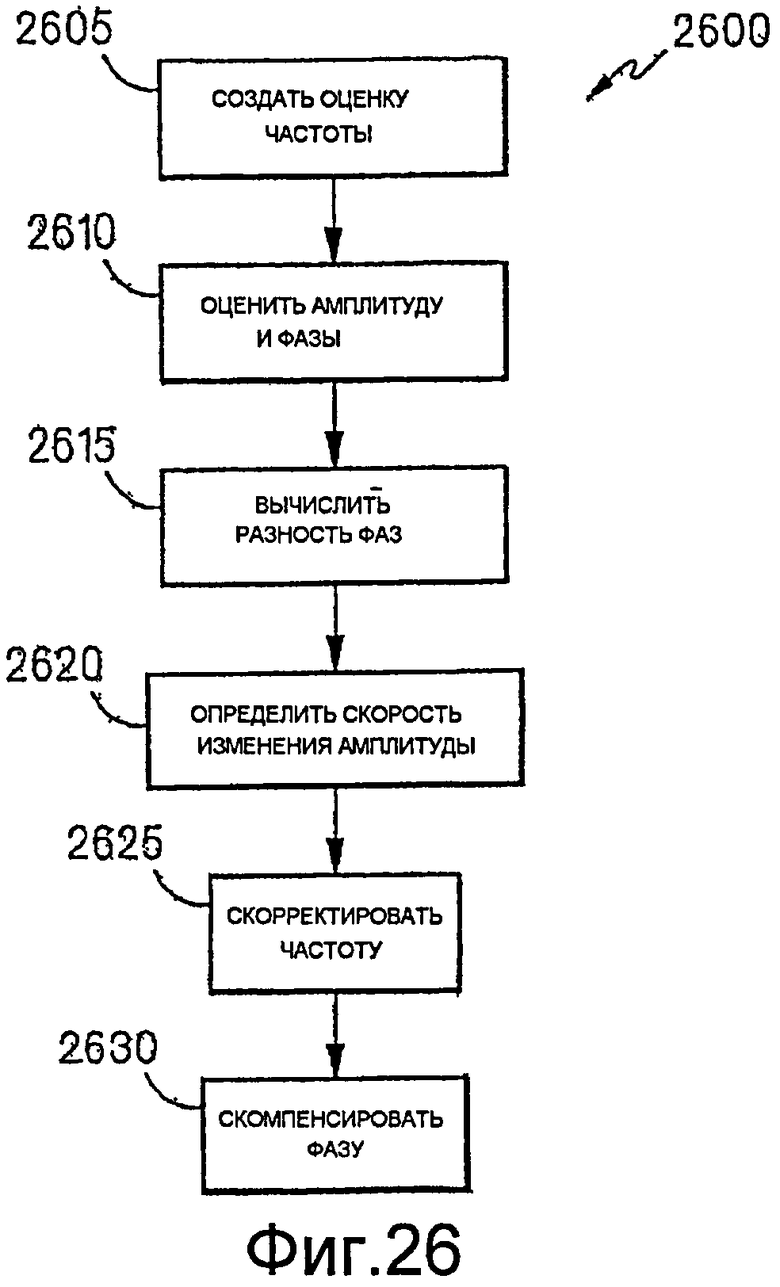
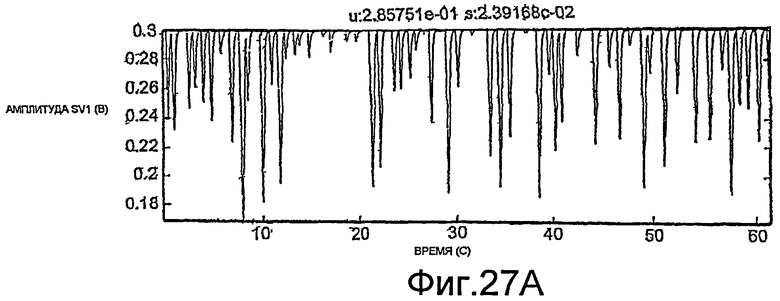
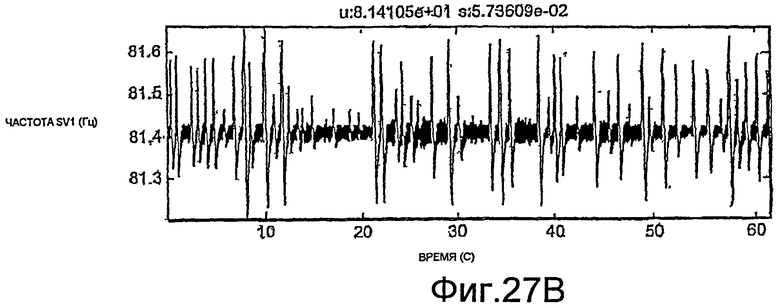
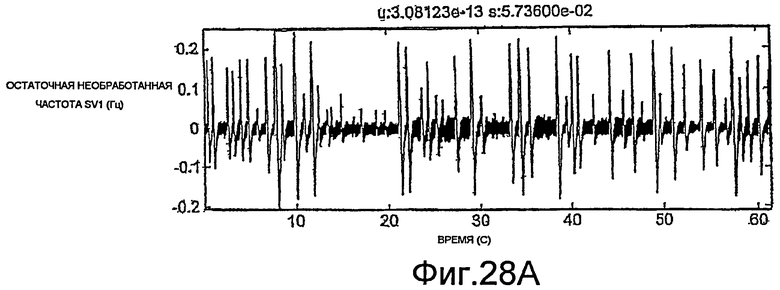
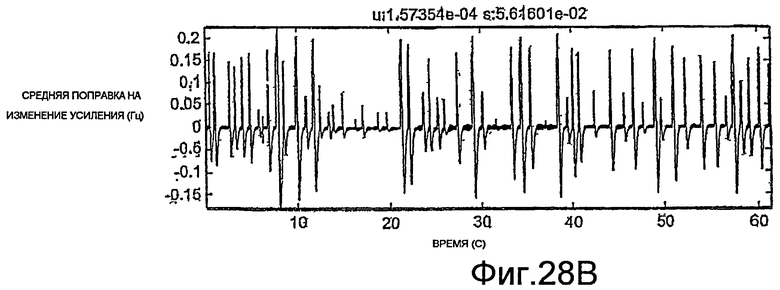
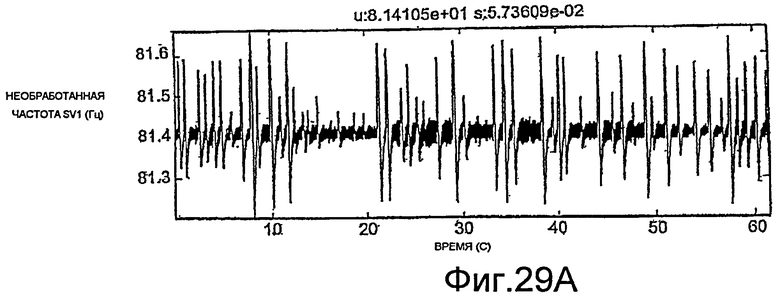
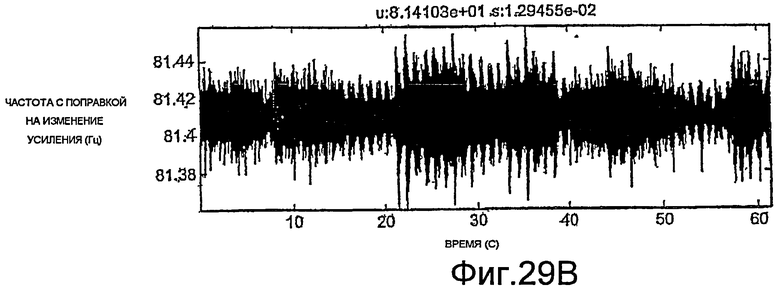
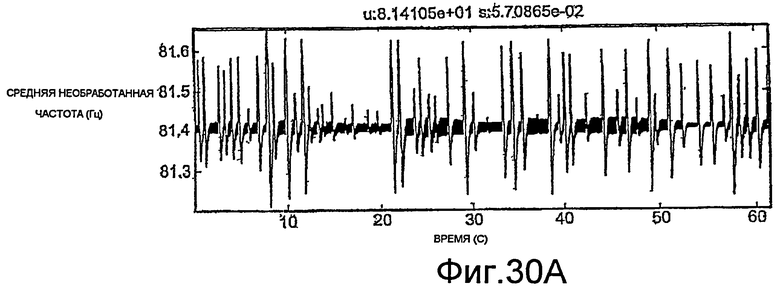
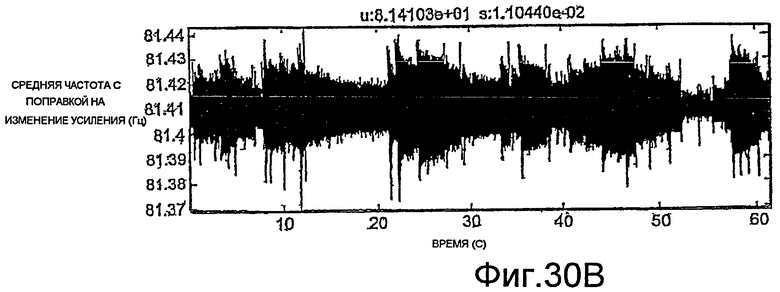
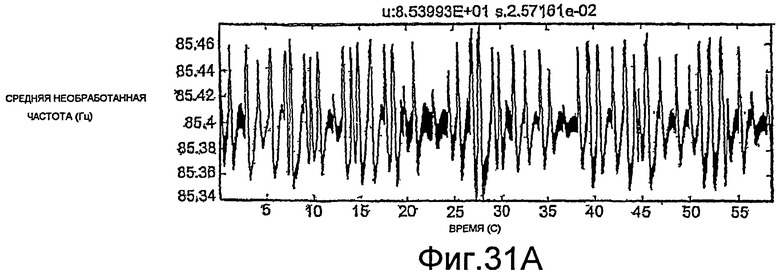
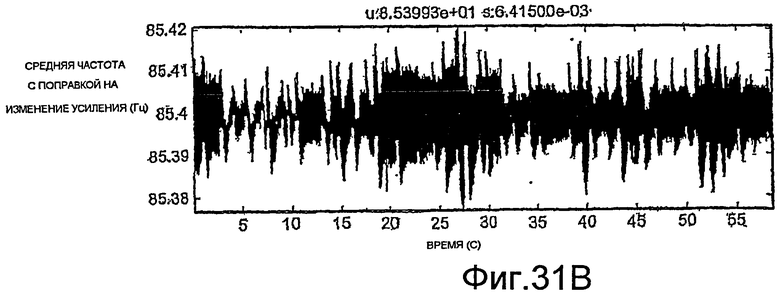
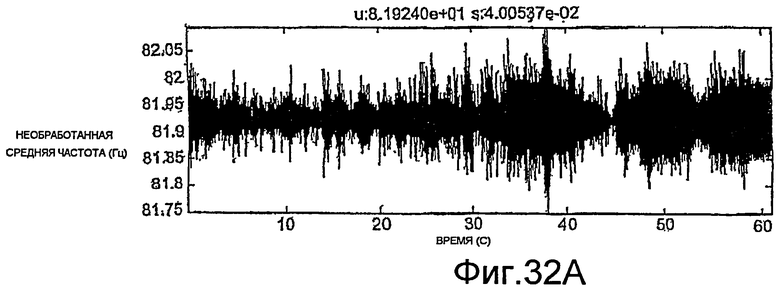
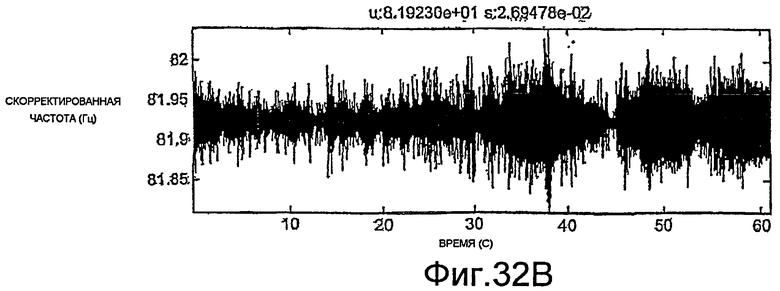
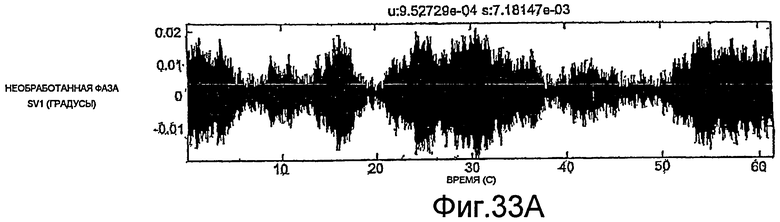
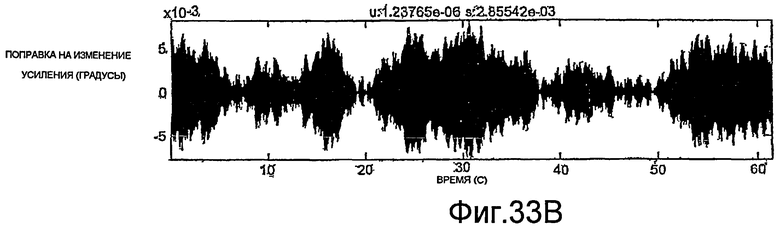
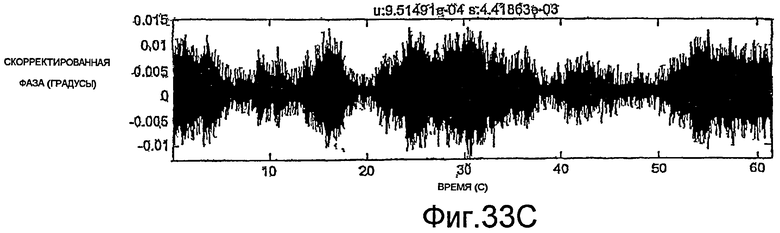
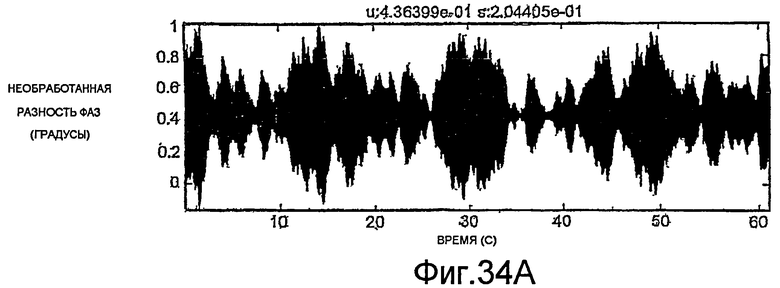
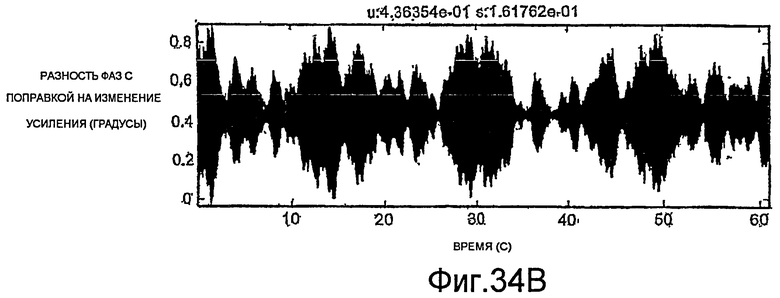
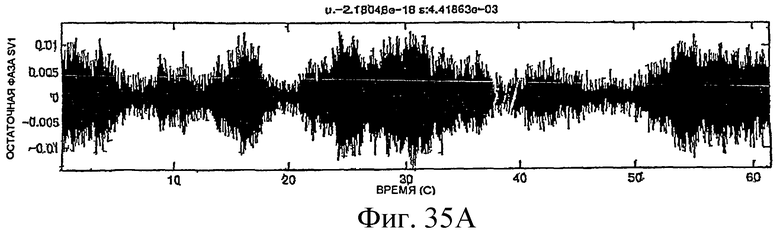
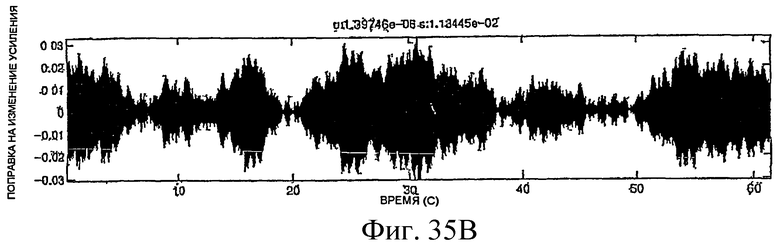
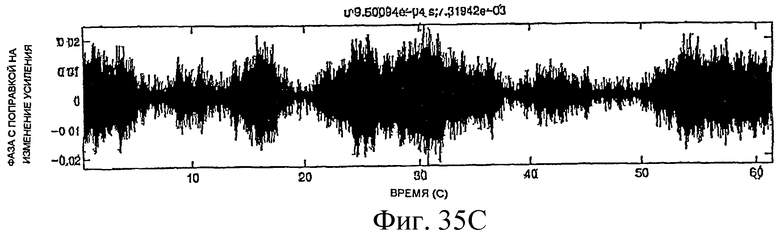
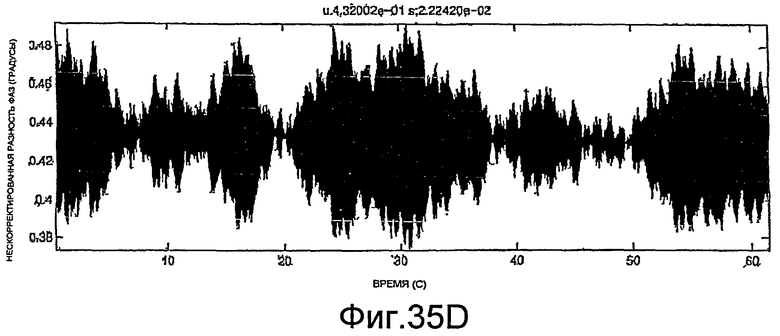
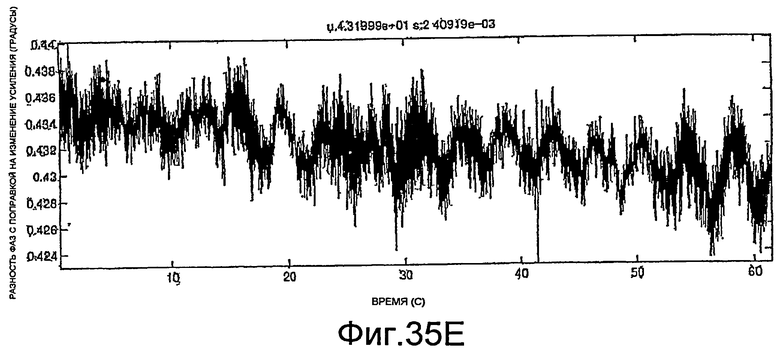
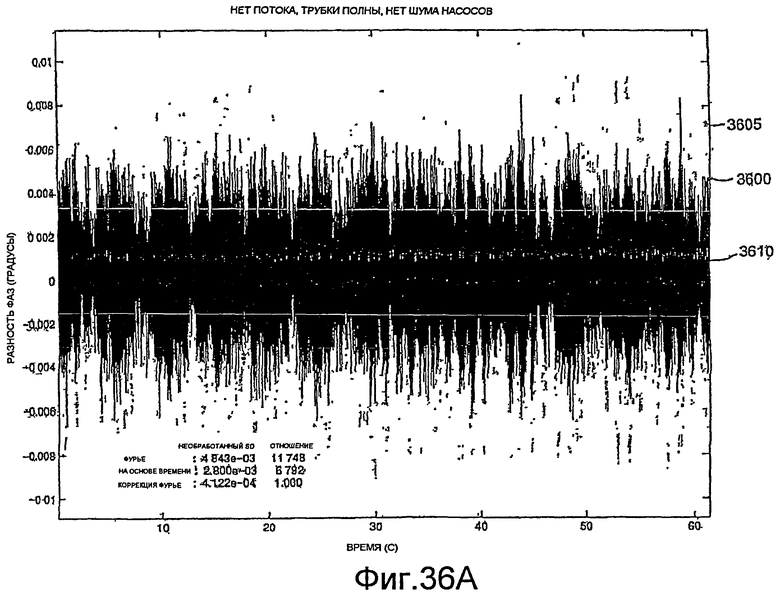
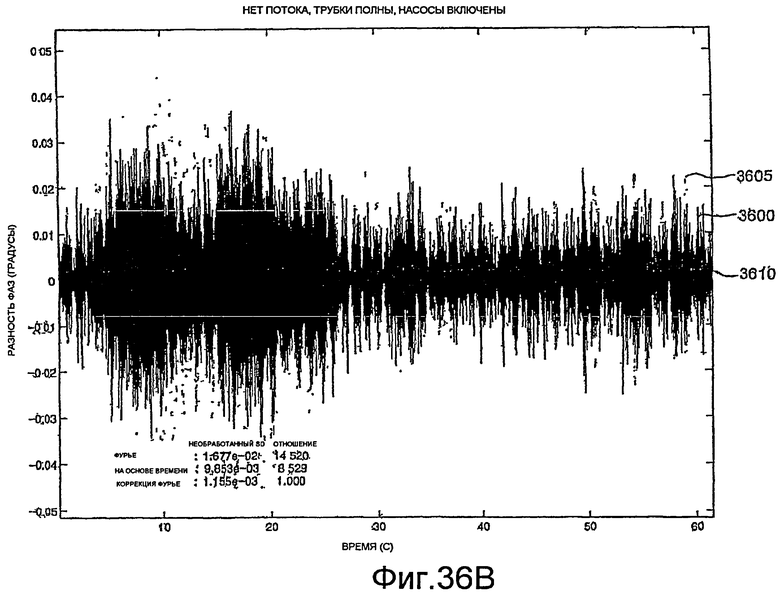
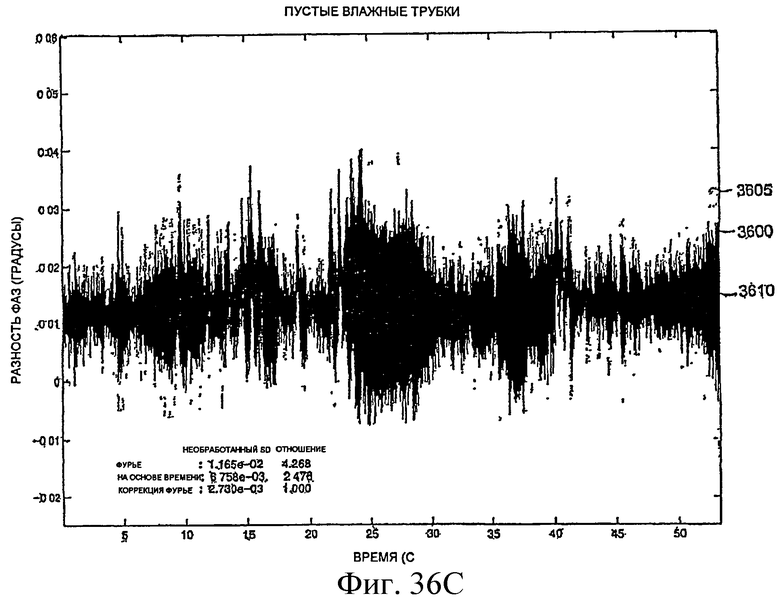
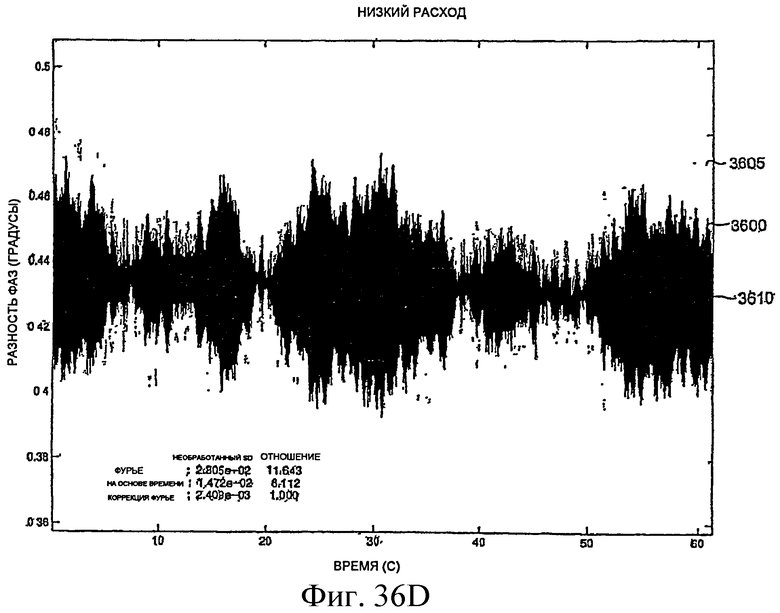
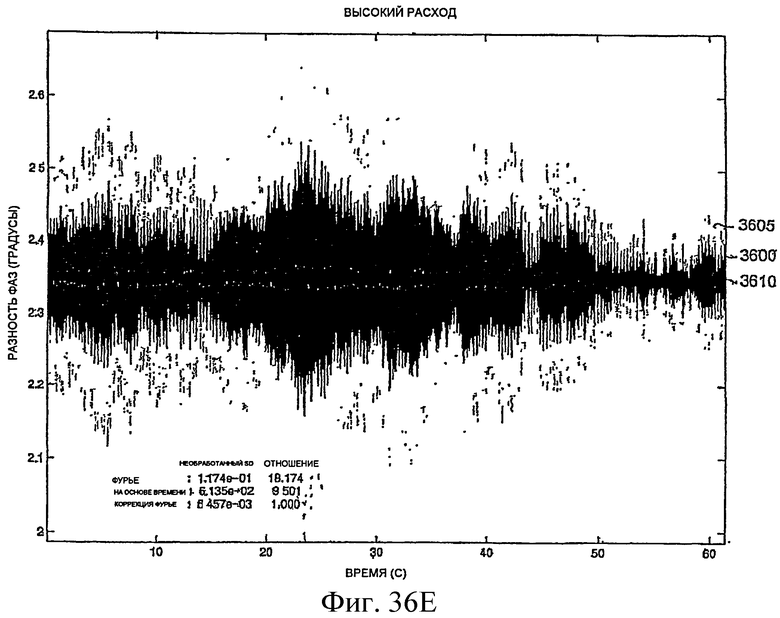
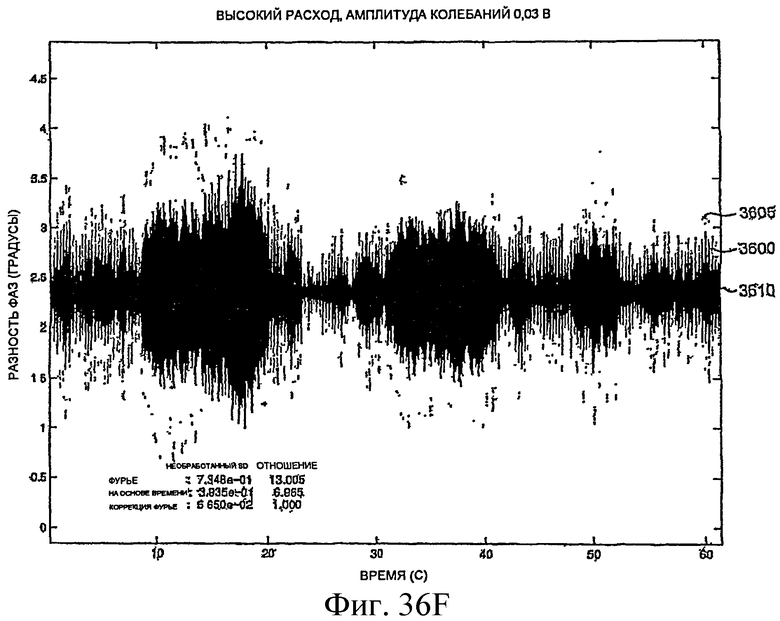
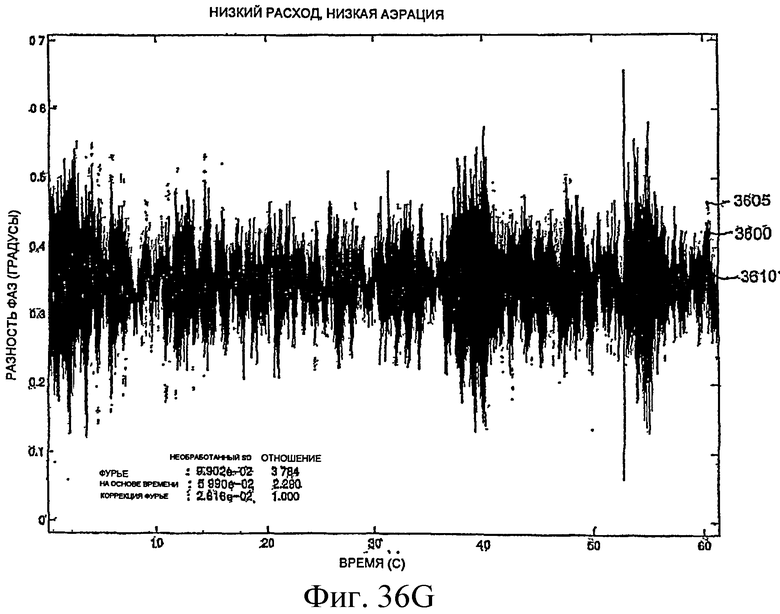
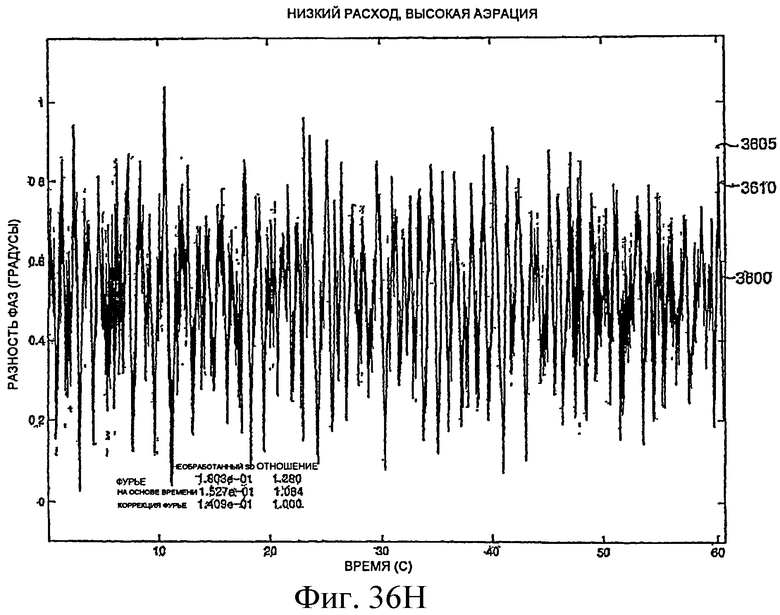
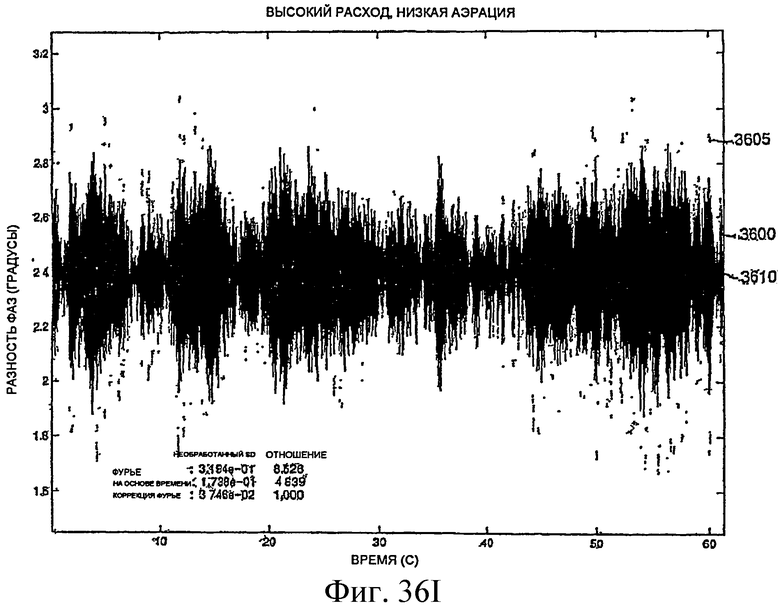
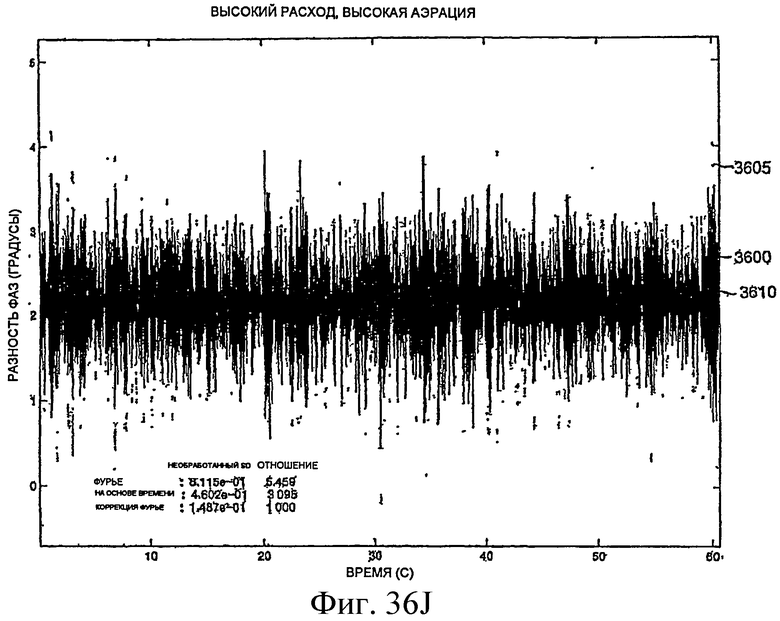
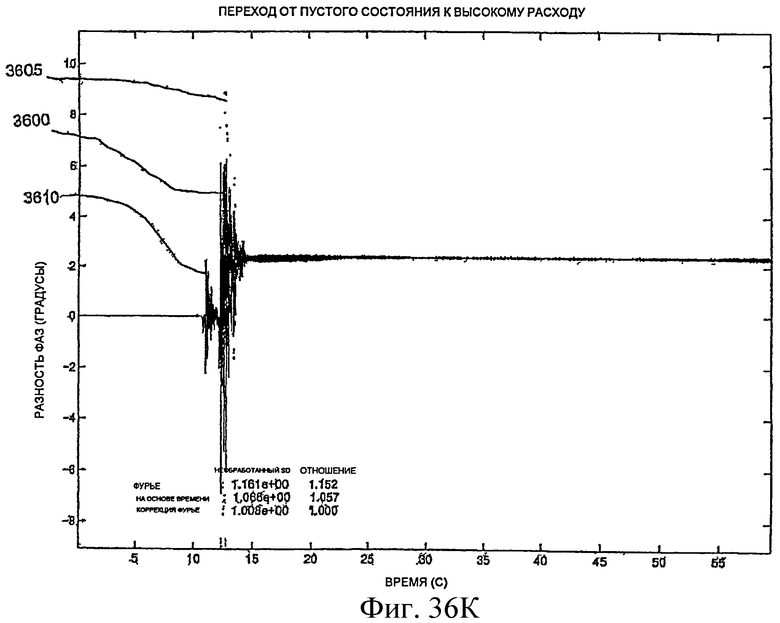
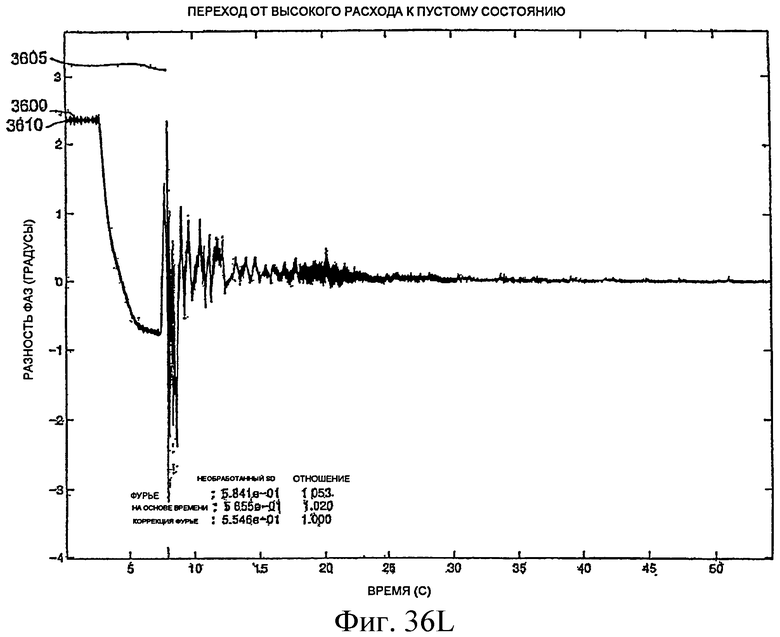
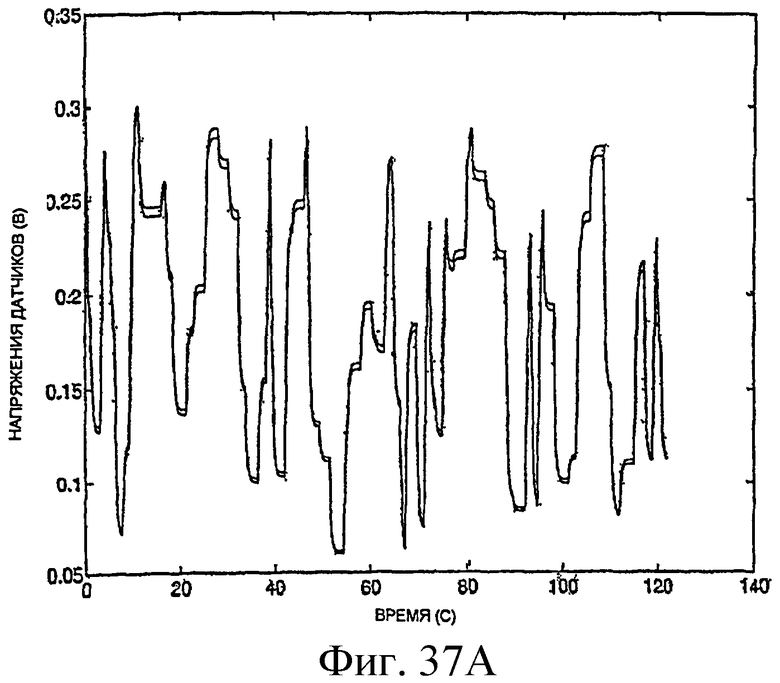
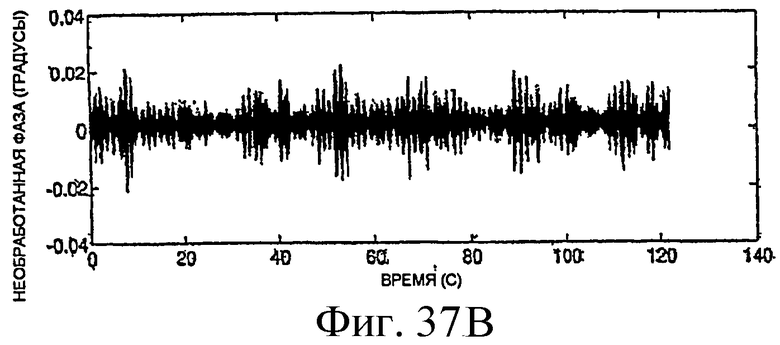
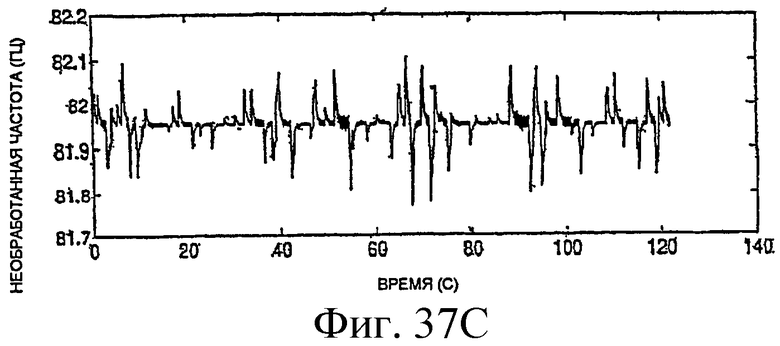
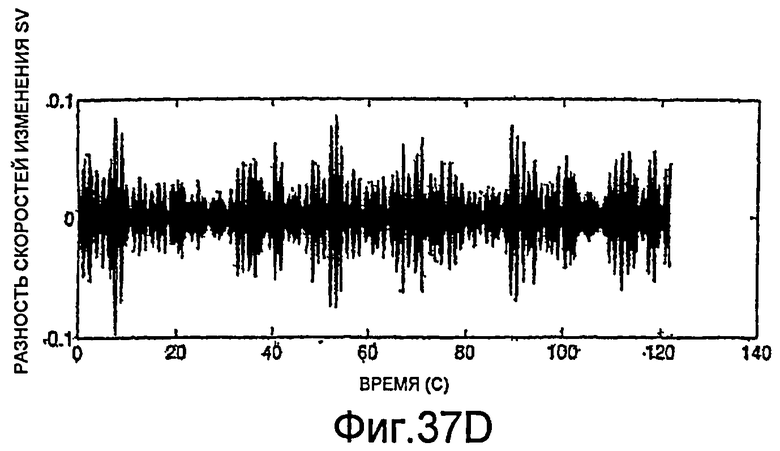
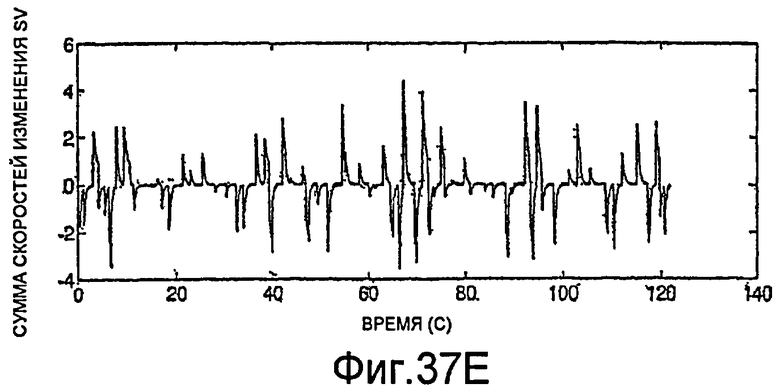
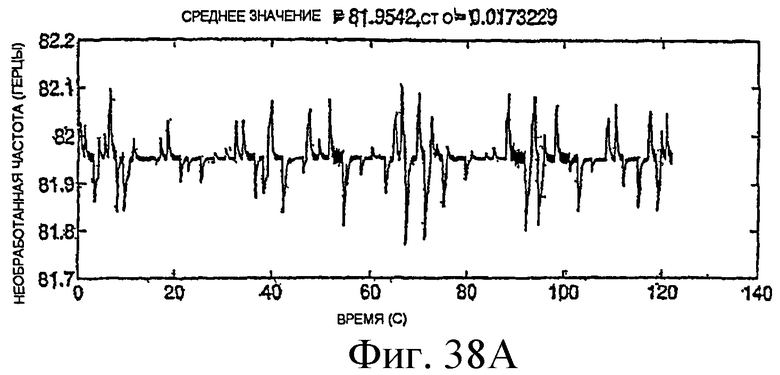
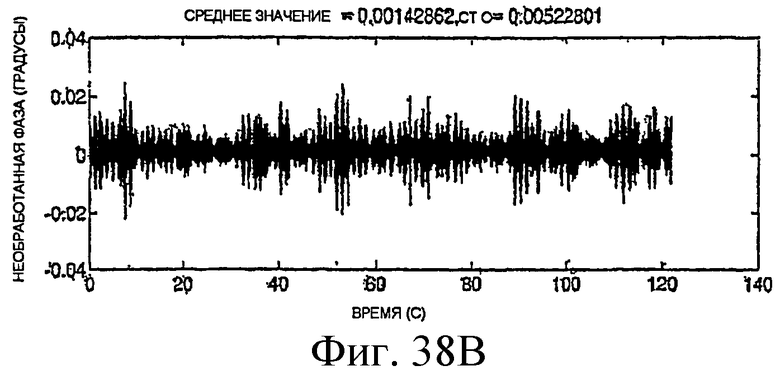
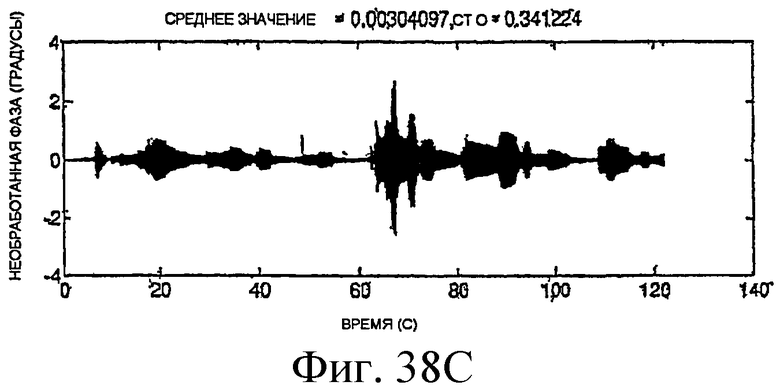
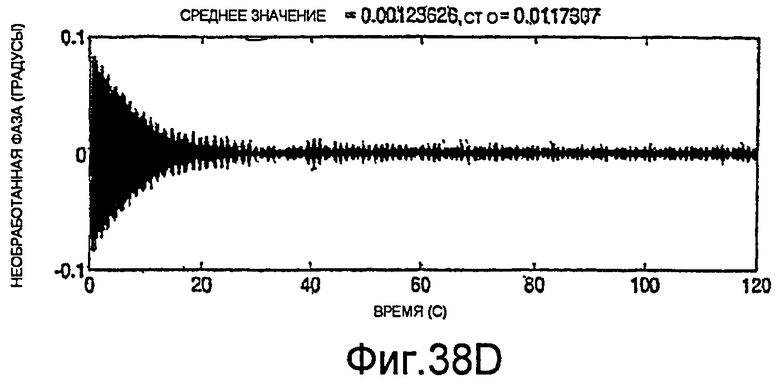
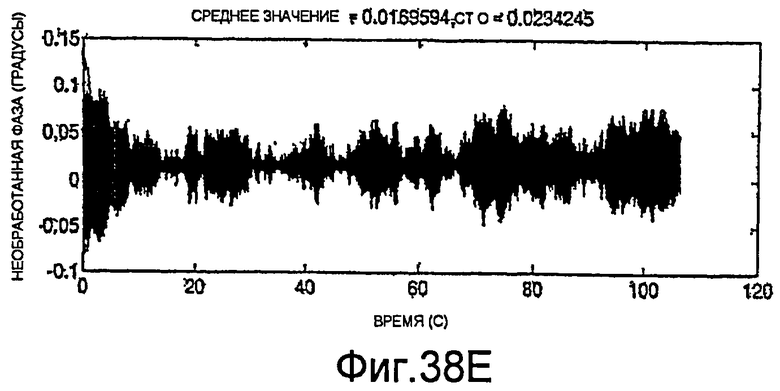
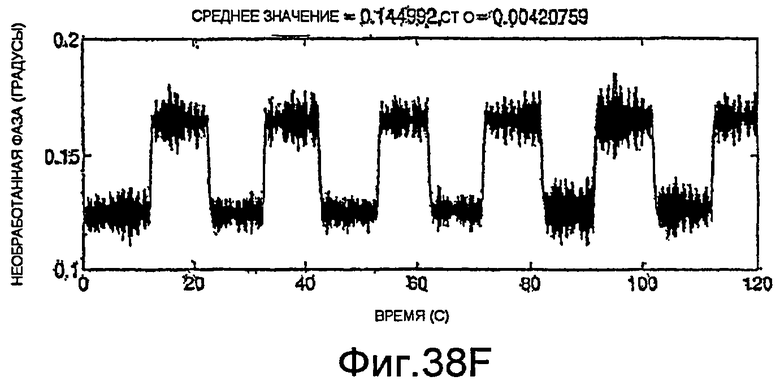
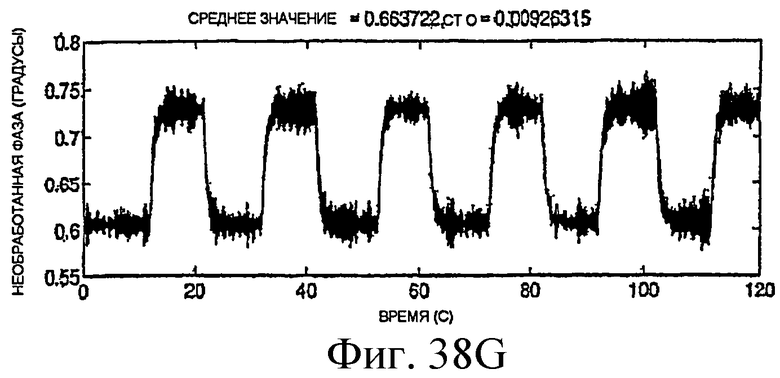
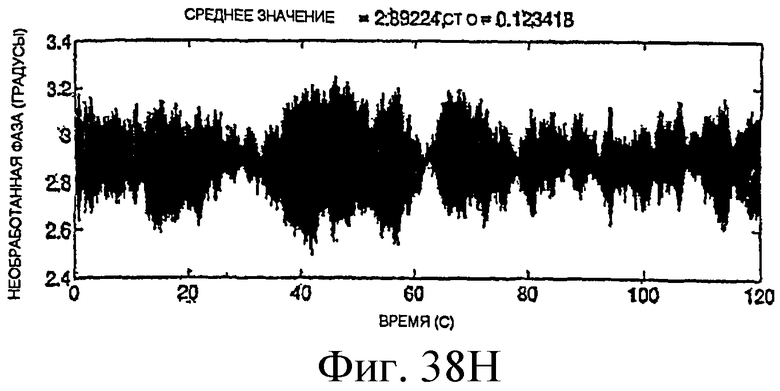
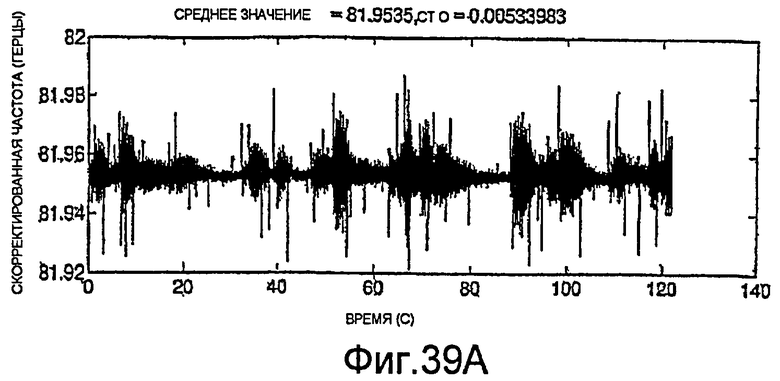
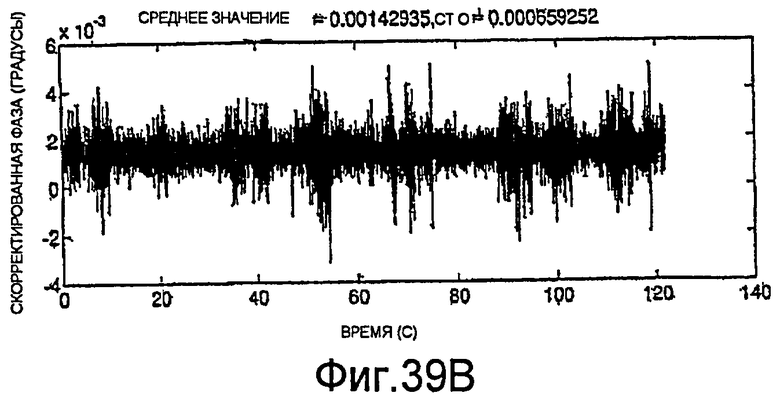
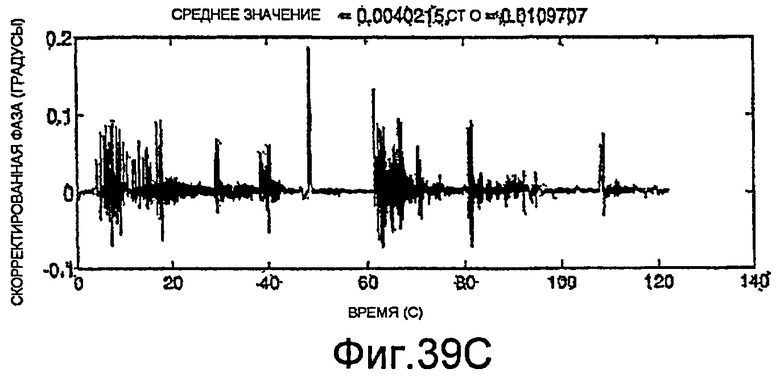
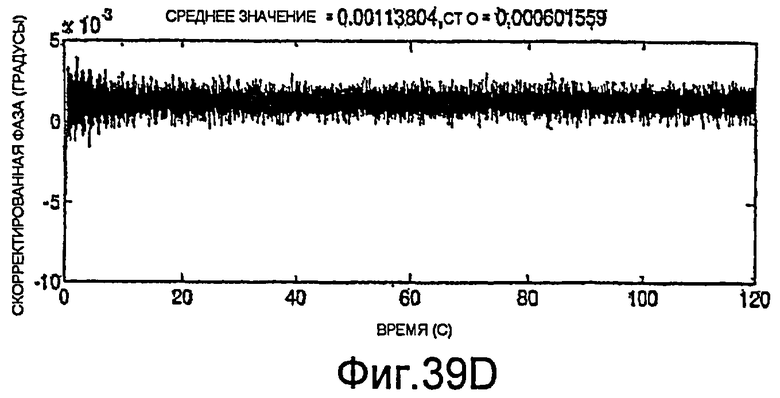
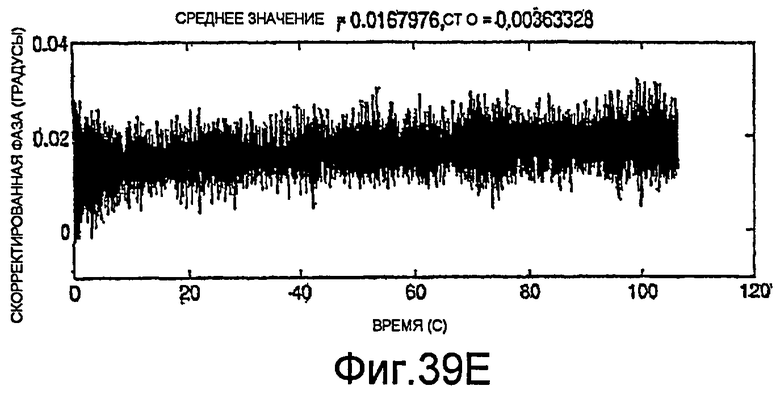
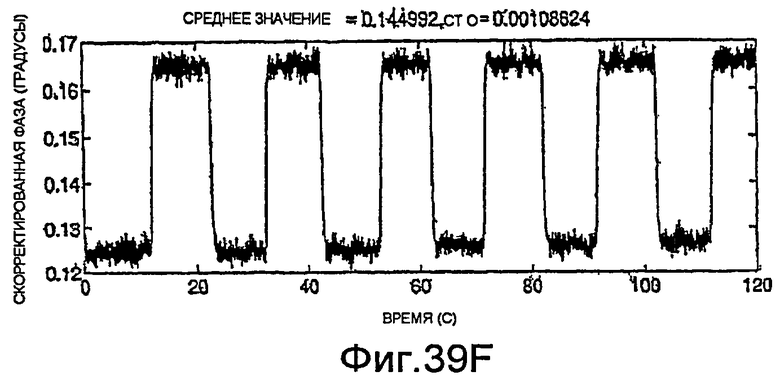
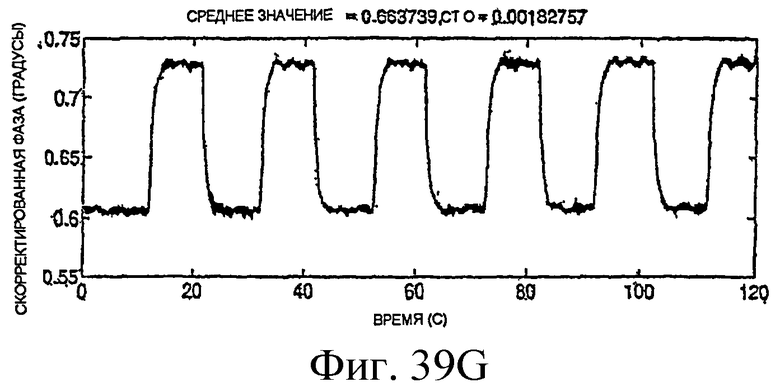
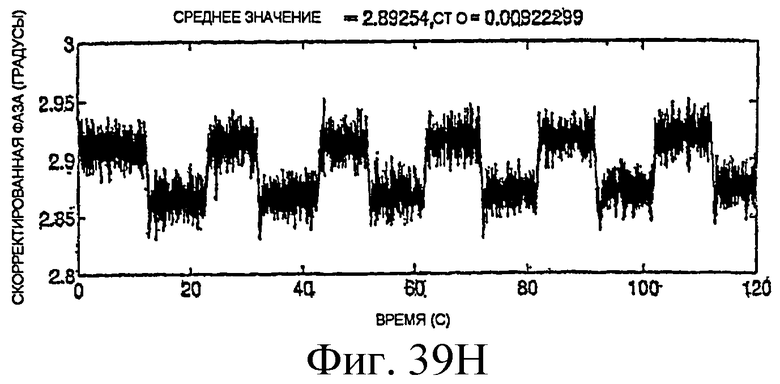
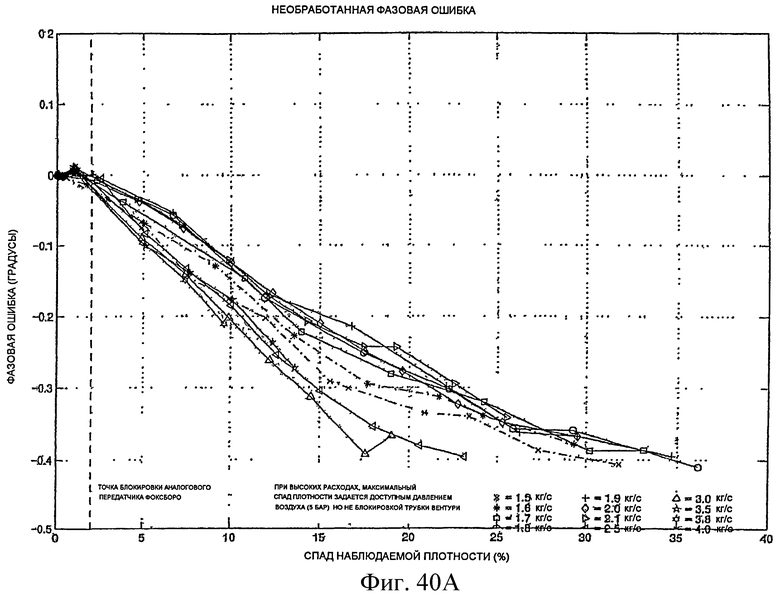
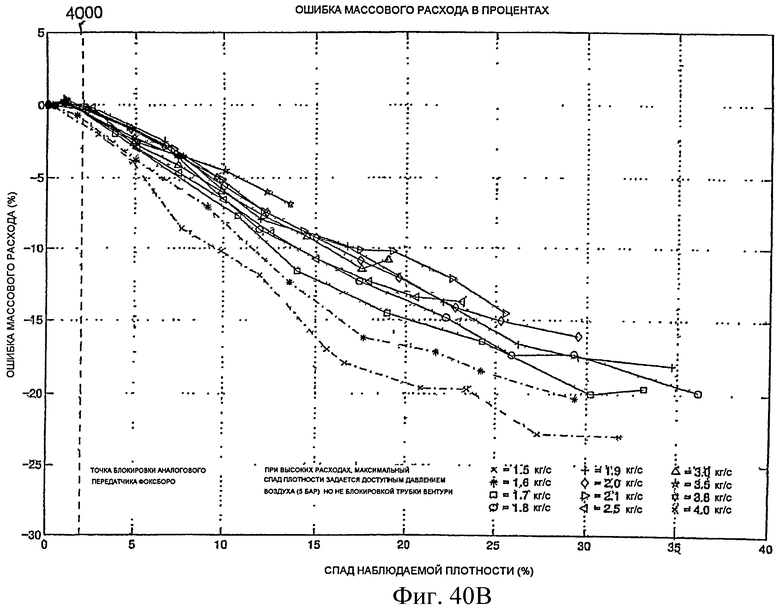
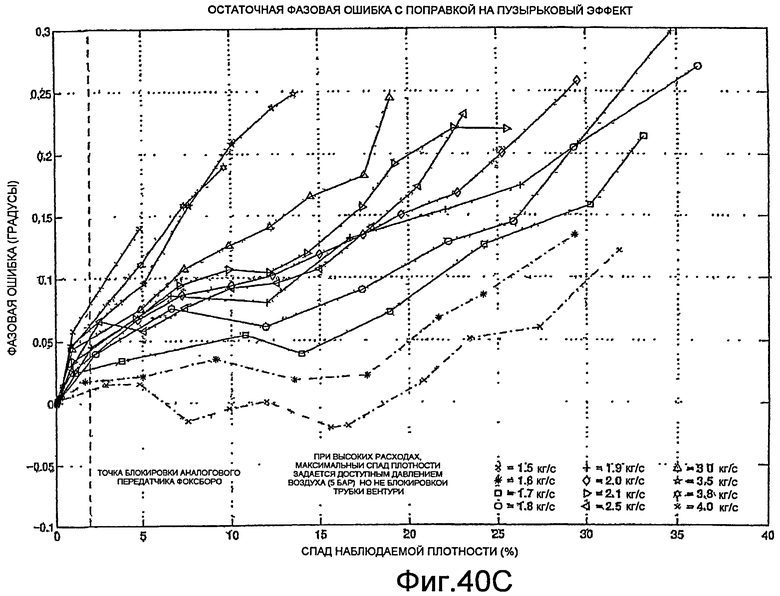
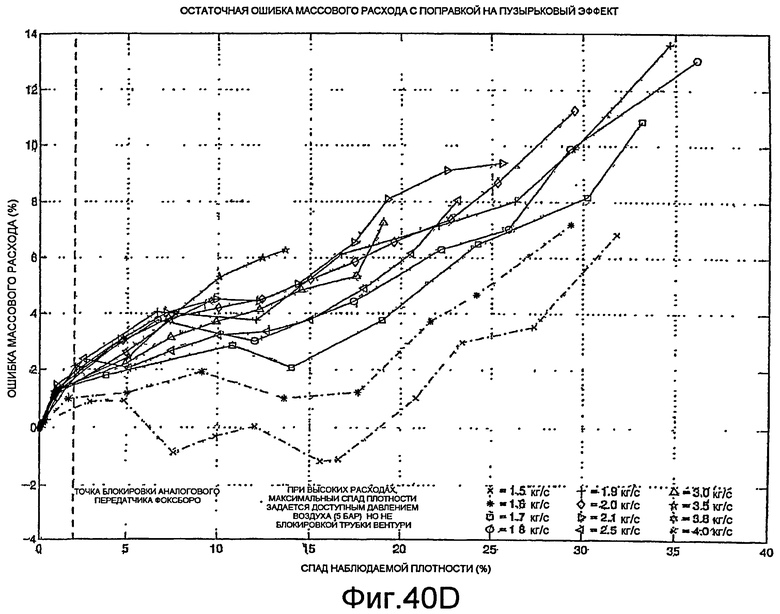
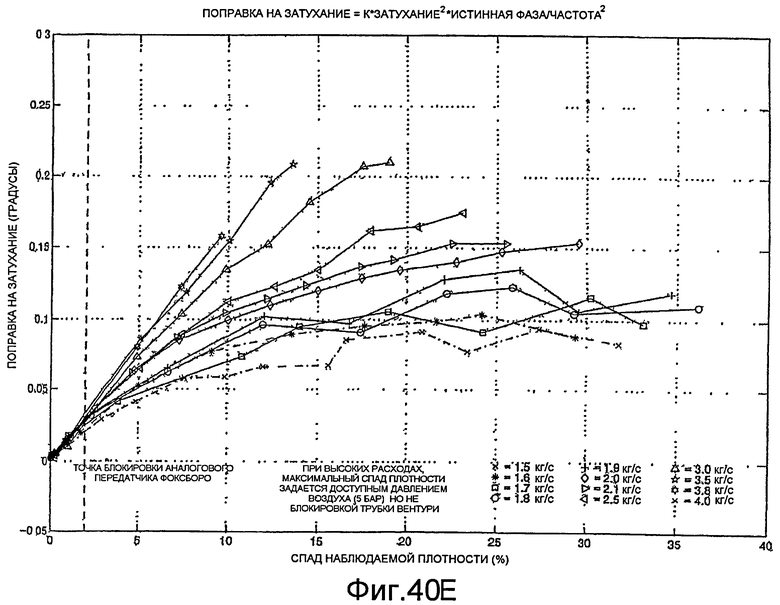
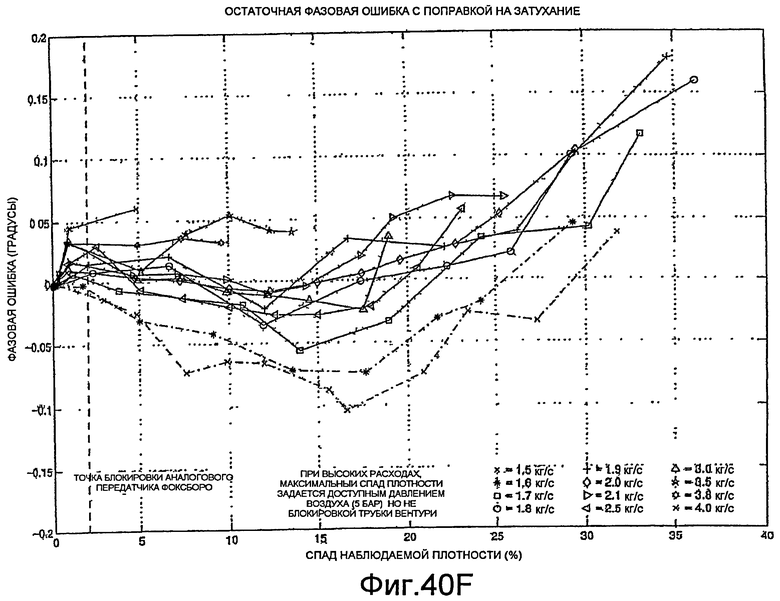
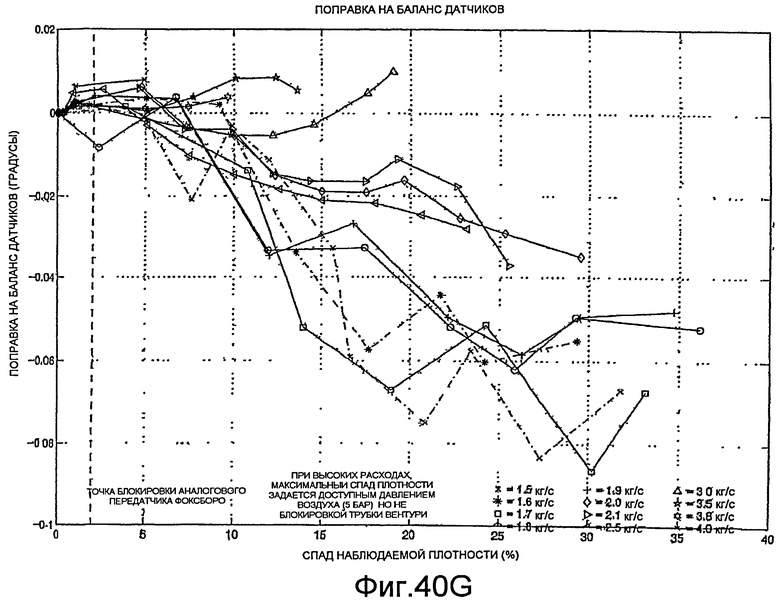
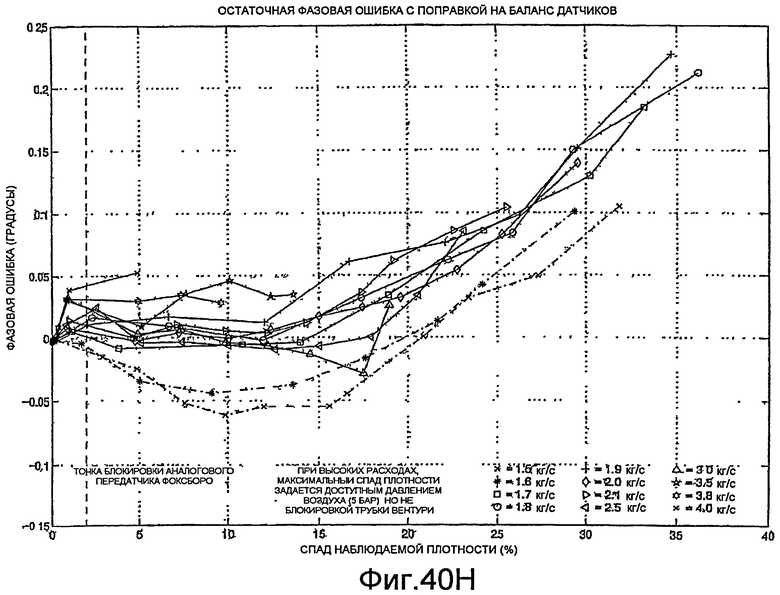
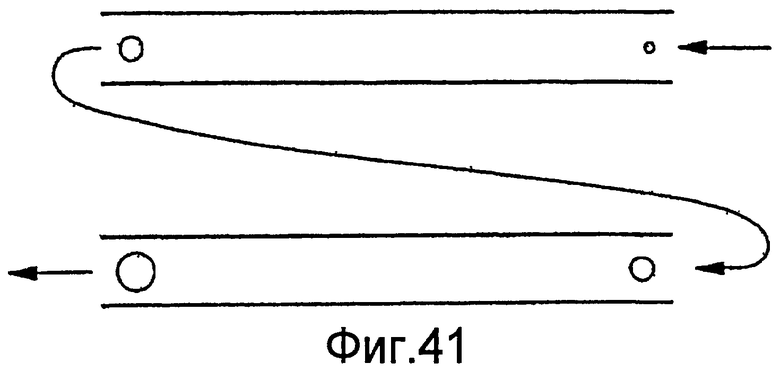
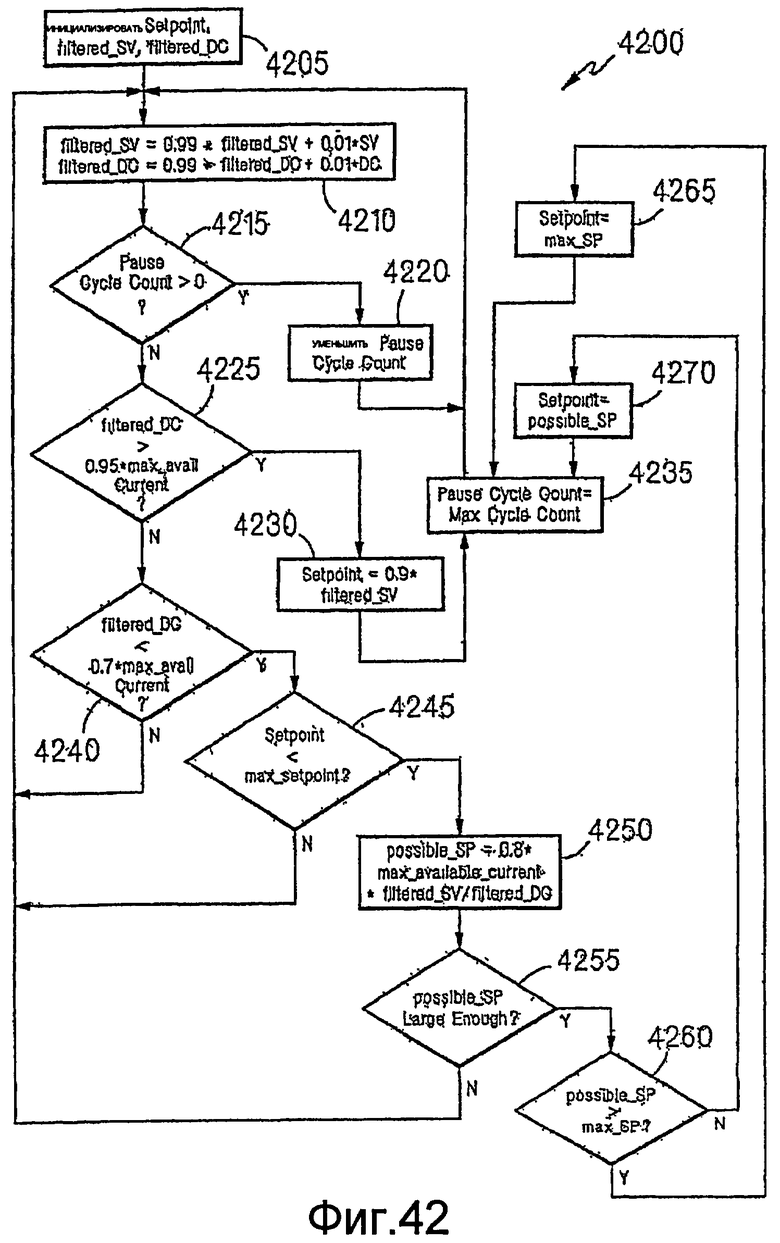
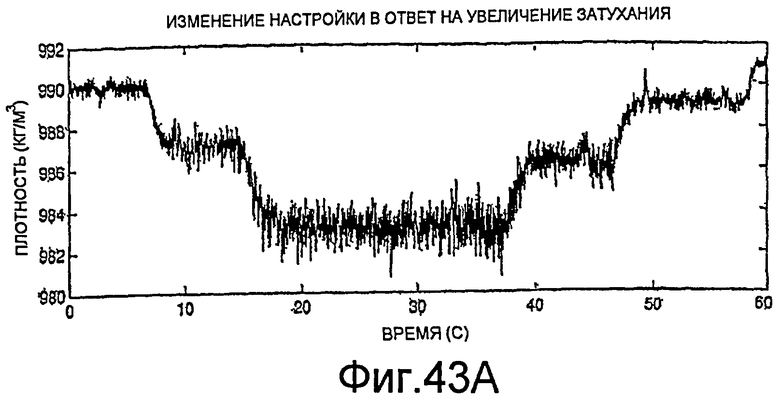
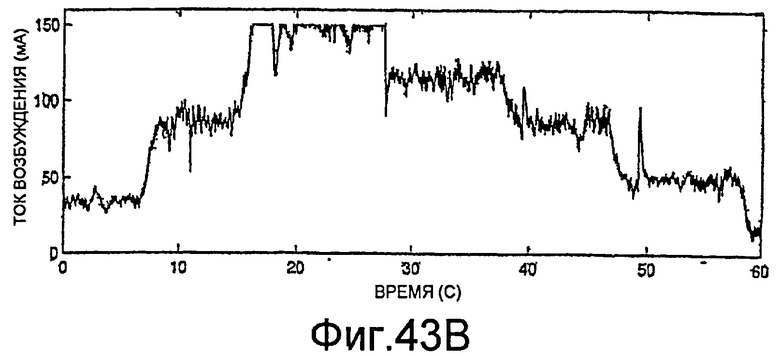
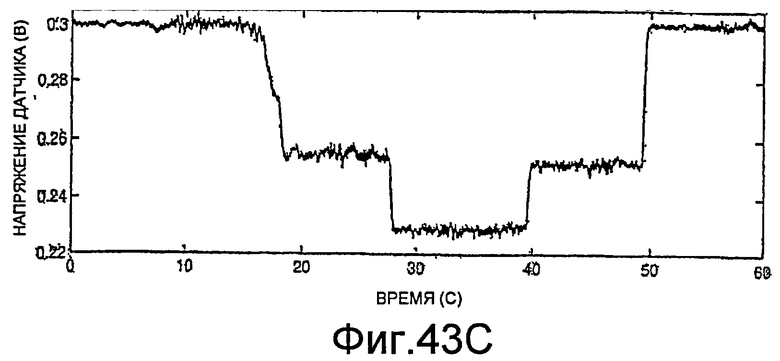
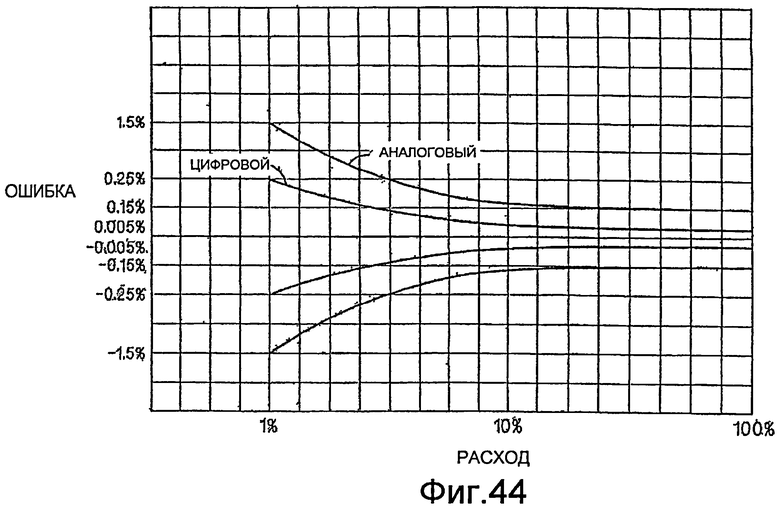
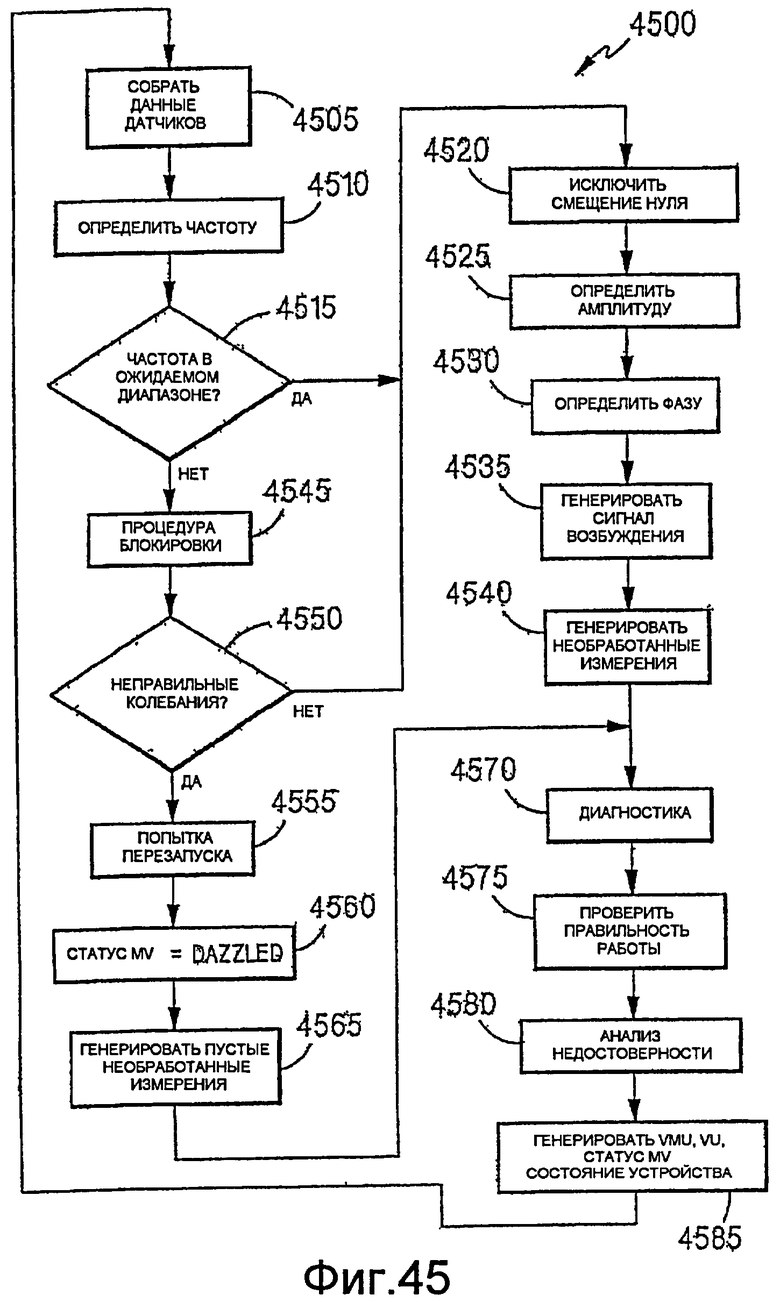
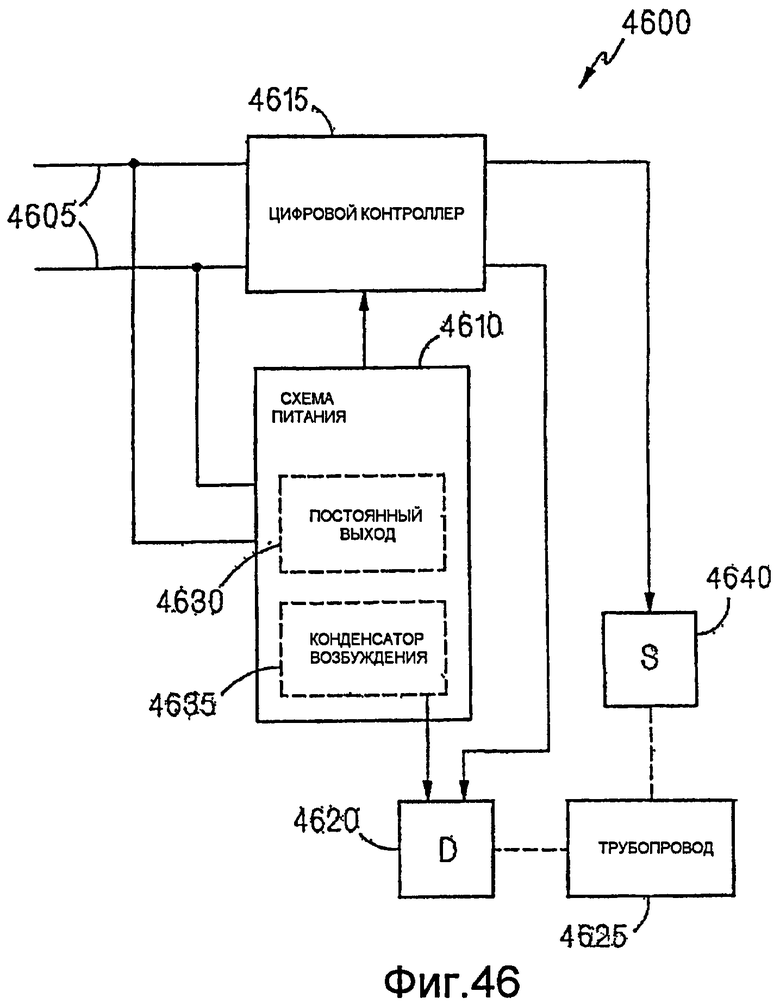
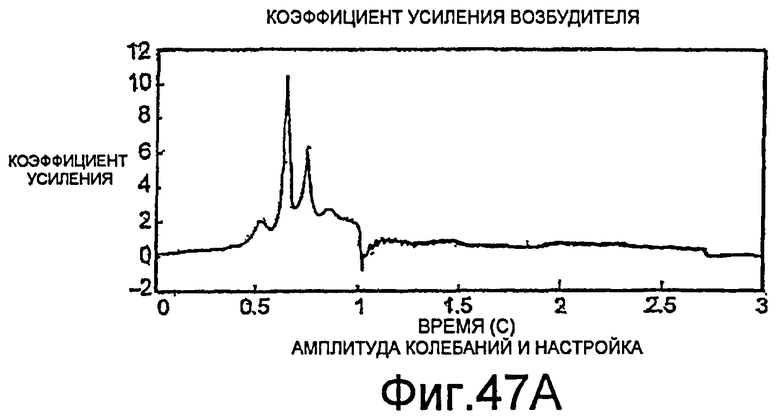
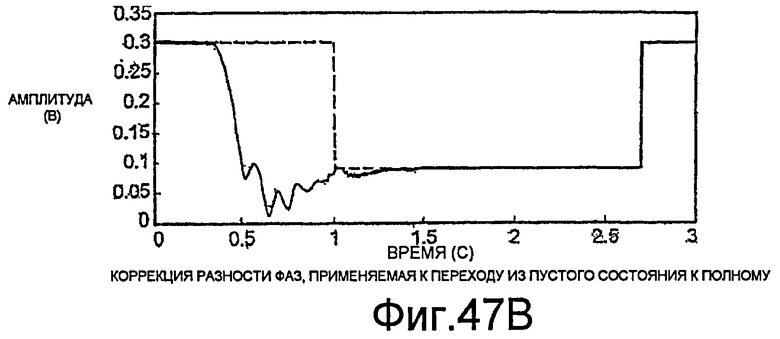
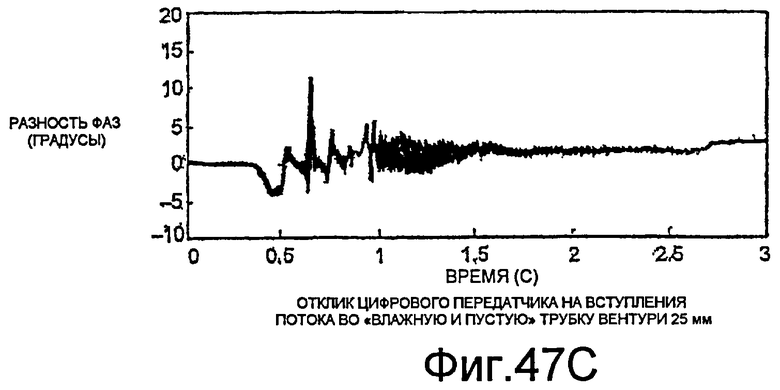
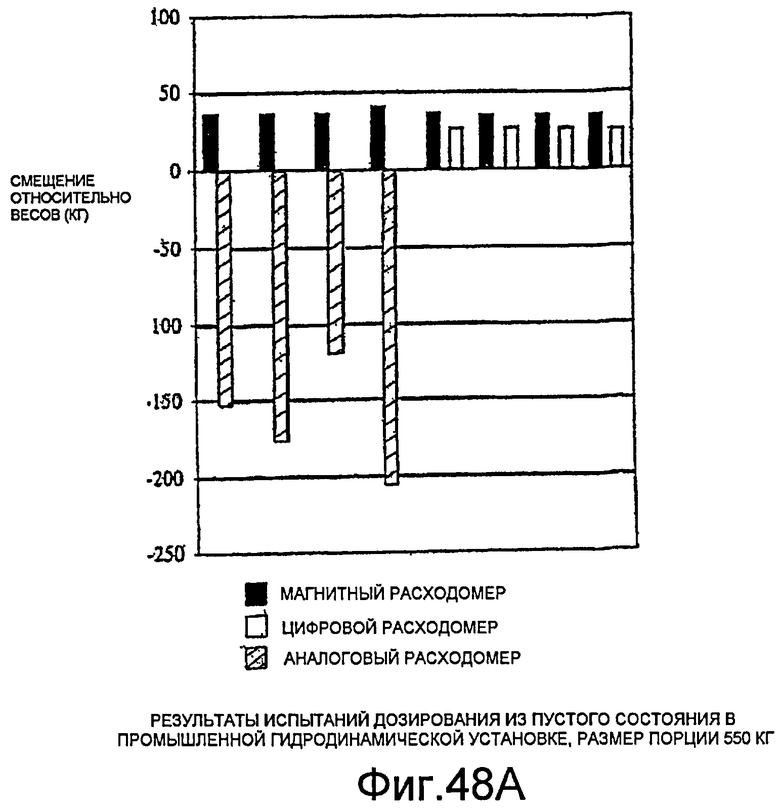
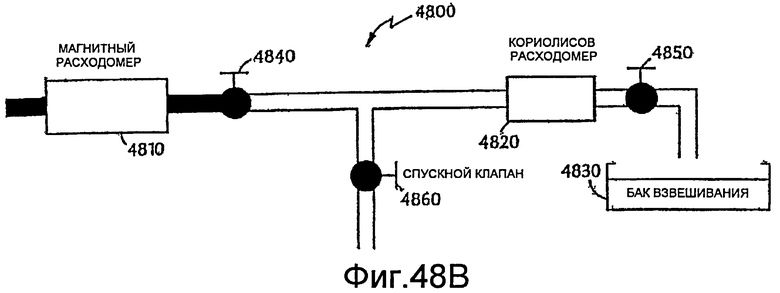
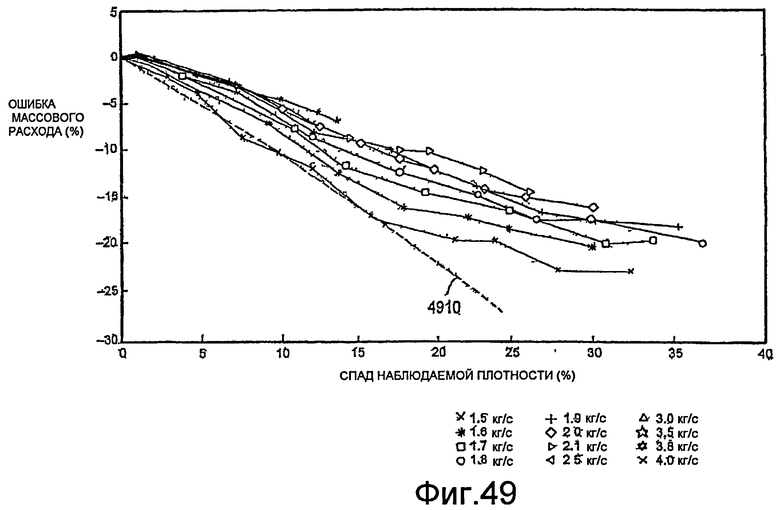
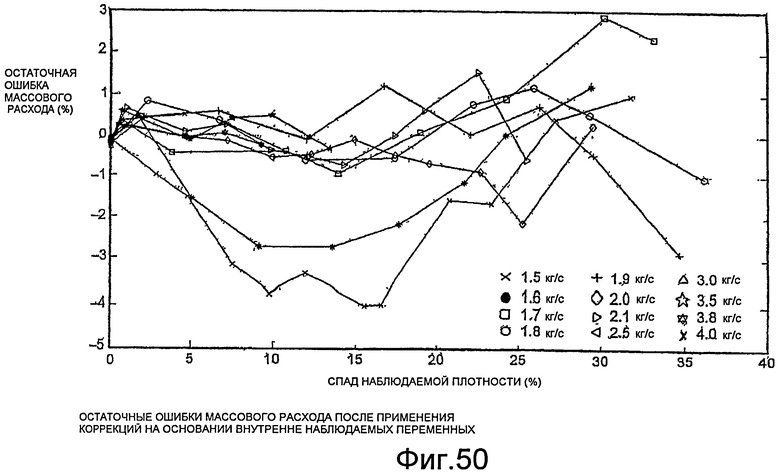
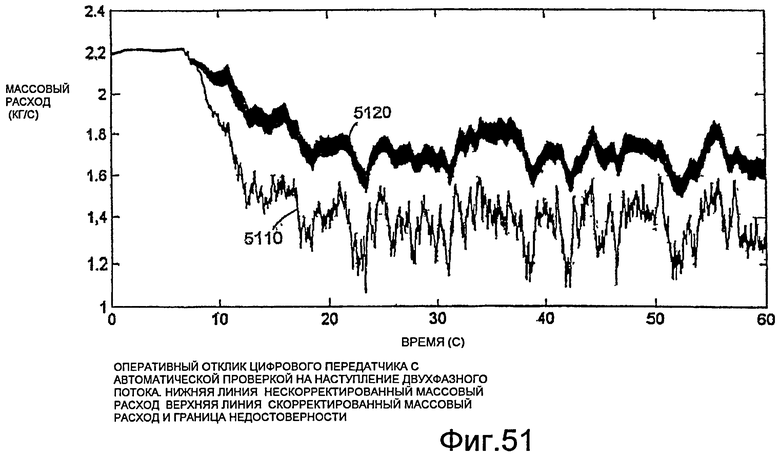
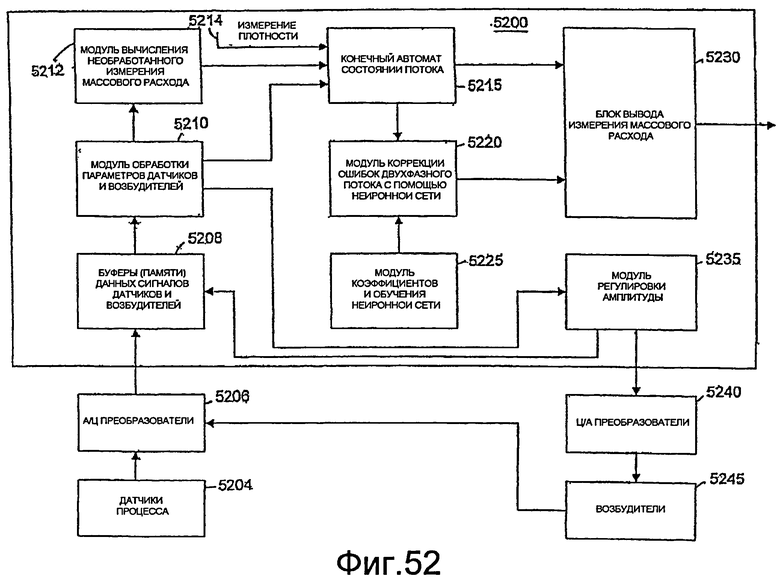
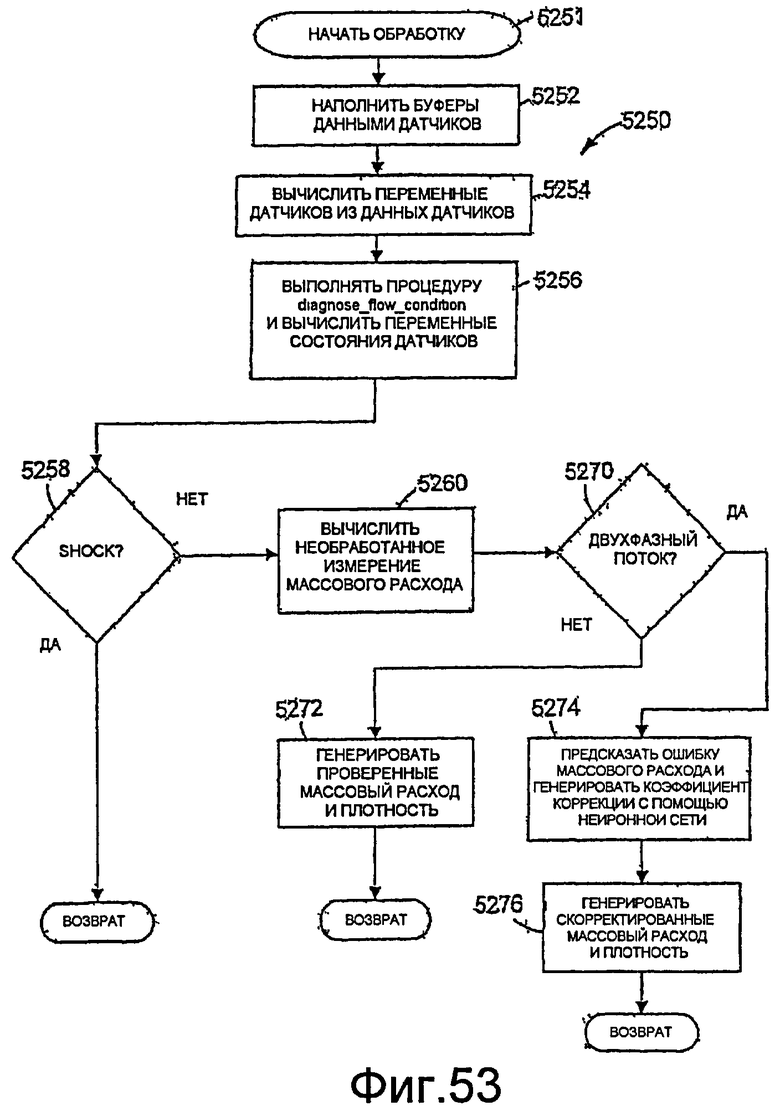
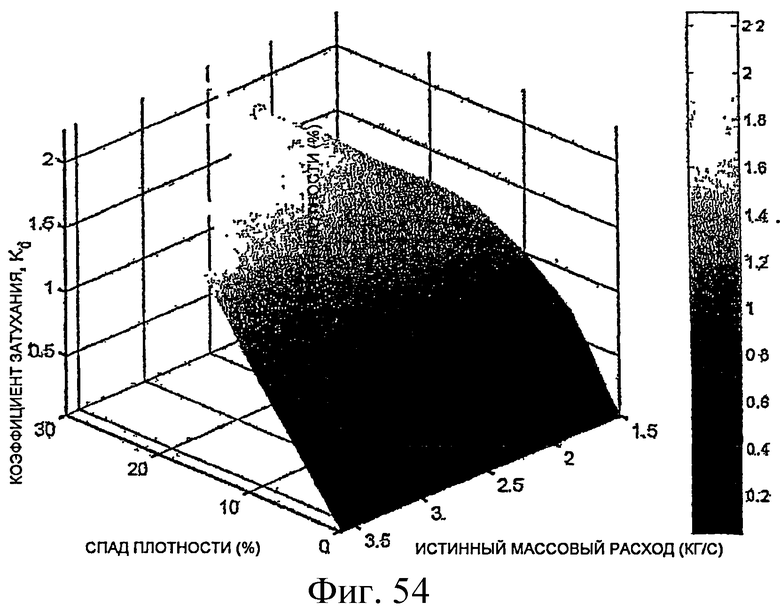
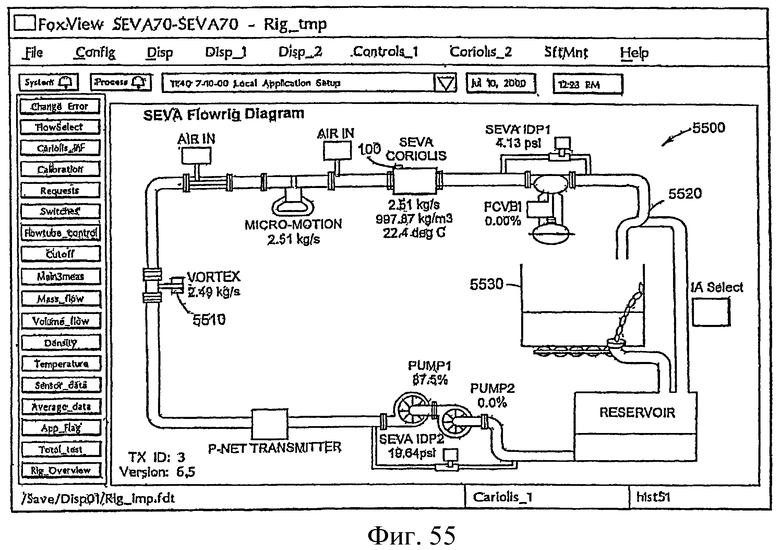
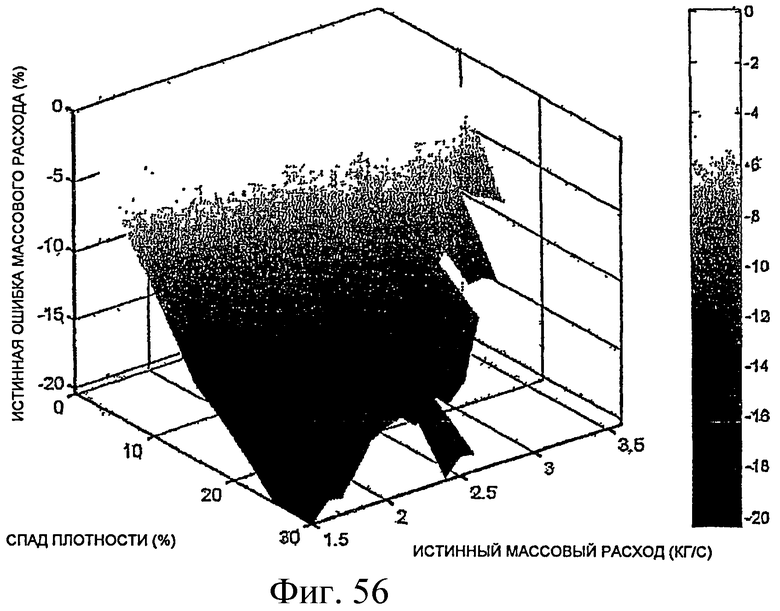
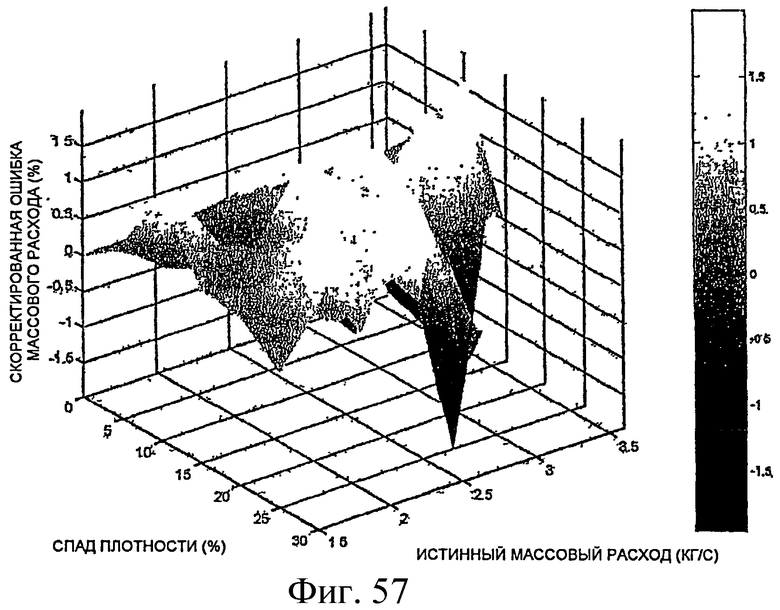
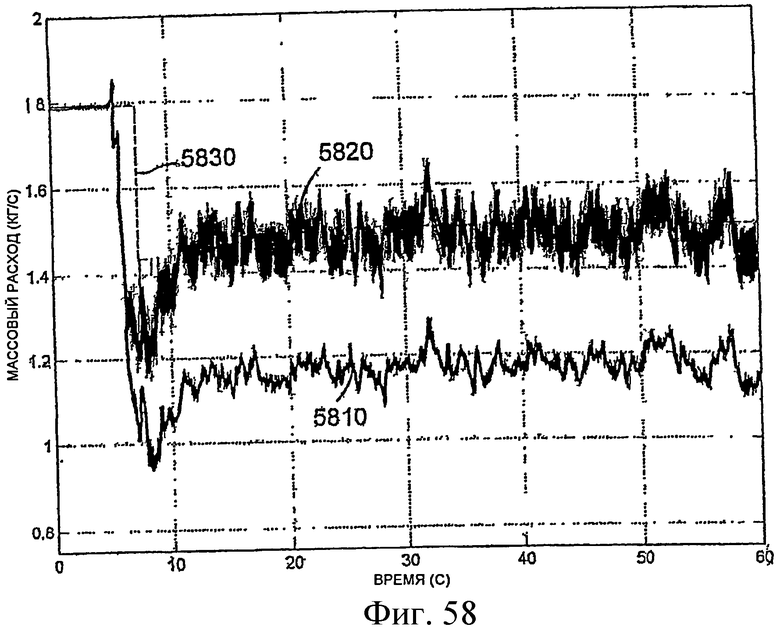
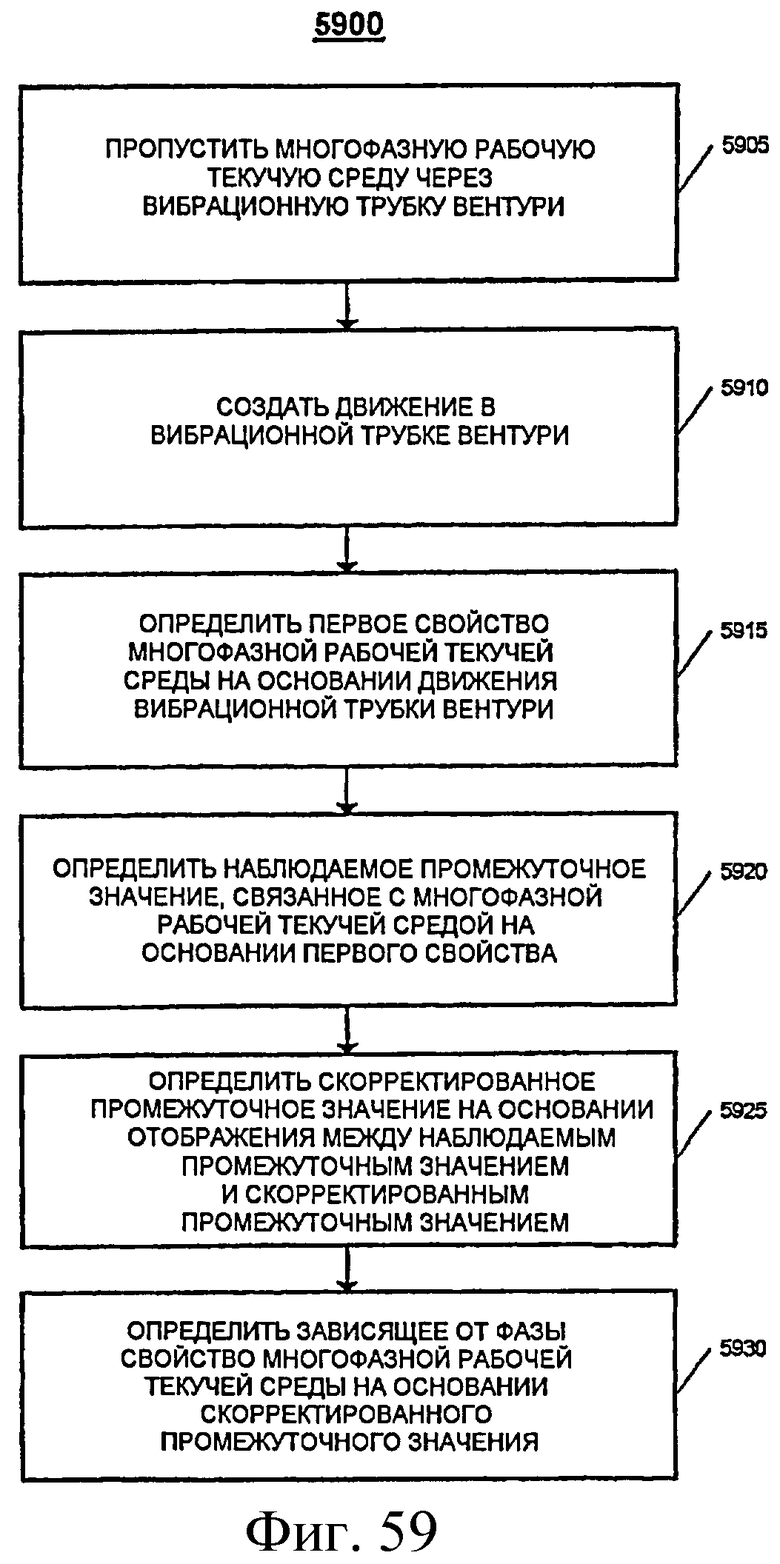
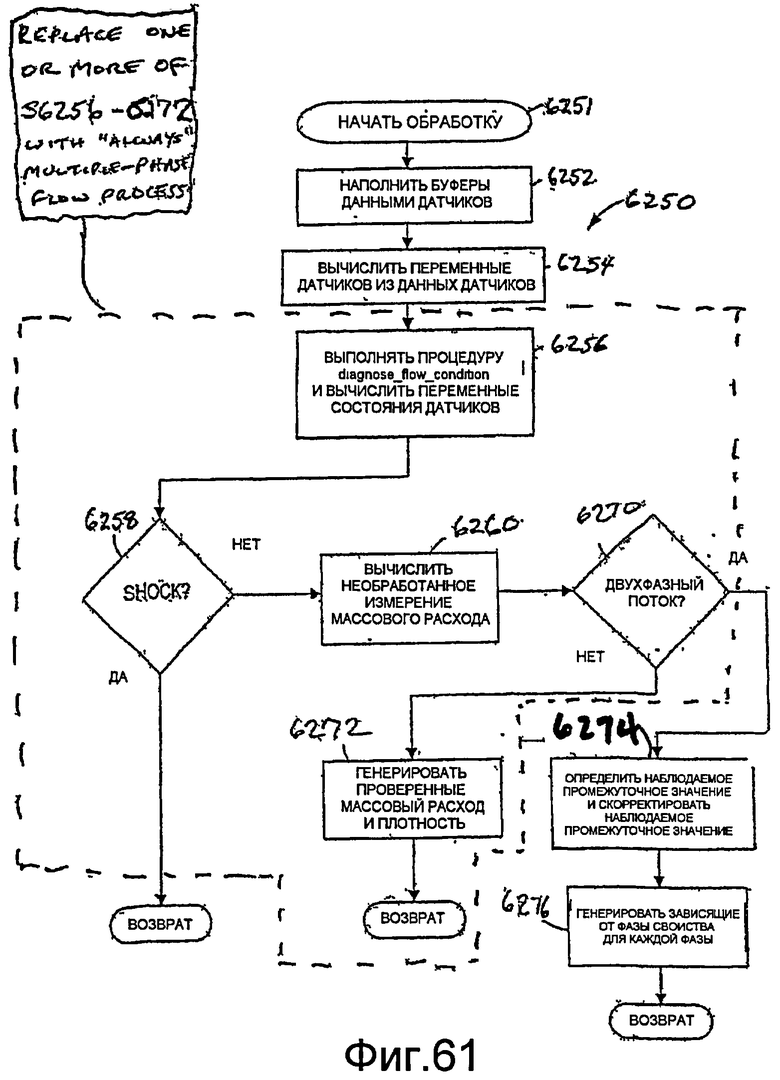
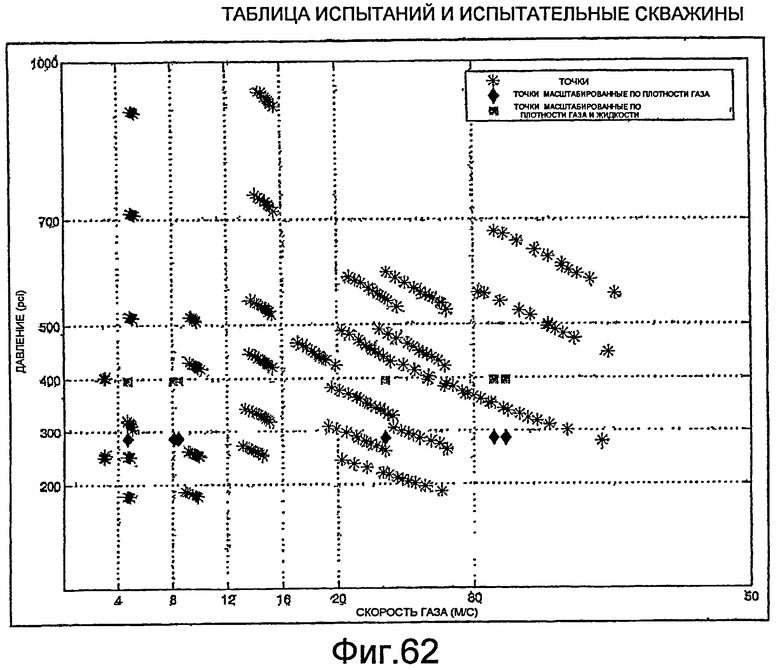
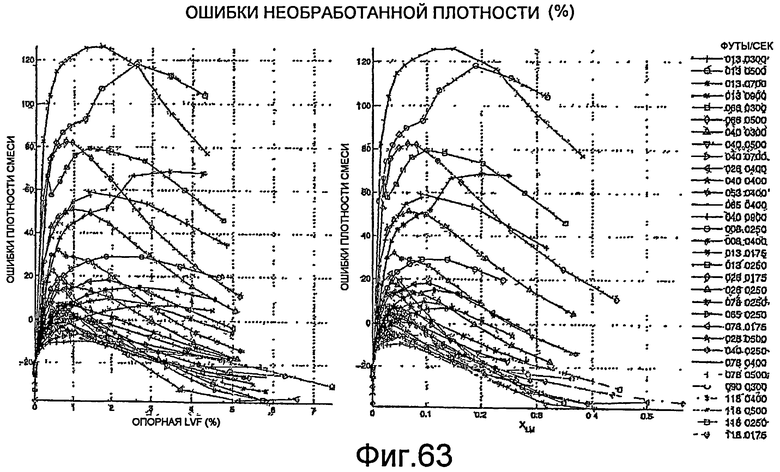
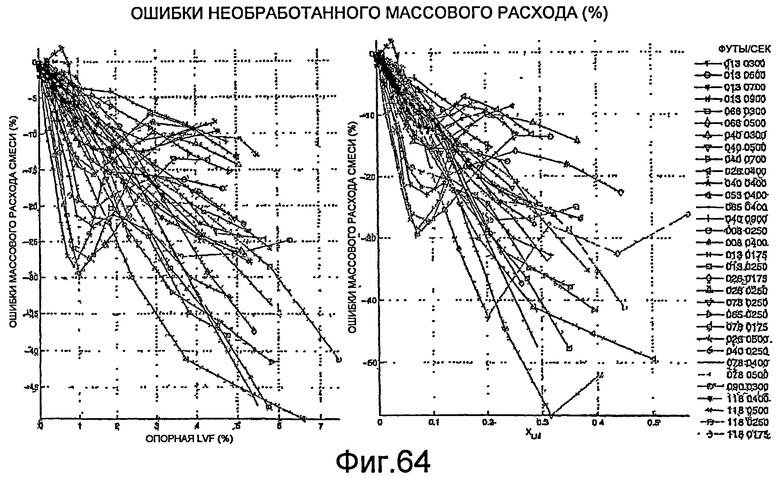
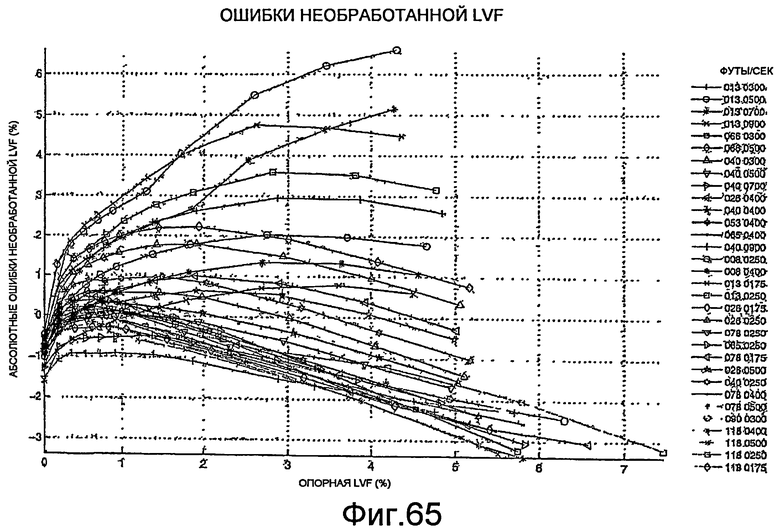
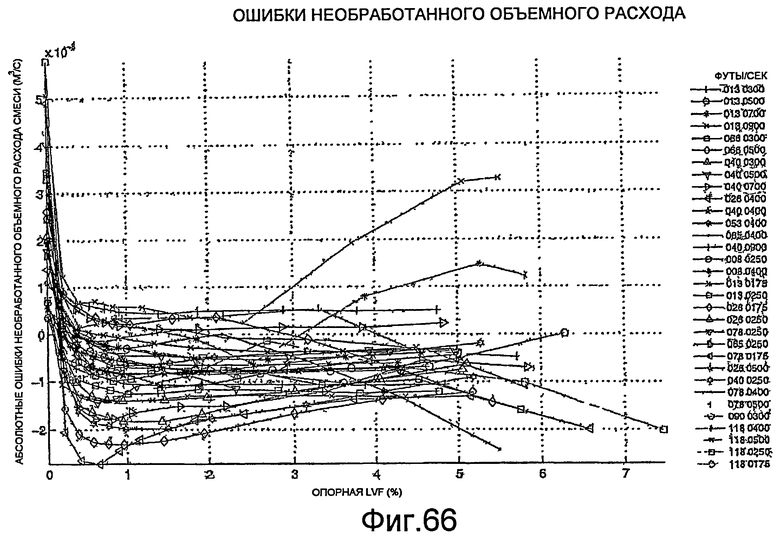
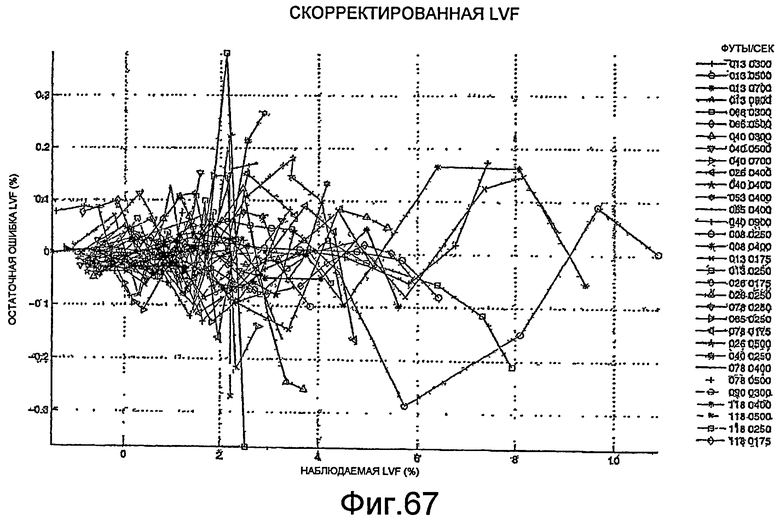
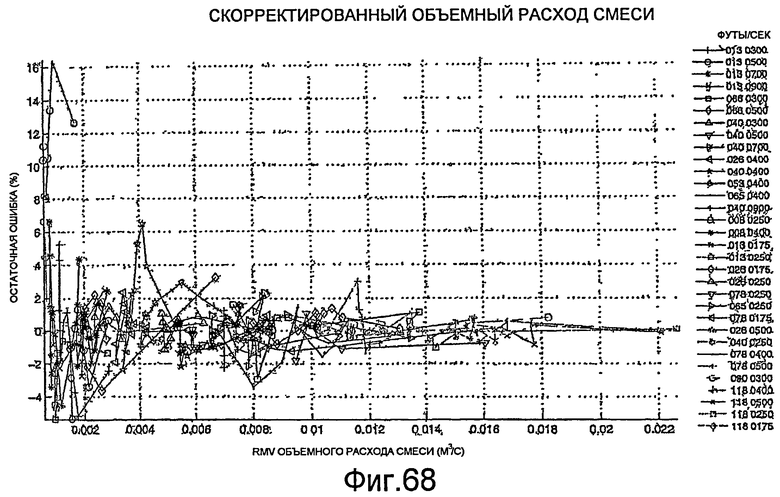
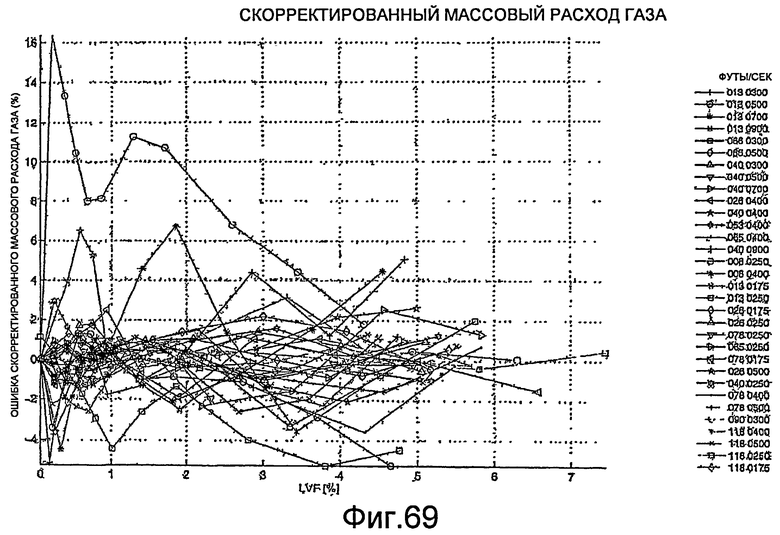
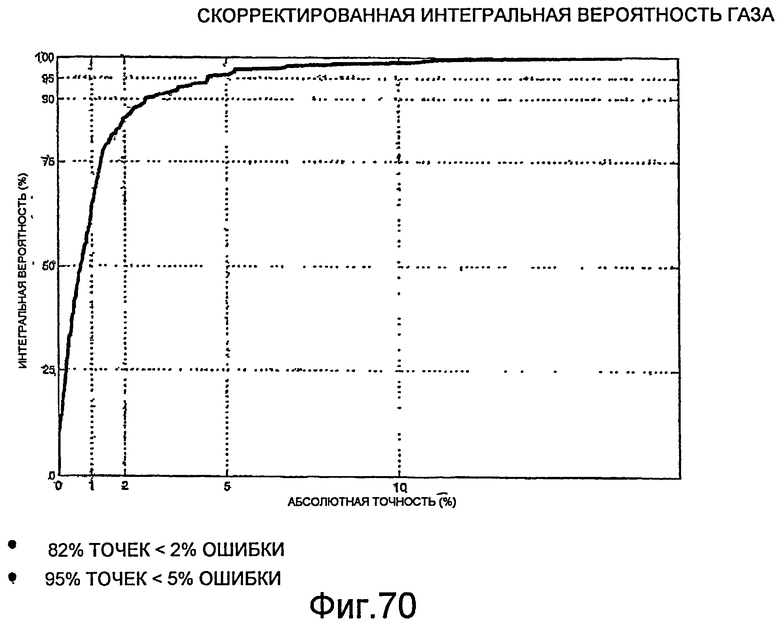
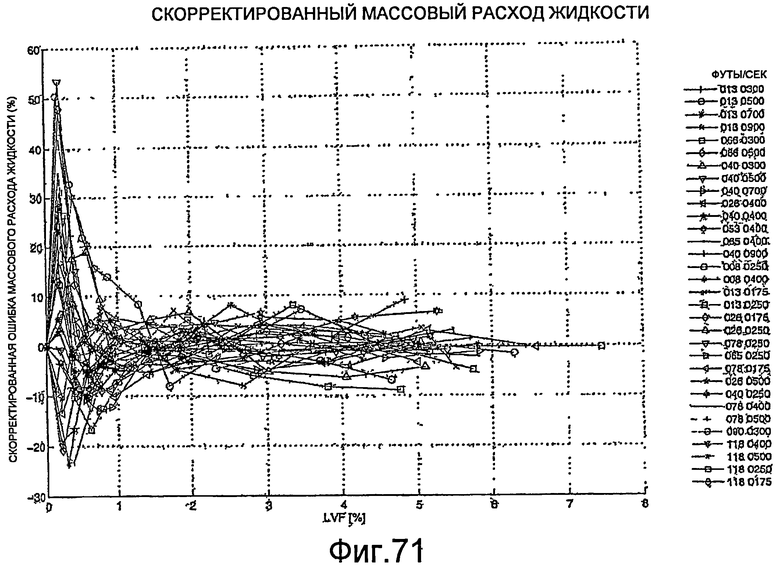
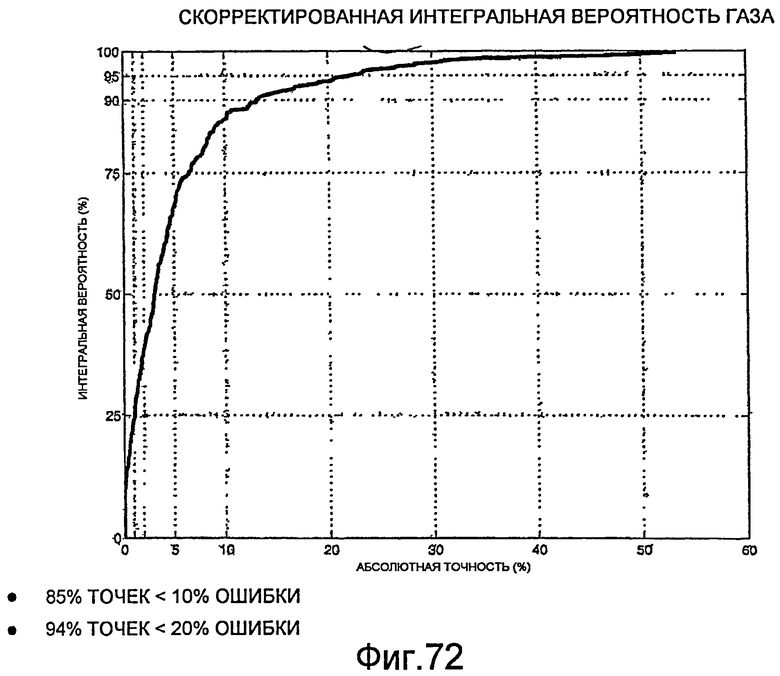
Многофазная рабочая текучая среда пропускается через вибрационную трубку Вентури. В вибрационной трубке Вентури создается движение. Первое наблюдаемое свойство многофазной рабочей текучей среды определяется на основании движения вибрационной трубки Вентури, и определяется наблюдаемое промежуточное значение, связанное с многофазной рабочей текучей средой, на основании первого наблюдаемого свойства. Скорректированное промежуточное значение определяется на основании отображения между наблюдаемым промежуточным значением и предыдущим скорректированным промежуточным значением. Зависящее от фазы свойство фазы многофазной рабочей текучей среды определяется на основании скорректированного промежуточного значения. Технический результат - повышение точности определения массового расхода и плотности каждой фазы многофазной текучей среды. 3 н. и 22 з.п. ф-лы, 72 ил., 5 табл.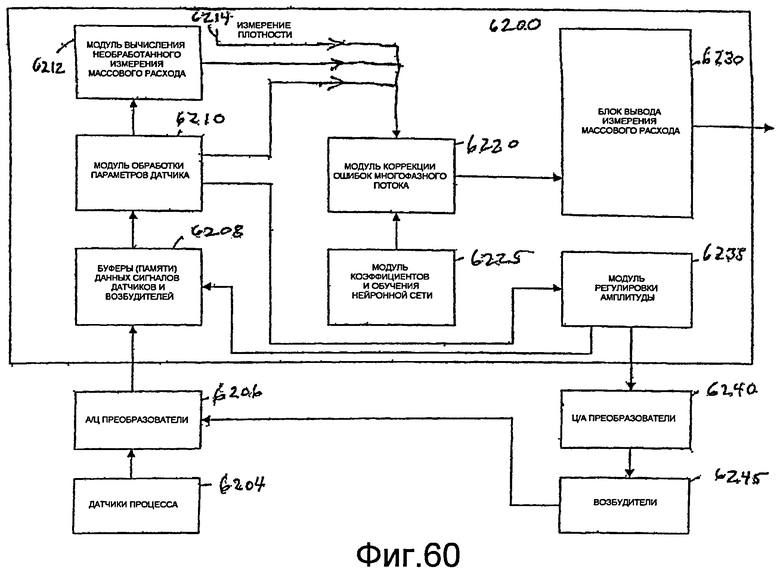
1. Способ определения свойства многофазной рабочей текучей среды, содержащий этапы, на которых
пропускают многофазную рабочую текучую среду через вибрационную трубку Вентури,
создают движение в вибрационной трубке Вентури,
определяют первое наблюдаемое свойство многофазной рабочей текучей среды на основании движения вибрационной трубки Вентури,
определяют наблюдаемое промежуточное значение, связанное с многофазной рабочей текучей средой, на основании первого наблюдаемого свойства,
определяют скорректированное промежуточное значение на основании отображения между наблюдаемым промежуточным значением и предыдущим скорректированным промежуточным значением, и
определяют зависящее от фазы свойство фазы многофазной рабочей текучей среды на основании скорректированного промежуточного значения.
2. Способ по п.1, в котором отображение является нейронной сетью.
3. Способ по п.2, дополнительно содержащий этапы, на которых определяют, что наблюдаемое промежуточное значение находится в первой заданной области значений до определения скорректированного промежуточного значения, и
определяют, что скорректированное промежуточное значение находится во второй заданной области значений до определения зависящего от фазы свойства фазы многофазной рабочей текучей среды.
4. Способ по п.1, в котором многофазная рабочая текучая среда является влажным газом.
5. Способ по п.4, в котором
многофазная рабочая текучая среда включает в себя первую фазу и вторую фазу,
первая фаза включает в себя негазообразную текучую среду, а вторая фаза включает в себя газ.
6. Способ по п.4, в котором многофазная рабочая текучая среда включает в себя
первую фазу, включающую в себя первую негазообразную текучую среду, и
вторую фазу, включающую в себя вторую негазообразную текучую среду, и
третью фазу, включающую в себя газ.
7. Способ по п.1, в котором на этапе определения первого наблюдаемого свойства многофазной рабочей текучей среды определяют второе наблюдаемое свойство многофазной рабочей текучей среды.
8. Способ по п.7, в котором первое наблюдаемое свойство многофазной рабочей текучей среды представляет собой массовый расход, а второе наблюдаемое свойство представляет собой плотность.
9. Способ по п.1, дополнительно содержащий этап, на котором принимают одно или более измерений, соответствующих дополнительному свойству рабочей текучей среды.
10. Способ по п.9, в котором
дополнительное свойство многофазной текучей среды включает в себя одно или более из температуры многофазной текучей среды, давления, связанного с многофазной текучей средой, и обводненности многофазной текучей среды, и
на этапе определения наблюдаемого промежуточного значения, связанного с многофазной рабочей текучей средой, на основании первого наблюдаемого свойства определяют промежуточное значение на основании первого наблюдаемого свойства и дополнительного свойства.
11. Способ по п.1, в котором на этапе определения наблюдаемого промежуточного значения, связанного с многофазной рабочей текучей средой, на основании первого наблюдаемого свойства определяют объемную долю, связанную с количеством негазообразной текучей среды в многофазной рабочей текучей среде, и объемный расход многофазной текучей среды.
12. Способ по п.1, в котором на этапе определения наблюдаемого промежуточного значения, связанного с многофазной рабочей текучей средой, на основании первого наблюдаемого свойства определяют первое число Фруда, соответствующее негазовой фазе многофазной текучей среды, и второе число Фруда, соответствующее газовой фазе многофазной текучей среды.
13. Способ по п.1, в котором на этапе определения зависящего от фазы свойства фазы многофазной рабочей текучей среды на основании скорректированного промежуточного значения определяют массовый расход негазовой фазы многофазной текучей среды.
14. Расходомер, содержащий
вибрационную трубку Вентури, причем трубка Вентури содержит многофазную текучую среду,
возбудитель, подключенный к трубке Вентури и способный придавать движение трубке Вентури, чтобы трубка Вентури вибрировала,
датчик, подключенный к трубке Вентури и способный воспринимать движение трубки Вентури и генерировать сигнал датчика, и
контроллер, принимающий сигнал датчика и выполненный с возможностью:
определения первого наблюдаемого свойства многофазной рабочей текучей среды на основании движения вибрационной трубки Вентури,
определения наблюдаемого промежуточного значения, связанного с многофазной рабочей текучей средой, на основании первого наблюдаемого свойства,
определения скорректированного промежуточного значения на основании отображения между наблюдаемым промежуточным значением и предыдущим скорректированным промежуточным значением, и
определения зависящего от фазы свойства фазы многофазной рабочей текучей среды на основании скорректированного промежуточного значения.
15. Расходомер по п.14, в котором отображение представляет собой нейронную сеть, способную определять ошибку в промежуточном значении, обусловленную наличием многофазной рабочей текучей среды.
16. Расходомер по п.14, в котором контроллер дополнительно выполнен с возможностью
определения того, что наблюдаемое промежуточное значение находится в первой заданной области значений до определения скорректированного промежуточного значения, и
определения того, что скорректированное промежуточное значение находится во второй заданной области значений до определения зависящего от фазы свойства фазы многофазной рабочей текучей среды.
17. Расходомер по п.14, в котором многофазная рабочая текучая среда является влажным газом.
18. Расходомер по п.14, в котором определение первого наблюдаемого свойства многофазной рабочей текучей среды включает в себя определение второго наблюдаемого свойства многофазной рабочей текучей среды.
19. Расходомер по п.18, в котором первое наблюдаемое свойство многофазной рабочей текучей среды представляет собой массовый расход, и второе наблюдаемое свойство представляет собой плотность.
20. Расходомер по п.18, в котором контроллер дополнительно выполнен с возможностью приема одного или более измерений, соответствующих второму наблюдаемому свойству рабочей текучей среды.
21. Расходомер по п.14, в котором определение наблюдаемого промежуточного значения, связанного с многофазной рабочей текучей средой, на основании первого наблюдаемого свойства включает в себя определение первого числа Фруда, соответствующего негазовой фазе многофазной текучей среды, и второго числа Фруда, соответствующего газовой фазе многофазной текучей среды.
22. Передатчик расходомера, содержащий
по меньшей мере, одно устройство обработки, и
запоминающее устройство, причем в запоминающем устройстве хранятся инструкции, предписывающие, по меньшей мере, одному устройству обработки
определять первое наблюдаемое свойство многофазной рабочей текучей среды на основании движения вибрационной трубки Вентури,
определять наблюдаемое промежуточное значение, связанное с многофазной рабочей текучей средой, на основании первого наблюдаемого свойства,
определять скорректированное промежуточное значение на основании отображения между наблюдаемым промежуточным значением и предыдущим скорректированным промежуточным значением, и
определять зависящее от фазы свойство фазы многофазной рабочей текучей среды на основании скорректированного промежуточного значения.
23. Передатчик по п.22, в котором многофазная рабочая текучая среда является влажным газом.
24. Передатчик по п.22, в котором в запоминающем устройстве дополнительно хранятся инструкции, предписывающие, по меньшей мере, одному устройству обработки принимать одно или более измерений, соответствующих второму наблюдаемому свойству рабочей текучей среды.
25. Передатчик по п.22, в котором определение наблюдаемого промежуточного значения, связанного с многофазной рабочей текучей средой, на основании первого наблюдаемого свойства включает в себя определение первого числа Фруда, соответствующего негазовой фазе многофазной текучей среды, и второго числа Фруда, соответствующего газовой фазе многофазной текучей среды.
| US 20060156831 А1, 20.07.2006 | |||
| US 2005061060 A1, 24.03.2005 | |||
| US 2005284237 A1, 29.12.2005 | |||
| US 2005216242 A1, 29.09.2005 | |||
| ДЕНСИМЕТР С ВИБРИРУЮЩЕЙ ТРУБКОЙ | 1993 |
|
RU2140068C1 |
Авторы
Даты
2012-06-20—Публикация
2007-08-28—Подача