Область техники
Изобретение относится к области квантовой физики, квантовой механики, атомной физики, квантовых компьютеров, сверхпроводимости, переключателей, модуляторов и может быть использовано в логических схемах, квантовых компьютерах и в других областях, где требуется сверхбыстрое переключение, модуляция и усиление сигнала.
Предшествующий уровень техники
Известен, основанный на эффекте Джосефсона [1-3], способ переключения бозонов между двумя связанными квантовыми состояниями «0» и «1» с волновыми функциями ψ0 и ψ1, характеризуемыми концентрациями бозонов |ψ00|2 и |ψ10|2, и коэффициентом связи K. В этом способе управляют переходом бозонов между двумя сверхпроводниками, разделенными тонким слоем изолятора. В качестве бозонов используют куперовские пары электронов - квазичастицы, имеющие целый спин и подчиняющиеся статистике Бозе-Эйнштейна. Заряд куперовской пары равен удвоенному заряду электрона: q=2e. К двум сверхпроводникам, разделенным тонким слоем изолятора, прикладывается электрическое напряжение. Если напряжение отсутствует, то между сверхпроводниками течет ток. Если прикладывают постоянное во времени напряжение U=Uconsn, то ток ослабевает или вообще прекращается. Если прикладывают переменное напряжение: U=Uconst+vcos(ωt), частота которого ω соответствует постоянной составляющей напряжения ω=qUconst/ħ, то через контакт пойдет ток. Таким образом, электрический ток, характеризующий переход бозонов между двумя пространственно-разделенными квантовыми состояниями, зависит от приложенного электрического напряжения. Иными словами, переходом бозонов можно управлять с помощью электрического напряжения. Этот способ является наиболее близким к заявленному способу и выбран в качестве прототипа.
Способ, выбранный в качестве прототипа, имеет недостаток, заключающийся в том, что переход бозонов осуществляется недостаточно эффективно, а возможности по управлению переходом бозонов ограничены.
Раскрытие изобретения
Технические результаты, достигаемые благодаря изобретению, заключаются в том, что значительно повышается чувствительность к изменению параметра α, который, как правило, представляет разность потенциалов, приложенную к переходу. Техническим результатом является также управление переходом бозонов путем сравнительно небольшого изменения их концентрации.
Указанные технические результаты достигаются в способе переключения бозонов между двумя связанными квантовыми состояниями «0» и «1» с волновыми функциями ψ0 и ψ1, характеризуемыми концентрациями бозонов |ψ00|2 и |ψ10|2, и коэффициентом связи К, причем суммарную концентрацию бозонов |ψ00|2+|ψ10|2 создают больше порогового значения, рассчитываемого заранее или подбираемого экспериментально исходя из того, что дифференциальный коэффициент усиления
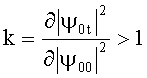
и вызывают переключение бозонов из одного квантового состояния в другое квантовое состояние, изменяя концентрацию бозонов, по меньшей мере, в одном из квантовых состояний (при этом меняют и суммарную концентрацию) или разность фаз этих квантовых состояний или разность потенциалов этих квантовых состояний. В результате переключения увеличение концентрации бозонов в одном квантовом состоянии равно уменьшению концентрации бозонов в другом квантовом состоянии.
Суммарную концентрацию бозонов |ψ00|2+|ψ1||2 можно создавать больше порогового значения, равного K/θ, где θ - коэффициент нелинейности ансамбля бозонов (в состояниях «0» и «1»).
Суммарную концентрацию бозонов |ψ00|2+|ψ10|2 можно создавать такой, что она удовлетворяет неравенству:
2K/|θ|<|Ψψ00|2+|ψ|2<6K/|θ|,
где θ - коэффициент нелинейности ансамбля бозонов.
При этом в начальный момент времени можно создавать концентрацию бозонов в состоянии «0», по меньшей мере, на порядок (в 10 раз) большей, чем концентрацию бозонов в состоянии «1», т.е. выполнять условие |ψ00|2>>|ψ10|2.
В начальный момент времени можно создавать концентрацию бозонов в состоянии «0» равной к концентрации бозонов в состоянии «1» или близкой, удовлетворяющей неравенству:
|ψ10|2-|ψ00|2<<|ψ10|2+|ψ00|2.
Бозоны могут полностью или частично находиться в состоянии бозе-эйнштейновского конденсата.
Квантовые состояния «0» и «1» с волновыми функциями ψ0 и ψ1 могут иметь различную энергию.
Квантовые состояния «0» и «1» с волновьми функциями ψ0 и ψ1 могут быть пространственно разделенными.
В качестве бозонов могут использоваться или куперовские пары электронов, или экситоны, или атомный конденсат, или молекулы с целым или нулевым спином, или магноны, или плазмоны.
Используемый в качестве бозонов атомный конденсат может состоять из атомов щелочных металлов.
Используемыми в качестве бозонов молекулами могут быть молекулы СО.
Переключать бозоны можно между двумя потенциальными ямами, туннельно-связанными между собой.
Для изменения концентрации бозонов, по меньшей мере, в одном из квантовых состояний, на используемый в качестве бозонов атомный конденсат могут воздействовать электромагнитным излучением. Воздействовать электромагнитным излучением могут с определенной частотой или изменяя частоту электромагнитного излучения или изменяя интенсивность излучения, воздействующего на атомный конденсат. Воздействовать могут электромагнитным излучением радиодиапазона.
Изменяя суммарную концентрацию бозонов в пределах 1%, например, путем изменения концентрации бозонов в одном из квантовых состояний, можно инициировать изменение концентраций в каждом из квантовых состояний более чем на 20%.
Переключать бозоны можно между двумя туннельно-связанным между собой и пространственно-разделенными каналам, по которым распространяются бозоны. При этом бозоны могут распространяться в обоих каналах в одном направлении. Каналы могут представлять собой два туннельно-связанных сверхпроводника, разделенных тонким изолятором. Сверхпроводники могут быть изготовлены в виде сверхпроводящих полосок, или пленок, или проводов.
В качестве бозонов могут быть плазмоны, которые распространяются по плазменному волноводу или по плазменным волноводам. Плазмоны могут распространяться вдоль двух плазменных волноводов, туннельно-связанных между собой. Поперек плазменного волновода можно пропускать электрический ток. В плазменный волновод можно дополнительно вводить оптическое излучение от полупроводникового диода или лазера.
Температура ансамбля бозонов может не превышать 10 градусов Кельвина, или 1 градус Кельвина, или даже не превышать 10-5 градуса Кельвина.
Указанные технические результаты достигаются в способе переключения бозонов между двумя связанными квантовыми состояниями «0» и «1» с волновыми функциями ψ0 и ψ1, характеризуемыми концентрациями бозонов |ψ00|2 и |ψ10|2, энергиями Е0 и E1, причем E0<E1, и коэффициентом связи K, при этом создают суммарную концентрацию бозонов |ψ00|2+|ψ10|2 больше порогового значения, предварительно воздействуют электромагнитным излучением с частотой ω, такой что |(E1-E0)-ωħ|<10|K|, (по сути это критерий связанности состояний, где α=(E1-E0)-ωħ является параметром расстройки или неидентичности состояний), а затем вызывают переключение бозонов из одного квантового состояния в другое квантовое состояние, изменяя частоту или интенсивность электромагнитного излучения.
Коэффициент связи может удовлетворять формуле 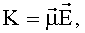 где
где 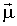 - средний электрический дипольный момент состояний,
- средний электрический дипольный момент состояний, 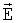 - напряженность электрического поля.
- напряженность электрического поля.
Коэффициент связи может удовлетворять формуле 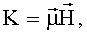 где
где 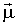 - средний магнитный дипольный момент состояний,
- средний магнитный дипольный момент состояний, 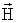 - напряженность магнитного поля.
- напряженность магнитного поля.
Электромагнитное излучение может быть оптическим или радиочастотным.
Предварительно могут воздействовать электромагнитным излучением с частотой ω, такой что 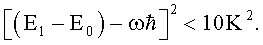
Краткое описание чертежей
Изобретение поясняется графиками на фигурах 1, 2, 3, 4, 5, 6, 7, 8, построенными на основе математического моделирования переключения в квантовой системе.
В соответствии с графиком на Фиг.1 перекачка во времени между двумя связанными квантовыми состояниями: в линейном случае (а); в нелинейном режиме (б) вблизи средней точки переключения М (r≈1), когда значение |ψ00|2 близко к критическому значению |ψ0M|2=4K|θ|. Параметр расстройки α=0.
|ψ1t|2=|ψ00|2+|ψ10|2-|ψ0t|2.
На Фиг.2 представлена зависимость |ψ0t|2/|ψ00|2 от |ψ00|2/|ψ0M|2. Переключение в квантовой нелинейной системе между двумя связанными квантовыми состояниями; α=0; ψ10=0. При изменении |ψ00|2 вблизи значения |Ψ0M|2 происходит резкое изменение конечного состояния |ψ0t|2·|ψ0M|2=4K/|θ|. Пунктиром обозначены: точка, где коэффициент дифференциального усиления k становится >1 и средняя точка переключения M, где k=mах. T=1.4π. Условие k>1 определяет пороговую концентрацию бозонов.
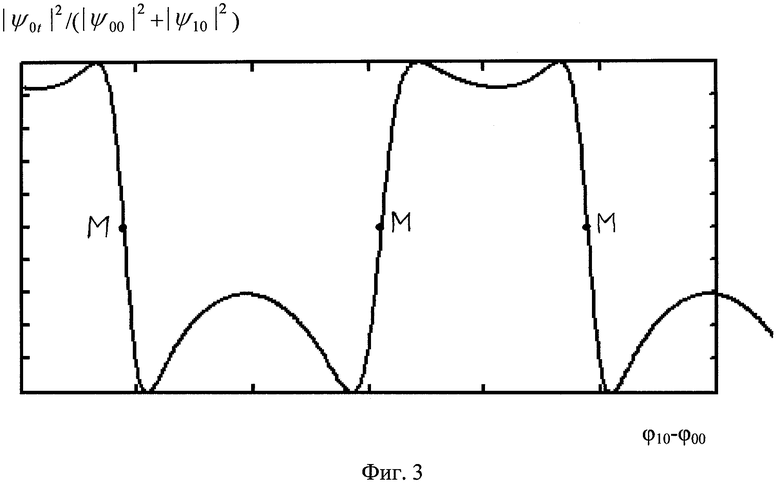
На Фиг.3 представлена зависимость |ψ0t|2/(|ψ00|2+|ψ10|2) от начальной разности фаз двух квантовых состояний φ10-φ00. T=1.6π. α=0. |ψ10|2/|ψ0M|2=0.005; |ψ00|2/|ψ0M|2=0.99.
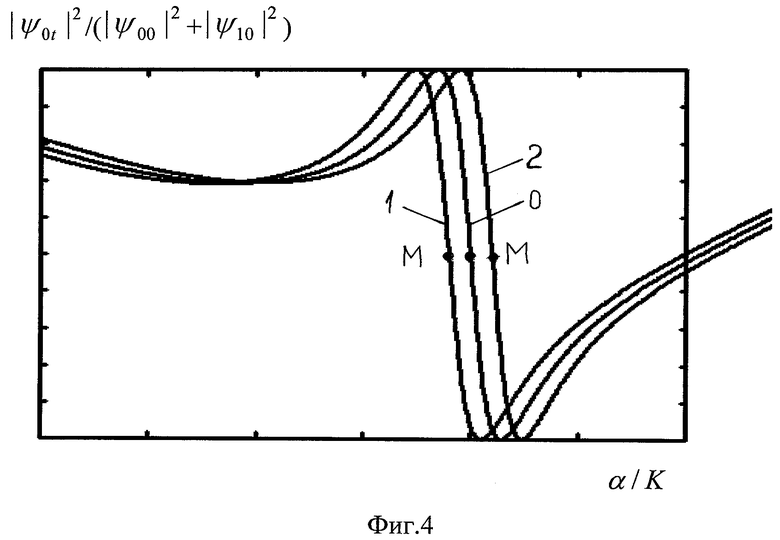
На Фиг.4 представлена зависимость |ψ0t|2/|ψ00|2 от ξ=α/K вблизи средней точки переключениям: M: |θ||ψ00|2/4K=0.99 (кривая 1), 1 (0), 1.01 (2). T=2π.
На Фиг.5 показаны две сверхпроводящих пленки (полоски, провода), разделенные тонким слоем изолятора.
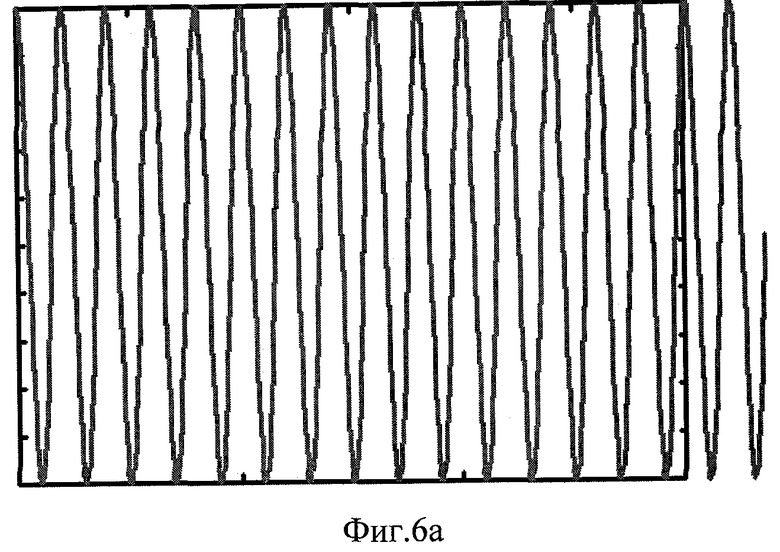
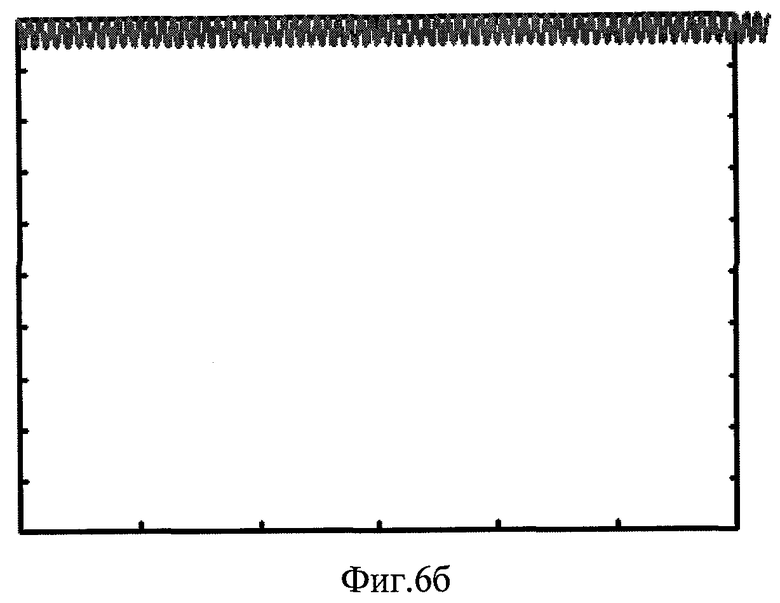
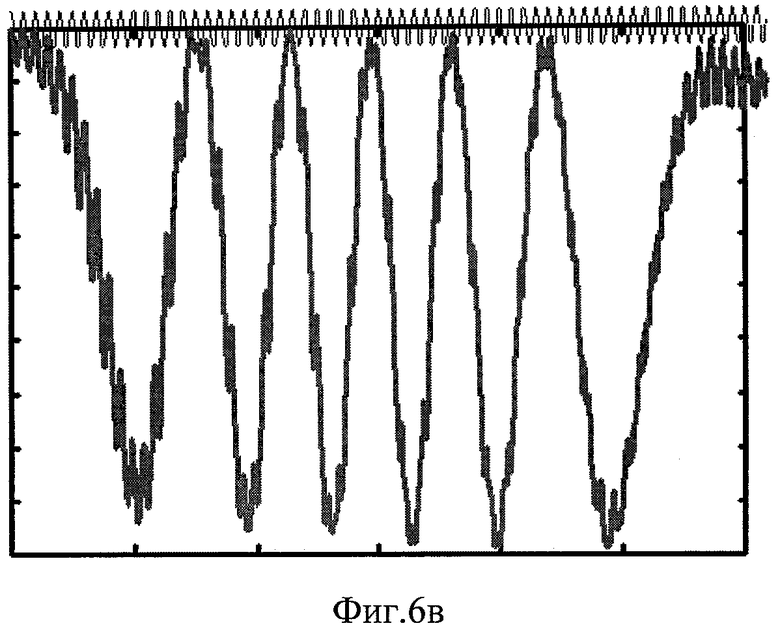
Фиг.6. Результаты моделирование известного «линейного» эффекта Джозефсона. Зависимости |Ψ0t|2/(|ψ00|2+|ψ10|2) от времени t при R0=|θ||ψ00|2/4K=0.1, ψ10=0 и различных напряжениях на переходе. Фиг.6а - напряжение на переход не подается; б - на переход подается постоянное напряжение, соответствующее удвоенному коэффициенту связи (α=2K); в - на переход подается постоянное и слабое переменное напряжение, причем частота переменного соответствует постоянной составляющей, а постоянная составляющая соответствует 2K (см. также пояснение в тексте).
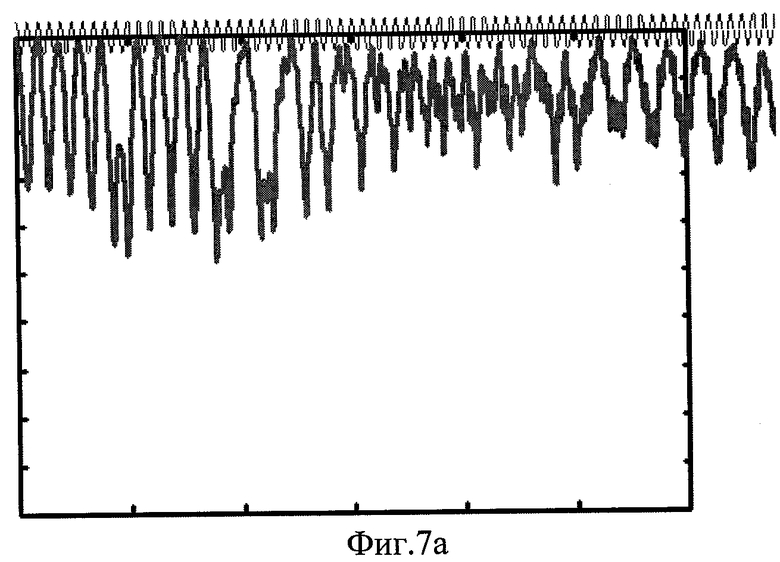
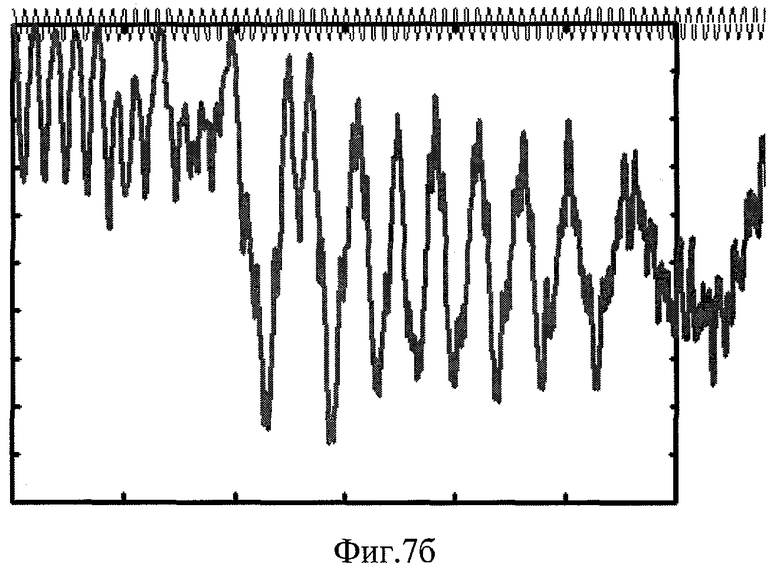
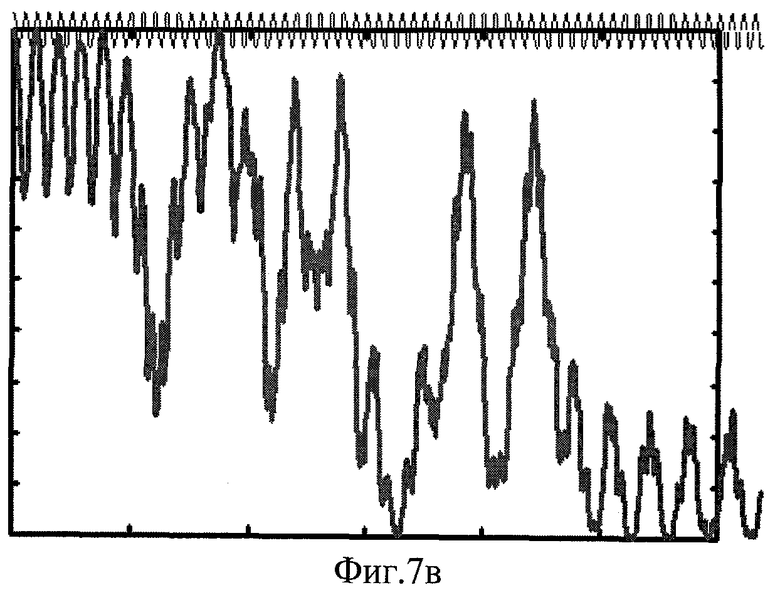
Фиг.7. Результаты моделирования нелинейного эффекта переключения. Зависимости |ψ0t|2/(|ψ00|2+|ψ10|2) от времени t при R0=|θ||ψ00|2/4K=1.9(а), R0=1.95(б), R0=2(в). Остальные параметры - те же, что для Фиг.6в. Аналогично Фиг.6в на переход подается постоянное и слабое переменное напряжение, причем частота переменной составляющей соответствует величине постоянной составляющей, а постоянная составляющая соответствует удвоенному коэффициенту связи (см. пояснение в тексте).
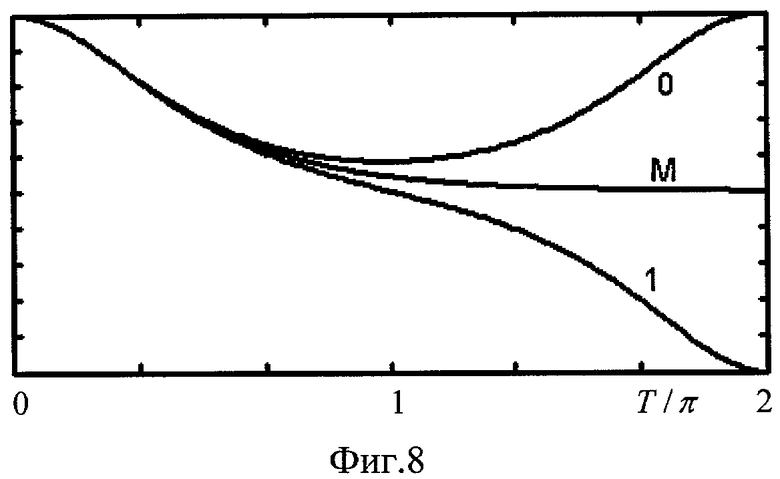
Фиг.8. Зависимости |ψ0t|2/(|ψ00|2+|ψ10|2) от «нормированного» времени Т/π при R0=|θ||ψ00|2/4K=0.985 (кривая «1»), R0=1.015 (кривая «0»), R0=1 (кривая «M») α=0.
Лучшие варианты использования изобретений
Класс систем с двумя связанными квантовыми состояниями подробно описан в книге Фейнмана [1]. Два связанных квантовых состояния, амплитуды их волновые функции которых аналогичны амплитудам однонаправленных распределенно-связанных волн (ОРСВ) и описываются уравнениями [1]:
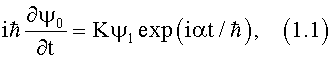
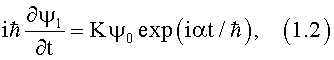
где K - коэффициент связи квантовых состояний; природа связи определяется спецификой квантовой системы [1-4], α=E1-E0 - параметр расстройки, характеризующий степень неидентичности состояний.
Между связанными квантовыми состояниями синусоидальный обмен энергией происходит во времени (фиг.1а). При α=0 и ψ1(t=0)=ψ10=0 вероятность j-ого состояния (j=0,1):
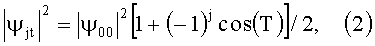
где T=2πtK/ħ, ψ00(t=0)=ψ00, ψj(t)=ψjt.
Если связанные квантовые состояния идентичны (α=0), то перекачка энергии полная, если неидентичные (α≠0), то перекачка неполная. Глубина перекачки ∝K2/(K2+α2), а частота перекачки ∝(K2+α2)1/2/ħ.
В 1987 году автором предсказано [5] явление переключения в нелинейных квантовых системах со связанными квантовыми состояниями и сказано следующее [5]:
«Эффект, аналогичный самопереключению (точнее аналогичный эффект неустойчивости), присущ, по-видимому, не только однонаправленным распределенно-связанным электромагнитным волнам и солитонам, набег фазы которых зависит от интенсивности, но также и другим системам, в частности квантовым системам (осцилляторам, электронам, атомам, другим частицам, квазичастицам и т.д.), волновые функций которых описываются связанными нелинейными уравнениями Шредингера типа:
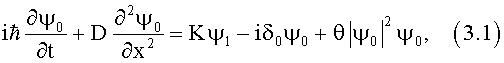
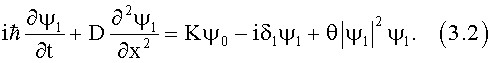
Эти уравнения, по-существу, совпадают с уравнениями, рассмотренными в [6-10], лишь координата заменяется временем, а время - координатой, если учитываются члены со вторыми производными [10]) и амплитуды двух связанных волн заменяются волновыми функциями ψ0 и ψ1 двух связанных между собой квантовых состояний. Если нелинейности нет, то между связанными состояниями идет периодический, синусоидальный во времени обмен энергией. Если есть нелинейность (θ≠0), то при выполнении условия, аналогичного условию самопереключения, которое в простейшем случае идентичных состояний и ψ0(t=0)=ψ00≠0, ψ1(t=0)=ψ10=0 соответствует |ψ00|2=4K/|θ|, период стремится к бесконечности и малое изменение начальных состояний |ψ00|2 и |ψ10|2, а также величины Re(ψ10ψ* 00) должно приводить к резкому изменению конечных (за заданный промежуток времени tK) состояний, т.е. величин |ψ0(tK)|2 и |ψ1(tK)|2».
Признаком этого нелинейного эффекта переключения является характерная форма кривых |ψ0|2 и |ψ1|2 во времени, вблизи средней точки переключения (см. фиг.1б). Переключение (фиг.2-4) может вызываться малым воздействием на систему в средней точке М и найти применение при создании квантовых компьютеров. В [5] оценка условия переключения дана для δ0=δ1=0, 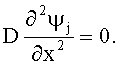
Отметим, что аналогичное явление самопереключения света было открыто и исследовано в работах [5-15], причем в [11, 12] оно впервые наблюдалось в экспериментах. Поэтому результаты теории [13, 14] могут быть использованы и для описания предлагаемого в данном изобретении способа переключения бозонов.
Связанные макроскопические квантовые состояния (СМКС) реализуются в двух нелинейных связанных потенциальных (квантовых) ямах, как правило - туннельно-связанных квантовых ямах (ТСКЯ). Эти макроскопические состояния реализуются за счет заполнения квантовых (потенциальных) ям квазичастицами с целым спином. Поэтому эти частицы могут образовывать бозе-эйнштейновский конденсат. К таким квантовым системам относится система из двух туннельно-связанных сверхпроводников с куперовскими парами электронов [1-3]. Другой системой этого класса являются ТСКЯ, в частности, туннельно-связанные квантовые точки с экситонами или биэкситонами. Имея целый спин, являясь бозонами, экситоны способны образовывать бозе-эйнштейновский конденсат и объединяться в кластеры. Третьим примером системы этого класса являются атомные бозе-эйнштейновские конденсаты [16] в магнитных ловушках, связанные между собой. Они формируются на основе сверхохлажденных атомов разреженных паров щелочных металлов (цезия, рубидия, натрия, лития) или атомарного водорода. Возможны и другие системы этого класса, например, на основе ТСКЯ или туннельно-связанных оптических волноводах (ТСОВ) с плазмонами.
ТСОВ аналогичны ТСКЯ. Глубина квантовой (потенциальной) ямы аналогична показателю преломления волноводного слоя. Поперечный профиль показателя преломления ТСОВ аналогичен профилю потенциальной энергии в ТСКЯ. Собственное значение энергии в квантовой яме аналогично эффективному показателю преломления оптического волновода. Куперовские пары электронов и другие бозоны аналогичны фотонам. Одной из таких квантовых систем, описанной в книге Фейнмана [1], являются два сверхпроводника, разделенные тонким (порядка 10А) изолятором. Такое устройство называется переходом Джосефсона [3] и описывается уравнениями [1]:
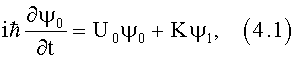
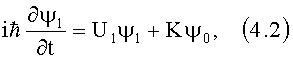
которые сводятся к уравнениям (1). Куперовские пары электронов так же, как фотоны, являются бозонами и могут скапливаться в одном низшем квантовом состоянии, образуя бозе-эйнштейновский конденсат.
В случае квантовых ям нелинейность обусловлена зависимостью энергии частиц (находящихся в квантовой яме), т.е. глубины квантовой ямы, от плотности этих частиц и, следовательно, от квадрата модуля волновой функции ψ*ψ=|ψ|2. Глубина квантовой ямы зависит от энергии взаимодействия частиц, находящихся в квантовой яме. С другой стороны, в сверхпроводнике реализуется макроскопическое квантовое состояние [1-3]. Когда ψ - волновая функция каждой из огромного числа частиц, поголовно пребывающих в одном и том же состоянии, то в этом случае Ψ*Ψ можно отождествить с плотностью частиц. Если в этих условиях все частицы несут одинаковые заряды, то мы можем пойти дальше и отождествить ψ*ψ с плотностью электричества [1].
Например, глубина квантовой ямы зависит от энергии электростатического взаимодействия куперовских пар, находящихся в квантовой яме. Она, в свою очередь, зависит от их суммарного заряда, который пропорционален квадрату модуля волновой функции. Этим объясняется наличие в уравнениях нелинейных членов θ0 |ψ0|2 ψ0 и θ1|ψ1|2 ψ1. Уравнения должны иметь вид:
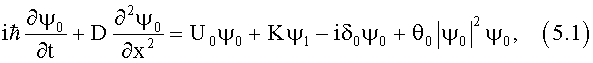
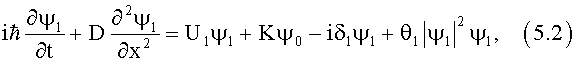
где 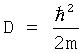 и, как правило, θ0=θ1=θ. Если пренебречь членами, содержащими θ и D, эти уравнения переходят в известные уравнения [1]. Параметр α=U1-U0 (приложенное напряжение) аналогичен параметру α=β1-β0 - разности эффективных показателей преломления ТСОВ. Это - параметр неидентичности ТСОВ или связанных квантовых состояний. Для прямоугольных квантовых ям членом, содержащим D, можно пренебречь. Кулоновское отталкивание куперовских пар должно способствовать их растеканию из потенциальной ямы. В этом смысле квантовая нелинейность аналогична нелинейности, которая ответственна за дефокусировку света. Для явления самопереключения волн знак нелинейности учитывается функцией sign(θ), входящей в решения и конечные формулы для модулей и фаз амплитуд [5, 13, 14].
и, как правило, θ0=θ1=θ. Если пренебречь членами, содержащими θ и D, эти уравнения переходят в известные уравнения [1]. Параметр α=U1-U0 (приложенное напряжение) аналогичен параметру α=β1-β0 - разности эффективных показателей преломления ТСОВ. Это - параметр неидентичности ТСОВ или связанных квантовых состояний. Для прямоугольных квантовых ям членом, содержащим D, можно пренебречь. Кулоновское отталкивание куперовских пар должно способствовать их растеканию из потенциальной ямы. В этом смысле квантовая нелинейность аналогична нелинейности, которая ответственна за дефокусировку света. Для явления самопереключения волн знак нелинейности учитывается функцией sign(θ), входящей в решения и конечные формулы для модулей и фаз амплитуд [5, 13, 14].
Для описания двух туннельно-связанных атомных конденсатов (в магнитных ловушках) можно использовать связанные уравнения:
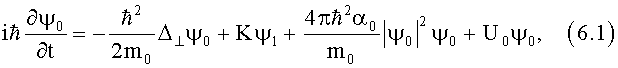
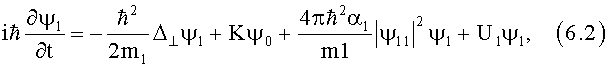
Уравнения (6) являются связанными нелинейными уравнениями Шредингера. При K=0 эти уравнения распадаются на два уравнения Гросса-Питаевского [16]. Потенциалы Uj, характеризуют магнитооптическую ловушку и их равенство U0=U1 соответствует α=0.
Обычно α0=α1=α. Уравнения (6) совпадают с уравнениями (5), (3), если положить 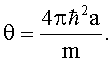 Нелинейные члены обусловлены столкновениями атомов, их рассеянием друг на друге; a - (грубо говоря) диаметр атомов, точнее - длина рассеяния или амплитуда s - рассеяния медленных атомов друг на друге. Число столкновений пропорционально концентрации частиц (бозонов). Поэтому нелинейные члены пропорциональны концентрации частиц (бозонов), ∝|ψj|2.
Нелинейные члены обусловлены столкновениями атомов, их рассеянием друг на друге; a - (грубо говоря) диаметр атомов, точнее - длина рассеяния или амплитуда s - рассеяния медленных атомов друг на друге. Число столкновений пропорционально концентрации частиц (бозонов). Поэтому нелинейные члены пропорциональны концентрации частиц (бозонов), ∝|ψj|2.
Итак, нелинейные члены в (5), (6) пропорциональны концентрации квазичастиц - бозонов и обусловлены их взаимодействием.
Аналогичные нелинейные связанные уравнения Шредингера применимы для описания других ТСКЯ с бозонами: экситонов (биэкситонов) в ТСКЯ, в частности, в туннельно-связанных квантовых точках; а также для описания плазмонов в ТСКЯ, в туннельно-связанных квантовых точках и в ТСОВ; связанных магнонов в нелинейном режиме и других систем.
Обозначим начальные и конечные значения волновых функций: ψj(t=0)=ψj0, ψj(t)=ψjt. Тогда модули и фазы амплитуд ψj=ρjехр(φj), ψjt=ρjtехр(iφjt), ψj0=ρj0ехр(iφj0), j=0,1. Решение (5) и (6) позволяет найти квадраты модулей волновых функций и разность фаз между ними в момент времени t через эти величины в начальный момент времени. Вместо этих трех величин для описания квантовой системы можно использовать три параметра Стокса [13].
В простейшем случае идентичных состояний: α=0, например, сверхпроводников при одинаковых потенциалах (U1=U0), и сосредоточения при t=0 всех бозонов в «нулевом» состоянии: Ψ00≠0, Ψ10=0 (например, в «нулевом» сверхпроводнике), явление переключения иллюстрируется фиг.2. Решение при этом имеет вид [8, 9, 13, 14]:
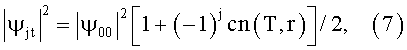
где T=2πtK/ħ - количество периодов перекачки энергии между двумя связанными квантовыми состояниями (в линейном режиме), умноженное на число π; r=|ψ00|2|θ|/4K - модуль эллиптической функции; j=0,1. При r=0 решение (7) переходит в (2).
Для неидентичных состояний (α≠0), например, сверхпроводников при различных потенциалах (U1≠U0) решения системы уравнений (5) и их анализ даны в [13, 14]. Так же, как для случая ψ00≠0, ψ10≠0. Эти решения выражаются через эллиптические функции с модулем r.
Переключение достигается вблизи средней точки переключения М (фиг.2), где r=1. Это условие переключения достигается при определенной, достаточно большой концентрации бозонов. В средней точке переключения (r=1) происходит автосинхронизация фаз квантовых состояний [13] и в процессе переключения фазы квантовых состояний меняются по закону [13, 14, 5].
На основе квантового переключения можно создать аналог оптического транзистора [5-15] - квантовый транзистор: изменение начальной плотности бозонов (в одной из ТСКЯ) вызывает во много раз большее изменение конечной плотности бозонов в обоих ТСКЯ. Этот квантовый транзистор можно использовать для усиления и модуляции сигналов и создания логических элементов для квантовых компьютеров. Его можно назвать бозонным транзистором. Коэффициент усиления изменения плотности бозонов (заряда - для куперовских пар) в средней точке переключения M: r=1 при α=0, ψ00≠0, ψ10=0 оценивается формулой [7, 8, 12]:
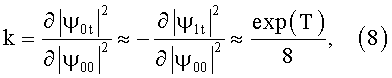
где физический смысл T=2πtK/ħ, пояснен выше. В более сложных случаях k оценивается формулами аналогичными [5, 9, 13, 14].
Следует отметить, что условие k>1 определяет пороговую концентрацию бозонов.
Переключение может осуществляться изменением начальной разности фаз двух квантовых состояний (фиг.3) при ψ00≠0, ψ10≠0.
Кроме того, резкое переключение может осуществляться изменением параметра α, который легко варьировать с помощью приложенной разности потенциалов (фиг.4); а также - изменением K. При этом система должна находиться вблизи средней точки переключения, т.е. r≠1. Это условие достигается при определенной, достаточно большой концентрации бозонов.
Переключение бозонов может происходить и при их распространении вдоль продольной координаты, которую обозначим как "z". В этом случае их взаимодействие и обмен энергией и плотностью между двумя состояниями происходит по мере распространения бозонов.
Для плазмонов это соответствует их взаимодействию в ТСОВ, при их распространении вдоль продольной координаты ТСОВ. Для куперовских пар - при их распространении вдоль туннельно-связанных сверхпроводников. В этом случае их самопереключение в точности аналогично самопереключению ОРСВ в нелинейно-оптической среде, в частности самопереключению фотонов в нелинейных ТСОВ [5-15], и описывается теми же формулами [5, 8, 9, 13, 14]. В частности, коэффициент усиления изменения плотности бозонов (заряда - для куперовских пар) в средней точке переключения M: r≠1 при α=0, ψ00≠0, ψ10=0 оценивается формулой [8, 12]:
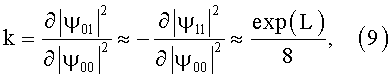
где физический смысл L=2πlK/λВ - число перекачек между связанными волнами де Бройля, соответствующими связанным бозонам (в частности - в туннельно-связанных ансамблях бозонов) в линейном режиме, когда θ ≡ 0, l - длина связи волн де Бройля для бозонов, λВ - длина волны де Бройля для бозонов. В более сложных случаях k оценивается формулами аналогичными [5, 13-14].
Рассмотренные переключения реализуются, как правило, при «гелиевых» температурах.
Аналогичное переключение возможно в условиях движения избыточного электрона или экситона в одномерных молекулярных цепях (белковых молекулах) [17], связанных между собой.
Аналогичное переключение также возможно в условиях взаимодействия двух связанных квантовых ангармонических осцилляторов.
Рассмотрим подробнее отличие заявленного способа от способа, основанного на эффекте Джозефсона. Для этого смоделируем эффект Джозефсона на основе численного решения уравнений. На фигурах 6 и 7 по оси абсцисс отложено время, а по оси ординат - нормированная концентрация бозонов в квантовом состоянии «0». Подчеркнем, что эффект Джозефсона - линейный, т.е. не зависит от концентрации бозонов (в отличие от используемого нами нелинейного эффекта). Линейный режим представлен на Фиг.6. При R0=|ψ00|2/|ψ0M|2=0.1, пусть напряжение между сверхпроводниками отсутствует, тогда между сверхпроводниками течет синусоидальный ток (Фиг.6а).
Теперь приложим к переходу постоянное во времени напряжение U=Uconst. Причем это напряжение соответствует удвоенному коэффициенту туннельной связи: U=α=Uconst=2·K. Тогда ток ослабевает или вообще прекращается. Точнее, его амплитуда уменьшается во много раз (Фиг.6б).
Теперь к переходу прикладывают переменное напряжение: U=α=Uconst+vcos(ωt) с малой амплитудой, частота которого ω соответствует постоянной составляющей напряжения ω=qUconst/ħ, причем по-прежнему Uconst=2·K. Иными словами, к переходу одновременно прикладывают постоянное напряжение Uconst=2·K и переменное напряжение с малой амплитудой v и определенной частотой, указанной выше. Тогда через контакт пойдет ток. Амплитуда тока между двумя сверхпроводниками увеличилась во много раз (Фиг.6в) и стала примерно такой, какой была на Фиг.6а. Т.е. глубина перекачки бозонов (куперовских пар) снова стала почти стопроцентной (Фиг.6в). Это так называемый нестационарный эффект Джозефсона. В верхней части Фиг.6в показано малое (для наглядности увеличенное в 100 раз на фигуре) переменное, синусоидальное, напряжение, приложенное к переходу. Нулевое значение напряжения (переменной составляющей) соответствует верхней горизонтальной оси на этой фигуре. Подчеркнем, что для всех трех Фигур 6 (а, б, в) выполнялся линейный режим: R0=|ψ00|2/|ψ0M|2=0.1<<1.
Теперь рассмотрим проявление эффекта, используемого в настоящем изобретении. Он является нелинейным и проявляется при существенно больших значениях R0=|ψ00|2/|ψ0M|2, а именно при превышении R0 порогового значения. Сохраним остальные параметры, такими же, как для Фиг.6в. Т.е. по-прежнему будем считать, что к переходу приложено напряжение, имеющее постоянную и переменную составляющие, соотношение между параметрами которых такое же, как для Фиг.6в. Но выберем R0=|ψ00|2/|ψ0M|2=1.9. Тогда результат будет таким, как на Фиг.7а, т.е. бозоны по истечении определенного времени сосредоточены, в основном, в нулевом состоянии. Зададим чуть большее значение начальной концентрации бозонов в состоянии «0», соответствующее R0=1.95. Тогда по истечении определенного времени бозоны поделятся примерно поровну между состояниями «0» и «1» (Фиг.7б). Если же еще немного увеличить начальную концентрацию бозонов, т.е. задать R0=2, то по истечении определенного времени большая часть бозонов переключится в состояние «1» (Фиг.7в).
Таким образом, наличие малой по амплитуде переменной составляющей напряжения на переходе позволяет осуществлять глубокое переключение (с участием порядка 100% бозонов) между состояниями «0» и «1» даже при достаточно большой (порядка 2·K) постоянной разности потенциалов на переходе (Фиг.7).
Подчеркнем, что для осуществления переключения предлагаемым способом не обязательно одновременно подавать постоянное напряжение и переменное напряжение на переход. Переключение можно осуществить и при нулевом постоянном напряжении на переходе (см. Фиг.8, Фиг.2).
Подчеркнем также, что в линейном режиме (в условиях эффекта Джозефсона) нельзя осуществить резкое переключение бозонов путем малого изменения величины ξ=α/K, например, за счет изменения подаваемого на переход напряжения. Иными словами, при малых параметрах R0=|θ||ψ00|2/4K, например, при R0=0.1 график зависимости |Ψ0t|2/|Ψ00|| от величины ξ=α/K на Фиг.4 представлял бы отрезок горизонтальной прямой. Т.е. концентрация бозонов почти не зависела бы от приложенного напряжения.
Приведем другие варианты осуществления изобретения.
Пример 1. Использовался атомный конденсат атомов натрия, в начальный момент времени находящийся в одной из пространственно разделенных туннельно-связанных магнитных ловушках («нулевой»), причем удалось достигнуть концентрации (плотности) атомов 0.5·1019 см3. Масса атома натрия m≈3.82·10-23 г. Согласно [16] можно считать α≈30 нм=3·10-8 см. Нелинейность составляла порядка 10-37 см3эрг. Коэффициент (энергия) туннельной связи составлял порядка 1,23·10-19 эрг. Эта соответствовало времени одной линейной перекачки порядка 4 нс. Такие параметры соответствуют средней точке переключения М: R0=|θ||ψ00|2/4K=1, т.е. модуль эллиптической функции примерно равен единице. При этих параметрах через время порядка 12 нс, соответствующее трем «линейным» перекачкам (т.е. в линейном режиме) между двумя туннельно-связанными квантовыми состояниями, количество атомов разделится между ловушками примерно поровну (кривая М на Фиг.8). Пусть теперь происходит увеличение числа атомов на 100 атомов в нулевой ловушке. Тогда через такое же время (порядка 12 нс) количество атомов в этой ловушке увеличивается примерно на 150000, а в другой ловушке - уменьшается примерно на такое же число - 150000. Коэффициент усиления изменения бозонов составляет примерно 1500.
Коэффициент связи можно менять (регулировать) с помощью изменения параметров лазерного или другого электромагнитного излучения за счет регулирования высоты и/или ширины потенциального барьера.
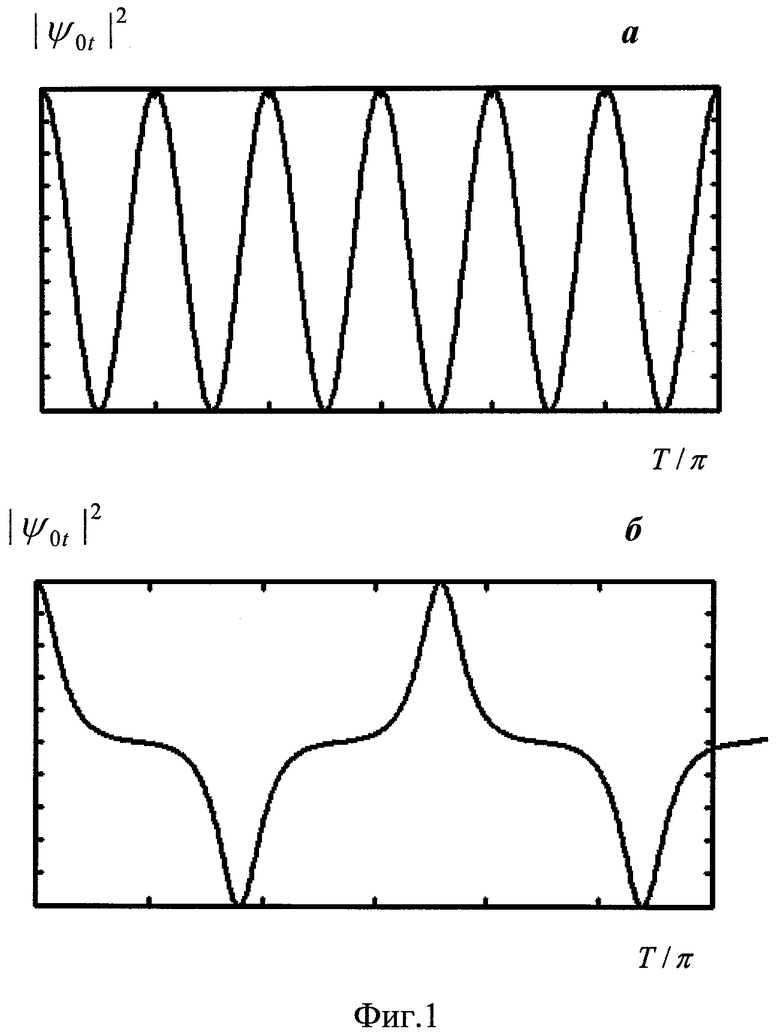
Обычно длина волны де Бройля материальных частиц, и в частности, атомов чрезвычайно мала и проникновение волны де Бройля через потенциальный барьер пренебрежимо мало при достаточно большом пространственном разнесении потенциальных ям (магнитных ловушек). В случае атомных конденсатов мы имеем исключение. Дело в том что (как уже отмечалось) температура атомного конденсата в магнитной ловушке может быть чрезвычайно мала (10-9 K). При таких температурах скорости атомов также чрезвычайно малы. Поэтому, при столь низких температурах, несмотря на значительную массу атомов, их импульсы также малы и, следовательно, длина волны де Бройля λ=h/p может быть достаточно большой. Поэтому коэффициент туннельной связи атомных конденсатов, находящихся в туннельно-связанных и магнитных ловушках (потенциальных ямах), может быть достаточно большим, даже если они находятся на значительном расстоянии друг от друга. Т.е. волны де Бройля могут проникать из одной потенциальной (квантовой) ямы в другую, даже если эти ямы находятся на значительном удалении друг от друга. Следовательно, между такими конденсатами могут происходить эффективный обмен, перенос массы - «телепортация» и переключение, описанное в данном изобретении.
Уменьшая температуру атомного конденсата (за счет «лазерного» охлаждения и «радиочастотного» воздействия) можно увеличивать длину волны де Бройля, тем самым увеличивая коэффициент туннельной связи. И наоборот, уменьшая температуру атомного конденсата, можно увеличивать длину волны де Бройля, тем самым увеличивая коэффициент туннельной связи. Т.е. таким образом регулировать коэффициент туннельной связи, настраиваясь в точку переключения.
Сделаем оценки. Пусть T=10-3 K, m=3.82·10-23 г, a≈30 нм=3·10-8 cм, учтем, что постоянная Больцмана kbol=1.38·10-23 Дж/K=1.38·10-30 эрг/К. Тогда длина волны де Бройля оценивается грубо с помощью формул 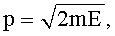
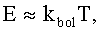 откуда
откуда 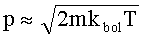 , и
, и 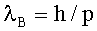 порядка 3 см.
порядка 3 см.
Пусть теперь T=10-9 K, m=3.82·10-23 г, a≈30 нм=3·10-8 cм. Тогда длина волны де Бройля оценивается грубо с помощью формул 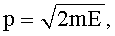
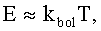 откуда
откуда 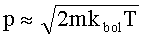 , и
, и 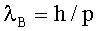 порядка 3080 см, т.е. порядка 30 м.
порядка 3080 см, т.е. порядка 30 м.
Для того чтобы происходило полное переключение бозонов, фаза их волновых функций во всех точках пространства (потенциальной ямы) должна быть одинакова. Для этого волновые функции должны представлять пространственные солитоны. Для этого, в свою очередь, волновые функции в начальный момент времени должны зависеть от пространственных координат по закону обратного гиперболического косинуса [15]. Это может быть достигнуто выбором надлежащей формы (пространственного профиля) потенциальной энергии в потенциальной (квантовой) яме. Теория переключения в этом случае может быть основана на подходе и результатах [15]. При этом в результатах и уравнениях [15] пространственная координата заменяется временем, а время - координатой.
Отметим, что конденсат атомов натрия при температуре порядка 10-9 K имеет аномально высокий коэффициент преломления, такой, что свет движется через конденсат со скоростью 17 м/с. Замечена также чрезвычайно сильная зависимость коэффициента пропускания света от интенсивности [18]. Поэтому, управляя концентрацией атомов в конденсате в магнитных ловушках (с помощью предложенного способа), можно модулировать интенсивность лазерного луча, пропускаемого сквозь конденсат, находящийся в этих магнитных ловушках.
Пример 2. Два пространственно разделенных туннельно-связанных сверхпроводника, разделенных тонким слоем изолятора толщиной 10 Å. Коэффициент туннельной связи составляет порядка 10-3. Это соответствует времени одной перекачки порядка 100 нс. Концентрация куперовских пар составляет порядка 1019 см-3. При нелинейности порядка 10-6 такая концентрация соответствует средней точке переключения М (см. Фиг.2). Изменение концентрации на 1% в одном из сверхпроводников вызывает увеличение концентрации куперовских пар в одном сверхпроводнике на 70%, а в другом сверхпроводнике концентрация куперовских пар уменьшается на 70%. Это изменение концентрации происходит через 200 не после момента времени, в который произошло первоначальное изменение концентрации на 1%.
Пример 3. Сверхпроводники изготовлены в виде сверхпроводящих полосок или пленок или проводов, разделенных тонким изолятором. Эти сверхпроводящие пленки разделены тонким слоем изолятора и туннельно-связаны между собой. Куперовские пары электронов распространяются вдоль этих сверхпроводящих пленок. Фактически указанные сверхпроводниковые пленки образуют волноводы для куперовских пар (бозонов), туннельно-связанные между собой.
Малое изменение плотности заряда на входном конце одного из сверхпроводников на 0.1% вызывает в 100 раз большее изменении плотности заряда на выходных концах сверхпроводников. Причем на выходных концах сверхпроводников изменения плотности заряда имеют противоположные знаки: на выходе нулевого сверхпроводника плотность заряда увеличивается на 10%, а на выходе первого сверхпроводника - уменьшается на 10%.
Данный способ переключения позволяет создать сверхбыстродействующий транзистор нового типа на основе переключения куперовских пар электронов, многократно усиливающий слабые изменения плотности заряда, тока и напряжения. На их основе можно сделать логические устройства. Эти устройства могут также найти применение для различных измерений, например магнитных, электрических и акустических полей, когда требуется большая чувствительность измеряемой аппаратуры.
Пример 4. Плазмоны распространяются вдоль двух плазменных волноводов, туннельно-связанных между собой. Первоначально плазмоны вводятся в один из плазменных волноводов («0») и по мере распространения перекачиваются в другой («1»). Длина одной перекачки составляет порядка 1 мм. На длине связи плазменных волноводов укладывалось примерно 2 перекачки плазмонов между волноводами (в линейном режиме). При достаточно большой концентрации плазмонов порядка 1019 см-3 возникал нелинейный режим взаимодействия между плазмонами, и наблюдалось резкое переключение плазмонов на выходе из одного волновода в другой. При изменении концентрации плазмонов на входе плазменного волновода «0» на 0.5%, на выходе этого волновода концентрация плазмонов увеличивалась на 35%, а на выходе первого волновода - уменьшалась на 35%.
По сравнению с оптическими транзисторами и переключателями фотонов описанные переключатели плазмонов имеют важное преимущество. Это - принципиально меньшие размеры используемых плазменных волноводов и самих переключателей плазмонов в целом. Размеры плазменных волноводов могут быть гораздо (на один-два порядка) меньше, чем размеры оптических волноводов в силу того, что длина волны плазмонов значительно (на один-два порядка) меньше длины оптической волны. Плазменные переключатели можно легко состыковать с плазменными проводами. Плазменные волноводы сами могут быть плазменными проводами. Скорости переключения плазмонов и фотонов соизмеримы между собой. Поэтому описанные в данной Заявке переключатели могут быть использованы при создании суперкомпьютеров и квантовых компьютеров.
Для изготовления переключателей, транзисторов и логических элементов предельно малых размеров предлагаемый способ имеет преимущество и перед известным способом переключения света и оптическими транзисторами [5-15]. И вот почему. Степень пространственной локализации бозонов, по меньшей мере, на порядок выше, чем степень пространственной локализации фотонов (света), ибо дебройлевская длина волны бозонов, по меньшей мере, на порядок меньше, чем длина волны света. Поэтому логические устройства и транзисторы на основе предлагаемого способа переключения могут иметь гораздо меньшие размеры, чем переключатели фотонов и найти применение в квантовых компьютерах.
ЛИТЕРАТУРА
1. Фейнман Р., Лейтон Р., Сэндс М. // Фейнмановские лекции по физике. Квантовая механика, тома 8, 9. М.: Мир, 1978 г.
2. Киттель Ч. // Введение в физику твердого тела. М.: Наука, 1978.
3. Josephson B.D. // Physics Letters, v.1, р.251-253 (1962).
4. Ярив А. // Квантовая электроника». М.: Сов. Радио, 1980.
5. Майер А.А. // Препринт ИОФАН №351, с.32. - М.: 1987. (Подписано к печати 3 сентября 1987 г.).
6. Майер А.А. // Патент СССР №1152397, приоритет от 22.09.1982.
7. Майер А.А. // Квантовая электроника, 1982, т.9, №11, с.2296-2302.
8. Майер А.А. // Квантовая электроника, 1984, т.11, №1, с.157-162.
9. Майер А.А. // Известия АН СССР, сер. физ., 1984, т.48, №7, с.1441-1446.
10. Майер А.А. // Квантовая электроника, 1987, т.14, №8, с.1596-1603.
11. Гусовский Д.Д., Дианов Е.М., Майер А.А. и др. // Препринт ИОФАН. М., 1986, №188, с.1-27 // Квантовая электроника, 1987, Т.14, №6, с.1144-1147.
12. Майер А.А., Сердюченко Ю.Н., Ситарский К.Ю. и др. // Препринт ИОФАН. М., 1986, №345, с.1-12; Квантовая электроника, 1987, т.14, №6, с.1157-1159.
13. Майер А.А. // УФН, т.165, №9, с.1037-1075, 1995 г.
14. Майер А.А. // УФН, с.166, №11, с.1171-1196, 1996 г.
15. Майер А.А., Лозинский А.С.//ДАН, сер. физ., 1997 г., т.356, №3, с.325-328.
16. Кадомцев Б.Б., Кадомцев М.Б.// УФН, т.167, №6, с.649-664, 1997 г.
17. Давыдов А.С. // «Нелинейные колебательные явления в биологии». В книге «Нелинейные волны. Распространение и взаимодействие». М.: Наука, 1981 г. Под редакцией А.В.Гапонова-Грехова.
18. А.В.Горохов. Соросовский образовательный журнал, том 7, №1, с.71-76, 2001 г.
Предложены способы переключения бозонов, находящихся в состоянии бозе-эйнштейновского конденсата, между двумя связанными квантовыми состояниями. В способе создают суммарную концентрацию бозонов, превышающую пороговое значение. Переключение осуществляется за счет изменения концентрации бозонов в одном из состояний, разности фаз квантовых состояний, разности потенциалов квантовых состояний или коэффициента связи. Способ позволяет реализовать бозонный переключатель, модулятор и транзистор. 2 н. 25 з.п. ф-лы, 8 ил.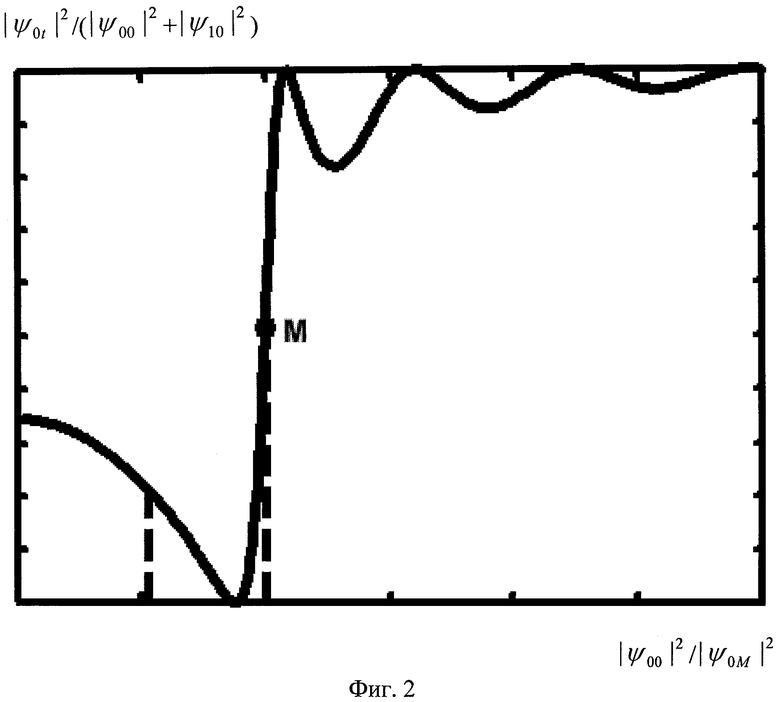
1. Способ переключения бозонов, полностью или частично находящихся в состоянии бозе-эйнштейновского конденсата, между двумя связанными квантовыми состояниями «0» и «1» с волновыми функциями ψ0 и ψ1, характеризуемыми концентрациями бозонов |ψ0|2 и |ψ1|2, и коэффициентом связи K, отличающийся тем, что создают суммарную концентрацию бозонов |ψ00|2+|ψ10|2 больше порогового значения и вызывают переключение бозонов из одного квантового состояния в другое квантовое состояние, изменяя концентрацию бозонов, по меньшей мере, в одном из квантовых состояний, или разность фаз этих квантовых состояний, или разность потенциалов этих квантовых состояний, или коэффициент связи.
2. Способ по п.1, отличающийся тем, что создают суммарную концентрацию бозонов |ψ00|2+|ψ10|2 больше порогового значения равного K/|θ|, где θ - коэффициент нелинейности ансамбля бозонов.
3. Способ по п.2, отличающийся тем, что создают суммарную концентрацию бозонов |ψ00|2+|ψ10|2 такой, что она удовлетворяет неравенству:
2K/|θ|<|ψ00|2+|ψ10|2<6K/|θ|, где θ - коэффициент нелинейности ансамбля бозонов.
4. Способ по п.3, отличающийся тем, что в начальный момент времени создают концентрацию бозонов в состоянии «0», по меньшей мере, на порядок (в 10 раз) большей, чем концентрацию бозонов в состоянии «1» (т.е. выполняется условие |ψ00|2>>|ψ10|2).
5. Способ по п.2, отличающийся тем, что в начальный момент времени создают концентрацию бозонов в состоянии «0» равной к концентрации бозонов в состоянии «1» или близкой, удовлетворяющей неравенству:
|ψ10|2-|ψ00|2<<|ψ10|2+|ψ00|2.
6. Способ по п.1, отличающийся тем, что температура ансамбля бозонов не превышает 10 K.
7. Способ по п.1, отличающийся тем, что, изменяя суммарную концентрацию бозонов в пределах 1% инициируют изменение концентраций в каждом из квантовых состояний более чем на 20%.
8. Способ по п.1, отличающийся тем, что квантовые состояния «0» и «1» с волновыми функциями ψ0 и ψ1 имеют различную энергию.
9. Способ по п.1, отличающийся тем, что квантовые состояния «0» и «1» с волновыми функциями ψ0 и ψ1 являются пространственно-разделенными.
10. Способ по п.9, отличающийся тем, что в качестве бозонов используются или куперовские пары электронов, или экситоны, или атомный конденсат, или молекулы с целым или нулевым спином, или магноны, или плазмоны.
11. Способ по п.9, отличающийся тем, что используемый в качестве бозонов атомный конденсат состоит из атомов щелочных металлов.
12. Способ по п.9, отличающийся тем, что в качестве бозонов используются молекулы CO.
13. Способ по п.9, отличающийся тем, что переключают бозоны между двумя потенциальными ямами, туннельно-связанными между собой.
14. Способ по п.9, отличающийся тем, что для изменения концентрации бозонов, по меньшей мере, в одном из квантовых состояний на используемый в качестве бозонов атомный конденсат воздействуют электромагнитным излучением.
15. Способ по п.14, отличающийся тем, что воздействуют электромагнитным излучением с определенной частотой или изменяя частоту электромагнитного излучения, или изменяя интенсивность излучения, воздействующего на атомный конденсат.
16. Способ по п.14, отличающийся тем, что воздействуют электромагнитным излучением радиодиапазона.
17. Способ по п.9, отличающийся тем, что переключают бозоны между двумя туннельно-связанным между собой и пространственно-разделенными каналами, по которым распространяются бозоны.
18. Способ по п.17, отличающийся тем, что бозоны распространяются в обоих каналах в одном направлении.
19. Способ по п.18, отличающийся тем, что каналы представляют собой два туннельно-связанных сверхпроводника в виде сверхпроводящих полосок, или пленок, или проводов, разделенных тонким изолятором.
20. Способ по п.17, отличающийся тем, что бозоны являются плазмонами и распространяются по плазменному волноводу или по плазменным волноводам.
21. Способ по п.20, отличающийся тем, что плазмоны распространяются вдоль двух плазменных волноводов, туннельно-связанных между собой.
22. Способ по п.20, отличающийся тем, что поперек плазменного волновода пропускают электрический ток или в плазменный волновод дополнительно вводят оптическое излучение от полупроводникового диода или лазера.
23. Способ переключения бозонов, полностью или частично находящихся в состоянии бозе-эйнштейновского конденсата, между двумя связанными квантовыми состояниями «0» и «1» с волновыми функциями ψ0 и ψ1, характеризуемыми концентрациями бозонов |ψ0|2 и |ψ1|2, энергиями E0 и E1, причем E0<E1, и коэффициентом связи K, отличающийся тем, что создают суммарную концентрацию бозонов |ψ00|2+|ψ10|2 больше порогового значения, предварительно воздействуют электромагнитным излучением с частотой ω, такой что |(E1-E0)-ωħ|<10|K|, а затем вызывают переключение бозонов из одного квантового состояния в другое квантовое состояние, изменяя частоту или интенсивность электромагнитного излучения.
24. Способ по п.23, отличающийся тем, что коэффициент связи удовлетворяет формуле 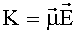 , где
, где 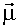 - средний электрический дипольный момент состояний,
- средний электрический дипольный момент состояний, 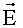 - напряженность электрического поля.
- напряженность электрического поля.
25. Способ по п.23, отличающийся тем, что коэффициент связи удовлетворяет формуле 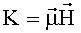 , где
, где 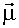 - средний магнитный дипольный момент состояний,
- средний магнитный дипольный момент состояний, 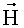 - напряженность магнитного поля.
- напряженность магнитного поля.
26. Способ по п.23, отличающийся тем, что электромагнитное излучение является оптическим.
27. Способ по п.23, отличающийся тем, что электромагнитное излучение является радиочастотным.
| Майер А.А | |||
| Оптические транзисторы и бистабильные элементы на основе нелинейной передачи света системами с однонаправленными связанными волнами | |||
| Квантовая электроника, 1982, т.9, №11, с.2296-2302 | |||
| Способ переключения сигнала в туннельно-связанных оптических волноводах | 1982 |
|
SU1152397A1 |
| СПОСОБ ПЕРЕКЛЮЧЕНИЯ И УПРАВЛЕНИЯ СОЛИТОНАМИ В ТУННЕЛЬНО-СВЯЗАННЫХ ОПТИЧЕСКИХ ВОЛНОВОДАХ СЛАБЫМ СИГНАЛОМ ДРУГОЙ НЕСУЩЕЙ ЧАСТОТЫ | 2003 |
|
RU2241245C2 |
| US 5651079 A, 22.07.1997. | |||
Авторы
Даты
2012-07-20—Публикация
2010-06-10—Подача