Изобретение относится к области инструментальных сейсмических исследований при сейсмическом микрорайонировании территорий гражданского и промышленного строительства.
Задачей данного изобретения является повышение достоверности оценки сейсмической опасности за счет учета влияния латеральной неоднородности скального основания и более глубоких горизонтов геологического разреза, а также определения потенциального ущерба для объектов хозяйственной деятельности, находящихся в зоне сейсмической активности.
Известен способ сейсмического микрорайонирования (патент RU №1251694 [1]), который реализуется следующим образом.
На площади, подлежащей сейсмическому микрорайонированию, проводят инженерно-геологическое картирование и выделяют участки с различными инженерно-геологическими условиями. Размещают исследуемые и опорные пункты наблюдений, оборудованные аппаратурой трехконтактной сейсмологической регистрации, равномерно по всей исследуемой площади. Проводят наблюдения и определяют варианты динамических параметров колебаний для различных частот заданного частотного диапазона исследований из различных очаговых зон, по секторам, не превышающим 30°. По результатам измерений устанавливают диапазон количественно значимых (например, J>0,5 балла) высокочастотных вариаций динамических параметров. В соответствии с полученными данными для всех выбранных направлений подхода используют данные в наиболее высокочастотном диапазоне fn. С учетом выделенных направлений на потенциально опасные очаговые зоны прокладывают опорные профили и перпендикулярные им, вдоль которых размещают первую группу дополнительных пунктов наблюдений. При этом расстояние между ними выбирают, не превышающее 1/3-1/4 длины волны высокочастотного диапазона исследований.
Проводят регистрацию сейсмических колебаний, распространяющихся от землетрясений (взрывов и других источников) из потенциально опасных и других очаговых зон, но вдоль направлений, наиболее близких к направлениям на потенциально опасные очаговые зоны, принимая во внимание, что в общем случае потенциально опасная очаговая зона представляет собой некоторый ограниченный объем геологической среды, расположенный на определенном расстоянии от пунктов наблюдений. По результатам наблюдений сейсмических волн вдоль опорных профилей определяют динамические параметры колебаний и строят графики их вариаций раздельно для различных направлений подхода волн от данной очаговой зоны. Причем вариации динамических параметров определяют относительно наблюдений на опорном пункте, расположенном в инженерно-геологических условиях, принятых за эталонные для данной территории сейсмического микрорайонирования, а также относительно средних значений динамических параметров, определяемых в зависимости от поставленной задачи по некоторой совокупности данных в пределах исследуемой территории или для всей территории микрорайонирования. Проводят пространственную фильтрацию данных вдоль профилей и по полученным графикам определяют периоды высокочастотных количественно значимых пространственных вариаций динамических параметров колебаний (например, более 0,5 балла).
Расстояния между пунктами наблюдений выбирают равными минимальным пространственным периодам количественно значимых вариаций.
В соответствии с полученным значением расстояния между пунктами наблюдений на площадке сейсмического микрорайонирования вдоль направлений, параллельных опорному профилю проводят наблюдения.
По второму варианту данный способ реализуется следующим образом. В условиях большой латеральной неоднородности геологического разреза периоды пространственных вариаций динамических параметров по площади могут сильно варьировать. В соответствии с этим после определения высокочастотных пространственных вариаций на опорных профилях выбирают расстояние между дополнительными пунктами наблюдений. Вследствие различий во внутреннем строении скального фундамента эти периоды на части территории оказываются отличными от значений на остальной территории.
Выполнение трехкомпонентной регистрации сейсмических колебаний по ортогональной ориентированной на потенциально опасные очаговые зоны сети профилей действительно повышает достоверность классификации возможного землетрясения.
Однако ввиду того, что в известном способе определение динамических параметров осуществляется путем анализа только наиболее высокочастотных сейсмических колебаний, то достижение технического результата, заключающегося в повышении достоверности прогноза, возможно только при стабильных во времени колебательных процессов и при отсутствии помех, обусловленных акустическими и гидродинамическими шумами природного и техногенного характера. И если в наземных условиях, с некоторыми допущениями, использование данного способа имеет положительный технический эффект, то в морских условиях для прогноза возможности возникновения цунами он практически не применим ввиду того, что на значительных расстояниях (больших размера очага) невозможно определить характер деформации дна, а существенная волна цунами возникает только при вертикальных или наклонных его движениях. Ложные же тревоги приводят к большим материальным потерям.
Задачей заявляемого технического решения является повышение достоверности определения наступления землетрясения.
Поставленная задача решается за счет того, что в способе сейсмического микрорайонирования, включающем размещение исследуемых и опорных пунктов наблюдений на участках с различными инженерно-геологическими условиями, регистрацию в них сейсмических колебаний от землетрясений из потенциально опасных и других очаговых зон, определение динамических параметров сейсмических колебаний и их вариаций в каждом исследуемом пункте наблюдений относительно опорных в заданном частотном диапазоне исследований, в котором дополнительно проводят трехкомпонентную регистрацию сейсмических колебаний по ортогональной ориентированной на потенциально опасные очаговые зоны сети профилей, причем расстояние между пунктами наблюдений не превышает 1/3-1/4 длины волны наиболее высокочастотных сейсмических колебаний, образующих информативные вариации амплитуд, а расстояние между профилями составляет 1/3-1/4 минимального пространственного периода информативных амплитудных вариаций высокочастотного диапазона сейсмических колебаний, в котором в отличие от прототипа, опорные пункты наблюдений также размещают под объектами хозяйственной деятельности, при определении динамических параметров сейсмических колебаний и их вариаций в каждом исследуемом пункте наблюдений относительно опорных, в заданном частотном диапазоне исследований учитывают распределение координат измерений, при этом высокочастотные сейсмические колебания, образующие информативные вариации амплитуд сейсмических колебаний выделяют по пространственно-временным объемам дискретных измерений путем построения дерева Кейли, при этом автоматически выделяют подбор измерений из всего массива измерений, имеющих минимальную погрешность измерений, по измерениям, имеющих минимальную погрешность измерений устанавливают величину экстремума сейсмического колебания, по которой определяют ущерб от экстремального значения сейсмических колебаний.
Сущность предлагаемого способа поясняется чертежами (фиг.1, 2).
Фиг.1. Дерево Кейли двоичного разбиения диапазона изменчивости сейсмической характеристики.
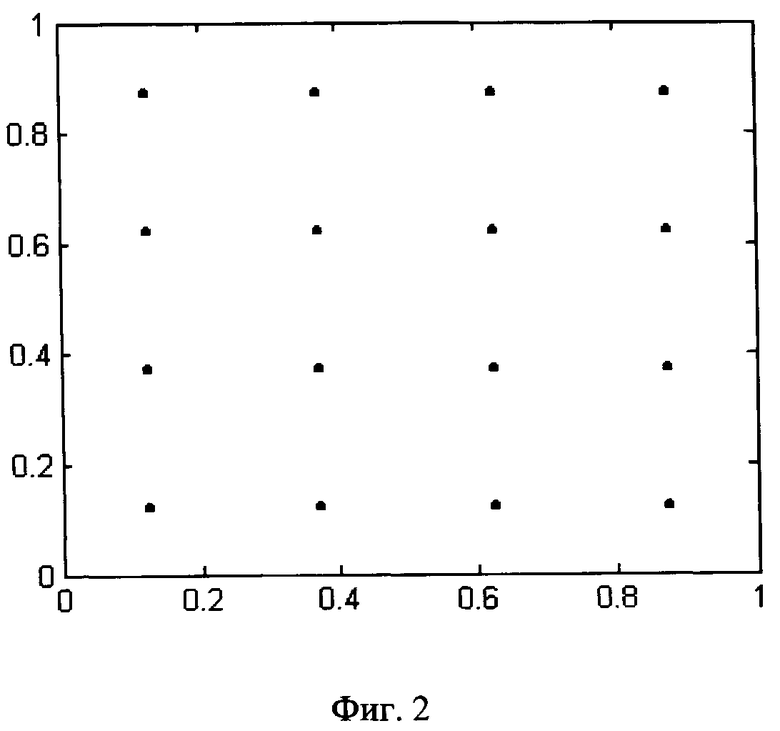
Фиг.2. Изображение кубической сетки при n=2, М=4.
Конкретный пример реализации способа.
Проводится сейсмическое микрорайонирование на площади размеров 1,5 км2. Грунтовые условия представлены тремя различными участками: скальные породы, галечниковые отложения и рыхлые осадки. На площади сейсмического микрорайонирования устанавливают сеть сейсмических станций и регистрируют записи от карьерных взрывов, находящихся на расстоянии 100 км. По результатам регистрации определяют диапазон высокочастотных количественно значимых вариаций. Разбивают профиль с расстоянием между пунктами регистрации около 200 м с ориентацией профиля в направлении на место расположения взрывов. По результатам регистрации колебаний по профилю определяют период пространственных вариаций (400-600 м). Разбивают ортогональную сеть наблюдений с расстоянием между пунктами регистрации 150-200 м.
На одном из участков площадки сейсмического микрорайонирования из-за особенностей внутреннего строения скального основания расстояние между пунктами регистрации сгущается до 100 м.
В отличие от прототипа, в заявляемом способе опорные пункты наблюдений также размещают под объектами хозяйственной деятельности (морскими терминалами, береговыми буровыми комплексами и т.д.).
При определении динамических параметров сейсмических колебаний и их вариаций в каждом исследуемом пункте наблюдений относительно опорных, в заданном частотном диапазоне исследований учитывают распределение координат измерений, при этом высокочастотные сейсмические колебания, образующие информативные вариации амплитуд сейсмических колебаний, выделяют по пространственно-временным объемам дискретных измерений путем построения дерева Кейли (фиг.1).
При этом, в отличие от прототипа, в котором при анализе сейсмических колебаний используют действительные числа, в предлагаемом способе при анализе сейсмических колебаний используют p-адические числа (Владимиров B.C., Волович И.В., Зеленев Е.И. p-Адический анализ и математическая физика. М.: Наука, 1994. - 352 с. Козырев С.В. Методы и приложения ультраметрического и p-адического анализа: от теории всплесков до биофизики. Современные проблемы математики. М.: МИАН, 2008. - 170 с. Фридман А.А. Мир как пространство и время. - Ижевск: НИЦ "Регулярная и хаотическая динамика", 2001. - 96 с. Suppes P., Luce D.H. Foundation of Measurement. - San Diego: Academic Press. - 1990. - 125 pp.).
Мотивация к применению в сейсмических исследованиях числовых систем, отличных от действительных чисел, связана со следующими основными обстоятельствами.
Во-первых, система действительных чисел - бесконечна, тогда как в реальности сейсмические колебания всегда лежат в ограниченном диапазоне значений.
Во-вторых, в результате любых измерений сейсмических характеристик получают количественные значения в рациональных числах. Действительно, в любом физическом измерении может быть принципиально достигнута только конечная точность (Хармут X. Применение методов теории информации в физике. - М.: Мир, 1989. - 344 с.), т.е. оперируют только с числами, имеющими конечное число знаков (десятичных или, например, двоичных). Это рациональные числа. Однако, стартуя с поля рациональных чисел можно получить либо систему действительных чисел, либо одну из систем p-адических чисел. По теореме Островского других числовых систем из рациональных чисел получить невозможно. Исторически приоритет получили действительные числа, а p-адические по формальным свойствам равноправные с ними, имеют значительно меньшее применение. Это можно объяснить тем, что p-адические числа отрыты на 800 лет позже действительных - в конце XIX века, их не изучают в ВУЗах и они имеют непривычные свойства, относительно действительных чисел.
В-третьих, пространственно-временная структура сейсмических характеристик принципиально неоднородна. Их динамика из-за неоднородности структуры земного рельефа, а тем более гидросферы является турбулентной. Вихревые образования прослеживаются на всех масштабах пространства и времени и образуют сложную иерархическую структуру по размерам и времени существования. Состояние иерархии имеет естественное представление в виде древовидной графовой структуры (Benzi R., Biferale L., Trovatore E. Ultrametric Structure of Multiscale Energy Correlations in Turbulent Models // Physical Review Letters, V.79, №9, 1997. - pp.1670-1673). Описать подобные структуры действительными числами невозможно, т.к. важнейшей чертой вещественного континуума является его однородность.
В-четвертых, изменчивость сейсмических характеристик явно связана с рассматриваемым пространственно-временным масштабом. В первом приближении эта зависимость описывается степенной функцией:
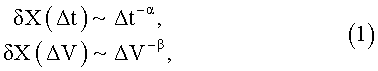
где δX - средняя изменчивость сейсмической характеристики на интервале времени Δt и на интервале пространства объемом ΔV, α, β - вещественные параметры, большие нуля. Заметим, что для соотношения (1) обнаруживается соответствие с древовидными структурами (Олемской А.И., Флат А.Я. Использование концепции фрактала в физике конденсированной среды. // УФН, Т.163, №12, 1993. - с.1-50).
Действительные числа, используемые при измерениях, принципиально не могут описывать сейсмические характеристики в требуемом пространственно-временном масштабе. Это "точечные" данные. Однако на практике они неявно применяются для описания состояния среды для пространственно-временных областей. Следствием этого, является то, что в принципе отсутствует возможность сравнения значений характеристик, измеренных в различных областях. Например, некорректно сравнивать значения температур, измеренных даже в один момент времени в разных городах, т.к. площади городов и интервалы изменчивости в них различны.
В-пятых, использование вещественных чисел приводит к проблеме согласования значений измерений, проведенных приборами с различной разрешающей способностью. Действительно, при округлении или уточнении числового значения возможно изменение непосредственно предыдущего (предыдущих) знаков числа по отношению к изменяемой позиции.
Представим один из возможных путей перехода к представлению акустических характеристик p-адическими числами, использование которых снимает указанные выше недостатки, возникающие при использовании вещественных чисел. Опишем этот переход с помощью трех последовательных этапов: введение иерархической структуры, определение на ней ультраметрического расстояния, переход к p-адическим числам.
Пусть дана сейсмическая характеристика Х и определен допустимый диапазон изменения ее значений X∈[Xmin,Xmax]=I. Проведем, например, простейшее двоичное деление этого диапазона, ему соответствует граф Кейли, представленный на фиг.1. На каждом уровне дробления каждому поддиапазону этого уровня ставится в соответствие символ 1 или 0. Каждый интервал на n-уровне дробления описывается последовательностью нулей и единиц, которые располагаются в порядке прохождений пути от корня дерева к требуемому интервалу, например, для n=3, x2={0,0,1}.
Дробление можно проводить не только двоичное, но для любого m>1, m - натуральное.
Кроме того, дробление можно продолжать до бесконечности. Тогда каждая точка разбиения x имеет бесконечное число координат
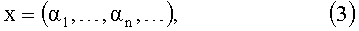
где каждая координата принимает конечное число значений
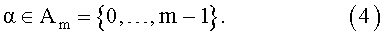
Обозначим пространство последовательностей (3) символом Zm. Введем расстояние ρ между элементами этого пространства следующим образом. Фиксируем действительное число 0<q<1. Пусть
x=(α0,α1,α2,…,αn,…), y=(β0,β1,β2,…,βn,…)∈Zm.
Положим
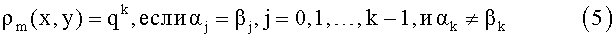
Эта функция является расстоянием (метрикой) и даже не архимедовым. Такое расстояние называется ультраметрикой. Это расстояние удовлетворяет усиленному неравенству треугольника:
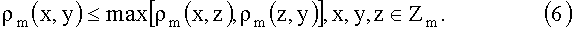
Для того, чтобы найти расстояние ρm(x,y) между двумя последовательностями цифр x и y, нужно найти первую позицию k такую, что последовательности имеют различные цифры на этой позиции. Выбор константы q не играет никакой роли. Стандартный выбор: q=1/m. Таким образом

Пример. Для двоичного разбиения m=2. Пусть x=(0,1,0,…) и, y=(0,1,1,…). Здесь k=2 и, следовательно, ρ2(x,y)=1/4.
Заметим, что до этого момента никаких числовых систем еще не появилось, только сейчас переходим к введению чисел. Сделаем это следующим образом. Заметим, что точку x=(α0,α1,α2,…,αk,…) пространства Zm можно отождествить с "числом"
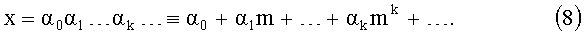
Этот ряд сходится в метрическом пространстве Zm. В частности, конечные последовательности x=α0α1…αk могут отождествляться с натуральными числами x=α0+α1m+…+αkmk.
Следовательно, множество всех конечных последовательностей может быть отождествлено с множеством натуральных чисел. Более того, множество натуральных чисел является плотным подмножеством в Zm: любой x∈Zm можно приблизить с произвольной точностью натуральными числами. Если x - натуральное число, то |x|m=m-k, тогда и только тогда, когда x делится на mk и не делится на mk+1.
Множество Zm называется множеством m-адических целых чисел.
На множестве m-адических целых чисел Zm можно ввести алгебраические операции, а именно сложение, вычитание и умножение. Эти операции являются естественными продолжениями стандартных операций на множестве натуральных чисел N={0,1,2,3,…}. Отметим, что деление в Zm не является корректно определенным (это числовое кольцо, но не числовое поле) и для этих числовых систем не развит аппарат математического анализа.
Для получения полноценных числовых не архимедовых систем (p-адических чисел) необходимо расширение числовых множеств Zm. Рассмотрим выражение вида:

где αj=0, 1, …, m-1 и s=0, ±1, ±2,…. Обозначим множество всех таких выражений символом Qm. Положим |x|m=m-s, если αs≠0. Это естественное продолжение нормирования, заданного на Zm. Если s=0, 1, 2, …, то x=αsms+…+αjmj+…. Тогда |x|m=m-s. С другой стороны, если s=-1, -2, …, то x=α-k/mk+…+αjmj+…, где k=-s. Тогда |x|m=m-s=mk.
Здесь отметим, что система действительных чисел R состоит из выражений вида:

Причем обычно используется десятичное основание, т.е. m=10. В вещественном случае может быть только конечное число членов с положительными степенями при m, а в m-адическом случае может быть бесконечное число членов с положительными степенями при m. Для отрицательных степеней все наоборот. Введем сложение, вычитание и умножение на Qm точно так же, как и на Zm, продолжая стандартные операции, заданные на множестве конечных сумм:

Заметим, что |xy|m≤|x|m|y|m. Если m=p является простым числом, то (как и для стандартного модуля в вещественном случае) |xy|p=|x|p|y|p. В общем случае деление на Qm не определено. Однако, если m=p, то деление определено корректно и, более того, существует аппарат математического анализа и теории вероятностей. Числовые системы типа Qp называются p-адическими числами.
Проведенное построение вполне возможно осуществить по имеющимся контактным и дистанционным измерениям сейсмических колебаний. При этом возможно ограничиться более "слабыми" числовыми системами Zm. Отметим характерный недостаток представленной иерархии числовых систем: отсутствие изморфизма между системами с различными m, и их большого многообразия - m - это любое натуральное число, большее 1, т.е. бесконечное число (как и простых).
Представляется верным утверждение о том, что закономерности природы не должны зависеть от используемых числовых систем для ее описания, т.е. должны проявляться в любой из них. Однако, верно и то, что в некоторых числовых системах эти закономерности имеют более простой вид, что позволяет быстрее их обнаружить.
Далее автоматически выделяют подбор измерений из всего массива измерений, имеющим минимальную погрешность измерений, по измерениям, имеющих минимальную погрешность измерений устанавливают величину экстремума сейсмического колебания, по которой определяют ущерб от экстремального значения сейсмических колебаний.
В практике обработки сейсмических наблюдений существует задача оценки среднего значения сейсмической характеристики в некотором пространственно-временном объеме по дискретным наблюдениям. Каждое дискретное наблюдение фиксируется четырьмя координатами: временем, широтой, долготой и глубиной (высотой). Другими словами, значение сейсмической характеристики в общем случае является функцией, заданной в четырехмерном координатном пространстве. В частных случаях эта размерность может принимать и меньшие значения. Размерность определяется числом координат точек наблюдений, значения которых меняются в массиве наблюдений. Например, для типичных задач по расчету среднего значения сейсмической характеристики по дискретным наблюдениям:
по дискретным во времени измерениям в географической точке с фиксированными координатами на фиксированной глубине;
по одновременным наблюдениям в некоторой пространственной области на фиксированной глубине;
по наблюдениям в некотором районе в разные моменты времени и в разных точках на фиксированной глубине;
по наблюдениям в некотором фиксированном районе за некоторый интервал времени в некотором интервале глубин.
Нумерация задач соответствует размерности пространства задания гидрометеорологической характеристики.
В настоящее время среднее арифметическое для любой задачи рассчитывают путем прямого суммирования всех измеренных значений, попадающих в рассматриваемый пространственно-временной объем, и делят на общее число измерений.
В действительности такой метод расчета среднего арифметического сейсмической характеристики не позволяет получить минимально возможную погрешность в оценке среднего. Причиной этого является то, что в принятом методе игнорируется распределение точек наблюдения по пространственно-временному объему. Более того, точность оценки среднего значения применяемого метода уменьшается с увеличением размерности пространства координат наблюдений.
Докажем это и приведем адекватный метод расчета среднего арифметического значения сейсмической характеристики, минимизирующий погрешность.
Задача определения среднего значения сейсмической характеристики по значениям характеристики в дискретных пространственно-временных точках с математической точки зрения является задачей оценки среднего арифметического значения непрерывной функции в пространственно-временном объеме по ее значениям в дискретных точках. Погрешность в оценке среднего арифметического, при условии изотропности изменчивости функции, определяется структурой «неравномерности» расположения точек измерения в пространственно-временном объеме. Наименьшую погрешность дают точки, равномерно распределенные по рассматриваемому объему. Точки называются равномерно распределенными в n-мерном единичном кубе, если в любом гиперкубе число точек пропорционально объему гиперкуба (Соболь И.М. Многомерные квадратурные формулы и функции Хаара. - М., Наука, 1969. - 288 с.).
Формально это определяется следующим образом. Обозначим через Kn единичный куб в n-мерном пространстве: Kn состоит из всех точек Р с декартовыми координатами Р=(x1,…,xn), которые удовлетворяют неравенствам 0≤хj≤1 (j=1, 2, …, n). Рассмотрим последовательность точек P0, P1, …, Pj, …, принадлежащих кубу Kn размерности n, и обозначим через SN(G) количество точек Pi с номерами 0≤i≤N-1, принадлежащими множеству G. Последовательность точек P0, P1, …, Pi,… - называется равномерно распределенной в Kn (сокращенно p.p.), если для любого n-го параллелепипеда π с ребрами, параллельными координатным осям,
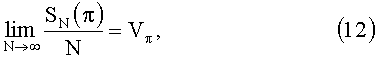
где Vπ - объем параллелепипеда π. Можно доказать, что если G произвольная область, расположенная в Kn и имеющая объем VG, то из (12) вытекает, что
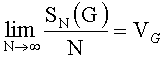 .
.
Таким образом, при больших N количество точек p.p. последовательности, принадлежащих любой области G, пропорционально объему G.
По теореме Вейля (Соболь И.М. Многомерные квадратурные формулы и функции Хаара. - М., Наука, 1969. - 288 с.) для того, чтобы {Pi} была p.p., необходимо и достаточно, чтобы для любой интегрируемой, по Риману, функции f(P) выполнялось соотношение
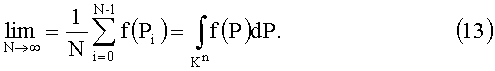
Выражение (2) является оценкой среднего арифметического. Оценка погрешности (13) определяется выражением
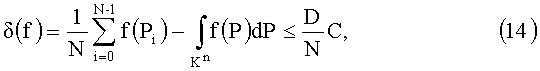
где С - константа, разная для функций с различной изменчивостью, D - отклонение распределения точек от p.p.
Отклонение D определяется следующим образом. Рассмотрим в Kn сетку, состоящую из N произвольных точек Р0, Р1, …, РN-1. Каждой точке Р из Kn поставим в соответствие параллелепипед πP с диагональю ОР (О - начало координат). Объем VP этого параллелепипеда равен произведению x1…xn координат точки Р. Отклонением сетки Р0, Р1, …, РN-1 называется число
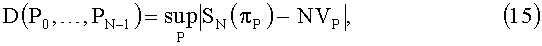
где верхняя грань берется по всем P∈Kn.
Для того, чтобы последовательность точек была p.p., необходимо и достаточно, чтобы при N→∝
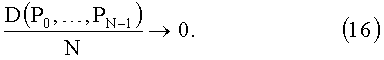
Характеристика D(P0,…,PN-1) является весьма сложной функцией от структуры расположения точек. Верхняя граница D≤N, нижняя граница ее до сих пор не известна (за исключением случая n=1, когда inf D=1/2). Существует предположение, что наилучшая возможная оценка D для n-мерной сетки, состоящей из N точек, равна

Необходимо отметить, что в большинстве случаев исследователи ошибочно полагают, что кубические сетки (их называют «регулярные», «равномерные» и т.п.) всегда очень «хорошие» и целью сбора информации является получение измерений на такой сетке. Кубическая сетка для N=М2 точек задается координатами
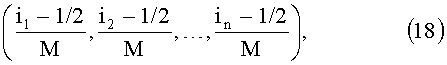
где i1, i2, …, in - независимо пробегают значения 1, 2, …, M. На фиг.2 изображена кубическая сетка при n=2, М=4.
Нетрудно проверить, что для таких сеток значение 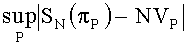 будет максимальным, например, в точке P'=(1/2M,1,1,…,1), когда SN(πp')=0, NVP'=N/2M=Мn-1/2. Следовательно,
будет максимальным, например, в точке P'=(1/2M,1,1,…,1), когда SN(πp')=0, NVP'=N/2M=Мn-1/2. Следовательно,

Из формулы (8) следует, что при n=1 кубические сетки оптимальны. Однако, с увеличением n равномерность сеток (18) ухудшается и порядки в формуле (19) приближаются к наихудшим, равным N. Уже при n=2 порядок (19) оказывается равным 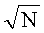 - такой же порядок соответствует случайным сеткам, состоящим из N независимых случайных точек, равномерно распределенных в Kn. Значит, при n≥3 сетки (18) асимптотически хуже случайных.
- такой же порядок соответствует случайным сеткам, состоящим из N независимых случайных точек, равномерно распределенных в Kn. Значит, при n≥3 сетки (18) асимптотически хуже случайных.
Пусть в Kn задано множество точек наблюдений за гидрометеорологической характеристикой Р0, Р1, …, РN-1. Этот набор точек далек от p.p. Необходимо определить такое подмножество точек 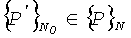 , которое образует сетку с наибольшей степенью равномерного распределения. Решение этой задачи будем искать следующим образом. Определим подходящую опорную сеть точек, имеющую p.p. Сравнивая координаты точек наблюдений с координатами точек опорной p.p. сетки, найдем искомое подмножество
, которое образует сетку с наибольшей степенью равномерного распределения. Решение этой задачи будем искать следующим образом. Определим подходящую опорную сеть точек, имеющую p.p. Сравнивая координаты точек наблюдений с координатами точек опорной p.p. сетки, найдем искомое подмножество 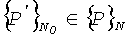 , которое будет давать минимальную ошибку с оценке среднего арифметического, в соответствии с (14).
, которое будет давать минимальную ошибку с оценке среднего арифметического, в соответствии с (14).
В вычислительной математике построено много вариантов сеток близких к p.p. Для нашей задачи целесообразно выбрать такую сетку с последовательностью точек Q0, Q1, …, Qi, …, которая удовлетворяет трем требованиям:
равномерность распределения сетки должна быть асимптотически оптимальной;
равномерность расположения точек должна наблюдаться не только при N→∝, но уже при малых N;
алгоритм расчета точек Qi должен быть достаточно простым.
Этим требованиям удовлетворяют, например, так называемые LPτ - последовательности (Соболь И.М. Многомерные квадратурные формулы и функции Хаара. - М., Наука, 1969. - 288 с.).
Не излагая теоретического обоснования p.p. свойств этих последовательностей приведем простой алгоритм расчета.
В этом алгоритме координаты (qi1,…,qin) точки Qi из LPτ - последовательности вычисляется по формуле
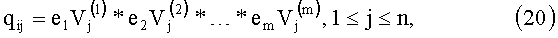
где i=em…e2e1 - представление i в двоичной системе, 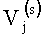 - двоично-рациональные числа вида
- двоично-рациональные числа вида 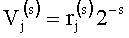 , числители которых табулированы.
, числители которых табулированы.
В таблице 1 представлены 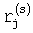 для 1≤s≤20 и 1≤j≤4, что позволяет легко вычислять точки Qi размерности n≤4 в количестве N≤220.
для 1≤s≤20 и 1≤j≤4, что позволяет легко вычислять точки Qi размерности n≤4 в количестве N≤220.
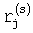
Алгоритм выбора репрезентативных точек можно представить в следующем виде:
Задано: множество из N точек наблюдений P0, P1, PN-1 в n-мерном кубе Kn, n=1, 2, 3, 4. Каждая точка наблюдений представлена нормированными координатами P=(x1,…,xn), 0≤xj≤1, j=1, 2, …, n.
Требуется: определить подмножество точек 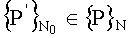 , которые дают наименьшую ошибку в оценке среднего арифметического функции, измеренной в этих точках (т.е наиболее репрезентативный набор точек измерений для оценки среднего или, что тождественно, образуют сетку с наибольшей степенью равномерного распределения).
, которые дают наименьшую ошибку в оценке среднего арифметического функции, измеренной в этих точках (т.е наиболее репрезентативный набор точек измерений для оценки среднего или, что тождественно, образуют сетку с наибольшей степенью равномерного распределения).
Инициация: Tk=T0=⌀ - набор точек-кандидатов на k шаге.
Последовательность операций решения:
Вычислить N точек Qk (k=1, …N) LPτ - последовательности по формуле (20).
Последовательно для каждого k от 1 до N для каждой точки Qk найти ближайшую в евклидовой метрике точку 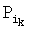 среди множества точек
среди множества точек 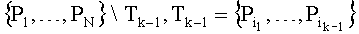 , и добавить ее в набор точек-кандидатов на k, образуя
, и добавить ее в набор точек-кандидатов на k, образуя 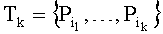 .
.
Вычислить отклонение Dk=D(Tk) для точки Рi по формуле (4).
Последовательно для каждого k от 1 до N найти D0k=max(D1,…,Dk).
Найти k0, для которого существует минимальное значение D0k.
Результат: набор точек 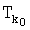 является искомым множеством точек наблюдений, дающим минимальную ошибку в оценке среднего арифметического. Таким образом, при расчете среднего арифметического значения сейсмической характеристики по дискретным наблюдениям в некотором пространственно-временном объеме для минимизации погрешности необходимо учитывать распределение координат измерений. На основе специального математического аппарата предложен метод расчета среднего арифметического значения гидрометеорологической характеристики по дискретным наблюдениям в некотором пространственно-временном объеме, дающий минимальную теоретическую погрешность в оценке, причем метод «автоматически» выявляет тот поднабор измерений из всего массива данных, который дает минимальную погрешность в оценке среднего арифметического. Для корректности вычислений необходимо ввести обычным путем локальные декартовы координаты для рассматриваемой пространственно-временной области.
является искомым множеством точек наблюдений, дающим минимальную ошибку в оценке среднего арифметического. Таким образом, при расчете среднего арифметического значения сейсмической характеристики по дискретным наблюдениям в некотором пространственно-временном объеме для минимизации погрешности необходимо учитывать распределение координат измерений. На основе специального математического аппарата предложен метод расчета среднего арифметического значения гидрометеорологической характеристики по дискретным наблюдениям в некотором пространственно-временном объеме, дающий минимальную теоретическую погрешность в оценке, причем метод «автоматически» выявляет тот поднабор измерений из всего массива данных, который дает минимальную погрешность в оценке среднего арифметического. Для корректности вычислений необходимо ввести обычным путем локальные декартовы координаты для рассматриваемой пространственно-временной области.
В задачах учета влияния сейсмических явлений на объекты хозяйственной деятельности, а также при проектировании различных береговых сооружений и оборудования, в задачах оценки надежности функционирования технических средств большое значение имеет выбор функции распределения сейсмических характеристик для оценки экстремальных значений, определяющих степень опасности влияния сейсмических условий.
Покажем, что экстремальные значения сейсмических характеристик распределены не по экспоненциальному закону, как это свойственно нормально распределенным случайным величинам, а по степенному закону. Это приводит к тому, что ущерб от экстремальных значений значительно выше, чем это обычно оценивается при использовании нормального закона распределения. Обоснованием может служить классическая теория экстремумов (Лидбеттер М., Ротсен X., Линдгрен Г. Экстремумы случайных последовательностей и процессов. - М.: Мир, 1989. - 392 с.), в которой рассматривается распределение максимума
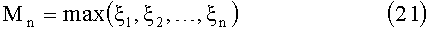
n независимых и одинаково распределенных случайных величин ξ, с функцией распределения F(x) при больших значениях n.
Основной результат этой теории утверждает, что если для некоторых последовательностей нормирующих констант а n>0, bn случайная величина а n(Мn-bn) имеет невырожденную предельную функцию распределения G(x), то эта функция G(x) должна иметь одну из трех возможных форм
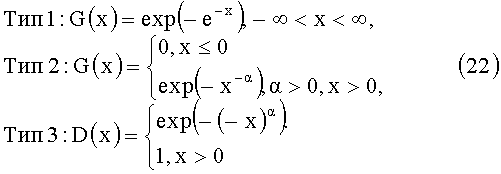
В частности доказывается, что "хвосты" всех функций распределения F(x) имеют только два типа:
- экспоненциальный (е-x) для типа 1 (например, для нормального закона распределения);
- степенной (x-α, α>0) для типов 2 и 3.
Покажем, что экстремальные значения акустических характеристик распределены по степенному закону. Логика доказательства следующая.
Прямыми статистическими оценками рядов наблюдений нельзя оценить поведение "хвоста" распределения в силу редкости экстремальных событий. Воспользуемся косвенный приемом, а именно тем, что поведение "хвостов" распределений разбивает все множество невырожденных распределений случайных величин на два класса эквивалентности - степенной и экспоненциальный. Причем линейные статистики не нарушают этого разбиения. Выберем такую статистику L(a n,bn) для временного хода акустической характеристики ξ(n), которая приводит к случайной величине η(n), распределенной по некоторому закону F*(y), для которой известен из классической теории экстремумов тип распределения ее "хвоста". Тогда такой же тип распределения "хвоста" будет у значений экстремумов акустической характеристики.
В качестве линейной статистики воспользуемся статистикой Герста, которая имеет вид (Федер Е. Фракталы. - М.: Мир, 1991. - 260 с.)
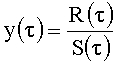 ,
,
где
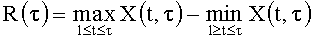
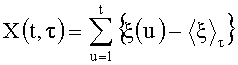 ,
,
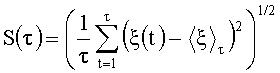 .
.
Оценим функцию распределения F*(y) случайной величины η, полученную с помощью этого преобразования.
Обработка временных рядов сейсмических характеристик приводит к следующей степенной зависимости
F*(y)~τH,
где 1/2<H<1.
Следовательно, статистика Герста определяет случайную функцию, распределенную по степенному закону, который, как доказывается в теории экстремумов, имеет степенное распределение "хвоста". Значит и "хвосты" сейсмических характеристик имеют степенное распределение.
Ущерб от экстремального значения сейсмической характеристики, очевидно, является некоторой степенной функцией от величины экстремума
Q~xn, n≤1.
Если в качестве количественной оценки влияния экстремальных значений сейсмических характеристик при проектировании использовать математическое ожидание ущерба
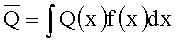 ,
,
где f(x) - функция плотности распределения "хвоста" сейсмической характеристики, то очевидно получаем:
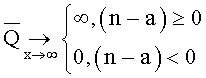
Для нормального закона распределения 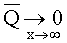 при любом n. Для наблюдаемых сейсмических процессов α~1, и вероятнее всего большое влияние "хвоста" распределения на величину ущерба от возникновения экстремального значения сейсмической характеристики.
при любом n. Для наблюдаемых сейсмических процессов α~1, и вероятнее всего большое влияние "хвоста" распределения на величину ущерба от возникновения экстремального значения сейсмической характеристики.
Способ может быть реализован на широкополосных акустических преобразователях, имеющих промышленную применимость, например, типа ЭХД-17 или ЭХД-20 и вычислительной техники, реализующей алгоритмы, приведенного в описании программно-математического обеспечения.
Источники информации
1. Патент RU №1251694.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ РЕГИСТРАЦИИ СЕЙСМИЧЕСКИХ СИГНАЛОВ НА АКВАТОРИИ МОРЯ ПРИ ПОИСКЕ ПОДВОДНЫХ ЗАЛЕЖЕЙ УГЛЕВОДОРОДОВ | 2011 |
|
RU2483330C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ПРЕДВЕСТНИКА ЗЕМЛЕТРЯСЕНИЯ | 2011 |
|
RU2483335C1 |
| СПОСОБ ОБНАРУЖЕНИЯ ВОЗМОЖНОСТИ НАСТУПЛЕНИЯ КАТАСТРОФИЧЕСКИХ ЯВЛЕНИЙ | 2011 |
|
RU2489736C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ПРЕДВЕСТНИКА ЗЕМЛЕТРЯСЕНИЯ | 2012 |
|
RU2490675C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ПРЕДВЕСТНИКА ЦУНАМИ | 2011 |
|
RU2457514C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ КОНЦЕНТРАЦИЙ ГАЗОВЫХ КОМПОНЕНТОВ СЛОЯ АТМОСФЕРЫ НА ГРАНИЦЕ С ГИДРОСФЕРОЙ | 2010 |
|
RU2438115C1 |
| СПОСОБ ОБНАРУЖЕНИЯ ВОЗМОЖНОСТИ НАСТУПЛЕНИЯ КАТАСТРОФИЧЕСКИХ ЯВЛЕНИЙ | 2007 |
|
RU2346300C1 |
| СПОСОБ ОБНАРУЖЕНИЯ ПОДВОДНЫХ ЗАЛЕЖЕЙ ГАЗОВЫХ ГИДРАТОВ | 2012 |
|
RU2490676C1 |
| СПОСОБ КАРТОГРАФИЧЕСКОГО ОТОБРАЖЕНИЯ ДВУХМЕРНЫХ РАСПРЕДЕЛЕНИЙ, ЗАДАННЫХ В ЦИФРОВОЙ ФОРМЕ | 2011 |
|
RU2484427C1 |
| СПОСОБ ВОССТАНОВЛЕНИЯ РЕЛЬЕФА МОРСКОГО ДНА ПРИ ИЗМЕРЕНИИ ГЛУБИН ПОСРЕДСТВОМ ГИДРОАКУСТИЧЕСКИХ СРЕДСТВ | 2011 |
|
RU2466426C1 |
Изобретение относится к области геофизики и может быть использовано при сейсмическом микрорайонировании территорий гражданского и промышленного строительства. Способ сейсмического микрорайонирования включает размещение исследуемых и опорных пунктов наблюдений на участках с различными инженерно-геологическими условиями. Опорные пункты наблюдений также размещают под объектами хозяйственной деятельности. Расстояние между пунктами наблюдений не превышает 1/3-1/4 длины волны наиболее высокочастотных сейсмических колебаний, образующих информативные вариации амплитуд, а расстояние между профилями составляет 1/3-1/4 минимального пространственного периода информативных амплитудных вариаций высокочастотного диапазона сейсмических колебаний. Высокочастотные сейсмические колебания, образующие информативные вариации амплитуд сейсмических колебаний выделяют по пространственно-временным объемам дискретных измерений путем построения дерева Кейли. Автоматически выделяют подбор измерений из всего массива измерений, имеющих минимальную погрешность измерений. По измерениям, имеющих минимальную погрешность измерений устанавливают величину экстремума сейсмического колебания, по которой определяют ущерб от экстремального значения сейсмических колебаний. Технический результат: повышение достоверности оценки сейсмической опасности. 2 ил.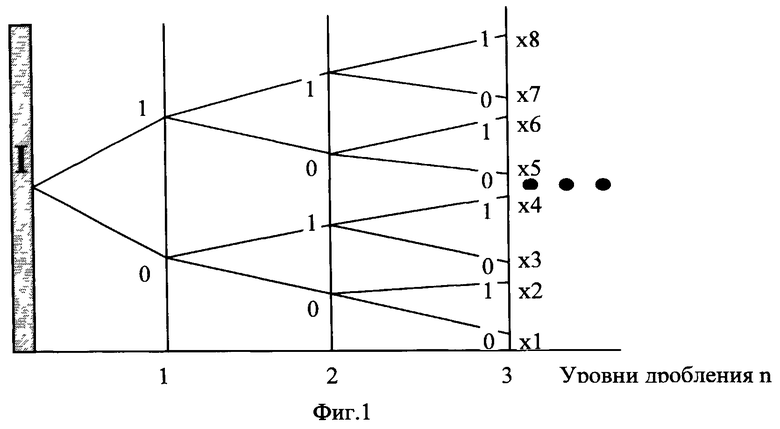
Способ сейсмического микрорайонирования, включающий размещение исследуемых и опорных пунктов наблюдений на участках с различными инженерно-геологическими условиями, регистрацию в них сейсмических колебаний от землетрясений из потенциально опасных и других очаговых зон, определение динамических параметров сейсмических колебаний и их вариаций в каждом исследуемом пункте наблюдений относительно опорных в заданном частотном диапазоне исследований, в котором дополнительно проводят трехкомпонентную регистрацию сейсмических колебаний по ортогональной ориентированной на потенциально опасные очаговые зоны сети профилей, причем расстояние между пунктами наблюдений не превышает 1/3-1/4 длины волны наиболее высокочастотных сейсмических колебаний, образующих информативные вариации амплитуд, а расстояние между профилями составляет 1/3-1/4 минимального пространственного периода информативных амплитудных вариаций высокочастотного диапазона сейсмических колебаний, отличающийся тем, что опорные пункты наблюдений также размещают под объектами хозяйственной деятельности, при определении динамических параметров сейсмических колебаний и их вариаций в каждом исследуемом пункте наблюдений относительно опорных в заданном частотном диапазоне исследований учитывают распределение координат измерений, при этом высокочастотные сейсмические колебания, образующие информативные вариации амплитуд сейсмических колебаний, выделяют по пространственно-временным объемам дискретных измерений путем построения дерева Кейли, при этом автоматически выделяют подбор измерений из всего массива измерений, имеющих минимальную погрешность измерений, по измерениям, имеющим минимальную погрешность, устанавливают величину экстремума сейсмического колебания, по которой определяют ущерб от экстремального значения сейсмических колебаний.
| СПОСОБ СЕЙСМИЧЕСКОГО МИКРОРАЙОНИРОВАНИЯ (ЕГО ВАРИАНТЫ) | 1984 |
|
RU1251694C |
| RU 1398630 С, 30.06.1994 | |||
| СПОСОБ СЕЙСМИЧЕСКОГО МИКРОРАЙОНИРОВАНИЯ | 1996 |
|
RU2099751C1 |
| СПОСОБ СЕЙСМИЧЕСКОГО МИКРОРАЙОНИРОВАНИЯ | 1996 |
|
RU2105997C1 |
| CN 101539632 A, 23.09.2009. | |||
Авторы
Даты
2012-08-20—Публикация
2011-06-29—Подача