Изобретение относится к информационно-телекоммуникационным технологиям и электронике и может быть использовано в современных цифровых системах широкополосной высокочастотной (ВЧ) радиосвязи и цифрового ВЧ радиовещания, когда средой распространения является изменчивая во времени и пространстве ионосфера Земли.
Способ основан на зондировании многомерного ионосферного векторного канала распространения сверхширокополосным линейно-частотно модулированным (ЛЧМ) сигналом и получении в результате характеристик частотной дисперсии и многомерности векторного канала путем оценки сжатых в частотной области элементов зондирующего сигнала. Применение способа позволит в реальном времени оценивать состояние многомерного векторного радиоканала распространения и возникающие искажения сигнала - переносчика информации, а также повысить достоверность получаемой по каналу информации. Использование способа обеспечит работу радиотехнических систем ВЧ-диапазона в широкой полосе частот и с минимальной мощностью, а также экономию вычислительных ресурсов и времени измерений.
Ионосфера Земли является средой с изменчивыми и ярко выраженными частотной дисперсией и многомерностью, зависящими от рабочей частоты и приводящими к сильным искажениям распространяющихся в ней радиосигналов. При этом многомерность определяется всевозможными трактами распространения сигнала от передатчика к приемнику, а частотная дисперсия - зависимостью времени распространения в тракте от частоты. Каждый j-й тракт характеризуется своей импульсной hj и частотной Hj характеристиками. При этом импульсная и частотные характеристики k-ого скалярного канала равны сумме соответствующих характеристик трактов
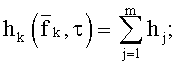
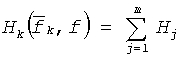
Видно, что скалярные каналы отличаются рабочей частотой 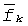 . Верхний индекс суммирования определяет размерность скалярного канала. В полосе прозрачности (наименьшая применимая частота (НПЧ) - максимальная применимая частота (МПЧ)) ионосферной линии связи можно организовать K=(МПЧ-НПЧ)/B скалярных каналов (где B - полоса частот скалярного канала) или один векторный канал с импульсной и частотными характеристиками
. Верхний индекс суммирования определяет размерность скалярного канала. В полосе прозрачности (наименьшая применимая частота (НПЧ) - максимальная применимая частота (МПЧ)) ионосферной линии связи можно организовать K=(МПЧ-НПЧ)/B скалярных каналов (где B - полоса частот скалярного канала) или один векторный канал с импульсной и частотными характеристиками 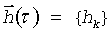 и
и 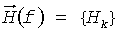 , где k=1, 2…K.
, где k=1, 2…K.
Негативное влияние дисперсии растет с ростом полосы сигнала, а многомерности - с ее уменьшением. Кроме того, степень влияния изменяется во времени из-за изменчивости среды. В такой ситуации для обеспечения качественной работы систем ВЧ-связи необходима оценка степени частотной дисперсии и многомерности различных скалярных каналов или одного векторного канала на линии ВЧ-связи и учета их в алгоритмах работы связных радиосистем. Это позволит повысить качество, достоверность и скорость передаваемой по ВЧ-каналам информации.
В связи с этим необходима разработка способа определения в реальном времени характеристик частотной дисперсии и многомерности векторного ионосферного ВЧ-радиоканала, позволяющего существенно повысить качество работы радиотехнических систем.
Известен способ, изложенный в работе [Арманд Н.А. Применение теоремы Котельникова к описанию дисперсии сигналов /Н.А.Арманд // Радиотехника и электроника. - 2004. - Т.49. №10. - С.1199-1204.], где импульсная характеристика неискаженного дисперсией скалярного канала распространения является основной гармоникой Котельникова, а искажения приводят к обогащению ее другими гармониками. Определение этих гармоник позволяет косвенно оценивать частотную дисперсию в скалярном канале при распространении.
Наиболее близким к заявляемому техническому решению (прототипом) является способ оценки многомерности скалярного ВЧ-канала по количеству сигналов, принимаемых в точке приема при отражении от ионосферы импульсных сигналов, представленный в работе [Иванов Д.В. Методы и математические модели исследования распространения в ионосфере сложных декаметровых сигналов и коррекции их дисперсионных искажений: Монография / Д.В.Иванов - Йошкар-Ола: МарГТУ, 2006. - 266 с.]. Он заключается в зондировании ионосферы импульсными сигналами на заданной рабочей частоте, приеме отраженных сигналов, определении их числа путем разделения отражений по времени группового запаздывания. Число разделенных импульсных отражений и определяет многомерность скалярного канала.
В реальных ВЧ-радиоканалах дисперсия и многомерность обычно существуют одновременно. Кроме того, известный способ не позволяет проводить анализ частотной дисперсии и многомерности векторного канала, соответствующего полосе прозрачности ионосферной линии связи.
Технический результат заключается в том, что заявляемый способ позволяет одновременно определять характеристики дисперсности и многомерности именно векторного ВЧ-радиоканала.
Технический результат достигается тем, что способ определения характеристик частотной дисперсии и многомерности векторного высокочастотного канала в полосе прозрачности ионосферной линии связи с использованием ЛЧМ сигналов, заключающийся в получении характеристик частотной дисперсии и многомерности элементов канала путем оценки сжатых в частотной области элементов зондирующего сигнала, отличающийся тем, что для зондирования векторного высокочастотного канала используется сверхширокополосный ЛЧМ сигнал; все скалярные ВЧ-каналы зондируются одновременно (что эквивалентно зондированию сверхширокополосного векторного ВЧ-канала); оцениваются многомерность скалярных каналов и дисперсионная характеристика сверхширокополосного векторного канала в виде полиномиальной функции, определяющая частотную дисперсию в нем.
Сущность технического решения в том, что сверхширокополосный векторный канал от НПЧ до МПЧ разбивается на скалярные каналы с полосами, удовлетворяющими условиям: дисперсия незначительная и принимаемые моды разрешаются по задержке. Скалярные каналы являются примыкающими и их полосы частот B=f2 f1 попадают в полосу прозрачности радиолинии. Далее производится зондирование сверхширокополосного векторного ВЧ-канала сверхширокополосным ЛЧМ сигналом с полосой, равной полосе прозрачности радиолинии. Этот сигнал в приемнике разбивается на парциальные ЛЧМ сигналы с примыкающими полосами частот 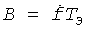 (Tэ - длительность парциального ЛЧМ сигнала,
(Tэ - длительность парциального ЛЧМ сигнала, 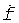 - скорость изменения его частоты), соответствующими полосам парциальных скалярных каналов. Итак, составляющими сверхширокополосного векторного канала являются К примыкающих скалярных каналов с различной средней частотой. Их зондирование обеспечивается сверхширокополосным ЛЧМ сигналом, примыкающие элементы которого, с различными средними частотами спектра, являются его парциальными сигналами. Каждый парциальный сигнал сжимается в частотной области путем умножения его на сигнал, когерентный излучаемому, и выделением из произведения колебания разностной частоты. При многомерном скалярном канале распространения на выходе приемника образуется звуковой сигнал, содержащий тоны разностной частоты, соответствующие трактам канала. Вычисляя спектры элементов, разделяем тоны колебания. Получаем многомерный спектр, упорядоченное множество компонент которого характеризует многомерный канал. Действительно, при выполнении условия
- скорость изменения его частоты), соответствующими полосам парциальных скалярных каналов. Итак, составляющими сверхширокополосного векторного канала являются К примыкающих скалярных каналов с различной средней частотой. Их зондирование обеспечивается сверхширокополосным ЛЧМ сигналом, примыкающие элементы которого, с различными средними частотами спектра, являются его парциальными сигналами. Каждый парциальный сигнал сжимается в частотной области путем умножения его на сигнал, когерентный излучаемому, и выделением из произведения колебания разностной частоты. При многомерном скалярном канале распространения на выходе приемника образуется звуковой сигнал, содержащий тоны разностной частоты, соответствующие трактам канала. Вычисляя спектры элементов, разделяем тоны колебания. Получаем многомерный спектр, упорядоченное множество компонент которого характеризует многомерный канал. Действительно, при выполнении условия 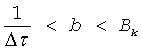 (Δτ - межмодовая задержка, Bk - полоса когерентного распространения) модуль спектра элемента сигнала разностной частоты для j-го мода имеет вид:
(Δτ - межмодовая задержка, Bk - полоса когерентного распространения) модуль спектра элемента сигнала разностной частоты для j-го мода имеет вид:
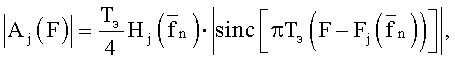
где 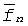 - средняя частота произвольного одномерного канала,
- средняя частота произвольного одномерного канала, 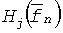 - ослабление сигнала в одномерном канале,
- ослабление сигнала в одномерном канале, 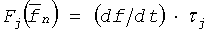 - частота тона, соответствующего j-й моды распространения, τj - задержка сигнала.
- частота тона, соответствующего j-й моды распространения, τj - задержка сигнала.
Ширина спектра равна 2/Тэ, поэтому при выполнении условия
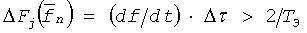
или 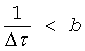
моды принимаемого сигнала разрешаются по задержке. Число принимаемых мод является численной характеристикой многомерности канала. Таким образом, определение многомерности векторного канала достигается выделением тонов колебаний разностной частоты для парциальных элементов ЛЧМ сигнала, соответствующих всем К скалярным каналам.
Для векторного канала можно построить частотную зависимость задержки сигналов в трактах распространения от средней частоты скалярного канала. Положения максимумов компонент многомерного спектра дает дискретную зависимость дисперсионной характеристики сверхширокополосного канала, представляющую собой зависимость задержки сигнала в среде от частоты. Действительно, тону частотой Fj можно поставить в соответствие задержку 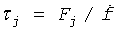 сигнала в тракте распространения, а длительности Тэ=Т/n элемента - полосу частот b=В/n компоненты многомерного излучаемого сигнала (T - длительность всего ЛЧМ сигнала, n - число элементов).
сигнала в тракте распространения, а длительности Тэ=Т/n элемента - полосу частот b=В/n компоненты многомерного излучаемого сигнала (T - длительность всего ЛЧМ сигнала, n - число элементов).
Непрерывную зависимость дисперсионной характеристики получим, представляя дискретную зависимость полиномом и решая задачу минимизации функционала:
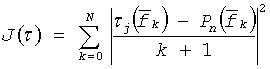
где 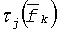 - дискретные отсчеты, Pn(f) - полиномиальная модель.
- дискретные отсчеты, Pn(f) - полиномиальная модель.
Таким образом, получение непрерывной зависимости задержки в тракте многомерной системы описанным способом обеспечивает определение дисперсионной характеристики векторного канала в полосе прозрачности ионосферной линии ВЧ-связи.
На фиг.1 представлена упрощенная схема многомерного скалярного канала в частотной области. Слева изображены тракты распространения с номерами 1, 2, …j…m {m - число трактов), соответствующие модам распространения от передатчика к приемнику на частоте 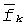 . В данном случае связь с ионосферным распространением ВЧ-радиоволн основана на идентификации мод распространения с трактами многомерной системы. Функции
. В данном случае связь с ионосферным распространением ВЧ-радиоволн основана на идентификации мод распространения с трактами многомерной системы. Функции 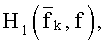
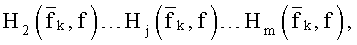
где 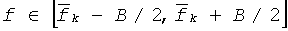 являются частотными характеристиками трактов распространения с номерами от 1 до m. Все тракты соединятся с сумматором. Справа приведена эквивалентная схема многомерного калярного канала на частоте
являются частотными характеристиками трактов распространения с номерами от 1 до m. Все тракты соединятся с сумматором. Справа приведена эквивалентная схема многомерного калярного канала на частоте 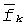 . Его частотная характеристика равна сумме частотных характеристик трактов.
. Его частотная характеристика равна сумме частотных характеристик трактов.
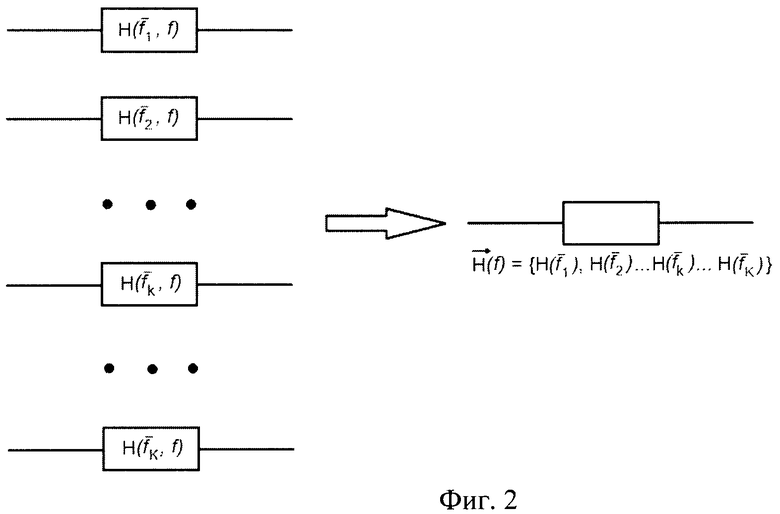
На фиг.2 представлена упрощенная схема векторного канала. Его компонентами (координатами) являются скалярные каналы, отличающиеся рабочими частотами 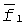 ,
, 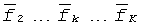 . При этом диапазон рабочих частот расположен от НПЧ до МПЧ ионосферной линии связи. Слева приведена схема допустимого множества скалярных каналов, а справа их эквивалент в виде векторного канала, компонентами векторной частотной характеристики которого
. При этом диапазон рабочих частот расположен от НПЧ до МПЧ ионосферной линии связи. Слева приведена схема допустимого множества скалярных каналов, а справа их эквивалент в виде векторного канала, компонентами векторной частотной характеристики которого 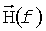 являются упорядоченное множество частотных характеристик возможных на линии связи скалярных каналов
являются упорядоченное множество частотных характеристик возможных на линии связи скалярных каналов 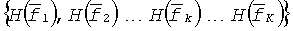 .
.
На фиг.3 показано расположение скалярных каналов на оси частот в полосе прозрачности радиолинии, приведены частотные скалярные каналы, отличающиеся средними частотами 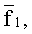
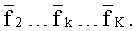 Совокупность скалярных каналов образует векторный канал. По оси частот (f) отложены занимаемые скалярными каналами частоты (от НПЧ до МПЧ), являющиеся аргументами их частотных характеристик.
Совокупность скалярных каналов образует векторный канал. По оси частот (f) отложены занимаемые скалярными каналами частоты (от НПЧ до МПЧ), являющиеся аргументами их частотных характеристик.
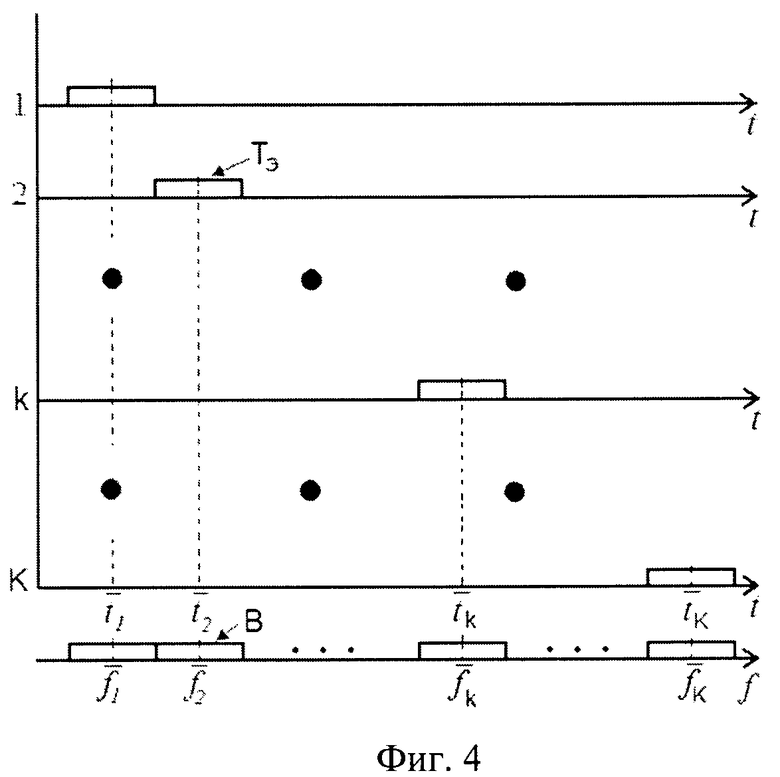
На фиг.4 показаны временные элементы сверхширокополосного зондирующего ЛЧМ сигнала и соответствующие им частотные скалярные каналы.
Представлены последовательные парциальные элементы зондирующего сверхширокополосного ЛЧМ сигнала и его элементы во временной области, t1, t2…tk…tK. Из-за линейной зависимости частоты от времени в данном сигнале этим временным элементам 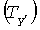 соответствуют полосы частот скалярных каналов (B) со средними частотами
соответствуют полосы частот скалярных каналов (B) со средними частотами 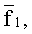
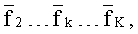 упорядоченное множество которых образует векторный канал.
упорядоченное множество которых образует векторный канал.
Верхние горизонтальные оси являются осями времени, а нижняя - осью частот.
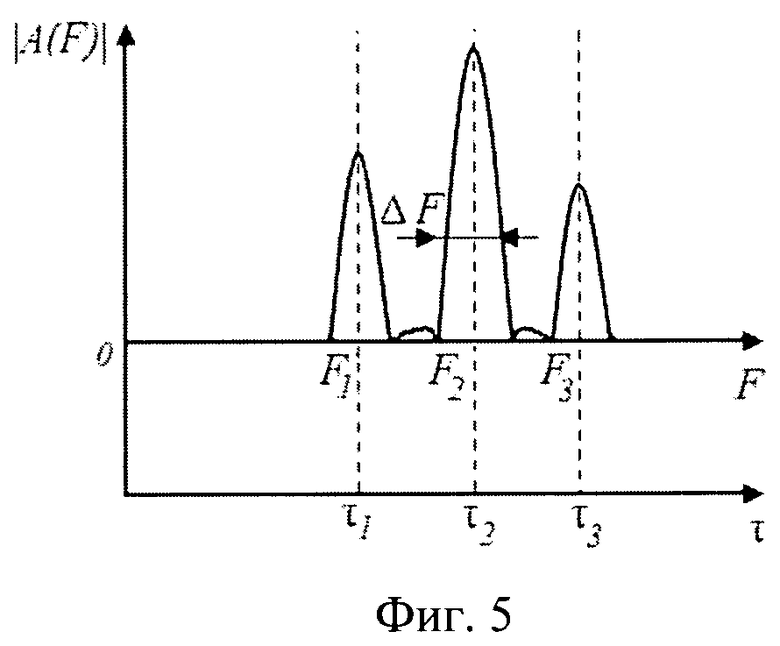
На фиг.5 представлены спектры парциального элемента сигнала разностной частоты, соответствующие трактам распространения. По вертикальной оси 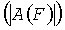 отложены спектральные амплитуды. По верхней горизонтальной оси - частота разностного сигнала. По нижней оси - время запаздывания сигнала при распространении в тракте. Частотам тонов F1, F2, F3 ставятся в соответствие задержки распространения в трактах многомерной системы τ1, τ2, τ3.
отложены спектральные амплитуды. По верхней горизонтальной оси - частота разностного сигнала. По нижней оси - время запаздывания сигнала при распространении в тракте. Частотам тонов F1, F2, F3 ставятся в соответствие задержки распространения в трактах многомерной системы τ1, τ2, τ3.
Можно выделить два направления использования способа. Когда параметры многомерности используются в имитаторах ВЧ-канала, для работы которых требуется задание количества трактов распространения, дисперсионная характеристика позволяет оценить дрожание фазы сигналов с псевдослучайной перестройкой рабочей частоты (ППРЧ) при когерентной обработке.
Действительно, фазу сигнала, прошедшего ионосферный канал по выделенному тракту, можно выразить через дисперсионную характеристику в виде
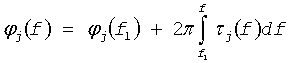
Дрожание фазы определяется разностью значений фазы на частотах fk и fk+1:
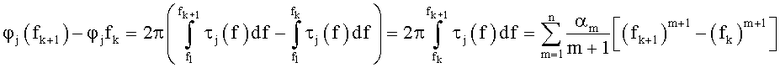
где было учтено, что 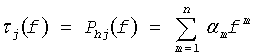
Учет дрожания фазы позволяет существенно улучшить помехоустойчивость и скрытность системы ВЧ связи с ППРЧ.
| название | год | авторы | номер документа |
|---|---|---|---|
| УСТРОЙСТВО ДЛЯ ОПРЕДЕЛЕНИЯ ОПТИМАЛЬНЫХ РАБОЧИХ ЧАСТОТ ИОНОСФЕРНОГО РАДИОКАНАЛА | 2009 |
|
RU2394371C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ МАКСИМАЛЬНО ПРИМЕНИМОЙ ЧАСТОТЫ ДЛЯ ИОНОСФЕРНОЙ РАДИОСВЯЗИ | 2012 |
|
RU2516239C2 |
| СПОСОБ ОДНОВРЕМЕННОГО ИЗМЕРЕНИЯ ЧАСТОТНЫХ ЗАВИСИМОСТЕЙ ДОПЛЕРОВСКОГО СМЕЩЕНИЯ ЧАСТОТЫ И ВРЕМЕНИ РАСПРОСТРАНЕНИЯ КОРОТКОВОЛНОВЫХ СИГНАЛОВ В ИОНОСФЕРНОЙ РАДИОЛИНИИ | 2006 |
|
RU2316898C1 |
| СПОСОБ СОЗДАНИЯ КАНАЛА РАДИОСВЯЗИ ЧЕРЕЗ ИСКУССТВЕННЫЙ ИОНОСФЕРНЫЙ РЕТРАНСЛЯТОР | 2012 |
|
RU2518900C2 |
| ИОНОСФЕРНЫЙ ЗОНД-РАДИОПЕЛЕНГАТОР | 2009 |
|
RU2399062C1 |
| СПОСОБ ВЫБОРА РАБОЧИХ ЧАСТОТ ДЛЯ РАДИОЛИНИЙ ИОНОСФЕРНЫХ ВОЛН | 2006 |
|
RU2307463C1 |
| ЛЧМ-ИОНОЗОНД | 2014 |
|
RU2581627C2 |
| СПОСОБ УПРАВЛЕНИЯ РАСПРОСТРАНЕНИЕМ КОРОТКИХ РАДИОВОЛН В ИОНОСФЕРНОМ ВОЛНОВОДЕ | 2009 |
|
RU2413363C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ПРОСТРАНСТВЕННОГО РАСПРЕДЕЛЕНИЯ ИОНОСФЕРНЫХ НЕОДНОРОДНОСТЕЙ | 2013 |
|
RU2529355C2 |
| Система автоматического управления декаметровой радиосвязью | 2022 |
|
RU2800643C1 |

Изобретение относится к информационно-телекоммуникационным технологиям и электронике и может быть использовано в современных цифровых системах широкополосной высокочастотной (ВЧ) радиосвязи и цифрового ВЧ - радиовещания, когда средой распространения является изменчивая во времени и пространстве ионосфера Земли. Технический результат состоит в одновременном оценивании частотной дисперсии и многомерности векторного широкополосного ВЧ-радиоканала. Для этого в полосе прозрачности ионосферной линии связи получают характеристику частотной дисперсии и многомерности элементов канала путем оценки сжатых в частотной области элементов зондирующего сигнала. Для зондирования векторного высокочастотного канала используется сверхширокополосный ЛЧМ сигнал; все скалярные ВЧ-каналы зондируются одновременно; оцениваются многомерность скалярных каналов и дисперсионная характеристика сверхширокополосного векторного канала в виде полиномиальной функции, определяющей частотную дисперсию в нем. Получение непрерывной зависимости задержки в тракте многомерной системы обеспечивает определение дисперсионной характеристики векторного канала в полосе прозрачности ионосферной линии ВЧ-связи. 5 ил.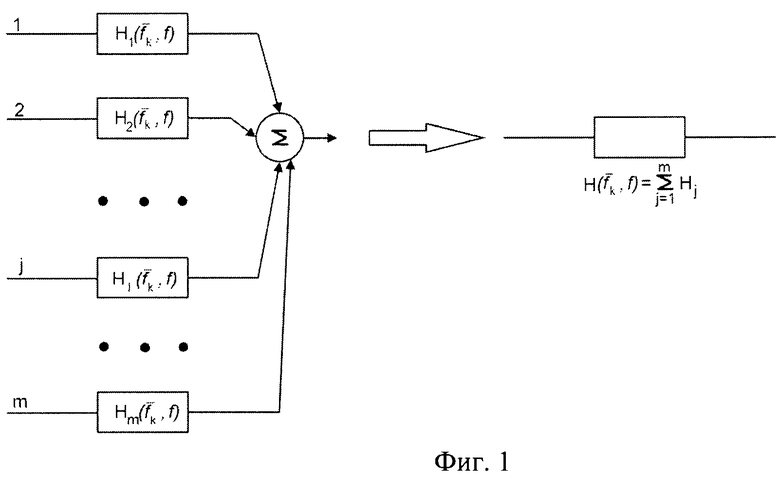
Способ определения характеристик частотной дисперсии и многомерности векторного высокочастотного ионосферного канала в полосе прозрачности ионосферной линии связи с использованием ЛЧМ сигналов, заключающийся в разбиении сверхширокополосного векторного канала, занимающего полосу прозрачности ионосферной линии ВЧ радиосвязи и расположенного от ее наименьшей применимой частоты до максимальной применимой частоты на К примыкающих скалярных частотных каналов, составляющих векторный канал; в зондировании векторного канала сверхширокополосным ЛЧМ сигналом с полосой, равной полосе прозрачности радиолинии; формировании в приемнике копии зондирующего сигнала; в разбиении принимаемого сигнала на парциальные ЛЧМ сигналы с примыкающими полосами частот, соответствующими полосам парциальных скалярных частотных каналов с различной средней частотой; выделении из них сигналов разностной частоты; в получении многомерного спектра сигналов разностной частоты, упорядоченное множество компонент которого характеризует зондируемый многомерный канал; отличающийся тем, что, с целью определения частотной дисперсии времени распространения и многомерности векторного ВЧ канала, выделяются тоны колебаний разностной частоты; определяются их спектральные максимумы, частоты которых соответствуют времени распространения элемента ЛЧМ сигнала в тракте; определяется общее количество трактов для каждого частотного канала; для каждого тракта определяется дискретная зависимость времени распространения от частоты (дисперсионная характеристика); по дискретным значениям путем минимизации функционала определяется непрерывная полиномиальная модель дисперсионной характеристики скалярного частотного канала.
| Горлов Н.И | |||
| Оптические направляющие системы.: Конспект лекций | |||
| - Новосибирск, 2003, лекция №5: Дисперсия и ее измерения | |||
| Способ определения профиля неоднородности среды с частотной дисперсией | 1988 |
|
SU1608597A1 |
| Способ определения градиента плотности среды с частотной дисперсией | 1983 |
|
SU1168880A1 |
Авторы
Даты
2013-02-20—Публикация
2011-08-25—Подача