Изобретение относится к инженерной биологии и биоиндикации загрязнения окружающей среды измерениями качества ростовых органов различных видов растений, преимущественно древесных растений, например проб в виде отдельных листьев древесных растений с равномерной выпукло-волновой листовой пластинкой, например, дуба.
Предлагаемое изобретение может быть также использовано при экологическом и технологическом мониторинге за молодыми древесными растениями, в частности за молодняками дуба.
Известен способ измерения формы древесного ствола по патенту №2201593, включающий разметку, по крайней мере, дважды, вначале по местам наименьших расстояний между неровностями, а затем по вершинам этих неровностей с измерением соответствующих расстояний от основания, причем некратные длины секций определяют по неровным участкам значительной кривизны.
Недостатком является измерение только диаметров ствола, что не позволяет на отдельных листьях этих же учетных деревьев точно измерять их волнистую форму. Для характеристики волнистой формы листа, например, дуба, требуется большее количество характерных точек. При этом требуется измерять не диаметры, то есть в предлагаемом техническом решении ширины листа в характерных точках от основания листа на черешке, а радиусы от главной жилки листа до края его волнистой боковой линии. Кроме того, не учитывается также асимметрия листа как важнейшего экологического показателя роста и развития древесного листа
Известен также способ измерения площади листьев у древесных растений (см. книгу: Федорова А.И., Никольская А.Н. Практикум по экологии и охране окружающей среды: Учеб. пос. М.: Гуманит. изд. центр ВЛАДОС, 2001. 288 с. С.123-126), включающий по методикам М.С.Миллера (Летние практические… 1973) подсчет квадратиков на миллиметровой бумаге для определения площади поверхности листа.
Недостатком является то, что на миллиметровой бумаге вычисляется только площадь по клеткам, а линия образующей формы листа не выделяется как объект исследования и поэтому не измеряется. При этом измерению площади подвергаются простые по форме листья. Не учитывается также асимметрия листа как важнейшего экологического показателя развития и роста древесного листа.
Технический результат - повышение функциональных возможностей измерения каждой стороны древесного листа от его главной жилки и точности индикации качества окружающей каждый лист древесного растения среды измерениями местоположения листа относительно ствола дерева и вычислением асимметрии формы поверхности листа, а также расширение функциональных возможностей способа подсчета квадратиков на миллиметровой бумаге для определения площади листа, дополнительно подсчета квадратиков для определения ординат каждой половины листа через разные расстояния от основания до вершины листа, то есть косвенно в динамике времени вегетационного периода учетного или срезанного листа учетного дерева.
Этот технический результат достигается тем, что способ измерения формы листьев у древесных растений, включающий взятие листьев от учетных деревьев, растущих в разных экологических условиях, обведение контура листа на миллиметровой бумаге и подсчет квадратиков на миллиметровой бумаге для определения площади листа, отличающийся тем, что каждый измеряемый лист размещают на подложке с закрепленным на ней листом миллиметровой бумаги, причем продольную ось листа растения по главной жилке совмещают с одной из сантиметровых линий сетки миллиметровой бумаги, затем лист прижимают к миллиметровой бумаге и обводят его по контуру пишущим устройством для получения четкой боковой линии листа, при этом по концам листа на миллиметровой бумаге отмечают положение главной продольной жилки, в дальнейшем измерения выполняют на миллиметровой бумаге по ширине каждой половинки нарисованного контура листа как расстояние от главной жилки до линии обвода контура листа, по измеренным значениям ширины половинок листа вычисляют переменную ширину листа как сумму половинок и их разность как абсолютную асимметрию листа, а также их отношение как коэффициент асимметрии листа, в дальнейшем по измеренным и рассчитанным значениям параметров листа статистическим моделированием выявляют биотехнические закономерности средней линии и волны контура у каждой половины листа, а по отношениям разницы между фактическими и расчетными по средней боковой линии значениями ширины у каждой половины листа судят о коэффициенте динамичности развития и роста формы листа.
При необходимости у древесного листа по основанию его черешка измеряют геодезические координаты по азимуту, высоте взятия листа и радиусу от продольной оси ствола учетного дерева, причем после срезания древесного листа как биологической пробы измерения формы листа выполняют на миллиметровой бумаге с контуром боковой линии листа в камеральных условиях, а для многократных измерений в динамике развития и роста в вегетационный период древесный лист принимают за учетный лист, около которого на ветке закрепляют метку, например, в виде бирки с номером учетного листа, привязанной на ветке ниткой.
Измерения выполняют на миллиметровой бумаге по ширине каждой половинки нарисованного контура листа как расстояние от главной жилки до линии обвода контура листа, при этом измерения ширины половинок листа выполняют с постоянным шагом через 2 мм или же переменным шагом, кратным 1 мм, по клеткам миллиметровой бумаги в зависимости от длины волны боковой линии листа.
Для повышения точности измерений и снижения погрешности моделирования боковой линии листа измерения вдоль главной продольной жилки листа выполняют до расстояния, при котором ординаты верхней и нижней половинок листа становятся меньше 3 мм.
По измеренным значениям ширины половинок листа y1 и y2 вычисляют переменную ширину В листа как сумму половинок и их разность как абсолютную асимметрию ΔВ листа, а также их отношение как коэффициент асимметрии As листа по формулам:
- переменная ширина древесного листа
В=y1+y2;
- абсолютная асимметрия древесного листа по ширине
ΔB=y1-y2;
- коэффициент поперечной асимметрии листа
As=ΔB/B.
Любой измеренный или расчетный параметр формы древесного листа по значениям идентифицируется биотехническим законом в виде детерминированной модели вида
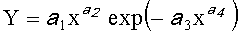 .
.
где Y - любой из перечисленных пяти параметров формы листа,
x - расстояние (абсцисса) вдоль главной продольной жилки листа от основания этого древесного листа, мм,
a 1…а 4 - параметры биотехнического закона, получающие конкретные числовые значения в зависимости от результатов измерений конкретного древесного листа с конкретным пространственным расположением относительно ствола дерева.
Для упрощенной методики обработки результатов измерений и расчетных параметров формы листа вычисляют следующие критерии оценки:
максимальная относительная погрешность Δmax (по модулю, %) статистической модели от фактических значений параметра в одной точке (для какого-то конкретного измерения) по формуле
Δmax⊃Δ=100(Yф-Y)/Yф=100ε/Yф;
коэффициент динамичности Kд max поведения объекта с максимальным возмущением в одной точке измерений по выражению
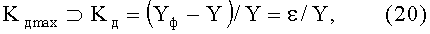
где ⊃ - знак отношения к множеству значений, из которых выбирается максимальное (по модулю) значение критерия,
Yф - фактические значения параметра формы листа,
Y - расчетные значения параметров листа,
ε - остаток (абсолютная погрешность) от детерминированной модели в виде биотехнического закона.
Для сопоставления с фенологическими наблюдениями, проведенными относительно учетного дерева, по измеренным значениям ширины половинок и других параметров формы листа статистическим моделированием выявляют трехчленные биотехнические закономерности по формуле:
Y=Y1+Y2+Y3,
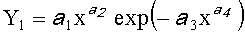 ,
,
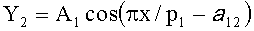 ,
, 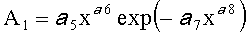 ,
, 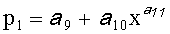 ,
,
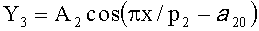 ,
, 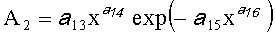 ,
, 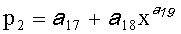 ,
,
где Y - показатель, то есть любой из измеренных или расчетных параметров древесного листа,
Y1 - детерминированная часть биотехнической закономерности,
Y2, Y3 - волновые составляющие модели, показывающие колебательное возмущение формы древесного листа в процессе адаптации к внешним воздействиям и внутреннем физиологическим процессам, происходящем в листе и материнском учетном дереве,
x - расстояние (абсцисса) вдоль главной продольной жилки листа от основания этого древесного листа, мм,
А1, А2 - амплитуды (половина) колебательного возмущения древесного листа в прошлом от начала вегетационного периода до момента взятия как биологической пробы,
p1, р2 - полупериоды колебания формы древесного листа вдоль главной продольной жилки, косвенно характеризующие течение времени вегетационного периода, мм,
а 1…а 20 - параметры трехчленной биотехнической закономерности,
получающие конкретные числовые значения в процессе идентификации в программной среде типа CurveExpert по измеренным и расчетным статистическим выборкам значений параметров формы древесного листа.
Для сопоставления с результатами фенологических наблюдений и физиологических измерений, по измеренным значениям ширины половинок и других параметров формы листа статистическим моделированием при доведении остатков после многочленной модели, меньших погрешности измерений ординат половинок листа, выявляют сложные и многочленные биотехнические закономерности по формуле:
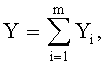
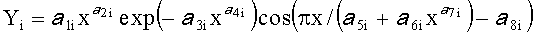 ,
,
где Y - показатель, то есть любой из измеренных или расчетных параметров древесного листа,
i - номер члена общей сложной формулы,
m - количество составляющих общей формулы, которое может быть различным для разных параметров формы листа, шт.,
x - расстояние вдоль длины главной жилки древесного листа, мм,
a 1…а 8 - параметры у одного члена формулы, физически представляемого как асимметричный вейвлет-сигнал с переменными амплитудой и частотой колебательного возмущения конкретного листа, заложенными в процессе развития и роста и в своем реактивном поведении за прошлый вегетационный период.
Кроме коэффициента корреляции, вычисляемого автоматически в программной среде типа CurveExpert, для более строгой оценки адекватности каждой многочленной биотехнической закономерности рассчитывается максимальная относительная погрешность Δmax, которая показывает не только адекватность составной из большого множества членов модели, но также характеризует и качество самоуправления растительного существа своим поведением, и этот критерий оценки определяется по формуле:
Δmax⊃Δ=100(YФ-Y)/Yф=100ε/Yф,
где ⊃ - знак отношения к множеству значений, из которых выбирается максимальное (по модулю) значение критерия,
Yф - фактические значения параметра формы листа,
Y - расчетные значения параметров листа,
ε - остаток (абсолютная погрешность) от сложной модели.
Для оценки замены табличной модели каждого из параметров формы древесного листа на ее математическую модель и одновременно важнейшей биоэкологической оценки качества поведения учетного или срезанного древесного листа сосчитывают критерии:
- количество m составляющих факторной функции, причем чем меньше количество составляющих, тем эффективнее вел себя древесный лист в процессах развития и роста при внешних и внутренних разнообразных воздействиях;
- количество n параметров выявленной статистической закономерности: чем меньше это количество, тем лучше «сработала» подсистема самоуправления древесным листом.
Для выяснения картины поведения древесного листа в прошлом на отдельных промежутках вегетационного периода до момента проведения измерений применяют следующие три критерия:
- значимость α1 первой составляющей характеризует стабильность и устойчивость будущего функционирования древесного листа, если он не был срезан для измерений, и этот оценочный показатель вычисляется как отношение расчетных значений по первой составляющей, к общему расчетному результату, то есть по математическому выражению:
α1=100Y1/Y,
где α1 - значимость первой составляющей,
Y1 - первая (трендовая) закономерность,
Y - расчетное значение параметра листа по общей модели (16)
- коэффициент приспособляемости k измеренного древесного листа к внешней среде показывает устойчивость в прошлом по отношению к различным волновым внешним и внутренним возмущениям и он исчисляется по формуле:
ki>1=Yi>1/Y1,
где ki>1 - коэффициент приспособляемости второй и последующей составляющей из общей многочленной модели,
i - номер члена общей сложной формулы,
Yi>1 - вторая и последующие составляющие из многочленной модели,
Y1 - первая составляющая общей многочленной модели;
- коэффициент динамичности Kд поведения в прошлом системы, в данном случае древесного листа как биологического существа, показывает стабильность в прошлом и возможную устойчивость к внешним воздействиям в будущем (до конца вегетационного периода) и указанный критерий самоуправления вычисляется по соотношению:
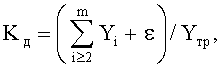
где Kд - коэффициент динамичности развития и роста древесного листа,
i - номер члена общей сложной формулы,
m - количество составляющих общей формулы, которое может быть различным для разных параметров формы листа, шт.,
ε - абсолютная погрешность (остатки) от общей многочленной формулы, то есть разница между фактически измеренными значениями параметров листа и рассчитанными значениями по многочленной формуле,
Yтр - тренд, в общем случае состоящий из нескольких первых не волновых составляющих статистической модели.
Сущность изобретения заключается в том, что каждый лист древесного растения принимается за биологический объект с геодезическими координатами относительно учетного дерева и, соответственно, относительно пространства места его произрастания с влияющими на развитие и рост древесного листа антропогенными и природными объектами.
Сущность изобретения заключается также в том, что лист измеряют непосредственно на растущем дереве многократно без его срезания и тогда этот измеряемый лист становится учетным древесным листом для экологического мониторинга в вегетационный период этого учетного листа, или же лист измеряют однократно после его срезания в камеральных условиях, причем выбор листа как срезаемой пробы или же листа как учетной особи зависит от целей экологических измерений фитоиндикацией.
Сущность изобретения заключается также и в том, что каждый измеряемый лист, срезанный или же оставляемый на доращивание, размещают на переносной или же стационарно размещенной в лаборатории подложке с закрепленным на ней листом миллиметровой бумаги, причем продольную ось учетного или же срезанного листа растения по главной жилке совмещают с одной из линий сетки миллиметровой бумаги, затем лист прижимают к миллиметровой бумаге и обводят его по контуру пишущим устройством для получения четкой боковой линии измеряемого листа.
Сущность изобретения заключается также и в том, что измерения выполняют по ширине каждой половинки листа как расстояние от главной жилки до линии обвода контура листа с постоянным или же переменным шагом в зависимости от длины волны боковой линии листа. Это позволяет в последующем точно промоделировать форму листа по обеим половинкам, а затем вычислить и показатели асимметричности листа. Чем меньше коэффициент асимметричности листа, тем лучше экологические условия его жизнедеятельности.
Сущность изобретения заключается также и в том, что динамичность по коэффициенту волнообразования формы листа, например у дуба, позволяет судить о требованиях учетного или срезанного листа дубового дерева к почве и загрязнениям воздуха. Причем чем меньше отношение волновой функции формы листа к ширине по средней боковой линии, тем лучше развивается и растет это лист и тогда лучше окружающая этот лист экологическая обстановка при условии хорошего транспорта минеральных веществ от корней к данному древесному листу.
Сущность изобретения заключается также и в том, что измерение параметров половинок у каждого геодезическими измерениям привязанного относительно ствола дерева учетного или срезанного листа позволяет по малой статистической выборке всего из 10-12 листьев (вместо 50-60 образцов листьев от нескольких деревьев по прототипу) даже от одного дерева оценивать (детектировать окружающую среду) экологические изменения вокруг него, затем сравнивать разные виды деревьев и обобщать все измеренные листья у нескольких деревьев для экологической оценки качества воздуха, и даже почвы с почвенными водами, территории произрастания нескольких учетных деревьев.
Новизна технического решения заключается в том, что измеряемый лист принимается за индивидуальную особь и это при измерениях ширины половинок листа через 1-2 миллиметра вдоль главной продольной жилки листа позволяет получить добротные статистические выборки для идентификации высокоадекватных к измеренным значениям биотехнические закономерности формы листа по двум половинам. А также по отношениям волны боковой линии к средней ширине листа в разных его местах по длине появляется возможность экологической оценки процесса формообразования древесного листа. Кроме того, по коэффициенту асимметрии листа можно судить о неравномерности биологических условий развития и роста листа.
Положительный эффект заключается в том, что техническое решение позволит постепенно перейти от камеральных однократных измерений срезанных листьев к многократным полевым измерениям одного и того же учетного листа в ходе экологического мониторинга в течение вегетационного периода этого листа. В связи с этим предлагаемое техническое решение становится пионерным для поиска новых научно-технических решений по мере накапливания и анализа статистическим моделированием данных камеральных и полевых измерений.
Таким образом, предлагаемое научно-техническое решение обладает существенными признаками, новизной и положительным эффектом. В научно-технической и патентной литературе информационных материалов, порочащих новизну предполагаемого изобретения, нами не обнаружено.
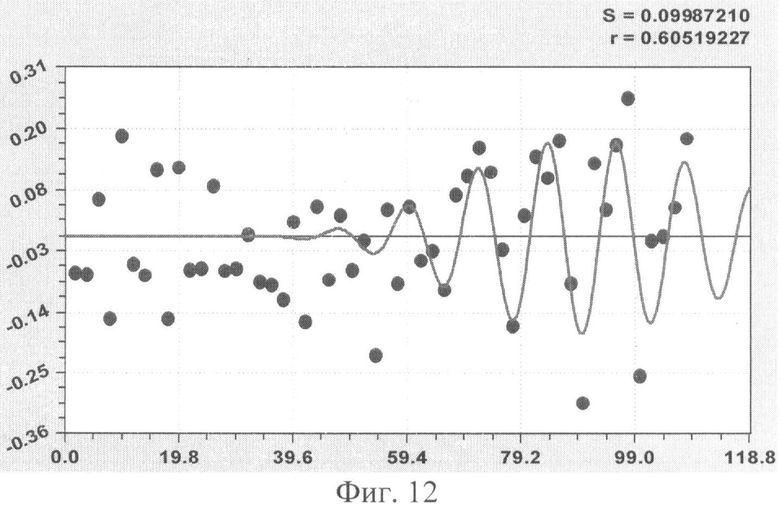
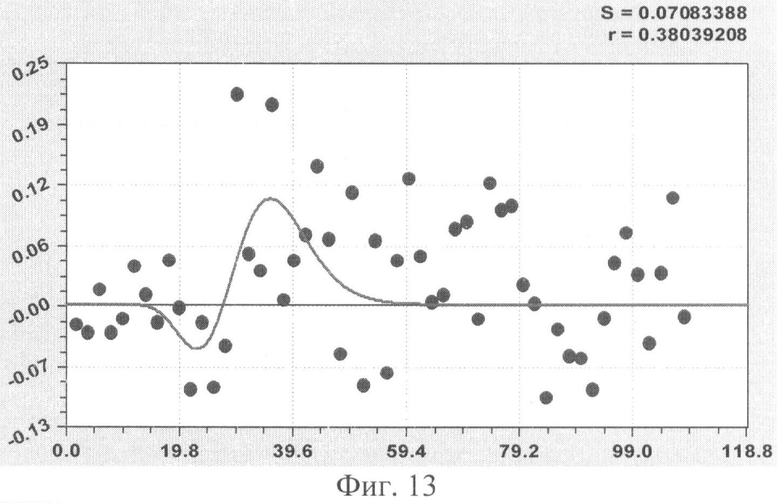
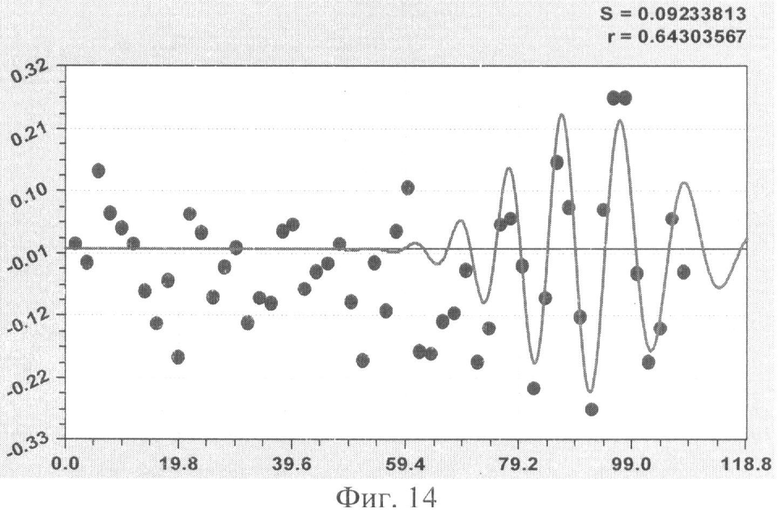
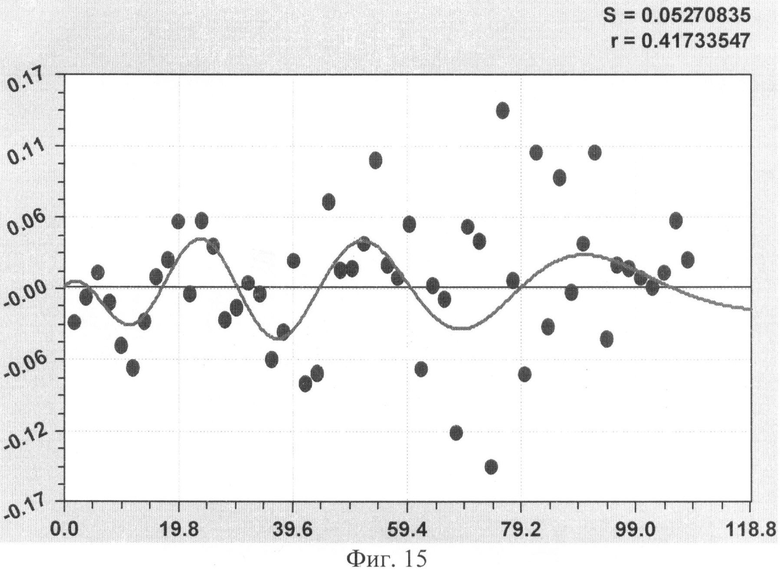
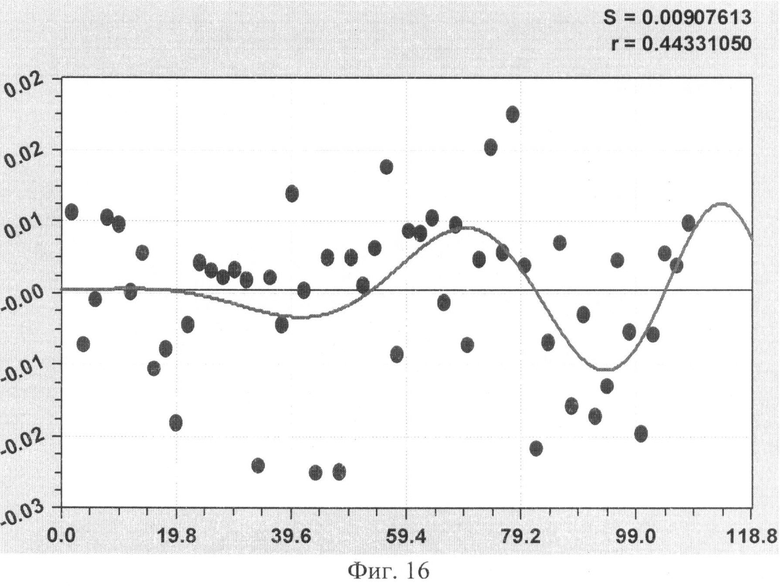
На фиг.1 приведен контур боковой линии дубового листа на фоне миллиметровой бумаги; на фиг.2 показан график детерминированного уравнения биотехнического закона изменения ординаты верхней полвины листа в зависимости от дискретного через 2 мм расстояния от основания до вершины древесного листа; на фиг.3 - то же на фиг.2 по нижней половине дубового листа; на фиг.4 - то же на фиг.2 по ширине дубового листа; на фиг.5 - то же на фиг.2 по абсолютной асимметрии листа; на фиг.6 - то же на фиг.2 по относительной асимметрии листа; на фиг.7 показан график трехчленного уравнения изменения ординаты верхней полвины листа в зависимости от дискретного через 2 мм расстояния от основания до вершины древесного листа; на фиг.8 - то же на фиг.7 по нижней половине дубового листа; на фиг.9 - то же на фиг.7 по ширине дубового листа; на фиг.10 - то же на фиг.7 по абсолютной асимметрии листа; на фиг.11 - то же на фиг.7 по относительной асимметрии листа; на фиг.12 показан график последней в общей модели волновой функции асимметричного вейвлет-сигнала изменения ординаты верхней половины дубового листа; на фиг.13 - то же на фиг.12 по нижней половине дубового листа; на фиг.14 - то же на фиг.12 по ширине дубового листа; на фиг.15 - то же на фиг.12 по абсолютной асимметрии листа; на фиг.16 - то же на фиг.12 по относительной асимметрии листа.
Способ измерения формы учетных листьев у древесных растений без их срезания включает такие основные действия.
Измерению подвергают каждый учетный лист, а обработку измеренных данных по множествам учетных листьев по их контурам на миллиметровой бумаге проводят по разным группировкам: с части дерева, с одного дерева, со всех деревьев и др. Поэтому способ измерения индивидуален, а выявление закономерностей - индивидуальное для листа и групповое для множества листьев даже с одного дерева дуба с геодезической привязкой каждого лист из принятого множества.
Вначале выбирают учетное дерево, например, дуба. Далее составляют описание свойств выбранного учетного дерева и места его произрастания с характеристикой объектов, окружающих и влияющих на экологическую обстановку вокруг учетного дерева. Составляют карту-схему расположения учетного дерева и на ней указывают места на кроне для выбора учетных листьев.
После этого осматривают крону учетного дерева и выбирают места для выбора по одному или нескольким учетным листьям на доступной для измеряющего человека высоте, например на высоте от одного до двух метров. Учетный лист выбирают из числа здоровых и не поврежденных листьев, имеющих примерно плоскую поверхность листовой пластины. На ветках около каждого выбранного учетного листа ставят метки, например, в виде цветной ленточки с бумажной или иной биркой, на которой наносят шифр учетного листа. Составляют журнал измерений с указанием шифра учетного дерева и учетных листьев на нем.
После отбора учетных листьев приступают вначале к их геодезическим измерениям по основанию черешков листьев. Для этого гибкой мерной лентой измеряют высоту расположения учетного листа над почвой или другой базовой поверхностью. Затем измеряют радиус расположения основания черешка листа от середины поперечного сечения ствола учетного дерева. Третьим параметром пространственно расположения учетного листа становится азимут этого радиуса, измеряемый компасом от северного направления.
При необходимости измеряют также угол поворота поверхности листа относительно радиуса основания черешка в вертикальной плоскости радиуса и угол разворота листа в перпендикулярной к радиусу плоскости.
При измерениях формы каждый учетный прикладывается на подложку с закрепленной на ней миллиметровой бумагой. При этом подложка с миллиметровой бумагой подносится к измеряемому учетному листу и, затем, лист прижимают к подложке.
Продольную ось листа растения по главной жилке совмещают с одной из сантиметровых линий сетки миллиметровой бумаги, затем лист прижимают к миллиметровой бумаге и обводят его по контуру пишущим устройством для получения четкой боковой линии листа.
По концам листа на миллиметровой бумаге отмечают положение главной продольной жилки, в дальнейшем измерения выполняют на миллиметровой бумаге по ширине каждой половинки нарисованного контура листа как расстояние от главной жилки до линии обвода контура листа.
По измеренным значениям ширины половинок листа вычисляют переменную ширину листа как сумму половинок и их разность как абсолютную асимметрию листа, а также их отношение как коэффициент асимметрии листа, в дальнейшем по измеренным и рассчитанным значениям параметров листа статистическим моделированием выявляют биотехнические закономерности средней линии и волны контура у каждой половины листа, а по отношениям разницы между фактическими и расчетными по средней боковой линии значениями ширины у каждой половины листа судят о коэффициенте динамичности развития и роста формы листа.
Измерения выполняют на миллиметровой бумаге по ширине каждой половинки нарисованного контура листа как расстояние от главной жилки до линии обвода контура листа, при этом измерения ширины половинок листа выполняют с постоянным шагом через 2 мм.
По измеренным значениям ширины половинок листа y1 и y2 вычисляют переменную ширину В листа как сумму половинок и их разность как абсолютную асимметрию ΔВ листа, а также их отношение как коэффициент асимметрии As листа по формулам:
- переменная ширина древесного листа
В=y1+y2;
- абсолютная асимметрия древесного листа по ширине
ΔB=y1-y2;
- коэффициент поперечной асимметрии листа
As=ΔB/B.
Любой измеренный или расчетный параметр формы древесного листа по значениям идентифицируется биотехническим законом в виде детерминированной модели вида
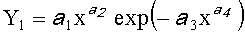 ,
,
где Y - любой из перечисленных пяти параметров формы листа,
x - расстояние (абсцисса) вдоль главной продольной жилки листа от основания этого древесного листа, мм,
а 1…а 4 - параметры биотехнического закона, получающие конкретные числовые значения в зависимости от результатов измерений конкретного древесного листа с конкретным пространственным расположением относительно ствола дерева.
Для сопоставления с результатами фенологических наблюдений и физиологических измерений по измеренным значениям ширины половинок и других параметров формы листа статистическим моделированием при доведении остатков после многочленной модели, меньших погрешности измерений ординат половинок листа, выявляют сложные и многочленные биотехнические закономерности по формуле:
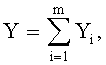
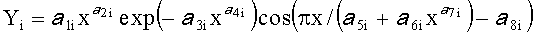 ,
,
где Y - показатель, то есть любой из измеренных или расчетных параметров древесного листа,
i - номер члена общей сложной формулы,
m - количество составляющих общей формулы, которое может быть различным для разных параметров формы листа, шт.,
x - расстояние вдоль длины главной жилки древесного листа, мм,
а 1…а 8 - параметры у одного члена формулы, физически представляемого как асимметричный вейвлет-сигнал с переменными амплитудой и частотой колебательного возмущения конкретного листа, заложенными в процессе развития и роста и в своем реактивном поведении за прошлый вегетационный период.
Кроме коэффициента корреляции, вычисляемого автоматически в программной среде типа CurveExpert, для более строгой оценки адекватности каждой многочленной биотехнической закономерности, рассчитывается максимальная относительная погрешность Δmax, которая показывает не только адекватность составной из большого множества членов модели, но также характеризует и качество самоуправления растительного существа своим поведением, и этот критерий оценки определяется по формуле:
Δmax⊃Δ=100(Yф-Y)/Yф=100ε/Yф,
где ⊃ - знак отношения к множеству значений, из которых выбирается максимальное (по модулю) значение критерия,
Yф - фактические значения параметра формы листа,
Y - расчетные значения параметров листа,
ε - остаток (абсолютная погрешность) от сложной модели.
Для оценки замены табличной модели каждого из параметров формы древесного листа на ее математическую модель и одновременно важнейшей биоэкологической оценки качества поведения учетного или срезанного древесного листа сосчитывают критерии:
- количество m составляющих факторной функции, причем чем меньше количество составляющих, тем эффективнее вел себя древесный лист в процессах развития и роста при внешних и внутренних разнообразных воздействиях;
- количество n параметров выявленной статистической закономерности: чем меньше это количество, тем лучше «сработала» подсистема самоуправления древесным листом.
Для выяснения картины поведения древесного листа в прошлом на отдельных промежутках вегетационного периода до момента проведения измерений применяют следующие три критерия:
- значимость α1 первой составляющей характеризует стабильность и устойчивость будущего функционирования древесного листа, если он не был срезан для измерений, и этот оценочный показатель вычисляется как отношение расчетных значений по первой составляющей, к общему расчетному результату, то есть по математическому выражению:
α1=100Y1/Y,
где α1 - значимость первой составляющей,
Y1 - первая (трендовая) закономерность,
Y - расчетное значение параметра листа по общей модели (16)
- коэффициент приспособляемости к измеренного древесного листа к внешней среде показывает устойчивость в прошлом по отношению к различным волновым внешним и внутренним возмущениям и он исчисляется по формуле:
ki>1=Yi>1/Y1,
где ki>1 - коэффициент приспособляемости второй и последующей составляющей из общей многочленной модели,
i - номер члена общей сложной формулы,
Yi>1 - вторая и последующие составляющие из многочленной модели,
Y1 - первая составляющая общей многочленной модели;
- коэффициент динамичности Kд поведения в прошлом системы, в данном случае древесного листа как биологического существа, показывает стабильность в прошлом и возможную устойчивость к внешним воздействиям в будущем (до конца вегетационного периода) и указанный критерий самоуправления вычисляется по соотношению:
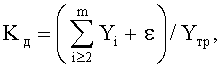
где Kд - коэффициент динамичности развития и роста древесного листа,
i - номер члена общей сложной формулы,
m - количество составляющих общей формулы, которое может быть различным для разных параметров формы листа, шт.,
ε - абсолютная погрешность (остатки) от общей многочленной формулы, то есть разница между фактически измеренными значениями параметров листа и рассчитанными значениями по многочленной формуле,
Yтр - тренд, в общем случае состоящий из нескольких первых не волновых составляющих статистической модели.
Способ измерения формы листьев у древесных растений, например у дуба, например, после срезания, высушивания и хранения в гербарии, по упрощенной методике исследований в школах, включает такие действия.
Во время экспедиций или школьных экскурсий для экономии времени листья срезают с предварительным геодезическим измерением местоположения каждого листа, высушивают и хранят в гербарии, а затем в камеральных условиях после завершении экспедиции или экскурсии измеряют форму листьев и сопоставляют по измеренным данным условия произрастания этих листьев.
Для этого каждый измеряемый лист размещают на подложке с закрепленным на ней листом миллиметровой бумаги, причем продольную ось листа растения по главной жилке совмещают с одной из сантиметровых линий сетки миллиметровой бумаги. Затем лист прижимают к миллиметровой бумаге и обводят его по контуру пишущим устройством для получения четкой боковой линии листа. При этом по концам листа на миллиметровой бумаге отмечают положение главной продольной жилки, в дальнейшем измерения выполняют на миллиметровой бумаге по ширине каждой половинки нарисованного контура листа как расстояние от главной жилки до линии обвода контура листа.
По измеренным значениям ширины половинок листа вычисляют переменную ширину листа как сумму половинок и их разность как абсолютную асимметрию листа, а также их отношение как коэффициент асимметрии листа, в дальнейшем по измеренным и рассчитанным значениям параметров листа статистическим моделированием выявляют биотехнические закономерности средней линии и волны контура у каждой половины листа, а по отношениям разницы между фактическими и расчетными по средней боковой линии значениями ширины у каждой половины листа судят о коэффициенте динамичности развития и роста формы листа.
Измерения выполняют на миллиметровой бумаге по ширине каждой половинки нарисованного контура листа как расстояние от главной жилки до линии обвода контура листа, при этом измерения ширины половинок листа выполняют с постоянным шагом через 2 мм.
Для повышения точности измерений и снижения погрешности моделирования боковой линии листа измерения вдоль главной продольной жилки листа выполняют до расстояния, при котором ординаты верхней и нижней половинок листа становятся меньше 3 мм.
По измеренным значениям ширины половинок листа y1 и y2 вычисляют переменную ширину В листа как сумму половинок и их разность как абсолютную асимметрию ΔВ листа, а также их отношение как коэффициент асимметрии As листа по формулам:
- переменная ширина древесного листа
В=y1+y2;
- абсолютная асимметрия древесного листа по ширине
ΔВ=y1-y2;
- коэффициент поперечной асимметрии листа
As=ΔB/B.
Любой измеренный или расчетный параметр формы древесного листа по значениям идентифицируется биотехническим законом в виде детерминированной модели вида
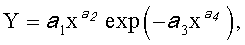
где Y - любой из перечисленных пяти параметров формы листа,
x - расстояние (абсцисса) вдоль главной продольной жилки листа от основания этого древесного листа, мм,
a 1…a 4 - параметры биотехнического закона, получающие конкретные числовые значения в зависимости от результатов измерений конкретного древесного листа с конкретным пространственным расположением относительно ствола дерева.
Для упрощенной методики обработки результатов измерений и расчетных параметров формы листа вычисляют следующие критерии оценки:
максимальная относительная погрешность Δmax (по модулю, %) статистической модели от фактических значений параметра в одной точке (для какого-то конкретного измерения) по формуле
Δmax⊃Δ=100(Yф-Y)/Yф=100ε/Yф;
коэффициент динамичности Kд max поведения объекта с максимальным возмущением в одной точке измерений по выражению
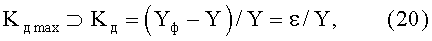
где ⊃ - знак отношения к множеству значений, из которых выбирается максимальное (по модулю) значение критерия,
Yф - фактические значения параметра формы листа,
Y - расчетные значения параметров листа,
ε - остаток (абсолютная погрешность) от детерминированной модели в виде биотехнического закона.
Пример. Форма листьев у многих древесных растений является индикатором годичного режима экологических условий. Дуб является требовательным к плодородию почвы и поверхностному водному режиму. Дубовые листья меняют волнистую форму в зависимости от условий произрастания. В итоге появляется практическая возможность фитоиндикации тех территорий, на которых произрастает хотя бы одно дерево дуба.
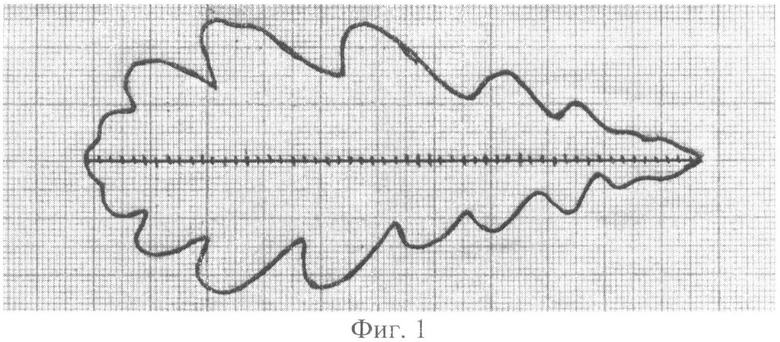
Вначале нужно научиться измерять и обрабатывать измеренные данные по отдельному дубовому листу. Для проведения измерений были взяты несколько дубовых листьев из гербария, то есть измерялась форма высохшего листа. Пример приведен по дубовому листу №1 (фиг.1), который был положен на миллиметровую бумагу наверх лицевой стороной с ориентацией продольной жилки относительно заметной сантиметровой линии на миллиметровке, а затем аккуратно обведен по контуру шариковой ручкой.
На контуре дубового листа отмечены расстояния вдоль продольной жилки с интервалом в 2 мм. Из картографических измерений известно, что шаг измерений в 2 мм, например, длины реки по карте, достаточен для получения относительно точно измеренных данных.
Для удобства измерений по ординатам вдоль оси листа на миллиметровой бумаге (см. фиг.1) вдоль оси х нанесены метки. Даже визуально видна асимметричность развития и роста каждой (верхней и нижней) стороны у дубового листа №1. Как известно, свойство асимметричного строения древесного листа применяется экологами для оценки качества окружающей растение среды. Однако главным недостатком является массовость измерений на обезличенном множестве древесных листьев. А это обстоятельство не позволяет проводить высокоточные экологические оценки по отдельным учетным или срезанным древесным листьям. Во всяком случае, вначале нужно измерить параметры отдельных листьев, и только затем, при необходимости, можно будет превратить результаты измерений у множества листьев в массовый статистический материал. Поэтому усреднение экологических данных вначале эксперимента недопустимо.
Исходя из такого методологического принципа контур каждого учетного или срезанного листа измеряется в отдельности
Результаты измерений текущей ширины каждой половины от главной жилки и расчетных параметров дубового листа приведены в таблице 1.
y1 - ордината верхней стороны древесного листа, мм;
y2 - ордината нижней стороны листа, мм;
B - переменная ширина древесного листа, мм;
ΔВ - абсолютная асимметрия древесного листа по ширине, мм;
As - относительная поперечная (коэффициент) асимметрия листа.
В зависимости от условий эксперимента все вышеуказанные пять параметров дубового листа могут стать показатели экологической оценки места произрастания данного учетного (возможность проведения многократных измерений в течение вегетационного периода) или срезанного (однократное измерение с учетом только одного момента времени вегетационного периода) листа.
Параметры y1 (вверх) и y2 (вниз) измеряются по клеткам миллиметровой бумаги относительно метки перпендикулярно линии главной жилки древесного листа.
Расчетные параметры формы древесного листа вычисляются по следующим формулам:
- переменная ширина древесного листа
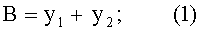
- абсолютная асимметрия древесного листа по ширине
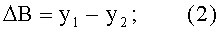
- коэффициент поперечной асимметрии листа
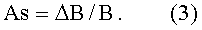
Погрешность измерений y1 и y2 определяется следующим образом.
Глазомерно можно оценивать размер половины клетки миллиметровой бумаги, поэтому цена деления ординат будет равна 0,5 мм (см. табл.1). В этом случае погрешность измерений составит ±0,25 мм. Эти же погрешности будут действительными для параметров в и ΔВ.
Пусть минимальная ширина листа будет равна 10 мм. Тогда погрешность коэффициента асимметрии будет равна ±0,25 мм/10 мм=0,025. в вершине древесного листа погрешность расчета коэффициента асимметрии будет возрастать.
Детерминированные модели. Любой параметр древесного листа изменяется по биотехническому закону вида
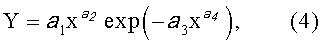
где Y - любой из выше перечисленных пяти параметров формы листа,
x - расстояние (абсцисса) вдоль главной продольной жилки листа от основания этого древесного листа, мм,
а 1…а 4 - параметры биотехнического закона (4), получающие конкретные числовые значения в зависимости от результатов измерений конкретного древесного листа с конкретным пространственным расположением относительно ствола дерева.
После параметрической идентификации исходной модели (4) для измерений по данным таблицы 1 были получены формулы при а 4=1:
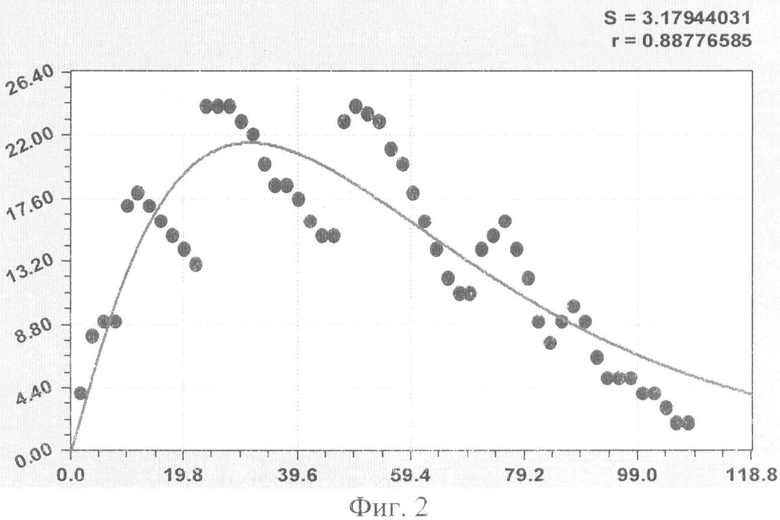
- ордината верхней стороны древесного листа (фиг.2)
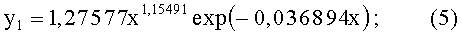
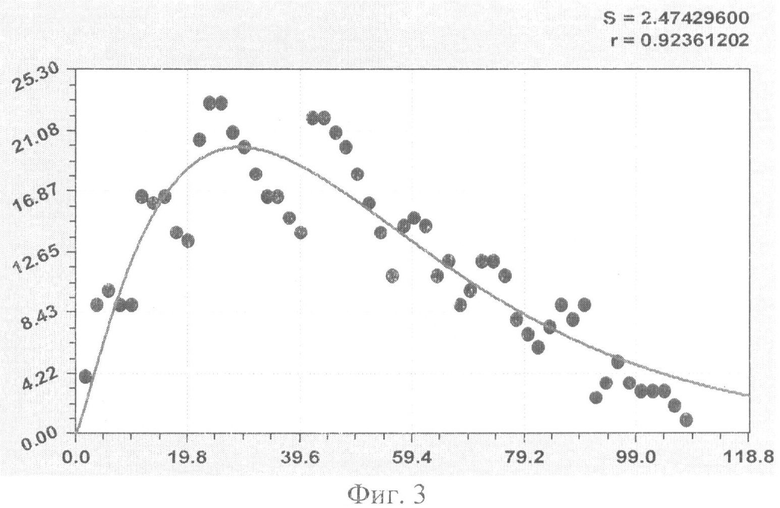
- ордината нижней стороны листа (фиг.3)
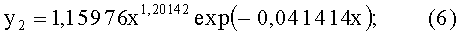
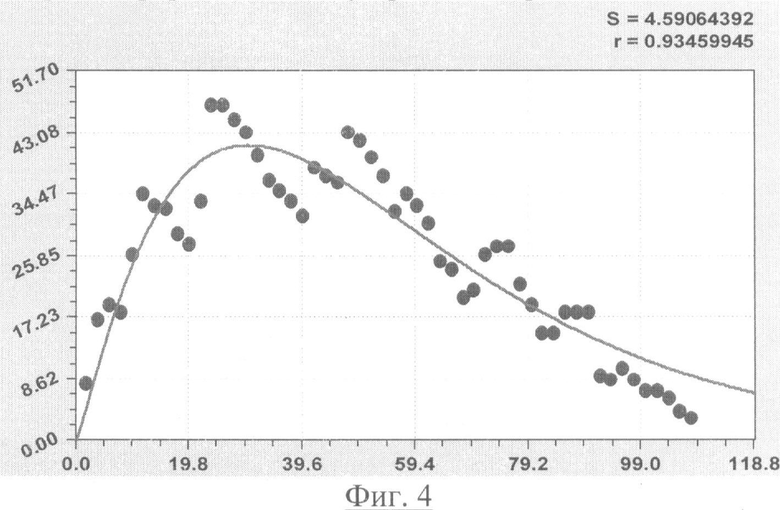
- переменная ширина древесного листа (фиг.4)
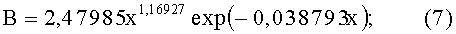
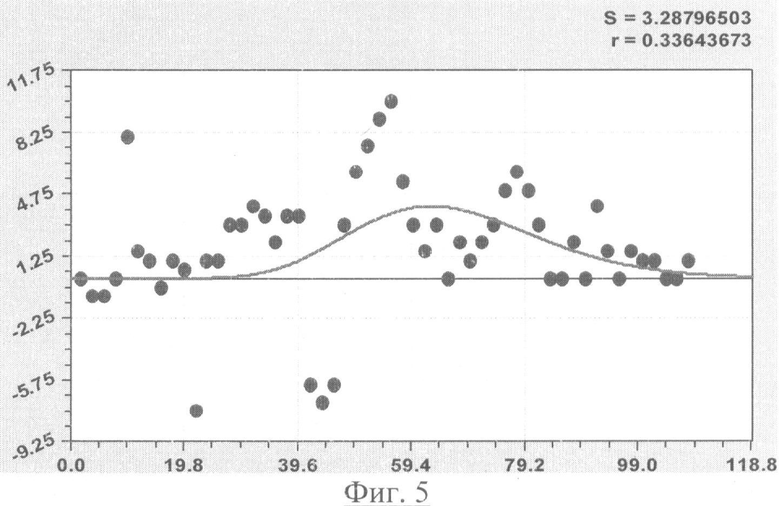
- абсолютная асимметрия древесного листа по ширине (фиг.5)
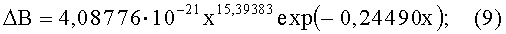
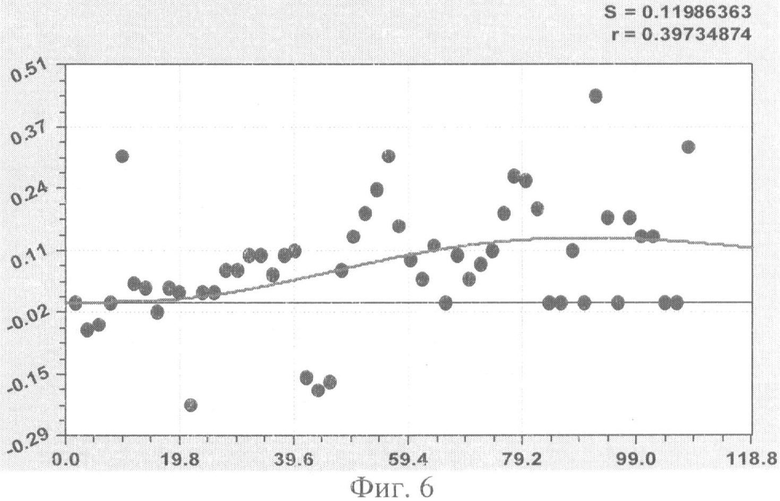
- коэффициент асимметрии древесного листа (фиг.6)
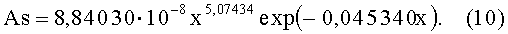
Показатели адекватности приведены в сводной таблице 2.
Трехчленные биотехнические закономерности. Они получаются присоединение к тренду (4) еще двух волновых функций, показывающих колебательное возмущение измеренного листа на воздействие окружающей среды и режима питания от материнского дерева.
После структурно-параметрической идентификации исходной модели (4) с дополнениями из программной среды CurveExpert для измерений по данным таблицы 1 были получены следующие формулы:
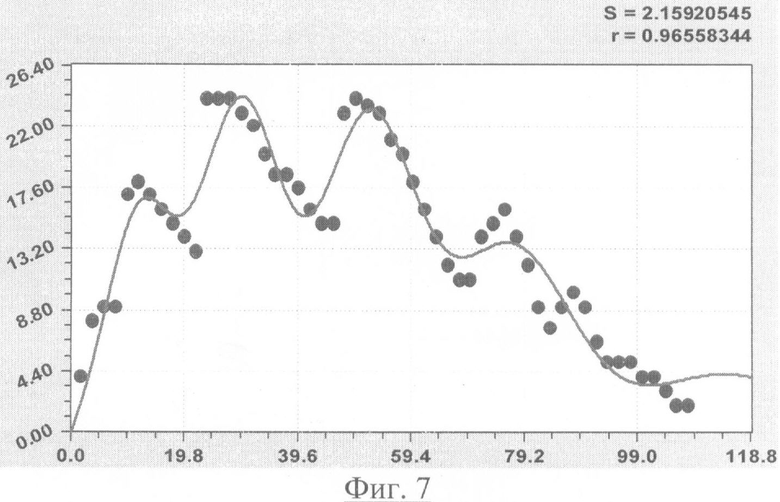
- ордината верхней стороны древесного листа (фиг.7)
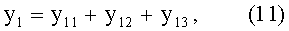
y11=1,25895x1,15357exp(-0,036093x1,00268), y12=A1cos(πx/p1-2,80170), А1=4,08511х3,56896ехр(-4,45060х0,29394), р1=10,22612+0,00015128х2,08577, y13=A2cos(πx/p2-2,03937), А2=0,018404х4,37368ехр(-3,31905х0,33558), р2=19,06494+0,00048418х2,15505,
причем обе волны позитивные (положительный знак перед членами);
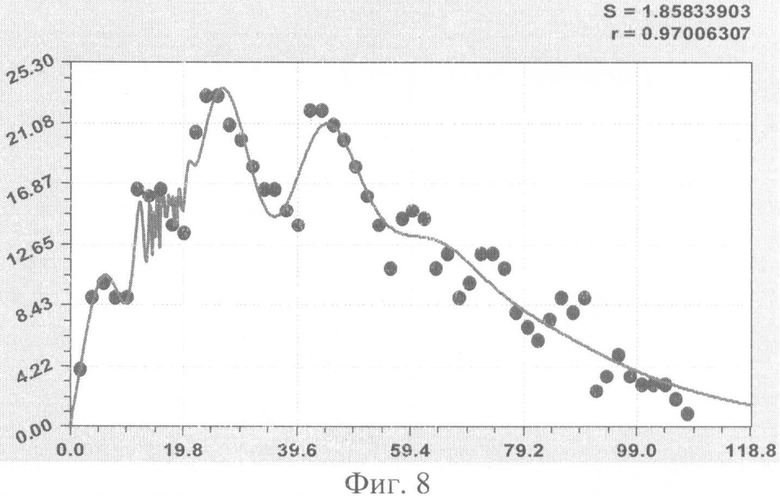
- ордината нижней стороны листа (фиг.8)
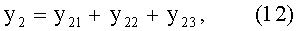
y21=2,33801x0,72298exp(-0,00090669x1,74936), y22=A1cos(πx/p1-0,67122), А1=4,64999·108х7,40640ехр(-21,46729х0,22376), р1=17,33859-0,55091x1,23001, y23=A2cos(πx/p2-0,60585), А2=-2,15395·10-7х6,82059ехр(-0,21047х0,99874), р2=0,14937+4,37718х0,18074,
и в этой формуле вторая волна имеет кризисную направленность;
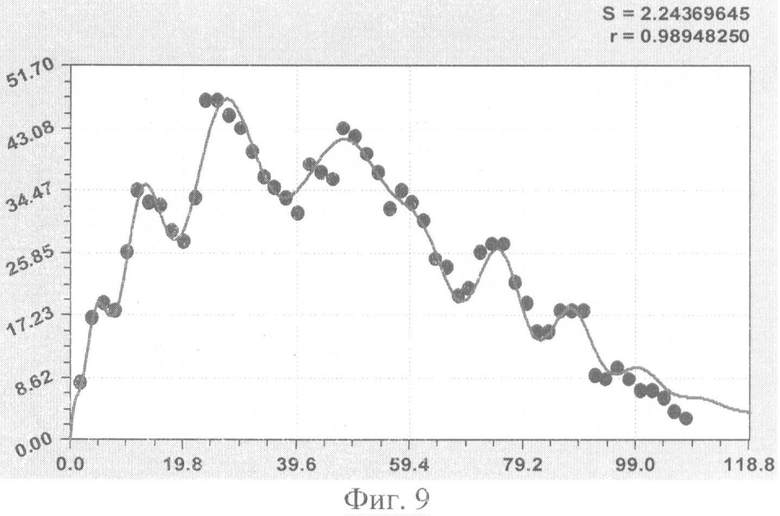
- переменная ширина древесного листа (фиг.9)
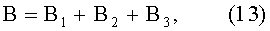
B1=6,12379х0,63350ехр(-0,00050846х1,84761), В2=A1cos(πx/p1-3,57208), А1=-0,88267х0,82603ехр(-0,0028001х1,61124), р1=0,97959+0,37293х0,67301, В3=A2cos(πx/p2-0,25654), А2=-1,01488·10-50х35,59702ехр(-0,59146х0,95771), р2=8,999402-0,00020813х1,89306,
с двумя кризисными волнами колебательного возмущения;
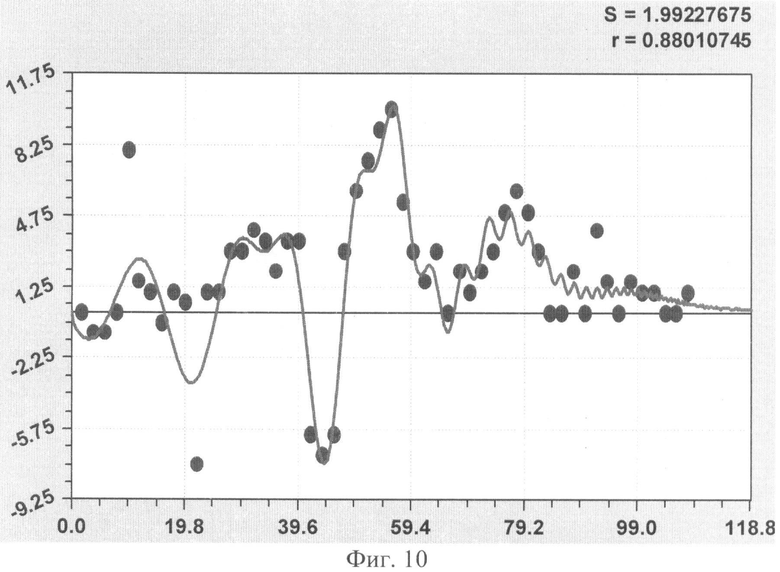
- абсолютная асимметрия древесного листа по ширине (фиг.10)
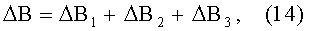
ΔB1=3,23897·10-15х11,01859ехр(-0,15596x1,82643), ΔВ2=A1cos(πx/р1-5,59263),
А1=-5,06571·10-12x10,86543ехр(-0,59166х0,81889),
р1=-57,74036+57,47201х0,033809, ΔВ3=A2cos(πx/p2+2,778625654),
А2=0,93869х0,43210ехр(-0,00017099х2,18205), р2=11,36777-0,099001х0,97717;
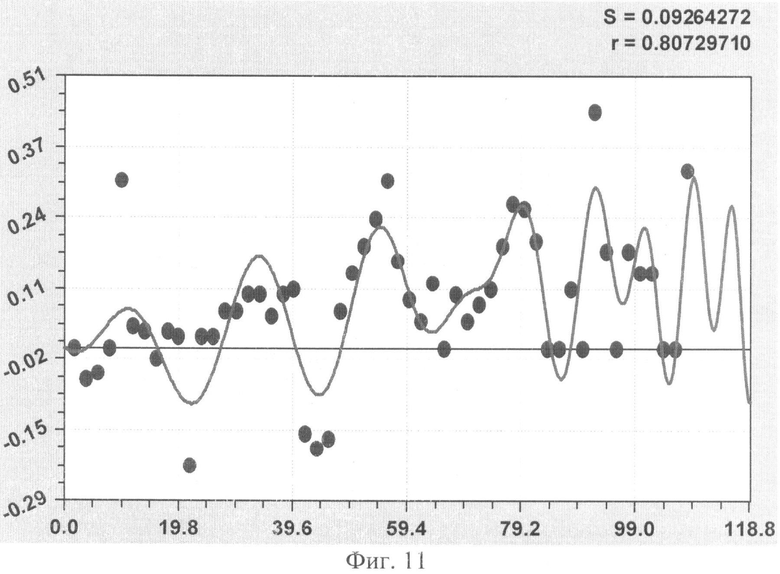
- коэффициент поперечной асимметрии древесного листа (фиг.11)
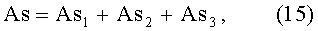
As1=8,73460·10-8х4,07500ехр(-0,044914х), As2=A1cos(πx/p1-2,61481),
А1=0,0091119х0,95855exp(-0,017318x1,05649), p1=11,99824-0,00019032х1,93552,
As3=A2cos(πx/р2+1,98063), А2=-3,61919·10-8х4,14550ехр(-0,17216х0,68268),
р2=15,24685-0,061024х1,03123.
По сути, эти статистические модели показывают волновую адаптацию листа к окружающей среде и условиям произрастания в прошлом вегетационном периоде, если измерения будут проводиться в конце осени.
Показатели адекватности всех 10 биотехнических закономерностей приведены в сводной таблице 2.
В ней дополнительно приведены следующие условные обозначения:
1) количество составляющих m статистической закономерности;
2) количество параметров n во всех составляющих модели;
3)коэффициент корреляции r, показывающий автоматически в правом верхнем углу на фигурах адекватность полученной закономерности;
4) максимальное количество mmax составляющих модели, независимых после трех членов друг от друга, после доведения процесса идентификации биотехнической волновой функции с погрешностью по остаткам менее погрешности проведенных измерений.
Основным статистическим критерием верификации полученных моделей является коэффициент корреляции.
Сравнение параметров формы листа. По значениям коэффициента корреляции, приведенных в данных таблице 2, можно сравнивать между собой все пять параметров формы дубового листа. По другим здоровым древесным листам получаются такие же сопоставления. Наибольшую адекватность имеет переменная ширина листа, поэтому во многих случаях, в особенности в экологических измерениях школьниками, достаточно измерять только ширину листа через расстояния в 2 мм по длине главной жилки (перспектива поиска новых технических решений - сканирование листа). Разница в ширине у различных древесных листов будет характеризовать особенности воздействий на развитие и рост листов окружающей каждого из них среды. Моделирование дает простую формулу типа (4).
По возможностям программной среды CurveExpert возможна совместная идентификация только трех составляющих. Но и в этом случае, как видно из данных таблицы 2, переменная ширина листа имеет преимущества перед другими параметрами формы листа.
Если имеются данные фенологических наблюдений за окружающей учетные или срезанные листья природной или иной, например городской, или условия жизнедеятельности в посадке дуба, среды, то появляется возможность, после полного моделирования до значимых с погрешностью измерений остатков, апостериорного объяснения поведения каждого листа в различные промежутки времени в течение прошлого вегетационного периода. Это - перспектива научного развития предлагаемого решения.
Общая конструкция биотехнической функции. Конструкция общей биотехнической закономерности из нескольких десятков составляющих, доведенной при моделировании по остаткам от предыдущих волновых составляющих ниже погрешности измерений, имеет вид
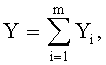
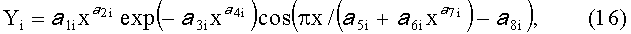
где Y - показатель, то есть любой из измеренных или расчетных параметров древесного листа,
i - номер члена общей формулы,
m - количество составляющих общей формулы, шт.,
х - расстояние вдоль длины главной жилки древесного листа, мм,
a 1…a 8 - параметры одного члена формулы, физически представляемого как асимметричный вейвлет-сигнал с переменными амплитудой и частотой колебательного возмущения конкретного листа в своем поведении за прошлый вегетационный период.
В таблице 3 приведены фрагменты общей формулы, с показом первых трех членов и последней составляющей, всех пяти показателей формы дубового листа №1.
Волновая кривая (примеры на фиг.12-16), у которой площади над и под осью абсцисс примерно равны, называется вейвлетом. Тогда получается, что древесный лист, как память компьютера, записывает собственное поведение в течение вегетационного периода.
Исследователю нужно только научиться расшифровать эти сигналы из прошлой жизни древесного листа и узнать, какое влияние оказали внешние известные воздействия.
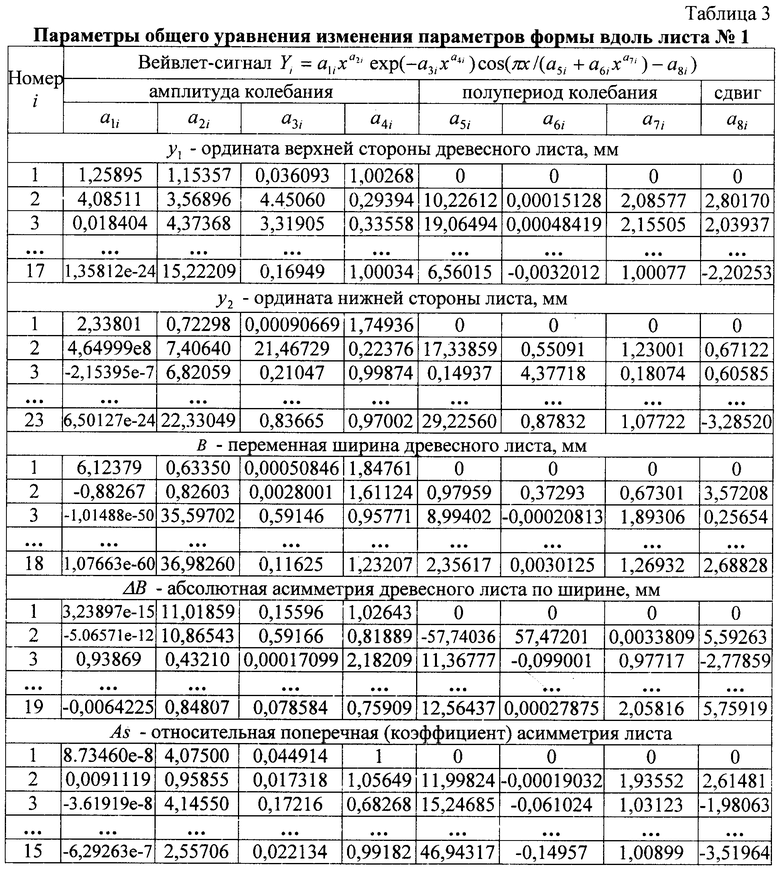
Идентификация общей модели сложна и применима только в фундаментальных исследованиях для изучения тонких процессов развития и роста древесного листа.
Критерии оценки. Они необходимы для сравнительного анализа параметров формы листа и выбора наиболее адекватного из них для последующего экологического мониторинга на данной территории.
Максимальная относительная погрешность Δmax показывает не только адекватность составной модели, но и характеризует качество управления листом своими физиологическими процессами. При этом должно соблюдаться условие, чтобы структурно-параметрическая идентификация исходной модели типа (16) была проведена до максимально возможного количества составляющих (в зависимости от точности измеренных и расчетных исходных данных).
Этот критерий одновременно является важнейшим для оценки замены табличной модели на ее математическую модель, в нашем примере волнистой формы древесного листа. Остальные три критерия позволяют выяснить картину поведения листа в прошлом, то есть в период от начала вегетационного периода до взятия листа и проведении измерений.
Значимость α1 трендовой (среднестатистической по динамике физической величины, принципиально отличающейся от средних арифметических и иных величин) закономерности факторной функции характеризует стабильность и устойчивость будущего функционирования древесного листа, если он не был срезан для измерений.
Этот оценочный показатель детерминированной части (%) факторной функции (может быть более одной составляющей) вычисляется как отношение расчетных значений, в нашем примере первой составляющей, к общему расчетному результату, то есть по математическому выражению
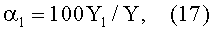
где Y1 - первая (трендовая) закономерность,
Y - расчетное значение параметра листа по общей модели (16)
Коэффициент приспособляемости k измеренного древесного листа к внешней среде показывает устойчивость в прошлом по отношению к различным волновым внешним и внутренним возмущениям.
Этот оценочный показатель исчисляется по формуле
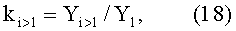
где Y1 - первая (трендовая) закономерность,
i - номер составляющей статистической закономерности типа (16).
Коэффициент динамичности Kд системы, в данном случае древесного листа как биологического существа, показывает стабильность в прошлом и возможную устойчивость к внешним воздействиям в будущем (до конца вегетационного периода).
Указанный критерий самоуправления вычисляется по соотношению
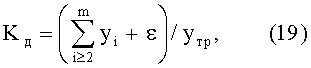
где yтр - тренд, в общем случае состоящий из нескольких первых не волновых составляющих статистической модели типа (16),
ε - абсолютная погрешность (остатки) от формулы (16), то есть разница между фактически измеренными значениями параметров листа по данным таблицы 1 и рассчитанными значениями по формуле (16).
Для нашего примера, когда трендом является только первая составляющая статистической модели, коэффициент динамичности поведения древесного листа в прошлом вычисляется по формуле
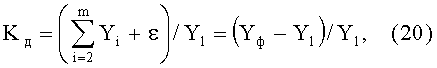
где Yф - фактические значения изучаемого параметра листа по данным измерений и результатов расчетов, приведенных в таблице 1.
Упрощенная методика обработки измеренных данных. Для практического применения школьниками и студентами необходима упрощенная методика обработки данных измерений по примеру таблицы 1.
Визуально на фигуре 1 видно, что различия в волнистом контуре края листа образуется из-за внешних воздействий.
При этом нужно измерить два параметра формы и рассчитать, как это было выполнено в таблице 1, еще три параметра, что не трудно и школьникам. Затем выполняется идентификация биотехнического закона по формуле (4).
Формула (4) и последующие тренды (5-10) имеют всего одну составляющую, поэтому показатели значимости и приспособляемости того или иного параметра листа не вычисляем.
По данным таблицы 1 в дальнейшем рассчитываются (табл.4):
1) максимальная относительная погрешность Δmax (по модулю, %) статистической модели от фактических значений параметра в одной точке (для какого-то конкретного измерения) по формуле
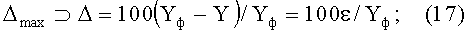
2) коэффициент динамичности Kд max поведения объекта с максимальным возмущением в одной точке измерений по выражению
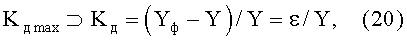
где ⊃ - знак отношения к множеству значений, из которых выбирается максимальное (по модулю) значение критерия,
Yф - фактические по таблице 1 значения параметра формы листа,
Y - расчетные по формулам (5-10) значения параметров листа,
ε - остаток (абсолютная погрешность) от формул (5-10).
Наиболее динамичными являются показатели абсолютной и относительной поперечной асимметрии древесного листа, поэтому они применяются для обработки более точных экспериментальных данных с выявлением всех возможных по погрешности измерений волновых составляющих модели типа (16).
С детерминированной моделью типа (9) и (10) коэффициент корреляции показывает слабую факторную связь в пределах 0,3-0,4.
Тогда для упрощенной методики рекомендуются всего три параметра древесного листа y1, y2 и В.
Как видно из данных таблицы 4, максимальная относительная погрешность биотехнического закона (4) наблюдается в конце ряда измеренных данных по ординате, то есть для листа №1 при абсциссе 108 мм.
Чтобы повысить эффективность предлагаемого способа оценки формы листа, можно отказаться от измерений в вершинке листа, если ординаты верхней и нижней половинок листа становятся меньше 3 мм. Из-за асимметричности листа предельно малая ширина листа может быть 5-6 мм. При такой методике измерений погрешность моделирования снижается в 2-4 раза. На экологическую оценку такое сокращение измерений не влияет.
На коэффициент динамичности волнистой кромки древесного листа не зависит от правой границы измерений вдоль главной жилки.
Из данных таблицы 4 видно, что наиболее динамичен участок листа №1 в интервале длины 2-4 мм от основания листа, то есть почти в самом начале вегетационного периода ив дальнейшем развитии роста задней части дубового листа.
Для сравнения отдельных листьев, взятых даже с одного дуба в разных геодезических направлениях, дополнительно рассматриваются влияния азимута и пространственного расположения каждого произрастающего древесного листа.
Преимуществом предлагаемого способа является техническая простота исполнения, так как требуется только миллиметровая бумага и подложка для ее фиксации при обводе контура учетного или же срезанного листа. Поэтому изобретение может быть широко реализовано в школьных экологических кружках, пришкольных лесничествах и даже в детских садах, а также в любых географических и иных экспедициях при дополнительном исследовании качества территории по листьям.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ ИЗМЕРЕНИЯ ПЛОЩАДИ ЛИСТЬЕВ У ДРЕВЕСНЫХ РАСТЕНИЙ | 2011 |
|
RU2466351C1 |
| СПОСОБ ИЗМЕРЕНИЯ ФЛУКТУИРУЮЩЕЙ АСИММЕТРИИ ЛИСТЬЕВ БЕРЕЗЫ | 2013 |
|
RU2556987C2 |
| СПОСОБ ИНДИКАЦИИ ЗАГРЯЗНЕННОСТИ ВОЗДУХА ПО ФЛУКТУИРУЮЩЕЙ АСИММЕТРИИ ЛИСТЬЕВ БЕРЕЗЫ | 2013 |
|
RU2580647C2 |
| СПОСОБ АНАЛИЗА ДИНАМИКИ РОСТА В ОНТОГЕНЕЗЕ ЗАГРЯЗНЕННЫХ ЛИСТЬЕВ БЕРЕЗЫ ОКОЛО АВТОМОБИЛЬНОЙ ДОРОГИ | 2015 |
|
RU2597643C1 |
| СПОСОБ СРАВНИТЕЛЬНОЙ ИНДИКАЦИИ ЗАГРЯЗНЕННОСТИ ВОЗДУХА ПО ФЛУКТУИРУЮЩЕЙ АСИММЕТРИИ ЛИСТЬЕВ БЕРЕЗЫ | 2013 |
|
RU2569748C2 |
| СПОСОБ ИЗМЕРЕНИЯ ДИНАМИКИ РОСТА ЛИСТЬЕВ ДЕРЕВА В ЧИСТЫХ ЭКОЛОГИЧЕСКИХ УСЛОВИЯХ | 2015 |
|
RU2597645C2 |
| Способ анализа онтогенеза чистых листьев дерева | 2015 |
|
RU2615363C2 |
| Способ факторного анализа онтогенеза учетных листьев дерева | 2015 |
|
RU2606189C2 |
| СПОСОБ ИСПЫТАНИЯ ПОБЕГОВ ДРЕВЕСНОГО РАСТЕНИЯ | 2005 |
|
RU2299435C2 |
| СПОСОБ СРАВНИТЕЛЬНОЙ ИНДИКАЦИИ ПО ФЛУКТУИРУЮЩЕЙ АСИММЕТРИИ ЛИСТЬЕВ БЕРЕЗЫ | 2013 |
|
RU2556985C2 |
Способ включает взятие листьев от учетных деревьев, растущих в разных экологических условиях, обведение контура листа на миллиметровой бумаге и подсчет квадратиков на миллиметровой бумаге для определения площади листа. Каждый измеряемый лист размещают на подложке с закрепленным на ней листом миллиметровой бумаги. Продольную ось листа растения по главной жилке совмещают с одной из сантиметровых линий сетки миллиметровой бумаги. Затем лист прижимают к миллиметровой бумаге и обводят его по контуру пишущим устройством для получения четкой боковой линии листа. По концам листа на миллиметровой бумаге отмечают положение главной продольной жилки. В дальнейшем измерения выполняют на миллиметровой бумаге по ширине каждой половинки нарисованного контура листа как расстояние от главной жилки до линии обвода контура листа. По измеренным значениям ширины половинок листа вычисляют переменную ширину листа как сумму половинок и их разность как абсолютную асимметрию листа, а также их отношение как коэффициент асимметрии листа. В дальнейшем по измеренным и рассчитанным значениям параметров листа статистическим моделированием выявляют биотехнические закономерности средней линии и волны контура у каждой половины листа. По отношениям разницы между фактическими и расчетными по средней боковой линии значениями ширины у каждой половины листа судят о коэффициенте динамичности развития и роста формы листа. Способ обеспечивает повышение точности измерения формы древесного листа от его главной жилки и точности индикации качества окружающей каждый лист древесного растения среды измерениями местоположения листа относительно ствола дерева и вычислением асимметрии формы поверхности листа. 11 з.п. ф-лы, 16 ил., 4 табл.
1. Способ измерения формы листьев у древесных растений, включающий взятие листьев от учетных деревьев, растущих в разных экологических условиях, обведение контура листа на миллиметровой бумаге и подсчет квадратиков на миллиметровой бумаге для определения площади листа, отличающийся тем, что каждый измеряемый лист размещают на подложке с закрепленным на ней листом миллиметровой бумаги, причем продольную ось листа растения по главной жилке совмещают с одной из сантиметровых линий сетки миллиметровой бумаги, затем лист прижимают к миллиметровой бумаге и обводят его по контуру пишущим устройством для получения четкой боковой линии листа, при этом по концам листа на миллиметровой бумаге отмечают положение главной продольной жилки, в дальнейшем измерения выполняют на миллиметровой бумаге по ширине каждой половинки нарисованного контура листа как расстояние от главной жилки до линии обвода контура листа, по измеренным значениям ширины половинок листа вычисляют переменную ширину листа как сумму половинок и их разность как абсолютную асимметрию листа, а также их отношение как коэффициент асимметрии листа, в дальнейшем по измеренным и рассчитанным значениям параметров листа статистическим моделированием выявляют биотехнические закономерности средней линии и волны контура у каждой половины листа, а по отношениям разницы между фактическими и расчетными по средней боковой линии значениями ширины у каждой половины листа судят о коэффициенте динамичности развития и роста формы листа.
2. Способ измерения формы листьев у древесных растений по п.1, отличающийся тем, что при необходимости у древесного листа по основанию его черешка измеряют геодезические координаты по азимуту, высоте взятия листа и радиусу от продольной оси ствола учетного дерева, причем после срезания древесного листа как биологической пробы измерения формы листа выполняют на миллиметровой бумаге с контуром боковой линии листа в камеральных условиях, а для многократных измерений в динамике развития и роста в вегетационный период древесный лист принимают за учетный лист, около которого на ветке закрепляют метку, например, в виде бирки с номером учетного листа, привязанной на ветке ниткой.
3. Способ измерения формы листьев у древесных растений по п.1, отличающийся тем, что измерения выполняют на миллиметровой бумаге по ширине каждой половинки нарисованного контура листа как расстояние от главной жилки до линии обвода контура листа, при этом измерения ширины половинок листа выполняют с постоянным шагом через 2 мм или же переменным шагом, кратным 1 мм, по клеткам миллиметровой бумаги в зависимости от длины волны боковой линии листа.
4. Способ измерения формы листьев у древесных растений по п.1, отличающийся тем, что для повышения точности измерений и снижения погрешности моделирования боковой линии листа измерения вдоль главной продольной жилки листа выполняют до расстояния, при котором ординаты верхней и нижней половинок листа становятся меньше 3 мм.
5. Способ измерения формы листьев у древесных растений по п.1, отличающийся тем, что по измеренным значениям ширины половинок листа y1 и y2 вычисляют переменную ширину В листа как сумму половинок и их разность как абсолютную асимметрию ΔВ листа, а также их отношение как коэффициент асимметрии As листа по формулам:
- переменная ширина древесного листа
B=y1+y2;
- абсолютная асимметрия древесного листа по ширине
ΔВ=y1-y2;
- коэффициент поперечной асимметрии листа
As=ΔB/B.
6. Способ измерения формы листьев у древесных растений по п.1, отличающийся тем, что любой измеренный или расчетный параметр формы древесного листа по значениям идентифицируется биотехническим законом в виде детерминированной модели вида
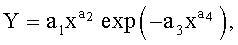
где Y - любой из перечисленных пяти параметров формы листа,
x - расстояние (абсцисса) вдоль главной продольной жилки листа от основания этого древесного листа, мм,
a1…a4 - параметры биотехнического закона, получающие конкретные
числовые значения в зависимости от результатов измерений конкретного древесного листа с конкретным пространственным расположением относительно ствола дерева.
7. Способ измерения формы листьев у древесных растений по п.6, отличающийся тем, что для упрощенной методики обработки результатов измерений и расчетных параметров формы листа вычисляют следующие критерии оценки: максимальная относительная погрешность Δmax (по модулю, %) статистической модели от фактических значений параметра в одной точке (для какого-то конкретного измерения) по формуле
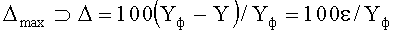 ;
;
коэффициент динамичности Kд max поведения объекта с максимальным возмущением в одной точке измерений по выражению
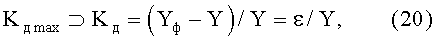
где 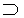 - знак отношения к множеству значений, из которых выбирается максимальное (по модулю) значение критерия,
- знак отношения к множеству значений, из которых выбирается максимальное (по модулю) значение критерия,
Yф - фактические значения параметра формы листа,
Y - расчетные значения параметров листа,
ε - остаток (абсолютная погрешность) от детерминированной модели в виде биотехнического закона.
8. Способ измерения формы листьев у древесных растений по п.1, отличающийся тем, что для сопоставления с фенологическими наблюдениями, проведенными относительно учетного дерева, по измеренным значениям ширины половинок и других параметров формы листа статистическим моделированием выявляют трехчленные биотехнические закономерности по формуле:
Y=Y1+Y2+Y3,
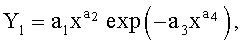
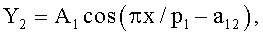
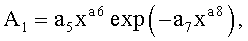
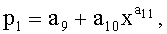
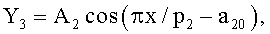
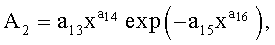
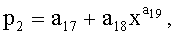
где Y - показатель, то есть любой из измеренных или расчетных параметров древесного листа,
Y1 - детерминированная часть биотехнической закономерности,
Y2, Y3 - волновые составляющие модели, показывающие колебательное возмущение формы древесного листа в процессе адаптации к внешним воздействиям и внутренним физиологическим процессам, происходящем в листе и материнском учетном дереве,
x - расстояние (абсцисса) вдоль главной продольной жилки листа от основания этого древесного листа, мм,
A1, A2 - амплитуды (половина) колебательного возмущения древесного листа в прошлом от начала вегетационного периода до момента взятия как биологической пробы,
p1, p2 - полупериоды колебания формы древесного листа вдоль главной продольной жилки, косвенно характеризующие течение времени вегетационного периода, мм,
a1…a20 - параметры трехчленной биотехнической закономерности, получающие конкретные числовые значения в процессе идентификации в программной среде типа CurveExpert по измеренным и расчетным статистическим выборкам значений параметров формы древесного листа.
9. Способ измерения формы листьев у древесных растений по п.1, отличающийся тем, что для сопоставления с результатами фенологических наблюдений и физиологических измерений, по измеренным значениям ширины половинок и других параметров формы листа статистическим моделированием при доведении остатков после многочленной модели, меньших погрешности измерений ординат половинок листа, выявляют сложные и многочленные биотехнические закономерности по формуле:
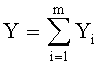 ,
,
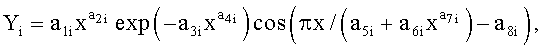
где Y - показатель, то есть любой из измеренных или расчетных
параметров древесного листа,
i - номер члена общей сложной формулы,
m - количество составляющих общей формулы, которое может быть различным для разных параметров формы листа, шт.,
x - расстояние вдоль длины главной жилки древесного листа, мм,
a1…a8 - параметры у одного члена формулы, физически представляемого как асимметричный вейвлет-сигнал с переменными амплитудой и частотой колебательного возмущения конкретного листа, заложенными в процессе развития и роста и в своем реактивном поведении за прошлый вегетационный период.
10. Способ измерения формы листьев у древесных растений по п.9, отличающийся тем, что кроме коэффициента корреляции, вычисляемого автоматически в программной среде типа CurveExpert, для более строгой оценки адекватности каждой многочленной биотехнической закономерности рассчитывается максимальная относительная погрешность Δmax, которая показывает не только адекватность составной из большого множества членов модели, но также характеризует и качество самоуправления растительного существа своим поведением, и этот критерий оценки определяется по формуле:
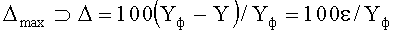 ,
,
где 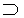 - знак отношения к множеству значений, из которых выбирается максимальное (по модулю) значение критерия,
- знак отношения к множеству значений, из которых выбирается максимальное (по модулю) значение критерия,
Yф - фактические значения параметра формы листа,
Y - расчетные значения параметров листа,
ε - остаток (абсолютная погрешность) от сложной модели.
11. Способ измерения формы листьев у древесных растений по п.9, отличающийся тем, что для оценки замены табличной модели каждого из параметров формы древесного листа на ее математическую модель и одновременно важнейшей биоэкологической оценки качества поведения учетного или срезанного древесного листа сосчитывают критерии:
- количество m составляющих факторной функции, причем чем меньше количество составляющих, тем эффективнее вел себя древесный лист в процессах развития и роста при внешних и внутренних разнообразных воздействиях;
- количество n параметров выявленной статистической закономерности: чем меньше это количество, тем лучше «сработала» подсистема самоуправления древесным листом.
12. Способ измерения формы листьев у древесных растений по п.9, отличающийся тем, что для выяснения картины поведения древесного листа в прошлом на отдельных промежутках вегетационного периода до момента проведения измерений применяют следующие три критерия:
- значимость αi первой составляющей характеризует стабильность и устойчивость будущего функционирования древесного листа, если он не был срезан для измерений, и этот оценочный показатель вычисляется как отношение расчетных значений по первой составляющей, к общему расчетному результату, то есть по математическому выражению:
α1=100Y1/Y,
где α1 - значимость первой составляющей,
Y1 - первая (трендовая) закономерность,
Y - расчетное значение параметра листа по общей модели (16),
коэффициент приспособляемости k измеренного древесного листа к внешней среде показывает устойчивость в прошлом по отношению к различным волновым внешним и внутренним возмущениям и он исчисляется по формуле:
ki>1=Yi>1/Y1,
где ki>1 - коэффициент приспособляемости второй и последующей составляющей из общей многочленной модели,
i - номер члена общей сложной формулы,
Yi>1 - вторая и последующие составляющие из многочленной модели,
Y1 - первая составляющая общей многочленной модели;
коэффициент динамичности Kд поведения в прошлом системы, в данном случае древесного листа как биологического существа, показывает стабильность в прошлом и возможную устойчивость к внешним воздействиям в будущем (до конца вегетационного периода) и указанный критерий самоуправления вычисляется по соотношению:
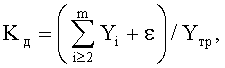
где Kд - коэффициент динамичности развития и роста древесного листа,
i - номер члена общей сложной формулы,
m - количество составляющих общей формулы, которое может быть различным для разных параметров формы листа, шт.,
ε - абсолютная погрешность (остатки) от общей многочленной формулы, то есть разница между фактически измеренными значениями параметров листа и рассчитанными значениями по многочленной формуле,
Yтр - тренд, в общем случае состоящий из нескольких первых не волновых составляющих статистической модели.
| ФЕДОРОВА А.И | |||
| и др | |||
| Практикум по экологии и охране окружающей среды | |||
| - М.: ВЛАДОС, 2001, с.123-126 | |||
| СПОСОБ ОПРЕДЕЛЕНИЯ ФОРМЫ КРОНЫ РАСТЕНИЯ | 2008 |
|
RU2373691C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ФОРМЫ КРОНЫ ДРЕВЕСНЫХ РАСТЕНИЙ | 1993 |
|
RU2050770C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ПЛОЩАДИ ЛИСТЬЕВ РАСТЕНИЙ | 1998 |
|
RU2145410C1 |
Авторы
Даты
2013-03-10—Публикация
2011-09-15—Подача