СПОСОБЫ И УСТРОЙСТВА ПОВЫШЕНИЯ ИНДЕКСА УГЛОВОЙ МОДУЛЯЦИИ Российский патент 2013 года по МПК H03C3/38 

Изобретение относится к радиотехнике и может быть использовано для формирования радиосигналов с угловой модуляцией в радиотехнических устройствах различного назначения, в том числе в технике создания преднамеренных радиоэлектронных помех.

Известен способ повышения индекса модуляции (способ Армстронга) (см. Гоноровский И.С. Частотная модуляция и ее применение. - М.: Государственное издательство литературы по вопросам связи и радио, 1948. - С.113-115; Артым А.Д. Теория и методы частотной модуляции. - М.-Л. Госэнергоиздат, 1961. - С.103), заключающийся в умножении исходной, достаточно низкой несущей частоты, которое сопровождается умножением индекса модуляции.

Недостатком способа является то, что при его реализации сильно снижается результирующая стабильность частоты передатчика и имеется принципиальный предел, связанный с тем, что исходная несущая частота f₀ не может быть выбрана сколь угодно низкой, поскольку она должна быть значительно больше наивысшей частоты модуляции F_макс.

Известен способ повышения индекса модуляции (см. Артым А.Д. Теория и методы частотной модуляции. - М.-Л. Госэнергоиздат, 1961. - С.138, 139), заключающийся в каскадном или цепочечном включении фазовых модуляторов, при котором напряжение высокой частоты последовательно проходит через ряд фазовых модуляторов, в каждом из которых индекс модуляции увеличивается на определенную величину, обычно одинаковую для всех модуляторов. Повышение индекса модуляции в N раз достигается введением N-го количества каскадов фазовых модуляторов вместо одного. Однако при большом значении N такой способ является практически нецелесообразным.

Известен способ повышения индекса модуляции (см. Гоноровский И.С. Частотная модуляция и ее применение. - М.: Государственное издательство литературы по вопросам связи и радио, 1948. - С.116, 117; Артым А.Д. Теория и методы частотной модуляции. - М.-Л. Госэнергоиздат, 1961. - С.139-141), заключающийся в умножении исходной, достаточно низкой несущей частоты, сопровождающееся умножением индекса модуляции, после чего применяется преобразование частоты, в результате которого девиация частоты и, соответственно, индекс модуляции остаются неизменными, но несущая частота уменьшается в определенное число раз. Понижение несущей частоты дает возможность произвести ее умножение и вновь повысить индекс модуляции и девиацию частоты.

Недостатком способа является значительное паразитное относительное изменение частоты, вызванное нестабильностью задающего генератора, в результате чего ухудшается стабильность несущей частоты.

Известен способ (см. Артым А.Д. Теория и методы частотной модуляции. - М.-Л. Госэнергоиздат, 1961. - С.139-142), заключающийся в том, что модулирующий сигнал через интегрирующие цепи, служащие для преобразования фазовой модуляции в частотную, подается на два модулятора в противоположных фазах, благодаря чему на их выходах девиация частоты имеет противоположные знаки. После умножения в n раз частота в одном канале с помощью кварцевого генератора и первого преобразователя понижается на величину f₁. Во втором преобразователе из частоты первого канала, также умноженной в n раз, вычитается преобразованная частота второго канала, в результате чего выделяется сигнал с частотой кварцевого генератора f₁, имеющий девиацию 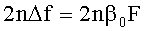$$2n\Delta f=2n{\beta }_{0}F$$ . При использовании фазового модулятора того же типа непосредственно на частоте f₁ девиация частоты равна β₀F. Таким образом, этот способ дает возможность повысить девиацию частоты Δf и индекс модуляции β₀ в 2n раз. При этом нестабильность задающего генератора не имеет значения, поскольку его частота f₀ в результате преобразований исключается.

Недостатком способа является то, что при необходимости многократного повышения индекса модуляции схема значительно усложняется, вследствие чего редко используется на практике.

Известен способ получения большого значения индекса модуляции (см. Артым А.Д. Теория и методы частотной модуляции. - М.-Л. Госэнергоиздат, 1961. - С.143-155) за счет разделения спектра модулирующих частот на N полос и выбора достаточно низкой исходной несущей частоты фазового модулятора f₀ с последующим ее умножением.

Недостаток способа заключается в сложности выполнения условий согласования фазовых модуляторов. Это обусловлено тем, что напряжение на входе фазового модулятора с понижением (или с повышением) частоты модулирующего напряжения может превысить величину, соответствующую максимальной девиации фазы, на которую рассчитан модулятор, в результате чего могут появиться недопустимо большие нелинейные искажения.

Общим недостатком перечисленных выше способов повышения индекса угловой модуляции является наличие в схемах управляемых реактивных элементов и частотно-избирательных цепей, что не позволяет с их помощью осуществлять угловую модуляцию при перестройках схем в широких диапазонах частот несущего колебания и одновременно на нескольких несущих частотах.

Наиболее близким по своей технической сущности к заявленному является способ повышения индекса модуляции (см. Попов П.А., Шерстюков С.А., Ромашов В.В., Жайворонок Д.А. Квадратурные формирователи радиосигналов: Монография / Под ред. П.А. Попова. - Воронеж: Воронежский институт МВД России, 2001. - С.31, 32).

Способ-прототип позволяет компенсировать амплитудно-фазовые искажения фазомодулированных сигналов (ФМС) при произвольно заданном значении индекса модуляции m_φ за счет использования балансных модуляторов в квадратурных каналах и синусно-косинусных (функциональных) преобразователей модулирующего напряжения. На фиг.1 приведена структурная схема, реализующая способ-прототип, в состав которой входят: ГВЧ - генератор высокой частоты, БМ1 и БМ2 - балансные модуляторы, ФВ - высокочастотный фазовращатель на π/2, C1 - высокочастотный линейный сумматор, ИМС - источник модулирующего сигнала, КП - косинусный преобразователь, СП - синусный преобразователь.

Способ-прототип включает:

- формирование с помощью высокочастотного генератора и фазовращателя на π/2 квадратурных составляющих, описываемых, соответственно, выражениями:

$${\text{u}}_{\text{1}}={\text{U}}_{\text{1}}\text{cos}\omega \text{t}{\text{, u}}_{\text{2}}=-{\text{U}}_{\text{1}}\text{sin}\omega \text{t}\text{, (1)}\text{, (2)}$$

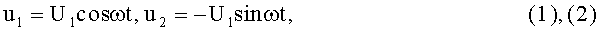
- формирование с помощью косинусного и синусного преобразователей модулирующего напряжения, соответственно, управляющих сигналов:

$${\text{e}}_{\text{k}}={\text{E}}_{\text{y}}\text{cos}\left[{\text{m}}_{\phi }\sin \Omega t\right]{\text{, e}}_{\text{c}}={\text{E}}_{\text{y}}\text{sin}\left[{\text{m}}_{\phi }\sin \Omega t\right]\text{; (3)}\text{, (4)}$$

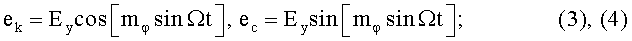
- квадратурное перемножение высокочастотных и низкочастотных составляющих (1) с (3) и (2) с (4) в балансных модуляторах с коэффициентами k_БМ=1;

- сложение высокочастотных квадратурных составляющих в линейном сумматоре, в результате которого формируется выходной ФМС:

$$\begin{array}{l}{\text{u}}_{\text{c}}={\text{U}}_{\text{1}}{\text{E}}_{\text{y}}\left[\cos \omega t\cos \left(m_{\phi }\sin \Omega t\right)-\sin \omega t\sin \left(m_{\phi }\sin \Omega t\right)\right]=\\ U_{c1}\cos \left(\omega t+m_{\phi }\sin \Omega t\right),\left(5\right)\end{array}$$

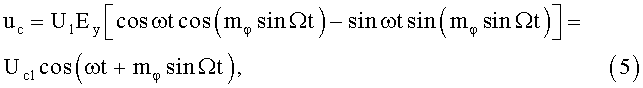
где U_c1=U₁E_y - постоянная амплитуда.

На фиг.2 приведены векторные диаграммы, поясняющие принцип работы схемы, представленной на фиг.1, при U₁=E_y=U_c1=1, Ωt=±π/2, соответственно, для значений m_φ=0, π/4, 5/4π. Из диаграмм следует, что в структурной схеме на фиг.1 возможно получение ФМС с любыми произвольно заданными индексами модуляции m_φ.

При реализации способа-прототипа не снижается результирующая стабильность частоты передатчика и отсутствует принципиальный предел, связанный с выбором несущей частоты, а также не требуются сложные согласования высокочастотного и низкочастотного трактов модулятора из-за отсутствия в схеме управляемых реактивных элементов и частотно-избирательных цепей. Данные факторы позволяют использовать способ-прототип для осуществления угловой модуляции в возбудителях при перестройках передатчиков в широких диапазонах частот несущего колебания.

Способ-прототип имеет недостатки:

- реализация больших значений индексов модуляции (выше 10π), с точки зрения вычислительных затрат, на практике затруднительно из-за ограничения количества членов разложения рядов Тейлора, аппроксимирующих значения выходных величин синусно-косинусного преобразователя;

- не предусмотрена возможность N-кратного увеличения значений индексов модуляции радиосигналов на первой гармонике колебания несущей частоты, где N=2, 3, 4…;

- отсутствует возможность формирования радиосигналов с угловой модуляцией одновременно на нескольких гармониках колебания несущей частоты и с различными значениями индексов модуляции.

Целями данного изобретения являются:

- разработка способов повышения индексов модуляции, позволяющих формировать радиосигналы с угловой модуляцией без принципиальных ограничений по значениям индексов модуляции при отсутствии в выходных радиосигналах передатчиков паразитной амплитудной модуляции (ПАМ) и не накапливающейся паразитной фазовой модуляции (ПФМ);

- увеличение количества гармоник колебания несущей частоты с одновременным увеличением на них значений индексов модуляции выходных ФМС, при отсутствии проявления ПАМ и ПФМ;

- уменьшение инерционности процесса угловой модуляции;

- существенное упрощение процессов частотообразования в возбудителях передатчиков;

- повышение быстродействия радиосистемы.

Поставленные цели достигаются тем, что в известном способе повышения индекса угловой модуляции, включающем формирование квадратурных высокочастотных составляющих, представление модулирующего напряжения в косинусном и синусном функциональных преобразователях ограниченным количеством членов разложений рядов Тейлора, зависящих от реализуемого индекса модуляции, последующих квадратурном перемножении высокочастотных и низкочастотных составляющих и линейном суммировании результатов квадратурного перемножения:

- увеличивают количество этапов квадратурных перемножений результатов вычислений косинусной и синусной функций модулирующего напряжения с квадратурными фазомодулированными составляющими и выполняют алгебраические линейные суммирования результатов квадратурных перемножений, получая при этом на выходе пропорциональное увеличение значений индексов модуляции на первой гармонике колебания несущей частоты;

- проводят многократные удвоения аргументов синусной и косинусной функций модулирующего напряжения и одновременно увеличивают количество этапов квадратурных перемножений и алгебраических линейных суммирований квадратурных фазомодулированных составляющих как с результатами вычислений косинусной и синусной функций модулирующего напряжения, так и с результатами многократных удвоений аргументов косинусной и синусной функций, получая при этом на выходе пропорциональное увеличение значений индексов модуляции на первой гармонике колебания несущей частоты;

- увеличивают количество этапов умножений колебания несущей частоты в сочетании с увеличением количества этапов квадратурных перемножений и линейных суммирований, как в двух предыдущих случаях, получая при этом требуемое количество гармоник колебания несущей частоты с одновременным увеличением на них (гармониках) значений индексов модуляции выходных ФМС и отсутствии проявления ПАМ и ПФМ;

- осуществляют процессы угловой модуляции вне кольца импульсно-фазовой автоматической подстройки частоты синтезатора, что способствует уменьшению инерционности процесса угловой модуляции, существенному упрощению процессов частотообразования в возбудителях передатчиков и повышению быстродействия радиосистемы в целом.

Перечисленная новая совокупность существенных признаков за счет того, что структуры модулирующих напряжений, сформированные в низкочастотной области функциональными преобразователями и удвоителями аргументов функций, транспонируют в область несущих частот с помощью этапов квадратурных перемножений и алгебраических суммирований, а также производят этапы многократного умножения колебания несущей частоты без использования управляемых реактивных элементов и частотно-избирательных цепей, позволяет достичь вышеуказанных целей изобретения.

Известен ряд устройств, реализующих формирование неискаженных ФМС с различными значениями индексов модуляции. Фазовый модулятор (см. Верещагин Е.М., Никитенко Ю.Г. Частотная и фазовая модуляция в технике связи. М.: Связь, 1974, С.125), содержит последовательно соединенные источник высокочастотного (модулируемого) сигнала, фазовращатель на π/2, первый амплитудный модулятор и сумматор, последовательно соединенные источник модулирующего сигнала и инвертор, выход которого подключен ко второму входу первого амплитудного модулятора, а также второй амплитудный модулятор, один вход которого соединен с выходом источника высокочастотного сигнала, второй вход - с выходом источника модулирующего сигнала, а выход второго амплитудного модулятора подключен ко второму входу сумматора, выход которого является выходом устройства.

Принцип работы этого устройства состоит в том, что от источника высокочастотного (модулируемого) сигнала напряжение несущей частоты подается на фазовращатель на π/2, после чего, два ортогональных колебания несущей частоты поступают на амплитудные модуляторы, где модулируются от источника модулирующего сигнала напряжением низкой частоты в противофазе. После амплитудных модуляторов колебания линейно складываются в сумматоре, на выходе которого и формируется ФМС.

Однако в этом устройстве формирование неискаженного ФМС возможно только при малых значениях индекса модуляции (m_φ≤0,5 рад), т.к. дальнейшее его увеличение вызывает нелинейность фазовой и неравномерность амплитудной модуляционных характеристик. Нелинейность фазовой модуляционной характеристики вызывает фазовые искажения выходного сигнала модулятора, которые в литературе называют нелинейными искажениями и которые можно рассматривать как ПФМ. Неравномерность амплитудной модуляционной характеристики является причиной амплитудных искажений выходного сигнала модулятора, проявляющихся в виде ПАМ.

Известен фазовый модулятор по свидетельству на полезную модель РФ №8185 от 16.01.98, М. Кл.4 H03C 3/38, опубл. 16.10.98, бюл. №10.

Фазовый модулятор содержит последовательно соединенные источник высокочастотного сигнала ИВС1, фазовращатель на π/2 ФВ2, первый амплитудный модулятор АМ3 и первый сумматор СУМ4, второй амплитудный модулятор АМ5, первый вход которого соединен с выходом ИВС1, а выход АМ5 подключен ко второму входу первого сумматора СУМ4, последовательно соединенные источник модулирующего сигнала ИМС6 и первый инвертор ИНВ7, последовательно соединенные первый перемножитель сигналов ПС8, первый аттенюатор АТ9, второй инвертор ИНВ10 и второй сумматор СУМ11, выход которого подключен ко второму входу первого амплитудного модулятора АМ3, последовательно соединенные второй перемножитель сигналов ПС12, второй аттенюатор АТ13, третий инвертор ИНВ14 и третий сумматор СУМ15, выход которого подключен ко второму входу второго амплитудного модулятора АМ5. При этом второй вход второго СУМ11 соединен с выходом второго аттенюатора АТ13, третий вход второго СУМ11 подключен к выходу первого инвертора ИНВ7, второй вход третьего сумматора СУМ15 соединен с выходом второго инвертора ИНВ10, третий вход третьего сумматора СУМ15 соединен с выходом источника ИМС6, первым и вторым входами первого ПС8, первым входом второго ПС12, второй вход которого соединен с выходом первого ПС8, а выходом устройства является выход первого сумматора СУМ4.

В фазовом модуляторе для получения неискаженного ФМС без ПАМ и с максимально возможным индексом модуляции m≤π/4 из модулирующего сигнала me, где e - мгновенное значение модулирующего напряжения, формируются сигналы, близкие, в данном случае, с большой степенью точности к функциям cos(me) и sin(me), вернее используются первые два члена разложения этих функций в ряд Тейлора: cos(me)=1-(me)²/2!, sin(me)=me-(me)³/3!.

После соответствующих преобразований на выходе устройства формируется практически неискаженный ФМС при индексе модуляции m≤π/4.

Недостатком устройства является ограничение по максимально возможному индексу модуляции, который не может быть больше m≤π/4. Ограничение связано с использованием амплитудных модуляторов в квадратурных ветвях, коэффициенты передачи которых не могут быть меньше нуля.

Известен фазовый модулятор по свидетельству на полезную модель РФ №7782 от 12.11.97, 6 H03C 3/38, опубл. 16.09.98, бюл. №9.

Фазовый модулятор содержит последовательно соединенные источник высокочастотного сигнала, фазовращатель на π/2, первый балансный модулятор и сумматор, последовательно соединенные источник модулирующего напряжения, квадратор, делитель напряжения, инвертор и второй балансный модулятор, выход которого соединен с третьим входом сумматора, а вход - с выходом источника высокочастотного сигнала. При этом выход источника модулирующего напряжения соединен со вторым входом первого балансного модулятора, второй вход сумматора подключен непосредственно к выходу источника высокочастотного сигнала, а выход сумматора является выходом устройства.

В устройстве имеет место практически неискаженная фазовая модуляция при работе в широком диапазоне частот несущего колебания с индексом модуляции m≤1.

Недостатком устройства является ограничение по максимально возможному индексу модуляции, который не может быть больше m≤1.

Известен квадратурный фазовый модулятор (КФМ) по свидетельству на полезную модель РФ №9555 от 26.03.98, 6 H03C 3/38, опубл. 16.03.99, бюл. №3.

Квадратурный фазовый модулятор содержит последовательно соединенные источник высокочастотного сигнала ИВС1, фазовращатель на π/2 ФВ2, первый амплитудный модулятор АМ3 и первый сумматор СУМ4, последовательно соединенные источник модулирующего сигнала ИМС5, первый инвертор ИНВ6 и второй сумматор СУМ7, выход которого соединен с модулирующим входом первого АМ3, последовательно соединенные третий сумматор СУМ8 и второй амплитудный модулятор АМ9, сигнальный вход которого соединен с выходом ИВС1, а выход - со вторым входом первого СУМ4, последовательно соединенные амплитудный детектор АД10

и инвертирующий усилитель ИУ11, выход которого соединен со вторыми входами второго СУМ7 и третьего СУМ8, при этом первый вход третьего СУМ8 соединен с выходом ИМС5, а выход первого СУМ4 соединен со входом АД10, последовательно соединенные фазовый детектор ФД12, четвертый сумматор СУМ13, усилитель У14, второй инвертор ИНВ15, выход которого соединен с третьим входом второго СУМ7. При этом второй вход четвертого СУМ13 соединен с выходом ИМС5, третий вход третьего СУМ8 соединен с выходом У14, первый вход ФД12 соединен с выходом ИВС1, а второй вход - с выходом первого СУМ14, который также является выходом устройства.

Характерным отличием этого устройства является включение фазового детектора во вспомогательный контур автоматического регулирования искажений фазы выходного сигнала, что обеспечивает глубокую компенсацию фазовых набегов и флуктуаций фазы в различных элементах преобразования входных сигналов. При этом одновременно происходит увеличение индекса модуляции.

Недостатком устройства является ограничение пропорциональной зависимости между фазой высокочастотного колебания и модулирующим напряжением в небольших пределах изменения фазы первого, т.е. при индексе модуляции m≤π/4. Это связано с тем, что коэффициенты передачи амплитудных модуляторов в квадратурных ветвях не могут быть меньше нуля, следовательно, максимальный индекс модуляции m_φmax, реализуемый в таком КФМ, принципиально не может быть больше π/4 (m_φmax≤0,78 рад).

Известен фазовый модулятор по свидетельству на полезную модель РФ №10306 от 27.11.98, 6 H03C 3/38, опубл. 16.06.99, бюл. №6.

Фазовый модулятор содержит последовательно соединенные источник высокочастотного (модулируемого) сигнала ИВС1 и фазовращатель на π/2 ФВ2, источник модулирующего сигнала ИМС3, первый сумматор СУМ4, второй сумматор СУМ5, третий сумматор СУМ6, последовательно соединенные аналого-цифровой преобразователь АЦП7, косинусный преобразователь кодов КПК8, первый цифроаналоговый преобразователь ЦАП9 и первый фильтр нижних частот ФНЧ10, выход которого соединен со вторым входом третьего СУМ6, последовательно соединенные синусный преобразователь кодов СПК11, второй цифро-аналоговый преобразователь ЦАП12 и второй фильтр нижних частот ФНЧ13, выход которого соединен со вторым входом второго СУМ5, первый (ДУС14) и второй (ДУС15) двухтактные усилители на полевых транзисторах с синфазным подключением транзисторов к нагрузке и разделительный конденсатор 16. При этом первый вход третьего СУМ6 соединен с выходом ИВС1, первый вход второго СУМ5 соединен с выходом фазовращателя на π/2 ФВ2, вход АЦП7 соединен с выходом ИМС3, вход СПК11 соединен с соединен с выходом АЦП7, вход первого ДУС14 соединен с выходом третьего СУМ6, а выход - с первым входом первого СУМ4, вход второго ДУС15 соединен с выходом ФВ2, а выход - со вторым входом первого СУМ4, выход которого через разделительный конденсатор С16 соединен с выходом устройства.

Устройство позволяет осуществлять неискаженную фазовую модуляцию без ПАМ и ПФМ с любым теоретически необходимым индексом модуляции.

Недостатки устройства:

- на практике получение значений индексов модуляции выше 10π связано с ограничением реализации рядов Тейлора 49-ю и 50-ю членами разложения, соответственно, для функций косинуса и синуса, аппроксимирующих значения выходных величин синусно-косинусного преобразователя, т.к. при увеличении количества членов разложений возрастают погрешности преобразований, вызывающие недопустимые отклонения амплитудной и фазовой модуляционных характеристик;

- отклонения фаз сигналов на выходе фазовращателя от π/2 на 10%, имеющие место в практических схемах при изменении частот несущих колебаний в пределах октавы, а также 5%-ная несимметричность квадратурных каналов, обусловленная использованием двухтактных усилителей на полевых транзисторах с синфазным подключением транзисторов к нагрузке в высокочастотных квадратурных ветвях, оказывают отрицательное влияние на точность формирования ФМС.

Наиболее близким по своей технической сущности к заявленному устройству является фазовый модулятор по свидетельству на полезную модель РФ №8184 от 16.01.98, 6 H03C 3/38, опубл. 16.10.98, бюл. №10.

Устройство-прототип (фиг.11) содержит последовательно соединенные источник высокочастотного сигнала ИВС, балансный модулятор БМ2 и линейный сумматор С1, последовательно соединенные фазовращатель на π/2 ФВ и балансный модулятор БМ1, выход которого соединен со вторым входом линейного сумматора C1, а вход ФВ соединен с выходом ИВС, последовательно соединенные перемножитель сигналов ПС1 и аттенюатор АТ1, последовательно соединенные перемножитель сигналов ПС2 и аттенюатор АТ2, источник модулирующих сигналов ИМС, линейный сумматор С2, выход которого соединен со вторым входом балансного модулятора БМ1, линейный сумматор С3, выход которого соединен со вторым входом балансного модулятора БМ2, пиковый детектор ПД, включенный между выходом источника модулирующего сигнала ИМС и первым входом сумматора С2, последовательно соединенные регулируемый аттенюатор-усилитель РАУ, перемножитель сигналов ПС3 и аттенюатор АТ3, выход которого соединен с третьим входом сумматора С2, последовательно соединенные перемножитель сигналов ПС4 и аттенюатор АТ4, выход которого соединен с третьим входом сумматора СУМ3, инвертор ИНВ1 между выходом АТ1 и вторым входом С2, инвертор ИНВ2 между выходом АТ2 и вторым входом С3. При этом выход РАУ соединен с первым входом С3 и первыми входами перемножителей сигналов ПС1, ПС2, ПС3 и ПС4, а выход ПС1 соединен со вторым входом ПС2, выход ПС2 соединен со вторым входом ПС3, выход ПС3 соединен со вторым входом ПС4. Выходом устройства является выход линейного сумматора С1.

Характерным для устройства-прототипа является то, что в нем происходит не только расширение диапазона возможных значений индекса модуляции от 0 до n, но и возможность точной установки заданного значения индекса модуляции, т.к. заданный индекс модуляции в этом устройстве равен коэффициенту передачи регулируемого аттенюатора-усилителя.

Недостатки устройства-прототипа:

- ограничение по индексу модуляции m≤n при формировании радиосигналов с фазовой (частотной) модуляцией;

- сложность технической реализации синусно-косинусного преобразователя модулирующего напряжения на аналоговой элементной базе;

- высокая (порядка 5%) погрешность синусно-косинусного преобразования, обусловленная неточностью перемножения (порядка 3-5%) в низкочастотных перемножителях сигналов и неточностью реализации математических операций деления, инвертирования и суммирования операционными усилителями, вызывает отклонения амплитудной (порядка 6%) и фазовой (порядка 7%) модуляционных характеристик от идеальных значений;

- отсутствует возможность повышения значений индексов модуляции более 3,14 рад, т.к. при превышении значения амплитуды модулирующего напряжения более 3,14 В в выходном ФМС появляются значительные амплитудно-фазовые искажения.

Целью изобретения является разработка устройств квадратурных формирователей радиосигналов с угловой модуляцией, реализующих заявляемые способы повышения индекса модуляции.

Поставленная цель достигается тем, что:

1) в известный фазовый модулятор, содержащий последовательно соединенные источник высокочастотного сигнала ИВС, первый балансный модулятор 1-й БМ1 и первый линейный сумматор 1-й С1, последовательно соединенные первый фазовращатель на π/2 1-й ФВ1 и второй балансный модулятор 2-й БМ2, выход которого соединен со вторым входом 1-го С1, а вход 1-го ФВ1 соединен с выходом ИВС, при этом 1-й БМ1, 2-й БМ2, 1-й ФВ1 и 1-й С1 составляют первый векторный модулятор 1-й ВМ1, дополнительно введены входной буфер, аналого-цифровой преобразователь АЦП, микропроцессорные косинусный КПМН и синусный СПМН преобразователи модулирующего напряжения, первый и второй цифроаналоговые преобразователи 1-й ЦАП1 и 2-й ЦАП2, первый и второй выходные буферы 1-й ВБ1 и 2-й ВБ2, первый и второй фильтры нижних частот 1-й ФНЧ1 и 2-й ФНЧ2, второй векторный модулятор 2-й ВМ2 в составе: 3-го БМ3, 4-го БМ4, 2-го ФВ2 и 2-го С2, при этом управляющие входы 1-го БМ1, 3-го БМ3 и 2-го БМ2, 4-го БМ4 соединены с выходами, соответственно, КПМН и СПМН через 1-й ЦАП1 и 2-й ЦАП2, 1-й ВБ1 и 2-й ВБ2, 1-й ФНЧ1 и 2-й ФНЧ2, а выходы 1-го С1 и 2-го С2 являются первым и вторым выходами устройства, на которых на первой гармонике колебания несущей частоты одновременно формируются ФМС с различными значениями индексов модуляции;

2) в устройство по п. 1) дополнительно введены каскады удвоителей аргументов косинусной и синусной функций модулирующего напряжения УАФ, в состав каждого из которых входят три перемножителя сигналов, один инвертор и два линейных сумматора, объединенных соответствующими связями, при этом косинусный и синусный входы УАФ соединены с выходами, соответственно, КПМН и СПМН, а управляющие входы балансных модуляторов соединены как с выходами КПМН и СПМН через ЦАП, ВБ и ФНЧ, так и с косинусными и синусными выходами УАФ, а выходы линейных сумматоров векторных модуляторов являются выходами устройства, на которых на первой гармонике колебания несущей частоты одновременно формируются ФМС с различными значениями индексов модуляции;

3) в устройство по п.2) дополнительно введены квадратурные умножители сигналов, состоящие из балансных модуляторов, фазовращателей на π/2 и линейных сумматоров, объединенные соответствующими связями, при этом, как и в двух предыдущих случаях, управляющие входы балансных модуляторов соединены с выходами УАФ, КПМН и СПМН, а выходы линейных сумматоров ВМ являются выходами устройства, на которых как на первой, так и на последующих гармониках колебания несущей частоты одновременно формируются ФМС с различными значениями индексов модуляции.

Перечисленная новая совокупность существенных признаков за счет того, что вводятся новые этапы, элементы и связи, позволяют достичь целей изобретения: разработка устройств квадратурных формирователей радиосигналов с угловой модуляцией, реализующих заявляемые способы повышения индекса модуляции.

Предложенные устройства с применением новых элементов значительно повышают быстродействие радиосистем с угловой модуляцией, упрощают процедуры частотообразования в возбудителях передатчиков и позволяют получить практически неискаженные ФМС с индексами модуляции π≤m≤N·10π одновременно как на первой, так и на последующих гармониках колебания несущей частоты.

Предлагаемые технические решения не следуют явным образом из уровня техники и, по мнению заявителя, обладают существенными отличиями, так как при поиске не выявлены аналоги, содержащие признаки, сходные с отличительными.

Заявляемые способы и устройства поясняются структурными схемами:

- на фиг.5 иллюстрируется 1-й способ повышения индекса угловой модуляции на первой гармонике колебания несущей частоте, основанный на вычислении синусной и косинусной функций модулирующего напряжения и квадратурном перемножении и суммировании;

- на фиг.6 иллюстрируется 2-й способ повышения индекса угловой модуляции на первой гармонике колебания несущей частоте, основанный на вычислении синусной и косинусной функций модулирующего напряжения, увеличении аргументов косинусной и синусной функций и квадратурном перемножении и суммировании;

- на фиг.7 иллюстрируется 3-й способ повышения индекса угловой модуляции одновременно на первой, второй и третьей гармониках колебания несущей частоты, основанный на вычислении косинусной и синусной функций модулирующего напряжения, удвоениях аргументов косинусной и синусной функций, квадратурном умножении и квадратурном перемножении и суммировании;

- на фиг.8 приведены этапы моделирования 1-го способа повышения индекса угловой модуляции;

- на фиг.9 приведены этапы моделирования 2-го способа повышения индекса угловой модуляции;

- на фиг.10 приведены этапы моделирования 3-го способа повышения индекса угловой модуляции;

- на фиг.11 приведена структурная схема устройства-прототипа;

- на фиг.12 приведена структура вычислений при кусочно-линейном методе;

- на фиг.13 изображены входные и выходные сигналы синусного преобразователя для аналитического и таблично-алгоритмического методов;

- на фиг.14 изображены входные и выходные сигналы косинусного преобразователя для аналитического и таблично-алгоритмического методов;

- на фиг.15 изображены входные и выходные сигналы синусного преобразователя для табличного метода с фильтрацией входного сигнала;

- на фиг.16 изображены входные и выходные сигналы косинусного преобразователя для табличного метода с низкочастотной фильтрацией входного сигнала;

- на фиг.17 приведен алгоритм программы реализации синусно-косинусного преобразования, использующий табличный метод и предварительную низкочастотную фильтрацию входного сигнала;

- на фиг.18 изображена частотная характеристика ФНЧ;

- на фиг.19 приведены временные формы (вверху) и спектральный вид (внизу) выходных сигналов: а) - СП; б) - КП, при частоте дискретизации f_d=1 МГц и разрядности сигналов равной 14;

- на фиг.20 приведена структурная схема квадратурного формирователя радиосигналов с угловой модуляцией, реализующая 1-й заявленный способ;

- на фиг.21 представлены осциллограммы (вверху) и спектрограммы (внизу) сигналов на выходах микропроцессорного функционального преобразователя модулирующего напряжения (МФПМН): а) - синусного; б) - косинусного, в режиме формирования индекса модуляции m_φ=10π;

- на фиг.22 и фиг.23 представлены, соответственно, осциллограмма и спектрограмма ФМС на выходе КФМ с использованием МФПМН, реализованного по табличному методу с предварительной фильтрацией, при заданном индексе модуляции m_φ=10π;

- на фиг.24 приведена структурная схема квадратурного формирователя радиосигналов с угловой модуляцией, реализующая 2-й заявленный способ;

- на фиг.25 приведена структурная схема квадратурного формирователя радиосигналов с угловой модуляцией, реализующая 3-й заявленный способ.

Заявленные способы повышения индексов угловой модуляции поясняются следующими алгоритмами.

Известно, что общим недостатком КФМ, использующих преобразование балансно-модулированных (БМС) или амплитудно-модулированных (АМС) сигналов в ФМС, является невозможность получения ФМС с большим индексом модуляции, так как при увеличении индекса модуляции в них возникают амплитудные и фазовые искажения (Armstrong E.M. A Method of Reducing Disfurbance in Radio-Sigualing by a System of Frequency Modulation. - Proe. IRE, 1936, v.24, №5. - p.689; Куликовский А.А. Частотная модуляция в радиовещании и радиосвязи. - М.-Л.: Госэнергоиздат, 1947. - 164 с.; Гоноровский И.С. Частотная модуляция и ее применение. - М.: Государственное издательство литературы по вопросам связи и радио, 1948. - 284 с.). Обычно, считается, что с помощью подобных модуляторов возможно формирование ФМС без амплитудно-фазовых искажений с индексом модуляции m_φ≤0,5 рад. Однако, как показывают расчеты, при m_φ=0,5 рад уже имеют место достаточно большие как амплитудные, так и фазовые (нелинейные) искажения.

Проанализируем известную структурную схему КФМ с использованием балансного модулятора (фиг.3), предложенную Армстронгом (Armstrong E.M. A Method of Reducing Disfurbance in Radio-Sigualing by a System of Frequency Modulation. - Proe. IRE, 1936, v.24, №5. - p.689), на которой приведены следующие обозначения: ГВЧ - генератор высокочастотного (несущего) колебания, ИМС - источник модулирующего сигнала, ФВ1 - фазовращатель на π/2, БМ - балансный модулятор, С1 - линейный сумматор.

Мгновенное значение напряжения несущего колебания

$${\text{u}}_{\text{1}}=\text{Ucos}\omega \text{t}\text{, (6)}$$

при этом напряжение после ФВ1

$${\text{u}}_{\text{2}}=\text{Ucos(}\omega \text{t}+\pi \text{/2)}=-\text{Usin}\omega \text{t}\text{. (7)}$$

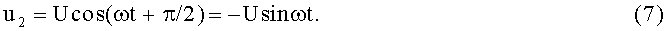
Мгновенное значение модулирующего гармонического сигнала

$$\text{e}=\text{Esin}\Omega \text{t}\text{. (8)}$$

В этом случае напряжение на выходе БМ

$${\text{u}}_{\text{3}}=-{\text{k}}_{\text{БМ}}\text{EUsin}\Omega \text{tsin}\omega \text{t}\text{, (9)}$$

где k_БМ - коэффициент передачи балансного модулятора [1/В],

а напряжение на выходе сумматора С1, при единичном коэффициенте передачи k_БМ=1

$${\text{u}}_{\text{c1}}={\text{u}}_{\text{1}}+{\text{u}}_{\text{3}}=\text{Ucos}\omega \text{t-UEsin}\Omega \text{tsin}\omega \text{t}={\text{U}}_{\text{c1}}\text{cos(}\omega \text{t}+{\varphi }_{\text{c1}}\text{)}\text{. (10)}$$

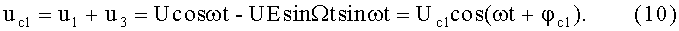
С учетом того, что амплитуда несущего колебания принята за единицу, запишем

$$U_{c1}==\sqrt{1+m_a^2{\sin }^2\Omega t},(11)$$

$${\varphi }_{\text{c1}}={\text{arctg(m}}_a\text{sin}\Omega \text{t)}\text{, (12)}$$

где m_a - коэффициент глубины амплитудной модуляции.

Из выражений (11) и (12) видно, что в выходном сигнале КФМ имеются амплитудные и фазовые искажения, проявляющиеся, соответственно, в виде ПАМ и ПФМ.

Используя (Корн Г., Корн Т. Справочник по математике для научных работников и инженеров. - 5-е изд. - М.: Наука, гл. ред. физ.-мат. лит., 1984. - 632 с.; Бронштейн И.Н., Семендяев К.А. Справочник по математике для инженеров и учащихся ВТУЗов. - 13-е изд., исправленное. - М.: Наука, гл. ред. физ.-мат. лит., 1986. - 544 с.), разложим (11) и (12) в степенные ряды и ограничимся первыми двумя членами. В этом случае U_с1=1+1/2m_a ²sin²Ωt или, используя формулу кратных углов для синуса, после преобразований имеем

$${\text{U}}_{\text{c1}}={\text{U}}_{\text{c10}}+{\text{U}}_{\text{c1пам}}\text{sin2}\Omega \text{t}\text{, (13)}$$

где U_c10=1+0,25m_a ² - постоянная амплитуда напряжения выходного сигнала КФМ, U_c1пам=0,25m_a ² - напряжение паразитной амплитудной модуляции,

$${\varphi }_{\text{с}1}={\varphi }_{\text{с}1\text{ м}}+{\varphi }_{\text{с}1\text{ пфм}}={\text{m}}_{\varphi }\text{sin}\Omega \text{t}+{\text{m}}_{\varphi \text{ пфм}}\text{sin3}\Omega \text{t}\text{, (14)}$$

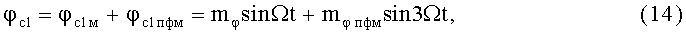
где индекс фазовой модуляции m_φ=m_a-1/4m_a ³, m_φпфм=1/12m_a ³.

Анализируя (13) и (14), можно видеть, что не учитывать U_с1пам и φ_с1пфм можно только при индексе модуляции m_φ≤0,1 рад, т.е. при m_a≤0,1.

Расчет U_с1пам и φ_с1пфм при m_a=0,1 показывает, что U_с1пам=0,0025, φ_с1пфм=0,000083, при m_a=0,5: U_с1пам=0,06, φ_с1пфм=0,01.

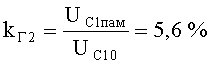
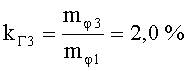
Следовательно, коэффициент ПАМ по второй гармонике модулирующего сигнала $$k_{Г2}=\frac{U_{C1пам}}{U_{C10}}=\mathrm{5,6}\%$$ , а коэффициент ПФМ по третьей гармонике модулирующего сигнала $$k_{Г3}=\frac{m_{\varphi 3}}{m_{\varphi 1}}=\mathrm{2,0}\%$$ .

Таким образом, при m_a=0,5 (m_φ=0,5 рад), как следует из результатов расчета, уже заметно проявляются амплитудно-фазовые искажения.

Из анализа структурной схемы (фиг.4) с двумя балансными модуляторами в квадратурных каналах, после соответствующих преобразований, следует, что на выходе линейного сумматора С формируется напряжение вида:

u_c=u₃+u₄=U_ccos(ωt+φ_c),

где $$U_C=\sqrt{1+e^2},{\varphi }_{\text{c}}=\text{arctg(e)}\text{. (15)}$$

Представив (15) двумя членами разложения по формуле Тейлора для многочлена, запишем выражения для U_c и φ_с, соответственно, в виде:

$${\text{U}}_{\text{c}}=\text{1}+{\text{1/2e}}^{\text{2}}\text{, }{\phi }_{\text{c}}=\text{e}+{\text{1/3e}}^{\text{3}}\text{. (16)}$$

Из (16) следует, что в выходном ФМС также, как и в структурной схеме на фиг.3, имеют место значительные ПАМ и ПФМ, о чем свидетельствуют, соответственно, квадратичное и кубическое слагаемые в этих выражениях.

Решение проблемы компенсации ПАМ и ПФМ в КФМ при значительном увеличении значений индекса угловой модуляции нашло отражение в способе-прототипе, представленном на фиг.1, и описанном алгоритмами (1)-(5). Это стало возможным за счет использования балансных модуляторов в квадратурных каналах и введения в схему новых элементов: косинусного и синусного преобразователей модулирующего напряжения. Однако в способе-прототипе не предусмотрена возможность одновременного N-кратного повышения абсолютных значений индексов модуляции радиосигналов с угловой модуляцией как на первой, так и на последующих гармониках колебания несущей частоты.

В связи с этим, предлагается 1-й способ повышения индекса угловой модуляции в КФМ на первой гармонике колебания несущей частоты (фиг.5), основанный на: формировании высокочастотного квадратурного колебания по отношению к колебанию несущей частоты; формировании синусной и косинусной составляющих модулирующего напряжения, являющихся результатом аппроксимаций функций синуса и косинуса ограниченным количеством членов разложений рядов Тейлора; первом квадратурном перемножении высокочастотных и низкочастотных составляющих и последующим линейном суммировании результатов квадратурного перемножения в первом линейном алгебраическом сумматоре, в результате получают ФМС на 1-й гармонике несущего колебания; втором квадратурном перемножении высокочастотных составляющих с выхода первого линейного алгебраического сумматора и низкочастотных составляющих с выходов косинусного и синусного преобразователей и последующим линейном алгебраическом суммировании результатов квадратурного перемножения во втором линейном алгебраическом сумматоре, в результате получают ФМС на 1-й гармонике несущего колебания и с удвоенным значением индекса модуляции; увеличивая количество этапов квадратурных перемножений и алгебраических линейных суммирований результатов вычислений косинусной и синусной функций модулирующего напряжения с соответствующими квадратурными высокочастотными составляющими, получают на выходе пропорциональное увеличение значений индексов модуляции.

На фиг.5 цифрами от 1 до 13 обозначены этапы формирования выходных ФМС (пунктирами показаны этапы способа-прототипа).

На 1-м - 8-м этапах последовательно выполняются алгоритмы (1)-(5).

На 9-м этапе производится формирование (сдвиг фазы на π/2) из ФМС:

u_лс1=U₁cosωtEcos[m_φsinΩt]-U₁sinωtEsin[m_φsinΩt]=U_c1cos(ωt+m_φsinΩt)

его квадратуры:

$${\text{u}}_{\text{3}}={\text{U}}_{\text{c1}}\text{sin(}\omega \text{t}+{\text{m}}_{\varphi }\text{sin}\Omega \text{t)}\text{. (17)}$$

10-й и 11-й этапы реализуют соответственно вторые синфазное и квадратурное перемножения высокочастотных составляющих ФМС (5) и (17) соответственно с косинусной (3) и синусной (4) составляющими модулирующего напряжения:

$${\text{u}}_{\text{сп2}}={\text{U}}_{\text{c1}}\text{cos(}\omega \text{t}+{\text{m}}_{\phi }\text{sin}\Omega {\text{t)Ecos[m}}_{\phi }\text{sin}\Omega \text{t]}\text{, (18)}$$

$${\text{u}}_{\text{кп2}}={\text{U}}_{\text{c1}}\text{sin(}\omega \text{t}+{\text{m}}_{\varphi }\text{sin}\Omega {\text{t)Esin[m}}_{\varphi }\text{sin}\Omega \text{t]}\text{. (19)}$$

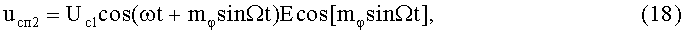
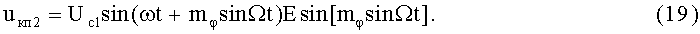
На 12-м этапе производят второе линейное алгебраическое суммирование составляющих (18) и (19) (2-й выход):

$$\begin{array}{l}{u}_{лс2}=U_{c1}\cos (\omega t+m_{\phi }\sin \Omega t)E\cos [m_{\phi }\sin \Omega t]-\\ -U_{c1}\sin (\omega t+m_{\phi }\sin \Omega t)E\sin [m_{\phi }\sin \Omega t]=\\ =U_{c1}{U}_{c2}\cos (\omega t+2m_{\phi }\sin \Omega t),(20)\end{array}$$

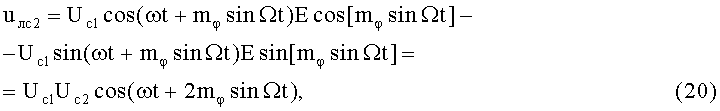
где U_c1U_c2 - постоянная амплитуда.

Из формулы (20) следует, что, в выходном ФМС произошло увеличение значения индекса модуляции в два раза, а ПАМ и ПФМ относительно сигнала (5) не проявляются.

На 13-м этапе на выходе N-го линейного алгебраического сумматора будет сформирован ФМС (N-й выход):

$${\text{u}}_{\text{лсN}}={\text{U}}_{\text{c1}}{\text{U}}_{\text{c2}}\dots {\text{U}}_{\text{cN}}\text{cos(}\omega \text{t}+\text{(N}+{\text{1)m}}_{\varphi }\text{sin}\Omega \text{t)}\text{, (21)}$$

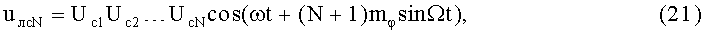
где U_c1U_c2U_cN - постоянная амплитуда, N - целое число.

Таким образом, на выходах 1-N, на фиксированной несущей частоте, одновременно формируются ФМС с различными значениями индексов модуляции. Очевидно, что с возрастанием порядкового номера этапов квадратурных перемножений и алгебраических линейных суммирований происходит пропорциональное увеличение значений индексов модуляции выходных ФМС: на 2-м выходе - в два раза, на 3-м выходе - в три раза (на фиг.5 не показано), на N-м выходе - в (N+1) раз, относительно начального значения индекса модуляции ФМС, сформированного на 1-м выходе.

На фиг.8 а-н приведены этапы моделирования данного способа, при аппроксимации функций синуса и косинуса 5-ю членами разложения рядов Тейлора, соответствующие формированию ФМС с индексом модуляции m_φ=π (Квадратурные формирователи радиосигналов: Монография / Попов П.А., Шерстюков С.А., Жайворонок Д.А., Ромашов В.В.; Под ред. П.А. Попова. - Воронеж: Воронежский институт МВД России, 2001. - C.36-43): рис.8а - соответствует 1-му этапу способа; б - 2-му этапу; в - 3-му этапу; г, д - 4-му этапу (на рис.д представлен спектр на выходе вычислителя косинусной функции модулирующего напряжения); е, ж - 5-му этапу (на рис.ж представлен спектр на выходе вычислителя синусной функции модулирующего напряжения); з - 6-му этапу; и - 7-му этапу; к, л - 8-му этапу (на рис.л представлен спектр на выходе первого линейного алгебраического сумматора); м - 10-му этапу; н - 11-му этапу; о, п - 12-му этапу (на рис.п представлен спектр на выходе второго линейного алгебраического сумматора); р, с - 13-му этапу (на рис.с представлен спектр на выходе N-го линейного алгебраического сумматора, при N=5).

2-й способ повышения индекса угловой модуляции в КФМ на первой гармонике колебания несущей частоты (фиг.6) отличается от 1-го способа на фиг.5 тем, что: на выходе вычислителей косинусной и синусной функций модулирующего напряжения производят соответствующим образом увеличение в 2, 4 … N раз значений аргументов этих функций; результаты первого удвоения аргументов косинусной и синусной функций перемножают с квадратурными колебаниями несущей частоты, соответственно, во вторых синфазном и квадратурном перемножителях, после чего, высокочастотные квадратурные компоненты складывают во втором линейном алгебраическом сумматоре, в результате получают ФМС на 1-й гармонике несущего колебания и с удвоенным значением индекса модуляции; из ФМС, полученного на выходе второго линейного алгебраического сумматора, производят формирование квадратурного колебания, после чего оба колебания перемножают с результатами вычислений косинусной и синусной функций, соответственно, в третьих синфазном и квадратурном перемножителях, а полученные высокочастотные квадратурные компоненты складывают в третьем линейном алгебраическом сумматоре, в результате получают ФМС на 1-й гармонике несущего колебания и с утроенным значением индекса модуляции; результаты второго удвоения аргументов косинусной и синусной функций перемножают с квадратурными колебаниями несущей частоты соответственно в четвертых синфазном и квадратурном перемножителях, после чего высокочастотные квадратурные компоненты складывают в четвертом линейном алгебраическом сумматоре, в результате получают ФМС на 1-й гармонике несущего колебания и с увеличенным в четыре раза значением индекса модуляции; увеличивая количество нечетных операций квадратурных перемножений и алгебраических линейных суммирований результатов вычислений косинусной и синусной функций модулирующего напряжения с соответствующими квадратурными высокочастотными составляющими, и - четных операций квадратурных перемножений и алгебраических линейных суммирований результатов удвоений аргументов косинусной и синусной функций с соответствующими квадратурными высокочастотными составляющими, получают на выходе пропорциональное увеличение значений индексов модуляции.

На фиг.6 цифрами от 1 до 25 обозначены этапы формирования выходных ФМС (пунктирами показаны этапы способа-прототипа и 1-го способа).

На 1-м - 5-м и 12 м - 14-м этапах выполняются алгоритмы (1)-(5).

На 6-м и 7-м этапах производят первые удвоения аргументов косинусной и синусной функций:

$${\text{e}}_{\text{k2}}={\text{E}}_{\text{2}}{\text{cos[2m}}_{\varphi }\text{sin}\Omega \text{t]}\text{, (22)}$$

$${\text{e}}_{\text{c2}}={\text{E}}_{\text{2}}{\text{sin[2m}}_{\varphi }\text{sin}\Omega \text{t]}\text{, (23)}$$

а на 8-м и 9-м этапах - вторые удвоения аргументов, соответственно, косинусной и синусной функций:

$${\text{e}}_{\text{k3}}={\text{E}}_{\text{3}}{\text{cos[4m}}_{\varphi }\text{sin}\Omega \text{t]}\text{, (24)}$$

$${\text{e}}_{\text{c3}}={\text{E}}_{\text{3}}{\text{sin[4m}}_{\varphi }\text{sin}\Omega \text{t]}\text{. (25)}$$

15-й и 16-й этапы реализуют вторые синфазное и квадратурное перемножения высокочастотных составляющих ФМС (1) и (2) соответственно с составляющими (22) и (23):

$${\text{u}}_{\text{сп2}}={\text{U}}_{\text{1}}\text{cos}\omega \text{t}\times {\text{E}}_{\text{2}}{\text{cos[2m}}_{\varphi }\text{sin}\Omega \text{t]}\text{, (26)}$$

$${\text{u}}_{\text{кп2}}={\text{U}}_{\text{1}}\text{sin}\omega \text{t}\times {\text{E}}_{\text{2}}{\text{sin[2m}}_{\varphi }\text{sin}\Omega \text{t]}\text{. (27)}$$

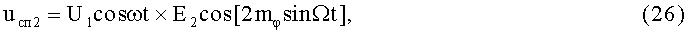
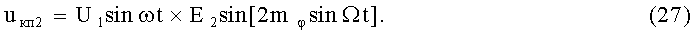
На 17-м этапе производят второе линейное алгебраическое суммирование результатов произведений (26) и (27) (2-й выход):

$$\begin{array}{l}{\text{u}}_{\text{лс2}}={\text{U}}_{\text{1}}\text{cos}\omega \text{t}\times {\text{E}}_{\text{2}}{\text{cos[m}}_{\varphi }\text{sin}\Omega {\text{t]-U}}_{\text{1}}\text{sin}\omega \text{t}\times {\text{E}}_{\text{2}}{\text{sin[m}}_{\varphi }\text{sin}\Omega \text{t]}=\\ ={\text{U}}_{\text{c2}}\text{cos(}\omega \text{t}+{\text{2m}}_{\varphi }\text{sin}\Omega \text{t)}\text{, (28)}\end{array}$$

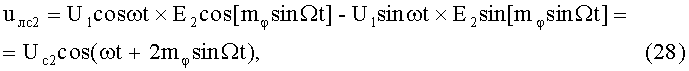
где U_c2 - постоянная амплитуда.

На 18-м этапе производится формирование квадратуры от ФМС (28):

$${\text{u}}_{\text{3}}={\text{U}}_{\text{c2}}\text{cos(}\omega \text{t}+{\text{2m}}_{\varphi }\text{sin}\Omega \text{t}+\pi \text{/2)}=-{\text{U}}_{\text{c2}}\text{sin(}\omega \text{t}+{\text{2m}}_{\varphi }\text{sin}\Omega \text{t)}\text{, (29)}$$

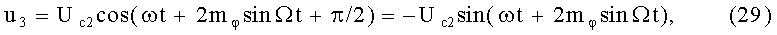
после чего на 19-м и 20-м этапах реализуют третьи синфазное и квадратурное перемножения высокочастотных составляющих ФМС (28) и (29) соответственно с косинусной (3) и синусной (4) составляющими модулирующего напряжения:

$${\text{u}}_{\text{сп3}}={\text{U}}_{\text{c2}}\text{cos(}\omega \text{t}+{\text{2m}}_{\varphi }\text{sin}\Omega \text{t)}\times {\text{E}}_{\text{1}}{\text{cos[m}}_{\varphi }\text{sin}\Omega \text{t]}\text{, (30)}$$

$${\text{u}}_{\text{кп3}}={\text{U}}_{\text{c2}}\text{sin(}\omega \text{t}+{\text{2m}}_{\varphi }\text{sin}\Omega \text{t)}\times {\text{E}}_{\text{1}}{\text{sin[m}}_{\varphi }\text{sin}\Omega \text{t]}\text{. (31)}$$

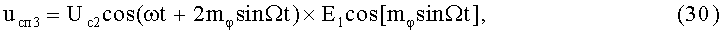
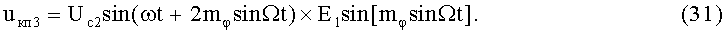
На 21-м этапе производят третье линейное алгебраическое суммирование результатов произведений (30) и (31) (3-й выход):

$$\begin{array}{l}{\text{u}}_{\text{лс3}}={\text{U}}_{\text{c2}}\text{cos(}\omega t+2m_{\varphi }\sin \Omega t)\times {\text{E}}_{\text{1}}\text{cos[}{m}_{\varphi }\sin \Omega t\text{])-}\\ {\text{-U}}_{\text{c2}}\text{sin(}\omega \text{t}+\text{2}{m}_{\varphi }\sin \Omega t\text{)}\times {\text{E}}_{\text{1}}\text{sin[}{m}_{\varphi }\sin \Omega t\text{]}=\\ ={\text{U}}_{\text{c3}}\text{cos(}\omega \text{t}+\text{3}{m}_{\varphi }\sin \Omega t\text{)}\text{, (32)}\end{array}$$

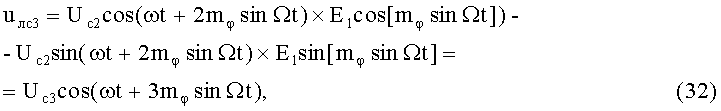
где U_c3 - постоянная амплитуда.

22-й и 23-й этапы реализуют четвертые синфазное и квадратурное перемножения высокочастотных составляющих ФМС (1) и (2) соответственно с составляющими (24) и (25):

$${\text{u}}_{\text{сп4}}={\text{U}}_{\text{1}}\text{cos}\omega \text{t}\times {\text{E}}_{\text{3}}\text{cos[4}{m}_{\varphi }\sin \Omega t\text{]}\text{, (33)}$$

$${\text{u}}_{\text{кп4}}={\text{-U}}_{\text{1}}\text{sin}\omega \text{t}\times {\text{E}}_{\text{3}}\text{sin[4}{m}_{\varphi }\sin \Omega t\text{]}\text{. (34)}$$

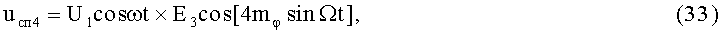
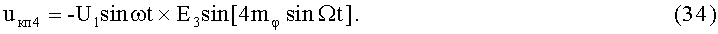
На 24-м этапе производят четвертое линейное алгебраическое суммирование результатов произведений (33) и (34) (4-й выход):

$$\begin{array}{l}{\text{u}}_{\text{лс4}}={\text{U}}_{\text{1}}\text{cos}\omega \text{t}\times {\text{E}}_{\text{3}}\text{cos[4}{m}_{\varphi }\sin \Omega t{\text{]-U}}_{\text{1}}\text{sin}\omega \text{t}\times {\text{E}}_{\text{3}}\text{sin[4}{m}_{\varphi }\sin \Omega t\text{]}=\\ ={\text{U}}_{\text{c4}}\text{cos(}\omega \text{t}+\text{4}{m}_{\varphi }\sin \Omega t\text{)}\text{, (35)}\end{array}$$

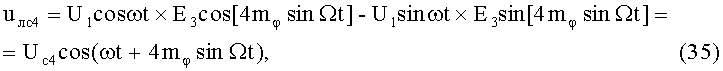
где U_c4 - постоянная амплитуда.

Для N-кратного увеличения количества этапов квадратурных перемножений и линейных алгебраических суммирований, для выходного ФМС можно записать (5-й выход):

$$\begin{array}{l}{\text{u}}_{\text{лс1-N}}={\text{U}}_{\text{c1-4}}{\text{E}}_{\text{y}}[\cos (\omega t+N\cdot m_{\varphi }\sin \Omega t)\cos (N\cdot m_{\varphi }\sin \Omega t)-\\ \text{-sin(}\omega \text{t}+\text{N}\cdot m_{\varphi }\sin \Omega t\text{)sin(N}\cdot m_{\varphi }\sin \Omega t\text{)}]=\\ ={\text{U}}_{\text{c1-N}}\text{cos(}\omega t+N\cdot m_{\varphi }\sin \Omega t)\text{, (36)}\end{array}$$

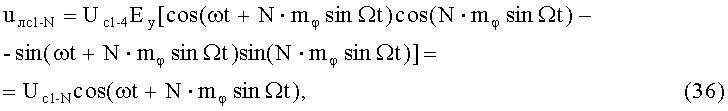
где 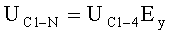$$U_{C1-N}=U_{C1-4}{E}_{у}$$ - постоянная амплитуда.

Из формул (28), (32), (35) и (36) можно видеть, как пропорционально увеличению количества этапов квадратурных перемножений и линейных суммирований происходит увеличение значений индексов модуляции выходных ФМС, при этом ПАМ и ПФМ относительно ФМС (5) не проявляются.

На фиг.9а-э приведены этапы моделирования данного способа: рис.9а, б - соответствует 6-му этапу способа (на рис.б представлен спектр на выходе первого удвоителя аргумента косинусной функции); в, г - 7-му этапу (на рис.г представлен спектр на выходе первого удвоителя аргумента синусной функции); д, е - 8-му этапу (на рис.е представлен спектр на выходе второго удвоителя аргумента косинусной функции); ж, з - 9-му этапу (на рис.з представлен спектр на выходе второго удвоителя аргумента синусной функции); и, к - 15-му этапу (на рис.к представлен спектр на выходе второго синфазного перемножителя); л, м - 16-му этапу (на рис.м представлен спектр на выходе второго квадратурного перемножителя); н, о - 17-му этапу (на рис.о представлен спектр на выходе второго линейного алгебраического сумматора); п, р - 19-му этапу (на рис.р представлен спектр на выходе третьего синфазного перемножителя); с, т - 20-му этапу (на рис.т представлен спектр на выходе третьего квадратурного перемножителя); у, ф - 21-му этапу (на рис.ф представлен спектр на выходе третьего линейного алгебраического сумматора); х, ц - 22-му этапу (на рис.ц представлен спектр на выходе четвертого синфазного перемножителя); ш, щ - 23-му этапу (на рис.щ представлен спектр на выходе четвертого квадратурного перемножителя); ы, э - 24-му этапу (на рис.э представлен спектр на выходе четвертого линейного алгебраического сумматора).

3-й способ повышения индекса угловой модуляции в КФМ одновременно на нескольких гармониках колебания несущей частоты (фиг.7) отличается от 2-го способа на фиг.6 тем, что: производят первое умножение колебания несущей частоты, в результате которого получают его вторую гармонику, и первое формирование квадратурного колебания второй гармоники; полученные результаты первого умножения и первого формирования квадратурного колебания перемножают с косинусной и синусной функциями модулирующего напряжения соответственно в первых синфазном и квадратурном перемножителях, после чего высокочастотные квадратурные компоненты складывают в первом линейном алгебраическом сумматоре, в результате получают ФМС на 2-й гармонике несущего колебания; производят второе умножение ФМС с выхода первого линейного алгебраического сумматора из 2-го способа, в результате которого получают ФМС на 2-й гармонике несущего колебания и с удвоенным значением индекса модуляции; выполняют второе формирование квадратурного колебания из ФМС на 2-й гармонике; полученные результаты второго умножения и второго формирования квадратурного колебания перемножают с косинусной и синусной функциями модулирующего напряжения, соответственно, во вторых синфазном и квадратурном перемножителях, после чего высокочастотные квадратурные компоненты складывают во втором линейном алгебраическом сумматоре, в результате получают ФМС на 2-й гармонике несущего колебания и с утроенным значением индекса модуляции; результаты первого умножения и первого формирования квадратурного колебания перемножают с результатами второго удвоения аргументов косинусной и синусной функций 2-го способа соответственно в третьих синфазном и квадратурном перемножителях, после чего высокочастотные квадратурные компоненты складывают в третьем линейном алгебраическом сумматоре, в результате получают ФМС на 2-й гармонике несущего колебания и с увеличенным в четыре раза значением индекса модуляции; производят третье умножение колебания несущей частоты, в результате которого получают его третью гармонику, и третье формирование квадратурного колебания третьей гармоники; полученные результаты третьего умножения и третьего формирования квадратурного колебания перемножают с косинусной и синусной функциями модулирующего напряжения соответственно в четвертых синфазном и квадратурном перемножителях, после чего, высокочастотные квадратурные компоненты складывают в четвертом линейном алгебраическом сумматоре, в результате получают ФМС на 3-й гармонике несущего колебания; результаты третьего умножения и третьего формирования квадратурного колебания перемножают с результатами первого удвоения аргументов косинусной и синусной функций 2-го способа соответственно в пятых синфазном и квадратурном перемножителях, после чего, высокочастотные квадратурные компоненты складывают в пятом линейном алгебраическом сумматоре, в результате получают ФМС на 3-й гармонике несущего колебания и с удвоенным значением индекса модуляции; выполняют четвертое формирование квадратурного колебания из ФМС на 3-й гармонике с удвоенным значением индекса модуляции; результаты пятого линейного алгебраического суммирования и четвертого формирования квадратурного колебания перемножают с косинусной и синусной функциями модулирующего напряжения 2-го способа соответственно в шестых синфазном и квадратурном перемножителях, после чего высокочастотные квадратурные компоненты складывают в шестом линейном алгебраическом сумматоре, в результате получают ФМС на 3-й гармонике несущего колебания и с утроенным значением индекса модуляции; результаты третьего умножения и третьего формирования квадратурного колебания перемножают с результатами второго удвоения аргументов косинусной и синусной функций 2-го способа соответственно в седьмых синфазном и квадратурном перемножителях, после чего высокочастотные квадратурные компоненты складывают в седьмом линейном алгебраическом сумматоре, в результате получают ФМС на 3-й гармонике несущего колебания и с увеличенным в четыре раза значением индекса модуляции; последовательно увеличивая количество этапов умножений колебания несущей частоты в сочетании с операциями квадратурных перемножений и алгебраических линейных суммирований, получают на выходе кратное увеличение значений индексов модуляции одновременно на различных гармониках колебания несущей частоты.

На фиг.7 цифрами от 1 до 28 обозначены этапы формирования выходных ФМС (пунктирами показаны этапы 2-го способа).

На 1-м и 2-м этапах выполняют соответственно первое умножение колебания несущей частоты (1-й выход) и формирование его квадратуры:

$${\text{u}}_{\text{ус1}}={{\text{(U}}_{\text{1}}\text{cos}\omega \text{t)}}^{\text{2}}{\text{-(U}}_{\text{1}}\text{sin}\omega {\text{t)}}^{\text{2}}={\text{U}}_{\text{1}}{}^{\text{2}}\text{cos2}\omega \text{t}\text{, (37)}$$

$${\text{u}}_{\text{фв1}}={\text{U}}_{\text{1}}{}^{\text{2}}\text{sin2}\omega \text{t}\text{. (38)}$$

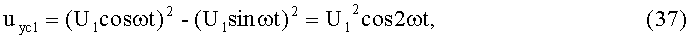
3-й и 4-й этапы реализуют первые синфазное и квадратурное перемножения 2-х гармоник колебаний несущей частоты (37) и (38) соответственно с составляющими (3) и (4):

$${\text{u}}_{\text{сп1}}={\text{U}}_{\text{1}}{}^{\text{2}}\text{cos2}\omega \text{t}\times {\text{E}}_{\text{1}}{\text{cos[m}}_{\varphi }\text{sin}\Omega \text{t]}\text{, (39)}$$

$${\text{u}}_{\text{кп1}}={\text{-U}}_{\text{1}}{}^{\text{2}}\text{sin2}\omega \text{t}\times {\text{E}}_{\text{1}}{\text{sin[m}}_{\varphi }\text{sin}\Omega \text{t]}\text{. (40)}$$

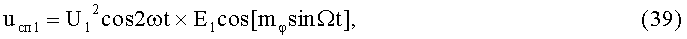
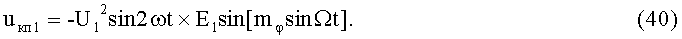
На 5-м этапе производят первое линейное алгебраическое суммирование результатов произведений (39) и (40) (2-й выход):

$$\begin{array}{l}{\text{u}}_{\text{с1}}={\text{U}}_{\text{1}}{}^{\text{2}}\text{cos2}\omega \text{t}\times {\text{E}}_{\text{1}}{\text{cos[m}}_{\varphi }\text{sin}\Omega {\text{t]-U}}_{\text{1}}{}^{\text{2}}\text{sin2}\omega \text{t}\times {\text{E}}_{\text{1}}{\text{sin[m}}_{\varphi }\text{sin}\Omega \text{t]}=\\ ={\text{U}}_{\text{c1}}\text{cos(2}\omega \text{t}+{\text{m}}_{\varphi }\text{sin}\Omega \text{t)}\text{, (41)}\end{array}$$

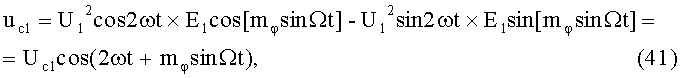
где U_c1 - постоянная амплитуда.

На 6-м и 7-м этапах производят соответственно второе умножение ФМС (3-й выход) и формирование его квадратуры:

$$\begin{array}{l}{\text{u}}_{\text{ус2}}={{\text{(U}}_{\text{c1}}}^{\text{cos(}}{\text{-(U}}_{\text{c1}}\text{sin(}\omega \text{t}+{\text{m}}_{\varphi }\text{sin}\Omega {\text{t))}}^{\text{2}}=\\ ={\text{U}}_{\text{c1}}{}^{\text{2}}\text{cos(2}\omega \text{t}+{\text{2m}}_{\varphi }\text{sin}\Omega \text{t)}\text{, (42)}\end{array}$$

$${\text{u}}_{\text{фв2}}=-{\text{U}}_{\text{c1}}{}^{\text{2}}\text{sin(2}\omega \text{t}+{\text{2m}}_{\varphi }\text{sin}\Omega \text{t)}\text{. (43)}$$

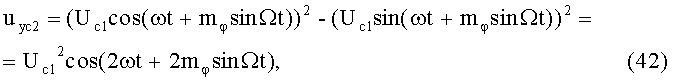
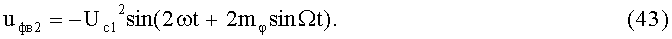
8-й и 9-й этапы реализуют первые синфазное и квадратурное перемножения сигналов (42) и (43) соответственно с составляющими (3) и (4):

$${\text{u}}_{\text{сп2}}={\text{U}}_{\text{c1}}{}^{\text{2}}\text{cos(2}\omega \text{t}+{\text{2m}}_{\varphi }\text{sin}\Omega \text{t)}\times {\text{E}}_{\text{1}}{\text{cos[m}}_{\varphi }\text{sin}\Omega \text{t]}\text{, (44)}$$

$${\text{u}}_{\text{кп2}}={\text{-U}}_{\text{c1}}{}^{\text{2}}\text{sin(2}\omega \text{t}+{\text{2m}}_{\varphi }\text{sin}\Omega \text{t)}\times {\text{E}}_{\text{1}}{\text{sin[m}}_{\varphi }\text{sin}\Omega \text{t]}\text{. (45)}$$

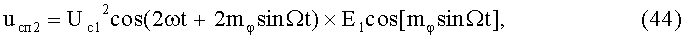
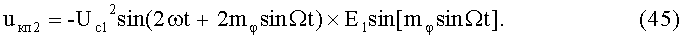
На 10-м этапе производят второе линейное алгебраическое суммирование результатов произведений (44) и (45) (4-й выход):

$$\begin{array}{l}{\text{u}}_{\text{c2}}={\text{U}}_{\text{c1}}{}^{\text{2}}\text{cos(2}\omega \text{t}+{\text{2m}}_{\varphi }\text{sin}\Omega \text{t)}\times {\text{E}}_{\text{1}}{\text{cos[m}}_{\varphi }\text{sin}\Omega \text{t]-}\\ {\text{-U}}_{\text{c1}}{}^{\text{2}}\text{sin(2}\omega \text{t}+{\text{2m}}_{\varphi }\text{sin}\Omega \text{t)}\times {\text{E}}_{\text{1}}{\text{sin[m}}_{\varphi }\text{sin}\Omega \text{t]}=\\ ={\text{U}}_{\text{c2}}\text{cos(2}\omega \text{t}+{\text{3m}}_{\varphi }\text{sin}\Omega \text{t)}\text{, (46)}\end{array}$$

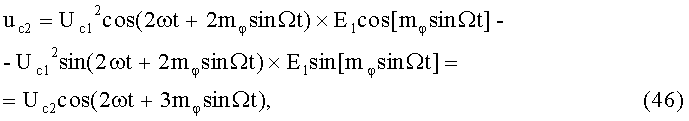
где U_c2 - постоянная амплитуда.

11-й и 12-й этапы реализуют третьи синфазное и квадратурное перемножения 2-х гармоник колебаний несущей частоты (37) и (38) соответственно с составляющими (24) и (25):

$${\text{u}}_{\text{сп3}}={\text{U}}_{\text{1}}{}^{\text{2}}\text{cos2}\omega \text{t}\times {\text{E}}_{\text{3}}{\text{cos[4m}}_{\varphi }\text{sin}\Omega \text{t]}\text{, (47)}$$

$${\text{u}}_{\text{кп3}}={\text{-U}}_{\text{1}}{}^{\text{2}}\text{sin2}\omega \text{t}\times {\text{E}}_{\text{3}}{\text{sin[4m}}_{\varphi }\text{sin}\Omega \text{t]}\text{. (48)}$$

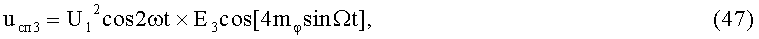
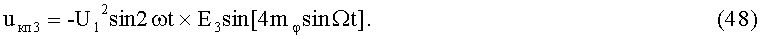
На 13-м этапе производят третье линейное алгебраическое суммирование результатов произведений (47) и (48) (5-й выход):

$$\begin{array}{l}{\text{u}}_{\text{с3}}={\text{U}}_{\text{1}}{}^{\text{2}}\text{cos2}\omega \text{t}\times {\text{E}}_{\text{3}}{\text{cos[4m}}_{\varphi }\text{sin}\Omega {\text{t]-U}}_{\text{1}}{}^{\text{2}}\text{sin2}\omega \text{t}\times {\text{E}}_{\text{3}}{\text{sin[4m}}_{\varphi }\text{sin}\Omega \text{t]}=\\ ={\text{U}}_{\text{c3}}\text{cos(2}\omega \text{t}+{\text{4m}}_{\varphi }\text{sin}\Omega \text{t)}\text{, (49)}\end{array}$$

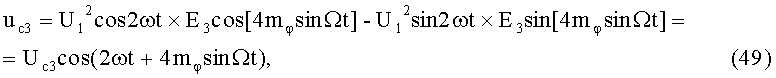
где U_c3 - постоянная амплитуда.

На 14-м и 15-м этапах производят соответственно третье умножение колебания несущей частоты (6-й выход) и формирование его квадратуры:

$${\text{u}}_{\text{ус3}}={\text{U}}_{\text{1}}\text{cos}\omega \text{t}\times {\text{U}}_{\text{1}}{}^{\text{2}}\text{cos2}\omega {\text{t-U}}_{\text{1}}\text{sin}\omega \text{t}\times {\text{U}}_{\text{1}}{}^{\text{2}}\text{sin2}\omega \text{t}={\text{U}}_{\text{с4}}{}^{\text{2}}\text{cos3}\omega \text{t}\text{, (50)}$$

$${\text{u}}_{\text{фв3}}=-{\text{U}}_{\text{с4}}{}^{\text{2}}\text{sin3}\omega \text{t}\text{. (51)}$$

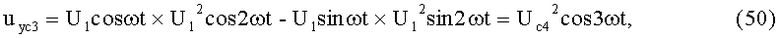
16-й и 17-й этапы реализуют четвертые синфазное и квадратурное перемножения 2-х гармоник колебаний несущей частоты (50) и (51) соответственно с составляющими (3) и (4):

$${\text{u}}_{\text{сп4}}={\text{U}}_{\text{с4}}{}^{\text{2}}\text{cos3}\omega \text{t}\times {\text{E}}_{\text{1}}{\text{cos[m}}_{\varphi }\text{sin}\Omega \text{t]}\text{, (52)}$$

$${\text{u}}_{\text{кп4}}={\text{-U}}_{\text{с4}}{}^{\text{2}}\text{sin3}\omega \text{t}\times {\text{E}}_{\text{1}}{\text{sin[m}}_{\varphi }\text{sin}\Omega \text{t]}\text{. (53)}$$

На 18-м этапе производят четвертое линейное алгебраическое суммирование результатов произведений (52) и (53) (7-й выход):

$$\begin{array}{l}{\text{u}}_{\text{с4}}{\text{=U}}_{\text{с4}}{}^{\text{2}}\text{cos3}\omega \text{t}\times {\text{E}}_{\text{1}}{\text{cos[m}}_{\varphi }\text{sin}\Omega {\text{t]-U}}_{\text{с4}}{}^{\text{2}}\text{sin3}\omega \text{t}\times {\text{E}}_{\text{1}}{\text{sin[m}}_{\varphi }\text{sin}\Omega \text{t]=}\\ {\text{=U}}_{\text{c4}}\text{cos(3}\omega {\text{t+m}}_{\varphi }\text{sin}\Omega \text{t)}\text{, (54)}\end{array}$$

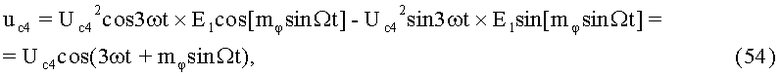
где U_c4 - постоянная амплитуда.

19-й и 20-й этапы реализуют пятые синфазное и квадратурное перемножения 2-х гармоник колебаний несущей частоты (50) и (51) соответственно с составляющими (22) и (23):

$${\text{u}}_{\text{сп5}}={\text{U}}_{\text{с4}}{}^{\text{2}}\text{cos3}\omega \text{t}\times {\text{E}}_{\text{2}}{\text{cos[2m}}_{\varphi }\text{sin}\Omega \text{t]}\text{, (55)}$$

$${\text{u}}_{\text{кп5}}={\text{-U}}_{\text{с4}}{}^{\text{2}}\text{sin3}\omega \text{t}\times {\text{E}}_{\text{2}}{\text{sin[2m}}_{\varphi }\text{sin}\Omega \text{t]}\text{. (56)}$$

На 21-м и 22-м этапах производят пятое линейное алгебраическое суммирование результатов произведений (55) и (56) (8-й выход) и формирование квадратуры полученного ФМС:

$$\begin{array}{l}{\text{u}}_{\text{с5}}{\text{=U}}_{\text{с4}}{}^{\text{2}}\text{cos3}\omega \text{t}\times {\text{E}}_{\text{2}}{\text{cos[2m}}_{\varphi }\text{sin}\Omega {\text{t]-U}}_{\text{с4}}{}^{\text{2}}\text{sin3}\omega \text{t}\times {\text{E}}_{\text{2}}{\text{sin[2m}}_{\varphi }\text{sin}\Omega \text{t]=}\\ {\text{=U}}_{\text{c5}}\text{cos(3}\omega {\text{t+2m}}_{\varphi }\text{sin}\Omega \text{t)}\text{, (57)}\end{array}$$

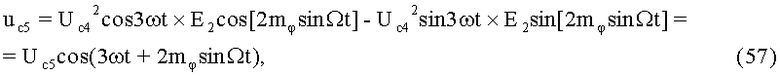
где U_c5 - постоянная амплитуда,

$${\text{u}}_{\text{фв4}}=-{\text{U}}_{\text{c5}}\text{sin(3}\omega \text{t}+{\text{2m}}_{\varphi }\text{sin}\Omega \text{t)}\text{. (58)}$$

23-й и 24-й этапы реализуют шестые синфазное и квадратурное перемножения сигналов (57) и (58) соответственно с составляющими (3) и (4):

$${\text{u}}_{\text{сп6}}={\text{U}}_{\text{c5}}\text{cos(3}\omega \text{t}+{\text{2m}}_{\varphi }\text{sin}\Omega \text{t)}\times {\text{E}}_{\text{1}}{\text{cos[m}}_{\varphi }\text{sin}\Omega \text{t]}\text{, (59)}$$

$${\text{u}}_{\text{кп6}}={\text{-U}}_{\text{c5}}\text{sin(3}\omega \text{t}+{\text{2m}}_{\varphi }\text{sin}\Omega \text{t)}\times {\text{E}}_{\text{1}}{\text{sin[m}}_{\varphi }\text{sin}\Omega \text{t]}\text{. (60)}$$

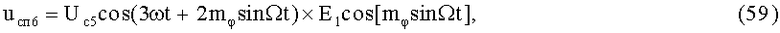
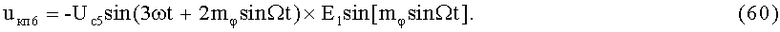
На 25-м этапе производят шестое линейное алгебраическое суммирование результатов произведений (59) и (60) (9-й выход):

$$\begin{array}{l}{\text{u}}_{\text{с6}}={\text{U}}_{\text{c5}}\text{cos(3}\omega \text{t}+{\text{2m}}_{\varphi }\text{sin}\Omega \text{t)}\times {\text{E}}_{\text{1}}{\text{cos[m}}_{\varphi }\text{sin}\Omega \text{t]-}\\ {\text{-U}}_{\text{c5}}\text{sin(3}\omega \text{t}+{\text{2m}}_{\varphi }\text{sin}\Omega \text{t)}\times {\text{E}}_{\text{1}}{\text{sin[m}}_{\varphi }\text{sin}\Omega \text{t]}=\\ ={\text{U}}_{\text{c6}}\text{cos(3}\omega \text{t}+{\text{3m}}_{\varphi }\text{sin}\Omega \text{t)}\text{, (61)}\end{array}$$

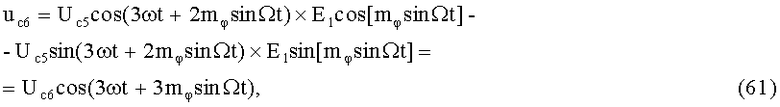
где U_c6 - постоянная амплитуда.

26-й и 27-й этапы реализуют седьмые синфазное и квадратурное перемножения сигналов (50) и (51) соответственно с составляющими (24) и (25):

$${\text{u}}_{\text{сп7}}={\text{U}}_{\text{с4}}{}^{\text{2}}\text{cos3}\omega \text{t}\times {\text{E}}_{\text{3}}{\text{cos[4m}}_{\varphi }\text{sin}\Omega \text{t]}\text{, (62)}$$

$${\text{u}}_{\text{кп7}}={\text{-U}}_{\text{с4}}{}^{\text{2}}\text{sin3}\omega \text{t}\times {\text{E}}_{\text{3}}{\text{sin[4m}}_{\varphi }\text{sin}\Omega \text{t]}\text{. (63)}$$

На 28-м этапе производят седьмое линейное алгебраическое суммирование результатов произведений (62) и (63) (10-й выход):

$$\begin{array}{l}{\text{u}}_{\text{с7}}{\text{=U}}_{\text{с4}}{}^{\text{2}}\text{cos3}\omega \text{t}\times {\text{E}}_{\text{3}}{\text{cos[4m}}_{\varphi }\text{sin}\Omega {\text{t]-U}}_{\text{с4}}{}^{\text{2}}\text{sin3}\omega \text{t}\times {\text{E}}_{\text{3}}{\text{sin[4m}}_{\varphi }\text{sin}\Omega \text{t]=}\\ {\text{=U}}_{\text{c7}}\text{cos(3}\omega {\text{t+4m}}_{\varphi }\text{sin}\Omega \text{t)}\text{, (64)}\end{array}$$

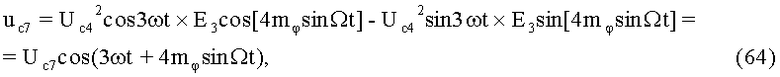
где U_c7 - постоянная амплитуда.

Для N-кратного увеличения количества этапов умножений колебания несущей частоты в сочетании с операциями квадратурных перемножений и алгебраических линейных суммирований, для выходных ФМС можно записать:

$${\text{u}}_{\text{cN}}={\text{U}}_{\text{cN}}\text{cos(N}\cdot \omega \text{t}+\text{N}\cdot {\text{m}}_{\varphi }\text{sin}\Omega \text{t)}\text{, (65)}$$

где U_cN - постоянная амплитуда.

Из формул (37), (41), (42), (46), (49), (50), (54), (57), (61), (64) и (65) следует, что пропорционально увеличению количества этапов умножений колебания несущей частоты в сочетании с увеличением количества этапов квадратурных перемножений и линейных суммирований происходит увеличение количества гармоник колебания несущей частоты с одновременным увеличением на них (гармониках) значений индексов модуляции выходных ФМС, при отсутствии проявления ПАМ и ПФМ.

На фиг.10а-д приведены спектры на выходах этапов моделирования 3-го способа (этапы формирования ФМС на 2-й и 3-й гармониках колебания несущей частоты, в сравнении с 1-й гармоникой, отмечены цифрами): рис.10а - соответствует 1-му и 14-му этапам; рис.10б - соответствует 5-му и 18-му этапам; рис.10в - соответствует 6-му и 21-му этапам; рис.10г - соответствует 10-му и 25-му этапам; рис.10д - соответствует 13-му и 28-му этапам.

Возможность реализации заявленных способов повышения индексов угловой модуляции поясняется следующим.

Для получения ФМС с индексами модуляции m>>1 целесообразно реализовывать цифровые синусные и косинусные преобразователи модулирующего напряжения (ЦСКПМН), которые можно рассматривать как функциональные преобразователи (ФП). В общем смысле [Смолов В.Б. Функциональные преобразователи информации. - Л.: Энергоиздат. Ленингр. отд-ние, 1981. - 248 с.], ФП являются вычислительными устройствами, предназначенными для автоматического воспроизведения элементарных функций Z одного Ф(X) или нескольких Ф (X₁, X₂, …, X_т) аргументов, зависящих от текущего времени: X_j=X_j(t). Поэтому функциональная характеристика ФП, определяющая связь между входными X_jвх и выходной Z_вых переменными, имеет вид

$${\text{Z}}_{\text{вых}}={\text{F}}_{\text{вых}}{\text{ (X}}_{\text{1вх}}{\text{, X}}_{\text{2вх}}\text{, }\dots {\text{, X}}_{\text{jвх}}\text{, }\dots {\text{, X}}_{\text{mвх}}\text{)}\text{, (66)}$$

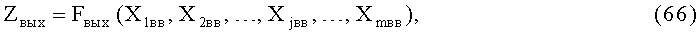
где Z_вых и X_jвх могут быть представлены физическими величинами в непрерывной или дискретной формах.

Оптимальными реализациями ЦСКПМН, с точки зрения простоты, точности преобразования, вычислительных и аппаратных затрат, являются кусочно-ступенчатые (КС) и кусочно-линейные (КЛ) ФП, которые могут быть использованы для точного воспроизведения функций синуса и косинуса при цифровом задании переменных.

В соответствии с классификацией [Смолов В.Б. Функциональные преобразователи информации. - Л.: Энергоиздат. Ленингр. отд-ние, 1981. - 248 с.], КС и КЛ ФП реализуются по блочно-структурному, структурно-программному и программно-арифметическому принципам действия, поэтому методика и конечная цель расчета параметров ФП указанных типов напрямую зависят от конкретной технической реализации устройств и сложности функционального преобразования.

Таблично-алгоритмические кусочно-ступенчатые цифровые ФП наряду с табличной записью в ПЗУ сокращенного объема значений заданной функции используют алгоритмические (программные или программно-структурные) операции сложения, умножения и деления. Очевидно, что программная реализация арифметических операций требует усложнения логической части ФП, а в ряде случаев они играют роль специализированных процессоров для более быстрого вычисления функций по сравнению с чисто программными процессорами. Кроме того, в подобных специализированных процессорах, наряду с программой, может быть использована более быстродействующая структурная реализация арифметических операций. Так же, как и табличные, таблично-алгоритмические КС и КЛ ФП технологически могут быть выполнены в виде процессоров обработки сигналов (ПОС) или программируемых логических интегральных схем (ПЛИС).

Для микропроцессорной реализации синусное и косинусное преобразования модулирующего напряжения запишем в виде:

$$\text{y(t)}=\text{sinx(t)}\text{, z(t)}=\text{cosx(t)}\text{, (67)}$$

где x(t) - входной сигнал, а y(t) и z(t) - соответственно выходные сигналы синусного и косинусного функциональных преобразователей.

В дискретной форме такого рода преобразования имеют вид:

$$\text{y(n)}=\text{sinx(n)}\text{, z(n)}=\text{cosx(n)}\text{, (68)}$$

где x(n), y(n)и z(n) соответственно входной и выходные отсчеты функциональных преобразователей, удовлетворяющие требованиям теоремы отсчетов Котельникова [Котельников В.А. Теория потенциальной помехоустойчивости. - М.-Л.: Госэнергоиздат, 1956].

Сравним аналитический, табличный и таблично-алгоритмический методы реализации функциональных преобразователей с точки зрения обеспечиваемой ими точности вычисления функций синуса и косинуса модулирующего напряжения. При аналитическом методе преобразования используется разложение в ряд функций:

$$\begin{array}{l}\sin \left[x(n)\right]=x(n)-\frac{x{(n)}^3}{3!}+\frac{x{(n)}^5}{5!}-\frac{x{(n)}^7}{7!}+\dots \left(\left|x(n)\right|<\infty \right),\\ \cos \left[x(n)\right]=1-\frac{x{(n)}^2}{2!}+\frac{x{(n)}^4}{4!}-\frac{x{(n)}^6}{6!}+\mathrm{...}\left(\left|x(n)\right|<\infty \right).(69)\end{array}$$

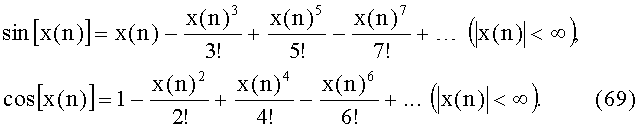
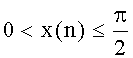
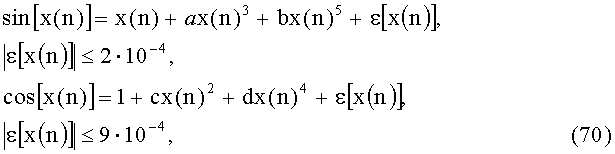
Очевидно, что использование бесконечных рядов, с позиции вычислительных затрат, не представляется возможным, поэтому на практике ограничивают количество членов ряда, аппроксимируя значение выходной величины синусно-косинусного преобразователя многочленами. Для $$0<x(n)\le \frac{\pi }{2}$$

$$$$ $$\begin{array}{l}\sin \left[x(n)\right]=x(n)+ax{(}^n+bx{(}^n+\epsilon \left[x\left(n\right)\right],\\ \left|\epsilon \left[x\left(n\right)\right]\right|\le 2\cdot {10}^{-4},\\ \cos \left[x(n)\right]=1+cx{(}^n+dx{(}^n+\epsilon \left[x\left(n\right)\right],\\ \left|\epsilon \left[x\left(n\right)\right]\right|\le 9\cdot {10}^{-4},\text{ (70)}\end{array}$$

где a=-0,16605, b=0,00761, c=-0,49670, d=0,03705.

Ошибка при n-битном представлении отсчетов x(n), выраженная в единицах младшего разряда, может быть найдена в соответствии с формулой

$$\delta =\epsilon \left[x\left(n\right)\right]\cdot 2^n,(71)$$

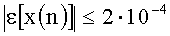
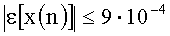
то есть при 8-битном представлении (n=8) отсчетов x(n) ошибка вычисления y(n) и z(n) не будет превышать 0,0512-х младшего разряда (одной двадцатой младшего разряда для $$\left|\epsilon \left[x\left(n\right)\right]\right|\le 2\cdot {10}^{-4}$$ ) и 0,2304-х младшего разряда (одной пятой младшего разряда для $$\left|\epsilon \left[x\left(n\right)\right]\right|\le 9\cdot {10}^{-4}$$ ).

Произведем оценку составляющих ошибок кусочно-линейной интерполяции для таблично-алгоритмического метода непосредственно в единицах младшего разряда цифрового кода отсчета x(n). Структура вычислений при кусочно-линейном методе представлена на рис.12.

Если входной параллельный код отсчета x(n) задан в виде выражения:

$$x(n)={\displaystyle \sum _{m=1}^{n}x(n)\cdot 2^{-m}}\text{ (72)}$$

и проведено разделение старших и младших разрядов на группы:

$$x{(n)}_{ст}={\displaystyle \sum _{m=1}^{g}x(n)\cdot 2^{-m}}\text{ и }x{(n)}_{мл}={\displaystyle \sum _{m=g+1}^{n}x(n)\cdot 2^{-m}},\text{ (73)}$$

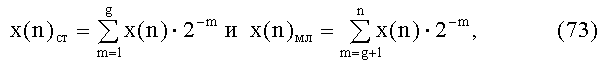
то формулу для аппроксимации функции sin x(n) между двумя соседними узлами аппроксимации можно записать в виде:

$$\sin \left[x{(n)}_{ст}+x{(n)}_{мл}\right]=\sin x{(n)}_{ст}+K_{i}x{(n)}_{мл},\text{ (74)}$$

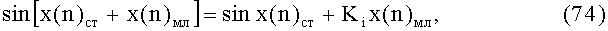
где K_i - скорость нарастания функции синуса или косинуса между двумя узлами аппроксимации, определяемая разрядами аргумента x(n)_ст.

Для упрощения структуры вычислений во всем диапазоне L изменений значений функций sinx(n) и cosx(n), будем брать равные кратные степени двойки интервалы между узлами аппроксимации. Длина интервала интерполяции l в этом случае будет равна:

$$l=\frac{L}{2^g},\text{ (75)}$$

где 2^g - число интервалов интерполяции.

Максимальная погрешность вычисления функций sinx(n) и cosx(n) в соответствии с (74):

$$\Delta \sin x(n)=\Delta \sin x{(n)}_{ст}+\Delta K_{i}x{(n)}_{мл}+{\Delta }_{умн}+\delta +{\Delta }_{окр}.\text{ (76)}$$

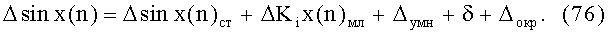
Здесь Δsinx(n)_ст и ΔK_i - ошибки оцифровки констант в ПЗУ для узлов аппроксимации, а именно функции sinx(n) и K_i, так как число разрядов представления функции конечно.

Если задать код функции sinx(n)_ст в узлах аппроксимации с η дополнительными разрядами и осуществить симметричное округление, то ошибка вычисления будет равна:

$$\Delta \sin x{(n)}_{ст}=\frac{1}{2}\cdot 2^{-(n+r)}.\text{ (77)}$$

Таблицу значений коэффициента K_i для узлов аппроксимации следует строить с учетом полученных значений погрешности функции синуса. Таким образом, эти погрешности, имея разный знак, будут в соответствии с (76) в значительной степени компенсировать друг друга. В дальнейшем будем считать, что ΔK_i=0.

Рассмотрим возможность уменьшения и других составляющих ошибок на примере структуры вычислений приведенной на рис.12, где в соответствии с (75) вычисление функции sinx(n) осуществляется путем задания таблиц опорных значений функции и скорости ее изменения по значениям старших разрядов аргумента в ПЗУ, интерполяции значения приращения функции, определяемого скоростью ее изменения, и младшими разрядами аргумента между опорными точками на выходе умножителя.

Второй сумматор осуществляет сложение суммарного кода текущей погрешности аппроксимации функции между опорными табличными значениями полиномом первого порядка и кодов усечения разрядных сеток операндов, одновременно формируемых в ПЗУ коррекции ошибок со значениями функции sinx(n), которое снимается с выхода умножителя. Если умножитель осуществляет вычисление произведения K_ix(n)_мл с учетом всех значащих цифр, округление при отбрасывании разрядов, вес которых меньше веса разряда 2^-(n+r), является симметричным, то ошибка умножения не будет превышать значения:

$${\Delta }_{умн}\le \frac{1}{2}\cdot 2^{-(n+r)}.\text{ (78)}$$

При отбрасывании r дополнительных разрядов и симметричном округлении значения функции во втором сумматоре:

$${\Delta }_{окр}=\frac{1}{2}{\displaystyle \sum _{l=n+1}^{n+r}{2}^{-l}}=\frac{2^{-n}-2^{-(n+r)}}{2}.\text{ (79)}$$

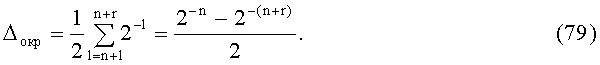
Значение погрешности аппроксимации функции полиномом первого порядка определяется выражением [Смолов В.Б. Функциональные преобразователи информации. - Л.: Энергоиздат. Ленингр. отд-ние, 1981. - 248 с.]:

$$\begin{array}{l}\delta =\frac{1}{2}\left[x(n)-x{(n)}_i\right]\cdot \left[x(n)-x{(n)}_{i+1}\right]\frac{d^2\sin x(n)}{dx{(n)}^2}=\\ =\frac{1}{2}\left[x(n)-x{(n)}_i\right]\cdot \left[x(n)-x{(n)}_{i+1}\right]\cdot \sin x(n),\text{ (80)}\end{array}$$

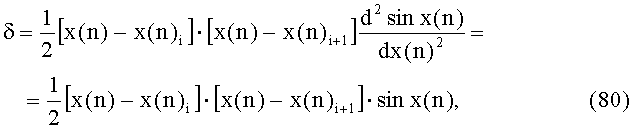
а максимальное значение ошибки аппроксимации (с учетом пересчета в радианную меру угла) не превосходит величины:

$${\delta }_{\max }=\frac{{\pi }^2{(2^{-g})}^2}{32}.\text{ (81)}$$

Алгоритм формирования значения кода коррекции ошибки аппроксимации строится в соответствии с (80), где текущее значение ошибки аппроксимации δ является функцией как старших, так и младших разрядов кода угла x(n). С этой целью, в соответствии с предварительно определенным числом дополнительных разрядов r и максимальным значением ошибки δ_max, вычисленным в соответствии с (81), определим число разрядов представления кода ошибки аппроксимации. По заданному числу выходных разрядов ПЗУ коррекции ошибки задается число первых разрядов из группы x(n)_ст, определяющих код функции sinx(n) в (80), и число первых разрядов из группы x(n)_мл, определяющих приращение аргумента внутри узла аппроксимации в (80). Указанные разряды являются входными для ПЗУ коррекции ошибки. Таким образом, максимальное значение ошибки аппроксимации можно уменьшить до значения:

$${\delta }_{\max }\le \frac{1}{2}\cdot 2^{-(n+r)}.\text{ (82)}$$

Естественно, что при этом в ПЗУ одновременно следует хранить и значение кода, обеспечивающего симметричное округление кода функции sinx(n) при окончательном отбрасывании дополнительных разрядов r во втором сумматоре, то есть, в таблицу кода коррекции, в соответствии с (80), следует добавить значение 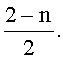$$\frac{2-n}{2}.$$ Окончательно, в соответствии с (77) - (82) для ошибки вычисления получим:

$$\Delta \sin x(n)=2^{-n}\left(2^{-r}+\frac{1}{2}\right).\text{ (83)}$$

При (n+r)=8 ошибка вычисления не будет превышать 0,00195, то есть не будет превышать половины младшего разряда при 8-разрядном представлении чисел на выходе преобразователя. Вычислительная сложность этого алгоритма несколько ниже, чем для аналитического метода, требующего до 20 операций сложения/умножения, и составляет только лишь 6 операций сложения/умножения на один выходной отсчет (фиг.12 представляет структуру вычислений таблично-алгоритмического метода).

В табл.1 сведены численные значения ошибок вычисления входного параллельного кода функции sinx(n) при различных значениях разрядности представления чисел n и количества дополнительных разрядов r. Из таблицы следует, что при увеличении значений n и r ошибка вычисления уменьшается, следовательно, повышается качество выходного сигнала.

Табл.1. Численные значения ошибок вычисления входного параллельного кода функции в зависимости от значений разрядности представления чисел и количества дополнительных разрядов. Значение разрядности представления чисел, n Количество дополнительных разрядов, r Значение ошибки вычисления, Δsinx(n) 8 10 1,957·10^-3 8 12 1,954·10^-3 10 12 4,885·10^-4 10 14 4,883·10^-4 12 14 1,221·10^-4 12 16 1,221·10^-4 14 16 3,052·10^-5 14 18 3,052·10^-5 16 18 7,629·10^-6 16 20 7,629·10^-6

Следует отметить, что при малой разрядности представления входных и выходных отсчетов (равной 8) и не высокой частоте дискретизации (равной 240 кГц), все рассмотренные выше методы обеспечивают достаточно высокую точность вычисления, но искажают форму преобразованного сигнала (фиг.13а, б и фиг.14а, б).

Выходной сигнал имеет ступенчатый характер, обусловленный недостаточно большим числом отсчетов, приходящимся на период. Особенно заметны искажения формы сигнала вблизи нулевых значений амплитуд, а также на высоких частотах и при больших значениях коэффициента k в выражении, определяющем диапазон изменений входной величины x(n)

$$-2\pi k\le x(n)\le 2\pi k.\text{ (84)}$$

Значительно лучшие результаты по качеству представления выходного сигнала (фиг.15а, б и фиг.16а, б) для малой разрядности входных/выходных отсчетов обеспечивает табличный способ преобразования с предварительной фильтрацией входного сигнала x(n) при помощи низкочастотного фильтра. На фиг.17 представлен алгоритм программы реализации синусно-косинусного преобразования, использующий табличный метод и предварительную фильтрацию входного сигнала.

Предлагаемый алгоритм обеспечивает ошибку преобразования, не превосходящую ошибки при таблично-алгоритмическом методе, но при этом, обеспечивает значительно лучшую форму выходного сигнала вблизи нулевых значений амплитуды. Вычислительная сложность предлагаемого метода преобразования несколько выше, чем у таблично-алгоритмического, но значительно ниже, чем у аналитического, и составляет 5 операций сложения/умножения.

Количество сложений/умножений определяется порядком используемого фильтра нижних частот. Качество выходного сигнала преобразователя будет тем выше, чем выше порядок фильтра. Однако, увеличение порядка фильтра влечет за собой неоправданно высокий рост вычислительных затрат.

Для фильтра 1-го порядка, использованного в макете, количество сложений/умножений равно 5, а для фильтра 2-го порядка равно 9, то есть, возрастает почти в 2 раза.

Фильтр НЧ 1-го порядка имеет передаточную характеристику вида

$$H(z)=\frac{b_0+b_1{z}^{-1}}{1+a_1{z}^{-1}}$$

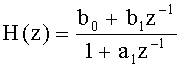
и реализуется при помощи разностного уравнения

$$y(n)=b_{0}x(n)+b_{1}x(n-1)-a_{1}y(n-1)$$ .

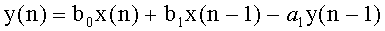
Частотная характеристика фильтра НЧ (использованного в макете), обеспечивающая частоту среза f=10 кГц, приведена на фиг.18.

Значительного увеличения качества сигнала в широкой полосе частот (до 10 кГц) и больших значениях K (до 10) можно достичь повышая частоту дискретизации и разрядность входного сигнала. На фиг.19 приведены результаты моделирования преобразователя для f=10 кГц, K=10 и разрядности входного сигнала, равной 14.

На фиг.20 приведена структурная схема устройства, реализующая 1-й заявленный способ, на которой в известный фазовый модулятор, содержащий последовательно соединенные источник высокочастотного сигнала ИВС, первый балансный модулятор 1-й БМ1 и первый линейный сумматор 1-й С1, выход которого является первым выходом устройства (соответствует 1-му выходу 1-го заявленного способа), последовательно соединенные первый фазовращатель на π/2 1-й ФВ1 и второй балансный модулятор 2-й БМ2, выход которого соединен со вторым входом 1-го С1, а вход 1-го ФВ1 соединен с выходом ИВС, дополнительно введены последовательно соединенные 3-й БМ3 и 2-й С2, выход которого является вторым выходом устройства (соответствует 2-му выходу 1-го заявленного способа), последовательно соединенные 2-й ФВ2 и 4-й БМ4, выход которого соединен со вторым входом 2-го С2, а входы 3-го БМ3 и 2-го ФВ2 соединены с выходом 1-го С1, последовательно соединенные входной буфер, вход которого соединен с выходом источника модулирующего сигнала ИМС, аналого-цифровой преобразователь АЦП и косинусный преобразователь модулирующего напряжения КПМН, состоящий из объединенных соответствующими связями первого шинного формирователя 1-го ШФ1, первого процессора обработки сигналов 1-го ПОС1, первого постоянного запоминающего устройства 1-го ПЗУ1, первого мультиплексора 1-го М1, первого цифроаналогового преобразователя 1-го ЦАП1, первого выходного буфера 1-го ВБ1 и первого фильтра нижних частот 1-го ФНЧ1, выход которого соединен с управляющими входами 1-го БМ1 и 3-го БМ3, последовательно соединенный с АЦП синусный преобразователь модулирующего напряжения СПМН, состоящий из объединенных соответствующими связями второго шинного формирователя 2-го ШФ2, второго процессора обработки сигналов 2-го ПОС2, второго постоянного запоминающего устройства 2-го ПЗУ2, второго мультиплексора 2-го М2, второго цифроаналогового преобразователя 2-го ЦАП2, второго выходного буфера 2-го ВБ2 и второго фильтра нижних частот 2-го ФНЧ2, выход которого соединен с управляющими входами 2-го БМ2 и 4-го БМ4. При этом сигнал с выхода тактового генератора поступает на синхронизирующие входы 1-го ПОС1 и 2-го ПОС2, делится на четыре и выдается на синхронизирующие выходы, выключатели S1.3 и S1.4 подсоединены непосредственно к старшим, а выключатели S1.1 и S1.2 - к младшим адресным шинам 1-го ПЗУ1 и 2-го ПЗУ2.

Работа устройства, выполненного в виде двух однотипных низкочастотных каналов КПМН и СПМН, осуществляется следующим образом. При этом КПМН и СПМН вычисляют, соответственно, функции y(n)=sin(x(n)) и y(n)=cos(x(n)). В каждом канале имеется ПОС, ПЗУ, ЦАП и ВБ. Входные выборки в каналы обработки поступают через ШФ от АЦП. При подаче питания на данное устройство начинает отрабатываться сигнал сброса процессоров, длительность которого составляет около 2,4 мс. Для ПОС достаточно, чтобы импульс сброса находился в активном состоянии в течение пяти циклов (один цикл 200 нс).

Процессоры работают от одного тактового генератора на частоте 20 МГц. Сигнал с выхода тактового генератора поступает на вход CLKIN процессоров. Внутри процессоров эта частота делится на четыре и выдается на вывод CLKOUT. Все команды в процессорах выполняются по положительному фронту сигнала CLKOUT. Для нормирования выходного сигнала ИМС (от 0 В до 2 В) на входе АЦП в схему введен дополнительный входной буфер, который выдает сигнал относительно эталонного входа VREF/2. АЦП работает с частотой преобразования 5 МГц (CLKOUT), то есть данные на выходе АЦП меняются через каждые 200 нс синхронно с началом каждого цикла работы процессоров. Следовательно, каждый процессор может считывать данные из АЦП в любом цикле своей работы.

После выполнения преобразований процессор записывает данные в ЦАП, который имеет внутренний регистр хранения данных. По фронту сигнала на выводе CLK происходит запись данных в ЦАП. Изменение положения выключателя S1 приводит к изменению выходного диапазона (табл.2).

Выключатель S1 определяет, с какой областью ПЗУ работает процессор. Выключатели S1.3 и S1.4 подсоединены непосредственно к старшим адресным линиям ПЗУ, при этом в целом, ПЗУ разделено на четыре независимых блока по 512 байт. Выключатели S1.1 и S1.2 к адресной шине ПЗУ подключены только тогда, когда процессор обращается к младшим 256-ти байтам. Такое подключение обеспечивает мультиплексор М. В результате, получается, что младшие 256 байт каждого из четырех блоков по 512 байт также разделены на четыре части, а в старших байтах находятся таблицы синуса или косинуса. Следовательно, реализуются 16 блоков по 64 байта и 4 блока по 256 байт (табл.3).

В каждой из 16-ти частей находятся разные программы, и в зависимости от положения выключателя S1, процессор выполняет действия по одной из этих программ. Разбиение ПЗУ предложенным способом выполнено для уменьшения времени выполнения основного цикла программы, так как из него (цикла), исключаются действия связанные с опросом положения выключателя S1. Например, выключатель находится в положении S1.1-, S1.2+, S1.3+, S1.4-, тогда после сброса процессора на его адресной шине выставится адрес 0000Н, а на адресной шине ПЗУ будет адрес 0280H (в табл.3 эта область указана цифрой 6).

Табл.2. Положения выключателей, определяющих изменение выходного диапазона.   Положение выключателей* S1.1 S1.2 S1.3 S1.4 Без преобразования - - - - π + - - - 2π - + - - 3π + + - - 4π - - + - 5π + - + - 6π - + + - 7π + + + - 8π - - - + 9π + - - + 10π - + - + Примечание (положение выключателей*): «+» - выключатель находится во включенном положении; «-» - выключатель находится в выключенном положении.

На фиг.21а, б показаны осциллограммы (вверху) и спектрограммы (внизу) сигналов на выходах микропроцессорных синусного (фиг.21а) и косинусного (фиг.21б) ФПМН. Для исследования выбраны следующие измерительные параметры: частота входного модулирующего сигнала f=1 кГц; разрядность входного сигнала n=8; положения выключателя S1: S1.1-, S1.2+, S1.3-, S1.4+; индекс модуляции m_φ=10π; частота дискретизации f_д=5 МГц; температура 25°C.

Анализ рисунков показывает, что формы выходных сигналов микропроцессорных синусного и косинусного преобразователей модулирующего напряжения совпадают с теоретическими. Спектральные составляющие для синусного преобразователя находятся на нечетных частотах от 1 кГц до 39 кГц, а для косинусного преобразователя - на четных частотах от 2 кГц до 40 кГц. Количество спектральных составляющих, как для СП, так и для КП составляет N=20, а их амплитуды, с точностью до 1%, совпадают с теоретическими, при этом в выходных спектрах не наблюдаются паразитные комбинационные составляющие. Также является очевидным, что временные формы выходных сигналов имеют сглаженный вид с не явно выраженным «ступенчатым» характером, что объясняется проявлением шумов квантования в результате работы цифровых устройств обработки и не высоким порядком выходных ФНЧ.

Далее, полученные структуры модулирующих напряжений е_КП и е_СП подают на управляющие входы, соответственно, 1-го БМ1, 3-го БМ3 и 2-го БМ2, 4-го БМ4 векторных модуляторов 1-го ВМ1 и 2-го ВМ2, в которых выполняются преобразования по алгоритмам (1)-(5) и (17)-(20). В результате, на выходах 1-го С1 и 2-го С2 формируются ФМС с индексами модуляции, соответственно, m=10π и m=20π.

На фиг.22 показана осциллограмма ФМС на выходе 1-го С1, на которой прослеживается линейный закон изменения фазового угла, соответствующий заданному значению индекса модуляции m=10π, и наблюдается постоянная огибающая ФМС, что свидетельствует об отсутствии в нем как ПФМ, так и ПАМ. На фиг.23 показана спектрограмма ФМС на выходе 1-го С1. Из анализа фиг.23 следует, что практическая ширина полосы частот, занимаемая ФМС, составляет 76 кГц, при частоте модулирующего напряжения 1 кГц. Учитывая составляющие спектра с амплитудами не менее 1% от амплитуды немодулированного сигнала, видно практически полное совпадение с теоретически рассчитанным спектром ФМС с индексом модуляции m=10π. Симметричная относительно несущей частоты форма спектра, а также отсутствие в спектре комбинационных составляющих, свидетельствуют о высокой точности формирования ФМС предложенным методом. Полученные экспериментальные результаты позволяют сделать вывод о том, что цифровой табличный метод с предварительной низкочастотной фильтрацией реализации СКПМН, при кусочно-линейной аппроксимации, является наиболее эффективным с точки зрения технической реализации алгоритмов формирования ФМС с использованием микропроцессорных СКПМН, позволяющих компенсировать амплитудно-фазовые искажения при заданном индексе модуляции m=10π.

На фиг.24 приведена структурная схема устройства, реализующая 2-й заявленный способ, в которую дополнительно введены последовательно соединенные 3-й БМ1-2 и 2-й С1-2, последовательно соединенные 2-й ФВ1-2 и 4-й БМ2-2, выход которого соединен со вторым входом 2-го С1-2, а входы 2-го ФВ1-2 и 3-го БМ1-2 соединены с выходом ИВС, последовательно соединенные 5-й БМ1-3 и 3-й С1-3, последовательно соединенные 3-й ФВ1-3 и 6-й БМ2-3, выход которого соединен со вторым входом 3-го С1-3, а входы 3-го ФВ1-3 и 5-го БМ1-3 соединены с выходом 2-го С1-2, последовательно соединенные 7-й БМ1-4 и 4-й С1-4, последовательно соединенные 4-й ФВ1-4 и 8-й БМ2-4, выход которого соединен со вторым входом 4-го С1-4, а входы 4-го ФВ1-4 и 7-го БМ1-4 соединены с выходом ИВС, последовательно соединенные 9-й БМ1-N и 5-й С1-N, последовательно соединенные 5-й ФВ1-N и 10-й БМ2-N, выход которого соединен со вторым входом 5-го С1-N, а вход 5-го ФВ1-N и высокочастотный вход 9-го БМ1-N могут быть соединены с выходами ИВС, выходами 1-го С1-1, 2-го С1-2, 3-го С1-3 и 4-го С1-4, управляющий вход 9-го БМ1-N может быть соединен с выходом КПМН, а также с косинусными выходами 1-го УАФ1, 2-го УАФ2 и 3-го УАФ N, управляющий вход 10-го БМ2-N может быть соединен с выходом СПМН, а также с синусными выходами 1-го УАФ1, 2-го УАФ2 и 3-го УАФ N, последовательно соединенные первый перемножитель сигналов 1-й ПС1-1 и первый низкочастотный линейный сумматор 1-й ЛС1-1, последовательно соединенные 2-й ПС2-1 и первый инвертор 1-й ИНВ1-1, выход которого соединен со вторым входом 1-го ЛС1-1, последовательно соединенные 2-й ЛС2-1, 3-й ПС3-1, 4-й ЛС2-2, 6-й ПС3-2, выход которого соединен с управляющим входом 8-го БМ2-4, объединенными первым и вторым входами 8-го ПС2-N и объединенными первым и вторым входами 6-го ЛС2-N, последовательно соединенные 4-й ПС1-2 и 3-й ЛС1-2, выход которого соединен с управляющим входом 7-го БМ1-4, объединенными первым и вторым входами 7-го ПС1-N и вторым входом 9-го ПС3-N, последовательно соединенные 5-й ПС2-2 и 2-й ИНВ1-2, выход которого соединен со вторым входом 3-го ЛС1-2, последовательно соединенные 7-й ПС1-N и 5-й ЛС1-N, выход которого может быть соединен с управляющим входом 9-го БМ1-N, последовательно соединенные 8-й ПС2-N и 3-й ИНВ1-N, выход которого соединен со вторым входом 5-го ЛС1-N, последовательно соединенные 6-й ЛС2-N и 9-й ПС3-N, выход которого может быть соединен с управляющим входом 10-го БМ2-N, при этом выход 1-го ЛС1-1 соединен с объединенными первым и вторым входами 4-го ПС1-2, вторым входом 6-го ПС3-2 и управляющим входом 3-го БМ1-2, выход 3-го ПС3-1 соединен с объединенными первым и вторым входами 4-го ЛС2-2, объединенными первым и вторым входами 5-го ПС2-2 и с управляющим входом 4-го БМ2-2, выход КПМН соединен с объединенными первым и вторым входами 1-го ПС1-1, вторым входом 3-го ПС3-1, управляющими входами 1-го БМ1-1 и 5-го БМ1-3, выход СПМН соединен с объединенными первым и вторым входами 2-го ПС2-1, объединенными первым и вторым входами 2-го ЛС2-1, управляющими входами 2-го БМ2-1 и 6-го БМ2-3. Причем 1-й ФВ1-1, 1-й БМ1-1, 2-й БМ2-1 и 1-й С1-1 составляют первый векторный модулятор 1-й ВМ1, 2-й ФВ1-2, 3-й БМ1-2, 4-й БМ2-2 и 2-й С1-2 составляют второй векторный модулятор 2-й ВМ2, 3-й ФВ1-3, 5-й БМ1-3, 6-й БМ2-3 и 3-й С1-3 составляют третий векторный модулятор 3-й ВМ3, 4-й ФВ1-4, 7-й БМ1-4, 8-й БМ2-4 и 4-й С1-4 составляют четвертый векторный модулятор 4-й ВМ4, 5-й ФВ1-N, 9-й БМ1-N, 10-й БМ2-N и 5-й С1-N составляют пятый векторный модулятор 5-й ВМ N, 1-й ПС1-1, 2-й ПС2-1, 3-й ПС3-1, 1-й ЛС1-1, 2-й ЛС2-1 и 1-й ИНВ1-1 составляют первый удвоитель аргументов функций 1-й УАФ1, 4-й ПС1-2, 5-й ПС2-2, 6-й ПС3-2, 3-й ЛС1-2, 4-й ЛС2-2 и 2-й ИНВ1-2, составляют второй удвоитель аргументов функций 2-й УАФ2, 7-й ПС1-N, 8-й ПС2-N, 9-й ПС3-N, 5-й ЛС1-N, 6-й ЛС2-N и 3-й ИНВ1-N составляют 3-й удвоитель аргументов функций 3-й УАФN, выходы 1-го ЛС1-1, 3-го ЛС1-2 и 5-го ЛС1-N являются косинусными выходами, соответственно, 1-го УАФ1, 2-го УАФ2 и 3-го УАФN, выходы 3-го ПС3-1, 6-го ПС3-2 и 9-го ПС3-N являются синусными выходами, соответственно, 1-го УАФ1, 2-го УАФ2 и 3-го УАФN, а выходы 1-го С1-1 - 4-го С1-4 и 5-го С1-N являются, соответственно, 1-4-ми и 5-м выходами устройства, соответствующие выходам 2-го заявленного способа.

Работа устройства осуществляется следующим образом.

На выходе ФПМН, в соответствии с выражениями e_k=E_ycos[m_φsinΩt] и e_c=E_ysin[m_φsinΩt], при управляющем напряжении E_y=1, формируются сигналы

$${\text{e}}_{\text{КП}}=\text{cos}\left[{\text{m}}_{\phi }\text{sin}\Omega \text{t}\right],(85)$$

$${\text{e}}_{\text{СП}}=\sin \left[{\text{m}}_{\phi }\text{sin}\Omega \text{t}\right],(86)$$

которые поступают на управляющие входы соответственно 1-го БМ1-1, 5-го БМ1-3 и 2-го БМ2-1, 6-го БМ2-3, а также на 1-й УАФ 1, в котором последовательно выполняются следующие алгоритмы преобразований:

$${\text{e}}_{\text{ПС1-1}}={\left(\text{cos}\left({\text{m}}_{\varphi }\text{sin}\Omega \text{t}\right)\right)}^2,(87)$$

$${\text{e}}_{\text{ПС2-1}}={\left(\sin \left({\text{m}}_{\varphi }\text{sin}\Omega \text{t}\right)\right)}^2,(88)$$

$${\text{e}}_{\text{ИНВ1-1}}=-{\left(\sin \left({\text{m}}_{\varphi }\text{sin}\Omega \text{t}\right)\right)}^2,(89)$$

$$e_{ЛС1-1}={\left(\cos \left({\text{m}}_{\varphi }\text{sin}\Omega \text{t}\right)\right)}^2-{\left(\sin \left({\text{m}}_{\varphi }\text{sin}\Omega \text{t}\right)\right)}^2=\cos \left(\text{2}\cdot {\text{m}}_{\varphi }\text{sin}\Omega \text{t}\right),(90)$$

$$e_{ЛС2-1}=\sin \left({\text{m}}_{\varphi }\text{sin}\Omega \text{t}\right)+\sin \left({\text{m}}_{\varphi }\text{sin}\Omega \text{t}\right)=2\cdot \sin \left({\text{m}}_{\varphi }\text{sin}\Omega \text{t}\right),(91)$$

$$e_{ПС3-1}=2\cdot \sin \left({\text{m}}_{\varphi }\text{sin}\Omega \text{t}\right)\cdot \cos \left({\text{m}}_{\varphi }\text{sin}\Omega \text{t}\right)=\sin \left(\text{2}\cdot {\text{m}}_{\varphi }\text{sin}\Omega \text{t}\right),(92)$$

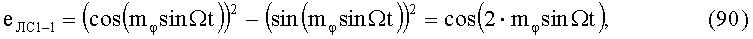
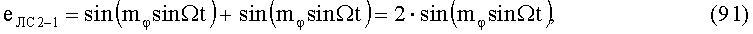
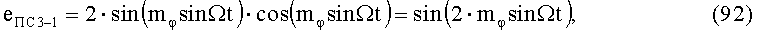
В свою очередь, во 2-м УАФ 2 напряжения (90) и (92) преобразуются по следующим алгоритмам:

$$e_{ЛС1-2}={\left(\cos \left(\text{2}\cdot {\text{m}}_{\varphi }\text{sin}\Omega \text{t}\right)\right)}^2,(93)$$

$$e_{ЛС2-2}={\left(\sin \left(\text{2}\cdot {\text{m}}_{\varphi }\text{sin}\Omega \text{t}\right)\right)}^2,(94)$$

$$e_{ИНВ1-2}=-{\left(\sin \left(\text{2}\cdot {\text{m}}_{\varphi }\text{sin}\Omega \text{t}\right)\right)}^2,(95)$$

$$e_{ЛС1-2}={\left(\cos \left(\text{2}\cdot {\text{m}}_{\varphi }\text{sin}\Omega \text{t}\right)\right)}^2-{\left(\sin \left(\text{2}\cdot {\text{m}}_{\varphi }\text{sin}\Omega \text{t}\right)\right)}^2=\cos \left(\text{4}\cdot {\text{m}}_{\varphi }\text{sin}\Omega \text{t}\right),(96)$$

$$e_{ЛС2-2}=\sin \left(\text{2}\cdot {\text{m}}_{\varphi }\text{sin}\Omega \text{t}\right)+\sin \left(\text{2}\cdot {\text{m}}_{\varphi }\text{sin}\Omega \text{t}\right)=2\cdot \sin \left(\text{2}\cdot {\text{m}}_{\varphi }\text{sin}\Omega \text{t}\right),(97)$$

$$e_{ПС3-2}=\text{2}\cdot \sin \left(\text{2}\cdot {\text{m}}_{\varphi }\text{sin}\Omega \text{t}\right)\cdot \cos \left(\text{2}\cdot {\text{m}}_{\varphi }\text{sin}\Omega \text{t}\right)=\sin \left(\text{4}\cdot {\text{m}}_{\varphi }\text{sin}\Omega \text{t}\right).(98)$$

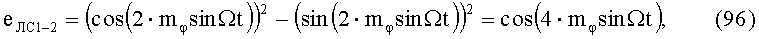
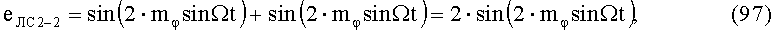
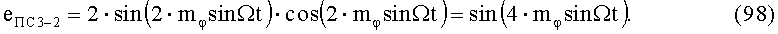
Из (90), (92) и (96), (98) следует, что на выходах 1-го УАФ 1 и 2-го УАФ 2 формируются напряжения функций косинуса и синуса с удвоенными значениями входных аргументов.

На выходе 1-го ВМ1, после перемножения напряжения (85) с u₁=U₁cosωt в 1-м БМ1-1 и напряжения (86) с u_ФВ1-1=-U₁sinωt во 2-м БМ2-1, последующего линейного сложения балансно-модулированных синфазной u_БМ1-1 и квадратурной u_БМ2-1 составляющих в 1-м С1-1, формируется ФМС:

$$\begin{array}{l}{\text{u}}_{\text{c1-1}}={\text{U}}_{\text{1}}{\text{E}}_{\text{y}}[\cos \omega t\cos ({\text{m}}_{\varphi }\text{sin}\Omega \text{t)-sin}\omega {\text{tsin(m}}_{\varphi }\text{sin}\Omega \text{t)}]=\\ ={\text{U}}_{\text{c1-1}}\text{cos(}\omega \text{t}+{\text{m}}_{\varphi }\text{sin}\Omega \text{t)}\text{, (99)}\end{array}$$

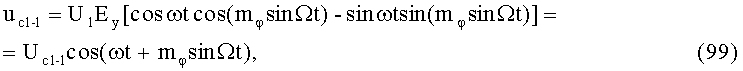
где U_c1-1=U₁E_y - постоянная амплитуда.

На выходе 2-го ВМ 2, после перемножения напряжения (90) с u₁=U₁cosωt в 3-м БМ1-2 и напряжения (92) с u_ФВ1-2=-U₁sinωt в 4-м БМ2-2, последующего линейного сложения балансно-модулированных синфазной u_БМ1-2 и квадратурной u_БМ2-2 составляющих во 2-м С1-2, формируется ФМС:

$$\begin{array}{l}{\text{u}}_{\text{c1-2}}={\text{U}}_{\text{1}}{\text{E}}_{\text{y}}[\cos \omega t\cos (2{\text{m}}_{\varphi }\text{sin}\Omega \text{t)-sin}\omega {\text{tsin(2m}}_{\varphi }\text{sin}\Omega \text{t)}]=\\ ={\text{U}}_{\text{c1-2}}\text{cos(}\omega \text{t}+{\text{2m}}_{\varphi }\text{sin}\Omega \text{t)}\text{, (100)}\end{array}$$

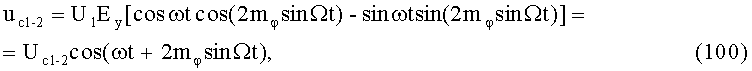
где U_c1-2=U₁E_y - постоянная амплитуда.

На выходе 3-го ВМ 3, после перемножения управляющего напряжения е_КП (85) c u_c1-2=U_c1-2cos(ωt+2m_φsinΩt) в 5-м БМ1-3 и напряжения е_СП (86) с u_ФВ1-3=-U_c1-2sin(ωt+2m_φsinΩt) в 6-м БМ2-3, последующего линейного сложения балансно-модулированных синфазной u_БМ1-3 и квадратурной u_БМ2-3 составляющих в 3-м С1-3, формируется ФМС:

$$\begin{array}{l}{\text{u}}_{\text{c1-3}}={\text{U}}_{\text{c1-2}}{\text{E}}_{\text{y}}[\cos (\omega t+2{\text{m}}_{\varphi }\text{sin}\Omega {\text{t)cos(m}}_{\varphi }\text{sin}\Omega \text{t)- }\\ \text{- sin(}\omega \text{t}+{\text{2m}}_{\varphi }\text{sin}\Omega {\text{t)sin(m}}_{\varphi }\text{sin}\Omega \text{t)]}={\text{U}}_{\text{c1-3}}\cos (\omega t+3{\text{m}}_{\varphi }\text{sin}\Omega \text{t)}\text{, (101)}\end{array}$$

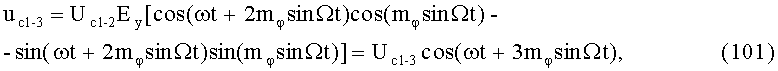
где U_c1-3=U_c1-2E_y - постоянная амплитуда.

На выходе 4-го ВМ 4, после перемножения напряжения 4е_КП (96) c u₁=U₁cosωt в 7-м БМ1-4 и напряжения 4е_СП (98) с u_ФВ1-4=-U₁sinωt в 8-м БМ2-4, последующего линейного сложения балансно-модулированных синфазной u_БМ1-4 и квадратурной u_БМ2-4 составляющих в 4-м С1-4, формируется ФМС:

$$\begin{array}{l}{\text{u}}_{\text{c1-4}}={\text{U}}_{\text{1}}{\text{E}}_{\text{y}}[\cos \omega t\cos (4{\text{m}}_{\varphi }\text{sin}\Omega \text{t)-sin}\omega {\text{tsin(4m}}_{\varphi }\text{sin}\Omega \text{t)}]=\\ ={\text{U}}_{\text{c1-4}}\text{cos(}\omega \text{t}+{\text{4m}}_{\varphi }\text{sin}\Omega \text{t)}\text{, (102)}\end{array}$$

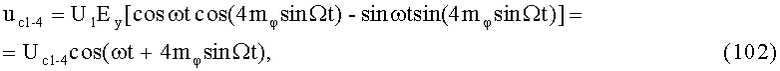
где U_c1-4=U₁E_y - постоянная амплитуда.

Из (99)-(102) следует, что при увеличении порядкового номера векторного модулятора, происходит соответствующее пропорциональное увеличение значений индексов модуляции выходных ФМС: на выходе 2-го ВМ 2 - в два раза, на выходе 3-го ВМ 3 - в три раза, на выходе 4-го ВМ 4 - в четыре раза, относительно начального значения индекса модуляции ФМС, сформированного на выходе 1-го ВМ1.

Таким образом, при увеличении каскадов удвоителей аргументов функций, на выходах векторных модуляторов имеется возможность формирования радиосигналов с угловой модуляцией на первой гармонике колебания несущей частоты с различными значениями индексов модуляции:

$$\begin{array}{l}{\text{u}}_{\text{c1-N}}={\text{U}}_{\text{c1-4}}{\text{E}}_{\text{y}}[\text{cos(}\omega \text{t}+\text{N}\cdot {\text{m}}_{\varphi }\text{sin}\Omega \text{t)cos(N}\cdot {\text{m}}_{\varphi }\text{sin}\Omega \text{t)-}\\ \text{-sin(}\omega \text{t}+\text{N}\cdot {\text{m}}_{\varphi }\text{sin}\Omega \text{t)sin(N}\cdot {\text{m}}_{\varphi }\text{sin}\Omega \text{t)]}={\text{U}}_{\text{c1-N}}\cos (\omega t+N\cdot {\text{m}}_{\varphi }\text{sin}\Omega \text{t)}\text{, (103)}\end{array}$$

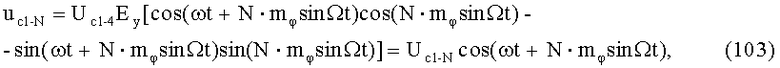
где U_C1-N=U_C1-4E_y - постоянная амплитуда.

Из (103) следует, что в выходных ФМС не проявляется ПАМ и не накапливается ПФМ.

На фиг.25 приведена структурная схема устройства, реализующая 3-й заявленный способ, в которую дополнительно введены последовательно соединенные 9-й БМ3-1 и 5-й С3-1, последовательно соединенные 9-й БМ3-1 и 5-й ФВ3-1, выход которого соединен со вторым входом 5-го С3-1, последовательно соединенные 10-й БМ4-1 и 6-й С4-1, последовательно соединенные 6-й ФВ4-1 и 11-й БМ4-2, выход которого соединен со вторым входом 6-го С4-1, последовательно соединенные 12-й БМ3-2 и 7-й С3-2, последовательно соединенные 12-й БМ3-2 и 7-й ФВ3-2, выход которого соединен со вторым входом 7-го С3-2, последовательно соединенные 13-й БМ4-3 и 8-й С4-2, последовательно соединенные 8-й ФВ4-2 и 14-й БМ4-4, выход которого соединен со вторым входом 8-го С4-2, последовательно соединенные 15-й БМ4-5 и 9-й С4-3, последовательно соединенные 9-й ФВ4-3 и 16-й БМ4-6, выход которого соединен со вторым входом 9-го С4-3, последовательно соединенные 17-й БМ5-1 и 10-й С5-1, последовательно соединенные 10-й ФВ5-1 и первый вход 18-го БМ5-2, последовательно соединенные 11-й ФВ5-2 и второй вход 18-го БМ5-2, выход которого соединен со вторым входом 10-го С5-1, последовательно соединенные 19-й БМ5-3 и 11-й С5-2, последовательно соединенные 12-й ФВ5-3 и 20-й БМ5-4, выход которого соединен со вторым входом 11-го С5-2, последовательно соединенные 21-й БМ5-5 и 12-й С5-3, последовательно соединенные 13-й ФВ5-4 и 22-й БМ5-6, выход которого соединен со вторым входом 12-го С5-3, последовательно соединенные 23-й БМ5-7 и 13-й С5-4, последовательно соединенные 14-й ФВ5-5 и 24-й БМ5-8, выход которого соединен со вторым входом 13-го С5-4, последовательно соединенные 25-й БМ5-9 и 14-й С5-5, последовательно соединенные 15-й ФВ5-6 и 26-й БМ5-10, выход которого соединен со вторым входом 14-го С5-5, при этом объединенные первый и второй входы 9-го БМ3-1 и 17-го БМ5-1, а также вход 10-го ФВ5-1 соединены с выходом ИВС, входы 6-го ФВ4-1, 9-го ФВ4-3 и 11-го ФВ5-2, второй вход 17-го БМ5-1, первые входы 10-го БМ4-1 и 15-го БМ4-5 соединены с выходом 5-го С3-1, объединенные первый и второй входы 13-го БМ3-2 соединены с выходом 1-го С1-1, вход 8-го ФВ4-2 и первый вход 13-го БМ4-3 соединены с выходом 7-го С3-2, входы 12-го ФВ5-3, 13-го ФВ5-4 и 15-го ФВ5-6 и первые входы 19-го БМ5-3, 21-го БМ5-5 и 25-го БМ5-9 соединены с выходом 10-го С5-1, вход 14-го ФВ5-5 и первый вход 23-го БМ5-7 соединены с выходом 12-го С5-3, вторые входы 10-го БМ4-1 и 11-го БМ4-2, 13-го БМ4-3 и 14-го БМ4-4, 19-го БМ5-3 и 20-го БМ5-4, 23-го БМ5-7 и 24-го БМ5-8 соединены с выходами соответственно КПМН и СПМН, вторые входы 15-го БМ4-5 и 16-го БМ4-6, 25-го БМ5-9 и 26-го БМ5-10 соединены с выходами соответственно 2-го УАКФ2 и 2-го УАСФ2, вторые входы 21-го БМ5-5 и 22-го БМ5-6 соединены с выходами, соответственно, 1-го УАКФ1 и 1-го УАСФ1. Причем 9-й БМ3-1, 5-й ФВ3-1 и 5-й С3-1 составляют первый квадратурный умножитель радиосигналов 1-й КУРС1-1, 12-й БМ3-2, 7-й ФВ3-2 и 7-й С3-2 составляют 2-й КУРС1-2, 17-й БМ5-1, 18-й БМ5-2, 10-й ФВ5-1, 11-й ФВ5-2 и 10-й С5-1 составляют 3-й КУРС2-1, 10-й БМ4-1, 11-й БМ4-2, 6-й ФВ4-1 и 6-й С4-1 составляют пятый векторный модулятор 5-й ВМ2-1, 13-й БМ4-3, 14-й БМ4-4, 8-й ФВ4-2 и 8-й С4-2 составляют 6-й ВМ2-2, 15-й БМ4-5, 16-й БМ4-6, 9-й ФВ4-3 и 9-й С4-3 составляют 7-й ВМ2-3, 19-й БМ5-3, 20-й БМ5-4, 12-й ФВ5-3 и 11-й С5-2 составляют 8-й ВМ3-1, 21-й БМ5-5, 22-й БМ5-6, 13-й ФВ5-4 и 12-й С5-3 составляют 9-й ВМ3-2, 23-й БМ5-7, 24-й БМ5-8, 14-й ФВ5-5 и 13-й С5-4 составляют 10-й ВМ3-3, 25-й БМ5-9, 26-й БМ5-10, 15-й ФВ5-6 и 14-й С5-5 составляют 11-й ВМ3-4, а выходы 5-го С3-1, 6-го С4-1, 7-го С3-2, 8-го С4-2, 9-го С4-3, 10-го С5-1, 11-го С5-2, 12-го С5-3, 13-го С5-4 и 14-го С5-5 линейных сумматоров являются соответственно 5 - 14 выходами устройства, соответствующие выходам 3-го заявленного способа.

Работа устройства осуществляется следующим образом.

С целью формирования на выходе 1-го КУРС1-1 второй гармоники колебания несущей частоты, сигнал, описываемый формулой (1), подается на объединенные входы 9-го БМ3-1, в результате на выходе 9-го БМ3-1 имеется напряжение:

$${\text{u}}_{\text{бм3-1}}={\text{U}}_{\text{1}}\text{cos}\omega \text{t}\times {\text{U}}_{\text{1}}\text{cos}\omega \text{t}={{\text{(U}}_{\text{1}}\text{cos}\omega \text{t)}}^{\text{2}}\text{, (104)}$$

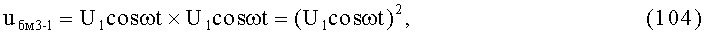
которое поступает на вход 5-го ФВ3-1 и первый вход 5-го С3-1. На выходе 5-го ФВ3-1 формируется квадратурный, относительно (104), сигнал:

$${\text{u}}_{\text{фв3-1}}={{\text{(U}}_{\text{1}}\text{cos}\omega \text{t)}}^{\text{2}}+\pi /\text{2}={\text{-(U}}_{\text{1}}\text{sin}\omega {\text{t)}}^{\text{2}}\text{, (105)}$$

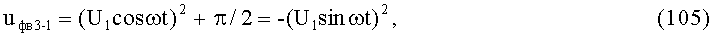
который линейно суммируется с сигналом (104) в 5-м С3-1. В результате на выходе 5-го С3-1 формируется 2-я гармоника колебания несущей частоты:

$${\text{u}}_{\text{c3-1}}={{\text{(U}}_{\text{1}}\text{cos}\omega \text{t)}}^{\text{2}}{\text{-(U}}_{\text{1}}\text{sin}\omega {\text{t)}}^{\text{2}}={\text{U}}_{\text{1}}{}^{\text{2}}\text{cos2}\omega \text{t}\text{, (106)}$$

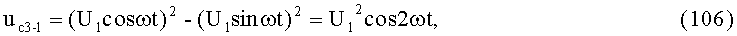
из которой на выходе 6-го ФВ4-1 получают квадратурное колебание вида:

$${\text{u}}_{\text{фв4-1}}={\text{U}}_{\text{1}}{}^{\text{2}}\text{cos2}\omega \text{t}+\pi \text{/2}=-{\text{U}}_{\text{1}}{}^{\text{2}}\text{sin2}\omega \text{t}\text{, (107)}$$

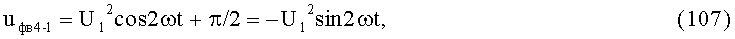
На выходе 5-го ВМ2-1, после перемножения напряжения (85) с (106) в 10-м БМ4-1 и напряжения (86) с (107) в 11-м БМ4-2, последующего линейного сложения балансно-модулированных синфазной u_БМ4-1 и квадратурной u_БМ4-2 составляющих в 6-м С4-1, формируется ФМС:

$$\begin{array}{l}{\text{u}}_{\text{c4-1}}={\text{U}}_{\text{1}}{}^{\text{2}}{\text{E}}_{\text{y}}[\cos 2\omega t\cos ({\text{m}}_{\varphi }\text{sin}\Omega \text{t})-\text{sin2}\omega {\text{tsin(m}}_{\varphi }\text{sin}\Omega \text{t)}]=\\ ={\text{U}}_{\text{c4-1}}\text{cos(2}\omega \text{t}+{\text{m}}_{\varphi }\text{sin}\Omega \text{t)}\text{, (108)}\end{array}$$

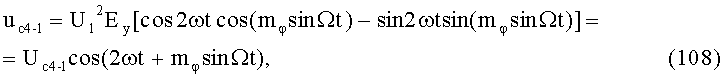
где U_c4-1=U₁ ²E_y - постоянная амплитуда.

Для получения удвоенного значения индекса модуляции на 2-й гармонике колебания несущей частоты, сигнал, описываемый формулой (99), подается на объединенные входы 12-го БМ3-2, в результате на выходе 12-го БМ3-2 имеется напряжение:

$$\begin{array}{l}{\text{u}}_{\text{бм3-2}}={\text{U}}_{\text{c1-1}}\text{cos(}\omega \text{t}+{\text{m}}_{\varphi }\text{sin}\Omega \text{t)}\times {\text{U}}_{\text{c1-1}}\text{cos(}\omega \text{t}+{\text{m}}_{\varphi }\text{sin}\Omega \text{t)}=\\ ={{\text{(U}}_{\text{c1-1}}}^{\text{cos(}}\text{, (109)}\end{array}$$

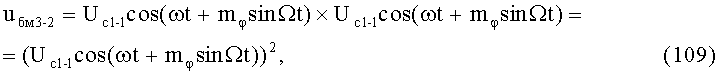
которое поступает на вход 7-го ФВ3-2 и первый вход 7-го С3-2. На выходе 7-го ФВ3-2 формируется квадратурный, относительно (109), сигнал:

$${\text{u}}_{\text{фв3-2}}={{\text{(U}}_{\text{c1-1}}\text{cos(}\omega \text{t}+{\text{m}}_{\varphi }\text{sin}\Omega \text{t))}}^{\text{2}}+\pi \text{/2}=-{{\text{(U}}_{\text{c1-1}}\text{sin(}\omega \text{t}+{\text{m}}_{\varphi }\text{sin}\Omega \text{t))}}^{\text{2}}\text{, (110)}$$

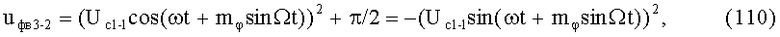
который линейно суммируется с сигналом (109) в С3-2. В результате на выходе 7-го С3-2 формируется ФМС на 2-й гармонике колебания несущей частоты и с удвоенным значением индекса модуляции:

$$\begin{array}{l}{\text{u}}_{\text{с3-2}}={{\text{(U}}_{\text{c1-1}}}^{\text{cos(}}{\text{-(U}}_{\text{c1-1}}\text{sin(}\omega \text{t}+{\text{m}}_{\varphi }\text{sin}\Omega {\text{t))}}^{\text{2}}=\\ ={\text{U}}_{\text{с3-2}}\text{ cos(2}\omega \text{t}+{\text{2m}}_{\varphi }\text{sin}\Omega \text{t)}\text{, (111)}\end{array}$$

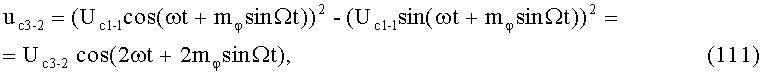
из которого, в свою очередь, на выходе 8-го ФВ4-2 получают квадратурное колебание вида:

$${\text{u}}_{\text{фв4-2}}={\text{U}}_{\text{с3-2}}\text{cos(2}\omega \text{t}+{\text{2m}}_{\varphi }\text{sin}\Omega \text{t)}+\pi \text{/2}=-{\text{U}}_{\text{с3-2}}\text{sin(2}\omega \text{t}+{\text{2m}}_{\varphi }\text{sin}\Omega \text{t)}\text{, (112)}$$

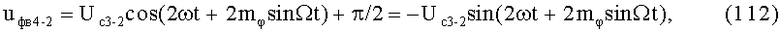
где U_с3-2=U_с1-1 ²E_y - постоянная амплитуда.

На выходе 6-го ВМ2-2, после перемножения напряжения (85) с (111) в 13-м БМ4-3 и напряжения (86) с (112) в 14-м БМ4-4, последующего линейного сложения балансно-модулированных синфазной u_БМ4-3 и квадратурной u_БМ4-4 составляющих в 8-м С4-2, формируется ФМС на 2-й гармонике колебания несущей частоты и с утроенным значением индекса модуляции:

$$\begin{array}{l}{\text{u}}_{\text{c4-2}}={\text{U}}_{\text{с3-2}}{\text{E}}_{\text{y}}[\cos (2\omega t+2{\text{m}}_{\varphi }\text{sin}\Omega {\text{t)cos(m}}_{\varphi }\text{sin}\Omega \text{t)-}\\ \text{-sin(2}\omega \text{t}+{\text{2m}}_{\varphi }\text{sin}\Omega {\text{t)sin(m}}_{\varphi }\text{sin}\Omega \text{t)}]=\\ ={\text{U}}_{\text{c4-2}}\text{cos(2}\omega \text{t}+{\text{3m}}_{\varphi }\text{sin}\Omega \text{t)}\text{, (113)}\end{array}$$

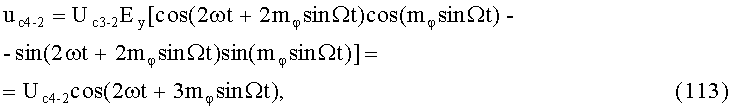
где U_c4-2=U_с3-2E_y - постоянная амплитуда.

На выходе 7-го ВМ2-3, после перемножения напряжения (96) с (106) в 15-м БМ4-5 и напряжения (98) с (107) в 16-м БМ4-6, последующего линейного сложения балансно-модулированных синфазной u_БМ4-5 и квадратурной u_БМ4-6 составляющих в 9-м С4-3, формируется ФМС на 2-й гармонике колебания несущей частоты и со значением индекса модуляции в четыре раза большем, чем в формуле (108):

$$\begin{array}{l}{\text{u}}_{\text{c4-3}}={\text{U}}_{\text{1}}{}^{\text{2}}{\text{E}}_{\text{y}}[\cos 2\omega t\cos (4{\text{m}}_{\varphi }\text{sin}\Omega \text{t)-sin2}\omega {\text{tsin(4m}}_{\varphi }\text{sin}\Omega \text{t)}]=\\ ={\text{U}}_{\text{c4-3}}\text{cos(2}\omega \text{t}+{\text{4m}}_{\varphi }\text{sin}\Omega \text{t)}\text{, (114)}\end{array}$$

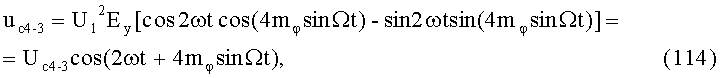
где U_c4-3=U₁ ²E_y - постоянная амплитуда.

С целью формирования на выходе 3-го КУРС2-1 третьей гармоники колебания несущей частоты вначале из сигналов, описываемых формулами (1) и (106), производят их квадратурные колебания (2) с помощью 10-го ФВ5-1 и (107) с помощью 11-го ФВ5-2. Затем, после перемножения напряжения (1) с (106) в 17-м БМ5-1 и напряжения (2) с (107) в 18-м БМ5-2, последующего линейного сложения балансно-модулированных синфазной u_БМ5-1 и квадратурной u_БМ5-2 составляющих в 10-м С5-1, выделяют на выходе 10-го С5-1 третью гармонику колебания несущей частоты:

$${\text{u}}_{\text{c5-1}}={\text{U}}_{\text{1}}{}^{\text{2}}{\text{U}}_{\text{1}}[\cos 2\omega t\cos \omega t-\sin 2\omega t\sin \omega t]=U_1{}^3\cos 3\omega t,(115)$$

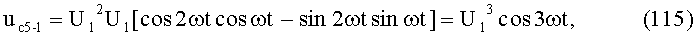
из которой на выходе 12-го ФВ5-3 получают квадратурное колебание вида:

$${\text{u}}_{\text{фв5-3}}={\text{U}}_{\text{1}}{}^{\text{3}}\text{cos3}\omega \text{t}+\pi \text{/2}=-{\text{U}}_{\text{1}}{}^{\text{3}}\text{sin3}\omega \text{t}\text{. (116)}$$

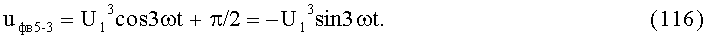
На выходе 8-го ВМ3-1, после перемножения напряжения (85) с (115) в 19-м БМ5-3 и напряжения (86) с (116) в 20-м БМ5-4, последующего линейного сложения балансно-модулированных синфазной u_БМ5-3 и квадратурной u_БМ5-4 составляющих в 11-м С5-2, формируется ФМС на 3-й гармонике колебания несущей частоты:

$$\begin{array}{l}{\text{u}}_{\text{c5-2}}={\text{U}}_{\text{1}}{}^{\text{3}}{\text{E}}_{\text{y}}[\cos 3\omega t\cos ({\text{m}}_{\varphi }\text{sin}\Omega \text{t)-sin3}\omega {\text{tsin(m}}_{\varphi }\text{sin}\Omega \text{t)}]=\\ ={\text{U}}_{\text{c5-2}}\text{cos(3}\omega \text{t}+{\text{m}}_{\varphi }\text{sin}\Omega \text{t)}\text{, (117)}\end{array}$$

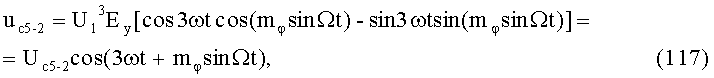
где U_c5-2=U₁ ³E_y - постоянная амплитуда.

На выходе 9-го ВМ3-2, после перемножения напряжения (90) с (115) в 21-м БМ5-5 и напряжения (92) с (116) в 22-м БМ5-6, последующего линейного сложения балансно-модулированных синфазной u_БМ5-5 и квадратурной u_БМ5-6 составляющих в 12-м С5-3, формируется ФМС на 3-й гармонике колебания несущей частоты и с удвоенным значением индекса модуляции:

$$\begin{array}{l}{\text{u}}_{\text{c5-3}}={\text{U}}_{\text{1}}{}^{\text{3}}{\text{E}}_{\text{y}}[\cos 3\omega t\cos (2{\text{m}}_{\varphi }\text{sin}\Omega \text{t)-sin3}\omega {\text{tsin(2m}}_{\varphi }\text{sin}\Omega \text{t)}]=\\ ={\text{U}}_{\text{c5-3}}\text{cos(3}\omega \text{t}+{\text{2m}}_{\varphi }\text{sin}\Omega \text{t)}\text{, (118)}\end{array}$$

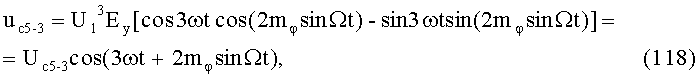
из которого, в свою очередь, на выходе 14-го ФВ5-5 получают квадратурное колебание вида:

$${\text{u}}_{\text{фв5-5}}={\text{U}}_{\text{c5-3}}\text{cos(3}\omega \text{t}+{\text{2m}}_{\varphi }\text{sin}\Omega \text{t)}+\pi /2=-U_{c5-3}\text{sin(3}\omega \text{t}+{\text{2m}}_{\varphi }\text{sin}\Omega \text{t)}\text{, (119)}$$

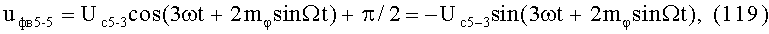
где U_c5-3=U₁ ³E_y - постоянная амплитуда.

На выходе 10-го ВМ3-3, после перемножения напряжения (85) с (118) в 23-м БМ5-7 и напряжения (86) с (119) в 24-м БМ5-8, последующего линейного сложения балансно-модулированных синфазной u_БМ5-7 и квадратурной u_БМ5-8 составляющих в 13-м С5-4, формируется ФМС на 3-й гармонике колебания несущей частоты и с утроенным значением индекса модуляции:

$$\begin{array}{l}{\text{u}}_{\text{c5-4}}={\text{U}}_{\text{c5-3}}{\text{E}}_{\text{y}}[\cos (3\omega t+2{\text{m}}_{\varphi }\text{sin}\Omega {\text{t)cos(m}}_{\varphi }\text{sin}\Omega \text{t)-}\\ \text{-sin(3}\omega \text{t}+{\text{2m}}_{\varphi }\text{sin}\Omega {\text{t)sin(m}}_{\varphi }\text{sin}\Omega \text{t)}]=\\ ={\text{U}}_{\text{c5-4}}\text{cos(3}\omega \text{t}+{\text{2m}}_{\varphi }\text{sin}\Omega \text{t)}\text{, (120)}\end{array}$$

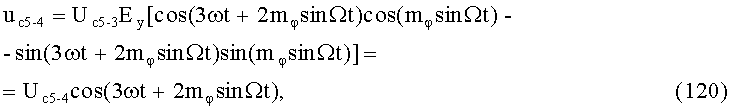
где U_c5-4=U_c5-3E_y - постоянная амплитуда.

На выходе 11-го ВМ3-4, после перемножения напряжения (96) с (115) в 25-м БМ5-9 и напряжения (98) с (116) в 26-м БМ5-10, последующего линейного сложения балансно-модулированных синфазной u_БМ5-9 и квадратурной u_БМ5-10 составляющих в 14-м С5-5, формируется ФМС на 3-й гармонике колебания несущей частоты и со значением индекса модуляции в четыре раза большем, чем в формуле (117):

$$\begin{array}{l}{\text{u}}_{\text{c5-5}}={\text{U}}_{\text{1}}{}^{\text{3}}{\text{E}}_{\text{y}}[\cos 3\omega t\cos (4{\text{m}}_{\varphi }\text{sin}\Omega \text{t)-sin3}\omega {\text{tsin(4m}}_{\varphi }\text{sin}\Omega \text{t)}]=\\ ={\text{U}}_{\text{c5-3}}\text{cos(3}\omega \text{t}+{\text{4m}}_{\varphi }\text{sin}\Omega \text{t)}\text{, (121)}\end{array}$$

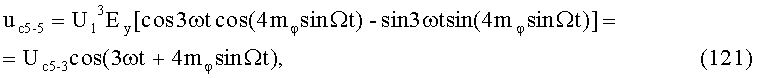
где U_c5-3=U₁ ³E_y - постоянная амплитуда.

При дальнейшем увеличении каскадов КУРС и ВМ, имеется возможность одновременного формирования неискаженных радиосигналов с угловой модуляцией как на первой, так и на последующих гармониках колебания несущей частоты с различными значениями индексов модуляции:

$${\text{u}}_{\text{c1-N}}={\text{U}}_{\text{c1-N}}\text{cos(N}\cdot \omega \text{t}+\text{N}\cdot {\text{m}}_{\varphi }\text{sin}\Omega \text{t)}\text{, (122)}$$

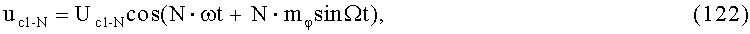
где U_c1-N - постоянная амплитуда.

Элементы заявляемых устройств повышения индекса угловой модуляции могут быть выполнены на следующей электронной компонентной базе: АЦП - на базе быстродействующей 8-разрядной микросхемы AD9280, ПОС - на TMS320C10, ПЗУ - на микросхемах КР556РТ7А, ЦАП - на базе 8-разрядной микросхемы TLC5602CN, схема сброса - на базе микросхемы триггера Шмита КР1533ТЛ2, шинный формирователь - на микросхеме КР1533АП5, мультиплексор - на микросхеме КР1533КП11А, тактовый генератор - на базе микросхем инверторов КР1533ЛН1 и кварцевого резонатора К1-4ДС-20000 кГц, входной и выходной буферы - на операционном усилителе КР140УД608, источник опорного напряжения для ЦАП - на стабилитронах, резисторах и конденсаторах, ВМ - на базе радиочастотных интегральных микросхем, например, HPMX2005 (диапазон рабочих частот от 25 до 250 МГц), AD6122 (от 110 до 220 МГц), HPMX2007 (от 220 до 400 МГц), AD8345 (от 400 до 960 МГц), AD8346 (от 960 до 2000 МГц), AD8343 (до 2500 МГц), симметрирующий высокочастотный трансформатор - на ETC1-1-13, высокочастотные перемножители сигналов - на микросхемах К174ПС1, ПС2, ПС4, низкочастотные перемножители сигналов - на прецизионных микросхемах К525ПС3Б или AD633, линейные сумматоры и инверторы - на операционных усилителях К1401УД2Б или TL084.

Таким образом, реализация и применение заявляемых способов и устройств повышения индекса угловой модуляции позволяет одновременно формировать на первой, второй, третьей и последующих гармониках колебания несущей частоты радиосигналы с угловой модуляцией без принципиальных ограничений по значениям индексов модуляции и при отсутствии в выходных радиосигналах передатчиков ПАМ и ПФМ. Кроме того, выполнение этапов формирования радиосигналов с угловой модуляцией вне кольца импульсно-фазовой автоматической подстройки частоты синтезаторов, позволяет значительно понизить инерционность процессов угловой модуляции, существенно упростить процессы частотообразования в возбудителях передатчиков и повысить быстродействие радиосистем. Указанные достоинства позволяют использовать заявляемые способы и устройства в технике создания преднамеренных радиоэлектронных помех системам радиоуправления взрывными устройствами и системам радиосвязи с псевдослучайной перестройкой радиочастоты.

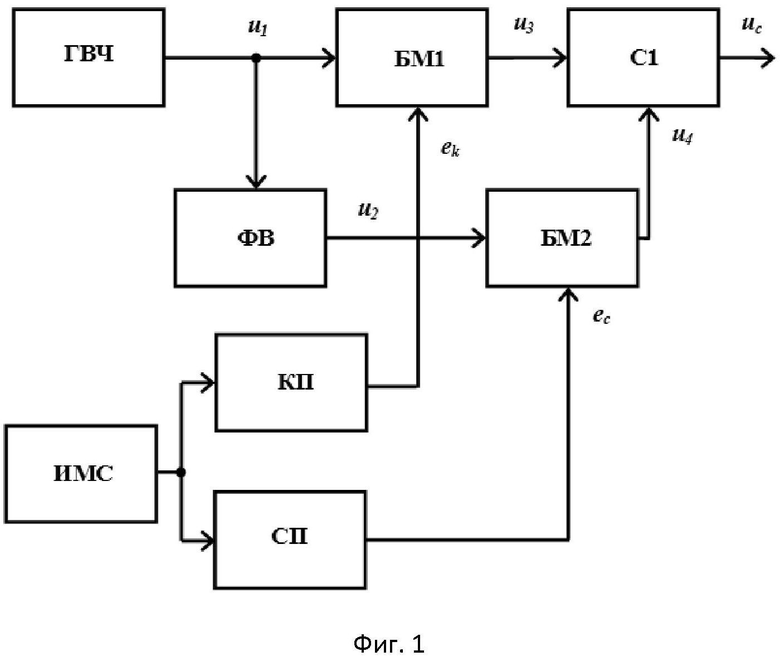
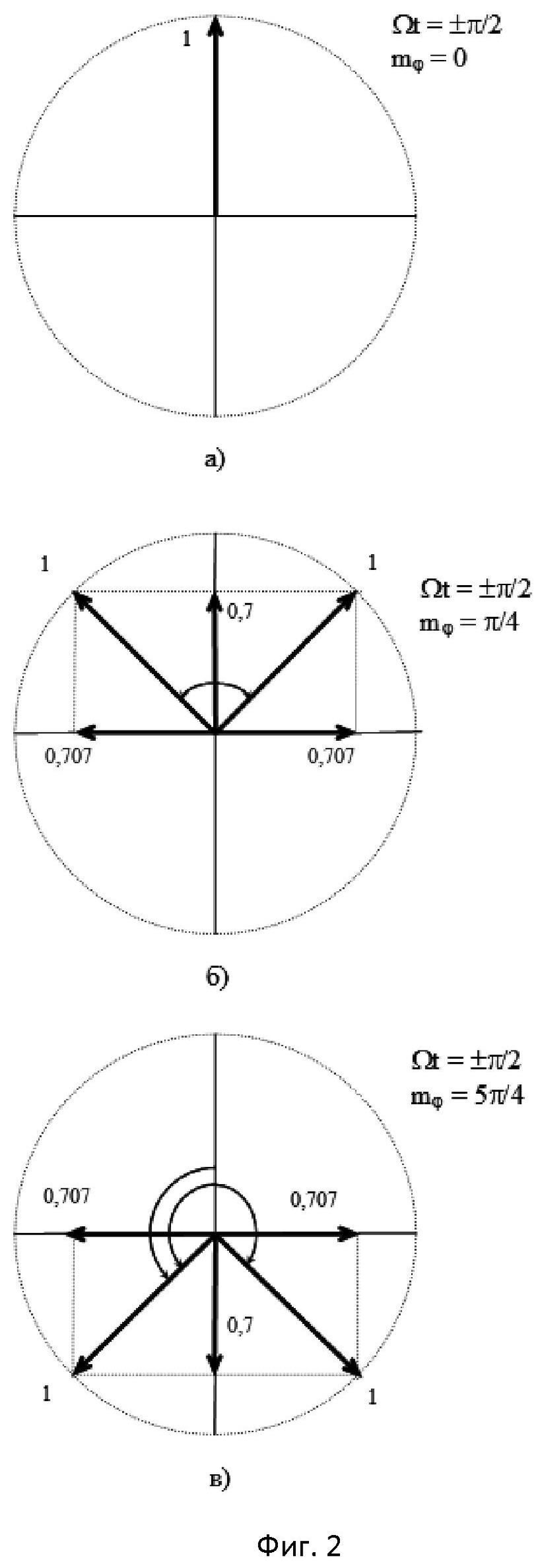
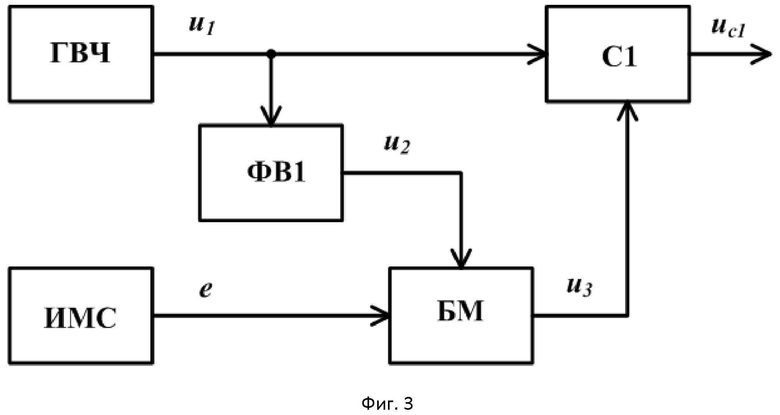
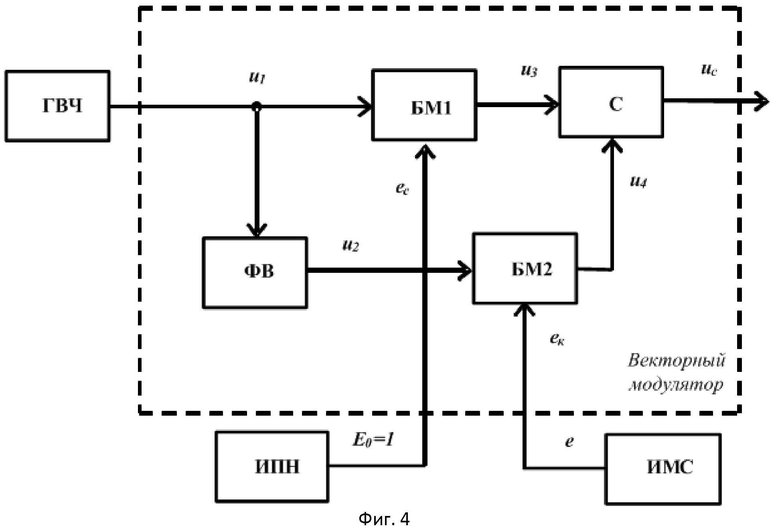
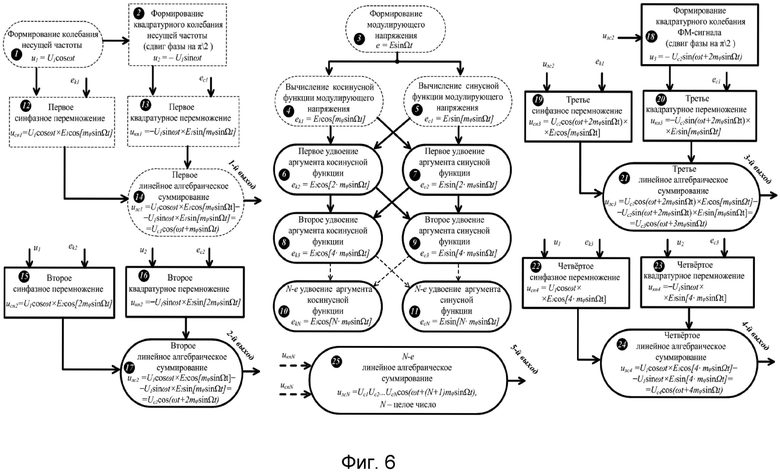
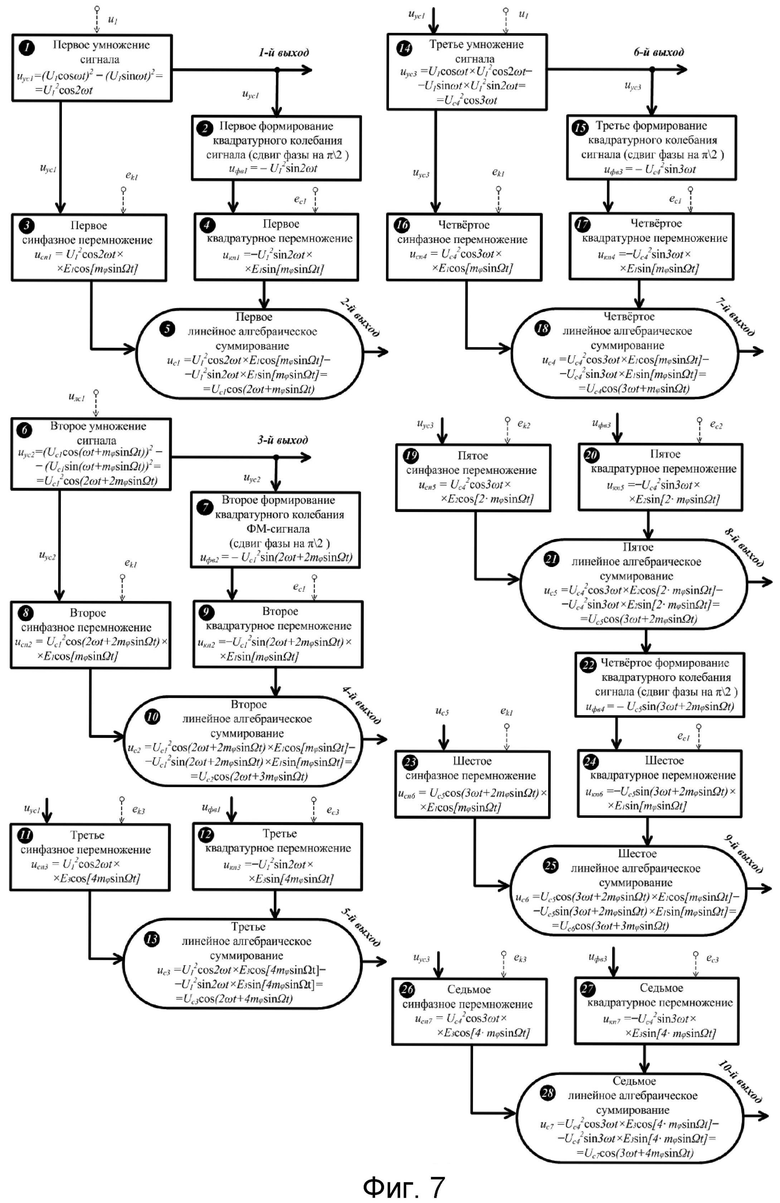
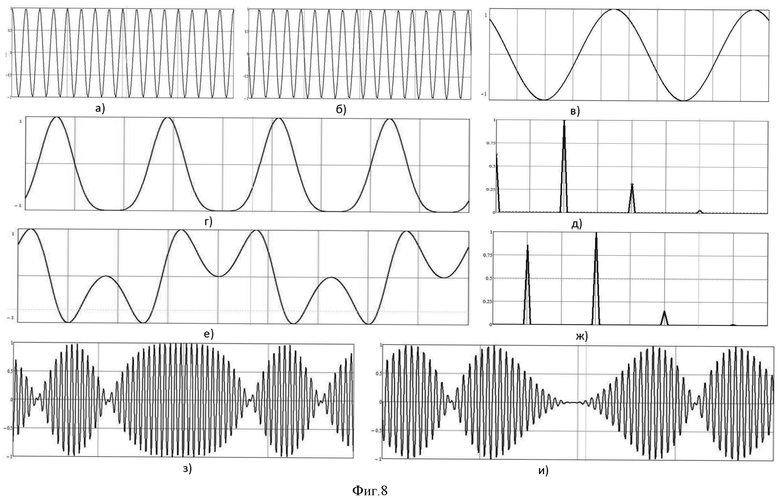
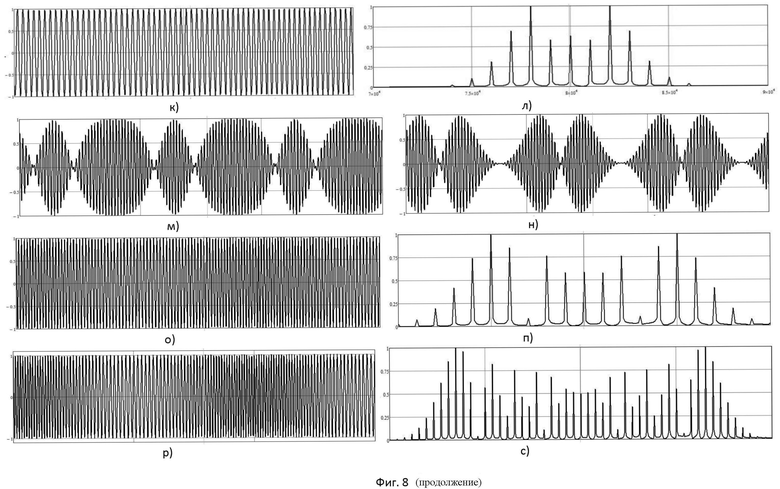
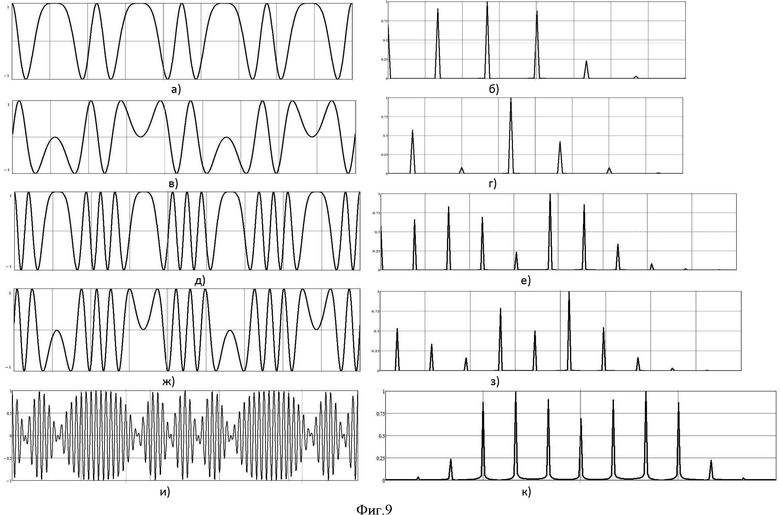
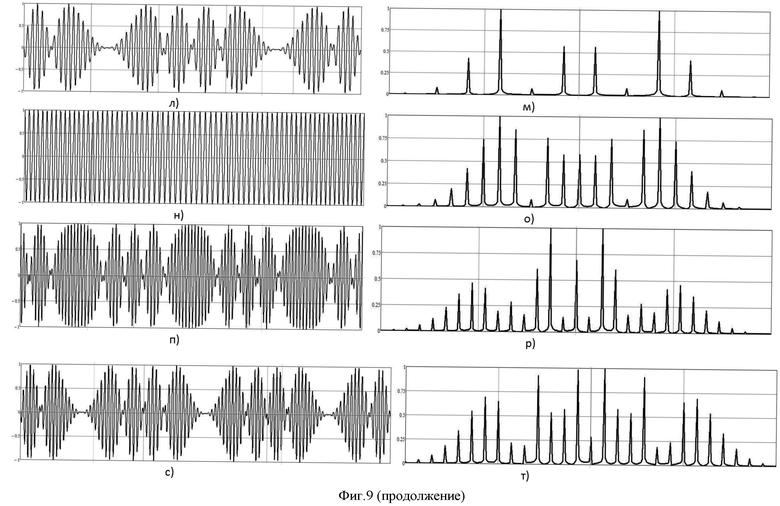
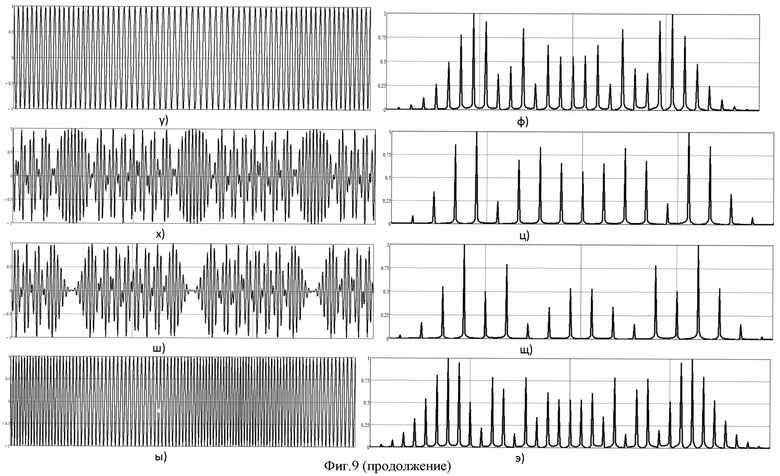
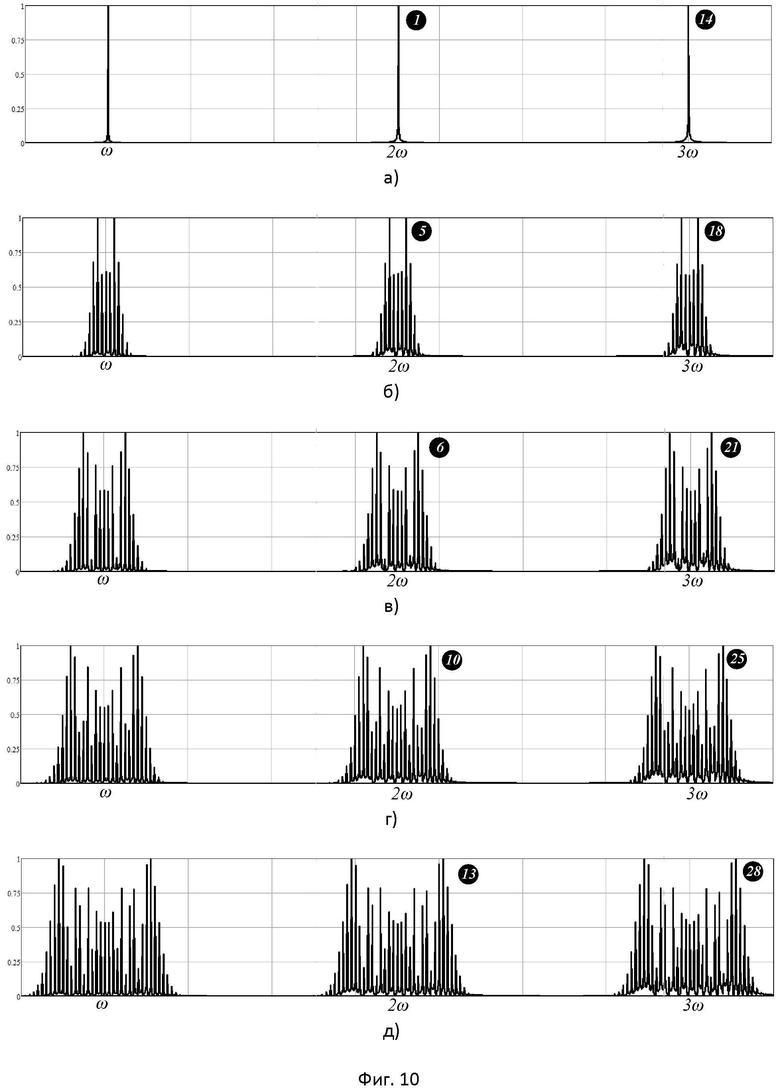
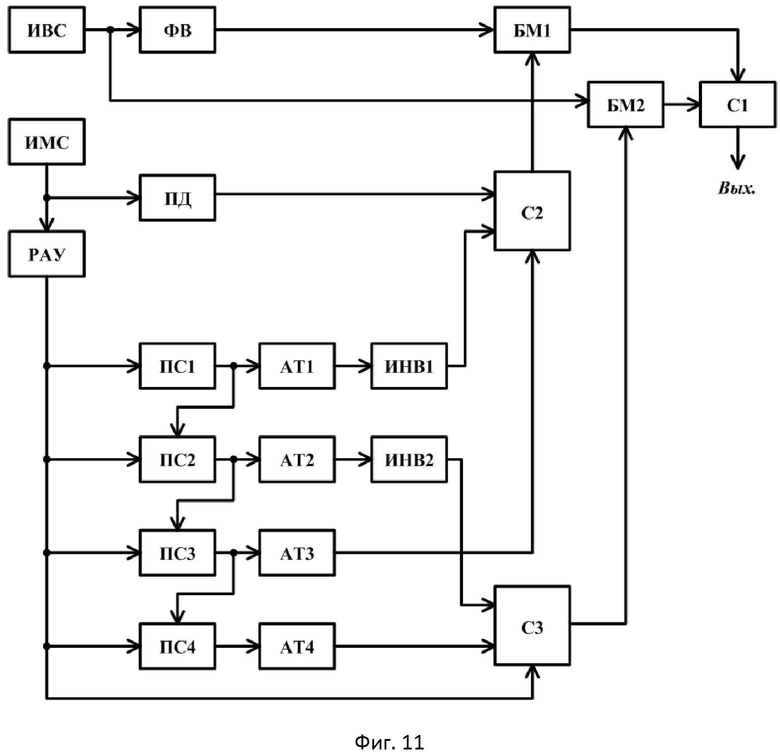
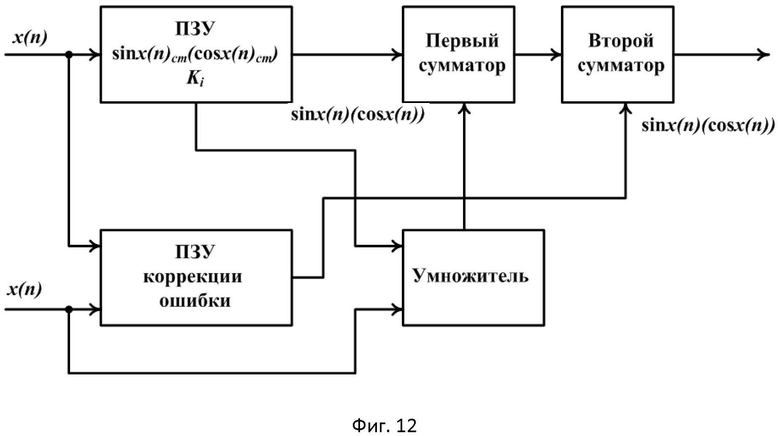
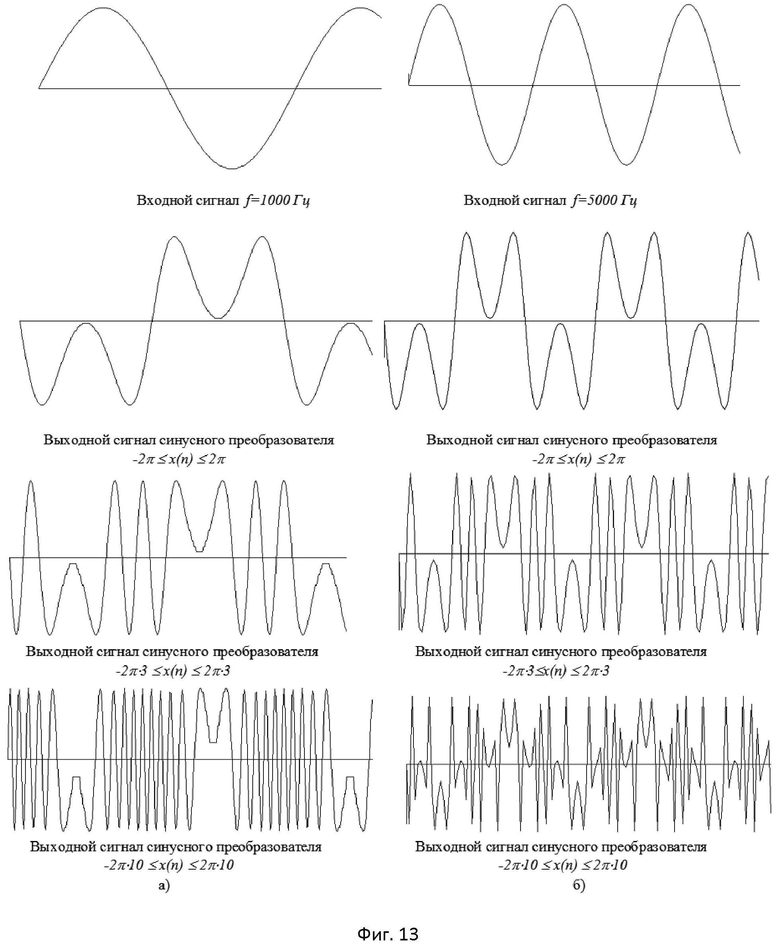
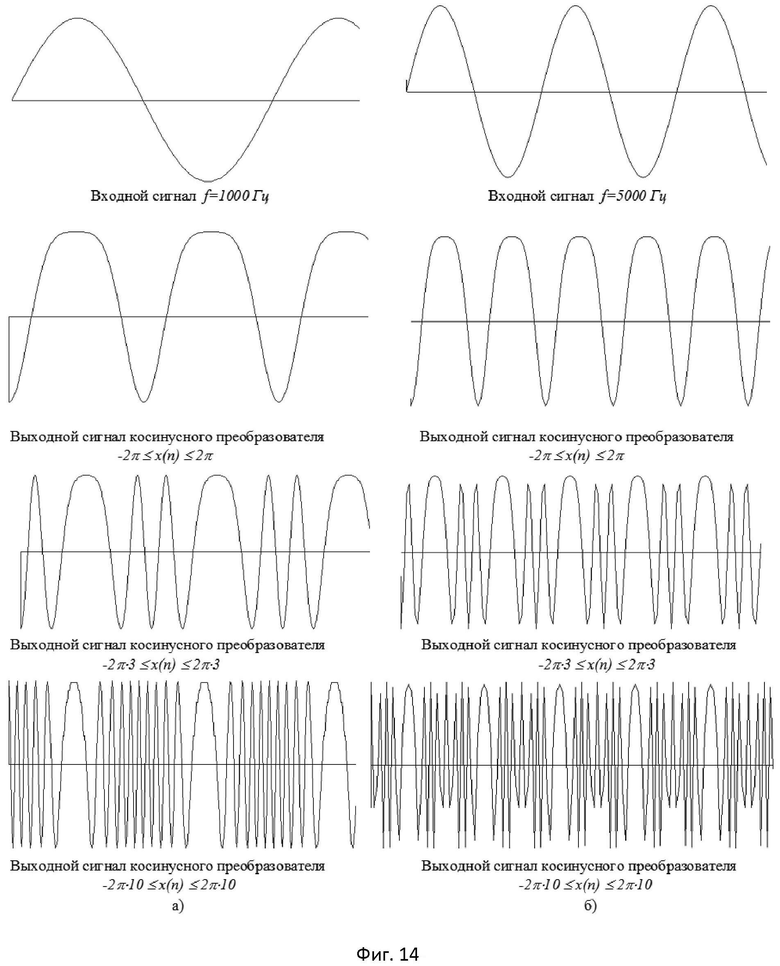
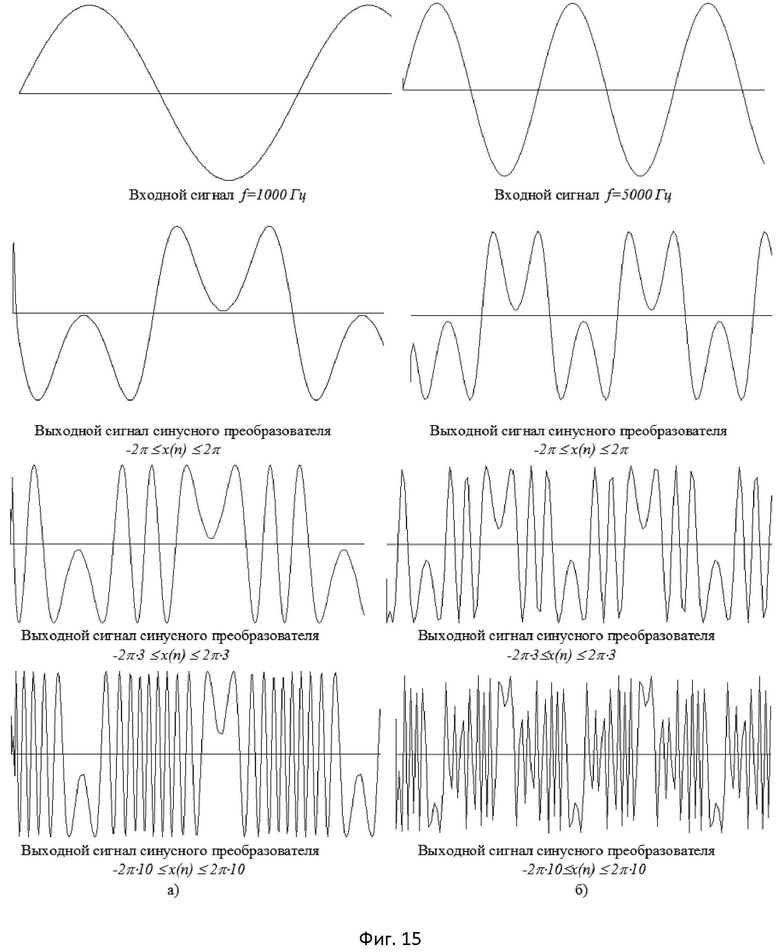
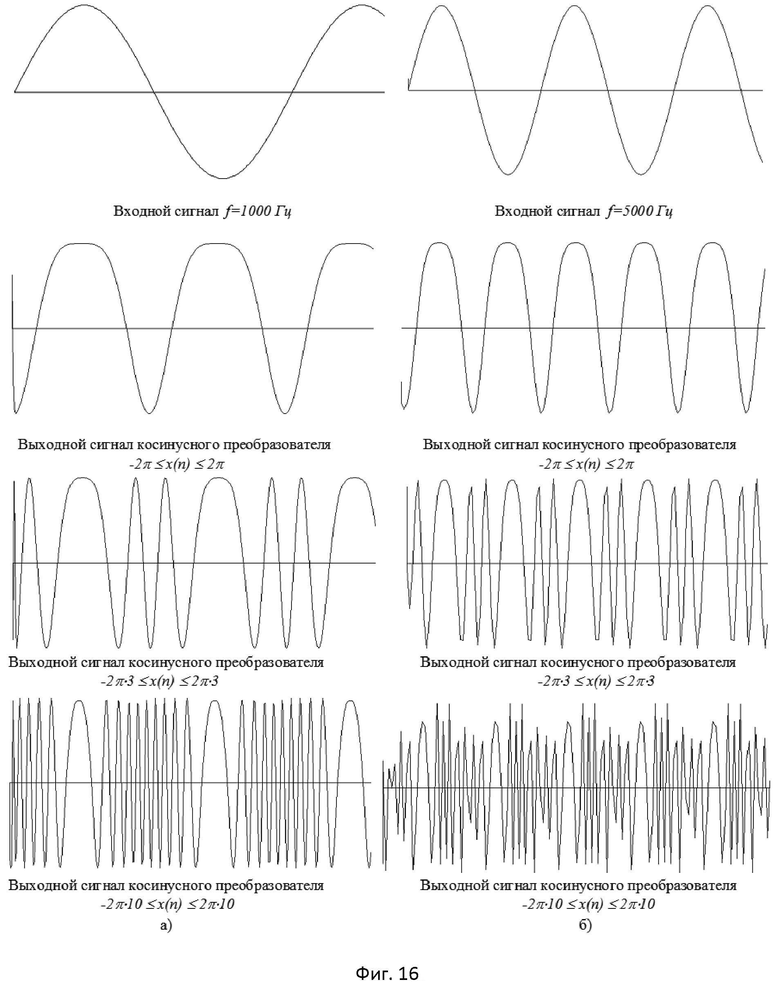
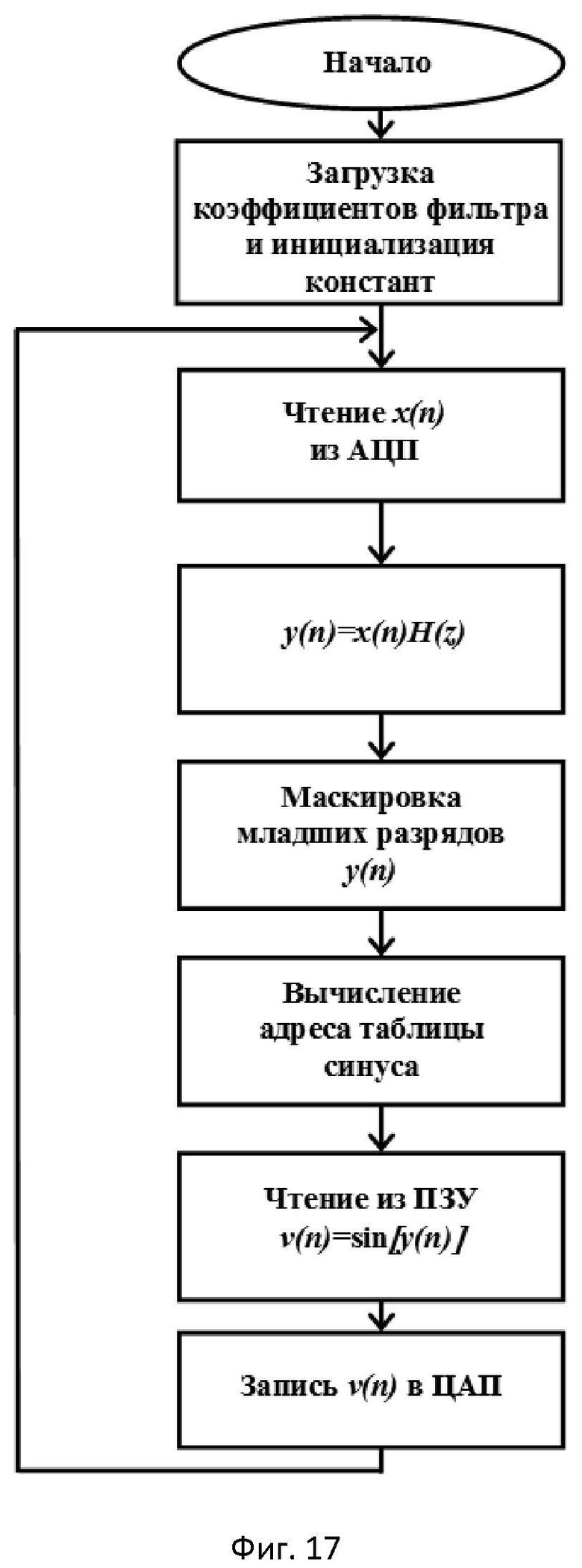
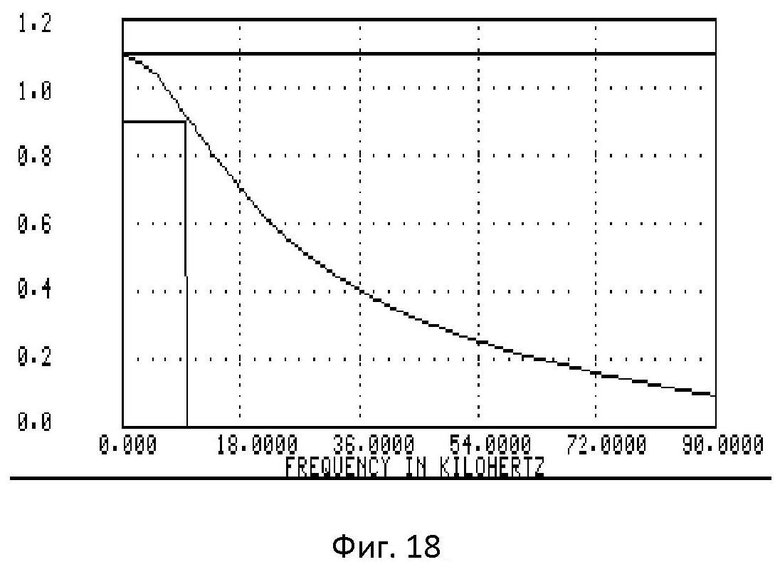
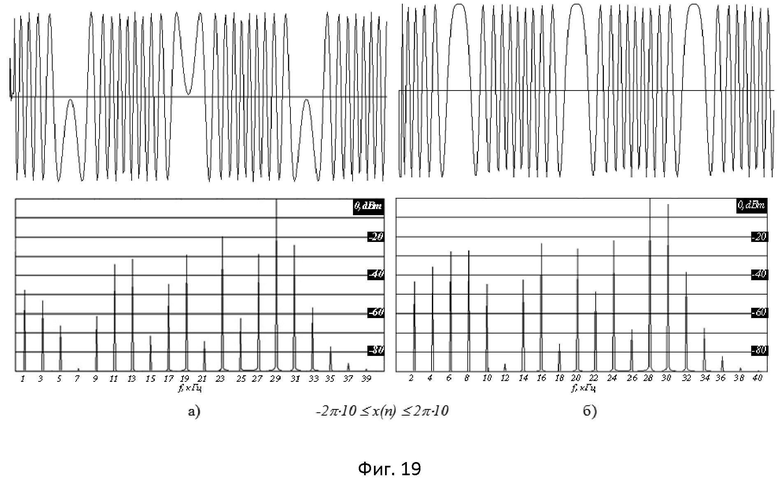
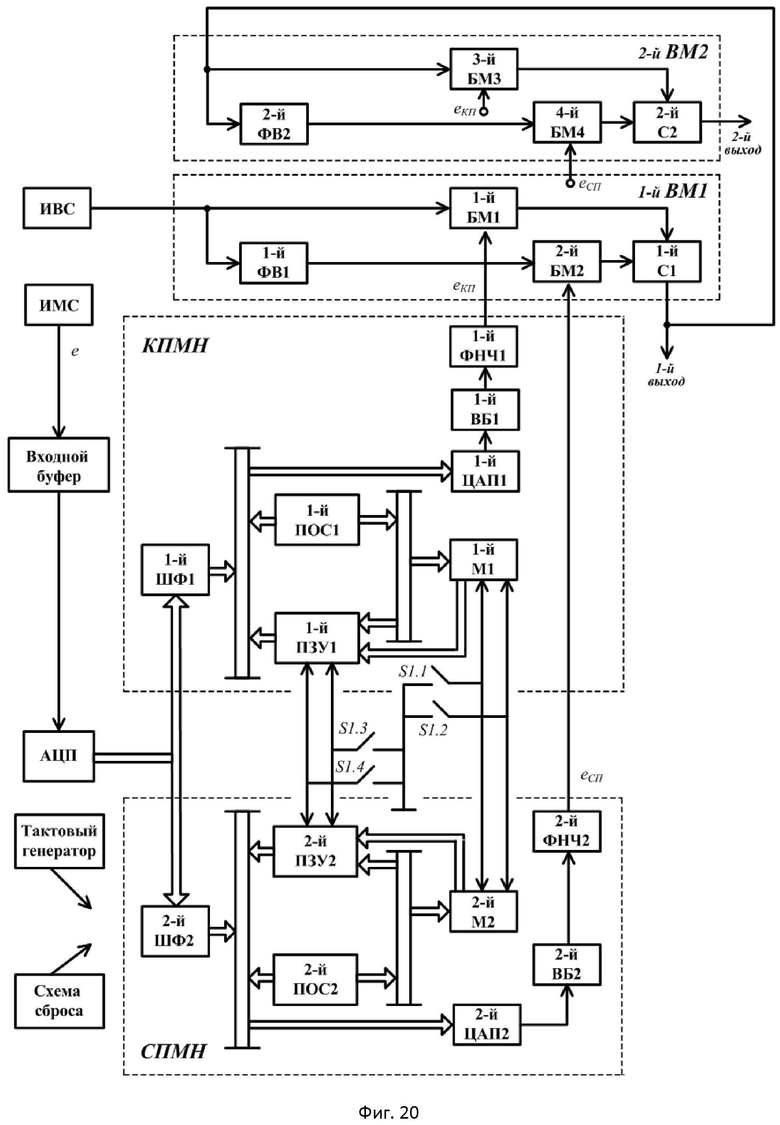
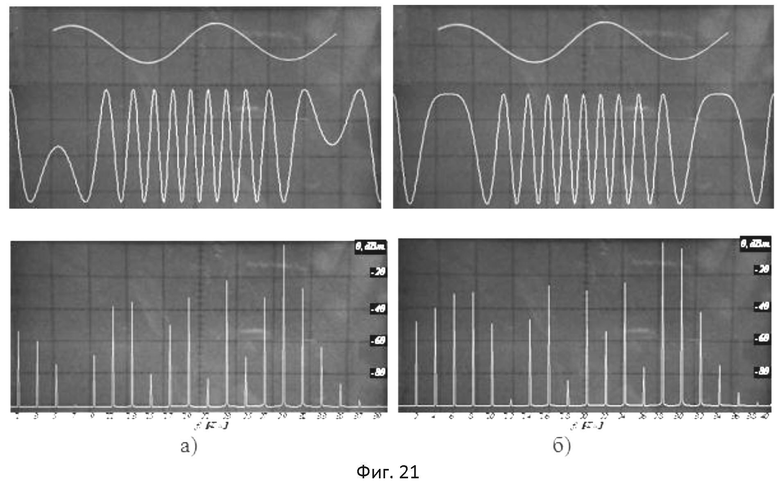
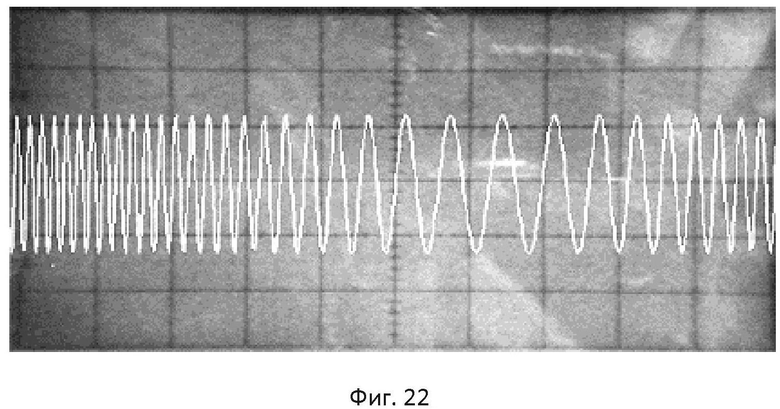
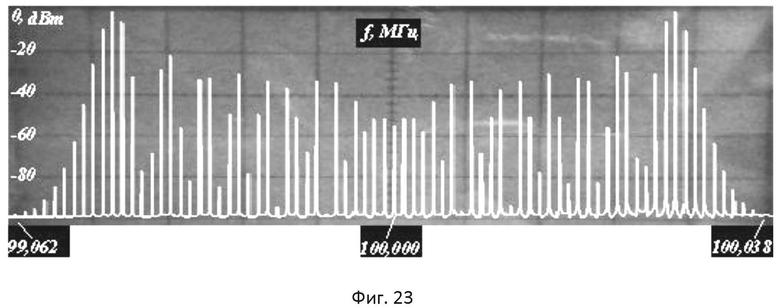
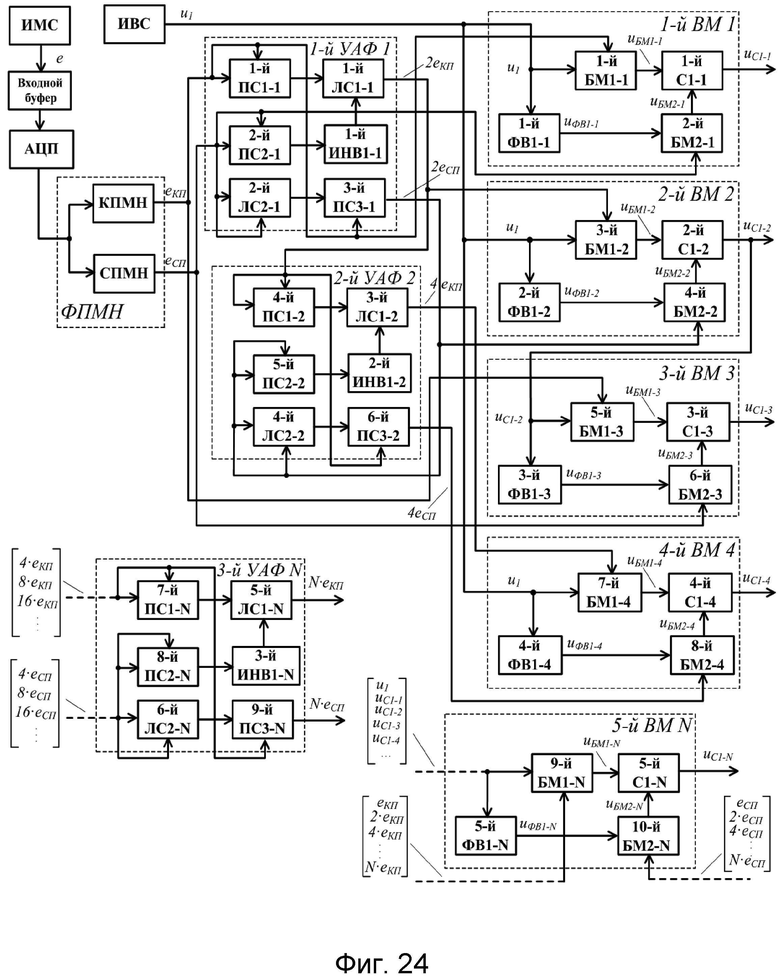
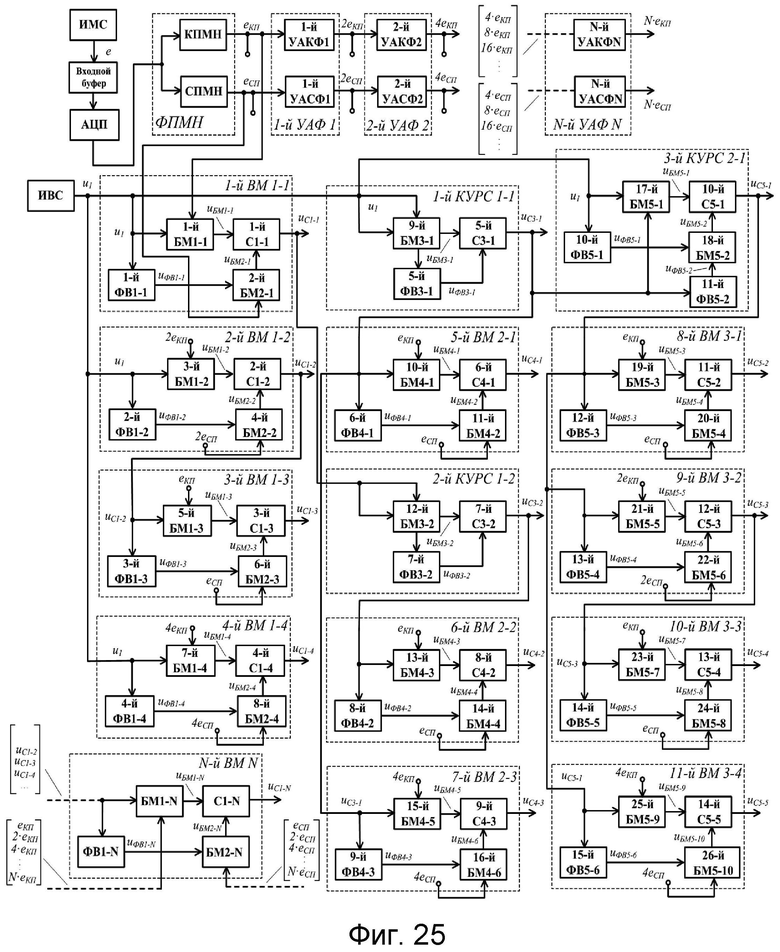
Изобретение относится к области радиотехники и может быть использовано для формирования радиосигналов с угловой модуляцией в радиотехнических устройствах различного назначения, в том числе в технике создания преднамеренных радиоэлектронных помех. Техническим результатом является формирование практически неискаженных фазомодулированных сигналов без ограничения величин индексов модуляции одновременно на первой, второй, третьей и последующих гармониках колебания несущей частоты. Первый способ повышения индекса угловой модуляции предназначен для увеличения значений индексов модуляции в выходных ФМ сигналах на первой гармонике колебания несущей частоты и характеризуется тем, что формируют квадратурное колебание по отношению к колебанию несущей частоты, формируют косинусную и синусную составляющие модулирующего напряжения, выполняют первый синфазное и квадратурное перемножения ВЧ и НЧ составляющих и первое линейное суммирование результатов первых перемножений, получают первое ФМ колебание с заданным значением индекса модуляции, дополнительно формируют квадратурное колебание по отношению к первому ФМ колебанию, осуществляют второе аналогичное попарное перемножение и второе линейное алгебраическое суммирование результатов вторых перемножений. 2 н. и 4 з.п. ф-лы, 25 ил., 3 табл.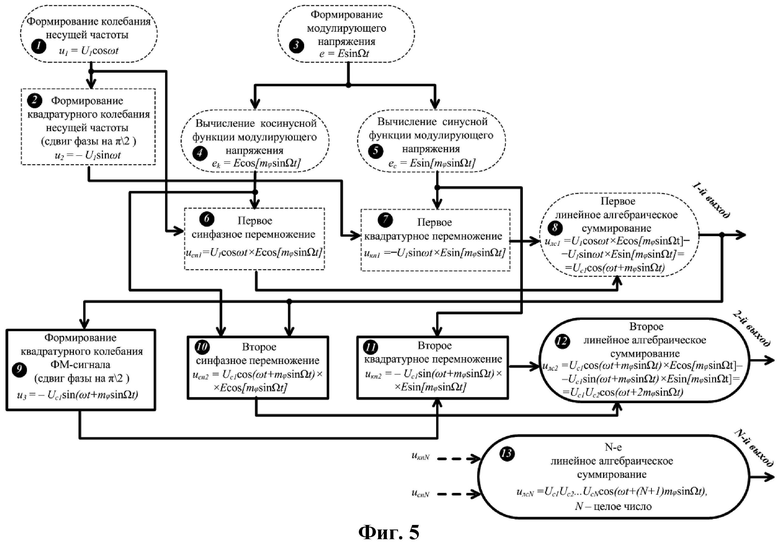

1. Способ повышения индекса угловой модуляции, заключающийся в том, что формируют квадратурное колебание по отношению к колебанию несущей частоты, формируют косинусную и синусную составляющие модулирующего напряжения, являющиеся результатом аппроксимаций функций косинуса и синуса ограниченным количеством членов разложений рядов Тейлора, выполняют первые синфазное и квадратурное перемножения высокочастотных и низкочастотных составляющих и первое линейное суммирование результатов первых перемножений, в результате получают первое фазомодулированное колебание с заданным значением индекса модуляции, отличающийся тем, что дополнительно формируют квадратурное колебание по отношению к первому фазомодулированному колебанию, выполняют второе попарное перемножение результатов косинусного и синусного преобразований с синфазной и квадратурной составляющими первого фазомодулированного колебания и второе линейное алгебраическое суммирование результатов вторых перемножений, в результате получают второе фазомодулированное колебание с удвоенным значением индекса модуляции на первой гармонике колебания несущей частоты; последовательно увеличивая количество этапов попарных перемножений косинусного и синусного преобразований с синфазными и квадратурными составляющими фазомодулированных сигналов и алгебраических линейных суммирований результатов перемножений, одновременно получают пропорциональное увеличение значений индексов модуляции в выходных фазомодулированных сигналах на первой гармонике колебания несущей частоты.

2. Способ по п.1, отличающийся тем, что на выходе вычислителей косинусной и синусной функций модулирующего напряжения последовательно производят увеличение в четное число раз значений аргументов этих функций; выполняют второе попарное перемножение результатов первого удвоения аргументов косинусной и синусной функций с синфазным и квадратурным колебаниями несущей частоты и второе линейное алгебраическое суммирование результатов вторых перемножений, в результате получают второе фазомодулированное колебание с удвоенным значением индекса модуляции на первой гармонике колебания несущей частоты; формируют квадратурное колебание по отношению ко второму фазомодулированному колебанию; выполняют третье попарное перемножение результатов косинусного и синусного преобразований модулирующего напряжения с синфазной и квадратурной составляющими второго фазомодулированного колебания и третье линейное алгебраическое суммирование результатов третьих перемножений, в результате получают третье фазомодулированное колебание с утроенным значением индекса модуляции на первой гармонике колебания несущей частоты; выполняют четвертое попарное перемножение результатов второго удвоения аргументов косинусной и синусной функций с синфазным и квадратурным колебаниями несущей частоты и четвертое линейное алгебраическое суммирование результатов четвертых перемножений, в результате получают четвертое фазомодулированное колебание с учетверенным значением индекса модуляции на первой гармонике колебания несущей частоты; последовательно увеличивая нечетное количество этапов попарных перемножений косинусного и синусного преобразований с синфазными и квадратурными составляющими четных фазомодулированных сигналов и алгебраических линейных суммирований результатов перемножений, одновременно получают пропорциональное увеличение нечетных значений индексов модуляции в выходных фазомодулированных сигналах на первой гармонике колебания несущей частоты; последовательно увеличивая четное количество этапов попарных перемножений результатов удвоений аргументов косинусной и синусной функций с синфазным и квадратурным колебаниями несущей частоты и алгебраических линейных суммирований результатов перемножений, одновременно получают пропорциональное увеличение четных значений индексов модуляции в выходных фазомодулированных сигналах на первой гармонике колебания несущей частоты.

3. Способ по п.2, отличающийся тем, что производят первое умножение колебания несущей частоты, в результате которого получают его вторую гармонику, и формируют квадратурное колебание второй гармоники; выполняют первое попарное перемножение результатов косинусного и синусного преобразований с синфазным и квадратурным колебаниями второй гармоники несущей частоты и первое линейное алгебраическое суммирование результатов первых перемножений, в результате получают первое фазомодулированное колебание с заданным значением индекса модуляции на второй гармонике колебания несущей частоты; выполняют второе попарное перемножение результатов косинусного и синусного преобразований модулирующего напряжения с синфазным и квадратурным колебаниями первой гармоники несущей частоты и второе линейное алгебраическое суммирование результатов вторых перемножений, в результате получают второе фазомодулированное колебание с заданным значением индекса модуляции на первой гармонике колебания несущей частоты; производят второе умножение второго фазомодулированного колебания, в результате получают третье фазомодулированное колебание с удвоенным значением индекса модуляции на второй гармонике колебания несущей частоты; формируют квадратурное колебание по отношению к третьему фазомодулированному колебанию; выполняют третье попарное перемножение результатов косинусного и синусного преобразований модулирующего напряжения с синфазной и квадратурной составляющими третьего фазомодулированного колебания и третье линейное алгебраическое суммирование результатов третьих перемножений, в результате получают четвертое фазомодулированное колебание с утроенным значением индекса модуляции на второй гармонике колебания несущей частоты; выполняют четвертое попарное перемножение результатов второго удвоения аргументов косинусной и синусной функций с синфазным и квадратурным колебаниями второй гармоники несущей частоты и четвертое линейное алгебраическое суммирование результатов четвертых перемножений, в результате получают пятое фазомодулированное колебание с учетверенным значением индекса модуляции на второй гармонике колебания несущей частоты; производят третье умножение колебания несущей частоты, в результате которого получают его третью гармонику, и формируют квадратурное колебание третьей гармоники; выполняют пятое попарное перемножение результатов косинусного и синусного преобразований с синфазным и квадратурным колебаниями третьей гармоники несущей частоты и пятое линейное алгебраическое суммирование результатов пятых перемножений, в результате получают шестое фазомодулированное колебание с заданным значением индекса модуляции на третьей гармонике колебания несущей частоты; выполняют шестое попарное перемножение результатов первого удвоения аргументов косинусной и синусной функций с синфазным и квадратурным колебаниями третьей гармоники несущей частоты и шестое линейное алгебраическое суммирование результатов шестых перемножений, в результате получают седьмое фазомодулированное колебание с удвоенным значением индекса модуляции на третьей гармонике колебания несущей частоты; формируют квадратурное колебание по отношению к седьмому фазомодулированному колебанию; выполняют седьмое попарное перемножение результатов косинусного и синусного преобразований модулирующего напряжения с синфазной и квадратурной составляющими седьмого фазомодулированного колебания и седьмое линейное алгебраическое суммирование результатов седьмых перемножений, в результате получают восьмое фазомодулированное колебание с утроенным значением индекса модуляции на третьей гармонике колебания несущей частоты; выполняют восьмое попарное перемножение результатов второго удвоения аргументов косинусной и синусной функций с синфазным и квадратурным колебаниями третьей гармоники несущей частоты и восьмое линейное алгебраическое суммирование результатов восьмых перемножений, в результате получают девятое фазомодулированное колебание с учетверенным значением индекса модуляции на третьей гармонике колебания несущей частоты; последовательно увеличивают количество этапов умножений колебания несущей частоты в сочетании с процедурами попарных перемножений и алгебраических линейных суммирований, в результате получают пропорциональное увеличение значений индексов модуляции в выходных фазомодулированных сигналах на четвертой и последующих гармониках колебания несущей частоты.

4. Устройство, реализующее способ по п.1, содержащее последовательно соединенные источник высокочастотного сигнала, первый балансный модулятор и первый линейный сумматор, выход которого является первым выходом устройства, последовательно соединенные первый фазовращатель на π/2 и второй балансный модулятор, выход которого соединен со вторым входом первого линейного сумматора, а вход первого фазовращателя на π/2 соединен с выходом источника высокочастотного сигнала, отличающееся тем, что, с целью увеличения значений индексов модуляции в выходных фазомодулированных сигналах на первой гармонике колебания несущей частоты, дополнительно введены последовательно соединенные третий балансный модулятор и второй линейный сумматор, выход которого является вторым выходом устройства, последовательно соединенные второй фазовращатель на π/2 и четвертый балансный модулятор, выход которого соединен со вторым входом второго линейного сумматора, а входы третьего балансного модулятора и второго фазовращателя на π/2 соединены с выходом первого линейного сумматора, последовательно соединенные входной буфер, вход которого соединен с выходом источника модулирующего сигнала, аналого-цифровой преобразователь и косинусный преобразователь модулирующего напряжения, состоящий из объединенных соответствующими связями первого шинного формирователя, первого процессора обработки сигналов, первого постоянного запоминающего устройства, первого мультиплексора, первого цифроаналогового преобразователя, первого выходного буфера и первого фильтра нижних частот, выход которого соединен с управляющими входами первого и третьего балансных модуляторов, последовательно соединенный с аналого-цифровым преобразователем синусный преобразователь модулирующего напряжения, состоящий из объединенных соответствующими связями второго шинного формирователя, второго процессора обработки сигналов, второго постоянного запоминающего устройства, второго мультиплексора, второго цифроаналогового преобразователя, второго выходного буфера и второго фильтра нижних частот, выход которого соединен с управляющими входами второго и четвертого балансных модуляторов, при этом сигнал с выхода тактового генератора поступает на синхронизирующие входы первого и второго процессоров обработки сигналов, делится на четыре и выдается на синхронизирующие выходы, выключатели S1.3 и S1.4 подсоединены непосредственно к старшим, а выключатели S1.1 и S1.2 - к младшим адресным шинам первого и второго постоянных запоминающих устройств.

5. Устройство по п.4, реализующее способ по п.2, отличающееся тем, что, с целью увеличения значений индексов модуляции в выходных фазомодулированных сигналах на первой гармонике колебания несущей частоты, дополнительно введены последовательно соединенные третий балансный модулятор и второй линейный сумматор, последовательно соединенные второй фазовращатель на π/2 и четвертый балансный модулятор, выход которого соединен со вторым входом второго линейного сумматора, а вход второго фазовращателя на π/2 и высокочастотный вход третьего балансного модулятора соединены с выходом источника высокочастотного сигнала, последовательно соединенные пятый балансный модулятор и третий линейный сумматор, последовательно соединенные третий фазовращатель на π/2 и шестой балансный модулятор, выход которого соединен со вторым входом третьего линейного сумматора, а вход третьего фазовращателя на π/2 и высокочастотный вход пятого балансного модулятора соединены с выходом второго линейного сумматора, последовательно соединенные седьмой балансный модулятор и четвертый линейный сумматор, последовательно соединенные четвертый фазовращатель на π/2 и восьмой балансный модулятор, выход которого соединен со вторым входом четвертого линейного сумматора, а вход четвертого фазовращателя на π/2 и высокочастотный вход седьмого балансного модулятора соединены с выходом источника высокочастотного сигнала, последовательно соединенные девятый балансный модулятор и пятый линейный сумматор, последовательно соединенные пятый фазовращатель на π/2 и десятый балансный модулятор, выход которого соединен со вторым входом пятого линейного сумматора, а вход пятого фазовращателя на π/2 и высокочастотный вход девятого балансного модулятора могут быть соединены с выходами источника высокочастотного, выходами первого, второго, третьего и четвертого линейных сумматоров, управляющий вход девятого балансного модулятора может быть соединен с выходом косинусного преобразователя модулирующего напряжения, а также с косинусными выходами первого, второго и третьего удвоителей аргументов функций, управляющий вход десятого балансного модулятора может быть соединен с выходом синусного преобразователя модулирующего напряжения, а также с синусными выходами первого, второго и третьего удвоителей аргументов функций, последовательно соединенные первый перемножитель сигналов и первый низкочастотный линейный сумматор, последовательно соединенные второй перемножитель сигналов и первый инвертор, выход которого соединен со вторым входом первого низкочастотного линейного сумматора, последовательно соединенные второй низкочастотный линейный сумматор, третий перемножитель сигналов, четвертый низкочастотный линейный сумматор, шестой перемножитель сигналов, выход которого соединен с управляющим входом восьмого балансного модулятора, объединенными первым и вторым входами восьмого перемножителя сигналов и объединенными первым и вторым входами шестого низкочастотного линейного сумматора, последовательно соединенные четвертый перемножитель сигналов, третий низкочастотный линейный сумматор, выход которого соединен с управляющим входом седьмого балансного модулятора, объединенными первым и вторым входами седьмого перемножителя сигналов и вторым входом девятого перемножителя сигналов, последовательно соединенные пятый перемножитель сигналов и второй инвертор, выход которого соединен со вторым входом третьего низкочастотного линейного сумматора, последовательно соединенные седьмой перемножитель сигналов и пятый низкочастотный линейный сумматор, выход которого может быть соединен с управляющим входом девятого балансного модулятора, последовательно соединенные восьмой перемножитель сигналов и третий инвертор, выход которого соединен со вторым входом пятого низкочастотного линейного сумматора, последовательно соединенные шестой низкочастотный линейный сумматор и девятый перемножитель сигналов, выход которого может быть соединен с управляющим входом десятого балансного модулятора, при этом выход первого низкочастотного линейного сумматора соединен с объединенными первым и вторым входами четвертого перемножителя сигналов, вторым входом шестого перемножителя сигналов и управляющим входом третьего балансного модулятора, выход третьего перемножителя сигналов соединен с объединенными первым и вторым входами четвертого низкочастотного линейного сумматора, объединенными первым и вторым входами пятого перемножителя сигналов и с управляющим входом четвертого балансного модулятора, выход косинусного преобразователя модулирующего напряжения соединен с объединенными первым и вторым входами первого перемножителя сигналов, вторым входом третьего перемножителя сигналов, управляющими входами первого и пятого балансных модуляторов, выход синусного преобразователя модулирующего напряжения соединен с объединенными первым и вторым входами второго перемножителя сигналов, объединенными первым и вторым входами второго низкочастотного линейного сумматора, управляющими входами второго и шестого балансных модуляторов, причем первый фазовращатель на π/2, первый и второй балансные модуляторы и первый линейный сумматор составляют первый векторный модулятор, второй фазовращатель на π/2, третий и четвертый балансные модуляторы и второй линейный сумматор составляют второй векторный модулятор, третий фазовращатель на π/2, пятый и шестой балансные модуляторы и третий линейный сумматор составляют третий векторный модулятор, четвертый фазовращатель на π/2, седьмой и восьмой балансные модуляторы и четвертый линейный сумматор составляют четвертый векторный модулятор, пятый фазовращатель на π/2, девятый и десятый балансные модуляторы и пятый сумматор составляют пятый векторный модулятор, первый, второй и третий перемножители сигналов, первый и второй низкочастотные линейные сумматоры и первый инвертор составляют первый удвоитель аргументов функций, четвертый, пятый и шестой перемножители сигналов, третий и четвертый низкочастотные линейные сумматоры и второй инверторы составляют второй удвоитель аргументов функций, седьмой, восьмой и девятый перемножители сигналов, пятый и шестой низкочастотные линейные сумматоры и третий инвертор составляют третий удвоитель аргументов функций, выходы первого, третьего и пятого низкочастотных линейных сумматоров являются косинусными выходами, соответственно, первого, второго и третьего удвоителей аргументов функций, выходы третьего, шестого и девятого перемножителей сигналов являются синусными выходами, соответственно, первого, второго и третьего удвоителей аргументов функций, а выходы первого - пятого линейных сумматоров являются, соответственно, первым - пятым выходами устройства.

6. Устройство по п.5, реализующее способ по п.3, отличающееся тем, что, с целью увеличения значений индексов модуляции в выходных фазомодулированных сигналах одновременно на второй, третьей и последующих гармониках колебания несущей частоты, дополнительно введены последовательно соединенные девятый балансный модулятор и пятый линейный сумматор, последовательно соединенные девятый балансный модулятор и пятый фазовращатель на π/2, выход которого соединен со вторым входом пятого линейного сумматора, последовательно соединенные десятый балансный модулятор и шестой линейный сумматор, последовательно соединенные шестой фазовращатель на π/2 и одиннадцатый балансный модулятор, выход которого соединен со вторым входом шестого линейного сумматора, последовательно соединенные двенадцатый балансный модулятор и седьмой линейный сумматор, последовательно соединенные двенадцатый балансный модулятор и седьмой фазовращатель на π/2, выход которого соединен со вторым входом седьмого линейного сумматора, последовательно соединенные тринадцатый балансный модулятор и восьмой линейный сумматор, последовательно соединенные восьмой фазовращатель на π/2 и четырнадцатый балансный модулятор, выход которого соединен со вторым входом восьмого линейного сумматора, последовательно соединенные пятнадцатый балансный модулятор и девятый линейный сумматор, последовательно соединенные девятый фазовращатель на π/2 и шестнадцатый балансный модулятор, выход которого соединен со вторым входом девятого линейного сумматора, последовательно соединенные семнадцатый балансный модулятор и десятый линейный сумматор, последовательно соединенные десятый фазовращатель на π/2 и первый вход восемнадцатого балансного модулятора, последовательно соединенные одиннадцатый фазовращатель на π/2 и второй вход восемнадцатого балансного модулятора, выход которого соединен со вторым входом десятого линейного сумматора, последовательно соединенные девятнадцатый балансный модулятор и одиннадцатый линейный сумматор, последовательно соединенные двенадцатый фазовращатель на π/2 и двадцатый балансный модулятор, выход которого соединен со вторым входом одиннадцатого линейного сумматора, последовательно соединенные двадцать первый балансный модулятор и двенадцатый линейный сумматор, последовательно соединенные тринадцатый фазовращатель на π/2 и двадцать второй балансный модулятор, выход которого соединен со вторым входом двенадцатого линейного сумматора, последовательно соединенные двадцать третий балансный модулятор и тринадцатый линейный сумматор, последовательно соединенные четырнадцатый фазовращатель на π/2 и двадцать четвертый балансный модулятор, выход которого соединен со вторым входом тринадцатого линейного сумматора, последовательно соединенные двадцать пятый балансный модулятор и четырнадцатый линейный сумматор, последовательно соединенные пятнадцатый фазовращатель на π/2 и двадцать шестой балансный модулятор, выход которого соединен со вторым входом четырнадцатого линейного сумматора, при этом объединенные первый и второй входы девятого и семнадцатого балансных модуляторов, а также вход десятого фазовращателя на π/2 соединены с выходом источника высокочастотного сигнала, входы шестого, девятого и одиннадцатого фазовращателей на π/2, второй вход семнадцатого балансного модулятора, первые входы десятого и пятнадцатого балансных модуляторов соединены с выходом пятого линейного сумматора, объединенные первый и второй входы тринадцатого балансного модулятора соединены с выходом первого линейного сумматора, вход восьмого фазовращателя на π/2 и первый вход тринадцатого балансного модулятора соединены с выходом седьмого линейного сумматора, входы двенадцатого, тринадцатого и пятнадцатого фазовращателей на π/2 и первые входы девятнадцатого, двадцать первого и двадцать пятого балансных модуляторов соединены с выходом десятого линейного сумматора, вход четырнадцатого фазовращателя на π/2 и первый вход двадцать третьего балансного модулятора соединены с выходом двенадцатого линейного сумматора, вторые входы десятого и одиннадцатого, тринадцатого и четырнадцатого, девятнадцатого и двадцатого, двадцать третьего и двадцать четвертого балансных модуляторов соединены с выходами, соответственно, косинусного и синусного преобразователей модулирующего напряжения, вторые входы пятнадцатого и шестнадцатого, двадцать пятого и двадцать шестого балансных модуляторов соединены с выходами вторых, соответственно, удвоителей аргументов косинусной и синусной функций, вторые входы двадцать первого и двадцать второго балансных модуляторов соединены с выходами первых, соответственно, удвоителей аргументов косинусной и синусной функций, причем девятый балансный модулятор, пятые фазовращатель на π/2 и линейный сумматор составляют первый квадратурный умножитель радиосигналов, двенадцатый балансный модулятор, седьмые фазовращатель на π/2 и линейный сумматор составляют второй квадратурный умножитель радиосигналов, семнадцатый и восемнадцатый балансные модуляторы, десятый и одиннадцатый фазовращатели на π/2 и десятый линейный сумматор составляют третий квадратурный умножитель радиосигналов, десятый и одиннадцатый балансные модуляторы, шестые фазовращатель на π/2 и линейный сумматор составляют пятый векторный модулятор, тринадцатый и четырнадцатый балансные модуляторы, восьмые фазовращатель на π/2 и линейный сумматор составляют шестой векторный модулятор, пятнадцатый и шестнадцатый балансные модуляторы, девятые фазовращатель на π/2 и линейный сумматор составляют седьмой векторный модулятор, девятнадцатый и двадцатый балансные модуляторы, двенадцатый фазовращатель на π/2 и одиннадцатый линейный сумматор составляют восьмой векторный модулятор, двадцать первый и двадцать второй балансные модуляторы, тринадцатый фазовращатель на π/2 и двенадцатый линейный сумматор составляют девятый векторный модулятор, двадцать третий и двадцать четвертый балансные модуляторы, четырнадцатый фазовращатель на π/2 и тринадцатый линейный сумматор составляют десятый векторный модулятор, двадцать пятый и двадцать шестой балансные модуляторы, пятнадцатый фазовращатель на π/2 и четырнадцатый линейный сумматор составляют одиннадцатый векторный модулятор, а выходы пятого - четырнадцатого линейных сумматоров являются, соответственно, пятым - четырнадцатым выходами устройства.