Изобретение относится к вычислительной технике и электросвязи, предназначено для решения задач защиты компьютерной информации. Наиболее предпочтительной областью использования изобретения является построение генераторов псевдослучайных чисел (ГПСЧ), а также криптографических примитивов хеширования, блочного и поточного шифрования.
В совокупности признаков заявленного изобретения используются следующие термины:
Стохастическое преобразование - непредсказуемое преобразование данных; примером стохастического преобразования может являться криптографическое преобразование;
Генератор псевдослучайных чисел (ГПСЧ) - генератор последовательности чисел, статистически не отличимой от последовательности случайных чисел с равномерным законом распределения; наиболее жесткие требования (по непредсказуемости, статистической безопасности, периоду формируемых последовательности и эффективности реализации) предъявляются к ГПСЧ, ориентированным на решение задач криптографической защиты информации;
Ключ - секретный параметр стохастического преобразования, представляет собой двоичную информацию, известную только законному пользователю;
Подключ - часть ключа;
Раунд - последовательность шагов, образующих одну итерацию итеративного (многораундового) стохастического преобразования;
Раундовый ключ (RoundKey) - ключевая информация, использующаяся при выполнении одного раунда преобразования, существует два способа формирования раундовых ключей: раундовый ключ может являться частью секретного ключа (пример - Российский стандарт криптозащиты ГОСТ 28147-89), последовательность раундовых ключей может получаться в результате работы процедуры «разворачивания» исходного ключа (пример - американский стандарт криптозащиты AES);
Раундовый подключ - часть раундового ключа;
Двоичный вектор - некоторая последовательность нулевых и единичных бит, например (01101010), двоичный вектор разрядности n может быть интерпретирован как элемент конечного поля GF(2n);
Замена (Substitution) - операция, выполняемая над двоичным вектором i∈GF(2n), при этом результат операции равен содержимому ячейки с индексом i таблицы замен размерности n×2n;
Перемешивание (Mix) - операция, выполняемая над двоичным вектором разрядности n, результат разрядности n которой зависит от всех входных бит и от их взаимного расположения; качественное перемешивание обладает свойствами рассеивания и перемешивания.
Известен способ нелинейного многораундового преобразования данных с архитектурой «Сеть Фейстеля», описанный в Российском стандарте криптографической защиты информации [Стандарт СССР ГОСТ 28147-89. Системы обработки информации. Защита криптографическая. Алгоритм криптографического преобразования]. Способ аналог включает в себя формирование ключа в виде последовательности из 8 подключей длиной 32 бита. Перед преобразованием 64-разрядный блок данных разбивается на два 32-разрядного подблока L и R, которые поочередно преобразуются путем выполнения 32 раундов преобразования. Один раунд преобразования заключается в следующем. По подблоку L формируется двоичный вектор F в соответствии с выражением F:=L, который преобразуется в зависимости от одного из подключей в соответствии с раундовой функцией преобразования Е. Преобразование двоичного вектора на i-м раунде записывается в виде F:=E{F, Ki), где Ki - подключ, используемый на i-м раунде. Полученное значение F:=E(F, Ki) поразрядно суммируется по модулю два ⊕ с подблоком R в соответствии с выражением R:=R⊕F. Вычисление раундовой функции E(F, Ki) осуществляется в соответствии со следующими шагами преобразования. Первоначально сформированный двоичный вектор F:=L преобразуется путем наложения на него текущего подключа Ki, являющегося фиксированным для данного раунда, с помощью операции сложения по модулю 232 в соответствии с формулой F:=(F+Ki) mod 232, после чего над двоичным вектором F выполняют операцию замены F:=S(F), затем операцию циклического сдвига влево (в сторону старших разрядов) на 11 разрядов F:=F<<<11. После каждого раунда шифрования, за исключением последнего, подблоки переставляются. Операция замены выполняется следующим образом. Двоичный вектор F разбивается на 8 двоичных векторов длиной по 4 бит каждый. Каждый 4-разрядный двоичный вектор заменяется двоичным вектором из соответствующей таблицы замен. Выбранные из таблиц замен восемь 4-разрядных векторов объединяются в преобразованный двоичный вектор F.
Недостатком данного способа построения нелинейного многораундового криптографического преобразования является низкое быстродействие, громоздкая процедура обоснования наличия свойств рассеивания и перемешивания информации, обязательных для криптографических преобразований, невозможность реализации с использованием гибридных суперкомпьютерных технологий.
Одним из путей решения проблемы построения быстродействующего итеративного криптографического преобразования является использование гибридных вычислительных технологий. Наиболее подходящей для реализации на GPU является архитектура Квадрат, предложенная авторами криптоалгоритмов Square и Rijndael, при этом последний в 2001 г. победил в конкурсе на принятие нового Американского стандарта криптозащиты AES (Advanced Encryption Standard).
Наиболее близким по своей технической сущности к заявленному способу итеративного криптографического преобразования данных является принятый за прототип способ многораундового 2D-преобразования с архитектурой «Квадрат», описанный в версии стандарта AES-128 [Daemen J., Rijmen V. AES Proposal: Rijndael. URL: http://csrc.nist.gov/archive/aes/rijndael/Rijndael-ainmended.pdf или Иванов M.A., Ковалев А.В., Чугунков И.В. и др. Стохастические методы защиты информации в компьютерных системах и сетях. М.: Кудиц-Пресс, 2009, с.241]. В данном способе все входные и выходные блоки данных, все промежуточные результаты преобразований, все раундовые ключи представляются в виде квадратного массива байтов 4×4, таким образом, разрядность всех блоков данных равна 128 битам. Преобразование выполняется путем формирования из секретного ключа с помощью процедуры разворачивания ключа последовательности раундовых ключей K0, K1,…, KR, где R - число раундов преобразования. По входному блоку М формируется блок State в соответствии с выражением State:=М. Затем выполняется операция начального поразрядного сложения по модулю два (XOR) блока State и раундового ключа (AddRoundKey) K0 в соответствии с выражением State:=State⊕K0, после чего выполняются R раундов преобразования. Преобразование блока данных на i-м раунде записывается в виде State:=E(State, Ki), где Е() - раундовая функция преобразования, Ki - раундовый ключ, используемый на i-м раунде. Полученное значение State:=E(State, Ki) поступает на вход следующего раунда. В состав каждого i-го раунда кроме последнего входят последовательно выполняемые преобразования замены байтов State:=SubBytes(State), циклического сдвига строк State:=ShiftRows(State), перемешивания столбцов State:=MixColimns(State) и сложения по модулю два (XOR) с раундовым ключом (AddRoundKey) Ki в соответствии с выражением State:=State⊕Ki. В состав последнего раунда входят последовательно выполняемые преобразования замены байтов, циклического сдвига строк и сложения (XOR) с раундовым ключом KR. Операция замены байтов выполняется следующим образом. Блок State разбивается на 16 байтов. Каждый байт заменяется байтом из фиксированной таблицы замен размерностью 8×256. Выбранные из таблицы замен 16 байтов объединяются в преобразованный блок State. Операция сдвига строк выполняется следующим образом. Блок State разбивается на 4 строки. Каждая j-я строка (j=0, 1, 2, 3) циклически сдвигается на j байтов. Сдвинутые строки объединяются в преобразованный блок State. Операция перемешивания столбцов выполняется следующим образом. Блок State разбивается на 4 столбца. При выполнении перемешивания байты столбца рассматриваются как коэффициенты многочлена А(х) степени 3 над полем GF(28). Суть операции перемешивания столбца - умножение по модулю х4+1 многочлена А(х) на многочлен 03х3+х2+х+02. Перемешанные столбцы объединяются в преобразованный блок State.
Таким образом, последовательность 10-раундового преобразования AES-128 имеет следующий вид: начальный шаг сложения с раундовым ключом, 9 раундов, каждый из которых состоит из четырех шагов (замены байтов, циклического сдвига строк, перемешивания столбцов и сложения с раундовым ключом), последний 10-й раунд, состоящий из трех шагов (замены байтов, циклического сдвига строк и сложения с раундовым ключом).
Недостатком известного решения является низкая криптостойкость и недостаточно высокое быстродействие.
К причинам, препятствующим достижению указанного ниже технического результата, относится использование только последовательной композиции раундовых преобразований, в результате, для обеспечения требуемого уровня криптостойкости необходимо выполнение большого числа раундов.
В основе изобретения лежит задача построения на основе последовательной и параллельной композиции раундовых функций шифрования нелинейного многораундового преобразования, допускающего максимальную степень параллелизма, что при реализации с использованием гибридных суперкомпьютерных технологий позволит в несколько раз повысить быстродействие алгоритма. При этом результат преобразований зависит от секретной информации, которую образуют ключ и таблица замен.
Техническим результатом изобретения является повышение криптостойкости и увеличение быстродействия итеративного криптографического преобразования данных.
Указанный технический результат при осуществлении изобретения достигается тем, что в итеративном криптографическом преобразовании данных, включающем
формирование из секретного ключа с помощью процедуры разворачивания ключа последовательности раундовых ключей K1, K2,…, KR, где R - число раундов преобразования;
формирование по входному блоку М блока С в соответствии с выражением С:=М;
выполнение R раундов преобразования, при этом преобразование блока данных на i-м раунде записывается в виде С:=Е(С, Ki), где Е() - раундовая функция преобразования, Кi - раундовый ключ, используемый на i-м раунде, полученное значение С:=Е(С, Ki) при i<R поступает на вход следующего раунда, а результат действия последнего раунда С:=Е(С, KR) является результатом преобразования;
новым согласно изобретению является то, что дополнительно
из каждого раундового ключа Ki формируют N раундовых подключей Ki1, Ki2,…, KiN, где N - число траекторий раундовых преобразований в каждом раунде;
при выполнении каждого i-го раунда создают N копий Сi1, Сi2,…, СiN входного блока данных С, каждую копию Cij подвергают стохастическому преобразованию Еij, которое записывается в виде Сij:=Eij(Cij, Kij), преобразованные значения Cij поступают на входы комбинационной схемы F, функцией которой является параллельная композиция различных траекторий раундовых преобразований, результат действия комбинационной схемы С:=F(Ci1, Сi2,…, СiN) объявляют результатом раунда.
В частном случае выполняют комбинационную схему в виде N - входового блока поразрядного сложения по модулю два.
Благодаря такому решению параллельная декомпозиция траекторий преобразований осуществляется самым простым из всех возможных способов.
Новым является то, что в частном случае стохастическое преобразование Eij включает
представление входного блока Cij, промежуточных результатов преобразования и раундового подключа Kij в виде квадратного массива бит размерностью 8×8;
сложение по модулю два (XOR) входного блока Cij и раундового подключа Кij;
разбиение результата на строки r1, r2,…, r8 и выполнение для каждой строки операции замены с использованием таблицы S размерностью 8×256;
разбиение результата на столбцы с1, с2,…, с8 и выполнение для каждого столбца операции замены с использованием таблицы S размерностью 8×256.
Благодаря совокупности перечисленных решений увеличивается криптостойкость преобразования за счет выполнения последовательной и параллельной композиции раундовых преобразований и повышается быстродействие за счет появления возможности сокращения числа раундов и выполнения всех раундовых преобразований Cij:=Еij(Сij, Kij) параллельно.
Суть предлагаемого способа иллюстрируют фиг.1-3.
На фиг.1 изображена структура итеративного криптографического преобразования.
На фиг.1 показаны входы 1i и выходы 2i последовательно выполняемых раундов 6i, а также раундовые ключи 31, 32,…, 3R, которые формируются из секретного ключа с помощью процедуры разворачивания ключа, где R - число раундов преобразования, i=1, 2,…, R. Последовательность шагов итеративного криптографического преобразования:
формирование по входному блоку 11 М блока С в соответствии с выражением С:=М;
выполнение R раундов преобразования, при этом преобразование блока данных 1i на i-м раунде записывается в виде С:=Е(С, Ki), где Ki - раундовый 3i ключ, используемый на i-м раунде, полученное значение 2i С:=Е(С, Ki) при i<R поступает на вход следующего раунда, а результат действия 2R последнего раунда С:=Е(С, KR) является результатом преобразования входного блока 11М.
Процедура разворачивания ключа может быть выполнена на основе ГПСЧ, в качестве начального состояния которого используется исходный секретный ключ, а с выхода которого снимается последовательность раундовых ключей.
На фиг.1 показаны раундовые 3ij подключи, i=1, 2,…, R, j=1, 2,…, N, использующиеся при выполнении стохастических преобразований 4i1, 4i2,…, 4iN, которые выполняются внутри каждого раунда 6i, а также комбинационная схема 7.
Внутри каждого раунда происходит формирование N копий входного блока 1i, каждая копия Cij подвергается стохастическому преобразованию 4ij, которое записывается в виде Cij:=Eij(Cij, Kij), преобразованные значения Cij поступают на входы комбинационной 5i схемы F, функцией которой является параллельная композиция различных траекторий раундовых преобразований, результат действия комбинационной 5i схемы С:=F(Ci1, Сi2,…, СiN) объявляется результатом 2i раунда 6i.
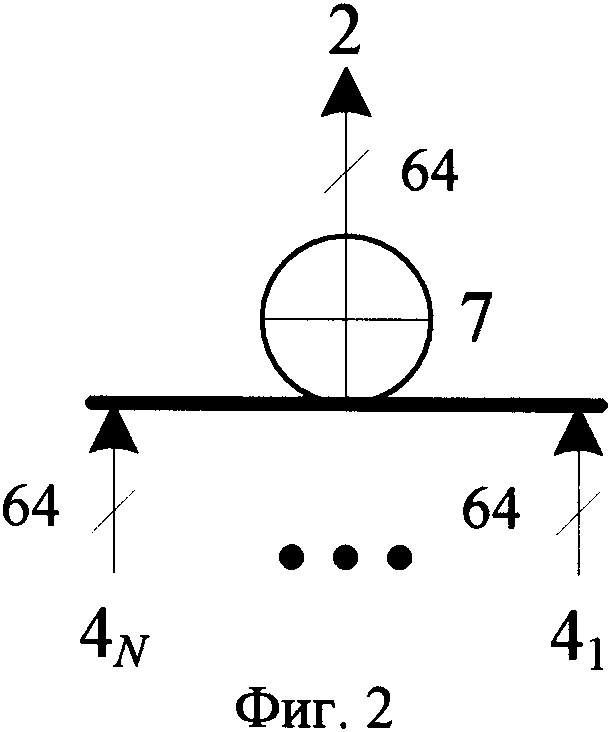
На фиг.2 показан вариант построения комбинационной 5 схемы на основе N-входового блока поразрядного сложения 7 по модулю два. На входы блока 7 поступают результаты преобразований с выходов блоков, осуществляющих стохастические преобразования 4i1, 4i2,…, 4iN. С выхода блока 5 снимается результат 2i i-го раунда.
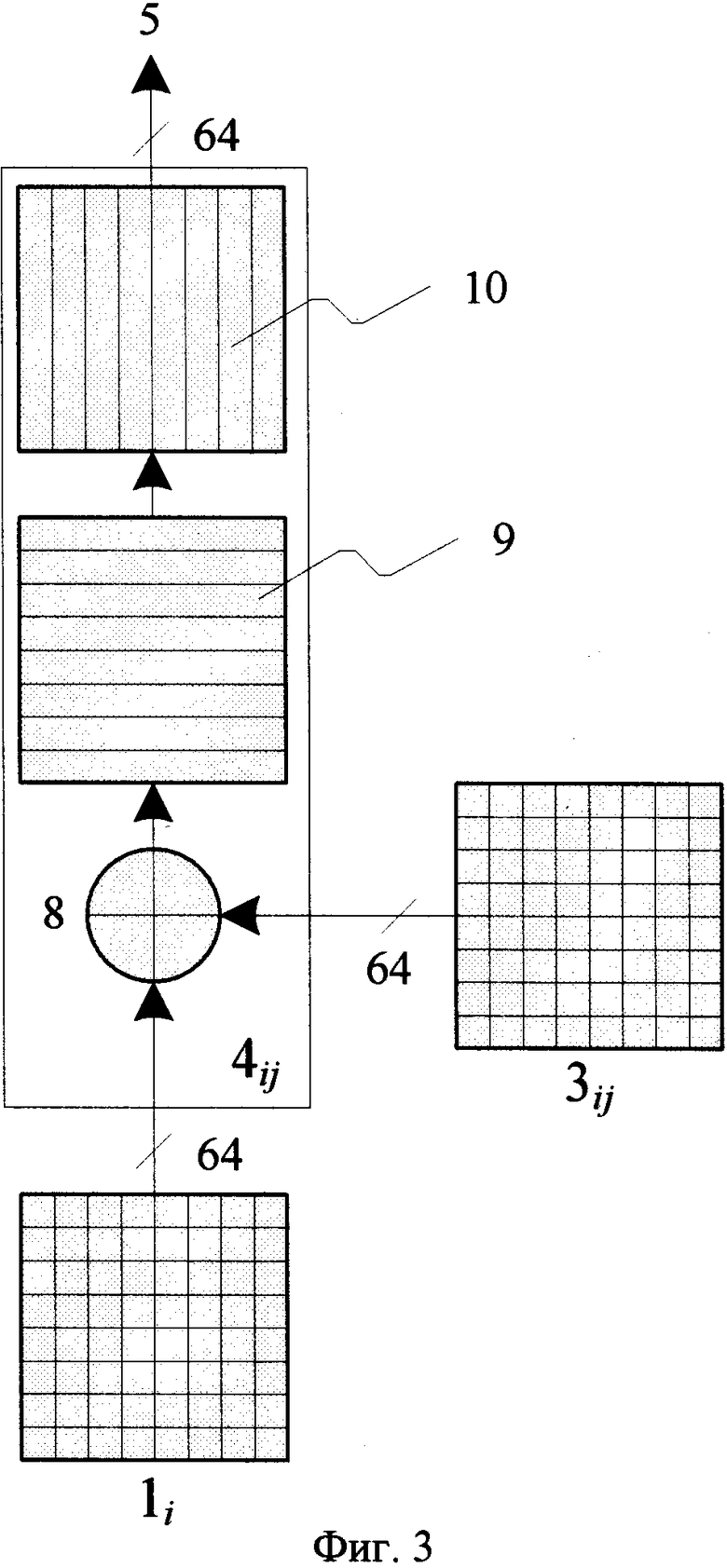
На фиг.3 показан пример преобразования 4. Рассматривается случай, когда все блоки 1i, 2i, все раундовые подключи 3ij, все промежуточные результаты преобразований в блоках 4ij представляются в виде квадратного массива бит 8×8, т.е. имеют разрядность 64 бита. На фиг.3 показана операция сложения 8 по модулю два, отдельные строки 9 и столбцы 10 блока данных.
Последовательность шагов итеративного криптографического преобразования имеет следующий вид.
- Формирование по входному 1i блоку М блока С в соответствии с выражением С:=М.
- 1-й раунд преобразований. Преобразование блока данных на первом раунде записывается в виде С:=Е(С, K1), где K1 - раундовый ключ первого раунда. Полученное значение 21 поступает на вход 12 второго раунда.
- 2-й раунд преобразований. Преобразование блока данных на втором раунде записывается в виде С:=Е(С, K2), где K2 - раундовый ключ второго раунда. Полученное значение 22 поступает на вход 13 третьего раунда.
- R-й раунд преобразований. Преобразование блока данных на последнем раунде записывается в виде С:=Е(С, KR), где KR - раундовый ключ последнего раунда. Полученное значение 2R является результатом итеративного криптографического преобразования блока данных 11М.
Более детально последовательность шагов итеративного криптографического преобразования можно описать следующим образом.
- Формирование по входному 11 блоку М блока С в соответствии с выражением С:=М.
- 1-й раунд преобразований. При выполнении первого раунда создается N копий С11, С12,…, С1N входного 11 блока данных С, каждая копия С1j подвергается стохастическому преобразованию 4ij, которое записывается в виде Cij:=E1j(C1j, K1j), где K1j - раундовые подключи первого раунда, j=1, 2,…, N, преобразованные значения C1j поступают на входы комбинационной 51 схемы F, функцией которой является параллельная композиция результатов выполнения различных траекторий раундовых преобразований, результат действия комбинационной 51 схемы С:=F(C11, С12,…, C1N) объявляется результатом 21 первого раунда. Полученное значение 21 поступает на вход 12 второго раунда.
- 2-й раунд преобразования. При выполнении второго раунда создается N копий С21, С22,…, С2N входного 12 блока данных С, каждая копия С2j подвергается стохастическому преобразованию 42j, которое записывается в виде С2j:=Е2j(С2j, K2j), где K2j - раундовые подключи второго раунда, j=1, 2,…, N преобразованные значения Cij поступают на входы комбинационной 52 схемы F, функцией которой является параллельная композиция результатов выполнения различных траекторий раундовых преобразований, результат действия комбинационной 52 схемы С:=F(C21, С22,…, C2N) объявляется результатом 22 второго раунда. Полученное значение 22 поступает на вход 13 третьего раунда.
- R-й раунд преобразований. При выполнении последнего раунда создается N копий CR1, CR2,…, CRN входного 1R блока данных С, каждая копия CRj подвергается стохастическому преобразованию 4Rj, которое записывается в виде CRj:=ERj(CRj, KRj), где KRj - раундовые подключи последнего раунда, j=1, 2,…, N, преобразованные значения CRj поступают на входы комбинационной 5R схемы F, функцией которой является параллельная композиция результатов выполнения различных траекторий раундовых преобразований, результат действия комбинационной 5R схемы С:=F(CR1, CR2,…, CRN) объявляется результатом 2R второго раунда. Полученное значение 2R является результатом итеративного криптографического преобразования блока данных 11М.
Рассмотрим пример реализации стохастического преобразования 4ij, показанный на фиг.4. Все блоки 1i входных данных, все промежуточные результаты, раундовые подключи 3ij имеют разрядность 64 бита и представляются в виде квадратного массива бит 8×8.
Последовательность операций при выполнении простейшего преобразования 4ij имеет следующий вид:
сложение 8 по модулю два (XOR) входного блока 1i и раундового подключа 3ij;
разбиение результата на строки 9 r1, r2,…, r8 и выполнение для каждой строки операции замены с использованием таблицы S размерностью 8×256;
разбиение результата на столбцы 10 с1, с2,…, c8 и выполнение для каждого столбца операции замены с использованием таблицы S размерностью 8×256.
При таком способе выполнения преобразования 4ij дополнительно появляется возможность повысить быстродействие за счет параллельного выполнения операций замены строк и столбцов.
Одним из известных путей повышения криптостойкости нелинейной функции шифрования является использование для ее построения последовательной и параллельной композиции простейших функций ƒ шифрования. Параллельная композиция суть побитовый XOR последовательностей с выходов двух блоков ƒ, в последовательной композиции выход одного блока ƒ является входом другого. Такой подход к построению шифра впервые был использован У. Маурером при создании самосинхронизирующегося поточного шифра [Иванов М.А., Ковалев А.В., Чугунков И.В. и др. Стохастические методы защиты информации в компьютерных системах и сетях. М.: Кудиц-Пресс, 2009, с.263]. Базовый компонент схемы Маурера - 3-битовый регистр сдвига с зависящей от ключа функцией ƒ выхода. Четыре таких компонента образуют блок следующего уровня - пару параллельно соединенных цепочек из двух базовых компонентов. На следующем уровне четыре таких блока собраны в последовательную композицию. На двух следующих уровнях эта конструкция повторяется. Результирующая последовательностная машина (ПМ) имеет входную память объемом 192 бита и 4 бита-компонента на каждый бит памяти. Внутреннее состояние ПМ служит входом для зависящей от ключа функции шифрования Fc. Для задания конструкций булевых функций ƒ ключ шифрования «разворачивается» в 256 байтов, каждый из которых определяет таблицу истинности соответствующей функции. Основная идея данной конструкции - построение ПМ, количество элементов памяти которой превышает разрядность входной памяти. Подобный подход к построению блочных итеративных шифров ранее не применялся, его использование при программной реализации криптографических преобразований стало возможным в связи с появлением гибридных суперкомпьютерных технологий. В результате стало возможным в пределах раунда параллельно (иначе говоря, без ущерба для быстродействия) выполнять различные траектории сложных преобразований, а затем на выходе осуществлять параллельную композицию полученных результатов. В результате задача инвертирования функции шифрования становится вычислительно неразрешимой при меньшем числе раундов преобразования. В том случае, когда число раундов остается неизменным, применение последовательной и параллельной композиции раундовых преобразований приводит к повышению криптостойкости шифра.
Таким образом, особенностью предлагаемого способа реализации итеративного криптографического преобразования является высокая степень параллелизма при выполнении различных траекторий раундовых преобразований с последующей параллельной композицией результатов их выполнения, что обеспечивает получение заявляемого технического результата - увеличение быстродействия при реализации с использованием гибридных суперкомпьютерных технологий за счет уменьшения числа раундов, требуемых для обеспечения заданного уровня криптостойкости, либо увеличение криптостойкости при сохранении исходного числа раундов.
В последние годы все большую популярность завоевывают гибридные вычислительные системы, сочетающие удобство классических вычислений на центральных процессорах (CPU) с массово-параллельными вычислениями на графических процессорах (GPU) [Боресков А.В., Харламов А.А. Основы работы с технологией CUDА. М.: ДМК Пресс, 2011], [CUDA Zone. URL http://developer.nvidia.com/ category/zone/cuda-zone]. Особенностью GPU является наличие большого числа (десятки и сотни) вычислительных ядер, работающих параллельно. В задачах, допускающих распараллеливание обработки потока исходных данных, выигрыш в производительности для системы CPU/GPU составляет до нескольких десятков раз по сравнению с классической CPU-системой. Многие из наиболее производительных современных суперкомпьютеров также имеют гибридную архитектуру CPU/GPU.
В гибридных системах CPU решает задачи управления выполнением программы в целом и проведения не очень "тяжелых" вычислений; наиболее критичные по производительности участки программы оформляются в виде специальных функций-ядер (kernel), которые запускаются на GPU. Современные производители графических процессоров, в частности, компания NVIDIA, предоставляют разработчикам программ для систем CPU/GPU мощные инструментальные средства. Полезной и приятной особенностью таких средств является то, что они являются бесплатными. В качестве примеров можно указать CUDA Toolkit [CUDA Toolkit. URL http://developer.nvidia.com/cuda-toolkit] и Parallel NSight [NVIDIA Parallel Nsight. URL http://developer.nvidia.com/ nvidia-parallel-nsight], которые интегрируются с современными популярными системами разработки ПО, такими как Microsoft Visual Studio и NetBeans.
Для программной реализации предложенного способа построения итеративного криптографического преобразования наиболее целесообразной представляется технология CUDA (Compute Unified Device Architecture - вычислительная унифицированная архитектура устройств) от компании NVIDIA [Боресков А.В., Харламов А.А. Основы работы с технологией CUDA. М.: ДМК Пресс, 2011], [CUDA Zone. URL http://developer.nvidia.com/category/zone/cuda-zone]. Минимальной вычислительной единицей в CUDA является нить (thread). По сути, нить есть набор конкретных действий над элементом данных, нити группируются в пучки (warp); все нити одного пучка физически параллельно выполняются на потоковом мультипроцессоре; из потоковых мультипроцессоров состоит графический процессор. Очень важной особенностью CUDA является то, что при программировании нити образуют трехмерные структуры, именуемые блоками (block). Блоки, в свою очередь, группируются в еще более крупную многомерную структуру, именуемую сеткой (grid). Другими словами, сетка есть совокупность всех нитей, выполняющих параллельную обработку данных, и вместе с тем представляющая собой гибкую многомерную иерархическую структуру. Таким образом, CUDA-программист может оперировать с одно-, двух- или трехмерными структурами для параллельной обработки исходных данных, в том числе комбинируя размерности этих структур.
Очевидно, что в пределах каждого раунда все траектории могут быть обработаны параллельно, а применение CUDA позволит существенно упростить процесс разработки ПО.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ НЕЛИНЕЙНОГО ТРЕХМЕРНОГО МНОГОРАУНДОВОГО ПРЕОБРАЗОВАНИЯ ДАННЫХ DOZEN | 2012 |
|
RU2503994C1 |
| СПОСОБ НЕЛИНЕЙНОГО ТРЕХМЕРНОГО МНОГОРАУНДОВОГО ПРЕОБРАЗОВАНИЯ ДАННЫХ | 2017 |
|
RU2683689C1 |
| СПОСОБ НЕЛИНЕЙНОГО ТРЕХМЕРНОГО МНОГОРАУНДОВОГО ПРЕОБРАЗОВАНИЯ ДАННЫХ RDOZEN | 2015 |
|
RU2591015C1 |
| СПОСОБ ТРЕХМЕРНОГО НЕЛИНЕЙНОГО ПРЕОБРАЗОВАНИЯ ЗАМЕНЫ | 2012 |
|
RU2519004C2 |
| СПОСОБ ХЕШИРОВАНИЯ ИНФОРМАЦИИ | 2020 |
|
RU2747517C1 |
| СПОСОБ КРИПТОГРАФИЧЕСКОГО ПРЕОБРАЗОВАНИЯ И УСТРОЙСТВО ДЛЯ ЕГО ОСУЩЕСТВЛЕНИЯ | 2018 |
|
RU2738321C1 |
| СПОСОБ БЛОЧНОГО ИТЕРАТИВНОГО ШИФРОВАНИЯ ЦИФРОВЫХ ДАННЫХ | 2000 |
|
RU2184423C2 |
| СПОСОБ ИТЕРАТИВНОГО ШИФРОВАНИЯ БЛОКОВ ДАННЫХ | 1999 |
|
RU2140714C1 |
| БЛОК ШИФРОВАНИЯ | 1998 |
|
RU2127024C1 |
| ШИФРУЮЩИЙ БЛОК | 1998 |
|
RU2140715C1 |
Изобретение относится к вычислительной технике и электросвязи, предназначено для решения задач защиты компьютерной информации. Наиболее предпочтительной областью использования изобретения является построение генераторов псевдослучайных чисел (ГПСЧ), а также криптографических примитивов хеширования, блочного и поточного шифрования.
Техническим результатом изобретения является повышение криптостойкости и увеличение быстродействия итеративного криптографического преобразования данных.
Указанный технический результат при осуществлении изобретения достигается тем, что в итеративном криптографическом преобразовании данных, включающем
формирование из секретного ключа с помощью процедуры разворачивания ключа последовательности раундовых ключей K1, K2,…, KR, где R - число раундов преобразования;
формирование по входному блоку М блока С в соответствии с выражением С:=М;
выполнение R раундов преобразования, при этом преобразование блока данных на i-м раунде записывается в виде С:=Е(С, Ki), где Е() - раундовая функция преобразования, Ki - раундовый ключ, используемый на i-м раунде, полученное значение С:=Е(С, Ki) при i<R поступает на вход следующего раунда, а результат действия последнего раунда С:=Е(С, KR) является результатом преобразования;
дополнительно
из каждого раундового ключа Ki формируют N раундовых подключей Ki1, Ki2,…, KiN, где N - число траекторий раундовых преобразований в каждом раунде;
при выполнении каждого i-го раунда создают N копий Сi1, Ci2,…, СiN входного блока данных С, каждую копию Cij подвергают стохастическому преобразованию Eij, которое записывается в виде Cij:=Eij(Cij, Kij), преобразованные значения Cij поступают на входы комбинационной схемы F, функцией которой является параллельная композиция различных траекторий раундовых преобразований, результат действия комбинационной схемы С:=F(Ci1, Сi2,…, CiN) объявляют результатом раунда.
В частном случае стохастическое преобразование Еij включает представление входного блока Cij, промежуточных результатов
преобразования и раундового подключа Kij в виде квадратного массива бит размерностью 8×8;
сложение по модулю два (XOR) входного блока Cij и раундового подключа Kij,
разбиение результата на строки r1, r2,…, r8 и выполнение для каждой строки операции замены с использованием таблицы S размерностью 8×256;
разбиение результата на столбцы с1, с2,…, с8 и выполнение для каждого столбца операции замены с использованием таблицы S размерностью 8×256.
Благодаря совокупности перечисленных решений увеличивается криптостойкость преобразования за счет выполнения последовательной и параллельной композиции раундовых преобразований и повышается быстродействие за счет появления возможности сокращения числа раундов и выполнения всех раундовых преобразований Cij:=Eij(Cij, Kij) параллельно. 2 з.п. ф-лы, 3 ил.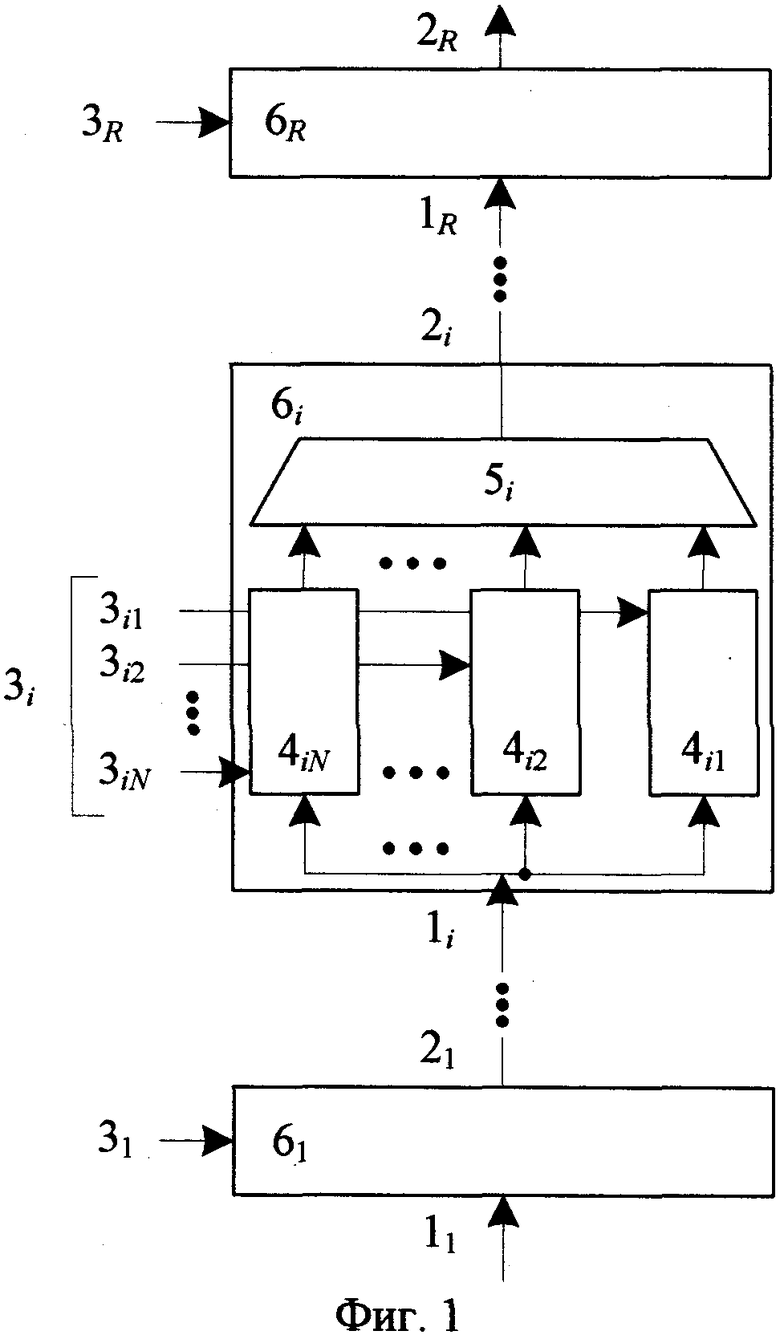
1. Способ итеративного криптографического преобразования данных, включающий формирование из секретного ключа с помощью процедуры разворачивания ключа последовательности раундовых ключей K1, K2, …, KR, где R - число раундов преобразования; формирование по входному блоку М блока С в соответствии с выражением С:=М; выполнение R раундов преобразования, при этом преобразование блока данных на i-м раунде записывается в виде С:=Е(С, Ki), где i=1, 2, …, R; а Кi - раундовый ключ, используемый на i-м раунде; полученное значение С:=Е(С, Ki) при i<R поступает на вход следующего раунда, а результат действия последнего раунда С:=Е(С, KR) выдают в качестве результата криптографического преобразования блока М; отличающийся тем, что из каждого раундового ключа Ki формируют N раундовых подключей Ki1, Ki2, …, KiN, где N - число траекторий раундовых преобразования в каждом раунде; при выполнении каждого i-го раунда создают N копий С1, С2, …, Cj, …, СN входного блока данных С; каждую копию Сj подвергают стохастическому преобразованию, которое записывается в виде Cj:=Ej(Cj, Kij), где j=1, 2, …, N; преобразованные значения С1, С2, …, Cj, …, СN поступают на N входов комбинационной схемы F, функцией которой является параллельная композиция различных траекторий раундовых преобразований; результат действия комбинационной схемы С:=F(C1, С2, …, СN) выдают в качестве результата раунда.
2. Способ по п.1, отличающийся тем, что N-входовую комбинационную схему выполняют в виде N-входового блока поразрядного сложения по модулю два.
3. Способ по п.1, отличающийся тем, что стохастическое раундовое преобразование включает представление входного блока, промежуточных результатов преобразования и раундового подключа в виде квадратного массива бит размерностью 8×8; сложение по модулю два входного блока и раундового подключа; разбиение результата на строки, выполнение для каждой строки операции замены с использованием таблицы S размерностью 8×256, выбранные из таблицы замен восемь преобразованных значений строк объединяют в преобразованный блок; разбиение результата на столбцы, выполнение для каждого столбца операции замены с использованием таблицы S размерностью 8×256, выбранные из таблицы замен восемь преобразованных значений столбцов объединяют в выходной блок, являющийся результатом стохастического раундового преобразования.
| СПОСОБ КРИПТОГРАФИЧЕСКОГО ПРЕОБРАЗОВАНИЯ БЛОКОВ ЦИФРОВЫХ ДАННЫХ | 2007 |
|
RU2359415C2 |
| Колосоуборка | 1923 |
|
SU2009A1 |
| Способ приготовления лака | 1924 |
|
SU2011A1 |
| Станок для изготовления деревянных ниточных катушек из цилиндрических, снабженных осевым отверстием, заготовок | 1923 |
|
SU2008A1 |
| US 6185304 B1, 06.02.2001 | |||
| Изложница с суживающимся книзу сечением и с вертикально перемещающимся днищем | 1924 |
|
SU2012A1 |
Авторы
Даты
2014-01-20—Публикация
2012-07-17—Подача