Изобретение относится к области контроля и диагностирования систем автоматического управления и их элементов.
Известен способ диагностирования динамических звеньев систем управления (Патент на изобретение №2439648 от 10.01.2012 по заявке №2010142159/08(060530), МКИ6 G05B 23/02, 2012), основанный на многократном интегрировании выходного сигнала блока с весами 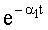
Недостатком этого способа является то, что он обеспечивает определение дефектов с невысокой различимостью, то есть обладает невысокой помехоустойчивостью.
Наиболее близким техническим решением (прототипом) является способ поиска неисправного блока в динамической системе (Патент на изобретение №2435189 от 27.11.2011 по заявке №2009123999/08(033242), МКИ6 G05B 23/02, 2011).
Недостатком этого способа является то, что он обеспечивает определение дефектов с невысокой различимостью, то есть обладает невысокой помехоустойчивостью.
Технической задачей, на решение которой направлено данное изобретение, является улучшение помехоустойчивости способа диагностирования непрерывных систем автоматического управления путем улучшения различимости дефектов. Это достигается путем применения адаптивного алгоритма диагностирования.
Поставленная задача достигается тем, что регистрируют реакцию заведомо исправной системы fjном(t), j=1,…,k и реакцию контролируемой системы fj(t) j=1,…,k на интервале t∈[0,TK] в k контрольных точках, задают минимальное значение квадрата нормы отклонения h сигналов контролируемой и заведомо исправной системы, величина h определяется экспериментально для конкретной контролируемой системы, формируют сигнал Н как квадрат нормы отклонения реакций контролируемой системы и заведомо исправной системы на заданном множестве контрольных точек: 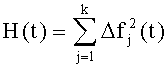
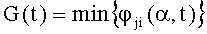
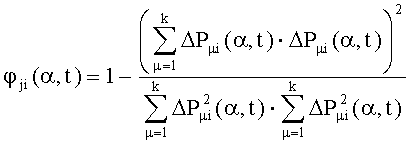
- косинус в квадрате угла между нормированными векторами интегральных оценок отклонений сигналов от номинальных значений при пробных отклонениях параметров для дефектов с номерами i и j, определяют интегральные оценки выходных сигналов Fjном(α), j=1,…,k системы, для чего в момент подачи тестового сигнала на вход системы с номинальными характеристиками одновременно начинают интегрирование сигналов системы управления в каждой из k контрольных точек с весами e-αt, где 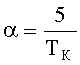
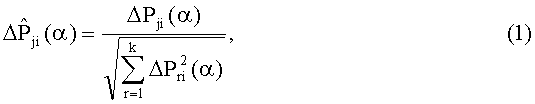
замещают систему с номинальными характеристиками контролируемой, на вход системы подают аналогичный тестовый сигнал x(t), определяют интегральные оценки сигналов контролируемой системы для k контрольных точек Fj(α), j=1,…,k для параметра интегрирования α, для значений времени, при которых H(t) больше заданной нормы h и G(t) больше выбранного минимума различимости g, определяют отклонения интегральных оценок сигналов контролируемой системы для k контрольных точек от номинальных значений ΔFj(α)=Fj(α)-Fjном(α), j=1,…,k, определяют нормированные значения отклонений интегральных оценок сигналов контролируемой системы из соотношения
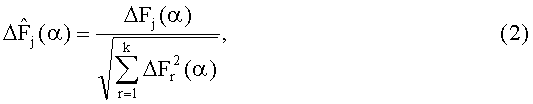
определяют диагностические признаки из соотношения
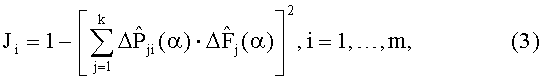
по минимуму значения диагностического признака определяют порядковый номер дефектного блока.
Сущность предлагаемого способа заключается в следующем.
Способ основан на использовании пробных отклонений параметров модели непрерывной динамической системы.
Для повышения достоверности диагностирования желательно увеличить расстояния между диагностическими признаками. При прочих равных условиях это позволяет повысить помехозащищенность алгоритма диагностирования. Увеличить расстояние между диагностическими признаками можно путем целенаправленного отбора диагностической информации в процессе формирования диагностических признаков. Для этих целей предлагается адаптивный алгоритм поиска одиночных структурных дефектов, функциональная схема которого приведена на фиг.1.
Здесь: ВХОД - входной сигнал;
1 - диагностическая модель;
2 - объект диагностирования;
3 - модель с пробным отклонением;
4 - блок перемножения сигналов;
5 - блок формирования признаков;
6 - блок выбора минимального из текущих значений коэффициентов различимости всех пар дефектов;
7 - блок сложения сигналов по контрольным точкам;
8 - ключевая схема с двумя управляющими сигналами;
ВЫХОД - вектор значений диагностических признаков.
Адаптивный алгоритм поиска одиночных дефектов блоков заключается в следующем:
- на функциональные блоки 1, 2 и 3 подается одинаковый входной сигнал ВХОД;
- формируется сигнал на выходе блока 7 (H(t)) как квадрат нормы отклонения временных характеристик на заданном множестве контрольных точек
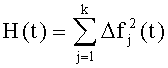
- формируется сигнал на выходе блока 5 (G(t)) как минимальное из текущих значений коэффициентов различимости всех пар дефектов
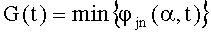
- мгновенные значения отклонений сигналов номинальной модели и объекта ΔF(t), а также отклонений сигналов номинальной модели и моделей с пробными отклонениями ΔPi(t) передаются через ключевую схему 8 на блок формирования признаков, при условии что H(t) больше заданного значения квадрата нормы h и G(t) больше выбранного минимума различимости g;
- формируется текущее значение диагностического признака в данный момент времени на выходе блока 8;
- после окончания времени контроля получаем вектор диагностических признаков ВЫХОД по значениям элементов которого определяется дефектный блок.
Таким образом, предлагаемый способ поиска неисправных блоков сводится к выполнению следующих операций:
1. В качестве динамической системы рассматривают систему, состоящую из произвольно соединенных динамических блоков, с количеством рассматриваемых одиночных дефектов блоков m.
2. Предварительно определяют время контроля ТК≥ТПП, где ТПП - время переходного процесса системы. Время переходного процесса оценивают для номинальных значений параметров динамической системы.
3. Определяют параметр интегрального преобразования сигналов из соотношения 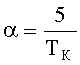
4. Фиксируют число контрольных точек k.
5. Для вычисления текущих мгновенных коэффициентов различимости в момент времени t предварительно определяют нормированные векторы 
6. Подают тестовый сигнал x(t) (единичный ступенчатый, линейно возрастающий, прямоугольный импульсный и т.д.) на вход системы управления с номинальными характеристиками. Принципиальных ограничений на вид входного тестового воздействия предлагаемый способ не предусматривает.
7. Регистрируют реакцию системы fjном(t), j=1,…,k на интервале t∈[0,ТК] в k контрольных точках и определяют текущие интегральные оценки выходных сигналов Fjном(α,t), j=1,…,k системы в момент времени t. Для этого в момент подачи тестового сигнала на вход системы управления с номинальными характеристиками одновременно начинают интегрирование сигналов системы управления в каждой из k контрольных точек с весами e-αt, где, 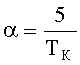
8. Определяют текущие интегральные оценки сигналов модели для каждой из k контрольных точек, полученные в результате пробных отклонений каждого из m одиночных дефектов блоков, для чего поочередно для параметров передаточной функции каждого структурного блока динамической системы вводят пробное отклонение этих параметров и выполняют пункты 6 и 7 применительно к реакциям моделей с пробными отклонениями для одного и того же тестового сигнала x(t). Полученные в результате интегрирования текущие оценки выходных сигналов для каждой из k контрольных точек и каждого из m пробных отклонений Pji(α,t), j=1,…,k; i=1,…,m регистрируют.
9. Определяют отклонения текущих интегральных оценок сигналов модели, полученные в результате пробных отклонений параметров структурных блоков ΔPji(α,t)=Pji(α,t)-Fjном(α,t), j=,…,k; i=1,…,m.
10. Определяют нормированные значения текущих отклонений интегральных оценок сигналов модели, полученные в результате пробных отклонений параметров одного из блоков в момент времени t по формуле:
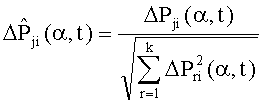
11. Задают минимальное значение квадрата нормы отклонения h сигналов контролируемой и заведомо исправной системы.
12. Формируют сигнал H(t) как квадрат нормы отклонения сигналов контролируемой и заведомо исправной системы на заданном множестве контрольных точек: 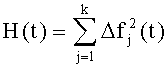
13. Задают минимальное из текущих значений в момент времени t коэффициентов различимости всех пар дефектов g.
14. Формируют сигнал G(t) как минимальное из выбранных мгновенных значений в момент времени t коэффициентов различимости пар дефектов: 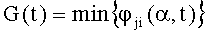
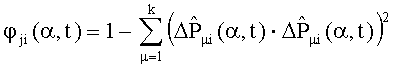
15. Для вычисления диагностических признаков определяют нормированные векторы 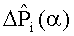
16. Определяют интегральные оценки выходных сигналов Fjном(α), j=1,…,k системы по реакциям системы fjном(t), j=1,…,k на интервале t∈[0,ТК] в k контрольных точках. Для этого в момент подачи тестового сигнала на вход системы управления с номинальными характеристиками одновременно начинают интегрирование сигналов системы управления в каждой из k контрольных точек с весами e-αt, где, 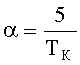
17. Определяют интегральные оценки сигналов модели для каждой из k контрольных точек, полученные в результате пробных отклонений каждого из m одиночных дефектов блоков, для чего поочередно для каждого структурного блока динамической системы вводят пробное отклонение его параметров передаточной функции и выполняют пункт 16 применительно к выходным сигналам моделей с пробными отклонениями для одного и того же тестового сигнала x(t). Полученные в результате интегрирования оценки выходных сигналов для каждой из k контрольных точек и каждого из m пробных отклонений Рji(α), j=1,…,k; i=1,…,m регистрируют.
18. Определяют отклонения интегральных оценок сигналов модели, полученные в результате пробных отклонений параметров структурного блока ΔPji(α)=Pji(α)-Fjном(α), j=1,…,k; i=1,…,m.
19. Определяют нормированные значения отклонений интегральных оценок сигналов модели, полученные в результате пробных отклонений параметров структурного блока по формуле:
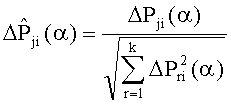
20. Определяют интегральные оценки сигналов контролируемой системы для k контрольных точек Fj(α), j=1,…,k, осуществляя операции, описанные в пункте 16 применительно к контролируемой системе.
21. Определяют отклонения интегральных оценок сигналов контролируемой системы для k контрольных точек от номинальных значений ΔFj(α)=Fj(α)-Fjном(α), j=1,…,k.
22. Вычисляют нормированные значения отклонений интегральных оценок сигналов контролируемой системы по формуле:
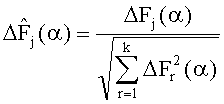
23. Вычисляют диагностические признаки наличия неисправного структурного блока по формуле (3).
24. По минимуму значения диагностического признака определяют дефектный блок.
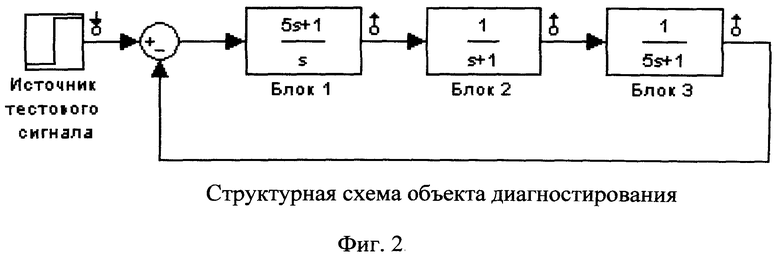
Рассмотрим реализацию предлагаемого способа поиска одиночного дефекта для системы, структурная схема которой представлена на фиг.2.
Передаточные функции блоков:
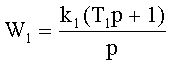
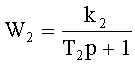
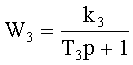
номинальные значения параметров: Т1=5 с; k1=1; k2=1; Т2=1 с; k3=1; Т3=5 с. При поиске одиночного дефекта в виде отклонения постоянной времени T1=4 с в блоке 1 путем подачи ступенчатого тестового входного сигнала единичной амплитуды и интегрального преобразования сигналов для параметра α=0.5 и ТК=10 с получены значения диагностических признаков по формуле (3) при использовании трех контрольных точек, расположенных на выходах блоков, и способа (прототипа) без адаптации: J1=0; J2=0.78; J3=0.074. Минимальное значение признака J1 однозначно указывает на наличие дефекта в блоке 1, а разность между третьим и первым признаками может количественно характеризовать фактическую различимость этого дефекта. Различимость дефекта ΔJ=J3-J1=0.074. Тот же дефект, найденный путем применения адаптации с параметрами адаптации h=0.041 и g=0.046, дает следующие значения диагностических признаков: J1=0.1697; J2=0.818; J3=0.8164 Различимость дефекта: ΔJ=J3-J1=0.6467. Анализ значений диагностических признаков показывает, что значения второго и третьего признака, полученные при использовании адаптивного алгоритма, больше, чем при использовании способа без адаптации (прототипа). Это позволяет сделать вывод, что фактическая различимость дефекта блока 1 выше при использовании заявляемого способа. Различимости дефектов блоков 2 и 3 при поиске их с использованием адаптивного алгоритма также не хуже, чем при использовании прототипа.
Моделирование процессов поиска дефектов в блоке 2 (в виде уменьшения параметра Т2 на 20%) для данного объекта диагностирования с использованием адаптивного алгоритма, параметрами адаптации h=0.041 и g=0.046 и при таком же входном сигнале дает следующие значения диагностических признаков:
J1=0.9497, J2=0.06825, J3=0.4042.
Различимость дефекта ΔJ=J3-J2=0.33595.
Для сравнения приведем диагностические признаки наличия неисправного блока без использования адаптивного алгоритма (прототип): J1=0.7827, J2=0, J3=0.7455. Различимость дефекта: ΔJ=J3-J2=0.7455.
Моделирование процессов поиска дефектов в блоке 3 (в виде уменьшения параметра Т3 на 20%) для данного объекта диагностирования при использовании адаптивного алгоритма с параметрами адаптации h=0.041 и g=0.046 дает следующие значения:
J1=0.7272, J2=0.64, J3=0.0004069.
Различимость дефекта: ΔJ=J2-J3=0.6395931.
Для сравнения приведем диагностические признаки наличия неисправного блока без использования адаптивного алгоритма (прототип):
J1=0.074, J2=0.7478, J3=0.
Различимость дефекта ΔJ=J1-J3=0.074.
Приведенные результаты показывают, что фактическая различимость нахождения дефектов с использованием адаптации более сбалансирована для разных дефектов блоков и, как правило, в разы выше, следовательно, выше будет и помехоустойчивость алгоритма.
Минимальное значение диагностического признака во всех случаях правильно указывает на дефектный блок.
Изобретение относится к диагностике систем автоматического управления. Техническим результатом является улучшение помехоустойчивости диагностирования систем управления путем улучшения различимости дефектов. Для этого регистрируют реакцию исправной и контролируемой системы, задают минимальное значение квадрата нормы отклонения сигналов контролируемой и исправной системы, формируют сигнал как квадрат нормы отклонения реакций контролируемой системы и исправной системы, задают минимальное из текущих значений, формируют сигнал как минимальное из текущих значений коэффициентов различимости всех пар дефектов, определяют интегральные оценки выходных сигналов, выходные сигналы блоков перемножения подают на входы блоков интегрирования, полученные оценки выходных сигналов регистрируют, фиксируют число структурных дефектов блоков, определяют интегральные оценки сигналов модели, полученные в результате интегрирования оценки выходных сигналов регистрируют, определяют отклонения интегральных оценок сигналов модели, определяют нормированные значения отклонений интегральных оценок сигналов модели, замещают систему с номинальными характеристиками контролируемой, на вход системы подают аналогичный тестовый сигнал, определяют интегральные оценки сигналов контролируемой системы, определяют отклонения интегральных оценок сигналов, определяют нормированные значения отклонений интегральных оценок сигналов, определяют диагностические признаки, по минимуму значения диагностического признака определяют порядковый номер дефектного блока. 2 ил.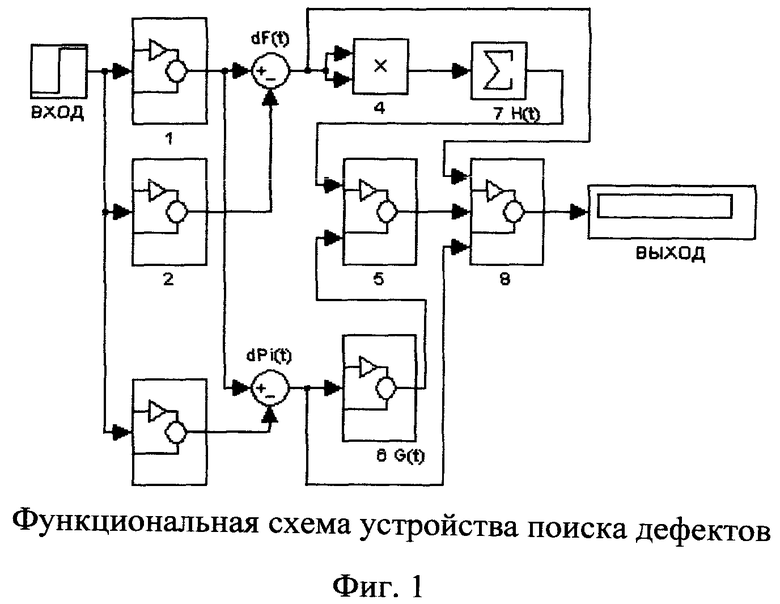
Способ поиска неисправного блока в непрерывной динамической системе, основанный на том, что фиксируют число динамических элементов, входящих в состав системы, определяют время контроля ТК≥ТПП, где ТПП - время переходного процесса системы, определяют параметр интегрального преобразования сигналов из соотношения 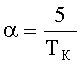
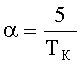
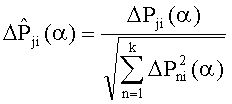
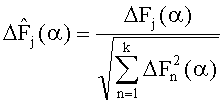
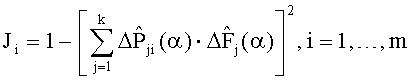
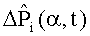
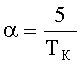
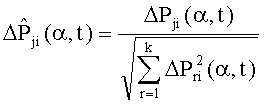
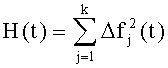
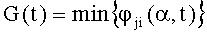
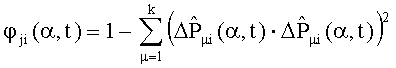
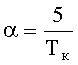
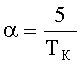
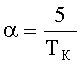
| СПОСОБ ПОИСКА НЕИСПРАВНОГО БЛОКА В ДИНАМИЧЕСКОЙ СИСТЕМЕ | 2009 |
|
RU2435189C2 |
| СПОСОБ ПОИСКА НЕИСПРАВНОСТЕЙ ДИНАМИЧЕСКОГО БЛОКА В НЕПРЕРЫВНОЙ СИСТЕМЕ | 2010 |
|
RU2429518C1 |
| Устройство для диагностики неисправностей технических объектов | 1988 |
|
SU1536357A1 |
| US 6766267 B2, 20.07.2004 | |||
Авторы
Даты
2014-04-20—Публикация
2013-05-07—Подача